Abstract
Three-dimensional flow via swirling porous disks and an annular sector is carried out using fully developed hybrid nanofluids. Here, a single-phase simulation based on thermophysical characteristics using various nanoparticle sizes and shapes is taken into account. A regression function connected with the permeable Reynolds number for injection and suction was created. We used the well-known and accurate “shooting approach” to apply to the governing, nonlinear, ordinary differential equation systems to obtain numerical results. Additionally, parametric research was employed to control the impact of embedded flow factors on concentration, velocity, and temperature. While the physical features of the bottom and upper disks, such as the skin friction coefficient and Nusselt number, are provided in a table, their characterization of the flow of several regulatory flow parameters, such as fluid velocity and temperature, is depicted graphically. The experimental range of nanoparticle fractions of 1% to 4% is considered with the Nusselt number having notable effects at = 4%. Both walls demonstrate the effects of an increase in injection factor, shear stress, and tensile stress. As the Eckert number rises at the lower wall, the rate of heat transfer dramatically increases, and the opposite is true for the upper wall. The rate of heat transmission is significantly impacted by the addition of different base fluids containing various kinds of nanoparticles. The aforementioned research created a solid foundation for the development of electronic computers with an emphasis on nanotechnology and biomedical devices.
MSC:
35Q30; 76D05; 76R10
1. Introduction
Nanofluids offer a more effective means of improving heat transfer. The capacity of common base liquids, similar to oil, ethylene glycol, and water, to improve the heat transport rate is insufficient. This perplexing situation was appropriately resolved by introducing extremely tiny solid particles into the basic liquids. Nanofluids are created by combining nano-measured pieces in suspension (e.g., 1–100 nm) in base liquids (oil, ethylene glycol, and water) and diffusing these tiny particles in the basic fluids. Metals (Fe, Al, Cu, Ag, Au) and oxides are common components in nanoparticles (Al2O3, TiO2). Despite the numerous challenges associated with heat transfer mechanisms using a variety of fluids, researchers are looking for new types of fluids with heat transport properties. As a result of this venture, a new form of nanofluid known as a “hybrid nanofluid” has been investigated, which has a greater thermal conductivity influence than regular nanofluids. This is a new form of heat transport fluid that has been utilized to increase the pace of heat transmission. Engine cooling, electronic cooling, drug reduction, cooling generators, lubrication, and nuclear cooling are just a few of the applications for hybrid nanofluids. Applications of hybrid nanofluids in the fields of refrigeration, heating, ventilation, and air conditioning, heat exchangers, heat pipes, coolants in machining and manufacturing, electronic cooling, automotive industry, generator cooling, transformer cooling, nuclear system cooling, biomedical, space, ships, and defense are among the main areas of research. The properties of hybrid nanofluids have been the subject of several scientific investigations during the last few decades. Ahmed et al. [1] analyzed the time-dependent squeezed flow of magneto-nanofluid between two parallel disks. Nanoparticles of various shapes are suspended in the base. In the base fluid, three distinct-shaped nanoparticles are suspended. Abbas et al. [2] analyzed the three distinct types of nanoparticles (copper, aluminum oxide, and titanium dioxide) with varied forms (spherical, cylindrical, and brick) were employed, using water as the basic nanofluid. With the base fluid, they evaluated copper–alumina nano-ingredients. Motlagh et al. [3] utilized aluminum oxide to refine heat transfer in an inclined cavity. The thermal characteristics of nanofluids are strongly influenced by their size, kind, production technique, dispersibility of their nanoparticles, compatibility, and purity of the base fluid and nanoparticles. Metal oxides (, MgO, , , CuO), metal nitride (AIN), CNT, and metals (Au, Ag, Ni, Cu) are the most often utilized nanoparticles in base fluids. A spinning disk was the focus of an investigation by Acharya et al. [4] into the hybrid nanofluid flowing in the presence of Hall current. They regarded and nanoparticles to be a novel type of nano-liquid. With multi-walled carbon nanotubes over a movable wedge in a permeable surface, Akbar et al. [5] calculated the magnetic influence on flow. Using an impermeable spinning disk with set radial freedom of speech and expression, Dinarvand et al. [6] studied and verified the incompressible, continuous, steady 3D limit surface fluid motion of a water ZnO-Au hybrid nanofluid. Ramesh [7] investigated how three distinct hybrid nanoparticles move across a spinning disk in a permeable plate explained by the Forchheimer surface. Convective conditions are used to evaluate heat transfer performance. Xu et al. [8] investigated the unsteady mixed convection of a hybrid nanofluid due to moving disks. A basic, relatively uniform modeling approach that explains hybrid nanofluids containing several types of nanoparticles was generated to model the difficulty. An MHD hybrid simulation for a heat production system with seven various kinds of nanoparticles was built by Abdelmalek et al. [9]. Hybridized nanocomponents are modeled based on their form and size factor to determine their thermal conductivity and fluid viscosity. The similarity transform for the constant three-dimensional Navier-Stokes equations of flow between two flexible disk was examined mathematically by Dinarvand et al. [10]. Hybrid nanofluids flow of heat transfer a rotating disk, according to Acharya et al. [11]. Over a spinning disc in a magnetic field, the steady flow of an incompressible viscous electrically conducted hybrid nanofluid is taken into consideration. Yin et al. [12] examined nanofluid heat transfer on a radially spaced rotating disk. The micropolar dusty fluid, Coriolis force effects on dynamics of MHD rotating fluid when lorentz force is significant considered by Lou et al. [13]. Ashraf et al. [14] studied the significance of bioconvection on MHD tangent hyperbolic nanofluid flow of irregular thickness across a slender elastic surface. Behnam et al. [15] aimed to semi-analytically examine the boundary layer flow of a SiC-TiO2/DO hybrid nanofluid under a steady vertical magnetic field over a porous spinning disk. The effect of contracting the spinning disk on nanofluids was studied by Hatami et al. [16]. For solution formation, they used the least square form. The 3D nanofluid flow over a stationary disk was analyzed by Mustafa et al. [17]. Under the influence of thermal energy and temperature difference effects, Dogonchi et al. [18] investigated the unstable squeezing flow and heat transfer of nanofluid between two simultaneous disks, some of which were penetrable but the others, stretchable/shrinkable. Researchers, Sajjan et al. [19], developed a Nonlinear Boussinesq and Rosseland approximations on 3D flow in an interruption of Ternary nanoparticles with various shapes of densities and conductivity properties. The incompressible hybrid nanofluid flow across an endless impermeable spinning disk was investigated in this paper. Hasnain et al. [20] conducted a theoretical analysis of heat transport enhancement in time-independent, three-dimensional, ternary, hybrid nanofluid flow, with base fluid water and motor oil under the impacts of thermal radiation, over a linear and nonlinearly stretched sheet. According to Khashi’ie et al. [21], magnetic nanofluids have been widely employed in both biological and environmental sectors, with a significant increase in numerical and experimental studies. As a result of the unique features of magnetic nanofluids, the goal of this research is to quantitatively investigate the three-dimensional flow of magnetic nanofluids (Fe3O4-H2O, CoFe2O4-H2O, Mn-ZnFe2O4-H2O) over a shrinking surface with suction and heat radiation effects. A numerical solutions of the partial differential equations for investigating the significance of partial slip due to lateral velocity and viscous dissipation, the case of blood-gold Carreau nanofluid and dusty fluid by Koriko et al. [22]. Shah et al. [23] conducted a numerical simulation of a thermally enhanced EMHD flow of a heterogeneous micropolar mixture comprising (60%)-ethylene glycol (EG), (40%)-water (W), and copper oxide nanomaterials (CuO).
Magnetic hydrodynamics (MHD), with its many significant uses, is also really relevant to be studied. The effect of a magnetic field on the motion of fluids is important to examine. Chemical reaction characteristics and boundary restriction inflow across a vertical surface were investigated by Rout et al. [24]. The chemical reaction in nano-liquid MHD flow was studied by Hayat et al. [25]. Rotation and chemical reactions were studied by Raddya et al. [26] in the MHD flow of nano-liquid. Hayat et al. [27] investigated chemical reactions in nanofluids flowing in MHD flow. Vajravelu et al. [28] analyzed the impact on the time-dependent MHD 3D heat and mass transfer flow of nanofluids squeezed among two simultaneous transpiration disks with velocity slip and heat reduction. Meanwhile, Das et al. [29] investigated that a pair of connected disks with magnetic fields and slip effects are squeezed by a mathematically modeled flow of nanofluid. Mohyud-Din et al. [30] explored the effects of an analogous disk on the compressed MHD flow of (N) that is impacted by both momentum and thermal slip. The mass and energy change in a convective heat transfer flow over a rotating disk with a uniform thin layer was investigated by Qayyum et al. [31]. Aziz et al. [32] found that the heat and mass transport of MHD through a spinning disk with viscous dissipation/emission and slip impact is approached by three-dimensional viscous nano-liquid flow. Elnaqeeb et al. [33] analyzed the natural convection flows of carbon nanotubes nanofluids with Prabhakar-like thermal transport. Uddin et al. [34] discussed heat generation and slip effects due to a revolving disk for the MHD 3D flow of nanofluids. The observed effects of MHD, viscous dissipation, and Joule heating were also reported by Khan et al. [35]. Nonlinear differential structures were calculated by the application of proper transformations using the built-in shooting process. Khan et al. [36] investigated the thermal transmission across two extending disks using MHD flow in the absence of viscous dissipation and Joule heating. MHD slip flow was calculated by Imtiaz et al. [37] through the spinning disk. Doh et al. [38] measured the flow of MHD fluid into a spinning disk. The MHD thin-film stream of nanofluid across a spinning disk was discussed by Shah et al. [39]. Rasool et al. [40] examined a numerical investigation of EMHD nanofluid flows over a convectively heated riga pattern positioned horizontally in a Darcy-Forchheimer porous medium. Rostami et al. [41] constructed a (SiO2-Al2O3/water) hybrid nanofluid boundary layer flow on a vertical, porous, flat disk with a suspended step, employing continuous, convective, MHD-coupled heat transfer. In the work of Ghadikolaeia et al. [42], Cu–Al2O3 hybrid nanoparticles were evaluated in the presence of nonlinear thermal radiation, variable thermal conductivity, and varied morphologies of NPs (bricks, rods, platelets, and blades). Many researchers have been worked on analyzing the MHD hybrid nanofluid fluid flow of heat transfer [43,44,45,46,47].
It seems from the literature that no studies have been conducted to date to assess the effects of shape and size parameters on 3D MHD heat transfer in the hybrid nanofluids, Ag-Al2O3/H2O, involving two orthogonal moving porous disks. Additionally, the effects of the applied magnetic field, shape and size factors, porosity parameter, Reynolds number, Prandtl number, Forchheimer number, and chemical reaction parameter should all be assessed. The main goals of the current research work are to develop the thermal characteristics of a carrier fluid, such as water, for practical and commercial reasons, as well as to assess the effects of hybridizing nanofluid flow over the surface of two orthogonal moving porous disks under magnetic influences. We also constructed and expressed this form of mathematics using the paradigm found in [48]. PDEs are regulated such that they may be transformed into dimensionless ordinary differential equations (ODEs). The fourth-order Runge–Kutta integration method and the “shooting method” were used to analyze the ODEs model numerically. The physical parameter data are described using tables and figures.
2. Mathematical Formulation
Consider the flow of incompressible, laminar, time-dependent MHD hybrid nanoparticles on the 3-dimensional fluid flow rate of heat transfer across a two orthogonally moving, porous disk. The disk is moving up and downward with a boundary 2r with a normalized velocity s’ (t) and the size of the diameters varies according to 2s(t). The impacts of magnetic fields and heat sources are specifically taken into consideration. Due to the low Reynolds number assumption, the induced magnetic field is disregarded. The practical model has a cylinder-shaped coordinate system . Here, v = (u (r, 0, and z), v (r, 0, and z), w (r, 0, and z)) is the fluid flow velocity. > are the set temperatures for the lower and upper walls of the permeable channel, respectively, as shown in the physical model (Figure 1). The following methodology can be used to represent the governing equation from Kashif et al. [49] which was extended to a 3-dimensional hybrid nanofluid:
where represents the strong magnetic field, stands for pressure, demonstrates the electrical conductivity, represents the temperatures, illustrates the viscosity of the hybrid nanofluid, is the density of the hybrid nanofluid, and the kinematic viscosity of the hybrid nanofluid is represented by , the specific heat capacitance of the hybrid nanofluid is , is the thermal conductivity of the hybrid nanofluid, the Brownian diffusion constant is shown, denotes the permeability of the porous medium, and is the non-uniform inertia coefficient.
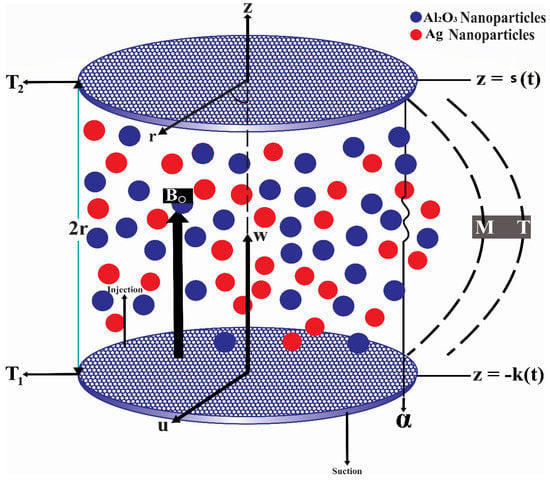
Figure 1.
Physical model.
The upper and lower porous surface boundary conditions for the above model are
where A is the wall permeability factor and the dash denotes the derivative with respect to time . After eliminating the pressure term from the governing equations, we add the following transformation of similarity [12]:
where the similarity variable is represented by .
First of all, the continuity equation is satisfied by the similarity variables stated in Equation (1). Furthermore, the similarity variables are used in the governing equations to acquire Equations (2) and (5).
with the boundary conditions
where α = is the wall expansion ratio, is the permeable Reynolds number, is the Prandtl number, is the porosity parameter, is the Eckert number, is the Forchheimer number, is the magnetic parameter, is the viscosity of the hybrid nanofluid, and represents the thermal diffusivity of the hybrid nanofluid.
Finally, we set , = and consider the case, following the work of Majdalani et al. [50], that when is a constant, = () and , which leads to = 0, = 0 and = 0. Thus, we have the following equations:
2.1. Practical and Engineering Interests
Skin friction and Nusselt number are physical characteristics that are essential for engineering applications in constructing nanoscale equipment. On both porous surfaces, all of these factors have been calculated.
2.2. Skin Friction Coefficients
The following parameter or indicate the skin friction coefficients for the top and bottom porous disks respectively
Here, represents the local Reynolds number and is the shear stress. The expression is defined as
When the upper and lower disks have radial and tangential shear stresses, they are denoted by and :
2.3. Nusselt Numbers
The top and bottom of a porous disk are the flow of heat transfer (Nusselt numbers), represented by and , and given as
Here, the heat flux is denoted as , which follows that
where .
2.4. Numerical Solution
By using the thermophysical properties of hybrid nanofluids in the nonlinear ODEs Equations (12)–(14):
where
By inputting the values of , , , , , and in Equations (18)–(20), the final results are
2.5. Solution of the Problem
We used the RK methodology with shooting methods to determine strategies to solve the current flow model (see Figure 2). To start the procedure, the change must be as follows:

Figure 2.
Flow chart of the numerical procedure (shooting method).
Finally, modify the model in the manner shown below from Equations (21)–(23):
By using substitution, embedded in Equation (24), the following system is attained:
Consequently, the initial condition is
Now, utilizing mathematics and a proper beginning condition, the aforementioned system is solved. The RK method, along with using the numerical “shooting method”, have both been considered in this case. This method makes handling the requisite dimensionless ODEs simple. First, we use the shooting approach to create the starting condition, ensuring that boundary criteria are met and the necessary level of precision is attained.
3. Results and Discussion
This section will use the built-in shooting technique to numerically calculate the acquired systems. The diverse variables physically focus on concentration, temperature, and velocity in this case. The relevant factors are discussed in-depth, i.e., the Reynolds number (Re), expansion ratio (), magnetic parameter (M), Prandtl number (), volume fractions and , diameter of the nanoparticles and , Forchheimer number , porosity parameter (, Eckert number (), and size factor (n). Here, all the observation is described utilizing the numerical and graphical outcomes of , ethylene glycol, engine oil, , ethylene glycol, engine oil, ethylene glycol, engine oil, , ethylene glycol, and engine oil nanoparticles. Table 1 focuses heavily on the thermophysical characteristics of hybrid nanofluid, while Table 2 shows the thermophysical characteristics of the various base fluid and nanoparticle types.

Table 1.
Thermophysical properties of hybrid nanofluid [51].

Table 2.
Different base fluids’ and nanoparticles’ thermophysical properties (Sheikholeslami and Ganji [52]).
Here, denotes the thermal conductivity for the shape base fluid, is the thermal conductivity of the base fluid, , , and represent the thermal conductivity of the 1st and 2nd nanoparticles and base fluid, denotes the effect viscosity, is the size of the factor, denotes the viscosity of the base fluid, and are the first and second particle’s diameters, and are the volume fraction of the first and second particles, and and illustrate the 1st and 2nd solid particle densities show in Table 1.
Table 3a,b analyzed the effects of different size factors (spherical, bricks, cylinder, platelet, and laminar) and several types of nanoparticles and base fluid comparisons shown in heat transfer. With the several kinds of hybridizing nanoparticles (HNFD1, HNFD2, HNFD3, HNFD4, HNFD5, HNFD6, HNFD7, HNFD8, HNFD9, HNFD10, HNFD11, HNFD12), the flow of heat transfer (Nusselt number) is improved if we raise the values of both nanoparticle volumes fractions and . Moreover, compared to other shape factors and hybridizing nanoparticles, the laminar shape factor (HNFD1) is superior for the flow of heat transmission (Nusselt number).

Table 3.
(a) Numerical size factor effect of heat transfer in different hybridized nanofluids. (b) Numerical size factor effect of heat transfer in different hybridized nanofluids.
Table 4 shows the numerical effects of shear stress and tensional stress on non-dimensional parameters. Increases the values of the , , , , and then the flow of fluid gradually increases in shear and tensional stress. Moreover, to enhance the values of the porosity parameter and diameter of the first and second nanoparticles, the shear and tensional stress values were reduced in both porous disks. Table 5 represents the impact of the inflow of heat transfer ( for both porous disks. As a result, as we raise the values of (, the flow of heat transfer for the lower disk increases while strictly dropping for the upward disk. Physically, the Eckert number is the product of the specific enthalpy difference between the wall and the fluid and the kinetic energy. As a result, a rise in the Eckert number results in work being performed against the viscous fluid stresses, which converts kinetic energy into internal energy. Table 6 demonstrates the impact of Re, and on the Nusselt number. The Nusselt number grows significantly when the Re and values are higher than the rate of heat transfer. Physically, a dimensionless number called the Prandtl number connects a fluid’s viscosity to its thermal conductivity. As a result, it evaluates the relationship between the transmission of momentum and a fluid’s capability for heat transport. Additionally, the flow of heat transfer is decreased since the expansion ratio is greater than working. Before visualizing the findings, we used Table 7 to confirm our findings against previously published research publications. An outstanding coincidence was observed, supporting the accuracy of the Mathematica code for the “shooting method”. By providing the values for the following parameters, the present analysis is estimated: , , .

Table 4.
Shear stress and tensional stress impact several non-dimensional parameters.

Table 5.
Eckert parameter Ec effects on numerical heat transfer for Re = 3, α = 2 and Pr = 6.2.

Table 6.
Different nondimensional parameter effects on the Nusselt number.

Table 7.
Comparison of the upper disk’s flow of heat transfer rate for fixed values of Re = 0, Pr = 2.92, M = 0.
Figure 3 displays the thermal conductivity of hybrid nanofluid with several types of nanoparticles and only one base fluid water (HNDF1, HNDF4, HNDF7, HNDF10) or different types of size factors used (spherical, bricks, cylinder, platelet, and laminar). Figure 3 shows four sections: for section, no. 1 we used HNDF1; no. 2, HNDF4; no. 3, HNDF7; and no. 4, HNDF10. The sections were used with increasing values of the volume fractions and several types of shape factors (spherical, bricks, cylinder, platelet, and laminar), but we noticed that when the NP volume fraction level was 0.04 in HNFDs1, better thermal conductivity efficiency was attained at 16.2. This implies that if we progressively raise the quantitative value of and , the thermal conductivity will rise along with the form factor. Figure 4 demonstrates the effect of viscosity-hybrid nanofluid with volume fractions of and and diameters of and for both NP under the various form and size factor value diameters used (spherical, bricks, cylindrical, platelet, laminar). Additionally, with a size factor of 16.2, the influence of viscosity is particularly strong as well as diameters of 25 when the NP’s volume fraction and is 0.04, as shown in Figure 4. We found that increasing the volume fraction and shape or size parameter numbers increased the thermal conductivity and viscosity of the hybrid nanofluid in Figure 3 and Figure 4. In this instance, laminar-shaped nanomaterials outperform other NP forms in terms of heat and mass transferability.
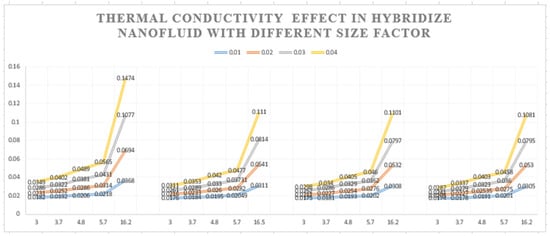
Figure 3.
The impact of the hybrid nanoparticle size on thermal conductivity coloration.

Figure 4.
The quantity of hybrid NP affects the viscosity coloring process.
Figure 5 reveals the Forchheimer number impact of the radial velocity profile influenced by the fixed values . A commonly analyzed that the Forchheimer number is greater than zero impact of the normal boundary layer increases for an upper and lower porous disk.
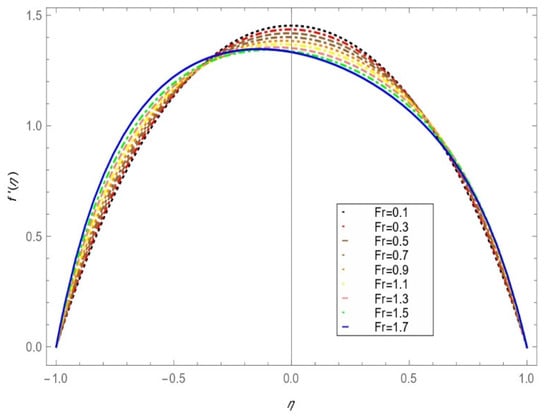
Figure 5.
Radial velocity profile effect of the Forchheimer number for .
Figure 6 presents the impact of the Forchheimer number on the tangential velocity profile. The momentum boundary layer of the tangential velocity profile is reduced in the upper and lower disk if we raise the values of the Forchheimer number.

Figure 6.
Tangential velocity profile effect of the Forchheimer number for , .
Figure 7 demonstrates the porosity parameter effect in the radial velocity profile. If we raise the values of the porosity parameter (), then the radial velocity profile values rise to the middle of the wall and are reduced for both porous disks. Figure 8 shows that the impact of the porosity parameter () is analyzed by the tangential velocity profile. Raising the values of then gradually increases the flow of fluid to the center of the wall and the same behavior of the upper disk is observed but the opposite behavior is shown in the lower disk.

Figure 7.
Radial velocity profile effect of the porosity parameter for , .

Figure 8.
Tangential velocity profile effect of the porosity parameter for .
The expansion ratio impact on the radial velocity profile is shown in Figure 9. If the expansion ratio is greater or less than zero, the flow of the momentum boundary layer thickness rises to the middle of the wall but the flow of the hybrid nanofluid is reduced in both porous disks. Figure 10 represents the effect of the temperature profile for the fixed values of . In this case, a rise in the values of the flow of thermal transfer rates acts oppositely in both porous disks.

Figure 9.
Radial velocity profile effect of the expansion ratio for .

Figure 10.
Temperature profile effect of the expansion ratio for .
Figure 11 illustrates the effects of magnetic parameters on the radial velocity profiles with constant values of . When the magnetic parameter values are greater than zero, the flow of the momentum boundary layer thickness is enhanced for the upper and lower disk. This outcome is consistent with the idea that the applied magnetic field acts as a resistance force that is essential for slowing down and controlling fluid movement. Furthermore, Figure 12 shows the tangential velocity profile flow of the momentum boundary layer acting oppositely in the upper and lower porous disk.

Figure 11.
Radial velocity profile effect of the magnetic parameter for .

Figure 12.
Impact of M on the tangential velocity profile for .
The permeable Reynolds number impact of the radial velocity profile and temperature profile is displayed in Figure 13 and Figure 14. Physically, the Reynolds number is equal to the ratio of the inertia force over the viscous forces. Geometrically, we used the Reynolds numbers less than 2000 so that the flow was laminar or the shapes were graphically symmetrical. Furthermore, if the permeable Reynolds number values grow, then the flow of momentum and the thermal boundary is decreasing the middle of the wall but is enhanced for both boundary layer porous disks.

Figure 13.
Radial velocity profile effect of the Reynolds number for .

Figure 14.
Temperature profile effect of the Reynolds number for .
4. Conclusions
The hybrid nanofluid flow of heat transfer under the impact of shape and size factors, unsteady, three-dimensional, Newtonian, MHD fluid flow across two orthogonally moving porous coaxial disks. We use several NP types for this purpose. The basic fluids utilized were water, engine oil, and ethylene glycol. Metallic and metallic-oxide NP were also employed. Using velocity and temperature profiles, the impacts of nanoparticle shape and size variables were investigated. It was found that the form of the particle has a significant impact on the velocity and temperature profiles. The following are the key findings:
- Laminar nanoparticles 16.2 within the volume fraction of 4 percent in HNFD1 have the maximum thermal conductivity and viscosity intensity, as compared to other shapes spherical, brick, cylindrical, and platelet nanoparticles, respectively.
- The flow rate of heat transfer is enhanced on both porous disks by increasing the expansion of the value ratio and permeable Reynolds number .
- Enhance the values of permeability Reynolds number , Forchheimer number , and magnetic parameter , the momentum boundary layer increases in the upper and lower porous surface.
- Shear stress and tensional stress flow rates are slowed down if the porosity parameter, as well as the diameters of the nanoparticles, , and , are larger than zero.
- Heat transfer rates are raised on both porous disks by increasing the values of Prandtl number and Reynolds number .
- Eckert number parameter values are raised and the flow of heat transfer rates in both porous disks is reduced.
Author Contributions
Conceptualization, M.M.A. and N.A.S.; methodology, A.A.H.; software, Q.R.; validation, M.Z.A.Q., F.S.H. and J.D.C.; formal analysis, B.A.; investigation, M.M.A. and N.A.S.; resources, B.A.; data curation, A.A.H.; writing—original draft preparation, Q.R., M.Z.A.Q. and B.A.; writing—review and editing, All authors. All authors have read and agreed to the published version of the manuscript.
Funding
This work received no external funding.
Data Availability Statement
Not applicable.
Acknowledgments
Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2022R132), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia. This work was supported by the Technology Innovation Program (20018869, Development of Waste Heat and Waste Cold Recovery Bus Air-conditioning System to Reduce Heating and Cooling Load by 10%), funded by the Ministry of Trade, Industry and Energy (MOTIE, Korea).
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Strength of magnetic field [T] | |
| Dimensionless form radial velocity | |
| Dimensionless form tangential velocity | |
| Prandtl number (m2 s−1) | |
| Skin friction coefficient | |
| Dimensionless form temperature | |
| Fixed pressure at a specific heat capacity (J/(kg K) | |
| Nusselt number | |
| Dynamic viscosity (kg m−1 s−1) | |
| Eckert number | |
| r z | Cylindrical coordinates system |
| Dimensionless parameter | |
| Porosity parameter | |
| M | Magnetic field (wb/m2) |
| Forchheimer number | |
| (u, v, w) | Velocity components [gr or m/s] |
| Re | Reynolds number |
| α | Expansion ratio |
| and | Diameter of 1st and 2nd nanoparticles |
| Electrical conductivity [()/kg] | |
| Kinematic viscosity [/s] | |
| Thermal diffusivity of hybrid nanofluid [/s] | |
| Density [kg/ | |
| Volumetric heat capacity [J/(m3 K)] | |
| 1st nanoparticle volume fraction | |
| 2nd nanoparticle volume fraction | |
| Subscripts | |
| () | Base fluid (NFs) nanofluids |
| (HNFDs) | Hybrid nanofluids |
| HNFD1 | |
| HNFD2 | |
| HNFD3 | oil |
| HNFD4 | Ag-TiO2/H2O |
| HNFD5 | Ag-TiO2/ |
| HNFD6 | Ag-TiO2/ oil |
| HNFD7 | Cu-Al2O3/H2O |
| HNFD8 | Cu-Al2O3/ |
| HNFD9 | Cu-Al2O3/ oil |
| HNFD10 | Cu-TiO2/H2O |
| HNFD11 | Cu-TiO2/ |
| HNFD12 | Cu-TiO2/ oil |
| NP | Nanoparticles |
| MHD | Magnetohydrodynamics |
| PDE | Partial differential equation |
References
- Ahmed, N.; Adnan; Khan, U.; Mohyud-Din, S.T. Influence of shape factor on flow of magneto-nanofluid squeezed between parallel disks. Alex. Eng. J. 2018, 57, 1893–1903. [Google Scholar] [CrossRef]
- Abbas, W.; Magdy, M.M. Heat and Mass Transfer Analysis of Nanofluid Flow Based on, and over a Moving Rotating Plate and Impact of Various Nanoparticle Shapes. Math. Probl. Eng. 2020, 2020, 9606382. [Google Scholar] [CrossRef]
- Motlagh, S.Y.; Soltanipour, H. Natural convection of Al2O3-water nanofluid in an inclined cavity using Buongiorno’s two-phase model. Int. J. Therm. Sci. 2017, 111, 310–320. [Google Scholar] [CrossRef]
- Acharya, N.; Bag, R.; Kundu, P.K. Influence of Hall current on radiative nanofluid flow over a spinning disk: A hybrid approach. Phys. E Low-Dimens. Syst. Nanostruct. 2019, 111, 103–112. [Google Scholar] [CrossRef]
- Akbar, N.S.; Raza, M.; Ellahi, R. Influence of induced magnetic field and heat flux with the suspension of carbon nanotubes for the peristaltic flow in a permeable channel. J. Magn. Magn. Mater. 2015, 381, 405–415. [Google Scholar] [CrossRef]
- Dinarvand, S.; Nademi Rostami, M. An innovative mass-based model of aqueous zinc oxide–gold hybrid nanofluid for von Kármán’s swirling flow. J. Therm. Anal. Calorim. 2019, 138, 845–855. [Google Scholar] [CrossRef]
- Ramesh, G.K. Three different hybrid nanometrial performances on rotating disk: A non-Darcy model. Appl. Nanosci. 2018, 9, 179–187. [Google Scholar] [CrossRef]
- Xu, H. Modelling unsteady mixed convection of a nanofluid suspended with multiple kinds of nanoparticles between two rotating disks by generalized hybrid model. Int. Commun. Heat Mass Transf. 2019, 108, 104275. [Google Scholar] [CrossRef]
- Abdelmalek, Z.; Qureshi, M.Z.A.; Bilal, S.; Raza, Q.; Sherif, E.-S.M. A case study on morphological aspects of distinct magnetized 3D hybrid nanoparticles on fluid flow between two orthogonal rotating disks: An application of thermal energy systems. Case Stud. Therm. Eng. 2020, 23, 100744. [Google Scholar] [CrossRef]
- Dinarvand, S.; Rashidi, M.M.; Shahmohamadi, H. Analytic approximate solution of three-dimensional Navier-Stokes equations of flow between two stretchable disks. Numer. Methods Partial Differ. Equ. 2010, 26, 1594–1607. [Google Scholar] [CrossRef]
- Acharya, N.; Maity, S.; Kundu, P.K. Framing the hydrothermal features of magnetized TiO2–CoFe2O4 water-based steady hybrid nanofluid flow over a radiative revolving disk. Multidiscip. Model. Mater. Struct. 2019, 16, 765–790. [Google Scholar] [CrossRef]
- Yin, C.; Zheng, L.; Zhang, C.; Zhang, X. Flow and heat transfer of nanofluids over a rotating disk with uniform stretching rate in the radial direction. Propuls. Power Res. 2017, 6, 25–30. [Google Scholar] [CrossRef]
- Lou, Q.; Ali, B.; Rehman, S.U.; Habib, D.; Abdal, S.; Shah, N.A.; Chung, J.D. Micropolar dusty fluid: Coriolis force effects on dynamics of MHD rotating fluid when lorentz force is significant. Mathematics 2022, 10, 2630. [Google Scholar] [CrossRef]
- Ashraf, M.Z.; Rehman, S.U.; Farid, S.; Hussein, A.K.; Ali, B.; Shah, N.A.; Weera, W. Insight into significance of bioconvection on MHD tangent hyperbolic nanofluid flow of irregular thickness across a slender elastic surface. Mathematics 2022, 10, 2592. [Google Scholar] [CrossRef]
- Fallah, B.; Dinarvand, S.; Eftekhari Yazdi, M.; Rostami, M.N.; Pop, I. MHD flow and heat transfer of SiC-TiO2/DO hybrid nanofluid due to a permeable spinning disk by a novel algorithm. J. Appl. Comput. Mech. 2019, 5, 976–988. [Google Scholar]
- Hatami, M.; Sheikholeslami, M.; Ganji, D.D. RETRACTED: Laminar flow and heat transfer of nanofluid between contracting and rotating disks by least square method. Powder Technol. 2014, 253, 769–779. [Google Scholar] [CrossRef]
- Mustafa, M.; Khan, J.A.; Hayat, T.; Alsaedi, A. On Bödewadt flow and heat transfer of nanofluids over a stretching stationary disk. J. Mol. Liq. 2015, 211, 119–125. [Google Scholar] [CrossRef]
- Dogonchi, A.; Chamkha, A.J.; Seyyedi, S.M.; Ganji, D. Radiative nanofluid flow and heat transfer between parallel disks with penetrable and stretchable walls considering Cattaneo-Christov heat flux model. Heat Transfer Asian Res. 2018, 47, 735–753. [Google Scholar] [CrossRef]
- Sajjan, K.; Shah, N.A.; Ahammad, N.A.; Raju, C.S.K.; Kumar, M.D.; Weera, W. Nonlinear Boussinesq and Rosseland approximations on 3D flow in an interruption of Ternary nanoparticles with various shapes of densities and conductivity properties. AIMS Math. 2022, 7, 18416–18449. [Google Scholar] [CrossRef]
- Hasnain, J.; Abid, N. Numerical investigation for thermal growth in water and engine oil-based ternary nanofluid using three different shaped nanoparticles over a linear and nonlinear stretching sheet. Numer. Heat Transfer Part A Appl. 2022, 1–12. [Google Scholar] [CrossRef]
- Khashi’ie, N.S.; Wahid, N.S.; Arifin, N.M.; Pop, I. Insight into three-dimensional flow of three different dynamics of nanofluids subject to thermal radiation: The case of water–cobalt ferrite, water–manganese–zinc ferrite, and water–magnetite. Heat Transfer 2022, 51, 4434–4450. [Google Scholar] [CrossRef]
- Koriko, O.K.; Adegbie, K.S.; Animasaun, I.L.; Olotu, M.A. Numerical solutions of the partial differential equations for investigating the significance of partial slip due to lateral velocity and viscous dissipation: The case of blood-gold Carreau nanofluid and dusty fluid. Numer. Methods Part. Differ. Equ. 2021, 7, 1–15. [Google Scholar] [CrossRef]
- Shah, N.A.; Wakif, A.; El-Zahar, E.R.; Ahmad, S.; Yook, S.-J. Numerical simulation of a thermally enhanced EMHD flow of a heterogeneous micropolar mixture comprising (60%)-ethylene glycol (EG), (40%)-water (W), and copper oxide nanomaterials (CuO). Case Stud. Therm. Eng. 2022, 35, 102046. [Google Scholar] [CrossRef]
- Rout, B.R.; Parida, S.K.; Panda, S. MHD Heat and Mass Transfer of Chemical Reaction Fluid Flow over a Moving Vertical Plate in Presence of Heat Source with Convective Surface Boundary Condition. Int. J. Chem. Eng. 2013, 2013, 296834. [Google Scholar] [CrossRef]
- Hayat, T.; Qayyum, A.; Alsaedi, A. Effects of heat and mass transfer in flow along a vertical stretching cylinder with slip conditions. Eur. Phys. J. Plus 2014, 129, 63. [Google Scholar] [CrossRef]
- Reddy, J.R.; Sugunamma, V.; Sandeep, N.; Sulochana, C. Influence of chemical reaction, radiation and rotation on MHD nanofluid flow past a permeable flat plate in porous medium. J. Niger. Math. Soc. 2016, 35, 48–65. [Google Scholar] [CrossRef]
- Hayat, T.; Rashid, M.; Imtiaz, M.; Alsaedi, A. Magnetohydrodynamic (MHD) flow of Cu-water nanofluid due to a rotating disk with partial slip. AIP Adv. 2015, 5, 067169. [Google Scholar] [CrossRef]
- Vajravelu, K.; Prasad, K.V.; Ng, C.-O.; Vaidya, H. MHD squeeze flow and heat transfer of a nanofluid between parallel disks with variable fluid properties and transpiration. Int. J. Mech. Mater. Eng. 2017, 12, 9. [Google Scholar] [CrossRef]
- Das, K.; Jana, S.; Acharya, N. Slip effects on squeezing flow of nanofluid between two parallel disks. Int. J. Appl. Mech. Eng. 2016, 21, 5–20. [Google Scholar] [CrossRef]
- Mohyud-Din, S.T.; Khan, S.I.; Bin-Mohsin, B. Velocity and temperature slip effects on squeezing flow of nanofluid between parallel disks in the presence of mixed convection. Neural Comput. Appl. 2016, 28, 169–182. [Google Scholar] [CrossRef]
- Qayyum, S.; Imtiaz, M.; Alsaedi, A.; Hayat, T. Analysis of radiation in a suspension of nanoparticles and gyrotactic microorganism for rotating disk of variable thickness. Chin. J. Phys. 2018, 56, 2404–2423. [Google Scholar] [CrossRef]
- Aziz, A.; Alsaedi, A.; Muhammad, T.; Hayat, T. Numerical study for heat generation/absorption in flow of nanofluid by a rotating disk. Results Phys. 2018, 8, 785–792. [Google Scholar] [CrossRef]
- Elnaqeeb, T.; Shah, N.A.; Mirza, I.A. Natural convection flows of carbon nanotubes nanofluids with Prabhakar-like thermal transport. Math. Meth. Appl. Sci. 2020, 1–14. [Google Scholar] [CrossRef]
- Uddin, I.; Akhtar, R.; Khan, M.A.R.; Zhiyu, Z.; Islam, S.; Shoaib, M.; Raja, M.A.Z. Numerical treatment for fluidic system of activation energy with non-linear mixed convective and radiative flow of magneto nanomaterials with Navier’s velocity slip. AIP Adv. 2019, 9, 055210. [Google Scholar] [CrossRef]
- Khan, M.I.; Hayat, T.; Alsaedi, A. A modified homogeneous-heterogeneous reactions for MHD stagnation flow with viscous dissipation and Joule heating. Int. J. Heat Mass Transf. 2017, 113, 310–317. [Google Scholar] [CrossRef]
- Khan, N.; A Sajid, M.; Mahmood, T. Heat transfer analysis for magnetohydrodynamics axisymmetric flow between stretching disks in the presence of viscous dissipation and Joule heating. AIP Adv. 2015, 5, 057115. [Google Scholar] [CrossRef]
- Imtiaz, M.; Hayat, T.; Alsaedi, A.; Asghar, S. Slip flow by a variable thickness rotating disk subject to magnetohydrodynamics. Results Phys. 2017, 7, 503–509. [Google Scholar] [CrossRef]
- Doh, D.; Muthtamilselvan, M. Thermophoretic particle deposition on magnetohydrodynamic flow of micropolar fluid due to a rotating disk. Int. J. Mech. Sci. 2017, 130, 350–359. [Google Scholar] [CrossRef]
- Shah, Z.; Dawar, A.; Kumam, P.; Khan, W.; Islam, S. Impact of Nonlinear Thermal Radiation on MHD Nanofluid Thin Film Flow over a Horizontally Rotating Disk. Appl. Sci. 2019, 9, 1533. [Google Scholar] [CrossRef]
- Rasool, G.; Shah, N.A.; El-Zahar, E.R.; Wakif, A. Numerical investigation of EMHD nanofluid flows over a convectively heated riga pattern positioned horizontally in a Darcy-Forchheimer porous medium: Application of passive control strategy and generalized transfer laws. Waves Random Complex Media 2022, 1–20. [Google Scholar] [CrossRef]
- Rostami, M.N.; Dinarvand, S.; Pop, I. Dual solutions for mixed convective stagnation-point flow of an aqueous silica–alumina hybrid nanofluid. Chin. J. Phys. 2018, 56, 2465–2478. [Google Scholar] [CrossRef]
- Ghadikolaei, S.; Hosseinzadeh, K.; Hatami, M.; Ganji, D. MHD boundary layer analysis for micropolar dusty fluid containing Hybrid nanoparticles (Cu-Al2O3) over a porous medium. J. Mol. Liq. 2018, 268, 813–823. [Google Scholar] [CrossRef]
- Qureshi, M.Z.A.; Bilal, S.; Malik, M.Y.; Raza, Q.; Sherif, E.-S.M.; Li, Y.-M. Dispersion of metallic/ceramic matrix nanocomposite material through porous surfaces in magnetized hybrid nanofluids flow with shape and size effects. Sci. Rep. 2021, 11, 12271. [Google Scholar] [CrossRef] [PubMed]
- Raza, Q.; Qureshi, M.Z.A.; Khan, B.A.; Hussein, A.K.; Ali, B.; Shah, N.A.; Chung, J.D. Insight into Dynamic of Mono and Hybrid Nanofluids Subject to Binary Chemical Reaction, Activation Energy, and Magnetic Field through the Porous Surfaces. Mathematics 2022, 10, 3013. [Google Scholar] [CrossRef]
- Raza, Q.; Qureshi, M.Z.A.; Ali, B.; Hussein, A.K.; Khan, B.A.; Shah, N.A.; Weera, W. Morphology of Hybrid MHD Nanofluid Flow through Orthogonal Coaxial Porous Disks. Mathematics 2022, 10, 3280. [Google Scholar] [CrossRef]
- Qureshi, M.Z.; Raza, Q.; Ramzan, A.; Faisal, M.; Ali, B.; Shah, N.A.; Weera, W. Activation Energy Performance through Magnetized Hybrid Fe3O4–PP Nanofluids Flow with Impact of the Cluster Interfacial Nanolayer. Mathematics 2022, 10, 3277. [Google Scholar] [CrossRef]
- Habib, D.; Salamat, N.; Ahsan, M.; Abdal, S.; Siddique, I.; Ali, B. Significance of bioconvection and mass transpiration for MHD micropolar Maxwell nanofluid flow over an extending sheet. Waves Random Complex Media 2022, 1–15. [Google Scholar] [CrossRef]
- Ali, K.; Akbar, M.Z.; Iqbal, M.F.; Ashraf, M. Numerical simulation of heat and mass transfer in unsteady nanofluid between two orthogonally moving porous coaxial disks. AIP Adv. 2014, 4, 107113. [Google Scholar] [CrossRef]
- Ali, K.; Iqbal, M.F.; Akbar, Z.; Ashraf, M. Numerical simulation of unsteady water-based nanofluid flow and heat transfer between two orthogonally moving porous coaxial disks. J. Theor. Appl. Mech. 2014, 52, 1033–1046. [Google Scholar] [CrossRef][Green Version]
- Majdalani, J.; Zhou, C.; Dawson, C.A. Two-dimensional viscous flow between slowly expanding or contracting walls with weak permeability. J. Biomech. 2002, 35, 1399–1403. [Google Scholar] [CrossRef]
- Saba, F.; Ahmed, N.; Khan, U.; Waheed, A.; Rafiq, M.; Mohyud-Din, S.T. Thermophysical Analysis of Water Based (Cu–Al2O3) Hybrid Nanofluid in an Asymmetric Channel with Dilating/Squeezing Walls Considering Different Shapes of Nanoparticles. Appl. Sci. 2018, 8, 1549. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Ganji, D.D. Nanofluid flow and heat transfer between parallel plates considering Brownian motion using DTM. Comput. Methods Appl. Mech. Eng. 2014, 283, 651–663. [Google Scholar] [CrossRef]
- Hussain, M.F.; Akbar, M.Z. Numerical Analysis of Nanofluids with Convective Heat Transfer through Porous Disks. Casp. J. Comput. Math. Eng. 2017, 2, 5–26. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).