Robust Stability Analysis of Filtered PI and PID Controllers for IPDT Processes
Abstract
1. Introduction
2. PI, PID, and PIDA Controller for the IPDT Plant Tuned with the MRDP Method
2.1. Optimal “Ideal” Controller Design
2.2. PID Controllers with Proper Transfer Functions and the Delay Equivalence
3. Robustness Issues
Robust Stability Analysis
4. Robust Stability of PI Controllers
4.1. Unfiltered PI Controllers
4.2. Filtered PI Controller with the First-Order Filter
4.3. Filtered PI Controller with the Second-Order Filter
4.4. Discussion on the Filtered PI Control
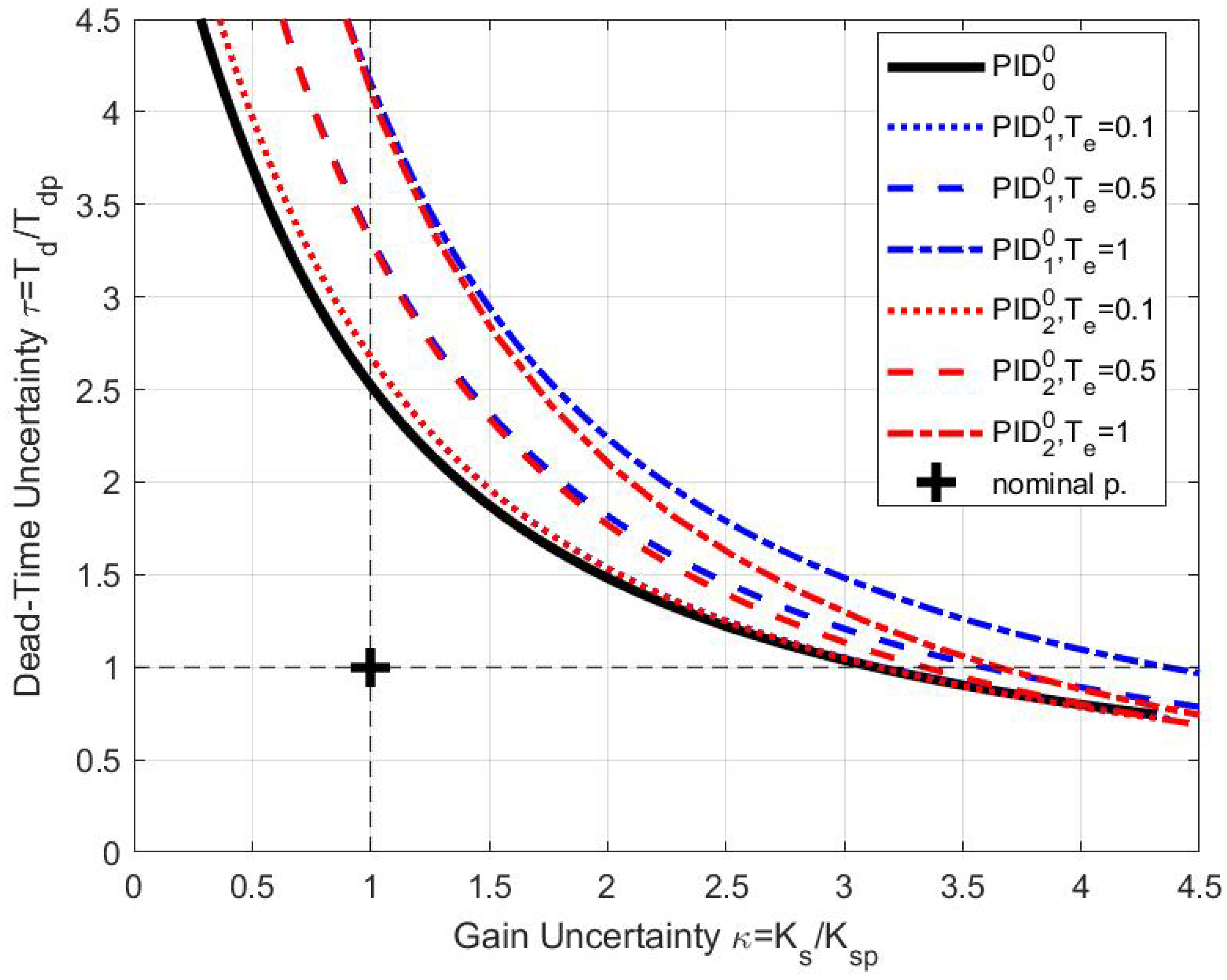
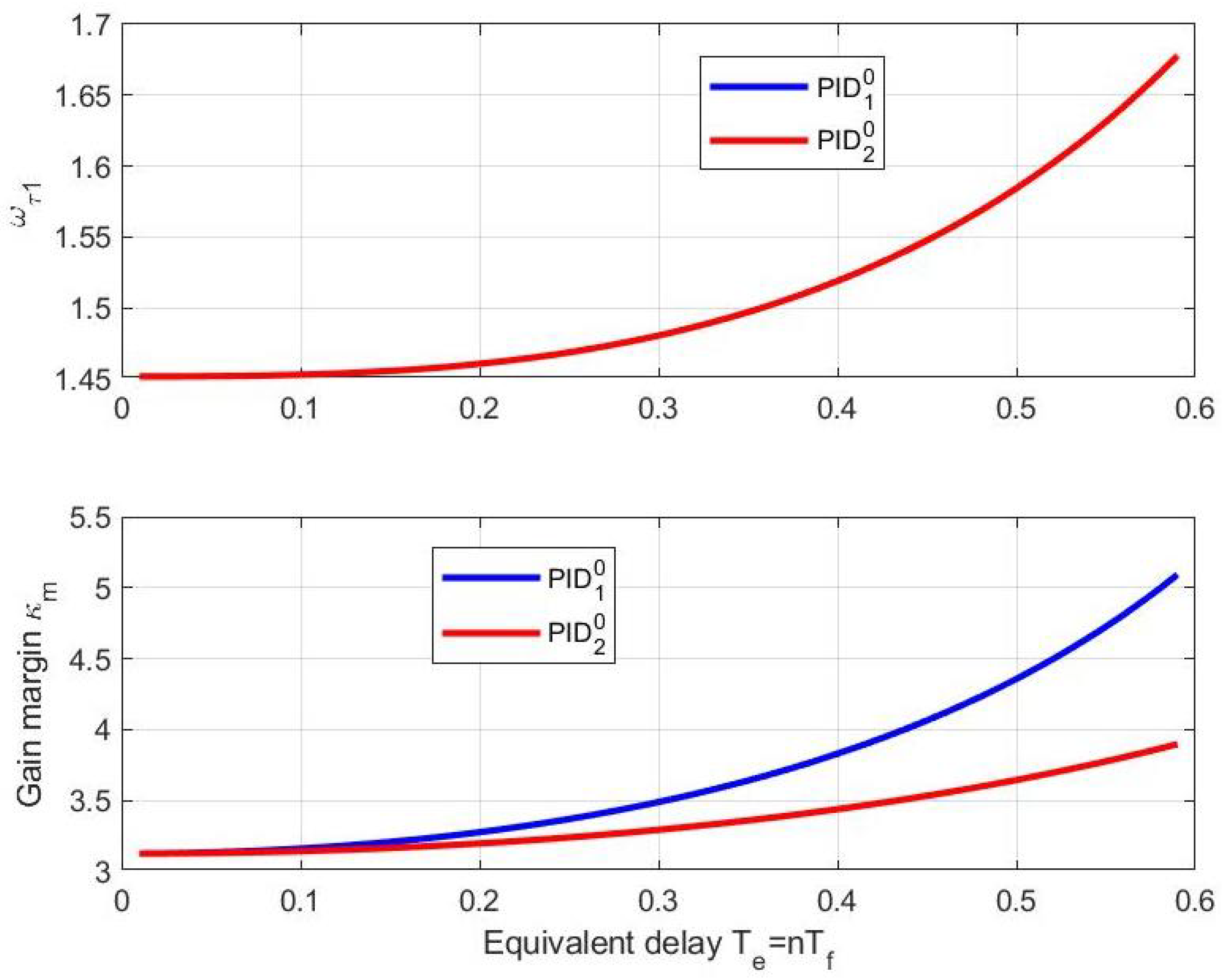
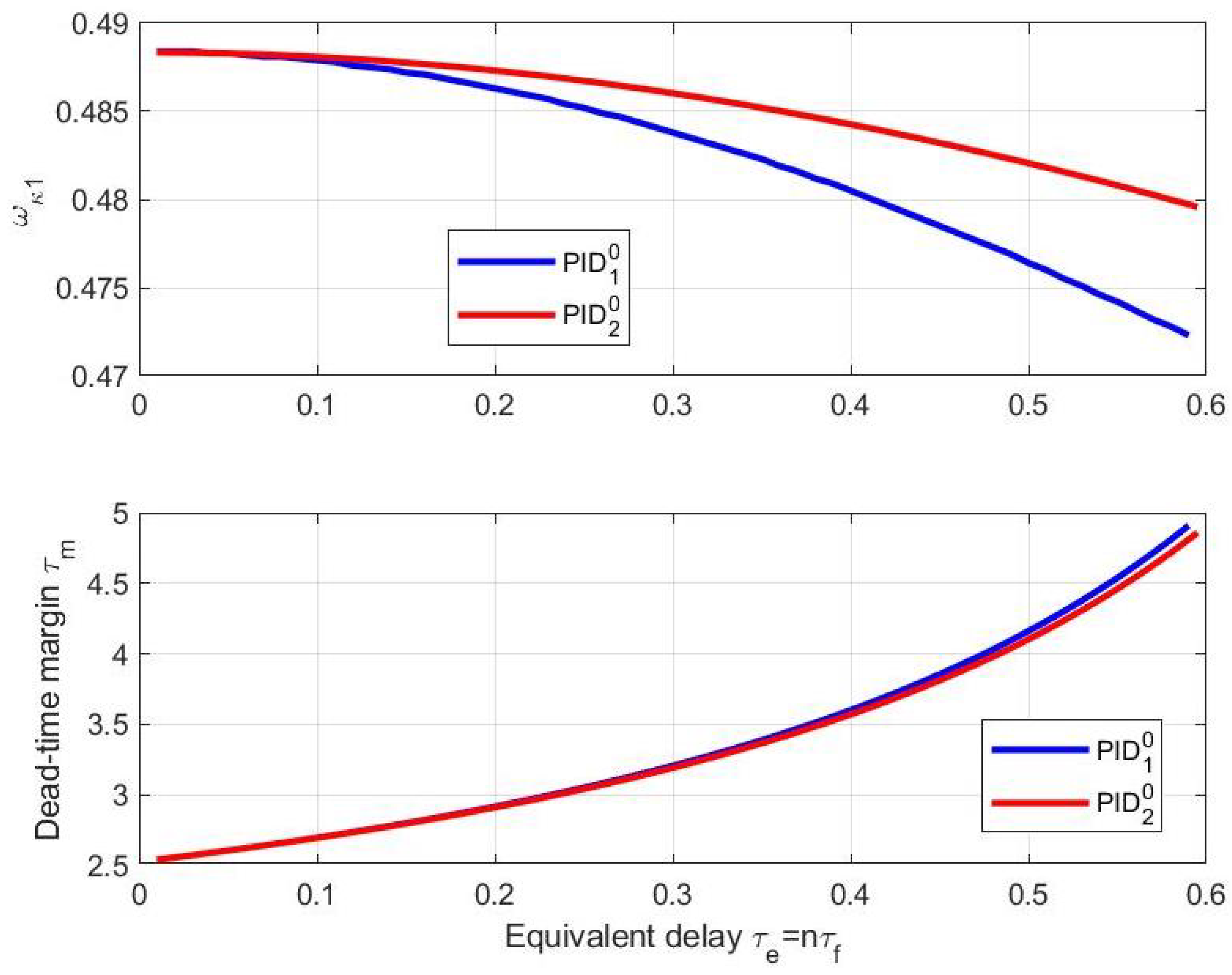
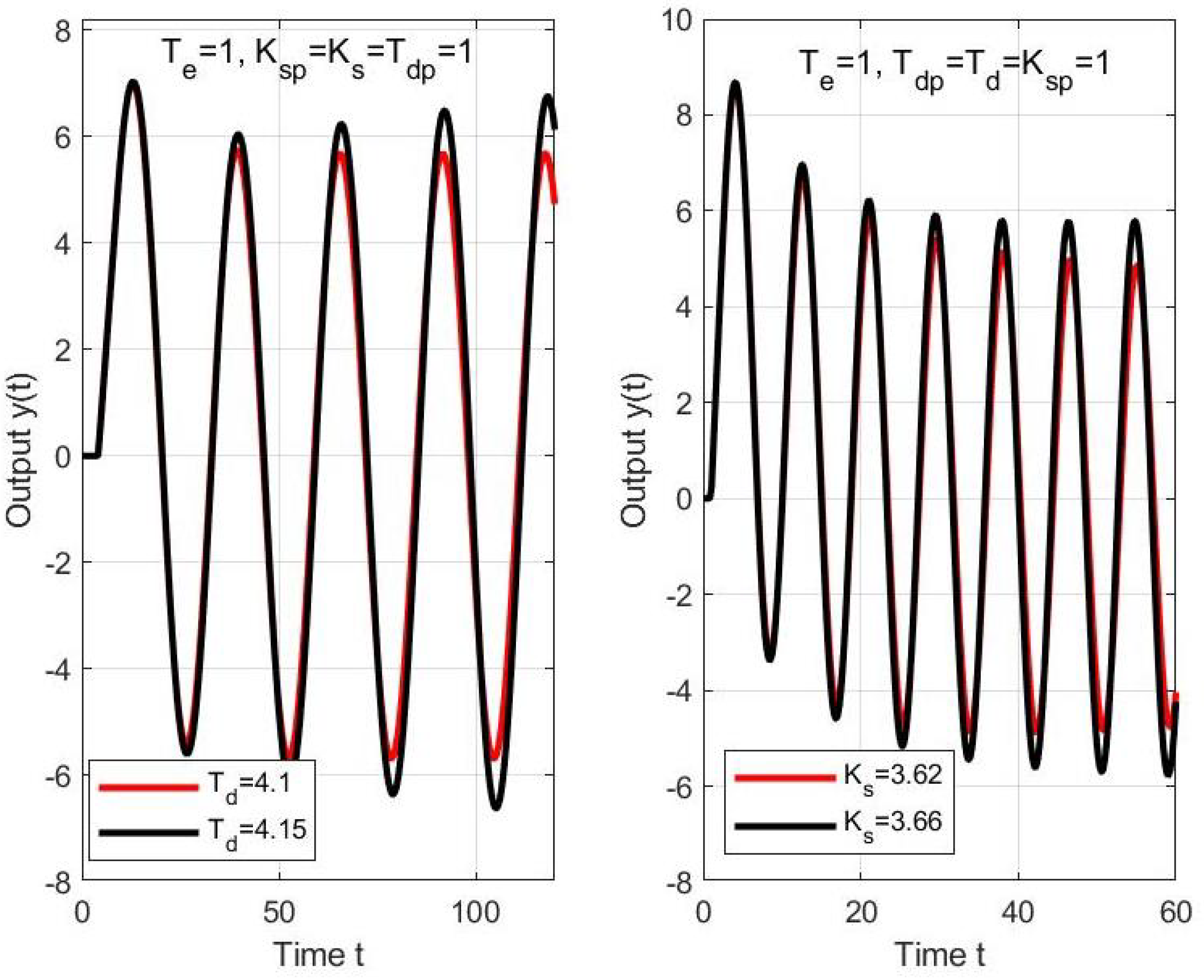
5. Robust Stability of Filtered PID Control
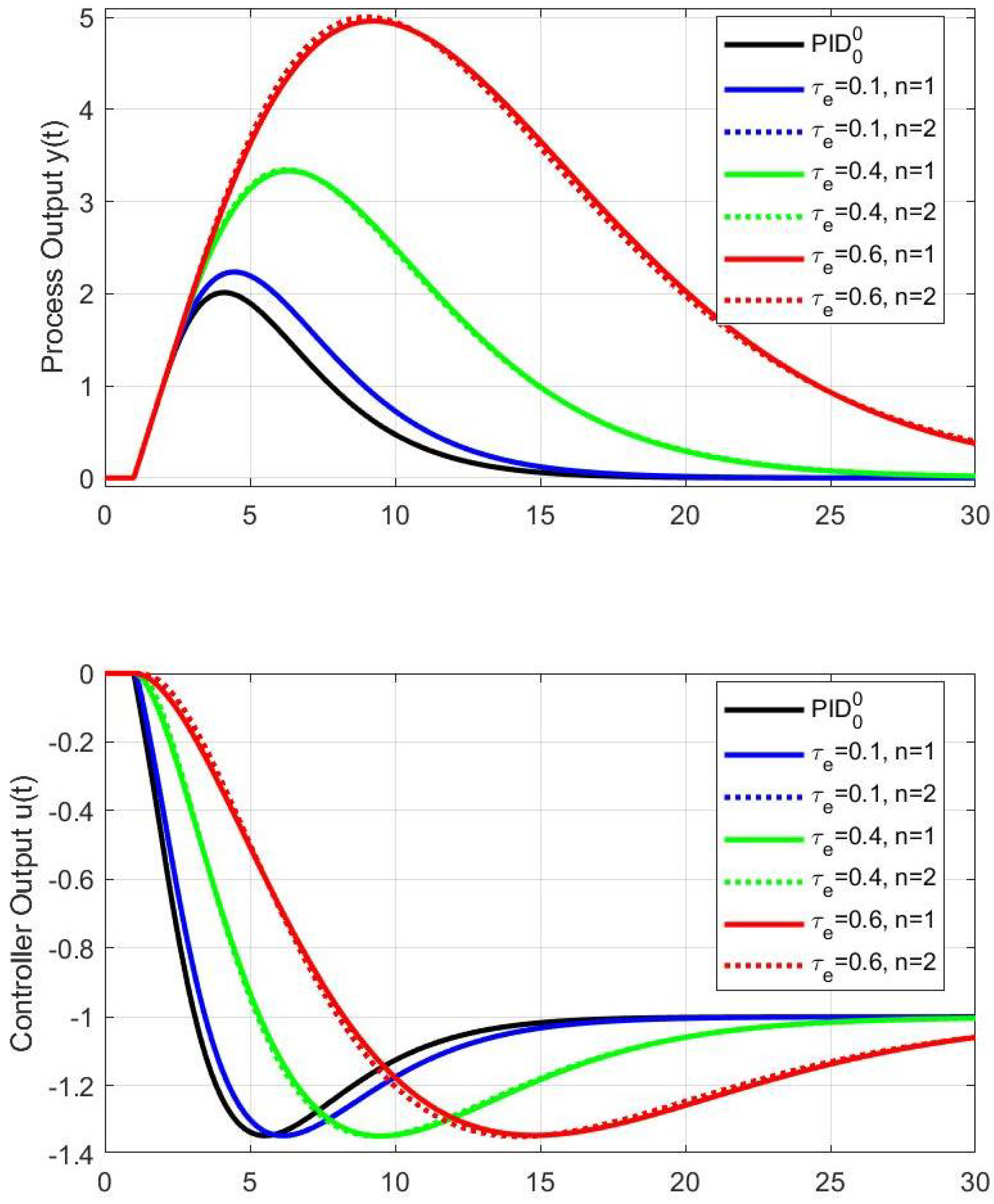
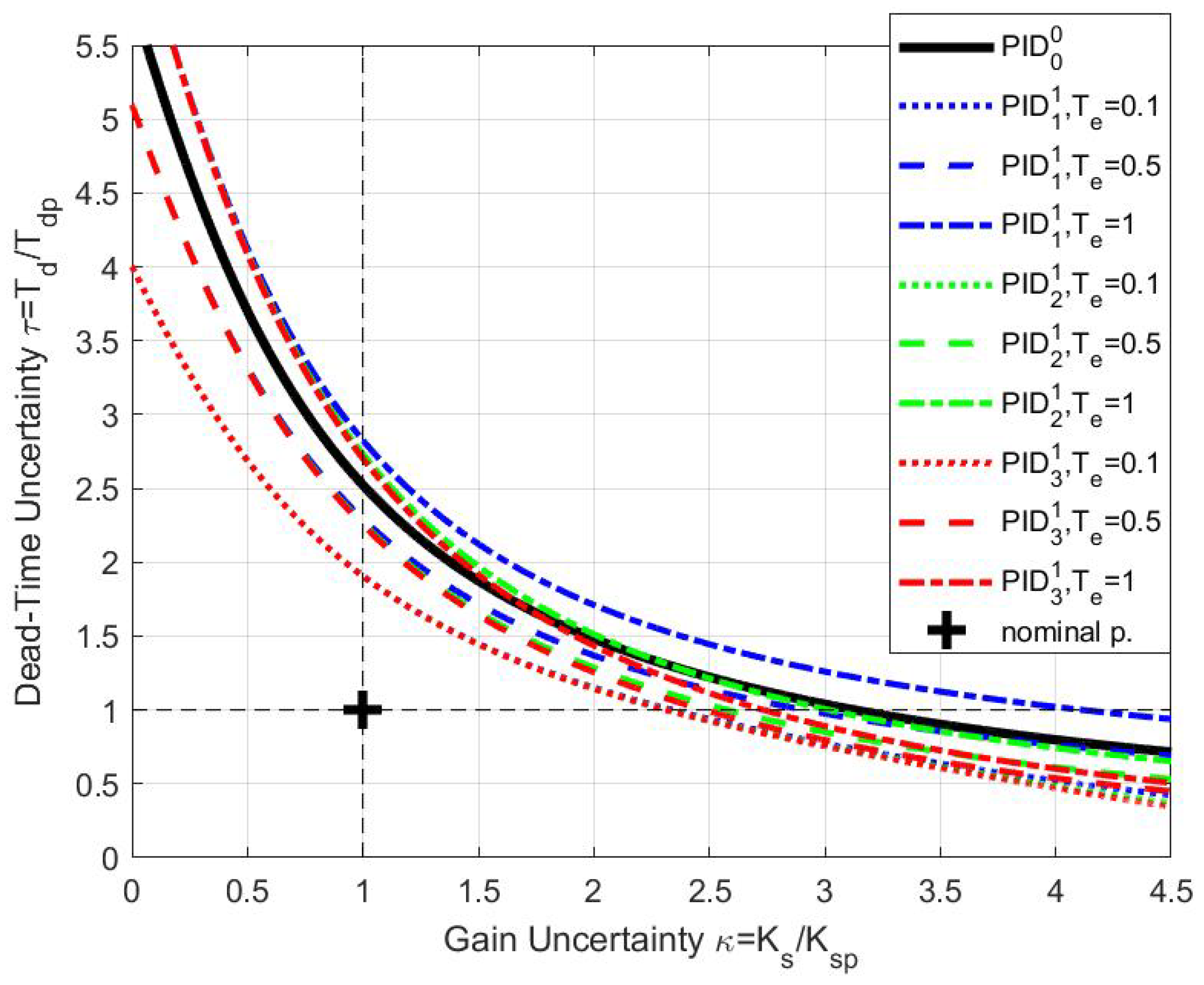
5.1. PID with the First-Order Filters
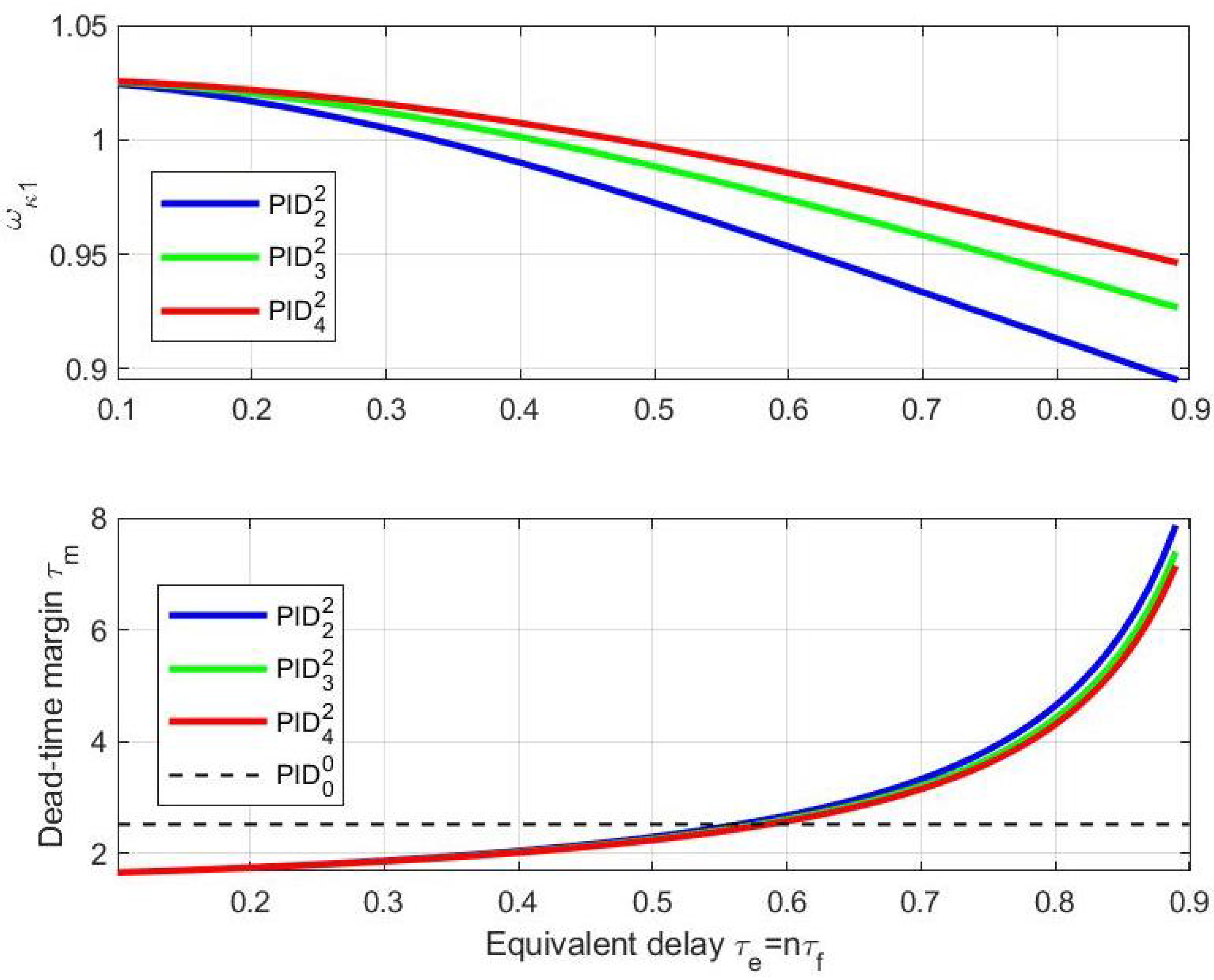
5.2. PID with the Second-Order Filter
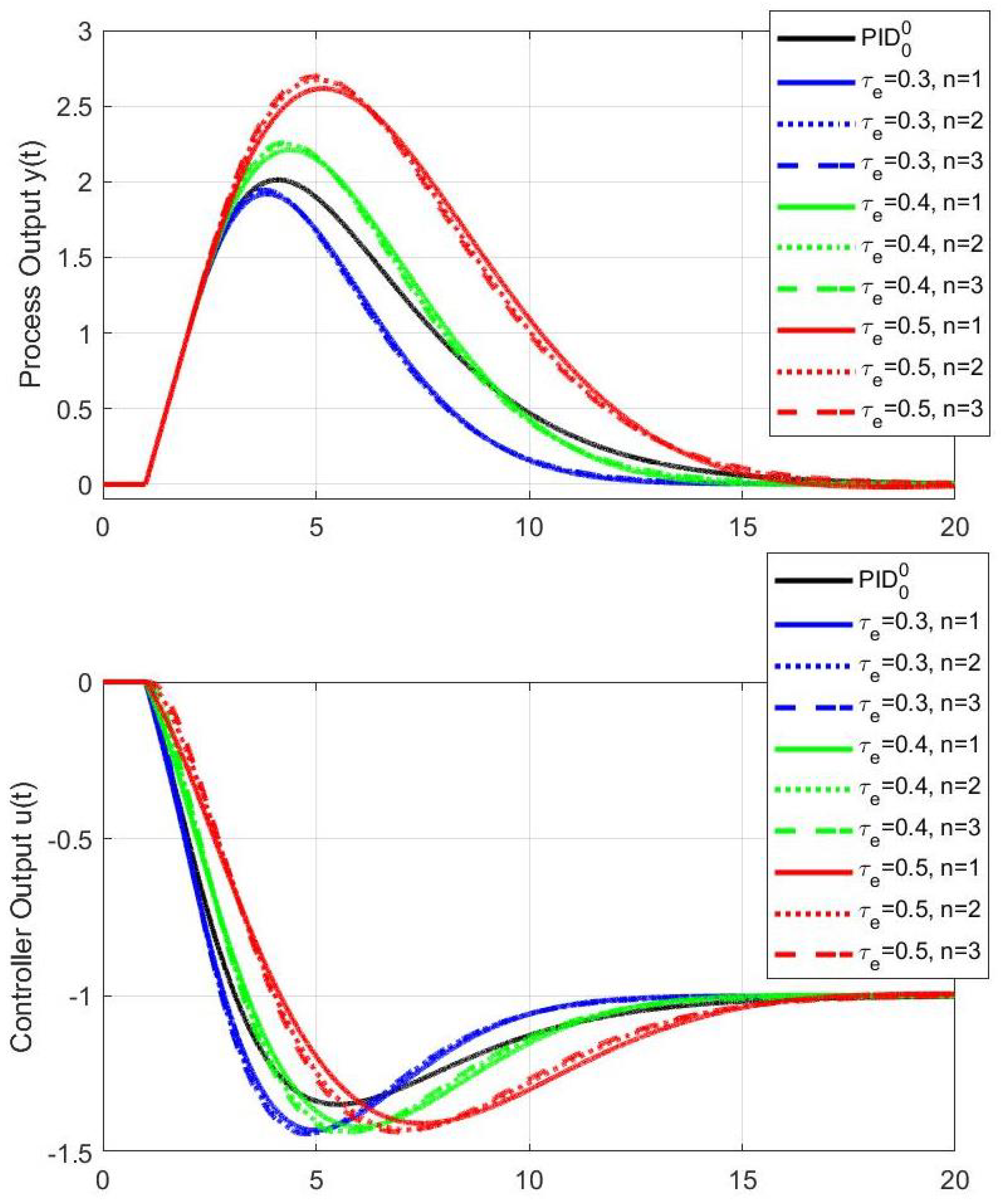
5.3. PID with the Third-Order Filter
5.4. Discussion about Filtered PID Control
6. Robust Stability of PIDA Controller
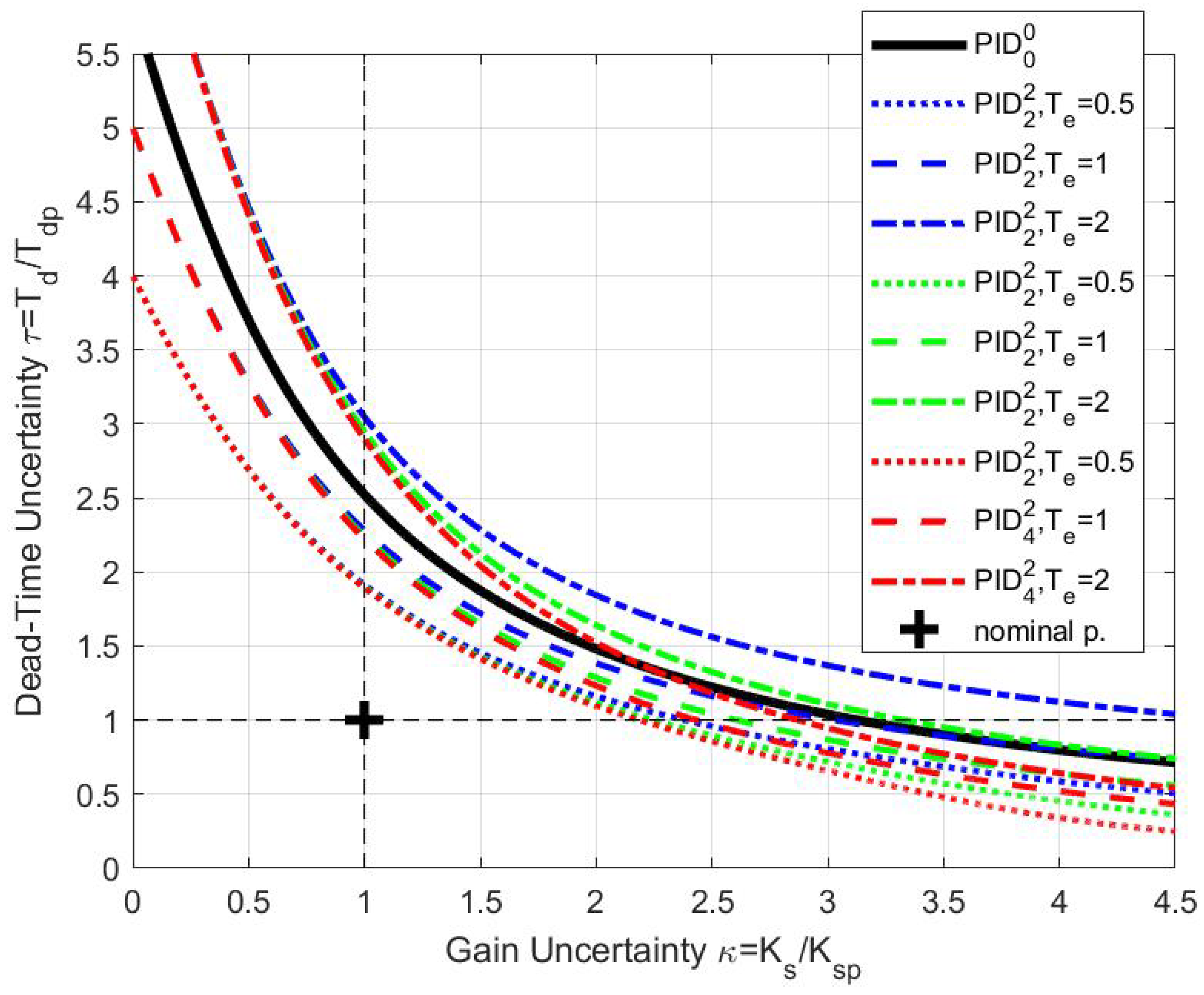
6.1. PIDA with the Second-Order Filters
6.2. PIDA with the Third-Order Filters
6.3. PIDA with the Fourth-Order Filters
6.4. Discussion on the Filtered PIDA Control
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Boundary Point | |
| Integral Absolute Error | |
| IPDT | Integrator Plus Dead-Time |
| MRDP | Multiple Real Dominant Pole |
| PI | Proportional-Integral |
| PID | Proportional-Integral-Derivative |
| PIDA | Proportional-Integral-Derivative-Accelerative |
References
- Visioli, A. Practical PID Control; Springer: London, UK, 2006. [Google Scholar]
- Åström, K.J.; Hägglund, T. Advanced PID Control; ISA, Research Triangle Park: Raleigh, NC, USA, 2006. [Google Scholar]
- Isaksson, A.; Graebe, S. Derivative filter is an integral part of PID design. Control Theory Appl. IEE Proc. 2002, 149, 41–45. [Google Scholar] [CrossRef]
- Ruel, P.E. Using filtering to improve performance. In Proceedings of the ISA Expo 2003, Houston, TX, USA, 21–23 October 2003. [Google Scholar]
- Hägglund, T. Signal Filtering in PID Control. IFAC Proc. Vol. 2012, 45, 1–10. [Google Scholar] [CrossRef]
- Micic, A.D.; Matausek, M.R. Optimization of PID controller with higher-order noise filter. J. Process Control 2014, 24, 694–700. [Google Scholar] [CrossRef]
- Segovia, V.R.; Hägglund, T.; Åström, K. Measurement noise filtering for PID controllers. J. Process Control 2014, 24, 299–313. [Google Scholar] [CrossRef]
- Fišer, J.; Zítek, P.; Vyhlídal, T. Dominant four-pole placement in filtered PID control loop with delay. IFAC-PapersOnLine 2017, 50, 6501–6506. [Google Scholar] [CrossRef]
- Peker, F.; Kaya, I. Optimal integral-proportional derivative controller design for input load disturbance rejection of time delay integrating processes. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2022; in press. [Google Scholar]
- Huba, M. Filter choice for an effective measurement noise attenuation in PI and PID controllers. In Proceedings of the ICM2015, Casablanca, Morocco, 20–23 December 2015. [Google Scholar]
- Huba, M.; Bisták, P.; Huba, T. Filtered PI and PID control of an Arduino based thermal plant. IFAC-PapersOnLine 2016, 49, 336–341. [Google Scholar] [CrossRef]
- Majhi, S.; Kotwal, V.; Mehta, U. FPAA-Based PI controller for DC servo position control system. IFAC Proc. Vol. 2012, 45, 247–251. [Google Scholar] [CrossRef]
- Hasler, J. Large-Scale Field-Programmable Analog Arrays. Proc. IEEE 2020, 108, 1283–1302. [Google Scholar] [CrossRef]
- Valele, W.; Virambath, R.; Mehta, U.; Azid, S. Fractional analog scheme for efficient stabilization of a synchronous buck converter. J. Electr. Eng. 2020, 71, 116–121. [Google Scholar] [CrossRef]
- Huba, M.; Vrančić, D.; Bisták, P. PID Control with Higher Order Derivative Degrees for IPDT Plant Models. IEEE Access 2021, 9, 2478–2495. [Google Scholar] [CrossRef]
- Vrančić, D.; Huba, M. High-Order Filtered PID Controller Tuning Based on Magnitude Optimum. Mathematics 2021, 9, 1340. [Google Scholar] [CrossRef]
- Oldenbourg, R.; Sartorius, H. Dynamik Selbsttätiger Regelungen; R.Oldenbourg-Verlag: München, Germany, 1944. [Google Scholar]
- Vítečková, M.; Víteček, A. Two-degree of Freedom Controller Tuning for Integral Plus Time Delay Plants. ICIC Express Lett. Int. J. Res. Surv. Jpn. 2008, 2, 225–229. [Google Scholar]
- Vítečková, M.; Víteček, A. 2DOF PI and PID controllers tuning. In Proceedings of the 9th IFAC Workshop on Time Delay Systems, Guangzhou, China, 29 September–1 October 2010; Volume 9, pp. 343–348. [Google Scholar]
- Vítečková, M.; Víteček, A. 2DOF PID controller tuning for integrating plants. In Proceedings of the 2016 17th Int. Carpathian Control Conf. (ICCC), High Tatras, Slovakia, 29 May–1 June 2016; pp. 793–797. [Google Scholar]
- Víteček, A.; Vítečková, M. Series Two Degree of Freedom PID Controller for Integrating Plants with Time Delay. In Proceedings of the 2019 20th International Carpathian Control Conference (ICCC), Kraków-Wieliczka, Poland, 26–29 May 2019; pp. 1–4. [Google Scholar]
- Vítečková, M.; Víteček, A.; Janáčová, D. Robustness and Muliple Dominant Pole Method. In Proceedings of the 2020 21th ICCC, High Tatras, Slovakia, 27–29 October 2020; pp. 1–4. [Google Scholar]
- Huba, M. Designing Robust Controller Tuning for Dead Time Systems. In Int. Conf. System Structure and Control; IFAC: Ancona, Italy, 2010. [Google Scholar]
- Huba, M. Performance measures, performance limits and optimal PI control for the IPDT plant. J. Process Control 2013, 23, 500–515. [Google Scholar] [CrossRef]
- Huba, M. Comparing 2DOF PI and Predictive Disturbance Observer Based Filtered PI Control. J. Process Control 2013, 23, 1379–1400. [Google Scholar] [CrossRef]
- Oaxaca-Adams, G.; Villafuerte-Segura, R.; Aguirre-Hernández, B. On non-fragility of controllers for time delay systems: A numerical approach. J. Frankl. Inst. 2021, 358, 4671–4686. [Google Scholar] [CrossRef]
- Oaxaca-Adams, G.; Villafuerte-Segura, R. On controllers performance for a class of time-delay systems: Maximum decay rate. Automatica 2023, 147, 110669. [Google Scholar] [CrossRef]
- Huba, M.; Chamraz, S.; Bisták, P.; Vrančić, D. Making the PI and PID Controller Tuning Inspired by Ziegler and Nichols Precise and Reliable. Sensors 2021, 18, 6157. [Google Scholar] [CrossRef] [PubMed]
- Huba, M.; Gao, Z. Uncovering Disturbance Observer and Ultra-Local Plant Models in Series PI Controllers. Symmetry 2022, 14, 640. [Google Scholar] [CrossRef]
- Huba, M. Disturbance Observer in PID Controllers for First-Order Time-Delayed Systems. In Proceedings of the 13th IFAC Symposium Advances in Control Education, Hamburg, Germany, 24–27 July 2022. [Google Scholar]
- Huba, M.; Bisták, P. Should we forget the PID control? In Proceedings of the 2022 20th International Conference on Emerging eLearning Technologies and Applications (ICETA), High Tatras, Slovakia, 20–21 October 2022. [Google Scholar]
- Huba, M.; Vrančić, D. Comparing filtered PI, PID and PIDD2 control for the FOTD plants. In Proceedings of the 3rd IFAC Conference on Advances in Proportional-Integral-Derivative Control, Ghent, Belgium, 9–11 May 2018; pp. 954–959. [Google Scholar]
- Huba, M.; Vrančić, D. Introduction to the Discrete Time PID Control for the IPDT Plant. In Proceedings of the 15th IFAC Int. Conference on Programmable Devices and Embedded Systems, Ostrava, Czech Republic, 23–25 May 2018; pp. 119–124. [Google Scholar]
- Tepljakov, A.; Alagoz, B.B.; Yeroglu, C.; Gonzalez, E.; HosseinNia, S.H.; Petlenkov, E. FOPID Controllers and Their Industrial Applications: A Survey of Recent Results. IFAC-PapersOnLine 2018, 51, 25–30. [Google Scholar] [CrossRef]
- Huba, M.; Vrančić, D.; Bisták, P. PID Control for IPDT Plants. Part 1: Disturbance Response. In Proceedings of the 26th Mediterranean Conference on Control and Automation (MED), Zadar, Croatia, 19–22 June 2018. [Google Scholar]
- Huba, M. Performance Measures and the Robust and Optimal Control Design. In Proceedings of the 3rd IFAC Conference on Advances in Proportional-Integral-Derivative Control, Ghent, Belgium, 9–11 May 2018; pp. 960–965. [Google Scholar]
- Huba, M.; Vrančić, D. Extending the Model-Based Controller Design to Higher-Order Plant Models and Measurement Noise. Symmetry 2021, 2021, 798. [Google Scholar] [CrossRef]
- Huba, M.; Vrančić, D. Tuning of PID Control for the Double Integrator Plus Dead-Time Model by Modified Real Dominant Pole and Performance Portrait Methods. Mathematics 2022, 10, 971. [Google Scholar] [CrossRef]
- Fortuna, L.; Frasca, M. Optimal and Robust Control: Advanced Topics with MATLAB, 1st ed.; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Ackermann, J. Robust Control: The Parameter Space Approach, 2nd ed.; Springer: Berlin, Germany, 2002. [Google Scholar]
- Zítek, P.; Fišer, J.; Vyhlídal, T. Dimensional analysis approach to dominant three-pole placement in delayed PID control loops. J. Process Control 2013, 23, 1063–1074. [Google Scholar] [CrossRef]
- Huba, M.; Oliveira, P.M.; Bisták, P.; Vrančić, D. A Set of Active Disturbance Rejection Controllers Based on Integrator Plus Dead-Time Models. Appl. Sci. 2021, 2021, 1671. [Google Scholar] [CrossRef]
- Ferrari, M.; Visioli, A. A software tool to understand the design of PIDA controllers. IFAC-PapersOnLine 2022, 55, 249–254. [Google Scholar] [CrossRef]
- Visioli, A.; Sánchez-Moreno, J. A relay-feedback automatic tuning methodology of PIDA controllers for high-order processes. Int. J. Control, 2022; in press. [Google Scholar]
- Huba, M.; Vrančić, D. Delay Equivalences in Tuning PID Control for the Double Integrator Plus Dead-Time. Mathematics 2021, 9, 328. [Google Scholar] [CrossRef]
- Ziegler, J.G.; Nichols, N.B. Optimum settings for automatic controllers. Trans. ASME 1942, 64, 759–768. [Google Scholar] [CrossRef]
- Fliess, M.; Join, C. Model-free control. Int. J. Control 2013, 86, 2228–2252. [Google Scholar] [CrossRef]
- Gao, Z. On the centrality of disturbance rejection in automatic control. ISA Trans. 2014, 53, 850–857. [Google Scholar] [CrossRef]
- Mercader, P.; Banos, A. A PI tuning rule for integrating plus dead time processes with parametric uncertainty. ISA Trans. 2017, 67, 246–255. [Google Scholar] [CrossRef]
- Huba, M.; Bélai, I. Limits of a Simplified Controller Design Based on IPDT models. ProcIMechE Part I J. Syst. Control Eng. 2018, 232, 728–741. [Google Scholar] [CrossRef]
- Neimark, J.I. D-decomposition of the space of quasi-polynomials (on the stability of linearized distributive systems. Am. Math. Soc. Transl. 1973, 102, 95–131. [Google Scholar]
- Householder, A.S. The Numerical Treatment of a Single Nonlinear Equation; McGraw-Hill: New York, NY, USA, 1970. [Google Scholar]



| K | 0.4612 | 0.78361 | 1.08268 |
| 5.8284 | 3.73205 | 3.00000 | |
| 0 | 0.26289 | 0.37500 | |
| 0 | 0 | 0.04167 |
| - | |||
|---|---|---|---|
| 12.639 | 4.763 | 2.771 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huba, M.; Bistak, P.; Vrancic, D. Robust Stability Analysis of Filtered PI and PID Controllers for IPDT Processes. Mathematics 2023, 11, 30. https://doi.org/10.3390/math11010030
Huba M, Bistak P, Vrancic D. Robust Stability Analysis of Filtered PI and PID Controllers for IPDT Processes. Mathematics. 2023; 11(1):30. https://doi.org/10.3390/math11010030
Chicago/Turabian StyleHuba, Mikulas, Pavol Bistak, and Damir Vrancic. 2023. "Robust Stability Analysis of Filtered PI and PID Controllers for IPDT Processes" Mathematics 11, no. 1: 30. https://doi.org/10.3390/math11010030
APA StyleHuba, M., Bistak, P., & Vrancic, D. (2023). Robust Stability Analysis of Filtered PI and PID Controllers for IPDT Processes. Mathematics, 11(1), 30. https://doi.org/10.3390/math11010030







