Abstract
This manuscript mainly focused on the nonlocal controllability of Hilfer fractional stochastic differential equations via almost sectorial operators. The key ideas of the study are illustrated by using ideas from fractional calculus, the fixed point technique, and measures of noncompactness. Then, the authors establish new criteria for the mild existence of solutions and derive fundamental characteristics of the nonlocal controllability of a system. In addition, researchers offer theoretical and real-world examples to demonstrate the effectiveness and suitability of our suggested solutions.
Keywords:
Hilfer fractional derivative; stochastic differential system; nonlocal controllability; measures of noncompactness; Darbo–Sadovskii fixed-point theorem; almost sectorial operators MSC:
34K30; 34K50; 47H08; 47H10
1. Introduction
The monographs of Ahmad et al. [1], Diethelm [2], Lakshmikantham and Vatsala [3], Miller and Ross [4], Podlubny [5], and Zhou [6,7] present several approaches to the subject of fractional calculus. On the other hand, differential equations with arbitrary order derivatives are presented as an extension of fractional differential equations. They are often used to explain the behavior of phase evolution and temporal interactions in a variety of applied sciences domains; for a list of references, see [8,9,10,11,12,13,14,15,16,17,18,19].
As far as we know, the concept of controllability is a vital qualitative and quantitative characterization of the control system, whereas the controllability feature is significant in a variety of control problems in both limited and unlimited systems. The controllability of a fractional wave equation has recently gained a lot of attention in this research. Using the Mönch fixed-point approach and measures of noncompactness (MNC), the investigator’s Wang and Zhou [20] recently discovered a few requirements providing the complete controllability of fractional evolution systems (FES) without assuming the adaptability of specific response technicians. Wang et al. [21] identified two essential requirements for nonlocal controllability in a fractional evolution system. For certain weak noncompactness criteria, these theorems ensure that the controllability findings will work as intended. Ji et al. [22] deduced the nonlocal controllability of an impulsive differential evolution system using the Mönch fixed-point theorem via the measures of noncompactness. Numerous writers have made important contributions to the exact and approximate controllability of various nonlinear dynamical systems with or without delays. In [22,23,24], researchers developed a new set of necessary requirements for the exact controllability of differential systems. For a summary of recent studies on the existence and controllability of the differential system with the fractional number , see [12,25].
Stochastic models should be examined instead of deterministic ones since noise and uncontrolled fluctuations are common and inherent in both natural and artificial systems. Unpredictability is reflected in the mathematical depiction of some events in stochastic differential equations. The use of stochastic differential equations (SDEs) to describe various phenomena in population dynamics, physics, electrical engineering, geography, psychology, biochemistry, and some other fields of physics and technology has recently attracted a lot of interest. SDEs can be applied in both finite and infinite dimensions. See, for example, [9,26,27,28] for a thorough introduction to stochastic differential equations and their applications.
Researchers employed almost sectorial operators to advance the fractional existence of fractional calculus. A new method was developed to find a mild solution for the system under investigation. Additionally, researchers developed a theory to analyze different attributes of connected semigroups produced by almost sectorial operators applying semigroups, fractional calculus, MNC, Wright-type functions, multivalued analysis, Laplace transforms, and a fixed-point approach. For further details, see [24,29,30,31,32,33].
Another sort of fractional derivative, including the R-L and Caputo fractional derivatives, was given by Hilfer [34]. Currently, investigators place a high value on Hilfer fractional differential calculus. Recently, many academics have shown considerable interest in this area, which has inspired work in [35,36,37,38,39,40]. The researchers in [41,42,43] employed Schauder’s fixed-point theorem to obtain their results via almost sectorial operators. The author used the Mönch fixed-point principle via the MNC to establish their conclusions in [21,22,44,45]. The Darbo–Sadovskii fixed-point approach via MNC was used by the authors to construct the concepts of differential systems [46,47]. Further, [48] investigated whether there is a mild solution for HF differential systems using almost sectorial operators. Inspired by the above article, we have developed the nonlocal controllability of the Hilfer fractional (HF) stochastic differential equations via almost sectorial operators by using the Darbo–Sadovskii fixed-point theorem via measures of noncompactness. However, to the best of our knowledge and investigation, no research has been conducted on this research problem.
In this article, researchers describe their latest finding on the nonlocal controllability of the HF stochastic differential equations via almost sectorial operators of the form
where A is an almost sectorial operator that represents an analytic semigroup on Z. denotes the Hilfer fractional derivative (HFD) of order and type . Let be the state in a Hilbert space Z with and be the control function in , where U is the Hilbert space. Here, is the bounded linear operator. Set and let be the Z-valued function, and the nonlocal term is given by .
The article’s framework may be divided into the following categories: In Section 2, researchers propose the fundamental characteristics of fractional calculus, semigroups, almost sectorial operators, and measures of non-compactness. The authors describe the system’s nonlocal controllability in Section 3. Finally, in Section 4, the authors give theoretical and practical implementations to make the conversation as successful as possible.
2. Preliminaries
In this chapter, we discuss fundamental definitions, theorems, and lemmas that are utilized throughout the whole work.
The two real Hilbert spaces are represented by the symbols and . Let be a complete probability space associated with a complete family of right continuous growing sub -algebra such that . Let be a Q-Wiener process defined on with the covariance operator Q such that . Then, we claim that a complete orthonormal system , exists in U, a finite sequence of positive real integers such that and of independent Brownian motion such that
Assume that the space of all Q-Hilbert-Schmidt operators with the scalar product is represented by the notation . Consider the resolvent operator of A, , where is uniformly bounded, that is, , and . The fractional power operator on its domain may therefore be derived for . Furthermore, is dense in Z.
The following important properties of will be discussed as follows.
Theorem 1.
- 1.
- Suppose , then is a Banach space with .
- 2.
- Assume that , then , A is compact and the embedding is also compact.
- 3.
- For all , exists such that
The set of all strongly continuous, square-integrable, Z-valued random variables, denoted by , is a Banach space associated with , where E is defined as . A necessary subspace of is given by
Let be the set of all continuous functions from V to Z, where and with . Let the Banach space exist and be finite and its be denoted by . Set . Let be noted. Consequently,
Definition 1
([31]). For , we denote the family of closed linear operators , the sector and that satisfies
- (i)
- ;
- (ii)
- , for all and let be a constant,
then is called an almost sectorial operator on Z.
Proposition 1
([31]). Suppose for and . Then, the following are satisfied:
- (a)
- , for all
- (b)
- , where the constant ;
- (c)
- The range of , is contained in . Particularly, for all withand hence there exists a constant such that
- (d)
- Suppose that , then
- (e)
- , and .
Definition 2
([6]). For the function with lower limit c, the R-L fractional integral of order γ is provided by
Definition 3
([6]). The R-L derivative of order , of the function is presented by
Definition 4
([6]). The Caputo derivative of order for a function is denoted by
Definition 5
([34]). The HFD of order and type for the function is presented by
Definition 6
([48]). Define the Wright function by
such that
Theorem 2
([6]). In the uniform operator topology, and are continuous, for , for every , and the continuity is uniform on .
Lemma 1
([48]). If is a compact operator, then and are also compact linear operators.
Lemma 2
([48]). Assume that is a compact operator. Then, is equicontinuous.
Lemma 3
Lemma 4
([36]). Let be a solution of the integral equation given by Lemma 3 then satisfies
where
Definition 7.
An -adapted stochastic process is called a mild solution of the Cauchy system (1) and (2), given , and exists such that on and satisfies
Lemma 5
([48]).
- 1.
- are strongly continuous, for .
- 2.
- If are bounded linear operators on Z, for any fixed , then we obtainwhere, .
Definition 8
([21]). Suppose is the positive cone of an order Banach space . Let Φ be the function defined on the set of all bounded subsets of the Banach space Z with values in known as on Z if and only if for very bounded subset , where denoted the closed convex hull of Ω.
Definition 9.
We will now review a few concepts related to the Hausdorff MNC.
Definition 10
([22]). For a bounded set in a Banach space Z, the Hausdorff χ is denoted as
Lemma 6
([22]). Suppose Z is a Banach space and are bounded. Then, the following properties satisfy:
- (i)
- is precompact if and only if ;
- (ii)
- where and denotes the closure and convex hull of , respectively;
- (iii)
- If then ;
- (iv)
- such that ;
- (v)
- ;
- (vi)
- , when Z be a real Banach space;
- (vii)
- If the operator is Lipschitz-continuous with constant , then we know for all bounded subset , where is a Banach space and t represents the Hausdorff in .
Definition 11
([22]). The operator is said to be an if a positive constant exists such that for all bounded closed subsets .
Theorem 3
([21]). If is a sequence of Bochner integrable functions from V to Z with the measurement , for every and for any , where , then the function is in and satisfies
Lemma 7
([21]). Let be a bounded set; then, a countable set exists such that .
We mean by the Hausdorff MNC in the space ∁.
Lemma 8
([21]). Let be bounded and equicontinuous; then,
- 1.
- is continuous on ,
- 2.
- .
Lemma 9
([6]). (The Darbo–Sadovskii theorem) Let be a bounded, convex, and closed set. is a continuous and operator. Then, Ψ has at least one fixed point in .
3. Controllability
We require the following hypotheses:
- (H1)
- Let A be the almost sectorial operator of the analytic semigroup in Z such that where is a constant.
- (H2)
- The function satisfies:
- (a)
- The Caratheodory condition: is strongly measurable for all , and is continuous for a.e. ;
- (b)
- There is a constant and and non-decreasing continuous function such that , where g satisfies ;
- (c)
- There is a constant and such that, for all bounded subsets for a.e. .
- (H3)
- (a)
- The linear operator is bounded, denoted by , and it has an inverse operator , which take the values in , and there are two positive values and such that
- (b)
- There is a constant and such that, for all bounded sets .
- (H4)
- The function is a continuous, compact operator, and there exists such that .
For our convenience, we introduce
.
Theorem 4.
Suppose that the hypotheses – hold; then, the HF stochastic differential system (1) and (2) has a solution on V provided with .
Proof.
The operator is defined as
To prove that has a fixed point.
From hypotheses (), for an arbitrary function , we describe the control by
As we can see, , which means that steer the Hilfer fractional stochastic differential system (1) and (2) to in the finite time c. This suggests that the system (1) and (2) can be nonlocally controllable on V.
Step 1: We have to show that a positive value P exists such that . Assume that the statement is false, i.e., for all , exists, but is not in ,
Hence,
where
The above inequality is divided by , and by applying the limit as , we obtain , which is the contradiction. Therefore, .
Step 2: Prove that is continuous. Let such that in . Then, we have
From the hypotheses and , and the Lebesgue dominated convergence theorem [49], we write
where
From the above equations, we obtain . So, is continuous on .
Step 3: To demonstrate that is equicontinuous, let , and ; then, exists such that
Thus, we write
By the strong continuity of , we obtain
tends to zero as .
From the Lebesgue’s dominated convergence theorem [49], we obtain .
By Theorem 2, is uniformly continuous in the operator norm topology. So, we obtain as .
Then, as , by using the dominated convergence theorem. Next,
Similar to the proof of and , we obtain that and tend to zero as , and tends to zero as . Therefore, is equicontinuous on V.
Step 4: To show is a -contraction operator.
Let ; then, from Lemma 7, there exists a countable set such that . By the equicontinuous of , we know that D is also equicontinuous. Therefore, from Lemma 7, we obtain
Hence, we have
Since N is compact and is relatively compact, we obtain
That is,
where .
Therefore, from Definition (11), is a -contraction operator. As a result, has at least one fixed point according to Lemma 7, and the mild solution also exists. □
4. Example
4.1. Example-I
Assume that the following HF stochastic differential equation is in the form:
where , and are the of order , type , is the Riemann–Liouville integral, and the function is continuous in t and . Let be a one-dimensional standard Brownian motions in Z denoted by on the filtered probability space . Let ; then, the operator is determined by , where and
where is the orthogonal set of eigenvectors of A. Here, A is the almost sectorial operator of the semigroup in Z and given by is not a compact semigroup on Z with where is the Hausdorff MNC and exists such that . Furthermore, is equicontinuous for and .
Let
It is clear that G is Lipschitz-continuous for the second variable with constant and satisfies . Let the function be defined by and the nonlocal term be defined as
Then, is a bounded linear operator and N is the compact operator satisfied . For , the operator W is defined as
For ,
where the Wright-type function, . Suppose that W satisfies ; then, all of the statements of Theorem 4 are accomplished. Therefore, the HF stochastic differential Equations (1) and (2) are nonlocal controllable on V.
4.2. Example-II
Digital filters perform an incredibly considerable aspect in the field of digital signal processing (DSP). The execution of digital filters is extraordinary, and each of the essential factors of DSP has grown in acclaim. Commonly, we classify filters with two main usages: one is signal separation, and the other is signal restoration. Digital filters are an important entity in various fields of signal processing and have unexceptionally received high-level prominence in the field of biomedical signal processing too. As most biomedical signals are low-frequency by nature, the general problem in processing those signals is the small amplitude of the signal, which is naturally dominated by artefacts and various other noises. The efficiency of the system lies in retrieving those signals in a substantial amount of time so as not to generate a high level of delay in processing and analyzing those signals. In general, biomedical systems consist of complex cascaded blocks such that the delay in producing the output of each block cumulatively affects the generation of the final output. The speed, as well as the accuracy, of processing is highly essential in modelling any biomedical system to retrieve such error-free processed signals.
Further, the biological signals are the ones with minimal amplitudes and lower frequencies (a few brain signals range from 1–4 Hz). The entire requirement of error-free signal generation shall be attributed to the proper controllability of the modelled system obtained through the solution. The signal processing unit is implemented through a block diagram as depicted in Figure 1 using MATLAB-Simulink software with the aid of the proposed system of Equations (1) and (2) that shall be suitable for a few biomedical applications. The magnitude response of the digital filter implemented using a fractional differentiation model, as shown in Figure 2, exhibits a sharp cut-off frequency with better signal-restoration capability [50,51]. Therefore, the output is obtained, which is bounded and controllable with better stability in the amplitude in the low-frequency corner.
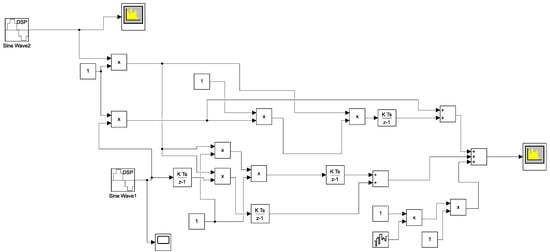
Figure 1.
Digital filter model.
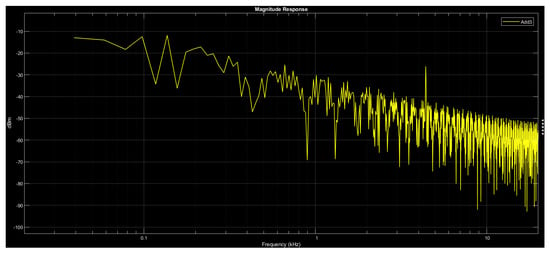
Figure 2.
Magnitude response.
Motivated by the filter systems defined in [52,53,54], we present our filter system in Figure 1 and Figure 2. Figure 1 describes the rough pattern of the digital filter model, and Figure 2 describes the frequency response of the digital filter, which aids in enhancing the usefulness of the solution with a minimum measure of inputs.
- 1.
- Product modulator 1 receives the input , and G produces .
- 2.
- Product modulator 2 receives the input , and B produces .
- 3.
- Product modulator 3, receives the input , and at time produces .
- 4.
- The integrator performs the integral ofover the period s.
Furthermore,
- (i)
- Inputs are combined and multiplied with an output of the integrator over .
- (ii)
- Inputs are combined and multiplied with an output of the integrator over .
Finally, we move all of the outputs from the integrators to the summer network. Therefore, the output of is attained; it is bounded and controllable.
5. Conclusions
This manuscript concentrated on the almost sectorial operator-based nonlocal controllability of HF stochastic differential equations. By applying findings and concepts from fractional calculus, almost sectorial operators, MNC, and the fixed-point method, the primary outcomes are obtained. Researchers established the necessary criteria for the mild solution’s existence and the system’s nonlocal controllability. Finally, we offer a tool for putting theoretical findings into practice. Future research will focus on almost sectorial operators’ approximate controllability of HF stochastic differential systems with infinite and finite delay.
These are the contributions we made: (1) The authors present a number of requirements for the nonlocal controllability of HF stochastic differential equations via almost sectorial operators. (2) As far as we are aware, there has not been an investigation into the existence and nonlocal controllability of the HF stochastic differential system using almost sectorial operators. (3) To wrap up, we offer an example of the results.
Author Contributions
Conceptualization, S.S. and S.E.A.; methodology, R.U.; formal analysis, R.U.; investigation, S.A.-O. and M.H.K.; resources, S.E.A.; writing—original draft preparation, S.S. and S.A.-O.; writing—review and editing, S.S., R.U., and M.H.K.; supervision, R.U. and S.E.A.; project administration, R.U., S.E.A., and S.A.-O.; and funding acquisition, S.E.A. All authors have read and agreed to the published version of the manuscript.
Funding
The authors would like to thank the Deanship of Scientific Research at Umm Al-Qura University for supporting this work by Grant Code: (22UQU4282396DSR18).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare that they have no competing interests.
References
- Ahmad, B.; Alsaedi, A.; Ntouyas, S.K.; Tariboon, J. Hadamard-Type Fractional Differential Equations, Inclusions and Inequalities; Springer International Publishing AG: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Diethelm, K. The Analysis of Fractional Differential Equations: An Application-Oriented Exposition Using Differential Operators of Caputo Type; Lecture Notes in Mathematics; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Lakshmikantham, V.; Vatsala, A.S. Basic theory of fractional differential equations. Nonlinear Anal. Theory Methods Appl. 2008, 69, 2677–2682. [Google Scholar] [CrossRef]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Differential Equations; John Wiley: New York, NY, USA, 1993. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Zhou, Y. Basic Theory of Fractional Differential Equations; World Scientific: Singapore, 2014. [Google Scholar]
- Zhou, Y. Fractional Evolution Equations and Inclusions: Analysis and Control; Elsevier: New York, NY, USA, 2015. [Google Scholar]
- Agarwal, R.P.; Lakshmikanthan, V.; Nieto, J.J. On the concept of solution for fractional differential equations with uncertainty. Nonlinear Anal. Theory Methods Appl. 2010, 72, 2859–2862. [Google Scholar] [CrossRef]
- Dineshkumar, C.; Udhayakumar, R.; Vijayakumar, V.; Nisar, K.S. Results on approximate controllability of neutral integro-differential stochastic system with state-dependent delay. Numer. Methods Partial Differ. Equ. 2020. [Google Scholar] [CrossRef]
- Khaminsou, B.; Thaiprayoon, C.; Sudsutad, W.; Jose, S.A. Qualitative analysis of a proportional Caputo fractional Pantograph differential equation with mixed nonlocal conditions. Nonlinear Funct. Anal. Appl. 2021, 26, 197–223. [Google Scholar]
- Sivasankar, S.; Udhayakumar, R. New Outcomes Regarding the Existence of Hilfer Fractional Stochastic Differential Systems via Almost Sectorial Operators. Fractal Fract. 2022, 6, 522. [Google Scholar] [CrossRef]
- Williams, W.K.; Vijayakumar, V.; Udhayakumar, R.; Nisar, K.S. A new study on existence and uniqueness of nonlocal fractional delay differential systems of order 1 < r < 2 in Banach spaces. Numer. Methods Partial Differ. Equ. 2020, 37, 949–961. [Google Scholar]
- Serrano, E.Z.; Munoz-Pacheco, J.M.; Serrano, F.E.; Sánchez-Gaspariano, L.A.; Volos, C. Experimental verification of the multi-scroll chaotic attractors synchronization in PWL arbitrary-order systems using direct coupling and passivity-based control. Integr. VLSI J. 2021, 81, 56–70. [Google Scholar] [CrossRef]
- Ding, Y.; Liu, X.; Chen, P.; Luo, X.; Luo, Y. Fractional-Order Impedance Control for Robot Manipulator. Fractal Fract. 2022, 6, 684. [Google Scholar] [CrossRef]
- Abdelhadi, M.; Alhazmi, S.; Al-Omari, S. On a Class of Partial Differential Equations and Their Solution via Local Fractional Integrals and Derivatives. Fractal Fract. 2022, 6, 210. [Google Scholar] [CrossRef]
- Hasan, S.; Harrouche, N.; Al-Omari, S.K.Q.; Al-Smadi, M.; Momani, S.; Cattani, C. Hilbert solution of fuzzy fractional boundary value problems. Appl. Math. Comput. 2022, 41, 1–22. [Google Scholar]
- Edwan, R.; Al-Omari, S.; Al-Smadi, M.; Momani, S.; Fulga, A. A new formulation of finite-difference and finite volume methods for solving a space-fractional convection-diffusion model with less error estimates. Adv. Differ. Equ. 2021, 2021, 1–19. [Google Scholar] [CrossRef]
- Momani, S.; Djeddi, N.; Al-Smadi, M.; Al-Omari, S. Numerical investigation for Caputo-Fabrizio fractional Riccati and Bernoulli equations using iterative reproducing kernel method. Appl. Numer. Math. 2021, 170, 418–434. [Google Scholar] [CrossRef]
- Al-Smadi, M.; Djeddi, N.; Momani, S.; Al-Omari, S.; Araci, S. An attractive numerical algorithm for solving nonlinear Caputo-Fabrizio fractional Abel differential equation in a Hilbert space. Adv. Differ. Equ. 2021, 271, 1–19. [Google Scholar] [CrossRef]
- Wang, J.R.; Zhou, Y. Complete controllability of fractional evolution systems. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 4346–4355. [Google Scholar] [CrossRef]
- Wang, J.R.; Fin, Z.; Zhou, Y. Nonlocal controllability of semilinear dynamic systems with fractional derivative in Banach spaces. J. Optim. Theory Appl. 2012, 154, 292–302. [Google Scholar] [CrossRef]
- Ji, S.; Li, G.; Wang, M. Controllability of impulsive differential systems with nonlocal conditions. Appl. Math. Comput. 2011, 217, 6981–6989. [Google Scholar] [CrossRef]
- Balachandran, K.; Sakthivel, R. Controllability of integro-differential systems in Banach spaces. Appl. Math. Comput. 2001, 118, 63–71. [Google Scholar]
- Wang, R.N.; Chen, D.H.; Xiao, T.J. Abstract fractional Cauchy problems with almost sectorial operators. J. Differ. Equ. 2012, 252, 202–235. [Google Scholar] [CrossRef]
- Mohan Raja, M.; Vijayakumar, V.; Udhayakumar, R. Results on existence and controllability of fractional integro-differential system of order 1 < r < 2 via measure of noncompactness. Chaos Solitons Fractals. 2020, 139, 110299. [Google Scholar]
- Evans, L.C. An Introduction to Stochastic Differential Equations; University of California: Berkeley, CA, USA, 2013. [Google Scholar]
- Mao, X. Stochastic Differential Equations and Applications; Horwood: Chichester, UK, 1997. [Google Scholar]
- Sivasankar, S.; Udhayakumar, R. A note on approximate controllability of second-order neutral stochastic delay integro-differential evolution inclusions with impulses. Math. Methods Appl. Sci. 2022, 45, 6650–6676. [Google Scholar] [CrossRef]
- Li, F. Mild solutions for abstract differential equations with almost sectorial operators and infinite delay. Adv. Differ. Equ. 2013, 327, 1–11. [Google Scholar] [CrossRef][Green Version]
- Pazy, A. Semigroups of Linear Operators and Applications to Partial Differential Equations. Applied Mathematical Sciences; Springer: New York, NY, USA, 1983. [Google Scholar]
- Periago, f.; Straub, B. A functional calculus for almost sectorial operators and applications to abstract evolution equations. J. Evol. Equ. 2002, 2, 41–68. [Google Scholar] [CrossRef]
- Sivasankar, S.; Udhayakumar, R. Hilfer Fractional Neutral Stochastic Volterra Integro-Differential Inclusions via Almost Sectorial Operators. Mathematics 2022, 10, 2074. [Google Scholar] [CrossRef]
- Zhang, L.; Zhou, Y. Fractional Cauchy problems with almost sectorial operators. Appl. Math. Comput. 2014, 257, 145–157. [Google Scholar] [CrossRef]
- Hilfer, R. Application of Fractional Calculus in Physics; World Scientific: Singapore, 2000. [Google Scholar]
- Dineshkumar, C.; Udhayakumar, R. New results concerning to approximate controllability of Hilfer fractional neutral stochastic delay integro-differential system. Numer. Methods Partial Differ. Equ. 2020, 37, 1072–1090. [Google Scholar] [CrossRef]
- Gu, H.; Trujillo, J.J. Existence of integral solution for evolution equation with Hilfer fractional derivative. Appl. Math. Comput. 2015, 257, 344–354. [Google Scholar]
- Varun Bose, C.S.; Udhayakumar, R. Existence of Mild Solutions for Hilfer Fractional Neutral Integro-Differential Inclusions via Almost Sectorial Operators. Fractal Fract. 2022, 6, 532. [Google Scholar] [CrossRef]
- Kavitha, K.; Vijayakumar, V.; Udhayakumar, R. Results on controllability of Hilfer fractional neutral differential equations with infinite delay via measure of noncompactness. Chaos Solitons Fractals. 2020, 139, 110035. [Google Scholar] [CrossRef]
- Varun Bose, C.S.; Udhayakumar, R. A note on the existence of Hilfer fractional differential inclusions with almost sectorial operators. Math. Methods Appl. Sci. 2022, 45, 2530–2541. [Google Scholar] [CrossRef]
- Yang, M.; Wang, Q. Existence of mild solutions for a class of Hilfer fractional evolution equations with nonlocal conditions. Fract. Calc. Appl. Anal. 2017, 20, 679–705. [Google Scholar] [CrossRef]
- Bedi, P.; Kumar, A.; Abdeljawad, T.; Khan, Z.A.; Khan, A. Existence and approximate controllability of Hilfer fractional evolution equations with almost sectorial operators. Adv. Differ. Equ. 2020, 615, 1–15. [Google Scholar] [CrossRef]
- Jaiswal, A. Bahuguna, D. Hilfer fractional differantial equations with almost sectorial operators. Differ. Equ. Dyn. Syst. 2020. [Google Scholar] [CrossRef]
- Karthikeyan, K.; Debbouche, A.; Torres, D.F.M. Analysis of Hilfer fractional integro-differential equations with almost sectorial operators. Fractal Fract. 2021, 5, 22. [Google Scholar] [CrossRef]
- Singh, V. Controllability of Hilfer fractional differential systems with non-dense domain. Numer. Funct. Anal. Optim. 2019, 40, 1572–1592. [Google Scholar] [CrossRef]
- Sivasankar, S.; Udhayakumar, R.; Subramanian, V.; AlNemer, G.; Elshenhab, A.M. Existence of Hilfer Fractional Stochastic Differential Equations with Nonlocal Conditions and Delay via Almost Sectorial Operators. Mathematics 2022, 10, 4392. [Google Scholar] [CrossRef]
- Atraoui, M.; Bouaouid, M. On the existence of mild solutions for nonlocal differential equations of the second order with conformable fractional derivative. Adv. Differ. Equ. 2021, 447, 1–11. [Google Scholar] [CrossRef]
- Bouaouid, M.; Hannabou, M.; Hilal, K. Nonlocal conformable fractional differential equations with a measure of noncompactness in Banach spaces. J. Math. 2020, 2020, 5615080. [Google Scholar] [CrossRef]
- Zhou, M.; Li, C.; Zhou, Y. Existence of mild solutions for Hilfer fractional differential evolution equations with almost sectorial operators. Axioms 2022, 11, 144. [Google Scholar] [CrossRef]
- Don, H.; Jainzhong, W.; Robert, G. The Lebesgue Integral; Real Analysis with an Introduction to Wavelets and Application; Academic Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Broner, N. The effects of low frequency noise on people-A review. J. Sound Vib. 1978, 58, 483–500. [Google Scholar] [CrossRef]
- Agnew, D.C.; Hodgkinson, K. Designing Compact Causal Digital Filters for Low-Frequency Strainmeter Data. Bull. Seismol. Soc. Am. 2007, 97, 91–99. [Google Scholar] [CrossRef]
- Chandra, A.; Chattopadhyay, S. Design of hardware efficient FIR filter: A review of the state of the art approaches. Eng. Sci. Technol. Int. J. 2016, 19, 212–226. [Google Scholar] [CrossRef]
- Vijayakumar, V.; Udhayakumar, R. Results on approximate controllability for non-densely defined Hilfer fractional differential system with infinite delay. Chaos Solitons Fractals. 2020, 139, 110019. [Google Scholar] [CrossRef]
- Zahoor, S.; Naseem, S. Design and implementation of an efficient FIR digital filter. Cogent. Eng. 2017, 4, 1323373. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).