On Join-Dense Subsets of Certain Families of Aggregation Functions

Abstract

Several important classes of aggregation functions defined on a bounded lattice form a lattice with respect to the pointwise operations of join and meet, respectively. The lattice structure of such classes is usually very complex; thus, it is very useful to characterize them by some appropriate sets of functions. In this paper, we focus on the three important classes of aggregation functions, namely the lattice of all aggregation functions, the lattice of idempotent aggregation functions, and the lattice of Sugeno integrals (defined on distributive lattices) and characterize their lattices by means of join-dense subsets. Moreover, the minimality of these sets is discussed.

1. Introduction

Aggregation is a process when several (usually numerical) data are merged into a single output. The process of aggregation is mathematically described by functions called aggregation functions, satisfying certain widely accepted natural conditions, see [1]. In experimental sciences, probably the most often used examples of aggregation functions are means (especially the arithmetic mean). Nowadays, aggregation functions appear in many other branches of science such as pure mathematics (functional equations, theory of means and averages, measure and integration theory), applied mathematics (probability, statistics, decision mathematics), computer and engineering sciences (artificial intelligence, operation research, data fusion, automatic reasoning, etc.). Surprisingly, their applications are also in social sciences, economy, life sciences, etc.

The prominent role in aggregation theory is played by Sugeno integrals. Recall that Sugeno introduced his integral (originally called F-integral) in [2] by means of fuzzy connectives min and max, generalizing the classical Lebesgue integral in the framework of expected values of fuzzy sets. Since min and max are in fact lattice connectives on linear scales, this integral was later on extended by Marichal [3] on bounded distributive lattices. In this case, the Sugeno integral is an idempotent weighted lattice polynomial function. Nowadays, Sugeno integrals have numerous applications in several different branches of science, especially in multicriteria decision support dealing with ordinal scales, fuzzy set theory, decision making, data fusion, pattern recognition, etc.

It is an important fact that several classes of aggregation functions on a bounded lattice L form a lattice with respect to the pointwise operations of join and meet. In particular, the set ${\mathsf{Agg}}^n\left(L\right)$ of all aggregation functions on L, the set ${\mathsf{Id}}^n\left(L\right)$ of idempotent aggregation functions on L, and the set ${\mathsf{Sug}}^n\left(L\right)$ of Sugeno integrals on L are of this kind.

To justify the role of join-dense subsets in (complete) lattices, these form their building blocks. To be more specific, we can mention, e.g., the so-called formal concept analysis (FCA) [4], an area of research which is based on a set-theoretical model for concepts and conceptual hierarchies. This relatively new approach to data analysis allows the formal representation of conceptual knowledge. The main theorem of FCA states (among others) that all the concepts are completely determined by their object concepts, which form a join-dense subset in a corresponding concept lattice.

The purpose of this paper is to give a better insight into the structure of the above-mentioned lattices of aggregation functions. Namely, we aim to characterize join-dense subsets in these lattices.

The paper is divided into two parts. After an introduction, we recall basic facts and definitions which are necessary for the paper. In the second part, we describe join-dense subsets of the lattices of all aggregation functions, idempotent aggregation functions, and Sugeno integrals as well. Moreover, minimality of these join-dense subsets is discussed.

2. Preliminaries

In this section, basic notions concerning aggregation functions defined on bounded lattices are recalled. We assume that the reader is familiar with the basic notions of lattice theory; for this, we refer to the standard monograph [5].

Let L be a bounded lattice with 0 and 1 representing its bottom and top element, respectively. A mapping $f:L^n\to L$, $n\in \mathbb{N}$ a positive integer, is called an n-ary aggregation function on L (see [1]), if it is monotone and it fulfils two boundary conditions, i.e., for any $\mathbf{x}=(x_1,\dots ,x_n),\mathbf{y}=(y_1,\dots ,y_n)\in L^n$

$$f\left(\mathbf{x}\right)\le f\left(\mathbf{y}\right), \mathrm{if} x_i\le y_i \mathrm{for} \mathrm{all} i=1,\dots ,n$$

and

$$f(0,\dots ,0)=0\mathrm{and}f(1,\dots ,1)=1.$$

The system of all n-ary aggregation functions defined on a bounded lattice L is denoted by ${\mathsf{Agg}}^n\left(L\right)$. This system is closed under pointwise operations of join and meet, respectively, i.e., given $f,g\in {\mathsf{Agg}}^n\left(L\right)$, the functions $f\vee g$ and $f\wedge g$ defined for all $\mathbf{x}\in L^n$ by

$$(f\vee g)\left(\mathbf{x}\right)=f\left(\mathbf{x}\right)\vee g\left(\mathbf{x}\right)\mathrm{and}(f\wedge g)\left(\mathbf{x}\right)=f\left(\mathbf{x}\right)\wedge g\left(\mathbf{x}\right)$$

are aggregation functions. Hence, ${\mathsf{Agg}}^n\left(L\right)$ forms a lattice.

An n-ary aggregation function f on a bounded lattice L is said to be idempotent if it satisfies $f(x,\dots ,x)=x$ for all $x\in L$. The family of all n-ary idempotent aggregation functions defined on L is denoted by ${\mathsf{Id}}^n\left(L\right)$. As join and meet of two idempotent aggregation functions belong to ${\mathsf{Id}}^n\left(L\right)$, it follows that this family forms a lattice, particularly a sublattice of ${\mathsf{Agg}}^n\left(L\right)$.

For a positive integer, $n\ge 1$, the symbol $\left[n\right]$ denotes the set of all positive integers less than or equal to n, i.e., $\left[n\right]=\{1,\dots ,n\}$. An L-valued capacity (see [3]), also known as an L-valued fuzzy measure, is a monotone set function $\mu :\mathrm{P}\left(\right[n\left]\right)\to L$ from the power set of $\left[n\right]$ to L such that $\mu (\varnothing )=0$ and $\mu \left(\right[n\left]\right)=1$. The family of all L-valued capacities defined on the power set $\mathrm{P}\left(\right[n\left]\right)$ is denoted by ${\mathsf{Cap}}^n\left(L\right)$. Obviously, it forms a lattice.

Let L be a bounded distributive lattice and $\mu :\mathrm{P}\left(\right[n\left]\right)\to L$ be an L-valued capacity. The Sugeno integral of an n-tuple $\mathbf{x}=(x_1,\dots ,x_n)\in L^n$ with respect to $\mu$ is defined by the following two equivalent formulas (see [3,6])

$${\mathsf{S}}_{\mu }\left(\mathbf{x}\right)=\underset{X\subseteq \left[n\right]}{\bigvee }(\mu \left(X\right)\wedge \underset{i\in X}{\bigwedge }{x}_i)$$

(1)

and

$${\mathsf{S}}_{\mu }\left(\mathbf{x}\right)=\underset{X\subseteq \left[n\right]}{\bigwedge }(\mu (\left[n\right]\setminus X)\vee \underset{i\in X}{\bigvee }{x}_i),$$

(2)

which are commonly known as the disjunctive and the conjunctive normal representation of the Sugeno integral, respectively. The family of all n-ary Sugeno integrals defined on a bounded distributive lattice L is denoted by ${\mathsf{Sug}}^n\left(L\right)$.

It can be easily verified that the Sugeno integral is an idempotent aggregation function, and it extends an L-capacity $\mu$ in the sense that ${\mathsf{S}}_{\mu }\left({\mathbf{e}}_S\right)=\mu \left(S\right)$ for all $S\subseteq \left[n\right]$, where ${\mathbf{e}}_S\in L^n$ represents the characteristic function of the subset S such that ${\left({\mathbf{e}}_S\right)}_i=1$ provided $i\in S$ and ${\left({\mathbf{e}}_S\right)}_i=0$ otherwise. It can be shown that this extension is unique in the class of lattice polynomial functions of L, see [3,6,7,8]. Recall that the lattice polynomial functions of a lattice L are functions corresponding to formal expressions involving a finite number of variables, lattice operations, and constants.

Using (1) and the distributivity of L, for L-capacities ${\mu }_1,{\mu }_2:\mathrm{P}\left(\left[n\right]\right)\to L$ and for all $\mathbf{x}\in L^n$ we obtain

$$\begin{array}{ll}{\mathsf{S}}_{{\mu }_1\vee {\mu }_2}\left(\mathbf{x}\right)=& \underset{X\subseteq \left[n\right]}{\bigvee }(({\mu }_1\left(X\right)\vee {\mu }_2\left(X\right))\wedge \underset{i\in X}{\bigwedge }{x}_i)=\underset{X\subseteq \left[n\right]}{\bigvee }(({\mu }_1\left(X\right)\wedge \underset{i\in X}{\bigwedge }{x}_i)\vee ({\mu }_2\left(X\right)\wedge \underset{i\in X}{\bigwedge }{x}_i))=\\ & \underset{X\subseteq \left[n\right]}{\bigvee }({\mu }_1\left(X\right)\wedge \underset{i\in X}{\bigwedge }{x}_i)\vee \underset{X\subseteq \left[n\right]}{\bigvee }({\mu }_2\left(X\right)\wedge \underset{i\in X}{\bigwedge }{x}_i)={\mathsf{S}}_{{\mu }_1}\left(\mathbf{x}\right)\vee {\mathsf{S}}_{{\mu }_2}\left(\mathbf{x}\right).\end{array}$$

Similarly, from (2), the formula ${\mathsf{S}}_{{\mu }_1\wedge {\mu }_2}\left(\mathbf{x}\right)={\mathsf{S}}_{{\mu }_1}\left(\mathbf{x}\right)\wedge {\mathsf{S}}_{{\mu }_2}\left(\mathbf{x}\right)$ follows; hence, ${\mathsf{Sug}}^n\left(L\right)$ forms a sublattice of ${\mathsf{Id}}^n\left(L\right)$ and the correspondence $\mu \mapsto {\mathsf{S}}_{\mu }$ is a bijective lattice homomorphism (isomorphism) between ${\mathsf{Cap}}^n\left(L\right)$ and ${\mathsf{Sug}}^n\left(L\right)$. Summarising the mentioned facts, we obtain the following proposition.

Proposition 1. 

Let L be a bounded distributive lattice. For all positive integers $n\in \mathbb{N}$, the lattices ${\mathsf{Cap}}^n\left(L\right)$ and ${\mathsf{Sug}}^n\left(L\right)$ are isomorphic.

Hence, with respect to this assertion, the lattice ${\mathsf{Cap}}^n\left(L\right)$ instead of ${\mathsf{Sug}}^n\left(L\right)$ is investigated.

3. Join-Dense Subsets

In this section, we describe join-dense subsets of the lattices of all aggregation functions, idempotent aggregation functions, and Sugeno integrals as well. The first part is devoted to sufficient conditions guaranteeing the existence of join-dense subsets in general systems of functions. We start with the definition of a join-dense subset and the related notions. A subset D of a bounded lattice L is join-dense if $0\in D$ and for every $x\in L$

$$x=\bigvee \{b\in D:b\le x\}.$$

A join-dense subset D of L is minimal (with respect to the inclusion relation), provided no $D^{\prime }⊊D$ is a join-dense subset of L.

Remark 1. 

If L contains the bottom element 0, then by the definition of the least upper bound, we have $0=\bigvee \varnothing$. Therefore, the requirement $0\in D$ in our definition of a join-dense subset is only formal since we are only interested in expressions involving nonempty joins of aggregation functions in this paper.

An element q of a lattice L is said to be completely join-irreducible if $q=\bigvee X$ implies $q\in X$ for all (possibly infinite) subsets $X\subseteq L$. If q is a completely join-irreducible element, then q has the unique lower cover, which is equal to the join of all elements lying below q. Let ${\mathrm{J}}^{*}\left(L\right)$ denote the set of completely join-irreducible elements of L. Note that if L contains the bottom element, then formally, $0\notin {\mathrm{J}}^{*}\left(L\right)$ since $0=\bigvee \varnothing$.

Theorem 1. 

Let L be a bounded lattice. There exists a minimal join-dense subset of L if and only if every element of L is a join of completely join-irreducible elements. In this case, the minimal join-dense subset is unique and it is equal to ${\mathrm{J}}^{*}\left(L\right)\cup \left\{0\right\}$.

Proof. 

Let D be a join-dense subset of L. Obviously, ${\mathrm{J}}^{*}\left(L\right)\subseteq D$. Further, assume that $c\in D$ for some $c\notin {\mathrm{J}}^{*}\left(L\right)$. Then, $c=\bigvee S$ for some nonempty subset $S\subseteq L$ such that $c\notin S$. As D is join-dense and $a<c$ for all $a\in S$, we obtain that $a=\bigvee S_a$ for some $S_a\subseteq D\setminus \left\{c\right\}$. In this case,

$$c=\underset{a\in S}{\bigvee }\bigvee S_a=\bigvee (\bigcup _{a\in S}{S}_a)$$

holds, where ${\bigcup }_{a\in S}{S}_a\subseteq D\setminus \left\{c\right\}$. However, this shows that $D\setminus \left\{c\right\}$ is join-dense as well.

Now, assume that every element of L is a join of completely join-irreducible elements. Then, $D={\mathrm{J}}^{*}\left(L\right)\cup \left\{0\right\}$ is minimal join-dense, since no $q\in {\mathrm{J}}^{*}\left(L\right)\cup \left\{0\right\}$ can be omitted from D.

Conversely, if not every element of L is a join of completely join-irreducible elements, then every join-dense subset of L contains some element $c\notin {\mathrm{J}}^{*}\left(L\right)\cup \left\{0\right\}$. However, then D is not minimal, since according to the previous claim, $D\setminus \left\{c\right\}$ is also join-dense. Hence, there is no minimal join-dense subset of L. □

Note that there are examples of lattices fulfilling the assumptions of the previous theorem, e.g., if a lattice fulfils the DCC (descending chain condition), then every element is a join of join-irreducible elements. Other typical example satisfying Theorem 1 is the power set $\mathrm{P}\left(X\right)$. In this case, the completely join-irreducible elements are precisely singletons $\left\{x\right\}$, $x\in X$, and it is obvious that each nonempty subset $A\subseteq X$ is the union of singletons $\left\{a\right\}$, $a\in A$. On the other hand, the real unit interval $[0,1]$ represents an example of a complete lattice without completely join-irreducible elements. Consequently, there in no minimal join-dense subset of this lattice.

Now, we turn our attention to the systems of functions forming a lattice.

Let X be a nonempty set, L a lattice, and $f_t:X\to L$, $t\in T$ be a system of functions indexed by some set $T\ne \varnothing$. Then, since the join operation is computed pointwise, for a function $g:X\to L$, it holds that

$$g=\underset{t\in T}{\bigvee }{f}_t$$

if and only if:

(1)

$f_t\le g$ for all $t\in T$;

(2)

For all $x\in X$, there is $T_x\subseteq T$ such that ${\bigvee }_{t\in T_x}{f}_t\left(x\right)=g\left(x\right)$.

Particularly, this means that the function g can be expressed as a join of some system of functions if and only if each function of this system is below g, and in every coordinate $x\in X$, the value $g\left(x\right)$ is a join of values of a certain subsystem of the considered system of functions.

Let $\mathcal{F}\subseteq L^X$ be a family of functions from X to a lattice L. For $y\in X$ and $b\in L$, denote by $S_{y,b}^{\mathcal{F}}$ the set of all functions from $\mathcal{F}$ attaining the value b at y, i.e., $S_{y,b}^{\mathcal{F}}=\{f\in \mathcal{F}:f\left(y\right)=b\}$. Further, let $D\subseteq L$ be a subset of a lattice L. We set $I_{\mathcal{F}}^D=\{(y,b)\in X\times D:S_{y,b}^{\mathcal{F}}\ne \varnothing \}$, i.e., $I_{\mathcal{F}}^D\subseteq X\times D$ denotes the set of pair of indexes $(y,b)$ for which $S_{y,b}^{\mathcal{F}}$ is nonempty. If $D=L$ we simply write $I_{\mathcal{F}}$.

Theorem 2. 

Let $\mathcal{F}$ be a family of functions closed under the join operation, such that the set $S_{y,b}^{\mathcal{F}}$ contains the smallest element $h_{y,b}$ for all $(y,b)\in I_{\mathcal{F}}$. Then, the set $\{h_{y,b}:(y,b)\in I_{\mathcal{F}}\}$ is join-dense in $\mathcal{F}$.

Proof. 

Let $f:X\to L$ be a function from the family $\mathcal{F}$. Then, $S_{y,f\left(y\right)}^{\mathcal{F}}\ne \varnothing$ for all $y\in X$. As $h_{y,f\left(y\right)}$ is the smallest function of the set $S_{y,f\left(y\right)}^{\mathcal{F}}$, it follows that $h_{y,f\left(y\right)}\left(x\right)\le f\left(x\right)$ for all $x\in X$ while $h_{y,f\left(y\right)}\left(y\right)=f\left(y\right)$. Consequently, for all $x\in X$, we obtain

$$\underset{y\in X}{\bigvee }{h}_{y,f\left(y\right)}\left(x\right)\le f\left(x\right)=h_{x,f\left(x\right)}\left(x\right)\le \underset{y\in X}{\bigvee }{h}_{y,f\left(y\right)}\left(x\right).$$

Hence, ${\bigvee }_{y\in X}{h}_{y,f\left(y\right)}=f$, showing that $\{h_{y,b}:(y,b)\in I_{\mathcal{F}}\}$ is join-dense in $\mathcal{F}$. □

Remark 2. 

It is possible that $h_{y_1,b_1}=h_{y_2,b_2}$ for some $y_1,y_2\in X$ and $b_1,b_2\in L$. For example, if a lattice L has the bottom element 0, then for $\mathcal{F}=L^X$ consisting of all functions from X to L, we obtain $h_{y_1,0}=h_{y_2,0}$ for all $y_1,y_2\in X$.

If $\mathcal{F}$ is closed under the pointwise meet operation, then any set $S_{y,b}^{\mathcal{F}}$ for $(y,b)\in I_{\mathcal{F}}$ contains the smallest element. In this case $h_{y,b}={\bigwedge }_{f\in S_{y,b}^{\mathcal{F}}}f$.

If an element $c\in L$ can be expressed as $c={\bigvee }_{b\in S}b$, $S\subseteq L$, it is quite natural to require that the function $h_{y,c}$ can also be expressed as a join of the functions $h_{y,b}$, $b\in S$. However, this is possible only if there are enough “good” functions defined in y which are below $h_{y,c}$. The following theorem describes a sufficient condition for this case.

Theorem 3. 

Let $D\subseteq L$ be a subset and $\mathcal{F}$ be a family of functions closed under the join and meet operations, such that for all $x\in X$ and $c\in L$, the relation $(x,c)\in I_{\mathcal{F}}$ implies $(x,b)\in I_{\mathcal{F}}$ for all $b\le c$, $b\in D$. If D is a join-dense subset of L, then $D_{\mathcal{F}}=\{h_{y,b}:(y,b)\in I_{\mathcal{F}}^D,\}$ is a join-dense subset of $\mathcal{F}$. If D is minimal, then $D_{\mathcal{F}}$ is minimal as well.

Proof. 

Let $D\subseteq L$ be a join-dense subset. First, we show that $D_{\mathcal{F}}$ is join-dense in $\mathcal{F}$. With respect to Theorem 2, it suffices to show that for all $y\in X$

$$h_{y,c}=\underset{b\in S_c}{\bigvee }{h}_{y,b}$$

where $S_c\subseteq D$ is such that $c={\bigvee }_{b\in S_c}b$. As $\mathcal{F}$ is closed under the meet operation, it follows that $h_{y,c}\ge h_{y,c}\wedge h_{y,b}\ge h_{y,b}$ for all $b\in S_c$, where the last inequality is due to the fact that $h_{y,b}$ is the smallest function with the value b at the point y. Hence, $h_{y,c}\ge {\bigvee }_{b\in S_c}{h}_{y,b}$ holds. On the other side

$$\underset{b\in S_c}{\bigvee }{h}_{y,b}\left(y\right)=\underset{b\in S_c}{\bigvee }b=c,$$

which yields $h_{y,c}\le {\bigvee }_{b\in S_c}{h}_{y,b}$ since $h_{y,c}$ is the smallest function in $\mathcal{F}$ with property $h_{y,c}\left(y\right)=c$.

Further, assume that $D_{\mathcal{F}}$ is not a minimal join-dense subset of $\mathcal{F}$. Then, there is $h_{y,b}\in D_{\mathcal{F}}$ for some $y\in X,b\in D$ such that $D_{\mathcal{F}}\setminus \left\{h_{y,b}\right\}$ is join-dense. In this case

$$h_{y,b}=\underset{h\in S}{\bigvee }h$$

(3)

for some subset $S\subseteq D_{\mathcal{F}}\setminus \left\{h_{y,b}\right\}$. Particularly, for the element y, we obtain

$$b=h_{y,b}\left(y\right)=\underset{h\in S}{\bigvee }h\left(y\right).$$

Since $b\in D$ and D is a minimal join-dense subset of L, it follows that $b=h\left(y\right)$ for some $h=h_{y_1,b_1}\in S$. From (3), we obtain $h_{y_1,b_1}\le h_{y,b}$ while $h_{y_1,b_1}\left(y\right)=b$ implies the converse inequality, yielding that these two functions are equal. This represents a contradiction, since $h_{y_1,b_1}\in D_{\mathcal{F}}\setminus \left\{h_{y,b}\right\}$ was assumed. □

In what follows, we subsequently apply the obtained results to the lattice ${\mathsf{Agg}}^n\left(L\right)$ of all aggregation functions, the lattice ${\mathsf{Id}}^n\left(L\right)$ of idempotent aggregation functions, and the lattice of Sugeno integrals ${\mathsf{Sug}}^n\left(L\right)$. Recall that ${\mathsf{Id}}^n\left(L\right)\subseteq {\mathsf{Agg}}^n\left(L\right)$ holds for an arbitrary bounded lattice L. Moreover, if L is distributive, then the following inclusions are valid

$${\mathsf{Sug}}^n\left(L\right)\subseteq {\mathsf{Id}}^n\left(L\right)\subseteq {\mathsf{Agg}}^n\left(L\right).$$

3.1. Aggregation Functions

The aim of this section is to characterize the least functions from the sets $S_{\mathbf{a},b}^{\mathcal{F}}$, $\mathbf{a}\in L^n$, $b\in L$, where $\mathcal{F}={\mathsf{Agg}}^n\left(L\right)$. From the definition of an aggregation function, it can be easily seen that these are empty whenever $\mathbf{a}={\mathbf{e}}_{\varnothing }=(0,\dots ,0)$ and $b>0$, as well as in the case $\mathbf{a}={\mathbf{e}}_{\left[n\right]}=(1,\dots ,1)$ and $b<1$. In the sequel, the symbol $L_{*}^n$ denotes the set $L^n\setminus \{(0,\dots ,0),(1,\dots ,1)\}$, i.e., $L^n$ without its smallest and greatest elements, respectively. For $\mathbf{a}\in L_{*}^n$ and $b\in L$, define the following n-ary function.

$${\chi }_{\mathbf{a},b}^n\left(\mathbf{x}\right)=\left\{\begin{array}{c}0, \mathrm{if} \mathbf{x}\ngeqq \mathbf{a}\hfill \\ b, \mathrm{if} \mathbf{x}\ge \mathbf{a} \mathrm{and} \mathbf{x}<(1,\dots ,1)\hfill \\ 1, \mathrm{if} \mathbf{x}=(1,\dots ,1).\hfill \end{array}\right.$$

(4)

The following lemma shows that the function defined by (4) is the least in the respective set $S_{\mathbf{a},b}^{\mathcal{F}}$, $\mathcal{F}={\mathsf{Agg}}^n\left(L\right)$.

Lemma 1. 

Let $\mathbf{a}\in L_{*}^n$, $b\in L$ be elements and $f:L^n\to L$ be an aggregation function with $f(\mathbf{a})=b$. Then, ${\chi }_{\mathbf{a},b}^n$ is an aggregation function such that ${\chi }_{\mathbf{a},b}^n\left(\mathbf{a}\right)=b$ and ${\chi }_{\mathbf{a},b}^n\left(\mathbf{x}\right)\le f\left(\mathbf{x}\right)$ for all $\mathbf{x}\in L^n$.

Proof. 

From (4), it can be easily seen that the function ${\chi }_{\mathbf{a},b}^n$ is monotone, it fulfils the boundary conditions, and that ${\chi }_{\mathbf{a},b}^n\left(\mathbf{a}\right)=b$.

Further, assume that f is an aggregation function with $f\left(\mathbf{a}\right)=b$. Obviously ${\chi }_{\mathbf{a},b}^n\left(\mathbf{x}\right)=0\le f\left(\mathbf{x}\right)$ for all $\mathbf{x}\in L^n$ with $\mathbf{x}\ngeqq \mathbf{a}$. For $\mathbf{x}\ge \mathbf{a}$, $\mathbf{x}\ne (1,\dots ,1)$, we obtain ${\chi }_{\mathbf{a},b}^n\left(\mathbf{x}\right)=b\le f\left(\mathbf{x}\right)$ since f is monotone. Finally, ${\chi }_{\mathbf{a},b}^n(1,\dots ,1)=f(1,\dots ,1)=1$. □

For the completeness, remark that for any $\mathbf{a}\in L_{*}^n$, it holds that ${\chi }_{{\mathbf{e}}_{\varnothing },0}^n={\chi }_{{\mathbf{e}}_{\left[n\right]},1}^n={\chi }_{\mathbf{a},0}^n$. In this case, all mentioned functions represent the least aggregation function in the full system $\mathcal{F}={\mathsf{Agg}}^n\left(L\right)$.

Let $D_L$ be a join-dense subset of the lattice L. It can be easily seen that for $\mathbf{a}\in L_{*}^n$ and $c\in L$, the condition $(\mathbf{a},c)\in I_{\mathcal{F}}$ yields $(\mathbf{a},b)\in I_{\mathcal{F}}$ for all $b\le c$, $b\in D_L$. Thus, for all $\mathbf{a}\in L_{*}^n$, the system of functions $\{{\chi }_{\mathbf{a},b}^n:\mathbf{a}\in L_{*}^n,b\in D_L\}$ fulfils the conditions of Theorem 3. Let us point out that the elements $(0,\dots ,0)$ and $(1,\dots ,1)$ do not play any role when generating the system ${\mathsf{Agg}}^n\left(L\right)$ since the values of the aggregation functions are uniquely determined in them.

For the system $\mathcal{F}={\mathsf{Agg}}^n\left(L\right)$, we obtain the following statement.

Theorem 4. 

Let $n\in \mathbb{N}$ be a positive integer, L be a bounded lattice, $D_L\subseteq L$ be a subset of L and $D_{{\mathsf{Agg}}^n\left(L\right)}=\{{\chi }_{\mathbf{a},b}^n:\mathbf{a}\in L_{*}^n,b\in D_L\}$. Then, $D_L$ is a join-dense subset of L if and only if $D_{{\mathsf{Agg}}^n\left(L\right)}$ is a join-dense subset of the lattice ${\mathsf{Agg}}^n\left(L\right)$. Moreover, $D_L$ is minimal if and only if $D_{{\mathsf{Agg}}^n\left(L\right)}$ is minimal.

Proof. 

Assume that $D_L$ is a join-dense subset of L. Then, with respect to Lemma 1, the system $D_{{\mathsf{Agg}}^n\left(L\right)}$ satisfies the assumptions of Theorem 3. Hence, $D_{{\mathsf{Agg}}^n\left(L\right)}$ is join-dense in ${\mathsf{Agg}}^n\left(L\right)$ and if $D_L$ is minimal, then $D_{{\mathsf{Agg}}^n\left(L\right)}$ is minimal as well.

To show the converse, suppose that $D_{{\mathsf{Agg}}^n\left(L\right)}$ is a join-dense subset of ${\mathsf{Agg}}^n\left(L\right)$. Our aim is to show that $D_L$ is join-dense in L. Let $0\ne c\in L$ be an arbitrary element. Take any $\mathbf{a}\in L_{*}^n$. As $D_{{\mathsf{Agg}}^n\left(L\right)}$ is join-dense, there is a subset $T\subseteq D_{{\mathsf{Agg}}^n\left(L\right)}$ such that

$${\chi }_{\mathbf{a},c}^n=\underset{f\in T}{\bigvee }f,$$

where each $f\in T$ is of the form $f={\chi }_{\mathbf{b},b}$ for some $\mathbf{b}\in L_{*}^n$ and $b\in D_L$. Put $T_0=\{f\in T:f\left(\mathbf{a}\right)=b\ne 0)\}$. Obviously $\{f\left(\mathbf{a}\right):f\in T_0)\}\subseteq D_L$ and we obtain

$$c={\chi }_{\mathbf{a},c}^n\left(\mathbf{a}\right)=\underset{f\in T}{\bigvee }f\left(\mathbf{a}\right)=\underset{f\in T_0}{\bigvee }f\left(\mathbf{a}\right),$$

i.e., the element c is a join of some subset of elements from $D_L$. Note that 0 must belong to $D_L$, otherwise, $D_{{\mathsf{Agg}}^n\left(L\right)}$ does not contain the smallest aggregation function.

Further, assume that $D_L$ is not minimal. Then, there is $d\in D_L$ such that $d={\bigvee }_{b\in S}b$ for some $S\subseteq D_L\setminus \left\{d\right\}$. Consequently for any $\mathbf{a}\in L_{*}^n$, we obtain ${\chi }_{\mathbf{a},d}^n={\bigvee }_{b\in S}{\chi }_{\mathbf{a},b}^n$, which yields that $D_{{\mathsf{Agg}}^n\left(L\right)}$ is not minimal. □

Observe that if $D_{{\mathsf{Agg}}^n\left(L\right)}$ is a minimal join-dense set, then, with respect to Theorem 1, all completely join-irreducible elements of ${\mathsf{Agg}}^n\left(L\right)$ are identified. In this case, ${\mathrm{J}}^{*}\left({\mathsf{Agg}}^n\left(L\right)\right)=D_{{\mathsf{Agg}}^n\left(L\right)}\setminus \left\{0_{{\mathsf{Agg}}^n\left(L\right)}\right\}$, where $0_{{\mathsf{Agg}}^n\left(L\right)}$ denotes the smallest aggregation function.

3.2. Idempotent Aggregation Functions

In what follows, we describe join-dense subsets of the lattice of all idempotent aggregation functions ${\mathsf{Id}}^n\left(L\right)$. At first, we recall the following easy statement characterizing idempotent functions as functions lying between the lattice operations meet and join. More precisely, these two functions represent the least and the greatest element in the lattice ${\mathsf{Id}}^n\left(L\right)$.

Lemma 2. 

A monotone function $f:L^n\to L$ is idempotent if and only if, for all $\mathbf{x}=(x_1,\dots ,x_n)\in L^n$, it satisfies

$$\underset{i=1}{\overset{n}{\bigwedge }}{x}_i\le f(x_1,\dots ,x_n)\le \underset{i=1}{\overset{n}{\bigvee }}{x}_i.$$

(5)

For $\mathbf{a}\in L^n$ and $b\in L$, define the following n-ary function

$${\iota }_{\mathbf{a},b}^n\left(\mathbf{x}\right)=\left\{\begin{array}{c}{\displaystyle b\vee \underset{i=1}{\overset{n}{\bigwedge }}{x}_i, \mathrm{if} \mathbf{x}\ge \mathbf{a}}\hfill \\ {\displaystyle \underset{i=1}{\overset{n}{\bigwedge }}{x}_i,\mathrm{otherwise}.}\hfill \end{array}\right.$$

(6)

Due to (5) of Lemma 2, for a given $\mathbf{a}\in L^n$, not all the values $b\in L$ are admissible. The following lemma gives sufficient conditions for the function ${\iota }_{\mathbf{a},b}^n$ to be idempotent.

Lemma 3. 

Assume that $b\in L$ and $\mathbf{a}=(a_1,\dots ,a_n)\in L^n$ satisfy $b\le {\bigvee }_{i=1}^n{a}_i$. Then, the function ${\iota }_{\mathbf{a},b}^n$ is an idempotent aggregation function.

Proof. 

First, we show that ${\iota }_{\mathbf{a},b}^n$ is monotone. Assume $\mathbf{x}\le \mathbf{y}$. If $\mathbf{x}\ge \mathbf{a}$, then $\mathbf{y}\ge \mathbf{a}$ as well, thus we obtain ${\iota }_{\mathbf{a},b}^n\left(\mathbf{x}\right)=b\vee {\bigwedge }_{i=1}^n{x}_i\le b\vee {\bigwedge }_{i=1}^n{y}_i={\iota }_{\mathbf{a},b}^n\left(\mathbf{y}\right)$. If $\mathbf{x}\ngeqq \mathbf{a}$, then ${\iota }_{\mathbf{a},b}^n\left(\mathbf{x}\right)={\bigwedge }_{i=1}^n{x}_i\le {\bigwedge }_{i=1}^n{y}_i\le {\iota }_{\mathbf{a},b}^n\left(\mathbf{y}\right)$.

To prove that ${\iota }_{\mathbf{a},b}^n$ is idempotent, hence that it also satisfies the boundary conditions, assume first that $(x,\dots ,x)\ge \mathbf{a}$. Consequently, with respect to the assumptions, $b\le {\bigvee }_{i=1}^n{a}_i\le x$, and we obtain ${\iota }_{\mathbf{a},b}^n(x,\dots ,x)=b\vee {\bigwedge }_{i=1}^{n}x=b\vee x=x$. For $(x,\dots ,x)\ngeqq \mathbf{a}$, we obtain ${\iota }_{\mathbf{a},b}^n(x,\dots ,x)={\bigwedge }_{i=1}^{n}x=x$. □

In what follows, we show that for $\mathcal{F}={\mathsf{Id}}^n\left(L\right)$, the function defined by (6) is the least idempotent functions in the respective set $S_{\mathbf{a},b}^{\mathcal{F}}$.

Lemma 4. 

Let $\mathbf{a}\in L^n$ be an element and $f:L^n\to L$ be an idempotent aggregation function with $b=f\left(\mathbf{a}\right)$. Then, ${\iota }_{\mathbf{a},b}^n\in {\mathsf{Id}}^n\left(L\right)$, ${\iota }_{\mathbf{a},b}^n\left(\mathbf{a}\right)=b$ and ${\iota }_{\mathbf{a},b}^n\left(\mathbf{x}\right)\le f\left(\mathbf{x}\right)$ for all $\mathbf{x}\in L^n$.

Proof. 

Since f is idempotent, due to (5) of Lemma 2, it follows that $b=f\left(\mathbf{a}\right)\le {\bigvee }_{i=1}^n{a}_i$. Consequently, according to Lemma 4, ${\iota }_{\mathbf{a},b}^n$ is idempotent. Moreover, using $b=f\left(\mathbf{a}\right)\ge {\bigwedge }_{i=1}^n{a}_i$, from (6), we obtain ${\iota }_{\mathbf{a},b}^n\left(\mathbf{a}\right)=b\vee {\bigwedge }_{i=1}^n{a}_i=b$.

In order to show that ${\iota }_{\mathbf{a},b}^n$ is below f, assume first that $\mathbf{x}\ge \mathbf{a}$. In this case $f\left(\mathbf{x}\right)\ge f\left(\mathbf{a}\right)=b$, as well as $f\left(\mathbf{x}\right)\ge {\bigwedge }_{i=1}^n{x}_i$, which yields $f\left(\mathbf{x}\right)\ge b\vee {\bigwedge }_{i=1}^n{x}_i={\iota }_{\mathbf{a},b}^n\left(\mathbf{x}\right)$. For $\mathbf{x}\ngeqq \mathbf{a}$, we directly obtain $f\left(\mathbf{x}\right)\ge {\bigwedge }_{i=1}^n{x}_i={\iota }_{\mathbf{a},b}^n\left(\mathbf{x}\right)$. □

For $n=1$, there is only one idempotent aggregation function, namely, the identity function on L. Hence, in what follows, we deal with the case $n\ge 2$.

Theorem 5. 

Let $n\in \mathbb{N}$, $n\ge 2$ be a positive integer, $D_L\subseteq L$ be a subset of a bounded lattice L such that $0\in D_L$ and $D_{{\mathsf{Id}}^n\left(L\right)}=\{{\iota }_{\mathbf{a},b}^n:\mathbf{a}\in L_{*}^n,b\in D_L,b\le {\bigvee }_{i=1}^n{a}_i\}$. Then, $D_L$ is a join-dense subset of L if and only if $D_{{\mathsf{Id}}^n\left(L\right)}$ is a join-dense subset of the lattice ${\mathsf{Id}}^n\left(L\right)$. If $D_{{\mathsf{Id}}^n\left(L\right)}$ is minimal, then $D_L$ is also minimal.

Proof. 

Let $D_L$ be a join-dense subset of L. According to Theorem 2 and with respect to Lemma 4, it suffices to show that each function ${\iota }_{\mathbf{a},c}^n\in {\mathsf{Id}}^n\left(L\right)$ for $\mathbf{a}\in L_{*}^n$ and $c\in L$ can be expressed as a join of some subset of the set $D_{{\mathsf{Id}}^n\left(L\right)}$. Let $c\in L$ and $\mathbf{a}\in L_{*}^n$ be arbitrary elements such that ${\iota }_{\mathbf{a},c}^n\in {\mathsf{Id}}^n\left(L\right)$. Then, $c={\bigvee }_{b\in S}b$ for some $S\subseteq D_L$. As ${\iota }_{\mathbf{a},c}^n$ is idempotent, it follows that $c\le {\bigvee }_{i=1}^n{a}_i$. Hence, $b\le {\bigvee }_{i=1}^n{a}_i$ for all $b\in S$ also holds, and ${\iota }_{\mathsf{a},b}^n\in {\mathsf{Id}}^n\left(L\right)$. Consequently, we obtain

$${\iota }_{\mathbf{a},c}^n\left(\mathbf{x}\right)=\underset{b\in S}{\bigvee }{\iota }_{\mathbf{a},b}^n\left(\mathbf{x}\right)=\left\{\begin{array}{c}{\displaystyle \underset{b\in S}{\bigvee }(b\vee \underset{i=1}{\overset{n}{\bigwedge }}{x}_i)=\underset{b\in S}{\bigvee }b\vee \underset{i=1}{\overset{n}{\bigwedge }}{x}_i=c\vee \underset{i=1}{\overset{n}{\bigwedge }}{x}_i, \mathrm{if} \mathbf{x}\ge \mathbf{a}}\hfill \\ {\displaystyle \underset{b\in S}{\bigvee }(\underset{i=1}{\overset{n}{\bigwedge }}{x}_i)=\underset{i=1}{\overset{n}{\bigwedge }}{x}_i,\mathrm{otherwise}.}\hfill \end{array}\right.$$

This shows that $D_{{\mathsf{Id}}^n\left(L\right)}$ is a join-dense subset of the lattice ${\mathsf{Id}}^n\left(L\right)$.

Conversely, assume that $D_{{\mathsf{Id}}^n\left(L\right)}$ is join-dense. Consider the element ${\mathbf{e}}_{\left\{1\right\}}=(1,0,0,\dots ,0)$. It can be easily seen that ${\iota }_{\mathbf{a},b}^n\left({\mathbf{e}}_{\left\{1\right\}}\right)=b$ or ${\iota }_{\mathbf{a},b}^n\left({\mathbf{e}}_{\left\{1\right\}}\right)=0$ for all functions ${\iota }_{\mathbf{a},b}^n\in D_{{\mathsf{Id}}^n\left(L\right)}$. Let $c\in L$ be an arbitrary element. Since the function ${\iota }_{{\mathbf{e}}_{\left\{1\right\}},c}^n$ can be expressed as a join of functions from some subset $S\subseteq D_{{\mathsf{Id}}^n\left(L\right)}$, we obtain

$$c={\iota }_{{\mathbf{e}}_{\left\{1\right\}},c}^n\left({\mathbf{e}}_{\left\{1\right\}}\right)=\underset{f\in S}{\bigvee }f\left({\mathbf{e}}_{\left\{1\right\}}\right),$$

where $\{f\left({\mathbf{e}}_{\left\{1\right\}}\right):f\in S\}\subseteq D_L$. This shows that $D_L$ is join-dense in L.

Now assume that $D_L$ is not a minimal join-dense subset of L. Then, there is $d\in D_L$, $d\ne 0$ such that $D_L\setminus \left\{d\right\}$ is join-dense. Consequently, $d={\bigvee }_{b\in S}b$ for some $S\subseteq D_L\setminus \left\{d\right\}$, and we obtain

$${\iota }_{{\mathbf{e}}_{\left\{1\right\}},d}^n=\underset{b\in S}{\bigvee }{\iota }_{{\mathbf{e}}_{\left\{1\right\}},b}^n,$$

which yields that $D_{{\mathsf{Id}}^n\left(L\right)}$ is not minimal. □

Let us remark that the minimality of $D_L$ does not imply the minimality of $D_{{\mathsf{Id}}^n\left(L\right)}$ in general, see the following example.

Example 1. 

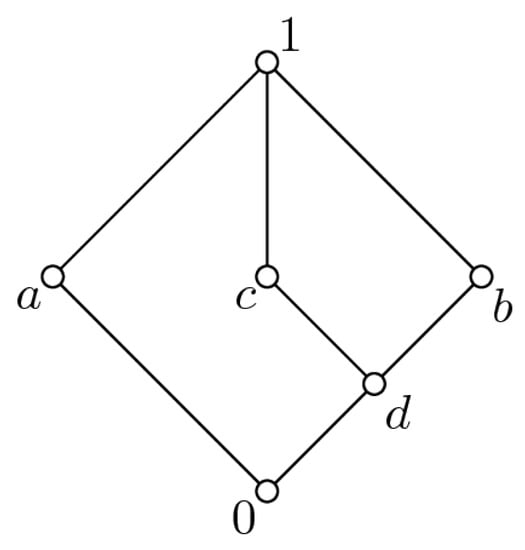
Consider the lattice L depicted in Figure 1. In this case, the minimal join-dense subset consists of elements $\{0,a,b,c,d\}$. For the element $\mathbf{a}=(b,c)$, the binary function ${\iota }_{\mathbf{a},a}^2$ is idempotent, since $a\le b\vee c=1$. Then, ${\iota }_{\mathbf{a},a}^2\left(\mathbf{a}\right)=a\vee (b\wedge c)=a\vee d=1$, which yields that ${\iota }_{\mathbf{a},a}^2={\iota }_{\mathbf{a},1}^2$. However, the function ${\iota }_{\mathbf{a},a}^2={\iota }_{\mathbf{a},1}^2$ is not join-irreducible as ${\iota }_{\mathbf{a},1}^2={\iota }_{\mathbf{a},b}^2\vee {\iota }_{\mathbf{a},c}^2$. Consequently, the set $D_{{\mathsf{Id}}^2\left(L\right)}$ is not minimal join-dense since it contains the reducible element ${\iota }_{\mathbf{a},1}^2$.

Figure 1. Example of a lattice L with $D_L$ minimal, while $D_{{\mathsf{Id}}^2\left(L\right)}$ is not.

3.3. Sugeno Integrals

In this section, we describe join-dense subsets in the lattice of all Sugeno integrals. In what follows, L denotes a bounded distributive lattice. According to Proposition 1, the lattice ${\mathsf{Sug}}^n\left(L\right)$ and the lattice ${\mathsf{Cap}}^n\left(L\right)$ of all L-capacities on L are isomorphic. Thus, we deal with the system ${\mathsf{Cap}}^n\left(L\right)$.

Let $n\in \mathbb{N}$ be a positive integer. For a proper nonempty subset $\varnothing \ne Y⊊\left[n\right]$ and $b\in L$, define a capacity $c_{Y,b}^n:\mathrm{P}\left(\left[n\right]\right)\to L$ by

$$c_{Y,b}^n\left(X\right)=\left\{\begin{array}{c}0,\mathrm{if}Y⊈X\hfill \\ b,\mathrm{if}Y\subseteq X\mathrm{and}X\ne \left[n\right]\hfill \\ 1,\mathrm{if}X=\left[n\right].\hfill \end{array}\right.$$

(7)

Similarly as in the proof of Lemma 1, it can be verified that if $\mu$ is an L-capacity with $\mu \left(Y\right)=b$, then $c_{Y,b}\left(X\right)\le \mu \left(X\right)$ for all $X\subseteq \left[n\right]$, i.e., $c_{Y,b}$ represents the smallest L-capacity with the value b for subset Y.

Analogously to the case of aggregation functions, the value of any L-capacity is uniquely determined in ∅ and for the set $\left[n\right]$. Consequently, these two sets play no role in the description of join-dense subsets of the lattice ${\mathsf{Cap}}^n\left(L\right)$. For $n=1$, it is obvious that there is only one L-capacity (and only one Sugeno integral, the identity function). Hence, for $n\ge 2$, using the same arguments as in the proof of Theorem 4 and applying Theorem 3, we obtain the following statement.

Theorem 6. 

Let $n\in \mathbb{N}$ be a positive integer, $n\ge 2$, $D_L\subseteq L$ be a subset of a bounded distributive lattice L and $D_{{\mathsf{Cap}}^n\left(L\right)}=\{c_{Y,b}^n:\varnothing \ne Y⊊\left[n\right],b\in D_L\}$. Then, $D_L$ is a join-dense subset of the lattice L if and only if $D_{{\mathsf{Cap}}^n\left(L\right)}$ is a join-dense subset of ${\mathsf{Cap}}^n\left(L\right)$. Moreover, $D_L$ is minimal if and only if $D_{{\mathsf{Cap}}^n\left(L\right)}$ is minimal.

Using formula (1) for the evaluation of a Sugeno integral with respect to the capacity $c_{Y,b}$ given by (7), we obtain

$${\mathsf{S}}_{c_{Y,b}}\left(\mathbf{x}\right)=\underset{X\subseteq \left[n\right]}{\bigvee }(c_{Y,b}\left(X\right)\wedge \underset{i\in X}{\bigwedge }{x}_i)=\underset{i\in \left[n\right]}{\bigwedge }{x}_i\vee \underset{Y\subseteq X⊊\left[n\right]}{\bigvee }(b\wedge \underset{i\in X}{\bigwedge }{x}_i)=\underset{i\in \left[n\right]}{\bigwedge }{x}_i\vee (b\wedge \underset{i\in Y}{\bigwedge }{x}_i).$$

Concluding, $D_{{\mathsf{Sug}}^n\left(L\right)}=\{{\mathsf{S}}_{c_{Y,b}}:\varnothing \ne Y⊊\left[n\right],b\in D_L\}$ is a join-dense subset of the lattice ${\mathsf{Sug}}^n\left(L\right)$. Moreover, $D_L$ is minimal if and only if $D_{{\mathsf{Sug}}^n\left(L\right)}$ is minimal.

4. Conclusions

Aggregation functions play an important role in various applications in fuzzy set theory, multicriteria decision-making, data mining, etc. As we have shown in our recent publications, their systems defined on bounded lattices form a very rich and complex structure. Thus, it turns out to be important and useful to study how these systems can be expressed in an easier way. This paper was devoted to a description of the so-called join-dense subsets of the three important classes of aggregation functions, namely, the lattice of all aggregation functions, the lattice of idempotent aggregation functions, and the lattice of Sugeno integrals (defined on distributive lattices).

While the description of minimal join-irreducible elements for the cases of aggregation functions and Sugeno integrals is relatively straightforward, this is not the case for the lattice of idempotent aggregation functions. Here, the minimality is directly connected to the existence of completely join-irreducible elements. This problem will be the objective of our future study. Particularly, our aim will be to provide a full description of minimal join-dense subsets of the lattices ${\mathsf{Id}}^n\left(L\right)$ by means of minimal join-dense subsets of the underlying lattice L. Another future direction of our research will be to investigate the possibility of approximating aggregation functions by using the joins of suitable subsets of the corresponding join-dense subsets.