Scalar Field Cosmology from a Modified Poisson Algebra

Abstract

We investigate the phase space of a scalar field theory obtained by minisuperspace deformation. We consider quintessence or phantom scalar fields in the action that arises from minisuperspace deformation on the Einstein–Hilbert action. We use a modified Poisson algebra where Poisson brackets are the $\alpha$-deformed ones and are related to the Moyal–Weyl star product. We discuss early- and late-time attractors and reconstruct the cosmological evolution. We show that the model can have the $\mathrm{\Lambda CDM}$ model as a future attractor if we initially consider a massless scalar field without a cosmological constant term.

1. Introduction

Cosmological observations indicate that the universe has gone through two acceleration phases [1,2,3,4], an early acceleration phase known as inflation and the present acceleration phase. The source of the cosmic acceleration is unknown. In the context of General Relativity, cosmic acceleration occurs when the cosmic fluid is dominated by a vacuum-like source known as dark energy (DE) with the property of having a negative value of the equation of state (EoS) parameter.

The cosmological constant $\mathsf{\Lambda }$ leads to the $\mathsf{\Lambda }$-cosmology being indeed the simplest candidate for DE; however, it suffers from two problems, the fine-tuning and the coincidence problems [5,6]. Furthermore, the detailed analysis of the recent cosmological observations shows that the $\mathsf{\Lambda }$-cosmology cannot solve tensions arising from the statistical analysis of the data, such as the $H_0$-tension [7]. There are various DE alternatives to the cosmological constant, which have been proposed to overpass the above-mentioned problems; see, for instance [8,9,10,11,12,13,14,15,16,17] and the references therein.

Scalar fields play a significant role in the description of cosmic acceleration. Indeed, introducing a scalar field in the field equations provides new degrees of freedom in the gravitational dynamics that provide acceleration effects. The most straightforward mechanism for describing the early acceleration phase of the universe, that is of the inflationary epoch, is that of the inflaton field [18,19,20,21,22,23,24,25]. During inflation [26,27], the scalar field dominates the cosmological dynamics and provides the antigravity effects. Similarly, for the description of the late-time acceleration [28], a tracker scalar field can be introduced [12], which roles down the potential energy $V\left(\varphi \right)$ to have DE effects [29,30,31,32,33]. Another novelty of the scalar fields is that they can reproduce various DE alternatives such as the Chaplygin gas and others [34,35].

In quintessence scalar field cosmology [8], the EoS parameter of the scalar field is constrained to the range $\left|w_{\varphi }\right|\le 1$, where $w_{\varphi }=1$ corresponds to a stiff fluid, where only the kinetic part of the scalar field dominates, while the limit $w_{\varphi }=-1$ corresponds to the case where only the scalar field potential dominates, leading to the $\mathsf{\Lambda }$-cosmology. Recall that acceleration occurs when $-1\le w_{eff}<-1/3.$ There is a family of scalar field models, known as phantom scalar fields, where $w_{\varphi }$ can cross the limit $-1$ and take smaller values, which is possible, for example, when there exists a negative kinetic energy [36,37,38,39].

During the very early stages of the universe, we expect that quantum effects play an important role in cosmic evolution. Until now, there is not a unique theory of quantum gravity; that is why various approaches have been considered in the literature by various groups [40,41,42,43,44,45,46,47,48]. String theory, double-special relativity, and the generalized uncertainty principle require the existence of a minimum length scale of the order of the Planck length $l_{\mathrm{pl}}$ [49,50,51,52,53,54,55,56]. As a result of the modification of the Heisenberg uncertainty in the latter approaches, a deformation parameter is introduced, which leads to the deformation of the coordinate representation of the operators of the momentum position, that is to a deformation of the Poisson algebra [57].

Noncommutative theories, quantum cosmology, quantum deformation, deformed phase space, Brans–Dicke theory, and noncommutative minisuperspace, as alternatives of the cosmological constant, have been treated, for example, in [58,59,60,61,62,63,64] and the references therein.

In [65], the phase space for the cosmological dynamics in quintessence cosmology was modified by a deformed Poisson algebra among the coordinates and the canonical momenta. The main result was that the deformation parameter is related to the accelerating scale factor provided by the deformed Poisson algebra in the absence of a cosmological constant. A similar result was determined recently in [66] and the case of a phantom scalar field.

The Moyal–Weyl star product provides a simple prescription for constructing noncommutative field theories on the noncommutative manifold [65] with $[{\widehat{x}}^{\mu },{\widehat{x}}^{\nu }]=i{\theta }^{\mu \nu }$. One replaces all the pointwise products in ordinary field theory with one of the star products. For example, the noncommutative action for a real massless scalar field $\mathsf{\Phi }$ in four dimensions is

$$S_{\varphi }=\frac{1}{2}\int d{}^{4}x{D}^{\mu }\mathsf{\Phi }{★}_{\alpha }{D}_{\mu }\mathsf{\Phi },$$

(1)

where the ordinary derivative ${\partial }_{\mu }$ appearing in the commutative scalar field action is replaced by the noncommutative covariant derivative $D_{\mu }$ and the action is invariant under the noncommutative gauge transformation.

In this paper, we are interested in studying the effects of the deformed Poisson algebra in the cosmological evolution. Specifically, we perform a detailed phase space analysis to investigate the existence of equilibrium points and reconstruct the cosmological parameters’ evolution. Such an analysis provides important information about the theory’s viability and can give us important results for the nature of the deformation parameter. For this analysis, one can introduce auxiliary variables, which transform the cosmological equations into an autonomous dynamical system [67,68,69,70,71,72,73,74,75,76,77,78,79,80,81]. Hence, we obtain a system of the form ${\mathbf{X}}^{\prime }=\mathbf{f}\left(\mathbf{X}\right)$, where $\mathbf{X}$ is the column vector of the auxiliary variables and $\mathbf{f}\left(\mathbf{X}\right)$ is an autonomous vector field. The derivative is with respect to a logarithmic time scale. The stability analysis comprises several steps. First, the critical points ${\mathbf{X}}_{\mathbf{c}}$ are extracted under the requirement of ${\mathbf{X}}^{\prime }=\mathbf{0}$. Then, one considers linear perturbations around ${\mathbf{X}}_{\mathbf{c}}$ as $\mathbf{X}={\mathbf{X}}_{\mathbf{c}}+\mathbf{U}$, with $\mathbf{U}$ the column vector of the auxiliary variable’s perturbations. Therefore, up to first order, we obtain ${\mathbf{U}}^{\prime }=\mathsf{\Xi }·\mathbf{U}$, where the matrix $\mathsf{\Xi }$ contains the coefficients of the perturbed equations. Finally, the type stability of each hyperbolic critical point is determined by the eigenvalues of $\mathsf{\Xi }$. That is, the point is stable (unstable) if the real parts of the eigenvalues are negative (positive) or a saddle point if the eigenvalues have real parts with different signs.

The structure of the paper is as follows. In Section 2, we introduce the modified Poisson algebra. In Section 3, we derive the modified field equations in the case of scalar field cosmology in an isotropic and homogeneous spatially flat universe. Section 4 and Section 5 include the main results of this study, where we present the detailed analysis of the phase space for the modified field equations. Finally, in Section 6, we summarize our results and conclude.

2. Modified Poisson Algebra

We consider the modified Poisson algebra [65]:

$$\begin{array}{cc}\hfill & {\{x_1,x_j\}}_{\alpha }={\theta }_{ij},\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill & {\{p_i,p_j\}}_{\alpha }={\beta }_{ij},\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill & {\{x_i,p_j\}}_{\alpha }={\delta }_{ij}+{\sigma }_{ij},\hfill \end{array}$$

(4)

where the Moyal–Weyl brackets are defined through the relation:

$${\{f,g\}}_{\alpha }=f{★}_{\alpha }g-g{★}_{\alpha }f$$

(5)

in which the product between f and g is substituted by the Moyal–Weyl star product:

$$\left(f{★}_{\alpha }g\right)=exp\left[\frac{1}{2}{\alpha }^{ab}{\partial }_a^{\left(1\right)}{\partial }_b^{\left(2\right)}\right]f\left(x_1\right)g\left(x_2\right){|}_{x_1=x_2=x},$$

(6)

such that

$$\alpha =\left(\begin{array}{cc}{\theta }_{ij}& {\delta }_{ij}+{\sigma }_{ij}\\ -{\delta }_{ij}-{\sigma }_{ij}& {\beta }_{ij}\end{array}\right),$$

(7)

where ${\theta }_{ij}$ and ${\beta }_{ij}$ are $2\times 2$ antisymmetric matrices indicating the noncommutativity in the coordinates and momenta, respectively. Particular deformations:

$${\theta }_{ij}=-\theta {ϵ}_{ij},{\beta }_{ij}=\beta {ϵ}_{ij},$$

(8)

where ${ϵ}_{ij}$ is the two-index Levi-Civita symbol, are considered.

By removing the sub-index in ${☆}_{\alpha }$, the ★-Friedman equations can be derived for the ★-FLRW metric as follows [82].

$$R_{\mu \nu }-\frac{1}{2}R★g_{\mu \nu }+\mathsf{\Lambda }{g}_{\mu \nu }=\kappa T_{\mu \nu }$$

(9)

with the energy–momentum tensor:

$$T_{\mu \nu }=p★g_{\mu \nu }+(\rho +p)★U_{\mu }★U_{\nu }$$

(10)

where $U_{\mu }={\delta }_{\mu }^0$ is the co-moving observer and p and $\rho$ are the total pressure and fluid energy three-density, respectively.

To avoid the complexities of ★-algebras, one may consider the field equations arising from the point-like action for a scalar field with action [83]:

$$S=\int dtN\left(-3\frac{a{\dot{a}}^2}{N^2}\right)+\frac{1}{2}\int dtN{a}^3\left(ϵ\frac{{\dot{\varphi }}^2}{N^2}-2V\left(\varphi \right)\right).$$

(11)

We define the point-like Lagrangian [83]:

$$\mathcal{L}(N,a,\varphi ,\dot{a},\dot{\varphi }):=\frac{1}{N}\left(-3a{\dot{a}}^2+\frac{1}{2}{a}^3ϵ{\dot{\varphi }}^2\right)-a^{3}NV\left(\varphi \right),$$

(12)

while, for simplicity, we consider a constant potential $V\left(\varphi \right)=\tilde{\mathsf{\Lambda }}$. The sign $ϵ=1$ corresponds to quintessence, and the sign $ϵ=-1$ corresponds to the phantom field.

With the variation with respect to $\{N,a,\varphi \}$ and the replacement $N=1$ after variation, we obtain the Euler–Lagrange equations:

$$\begin{array}{cc}\hfill & \frac{1}{2}\left(6a{\dot{a}}^2-a^3\left(2\tilde{\mathsf{\Lambda }}+ϵ{\dot{\varphi }}^2\right)\right)=0,\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill & \frac{3}{2}\left(4a\ddot{a}+2{\dot{a}}^2+a^2\left(ϵ{\dot{\varphi }}^2-2\tilde{\mathsf{\Lambda }}\right)\right)=0,\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill & -ϵa^2\left(3\dot{a}\dot{\varphi }+a\ddot{\varphi }\right)=0.\hfill \end{array}$$

(15)

Introducing the Hubble parameter $H=\dot{a}/a$, the previous equations can be written as [83]:

$$\begin{array}{cc}\hfill & 3H^2=\tilde{\mathsf{\Lambda }}+\frac{1}{2}ϵ{\dot{\varphi }}^2,\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill & 2\dot{H}=-3H^2+\tilde{\mathsf{\Lambda }}-\frac{1}{2}ϵ{\dot{\varphi }}^2,\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill & \ddot{\varphi }+3H\dot{\varphi }=0.\hfill \end{array}$$

(18)

For the Lagrangian function (12), we define the generalized momenta by $p_i=\frac{\partial \mathcal{L}}{\partial {\dot{q}}^i}$, where $q^i\in \{a,\varphi \}$, $p_i\in \{p_a,p_{\varphi }\}$, namely

$$\begin{array}{cc}\hfill p_a& \equiv -\frac{6a\dot{a}}{N},p_{\varphi }\equiv \frac{ϵa^3\dot{\varphi }}{N}.\hfill \end{array}$$

(19)

Hence, we can introduce the Hamiltonian function $\mathcal{H}=p_a\dot{a}+p_{\varphi }\dot{\varphi }-\mathcal{L}$, which is written as

$$\mathcal{H}=N\left(-\frac{{p_a}^2}{12a}+\frac{ϵ{p_{\varphi }}^2}{2a^3}+\tilde{\mathsf{\Lambda }}{a}^3\right)$$

(20)

We define the canonical coordinates [83]:

$$x={\lambda }^{-1}{\left(ϵa\right)}^{3/2}sinh\left(\sqrt{ϵ}\lambda \varphi \right),y={\lambda }^{-1}{a}^{3/2}cosh\left(\sqrt{ϵ}\lambda \varphi \right),$$

(21)

with the inverse:

$$a={\left(\lambda y\sqrt{1-\frac{ϵx^2}{y^2}}\right)}^{2/3},\varphi =\frac{{tanh}^{-1}\left(\sqrt{ϵ}x/y\right)}{\lambda \sqrt{ϵ}},$$

(22)

where ${\lambda }^{-1}=\sqrt{8/3}$, and we consider the simpler case where the matter content is an ordinary ($ϵ=+1$) or a phantom ($ϵ=-1$) scalar field in the action. Then, (12) becomes

$$\mathcal{L}(N,a,\varphi ,\dot{a},\dot{\varphi }):=\frac{1}{N}\left(-3a{\dot{a}}^2+\frac{1}{2}{a}^3ϵ{\dot{\varphi }}^2\right)-a^{3}NV\left(\varphi \right).$$

(23)

Generalized momenta are given by

$$\begin{array}{c}\hfill P_x=\frac{ϵ\dot{x}}{N},P_y=-\frac{\dot{y}}{N}.\end{array}$$

(24)

Hence, the problem can be formulated from the canonical Hamiltonian:

$${\mathcal{H}}_c=ϵN\left(\frac{1}{2}{P}_x^2+\frac{{\omega }^2}{2}{x}^2\right)-N\left(\frac{1}{2}{P}_y^2+\frac{{\omega }^2}{2}{y}^2\right),$$

(25)

where ${\omega }^2=-3\tilde{\mathsf{\Lambda }}/4$, and we use the comoving frame $N=1$. For the choice $ϵ=+1$, see the related work [65].

We have the evolution equations for $(\dot{x},\dot{y})$ as given by (24):

$$\dot{x}=ϵP_x,\dot{y}=-P_y$$

(26)

Hamilton’s equations ${\dot{p}}_i=-\frac{\partial \mathcal{H}}{\partial q^i}$, where $\mathcal{H}={\mathcal{H}}_c$ and $q^i\in \{x,y\}$, $p_i\in \{P_x,P_y\}$, lead to

$$\dot{P_x}=-ϵ{\omega }^{2}x,\dot{P_y}={\omega }^{2}y.$$

(27)

which lead to the following equations for $ϵ=\pm 1$:

$$\ddot{x}+{\omega }^{2}x=0,\ddot{y}+{\omega }^{2}y=0,$$

(28)

with conserved quantity:

$${\tilde{y}}^2-ϵ{\tilde{x}}^2=1,(\tilde{x},\tilde{y})=\lambda a^{-3/2}·(x,y).$$

(29)

By the definition ${\omega }^2=-3/4\tilde{\mathsf{\Lambda }}$, the solutions are

$$\begin{array}{cc}\hfill & x\left(t\right)=c_1{e}^{\frac{1}{2}\sqrt{3}\sqrt{\tilde{\mathsf{\Lambda }}}t}+c_2{e}^{-\frac{1}{2}\sqrt{3}\sqrt{\tilde{\mathsf{\Lambda }}}t},\hfill \end{array}$$

(30)

$$\begin{array}{cc}\hfill & y\left(t\right)=c_3{e}^{\frac{1}{2}\sqrt{3}\sqrt{\tilde{\mathsf{\Lambda }}}t}+c_4{e}^{-\frac{1}{2}\sqrt{3}\sqrt{\tilde{\mathsf{\Lambda }}}t}.\hfill \end{array}$$

(31)

Then,

$$\begin{array}{cc}\hfill \varphi \left(t\right)& =\frac{{coth}^{-1}\left(\frac{{ϵ}^{3/2}\left(c_3{e}^{\sqrt{3}\sqrt{\tilde{\mathsf{\Lambda }}}t}+c_4\right)}{c_1{e}^{\sqrt{3}\sqrt{\tilde{\mathsf{\Lambda }}}t}+c_2}\right)}{\lambda \sqrt{ϵ}},\hfill \end{array}$$

(32)

$$\begin{array}{cc}\hfill a\left(t\right)& =e^{-\sqrt{\frac{\tilde{\mathsf{\Lambda }}}{3}}t}{\left(\lambda \left(c_3{e}^{\sqrt{3}\sqrt{\tilde{\mathsf{\Lambda }}}t}+c_4\right)\right)}^{2/3}{\left(1-\frac{ϵ\left(c_1{e}^{\sqrt{3}\sqrt{\tilde{\mathsf{\Lambda }}}t}+c_2\right){}^2}{\left(c_3{e}^{\sqrt{3}\sqrt{\tilde{\mathsf{\Lambda }}}t}+c_4\right){}^2}\right)}^{1/3},\hfill \end{array}$$

(33)

such that

$$\begin{array}{cc}\hfill & \varphi \sim \frac{ln\left(1-\frac{2c_1}{c_1-c_3{ϵ}^{3/2}}\right)}{2\lambda \sqrt{ϵ}},a\sim c_3{}^{2/3}{\lambda }^{2/3}\sqrt[3]{1-\frac{c_1{}^2ϵ}{c_3{}^2}}{e}^{\frac{\sqrt{\tilde{\mathsf{\Lambda }}}t}{\sqrt{3}}}\hfill \end{array}$$

(34)

as $t\to \infty$. That is, a de Sitter solution is obtained.

The elements of the new configuration space, $(x,y)$, and their conjugate momenta fulfil the following commutation relations based on the Poisson bracket:

$$\begin{array}{c}\hfill \{x_k,x_j\}=0,\{P_{x_k},P_{x_j}\}=0,\{x_k,P_{x_j}\}={\delta }_{kj}\end{array}$$

(35)

where k and j can take 1 and 2, that is $(x_1,x_2)=(x,y)$ and ${\delta }_{kj}$ is the usual Kronecker delta.

To obtain a modified scenario, we take classical phase space variables $(x,y,P_x,P_y)$ and perform the transformation (see the related work [65]):

$$\left(\begin{array}{c}\widehat{x}\\ \widehat{y}\end{array}\right)=\left(\begin{array}{c}x\\ y\end{array}\right)+\frac{\theta }{2}\left(\begin{array}{c}{P}_y\\ -P_x\end{array}\right)$$

(36)

and

$$\left(\begin{array}{c}{\widehat{P}}_x\\ {\widehat{P}}_y\end{array}\right)=\frac{\beta }{2}\left(\begin{array}{c}-y\\ x\end{array}\right)+\left(\begin{array}{c}{P}_x\\ P_y\end{array}\right)$$

(37)

The modified Poisson Algebra is given by

$$\{\widehat{y},\widehat{x}\}=\theta ,\{{\widehat{P}}_y,{\widehat{P}}_x\}=\beta$$

(38)

and

$$\{\widehat{x},{\widehat{P}}_x\}=1+\sigma ,\{\widehat{y},{\widehat{P}}_y\}=1+\sigma ,$$

(39)

where $\sigma =\theta \beta /4$. Now, we change the notation $\{\widehat{x},\widehat{y},{\widehat{P}}_x,{\widehat{P}}_y\}$ to $\{x,y,p_x,p_y\}$.

The modified Hamiltonian will be

$${\mathcal{H}}_{mod.}=\frac{1}{2}ϵp_x^2-\frac{1}{2}{p}_y^2-\frac{{\omega }_1^2}{2}\left(x{p}_y+ϵy{p}_x\right)+\frac{{\omega }_2^2}{2}(ϵx^2-y^2),$$

(40)

where

$$\begin{array}{cc}\hfill & p_x=\dot{x}+\frac{1}{2}{\omega }_{1}y,p_y=\frac{-x{\omega }_1^2ϵ-2\dot{y}}{2ϵ},\hfill \end{array}$$

(41)

and and we define the parameters

$$\begin{array}{cc}\hfill & {\omega }_1^2=\frac{4\beta -4ϵ{\omega }^2\theta }{4-ϵ{\omega }^2{\theta }^2},{\omega }_2^2=\frac{4{\omega }^2-ϵ{\beta }^2}{4-ϵ{\omega }^2{\theta }^2},\hfill \end{array}$$

(42)

$$\begin{array}{cc}\hfill & \mathsf{\Lambda }=-\frac{4\left((\beta -1)\beta ϵ+(\theta -4){\omega }^2\right)}{3\left({\theta }^2{\omega }^2ϵ-4\right)}.\hfill \end{array}$$

(43)

If $\omega =0$, the latter definitions are

$$\begin{array}{cc}\hfill & {\omega }_1^2=\beta ,{\omega }_2^2=-\frac{ϵ{\beta }^2}{4},\mathsf{\Lambda }=\frac{(\beta -1)\beta ϵ}{3}.\hfill \end{array}$$

(44)

We can infer from these that the cosmological constant term is introduced from the modification of the Poisson algebra if our initial model does not include a cosmological constant term. The equations of motion derived from ${\mathcal{H}}_{mod.}$ are

$$\ddot{x}+{\omega }_1^2\dot{y}-\frac{3}{4}\mathsf{\Lambda }x=0,$$

(45)

and

$$\ddot{y}+ϵ{\omega }_1^2\dot{x}-\frac{3}{4}\mathsf{\Lambda }y=0,$$

(46)

These equations have the solutions:

$$\begin{array}{cc}\hfill x\left(t\right)& =c_{1}cosh\left(\frac{t{{\omega }_1}^2}{2}\right)cosh\left(\frac{1}{2}t\sqrt{3\mathsf{\Lambda }+{{\omega }_1}^4}\right)-c_{3}sinh\left(\frac{t{{\omega }_1}^2}{2}\right)cosh\left(\frac{1}{2}t\sqrt{3\mathsf{\Lambda }+{{\omega }_1}^4}\right)\hfill \end{array}$$

$$\begin{array}{cc}\hfill & +\frac{sinh\left(\frac{1}{2}t\sqrt{3\mathsf{\Lambda }+{{\omega }_1}^4}\right)\left(\left(c_3{{\omega }_1}^2+2c_2\right)cosh\left(\frac{t{{\omega }_1}^2}{2}\right)-\left(c_1{{\omega }_1}^2+2c_4\right)sinh\left(\frac{t{{\omega }_1}^2}{2}\right)\right)}{\sqrt{3\mathsf{\Lambda }+{{\omega }_1}^4}},\hfill \\ \hfill y\left(t\right)& =c_{3}cosh\left(\frac{t{{\omega }_1}^2}{2}\right)cosh\left(\frac{1}{2}t\sqrt{3\mathsf{\Lambda }+{{\omega }_1}^4}\right)-c_{1}sinh\left(\frac{t{{\omega }_1}^2}{2}\right)cosh\left(\frac{1}{2}t\sqrt{3\mathsf{\Lambda }+{{\omega }_1}^4}\right)\hfill \end{array}$$

(47)

$$\begin{array}{cc}\hfill & +\frac{sinh\left(\frac{1}{2}t\sqrt{3\mathsf{\Lambda }+{{\omega }_1}^4}\right)\left(\left(c_1{{\omega }_1}^2+2c_4\right)cosh\left(\frac{t{{\omega }_1}^2}{2}\right)-\left(c_3{{\omega }_1}^2+2c_2\right)sinh\left(\frac{t{{\omega }_1}^2}{2}\right)\right)}{\sqrt{3\mathsf{\Lambda }+{{\omega }_1}^4}}.\hfill \end{array}$$

(48)

Some solutions of this form have been found before in the literature, e.g., [84,85].

3. Modified Friedmann Equations

Equations (45) and (46) are equivalent to

$$\begin{array}{cc}\hfill & \ddot{a}=-\frac{{\dot{a}}^2}{2a}-\frac{1}{6}a\left(4\lambda ϵ\dot{\varphi }\left(\lambda \dot{\varphi }+{{\omega }_1}^2\right)+4{{\omega }_2}^2+{\omega }_1^2ϵ\right),\hfill \end{array}$$

(49)

$$\begin{array}{cc}\hfill & \ddot{\varphi }=-\frac{3\dot{a}\left(2\lambda \dot{\varphi }+{{\omega }_1}^2\right)}{2\lambda a}\hfill \end{array}$$

(50)

with the first integral

$$-3H^2+\frac{1}{2}ϵ{\dot{\varphi }}^2-\frac{4{{\omega }_2}^2}{3}-\frac{{{\omega }_1}^2ϵ}{3}=0.$$

(51)

where $H=\dot{a}/a$ is the Hubble parameter.

3.1. Vacuum Case

Using the reparameterization (43), the modified Friedman equation reads

$$3H^2=\frac{1}{2}ϵ{\dot{\varphi }}^2+\mathsf{\Lambda }.$$

(52)

The modified Klein–Gordon equation is

$$\ddot{\varphi }=-H\left(\sqrt{6}{\omega }_1^2+3\dot{\varphi }\right)$$

(53)

The Raychaudhuri equation is

$$\dot{H}=-\frac{3H^2}{2}-\frac{ϵ{\omega }_1^2\dot{\varphi }}{\sqrt{6}}-\frac{1}{4}ϵ{\dot{\varphi }}^2+\frac{\mathsf{\Lambda }}{2},$$

(54)

Alternatively, by removing $H^2$ and using (52), we obtain

$$\dot{H}=-\frac{ϵ{\omega }_1^2\dot{\varphi }}{\sqrt{6}}-\frac{1}{2}ϵ{\dot{\varphi }}^2.$$

(55)

With the definitions:

$${\rho }_{\varphi }=\frac{1}{2}ϵ{\dot{\varphi }}^2+\mathsf{\Lambda },P_{\varphi }=\frac{1}{2}ϵ{\dot{\varphi }}^2+\sqrt{\frac{2}{3}}{\omega }_1^2ϵ\dot{\varphi }-\mathsf{\Lambda },$$

(56)

the Klein–Gordon equation can be written as the conservation equation:

$${\dot{\rho }}_{\varphi }+3H({\rho }_{\varphi }+P_{\varphi })=0.$$

(57)

Moreover, we define the effective EoS parameter of $\varphi$ as

$$w_{\varphi }:=\frac{P_{\varphi }}{{\rho }_{\varphi }}=\frac{ϵ{\dot{\varphi }}^2+2\sqrt{\frac{2}{3}}{\omega }_1^2ϵ\dot{\varphi }-2\mathsf{\Lambda }}{ϵ{\dot{\varphi }}^2+2\mathsf{\Lambda }}.$$

(58)

3.2. Including Matter

The Friedman equation reads

$$3H^2=\frac{1}{2}ϵ{\dot{\varphi }}^2+{\rho }_m+\mathsf{\Lambda }.$$

(59)

The modified Klein–Gordon equation is

$$\ddot{\varphi }=-H\left(\sqrt{6}{\omega }_1^2+3\dot{\varphi }\right)$$

(60)

which can be written using (56) as

$${\dot{\rho }}_{\varphi }+3H({\rho }_{\varphi }+P_{\varphi })=0.$$

(61)

We have the matter conservation equation:

$${\dot{\rho }}_m+3H(1+w_m){\rho }_m=0.$$

(62)

The Raychaudhuri equation is

$$\dot{H}=-\frac{{\omega }_1^2ϵ\dot{\varphi }}{\sqrt{6}}-\frac{1}{2}ϵ{\dot{\varphi }}^2-\frac{1}{2}\left(w_m+1\right){\rho }_m.$$

(63)

4. Dynamical Systems’ Analysis in the Vacuum Case

In this section, we proceed with the analysis of the phase space for the modified cosmological field equations. In order to perform such an analysis, we define dimensionless variables in the Hubble normalization approach, that is

$${\mathsf{\Sigma }}_{\varphi }=\frac{\dot{\varphi }}{\sqrt{6}H},\mathsf{\Sigma }=\frac{{\omega }_1^2}{H},$$

(64)

which satisfies the constraint equation:

$${\mathsf{\Sigma }}_{\varphi }^2ϵ+\mu {\mathsf{\Sigma }}^2=1,$$

(65)

where we have introduced the constant $\mu =\mathsf{\Lambda }/\left(3{\omega }_1^4\right)$, or, alternatively,

$${\mathsf{\Sigma }}_{\varphi }^2ϵ+{\mathsf{\Omega }}_{\mathsf{\Lambda }}=1.$$

(66)

where, for convenience, we define the fractional energy density of $\mathsf{\Lambda }$ as

$${\mathsf{\Omega }}_{\mathsf{\Lambda }}:=\frac{\mathsf{\Lambda }}{3H^2}=\mu {\mathsf{\Sigma }}^2,\mu >0.$$

(67)

Thus, the dynamical system (52), (53), and (55) can be written as a dynamical system:

$$\begin{array}{cc}\hfill & {\mathsf{\Sigma }}_{\varphi }^{\prime }=(3{\mathsf{\Sigma }}_{\varphi }+\mathsf{\Sigma })\left({\mathsf{\Sigma }}_{\varphi }^2ϵ-1\right),\hfill \end{array}$$

(68)

$$\begin{array}{cc}\hfill & {\mathsf{\Sigma }}^{\prime }=ϵ{\mathsf{\Sigma }}_{\varphi }\mathsf{\Sigma }(3{\mathsf{\Sigma }}_{\varphi }+\mathsf{\Sigma }),\hfill \end{array}$$

(69)

where we have introduced the new time derivative $f^{\prime }=H^{-1}\dot{f}$.

4.1. Analysis of the 2D Flow

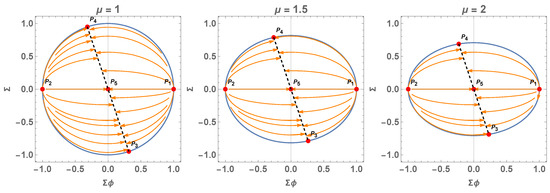
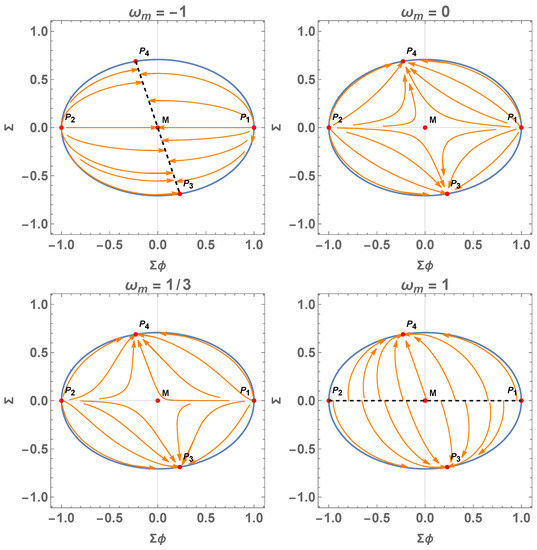
In this section, we analyze the 2D flow associated with the dynamical system (68) and (69). We obtain the (lines of) equilibrium points of the system (68) and (69), which are summarized in

Table 1. Equilibrium points of System (68)–(69) for $ϵ=+1$ with their eigenvalues and stability. $P_5$ is a sink, but does not satisfy the condition (65).

Label	Existence	Coordinates $({\mathsf{\Sigma }}_{\mathit{\varphi }},\mathsf{\Sigma })$	Eigenvalues	Stability
$P_{1,2}$	$ϵ=+1$	$(\pm 1,0)$	$\{3,6\}$	Unstable
$L_1$	always	$({\mathsf{\Sigma }}_{\varphi },-3{\mathsf{\Sigma }}_{\varphi })$	$\{-3,0\}$	Stable
$P_{3,6}$	$ϵ=\pm 1$	$\left(\frac{ϵ}{\sqrt{9\mu +ϵ}},-\frac{3ϵ}{\sqrt{9\mu +ϵ}}\right)$	$\{-3,0\}$	Stable
$P_{4,7}$	$ϵ=\pm 1$	$\left(-\frac{ϵ}{\sqrt{9\mu +ϵ}},\frac{3ϵ}{\sqrt{9\mu +ϵ}}\right)$	$\{-3,0\}$	Stable
$P_5$	∄	$(0,0)$	$\{-3,0\}$	Stable

for $ϵ=\pm 1$ along with with their coordinates, eigenvalues, and stability.

4.1.1. Case $ϵ=+1$

In the case $ϵ=+1$, there exist kinetic-dominated solutions, given by the points $P_1$ and $P_2$. They represent stiff solutions ($w_{\varphi }=1$).

There is a line of equilibrium points $L_1$, which corresponds to

$$\dot{\varphi }+\frac{\sqrt{6}}{3}{\omega }_1^2=0\Rightarrow \varphi =-\frac{\sqrt{6}}{3}{\omega }_1^{2}t+c_1.$$

(70)

Then, from (55), we have at the lines of the equilibrium points

$$\begin{array}{cc}\hfill & \dot{H}=0\Rightarrow H=H_0,\Rightarrow a=e^{H_0(t-t_U)}.\hfill \end{array}$$

(71)

where $H_0$ satisfies $3H_0^2=\mathsf{\Lambda }+\frac{{\omega }_1^4ϵ}{3}$. That is a de Sitter solution.

Moreover, imposing the condition (65), the lines are reduced to the points $P_3$ and $P_4$ that belong to the lines of the equilibrium points $3{\mathsf{\Sigma }}_{\varphi }+\mathsf{\Sigma }=0$.

For these equilibrium points, we have $\dot{\varphi }=\sqrt{6}{{\mathsf{\Sigma }}_{\varphi }}_{1,2}H$, where ${{\mathsf{\Sigma }}_{\varphi }}_{1,2}=\pm 1/\sqrt{9\mu +1}$. Hence,

$$\dot{H}+{{\mathsf{\Sigma }}_{\varphi }}_{1,2}H\left(3{{\mathsf{\Sigma }}_{\varphi }}_{1,2}H+\sqrt{\mathsf{\Lambda }/\left(3\mu \right)}\right)=0.$$

(72)

That is,

$$H=\frac{\sqrt{3}{H}_0\sqrt{\frac{\mathsf{\Lambda }}{\mu }}}{\left(9H_0{{\mathsf{\Sigma }}_{\varphi }}_{1,2}+\sqrt{3}\sqrt{\frac{\mathsf{\Lambda }}{\mu }}\right)e^{(t-t_U){{\mathsf{\Sigma }}_{\varphi }}_{1,2}\sqrt{\frac{\mathsf{\Lambda }}{3\mu }}}-9H_0{{\mathsf{\Sigma }}_{\varphi }}_{1,2}}.$$

(73)

The line $L_1$ also contains the point $P_5$, which is a sink, but does not satisfy the condition (65).

Figure 1 presents a phase plot for System (68)–(69) for $ϵ=+1$ and different values of $\mu$. The dashed black line corresponds to $L_1$.

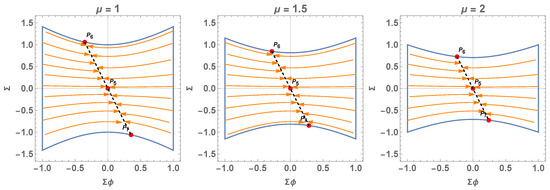
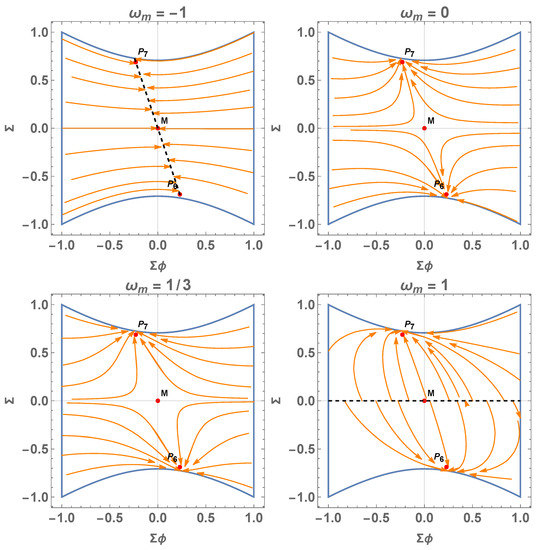
4.1.2. Case $ϵ=-1$

For the case $ϵ=-1$, the equilibrium points of the system (68) and (69) are, as before, the line $L_1$, which contains $P_5$ (which does not satisfy (65). Moreover, imposing the condition (65), the lines are reduced to the points $P_6$ and $P_7$ that belong to the lines of equilibrium points $3{\mathsf{\Sigma }}_{\varphi }+\mathsf{\Sigma }=0$, where ${{\mathsf{\Sigma }}_{\varphi }}_{1,2}=\mp 1/\sqrt{9\mu -1}$.

For these equilibrium points, we have $\dot{\varphi }=\sqrt{6}{{\mathsf{\Sigma }}_{\varphi }}_{1,2}H$. Hence,

$$\dot{H}-{{\mathsf{\Sigma }}_{\varphi }}_{1,2}H\left(3{{\mathsf{\Sigma }}_{\varphi }}_{1,2}H+\sqrt{\mathsf{\Lambda }/\left(3\mu \right)}\right)=0.$$

(74)

That is,

$$H=\frac{\sqrt{3}{H}_0\sqrt{\frac{\mathsf{\Lambda }}{\mu }}}{\left(9H_0{{\mathsf{\Sigma }}_{\varphi }}_{1,2}+\sqrt{3}\sqrt{\frac{\mathsf{\Lambda }}{\mu }}\right)e^{-(t-t_U){{\mathsf{\Sigma }}_{\varphi }}_{1,2}\sqrt{\frac{\mathsf{\Lambda }}{3\mu }}}-9H_0{{\mathsf{\Sigma }}_{\varphi }}_{1,2}}.$$

(75)

Figure 2 presents a phase plot for System (68)–(69) for $ϵ=-1$ and different values of $\mu$. The dashed black line corresponds to $L_1$.

4.2. The 1D Reduced System

Using (65) to reduce the dimensionality and for $\mathsf{\Sigma }\ge 0$, we have

$$\mathsf{\Sigma }=\sqrt{(1-{\mathsf{\Sigma }}_{\varphi }^2ϵ)/\mu }.$$

(76)

Then, we have the reduced dynamical system:

$$\begin{array}{cc}\hfill & {\mathsf{\Sigma }}_{\varphi }^{\prime }=-\left(3{\mathsf{\Sigma }}_{\varphi }+\sqrt{(1-{\mathsf{\Sigma }}_{\varphi }^2ϵ)/\mu }\right)\left(1-{\mathsf{\Sigma }}_{\varphi }^2ϵ\right),\hfill \end{array}$$

(77)

This patch covers only the equilibrium points (68)–(69) with $\mathsf{\Sigma }>0$ and ${\mathsf{\Sigma }}_{\varphi }=0$, say $P_1:{\mathsf{\Sigma }}_{\varphi }=1$, $P_2:{\mathsf{\Sigma }}_{\varphi }=-1$ and $P_4:{\mathsf{\Sigma }}_{\varphi }=-1/\sqrt{9\mu +1}$. Moreover, the equilibrium point of the 1D system (77) is $P_6:{\mathsf{\Sigma }}_{\varphi }=-1/\sqrt{9\mu -1}$.

Table 2. Equilibrium points of System (77) for $ϵ=\pm 1$ with their eigenvalues and stability.

Label	Existence	Coordinates ${\mathit{\Sigma }}_{\mathit{\varphi }}$	Eigenvalue	Stability
$P_{1,2}$	$ϵ=+1$	$\pm 1$	6	Unstable
$P_3$	$ϵ=+1,\mu >-\frac{1}{9}$	$\frac{1}{\sqrt{9\mu +1}}$	$-3$	Stable
$P_6$	$ϵ=-1,\mu >\frac{1}{9}$	$-\frac{1}{\sqrt{9\mu -1}}$	$-3$	Stable

presents the equilibrium points of System (77) for $ϵ=\pm 1$ with their eigenvalues and stability.

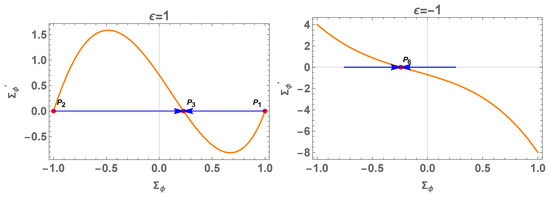
Figure 3 presents a phase plot for the reduced 1D equation (77) for $ϵ=\pm 1$ and $\mu =2$.

On the other hand, using

$$\mathsf{\Sigma }=-\sqrt{(1-{\mathsf{\Sigma }}_{\varphi }^2ϵ)/\mu },$$

(78)

we have the reduced dynamical system:

$$\begin{array}{cc}\hfill & {\mathsf{\Sigma }}_{\varphi }^{\prime }=-\left(3{\mathsf{\Sigma }}_{\varphi }-\sqrt{(1-{\mathsf{\Sigma }}_{\varphi }^2ϵ)/\mu }\right)\left(1-{\mathsf{\Sigma }}_{\varphi }^2ϵ\right),\hfill \end{array}$$

(79)

This patch covers only the equilibrium points (68)–(69) with $\mathsf{\Sigma }<0$ and ${\mathsf{\Sigma }}_{\varphi }=0$, say $P_1:{\mathsf{\Sigma }}_{\varphi }=1$, $P_2:{\mathsf{\Sigma }}_{\varphi }=-1$ and $P_3:{\mathsf{\Sigma }}_{\varphi }:=1/\sqrt{9\mu +1}$. Moreover, the equilibrium point of the 1D system (79) is $P_7:{\mathsf{\Sigma }}_{\varphi }=1/\sqrt{9\mu -1}$, which belongs to the lines of the equilibrium points $3{\mathsf{\Sigma }}_{\varphi }+\mathsf{\Sigma }=0$.

Table 3. Equilibrium points of System (79) for $ϵ=\pm 1$ with their eigenvalues and stability.

Label	Existence	Coordinates ${\mathsf{\Sigma }}_{\mathit{\varphi }}$	Eigenvalue	Stability
$P_{1,2}$	$\pm 1$	$ϵ=+1$	6	Unstable
$P_4$	$ϵ=+1,\mu >-\frac{1}{9}$	$-\frac{1}{\sqrt{9\mu +1}}$	$-3$	Stable
$P_7$	$ϵ=-1,\mu >\frac{1}{9}$	$\frac{1}{\sqrt{9\mu -1}}$	$-3$	Stable

presents the equilibrium points of System (79) for $ϵ=\pm 1$ with their eigenvalues and stability.

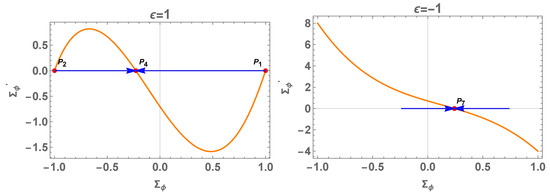
Figure 4 presents a phase plot for the reduced 1D equation (79) for $ϵ=\pm 1$ and $\mu =2$.

5. Dynamical Systems’ Analysis by Including Matter

We define

$${\mathsf{\Sigma }}_{\varphi }=\frac{\dot{\varphi }}{\sqrt{6}H},\mathsf{\Sigma }=\frac{{\omega }_1^2}{H},{\mathsf{\Omega }}_m=\frac{{\rho }_m}{3H^2},$$

(80)

which satisfy

$${{\mathsf{\Sigma }}_{\varphi }}^2ϵ+\mu {\mathsf{\Sigma }}^2+{\mathsf{\Omega }}_m=1.$$

(81)

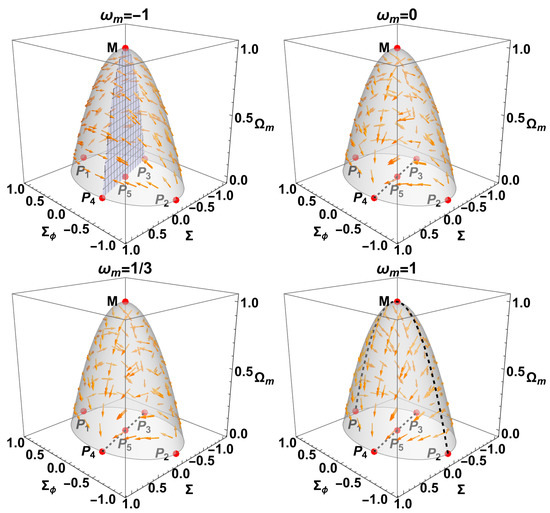
5.1. The 3D System

The system (52), (53), and (52) can be written as the dynamical system given by

$$\begin{array}{cc}\hfill & {{\mathsf{\Sigma }}_{\varphi }}^{\prime }=\frac{3}{2}(w_m+1){\mathsf{\Sigma }}_{\varphi }{\mathsf{\Omega }}_m+(3{\mathsf{\Sigma }}_{\varphi }+\mathsf{\Sigma })\left({{\mathsf{\Sigma }}_{\varphi }}^2ϵ-1\right),\hfill \end{array}$$

(82)

$$\begin{array}{cc}\hfill & {\mathsf{\Sigma }}^{\prime }=\frac{3}{2}(w_m+1)\mathsf{\Sigma }{\mathsf{\Omega }}_m+{\mathsf{\Sigma }}_{\varphi }\mathsf{\Sigma }ϵ(3{\mathsf{\Sigma }}_{\varphi }+\mathsf{\Sigma }),\hfill \end{array}$$

(83)

$$\begin{array}{cc}\hfill & {\mathsf{\Omega }}_m^{\prime }={\mathsf{\Omega }}_m(3w_m({\mathsf{\Omega }}_m-1)+2{\mathsf{\Sigma }}_{\varphi }ϵ(3{\mathsf{\Sigma }}_{\varphi }+\mathsf{\Sigma })+3({\mathsf{\Omega }}_m-1)).\hfill \end{array}$$

(84)

Table 4. Equilibrium points of System (82), (83), and (84) for $ϵ=\pm 1$ with their eigenvalues and stability.

Label	Existence	Coordinates $({\mathsf{\Sigma }}_{\mathit{\varphi }},\mathsf{\Sigma },{\mathsf{\Omega }}_{\mathit{m}})$	Eigenvalues	Stability
$P_{1,2}$	$ϵ=+1$	$(\pm 1,0,0)$	$\{3,6,3(1-{\omega }_m)\}$	Unstable
$L_1$	always	$({\mathsf{\Sigma }}_{\varphi },-3{\mathsf{\Sigma }}_{\varphi },0)$	$\{-3,0,-3({\omega }_m+1)\}$	Stable
$P_{3,6}$	$ϵ=\pm 1$	$\left(\frac{ϵ}{\sqrt{9\mu +ϵ}},-\frac{3ϵ}{\sqrt{9\mu +ϵ}},0\right)$	$\{-3,0,-3({\omega }_m+1)\}$	Stable
$P_{4,7}$	$ϵ=\pm 1$	$\left(-\frac{ϵ}{\sqrt{9\mu +ϵ}},\frac{3ϵ}{\sqrt{9\mu +ϵ}},0\right)$	$\{-3,0,-3({\omega }_m+1)\}$	Stable
$P_5$	∄	$(0,0,0)$	$\{-3,0,-3({\omega }_m+1)\}$	Stable
M	$ϵ=\pm 1$	$(0,0,1)$	$\left\{\frac{3({\omega }_m-1)}{2},\frac{3({\omega }_m+1)}{2},3({\omega }_m+1)\right\}$	Stable for ${\omega }_m=-1$
				Unstable for ${\omega }_m=1$
				Saddle otherwise

presents the equilibrium points of System (82), (83), and (84) for $ϵ=\pm 1$ with their eigenvalues and stability.

5.1.1. Case $ϵ=+1$

For the case $ϵ=+1$, the equilibrium points of the system (82), (83), and (84) are $P_1$, $P_2$, which are kinetic-dominated solutions. The line of equilibrium points $L_1$ represents the de Sitter solutions. This line contains the points $P_3$, $P_4$, and $P_5$. Additionally, we have the matter-dominated solution $M:\left({\mathsf{\Sigma }}_{\varphi },\mathsf{\Sigma },{\mathsf{\Omega }}_m\right)=(0,0,1)$.

Figure 5 presents a 3D phase plot for System (82), (83), and (84) for $ϵ=1$, $\mu =2$, and different values of ${\omega }_m$.

5.1.2. Case $ϵ=-1$

For the case $ϵ=-1$, the equilibrium points of the system (82), (83), and (84) are the line of equilibrium points $L_1$, which represents the de Sitter solutions. This line contains the points $P_5$, $P_6$, and $P_7$. Additionally, we have the matter-dominated solution $M:\left({\mathsf{\Sigma }}_{\varphi },\mathsf{\Sigma },{\mathsf{\Omega }}_m\right)=(0,0,1)$.

Figure 6 presents a 3D phase plot for System (82), (83), and (84) for $ϵ=-1$, $\mu =2$, and different values of ${\omega }_m$.

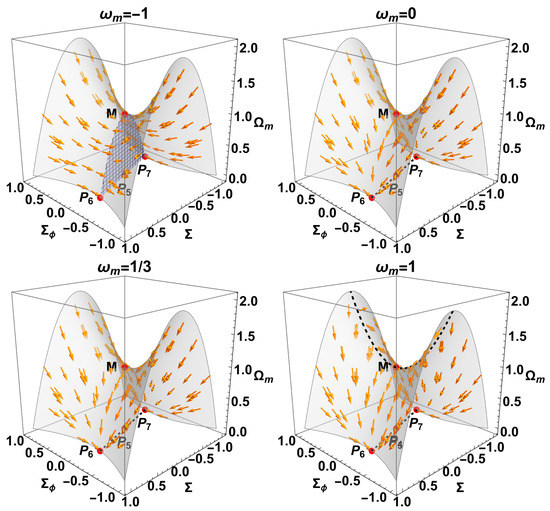
5.2. Reduced 2D System

Eliminate ${\mathsf{\Omega }}_m$ from (81) to obtain the reduced system:

$$\begin{array}{cc}\hfill & {{\mathsf{\Sigma }}_{\varphi }}^{\prime }=-\frac{1}{2}\left({{\mathsf{\Sigma }}_{\varphi }}^2ϵ-1\right)(3(w_m-1){\mathsf{\Sigma }}_{\varphi }-2\mathsf{\Sigma })-\frac{3}{2}\mu (w_m+1){\mathsf{\Sigma }}_{\varphi }{\mathsf{\Sigma }}^2,\hfill \end{array}$$

(85)

$$\begin{array}{cc}\hfill & {\mathsf{\Sigma }}^{\prime }=\frac{3}{2}(w_m+1)\mathsf{\Sigma }\left(1-{{\mathsf{\Sigma }}_{\varphi }}^2ϵ-\mu {\mathsf{\Sigma }}^2\right)+{\mathsf{\Sigma }}_{\varphi }\mathsf{\Sigma }ϵ(3{\mathsf{\Sigma }}_{\varphi }+\mathsf{\Sigma }).\hfill \end{array}$$

(86)

5.2.1. Case $ϵ=+1$

The equilibrium points of the system (85) and (86) are $P_{1,2}$ $L_1$, $P_3$, $P_4,$ and M, as summarized in

Table 5. Equilibrium points of System (85) and (86) for $ϵ=+1$ with their eigenvalues and stability.

Label	Coordinates $({\mathsf{\Sigma }}_{\mathit{\varphi }},\mathsf{\Sigma })$	Eigenvalues	Stability
$P_{1,2}$	$(\pm 1,0)$	$\{3,6\}$	Unstable
$L_1$	$({\mathsf{\Sigma }}_{\varphi },-3{\mathsf{\Sigma }}_{\varphi })$	$\{-3,-3(\omega +1\left)\right\}$	Stable
$P_3$	$\left(\frac{1}{\sqrt{9\mu +1}},-\frac{3}{\sqrt{9\mu +1}}\right)$	$\{-3,-3(\omega +1\left)\right\}$	Stable
$P_4$	$\left(-\frac{1}{\sqrt{9\mu +1}},\frac{3}{\sqrt{9\mu +1}}\right)$	$\{-3,-3(\omega +1\left)\right\}$	Stable
M	$(0,0)$	$\left\{\frac{3({\omega }_m-1)}{2},3({\omega }_m+1)\right\}$	Stable for $\omega =-1$
			Unstable for $\omega =1$
			Saddle otherwise

.

Figure 7 presents the 2D projections of the system (85)–(86) for $ϵ=+1$, $\mu =2$, and different values of ${\omega }_m$.

5.2.2. Case $ϵ=-1$

The equilibrium points of the system (85) and (86) for $ϵ=-1$ are summarized in

Table 6. Equilibrium points of System (85) and (86) for $ϵ=-1$ with their eigenvalues and stability.

Label	Coordinates $({\mathsf{\Sigma }}_{\mathit{\varphi }},\mathsf{\Sigma })$	Eigenvalues	Stability
$L_1$	$({\mathsf{\Sigma }}_{\varphi },-3{\mathsf{\Sigma }}_{\varphi })$	$\{-3,-3({\omega }_m+1)\}$	Stable
$P_6$	$\left(\frac{1}{\sqrt{9\mu -1}},-\frac{3}{\sqrt{9\mu -1}}\right)$	$\{-3,-3(\omega +1\left)\right\}$	Stable
$P_7$	$\left(-\frac{1}{\sqrt{9\mu -1}},\frac{3}{\sqrt{9\mu -1}}\right)$	$\{-3,-3(\omega +1\left)\right\}$	Stable
M	$(0,0)$	$\left\{\frac{3({\omega }_m-1)}{2},3({\omega }_m+1)\right\}$	Stable for $\omega =-1$
			Unstable for $\omega =1$
			Saddle otherwise

.

Figure 8 presents the 2D projection of (85)–(86) for $ϵ=-1$, $\mu =2$, and different values of ${\omega }_m$.

6. Conclusions

In this study, we investigated the effects of the modification of the Poisson algebra on the dynamics of scalar field cosmology. Specifically, we performed a detailed phase space analysis by studying the equilibrium points and their stability, reconstructing the cosmological history.

The modified Poisson algebra modifies the field equations, introducing a cosmological constant term. The pressure component of the scalar field’s energy-momentum tensor is different from that of the canonical scalar field. Moreover, a mass term for the scalar field is introduced, which is described by the cosmological constant.

As a result, the equilibrium points provided by the modified field equations are different from those of the usual scalar field model. From the analysis, we can conclude that the modified equations can provide more than one accelerating universe, described by the de Sitter solution. Hence, cosmic inflation and late-time acceleration are provided by the specific theory.

In the matter-less case, we divided the study into two subcases, one for $ϵ=1$ and one for $ϵ=-1$. We have six families of physically acceptable equilibrium points that can describe stiff fluid solutions and de Sitter spacetime in the asymptotic regime.

In the case with the matter, we also considered the subcases $ϵ=\pm 1,$ and in total, we obtained eight families of equilibrium points, the same ones as in the case without matter and one additional equilibrium point that describes matter.

In future work, we plan to further investigate the modified field equations with the introduction of a nonzero scalar field potential. In contrast, an interacting term between the scalar field and the matter source will be considered.

The steps in this paper allow exploring the cosmological models’ feasibility in concordance with the observational data set from measurements of Supernovae Ia, Cosmic Chronometers, baryon acoustic oscillation and cosmic microwave background. However, the observational test is out of the scope of the present research.