Future Failure Time Prediction Based on a Unified Hybrid Censoring Scheme for the Burr-X Model with Engineering Applications

Abstract

Industries are constantly seeking ways to avoid corrective maintenance in order to reduce costs. Performing regular scheduled maintenance can help to mitigate this problem, but not necessarily in the most efficient way. In many real life applications, one wants to predict the future failure time of equipment or devices that are expensive, or with long lifetimes, to save costs and/or time. In this paper, statistical prediction was studied using the classical and Bayesian approaches based on a unified hybrid censoring scheme. Two prediction schemes were used: (1) a one-sample prediction scheme that predicted the unobserved future failure times of devices that did not complete the lifetime experiments; and (2) a two-sample prediction scheme to predict the ordered values of a future independent sample based on past data from a certain distribution. We chose to apply the results of the paper to the Burr-X model, due to the importance of this model in many fields, such as engineering, health, agriculture, and biology. Point and interval predictors of unobserved failure times under one- and two-sample prediction schemes were computed based on simulated data sets and two engineering applications. The results demonstrate the ability of predicting the future failure of equipment using a statistical prediction branch based on collected data from an engineering system.

1. Introduction

Industries are constantly seeking ways to avoid corrective maintenance in order to reduce costs. Performing regular scheduled maintenance can help to mitigate this problem, but not necessarily in the most efficient way, see [1,2,3]. In condition-based maintenance, the main goal is to come up with ways to treat and transform data from an engineering system, so that it can be used to build a data set to make statistical predictions about how the equipment will act in the future and when it will break down.

In many practical situations, one desires to predict future observations from the same population of previous data. This may be done by constructing an interval that will include future observations with a certain probability.

Predictive interval accuracy depends on sample size; full testing is impractical in real testing, owing to the advancement of industrial design and technology, which results in very reliable products with long lifespans. Censoring has been implemented in this case for a variety of reasons, including a lack of available resources and the need to save costs. In general, only a small percentage of failure times are recorded when a $CS$ is engaged in a test environment.

Let $X_{1:n},X_{2:n},\dots ,X_{n:n}$ be the ordered failure times of n identical units placed on a life-test, from a certain distribution with $PDF$, $f(x;\mathit{\theta })$, where $\mathit{\theta }$ is the vector of parameters and $RF$, $R(x;\mathit{\theta })$. For fixed $k,r\in \{1,2,\dots ,n\}$ and $T_1<T_2\in (0,\infty )$ with $k<r$ and upon the relation between $T_1,T_2,X_k$ and $X_r$, an $UHCS$ is defined by Balakrishnan with six decisions, as follows:

(1)

Stopping the experiment at $T_1$ if $0<X_{k:n}<X_{r:n}<T_1<T_2$;

(2)

Stopping the experiment at $X_{r:n}$ if $0<X_{k:n}<T_1<X_{r:n}<T_2$;

(3)

Stopping the experiment at $T_2$ if $0<X_{k:n}<T_1<T_2<X_{r:n}$;

(4)

Stopping the experiment at $X_{r:n}$ if $0<T_1<X_{k:n}<X_{r:n}<T_2$;

(5)

Stopping the experiment at $T_2$ if $0<T_1<X_{k:n}<T_2<X_{r:n}$;

(6)

Stopping the experiment at $X_{k:n}$ if $0<T_1<T_2<X_{k:n}<X_{r:n}$.

Let $d_i$ denote the number of failures until time $T_i$, $i=1,2$. Then, the $LF$ of this $UHCS$ censored sample is as follows:

$$\begin{array}{c}\hfill L(\mathit{\theta };data)=\left\{\begin{array}{cc}& \frac{n!}{(n-d)!}\left[{\prod }_{i=1}^{d}f(x_i;\mathit{\theta })\right]{\left[R(T_1;\mathit{\theta })\right]}^{(n-d)},d_1=d_2=d=r,\dots ,n,\hfill \\ \hfill & \frac{n!}{(n-r)!}\left[{\prod }_{i=1}^{r}f(x_i;\mathit{\theta })\right]{\left[R(x_r;\mathit{\theta })\right]}^{(n-r)},d_1=k,\dots ,r-1,d_2=r,\hfill \\ \hfill & \frac{n!}{(n-d_2)!}\left[{\prod }_{i=1}^{d_2}f(x_i;\mathit{\theta })\right]{\left[R(T_2;\mathit{\theta })\right]}^{(n-d_2)},d_1=k,\dots ,r-1,d_2=k,\dots ,r-1,d_1\le d_2\hfill \\ \hfill & \frac{n!}{(n-r)!}\left[{\prod }_{i=1}^{r}f(x_i;\mathit{\theta })\right]{\left[R(x_r;\mathit{\theta })\right]}^{(n-r)},d_1=0,1,\dots ,k-1,d_2=r,\hfill \\ \hfill & \frac{n!}{(n-d_2)!}\left[{\prod }_{i=1}^{d_2}f(x_i;\mathit{\theta })\right]{\left[R(T_2;\mathit{\theta })\right]}^{(n-d_2)},d_1=0,\dots ,k-1,d_2=k,\dots ,r-1,\hfill \\ \hfill & \frac{n!}{(n-k)!}\left[{\prod }_{i=1}^{k}f(x_i;\mathit{\theta })\right]{\left[R(x_k;\mathit{\theta })\right]}^{(n-k)},d_2=0,\dots ,k-1.\hfill \end{array}\right.\end{array}$$

(1)

Many well-known censoring schemes can be considered as special cases from the studied $UHCS$, such as generalized type-I HCS, see [4] when $T_1\to 0$, generalized type-II HCS, see [4] when $k=1$, type-I HCS, see [5], when $T_1\to 0$ and $k=1$, type-II HCS, see [5], when $T_2\to \infty$ and $k=1$, type-I censoring, see [6], when $T_1\to 0$, $k=1$, $r=n$ and type-II censoring, see [6], when $T_1\to 0$, $T_2\to \infty$ and $k=1$.

Among the advantages of $UHCS$ is that it is more flexible than the generalized type-I $HCS$ and generalized type-II $HCS$; moreover, it guarantees us more observations, which will increase the accuracy of the predictive intervals.

Ref. [7] proposes the Burr-X distribution as a member of the Burr distribution family. This model is extremely useful in the fields of statistics and operations research. Engineering, health, agriculture, and biology are just some of the fields where it can be used to great effect.

A random variable X is said to have a Burr-X with a vector of parameters $\mathit{\theta }=(\alpha ,\beta )$ if the $PDF$ is given by

$$\begin{array}{c}\hfill f(x;\alpha ,\beta )=2\alpha \beta x{e}^{-\beta x^2}{(1-e^{-\beta x^2})}^{\alpha -1},x>0,(\alpha >0,\beta >0).\end{array}$$

(2)

The corresponding $CDF$ and $RF$ are given, respectively, as:

$$\begin{array}{c}\hfill F(x;\alpha ,\beta )={(1-e^{-\beta x^2})}^{\alpha },x>0,(\alpha >0,\beta >0),\end{array}$$

(3)

$$\begin{array}{c}\hfill R(x;\alpha ,\beta )=1-{(1-e^{-\beta x^2})}^{\alpha },x>0,(\alpha >0,\beta >0).\end{array}$$

(4)

For more details about some Burr models with related inferences using classical and Bayesian approaches, see [8,9,10,11,12,13,14,15,16,17,18].

Many contributions found in this paper, such as: studying the prediction problem in a $UHCS$ using the classical and Bayesian approaches with making some comparisons between the two approaches, analyzing two engineering real data sets using Burr-X distribution and applying the obtained results on these real data sets as illustrative examples.

This paper is organized as follows: the point and interval prediction problems under one- and two-sample prediction schemes were studied using the classical and Bayesian approaches in Section 2 and Section 3, respectively. In Section 4, the obtained results were applied on simulated and real data sets. Our conclusions are summarized in Section 5.

2. One-Sample Prediction

Assume that n items are placed in a life-time experiment and that this experiment will be terminated at a fixed time $T^{*}$ and the number of failures until this time is D. The previous ordered failures denoted by $\mathit{x}=(x_{1:n},x_{2:n},\dots ,x_{D:n})$, which can be written for simplicity as $\mathit{x}=(x_1,x_2,\dots ,x_D)$, called (Informative sample). In Balakrishnan’s $UHCS$, $T^{*}$ will equal $T_1$ in the first case, $x_r$ in the second case, $T_2$ in the third case, $x_r$ in the fourth case, $T_2$ in the fifth case and $x_k$ in the sixth case. Moreover, D will equal $d_1$ in the first case, r in the second case, $d_2$ in the third case, r in the fourth case, $d_2$ in the fifth case, and k in the sixth case. In the one-sample prediction scheme, the future failure time $x_{D+s}\equiv y_s,s=1,2,\dots ,n-D$ will be predicted based on the informative sample.

In this section, the $PPs$ and $IPs$ of the future unknown failure time $y_s$ will be computed using classical and Bayesian methods.

First, the conditional $PDF$ of the future failure time $y_s$ given the vector of parameters $\mathit{\theta }$ should be derived as follows:

Based on the informative sample $\mathit{x}=(x_1,x_2,\dots ,x_D)$, the $PDF$ of $y_s$ given $\mathit{\theta }$ will be the $PDF$ of the sth ordered value from $n-D$ ordered values after $T^{*}$, which can be written as (see [15,19,20,21]):

$$\begin{array}{c}\hfill g_1(y_s;\mathit{\theta })\propto {[R(T^{*};\mathit{\theta })-R(y_s;\mathit{\theta })]}^{s-1}{\left[R(y_s;\mathit{\theta })\right]}^{n-D-s}{\left[R(T^{*};\mathit{\theta })\right]}^{-(n-D)}f(y_s;\mathit{\theta }),y_s>T^{*}.\end{array}$$

(5)

Using this $PDF$, the conditional $PDF$ of the future failure time $y_s$ given $\mathit{\theta }$ based on all cases of Balakrishnan’s $UHCS$ is:

$$\begin{array}{c}\hfill g_1(y_s;\mathit{\theta })\propto \left\{\begin{array}{cc}& {[R(T_1;\mathit{\theta })-R(y_s;\mathit{\theta })]}^{s-1}{\left[R(y_s;\mathit{\theta })\right]}^{n-d-s}{\left[R(T_1;\mathit{\theta })\right]}^{-(n-d)}f(y_s;\mathit{\theta }),y_s>T_1,\hfill \\ \hfill & d_1=d_2=d=r,\dots ,n,\hfill \\ \hfill & {[R(x_r;\mathit{\theta })-R(y_s;\mathit{\theta })]}^{s-1}{\left[R(y_s;\mathit{\theta })\right]}^{n-r-s}{\left[R(x_r;\mathit{\theta })\right]}^{-(n-r)}f(y_s;\mathit{\theta }),y_s>x_r,\hfill \\ \hfill & d_1=k,\dots ,r-1,d_2=r,\hfill \\ \hfill & {[R(T_2;\mathit{\theta })-R(y_s;\mathit{\theta })]}^{s-1}{\left[R(y_s;\mathit{\theta })\right]}^{n-d_2-s}{\left[R(T_2;\mathit{\theta })\right]}^{-(n-d_2)}f(y_s;\mathit{\theta }),y_s>T_2,\hfill \\ \hfill & d_1=k,\dots ,r-1,d_2=k,\dots ,r-1,d_1\le d_2\hfill \\ \hfill & {[R(x_r;\mathit{\theta })-R(y_s;\mathit{\theta })]}^{s-1}{\left[R(y_s;\mathit{\theta })\right]}^{n-r-s}{\left[R(x_r;\mathit{\theta })\right]}^{-(n-r)}f(y_s;\mathit{\theta }),y_s>x_r,\hfill \\ \hfill & d_1=0,1,\dots ,k-1,d_2=r,\hfill \\ \hfill & {[R(T_2;\mathit{\theta })-R(y_s;\mathit{\theta })]}^{s-1}{\left[R(y_s;\mathit{\theta })\right]}^{n-d_2-s}{\left[R(T_2;\mathit{\theta })\right]}^{-(n-d_2)}f(y_s;\mathit{\theta }),y_s>T_2,\hfill \\ \hfill & d_1=0,\dots ,k-1,d_2=k,\dots ,r-1,\hfill \\ \hfill & {[R(x_k;\mathit{\theta })-R(y_s;\mathit{\theta })]}^{s-1}{\left[R(y_s;\mathit{\theta })\right]}^{n-k-s}{\left[R(x_k;\mathit{\theta })\right]}^{-(n-k)}f(y_s;\mathit{\theta }),y_s>x_k,d_2=0,\dots ,k-1.\hfill \end{array}\right.\end{array}$$

(6)

2.1. Classical Method (Maximum Likelihood Prediction)

In this subsection, the $PPs$ and $IPs$ of $y_s$ were obtained using the following $PLF$ (see [22]):

$$\begin{array}{c}\hfill g_1^{*}(y_s;\mathit{\theta },\mathit{x})\propto L(\mathit{\theta };\mathit{x})g_1(y_s;\mathit{\theta }),y_s>T^{*}.\end{array}$$

(7)

Substituting from (1) and (6) in (7), we have

$$\begin{array}{c}\hfill g_1^{*}(y_s;\mathit{\theta },\mathit{x})\propto \left\{\begin{array}{cc}& \left[{\prod }_{i=1}^{d}f(x_i;\mathit{\theta })\right]{[R(T_1;\mathit{\theta })-R(y_s;\mathit{\theta })]}^{s-1}{\left[R(y_s;\mathit{\theta })\right]}^{n-d-s}f(y_s;\mathit{\theta }),y_s>T_1,\hfill \\ \hfill & d_1=d_2=d=r,\dots ,n,\hfill \\ \hfill & \left[{\prod }_{i=1}^{r}f(x_i;\mathit{\theta })\right]{[R(x_r;\mathit{\theta })-R(y_s;\mathit{\theta })]}^{s-1}{\left[R(y_s;\mathit{\theta })\right]}^{n-r-s}f(y_s;\mathit{\theta }),y_s>x_r,\hfill \\ \hfill & d_1=k,\dots ,r-1,d_2=r,\hfill \\ \hfill & \left[{\prod }_{i=1}^{d_2}f(x_i;\mathit{\theta })\right]{[R(T_2;\mathit{\theta })-R(y_s;\mathit{\theta })]}^{s-1}{\left[R(y_s;\mathit{\theta })\right]}^{n-d_2-s}f(y_s;\mathit{\theta }),y_s>T_2,\hfill \\ \hfill & d_1=k,\dots ,r-1,d_2=k,\dots ,r-1,d_1\le d_2\hfill \\ \hfill & \left[{\prod }_{i=1}^{r}f(x_i;\mathit{\theta })\right]{[R(x_r;\mathit{\theta })-R(y_s;\mathit{\theta })]}^{s-1}{\left[R(y_s;\mathit{\theta })\right]}^{n-r-s}f(y_s;\mathit{\theta }),y_s>x_r,\hfill \\ \hfill & d_1=0,1,\dots ,k-1,d_2=r,\hfill \\ \hfill & \left[{\prod }_{i=1}^{d_2}f(x_i;\mathit{\theta })\right]{[R(T_2;\mathit{\theta })-R(y_s;\mathit{\theta })]}^{s-1}{\left[R(y_s;\mathit{\theta })\right]}^{n-d_2-s}f(y_s;\mathit{\theta }),y_s>T_2,\hfill \\ \hfill & d_1=0,\dots ,k-1,d_2=k,\dots ,r-1,\hfill \\ \hfill & \left[{\prod }_{i=1}^{k}f(x_i;\mathit{\theta })\right]{[R(x_k;\mathit{\theta })-R(y_s;\mathit{\theta })]}^{s-1}{\left[R(y_s;\mathit{\theta })\right]}^{n-k-s}f(y_s;\mathit{\theta }),y_s>x_k,\hfill \\ \hfill & d_2=0,\dots ,k-1.\hfill \end{array}\right.\end{array}$$

(8)

Substituting from (2)–(4) in (8), we have

$$\begin{array}{c}\hfill g_1^{*}(y_s;\alpha ,\beta ,\mathit{x})\propto \left\{\begin{array}{cc}& {\alpha }^{d+1}{\beta }^{d+1}{y}_s{e}^{-\beta y_s^2}{(1-e^{-\beta y_s^2})}^{\alpha -1}\left[{\prod }_{i=1}^d{x}_i{e}^{-\beta x_i^2}{(1-e^{-\beta x_i^2})}^{\alpha -1}\right]\times \hfill \\ \hfill & {[{(1-e^{-\beta y_s^2})}^{\alpha }-{(1-e^{-\beta T_1^2})}^{\alpha }]}^{s-1}{[1-{(1-e^{-\beta y_s^2})}^{\alpha }]}^{n-d-s},y_s>T_1,\hfill \\ \hfill & d_1=d_2=d=r,\dots ,n,\hfill \\ \hfill & {\alpha }^{r+1}{\beta }^{r+1}{y}_s{e}^{-\beta y_s^2}{(1-e^{-\beta y_s^2})}^{\alpha -1}\left[{\prod }_{i=1}^r{x}_i{e}^{-\beta x_i^2}{(1-e^{-\beta x_i^2})}^{\alpha -1}\right]\times \hfill \\ \hfill & {[{(1-e^{-\beta y_s^2})}^{\alpha }-{(1-e^{-\beta x_r^2})}^{\alpha }]}^{s-1}{[1-{(1-e^{-\beta y_s^2})}^{\alpha }]}^{n-r-s},y_s>x_r,\hfill \\ \hfill & d_1=k,\dots ,r-1,d_2=r,\hfill \\ \hfill & {\alpha }^{d_2+1}{\beta }^{d_2+1}{y}_s{e}^{-\beta y_s^2}{(1-e^{-\beta y_s^2})}^{\alpha -1}\left[{\prod }_{i=1}^{d_2}{x}_i{e}^{-\beta x_i^2}{(1-e^{-\beta x_i^2})}^{\alpha -1}\right]\times \hfill \\ \hfill & {[{(1-e^{-\beta y_s^2})}^{\alpha }-{(1-e^{-\beta T_2^2})}^{\alpha }]}^{s-1}{[1-{(1-e^{-\beta y_s^2})}^{\alpha }]}^{n-d_2-s},y_s>T_2,\hfill \\ \hfill & d_1=k,\dots ,r-1,d_2=k,\dots ,r-1,d_1\le d_2\hfill \\ \hfill & {\alpha }^{r+1}{\beta }^{r+1}{y}_s{e}^{-\beta y_s^2}{(1-e^{-\beta y_s^2})}^{\alpha -1}\left[{\prod }_{i=1}^r{x}_i{e}^{-\beta x_i^2}{(1-e^{-\beta x_i^2})}^{\alpha -1}\right]\times \hfill \\ \hfill & {[{(1-e^{-\beta y_s^2})}^{\alpha }-{(1-e^{-\beta x_r^2})}^{\alpha }]}^{s-1}{[1-{(1-e^{-\beta y_s^2})}^{\alpha }]}^{n-r-s},y_s>x_r,\hfill \\ \hfill & d_1=0,1,\dots ,k-1,d_2=r,\hfill \\ \hfill & {\alpha }^{d_2+1}{\beta }^{d_2+1}{y}_s{e}^{-\beta y_s^2}{(1-e^{-\beta y_s^2})}^{\alpha -1}\left[{\prod }_{i=1}^{d_2}{x}_i{e}^{-\beta x_i^2}{(1-e^{-\beta x_i^2})}^{\alpha -1}\right]\times \hfill \\ \hfill & {[{(1-e^{-\beta y_s^2})}^{\alpha }-{(1-e^{-\beta T_2^2})}^{\alpha }]}^{s-1}{[1-{(1-e^{-\beta y_s^2})}^{\alpha }]}^{n-d_2-s},y_s>T_2,\hfill \\ \hfill & d_1=0,\dots ,k-1,d_2=k,\dots ,r-1,\hfill \\ \hfill & {\alpha }^{k+1}{\beta }^{k+1}{y}_s{e}^{-\beta y_s^2}{(1-e^{-\beta y_s^2})}^{\alpha -1}\left[{\prod }_{i=1}^k{x}_i{e}^{-\beta x_i^2}{(1-e^{-\beta x_i^2})}^{\alpha -1}\right]\times \hfill \\ \hfill & {[{(1-e^{-\beta y_s^2})}^{\alpha }-{(1-e^{-\beta x_k^2})}^{\alpha }]}^{s-1}{[1-{(1-e^{-\beta y_s^2})}^{\alpha }]}^{n-k-s},y_s>x_k,\hfill \\ \hfill & d_2=0,\dots ,k-1.\hfill \end{array}\right.\end{array}$$

(9)

2.1.1. Point Predictor

In this subsection, the $PPs$ of $y_s$ will be obtained using two methods.

Method (1):

obtaining the values of $\alpha ,\beta$, and $y_s$, which maximize the logarithm of the $PLF$, and will be denoted by ${\alpha }^{*},{\beta }^{*}$, and $y_s^{*}$, respectively. The values ${\alpha }^{*}$ and ${\beta }^{*}$ will be called the $PMLEs$ and the value $y^{*}$ will be called the $MLP$ of $y_s$.

To maximize the logarithm of the $PLF$, we will differentiate $log\left(g_1^{*}(y_s;\alpha ,\beta ,\mathit{x})\right)$ with respect to $\alpha ,\beta$, and $y_s$, set the resulting derivatives to zero and solve the resulting nonlinear equations. The solution of the resulting nonlinear equations will be ${\alpha }^{*},{\beta }^{*}$, and $y^{*}$.

Method (2):

first, the $MLEs$ of the parameters $\alpha$ and $\beta$, denoted by $\widehat{\alpha }$ and $\widehat{\beta }$, will be obtained, then replace $\alpha$ and $\beta$ by $\widehat{\alpha }$ and $\widehat{\beta }$, respectively, in the $PLF$, to obtain the $MLPF$ in the form: $g_1^{**}(y_s;\mathit{x})=g_1^{*}(y_s;\widehat{\alpha },\widehat{\beta },\mathit{x}),$ and finally the $MLP$ of $y_s$ will be equal to ${\int }_{T^{*}}^{\infty }{y}_s{g}_1^{**}(y_s;\mathit{x})d{y}_s$, which represents the mathematical expectation of the random variable $Y_s$. To obtain the ($MLEs$) of $\alpha$ and $\beta$, we will differentiate the logarithm of the $LF$ then set the resulting equations to zero and solve the resulting nonlinear equations. The solution of the resulting nonlinear equations will be $\widehat{\alpha }$ and $\widehat{\beta }$.

Based on the studied $UHCS$, $g_1^{**}(y_s;\mathit{x})$ can be written in the form:

$$\begin{array}{c}\hfill g_1^{**}(y_s;\mathit{x})=A{y}_s{e}^{-\widehat{\beta }{y}_s^2}{(1-e^{-\widehat{\beta }{y}_s^2})}^{\widehat{\alpha }-1}{[{(1-e^{-\widehat{\beta }{y}_s^2})}^{\widehat{\alpha }}-{(1-e^{-\widehat{\beta }{T}^{{*}^2}})}^{\widehat{\alpha }}]}^{s-1}{[1-{(1-e^{-\widehat{\beta }{y}_s^2})}^{\widehat{\alpha }}]}^{n-D-s},y_s>T^{*},\end{array}$$

(10)

where A is a normalizing constant and has the value

$$\begin{array}{c}\hfill A=\frac{1}{{\int }_{T^{*}}^{\infty }\left(y_s{e}^{-\widehat{\beta }{y}_s^2}{(1-e^{-\widehat{\beta }{y}_s^2})}^{\widehat{\alpha }-1}{[{(1-e^{-\widehat{\beta }{y}_s^2})}^{\widehat{\alpha }}-{(1-e^{-\widehat{\beta }{T}^{{*}^2}})}^{\widehat{\alpha }}]}^{s-1}{[1-{(1-e^{-\widehat{\beta }{y}_s^2})}^{\widehat{\alpha }}]}^{n-D-s}\right)d{y}_s}.\end{array}$$

(11)

So, the $MLP$ of $y_s$ will be

$$\begin{array}{cc}\hfill y_s^{*}=E\left[Y_s\right]=& {\int }_{T^{*}}^{\infty }{y}_s{g}_1^{**}(y_s;\mathit{x})d{y}_s=\hfill \\ \hfill & \frac{{\int }_{T^{*}}^{\infty }\left(y_s^2{e}^{-\widehat{\beta }{y}_s^2}{(1-e^{-\widehat{\beta }{y}_s^2})}^{\widehat{\alpha }-1}{[{(1-e^{-\widehat{\beta }{y}_s^2})}^{\widehat{\alpha }}-{(1-e^{-\widehat{\beta }{T}^{{*}^2}})}^{\widehat{\alpha }}]}^{s-1}{[1-{(1-e^{-\widehat{\beta }{y}_s^2})}^{\widehat{\alpha }}]}^{n-D-s}\right)d{y}_s}{{\int }_{T^{*}}^{\infty }\left(y_s{e}^{-\widehat{\beta }{y}_s^2}{(1-e^{-\widehat{\beta }{y}_s^2})}^{\widehat{\alpha }-1}{[{(1-e^{-\widehat{\beta }{y}_s^2})}^{\widehat{\alpha }}-{(1-e^{-\widehat{\beta }{T}^{{*}^2}})}^{\widehat{\alpha }}]}^{s-1}{[1-{(1-e^{-\widehat{\beta }{y}_s^2})}^{\widehat{\alpha }}]}^{n-D-s}\right)d{y}_s},\hfill \end{array}$$

(12)

where

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}& D=d,y_s>T^{*},T^{*}=T_1,d_1=d_2=d=r,\dots ,n,\hfill \\ \hfill & D=r,y_s>T^{*},T^{*}=x_r,d_1=k,\dots ,r-1,d_2=r,\hfill \\ \hfill & D=d_2,y_s>T^{*},T^{*}=T_2,d_1=k,\dots ,r-1,d_2=k,\dots ,r-1,d_1\le d_2\hfill \\ \hfill & D=r,y_s>T^{*},T^{*}=x_r,d_1=0,1,\dots ,k-1,d_2=r,\hfill \\ \hfill & D=d_2,y_s>T^{*},T^{*}=T_2,d_1=0,\dots ,k-1,d_2=k,\dots ,r-1,\hfill \\ \hfill & D=k,y_s>T^{*},T^{*}=x_k,d_2=0,\dots ,k-1.\hfill \end{array}\right.\end{array}$$

(13)

2.1.2. Interval Predictor

A $(1-\tau )\times 100\%$ $MLPI$ $(L{M}_1,U{M}_1)$ of the future failure time $y_s$ can be obtained by solving the following two nonlinear equations:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\int }_{L{M}_1}^{\infty }{g}_1^{**}(y_s;\mathit{x})d{y}_s=1-\frac{\tau }{2},\hfill \\ {\int }_{U{M}_1}^{\infty }{g}_1^{**}(y_s;\mathit{x})d{y}_s=\frac{\tau }{2}.\hfill \end{array}\right.\end{array}$$

(14)

From (10) and (11) in (14), the two nonlinear equations in (14) can be rewritten to be of the form

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}& \frac{{\int }_{L{M}_1}^{\infty }\left(y_s{e}^{-\widehat{\beta }{y}_s^2}{(1-e^{-\widehat{\beta }{y}_s^2})}^{\widehat{\alpha }-1}{[{(1-e^{-\widehat{\beta }{y}_s^2})}^{\widehat{\alpha }}-{(1-e^{-\widehat{\beta }{T}^{{*}^2}})}^{\widehat{\alpha }}]}^{s-1}{[1-{(1-e^{-\widehat{\beta }{y}_s^2})}^{\widehat{\alpha }}]}^{n-D-s}\right)d{y}_s}{{\int }_{T^{*}}^{\infty }\left(y_s{e}^{-\widehat{\beta }{y}_s^2}{(1-e^{-\widehat{\beta }{y}_s^2})}^{\widehat{\alpha }-1}{[{(1-e^{-\widehat{\beta }{y}_s^2})}^{\widehat{\alpha }}-{(1-e^{-\widehat{\beta }{T}^{{*}^2}})}^{\widehat{\alpha }}]}^{s-1}{[1-{(1-e^{-\widehat{\beta }{y}_s^2})}^{\widehat{\alpha }}]}^{n-D-s}\right)d{y}_s}=1-\frac{\tau }{2},\hfill \\ \hfill & \frac{{\int }_{U{M}_1}^{\infty }\left(y_s{e}^{-\widehat{\beta }{y}_s^2}{(1-e^{-\widehat{\beta }{y}_s^2})}^{\widehat{\alpha }-1}{[{(1-e^{-\widehat{\beta }{y}_s^2})}^{\widehat{\alpha }}-{(1-e^{-\widehat{\beta }{T}^{{*}^2}})}^{\widehat{\alpha }}]}^{s-1}{[1-{(1-e^{-\widehat{\beta }{y}_s^2})}^{\widehat{\alpha }}]}^{n-D-s}\right)d{y}_s}{{\int }_{T^{*}}^{\infty }\left(y_s{e}^{-\widehat{\beta }{y}_s^2}{(1-e^{-\widehat{\beta }{y}_s^2})}^{\widehat{\alpha }-1}{[{(1-e^{-\widehat{\beta }{y}_s^2})}^{\widehat{\alpha }}-{(1-e^{-\widehat{\beta }{T}^{{*}^2}})}^{\widehat{\alpha }}]}^{s-1}{[1-{(1-e^{-\widehat{\beta }{y}_s^2})}^{\widehat{\alpha }}]}^{n-D-s}\right)d{y}_s}=\frac{\tau }{2}.\hfill \end{array}\right.\end{array}$$

(15)

By solving the previous system, the $MLPI$ of $y_s$, $(L{M}_1,U{M}_1)$, can be computed.

2.2. Bayesian Method (Bayesian Prediction)

Using the following bivariate prior suggested by [23,24]:

$$\begin{array}{cc}\hfill \pi (\alpha ,\beta )\propto & {\alpha }^{c_1+c_3-1}{\beta }^{c_3-1}{e}^{-\alpha (\beta +c_2)},\alpha >0,\beta >0,(c_1>0,c_2>0,c_3>0),\hfill \end{array}$$

(16)

where $c_1,c_2$, and $c_3$ are the prior parameters ( also known as hyperparameters) and $LF$ (1) replace $f(x_i;\mathit{\theta })$ and $R(x_i;\mathit{\theta })$ by its definitions from (2) and (4), the posterior $PDF$ of $\alpha$ and $\beta$ can be written as:

$$\begin{array}{c}\hfill {\pi }^{*}(\alpha ,\beta ;\mathit{x})\propto \left\{\begin{array}{cc}& {\alpha }^{d+c_1+c_3-1}{\beta }^{d+c_3-1}{e}^{-\alpha (\beta +c_2)}\left[{\prod }_{i=1}^d{x}_i{e}^{-\beta x_i^2}{(1-e^{-\beta x_i^2})}^{\alpha -1}\right]\times \hfill \\ \hfill & {[1-{(1-e^{-\beta T_1^2})}^{\alpha }]}^{n-d-s},d_1=d_2=d=r,\dots ,n,\hfill \\ \hfill & {\alpha }^{r+c_1+c_3-1}{\beta }^{r+c_3-1}{e}^{-\alpha (\beta +c_2)}\left[{\prod }_{i=1}^r{x}_i{e}^{-\beta x_i^2}{(1-e^{-\beta x_i^2})}^{\alpha -1}\right]\times \hfill \\ \hfill & {[1-{(1-e^{-\beta x_r^2})}^{\alpha }]}^{n-r-s},d_1=k,\dots ,r-1,d_2=r,\hfill \\ \hfill & {\alpha }^{d_2+c_1+c_3-1}{\beta }^{d_2+c_3-1}{e}^{-\alpha (\beta +c_2)}\left[{\prod }_{i=1}^{d_2}{x}_i{e}^{-\beta x_i^2}{(1-e^{-\beta x_i^2})}^{\alpha -1}\right]\times \hfill \\ \hfill & {[1-{(1-e^{-\beta T_2^2})}^{\alpha }]}^{n-d_2-s},d_1=k,\dots ,r-1,d_2=k,\dots ,r-1,d_1\le d_2\hfill \\ \hfill & {\alpha }^{r+c_1+c_3-1}{\beta }^{r+c_3-1}{e}^{-\alpha (\beta +c_2)}\left[{\prod }_{i=1}^r{x}_i{e}^{-\beta x_i^2}{(1-e^{-\beta x_i^2})}^{\alpha -1}\right]\times \hfill \\ \hfill & {[1-{(1-e^{-\beta x_r^2})}^{\alpha }]}^{n-r-s},d_1=0,1,\dots ,k-1,d_2=r,\hfill \\ \hfill & {\alpha }^{d_2+c_1+c_3-1}{\beta }^{d_2+c_3-1}{e}^{-\alpha (\beta +c_2)}\left[{\prod }_{i=1}^r{x}_i{e}^{-\beta x_i^2}{(1-e^{-\beta x_i^2})}^{\alpha -1}\right]\times \hfill \\ \hfill & {[1-{(1-e^{-\beta T_2^2})}^{\alpha }]}^{n-d_2-s},d_1=0,\dots ,k-1,d_2=k,\dots ,r-1,\hfill \\ \hfill & {\alpha }^{k+c_1+c_3-1}{\beta }^{k+c_3-1}{e}^{-\alpha (\beta +c_2)}\left[{\prod }_{i=1}^k{x}_i{e}^{-\beta x_i^2}{(1-e^{-\beta x_i^2})}^{\alpha -1}\right]\times \hfill \\ \hfill & {[1-{(1-e^{-\beta x_k^2})}^{\alpha }]}^{n-k-s},d_2=0,\dots ,k-1.\hfill \end{array}\right.\end{array}$$

(17)

Using the previous posterior $PDF$ and the conditional $PDF$ of $y_s$ given $\alpha$ and $\beta$, (6), after using the definition of $f(x_i;\mathit{\theta })$ and $R(x_i;\mathit{\theta })$ from (2) and (4), the Bayesian predictive $PDF$ of $y_s$ given $\mathit{x}$ will be as follows (see [22]):

$$\begin{array}{c}\hfill h_1^{*}(y_s;\mathit{x})={\int }_0^{\infty }{\int }_0^{\infty }{h}_1(y_s;\alpha ,\beta ,\mathit{x})d\beta d\alpha ,\end{array}$$

(18)

where

$$\begin{array}{cc}\hfill h_1(y_s;\alpha ,\beta ,\mathit{x})=& {\pi }^{*}(\alpha ,\beta ;\mathit{x})g_1(y_s;\alpha ,\beta )=\hfill \\ \hfill & \left\{\begin{array}{c}{A}_1{y}_s{\alpha }^{d+c_1+c_3}{\beta }^{d+c_3}{e}^{-(\alpha (\beta +c_2)+\beta y_s^2)}{(1-e^{-\beta y_s^2})}^{\alpha -1}\times \hfill \\ [{\prod }_{i=1}^d{x}_i{e}^{-\beta x_i^2}{(1-e^{-\beta x_i^2})}^{\alpha -1}]{[{(1-e^{-\beta y_s^2})}^{\alpha }-{(1-e^{-\beta T_1^2})}^{\alpha }]}^{s-1}\times \hfill \\ {[1-{(1-e^{-\beta y_s^2})}^{\alpha }]}^{n-d-s},y_s>T_1,d_1=d_2=d=r,\dots ,n,\hfill \\ A_2{y}_s{\alpha }^{r+c_1+c_3}{\beta }^{r+c_3}{e}^{-(\alpha (\beta +c_2)+\beta y_s^2)}{(1-e^{-\beta y_s^2})}^{\alpha -1}\times \hfill \\ [{\prod }_{i=1}^r{x}_i{e}^{-\beta x_i^2}{(1-e^{-\beta x_i^2})}^{\alpha -1}]{[{(1-e^{-\beta y_s^2})}^{\alpha }-{(1-e^{-\beta x_r^2})}^{\alpha }]}^{s-1}\times \hfill \\ {[1-{(1-e^{-\beta y_s^2})}^{\alpha }]}^{n-r-s},y_s>x_r,d_1=k,\dots ,r-1,d_2=r,\hfill \\ A_3{y}_s{\alpha }^{d_2+c_1+c_3}{\beta }^{d_2+c_3}{e}^{-(\alpha (\beta +c_2)+\beta y_s^2)}{(1-e^{-\beta y_s^2})}^{\alpha -1}\times \hfill \\ [{\prod }_{i=1}^{d_2}{x}_i{e}^{-\beta x_i^2}{(1-e^{-\beta x_i^2})}^{\alpha -1}]{[{(1-e^{-\beta y_s^2})}^{\alpha }-{(1-e^{-\beta T_2^2})}^{\alpha }]}^{s-1}\times \hfill \\ {[1-{(1-e^{-\beta y_s^2})}^{\alpha }]}^{n-d_2-s},y_s>T_2,d_1=k,\dots ,r-1,d_2=k,\dots ,r-1,d_1\le d_2\hfill \\ A_4{y}_s{\alpha }^{r+c_1+c_3}{\beta }^{r+c_3}{e}^{-(\alpha (\beta +c_2)+\beta y_s^2)}{(1-e^{-\beta y_s^2})}^{\alpha -1}\times \hfill \\ [{\prod }_{i=1}^r{x}_i{e}^{-\beta x_i^2}{(1-e^{-\beta x_i^2})}^{\alpha -1}]{[{(1-e^{-\beta y_s^2})}^{\alpha }-{(1-e^{-\beta x_r^2})}^{\alpha }]}^{s-1}\times \hfill \\ {[1-{(1-e^{-\beta y_s^2})}^{\alpha }]}^{n-r-s},y_s>x_r,d_1=0,1,\dots ,k-1,d_2=r,\hfill \\ A_5{y}_s{\alpha }^{d_2+c_1+c_3}{\beta }^{d_2+c_3}{e}^{-(\alpha (\beta +c_2)+\beta y_s^2)}{(1-e^{-\beta y_s^2})}^{\alpha -1}\times \hfill \\ [{\prod }_{i=1}^{d_2}{x}_i{e}^{-\beta x_i^2}{(1-e^{-\beta x_i^2})}^{\alpha -1}]{[{(1-e^{-\beta y_s^2})}^{\alpha }-{(1-e^{-\beta T_2^2})}^{\alpha }]}^{s-1}\times \hfill \\ {[1-{(1-e^{-\beta y_s^2})}^{\alpha }]}^{n-d_2-s},y_s>T_2,d_1=0,...,k-1,d_2=k,\dots ,r-1,\hfill \\ A_6{y}_s{\alpha }^{k+c_1+c_3}{\beta }^{k+c_3}{e}^{-(\alpha (\beta +c_2)+\beta y_s^2)}{(1-e^{-\beta y_s^2})}^{\alpha -1}\times \hfill \\ [{\prod }_{i=1}^k{x}_i{e}^{-\beta x_i^2}{(1-e^{-\beta x_i^2})}^{\alpha -1}]{[{(1-e^{-\beta y_s^2})}^{\alpha }-{(1-e^{-\beta x_k^2})}^{\alpha }]}^{s-1}\times \hfill \\ {[1-{(1-e^{-\beta y_s^2})}^{\alpha }]}^{n-k-s},y_s>x_k,d_2=0,\dots ,k-1,\hfill \end{array}\right.\hfill \end{array}$$

(19)

where $A_i,i=1,2,\dots ,6$ are normalizing constants.

The $BP$ of $y_s$ will equal to (see [22]):

$$\begin{array}{c}\hfill y_s^{**}=E\left[Y_s\right]={\int }_{T^{*}}^{\infty }{y}_s{h}_1^{*}(y_s;\mathit{x})d{y}_s,\end{array}$$

(20)

and the $(1-\tau )\times 100\%$ $BPI$, $(L{B}_1,U{B}_1)$, of $y_s$ can be obtained by solving the following two nonlinear equations:

$$\left\{\begin{array}{c}{\int }_{L{B}_1}^{\infty }{h}_1^{*}(y_s;\mathit{x})d{y}_s=1-\frac{\tau }{2},\hfill \\ {\int }_{U{B}_1}^{\infty }{h}_1^{*}(y_s;\mathit{x})d{y}_s=\frac{\tau }{2}.\hfill \end{array}\right.$$

(21)

It is clear that the previous system contains double integration on $\alpha$ and $\beta$, which will make the problem of finding the solution for this system very complicated. In this situation, the Gibbs sampler and Metropolis–Hastings algorithm were used to generate a random sample $({\alpha }^{\left(1\right)},{\beta }^{\left(1\right)}),({\alpha }^{\left(2\right)},{\beta }^{\left(2\right)}),\dots ,({\alpha }^{\left(K\right)},{\beta }^{\left(K\right)})$ from the posterior $PDF$ $\left(17\right)$; the the system (21) will be of the form

$$\left\{\begin{array}{c}\frac{{\sum }_{i=1}^K{\int }_{L{B}_1}^{\infty }{h}_1(y_s;{\alpha }^{\left(i\right)},{\beta }^{\left(i\right)},\mathit{x})d{y}_s}{{\sum }_{i=1}^K{\int }_{T^{*}}^{\infty }{h}_1(y_s;{\alpha }^{\left(i\right)},{\beta }^{\left(i\right)},\mathit{x})d{y}_s}=1-\frac{\tau }{2},\hfill \\ \frac{{\sum }_{i=1}^K{\int }_{U{B}_1}^{\infty }{h}_1(y_s;{\alpha }^{\left(i\right)},{\beta }^{\left(i\right)},\mathit{x})d{y}_s}{{\sum }_{i=1}^K{\int }_{T^{*}}^{\infty }{h}_1(y_s;{\alpha }^{\left(i\right)},{\beta }^{\left(i\right)},\mathit{x})d{y}_s}=\frac{\tau }{2}.\hfill \end{array}\right.$$

(22)

By solving this system, the $BPI$, $(L{B}_1,U{B}_1)$, for $y_s$ will be obtained.

For more details about the Gibbs sampler and Metropolis–Hastings algorithms, see, for example [25,26,27,28].

3. Two-Sample Prediction

Assume that $\mathit{x}=(x_1,x_2,\dots ,x_D)$ and $\mathbf{z}=(z_1,z_2,\dots ,z_m)$ represent the informative sample, from the studied $UHCS$ and a future ordered sample of size m, respectively. It is assumed that the two samples are independent.

In this section, $PPs$ and $IPs$ of the observation $z_s,s=1,2,\dots ,m$ will be obtained using the classical and Bayesian methods. The conditional $PDF$ of the observation $z_s$ given the vector of parameters $\mathit{\theta }$ is the $PDF$ of the sth ordered value from the m ordered values, which can be written as (see [15,22]):

$$\begin{array}{c}\hfill g_2(z_s;\mathit{\theta })\propto {[1-R(z_s;\mathit{\theta })]}^{s-1}{\left[R(z_s;\mathit{\theta })\right]}^{m-s}f(z_s;\mathit{\theta }),z_s>0.\end{array}$$

(23)

Using the definitions of $R(x;\mathit{\theta })$ and $f(x;\mathit{\theta })$ from (2) and (4) in (23), the conditional $PDF$ of the observation $z_s$ given $\mathit{\theta }$ will be:

$$\begin{array}{c}\hfill g_2(z_s;\alpha ,\beta )\propto \alpha \beta z_s{e}^{-\beta z_s^2}{(1-e^{-\beta z_s^2})}^{s\alpha -1}{[1-{(1-e^{-\beta z_s^2})}^{\alpha }]}^{m-s},z_s>0.\end{array}$$

(24)

Based on the two-sample scheme and the same prior (16), the $IPs$ and $PPs$ of $z_s$ can be summarized as follows in the following subsections.

3.1. Maximum Likelihood Prediction (Point and Interval Predictors)

The $MLPF$ can be obtained from (24) after replacing each parameter by its $MLE$ to be of the form

$$\begin{array}{c}\hfill g_2^{**}(z_s;\mathit{x})=B{z}_s{e}^{-\widehat{\beta }{z}_s^2}{(1-e^{-\widehat{\beta }{z}_s^2})}^{s\widehat{\alpha }-1}{[1-{(1-e^{-\widehat{\beta }{z}_s^2})}^{\widehat{\alpha }}]}^{m-s},z_s>0,\end{array}$$

(25)

where B is a normalizing constant has the value

$$\begin{array}{c}\hfill B=\frac{1}{{\int }_0^{\infty }\left(z_s{e}^{-\widehat{\beta }{z}_s^2}{(1-e^{-\widehat{\beta }{z}_s^2})}^{s\widehat{\alpha }-1}{[1-{(1-e^{-\widehat{\beta }{z}_s^2})}^{\widehat{\alpha }}]}^{m-s}\right)d{z}_s}.\end{array}$$

(26)

So, the $MLP$ of $z_s$ will be

$$\begin{array}{cc}\hfill z_s^{*}=E\left[Z_s\right]=& {\int }_0^{\infty }{z}_s{g}_2^{**}(z_s;\mathit{x})d{z}_s=\hfill \\ \hfill & \frac{{\int }_0^{\infty }\left(z_s^2{e}^{-\widehat{\beta }{z}_s^2}{(1-e^{-\widehat{\beta }{z}_s^2})}^{s\widehat{\alpha }-1}{[1-{(1-e^{-\widehat{\beta }{z}_s^2})}^{\widehat{\alpha }}]}^{m-s}\right)d{z}_s}{{\int }_0^{\infty }\left(z_s{e}^{-\widehat{\beta }{z}_s^2}{(1-e^{-\widehat{\beta }{z}_s^2})}^{s\widehat{\alpha }-1}{[1-{(1-e^{-\widehat{\beta }{z}_s^2})}^{\widehat{\alpha }}]}^{m-s}\right)d{z}_s},\hfill \end{array}$$

(27)

A $(1-\tau )\times 100\%$ $MLPI$ $(L{M}_2,U{M}_2)$ of $z_s$ can be obtained by solving the following two nonlinear equations:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\int }_{L{M}_2}^{\infty }{g}_2^{**}(z_s;\mathit{x})d{z}_s=1-\frac{\tau }{2},\hfill \\ {\int }_{U{M}_2}^{\infty }{g}_2^{**}(z_s;\mathit{x})d{z}_s=\frac{\tau }{2}.\hfill \end{array}\right.\end{array}$$

(28)

From (25) and (26) in (28), the two nonlinear equations in (28) can be rewritten, to be of the form

$$\left\{\begin{array}{cc}& \frac{{\int }_{L{M}_2}^{\infty }\left(z_s{e}^{-\widehat{\beta }{z}_s^2}{(1-e^{-\widehat{\beta }{z}_s^2})}^{s\widehat{\alpha }-1}{[1-{(1-e^{-\widehat{\beta }{z}_s^2})}^{\widehat{\alpha }}]}^{m-s}\right)d{z}_s}{{\int }_0^{\infty }\left(z_s{e}^{-\widehat{\beta }{z}_s^2}{(1-e^{-\widehat{\beta }{z}_s^2})}^{s\widehat{\alpha }-1}{[1-{(1-e^{-\widehat{\beta }{z}_s^2})}^{\widehat{\alpha }}]}^{m-s}\right)d{z}_s}=1-\frac{\tau }{2},\hfill \\ \hfill & \frac{{\int }_{U{M}_2}^{\infty }\left(z_s{e}^{-\widehat{\beta }{z}_s^2}{(1-e^{-\widehat{\beta }{z}_s^2})}^{s\widehat{\alpha }-1}{[1-{(1-e^{-\widehat{\beta }{z}_s^2})}^{\widehat{\alpha }}]}^{m-s}\right)d{z}_s}{{\int }_0^{\infty }\left(z_s{e}^{-\widehat{\beta }{z}_s^2}{(1-e^{-\widehat{\beta }{z}_s^2})}^{s\widehat{\alpha }-1}{[1-{(1-e^{-\widehat{\beta }{z}_s^2})}^{\widehat{\alpha }}]}^{m-s}\right)d{z}_s}=\frac{\tau }{2}.\hfill \end{array}\right.$$

(29)

By solving the previous system, the $MLPI$ of $z_s$, $(L{M}_2,U{M}_2)$, can be computed.

3.2. Bayesian Prediction (Point and Interval Predictors)

The Bayesian predictive $PDF$ of $z_s$ given $\mathit{x}$ will be as follows:

$$\begin{array}{c}\hfill h_2^{*}(z_s;\mathit{x})={\int }_0^{\infty }{\int }_0^{\infty }{h}_2(z_s;\alpha ,\beta ,\mathit{x})d\beta d\alpha ,\end{array}$$

(30)

where

$$\begin{array}{cc}\hfill h_2(z_s;\alpha ,\beta ,\mathit{x})=& {\pi }^{*}(\alpha ,\beta ;\mathit{x})g_2(z_s;\alpha ,\beta )=\hfill \\ \hfill & \left\{\begin{array}{c}{B}_1{z}_s{\alpha }^{d+c_1+c_3}{\beta }^{d+c_3}{e}^{-(\alpha (\beta +c_2)+\beta z_s^2)}{(1-e^{-\beta z_s^2})}^{s\alpha -1}\times \hfill \\ [{\prod }_{i=1}^d{x}_i{e}^{-\beta x_i^2}{(1-e^{-\beta x_i^2})}^{\alpha -1}]{[1-{(1-e^{-\beta z_s^2})}^{\alpha }]}^{m-s}\times \hfill \\ [1-(1-e^{-\beta T_1^2}{{)}^{\alpha }]}^{n-d},z_s>0,d_1=d_2=d=r,\dots ,n,\hfill \\ B_2{z}_s{\alpha }^{r+c_1+c_3}{\beta }^{r+c_3}{e}^{-(\alpha (\beta +c_2)+\beta z_s^2)}{(1-e^{-\beta z_s^2})}^{s\alpha -1}\times \hfill \\ [{\prod }_{i=1}^r{x}_i{e}^{-\beta x_i^2}{(1-e^{-\beta x_i^2})}^{\alpha -1}]{[1-{(1-e^{-\beta z_s^2})}^{\alpha }]}^{m-s}\times \hfill \\ [1-(1-e^{-\beta x_r^2}{{)}^{\alpha }]}^{n-r},z_s>0,d_1=k,\dots ,r-1,d_2=r,\hfill \\ B_3{z}_s{\alpha }^{d_2+c_1+c_3}{\beta }^{d_2+c_3}{e}^{-(\alpha (\beta +c_2)+\beta z_s^2)}{(1-e^{-\beta z_s^2})}^{s\alpha -1}\times \hfill \\ {\prod }_{i=1}^{d_2}{x}_i{e}^{-\beta x_i^2}{(1-e^{-\beta x_i^2})}^{\alpha -1}]{[1-{(1-e^{-\beta z_s^2})}^{\alpha }]}^{m-s}\times \hfill \\ [1-(1-e^{-\beta T_2^2}{{)}^{\alpha }]}^{n-d_2},z_s>0,d_1=k,\dots ,r-1,d_2=k,\dots ,r-1,d_1\le d_2\hfill \\ B_4{z}_s{\alpha }^{r+c_1+c_3}{\beta }^{r+c_3}{e}^{-(\alpha (\beta +c_2)+\beta z_s^2)}{(1-e^{-\beta z_s^2})}^{s\alpha -1}\times \hfill \\ {\prod }_{i=1}^r{x}_i{e}^{-\beta x_i^2}{(1-e^{-\beta x_i^2})}^{\alpha -1}]{[1-{(1-e^{-\beta z_s^2})}^{\alpha }]}^{m-s}\times \hfill \\ [1-(1-e^{-\beta x_r^2}{{)}^{\alpha }]}^{n-r},z_s>0,,d_1=0,1,\dots ,k-1,d_2=r,\hfill \\ B_5{z}_s{\alpha }^{d_2+c_1+c_3}{\beta }^{d_2+c_3}{e}^{-(\alpha (\beta +c_2)+\beta z_s^2)}{(1-e^{-\beta z_s^2})}^{s\alpha -1}\times \hfill \\ {\prod }_{i=1}^{d_2}{x}_i{e}^{-\beta x_i^2}{(1-e^{-\beta x_i^2})}^{\alpha -1}]{[1-{(1-e^{-\beta z_s^2})}^{\alpha }]}^{m-s}\times \hfill \\ [1-(1-e^{-\beta T_2^2}{{)}^{\alpha }]}^{n-d_2},z_s>0,d_1=0,\dots ,k-1,d_2=k,\dots ,r-1,\hfill \\ B_6{z}_s{\alpha }^{k+c_1+c_3}{\beta }^{k+c_3}{e}^{-(\alpha (\beta +c_2)+\beta z_s^2)}{(1-e^{-\beta z_s^2})}^{s\alpha -1}\times \hfill \\ {\prod }_{i=1}^k{x}_i{e}^{-\beta x_i^2}{(1-e^{-\beta x_i^2})}^{\alpha -1}]{[1-{(1-e^{-\beta z_s^2})}^{\alpha }]}^{m-s}\times \hfill \\ [1-(1-e^{-\beta x_k^2}{{)}^{\alpha }]}^{n-k},z_s>0,,d_2=0,\dots ,k-1,\hfill \end{array}\right.\hfill \end{array}$$

(31)

where $B_i,i=1,2,\dots ,6$ are normalizing constants.

The $BP$ of $z_s$ will equal

$$\begin{array}{c}\hfill z_s^{**}=E\left[Z_s\right]={\int }_0^{\infty }{z}_s{h}_2^{*}(z_s;\mathit{x})d{z}_s,\end{array}$$

(32)

and the $(1-\tau )\times 100\%$ $BPI$, $(L{B}_2,U{B}_2)$, of $z_s$ can be obtained by solving the following two nonlinear equations:

$$\left\{\begin{array}{c}{\int }_{L{B}_2}^{\infty }{h}_2^{*}(z_s;\mathit{x})d{z}_s=1-\frac{\tau }{2},\hfill \\ {\int }_{U{B}_2}^{\infty }{h}_2^{*}(z_s;\mathit{x})d{z}_s=\frac{\tau }{2}.\hfill \end{array}\right.$$

(33)

Using $({\alpha }^{\left(1\right)},{\beta }^{\left(1\right)}),({\alpha }^{\left(2\right)},{\beta }^{\left(2\right)}),\dots ,({\alpha }^{\left(K\right)},{\beta }^{\left(K\right)})$, which are generated from the posterior $PDF$ $\left(15\right)$, then the system (33) will be of the form

$$\left\{\begin{array}{c}\frac{{\sum }_{i=1}^K{\int }_{L{B}_2}^{\infty }{h}_2(z_s;{\alpha }^{\left(i\right)},{\beta }^{\left(i\right)},\mathit{x})d{z}_s}{{\sum }_{i=1}^K{\int }_0^{\infty }{h}_2(z_s;{\alpha }^{\left(i\right)},{\beta }^{\left(i\right)},\mathit{x})d{z}_s}=1-\frac{\tau }{2},\hfill \\ \frac{{\sum }_{i=1}^K{\int }_{U{B}_2}^{\infty }{h}_2(z_s;{\alpha }^{\left(i\right)},{\beta }^{\left(i\right)},\mathit{x})d{z}_s}{{\sum }_{i=1}^K{\int }_0^{\infty }{h}_2(z_s;{\alpha }^{\left(i\right)},{\beta }^{\left(i\right)},\mathit{x})d{z}_s}=\frac{\tau }{2}.\hfill \end{array}\right.$$

(34)

By solving this system, the $BPI$, $(L{B}_2,U{B}_2)$, for $z_s$ will be obtained.

From the results of the second and third sections, it is clear that the classical method of prediction and inference in general, called the maximum likelihood approach, depends only on an informative sample from the studied distribution under a suggested censoring scheme, and does not depend on any additional information about the parameters of the population. However, for the Bayes method, it depends on the same informative sample, but in addition to additional information about the parameters of the population represented in the prior distribution of the parameters. This obviously leads to better results. The results obtained based on the samples in the next section will verify this fact.

In case of absence of information on the population parameters, we have two choices. The first is to use the Bayes approach under a vague prior and the second is to use the classical method.

4. Results

In this section, one- and two-sample $PPs$ and $IPs$ using the classical and Bayesian approaches were obtained based on simulated and real data sets.

4.1. Simulated Results

The predictive process is a process that takes in historical data to predict which areas and parts of an asset will fail and at what time. The technician can receive relevant and accurate data points, remotely. The collected data are then analyzed and predictive algorithms to determine which part are more likely to fail. This information is communicated to workers via collaboration tools and data visualization, with which they can perform maintenance work only on the parts that require it. By implementing a predictive maintenance solution (Figure 1), organizations will know when to schedule a specific part replacement and be alerted to future degradations due to faulty parts.

Figure 1. Reactive periodic proactive predictive four stage engineering process.

In this section, the $PPs$ and $IPs$ of future failure times are computed, in one- and two-sample schemes, using the classical and Bayesian methods based on a generated $UHCS$ informative sample for different values of $r,k,T_1$, and $T_2$ as follows:

• For a given set of prior parameters $c_1,c_2$, and $c_3$, the population parameters $\alpha$ and $\beta$ are generated from the joint prior (16).
• Making use of $\alpha$ and $\beta$ obtained in step 1, a sample of size n of upper ordered values from Burr-X is generated.
• For different values of $n,r,k,T_1$, and $T_2$, a $UHCS$ informative sample is generated from the complete sample in step 2.
• For different values of $n,r,k,T_1$, and $T_2$, the $PPs$ and $IPs$ of the future failure times are computed using classical and Bayes methods in a one-sample scheme, as explained in Section 2.
• The same is done in a two-sample scheme, as explained in Section 3.
• For each future failure time, the $PP$, $IP$, length of the $IP$, and the $CP$ of the $IP$ are computed.
• The results are summarized in Table 1 and Table 2.
  Table 1. $PPs$ and $IPs$ of the future failure time $y_s,s=1,2,3,4$, based on the generated Balakrishnan $UHCS$ informative sample. $(\alpha =3.1811,\beta =1.5779)$, $(c_1=4.8,c_2=2.5$, $c_3=4.5)$.

  Values of $(T_1,T_2)$		$(1.5,1.6)$
  		$Generated{y}_1$	$Generated{y}_2$	$Generated{y}_3$	$Generated{y}_4$
  $(r,k)$		$PP$ of $y_1$	$PP$ of $y_2$	$PP$ of $y_3$	$PP$ of $y_4$
  $(n,D)$	$Method$	$IP$ of $y_1$	$IP$ of $y_2$	$IP$ of $y_3$	$IP$ of $y_4$
  		$Length$	$Length$	$Length$	$Length$
  		$CP$	$CP$	$CP$	$CP$
  $(10,5)$	$ML$	1.03809	1.11608	1.57305	1.65624
  $(20,12)$		0.91676	1.0914	1.4711	1.6674
  		(0.87340,1.12306)	(0.82512,1.13621)	(1.10036,1.61367)	(1.42708,1.97736)
  		0.24966	0.31109	0.51331	0.55028
  		0.9176	0.92177	0.93001	0.93816
  	$Bayes$	1.03809	1.11608	1.57305	1.65624
  		0.91053	1.1537	1.5018	1.6214
  		(0.87103,0.98636)	(1.02104,1.22278)	(1.16172,1.47264)	(1.29082,1.70564)
  		0.11523	0.20174	0.31092	0.41482
  		0.9037	0.9165	0.9275	0.9310
  $(10,7)$	$ML$	1.03809	1.11608	1.57305	1.65624
  $(20,14)$		1.18077	1.32147	1.59917	1.79101
  		(1.09166,1.22885)	(1.21106,1.42664)	(1.38102,1.68120)	(1.49016,1.88918 )
  		0.13719	0.21558	0.30018	0.39902
  		0.9001	0.91130	0.92719	0.92991
  	$Bayes$	1.03809	1.11608	1.57305	1.65624
  		1.17914	1.34221	1.62017	1.77082
  		(1.11057,1.23958)	(1.20184,1.4052)	(1.42061,1.69377)	(1.58062,1.94235)
  		0.12901	0.20336	0.27316	0.36173
  		0.8997	0.91055	0.9206	0.9227
  Values of $(T_1,T_2)$		$(1.3,1.5)$
  $(25,5)$	$ML$	0.66209	0.89038	0.91005	1.75215
  $(30,25)$		0.58144	0.9102	0.88152	1.70119
  		(0.40068,0.79311)	(0.60106,1.09158)	(0.74061,1.27075)	(1.12105,1.85211)
  		0.39243	0.49052	0.53014	0.73106
  		0.95161	0.96173	0.96106	0.97015
  	$Bayes$	0.662089	0.890378	0.910053	1.75215
  		0.64825	0.86239	0.94931	1.69046
  		(0.50151,0.86203)	(0.76175,1.16289)	(0.95276,1.46868)	(1.39173,1.90765)
  		0.36052	0.40114	0.51592	0.61058
  		0.9483	0.9553	0.9581	0.98813
  $(25,10)$	$ML$	0.662089	0.890378	0.910053	1.75215
  $(30,25)$		0.66131	0.86561	0.94072	1.78334
  		(0.49106,0.78122)	(0.73083,1.11254)	(0.807016,1.26818)	(1.24608,1.94780)
  		0.29016	0.38171	0.46117	0.70172
  		0.94814	0.95231	0.95618	0.96131
  	$Bayes$	0.662089	0.890378	0.910053	1.75215
  		0.67013	0.88172	0.90157	1.74105
  		(0.58043,0.79278)	(0.72063,1.07077)	(0.83803,1.24985)	(1.14473,1.82615)
  		0.21225	0.35041	0.41182	0.68142
  		0.9381	0.9481	0.9511	0.9591
  $(25,15)$	$ML$	1.42077	1.50944	1.54494	1.63888
  $(30,21)$		1.39354	1.48593	1.51207	1.65472
  		(1.31075,1.56622)	(1.32194,1.86571)	(1.34528,1.70186)	(1.45619,1.84651)
  		0.25547	0.27377	0.35658	0.45032
  		0.9695	0.9726	0.9799	0.9801
  	$Bayes$	1.42077	1.50944	1.54494	1.63888
  		1.43406	1.49225	1.53821	1.64152
  		(1.40089,1.52250)	(1.40916,1.59487)	(1.42534,1.67038)	(1.50294,1.77342)
  		0.12161	0.18571	0.24504	0.27048
  		0.9217	0.9317	0.9502	0.9573
  Values of $(T_1,T_2)$		$(0.8,2.5)$
  $(25,20)$	$ML$	1.42077	1.50944	1.54494	1.63888
  $(30,25)$		1.40593	1.49593	1.57207	1.61472
  		(1.32194,1.56571)	(1.32194,1.58239)	(1.34528,1.68186))	(1.25619,1.70651)
  		0.24377	0.26045	0.33658	0.45032
  		0.9504	0.9551	0.9623	0.9708
  	$Bayes$	1.42077	1.50944	1.54494	1.63888
  		1.41948	1.51021	1.54843	1.63451
  		(1.35285,1.47209)	(1.40421,1.65515)	(1.48797,1.81620)	(1.52675,1.95603)
  		0.11924	0.25094	0.32823	0.42928
  		0.9495	0.9525	0.9605	0.9693
  Values of $(T_1,T_2)$		$(0.8,1.1)$
  $(30,20)$	$ML$	1.42061	1.52062	1.63815	1.64518
  $(40,23)$		1.41092	1.49332	1.61337	1.66319
  		(1.32901,1.59942)	(1.40162,1.69674)	(1.48054,1.78922)	(1.50512,2.14725)
  		0.27041	0.29512	0.34116	0.64213
  		0.9601	0.9664	0.9718	0.9804
  	$Bayes$	1.42061	1.52062	1.63815	1.64518
  		1.41941	1.51804	1.64183	1.65184
  		(1.34162,1.56357)	(1.44076,1.69407)	(1.52184,1.82301)	(1.59042,2.00790)
  		0.22195	0.25331	0.30117	0.41748
  		9594	0.9614	0.9695	0.9748
  Values of $(T_1,T_2)$		$(0.5,0.8)$
  $(30,25)$	$ML$	1.51436	1.60734	1.71813	1.72479
  $(40,25)$		1.49201	1.58801	1.77419	1.75118
  		(1.40162,1.663278)	(1.45281,1.74086)	(1.59042,1.91318)	(1.66492,2.25535)
  		0.23116	0.28805	0.32276	0.59043
  		0.9584	0.9615	0.9697	0.978
  	$Bayes$	1.51436	1.60734	1.71813	1.72479
  		1.50184	1.58294	1.70174	1.73182
  		(1.41062,1.62090)	(1.50372,1.74565)	(1.60152,1.88221)	(1.64107,1.98290)
  		0.21028	0.24193	0.28069	0.34183
  		0.9533	0.9557	0.9614	0.9736

  Table 2. $PPs$ and $IPs$ of the future failure time $z_s,s=1,2,3,4$, based on the generated Balakrishnan $UHCS$ informative sample. $(\alpha =3.1811,\beta =1.5779)$, $(c_1=4.8,c_2=2.5$, $c_3=4.5)$.

  Values of $(T_1,T_2)$		$(1.5,1.6)$
  		$Generated{z}_1$	$Generated{z}_2$	$Generated{z}_3$	$Generated{z}_4$
  $(r,k)$		$PP$ of $z_1$	$PP$ of $z_2$	$PP$ of $z_3$	$PP$ of $z_4$
  $(n,D)$	$Method$	$IP$ of $z_1$	$IP$ of $z_2$	$IP$ of $z_3$	$IP$ of $z_4$
  		$Length$	$Length$	$Length$	$Length$
  		$CP$	$CP$	$CP$	$CP$
  $(10,5)$	$ML$	0.41303	0.78654	1.09878	1.31352
  $(20,12)$		0.37017	0.69154	0.95124	1.24012
  		(0.25175,0.46227)	(0.43129,0.80322)	(0.71182,1.30162)	(1.00273,1.59152)
  		0.21052	0.37193	0.4898	0.58879
  		0.88153	0.9152	0.9205	0.9317
  	$Bayes$	0.41303	0.78654	1.09878	1.31352
  		0.38718	0.71032	0.97182	1.27104
  		(0.33152,0.53268)	(0.51037,0.82988)	(0.81094,1.20606)	(1.17213,1.65357)
  		0.20116	0.31951	0.39512	0.48144
  		0.8781	0.9013	0.9114	0.9226
  $(10,7)$	$ML$	0.41303	0.78654	1.09878	1.31352
  $(20,14)$		0.38053	0.71108	0.98155	1.30153
  		(0.35102,0.54184)	(0.51005,0.82108)	(0.81106,1.22128)	(1.10924,1.63025)
  		0.19082	0.31103	0.41022	0.52101
  		0.8771	0.9010	0.9113	0.9215
  	$Bayes$	0.41303	0.78654	1.09878	1.31352
  		0.39012	0.73318	1.1192	1.34417
  		(0.38065,0.56341)	(0.54194,0.83207)	(0.79168,1.16883)	(1.01845,1.50039)
  		0.18276	0.29013	0.37715	0.48194
  		0.8771	0.8917	0.9016	0.9106
  Values of $(T_1,T_2)$		$(1.3,1.5)$
  $(25,5)$	$ML$	0.41303	0.78654	1.09878	1.31352
  $(30,25)$		0.38026	0.82165	1.16271	1.41152
  		(0.15243,0.42406)	(0.40072,0.90224)	(0.87932,1.44074)	(1.27194,1.88367)
  		0.27163	0.50152	0.56152	0.61173
  		0.9201	0.9332	0.9441	0.9505
  	$Bayes$	0.41303	0.78654	1.09878	1.31352
  		0.39012	0.73515	0.92166	1.28061
  		(0.27251,0.52427)	(0.50041,0.96225)	(0.88015,1.40234)	(1.18145,1.78310)
  		0.25176	0.46184	0.52219	0.60165
  		0.9115	0.9271	0.9396	0.9471
  $(25,10)$	$ML$	0.41303	0.78654	1.09878	1.31352
  $(30,25)$		0.40712	0.0.81026	0.99172	1.28017
  		(0.35143,0.59310)	(0.53183,0.99795)	(0.80384,1.29498)	(0.93317,1.51480)
  		0.24167	0.46612	0.0.49114	0.0.58163
  		0.9195	0.9307	0.9421	0.9497
  	$Bayes$	0.41303	0.78654	1.09878	1.31352
  		0.41005	0.79015	1.01823	1.31561
  		(0.37041,0.60357)	(0.55272,0.97563)	(0.79043,1.24077)	(0.93962,1.49109)
  		0.23316	0.42291	0.45037	0.55147
  		0.9061	0.9298	0.9402	0.9488
  $(25,15)$	$ML$	0.41303	0.78654	1.09878	1.31352
  $(30,21)$		0.40815	0.77804	0.1.10926	1.28915
  		(0.31629,0.57135)	(0.56052,0.86964)	(0.80057,1.24265)	(1.01748,1.55254)
  		0.25506	0.30912	0.44208	0.53506
  		0.9479	0.95514	0.9609	0.9716
  	$Bayes$	0.41303	0.78654	1.09878	1.31352
  		0.41105	0.78052	1.08805	1.30615
  		(0.30225,0.547738)	(0.52817,0.82633)	(0.93183,1.3335)	(1.13052,1.64131)
  		0.24513	0.29816	0.40167	0.0.51079
  		0.9397	0.9520	0.9593	0.9675
  Values of $(T_1,T_2)$		$(0.8,2.5)$
  $(25,20)$	$ML$	0.41303	0.78654	1.09878	1.31352
  $(30,25)$		0.41201	0.80152	1.11026	1.28961
  		(0.43172,0.65335)	(0.60332,0.85448)	(0.82184,1.20366)	(1.10286,1.56910)
  		0.22163	0.25116	0.38182	0.46624
  		0.9418	0.9536	0.9592	0.9663
  	$Bayes$	0.41303	0.78654	1.09878	1.31352
  		0.41052	0.79316	0.1.12052	1.29164
  		(0.45132,0.66194)	(0.65293,0.89786)	(0.87281,1.23444)	(1.17148.1.60341)
  		0.21062	0.24493	0.0.36163	0.43193
  		0.9406	0.9513	0.9554	0.9614
  Values of $(T_1,T_2)$		$(0.8,1.1)$
  $(30,20)$	$ML$	0.41303	0.78654	1.09878	1.31352
  $(40,23)$		0.41903	0.79016	0.99173	0.1.3201
  		(0.32183,0.58324)	(0.53148,0.83165)	(0.81064,1.22247)	(1.10573,1.68725)
  		0.26141	0.30017	0.41183	0.58152
  		0.9726	0.9775	0.9802	0.9892
  	$Bayes$	0.41303	0.78654	1.09878	1.31352
  		0.41525	0.77812	0.1.03124	1.31902
  		(0.35149,0.59301)	(0.56028,0.84226)	(0.79104,1.18118)	(0.97823,1.51955)
  		0.24152	0.28198	0.39014	0.54132
  		0.9618	0.9693	0.9715	0.9801
  Values of $(T_1,T_2)$		$(0.5,0.8)$
  $(30,25)$	$ML$	0.41303	0.78654	1.09878	1.31352
  $(40,25)$		0.4111	0.7902	0.1.1058	0.1.3111
  		(0.31047,0.56566)	(0.55061,0.84878)	(0.81718,1.20735)	(1.03081,1.59187)
  		0.25519	0.29817	0.39017	0.56106
  		0.9594	0.9615	0.9694	0.9772
  	$Bayes$	0.41303	0.78654	1.09878	1.31352
  		0.40183	0.79163	1.10815	1.29284
  		(0.28071,0.52488)	(0.51148,0.80667)	(0.79208,1.15819)	(1.10273,1.62478)
  		0.24417	0.29519	0.36611	0.52205
  		0.9523	0.9594	0.9611	0.9731

  From Table 1 and Table 2, observe the following:

  (a)

  For fixed $r,k,T_1$, and $T_2$, the length and the $CP$ of the $IP$ increase by increasing s because the element $y_s$ or $z_s$ will be larger, which will widen its predictive interval and, therefore, its $CP$.

  (b)

  In all six cases of the studied $UHCS$:

  • The length and the $CP$ of the $IP$ decreases by increasing the ratio $\frac{D}{n}$, which means that the results will be better by increasing the available information.
  • In the cases with constant ratio $\frac{D}{n}$ and fixed $r,T_1$, and $T_2$, the length and the $CP$ of the $IP$ decrease by increasing k, which show us that the results will be better by increasing k.

  (c)

  In all cases, the lengths of the $IPs$ are shorter in case of the Bayesian method than that computed by the classical method, which means that the Bayesian method is better than the classical method.

  (d)

  In all cases, the Bayesian $CPs$ are less than that computed by the classical method, which is also a criterion indicating that the results obtained by using the Bayes method is better than that obtained using the classical method.

  (e)

  The values $r,k,T_1$, and $T_2$ have been chosen so as to give all six cases of the studied $UHCS$.

4.2. Data Analysis

In this section, two real data sets are introduced; they were analyzed using Burr-X. The studied real data sets are from [8]. The first data set represents the failure times in the hours of 15 devices, and the second represents the first failure times in the months of 20 electronic cards. These real data sets are:

Data I:

0.19, 0.78, 0.96, 1.31, 2.78, 3.16, 4.15, 4.76, 4.85, 6.5, 7.35, 8.01, 8.27, 12.06 and 31.75.

Data II:

0.9, 1.5, 2.3, 3.2, 3.9, 5.0, 6.2, 7.5, 8.3, 10.4, 11.1, 12.6, 15.0, 16.3, 19.3, 22.6, 24.8, 31.5, 38.1 and 53.0.

In Table 3, the $MLEs$ of the parameters $\alpha$ and $\beta$ and the corresponding Kolmogorov–Smirnov ($K-S$) test statistic were computed under the Burr-X model.

Table 3. $MLEs$ of the parameters and the associated $K-S$ based on the real data sets I and II.

Data Set No.	$\mathit{M}\mathit{L}\mathit{E}{s}$	$\mathit{K}-\mathit{S}$
I	$\widehat{\alpha }=0.436377$, $\widehat{\beta }=0.0218652$	0.193849
II	$\widehat{\alpha }=0.611733$, $\widehat{\beta }=0.140011$	0.247625

Under the significance level ($0.05$) and using the Kolmogorov–Smirnov table, the critical value for the $K-S$ test statistic is $0.33760$, which is greater than the computed $K-S$ test statistics for the two real data sets under the $Burr$-X model. This means that the studied model fits the two biological data sets well.

$PPs$ and $IPs$ of the remaining future failure times ($y_s,s=1,2,3,4$) and of the first four observations ( $z_s,s=1,2,3,4$) from an independent ordered sample based on a generated Balakrishnan $UHCS$ informative sample from the given real data sets, were computed; they are summarized in Table 4, Table 5, Table 6 and Table 7.

Table 4. $PPs$ and $IPs$ of the future failure time $y_s,s=1,2,3,4$ based on a generated Balakrishnan $UHCS$ informative sample from real data set I.

Values of $(T_1,T_2)$		$(1.1,7.5)$
True $y_s$	$Method$	$y_1$	$y_2$	$y_3$	$y_4$
$(r,k)$		$PP$ of $y_1$	$PP$ of $y_2$	$PP$ of $y_3$	$PP$ of $y_4$
$(n,D)$		$IP$ of $y_1$	$IP$ of $y_2$	$IP$ of $y_3$	$IP$ of $y_4$
$CaseNo.$		$Length$	$Length$	$Length$	$Length$
$(12,5)$	$ML$	8.01	8.27	12.06	31.75
$(15,11)$		7.5715	8.1129	11.3816	33.8818
5		(6.77191,9.97962)	(7.17305,10.60674)	(10.48435,14.55529)	(25.66194,39.64581)
		3.20771	3.43369	4.07094	13.98387
	$Bayes$	8.01	8.27	12.06	31.75
		7.70925	8.19027	11.69016	32.20172
		(7.21062,9.51244)	(7.50592,10.42419)	(10.88017,14.53119)	(27.44018,38.34811)
		2.30182	2.91827	3.65102	10.90793

Table 5. $PPs$ and $IPs$ of the future failure time $y_s,s=1,2,3,4$, based on a generated Balakrishnan’s $UHCS$ informative sample from real data set II.

Values of $(T_1,T_2)$		$(1.3,1.8)$
True $y_s$	$Method$	$y_1$	$y_2$	$y_3$	$y_4$
$(r,k)$		$PP$ of $y_1$	$PP$ of $y_2$	$PP$ of $y_3$	$PP$ of $y_4$
$(n,D)$		$IP$ of $y_1$	$IP$ of $y_2$	$IP$ of $y_3$	$IP$ of $y_4$
$CaseNo.$		$Length$	$Length$	$Length$	$Length$
$(12,5)$	$ML$	5.0	6.2	7.5	8.3
$(15,5)$		4.6827	6.0196	7.3891	8.9017
6		(3.51081,6.01779)	(4.89192,7.91478)	(6.09047,9.82138)	(6.12081,10.55201)
		2.50698	3.02286	3.73091	4.43120
	$Bayes$	5.0	6.2	7.5	8.3
		4.7908	6.3005	7.4213	8.5105
		(3.78207,5.66372)	(5.03927,7.07429)	(6.24718,8.57770)	(6.74039,10.55102)
		1.88165	2.03502	2.33052	3.81063

Table 6. $PPs$ and $IPs$ of the future failure time $z_s,s=1,2,3,4$, based on a generated Balakrishnan $UHCS$ informative sample from real data set I.

Values of $(T_1,T_2)$		$(1.1,7.5)$
Generated $z_s$	$Method$	$z_1$	$z_2$	$z_3$	$z_4$
$(r,k)$		$PP$ of $z_1$	$PP$ of $z_2$	$PP$ of $z_3$	$PP$ of $z_4$
$(n,D)$		$IP$ of $z_1$	$IP$ of $z_2$	$IP$ of $z_3$	$IP$ of $z_4$
$CaseNo.$		$Length$	$Length$	$Length$	$Length$
$(12,5)$	$ML$	0.38819	0.49016	0.52015	0.60823
$(15,11)$		0.42115	0.50284	0.51082	0.58807
5		(0.34905,0.51106)	(0.36373,0.54428)	(0.39017,0.60024)	(0.48165,0.7626)
		0.16201	0.18055	0.21007	0.28095
	$Bayes$	0.38819	0.49016	0.52015	0.60823
		0.41066	0.48107	0.52713	0.60153
		(0.36105,0.49267)	(0.40552,0.56075)	(0.48174,0.65461)	(0.52315,0.76499)
		0.13162	0.15523	0.17287	0.24184

Table 7. $PPs$ and $IPs$ of the future failure time $z_s,s=1,2,3,4$, based on a generated Balakrishnan $UHCS$ informative sample from real data set II.

Values of $(T_1,T_2)$		$(1.3,1.8)$
Generated $z_s$	$Method$	$z_1$	$z_2$	$z_3$	$z_4$
$(r,k)$		$PP$ of $z_1$	$PP$ of $z_2$	$PP$ of $z_3$	$PP$ of $z_4$
$(n,D)$		$IP$ of $z_1$	$IP$ of $z_2$	$IP$ of $z_3$	$IP$ of $z_4$
$CaseNo.$		$Length$	$Length$	$Length$	$Length$
$(12,5)$	$ML$	0.28003	0.41052	0.48105	0.50185
$(15,5)$		0.30119	0.38826	0.41918	0.46817
6		(0.20275,0.37427)	(0.25594,0.4890)	(0.30142,0.71214)	(0.35107,0.82210)
		0.171752	0.23306	0.41072	0.47103
	$Bayes$	0.28003	0.41052	0.48105	0.50185
		0.29014	0.39082	0.45119	0.48017
		(0.26023,0.42308)	(0.27684,0.48890)	(0.33206,0.61621)	(0.39082,0.70595)
		0.16285	0.21206	0.28415	0.31513

From previous tables and figures, we can observe (for fixed $r,k,T_1$, and $T_2$):

• Increase the length of the predictive intervals by increasing s, because, as mentioned previously, the element $y_s$ or $z_s$ will be larger, which will widen its predictive interval.
• The length of the predictive intervals computed by the Bayesian method is less that that computed by the classical method, which means that Bayes technique is better than the other technique.
• For Bayes and classical approaches, and for all values of s, the exact value of $y_s$ lies in its predictive interval.
• From Figure 2A,B, Figure 3A,B, Figure 4A,B and Figure 5A,B, we can observe that:
  

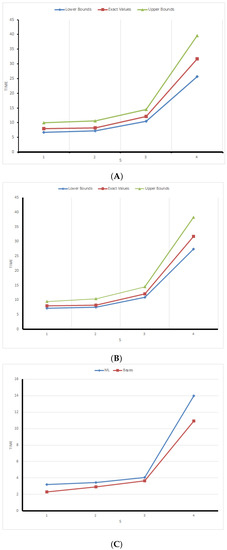  Figure 2. (A) ML one-sample predictive intervals based on sample I; (B) Bayesian one-sample predictive intervals based on sample I; (C) lengths of the one-sample predictive intervals based on sample I.
  

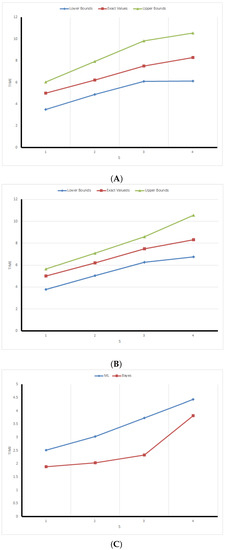  Figure 3. (A) ML one-sample predictive intervals based on sample II; (B) Bayesian one-sample predictive intervals based on sample II; (C) lengths of one-sample predictive intervals based on sample II.
  

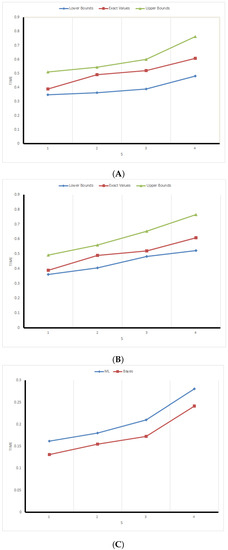  Figure 4. (A) ML two-sample predictive intervals based on sample I; (B) Bayesian two-sample predictive intervals based on sample I; (C) lengths of two-sample predictive intervals based on sample I.
  

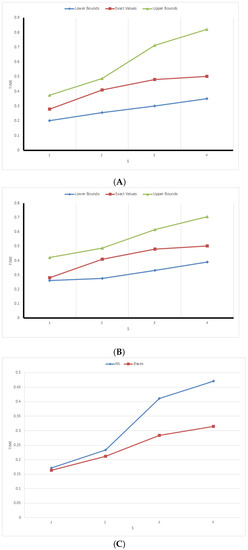  Figure 5. (A) ML two-sample predictive intervals based on sample II; (B) Bayesian two-sample predictive intervals based on sample II; (C) lengths of two-sample predictive intervals based on sample II.

  (a)

  The red broken refracted line, which represents the true value of the observation to be predicted, is located between the two broken lines that represent the lower and upper bounds of the predictive internals, which confirms with 3.

  (b)

  The lower bounds increase by increasing s.

  (c)

  The upper bounds also increase by increasing s.

• From Figure 2C, Figure 3C, Figure 4C and Figure 5C, we can observe:

  (a)

  The length of the predictive interval increase by increasing s, which confirms with 1.

  (b)

  The lengths of the predictive intervals obtained using the Bayes approach are less than that obtained by the classical approach, which confirms with 2.

5. Conclusions

In this paper, the $PPs$ and $IPs$ of the future failure times from Burr-X were computed based on a $UHCS$ (suggested by Balakrishnan et al. (2008) ) informative sample using different values of $r,k,T_1$, and $T_2$, using classical and Bayesian approaches, making some comparisons between the two approaches. Two engineering real data sets were introduced and analyzed using the Burr-X model to emphasize that the studied model fits the given real data sets well. Based on a generated $UHCS$ informative sample from the given real data sets, the $PPs$ and $IPs$ of the future failure times under one- and two-sample schemes were computed using classical and Bayesian approaches; it was found that the predictive intervals using the Bayesian approach were shorter than those computed by the classical approach, which means that the Bayesian approach is better than the other approach. In addition to the tabular description of the results related to the real data sets, graphical descriptions were also introduced. The results of the work confirm that it is possible to use statistical prediction to perform predictive tasks in relation to the conditions of industrial equipment.