On the Autocorrelation Function of 1/f Noises
Abstract
:1. Introduction
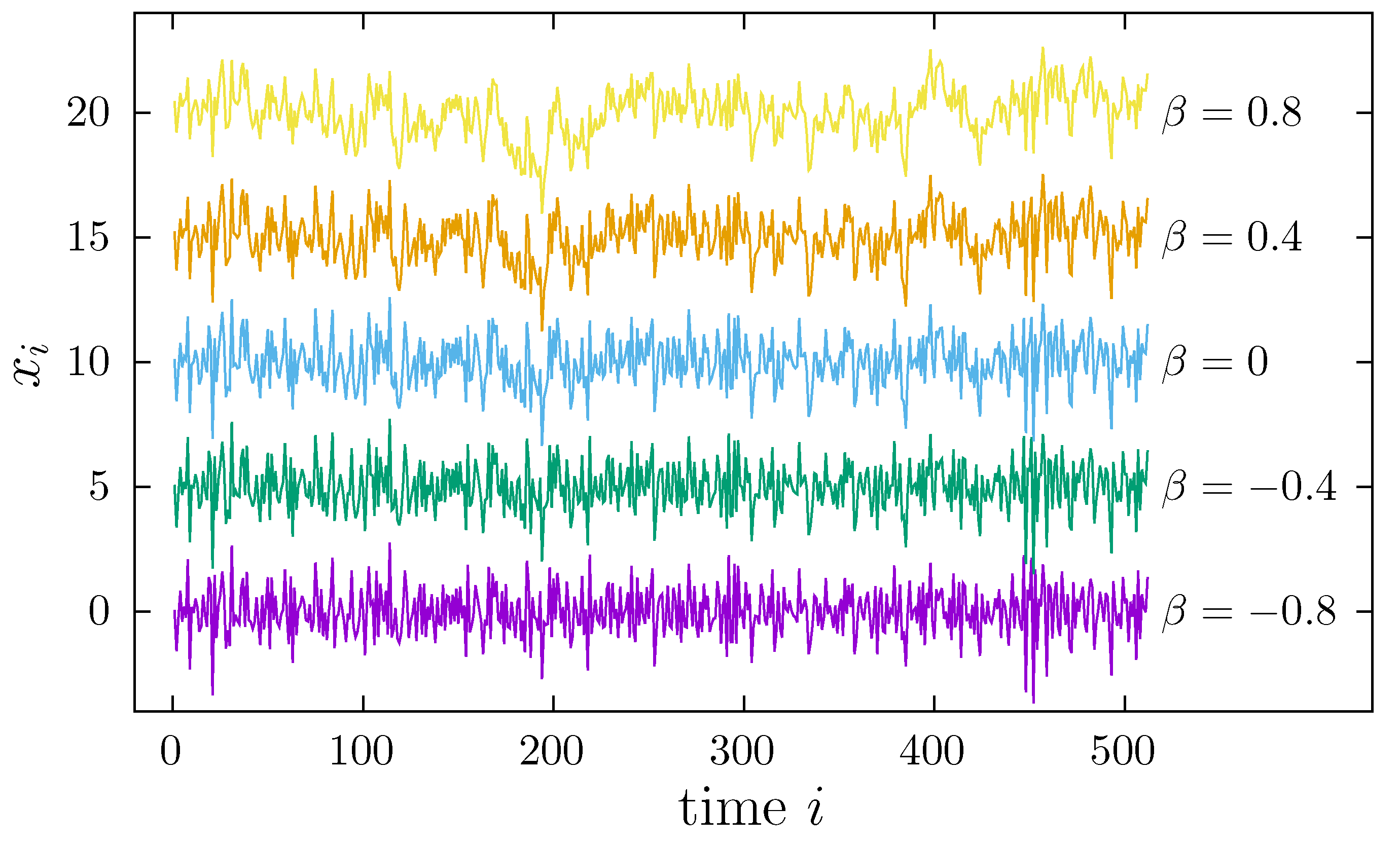
2. Fourier Filtering Method and Noises
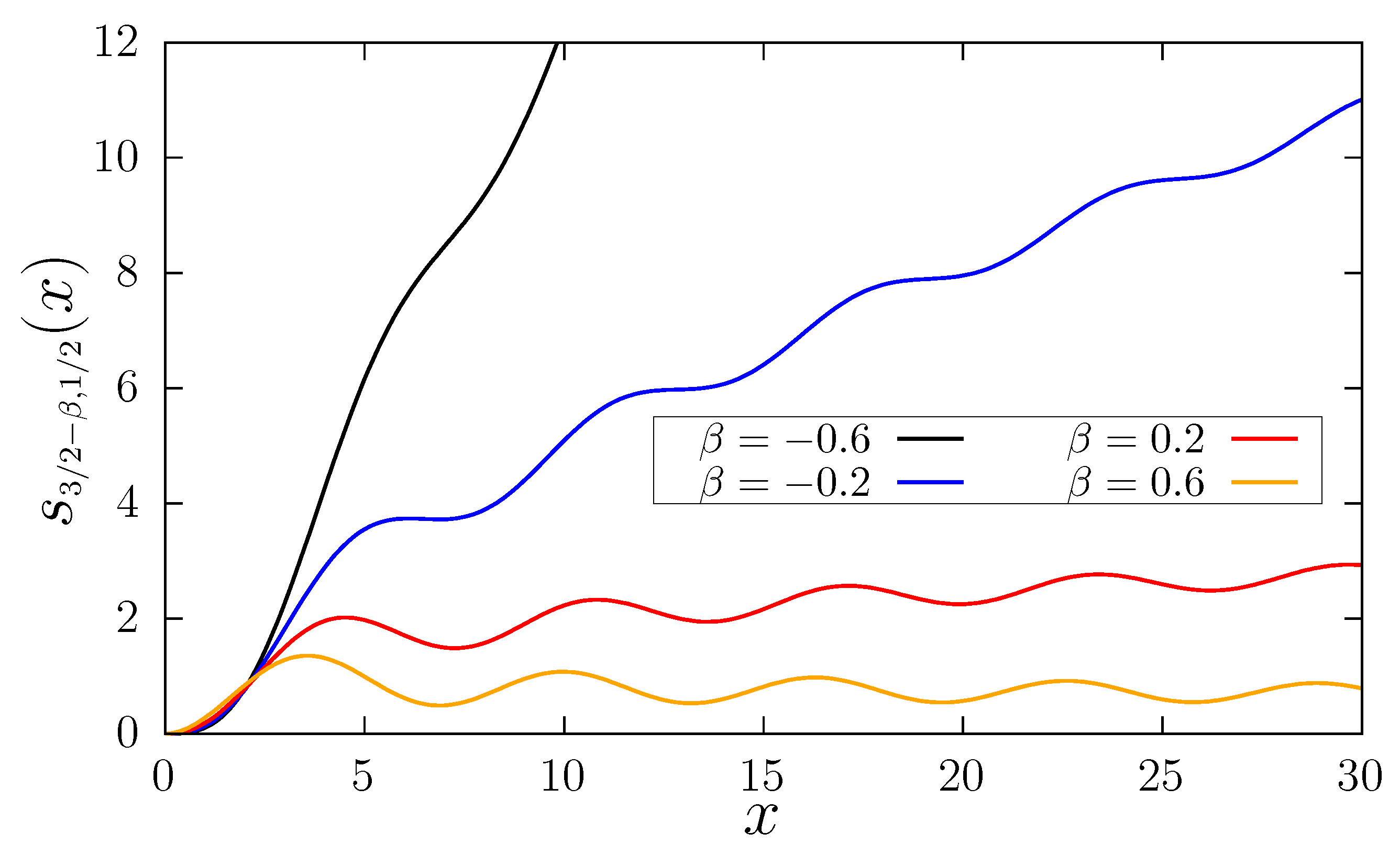
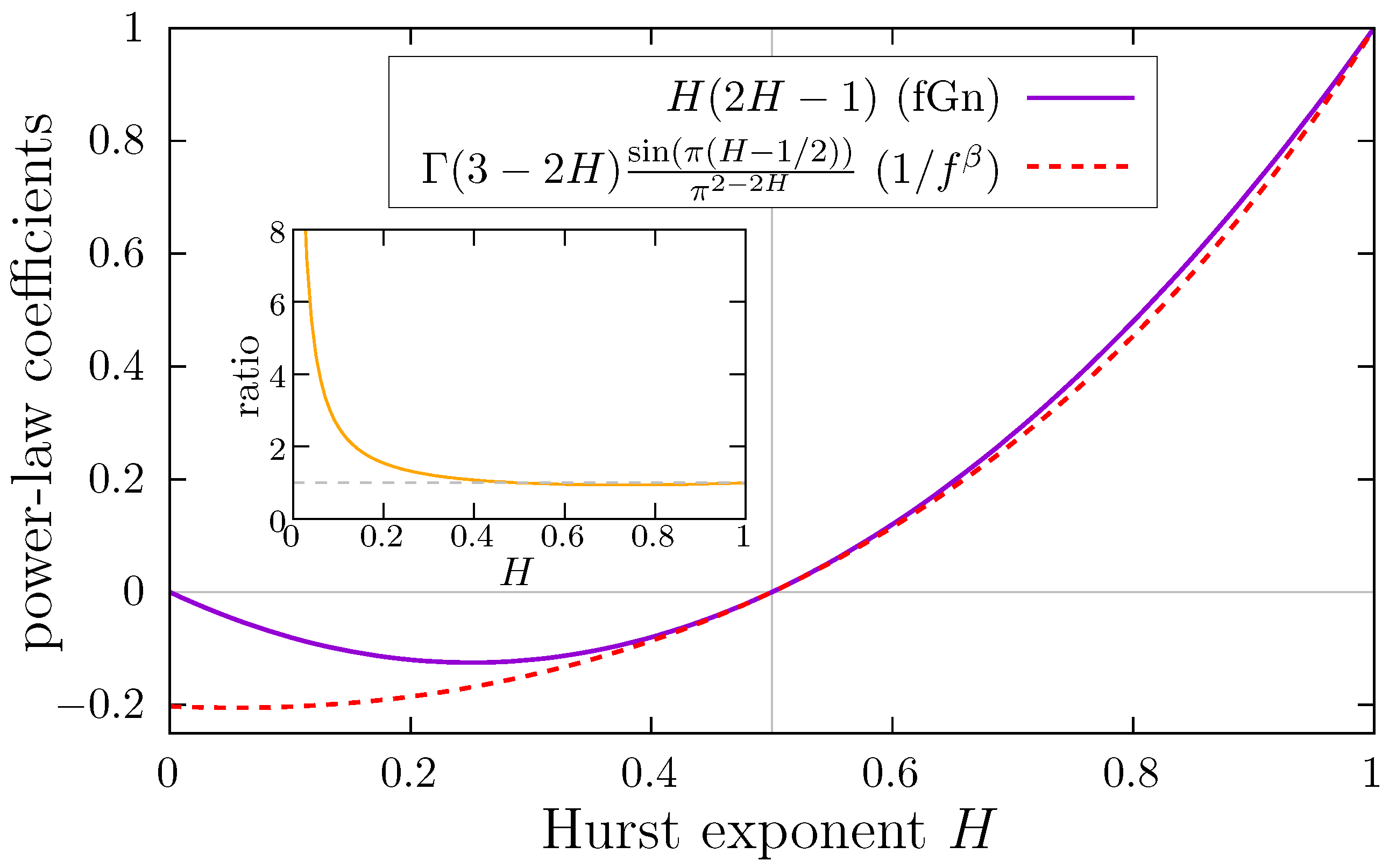
3. Autocorrelation Function of Noises
4. Applications
4.1. Comparing fGn and Noises
4.2. Fluctuation Analysis of Noises
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Hurst, H.E. Long-term storage capacity of reservoirs. Trans. Am. Soc. Civ. Eng. 1951, 116, 770–779. [Google Scholar] [CrossRef]
- Peters, E.E. Fractal Market Analysis: Applying Chaos Theory to Investment and Economics; John Wiley & Sons: Hoboken, NJ, USA, 1994. [Google Scholar]
- Peng, C.K.; Mietus, J.; Hausdorff, J.M.; Havlin, S.; Stanley, H.E.; Goldberger, A.L. Long-range anticorrelations and non-Gaussian behavior of the heartbeat. Phys. Rev. Lett. 1993, 70, 1343–1346. [Google Scholar] [CrossRef] [PubMed]
- Ivanov, P.C. Long-range dependence in heartbeat dynamics. In Processes with Long Range Correlations: Theory and Applications (Lecture Notes in Physics Vol. 621); Rangajaran, G., Ding, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2003; pp. 339–372. [Google Scholar]
- Ivanov, P.C. From 1/f noise to multifractal cascades in heartbeat dynamics. Chaos 2001, 11, 641–652. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Peng, C.K.; Mietus, J.E.; Liu, Y.; Lee, C.; Hausdorff, J.M.; Stanley, H.E.; Goldberger, A.L.; Lipsitz, L.A. Quantifying fractal dynamics of human respiration: Age and gender effects. Ann. Biomed. Eng. 2002, 30, 683–692. [Google Scholar] [CrossRef]
- Likenkaer-Hansen, K.; Nikouline, V.V.; Palva, J.M.; Ilmoniemi, R.J. Long-range temporal correlations and scaling behavior in human brain oscillations. J. Neurosci. 2001, 21, 1370–1377. [Google Scholar] [CrossRef] [Green Version]
- Duarte, M.; Zatsiorski, V.M. On the fractal properties of natural human standing. Neurosci. Lett. 2000, 283, 173–176. [Google Scholar] [CrossRef]
- Blázquez, M.T.; Anguiano, M.; de Saavedra, F.; Lallena, A.M.; Carpena, P. Study of the human postural control system during quiet standing using detrended fluctuation analysis. Physica A 2009, 388, 1857–1866. [Google Scholar] [CrossRef]
- Peng, C.K.; Buldyrev, S.V.; Goldberger, A.L.; Havlin, S.; Sciortino, F.; Simons, M.; Stanley, H.E. Long-range correlations in nucleotide sequences. Nature 1992, 356, 168–170. [Google Scholar] [CrossRef]
- Contreras-Reyes, J.E. Lerch distribution based on maximum nonsymmetric entropy principle: Application to Conway’s Game of Life cellular automaton. Chaos Solitons Fractals 2021, 151, 111272. [Google Scholar] [CrossRef]
- Bartos, I.; Jánosi, I.M. Nonlinear correlations of daily temperature records over land. Nonlin. Process. Geophys. 2006, 13, 571–576. [Google Scholar] [CrossRef] [Green Version]
- Varotsos, A.; Sarlis, N.V.; Skordas, E.S. Long-range correlations in the electric signals that precede rupture. Phys. Rev. E 2002, 66, 011902. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mandelbrot, B.B.; Van Ness, J.W. Fractional Brownian motions, fractional noises ans applications. SIAM Rev. 1968, 10, 422–437. [Google Scholar] [CrossRef]
- Davies, R.B.; Harte, D.S. Test for Hurst Effect. Biometrika 1987, 74, 95–101. [Google Scholar] [CrossRef]
- Dieker, A.B.; Mandjes, M. On spectral simulation of fractional Brownian motion. Probab. Eng. Inf. Sci. 2003, 17, 417–434. [Google Scholar] [CrossRef] [Green Version]
- Makse, H.A.; Havlin, S.; Schwartz, M.; Stanley, H.E. Method for generating long-range correlations for large systems. Phys. Rev. E 1996, 53, 5445–5449. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rangarajan, G.; Ding, M. Integrated approach to the assessment of long range correlation in time series data. Phys. Rev. E 2000, 61, 4991. [Google Scholar] [CrossRef] [Green Version]
- Coronado, A.V.; Carpena, P. Size Effects on Correlation Measures. J. Biol. Phys. 2005, 31, 121–133. [Google Scholar] [CrossRef] [Green Version]
- Hu, K.; Ivanov, P.C.; Chen, Z.; Carpena, P.; Stanley, H.E. Effect of trends on detrended fluctuation analysis. Phys. Rev. E 2001, 64, 011114. [Google Scholar] [CrossRef] [Green Version]
- Chen, Z.; Hu, K.; Carpena, P.; Bernaola-Galván, P.; Stanley, H.E.; Ivanov, P.C. Effect of nonlinear filters on detrended fluctuation analysis. Phys. Rev. E 2005, 71, 011104. [Google Scholar] [CrossRef] [Green Version]
- Carpena, P.; Gómez-Extremera, M.; Carretero-Campos, C.; Bernaola-Galván, P.A.; Coronado, A.V. Spurious Results of Fluctuation Analysis Techniques in Magnitude and Sign Correlations. Entropy 2017, 19, 261. [Google Scholar] [CrossRef]
- Carpena, P.; Gómez-Extremera, M.; Bernaola-Galván, P.A. On the Validity of Detrended Fluctuation Analysis at Short Scales. Entropy 2022, 24, 61. [Google Scholar] [CrossRef] [PubMed]
- Carpena, P.; Bernaola-Galván, P.; Coronado, A.V.; Hackenberg, M.; Oliver, J.L. Identifying characteristic scales in the human genome. Phys. Rev. E 2007, 75, 032903. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Carretero-Campos, C.; Bernaola-Galván, P.A.; Ivanov, P.C.; Carpena, P. Phase transitions in the first-passage time of scale-invariant correlated processes. Phys. Rev. E 2012, 85, 011139. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kalraa, D.S.; Santhanamb, M.S. Inferring long memory using extreme events. Chaos 2021, 31, 113131. [Google Scholar] [CrossRef]
- de Moura, F.A.B.F.; Lyra, M.L. Delocalization in the 1D Anderson model with long-range correlated disorder. Phys. Rev. Lett. 1998, 81, 3735–3738. [Google Scholar] [CrossRef]
- Nguyen, B.P.; Thoa, T.K.; Kim, K. Numerical study of the transverse localization of waves in one-dimensional lattices with randomly distributed gain and loss: Effect of disorder correlations. Waves Random Complex Media 2022, 32, 390–405. [Google Scholar] [CrossRef]
- Pires, J.P.S.; Khan, N.A.; Lopes, J.M.V.P.; dos Santos, J.M.B.L. Global delocalization transition in the de Moura-Lyra model. Phys. Rev. B 2019, 99, 205148. [Google Scholar] [CrossRef] [Green Version]
- Carpena, P.; Bernaola-Galván, P.; Gómez-Extremera, M.; Coronado, A.V. Transforming Gaussian correlations. Applications to generating long-range power-law correlated time series with arbitrary distribution. Chaos 2020, 30, 083140. [Google Scholar] [CrossRef]
- Bryce, R.M.; Sprague, K.B. Revisiting detrended fluctuation analysis. Sci. Rep. 2012, 2, 315. [Google Scholar] [CrossRef] [Green Version]
- Abramowitz, M.; Stegun, I. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; Ninth Printing; Dover Publications: New York, NY, USA, 1964. [Google Scholar]
- Olver, F.W.J.; Lozier, D.W.; Boisvert, R.F.; Clark, C.W. NIST Handbook of Mathematical Functions; Cambridge University Press: New York, NY, USA, 2010. [Google Scholar]
- Beran, J. Statistics for Long-Memory Processes; Chapman and Hall/CRC: New York, NY, USA, 1994. [Google Scholar]
- Karlin, S.; Brendel, V. Patchiness and correlations in DNA sequences. Science 1993, 259, 677–680. [Google Scholar] [CrossRef]
- Peng, C.K.; Buldyrev, S.V.; Havlin, S.; Simons, M.; Stanley, H.E.; Goldberger, A.L. Mosaic organization of DNA nucleotides. Phys. Rev. E 1994, 49, 1685–1689. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Höll, M.; Kantz, H. The relationship between the detrended fluctuation analysis and the autocorrelation function of a signal. Eur. Phys. J. B 2015, 88, 327. [Google Scholar] [CrossRef]
- Gradshteyn, I.S.; Ryzhik, I.M. Tables of Integrals, Series and Products, 7th ed.; Jeffrey, A., Zwillinger, D., Eds.; Academic Press: Cambridge, MA, USA, 2007. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carpena, P.; Coronado, A.V. On the Autocorrelation Function of 1/f Noises. Mathematics 2022, 10, 1416. https://doi.org/10.3390/math10091416
Carpena P, Coronado AV. On the Autocorrelation Function of 1/f Noises. Mathematics. 2022; 10(9):1416. https://doi.org/10.3390/math10091416
Chicago/Turabian StyleCarpena, Pedro, and Ana V. Coronado. 2022. "On the Autocorrelation Function of 1/f Noises" Mathematics 10, no. 9: 1416. https://doi.org/10.3390/math10091416
APA StyleCarpena, P., & Coronado, A. V. (2022). On the Autocorrelation Function of 1/f Noises. Mathematics, 10(9), 1416. https://doi.org/10.3390/math10091416






