Abstract
This study entailed an in-depth exploration of the meanings identified by a group of 105 fourth year primary schoolchildren when solving a task involving partitioning. The research was based on a semantic triangle consisting of a conceptual structure, representation systems, and sense. The content of children’s answers was analysed qualitatively. One of the most prominent findings was that purposes or usages were recognised based on multiple strategies, new categories of which, not envisaged in earlier research, were defined. Most of the students deployed graphic, verbal, and numerical representation and established relationships among them. Concepts such as the part-whole relationship and fractioning appeared in their description of conceptual structure, although errors were detected in terms of inequities and confusion between numerator and denominator.
Keywords:
partitioning; distribution; semantic triangle; primary education; representation; strategies MSC:
00A35; 97F90
1. Introduction
Problems involving equitable partitioning are normally introduced as classroom tasks beginning in pre-school, for the notion is familiar to children and the tasks where it appears can be modelled with manipulatives [1,2]. These kinds of tasks are intended either to divide or develop equal sized parts from continuous wholes, or equal sized groups from discrete collections, as fair shares. The importance of solving tasks involving partitioning is attested to by the growing number of studies on the subject. Much of the research on partitioning has focused on the strategies adopted by schoolchildren [3,4,5,6]. The findings show that young students tend to use a variety of intuitive strategies when confronted with such tasks [2,5,7,8,9,10], although some fail to bear in mind the total number of parts (lack of exhaustivity) or their size (misunderstanding of fractions) [5,11]. Such studies have also found the choice of partitioning strategies to depend on prior knowledge and experience, the situation involved, the type and number of objects partitioned, and the number of partitions [3,9,10,12]. Ever fuller understanding of young children’s partitioning strategies has spawned taxonomies that have been steadily refined with advances in research over the years [3,12]. Taxonomies afford teachers and researchers a framework for assessing children’s progress toward abstraction of the idea of partitioning as well as for planning and delivering classroom lessons commensurate with that progress.
Students’ ability to solve routine tasks involving mathematical content in certain situations does not necessarily denote their understanding of the meaning of such content [13]. Thompson [14] contended that the primary reason students have difficulties in problem solving is their failure to understand the concepts involved, the meaning of which should be the key to future learning in the discipline. Although many studies have focused on children’s understanding of fractions [7,8,9,10,11,12], none detected in a review of the literature broached the issue from the perspective of meanings. Since ‘the meaning of a concept can, therefore, be associated with what the person can do by means of the concept’ [15] (p. 85), here the elements characterising meaning, as expressed by a group of primary schoolchildren when solving a partitioning task, are explored in depth. In the approach adopted here, meaning is interpreted around the semantic triangle defined by structure, representation, and sense or usage [13]. Establishing partitioning as the sense, the study consisted in describing the elements of conceptual structure and the representation systems stated by students.
2. Meaning in Mathematics Classroom Content
The notion of meaning is often used informally in education research [15,16]. Recent studies on the meaning of mathematics classroom concepts show that semantics constitute a sound approach to exploring mathematics teaching and learning [13]. That premise is firmly supported by the idea that the meaning of mathematical content is essential to explaining the fundamentals of students’ mathematical knowledge, as well as to describing their understanding and adopting decisions for teaching design [14]. Since for the learner ‘meaning … refers to a complex pattern’ [15] (p. 97), here the meaning of mathematics classroom content is broached in terms of a semantic triangle.
A number of semantic triangles have been put forward in mathematics education research, including interpretation–objectification–generalization [17]; mathematics–learners of mathematics–signs [18]; reference situations–operational invariants–symbolic representations [19]; sign/symbol–object/reference context–mathematical concept [20]; and conceptual structure–domains of applications–representation tools [21]. Such proposals build on three categories to endow mathematical content with meaning. In this study conceptualisation draws essentially from Rico’s approach [13]. Borrowing from Frege [22], he suggested that the meaning of classroom mathematics content is determined by three inter-related components: conceptual structure, representation systems, and sense or usage. That system of components helps teachers and researchers determine how students understand content. The framework chosen to attain such understanding identifies, organises, synthesises, analyses, and interprets the elements of content, their interrelationships, and processing and conversion rules, all of which have a significant impact on the aforementioned components [23].
2.1. Conceptual Structure
In mathematics the term structure generally refers to a set of elements and an associated series of finite operations and relationships. The structure of the natural numbers, for instance, comprises a set accommodating the arithmetic operations and characterised by specific properties such as order or sequence.
According to Rico [13], conceptual structure is based on a network of conceits and relationships and each concept learnt forms part of a pre-existing structure. Delimiting the conceptual structure of a mathematical matter delimits concepts and procedures and the connections between them.
Along the lines defined by both Bell et al. and Hiebert and Lefevre [24,25], here conceptual structure is understood to be organised into two dimensions, conceptual and procedural. Specifically, content is deemed to lie within the conceptual dimension whilst strategies, defined as processes relating content and reasoning and expressed as a series of arguments, form part of the procedural dimension.
2.2. Representation Systems
For mathematical ideas to be communicated and applied they must be represented in some way, whilst to be pondered in any depth they must be represented in a number of ways. Generally speaking, the term (external) representation refers to physically embodied, observable expressions such as written symbols, diagrams, pictures, spoken language, or computer microworlds [26]. According to Kaput [27], any discussion of representation must distinguish between the representing and the represented worlds. Representing an idea converts a mentally pictured concept into a physical presence.
Morgan and Kynigos [28] equated representation to the expression of meaning. The way representation is arranged also denotes meaning. In the semantic triangle proposed here, representation is a tool for establishing meaning. In mathematics education certain words, diagrams, algebraic notations, etc. are used in keeping with convention. Deploying various types of representation entails the use of several forms of communication that differ in their potential for building meaning. Each representation system has specific rules that describe mathematical concepts in specific ways, emphasising and delimiting certain important properties while blurring or masking others [29].
2.3. Sense
This component relates to the purpose attributed to mathematics. Freudenthal [30] noted that mathematical concepts and structures are linked to specific developments. The expression ‘sense or usage’ refers here to developments or matters that translate into the applicability of mathematical concepts, which derive their meaning from developments and matters transpiring in the physical, social, and cultural worlds [31] (p. 175). In mathematics classrooms they are introduced in the form of tasks closely associated with the meaning of the concept at hand. To acquire a command of such meanings, children must engage in solving a variety of tasks of this nature.
The three components of the semantic triangle proposed determine a way to broach the meaning of mathematical concepts, an approach that serves a dual purpose. On the one hand it constitutes a tool for analysing the topics addressed in classroom mathematics, describing and establishing the meanings of topics in terms of conceptual structure, representation systems, and sense. On the other, it can be deployed to analyse and describe meanings as expressed by students. The present study focuses on the latter, establishing a component of the semantic triangle (the sense of partitioning), and exploring the other components (conceptual structures and representation systems) stated by students.
3. Methodology
The approach adopted in this qualitative-descriptive study was interpretational [32].
The subjects were 105 fourth year primary school (9- to 10-year old) students enrolled in three schools, each in a different Spanish city (Table 1). All featured similar characteristics and a middle-class socio-economic background.

Table 1.
Schools and students participating in the study.
The task they were assigned (Figure 1), drawn from studies conducted by Lamon ([7,33], p. 140), has also been used in earlier studies such as [34], where it provided successful results in relation to the analysis of strategies and performance of schoolchildren.
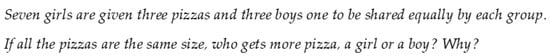
Figure 1.
Task.
It was presented verbally only to ensure students would feel free to use whatever representation system they preferred in their solutions.
The students received the exercise in writing during a normal classroom session. They were then given as much time as needed to solve the task individually on paper. One of the researchers was present during the session.
Data Analysis
We performed a content analysis of the students’ written answers [35], with a focus on the meanings expressed. Since sense was established by the task, partitioning, the analysis categories were established for each of the other two semantic components: representation systems and conceptual structure.
Mathematical content and strategies were the items addressed under conceptual structure [25]. The categories used to analyse the mathematical content (Table 2) arose inductively from the students’ exercises. The basis used for analysing the strategies was Lamon’s categories [33], established on the grounds of the relationship existing between quantities. As a result of the analysis of the students’ replies, the list of categories was lengthened to include labelled pieces, where subjects divided pizzas into the same number of pieces and calculated the number of pieces boys and girls would eat once they were distributed. Further additions to the system included the strategies pre-within, incomplete between or incomplete pieces as variations on the strategies within, between, and pieces. A description of the categories and their variations is provided in Table 3.

Table 2.
Categories obtained after analysing contents.

Table 3.
Categories used to analyse strategies.
In keeping with Castro and Castro [36] and Lupiáñez [37,38], three categories were defined for the representation systems used: graphic, symbolic-numerical, and verbal (Table 4). When students used more than one type of representation, their replies were analysed to determine whether or not they associated the systems used to one another.

Table 4.
Categories used to analyse representations.
In some cases, students used more than one representation system, strategy, or mathematical content in their answers. In the next section, some examples of students’ resolutions are described, so pronouns are gendered indiscriminately throughout the text to protect students’ identity.
4. Results
The present study establishes the sense (partitioning) and explores the conceptual structures (strategies and contents) and representation systems observed in students. For this reason, findings are discussed under three subsections, two of them referring to conceptual structure (strategies and contents) and the last one, referring to representations.
4.1. Conceptual Structure: Strategies
The frequency of use of each strategy is given in Table 5.

Table 5.
Frequency of use of each strategy.
A total of 78.1% of the students broached the task with just one strategy, whilst 19% deployed two. The most prevalent category among the latter was pre-within, with 18 of the 20 students involved using it. Two students used incomplete pieces in combination with the incomplete between strategy. The former constituted a first approach to the within strategy. In it, students compared quantities of the same nature (number of boys to number of girls and number of pizzas for one to number of pizzas for the other), although they failed to compare the results to respond to the question posed. This strategy was, significantly, one of the ones used by most of the students who combined two. An example of its application in combination with pieces is reproduced in Figure 2, in which the student divides each pizza into eight pieces and shares them among the members of each group. The girls get 3.5 pieces and boys get 2.5 pieces. Although the decimal part of these numbers does not exactly match the decimal part of the divisions 24:7 and 8:3, we interpret that the respondent student means that the girls and the boys eat a whole of a piece plus a small portion (not necessarily a half). This part of the task corresponds to the “pieces” strategy. However, in the solution the respondent indicates that the girls eat more because they have more pizzas, that is, he compares the number of pizzas for each group (girls-boys), independently of the number of people in each group (n. of girl vs n. of boys). That is a “pre-within” strategy.
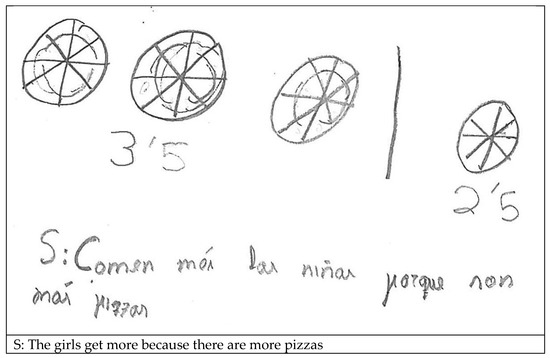
Figure 2.
Example of application of the pre-within combined with the pieces strategy.
The pieces strategy was also prominently used, specifically by 19 students, two of whom applied it in combination with the pre-within strategy. A further 11 students tried to deploy it but failed to complete the procedure, for they only divided the pizza into pieces: i.e., they used the pieces strategy incompletely. The answer given by one student who applied the pieces strategy is depicted in Figure 3, left, whilst an example of the incomplete use of the strategy is shown on the right.
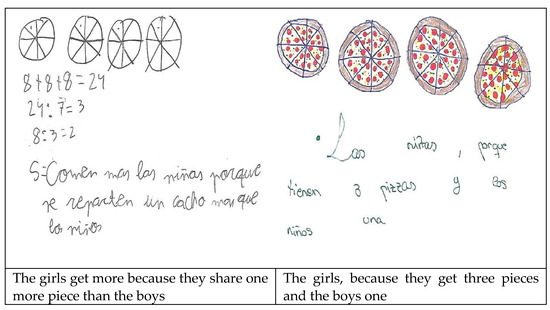
Figure 3.
Examples of pieces and incomplete pieces strategies.
In the between strategy, another way to broach the task, relationships were established between the number of pizzas and the number of students to compare them and find the answer. That strategy was used by 12 students. The other 24 who began to apply it but failed to complete the comparison were coded as using the incomplete between strategy. Figure 4 shows how one student related the number of girls’ pizzas to the number of girls (7/3) and the number of boys’ pizzas to the number of boys (1/3) but failed to find or therefore compare the results. She also confounded numerator and denominator in the first fraction.

Figure 4.
Examples of incomplete between strategy.
An example of unitizing strategy is reproduced in Figure 5, where the pizzas were divided into thirds and one-third of a pizza used as the unit of comparison. This student consequently drew a pizza divided into thirds for the boys and three divided into thirds for the girls, noting that two-thirds would be left over for the girls.
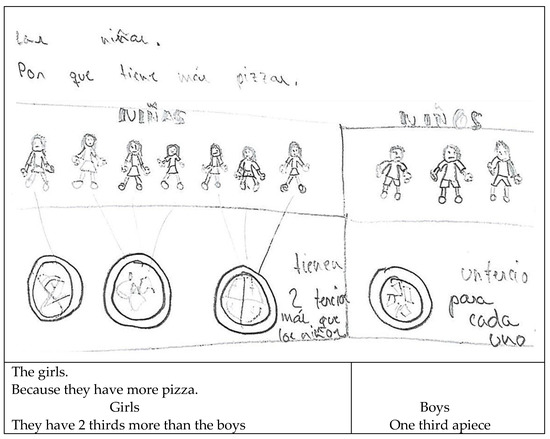
Figure 5.
Example of the unitisation strategy.
In addition, 16 students used strategies that could not be classified under any of the established categories and three showed none at all in their replies. In the answer reproduced in Figure 6 the student divided one pizza into fourths and one in half while leaving the third undivided to provide one piece for each girl, albeit of unequal sizes. He also divided the pizza for the boys into different sized pieces.
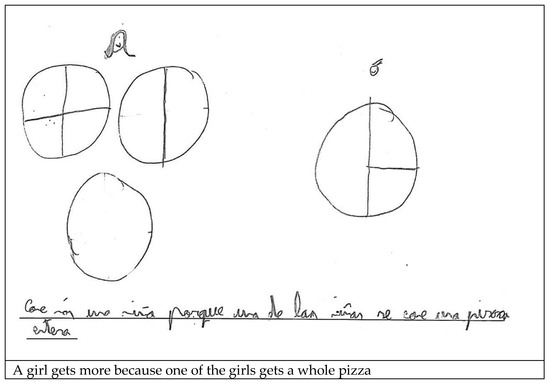
Figure 6.
Uncategorised strategy.
4.2. Conceptual Structure: Contents
The students used different mathematical contents to solve the task posed. The frequency of use of each content graphed in Figure 7 indicates that the part-whole relationship was a key component in the task posed, as it appeared in 80 of the 105 solutions. That notwithstanding, 44 of the students exhibited difficulties in partitioning the units, failing to bear in mind that the parts were to be equal, as observed in the exercise depicted in Figure 6.
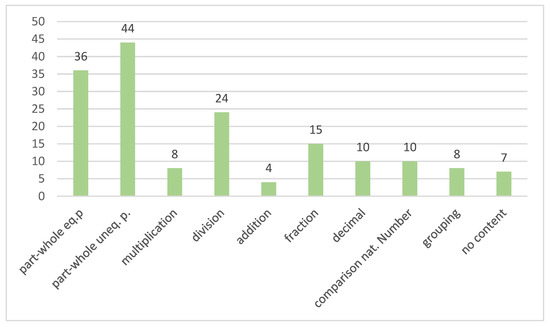
Figure 7.
Frequency of use of each content.
Other notions that appeared frequently were division and fractioning, although in the latter students found it difficult to determine quantities for the numerator and denominator, as illustrated in Figure 4.
Lastly, although less frequently, other mathematical contents were found, such as multiplication, addition, decimals, comparison of natural numbers, or grouping.
Figure 8 provides an example of a solution that combines the whole-part relationship with unequal parts, multiplication, division, and decimals to solve the task posed. The student first divided each unit into seven pieces, obviating the need for equality among the parts. She then multiplied or divided to find the number of parts each girl and boy would get, finding a decimal number in one of the results. Lastly, she compared the results and found the greater of the quantities.
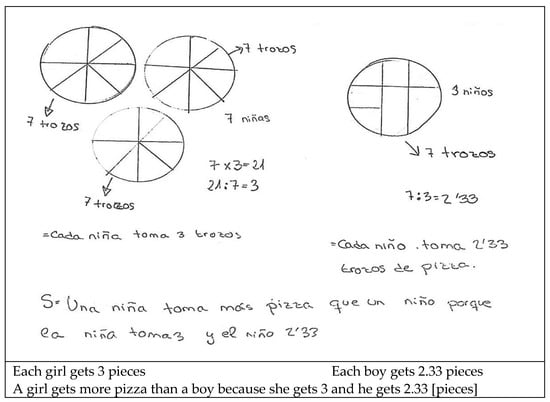
Figure 8.
Combination of various mathematical contents to find the solution.
4.3. Representation Systems
As the examples illustrated above show, the students used a number of representation systems to find the answer to the task. A total of 80% of the participants used more than one system, with graphic and verbal representation prevailing. The graphic system was used by 85 students, most of whom drew circles to represent the pizzas, although some represented the number of girls and boys involved in each case (Figure 5). Verbal representation was used by 86 students to answer the question posed and explain their reasoning. Symbolic-numerical representation was present in 43 exercises, mostly in the form of natural numbers.
The fact that students were able to use more than one system informed a study of whether they established relationships between the types of representation used. The frequency of use of each type when multiple systems were used is given in Table 6, along with the number of times two or more were interrelated.

Table 6.
Frequency of use of each strategy.
As Table 5 shows, of the 83 participants who used more than one type of representation, only 48 established interrelationships between them. In Figure 3, left, the student related the graphic, numerical, and verbal systems, whereas the participant on the right used but failed to interrelate graphic and verbal representation. More specifically, in the former the participant drew the pizzas and divided each into eight parts, using graphic representation. She then determined the number of pieces each girl and each boy would get using symbols and numbers. Lastly, she answered the question verbally. The latter student used the combination of representation systems most frequently observed in this sample: graphic and verbal.
The graphic and symbolic and symbolic and verbal systems were combined less frequently: an example of the former is given in Figure 4 and of the latter in Figure 9.

Figure 9.
Solution to the task combining symbolic and verbal representation.
5. Discussion and Conclusions
The aim of this study was to conduct an in-depth analysis of the characteristics of the meanings identified by a group of primary schoolchildren when solving a partitioning task. That entailed interpreting meaning in terms of a semantic triangle—conceptual structure, representation systems, and sense [13], particularly, we established a sense (partitioning) and describing the elements of conceptual structure (strategies and contents) and the representations stated by the students.
In relation to the procedural dimension of the conceptual structure, the strategies, the subjects in this study, like those participating in earlier research [5], used a variety of intuitive strategies to solve the task posed. In light of their responses the list of strategies categories proposed in [12] had to be lengthened. More specifically, the additions included approaches such as pieces and several more elementary strategies: pre-within, incomplete between, and incomplete pieces. In the latter three, students attempted to apply a strategy but failed to use the information found to answer the question posed. The strategies most frequently used were pre-within, between, incomplete between, and pieces, whilst the strategy within was not deployed by any of the students. Most of the students using more than one strategy (20%) combined pre-within with some other of the remaining strategies. One question that might be posed is whether our participants did not use the strategy within because they are not mature enough to perform this strategy.
On the conceptual dimension of the conceptual structure, the content, we observed that the part-whole relationship was the most prevalent category in students’ replies. The difficulties encountered by a substantial 49.1% of the students to divide the whole into equal parts denotes a need to broach equity-related issues from the earliest years of primary education. Those findings corroborate the results on partitioning and fractions reported by Dávila [11], whose students identified the number of parts but not their size. The primary school participants in this study supplemented the procedures initially applied with operations such as division (22.85%) and fractioning (14.28%). Those who used division exhibited difficulties in the use of the algorithm, whilst fractions were not always correctly represented, with some students confounding numerator and denominator. Much as the participants in the Lamon [7] study, here most the students compared natural numbers only.
Finally, concerning the last component of the semantic triangle, representation systems, we found that most prevalently used to solve the task was graphic representation in the form of circles divided into (on occasion unequal) pieces (81.9% of participants). Similar findings were observed in a study with pre-service primary school teachers [39]. Verbal representation was applied by 81.9% of the students to explain processes, describe details of the task and reply to the question posed, whilst 40.1% used numerical-symbolic representation in the form of numbers, fractions, or operations. A full 80% of the students used more than one type of representation, although only 46% established a relationship between the systems deployed.
In general, these results corroborate other authors’ [1,2] recommendation to introduce tasks involving partitioning or sharing in primary school. In addition to affording a context familiar to schoolchildren, when properly chosen for a given level of schooling their solutions are neither immediate nor foreseeable. This encourages schoolchildren to apply a variety of representations, strategies, and contents, providing teachers with relevant information about their students’ approach to such tasks.
Author Contributions
Conceptualization, M.F. and E.C.-R.; methodology, M.F., E.C.-R. and A.B.M.; validation, M.F., E.C.-R. and A.B.M.; formal analysis, M.F.; investigation, M.F. and E.C.-R.; data curation, M.F.; writing—original draft preparation, E.C.-R. and A.B.M.; writing—review and editing, E.C.-R., A.B.M. and J.F.R.-H.; supervision, E.C.-R., A.B.M. and J.F.R.-H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funding from Junta de Andalucía Research Group FQM-193 on numerical and algebraic thinking.
Institutional Review Board Statement
Ethical review and approval were waived for this study due to its anonymized nature. The activities were revised and authorized by the respective teachers. The parents were informed prior to the study that their children could be included in research studies.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to privacy restrictions.
Acknowledgments
This research was conducted within the project referenced PID2020-113601GB-I00, financed by the Spanish National Research Agency (AEI). Furthermore, it was supported by Junta de Andalucía Research Group FQM-193 on numerical and algebraic thinking.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bosch, M.A.; Castro, E.; Segovia, I. El pensamiento multiplicativo en los primeros niveles. Una investigación en curso. PNA 2007, 1, 179–190. [Google Scholar]
- Steffe, L.P. A new hypothesis concerning children’s fractional knowledge. J. Math. Behav. 2001, 20, 267–307. [Google Scholar] [CrossRef]
- Charles, K.; Nason, R. Young children’s partitioning strategies. Educ. Stud. Math. 2000, 43, 191–221. [Google Scholar] [CrossRef]
- De León, H.J. Procedimientos de niños de primaria en la solución de problemas de reparto. Relime 1998, 1, 5–28. [Google Scholar]
- Olguín, E.M.; Valdemoros, M.E. El reparto con fracciones mediante “escenarios didácticos”. In Acta Latinoaméricana de Matemática Educativa; Flores, R., Ed.; Comité Latinoamericano de Matemática Educativa A.C.: Mexico City, Mexico, 2012; pp. 583–592. [Google Scholar]
- Ramírez-Uclés, R.; Castro-Rodríguez, E.; Piñeiro, J.L.; Ruiz-Hidalgo, J.F. What makes a task a problem in early childhood education? Eur. Early Child. Educ. Res. J. 2018, 26, 574–588. [Google Scholar] [CrossRef]
- Lamon, S.J. Ratio and Proportion: Connecting Content and Children’s Thinking. J. Res. Math. Educ. 1993, 24, 41–61. [Google Scholar] [CrossRef]
- Pitkethly, A.; Hunting, R.P. A review of recent research in the area of initial fraction concepts. Educ. Stud. Math. 1996, 30, 5–38. [Google Scholar] [CrossRef]
- Pothier, Y.; Sawada, D. Partitioning: The emergence of rational number ideas in young children. J. Res. Math. 1983, 14, 307–317. [Google Scholar]
- Streefland, L. Fractions in Realistic Mathematics Education; Kluwer Academic: Dordrecht, The Netherlands, 1991. [Google Scholar]
- Dávila, M. El reparto y las fracciones. Educ. Mat. 1992, 4, 32–45. [Google Scholar]
- Lamon, S.J. The development of unitizing: Its role in children’s partitioning strategies. J. Res. Math. Educ. 1996, 27, 170–193. [Google Scholar] [CrossRef]
- Rico, L. Aproximación a la investigación en Didáctica de la Matemática. AIEM 2012, 1, 29–63. [Google Scholar] [CrossRef]
- Thompson, P.W. Researching mathematical meanings for teaching. In Handbook of International Research in Mathematics Education; English, L., Kirshner, D., Eds.; Routledge: New York, NY, USA, 2016; pp. 435–461. [Google Scholar]
- Skovsmose, O. Meaning in mathematics education. In Meaning in Mathematics Education; Kilpatrick, J., Hoyles, C., Skovsmose, O., Eds.; Springer: New York, NY, USA, 2005; pp. 83–100. [Google Scholar]
- Godino, J.D.; Burgos, M.; Gea, M. Analysing theories of meaning in mathematics education from the onto-semiotic approach. Int. J. Math. Educ. Sci. Technol. 2021, in press. [Google Scholar] [CrossRef]
- Radford, L. Gestures, speech, and the sprouting of signs: A semiotic-cultural approach to learners’ types of generalization. Math. Think. Learn. 2003, 5, 37–70. [Google Scholar] [CrossRef]
- Sáenz-Ludlow, A. Learning mathematics: Increasing the value of initial mathematical wealth. Relime 2006, 9, 225–245. [Google Scholar]
- Vergnaud, G. La théorie des champs conceptuels. Rech. Didact. Mat. 1990, 10, 133–170. [Google Scholar]
- Steinbring, H. What makes a sign a mathematical sign? An epistemological perspective on mathematical interaction. Educ. Stud. Math. 2006, 61, 133–162. [Google Scholar] [CrossRef][Green Version]
- Biehler, R. Reconstruction of meaning as a didactical task: The concept of function as an example. In Meaning in Mathematics Education. Mathematics Education Library; Kilpatrick, J., Hoyles, C., Skovsmose, O., Valero, P., Eds.; Springer: New York, NY, USA, 2005; Volume 37, pp. 61–81. [Google Scholar]
- Frege, G. Escritos Filosóficos; Tecnos: Madrid, España, 1996. [Google Scholar]
- Rico, L.; Ruiz Hidalgo, J.F. Ideas to work for the curriculum change in school mathematics. In Proceedings of the 24th ICMI Study: School Mathematics Curriculum Reforms: Challenges, Changes and Opportunities, Tsukuba, Japan, 25–30 November 2018. [Google Scholar]
- Bell, A.W.; Costello, J.; Küchemann, D. A Review of Research in Mathematical Education. Reserch on Learning and Teaching; NFER-NELSON: New Jersey, NJ, USA, 1983. [Google Scholar]
- Hiebert, J.; Lefevre, P. Conceptual and procedural knowledge in mathematics: An introductory analysis. In Conceptual and Procedural Knowledge in Mathematics: The Case of Mathematics; Hiebert, J., Ed.; Lawrence Erlbaum Associates: Windsor, England, 1986; pp. 1–28. [Google Scholar]
- Goldin, G.A.; Kaput, J. A joint perspective on the idea of representation in learning and doing mathematics. In Theories in Mathematical Learning; Steffe, L., Nesher, P., Cobb, P., Golding, G., Greer, B., Eds.; Erlbaum: Hillsdale, NJ, USA, 1996; pp. 397–430. [Google Scholar]
- Kaput, J. Towards a theory of symbol use in mathematics. In Problems of Representation in the Teaching and Learning of Mathematics; Janvier, C., Ed.; LEA: Hillsdale, NJ, USA, 1987; pp. 159–195. [Google Scholar]
- Morgan, C.; Kynigos, C. Digital artefacts as representations: Forging connections between a constructionist and a social semiotic perspective. Edu. Stud. Math. 2014, 85, 357–379. [Google Scholar] [CrossRef]
- Rico, L. Sobre las nociones de representación y comprensión en la investigación en educación matemática. PNA 2009, 4, 1–14. [Google Scholar]
- Freudenthal, H. Didactical Phenomenology of Mathematical Structures; Reidel: Dordrecht, The Netherlands, 1983. [Google Scholar]
- Van den Heuvel-Panhuizen, M. Didactical phenomenology (Freudenthal). In Encyclopedia of Mathematics Education; Lerman, S., Ed.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 174–176. [Google Scholar]
- Hernández, R.; Fernández, C.; Baptista, M.P. Metodología de investigación, 6th ed.; McGraw Hill Education: Mexico City, Mexico, 2014. [Google Scholar]
- Lamon, S.J. Ratio and Proportion: Children’s cognitive and metacognitive processes. In Rational Numbers: An Integration of Research; Carpenter, T.P., Fennema, E., Romberg, T.A., Eds.; Lawrence Erlbaum Associates: New Jersey, NJ, USA, 1993; pp. 131–156. [Google Scholar]
- Charalambous, C.Y.; Pitta-Pantazi, D. Drawing on a theoretical model to study students’ understandings of fractions. Educ. Stud. Math. 2007, 64, 293–316. [Google Scholar] [CrossRef]
- Cohen, L.; Manion, L.; Morrison, K. Research Methods in Education, 6th ed.; Routledge, Taylor & Francis Group: New York, NY, USA, 2007. [Google Scholar]
- Castro, E.; Castro, E. Representaciones y modelización. In La Educación Matemática en la Enseñanza Secundaria; Romero, R.L., Ed.; Horosi: Barcelona, Spain, 1997; pp. 95–124. [Google Scholar]
- Lupiáñez, J.L. Análisis didáctico. La planificación desde una perspectiva curricular. In Análisis Didáctico en Educación Matemática; Rico, L., Lupiáñez, J.L., Molina, M., Eds.; Comares: Granada, Spain, 2013; pp. 81–102. [Google Scholar]
- Lupiáñez, J.L. Sistemas de representación. In Elementos de Didáctica de la Matemática para el Profesor de Secundaria; Rico, L., Moreno, A., Eds.; Pirámide: Madrid, Spain, 2016; pp. 119–137. [Google Scholar]
- Castro-Rodríguez, E.; Pitta-Pantazi, D.; Rico, L.; Gómez, P. Prospective teachers’ understanding of the multiplicative part-whole relationship of fraction. Educ. Stud. Math. 2016, 92, 129–146. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).