A Study of the Complexity of Problems Posed by Talented Students in Mathematics

Abstract

Problem posing and mathematical talent are topics of interest to the community of researchers in Mathematics Education, but few studies reveal talented students’ abilities to solve problem-posing tasks. The data were collected using a problem invention instrument composed of four questionnaires that include free, semi-structured tasks and problem invention structures. The sample consisted of 23 students considered as mathematically talented and 22 students from a standard public school. The results show that the problems posed by the talent group are more complex than those invented by the standard group. The former are longer and show greater diversity of ideas while also requiring more steps to be solved, presenting a higher level of complexity according to the PISA framework, and requiring significant cognitive effort. In conclusion, the problem invention instrument used and the variables defined enabled us to analyze the complexity of the problems posed by the group of talented students. The statistical analysis performed reinforces the differences found in the complexity of the productions by the two groups studied.

1. Introduction

The context of this research involves two main lines of study: student problem posing and mathematical talent. Both topics have awakened the interest of mathematics researchers and educators, as shown by the numerous publications, for example [1,2,3,4] and scholarly meetings [5,6,7] dedicated to the two topics.

Problem posing has formed part of problem solving for several years [1]. However, only in recent decades have Mathematics Education researchers paid problem posing more attention and identified it as a line of research [8]. Its importance has been expressed by scientists, mathematicians and a large number of researchers in Mathematics Education, which is evidenced by the publications that link the invention of problems with the mathematical training of students at all educational levels [2,9].

In fact, those who support problem-posing activities hold that they are cognitively more difficult tasks than solving problems (Mestre, 2002; cited by [10]) since it requires an effort of personal interpretation when analyzing a proposed situation and giving meaning to the mathematical concepts involved [3]. In addition, they promote students’ participation in a genuine mathematical activity, challenging them to find many problems, methods, and solutions, and put their creativity into practice [11].

Similarly, when students invent problems they achieve complex levels of reflection that require them to use their knowledge, skills, and prior mathematical experience, leading them to a stage of reasoning in which they can construct mathematical knowledge [4]. Ref. [12] also stressed the predominant role of problem posing in mathematics classes:

“The process of creating problems represents one of the forms of authentic mathematical research. Properly implemented in class activities, it has the potential to go beyond the limitations of word problems—at least as they are typically treated. Promoting creation of problems is one way to achieve development of different student potentialities and stimulate greater mental flexibility.”

(p. 53)

Unfortunately, studies on problem posing are recent, and the topic has received attention as a research topic for only a little over two decades [13]. Further, studies of problem posing are less frequent and constitute a shorter line of research than studies in the field of problem solving [14]. Thus, relatively little is known of the cognitive processes involved in problem posing (Cai et al., 2013; cited in [15]).

In relation to mathematical talent, the literature agrees that these types of students are recognized aptitudes and skills towards mathematics that differentiate them from subjects with average intelligence and that makes them capable of performing tasks in this field with greater success in this discipline [16].

Likewise, it is agreed that the training and development of this type of student constitutes one of the most important actions that educational systems can offer to society due to the excellence and great performance that they can have when they reach the world of work [17]. Research continues to confirm the potential of students with talent in mathematics [18]; however, traditionally more attention has been paid to those who show special educational needs [19], forgetting the difficulties they may have in adapting to the educational system because their skills are not taken care of which can lead to demotivation, inhibition of their skills, and even school failure [5].

The field recognizes a need to strengthen the process of identifying and characterizing students with mathematical talent, and this process should not focus only on tests based on numerical calculation or problem-solving tasks [20]. It must include other aspects of content that lead subjects to demonstrate their mathematical reasoning capabilities through analysis of the quality of their responses to specific tasks [21].

Based on the foregoing, problem-posing tasks emerge as a cognitive activity that enables students to show the content, abilities, and skills they have learned, as well as their level of reasoning and creativity [22,23]. A line of research thus focuses on analyzing whether students with mathematical talent have a greater problem-posing capability than their classmates who are less skilled in mathematics.

On this issue, [23] reported that mathematically talented students were able to see problems that arose naturally from provided information, whereas their classmates with less skill in mathematics had difficulty doing so even when the interviewer intervened. The author argued that students with high mathematical abilities are better at recognizing the structure of mathematical problems.

The study by [24] showed that problems posed by more skilled students involved greater calculation difficulty, more operations, and a more complex numerical system. The more skilled students also used mathematical language more fluently than their less capable classmates.

Ref. [25] reported that students with greater mathematical ability not only generated more mathematics problems but that the problems were also more complex, as they involved a greater number of semantic relationships. Similarly, Ref. [22] found that the problems posed by a group of talented students were richer in length of statement, type of interrogative proposition, type of number, and number of processes and steps involved in solving the problem than the problems posed by a standard group from a public school. The study also concluded that the productions of the students with talent were perceived as more difficult; on reading the statement, a procedure for solving such problems could not immediately be identified.

Considering that problem-posing tasks involve students in significant cognitive activity, that the literature confirms a need to deepen the characterization of talented students, and that some studies show the capability of this type of student when they pose problems, our study aims to analyze the complexity of problems invented by a group of students identified as having mathematical talent during problem-posing tasks and to compare this complexity to the actions of a group of students from a standard public school provided the same tasks. Although research on mathematical talent and research on problem posing is abundant, the relationship between them is less so. The interest in trying to explore whether the invention of problems can be used to diagnose mathematical talent is of great relevance. We believe this study can provide relevant information, not only for the process of identification and characterization of mathematical talent that has focused on standardized tests, but also for its subsequent intervention.

To achieve this goal, we must define the variables of specific interest for studying the complexity of mathematical problems. The following describes these variables.

Study Variables Related to the Complexity of Mathematical Problems

One group of variables of interest when studying mathematics problems is related to the mathematical complexity of the problem. For [6], one such variable was the use of complex ideas required to solve the problem. The number of steps to solve the problem, type of operational structure, number of different calculation processes required to solve the problem [22], and complexity of the mathematical relationships involved [11] have also been considered.

Another widely known variable, proposed by the PISA framework [26], is the type of cognitive demand required to solve different types of problems, in which three levels of progressive complexity were determined: reproduction, connection, and reflection. The authors of [27] also mentioned the variable cognitive demand, which is linked to cognitive effort the student must make to solve mathematical problems. These authors determine the following four levels to evaluate the reflection and reasoning required to solve problems successfully: memorization, procedures without connections, procedures with connections, and performing mathematics.

Some syntactical variables have also been related to the complexity of a mathematical problem, including the problem’s presentation format, length of the statement, grammatical complexity, type and size of numbers, and type of question [28].

Ref. [29] used number of propositions to study the variable length of statement and conceptualized length as the number of “explicit expressions in the text of the statement that assign a numerical value or quantity of a variable or establish a quantitative relationship between two variables” (p. 65). The order of magnitude of the numbers has also been considered. Problems with small numbers are less difficult to solve, as they can be solved by using objects or one’s fingers or performing mental calculation [30].

Regarding the type of problem, Ref. [31] identified assignment and relational problems. In assignment problems, one does not know the value of the amount assigned, and the question asks one to find this value. In relational problems, the question involves specifying the meaning of a comparison between two related quantities. Ref. [11] added a third problem type, conditional problems, in which the question establishes a condition. They argue that a conditional or relational question is harder to solve than an assignment problem.

2. Methodology

This study used a mixed design, which combines aspects of simple quantitative and qualitative design. It is also a descriptive study [32] that seeks to expand the information on subjects with mathematical talent by analyzing the problems these subjects pose at a specific time, with predominant focus on the description and characterization in qualitative and quantitative terms.

2.1. Participants

Two groups of students were chosen that were already formed prior to the study. The first, the talent group, was composed of 23 students 16 and 17 years of age from the Costa Rican Scientific School (Colegio Científico de Costa Rica) at the National University (Universidad Nacional) in the Brunca Region. This school forms part of a system of nine different secondary schools that fosters talent development in the sciences for two academic years. To ensure that this group provided a real sample of students with talent, the students were provided Raven’s Progressive Matrices Test [33]; those chosen for the study scored above the 75th percentile.

The second group, the standard group, was composed of 22 students, also 16 and 17 years of age, from a standard public high school in the same region. This group was chosen because it comprised a set of standard public school students who were not identified as talented.

It should be noted that both groups were selected through intentional sampling because their location was close to one of the authors of this work. Furthermore, all students who participated in the study mentioned that they did not received prior preparation regarding solving problem-posing tasks, nor had their teachers carried out such activities in their classes. Finally, all students were informed about the study and told that the information collected would be treated confidentially.

2.2. Instrument

This study used a problem-posing instrument composed of four questions that included free, semi-structured, and structured problem-posing tasks [34]. The first questionnaire had two semi-structured problem-posing tasks that required posing problems from textual information or statements. The second had two semi-structured tasks in which the students posed statements from an image or newspaper clipping. The third questionnaire was composed of a single task that required first solving a problem and then posing a problem based on the problem solved but modifying the data, information, or question. Finally, the fourth questionnaire was composed of two free problem-posing tasks that asked students to formulate and reformulate their own problem, with no restrictions. It is important to mention that the proposed tasks were diverse and encouraged the invention of problems from different fields of knowledge of mathematics or even extramathematics.

To study the reliability of the instrument, Cronbach’s alpha was used, which in the case of this study obtained a Cronbach’s alpha of 0.801. Regarding the validity of the instrument, it was verified with the help of experts in the area that the proposed tasks corresponded to a representative sample of the universe of different types of tasks that can be used. To achieve this, a review was carried out on the classification and design of problem invention tasks; as well as the recommendations provided by some authors for its implementation. Then, a number of tasks were chosen and implemented in a pilot study with the aim of validating whether the proposed situations were the most suitable as reagents, as well as determining whether the stipulated time was sufficient to complete the tasks.

2.3. Categories of Analysis

This study defined eight study variables organized into two categories of analysis, termed syntactical complexity and mathematical complexity. The following describes each category and the variables considered.

2.3.1. Category I: Syntactical Complexity

This category analyzed the students’ ability to pose complex problems related to length and diversity of ideas, type and quantity of numbers used, and type of question. The following variables were analyzed in this category: (a) length of statement, (b) number of dissimilar propositions, (c) numerical flexibility, and (d) type of question.

2.3.2. Category II: Mathematical Complexity

This category analyzes the student’s capability to pose problems that are complex from a mathematical point of view. The following variables were analyzed: (a) number of steps needed to solve the problem, (b) use of complex ideas, (c) complexity level according to PISA, and (d) cognitive demand.

2.4. Data Analysis

A statistical analysis of frequency performed using SPSS v22 (IBM Corp. Released 2013. IBM SPSS Statistics for Windows, Version 22.0. Armonk, NY, USA: IBM Corp) enabled us to quantify and contrast the presence/absence of the above-mentioned variables in both groups. We conducted normality and hypothesis tests at a confidence level of 95% to confirm statistically the differences found in quantitative variables. For the qualitative variables, we performed a bivariate analysis using contingency tables and the Chi-square test at a confidence level of 95% in the cases in which 80% of the cells had an expected frequency above five.

3. Results

This section presents the main results obtained from analyzing the productions according to the eight study variables. We present first the general characteristics of the statements and then the results obtained according to the categories defined. For this, a statistical analysis of frequencies was carried out using the statistical package SPSS version 22, which made it possible to quantify and contrast the presence or absence of these variables in both groups of students. Similarly, normality and hypothesis tests were performed and a confidence level of 95% (sampling error of 5%) was established to statistically confirm the differences found in the quantitative variables. To study the differences in the qualitative variables, a bivariate analysis was performed using contingency tables and the Chi-square test was used with a confidence level of 95% in cases where 80% of the boxes had an expected frequency higher than five.

3.1. General Characteristics of the Problems Posed

The study obtained a total of 303 mathematics problems obtained from 315 possible productions (96.19%), as seven productions were left blank (five from the standard group and two from the talent group). Two productions also lacked requirements and three provided ambiguous responses; all five of these posed by the talent group. Of the 303 statements, 154 were mathematical problems posed by the talent group and 149 by the standard group.

Regarding the solvability of the mathematical problems, 91.09% of the problems posed by both groups were solvable (276 problems). More specifically, 92.20% of the problems from the talent group (142 statements) and 89.93% from the standard group (134 statements) were solvable.

Of the 27 unsolvable problems, 12 were posed by the talent group and 15 by the standard group. Of these, 81.48% (22 statements) were incomplete because they did not include all the information needed to solve them, 14.81% (4 statements) had some mathematical incompatibility, and 3.70% (1 statement) had some contradiction.

One example of a problem that was incomplete due to lack of data was posed by a student in the talent group in response to a task that referred to the load on a train: “If the train can carry a total of 1000 kg and it is carrying 1768 kg of goods, what is the maximum number of persons who can ride in each car, assuming that the same number of persons rides in each car?”

The following is a problem that presents a conceptual mathematical incompatibility because a circle has no lateral area: “If a circle has a lateral area of 36 cm² and a basal area of 20 cm². Find the measure of its radius, its diameter, and its total area.”

The following problem presents a contradiction because according to the information shown by the student an isosceles triangle is formed, but no isosceles triangle is formed in the problem: “If the trees form an isosceles triangle, the height of one of them is 75 cm and the measurement of the crown to the base of the other tree is 115 cm. The other measurements are 200 cm and 80 cm distance between the trees. What is the area of that triangle? (Figure 1)

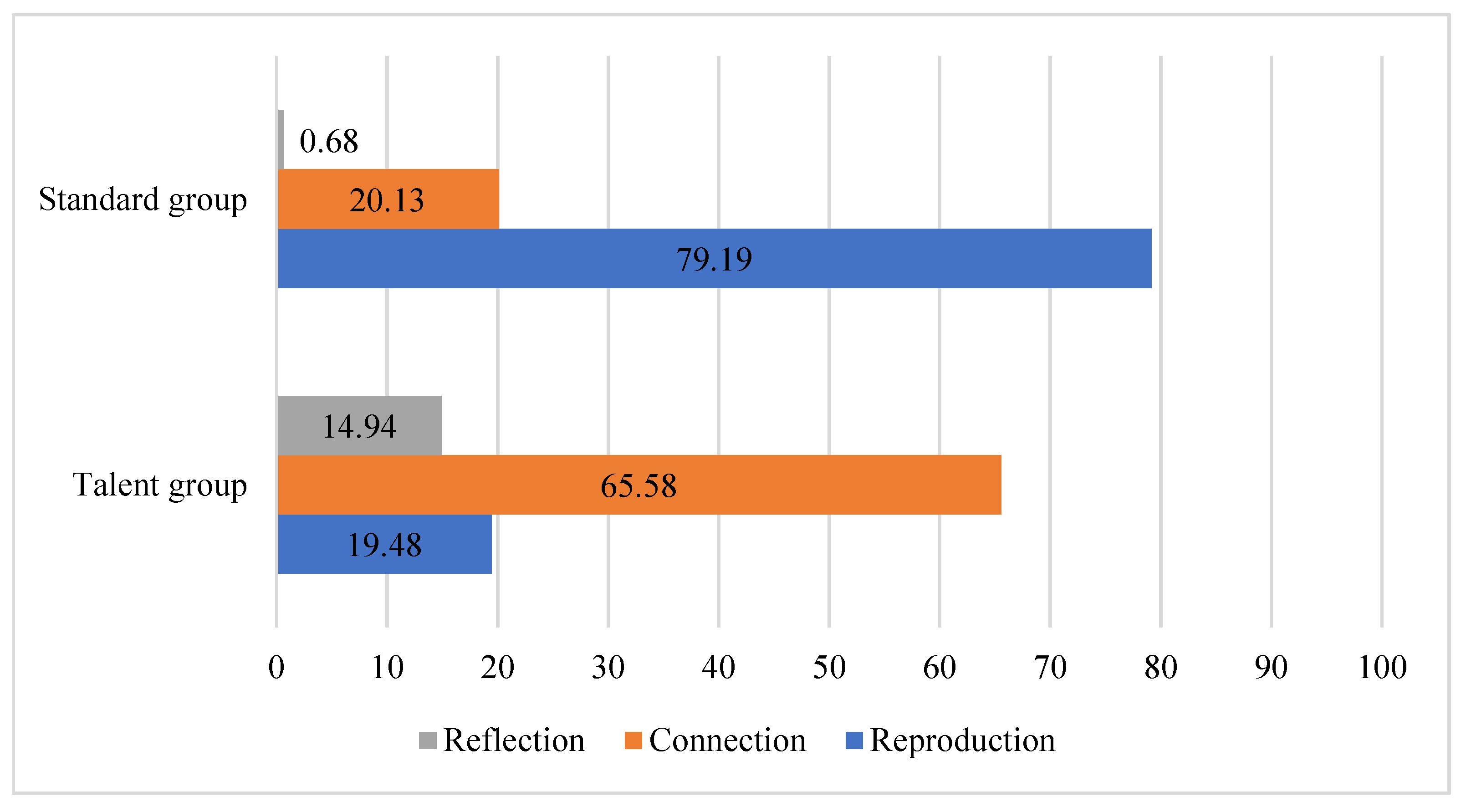
3.2. Analysis by Syntactical Complexity

Next, we present the results obtained according to the four variables considered in this category.

Length of statement: studied according to the number of propositions present in the statement that assigned a numerical value or quantity to a variable or established a quantitative relationship between two variables [21].

The general average of the number of propositions in problems posed by the talent group (5.55) is higher than that of the standard group (4.00). The Kolmogorov–Smirnov contrast of hypotheses enabled us to conclude that the data were not distributed normally since the associated p-value is 0.0. The Mann–Whitney test verified significant differences between the average number of propositions contained in the problems of both groups, as the associated p-value was 0.0.

These differences were also reflected in the number of problems that posed five or more propositions: 64.5% of the problems posed by the talent group had this characteristic, as opposed to 30.9% of the standard group’s problems. Further, most statements posed by the standard group (63.1%) were composed of two to four propositions, whereas 46.5% of those posed by the talent group had six or more propositions. The following is a problem posed by a student from the talent group and who has more than six propositions. In this task, students were asked to invent a problem that was difficult to solve based on the following situation: “A train with four passenger cars and two freight cars leaves a Cartago station at 9:00 a.m. bound for Alajuela. The train can carry a total of 294 passengers and 2365 kg of freight”.

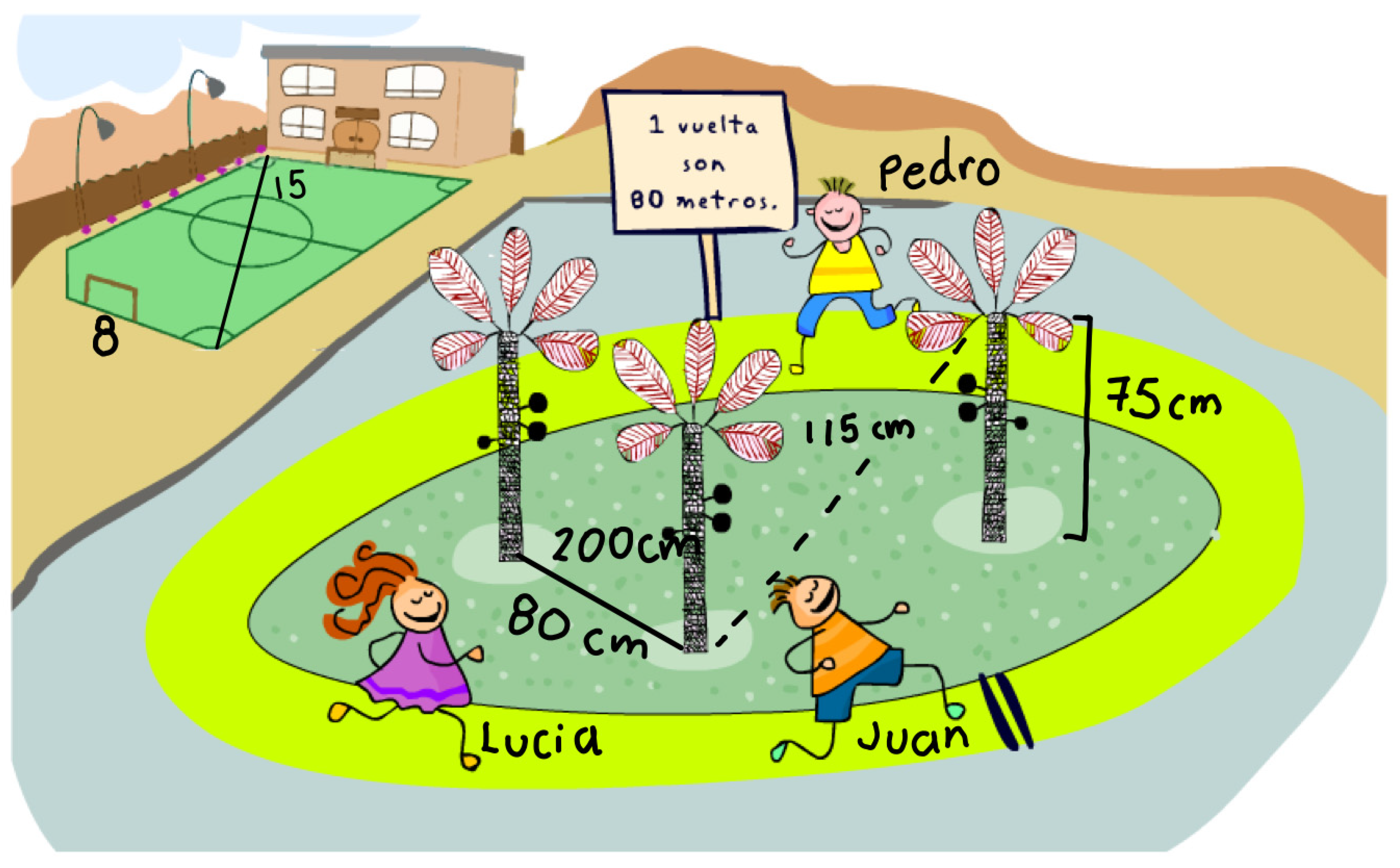
“If the train at its maximum capacity can reach a maximum speed of 500 km/h, in addition the average weight of each person is 75 kg and if a passenger car and three freight cars are added, it can reach a maximum speed of 400 km/h At what time does he arrive in Alajuela if in the middle of the journey he makes a 20-min stop and returns his number of wagons to the first mentioned, knowing that it travels at a maximum speed at all times and that from Cartago to Alajuela there are 5554 km?”

Number of dissimilar propositions: studied the quantities of dissimilar propositions (i.e., that contribute a different type of information) in the problem statement [29]. For example, in the propositions, “Juan walks around the square three times,” “María walks around the square seven times,” and “Pedro walks around the square two more times than María,” the first two propositions are more similar, while the third adds a comparative relationship, making it different from the first two.

The average number of dissimilar propositions is greater in the talent group (3.64) than in the standard group (2.42). The Kolmogorov–Smirnov hypothesis test showed, at a significance level of 0.05, that the data are not distributed normally (p-value 0.0). The Mann–Whitney test showed significant differences between the groups’ averages at a significance level of 0.05, with an associated p-value of 0.0.

Table 1. Number of dissimilar propositions.

Number of Propositions	Talent Group	Standard Group
One proposition	4 (2.60) 1	18 (12.08)
Two propositions	27 (17.53)	69 (46.31)
Three propositions	48 (31.17)	47 (31.54)
Four propositions	41 (26.62)	11 (7.38)
Five or more propositions	31 (22.08)	4 (2.68)
Total	154	149

¹ Quantity (percentages).

lists the results for this variable.

We see that most problems from the standard group have two or fewer dissimilar propositions (58.39%), whereas 20.13% from the talent group have this number. The proportion of problems with four or more different propositions is also higher in the talent group than in the standard group (48.7% and 10.06%, respectively). On the other hand, 50% of the statements in the talent group contained three or more propositions, whereas 50% of the problems in the standard group contained two or fewer propositions.

The following is a problem posed by a student from the standard group that contains five propositions, but only two of them provide different types of information.

“In a train with six cars for passengers, two for parcels and another two to transport animals, it leaves the Pérez Zeledón station at 7:00 am and arrives in San José at 11:00 am. Find out how long it takes to get there and how many people it carries in each car if there are 253 people in total.”

Numerical flexibility: analyzed use of different sets of numbers included in the statements. The results show that both groups preferred to use natural numbers in their statements: 97.42% in the talent group and 99.33% in the standard group. The talent group also used a higher proportion of problems with rational numbers (19.33%) than the standard group (9.4%).

Regarding the quantity of sets of numbers, both groups used only one set in most of their problems; 79.35% and 87.25% of the problems in the talent and standard groups, respectively. We also observe that the talent group posed a greater proportion of statements with two sets than their peers in the standard group. The statistical analysis showed significant differences in the two groups’ number of numerical sets (Chi-square $=3.802, \mathrm{gl}=1, p < 0.05)$.

Type of question: studied type of question presented in the problem statement (assignment, relational, or conditional). The results show that most interrogative propositions included by the students in the talent and standard groups were assignment propositions (76.77% and 84.56%, respectively). These propositions asked solvers to calculate a specific quantity or value, without establishing relationships or conditions in the question. Both groups also used a very small number of relational interrogative propositions.

Here is a problem posed by a student in the standard group that contained an assignment-type interrogative proposition: “If that same train transports $\frac{1}{8}$ of the goods and each passenger car has double the number of men as women, how many kilograms of goods is the train carrying, and how many men are travelling on this train?” A problem with a conditional interrogative proposition posed by a student in the talent group was: “If the train starts its journey at a speed of 40 $\frac{\mathrm{km}}{\mathrm{h}}$ and $\frac{3}{8}$ of the trip was a stop of 10 min, after which the train continued for the rest of its journey at double the previous speed, at what time did the train reach its destination, if we know that the distance between the two places equals the product of the number of divisors of the passengers and kilograms of goods?”

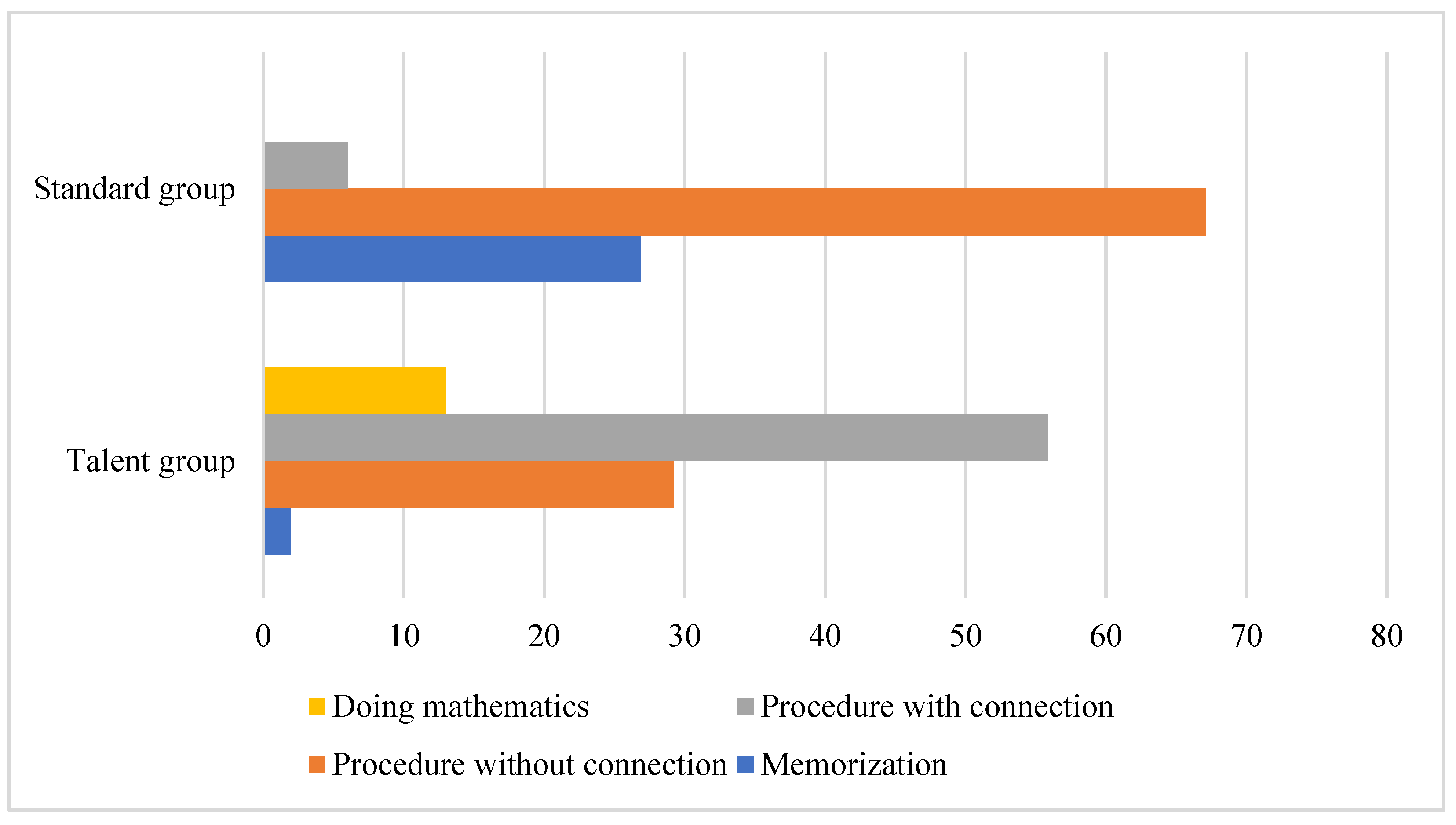
3.3. Analysis by Mathematical Complexity

Next, we present the results obtained, according to the four variables considered in this category.

Number of steps needed to solve the problem: studied the number of different steps needed to solve the problems, such that two steps are the same if they involve the same calculation process [22]. The results show that the average number of steps to solve the problems posed by the talent group (4.23) is greater than that for the standard group (2.32). The Kolmogorov–Smirnov hypothesis test showed, at a 0.05 significance level, that the data were not distributed normally (p-value 0.0). The Mann–Whitney test verified, at a 0.05 significance level, significant differences between the averages of the two groups (p-value 0.0).

Further, the average of this variable is 3.29 steps. Approximately 90% of the problems posed by the standard group required fewer than this number of steps to be solved, whereas approximately 30% of the problems in the talent group required fewer than 3.29 steps to be solved.

Table 2. Number of steps needed to solve the problem.

Number of Steps	Talent Group	Standard Group
One step	2 (1.30) 1	26 (17.45)
Two steps	24 (15.58)	68 (45.64)
Three steps	32 (20.78)	41 (27.52)
Four steps	29 (18.83)	11 (7.38)
Five or more steps	67 (43.51)	3 (2.01)
Total	154	149

¹ Quantity (percentages).

lists these results, showing the difference between the number of steps needed to solve the problems in both groups: the number of problems that required four or more steps is greater in the talent group (62.34%) than in the standard group (9.39%). Further, 63.09% of the statements posed by the standard group required two steps or fewer to be solved, whereas only 16.88% of the talent group’s statements required this number.

The following are two problems posed by a student from the standard and talent group, respectively. The indication asked to invent a difficult problem to solve from the following image (Figure 2).

The first one is solved using two steps, while the second one requires four steps to be solved.

“If boy A has run a distance of 560 m and girl B has a total of 480 m, how many laps does boy C need to catch up with boy A, knowing that boy C has run a distance of 160 m?”

“Juan, Carlos and María are doing a race that consists of 5 laps. If while Maria completes the first lap, Carlos goes for the third and Juan for the second, Juan goes at a speed of 15 (m)/s and Carlos goes at a speed of 20 m/s. How fast must Maria go to be the winner?”

Use of complex ideas: the variable that studies complex mathematical ideas that the students included in the problems. An idea is considered as complex when it is generally understood only by students in grades higher than the grade of the student using it. The results show that no student in the standard group included complex ideas in their statement and that only 8.44% of the problems in the talent group included complex ideas (13 statements). Regarding the results, the talent group was expected to incorporate this type of idea with greater frequency in their statements, since one specific characteristic of these students is in-depth understanding of complex ideas [35].

The following is a problem posed by a student in the talent group that includes at least one complex idea (angular acceleration): “Three kids run around a circle of 80 m, and if the angular acceleration is 5 rad/s², what is the distance x of the advantage that the first runner has over the others and the second runner over the girl, taking into account that his angular velocity is equal to 10 rad/s.”

Complexity level according to PISA: analyzed level of complexity of a mathematical problem according to the PISA framework (reproduction, connection, and reflection). Progressive in complexity, these levels are organized according to the number of concepts involved and their distance from merely school situations in the statement. Figure 3 presents the results for this variable.

We observe that most of the problems posed by the talent group are connection problems (65.58%) and involve several mathematical ideas or concepts, as well as several steps to solve, whereas the standard group proposed a large number of reproduction problems (79.19%), most of which required a procedure to solve them and expressed situations common in the school context. Further, both groups posed few reflection problems, but the talent group posed more than the standard group. The statistical analysis showed significant differences in the level of complexity between the groups according to the PISA framework (Chi-square $=105.91, \mathrm{gl}=2, p < 0.00)$.

The following problem was invented by a student from the standard group and is classified as reproduction, since it established an additive arithmetic situation common to the mathematics classroom: “María decided to go to the supermarket to buy some items on sale. Her list contained: mayonnaise, tomato sauce, orange juice, Corn Flakes, oat milk, oil, and refried beans. If she buys one unit of each product on her list, how much money will María save?”

An example of a connection problem from the talent group reads as follows: “Three children decide to compete in a race of speed, in which the winner will run two laps around a circular area (starting from the finish line). Supposing that, at the start of the second lap, the girl who had an advantage of 20 m and a speed of 4 m/s trips and remains on the ground for 6 s before getting up and continuing to run at the same speed she was running before the accident. The boy who had been behind her wins the race. From the finish line (start of the second lap), at what (minimum) speed did the boy have to run to beat the girl?” This is a connection problem due to the number of relationships established among data items (uniform speed with discontinuous space, establishment of a relative place of reference, and proposal to calculate minimum speed). It also reflects a situation uncommon in the classroom.

Cognitive demand: analyzed the level of thinking that the task requires of students to resolve it successfully. The authors of [27] considered the following four categories of cognitive demand, which have progressive levels of complexity and are mutually exclusive: memorization, procedure without connection, procedure with connection, and performing mathematics. Figure 4 presents the results obtained for this variable.

The previous figure shows that the students in the talent group posed problems with high cognitive demand that involved connecting different mathematical concepts and significant cognitive effort, as their statements were classified as procedures with connection (55.84%) or performing mathematics (12.99%). In the standard group, a significant number of problems were low in cognitive demand (93.96%); memorization or procedures without connection. These problems generally require a procedure to be solved, and it is easy to determine a process to solve them. The statistical analysis showed significant differences in cognitive demand between the groups (Chi-square $=135.06, \mathrm{gl}=3, p < 0.00)$.

The following is a problem posed by a student in the talent group, whose cognitive demand is at the level of procedure with connection as it requires cognitive effort and several procedures to solve, as well as connecting of different mathematical concepts (see Figure 5). The task asked students to invent a problem that they could solve, but that they considered difficult for their classmates.

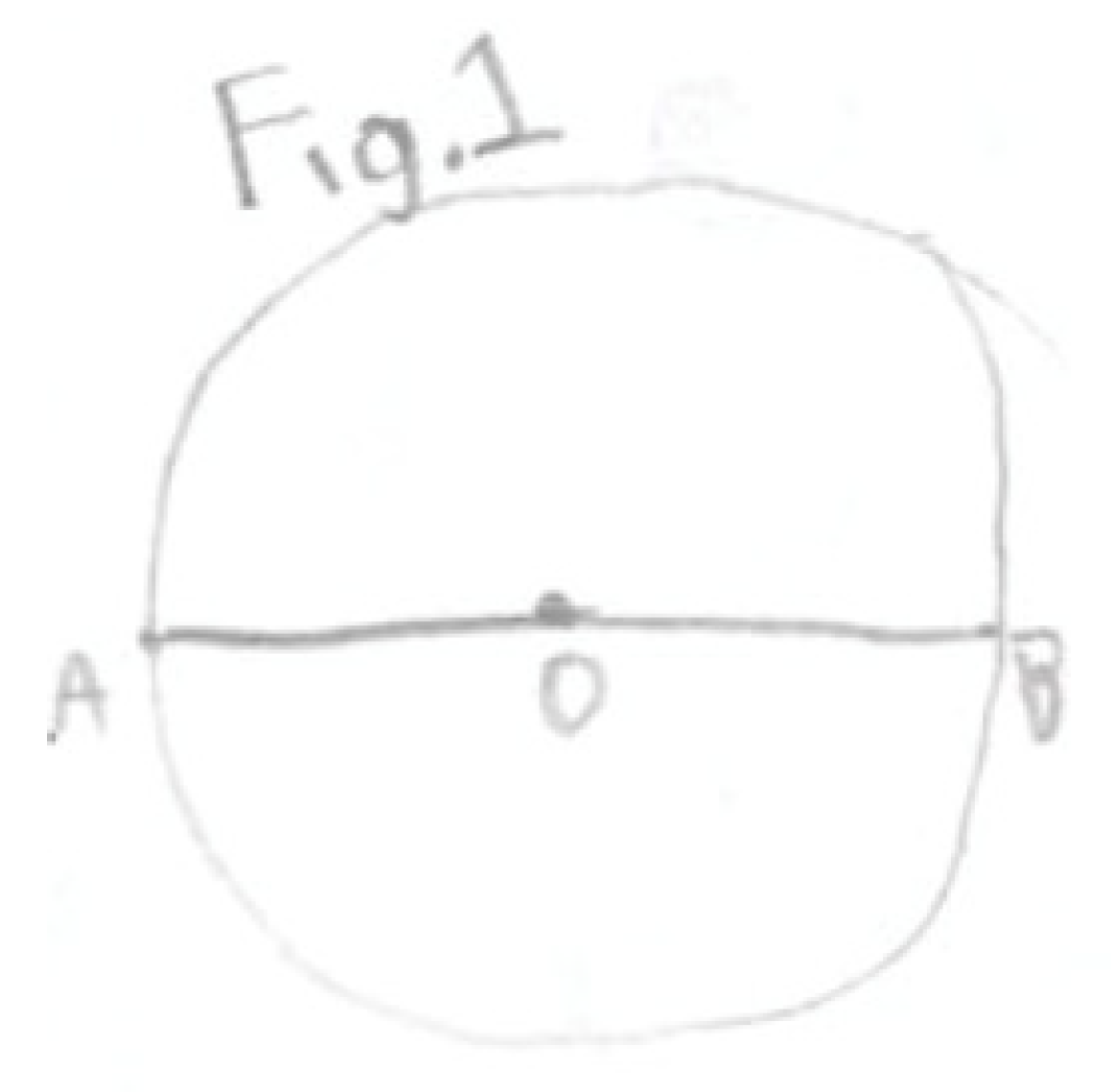
“If I have a hexagonal prism whose volume is $\frac{7}{5}\pi$ of the volume of the sphere in Fig. 1; AB is three units greater than the radius of the hexagon, whose perimeter is equivalent to $fog$ where $f\left(x\right)=3x$ and $g\left(x\right)=x+3$ m; and x is equal to the value in degrees of $\frac{\pi }{4}$; what is the area of the hexagonal prism?”

The following is a problem posed by a student from the standard group that was classified as procedure without connection, since it requires a procedure that is easy to see: “If on the route from Cartago to Alajuela, the train stops to add cars and adds three passenger cars but this time the cars are larger, each car can hold 177 people, and all cars are full, how many people are on the train in all?”

4. Discussion and Conclusions

First, we believe that the problem-posing instrument and the variables used in this study enable us to analyze the complexity of problems posed by the two groups. Similarly, this instrument allowed students to demonstrate their skills and abilities in mathematics, obtaining a high response rate and a variety of problems. In addition, according to the analysis of the instrument carried out, it has good reliability.

Analyzing the students’ productions based on the ten study variables defined enabled us to study the complexity of the problems the students posed. We also found some differences between the two groups’ productions confirmed through statistical tests.

We conclude that the problems posed by the talent group have some characteristics that made them more complex than those posed by the standard group. First, the statements were longer, as they were composed of a greater number of propositions. The statements also contained more dissimilar propositions, enabling us to conclude that the talent group students posed not only longer problems but also ones with more diverse ideas.

Similarly, we conclude that the problems from the talent group require more steps to be solved and show a higher level of complexity according to the PISA framework, since they imply connection of several ideas or mathematical concepts. They also require greater cognitive effort, as they must be solved carefully; the answer cannot be deduced explicitly from the proposal or involve complex, nonprocedural reasoning, requiring that one explore and understand the nature of the mathematical concepts involved. Most of the problems posed by the standard group, in contrast, required common procedures that involved simple calculations and were drawn from the student’s own environment.

We thus agree with [22] that the differences found are perceived in the feeling of difficulty in solving the problems. The talent group’s productions were not as easy to solve after reading the statement or even analyzing the solution the student provided. However, in the standard group it was relatively easy to find a procedure to solve the problems.

The study allows us to conclude that despite the fact that there is little research that addresses the invention of problems as an instrument to identify students with mathematical talent, this research provides elements that confirm that this type of activity can be used with such purpose. This is because it was shown that the students of the talent group present some characteristics when they face problem-posing tasks that differentiate them from their peers in a standard public school. In addition, these differences were reflected in the sensation of difficulty perceived when analyzing the solution of each problem since those written by the talent group are more difficult and do not immediately identify a procedure to solve them.

Finally, it is important to stress that the problems posed by the talent group were not more complex in numerical flexibility, type of question, or use of complex ideas. The statistical analyses of these variables did not show significant differences between the two groups.

All this analysis shows two important results: First, problem posing can be used as an activity to diagnose mathematical talent, as certain characteristics of the statements identify this type of student. Second, problem posing is an activity of considerable educational interest, especially in the mathematic classroom at all levels, because it reveals facets of students’ mathematical knowledge that are not easily identified using other instruments.

5. Limitations

This study presented limitations related to the study subjects since these are a small group of students within the school population and the study was carried out with a group in a certain region of Costa Rica, so it is necessary to replicate the experience in other regions or countries to generalize the results. Another aspect was the time they had to complete the tasks, two 80 min sessions; it is recommended to have more time because when problems are invented a period of time is needed for the ideas and relationships to between the data emerge and evolve.

Lastly, we consider it necessary for the students to have knowledge about problem posing; it was observed that they had difficulties in carrying out the activity because sometimes they did not know how to start or what problem to invent. This occurred more strongly in the first proposed tasks.