Abstract
In this paper, we propose an efficient numerical method for solving an initial boundary value problem for a coupled system of equations consisting of a nonlinear parabolic partial integro-differential equation and an elliptic equation with a nonlinear term. This problem has an important applied significance in petroleum engineering and finds application in modeling two-phase nonequilibrium fluid flows in a porous medium with a generalized nonequilibrium law. The construction of the numerical method is based on employing the finite element method in the spatial direction and the finite difference approximation to the time derivative. Newton’s method and the second-order approximation formula are applied for the treatment of nonlinear terms. The stability and convergence of the discrete scheme as well as the convergence of the iterative process is rigorously proven. Numerical tests are conducted to confirm the theoretical analysis. The constructed method is applied to study the two-phase nonequilibrium flow of an incompressible fluid in a porous medium. In addition, we present two examples of models allowing for prediction of the behavior of a fluid flow in a porous medium that are reduced to solving the nonlinear integro-differential equations studied in the paper.
Keywords:
nonequilibrium fluid flows in porous media; nonlinear integro-differential equation; finite element method MSC:
76M10
1. Introduction
Fluid flows through porous media are of fundamental significance to a wide range of natural and industrial processes in groundwater hydrology, enhanced oil recovery, climate engineering and many others. These processes are generally described by a system of partial differential equations. However, in certain circumstances, these equations may not provide an adequate and accurate representation of the fluid flow process due to neglecting important properties of the porous medium [1,2,3].
For example, a number of authors have conceived that the dynamics of fluid flow in a porous medium are influenced not only by the current state of the process but also by its previous states [4,5]. In particular, a number of studies have shown significant discrepancies between experimental results on wells and simulation results based on classical models [1,6]. These hereditary properties of the process, known as memory, can appear when modeling non-local transfer of reaction and contaminants, thermal conductivity [4,7,8,9,10], and many others.
The memory effects can be taken into account by the inclusion of a non-trivial memory term in the model equation, which is often represented as a convolution of the function or its derivative with some kernel [11]. Thus, a fluid flow model in a porous media taking into account memory effects can be described by partial integro-differential equations.
Another example of the application of nonlinear partial integro-differential equations are models describing multi-phase nonequilibrium fluid flow in a porous medium. One of these models was proposed in [12,13], which generalized the classical nonequilibrium model of G. Barenblatt [14]. The idea behind this generalization lies in the assumption that all flows are nonequilibrium and differ only in the degree of nonequilibrium. In this regard, the authors of [12,13] introduced a function for each flow varying between 0 and 1 that shows to what extent the flow is non-equilibrium. Moreover, the limit values, 0 and 1, correspond to completely equilibrium and completely non-equilibrium cases.
The nonlinear integro-differential equation in the model studied in [12] describes the distribution of effective water saturation. The consideration of nonequilibrium effects appears to be necessary at all stages in the development of oil fields since the pressure drop versus time obtained during laboratory studies of porous media in order to determine the relative phase permeability functions significantly differ from the theoretical curves calculated in the framework of the classical filtration theory [15]. The effect of nonequilibrium can be significant: the time of saturation establishment in the conditions of oil fields can reach the order of a year [14].
The above two examples clearly demonstrate that nonlinear integro-differential equations make it possible to describe extremely important processes occurring in porous media.
Nonlinear integro-differential equations are known to admit an analytical solution only in a few particular cases due to their complexity. Over the last several decades, many techniques have been developed for the approximate solution of these equations, which include, for example, the combination of the radial basis functions and finite difference method [16], space-time spectral collocation method [17], Galerkin method with a non-classical -projection [18].
Recently, much interest has been paid to collocation methods—namely, the Legendre wavelet method [17,19,20], Haar wavelet method [21,22,23], Euler wavelets [24], collocation method by sigmoidal functions [25], variational iteration method [26,27,28,29], homotopy perturbation method [30,31,32], moving least square method [33], Adomian’s decomposition method [34] and its combination with the homotopy analysis method [35,36], parametric iteration method and spectral collocation method [37], and differential transform method [38].
Considering the importance of the subject and motivated by the model proposed in [12,13], we devote our study to an initial boundary problem for a nonlinear system of three coupled equations. The first equation of the system is a non-linear convection–diffusion-reaction equation with an additional time-dependent integral term, which, in [12], describes the dynamics of the effective water saturation through a porous medium. The second and third equations together constitute an elliptic equation containing a nonlinear term and describe the dynamics of the pressure field.
The problem under consideration has been numerically solved in a few works. The paper [12] introduced an explicit difference scheme to numerically implement the integro-differential equation, whereas the elliptic equation was solved using the successive over-relaxation iterative method. In contrast, in [39], an implicit finite difference scheme was utilized to solve the partial integro-differential equation, which was then implemented by the alternate directions method. The elliptic equation was solved using the iterative procedure of establishement method. The stability and convergence analysis of the constructed method has been discussed.
Although the numerical schemes constructed in [12,39] made it possible to assess the impact of nonequilibrium effects on the fluid flow within the framework of the constructed model, in our opinion, insufficient attention was paid to the handling of nonlinear terms which were treated as known functions, and their values were taken from previous time layers. This approach is known to lower the convergence order with respect to the time variable.
Unfortunately, the literature review did not reveal any other works aimed at solving the filtration problem under study. However there are a few alternative efficient approaches of solving nonlinear partial integro-differential equations similar to the first equation of the system under consideration. For example, the papers [4,8,40] have utilized a two-grid finite element or block-centered finite difference method to the nonlinear non-Fickian flow model such that a rough approximation was obtained on a coarse grid, and then the corresponding linearized problem was solved on a fine grid.
In [41], this equation was reduced to a system of ordinary differential equations by virtue of a combination of group preserving scheme and spectral meshless radial point interpolation, which was then solved by the method of lines. There are also known implementations of the non-linear non-Fickian flow model by the finite volume element method [42], mixed finite element method [43], expanded -Galerkin mixed finite element method [44].
The authors of [45] proposed a numerical method based on the matrix collocation method descended from the use of Laguerre and Taylor polynomials. In [46], the Kirchhoff transformation of the dependent variable was applied, and then the solution was obtained using Galerkin approximations.
Our work uses a different approach. We constructed a numerical method based on the use of a finite difference approximation in time and a finite element approximation in the spatial direction. To achieve a global second convergence order in time, we employ different approximations of the time derivative for the first and subsequent time layers. The integral term is approximated using the Lagrange interpolation formula. For treatment of one nonlinear term, Newton’s method is applied, and the remaining nonlinear terms are linearized using a second-order difference approximation.
Secondly, we rigorously prove the stability and convergence of the fully discrete scheme as well as the convergence of Newton’s iterative process. Further, the theoretical convergence order is confirmed by numerical tests conducted for a problem with a known exact solution. We also present a comparative analysis with the results obtained by the finite difference method proposed in [12].
Thirdly, we apply the constructed numerical method to modeling a two-phase nonequilibrium flow of an incompressible fluid in a porous medium according to the model proposed in [12]. The numerical scheme has shown itself to be stable for a wide range of time step values.
Fourthly, as a supplement, we consider two examples of fluid flow problems in porous media, which are reduced to solving the nonlinear integro-differential equation considered in the paper. The first problem is concerned with a special case of nonequilibrium filtration referred to as the countercurrent filtration problem. The second problem deals with the filtration process in a fractured porous medium.
The main contribution of our paper is an approach that make it possible to effectively account for nonlinear terms, thus, maintaining a balance between computational complexity and the achievement of the global second-order convergence.
The paper is structured as follows. The next section presents the problem statement and defines the assumptions under which the problem is solved. Section 2.2 is devoted to the construction of the fully discrete scheme and Newton’s iterative method. In Section 2.3 and Section 2.4, the stability and convergence of the fully discrete schemes are discussed. Section 2.5 determines the conditions under which the quadratic convergence of Newton’s method is achieved. The remainder of the paper is aimed at providing numerical tests to show the effectiveness and applicability of the proposed method. First, we confirm the theoretical convergence order on the example of a problem with a known exact solution in Section 3.1. Finally, we show the applicability of the proposed method to solving three filtration problems in Section 3.2 and Section 4.
2. Materials and Methods
2.1. Formulation of the Problem
Problem 1.
Find η, and p in , where , , satisfying the equations
and the initial and boundary conditions:
where , λ, and σ are some positive constants; , , , , , , , and are given functions; is the outer unit normal to the boundary .
Although the boundary condition of the first kind for is considered in the analysis, the results obtained can be extended to other kinds of boundary conditions with minor modifications. Further, we assume that for simplicity of presentation.
The following assumptions are used throughout the paper.
Assumption 1.
Problem 1 has a unique solution that has a sufficient number of derivatives required for the analysis.
Assumption 2.
and are positive non-decreasing functions. Furthermore, there exist finite positive real numbers , , , , , such that, for all :
(a) .
(b)
(c) .
(d)
Assumption 3.
The components of the vector are subject to the following restrictions:
(a) .
(b) is Lipschitz continuous with respect to η and there exists a positive constant such that .
Assumption 4.
The vector can be represented as the sum of two vectors:
where the vector is such that
(a) .
(b) There exist positive constants such that and .
We adopt the standard notations of Lebesgue spaces and Sobolev spaces with the special case denoted by [47]. Further, and denote the scalar product and norm in . Let us introduce the functional spaces
Then, a weak formulation of Problem 1 reads as follows.
Problem 2.
Find satisfying the identities
for any , , , where .
2.2. Derivation of a Fully Discrete Scheme
To construct a numerical scheme, we first discretize the time interval by points , such that , where is the time discretization parameter, and denote . In addition, we use the notation and due to the implicit temporal dependence.
At first, we approximate the time derivative and the integral term in (2). To achieve the global second order in temporal variable, we employ the following approximations of the time derivative at :
where , , , .
Next, to approximate the third term in (2), represent the integral as below:
with , we then apply the Lagrange interpolation formula for
Consider the differences
Note that . Furthermore, Assumption 2 implies that . A similar assertion is valid concerning the components of the vectors and due to Assumption 4.
Let us rewrite Problem 2 with the use of the obtained approximations.
Problem 3.
Let , be known, in particular, . Find , satisfying the following identities for any , , : when :
when :
Next, we introduce a quasi-uniform triangulation in with a diameter h and let , , be certain finite element spaces. Further, truncating the errors in (3)–(8), we define a fully discrete finite element procedure.
Problem 4.
Let , be known, in particular, be the -projection of . Find , satisfying the following identities for all , , :
when :
when :
Equations (9) and (12) are in fact nonlinear. We apply Newton’s method for their linearization. To this end, we iterate the above procedure for the iterative parameter and denote the value of the function on the sth iteration by . Then, the iterative method is defined as follows.
Problem 5.
Let , be known, in particular, be the -projection of . In addition, let , be given for n, in particular, . Find , satisfying the following identities for all , , : when :
when :
Thus, Problem 1 is numerically solved in accordance with the following algorithm. First, the pair is determined simultaneously from Equations (16) and (17) employing a known initial value . Further, by taking as an initial approximation, the iterative process for computing , is conducted by (15) until for a given .
For subsequent time layers, the calculation is performed in a similar manner. For , the pair is determined simultaneously from Equations (19) and (20) with the use of known values and . Iterations are then performed by Equation (18) to determine , , where .
To analyze the convergence of the proposed numerical method, it suffices to verify that as while as . The former statement will be rigorously proven in Section 2.4, and the convergence of Newton’s method will be shown in Section 2.5.
2.3. Stability of the Scheme
In this section, we discuss the stability of the scheme (9)–(14). For the sake of completeness, let us formulate the discrete analogue of the Gronwall’s lemma, which will be used several times in obtaining the main results.
Lemma 1
([48]). If and are two positive sequences, is a monotone positive sequence, and these satisfy the inequalities , , , then the following estimate holds:
Now, let us prove a few auxiliary lemmas.
Lemma 2.
Let , , , be the solution of Problem 4. The following inequalities hold under Assumptions 2 and 4:
where C is a constant independent of τ.
Proof.
Lemma 3.
Let , , , be the solution of Problem 4. The following inequality holds for all such that
under Assumptions 2 and 3:
where C is a constant independent of τ.
Proof.
Let us take in (12):
and estimate the terms , . By a direct check, one can verify that is bounded from below by the quantity
Under Assumptions 2 and 3, the condition where is defined in (24), by using the inequality (23) and noting that for , it is easy to obtain that
where is an arbitrarily small number.
Making use of the inequalities (26)–(32) in (25) and summing the resulting inequality over n from 2 to n, we obtain:
By applying the discrete Gronwall’s lemma, we arrive at
Estimating the terms , ,..., in (36) in a similar manner as in obtaining the inequalities (27)–(32), we conclude that, for all satisfying the condition (24):
Finally, by taking the square root of both parts of the last inequality, then using the fact that and observing that , we arrive at the assertion of the lemma. □
Theorem 1.
Let , , , be the solution of Problem 4. Then, , satisfies the inequality
for all such that
under Assumptions 2–4, where is a constant independent of τ.
Proof.
Lemmas 2 and 3 imply that, under the specified conditions:
Applying the discrete Gronwall’s lemma to this inequality, we obtain the assertion of the theorem. □
2.4. Convergence of the Scheme
Let us introduce the projections , , such that
satisfying the approximation properties
where m and l depend on the choice of the finite element spaces.
Let us decompose the errors as follows:
Lemma 4.
Let , , , be the solution of Problem 4 and be the solution of Problem 1. The following inequalities hold under Assumptions 1 and 4:
where C is a constant independent of the mesh parameters.
Proof.
Lemma 5.
Let , , , be the solution of Problem 4 and be the solution of Problem 1. The following inequality holds for all ,
under Assumptions 1–3:
where C is a constant depending on the norms of the solution of Problem 1 but independent of the mesh parameters.
Proof.
Subtract (3) and (6) from (9) and (12), respectively. Then, take and use the notation (41) to obtain: when :
when :
The term is estimated as follows:
Using the obtained inequalities in (49) and summing the resulting inequality with respect to n from 2 to n implies:
Applying the discrete Gronwall’s lemma gives
Under the condition , where is defined in (47), we obtain
Taking the square root of both parts of the inequality, we arrive at the assertion of the lemma. □
Theorem 2.
Let , , , be the solution of Problem 4 and be the solution of Problem 1. Then, satisfies the inequality
for all such that
under Assumptions 1–4, where C is a constant depending on the norms of the solution of Problem 1 but independent of the mesh parameters.
Proof.
Lemmas 4 and 5 imply that, for all :
or
By applying the discrete Gronwall’s lemma to the last inequality, we obtain the assertion of the theorem. □
2.5. Convergence of Newton’s Method
Let us determine the conditions ensuring the quadratic convergence of Newton’s iterative process (15), (18) using the technique proposed in [49].
Theorem 3.
Proof.
Subtract (15) and (18) from (9) and (12) to obtain
where , and , . Choose and estimate the terms in (53). Let us dwell in more detail on the estimate of the last term on the left-hand side of (53). By using Assumption 3 and the inequality [49]
valid for a differentiable function g with a Lipschitz-continuous derivative, we obtain
Further, using the inequality [49], we have
whence, for sufficiently small , we conclude that
This inequality implies the assertion of the theorem. □
3. Results
3.1. Verification of the Convergence Order
This section provides an analysis of a few numerical tests conducted to validate the proposed numerical method. The purpose of the first computational experiment was to determine the empirical convergence order and compare it with the theoretical convergence order predicted in Theorem 2.
Consider Problem 1 in , where , with the following input data:
The exact solution of the problem is as follows: ,
, .
One can verify that Assumptions 2–4 are satisfied for the selected data. The following finite element spaces were chosen:
where is the set of polynomials of degree at most l. Therefore, we expected the second convergence order both in temporal and spatial variables.
A partition containing nodes was introduced on each side of the square , and a quasi-uniform triangulation of was generated on its basis. The diameter of the triangulation obtained in this way was . The iterative process (15) and (18) was performed until . In all numerical tests, this condition was achieved in two to three iterations.
The numbers and in Theorems 1 and 2 that impose a constraint on the time step at were approximately equal to 0.46875 and 0.11719, respectively. In particular, the stability and convergence of the scheme is predicted to be achieved for all according to these theorems. By successively halving the time step in the range from to , we calculated the corresponding errors in the -norm and the convergence order by the formula .
The calculation results are presented in the second and third columns of Table 1. It follows from the table that the actual convergence order slightly exceeded 2.0, which fully confirms the temporal convergence order predicted in Theorem 2.

Table 1.
Convergence analysis for with respect to the temporal variable conducted with a fixed spatial discretization parameter, .
This problem was also solved by the numerical scheme proposed in [12] for comparison. To this end, a uniform grid is introduced in the square with a step with . Conducting a computational experiment as described above, we obtained the actual order of convergence of this method. The calculation results are presented in the fourth and fifth columns of Table 1, which clearly show that this method converges with the first order in the temporal variable. Thus, it follows from a comparison of the results that the method proposed in this paper is more efficient for solving the problem.
A similar computational experiment was conducted by reducing the parameters and by half at a fixed time step to verify the convergence order with respect to the spatial variable. The results of the experiment showed the second order of convergence for both methods. Therefore, the numerical tests performed fully confirmed the order of convergence predicted in Theorem 2.
3.2. Modeling the Two-Phase Non-Equilibrium Flow in Porous Media
We now consider a more realistic example. Let us consider the following equations describing non-equilibrium flow of a two-phase incompressible fluid in a porous medium [12,13]:
where and s are the effective and true water saturations, respectively; is the volumetric velocity of the flow; p is the pressure; and m are the absolute permeability and porosity of the medium; is the replacement time; is the degree of non-equilibrium; is the porosity; and and are the relative phase permeabilities corresponding to the phases of water w and oil o.
Equation (57) extends the non-equilibrium law by G. Barenblatt [50] and is referred to as the generalized law of non-equilibrium in [12]. The essence of this generalization lies in the assumption that all flows are nonequilibrium and differ only in the degree of nonequilibrium. The function determines the degree of nonequilibrium and takes values between 0 and 1, where the limit values and correspond to a completely nonequilibrium flow and a completely equilibrium flow, respectively.
We adopt a few assumptions regarding physical data. In contrast to [12], we exclude the explicit dependence of the capillary pressure function on x assuming its dependence only on . In addition, the porosity and replacement time are assumed to be constants. In this case, the coefficients in (54)–(57) are defined as follows:
where and are the water and oil densities, and is the gravity vector. Further, we employ a slightly modified LET-type model [51] to determine the relative phase permeabilities:
with, say, , and assume that the capillary pressure function is defined as
where A and B are positive constants. In this case, , , . The rest of the parameters are chosen as follows: , , , , , , . Note that , k and a in fact do not depend on . Therefore, Assumptions 2–4 are fulfilled.
The calculations were performed on a mesh with a diameter . Establishing the exact values of the constants and in Theorems 1 and 2 was found to be quite difficult. However due to the smallness of entering , the restriction on was insignificant. In practice, the numerical scheme has shown itself to be stable for a wide range of time step values. The numerical test was conducted for until the flow became steady. The values of the obtained effective saturation at different times are illustrated in Figure 1.
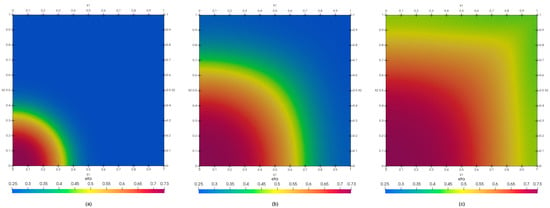
Figure 1.
Dynamics of the effective saturation at different times t. (a) t = 1000 , (b) t = 4000 , and (c) t = 9000 with = 10.
Note that discussion of the simulation results is beyond of this paper’s remit since the aim of this study is to show the applicability of the numerical method. This issue is discussed in detail in [39].
4. Discussion
Based on the theoretical analysis performed and the results of numerical experiments, the following conclusions can be drawn.
(1) The proposed computational method makes it possible to obtain an approximate solution to the filtration problem, which includes a nonlinear partial integro-differential equation. The results of computational experiments conducted for a model problem with different mesh configurations fully confirmed the results of the theoretical analysis.
We demonstrated that the empirical convergence order in the temporal variable in the -norm slightly exceeded 2.00, while the spatial convergence order was consistently close to 2.00 for the chosen finite element spaces. This result agrees well with the results of Theorem 2 and significantly improves the result obtained in [12].
(2) It should be noted that the construction of a numerical scheme of the second convergence order in the temporal variable relies heavily on the properties of the functions adopted in classical filtration models. In most two-phase relative phase permeability models (see, for example, [52]), the function and its derivative vanishes at 0. Moreover, it is often assumed that the water saturation is uniformly distributed over the domain at the initial time. These simplifying considerations have allowed us to formulate Assumption 2(b) and Assumption 4(a).
(3) The proposed approach based on the combined use of Newton’s method and a second-order approximation made it possible to effectively handle nonlinear terms, thereby, maintaining a balance between computational complexity and achieving second-order convergence. Moreover, the results of solving the model problem, presented in Section 3.1, showed the quadratic convergence of Newton’s method.
It should be noted that the results obtained have more of a methodological nature. However, the proposed approach can be easily generalized for the case when all the coefficients in Equation (1) depend on the sought solution by applying Newton’s method or high-order approximations for their linearization.
(4) Note that the initial boundary value problem for Equation (1) is also of independent interest. Let us show the applicability of the proposed method on a particular case of the nonequilibrium filtration model when the total flow velocity is equal to zero. This case is known as countercurrent capillary impregnation [53]. Then, Equation (56) becomes an identity, and Equation (54) reduces to the following form:
The iterative method for solving this problem is to find satisfying the identities (15) and (18). The stability and convergence of a fully discrete scheme follows from Lemmas 3 and 5 with , and the convergence of the iterative method follows from Theorem 3.
Furthermore, the constructed numerical method can be applied to solving a filtration problem in a fractured porous medium. This generalized model is formulated under the assumption that the fluid and medium parameters depend on the fractional derivative of the pressure. Making use of a non-local change of variables allows one to reduce the obtained pressure equation to the non-linear partial integro-differential Equation (1). For a more detailed analysis, we refer the reader to Appendix A.
(5) Since the work is mainly aimed at a comprehensive study of the numerical method for solving Problem 1, little attention is paid to the interpretation of the results of modeling two-phase nonequilibrium fluid flow in porous media. In our opinion, this issue deserves more detailed consideration, which will be the subject of a separate paper.
(6) In subsequent works, the authors intend to focus on other aspects of the numerical solution of Problem 1. For example, the obtained results can be extended for the fractional differential generalizations of the filtration model by replacing the time derivatives with their fractional differential counterparts. Similar generalizations of well-known fluid dynamics models have been the subject of many works [54,55,56,57]. In addition, in subsequent papers, the authors intend to investigate the asymptotic stability of the proposed scheme (see, for example, [58,59,60]). Furthermore, the study of control problems with qualitative properties of controllability [61] is also promising.
The outcomes of this study can be used in solving other classes of problems involving integro-differential equations. The proposed approach also forms the basis for further research in this direction.
Author Contributions
Conceptualization, D.B. and N.T.; methodology, D.B. and N.T.; software, D.B.; validation, D.O., Y.Y. and K.B.; formal analysis, D.O., Y.Y. and K.B.; investigation, D.B. and D.O.; resources, D.B. and Y.Y.; data curation, Y.Y.; writing—original draft preparation, D.B. and D.O.; writing—review and editing, D.B. and D.O.; visualization, D.B.; supervision, D.B.; project administration, D.B.; funding acquisition, D.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Ministry of Education and Science of the Republic of Kazakhstan, grant number AP08053189.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Modeling the Flow in a Fractured Porous Medium
The proposed iterative schemes (15) and (18) can also be extremely useful in solving the problem of one-phase fluid flow in a fractured porous medium. Following [2], we consider the following fractional generalizations of the classical equation of state and the relation for porosity:
where , . In this paper, we used the fractional derivative and the fractional integral in the sense of Caputo–Fabrizio, which are defined as [62]
where we take .
Further, we consider the following generalized motion law similar to [2]:
where we slightly modified the last term. Substituting these relations into the classical continuity equation
we obtain the following nonlinear equation for pressure:
where , and Q is a linear term taking into account mass transfer from other continua. In practice, the functions and are often known, since they are expressed in terms of the empirically determined rock and fluid compressibility coefficients.
A numerical method of solving an initial boundary problem for a linear special case of Equation (A1) was proposed in [63]. Now, we consider a different approach. Following [2], let us make a non-local change of variables , and use the properties of fractional derivatives and integrals [64] to obtain
Let us confine ourselves to the case , , . Then, (A2) is reduced to the form
By observing that
we arrive at the equation
Thus, the problem of fluid flow in a fractured porous medium under study has been reduced to solving a nonlinear partial integro-differential equation studied in the paper. The numerical solution of the obtained equation is similar to that described in the Discussion section for Equation (58).
References
- Ferreira, J.A.; Pinto, L. An Integro-Differential Model for Non-Fickian Tracer Transport in Porous Media: Validation and Numerical Simulation. Math. Methods Appl. Sci. 2015, 39, 4736–4749. [Google Scholar] [CrossRef]
- Gazizov, R.K.; Lukaschuk, S.Y. Fractional-Differential Approach to Modeling Filtration Processes in Complex Inhomogeneous Porous Media. Vestnik UGATU 2017, 21, 104–112. (in Russian). [Google Scholar]
- Zhou, H.W.; Yang, S.; Zhang, S.Q. Modeling Non-Darcian Flow and Solute Transport in Porous Media with the Caputo–Fabrizio Derivative. Appl. Math. Model. 2019, 68, 603–615. [Google Scholar] [CrossRef]
- Liu, W.; Li, X.; Zhao, Q. A Two-Grid Expanded Mixed Element Method for Nonlinear Non-Fickian Model in Porous Media. Int. J. Comput. Math. 2014, 91, 1299–1314. [Google Scholar] [CrossRef]
- Hashan, M.; Jahana, T.U.; Zaman, L.N.; Imtiaz, S.; Hossain, M.E. Modelling of Fluid Flow Through Porous Media Using Memory Approach: A Review. Math. Comput. Simul. 2020, 177, 643–673. [Google Scholar] [CrossRef]
- Boganik, V.N.; Medvedev, A.I.; Pestrikova, N.A.; Gugnyakov, V. Improving the Reliability of Determining Permeability, Skin Factor, Flow Rate and Productivity Given by the Operation of Gas Wells. Tekhnologia TEK 2006, 3, 34–40. (In Russian) [Google Scholar]
- Wang, P.; Jiang, L.; Chen, S. A Nonconforming Scheme for Non-Fickian Flow in Porous Media. J. Inequalities Appl. 2017, 142, 1–16. [Google Scholar] [CrossRef]
- Li, X.; Rui, H. A Two-Grid Block-Centered Finite Difference Method for Nonlinear Non-Fickian Flow Model. Appl. Math. Comput. 2016, 281, 300–313. [Google Scholar] [CrossRef]
- Ewing, R.; Wang, H. A Summary of Numerical Methods for Time-Dependent Advection-Dominated Partial Differential Equations. J. Comput. Appl. Math. 2001, 128, 423–445. [Google Scholar] [CrossRef]
- Sharma, P.K.; Agarwal, P.; Mehdinejadiani, B. Study on Non-Fickian Behavior for Solute Transport Through Porous Media. J. Hydraul. Eng. 2020, 28, 171–179. [Google Scholar] [CrossRef]
- Peszynska, M. Analysis of an Integro-Differential Equation Arising Form Modelling of Flows with Fading Memory Through Fissured Media. J. Partial. Differ. Equ. 1995, 8, 173–195. [Google Scholar]
- Yermagambetov, T.K. Algorithm for Numerical Implementation of a Filtration Model with a Generalized Nonequilibrium Law. Proc. Natl. Acad. Sci. Repub. Kazakhstan Phys.-Math. Ser. 2010, 2, 94–96. [Google Scholar]
- Gabbasov, M.B. On the Solvability of a Problem of Nonequilibrium Inhomogeneous Countercurrent Capillary Filtration. In Abstracts of the Conference "Boundary Value Problems and Their Spectral Questions for Differential Equations"; Publishing House of Kazakh State University: Almaty, Kazakhstan, 1991. (In Russian) [Google Scholar]
- Barenblatt, G.I.; Vinnichenko, A.P. Non-equilibrium filtration of immiscible fluids. Adv. Mech. 1980, 3, 52–58. (In Russian) [Google Scholar]
- Faizulin, T.A. Mathematical Modeling of Relaxation Phenomena during the Flow of an Inhomogeneous Fluid in Porous Media. Ph.D. Thesis, Ufa State Aviation Technical University, Ufa, Russia, 2008. (In Russian). [Google Scholar]
- Avazzadeh, Z.; Beygi Rizi, Z.; Maalek Ghaini, F.M.; Loghmani, G.B. A Numerical Solution of Nonlinear Parabolic-Type Volterra Partial Integro-Differential Equations Using Radial Basis Functions. Eng. Anal. Bound. Elem. 2012, 36, 881–893. [Google Scholar] [CrossRef]
- Fakhar-Izadi, F.; Dehghan, M. Fully Spectral Collocation Method for Nonlinear Parabolic Partial Integro-Differential Equations. Appl. Numer. Math. 2018, 123, 99–120. [Google Scholar] [CrossRef]
- Cannon, J.R.; Lin, Y. Non-classical H1 Projection and Galerkin Methods for Non-Linear Parabolic Integro-Differential Equations. Calcolo 1988, 25, 187–201. [Google Scholar] [CrossRef]
- Singh, S.; Patel, V.K.; Singh, V.K. Convergence Rate of Collocation Method Based on Wavelet for Nonlinear Weakly Singular Partial Integro-Differential Equation Arising from Viscoelasticity. Numer. Methods Partial. Differ. Equ. 2018, 34, 1781–1798. [Google Scholar] [CrossRef]
- Mahdavi, S.; Kajani, M.T. Nonlinear Integro-Differential Equations. J. Math. Ext. 2010, 4, 107–117. [Google Scholar]
- Amin, R.; Mahariq, I.; Shah, K.; Awais, M.; Elsayed, F. Numerical Solution of the Second Order Linear and Nonlinear Integro-Differential Equations Using Haar Wavelet Method. Arab. J. Basic Appl. Sci. 2021, 28, 12–20. [Google Scholar] [CrossRef]
- Lepik, Ü. Haar Wavelet Method for Nonlinear Integro-Differential Equations. Appl. Math. Comput. 2006, 176, 324–333. [Google Scholar] [CrossRef]
- Erfanian, M.; Mansoori, A. Solving the Nonlinear Integro-Differential Equation in Complex Plane with Rationalized Haar Wavelet. Math. Comput. Simul. 2019, 165, 223–237. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, L. Solving Nonlinear Volterra Integro-Differential Equations of Fractional Order by Using Euler Wavelet Method. Adv. Differ. Equ. 2017, 27, 1–16. [Google Scholar] [CrossRef]
- Costarelli, D.; Spigler, R. A Collocation Method for Solving Nonlinear Volterra Integro-Differential Equations of Neutral Type by Sigmoidal Functions. J. Integral Equ. Appl. 2014, 26, 15–52. [Google Scholar] [CrossRef]
- Al-Saar, F. Solving Nonlinear Fredholm Integro-Differential Equations Via Modifications of Some Numerical Methods. Adv. Theory Nonlinear Anal. Its Appl. 2021, 5, 260–276. [Google Scholar] [CrossRef]
- Yildirim, A. Application of He’s Variational Iteration Method to Nonlinear Integro-Differential Equations. Z. Naturforschung A 2010, 65, 418–430. [Google Scholar] [CrossRef]
- Liu, Y.; Gurran, C.S. Solving Nonlinear Differential Difference Equations Using He’s Variational Iteration Method. Appl. Math. Comput. Sci. 2011, 3, 33–46. [Google Scholar]
- Batiha, B.; Noorani, M.S.M.; Hashim, I. Numerical Solutions of the Nonlinear Integro-Differential Equations. Int. J. Open Probl. Comput. Sci. Math. 2008, 1, 34–42. [Google Scholar]
- Roul, P.; Meyer, P. Numerical Solutions of Systems of Nonlinear Integro-Differential Equations by Homotopy-Perturbation Method. Appl. Math. Model. 2011, 35, 4234–4242. [Google Scholar] [CrossRef]
- Sekar, S.; Thirumurugan, A.S. Numerical Investigation of the Nonlinear Integro-Differential Equations Using He’s Homotopy Perturbation Method. Malaya J. Mat. 2017, 5, 389–394. [Google Scholar]
- Sharif, A.A.; Hamoud, A.A.; Ghadle, K.P. Solving Nonlinear Integro-Differential Equations by Using Numerical Techniques. Acta Univ. Apulensis 2020, 61, 45–53. [Google Scholar]
- Dehghan, M.; Salehi, R. The Numerical Solution of the Non-Linear Integro-Differential Equations Based on the Meshless Method. J. Comput. Appl. Math. 2012, 236, 2367–2377. [Google Scholar] [CrossRef]
- Al-Mazmumy, M.; Almuhalbedi, S.O. Solution of Nonlinear Integro Differential Equations by Two-Step Adomian Decomposition Method (TSAM). Int. J. Mod. Nonlinear Theory Appl. 2016, 5, 248–255. [Google Scholar] [CrossRef][Green Version]
- Abdou, M.A.; Youssef, M.I. On a Method for Solving Nonlinear Integro Differential Equation of Order n. J. Math. Comput. Sci. 2021, 25, 322–340. [Google Scholar] [CrossRef]
- Khanlari, N.; Paripour, M. Solving Nonlinear Integro-Differential Equations Using the Combined Homotopy Analysis Transform Method with Adomian Polynomials. Commun. Math. Appl. 2018, 9, 637–650. [Google Scholar]
- Daliri Birjandi, M.H.; Saberi-Nadjafi, J.; Ghorbani, A. An Efficient Numerical Method for a Class of Nonlinear Volterra Integro-Differential Equations. J. Appl. Math. 2018, 2018, 7461058. [Google Scholar] [CrossRef]
- Behiry, S.H. Nonlinear Integro-Differential Equations by Differential Transform Method with Adomian Polynomials. Math. Sci. Lett. 2013, 2, 209–221. [Google Scholar] [CrossRef][Green Version]
- Yermagambetov, T.K. Solvability and Numerical Study of the Model of Nonequilibrium Filtration of Two Incompressible Fluids with a Generalized Law of Nonequilibrium. Ph.D. Thesis, Al-Farabi Kazakh National University, Almaty, Kazakhstan, 2010. (In Russian). [Google Scholar]
- Chen, C.; Zhang, X.; Zhang, G.; Zhang, Y. A Two-Grid Finite Element Method for Nonlinear Parabolic Integro-Differential Equations. Int. J. Comput. Math. 2018, 96, 2010–2023. [Google Scholar] [CrossRef]
- Soradi-Zeid, S.; Mesrizadeh, M. The Method of Lines for Parabolic Integro-Differential Equations. J. Math. Model. 2020, 8, 291–308. [Google Scholar]
- Ewing, R.; Lazarov, R.; Lin, Y. Finite Volume Element Approximations of Nonlocal Reactive Flows in Porous Media. Numer. Methods Partial. Differ. Equ. 2000, 16, 285–311. [Google Scholar] [CrossRef]
- Sinha, R.K.; Ewing, R.; Lazarov, R. Mixed Finite Element Approximations of Parabolic Integro-Differential Equations with Nonsmooth Initial Data. SIAM J. Numer. Anal. 2009, 47, 3269–3292. [Google Scholar] [CrossRef]
- Al-Humedi, H.O.; Al-Abadi, A.K. Analysis of Error Estimate for Expanded H1-Galerkin MFEM of PIDEs with Nonlinear Memory. In Proceedings of the International Conference on Emerging Applications in Material Science and Technology, Namakkal, India, 30–31 January 2020; Volume 2235, p. 020010. [Google Scholar]
- Gürbüz, B.; Sezer, M. A New Computational Method Based on Laguerre Polynomials for Solving Certain Nonlinear Partial Integro Differential Equations. Acta Phys. Pol. A 2017, 132, 561–563. [Google Scholar] [CrossRef]
- Da, X. Finite Element Methods of the Two Nonlinear Integro-Differential Equations. Appl. Math. Comput. 1993, 58, 241–273. [Google Scholar] [CrossRef]
- Adams, R. Sobolev Spaces; Academic Press: New York, NY, USA, 1975. [Google Scholar]
- Brezzi, F.; Fortin, M. Mixed and Hybrid Finite Element Methods; Springer: New York, NY, USA, 1991. [Google Scholar]
- Radu, F.A.; Pop, I.S. Simulation of Reactive Contaminant Transport with Non-Equilibrium Sorption by Mixed Finite Elements and Newton Method. Comput. Geosci. 2011, 15, 431–450. [Google Scholar] [CrossRef]
- Barenblatt, G.I. Filtration of Two Nonmixing Fluids in a Homogeneous Porous Medium. Mech. Gas Fluids 1971, 5, 57–64. (In Russian) [Google Scholar] [CrossRef]
- Moghadasi, L.; Guadagnini, A.; Inzoli, F.; Bartosek, M. Interpretation of Two-phase Relative Permeability Curves Through Multiple Formulations and Model Quality Criteria. J. Pet. Sci. Eng. 2015, 135, 738–749. [Google Scholar] [CrossRef]
- Chen, Z. Reservoir Simulation: Mathematical Techniques in Oil Recovery; SIAM: Philadelphia, PA, USA, 2007; p. 17. [Google Scholar]
- Barenblatt, G.I.; Gilman, A.A. Mathematical model of nonequilibrium countercurrent capillary impregnation. Eng. Phys. J. 1987, 52, 456–461. [Google Scholar] [CrossRef]
- Caputo, M. Models of Flux in Porous Media with Memory. Water Resour. Res. 2000, 36, 693–705. [Google Scholar] [CrossRef]
- Agarwal, R.; Yadav, M.P.; Baleanu, D.; Purohit, S.D. Existence and Uniqueness of Miscible Flow Equation Through Porous Media with a Non Singular Fractional Derivative. AIMS Math. 2020, 5, 1062–1073. [Google Scholar] [CrossRef]
- Zhong, W.; Li, C.; Kou, J. Numerical Fractional-Calculus Model for Two-Phase Flow in Fractured Media. Adv. Math. Phys. 2013, 2013, 429835. [Google Scholar] [CrossRef]
- Vijayakumar, V.; Nisar, K.S.; Chalishajar, C.; Shukla, A.; Malik, M.; Alsaadi, A.; Aldosary, S.F. A Note on Approximate Controllability of Fractional Semilinear Integrodifferential Control Systems via Resolvent Operators. Fractal Fract. 2022, 6, 73. [Google Scholar] [CrossRef]
- Tian, H. Asymptotic Stability Analysis of the Linear θ-Method for Linear Parabolic Differential Equations with Delay. J. Differ. Equ. Appl. 2009, 15, 473–487. [Google Scholar] [CrossRef]
- Singh, A.; Shukla, A.; Vijayakumar, V.; Udhayakumar, R. Asymptotic Stability of Fractional Order (1, 2] Stochastic Delay Differential equations in Banach spaces. Chaos Solitons Fractals 2021, 150, 111095. [Google Scholar] [CrossRef]
- Larsson, S. The Long time Behavior of Finite-element Approximations of Solutions to Semilinear Parabolic Problems. SIAM J. Numer. Anal. 1989, 26, 348–365. [Google Scholar] [CrossRef]
- Vijayakumar, V.; Udhayakumar, R.; Dineshkumar, C. Approximate Controllability of Second Order Nonlocal Neutral Differential Evolution Inclusions. IMA J. Math. Control. Inf. 2021, 38, 192–210. [Google Scholar] [CrossRef]
- Caputo, M.; Fabrizio, M. Applications of New Time and Spatial Fractional Derivatives with Exponential Kernels. Progr. Fract. Differ. Appl. 2016, 2, 1–11. [Google Scholar] [CrossRef]
- Baigereyev, D.; Alimbekova, N.; Berdyshev, A.; Madiyarov, M. Convergence Analysis of a Numerical Method for a Fractional Model of Fluid Flow in Fractured Porous Media. Mathematics 2021, 9, 2179. [Google Scholar] [CrossRef]
- Atangana, A. Extension of Rate of Change Concept: From Local to Nonlocal Operators with Applications. Results Phys. 2020, 19, 103515. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).