1. Introduction
Optimal portfolio selection [
1,
2] is a cornerstone quantitative model and theory in the financial industry. It is a theory because it represents the first quantitative explanation of a “rational” investor selection model. It is also a quantitative model because the original proposal develops a geometric and analytic method to “select” a group of securities (portfolio) that lead to the highest investor’s satisfaction. By satisfaction, the Classic Economics theory (along with Classical Financial Economics) implies the highest possible return, given the lowest feasible risk exposure.
As a brief introduction, the portfolio with the highest satisfaction (that means the highest utility function) is the one with the maximum utility function (
) level selected with the following optimization problem:
In the previous expression,
is an
weights vector with the investment level of each of the
assets that will be part of the investment universe,
, or the set of the securities of interest. Moreover,
is an
expected value vector with the expected value of the return of each security in the portfolio, and
is a (personal) risk-aversion level that penalizes the risk exposure of the portfolio. Finally, there is an
covariance matrix that allows us to estimate the portfolio’s risk exposure (
), given the covariance or security’s co-linearities in the performance of each security, either individually or by the correlation with other securities in the investment universe, Ψ. According to References [
1,
2], the first term on the right-hand side of (1) is a “positive” or preferred quality (expected return). That is, the higher it is, the happier the investor is. Contrary to this, the second term is not good. The higher it is, the less comfortable (anxious) the investor is.
Even if the Quadratic equation in (1) is a simple Quadratic equation reached with a second-order Taylor expansion of , other functional forms could model the investor’s satisfaction. The choice of the best utility function is a task outside our scope. By assuming a mean–variance portfolio selection process, a lot of the literature tests the benefits of an optimal portfolio selection, maximizing (1), or related utility functions.
To perform the optimal portfolio selection
in (1), the portfolio manager (PM) must solve the following optimization problem:
In this problem, a and are security-specific or security-type lower and upper restriction vectors.
Among the issues discussed in the literature, there is no consensus on determining the expected returns vector
. In this problem,
and
b are security-specific lower and upper restriction vectors. This optimization problem applies only to a portfolio with risky securities. If an investor wants to include the impact of a risk-free (
) asset in the portfolio, (2) should be extended as follows:
Financial Economics Theory indicates that, in a well-informed, or almost well-informed market (that is strong or semi-strong efficient [
3] market), the expected return in an asset is the one given with the equilibrium risk premium (
) from the rate
of a risk-free asset, such as the US 3-month Treasury-bill. A risk premium modeled with a single (market) factor or portfolio’s risk premium (
), given that portfolio’s expected return
). This led to the Capital Asset Pricing Model (CAPM) or single-factor model [
4,
5], and its multifactor extensions, such as the Fama-French [
6,
7] and the Carhart [
8], as the most used in the financial practice. This assumption of an equilibrium risk-premium suggests that, given a strong or semi-strong informational efficiency, there is no way to have a better performance than the return of a market portfolio (
), that is a stock index or benchmark that it is assumed as the one that all the investors hold, given their added utility functions and preferences.
Despite this, a critical drawback of this “equilibrium theory” is the fact that no one knows this market portfolio, and the portfolio market proxy (stock index) could not be mean–variance efficient [
9,
10,
11]. That is, its risk–return trade-off is not the best that a given investor could reach. This drawback opens the possibility to add personal “views” or expected returns, given an economic or quantitative model. Views that could lead to outperform this benchmark or market portfolio. This conclusion suggests that we estimate the personal (quantitative or economic) views and mixing them with the equilibrium ones.
Another significant drawback of the optimization problem in (2) or (3) is that the input parameters,
and
, are unknown, and, usually, their sample estimators are used instead (
, ). As a consequence, and as Jorion [
12], Michaud [
13], and Best and Grauer [
14,
15] proved as true, the optimal portfolio selection in (2) or (3) is sensitive to these parameters, especially
.
In the original Markowitz [
1,
2] proposal, there is another concept known as the efficient set (
), which is a locus of all the portfolios that have (1) the lowest risk (
), given (2) a portfolio return (
. This locus
has a geometric risk–return representation known as the efficient frontier. From this efficient set,
, the investor selects the portfolio that solves the optimization problem given in (3). As previously mentioned, the efficient set depends on the values of the sample parameters,
and
. If these are subject to estimation (sample) error, the efficient portfolio set
and (3) are also subject to that error. This estimation error led to Bayesian estimation methods to reduce this estimation error. Among the primary suggestions, we can mention the one of Jorion [
16].
As noted in this brief historical review, the original portfolio selection model lacks in two issues:
The optimal portfolio, , is sensitive to estimation (sample) error in the security’s risk and return input parameters (, ).
The original model does not mix personal security views or security’s return forecast () with the general equilibrium returns (). There is a need to determine a properly expected return vector, , that blends the equilibrium market returns and the PM’s forecasts and views.
Several portfolio selection heuristics have been suggested for this purpose, with the Treynor and Black [
17] (TB) being one of the most mentioned. This heuristic mixes an “active portfolio” (
), a portfolio with investment levels different, with the ones of the market or equilibrium one (
). Despite its simplicity and being a CAPM portfolio selection heuristic, this optimal selection model was not used widely by practitioners for three reasons:
They do not have enough resources to estimate views in a large set of securities (such as the S&P 500 stock index).
Their qualitative views are not part of the active portfolio’s parameters estimation.
A feasible optimal portfolio (given the current restrictions) could not be mean–variance efficient. Either the TB or the Markowitz optimization problem in (2) or (3) could lead to “corner” portfolios. A “corner” portfolio is, in terms of the Quadratic programming algorithm that helps to optimize (2) or (3), a portfolio that is in “the corner” or edge of two or more converging linear restrictions.
As a potential solution to these three issues, Black and Litterman [
18] suggested a Bayesian framework in which the equilibrium returns of the market portfolio (or benchmark instead of a market portfolio, as Meucci [
19] suggested) are “priors” that are estimated as follows:
This result departs from the CAPM risk-premium of the
ith security’s return,
:
In the previous expression,
is the security’s sensitivity to percent market changes (
) and is considered the only risk factor, given some CAPM and equilibrium assumptions, such as homogeneous expectations (the same rational choice and views) among investors [
5,
20]. Moreover,
is the weight of the ith security in the market portfolio or benchmark. Following Black and Litterman, (5) can be expressed in matrix form as in (4). With this result, the equilibrium return the one estimated with the weight that the market invest in each security (
), the covariance among these (
), and the general market risk aversion (
). This last magnitude reflects the confidence level in the market equilibrium views. If
the PM is highly confident in
.
Black and Litterman (henceforth B–L) suggest a Gaussian framework to blend the personal views
in each asset (in a portfolio of
assets) with its corresponding equilibrium return
, given the confidence level printed in that view (
). With a
views vector
(
), a
“pick” matrix
(a matrix in which each row represents the investment level of each view in the portfolio), a
diagonal matrix with the trust level in each view (
), and the securities equilibrium returns vector (
), B–L suggested the Bayesian estimation of each security expected return as follows:
In the previous expression,
and
represent the confidence in the market and personal views, respectively. This rationale leads to the Bayesian estimation of the B–L covariance matrix as follows:
With the Bayesian parameters (6) and (7), Black and Litterman suggest running a conventional mean–variance portfolio selection process with the expectation that the resulting optimal weights () reflect the blend of the equilibrium and personal views. These authors also suggest that the optimal investment levels are diversified and do not show the investment level concentration as the selection made with the sample parameters (, ).
As we review in the next section, extensions to the original B–L model (5) and (6) exist. Moreover, there are tests for several applications.
A potential extension to the B–L model is to estimate the security-specific views with Markov-Switching (M-S) models [
21,
22,
23]. These models have some benefits, such as estimating location (mean,
) and scale (standard deviation, (
) parameters in different states of nature (regimes). In terms of behavioral-finance and security analysis, one regime (
) could be the period in which the volatility (stock price fluctuation) is low, and another the one (
) in which the volatility is low. Moreover, these models are useful to predict the probability (
) of beaing in each regime. These models are useful to forecast these regimes and, given the estimated parameters, a PM could predict portfolio performance in a multi-regime (states of nature) context to make investment decisions. The first paper that suggested M-S models for investment decisions is the one of Brooks and Persand [
24] in the UK fixed-income and stock markets. These authors found as useful their M-S trading algorithm to create alpha (extra return) from a passive or buy-and-hold portfolio management strategy in these markets.
Following Brooks and Persand, other authors, such as Kritzman et al. [
25]; Ang and Bekaert [
26,
27,
28]; Hauptman et al. [
29]; Engel, Wahl, and Zagst [
30]; De la Torre-Torres; Galeana-Figueroa and Alvarez-Garcia [
31,
32,
33]; or De la Torre, Martínez and Venegas [
34], tested the benefit of two or three-regime M-S models in trading algorithms. These authors tested their algorithms in stock, currency, agricultural or energy commodities, or even volatility futures trading. Practically all of these works (including the impact of trading costs and taxes) found M-S models to be useful in trading algorithms, similar to Brooks and Persand. The limitation of these works (except for the ones of Kritzman et al. [
25] and Ang and Bekaert [
26,
27,
28]) is that they tested their algorithms in single security versus a risk-free asset context. Their simulated portfolios only used M-S models to determine the investment levels in the risky asset (stocks, security futures, currencies, or volatility futures) and the risk-free ones.
As mentioned in our first test in this paper, we wanted to test if the use of M-S models to make security-specific return forecasts (views) are useful inputs for the B–L optimal portfolio selection in (6) and (7). Our position is that using two-regime M-S models for the security-specific views in a B–L portfolio selection context could lead to alpha generation in a US stocks portfolio.
Despite this, there are few works in the literature about the use of views () estimated with Markov-Switching (M-S) models. Departing from this scant literature, we wanted to extend the current reviews by testing if it is helpful to use M-S models to forecast the performance of each security in a US stocks portfolio.
Up to now, there have been tests in internationally diversified portfolios. Little is written in portfolios with a broader number of assets. An issue that leads to limited optimal solutions is if the PM uses a mean–variance Quadratic programming algorithm in the portfolio selection. Given this issue, and as a secondary aim, we wanted to test if the B–L estimation of portfolio parameters leads to properly diversified portfolios and a better mean–variance efficiency against a buy-and-hold strategy in the PM’s benchmark or market portfolio.
Our position is that using views generated with M-S models leads to a better performance than the buy-and-hold portfolio and more mean–variance efficient results.
Our paper is structured as follows: In the next section, we review the main results and tests made on the use of M-S models for trading decisions, the use of the B–L model, and the scant literature about the use of M-S models in a B–L context. This section explains our motivations and their academic and professional impact. The third section details how we gathered and processed the input data in our backtests. In the fourth section, we review our main findings. Finally, in the fourth section, we present our conclusions and guidelines for further research on the subject.
2. Literature Review and Research Motivations
This literature review discusses the rationale behind Markov-Switching (M-S) models and their main applications and extensions. The previous section briefly introduced the standard portfolio selection problems and one of the most studied extensions: the Black–Litterman (B–L) model. Following this extension, we discuss the scant literature about using M-S models in optimal portfolio selection. As mentioned previously, we discuss these works and the theoretical context of our research motivations (our tests’ motivations).
M-S models are one answer to modeling non-linearities in the mean or location parameter. By non-linearities, we mean that there are
breaks in these parameters, leading to the concept of a multimodal probability density function (pdf) with an
number of states of nature (regimes). This assumption implies multiple means (
) and, consequently, various scales or standard deviations (
). The first developments in statistics and econometrics assumed that a given time series (
) could be modeled with a linear conditional mean model (such as a time series model or a multifactor regression one [
35,
36,
37,
38]), along with either a linear (
) scale parameter or a non-linear, as is the case of a Generalized Autoregressive Conditional Hetesokedastic (GARCH) one [
39,
40,
41,
42]:
As noted in the previous model, in a GARCH variance, past realizations of the residuals (
) influence the actual volatility or variance level at
(ARCH term or second term in the right-hand side of the equation), along with past realizations of the volatility (variance) value (
). This model expresses a non-linear time-varying volatility model. The expression in (8) is an example of symmetric GARCH models. Still, there are other asymmetric or even fat-tailed extensions, such as the E-GARCH model of Nelson [
41]; the T-GARCH of Zakoian [
43]; or the leveraged GJR-GARCH of Glosten, Jaganathan, and Runkle [
42], among the most used (Please refer to Bauwens, Laurent, and Rombouts [
44] for a general introduction to these models).
A non-linear volatility model, such as (8), is usually generated from the residuals (
) of a linear location (
) parameter, that is, either a time-fixed (unconditional) arithmetic mean (
) or a conditional one. Examples of conditional mean models are the CAPM model, an APT [
11,
45] one, or other multifactor ones, such as the Fama and French [
6,
46] or the Carhart [
8] one. In all cases and related, these mean and volatility models are part of the Classical Financial Economics or Classic Financial Econometrics corpus of models and are specific applications to model some theoretically unexpected but observed anomalies, such as volatility clustering (periods of high volatility followed by high volatility ones). These conditional mean and volatility models assume a unimodal, Gaussian, Student’s
t, or Generalized Error Distribution (GED) pdf or log-likelihood function (LLF). This means that we use the following for the most general Gaussian and GARCH case:
Despite this strong result, Classical Financial Economics fails to explain some anomalies observed in financial markets, such as volatility clustering or the lack of significance of portfolio parameters due to framing. These anomalies lead to given return levels when investors feel optimistic about future securities markets’ prospects and different ones during distress periods. This result assumes multimodal pdfs with more than one location and scale parameter. One for each state of nature or regime,
.
The issues with having more than one location and scale parameters are that (1) it is necessary to know which parameters to use at . This issue means that the analyst should know from which pdf segment the realization comes. (2) If a PM wants to make an optimal portfolio selection with (2) or (3), she or he should know, in a multi-regime context, that the optimal portfolio is different in each regime.
As a solution to econometric modeling of multi-regime models, Tong [
47] suggested the Threshold Autoregressive (TAR) model in which the analyst can perform a different autoregressive time series model for two regimes given a discretionary threshold (
. Despite it simplicity, this model lacks the possibility of making forecasts about future values in the securities time series, about the likelihood of being in each regime at
, and its estimation is sensitive to the threshold,
.
As a suitable answer to this need, Hamilton [
21,
22,
23] proposed the Markov-Switching (M-S) model in which the analyst can assume the existence of
regimes or states of nature and can estimate the location and scale parameters for each regime, as in (9). To define which realization (
) comes from each regime, Hamilton’s model assumes that the
regime behaves as a first-order Markovian chain with its transition probability matrix (for the sake of simplicity and following the assumptions in our tests, we assume a two-regime world):
In this matrix represents the probabilities of transiting from the regime, , to the regime from to .
These transition probabilities are estimated from the filtered and then smoothed regime-specific probabilities from the time series (
):
These filtered regime-specific probabilities are usually smoothed with Kim’s [
48] algorithm. These are useful to estimate
in (11) and to infer the regime-specific location and scale parameters (
) with the use of Bayesian estimation methods that maximize the next LLF, given the parameter set of interest (
):
The M-S model, also known as Hamilton’s filter, is helpful for several forecasts and decision-making processes. The literature that discusses its use is widespread in the spectrum of applications. Among some of the papers that test their benefit in economic growth forecast, we found the works of Hamilton [
21], Humala [
49], Misas, and Ramirez [
50] or Camacho and Perez-Quiroz [
51]. These authors found applicable M-S models to estimate the change in the business cycle in an expansion (
) or contraction (
) regime. These authors also extended the original M-S model with the estimation or Autoregressive Moving Average (ARMA) or Vector Autoregression (VAR) models to determine the number of regimes in business cycles and also to measure a level of contagion among countries of Latin America or the US.
Another application of M-S models is to infer the presence of regimes and contagion effects between exchange rates, monetary policies, and economic growth. More specifically, the works of Alvarez-Plata and Schrooten [
52]; Mouratidis [
53,
54]; Chen [
55]; Canarella and Pollard [
56]; Walid, Chaker, Masood, and Fry [
57]; and Sottile [
58] found evidence that favors the use of M-S models to determine the following:
- (1)
The presence of these multiple regimes;
- (2)
The influence and spillover effects between currencies in developed and developing countries, their monetary policies, or even their risk-level estimates with time-varying volatility models in each regime—models such as the GARCH ones.
M-S models are helpful for regime-specific modeling in financial time series. This use is the most discussed in the literature. The works of Klein [
59]; Zheng, and Zuo [
60]; Ardia and Hoogerheide [
61,
62]; Ye, Zhu, Wu, and Miao [
63]; Shen and Holmes [
64]; De la Torre, Galeana, and Alvarez [
32]; Balcillar, Demirer and Hammoudeh [
65]; and Cabrera et al. [
66] are a sample of works that use M-S models or their previously mentioned extensions. They did this to model the presence of two or three regimes in the financial time series of the US, the leading European, Latin American, Asian, or Midwest stock indexes. These works found evidence that either favor the use of M-S models or show, in a two-regime context, that the spillover effect is more considerable in distress or high-volatility regimes (
). Some of these authors also found that the high-volatility smoothed probability from one market relates to the one of other stock markets.
The works mentioned in the previous paragraph motivate our work because they found evidence of two or more regimes in the time series of stock market indexes. To run our simulations, this result’s proof is essential to determine the use of M-S models in portfolio selection.
We also found works that proved the use of M-S models in other financial markets—cases such as the credit default swaps (CDSs) [
67,
68,
69] and oil futures [
70,
71,
72,
73], along with other commodities, such as carbon prices in the European Union emission trading scheme [
74] or Asian rice prices [
75].
Our research interest is in investment decisions or optimal portfolio selection from the several potential uses of M-S models. The first work suggesting this use is Brooks and Persand [
24]. These authors tested the use of M-S models in the Gilt-equity yield ratio. That is, the ratio of the 10-year UK treasury (Gilt) divided by the FTSE-100 stock index’s dividend yield. They estimated a Gaussian two-regime M-S model at
, using Gilt and FTSE-100 return data (
) from January 1975 to April 1997. They estimated, in each trading date, a two-regime M-S model with a location (mean or
) and scale parameter (
) for the low (high) volatility regime
(
). With the smoothed probability of each regime, they determined the investment level in stocks (
) and Gilts (
) with the next trading rule:
Their results suggest that their backtested strategy pays more return (alpha) against a buy-and-hold one either in the FTSE-100 or the performance of the UK 10-year Gilts. This paper strongly influences our tests because it is the first work suggesting M-S models for trading decisions.
Other works that extended Brooks and Persand [
24] are the ones of Hauptman et al. [
29]; Kritsjanpoller and Michell [
76]; and Engel, Wahl, and Zagst [
30]. These three works develop a sequential three-regime M-S estimation process in which they first infer a two-regime model (low,
, and high,
, volatility regimes). Given the regime-specific smoothed probabilities, they filtered the stock index return realizations generated in the second regime (
) and filtered these to infer a high (
) and an extreme (
volatility regime. Once they did this in the US, German, Brazilian, Chilean, Mexican, or Japanese stock markets, they used logit regression models to forecast the regime-specific probabilities. That is, they incorporated the effect—in
and
regimes’ smoothed probabilities—of other financial or economic factors, such as the 5-year and 3-month US Treasury bill (T-Bill) yield spread, the 10-year and 3-month US T-Bill one, the OECD leading indicator, and the corporate bond spread with the LIBOR rate (London Interbank Offered Rate). These three works found as appropriate the use of these factors to forecast the smoothed probabilities and to outperform a buy-and-hold investment strategy in their corresponding indexes.
The previous works focused on single index trading decisions. There are tests about this that are used from a portfolio-management perspective for active portfolio management. The papers of Ang and Bekaert [
26,
28]; and Kritzman, Page, and Turkington [
25] suggest the use of either M-S covariances (the former) or tilts in the portfolio investment levels of either an internationally diversified portfolio or a security type diversified one (the latter). Ang and Bekaert propose the estimation of M-S covariances by extending the single-index CAPM auxiliary regression into a two-regime context:
In the previous expression,
is the percentage return of the MSCI world stock index. By using the estimated two-regime
s in each portfolio’s security in a loadings vector
with (15) and maximizing (13), the authors estimated the two-regime covariance matrix and expected return vector, respectively:
In the previous expression, is the variance of the market factor’s (MSCI world index returns) residual (). With the parameters in (16) and (17), Ang and Bekaert estimated a mean–variance optimal portfolio selection as in (3) and found better asset allocation than in a single-index context.
Similar to this paper, Kritzman, Page, and Turkington tested the benefit of using M-S models in the S&P-500 US stock index to determine a tilts rule in the investment levels of US stocks, government bonds, and corporate bonds, along with some foreign equity. In their simulations, these authors used the Baum and Welch [
71] algorithm to estimate the Gaussian two-regime M-S model. In a backtest from February 1978 to March 2008, their results showed that using M-S models to reallocate securities in turbulent periods (
s = 2) leads to a better performance than a buy-and-hold strategy in the same portfolio. Moreover, these authors showed that the losses incurred in the simulated portfolio in
are lower than in the buy-and-hold one.
After the works of Ang and Bekaert [
26,
28]; and Kritzman, Page, and Turkington [
25], little has been written about the use of M-S models in optimal portfolio selection. Only the works of Dewandaru et al. [
77]; Mousavi, Naderi, and Hasanlou [
78]; and Ng, Li, and Yu [
79] extend the use of M-S models (and their extensions) in the US Dow Jones Islamic stock index, or the Iran stock exchange.
The papers that tested the benefits of M-S models in investment decisions focused their efforts on trading rules, such as the one of Brooks and Persand [
24] in (14), in other stock markets [
80], FX rates [
81], commodity markets [
31,
82], or a portfolio diversified in stocks and volatility futures [
33,
34]. However, as mentioned previously, little is written about using M-S models to estimate optimal portfolio selection parameters.
The papers that did these tests used either a tilt trading rule or M-S parameters in a classical portfolio (sample) context. These works used a sample expected return vector and covariance matrix (). The portfolios used were portfolios prone to estimation error and corner portfolios (highly concentrated portfolios, given the optimal selection restrictions).
Departing from this issue, the papers mentioned in the previous paragraphs motivate us to extend the current literature by using M-S models to estimate Gaussian, two-regime expected returns in a US stock portfolio. Instead of using a multifactor M-S parameter estimation, as in Ang and Bekaert [
26,
28], or a closed-form tilt rule, as in Kritzman, Page, and Turkington [
25], we wanted to use M-S expected return estimation as the PM personal views or forecast and mixed these with the expected equilibrium returns in the market. We believe that this could combine the expectations in the stock market (assuming a semi-strong informational efficiency in the market) with the personal expected returns, given the likelihood of being in distress or high volatility periods at
. For this reason, instead of using a sample context, we estimated the expected returns vector and covariance matrix in a Bayesian one. For this purpose, we used the Black–Litterman [
18,
83,
84] Bayesian estimation method of these parameters that we briefly describe next.
As we mentioned, Black and Litterman (B–L) depart from the equilibrium expected returns of a market portfolio, or, in the words of Meucci [
85], a PM’s benchmark. To estimate these equilibrium returns, the PM uses the sample covariance matrix of this benchmark or market portfolio (
), along with a general market risk-aversion parameter,
. Departing from Black [
86] from reverse optimization and market (benchmark) investment levels (
), the equilibrium returns are estimated as follows:
In the previous expression, the PM can estimate
as in the CAPM [
5] demonstration, given the rate of a risk-free asset (
) as the 3-month US T-Bills:
Furthermore, as Meucci [
87] or Fabozzi, Foccardi, and Kolm [
88] suggest, the value of
has a negligible impact in the B–L model. For this reason, we set
in our simulations.
To blend the equilibrium market views,
, with the PM
views, it is necessary to have a vector of those views (
), along with a
“pick matrix” (a vector or matrix with
in the assets favored with the kth view, or zero otherwise. The PM uses this matrix, along with a
diagonal scalar (matrix) with the level of uncertainty in that (or those) view (s),
. By following Theil’s [
89] mixed (Bayesian) estimation, assuming that the views (
) follow a Gaussian distribution, and also that the views are independent (that is why
is diagonal), the mixed estimation is as follows:
From the previous expression (also assuming that the views and prior or equilibrium returns are independent), we gain the following:
The solution for
in (20) is through Generalized Least Scares (GLS), as follows:
The previous expression is the Black–Litterman Bayesian method to estimate an expected returns vector as a blend of market equilibrium returns,
, with the personal views,
, subject to the confidence level in the former (
) and the latter (
). Moreover, Theil, Black, and Litterman suggest the following Bayesian estimation of the covariance matrix, departing from the sample covariance matrix,
, and the covariance of the views,
:
With the Bayesian multivariate parameters in (22) and (23), the PM could substitute these in an optimal portfolio selection problem, as in (3), and select an optimal portfolio with less estimation (sample) error or uncertainty. This selection could potentially lead to a more diversified market/personal views portfolio.
There are few works in the literature about using M-S models as views in an optimal portfolio selection process in a B–L Bayesian context. Our position is that using M-S models to estimate B–L views with (22) and (23) could lead to a more efficient ex-post and ex-ante portfolio. Moreover, their use leads to better portfolio performance.
Departing from this motivation, we simulated three portfolios that used (22) and (23), and one portfolio that used a sample mean vector () and covariance matrix (). We did this in a closed investment universe (closed set) of the 26 US stocks that (1) were members of the Dow Jones Industrial (DJI) stock index from 1998 to 2022 and (2) had historical prices at least since 1 January 2000.
The purpose of this closed investment universe of 26 stocks is that the Dow Jones stock index is an “almost” homogeneous index. Its “secret” screening process made by Dow Jones LLC allows for marginal leavers/joiners member changes. If a given PM fetches the index past rebalances, she or he can note small changes in this set. Moreover, we preferred a closed investment universe to estimate our “in-house” benchmark to avoid favorable performance impacts due to rebalancing. Given the blue-chip profile of the stock index and its screening process, we found that the 26-stocks set represents the most traded stocks in the US markets. Therefore, we assume that our results could be generalized to broader investment universes. We suggest testing this assumption as a guideline for further research.
We compared these four simulated portfolios against a market-weighted benchmark of this closed investment universe (market portfolio). Suppose we found a significantly higher Sharpe [
88] (ex-post and ex-ante) and better portfolio performance in our backtests. In that case, we would prove the benefit of using M-S models as a soft-computing technique to forecast expected returns (views) in a B–L optimal portfolio selection process.
As mentioned, there is scant literature about the use of M-S models in a B–L portfolio selection context. Therefore, we want to fill the gap in Academic knowledge and give proof to PMs about the benefit of using M-S models to forecast returns in a B–L context.
In the next section, we discuss how we gathered the data, how we processed it, and the algorithms and assumptions of our simulations.
3. Data Processing and Simulations Parameters
In the Introduction section, we presented our theoretical position (hypothesis): “The use of views generated with M-S models leads to a better performance than the buy-and-hold portfolio and more mean–variance efficient results”. To prove it, we downloaded the weekly historical data of US stocks (of the New York Stock Exchange (NYSE) and the National Association of Securities Dealers Automated Quotation (NASDAQ)) that fulfilled the following criteria:
To be a stock member of the Dow Jones Industrial (DJI) average or stock index on 14 February 2020.
To have historical data since 7 January 1998.
To be active in their corresponding exchange’s trading pit as of 14 February 2022.
We included only the stock traded (not delisted) at that date, fulfilling the last criteria.
We selected the 30 “best” stocks (known as blue chips) in the US with this screening process. This screening led us to an investment universe of the most traded stocks of the companies with the highest capitalization.
A feature of the DJI stock screening process [
90] is that its members are practically the same on several rebalancing dates. This feature allowed us to have a more homogeneous (and stable) investment set through time. Extending our tests to a broader set of the stocks that have been members of this index is a suggestion for further research.
The need to have a historical price record since 1 January 1998 is for M-S model estimation purposes. Because a higher information set leads to better estimation and includes more than one high-volatility regime (), we used this criterion to select our investment universe. As we mention here next, we estimated the M-S models with historical return data from this starting date (1 January 1998) to the simulated date (). This process implies that the information set (time-series length) increased each simulated week.
The third criterion is necessary for our simulations to allow a proper investment universe. The inclusion or exclusion process could lead to behavioral biases and performance in our simulated portfolios or benchmark performance.
Our investment universe is closed during all our simulations with these screening criteria. The benchmark and the simulated portfolios included the same stocks from 1 January 2000 to 14 February 2022. We used this simulation period to incorporate the most recent, and also the most relevant, financial and economic crises in the last 22 years. These crises refer to episodes that led to higher volatility levels in the US stock markets and to important price swings and behavioral issues that should be incorporated and forecasted by M-S models, including the 2007/2008 sub-prime crisis, the 2013 European debt issues, the 2016–2018 US trade tensions, or the most recent 2020-to-date COVID-19 market turbulence.
We performed our simulations in the form of a weekly portfolio analysis in a rebalancing context. We did this to make the first test of our suggested M-S portfolio selection strategy and because we wanted to reduce the presence of short-term (daily) or even intra-day noise. We believe that using monthly periods leads to highly smoothed time series, and M-S models could not estimate proper regime changes. In addition, the weekly simulation process is consistent with the weekly portfolio performance analysis and rebalancing (and also position reporting) practiced in most of the US mutual and pension funds. The use of weekly time series allows us to estimate and forecast regime changes in a more efficient way than using nosier daily ones. We also believe that the estimation of daily or even intraday rebalancing leads to the inclusion of other short-term factors and regime switches that need particular review.
We used an investment universe with the 26 stocks detailed in
Appendix A from the previous three-stocks investment universe selection criteria.
For the benchmark or market portfolio, we calculated a market-value-weighted index, using each stock’s market capitalization (
) at
, that is, the number of free-floating stocks of that company in the exchange times its current close price at the simulated week (
). We estimated the stock’s weight in the benchmark or market portfolio as a normalization of the current active stocks at week
:
We also estimated an
continuous-time percentage variation (
) vector:
With (24) and (22), we estimated the benchmark’s weekly percentage variation at
as follows:
We used this set of 1154 weeks (from 7 January 2000 to 14 February 2022) of percentage variations to calculate the benchmark’s base 100 value at .
We estimated Gaussian, two-regimes M-S models in each asset in the investment universe to simulate our active Bayesian portfolio. We maximized the LLF in (13) by filtering the parameters (10) to (11) of the two-regime process (9). This process allowed us to estimate the smoothed probabilities vector () for the periods used for M-S model estimation, the transition probability matrix as in (10), and the regime-specific means () and standard deviations (). We defined the high-volatility (low) regime () as the one with the highest (lowest) estimated standard deviation ().
To estimate the M-S in each portfolio’s stock, we used the Bayesian E-M algorithm [
91] with the MSwM library of Sanchez-Espigares and Lopez-Moreno [
92] in R. With these M-S models, we forecasted the regime-specific smoothed probabilities for the next week (
) as follows:
We estimated the expected returns in two possible scenarios with these forecasted probabilities. One that follows the Brooks and Persand [
24] trading rule is as follows:
The second scenario follows a trading rule similar to Scenario 2 of De la Torre-Torres, Galeana-Figueroa, and Alvarez-Garcia [
33]:
We named the simulated portfolios that used these two expected returns rules (28) and (29) BL1 (Black–Litterman 1) and BL2, respectively. With the expected returns (28) or (29) in each asset in the portfolio, we formed an
views vector,
. In a similar rationale, we estimated the M-S standard deviations of the BL1 and BL2 portfolios by substituting the regime-specific standard deviation with the regime-specific mean, as follows, respectively:
With each asset’s standard deviation, we formed the
confidence diagonal matrix,
:
In these two portfolios (BL1 and BL2), we estimated the market equilibrium views by using the market capitalization investment levels (24) and blended these with the M-S views vector, , to estimate the Bayesian B–L expected returns vector, , and covariance matrix, , with (21) and (22). In these two portfolios, we used an pick matrix, , in which the diagonal is one because each row represents the investment level in its corresponding view in .
By following Fabozzi, Foccardi, and Kolm [
88] and Meucci [
85,
93], we also simulated the third portfolio in that, instead of using an asset-specific view and confidence, it deals with the M-S views as an investment strategy view. That is, we estimated the M-S expected returns for each asset and then estimated a hypothetical portfolio that invested in each asset, given its expected return with (29) and the diagonal confidence matrix,
, as in (31). With these two parameters, we estimated this portfolio’s expected risk (
) and return (
) as follows:
In (32), is the diagonalization (diagonal elements extraction) of the view’s confidence matrix, . As noted, we preserve the independence between views assumption. Moreover, in (32) and (33), is the investment-level vector. We determined each security’s investment level with the following steps:
Departing from the market capitalization weights in (24), we changed their sign with the following rule:
With the previous transformation, we normalized
as follows:
In this third portfolio, BL3, we set the investment levels in each asset as follows to determine the investment levels in the
“pick” vector,
:
In this particular portfolio (BL3) in which there is only one view, one confidence level, and a Pick vector, the B–L expected return and risk were estimated as previously mentioned in (33) and (34). Then we used (22) and (23) to estimate the Bayesian expected return and covariance matrix.
In these three simulated portfolios (BL1, BL2, and BL3), we used their corresponding B–L or Bayesian expected returns vector () and covariance matrix () to select the optimal portfolio selection process with (3). To solve this problem, we performed Quadratic programing to determine the optimal investment weights vector ( the optimal portfolio’s expected return (), and the optimal portfolio’s expected risk (). To solve the problem in (3), we used the weekly equivalent rate of the secondary market yield of the US 3-month T-Bill as the risk-free rate ().
For estimation purposes of the Gaussian two-regime M-S models, we used the historical continuous-time return data from 1 January 1998 to the simulated date (t). This use means that, in each week, the information set or time-series length increased by a week and allowed us to estimate M-S models with a more complete dataset. We estimated the BL1, BL2, and BL3 optimal portfolio estimation during the 1154 weeks from 7 January 2000 to 14 February 2022. Moreover, we simulated our three portfolios since 7 January 2000 to include in the estimation periods the presence of crucial high volatility periods. The periods included the 1998 Vodka crisis, the 2000 “dot com” one, the 2003 Irak war period, the 2007/2008 sub-prime crisis, the 2013 European debt issues, the 2016–2018 US trade tensions, and the most recent 2020–2022 COVID-19 global pandemic crisis. We could not cover the Russian invasion of the Ukraine and subsequent war, given the paper preparation and the backtest updating time (1.5 min, on average, to estimate M-S models of a portfolio of 26 assets).
We compared the performance of our three B–L portfolios against the performance of the benchmark (market portfolio) and a fourth portfolio (SampP). This fourth portfolio used the sample mean returns as expected returns () and the sample covariance matrix ().
We used the fPortfolio [
92] R library to run the optimal portfolio selection problem. We assumed that short sales are not allowed, and there are no maximum investment-level restrictions.
To compare the performance of the simulated portfolios, we used two perspectives. The first is the ex-ante, which uses the expected returns, expected risks, and expected Sharpe [
94] ratio, respectively, in the four simulated portfolios and the benchmark, given their optimal o market capitalization weights:
The second is the ex-post perspective, which uses the previous three portfolio performance metrics, but, instead of using the expected portfolio return (
), it estimates the observed portfolio return, as in (26). That is, we used each security continuous-time return as in (25) and made the dot product of that vector with the simulated portfolio optimal or market capitalization weights:
Our hypothesis is true in BL1, BL2, or BL3 if their ex-ante and ex-post Sharpe ratios are statistically higher than those of the benchmark (buy-and-hold strategy or market portfolio) or the sample portfolio (SampP).
As noted in (41), we are not incorporating the impact of stock trading fees and taxes. We assumed this following the results of De la Torre-Torres, Galeana-Figueroa, and Alvarez-Garcia [
33]; and De la Torre-Torres, Aguilasocho-Montoya, and Alvarez-Garcia [
95], who found that the impact of these trading costs is not as high as expected in the US or European stocks. Another reason not to incorporate trading costs is to test ex-ante and ex-post mean–variance efficiency. Suppose the mean–variance (risk–return) relation is better in our B–L simulated portfolios against a buy-and-hold strategy or an optimal portfolio with sample parameters. In that case, we expect that the impact of trading fess will be negligible. This assumption holds because a PM incurs trading costs to manage the market, BL1, BL2, BL3, and SampP portfolios. Given this assumption, we suggest the impact of trading cost in simulations such as ours as a guideline for further research.
To perform our backtest or simulations, for each simulated week,
, we used the pseudocode of Algorithm 1:
| Algorithm 1: The steps followed in the portfolio simulation of BL1, BL2, BL3, and SampP. |
| Loop 2 from 7 January 2000 to 11 February 2022 (tas date or week counter): |
| Loop 1 For the four simulated portfolios in each date,t: |
- 1.
To calculate each security’s continuous-time return time series in the portfolio.
- 2.
To estimate, with a complete-time series matrix (with data of the dates that are all the same in the securities return), the sample covariance matrix, .
- 3.
To calculate the market investment of the benchmark (market portfolio) level vector, as in (24).
- 4.
To calculate the market equilibrium returns by using (18): .
- 5.
To estimate the views or security-specific expected returns vector (), according to the simulated portfolio. - 6.
To estimate the views confidence matrix (), with each security’s standard deviation, according to the simulated portfolio: - 7.
To define the pick matrix or vector in portfolio BL1, BL2, and BL3 In portfolios BL1 and BL, we used an diagonal matrix for the investment in each asset, given its corresponding view: In portfolio BL3, we defined the pick vector with the following rule: For this purpose, we used the weighting method in (35):
- 8.
By setting to calculate the B–L expected returns vector : - 9.
By setting (highly confident in market views) to calculate the B–L covariance matrix : - 10.
With the B–L parameters ( ), we made the optimal portfolio selection in (3) to determine the optimal investment levels in portfolios BL1, BL2, BL3, and SampP (are a zeros and ones vector for the cardinality restriction ): - 11.
With the portfolio-specific investment levels , in BL1, BL2, BL3, and SampP, we calculated the observed portfolio return as follows from (41) and (42): - 12.
In addition, with the portfolio-specific investment levels, , in BL1, BL2, BL3, and SampP, we calculated the expected portfolio return and risk exposure as follows from (38) and (39): - 13.
With the observed (ex-post) return, and the current risk-free date at , we estimated the observed Sharpe ratio as in (43): - 14.
In a parallel calculation, we estimated the expected (ex-ante) Sharpe ratio as in (40): - 15.
We stored, in a database, the expected return, risk exposure, ex-ante and ex-post Sharpe ratios, and Hirschmann–Herfindahl concentration level for the market, BL1, BL2, BL3, and SampP portfolios:
|
| End loop 2 |
| End loop 1 |
| End |
We compared the historical ex-post portfolio returns to test our null hypothesis that the portfolios that use security-specific M-S forecast in a B–L context are better than a buy-and-hold strategy. We made this comparison with a parametric one-way analysis of variance (ANOVA) test of the historical returns of the five simulated portfolios (market, BL1, BL2, BL3, and SampP) and a non-parametric Kruskal–Wallis test.
Similarly, we compared the ex-ante and ex-post Sharpe ratios, and we made a historical performance analysis of the five portfolios of interest. We analyzed the historical expected returns and observed the historical returns, historical risk exposure levels, and historical Sharpe ratios (ex-ante and ex-post) chart.
We present and discuss our simulation’s results in the next section.
4. Simulation Results’ Discussion and Hypothesis Testing
In
Table 1, we present the statistical summary of the five simulated portfolios’ values, and, in
Table 2, we present one of the portfolios’ returns. As noted in those tables, the market portfolio paid an accumulated return of 133.50%, and the sample parameters one (SampP) paid 133.94%. The B–L portfolios (BL1, BL2, and BL3) paid similar accumulated returns, with the BL3 portfolios (the portfolio that used M-S return forecasts to form an M-S portfolio and blended the views as a single portfolio or strategy) being the ones with the highest accumulated return.
This result is partly due to that portfolio’s mean weekly return (
Table 2). An interesting result in
Table 2 is that the standard deviation of BL3 is the highest of the three B–L portfolios, but, despite this, its standard deviation is lower than the one of the SampP portfolio.
Table 2 shows the estimated quasi-Sharpe ratio with the mean weekly return divided by the return’s standard deviation (both in
Table 2). As noted, the BL3 portfolio has the best performance or mean–variance (risk–return) relation.
Despite this starting result favoring our simulations, we tested if this result holds in the long term. For this purpose, we present the historical performance of the portfolios in
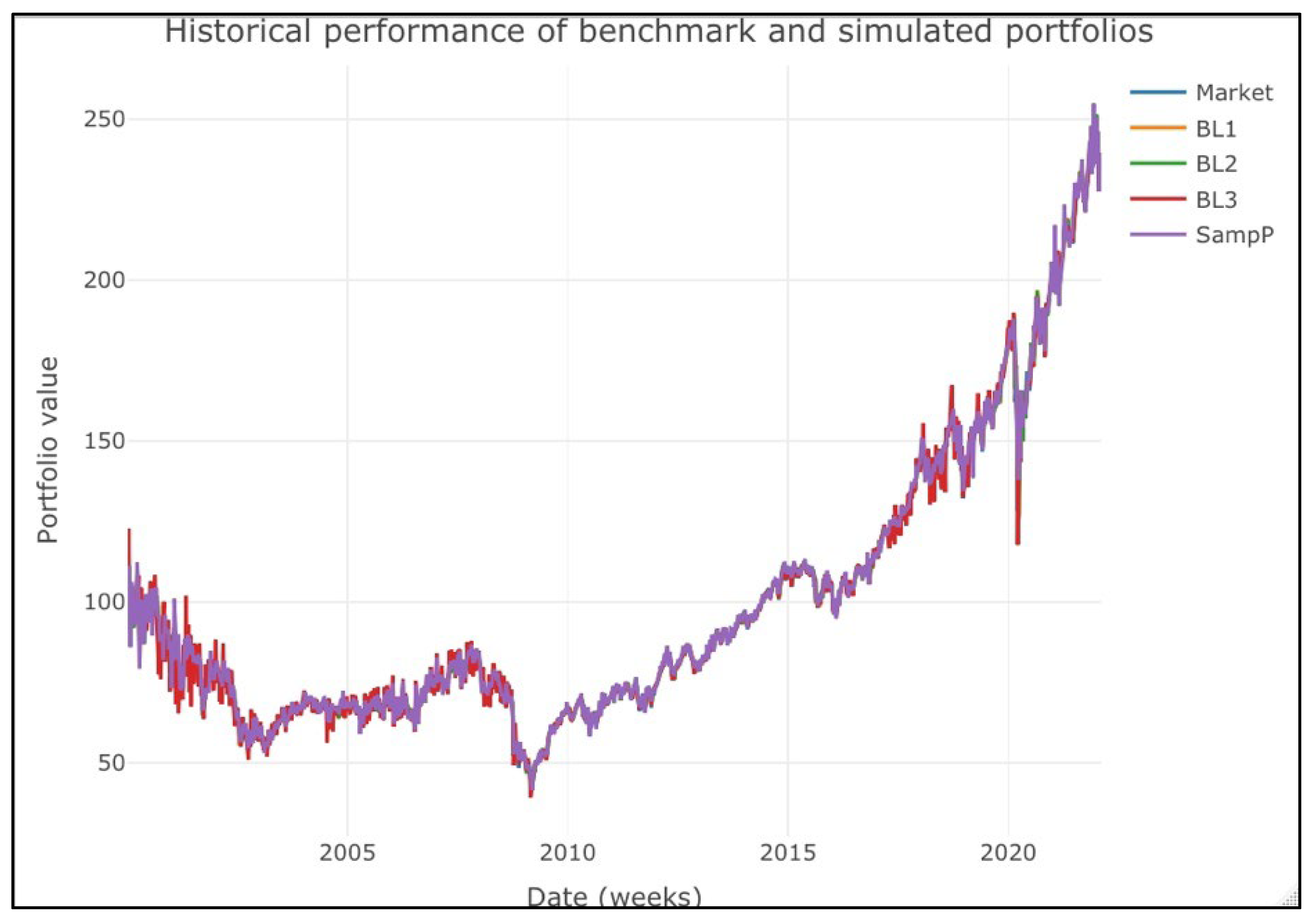
Figure 1. This figure gives another picture of their performance. The first finding is that using M-S forecasted returns in a B–L context did not add alpha against the benchmark or market portfolio. The market portfolio and all the active portfolios had a similar performance as the Dow Jones index from 2002 to 2007. This result suggests that the active, Bayesian portfolio selection with M-S models did not add alpha or extra returns against the market portfolio or sample parameters (SampP). This figure indicates that the performance of the simulated portfolios is statistically equal.
To have a more comprehensive picture of this possibility, we present, in
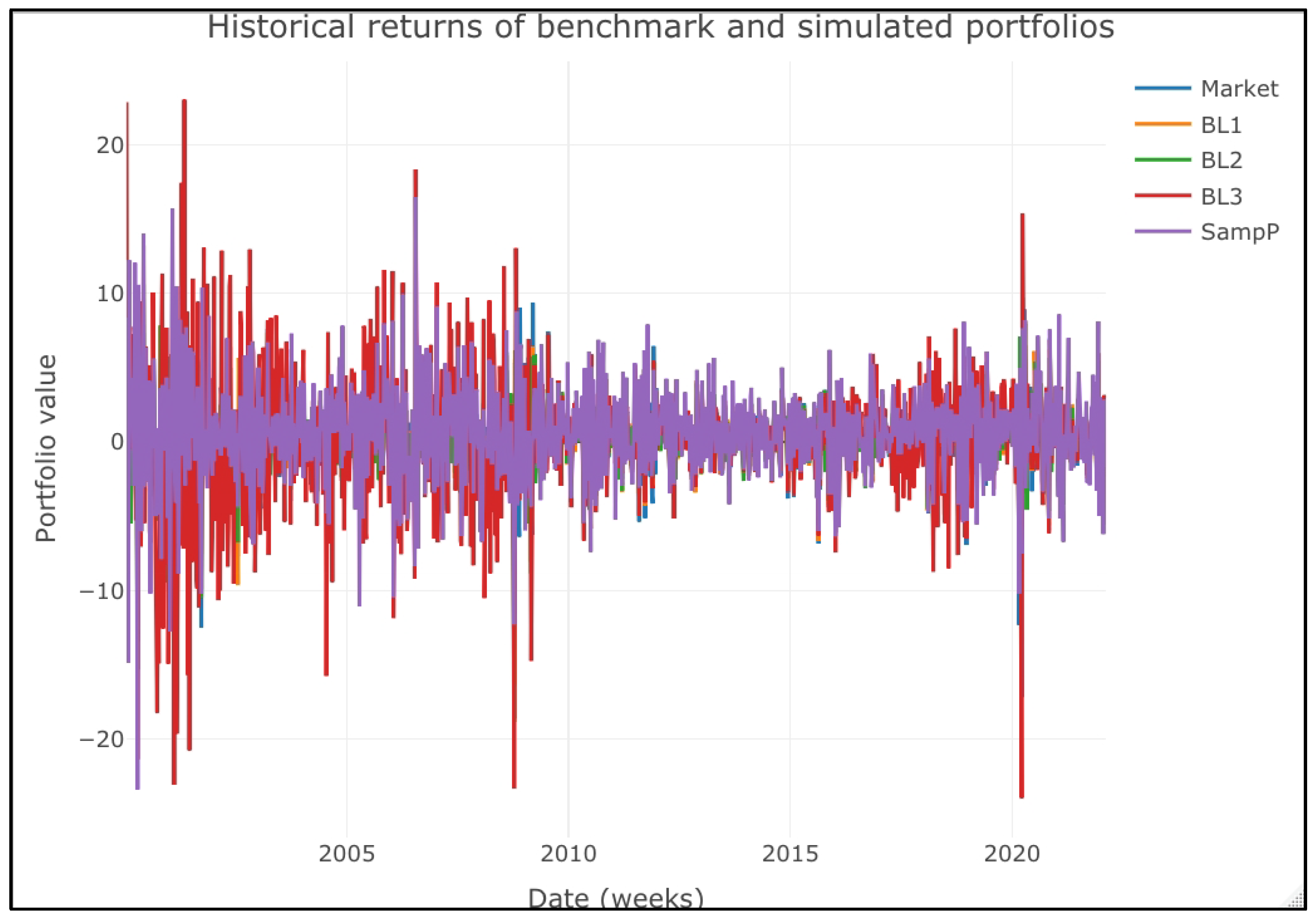
Figure 2, the historical values of the percentage returns of each portfolio. As noted, the SampP and the BL2 portfolios have the smallest return fluctuation (as summarized in
Table 2). Despite this result,
Figure 2 also suggests that these portfolios’ performance is statistically equal. If it is the case, we can find evidence that favors the alternative hypothesis that using M-S models to forecast views in a B–L context is not helpful to generate alpha, that is, to generate an extra return from the market portfolio.
To give more substantial support to this result, we estimated a one-way ANOVA test and a Kruskal–Wallis non-parametric one of the portfolio’s returns time series. We show the results in
Table 3 and
Table 4.
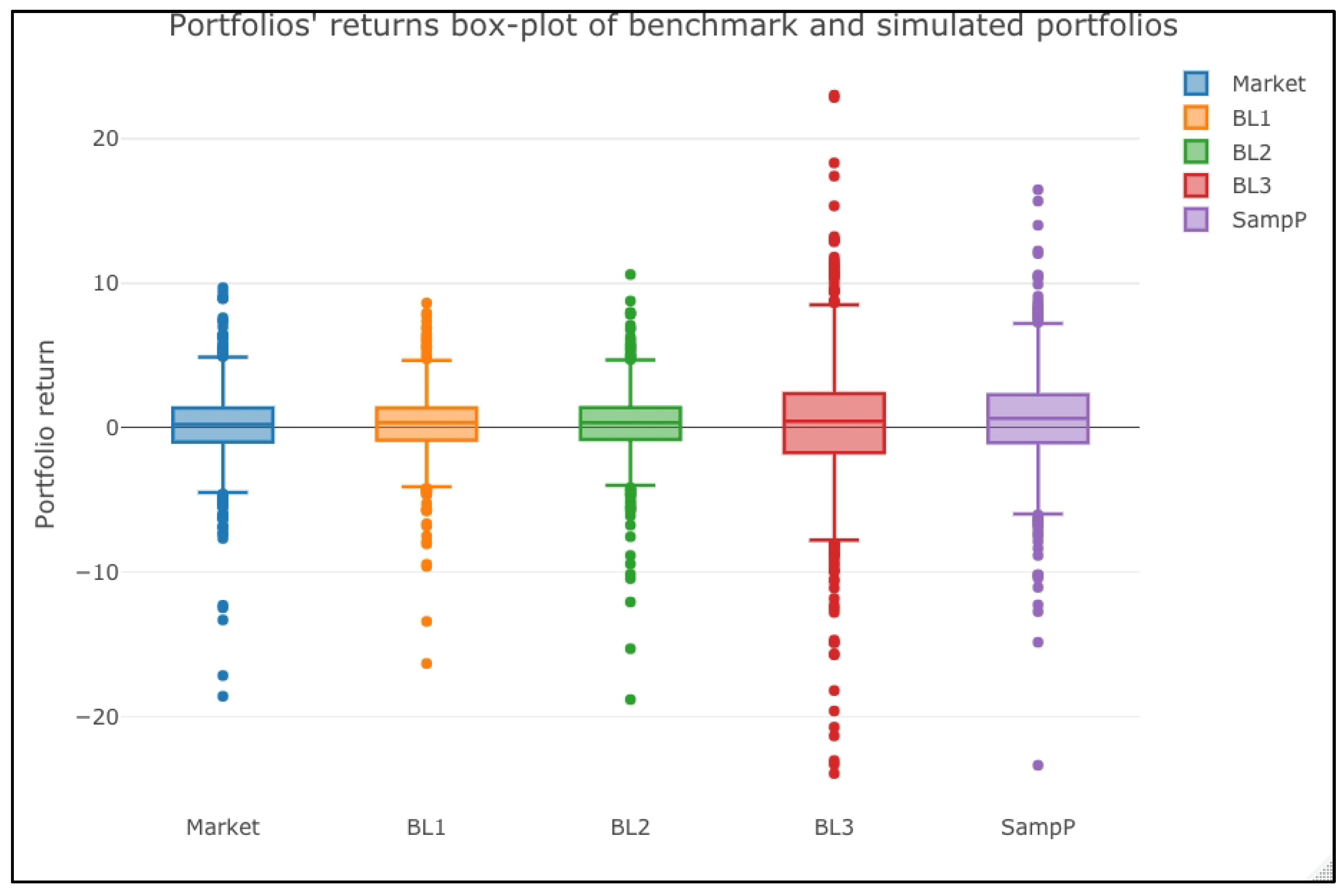
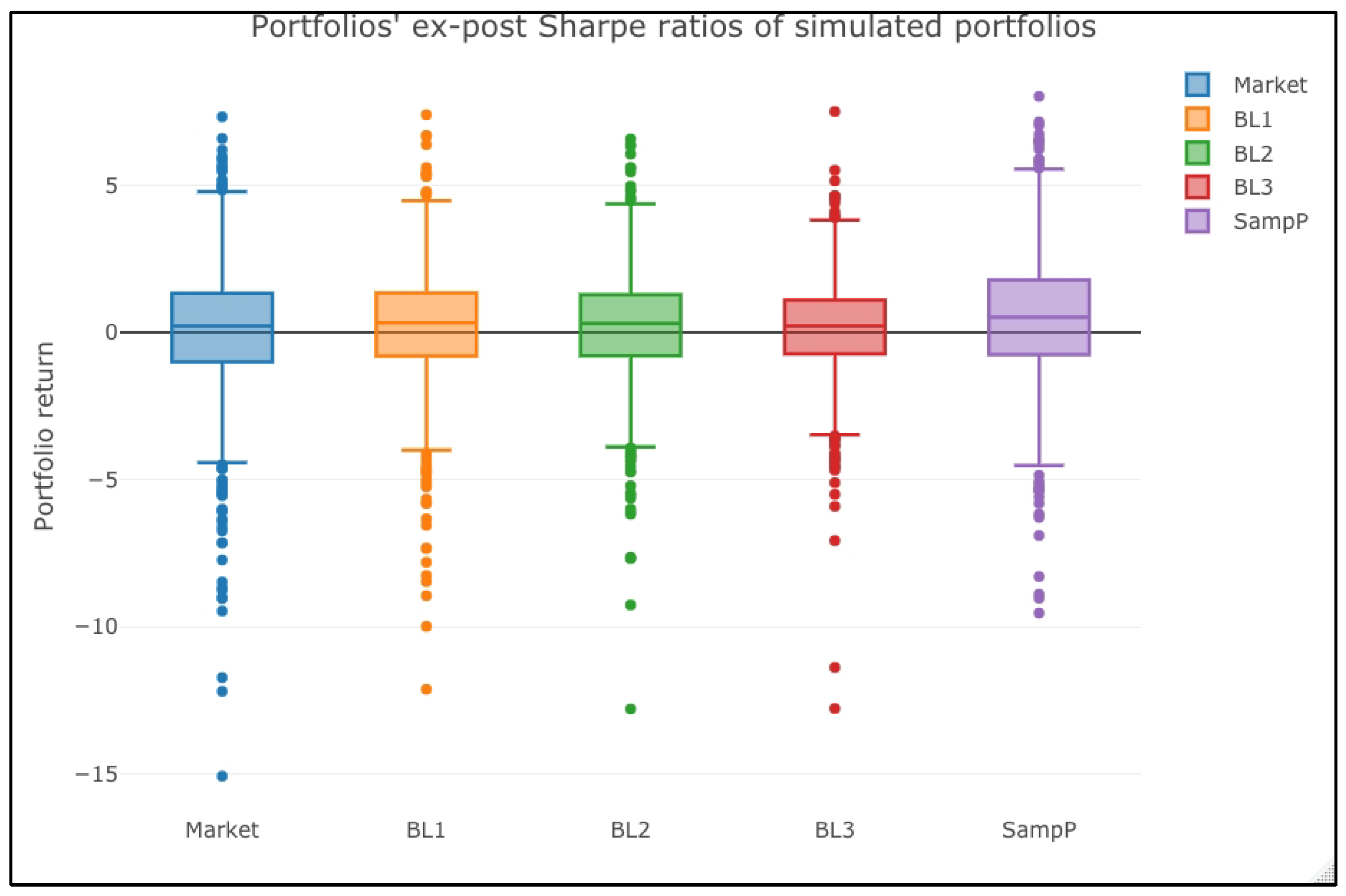
As noted from those tests, the means of the portfolios’ historical returns are statistically equal either in a Gaussian or in a non-parametric context. This test suggests that, even if the BL3 portfolio paid a marginally better performance, this better return improvement holds only in the short term.
Figure 3 shows the portfolios’ returns boxplot and depicts our conclusion.
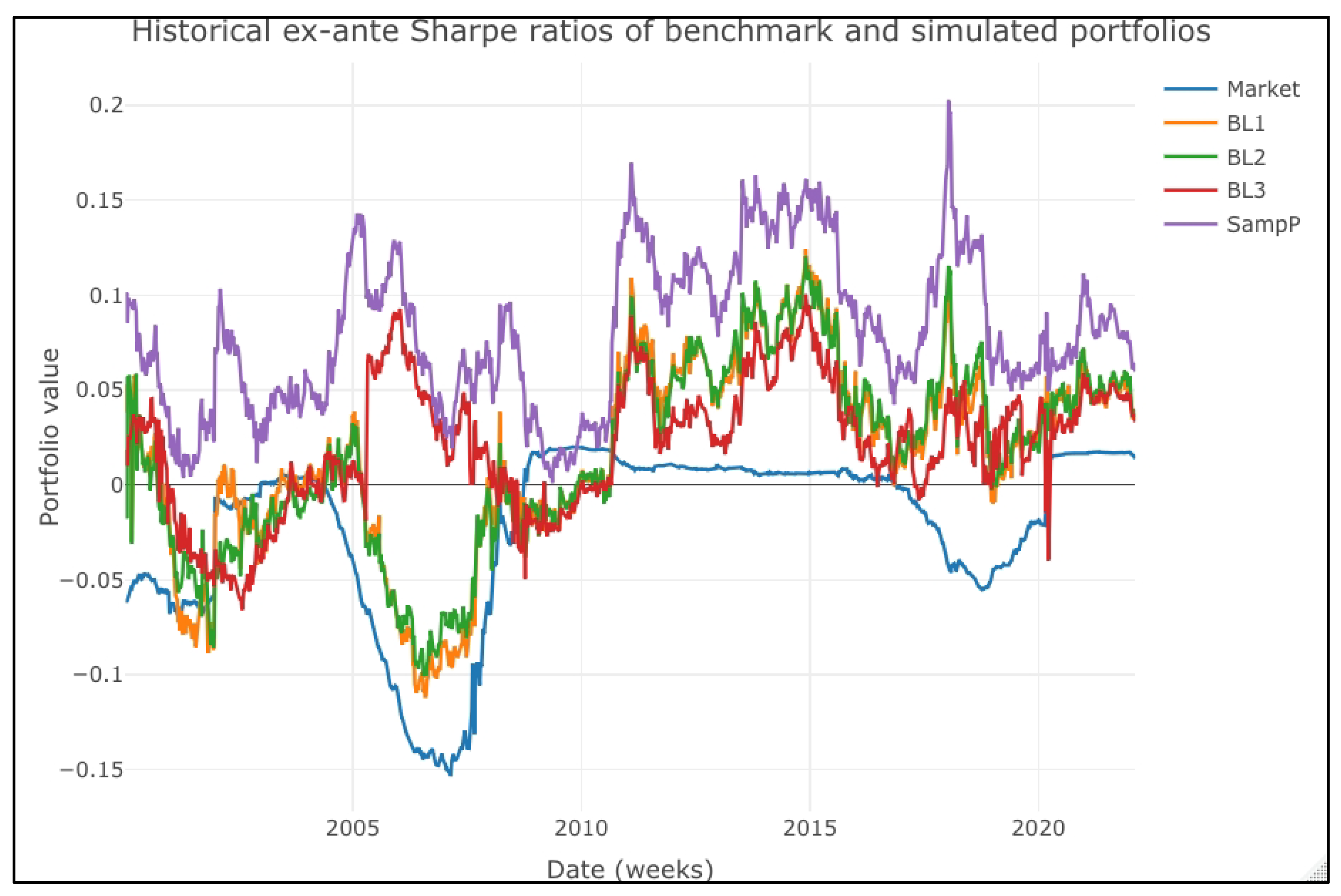
We made a historical review of the ex-ante and ex-post Sharpe ratios to extend our review. We compared the “expected” mean–variance efficiency of the simulated portfolios and then repeated the comparison of the observed values. We present the historical performances in
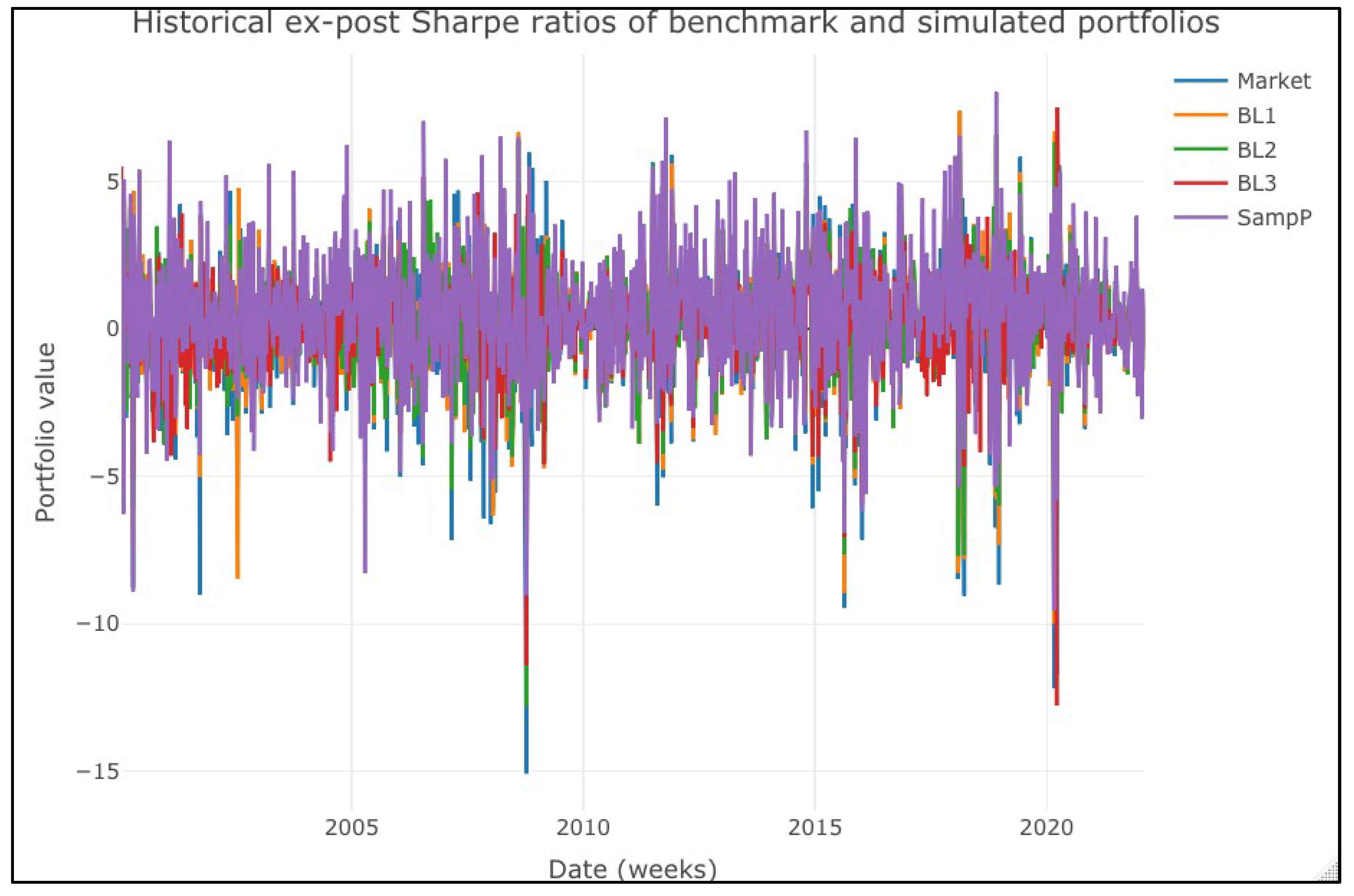
Figure 4 and
Figure 5. The means and boxes are practically aligned, suggesting that, even if some outliers suggest some differences in the portfolios’ performance, these are short-term lived. An interesting result is that the SampP portfolio always had positive values in the ex-ante portfolio (
Figure 4). Its ex-ante Sharpe ratio values are significantly higher than those in the BL1, BL2, and BL3 portfolios, a result that we confirmed with the one-way ANOVA test of
Table 5 and the Kruskal–Wallis test of
Table 6.
Moreover, in
Figure 4, we highlight that the market portfolio (the buy-and-hold strategy) has a lower ex-ante Sharpe ratio than the SampleP, BL1, BL2, and BL3 portfolios. This result is in line with several previous studies showing that a sample portfolio’s parameters or a B–L one led to better mean–variance portfolios. Despite this, we compared the ex-ante and ex-post results. What we expect in a given investment is different from what we have. That is, the results ex-ante and ex-post cannot be in line with each other.
In
Figure 5, we present a different result, one in line with the ex-post results of the simulated portfolios’ returns: the historical Sharpe ratios show no significant difference between portfolios. We confirmed these results in
Table 7 and
Table 8, in which we present the one-way ANOVA and Kruskal–Wallis tests, respectively.
Figure 6 and
Figure 7 present (also correspondingly) the boxplots of the ex-ante and ex-post Sharpe ratios. In line with
Figure 3, these present the visual contrast of these Sharpe ratios.
Figure 6 shows the ex-ante conclusion. The market portfolio has a significantly lower Sharpe ratio than the actively managed ones in the ex-ante context. Moreover, in the same perspective, the SampleP portfolio shows the highest expected mean–variance efficiency.
As expected and in line with our results,
Figure 7 confirms the results of
Figure 5 and
Table 7 and
Table 8 in an ex-post scenario. Using either an optimal portfolio with sample parameters or one with the B–L method leads to a similar performance to a buy-and-hold portfolio. That is, their mean–variance efficiency and returns are statistically equal. In practical terms, it means that the effort of estimating M-S returns (views) leads to a similar performance to a buy-and-hold strategy or a conventional sample optimal portfolio.
As a corollary of results, we can mention that using M-S models in an optimal portfolio selection with a Black–Litterman estimation method adds better performance and better mean–variance efficiency in the short term. In the long term, the performance of the simulated portfolios is statistically equal. Therefore, using M-S models in a Bayesian (B–L) context does not create alpha or extra returns from a market portfolio. This result implies, contrary to our expectations, that the use of M-S models for investment decisions in an optimal portfolio selection context is unnecessary and is preferable to engage in a buy-and-hold strategy. In Financial Economics terms, this means that there is a semi-strong, or even strong, market efficiency that makes “negligible” the improvements made with our active portfolio management algorithm.
5. Conclusions
The use of the Black and Litterman [
18] (B–L) Bayesian portfolio parameters estimation gave us a flexible method to incorporate personal security-specific views in the portfolio selection. Furthermore, it helped to reduce estimation error and highly concentrated optimal portfolios, that is, portfolios highly invested in a few securities.
In a parallel perspective, Markov-Switching models [
21,
22] (M-S) allowed us to estimate non-linear parameters by assuming that the stochastic process of a given time series has several
breaks and an
number of regimes or states of nature. They also allowed us to estimate the probability (
) of being in each regime at
, along with the state transition probabilities matrix
, and the regime-specific location (
) and scale (
) parameters. As noted, M-S models deal with the changes of regimes, assuming an unobserved first-order Markovian process.
In this paper, we first tested the use of M-S models to make regime-specific forecasts (views) of each security’s return in a US stock portfolio. More specifically, we assumed three possible types of views:
An
M-S views vector (
) in which the security-specific view is estimated with Gaussian two-regimes M-S models as follows:
We named this portfolio Black–Litterman 1 (BL1).
An
M-S views vector in which we estimated the security-specific view with the following rule (BL2):
In portfolios BL1 and BL2, we used the corresponding M-S model regime-specific standard deviations (scale parameters) to estimate an diagonal confidence matrix, .
A single M-S strategy portfolio in which we estimated the security-specific expected views as in BL1. With these and a similar estimation method for the expected standard error (), we estimated a single view (strategy view) and an confidence vector.
With these three views, we made an optimal tangency portfolio selection in weekly rebalancing periods from 7 January 2000 to February 2022.
Our position was that using M-S models with these three types of views could create alpha (extra return) from a buy-and-hold strategy of the 26 most important (most trades and biggest) stocks in the US stock markets. We compared the historical performance of our simulated portfolios against that benchmark or “market” portfolio, along with the performance of an optimal portfolio estimated with sample expected returns vector and covariance matrix (SampP).
Our results found that the third portfolio (BL3) had a better performance than the market portfolio and the other actively managed ones (including SampP). Despite this, we found that this result holds only in the short term. By comparing the five simulated portfolios (BL1, BL2, BL3, the market portfolio, and the sample parameters one), we found that, ex-ante (expected), the mean–variance efficiency is statistically higher in a sample parameter optimal portfolio (the conventional Markowitz portfolio selection with sample covariance matrix and expected returns vector). In an ex-post view (once the simulation performed the portfolio rebalancing and executed the trading algorithm that we detail in
Section 4), we found that the simulated portfolios’ returns and Sharpe ratios (mean–variance efficiency) are statistically equal. There is no return or mean–variance efficiency gain by using M-S models in optimal portfolio selection in the leading US stocks.
These first results suggest that the potential use of the Black–Litterman (B–L) portfolio parameter estimation, combined with M-S models, leads to better portfolio performance only in the short term. There is no significant difference in using a buy-and-hold or passive portfolio management strategy against the active one with this selection model. Our results are contrary to previous works suggesting that using the B–L portfolio selection process leads to alpha generation [
73,
86,
94]. We believe that our results could guide the passive versus active portfolio management discussion and use either M-S models or the B–L method in optimal portfolio selection.
We assume that our results are due to the strong link of B–L parameter estimation with market views. The B–L model is an active portfolio management one that departs from a passive or market portfolio as prior. Our results are contrary to the ones of previous research on the subject, such as the ones of Brooks and Persand [
64]; Kritzman, Page, and Turkington [
70]; Ang and Bekaert [
68,
69]; Hauptman et al. [
65]; Engel, Wahl, and Zagst [
67]; or De la Torre-Torres, Galeana-Figueroa and Alvarez-Garcia [
79], to mention a few.
A potential explanation is that these previous works deal with different investment-level tilt methods or use M-S models in a two assets portfolio context (the stock and volatility index with a risk-free asset). In our simulations, we tested the use of M-S models in the optimal selection of a stocks-only portfolio. Therefore, as the first guideline for further research, we suggest adding how much to invest in the stocks portfolio and a risk-free asset in the optimal portfolio selection with M-S models. A test of B–L and M-S simulated portfolios as a risky asset in an M-S trading decision, as in Brooks and Persand; Hauptman et al. [
65]; or De la Torre-Torres, Galeana-Figueroa, and Alvarez Garcia [
79].
Our tests depart from a sample covariance matrix to estimate the equilibrium security-specific expected returns. Ang and Bekaert [
26,
28] did not use a Bayesian parameter estimation as we did in our tests but used an M-S covariance matrix. Therefore, we suggest extending our work by using M-S covariance matrixes in the equilibrium returns estimation.
Furthermore, even if our investment universe of the 26 most influential US stocks is a good starting point, we suggest extending our tests to a more diversified portfolio (more stocks in the investment universe).
As a final research suggestion, we recommend relaxing the assumption of a time-fixed transition probabilities matrix and including behavioral factors, such as market sentiment or uncertainty, in the M-S parameter estimation.