Blasius Flow over a Permeable Moving Flat Plate Containing Cu-Al₂O₃ Hybrid Nanoparticles with Viscous Dissipation and Radiative Heat Transfer

Abstract

This study examines the Blasius flow with Cu-Al₂O₃ hybrid nanoparticles over a moving plate. Additionally, the effects of viscous dissipation and radiation are considered. Similarity transformation is employed to convert the respective model into similarity equations. The results are generated by using bvp4c in MATLAB. Findings reveal that two solutions are attained when both the free stream and the plate move in opposite directions. Moreover, the domains of the velocity ratio parameter are extended when suction is available. Besides, the upsurge of radiation and hybrid nanoparticles lead to the heat transfer enhancement. The rise in radiation heat energy incorporated in radiation parameter leads to the development of fluid temperature as well as the thermal boundary layer. Meanwhile, hybrid nanoparticles offer good thermal characteristics because of synergistic effects. However, the effects reduce with the rise in Eckert number. The first solution is stable and acceptable based on the temporal stability analysis. Furthermore, the critical/separation values of the physical parameters are also reported. With these findings, the optimized productivity will be achieved as well as the processes on certain products can be planned according to the desire output. This significant preliminary study provides future insight to the engineers and scientist on the real applications.

1. Introduction

In fluid dynamics, the flowing fluid over a fixed plate is a very well-known phenomenon in the boundary layer flow problem. This type of flow was introduced by Blasius [1]. Moreover, the flow over a moving plate in a quiescent fluid was pioneered by Sakiadis [2]. Then, the studies on these types of flows gained much attention from the researcher since they have important applications in industrial and engineering such as continuous casting, plastic extrusion, crystal growing, and glass fibre drawing [3]. The Blasius flow with radiation effect was examined by Bataller [4] and then continued by Aziz [5], Ishak et al. [6], and Ramesh et al. [7]. Next, Ishak et al. [8] studied the Blasius flow with constant surface heat flux. Moreover, the Blasius flow with the effect of various nanoparticles was reported by Ahmad et al. [9], Bachok et al. [10], and Makinde [11]. Besides, the simultaneous impact of entropy generation, radiation, and viscous dissipation has been reported by Afridi and Qasim [12]. They found that the local Nusselt number decreases for larger Eckert number and heating parameter and enhances with the rise of radiation parameter.

Choi and Eastman [13] were the first to introduce the high performance of heat transfer fluid called “nanofluid”. Mono nanofluid refers to a combination of a base fluid with a single nano-sized particles. To improve it further, a hybrid nanofluid is invented which consists of two distinct types of nanoparticles. Because of that, many related applications such as coolant in machining are considering hybrid nanofluid. Lately, the numerical analysis of hybrid nanofluids have been discussed by many researchers and have become a new hot topic in this field as studied by Takabi and Salehi [14]. Furthermore, Olatundun and Makinde [15] examined the Blasius flow with hybrid nanoparticles subjected to a convectively heated surface. They found that the heat transfer rate produced by hybrid nanofluid is higher than that of nanofluid. Moreover, the stability of the dual solutions of the hybrid nanofluid flow over a shrinking sheet was examined by Waini et al. [16]. Recently, several such studies with different physical aspects have been reported in Refs. [17,18,19,20,21,22,23]. The other study on particle suspension in fluid is reported by Abdelsalam and Zaher [24].

The heat transfer effect which visible in the high-temperature operating system, like solar power, rocket combustion chambers, hypersonic flights, and cooling system is physically influenced by the thermal/solar radiation. Being introduced by Rosseland [25], the radiation impact is widely studied. Khashi’ie et al. [26] observed the heat transfer increment with for the stretching flow with radiation. In addition, Waini et al. [27] found the heat transfer enhancement when considering sensor surface with thermal radiation. Further discussions are available in Refs. [28,29,30,31,32,33,34].

Furthermore, the viscous dissipation effect due to frictional heating is very significant to be considered because it has a direct impact on the heat transfer rate. The viscous dissipation converts the fluid’s kinetic energy to thermal energy and is commonly exemplified by the Eckert number which defines as the kinetic energy ratio of flow to heat transition enthalpy driving force. It seems that the viscous dissipation effect on natural convective flow was initiated by Gebhart [35]. The study of viscous dissipation on flow over various surfaces was considered by researchers, such as the flow over a disk [36,37], wedge [38,39], and cylinder [40,41]. Moreover, the flow over a stretching/shrinking sheet was studied by Mittal et al. [42] Koriko et al. [43], Gajjela and Nandkeolyar [44], Aly and Pop [45], Lund et al. [46], and Zainal et al. [47].

Upon the fulfillment of the research gap by the existing studies, this study examines the thermal and flow behavior of Blasius hybrid nanofluid past a moving flat plate with radiation and viscous dissipation effects. The hybrid nanofluid is composed by scattering a couple of distinct nanoparticles which are Al₂O₃ (alumina) and Cu (copper). Different from the work reported by Olatundun and Makinde [15], the present study considers the plate moving in the flowing fluid. The contribution of this study is not only limited to the discovery of non-unique solutions up to the separation value, but also highlight the stability analysis procedure. For the future benchmark, this preliminary study is important for the real industrial processes and applications. The present findings may provide idea to the engineers and scientist regarding the important and significant factors/parameters for their desired/optimized output.

2. Mathematical Formulation

For the physical model, the uniform upstream velocity $U_{\infty }$ moves in the $x$-axis direction as shown in Figure 1. Moreover, the plate is assumed to have a uniform velocity, $u=U_w$. Besides, the flow is subjected to the radiative heat flux $q_r$, which is applied normal to the surface in the positive $y$-direction. Additionally, the effect of the viscous dissipation is considered. Moreover, there is an assumption that the stable hybrid nanofluid is considered, which implies the exclusion of nanoparticle sedimentation/aggregation. The nanoparticles are assumed to have a uniform size with a spherical shape. It is assumed that both the base fluid and the nanoparticles are in a thermal equilibrium state, and they flow at the same velocity; see Khashi’ie et al. [48].

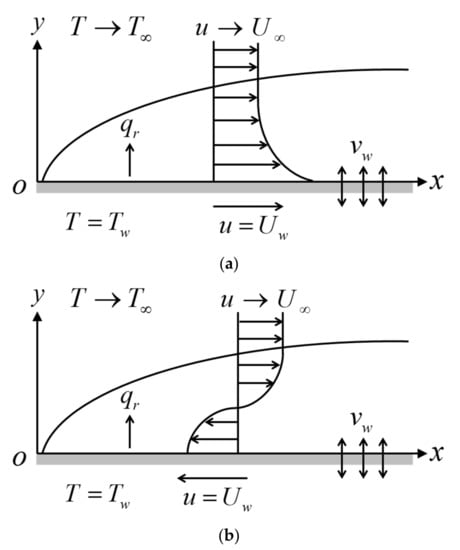
Figure 1. The flow configuration of the fluid and the plate move in the (a) same direction and (b) opposite directions.

Accordingly, the hybrid nanofluid equations are (see [9,12,15]):

$$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0,$$

(1)

$$u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=\frac{{\mu }_{hnf}}{{\rho }_{hnf}}\frac{{\partial }^{2}u}{\partial y^2},$$

(2)

$$u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\frac{k_{hnf}}{{\left(\rho C_p\right)}_{hnf}}\frac{{\partial }^{2}T}{\partial y^2}+\frac{{\mu }_{hnf}}{{\left(\rho C_p\right)}_{hnf}}{\left(\frac{\partial u}{\partial y}\right)}^2-\frac{1}{{\left(\rho C_p\right)}_{hnf}}\frac{\partial q_r}{\partial y},$$

(3)

subject to:

$$\begin{gathered} u=U_w, v=v_w\left(x\right), T=T_w \mathrm{at} y=0, \\ u\to U_{\infty }, T\to T_{\infty } \mathrm{as} y\to \infty , \end{gathered}$$

(4)

where $\left(u,v\right)$ is the corresponding velocities in $\left(x,y\right)$ axes, and $v_w\left(x\right)$ is the mass flux velocity. Furthermore, the temperature is given by $T$ with constant free stream and wall temperatures denoted as $T_{\infty }$ and $T_w$, respectively. Additionally, the expression of the radiative heat flux is [31]:

$$q_r=-\frac{4{\sigma }^{*}}{3k^{*}}\frac{\partial T^4}{\partial y},$$

(5)

where ${\sigma }^{\ast }$ and $k^{\ast }$ are the Stefan-Boltzmann constant and Rosseland mean absorption coefficient, respectively. Following Rosseland [25], $T^4\cong 4 T_{\infty }^3 T-3T_{\infty }^4,$ which transforms Equation (3) to:

$$u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\frac{1}{{(\rho C_p)}_{hnf}}\left[k_{hnf}+\frac{16{\sigma }^{*}{T}_{\infty }^3}{3k^{*}}\right]\frac{{\partial }^{2}T}{\partial y^2}+\frac{{\mu }_{hnf}}{{\left(\rho C_p\right)}_{hnf}}{\left(\frac{\partial u}{\partial y}\right)}^2.$$

(6)

Furthermore, Table 1 gives the characteristics of the Al₂O₃, Cu and water [32]. Note that, ${\phi }_1$ and ${\phi }_2$ denote Al₂O₃, and Cu nanoparticles, respectively, where ${\phi }_{hnf}={\phi }_1+{\phi }_2$. Meanwhile, Table 2 provides the hybrid nanofluid correlations [14].

Table 1. Physical properties of the respective base fluid and nanoparticles.

Properties	Base Fluid	Nanoparticles
	Water	Cu	Al2O3
$\rho \left(kg/m^3\right)$	997.1	8933	3970
$C_p \left(J/kgK\right)$	4179	385	765
$k \left(W/mK\right)$	0.613	400	40
Prandtl number, $\mathrm{Pr}$	6.2

Table 2. Thermophysical properties of hybrid nanofluid.

Thermophysical Properties	Correlations
Thermal conductivity	$\frac{k_{hnf}}{k_f}=\frac{\frac{{\phi }_1{k}_{n1}+{\phi }_2{k}_{n2}}{{\phi }_{hnf}}+2k_f+2\left({\phi }_1{k}_{n1}+{\phi }_2{k}_{n2}\right)-2{\phi }_{hnf}{k}_f}{\frac{{\phi }_1{k}_{n1}+{\phi }_2{k}_{n2}}{{\phi }_{hnf}}+2k_f-\left({\phi }_1{k}_{n1}+{\phi }_2{k}_{n2}\right)+{\phi }_{hnf}{k}_f}$
Heat capacity	${(\rho C_p)}_{hnf}=\left(1-{\phi }_{hnf}\right){(\rho C_p)}_f+{\phi }_1{(\rho C_p)}_{n1}+{\phi }_2{(\rho C_p)}_{n2}$
Density	${\rho }_{hnf}=\left(1-{\phi }_{hnf}\right){\rho }_f+{\phi }_1{\rho }_{n1}+{\phi }_2{\rho }_{n2}$
Dynamic viscosity	${\mu }_{hnf}=\frac{{\mu }_f}{{\left(1-{\phi }_{hnf}\right)}^{2.5}}$

Now, consider the dimensionless variables (see [9,15]):

$$\psi =\sqrt{U_{\infty }{\nu }_{f}x}f\left(\eta \right), \theta \left(\eta \right)=\frac{T-T_{\infty }}{T_w-T_{\infty }}, \eta =y\sqrt{\frac{U_{\infty } }{{\nu }_{f}x}},$$

(7)

where $u=\partial \psi /\partial y$ and $v=-\partial \psi /\partial x$ such that

$$u=U_{\infty } f^{\prime }\left(\eta \right), v=-\frac{1}{2}\sqrt{\frac{U_{\infty }{\nu }_f}{x}}\left[f\left(\eta \right)-\eta f^{\prime }\left(\eta \right)\right].$$

(8)

From Equation (8), by setting $\eta =0$, one obtains:

$$v_w\left(x\right)=-\frac{1}{2}\sqrt{\frac{U_{\infty }{\nu }_f}{x}}S,$$

(9)

where ${\nu }_f$ represents the base fluid kinematic viscosity. Additionally, $f\left(0\right)=S$ is the suction/injection parameter which determines the permeability of the surface. Here, $S<0$ (injection) and $S>0$ (suction) represent the permeable cases while $S=0$ represents an impermeable case.

On using Equations (7) and (8), Equation (1) is identically fulfilled. Now, Equations (2) and (6) reduce to:

$$\frac{{\mu }_{hnf}/{\mu }_f}{{\rho }_{hnf}/{\rho }_f} f^{‴}+\frac{1}{2}f{f}^{″}=0,$$

(10)

$$\frac{1}{\mathrm{Pr}}\frac{1}{{\left(\rho C_p\right)}_{hnf}/{\left(\rho C_p\right)}_f}\left(\frac{k_{hnf}}{k_f}+\frac{4}{3}R\right){\theta }^{″}+\frac{1}{2}f{\theta }^{\prime }+Ec\frac{{\mu }_{hnf}/{\mu }_f}{{\left(\rho C_p\right)}_{hnf}/{\left(\rho C_p\right)}_f}{f}^{″2}=0,$$

(11)

subject to:

$$\begin{gathered} f\left(0\right)=S, f^{\prime }\left(0\right)=\lambda , \theta \left(0\right)=1, \\ {f}^{\prime }\left(\eta \right)\to 1, \theta \left(\eta \right)\to 0 \mathrm{as} \eta \to \infty , \end{gathered}$$

(12)

where primes indicate the differentiation with respect to $\eta$. Moreover, $\mathrm{Pr}$ and $Ec$ are the Prandtl and the Eckert numbers, respectively, while $R$ and $\lambda$ are the radiation and the velocity ratio parameters, which are defined as:

$$\mathrm{Pr}=\frac{{\left(\mu C_p\right)}_f}{k_f}, Ec=\frac{U_{\infty }^2}{{\left(C_p\right)}_f\left(T_w-T_{\infty }\right)}, R=\frac{4{\sigma }^{*}{T}_{\infty }^3}{k^{*}{k}_f}, \lambda =\frac{U_w}{U_{\infty }}.$$

(13)

Here, $\lambda =0$ is for the static plate, while $\lambda <0$ $(\lambda >0)$ indicates the plate and the fluid move in the opposite (same) direction. It is worth mentioning that when ${\phi }_{hnf}=S=\lambda =0$, Equation (10) reduces to the classical Blasius flow.

The skin friction coefficient $C_f$ and the local Nusselt number $N{u}_x$ are given as [49]:

$$C_f=\frac{{\mu }_{hnf}}{{\rho }_f U_{\infty }^2}{\left(\frac{\partial u}{\partial y}\right)}_{y=0}, N{u}_x=\frac{x}{k_f\left(T_w-T_{\infty }\right)}\left(-k_{hnf} {\left(\frac{\partial T}{\partial y}\right)}_{y=0}+{(q_r)}_{y=0}\right).$$

(14)

Using (7) and (14), one receives:

$${\mathrm{Re}}_x^{1/2}{C}_f=\frac{{\mu }_{hnf}}{{\mu }_f}{f}^{″}\left(0\right), {\mathrm{Re}}_x^{-1/2}N{u}_x=-\left(\frac{k_{hnf}}{k_f}+\frac{4}{3}R\right){\theta }^{\prime }\left(0\right),$$

(15)

which with the local Reynolds number is ${\mathrm{Re}}_x=U_{\infty }x/{\nu }_f$.

3. Stability Analysis

This analysis is important to verify the stability of the obtained solutions [50,51,52]. Based on Equation (9), the semi-similar variables are:

$$\psi =\sqrt{U_{\infty }{\nu }_{f}x}f\left(\eta ,\tau \right), \theta \left(\eta ,\tau \right)=\frac{T-T_{\infty }}{T_w-T_{\infty }}, \eta =y\sqrt{\frac{U_{\infty } }{{\nu }_{f}x}}, \tau =\frac{Ut}{x},$$

(16)

with $u=\partial \psi /\partial y$ and $v=-\partial \psi /\partial x$ which are defined as

$$u=U_{\infty }\frac{\partial f}{\partial \eta }\left(\eta ,\tau \right), v=-\frac{1}{2}\sqrt{\frac{U_{\infty }{\nu }_f}{x}}\left[f\left(\eta ,\tau \right)-\eta \frac{\partial f}{\partial \eta }\left(\eta ,\tau \right)-2\tau \frac{\partial f}{\partial \tau }\left(\eta ,\tau \right)\right].$$

(17)

The transformed equations by applying Equations (16) and (17) into Equations (2) and (3) are:

$$\frac{{\mu }_{hnf}/{\mu }_f}{{\rho }_{hnf}/{\rho }_f}\frac{{\partial }^{3}f}{\partial {\eta }^3}+\frac{1}{2}f\frac{{\partial }^{2}f}{\partial {\eta }^2}-\frac{{\partial }^{2}f}{\partial \eta \partial \tau }+\tau \left(\frac{\partial f}{\partial \eta }\frac{{\partial }^{2}f}{\partial \eta \partial \tau }-\frac{\partial f}{\partial \tau }\frac{{\partial }^{2}f}{\partial {\eta }^2}\right)=0,$$

(18)

$$\begin{gathered} \frac{1}{\mathrm{Pr}}\frac{1}{{\left(\rho C_p\right)}_{hnf}/{\left(\rho C_p\right)}_f} \left(\frac{k_{hnf}}{k_f}+\frac{4}{3}R\right)\frac{{\partial }^2\theta }{\partial {\eta }^2}+\frac{1}{2}f\frac{\partial \theta }{\partial \eta }+Ec\frac{{\mu }_{hnf}/{\mu }_f}{{\left(\rho C_p\right)}_{hnf}/{\left(\rho C_p\right)}_f}{\left(\frac{{\partial }^{2}f}{\partial {\eta }^2}\right)}^2 \\ -\frac{\partial \theta }{\partial \tau }+\tau \left(\frac{\partial f}{\partial \eta }\frac{\partial \theta }{\partial \tau }-\frac{\partial f}{\partial \tau }\frac{\partial \theta }{\partial \eta }\right)=0, \end{gathered}$$

(19)

subject to:

$$\begin{gathered} f\left(0,\tau \right)-2\tau \frac{\partial f}{\partial \tau }\left(0,\tau \right)=S, \frac{\partial f}{\partial \eta }\left(0,\tau \right)=\lambda , \theta \left(0,\tau \right)=1, \\ \frac{\partial f}{\partial \eta }\left(\eta ,\tau \right)\to 0, \theta \left(\eta ,\tau \right)\to 0 \mathrm{as} \eta \to \infty . \end{gathered}$$

(20)

Then, the disturbance is applied to the steady solution $f=f_0\left(\eta \right)$ and $\theta ={\theta }_0\left(\eta \right)$ of Equations (10) and (11) by employing the following relations [52]:

$$f\left(\eta ,\tau \right)=f_0\left(\eta \right)+e^{-\gamma \tau }F\left(\eta ,\tau \right), \theta \left(\eta ,\tau \right)={\theta }_0\left(\eta \right)+e^{-\gamma \tau }G\left(\eta ,\tau \right),$$

(21)

where $F\left(\eta ,\tau \right)$ and $G\left(\eta ,\tau \right)$ are arbitrary functions and relatively small compared to $f_0\left(\eta \right)$ and ${\theta }_0\left(\eta \right)$, and $\gamma$ denotes the eigenvalue. Substituting Equation (21) into Equations (18) and (19) yields

$$\frac{{\mu }_{hnf}/{\mu }_f}{{\rho }_{hnf}/{\rho }_f}\frac{{\partial }^{3}F}{\partial {\eta }^3}+\frac{1}{2}\left(f_0\frac{{\partial }^{2}F}{\partial {\eta }^2}+f_0^{″}F\right)+\gamma \frac{\partial F}{\partial \eta }-\frac{{\partial }^{2}F}{\partial \eta \partial \tau }+\tau \left(\gamma f_0^{″}F-\gamma f_0^{\prime }\frac{\partial F}{\partial \eta }-f_0^{″}\frac{\partial F}{\partial \tau }+f_0^{\prime }\frac{{\partial }^{2}F}{\partial \eta \partial \tau }\right)=0,$$

(22)

$$\begin{gathered} \frac{1}{\mathrm{Pr}}\frac{1}{{\left(\rho C_p\right)}_{hnf}/{\left(\rho C_p\right)}_f} \left(\frac{k_{hnf}}{k_f}+\frac{4}{3}R\right)\frac{{\partial }^{2}G}{\partial {\eta }^2}+\frac{1}{2}\left(f_0\frac{\partial G}{\partial \eta }+{\theta }_0^{\prime }F\right)+2Ec\frac{{\mu }_{hnf}/{\mu }_f}{{\left(\rho C_p\right)}_{hnf}/{\left(\rho C_p\right)}_f}{f}_0^{″}\frac{{\partial }^{2}F}{\partial {\eta }^2}+\gamma G-\frac{\partial G}{\partial \tau }+ \\ \tau \left(\gamma {\theta }_0^{\prime }F-\gamma f_0^{\prime }G+f_0^{\prime }\frac{\partial G}{\partial \tau }-{\theta }_0^{\prime }\frac{\partial F}{\partial \tau }\right)=0 \end{gathered}$$

(23)

The boundary conditions become

$$\begin{gathered} F\left(0,\tau \right)-2\tau \left(\frac{\partial F}{\partial \tau }\left(0,\tau \right)-\gamma F\left(0,\tau \right)\right)=0,\hspace{1em}\frac{\partial F}{\partial \eta }\left(0,\tau \right)=0,\hspace{1em}G\left(0,\tau \right)=0, \\ \frac{\partial F}{\partial \eta }\left(\eta ,\tau \right)\to 0,\hspace{1em}\hspace{1em}G\left(\eta ,\tau \right)\to 0 \mathrm{as} \eta \to \infty . \end{gathered}$$

(24)

By setting $\tau =0$ implies $F(\eta ,\tau )=F_0(\eta )$ and $G(\eta ,\tau )=G_0(\eta )$ [37]. After linearization, the eigenvalue problems become

$$\frac{{\mu }_{hnf}/{\mu }_f}{{\rho }_{hnf}/{\rho }_f}{F}^{‴}+\frac{1}{2}\left(f_0{F}_0^{″}+f_0^{″}{F}_0\right)+\gamma F^{\prime }=0,$$

(25)

$$\frac{1}{\mathrm{Pr}}\frac{1}{{\left(\rho C_p\right)}_{hnf}/{\left(\rho C_p\right)}_f} \left(\frac{k_{hnf}}{k_f}+\frac{4}{3}R\right)G_0^{″}+\frac{1}{2}\left(f_0{G}_0^{\prime }+{\theta }_0^{\prime }{F}_0\right)+2Ec\frac{{\mu }_{hnf}/{\mu }_f}{{\left(\rho C_p\right)}_{hnf}/{\left(\rho C_p\right)}_f}{f}_0^{″}{F}_0^{″}+\gamma G_0=0,$$

(26)

subject to:

$$\begin{gathered} F_0\left(0\right)=0, F_0^{\prime }\left(0\right)=0, G_0\left(0\right)=0, \\ {F}_0^{\prime }\left(\eta \right)\to 0, G_0\left(\eta \right)\to 0 \mathrm{as} \eta \to \infty . \end{gathered}$$

(27)

To obtain $\gamma$ in Equations (25) and (26), $F^{″}\left(0\right)=1$ is employed to replace $F_0^{\prime }\left(\eta \right)\to 0 \mathrm{as} \eta \to \infty$ [53].

4. Results and Discussion

Equations (10)–(12) are programmed in the bvp4c solver and then, numerically computed. The 3-stage Lobatto IIIa formula is embedded in the bvp4c application [54]. Further, the total composition of Al₂O₃ and Cu concentrations are considered as $1\%$ of Al₂O₃ $\left({\phi }_1=1\%\right)$ and $1\%$ of Cu $\left({\phi }_2=1\%\right)$.

The values of $-\theta \prime \left(0\right)$ when ${\phi }_{hnf}=\lambda =R=Ec=0$ with different values of $\mathrm{Pr}$ are compared with Bataller [4] as shown in Table 3. Meanwhile, Table 4 shows the comparison of the skin friction coefficient ${\mathrm{Re}}_x^{1/2}{C}_f$ and the local Nusselt number ${\mathrm{Re}}_x^{-1/2}N{u}_x$ with Ahmad et al. [9] when ${\phi }_2=\lambda =R=Ec=0$ and $\mathrm{Pr}=6.2$ with several ${\phi }_1$. From these tables, the results are satisfactory to that mentioned literature. Moreover, the values of ${\mathrm{Re}}_x^{-1/2}N{u}_x$ are also provided in Table 4 and show an increasing pattern as ${\phi }_1$ increases. Additionally, the values ${\mathrm{Re}}_x^{1/2}{C}_f$ and ${\mathrm{Re}}_x^{-1/2}N{u}_x$ with different values of $\lambda , R, Ec,$ and $S$ when ${\phi }_{hnf}=2\%$ and $\mathrm{Pr}=6.2$ are provided in Table 5 for future reference.

Table 3. Values of $-\theta \prime \left(0\right)$ when ${\phi }_{hnf}=\lambda =R=Ec=0$ with different values of $\mathrm{Pr}$.

$\mathbf{P}\mathbf{r}.$	Bataller [4]	Present Results
0.7	0.29268	0.29268
5	0.57669	0.57669
6.2		0.62007
10	0.72814	0.72814
50	1.24729	1.24729
100	1.57183	1.57183

Table 4. Values of ${\mathrm{Re}}_x^{1/2}{C}_f$ and ${\mathrm{Re}}_x^{-1/2}N{u}_x$ when ${\phi }_2=\lambda =R=Ec=0$ and $\mathrm{Pr}=6.2$ with different ${\phi }_1$.

${\mathit{\phi }}_1$	Ahmad et al. [9]	Present Results
	$\mathbf{R}{\mathbf{e}}_{\mathit{x}}^{1/2}{\mathit{C}}_{\mathit{f}}$	$\mathbf{R}{\mathbf{e}}_{\mathit{x}}^{1/2}{\mathit{C}}_{\mathit{f}}$	$\mathbf{R}{\mathbf{e}}_{\mathit{x}}^{-1/2}\mathit{N}{\mathit{u}}_{\mathit{x}}$
0	0.3321	0.33206	0.62007
0.002	0.3339	0.33388	0.62241
0.004	0.3357	0.33571	0.62475
0.008	0.3394	0.33938	0.62943
0.01	0.3412	0.34123	0.63177

Table 5. Values ${\mathrm{Re}}_x^{1/2}{C}_f$ and ${\mathrm{Re}}_x^{-1/2}N{u}_x$ with different values of $\lambda , R, Ec,$ and $S$ when $\mathrm{Pr}=6.2$ and ${\phi }_{hnf}=2\%$.

$\mathit{\lambda }$	$\mathit{R}$	$\mathit{E}\mathit{c}$	$\mathit{S}$	First Solution		Second Solution
				$\mathbf{R}{\mathbf{e}}_{\mathit{x}}^{1/2}{\mathit{C}}_{\mathit{f}}$	$\mathbf{R}{\mathbf{e}}_{\mathit{x}}^{-1/2}\mathit{N}{\mathit{u}}_{\mathit{x}}$	$\mathbf{R}{\mathbf{e}}_{\mathit{x}}^{1/2}{\mathit{C}}_{\mathit{f}}$	$\mathbf{R}{\mathbf{e}}_{\mathit{x}}^{-1/2}\mathit{N}{\mathit{u}}_{\mathit{x}}$
−0.35	0	0	0	0.19675	0.05461	0.13639	0.01126
−0.3				0.27241	0.18844	0.06483	0.00031
−0.25				0.30670	0.28935	0.03467	0.00001
−0.2				0.32856	0.37636	0.01695	0.00000
−0.1				0.35216	0.52430	0.00148	0.00000
−0.3	0.5			0.27241	0.34743	0.06483	0.00660
	1			0.27241	0.49699	0.06483	0.02676
	1.5			0.27241	0.63822	0.06483	0.06050
	2			0.27241	0.77255	0.06483	0.10416
	3			0.27241	1.02468	0.06483	0.20909
	1	0.01		0.27241	0.48806	0.06483	0.02565
		0.03		0.27241	0.47018	0.06483	0.02342
		0.05		0.27241	0.45231	0.06483	0.02119
		0.1		0.27241	0.40762	0.06483	0.01561
		0.2		0.27241	0.31824	0.06483	0.00445
		0.1	−0.1	0.18325	0.18495	0.09451	0.04133
			0.1	0.34471	0.62723	0.05293	0.00862
			0.2	0.41264	0.85529	0.04630	0.00545
			0.3	0.47877	1.09161	0.04235	0.00370
			0.5	0.60909	1.58414	0.03902	0.00174

The variations of the local Nusselt number ${\mathrm{Re}}_x^{-1/2}N{u}_x$ against $R$ when $\lambda =-0.3,S=Ec=0,\mathrm{and}\mathrm{Pr}=6.2$ for various ${\phi }_{hnf}$ are presented in Figure 2. The increment in the values of ${\mathrm{Re}}_x^{-1/2}N{u}_x$ on both solutions are observed with the rising values of $R$ and ${\phi }_{hnf}$. The rise in radiation heat energy incorporated in radiation parameters leads to the development of fluid temperature, as well as the thermal boundary layer; Meanwhile, the rising values of ${\phi }_{hnf}$ contribute to the increment of ${\mathrm{Re}}_x^{-1/2}N{u}_x$. This is consistent with the fact that the hybrid nanofluid offers better thermal characteristics as compared to the base fluid and nanofluid containing single nanoparticles as a result of synergistic effects.

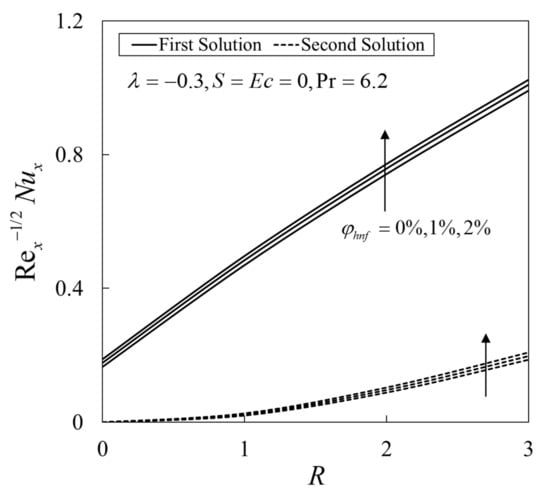
Figure 2. Variation of the local Nusselt number ${\mathrm{Re}}_x^{-1/2}N{u}_x$ with R for several values of ${\phi }_{hnf}$.

Moreover, the effect of $R$ and $Ec$ on ${\mathrm{Re}}_x^{-1/2}N{u}_x$ when $\lambda =-0.3,S=0,\mathrm{Pr}=6.2, \mathrm{and} {\phi }_{hnf}=2\%$ can be observed in Figure 3. The values of ${\mathrm{Re}}_x^{-1/2}N{u}_x$ on both solutions decline with the rise of $Ec$. Physically, the Eckert number is the ratio of the kinetic energy flow to the boundary layer’s enthalpy difference. By opposing fluid stresses, the Eckert number aids in the conversion of kinetic energy into internal energy. As a result, the enthalpy difference effect lessens due to the high intensity of kinetic energy. Thus, the thickness of the thermal layer increases which implies the increase in the fluid temperature. Therefore, the upshot of $Ec$ lead to a decrease in the temperature gradient and consequently reduce the heat transfer.

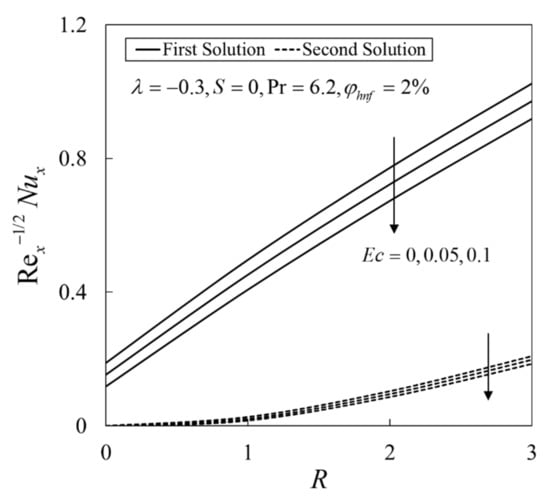
Figure 3. Variation of the local Nusselt number ${\mathrm{Re}}_x^{-1/2}N{u}_x$ with R for several values of $Ec$.

Moreover, the variations of the skin friction coefficient ${\mathrm{Re}}_x^{1/2}{C}_f$ and the local Nusselt number ${\mathrm{Re}}_x^{-1/2}N{u}_x$ against $\lambda$ when $R=1, Ec=0.1, \mathrm{Pr}=6.2, \mathrm{and} {\phi }_{hnf}=2\%$ for different values of $S$ are displayed in Figure 4 and Figure 5. Note that the values of ${\mathrm{Re}}_x^{1/2}{C}_f$ and ${\mathrm{Re}}_x^{-1/2}N{u}_x$ are greater for $S=0.1$ (suction case) followed by $S=0$ (impermeable case) and $S=-0.1$ (injection case). Besides, the dual solutions are observed when $\lambda <0$. The separation of the boundary layer occurs in this region where the critical points for $S=-0.1, 0,\mathrm{and} 0.1$ are given by ${\lambda }_{c1}=-0.31064,{\lambda }_{c2}=-0.35410,\mathrm{and}{\lambda }_{c3}=-0.40000$, respectively.

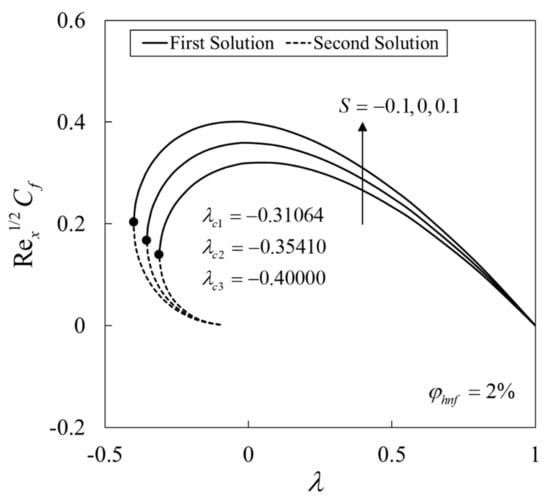
Figure 4. Variation of the skin friction coefficient ${\mathrm{Re}}_x^{1/2}{C}_f$ with $\lambda$ for several values of $S$.

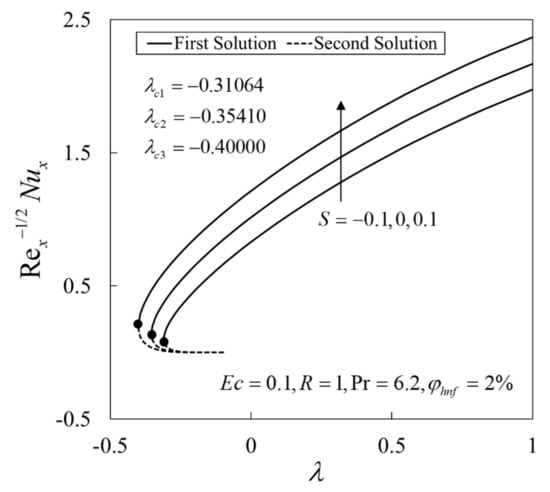
Figure 5. Variation of the local Nusselt number ${\mathrm{Re}}_x^{-1/2}N{u}_x$ with $\lambda$ for several values of S.

Furthermore, the consequence of pertinent parameters on the velocity profiles $f^{\prime }\left(\eta \right)$ and the temperature profiles $\theta \left(\eta \right)$ are displayed in Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13. Figure 6 and Figure 7 demonstrate the consequence of ${\phi }_{hnf}$ on the profiles of $f^{\prime }\left(\eta \right)$ and $\theta \left(\eta \right)$ when $\lambda =-0.39,S=0.1,R=1, Ec=0.1, \mathrm{Pr}=6.2$. Both branch solutions of $f^{\prime }\left(\eta \right)$ show an upward trend for the upsurge of ${\phi }_{hnf}$, while the observations are reversed for $\theta \left(\eta \right)$. Moreover, Figure 8 and Figure 9 illustrate the consequence of $\lambda <0$ on $f^{\prime }\left(\eta \right)$ and $\theta \left(\eta \right)$ when $S=0.1,{\phi }_{hnf}=2\%, R=1, Ec=0.1, \mathrm{Pr}=6.2$. Next, the profiles of $f^{\prime }\left(\eta \right)$ and $\theta \left(\eta \right)$ when $\lambda =-0.3,{\phi }_{hnf}=2\%,Ec=0.1,R=1, \mathrm{and}\mathrm{Pr}=6.2$ for different $S$ are provided in Figure 10 and Figure 11. Note that the values of $f^{\prime }\left(\eta \right)$ on the first solution are higher for suction case $\left(S=0.1\right)$. Contrary, suction case $\left(S=0.1\right)$ lowers the values of $\theta \left(\eta \right)$ on the first solution. Besides, Figure 12 and Figure 13 illustrate the impact of $R$ and $Ec$ on $\theta \left(\eta \right)$ for selected parameters. The first solution of $\theta \left(\eta \right)$ shows an increasing pattern, but the second solutions are fluctuated with the rise of $R$. Moreover, the values of $\theta \left(\eta \right)$ for both solutions enlarge with the increase of $Ec$.

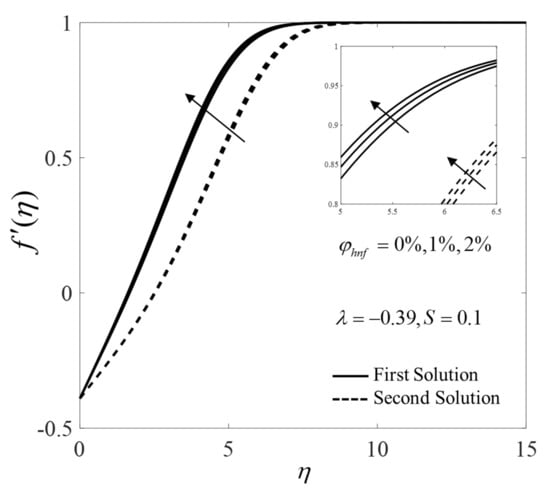
Figure 6. Velocity profile $f^{\prime }\left(\eta \right)$ for several values of ${\phi }_{hnf}$.

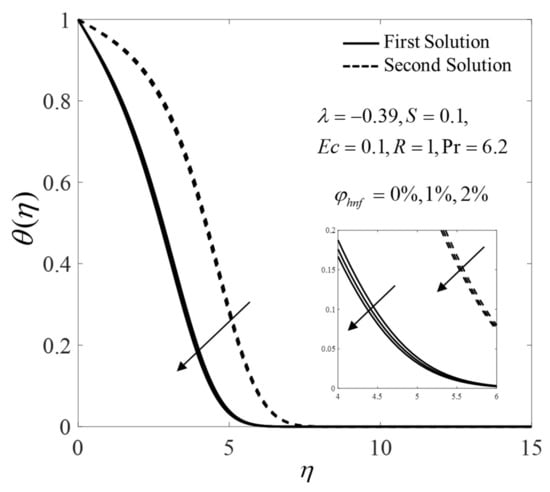
Figure 7. Temperature profile $\theta \left(\eta \right)$ for several values of ${\phi }_{hnf}$.

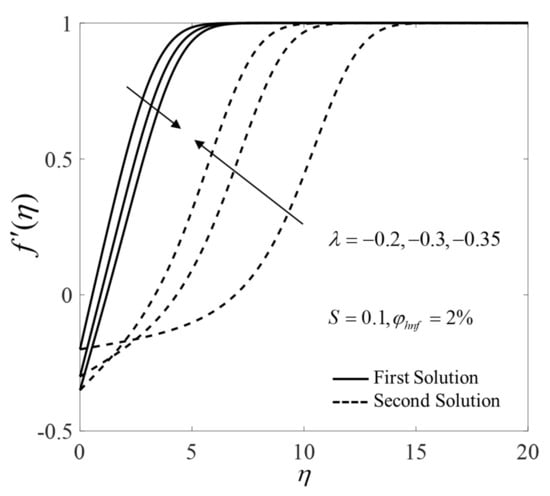
Figure 8. Velocity profile $f^{\prime }\left(\eta \right)$ for several values of $\lambda$.

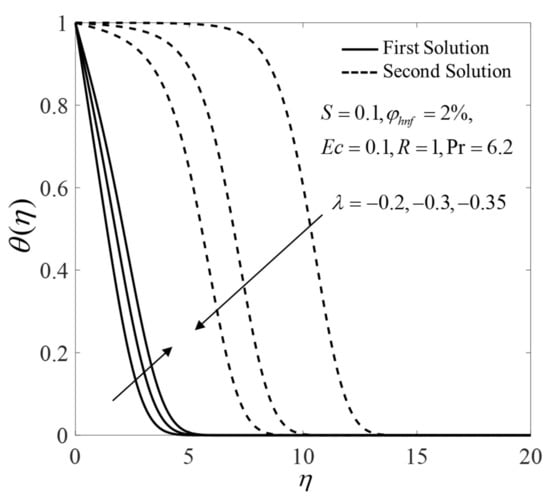
Figure 9. Temperature profile $\theta \left(\eta \right)$ for several values of $\lambda$.

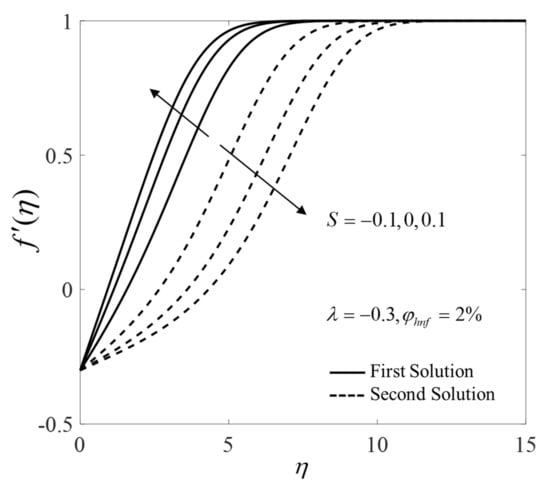
Figure 10. Velocity profile $f^{\prime }\left(\eta \right)$ for several values of $S$.

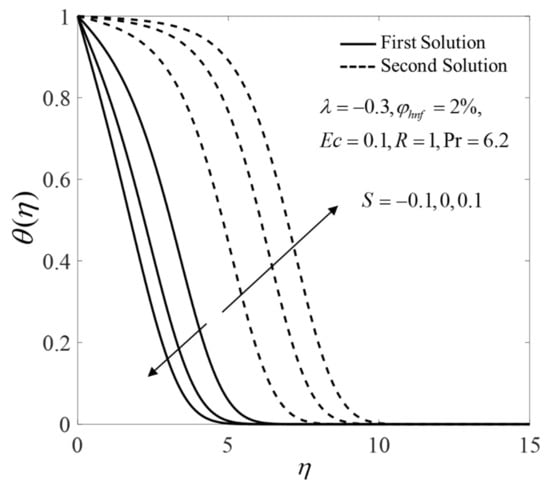
Figure 11. Temperature profile $\theta \left(\eta \right)$ for several values of $S$.

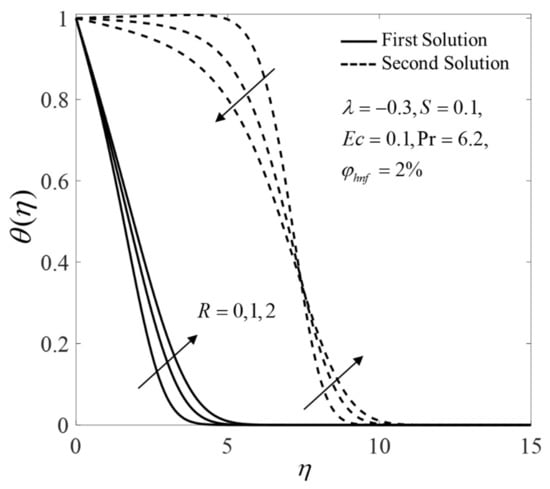
Figure 12. Temperature profile $\theta \left(\eta \right)$ for several values of $R$.

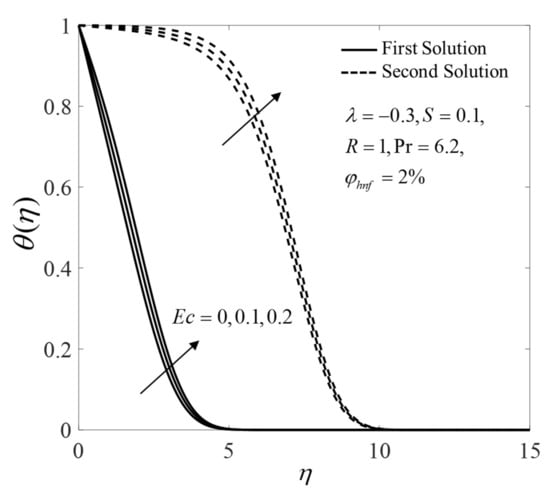
Figure 13. Temperature profile $\theta \left(\eta \right)$ for several values of $Ec$.

The variations of $\gamma$ against $\lambda$ when $S=-0.1,$ and ${\phi }_{hnf}=2\%$ are depicted in Figure 14. It is noted that $e^{-\gamma \tau }\to \infty$ when $\gamma <0$, whereas $e^{-\gamma \tau }\to 0$ when $\gamma >0$ as time evolves $\left(\tau \to \infty \right)$. The case $\gamma >0$ shows that the disturbance is diminished as time passes, which indicates the flow is stable over time. On the other hand, the flow is unstable in the long run for the case $\gamma <0$. Even the unstable solution may deprive of physical significance, they are still of interest since this solution is also a solution to the differential equation. This solution may appear in other situations, where its existence is more appreciated.

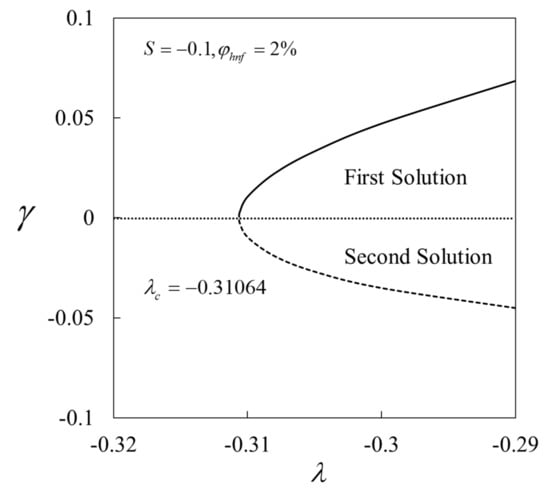
Figure 14. The smallest eigenvalue $\gamma$ against $\lambda$.

5. Conclusions

The heat transfer enhancement in the Blasius flow of a hybrid nanofluid over a moving plate with viscous dissipation and radiation effects are studied in this paper. Different from the classical Blasius flow which considered a viscous fluid flow over a static flat plate, in this study, both the fluid and the plate move either in the same or in the opposite directions. The numerical results indicate that two solutions exist when the plate and the free stream move in the opposite directions, while unique solution is obtained when they move in the same direction. The solutions exist up to a certain critical value, beyond which the separation occurs, thus no solution is possible. The findings of this study are summarized as follows:

• Two solutions are attained when $\lambda <0$ (when the plate and the free stream move in the opposite directions), while the solution is unique when $\lambda \ge 0$ (when the plate and the free stream move in the same directions).
• The critical value ${\lambda }_c$ is expanded by the addition of the suction/injection parameter which implies the retardation in boundary layer separation.
• The enhancement in the heat transfer rate is observed with the increase of ${\phi }_{hnf}$ and radiation parameter $R$.
• The increase of Eckert number $Ec$ lowers the heat transfer rate.
• The increase of $R$ and $Ec$ lead to an increase in $\theta \left(\eta \right)$ while opposite behaviour with the upsurge of ${\phi }_{hnf}$.
• The first solution is physically reliable and stable based on the temporal stability analysis.

These original results are important to other researchers in the selection of (i) the relevant parameters to optimize the heat transfer process and, (ii) the right parameters to generate all available solutions so that no misjudgment on flow and heat transfer features.