Blasius Flow over a Permeable Moving Flat Plate Containing Cu-Al2O3 Hybrid Nanoparticles with Viscous Dissipation and Radiative Heat Transfer
Abstract
:1. Introduction
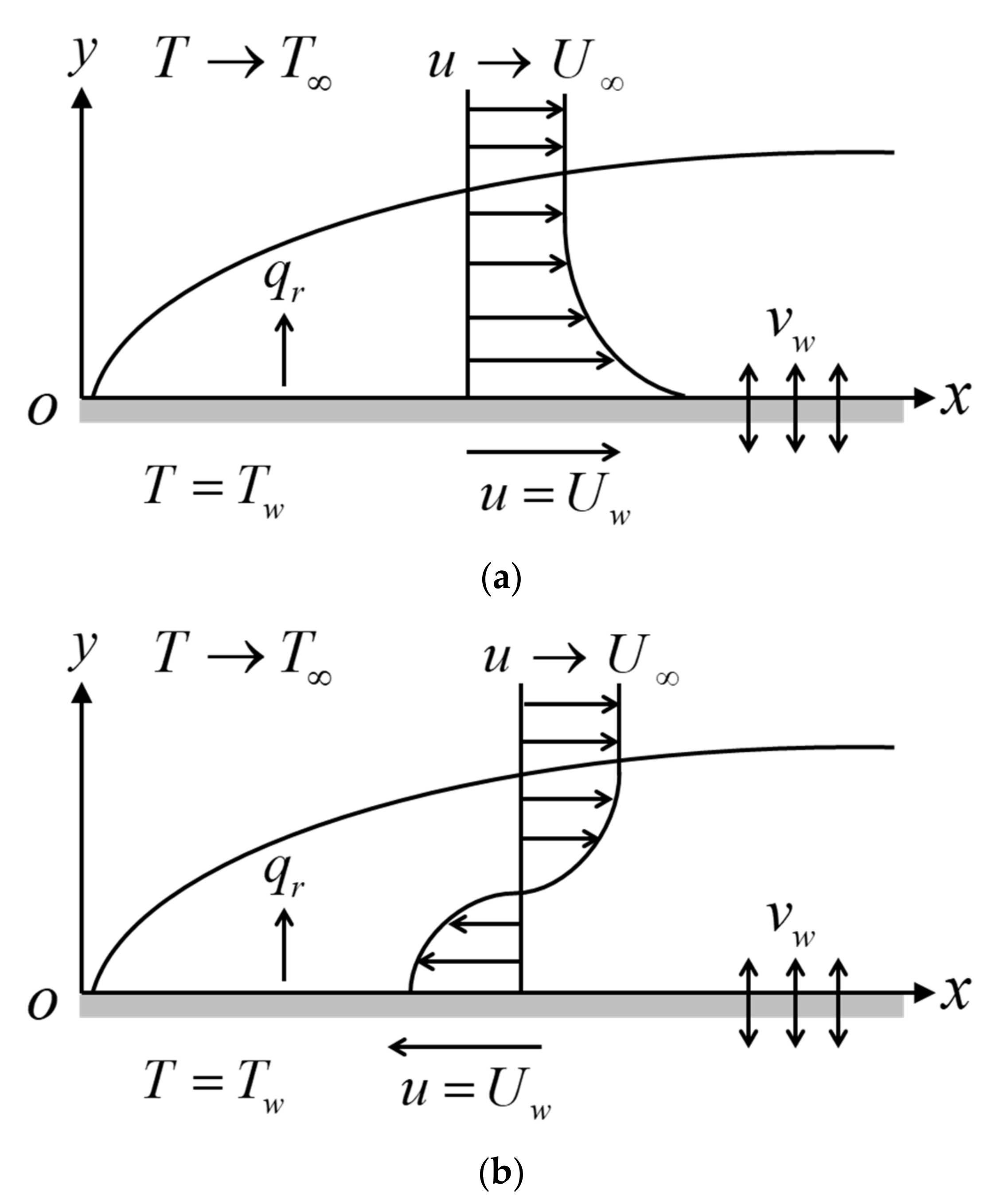
2. Mathematical Formulation
3. Stability Analysis
4. Results and Discussion
5. Conclusions
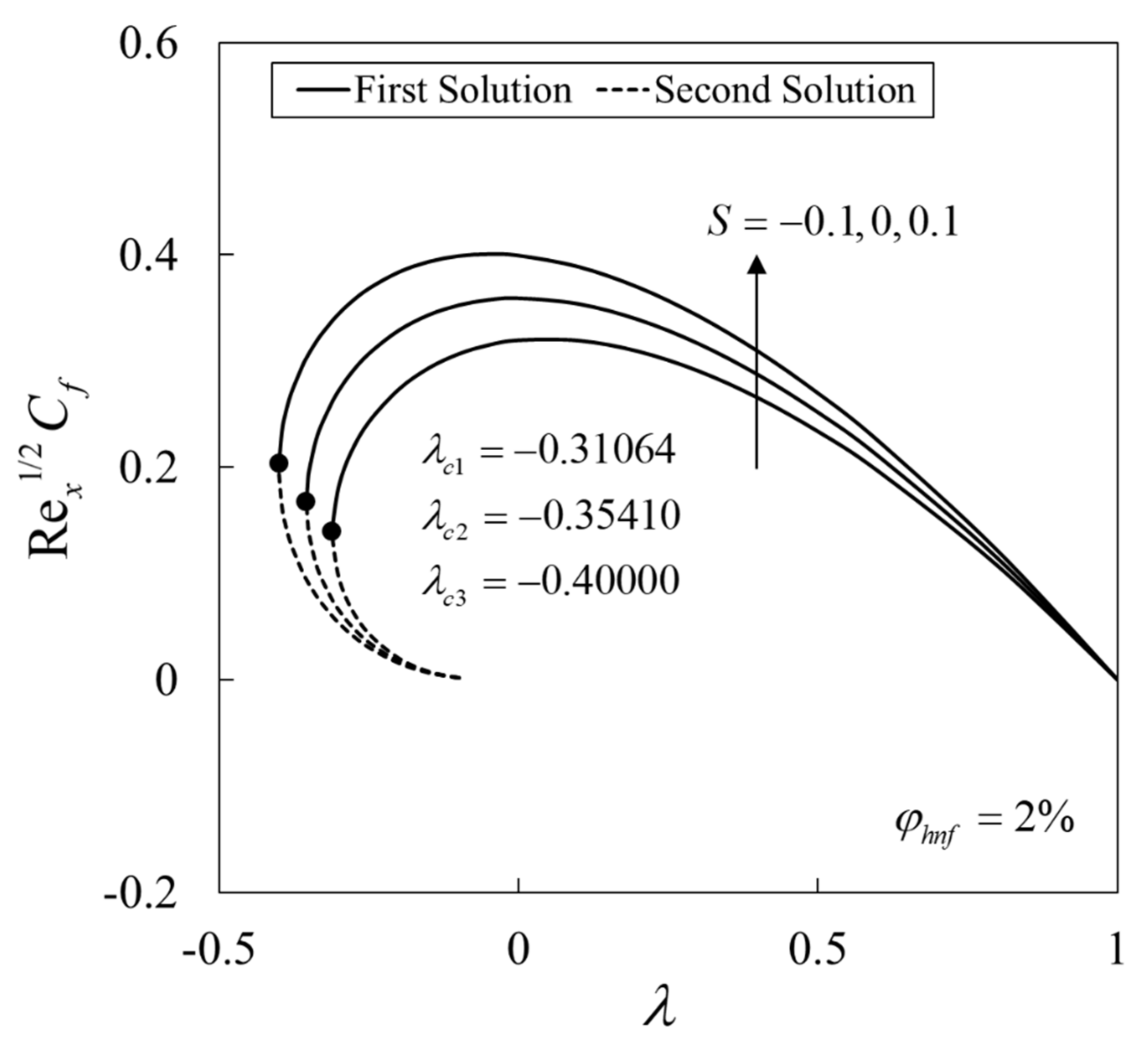
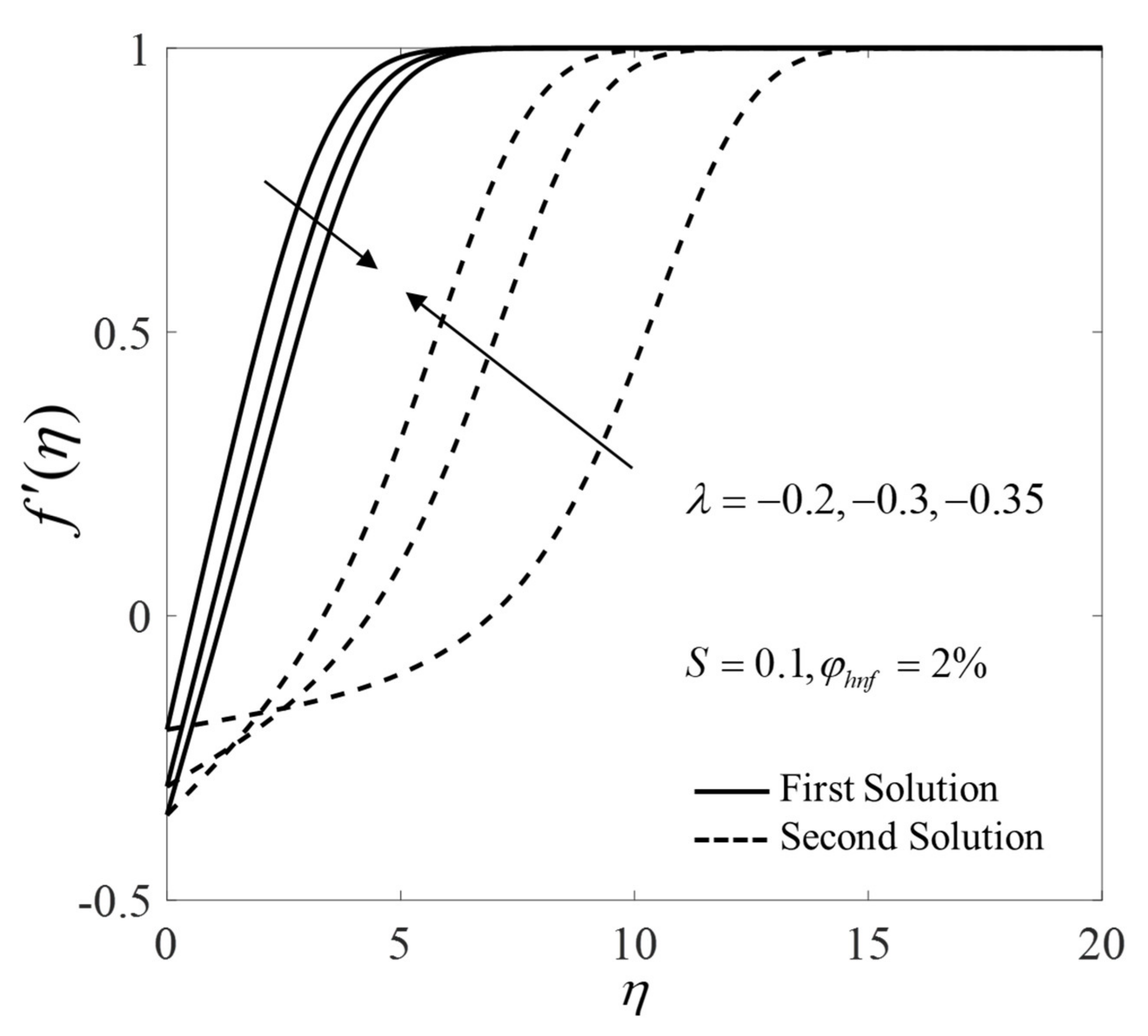
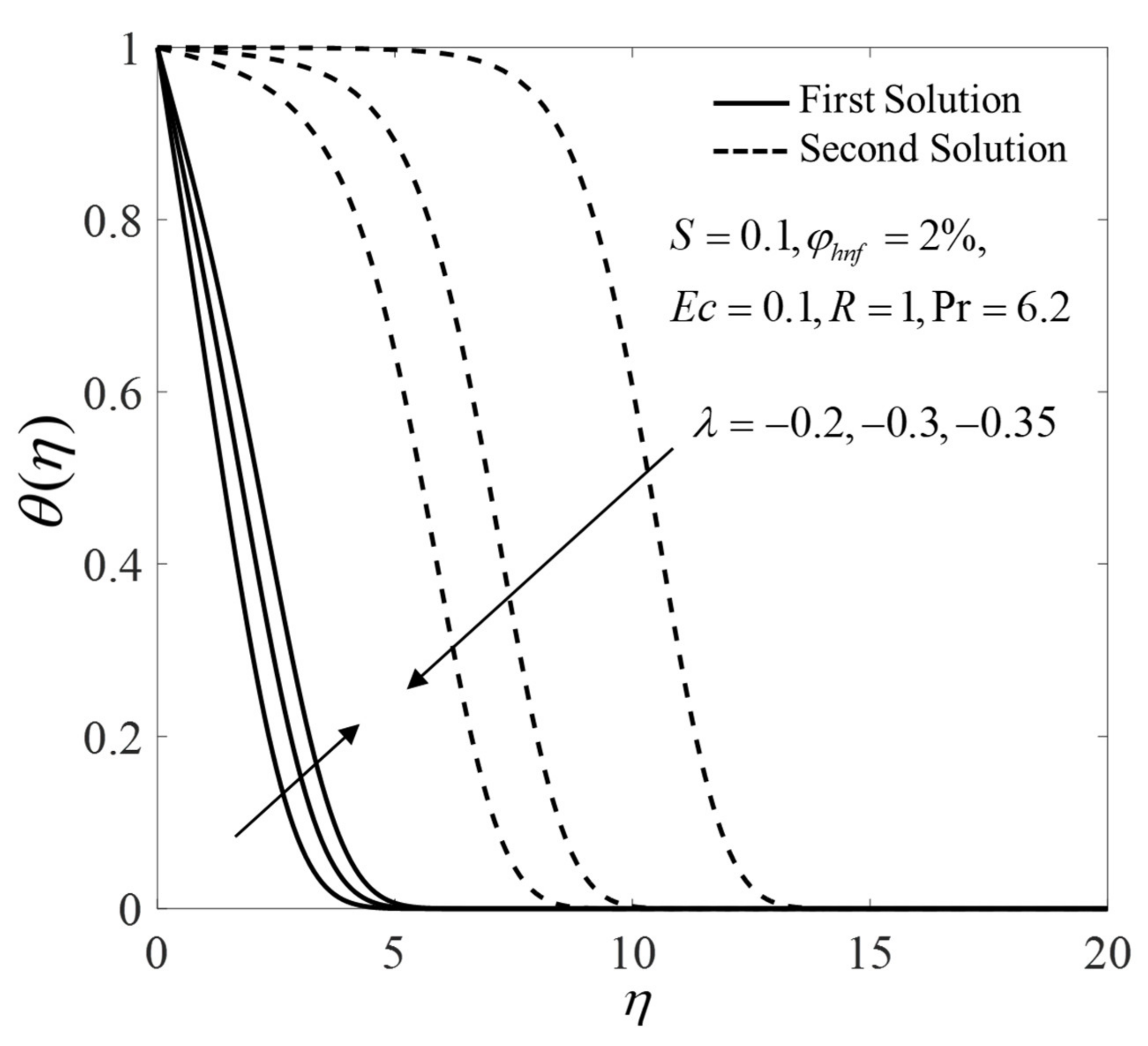
- Two solutions are attained when (when the plate and the free stream move in the opposite directions), while the solution is unique when (when the plate and the free stream move in the same directions).
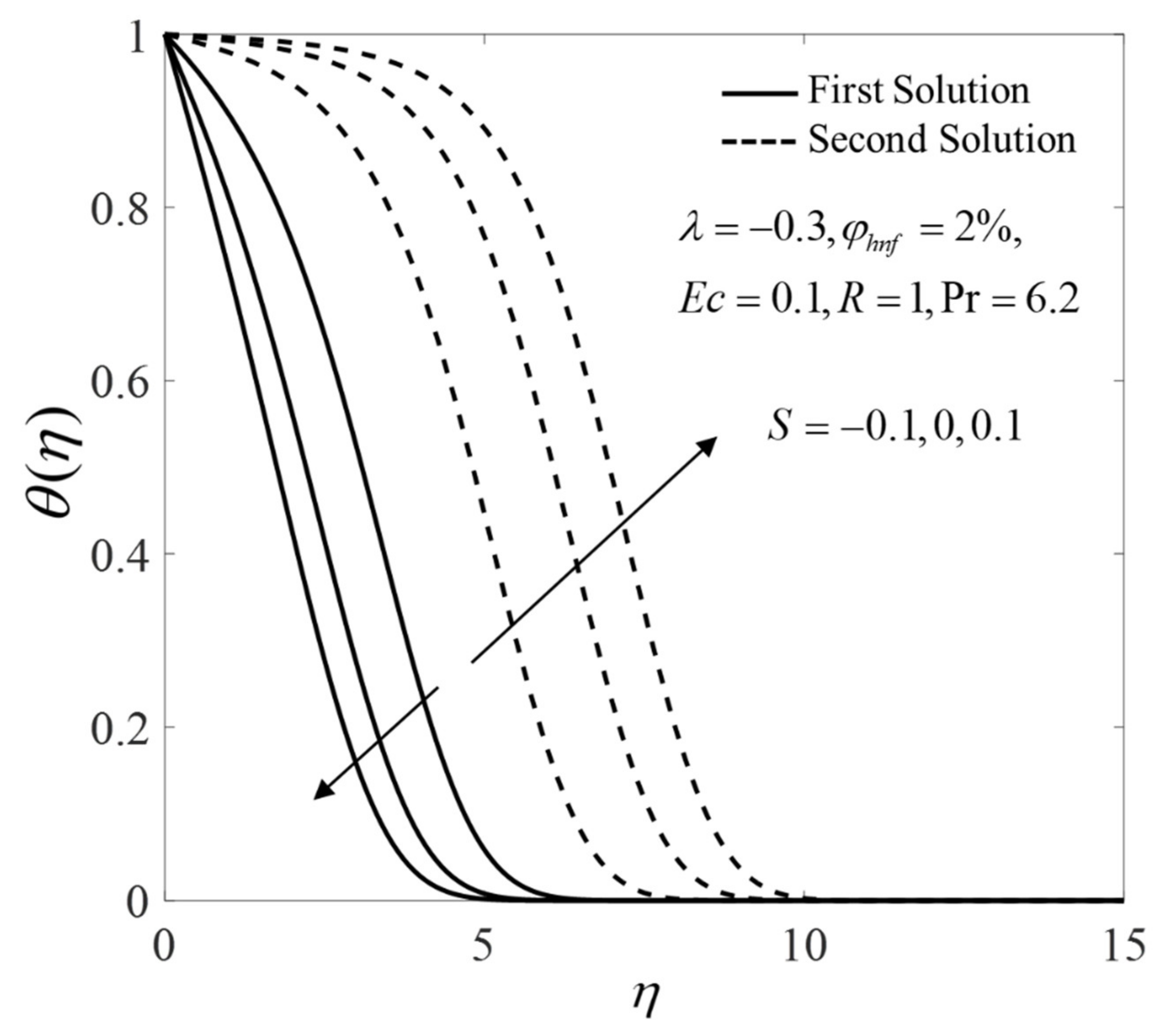
- The critical value is expanded by the addition of the suction/injection parameter which implies the retardation in boundary layer separation.
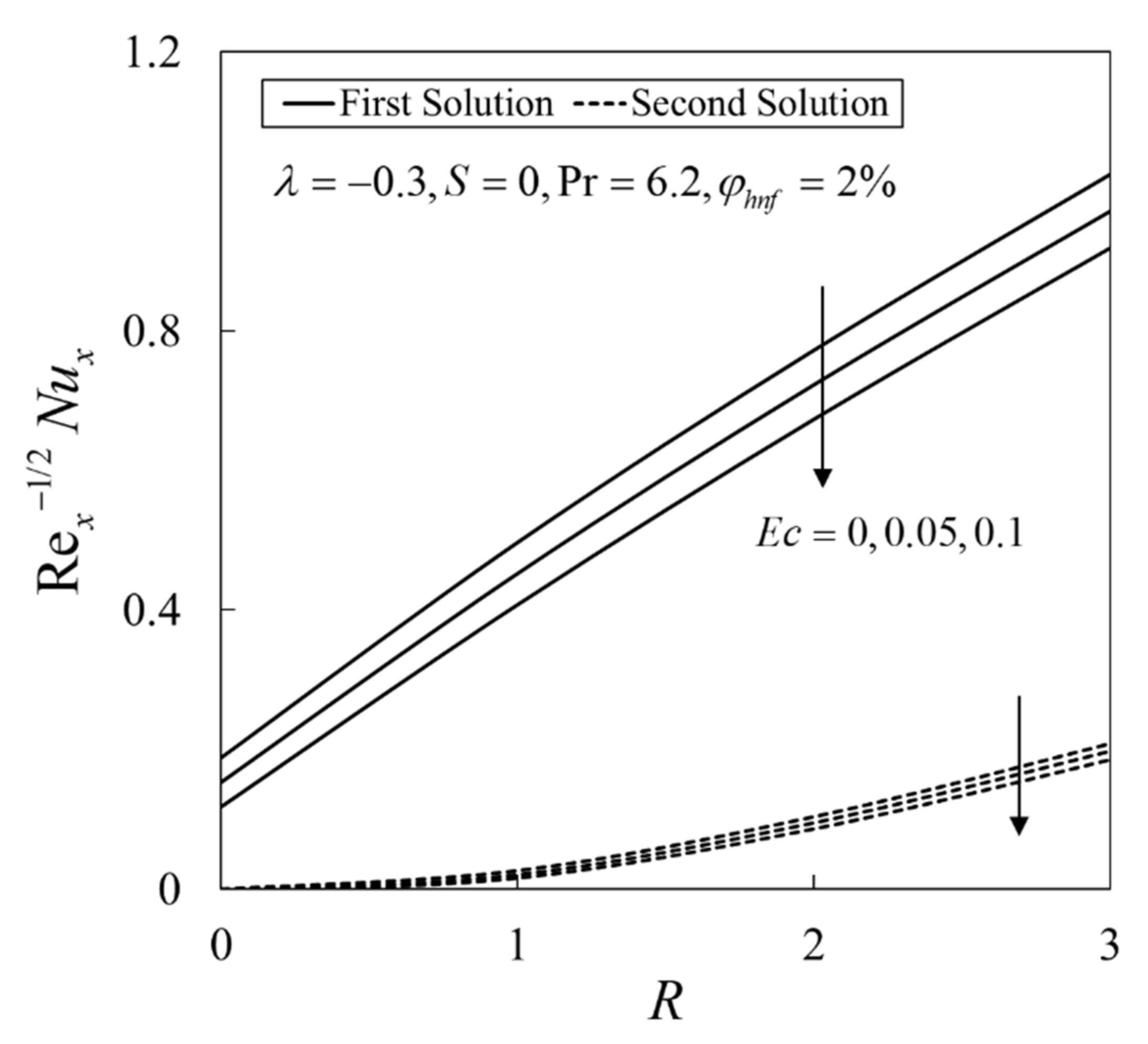
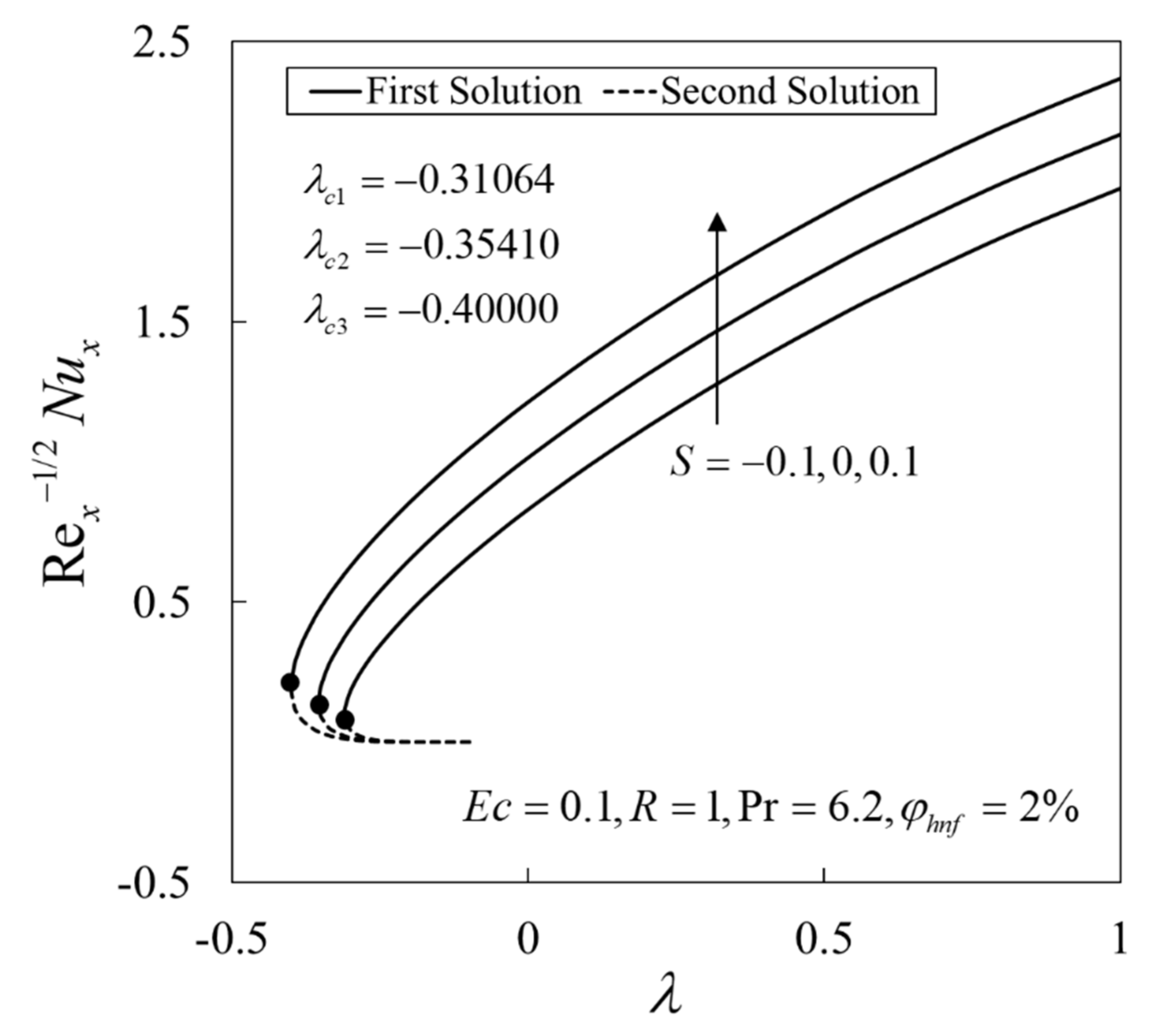
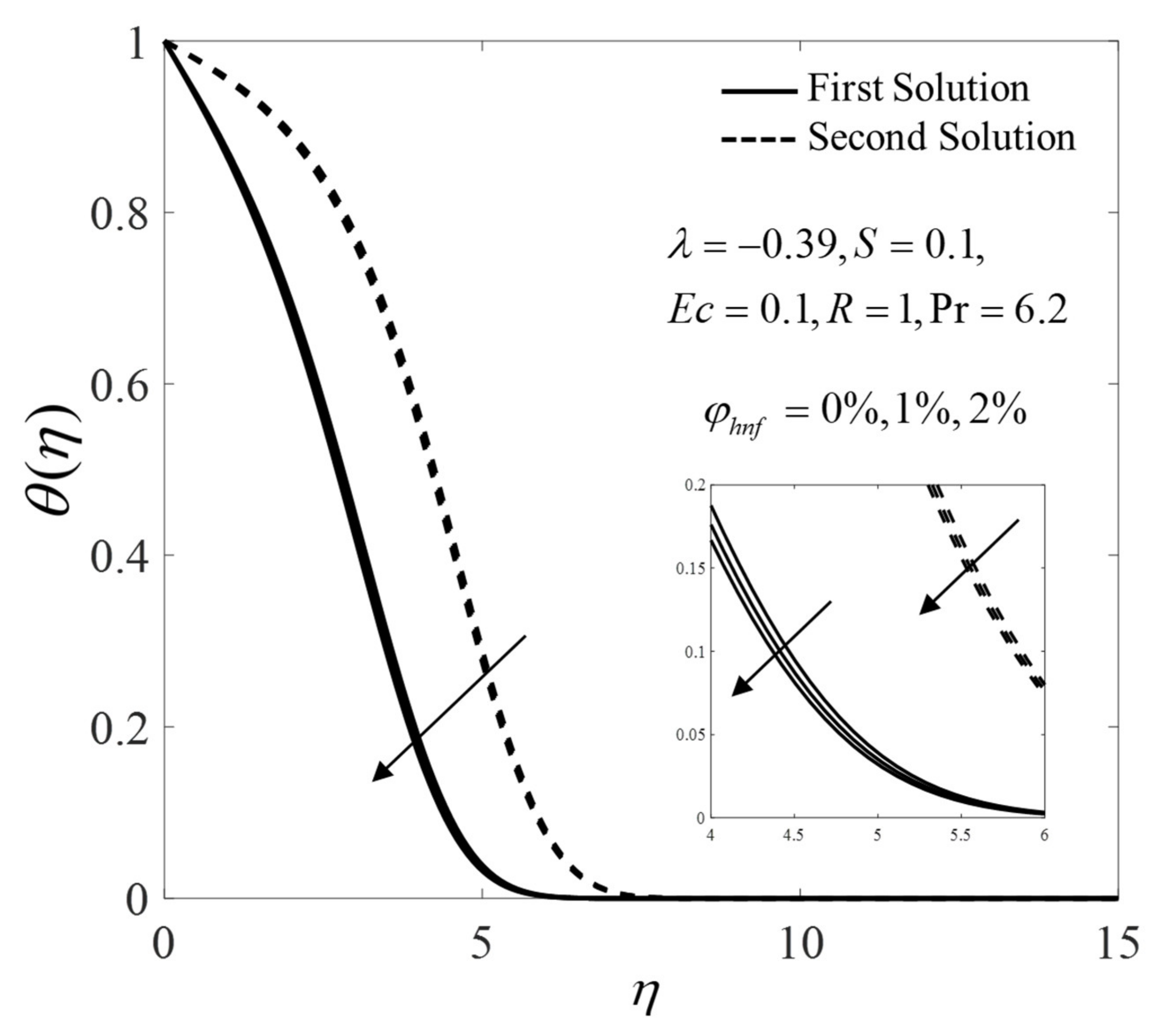
- The enhancement in the heat transfer rate is observed with the increase of and radiation parameter .
- The increase of Eckert number lowers the heat transfer rate.
- The increase of and lead to an increase in while opposite behaviour with the upsurge of .
- The first solution is physically reliable and stable based on the temporal stability analysis.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| skin friction coefficient | |
| specific heat at constant pressure () | |
| heat capacitance of the fluid () | |
| Eckert number | |
| dimensionless stream function | |
| arbitrary functions | |
| fluid thermal conductivity () | |
| coefficient for Rosseland mean absorption () | |
| local Nusselt number | |
| Pr | Prandtl number |
| radiative heat flux () | |
| thermal radiation parameter | |
| mass flux parameter | |
| local Reynolds number | |
| time (s) | |
| T | fluid temperature () |
| ambient temperature () | |
| surface temperature () | |
| velocity component in the x- and y- directions () | |
| mass flux velocity () | |
| constant velocity of the surface () | |
| constant velocity of the free stream () | |
| Cartesian coordinates (m) | |
| Greek symbols | |
| eigenvalue | |
| velocity ratio parameter | |
| dimensionless time variable | |
| similarity variable | |
| dimensionless temperature | |
| dynamic viscosity () | |
| kinematic viscosity of the fluid () | |
| density of the fluid () | |
| Stefan-Boltzmann constant () | |
| stream function | |
| nanoparticle volume fractions for Al2O3 (alumina) | |
| nanoparticle volume fractions for Cu (copper) | |
| hybrid nanoparticles volume fractions | |
| Subscripts | |
| base fluid | |
| hybrid nanofluid | |
| solid component for Al2O3 (alumina) | |
| solid component for Cu (copper) | |
| Superscript | |
| differentiation with respect to | |
References
- Blasius, H. Grenzschichten in Flüssigkeiten Mit Kleiner Reibung. Z. Für Angew. Math. Und Phys. 1908, 56, 1–37. [Google Scholar] [CrossRef]
- Sakiadis, B.C. Boundary-Layer Behaviour on Continuous Solid Surfaces: I. Boundary Layer Equations for Two-Dimensional and Axisymmetric Flow. Am. Inst. Chem. Eng. J. 1961, 7, 26–28. [Google Scholar] [CrossRef]
- Bachok, N.; Ishak, A.; Pop, I. Boundary-Layer Flow of Nanofluids over a Moving Surface in a Flowing Fluid. Int. J. Therm. Sci. 2010, 49, 1663–1668. [Google Scholar] [CrossRef]
- Bataller, R.C. Radiation Effects in the Blasius Flow. Appl. Math. Comput. 2008, 198, 333–338. [Google Scholar] [CrossRef]
- Aziz, A. A Similarity Solution for Laminar Thermal Boundary Layer over a Flat Plate with a Convective Surface Boundary Condition. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 1064–1068. [Google Scholar] [CrossRef]
- Ishak, A.; Yacob, N.A.; Bachok, N. Radiation Effects on the Thermal Boundary Layer Flow over a Moving Plate with Convective Boundary Condition. Meccanica 2011, 46, 795–801. [Google Scholar] [CrossRef]
- Ramesh, G.K.; Gireesha, B.J.; Subba, R.; Gorla, R. Study on Sakiadis and Blasius Flows of Williamson Fluid with Convective Boundary Condition. Nonlinear Eng. 2015, 4, 215–221. [Google Scholar] [CrossRef]
- Ishak, A.; Nazar, R.; Pop, I. Flow and Heat Transfer Characteristics on a Moving Flat Plate in a Parallel Stream with Constant Surface Heat Flux. Heat Mass Transf. 2009, 45, 563–567. [Google Scholar] [CrossRef]
- Ahmad, S.; Rohni, A.M.; Pop, I. Blasius and Sakiadis Problems in Nanofluids. Acta Mech. 2011, 218, 195–204. [Google Scholar] [CrossRef]
- Bachok, N.; Ishak, A.; Pop, I. Flow and Heat Transfer Characteristics on a Moving Plate in a Nanofluid. Int. J. Heat Mass Transf. 2012, 55, 642–648. [Google Scholar] [CrossRef]
- Makinde, O.D. Effects of Viscous Dissipation and Newtonian Heating on Boundary-Layer Flow of Nanofluids over a Flat Plate. Int. J. Numer. Methods Heat Fluid Flow 2013, 23, 1291–1303. [Google Scholar] [CrossRef]
- Afridi, M.I.; Qasim, M. Second Law Analysis of Blasius Flow with Nonlinear Rosseland Thermal Radiation in the Presence of Viscous Dissipation. Propuls. Power Res. 2019, 8, 234–242. [Google Scholar] [CrossRef]
- Choi, S.U.S.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles. In Proceedings of the 1995 ASME International Mechanical Engineering Congress and Exposition, FED 231/MD, San Francisco, CA, USA, 12–17 November 1995; Volume 66, pp. 99–105. [Google Scholar] [CrossRef] [Green Version]
- Takabi, B.; Salehi, S. Augmentation of the Heat Transfer Performance of a Sinusoidal Corrugated Enclosure by Employing Hybrid Nanofluid. Adv. Mech. Eng. 2014, 6, 147059. [Google Scholar] [CrossRef]
- Olatundun, A.T.; Makinde, O.D. Analysis of Blasius Flow of Hybrid Nanofluids over a Convectively Heated Surface. Defect Diffus. Forum 2017, 377, 29–41. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Unsteady Flow and Heat Transfer Past a Stretching/Shrinking Sheet in a Hybrid Nanofluid. Int. J. Heat Mass Transf. 2019, 136, 288–297. [Google Scholar] [CrossRef]
- Sarkar, J.; Ghosh, P.; Adil, A. A Review on Hybrid Nanofluids: Recent Research, Development and Applications. Renew. Sustain. Energy Rev. 2015, 43, 164–177. [Google Scholar] [CrossRef]
- Sidik, N.A.C.; Adamu, I.M.; Jamil, M.M.; Kefayati, G.H.R.; Mamat, R.; Najafi, G. Recent Progress on Hybrid Nanofluids in Heat Transfer Applications: A Comprehensive Review. Int. Commun. Heat Mass Transf. 2016, 78, 68–79. [Google Scholar] [CrossRef]
- Babu, J.A.R.; Kumar, K.K.; Rao, S.S. State-of-Art Review on Hybrid Nanofluids. Renew. Sustain. Energy Rev. 2017, 77, 551–565. [Google Scholar] [CrossRef]
- Huminic, G.; Huminic, A. Entropy Generation of Nanofluid and Hybrid Nanofluid Flow in Thermal Systems: A Review. J. Mol. Liq. 2020, 302, 112533. [Google Scholar] [CrossRef]
- Yang, L.; Ji, W.; Mao, M.; Huang, J. An Updated Review on the Properties, Fabrication and Application of Hybrid-Nanofluids along with Their Environmental Effects. J. Clean. Prod. 2020, 257, 120408. [Google Scholar] [CrossRef]
- Das, S.K.; Choi, S.U.S.; Yu, W.; Pradeep, T. Nanofluids: Science and Technology; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2008; ISBN 9780470074732. [Google Scholar]
- Ali, H.M. Hybrid Nanofluids for Convection Heat Transfer; Academic Press: London, UK, 2020; ISBN 9780128192801. [Google Scholar]
- Abdelsalam, S.I.; Zaher, A.Z. Leveraging Elasticity to Uncover the Role of Rabinowitsch Suspension through a Wavelike Conduit: Consolidated Blood Suspension Application. Mathematics 2021, 9, 2008. [Google Scholar] [CrossRef]
- Rosseland, S. Astrophysik Und Atom-Theoretische Grundlagen; Springer: Berlin, Germany, 1931; ISBN 9783662245330. [Google Scholar]
- Khashi’ie, N.S.; Arifin, N.M.; Rosca, N.C.; Rosca, A.V.; Pop, I. Three-Dimensional Flow of Radiative Hybrid Nanofluid Past a Permeable Stretching/Shrinking Sheet with Homogeneous-Heterogeneous Reaction. Int. J. Numer. Methods Heat Fluid Flow 2021, 32, 568–588. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Squeezed Hybrid Nanofluid Flow over a Permeable Sensor Surface. Mathematics 2020, 8, 898. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Hybrid Nanofluid Flow and Heat Transfer over a Nonlinear Permeable Stretching/Shrinking Surface. Int. J. Numer. Methods Heat Fluid Flow 2019, 29, 3110–3127. [Google Scholar] [CrossRef]
- Agbaje, T.M.; Mondal, S.; Motsa, S.S.; Sibanda, P. A Numerical Study of Unsteady Non-Newtonian Powell-Eyring Nanofluid Flow over a Shrinking Sheet with Heat Generation and Thermal Radiation. Alex. Eng. J. 2017, 56, 81–91. [Google Scholar] [CrossRef] [Green Version]
- Zainal, N.A.; Nazar, R.; Naganthran, K.; Pop, I. MHD Flow and Heat Transfer of Hybrid Nanofluid over a Permeable Moving Surface in the Presence of Thermal Radiation. Int. J. Numer. Methods Heat Fluid Flow 2021, 31, 858–879. [Google Scholar] [CrossRef]
- Muhammad, K.; Hayat, T.; Alsaedi, A. Heat Transfer Analysis in Slip Flow of Hybrid Nanomaterial (Ethylene Glycol + Ag + CuO) via Thermal Radiation and Newtonian Heating. Waves Random Complex Media 2021, 1–21. [Google Scholar] [CrossRef]
- Gangadhar, K.; Bhargavi, D.N.; Kannan, T.; Venkata Subba Rao, M.; Chamkha, A.J. Transverse MHD Flow of Al2O3-Cu/H2O Hybrid Nanofluid with Active Radiation: A Novel Hybrid Model. Math. Methods Appl. Sci. 2020, 1–19. [Google Scholar] [CrossRef]
- Hosseinzadeh, K.; Roghani, S.; Mogharrebi, A.R.; Asadi, A.; Ganji, D.D. Optimization of Hybrid Nanoparticles with Mixture Fluid Flow in an Octagonal Porous Medium by Effect of Radiation and Magnetic Field. J. Therm. Anal. Calorim. 2021, 143, 1413–1424. [Google Scholar] [CrossRef]
- Wakif, A.; Chamkha, A.; Thumma, T.; Animasaun, I.L.; Sehaqui, R. Thermal Radiation and Surface Roughness Effects on the Thermo-Magneto-Hydrodynamic Stability of Alumina–Copper Oxide Hybrid Nanofluids Utilizing the Generalized Buongiorno’s Nanofluid Model. J. Therm. Anal. Calorim. 2021, 143, 1201–1220. [Google Scholar] [CrossRef]
- Gebhart, B. Effects of Viscous Dissipation in Natural Convection. J. Fluid Mech. 1962, 14, 225–235. [Google Scholar] [CrossRef]
- Hayat, T.; Qayyum, S.; Khan, M.I.; Alsaedi, A. Entropy Generation in Magnetohydrodynamic Radiative Flow Due to Rotating Disk in Presence of Viscous Dissipation and Joule Heating. Phys. Fluids 2018, 30, 017101. [Google Scholar] [CrossRef]
- Farooq, U.; Afridi, M.I.; Qasim, M.; Lu, D.C. Transpiration and Viscous Dissipation Effects on Entropy Generation in Hybrid Nanofluid Flow over a Nonlinear Radially Stretching Disk. Entropy 2018, 20, 668. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, N.; Tassaddiq, A.; Alabdan, R.; Adnan; Khan, U.; Noor, S.; Mohyud-Din, S.T.; Khan, I. Applications of Nanofluids for the Thermal Enhancement in Radiative and Dissipative Flow over a Wedge. Appl. Sci. 2019, 9, 1976. [Google Scholar] [CrossRef] [Green Version]
- Ahmad, R.; Khan, W.A. Numerical Study of Heat and Mass Transfer MHD Viscous Flow over a Moving Wedge in the Presence of Viscous Dissipation and Heat Source/Sink with Convective Boundary Condition. Heat Transf.—Asian Res. 2014, 43, 17–38. [Google Scholar] [CrossRef]
- Tamoor, M.; Waqas, M.; Khan, M.I.; Alsaedi, A.; Hayat, T. Magnetohydrodynamic Flow of Casson Fluid over a Stretching Cylinder. Results Phys. 2017, 7, 498–502. [Google Scholar] [CrossRef]
- Zokri, S.M.; Arifin, N.S.; Mohamed, M.K.A.; Kasim, A.R.M.; Mohammad, N.F.; Salleh, M.Z. Mathematical Model of Mixed Convection Boundary Layer Flow over a Horizontal Circular Cylinder Filled in a Jeffrey Fluid with Viscous Dissipation Effect. Sains Malays 2018, 47, 1607–1615. [Google Scholar] [CrossRef]
- Mittal, A.S.; Patel, H.R.; Darji, R.R. Mixed Convection Micropolar Ferrofluid Flow with Viscous Dissipation, Joule Heating and Convective Boundary Conditions. Int. Commun. Heat Mass Transf. 2019, 108, 104320. [Google Scholar] [CrossRef]
- Koriko, O.K.; Adegbie, K.S.; Shah, N.A.; Animasaun, I.L.; Olotu, M.A. Numerical Solutions of the Partial Differential Equations for Investigating the Significance of Partial Slip Due to Lateral Velocity and Viscous Dissipation: The Case of Blood-Gold Carreau Nanofluid and Dusty Fluid. Numer. Methods Part. Differ. Equ. 2021. [Google Scholar] [CrossRef]
- Gajjela, N.; Nandkeolyar, R. Investigating the Magnetohydrodynamic Flow of a Couple Stress Dusty Fluid along a Stretching Sheet in the Presence of Viscous Dissipation and Suction. Heat Transf. 2021, 50, 2709–2724. [Google Scholar] [CrossRef]
- Aly, E.H.; Pop, I. MHD Flow and Heat Transfer near Stagnation Point over a Stretching/Shrinking Surface with Partial Slip and Viscous Dissipation: Hybrid Nanofluid versus Nanofluid. Powder Technol. 2020, 367, 192–205. [Google Scholar] [CrossRef]
- Lund, L.A.; Omar, Z.; Khan, I.; Raza, J.; Sherif, E.S.M.; Seikh, A.H. Magnetohydrodynamic (MHD) Flow of Micropolar Fluid with Effects of Viscous Dissipation and Joule Heating over an Exponential Shrinking Sheet: Triple Solutions and Stability Analysis. Symmetry 2020, 12, 142. [Google Scholar] [CrossRef] [Green Version]
- Zainal, N.A.; Nazar, R.; Naganthran, K.; Pop, I. Viscous Dissipation and MHD Hybrid Nanofluid Flow towards an Exponentially Stretching/Shrinking Surface. Neural Comput. Appl. 2021, 33, 11285–11295. [Google Scholar] [CrossRef]
- Khashi’ie, N.S.; Arifin, N.M.; Pop, I.; Nazar, R.; Hafidzuddin, E.H.; Wahi, N. Flow and Heat Transfer Past a Permeable Power-Law Deformable Plate with Orthogonal Shear in a Hybrid Nanofluid. Alex. Eng. J. 2020, 59, 1869–1879. [Google Scholar] [CrossRef]
- Cortell, R. Heat and Fluid Flow Due to Non-Linearly Stretching Surfaces. Appl. Math. Comput. 2011, 217, 7564–7572. [Google Scholar] [CrossRef] [Green Version]
- Oztop, H.F.; Abu-Nada, E. Numerical Study of Natural Convection in Partially Heated Rectangular Enclosures Filled with Nanofluids. Int. J. Heat Fluid Flow 2008, 29, 1326–1336. [Google Scholar] [CrossRef]
- Merkin, J.H. On Dual Solutions Occurring in Mixed Convection in a Porous Medium. J. Eng. Math. 1986, 20, 171–179. [Google Scholar] [CrossRef]
- Weidman, P.D.; Kubitschek, D.G.; Davis, A.M.J. The Effect of Transpiration on Self-Similar Boundary Layer Flow over Moving Surfaces. Int. J. Eng. Sci. 2006, 44, 730–737. [Google Scholar] [CrossRef]
- Harris, S.D.; Ingham, D.B.; Pop, I. Mixed Convection Boundary-Layer Flow near the Stagnation Point on a Vertical Surface in a Porous Medium: Brinkman Model with Slip. Transp. Porous Media 2009, 77, 267–285. [Google Scholar] [CrossRef]
- Shampine, L.F.; Gladwell, I.; Thompson, S. Solving ODEs with MATLAB; Cambridge University Press: Cambridge, UK, 2003; ISBN 9780521824040. [Google Scholar]



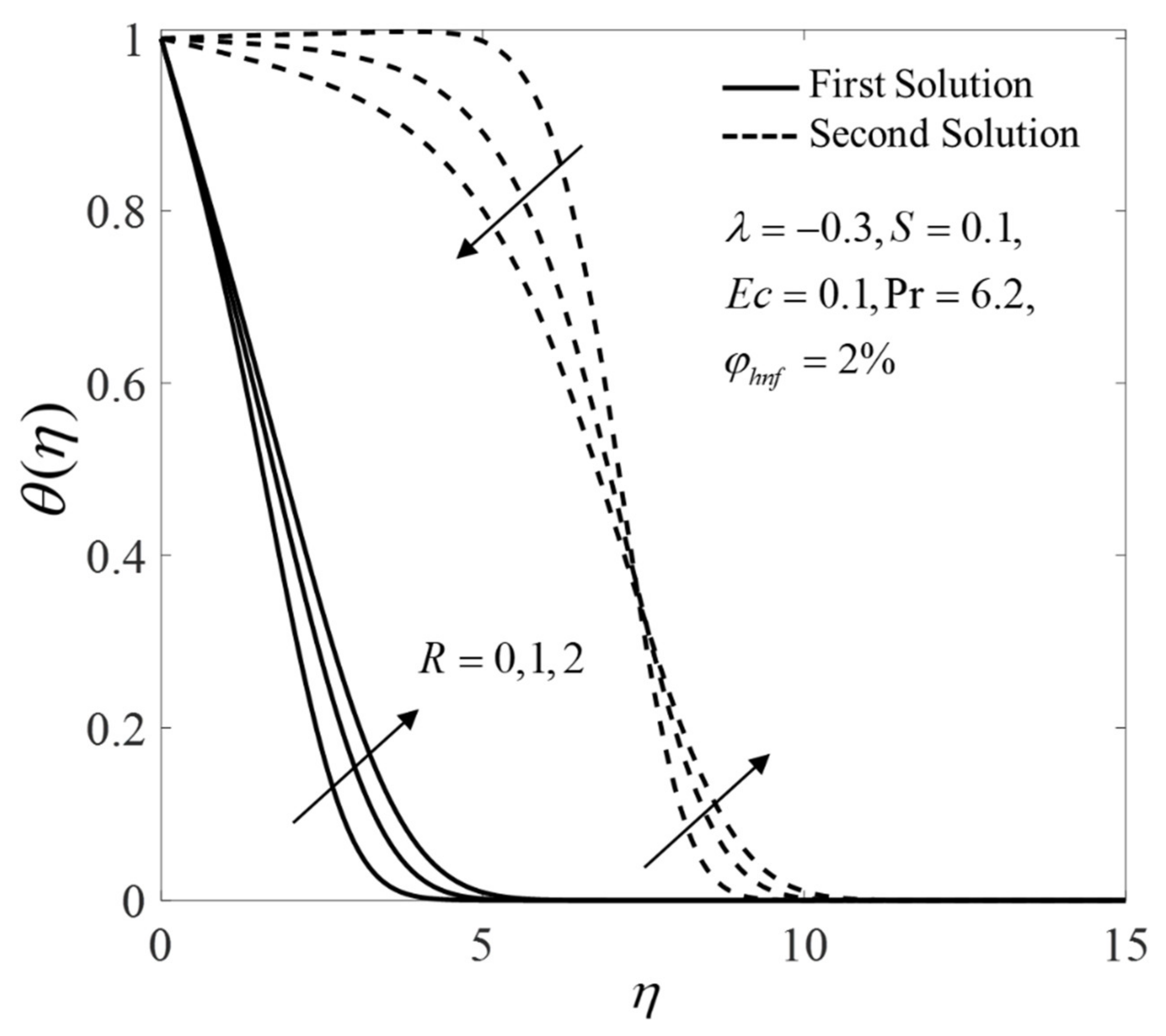
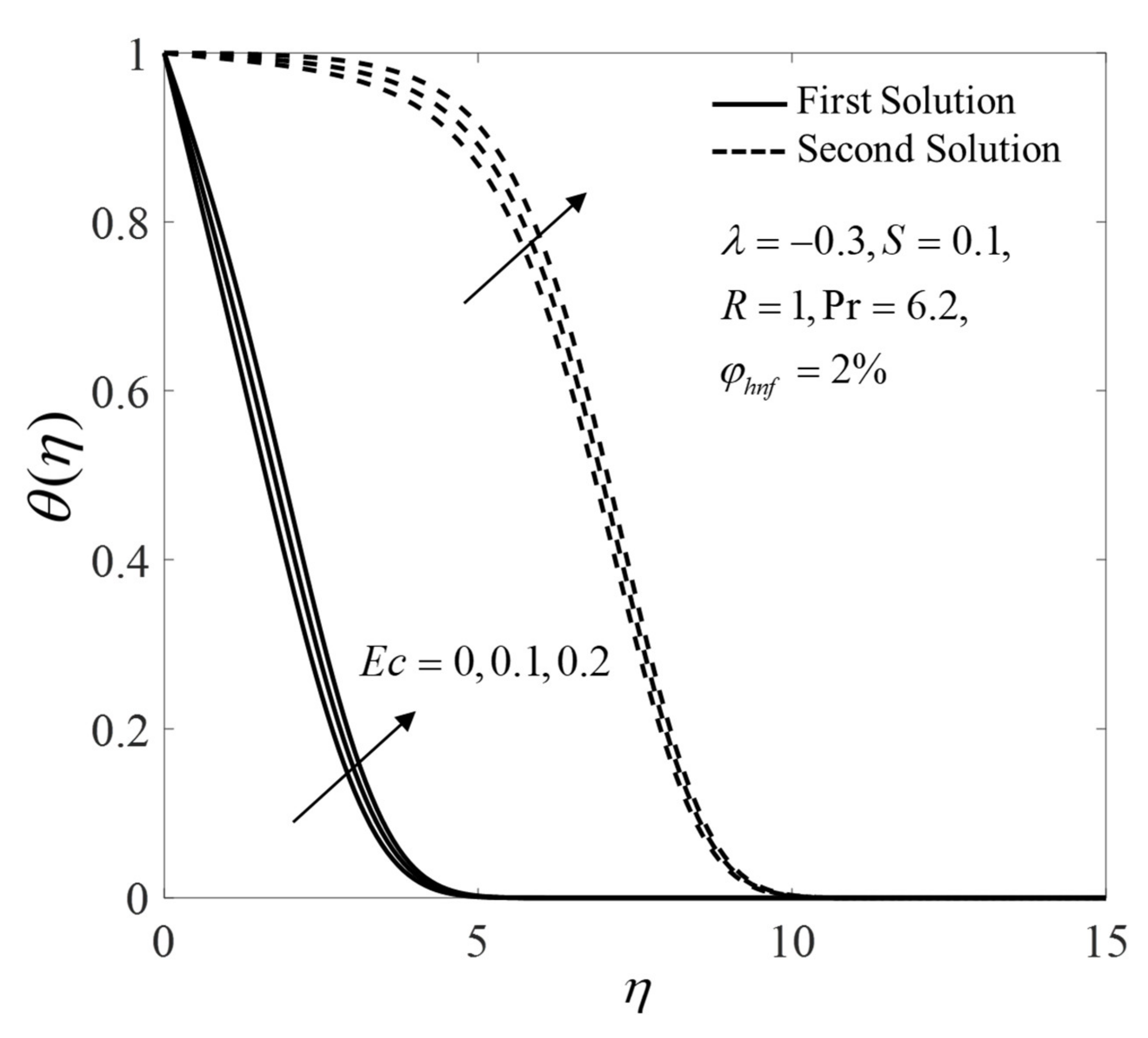

| Properties | Base Fluid | Nanoparticles | |
|---|---|---|---|
| Water | Cu | Al2O3 | |
| 997.1 | 8933 | 3970 | |
| 4179 | 385 | 765 | |
| 0.613 | 400 | 40 | |
| Prandtl number, | 6.2 | ||
| Thermophysical Properties | Correlations |
|---|---|
| Thermal conductivity | |
| Heat capacity | |
| Density | |
| Dynamic viscosity |
| Bataller [4] | Present Results | |
|---|---|---|
| 0.7 | 0.29268 | 0.29268 |
| 5 | 0.57669 | 0.57669 |
| 6.2 | 0.62007 | |
| 10 | 0.72814 | 0.72814 |
| 50 | 1.24729 | 1.24729 |
| 100 | 1.57183 | 1.57183 |
| Ahmad et al. [9] | Present Results | ||
|---|---|---|---|
| 0 | 0.3321 | 0.33206 | 0.62007 |
| 0.002 | 0.3339 | 0.33388 | 0.62241 |
| 0.004 | 0.3357 | 0.33571 | 0.62475 |
| 0.008 | 0.3394 | 0.33938 | 0.62943 |
| 0.01 | 0.3412 | 0.34123 | 0.63177 |
| First Solution | Second Solution | ||||||
|---|---|---|---|---|---|---|---|
| −0.35 | 0 | 0 | 0 | 0.19675 | 0.05461 | 0.13639 | 0.01126 |
| −0.3 | 0.27241 | 0.18844 | 0.06483 | 0.00031 | |||
| −0.25 | 0.30670 | 0.28935 | 0.03467 | 0.00001 | |||
| −0.2 | 0.32856 | 0.37636 | 0.01695 | 0.00000 | |||
| −0.1 | 0.35216 | 0.52430 | 0.00148 | 0.00000 | |||
| −0.3 | 0.5 | 0.27241 | 0.34743 | 0.06483 | 0.00660 | ||
| 1 | 0.27241 | 0.49699 | 0.06483 | 0.02676 | |||
| 1.5 | 0.27241 | 0.63822 | 0.06483 | 0.06050 | |||
| 2 | 0.27241 | 0.77255 | 0.06483 | 0.10416 | |||
| 3 | 0.27241 | 1.02468 | 0.06483 | 0.20909 | |||
| 1 | 0.01 | 0.27241 | 0.48806 | 0.06483 | 0.02565 | ||
| 0.03 | 0.27241 | 0.47018 | 0.06483 | 0.02342 | |||
| 0.05 | 0.27241 | 0.45231 | 0.06483 | 0.02119 | |||
| 0.1 | 0.27241 | 0.40762 | 0.06483 | 0.01561 | |||
| 0.2 | 0.27241 | 0.31824 | 0.06483 | 0.00445 | |||
| 0.1 | −0.1 | 0.18325 | 0.18495 | 0.09451 | 0.04133 | ||
| 0.1 | 0.34471 | 0.62723 | 0.05293 | 0.00862 | |||
| 0.2 | 0.41264 | 0.85529 | 0.04630 | 0.00545 | |||
| 0.3 | 0.47877 | 1.09161 | 0.04235 | 0.00370 | |||
| 0.5 | 0.60909 | 1.58414 | 0.03902 | 0.00174 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khashi’ie, N.S.; Waini, I.; Ishak, A.; Pop, I. Blasius Flow over a Permeable Moving Flat Plate Containing Cu-Al2O3 Hybrid Nanoparticles with Viscous Dissipation and Radiative Heat Transfer. Mathematics 2022, 10, 1281. https://doi.org/10.3390/math10081281
Khashi’ie NS, Waini I, Ishak A, Pop I. Blasius Flow over a Permeable Moving Flat Plate Containing Cu-Al2O3 Hybrid Nanoparticles with Viscous Dissipation and Radiative Heat Transfer. Mathematics. 2022; 10(8):1281. https://doi.org/10.3390/math10081281
Chicago/Turabian StyleKhashi’ie, Najiyah Safwa, Iskandar Waini, Anuar Ishak, and Ioan Pop. 2022. "Blasius Flow over a Permeable Moving Flat Plate Containing Cu-Al2O3 Hybrid Nanoparticles with Viscous Dissipation and Radiative Heat Transfer" Mathematics 10, no. 8: 1281. https://doi.org/10.3390/math10081281
APA StyleKhashi’ie, N. S., Waini, I., Ishak, A., & Pop, I. (2022). Blasius Flow over a Permeable Moving Flat Plate Containing Cu-Al2O3 Hybrid Nanoparticles with Viscous Dissipation and Radiative Heat Transfer. Mathematics, 10(8), 1281. https://doi.org/10.3390/math10081281









