Complex Modified Projective Difference Function Synchronization of Coupled Complex Chaotic Systems for Secure Communication in WSNs
Abstract
:1. Introduction
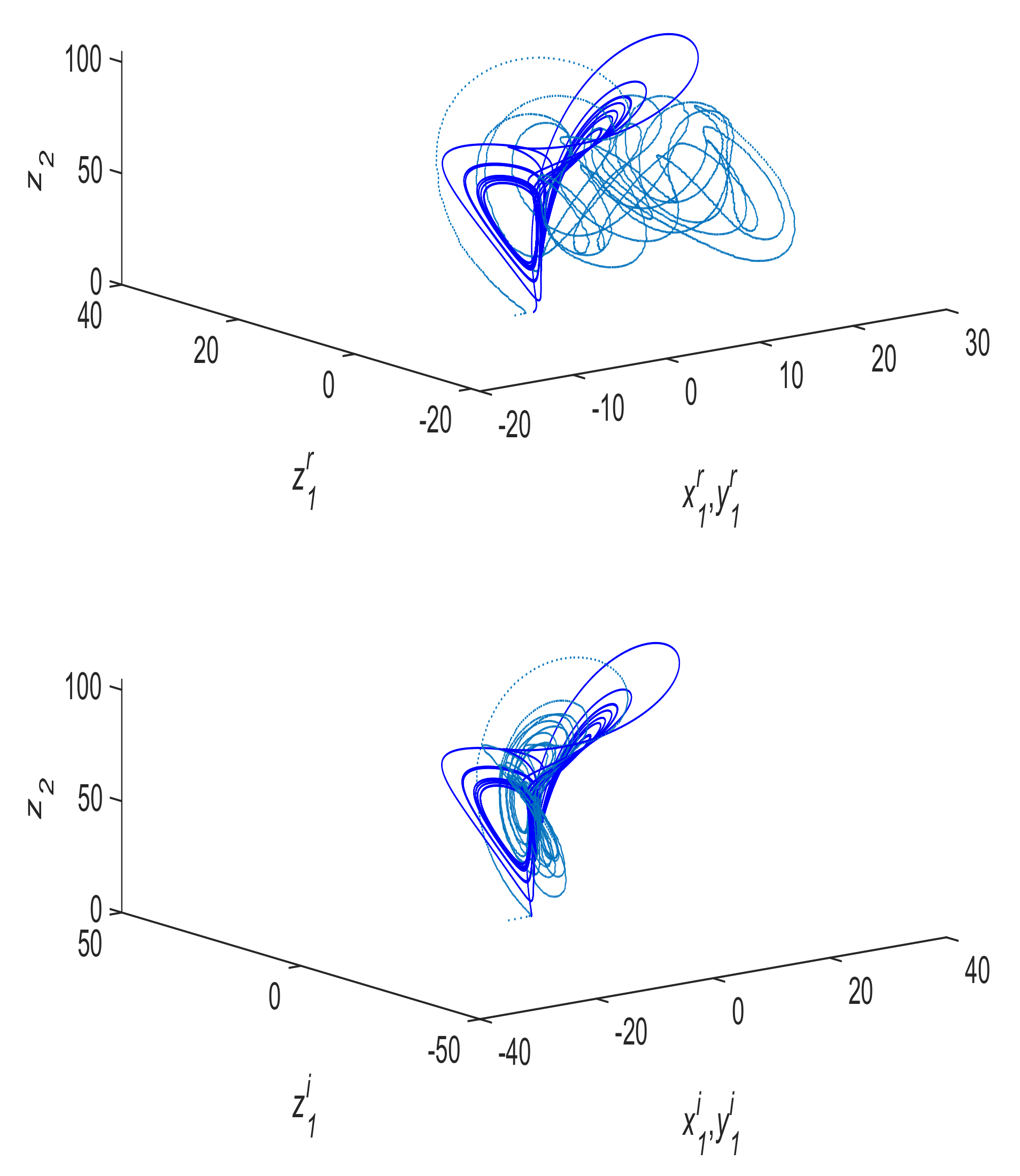
2. Complex Modified Projective Difference Function Synchronization (CMPDFS)
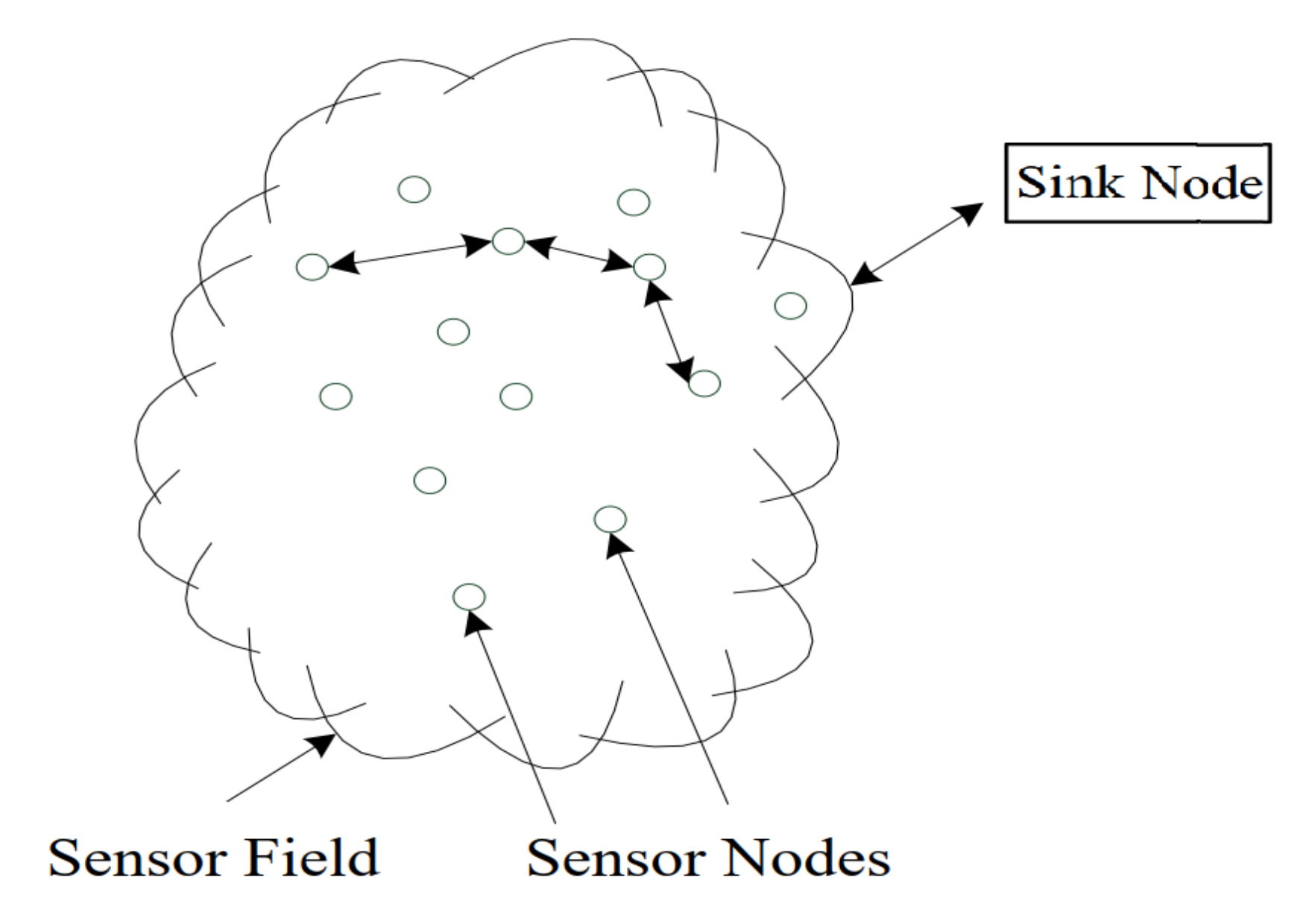
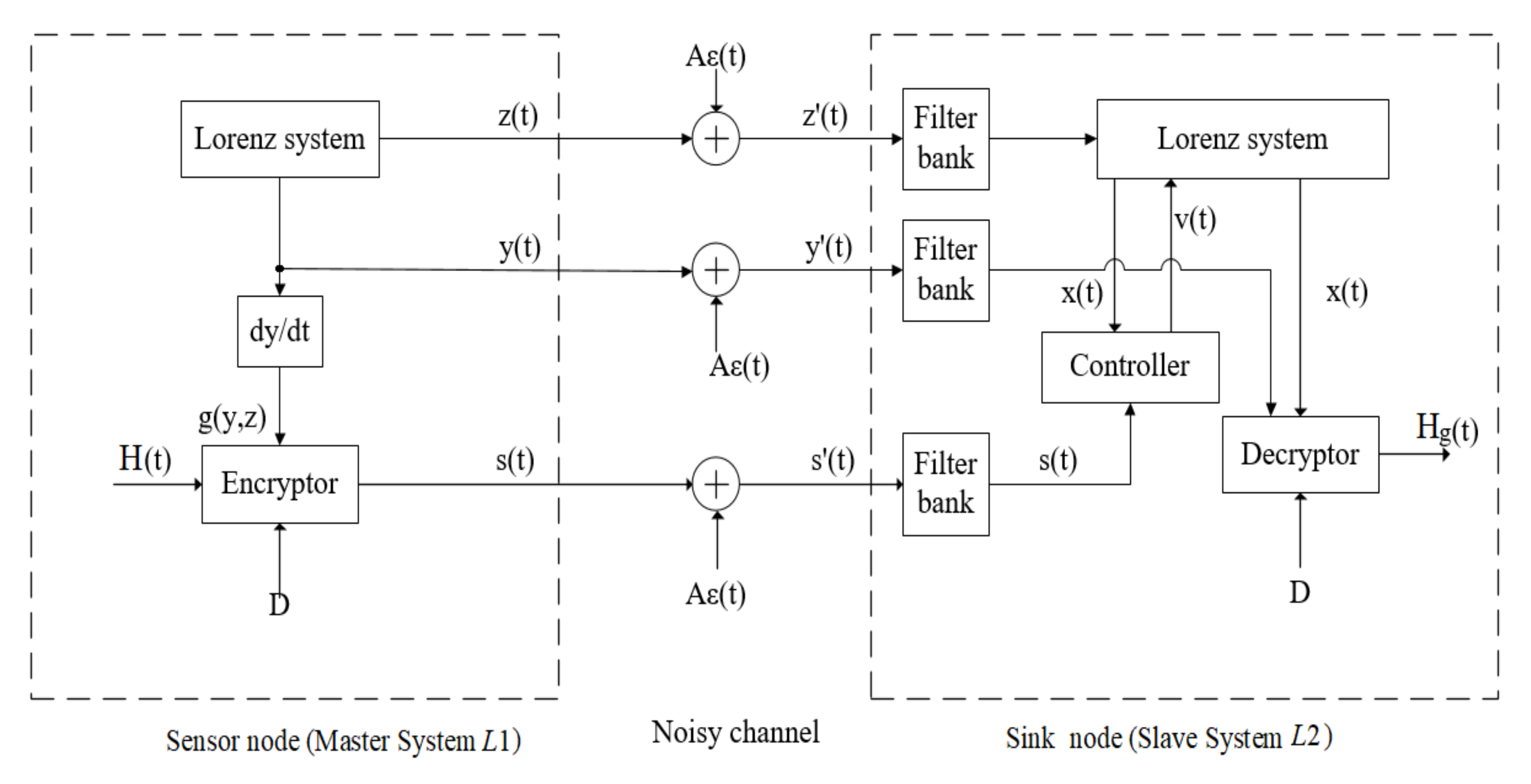
3. CMPDFS Communication Scheme for WSNs
3.1. CMPDFS Controller
3.2. The Communication Scheme for WSNs
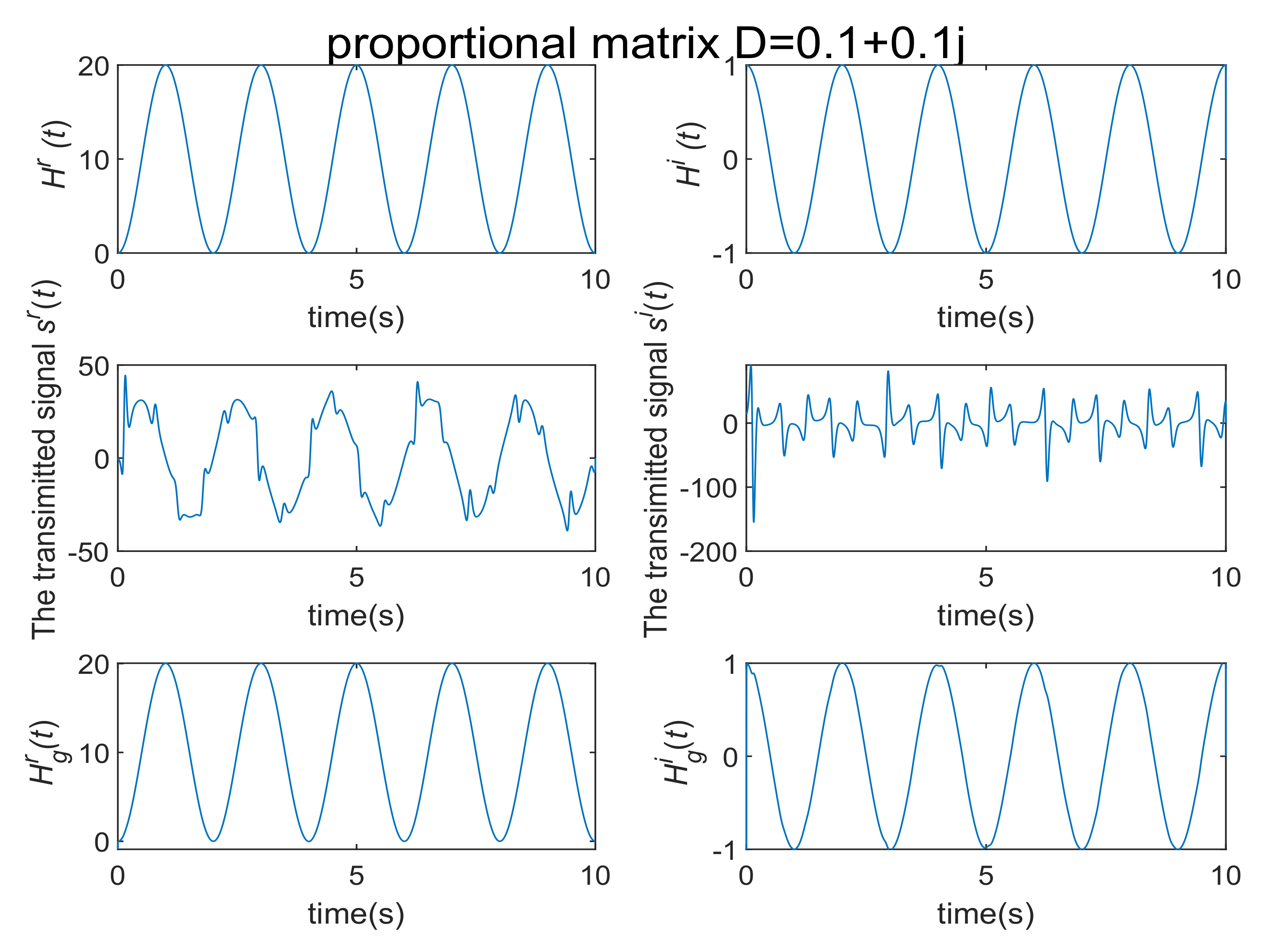
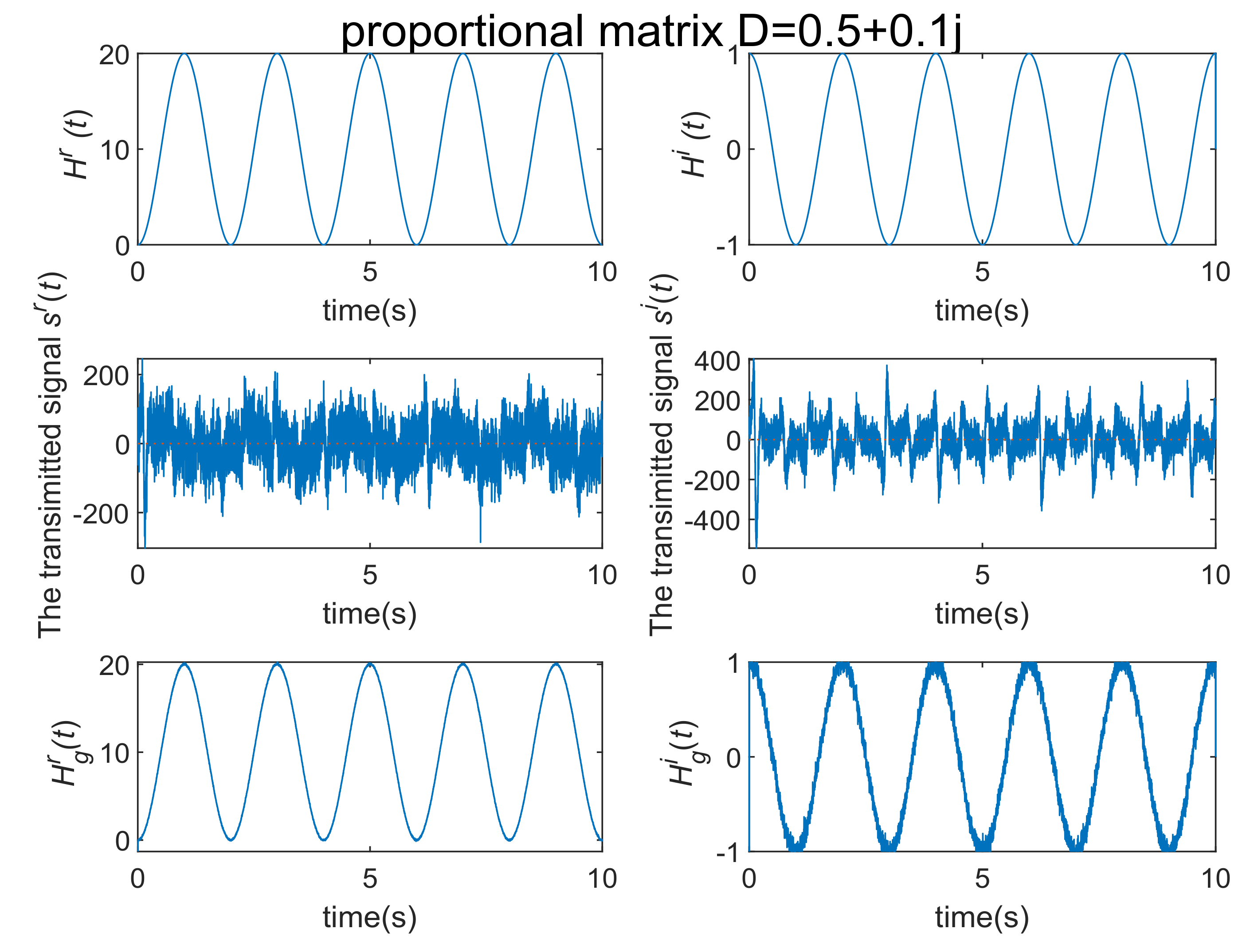
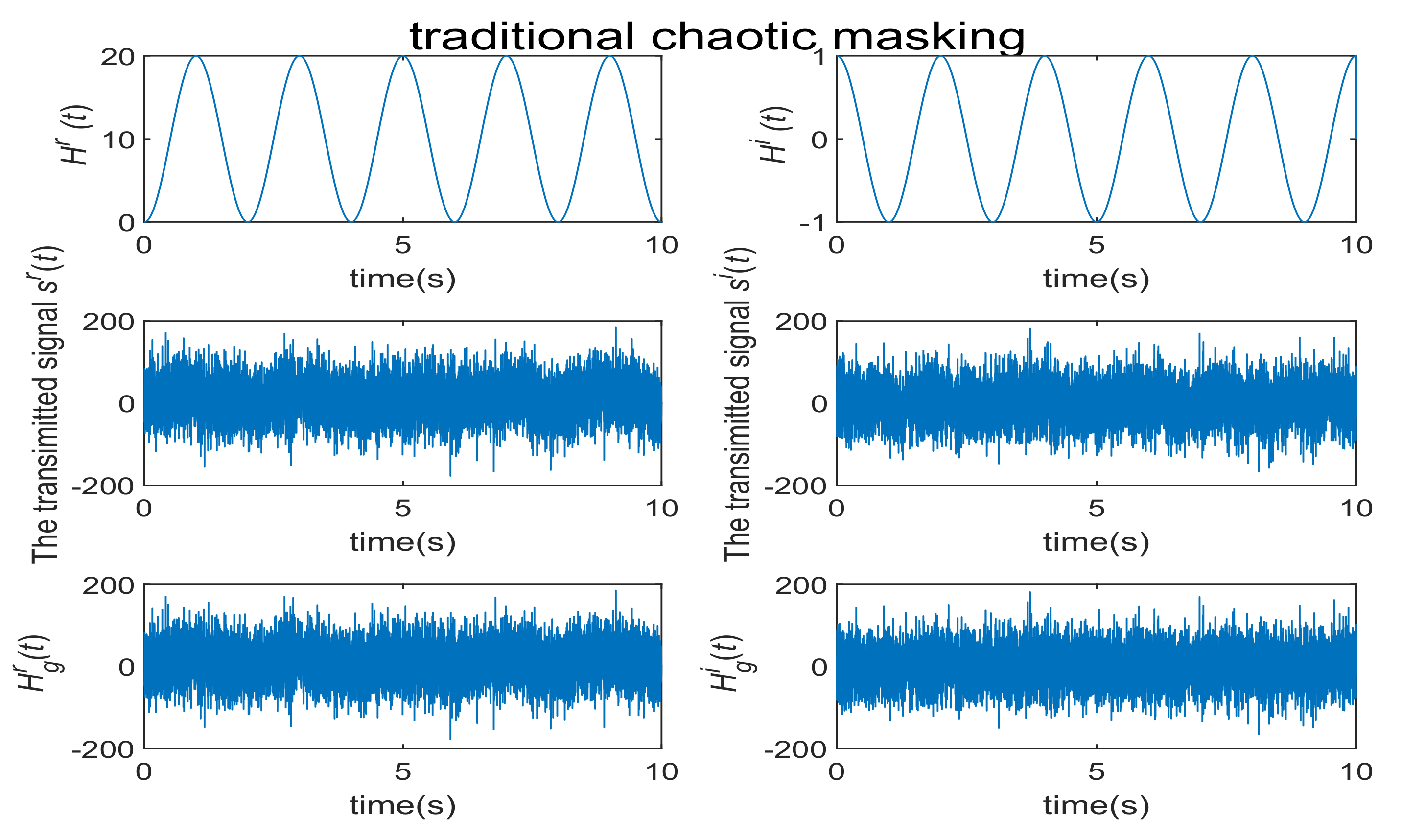
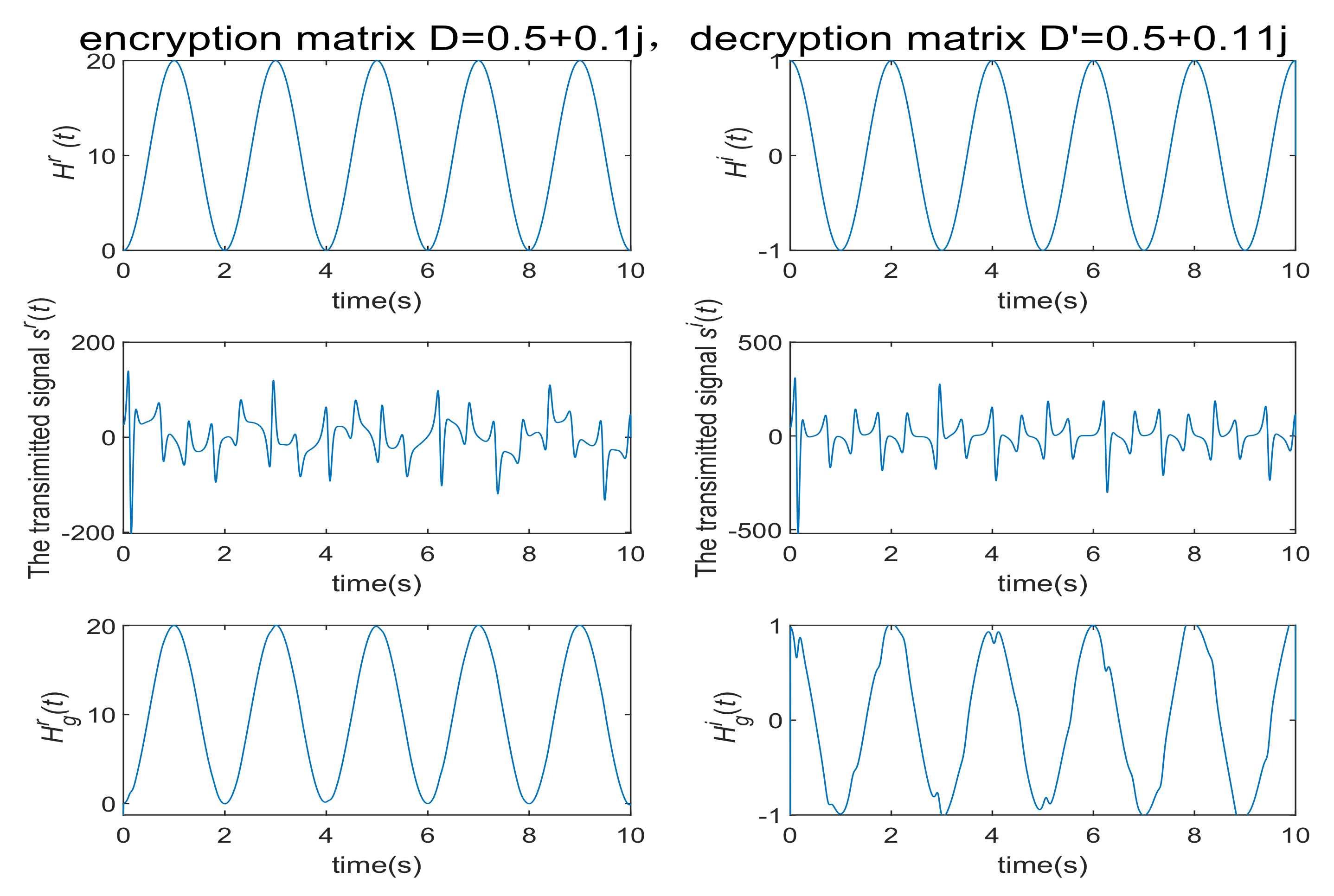
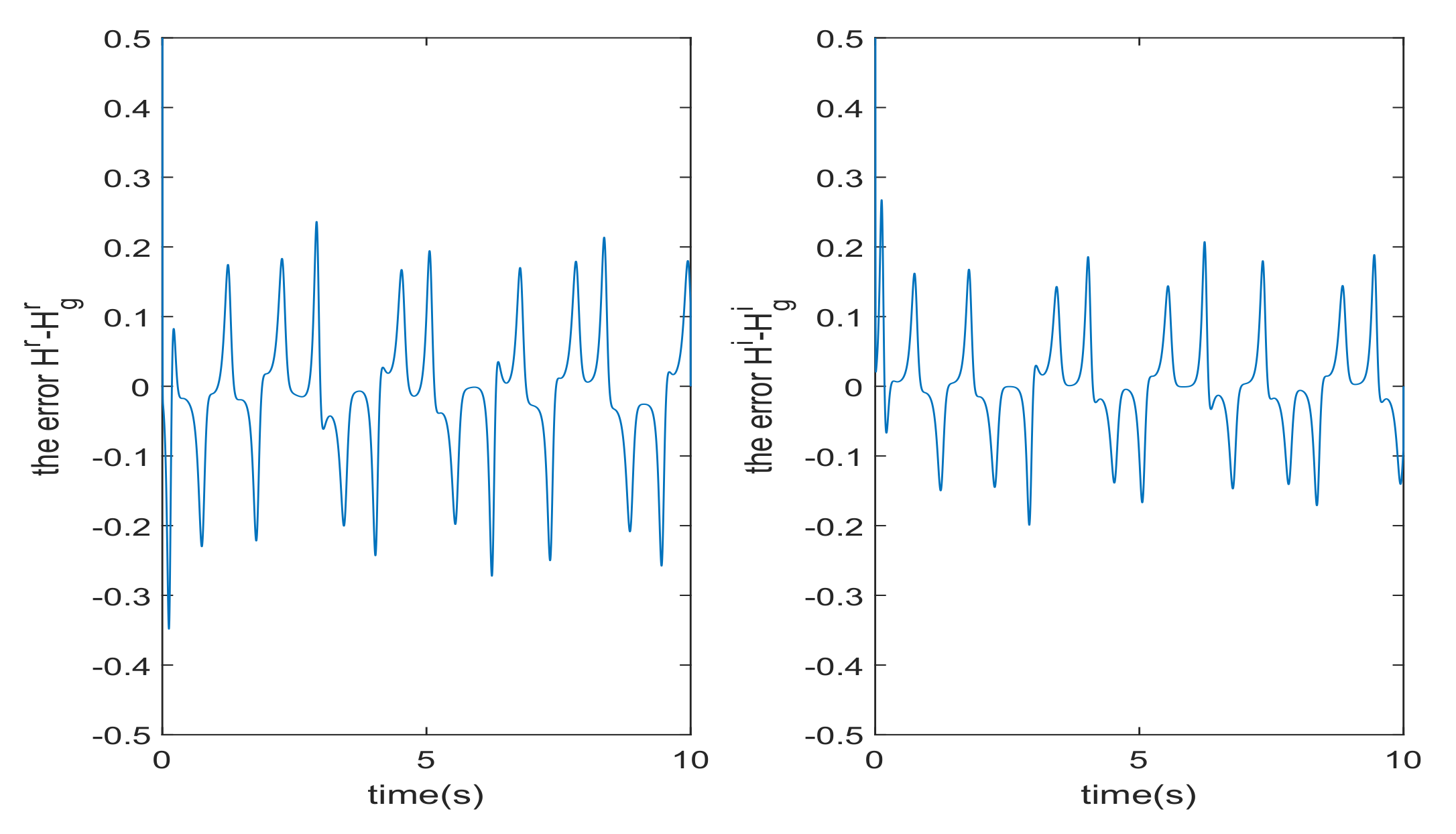
4. Numerical Simulations and Discussions
4.1. Communication Process without Noise
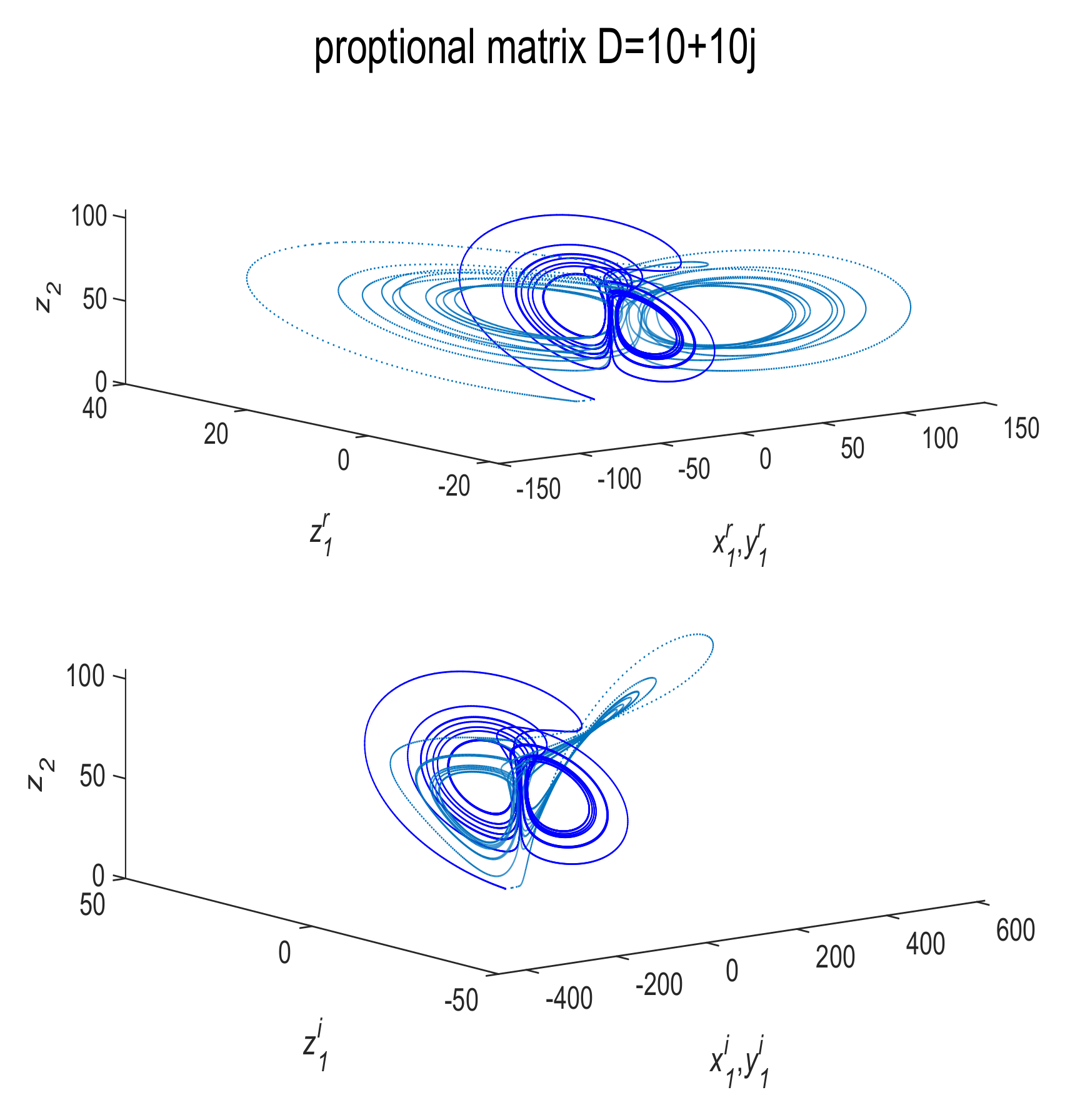
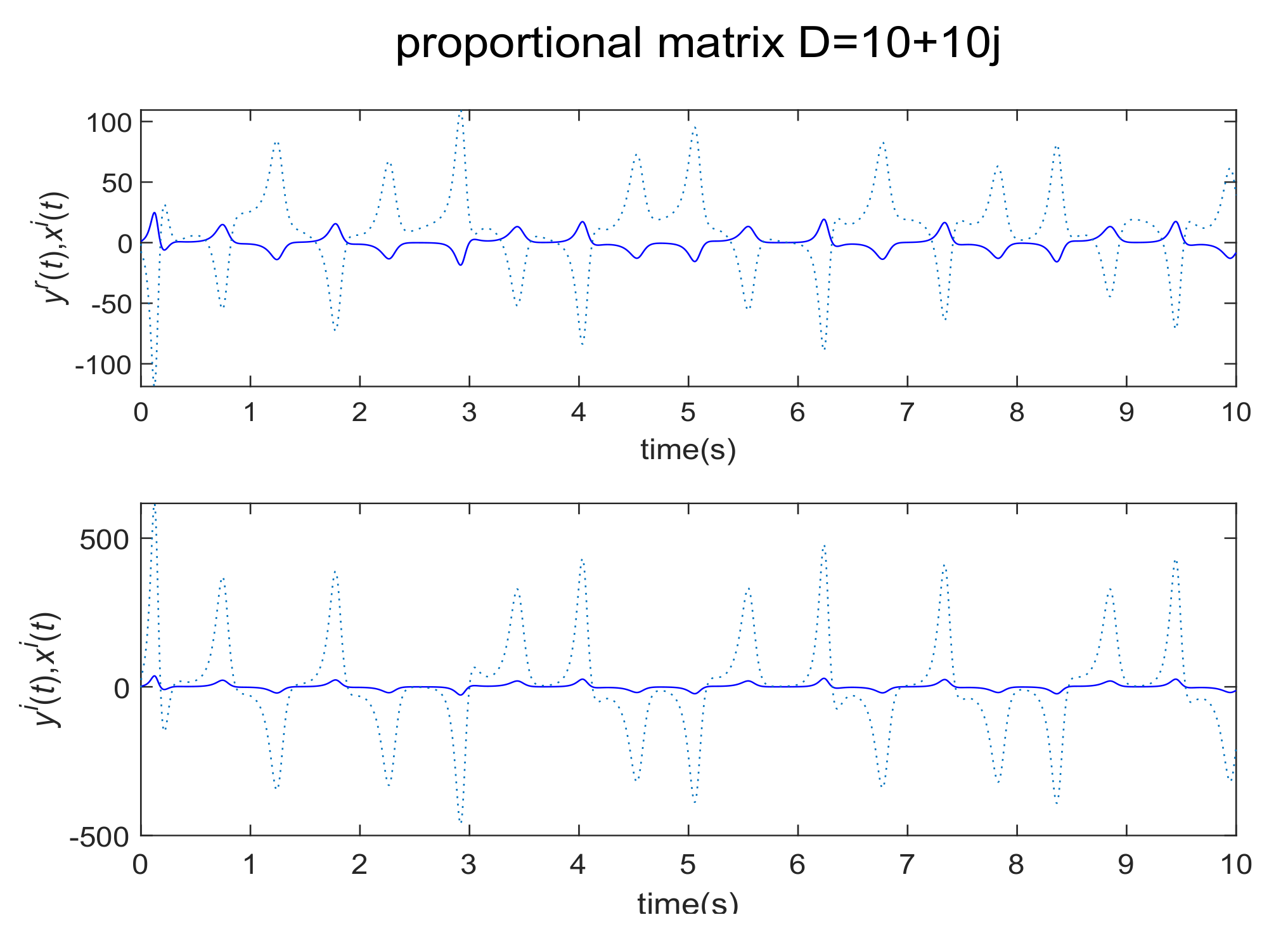
4.2. Communication Process with Noise
5. Security Analysis
5.1. Key Space Analysis
5.2. Key Sensitivity Analysis
5.3. Speed Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fowler, A.C.; Gibbon, J.D. The complex Lorenz equations. Phys. D Nonlinear Phenom. 1982, 4, 139–163. [Google Scholar] [CrossRef]
- Gibbon, J.D.; McGuinness, M.J. The real and complex Lorenz equations in rotating fluids and laser. Phys. D Nonlinear Phenom. 1982, 5, 108–122. [Google Scholar] [CrossRef]
- Fowler, A.C.; Gibbon, J.D.; McGuinnes, M.J. The real and complex Lorenz equations and their relevance to physical systems. Phys. 7D 1983, 7, 126–134. [Google Scholar] [CrossRef]
- Mahmoud, G.M.; Bountis, T.; Mahmoud, E.E. Active control and global synchronization for complex Chen and Lu¨ systems. Int. J. Bifurc. Chaos 2007, 17, 4295–4308. [Google Scholar] [CrossRef]
- Mahmoud, G.M.; Mahmoud, E.E.; Arafa, A.A. On projective synchronization of hyperchaotic complex nonlinear systems based on passive theory for secure communications. Phys. Scr. 2013, 87, 055002. [Google Scholar] [CrossRef]
- Cui, S.; Zhang, J. Chaotic Secure Communication Based on Single Feedback Phase Modulation and Channel Transmission. IEEE Photonics J. 2019, 11, 1–8. [Google Scholar] [CrossRef]
- Zhang, F.; Li, Z.; Sun, K.; Zhang, X.; Ji, P. A new hyperchaotic complex system with parametric attractors. Fractals 2021, 29, 2150230. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, F.; Zhang, X.; Zhao, Y. A new hyperchaotic complex system and its synchronization realization. Phys. Scr. 2021, 96, 045208. [Google Scholar] [CrossRef]
- Zhang, F.F.; Gao, R.; Liu, J. Acoustic wireless communication based on parameter modulation and complex Lorenz chaotic systems with complex parameters and parametric attractors. Chin. Phys. 2021, 30, 080503. [Google Scholar] [CrossRef]
- Aliabadi, F.; Majidi, M.H.; Khorashadizadeh, S. Chaos synchronization using adaptive quantum neural networks and its application in secure communication and cryptography. Neural Comput. Appl. 2022, 34, 6521–6533. [Google Scholar] [CrossRef]
- Alshammari, A.S. Synchronization of Two Chaotic Stream Ciphers in Secure CDMA Communication Systems. Eng. Technol. Appl. Sci. Res. 2020, 10, 5947–5952. [Google Scholar] [CrossRef]
- Bai, C.; Ren, H.-P.; Kolumbán, G. Double-Sub-Stream M-ary Differential Chaos Shift Keying Wireless Communication System Using Chaotic Shape-Forming Filter. IEEE Trans. Circuits Syst. I 2020, 67, 3574–3587. [Google Scholar] [CrossRef]
- Zheng, J.; Hu, H.P. A highly secure stream cipher based on analog-digital hybrid chaotic system. Inf. Sci. 2022, 587, 226–246. [Google Scholar] [CrossRef]
- Mahmoud, G.M.; Mahmoud, E.E. Phase and antiphase synchronization of two identical hyperchaotic complex nonlinear systems. Nonlinear Dyn. 2010, 61, 141–152. [Google Scholar] [CrossRef]
- Mahmoud, G.M.; Mahmoud, E.E. Complete synchronization of chaotic complex nonlinear systems with uncertain parameters. Nonlinear Dyn. 2010, 62, 875–882. [Google Scholar] [CrossRef]
- Liu, S.T.; Liu, P. Adaptive anti-synchronization of chaotic complex nonlinear systems with unknown parameters. Nonlinear Anal. RWA 2011, 12, 3046–3055. [Google Scholar] [CrossRef]
- Liu, P.; Liu, S.T. Anti-synchronization between different chaotic complex systems. Phys. Scr. 2011, 83, 065006. [Google Scholar] [CrossRef]
- Mahmoud, G.M.; Mahmoud, E.E. Lag synchronization of hyperchaotic complex nonlinear systems. Nonlinear Dyn. 2012, 67, 1613–1622. [Google Scholar] [CrossRef]
- Mahmoud, E.E. Adaptive anti-lag synchronization of two identical or non-identical hyperchaotic complex nonlinear systems with uncertain parameters. J. Frankl. Inst. 2012, 349, 1247–1266. [Google Scholar] [CrossRef]
- Liu, P.; Liu, S.T.; Li, X. Adaptive modified function projective synchronization of general uncertain chaotic complex systems. Phys. Scr. 2012, 85, 3743–3748. [Google Scholar] [CrossRef]
- Liu, P.; Liu, S.T. Robust adaptive full state hybrid synchronization of chaotic complex systems with unknown parameters and external disturbances. Nonlinear Dyn. 2012, 70, 585–599. [Google Scholar] [CrossRef]
- Mahmoud, E.E. Modified projective phase synchronization of chaotic complex nonlinear systems. Math. Comput. Simul. 2013, 89, 69–85. [Google Scholar] [CrossRef]
- Luo, C.; Wang, X.Y. Hybrid modified function projective synchronization of two different dimensional complex nonlinear systems with parameters identification. J. Frankl. Inst. 2013, 350, 2646–2663. [Google Scholar] [CrossRef]
- Liu, J.; Liu, S.T.; Yuan, C.H. Adaptive complex modified projective synchronization of complex chaotic (hyperchaotic) systems with uncertain complex parameters. Nonlinear Dyn. 2015, 79, 1035–1047. [Google Scholar] [CrossRef]
- Zhang, F.F.; Liu, S.T. Self time-delay synchronization of time-delay coupled complex chaotic system and its applications to communication. Int. J. Mod. Phys. C 2014, 25, 1350102. [Google Scholar] [CrossRef]
- Zhang, F.F. Complete synchronization of coupled multiple-time-delay complex chaotic system with applications to secure communication. Acta Phys. Pol. 2015, 46, 1473–1486. [Google Scholar] [CrossRef]
- Liu, J.; Liu, S.T.; Sprott, J.C. Adaptive complex modified hybrid function projective synchronization of different dimensional complex chaos with uncertain complex parameters. Nonlinear Dyn. 2016, 83, 1109–1121. [Google Scholar] [CrossRef]
- Liu, J.; Liu, S.T. Complex modified function projective synchronization of complex chaotic systems with known and unknown complex parameters. Appl. Math. Model. 2017, 48, 440–450. [Google Scholar] [CrossRef]
- Mahmoud, E.E.; Abo-Dahab, S.M. Dynamical properties and complex anti synchronization with applications to secure communications for a novel chaotic complex nonlinear model. Chaos Soliton Fractals 2018, 106, 273–284. [Google Scholar] [CrossRef]
- Liu, J.; Wang, Z.; Shu, M.; Zhang, F.; Leng, S.; Sun, X. Secure communication of fractional complex chaotic systems based on fractional difference function synchronization. Complexity 2019, 2019, 7242791. [Google Scholar] [CrossRef] [Green Version]
- Guo, J.; Ma, C.; Wang, X.; Zhang, F.; van Wyk, M.A.; Kou, L. A new synchronization method for time-delay fractional complex chaotic system and its application. Mathematics 2021, 9, 3305. [Google Scholar] [CrossRef]
- Jayawickrama, C.; Kumar, S.; Chakrabartty, S.; Song, H. A novel chaotic modulation approach of packaged antenna for secured wireless medical sensor network in E-healthcare applications. Microw. Opt. Technol. Lett. 2020, 62, 933–942. [Google Scholar] [CrossRef]
- Niu, Z.; Zheng, M.; Zhang, Y.; Wang, T. A new asymmetrical encryption algorithm based on semitensor compressed sensing in WBANs. IEEE Internet Things 2020, 7, 734–750. [Google Scholar] [CrossRef]
- Olga, I.M.; Alexey, A.K.; Alexander, E.H. Generalized synchronization of chaos for secure communication: Remarkable stability to noise. Phys. Lett. A 2010, 374, 2925–2931. [Google Scholar]
- Narendra, K.P. Design and analysis of a novel digital image encryption scheme. Int. J. Netw. 2012, 4, 95–108. [Google Scholar]
- Jie, Z.; Nan, Z.; Hua, G. Fast color image encryption scheme based on 3D orthogonal Latin squares and matching matrix. Opt. Laser Technol. 2020, 131, 106437. [Google Scholar]


| The Symbol | Meanings |
|---|---|
| n | The dimension of system |
| q | The dimension of uncoupled variables |
| The drive system | |
| The response system | |
| , | The complex state vector of the drive system |
| The complex state vector of the response system | |
| r | The real part of a complex variable |
| i | The imaginary part of a complex variable |
| , , | Nonlinear function of complex variables |
| The designed controller | |
| The error vector | |
| The difference function vector | |
| The modified projective matrix which is the private key | |
| The transmitted signal without noise | |
| The transmitted signal with noise | |
| The noise where A is the amplitude of the noise | |
| The recovered signal | |
| The control strength matrix | |
| The probability density function of Gaussian distribution | |
| The square of error in the real part of the recovered signal | |
| The square of error in the imaginary part of the recovered signal |
| D | ||||
|---|---|---|---|---|
| 10 + 10j | 119.2935 | 615 | 6.7627 | 92.8656 |
| 10 + j | 211.2523 | 392.0710 | 7.6200 | 46.0385 |
| 10 + 0.1j | 244.3068 | 369.7529 | 10.8091 | 42.2822 |
| 1 + j | 11.9294 | 61.5253 | 0.1927 | 2.4379 |
| 1 + 0.1j | 21.1252 | 39.2071 | 0.3279 | 1.7356 |
| 0.5 + 0.1j | 8.7262 | 20.8434 | 0.2395 | 1.1375 |
| 0.1 + 0.1j | 1.1929 | 6.1525 | 0.2062 | 0.7844 |
| 0.1 + 0.02j | 1.7452 | 4.1687 | 0.2184 | 0.7573 |
| 0.01 + 0.02j | 0.4866 | 0.8632 | 0.2128 | 0.6959 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, F.; Gao, R.; Huang, Z.; Jiang, C.; Chen, Y.; Zhang, H. Complex Modified Projective Difference Function Synchronization of Coupled Complex Chaotic Systems for Secure Communication in WSNs. Mathematics 2022, 10, 1202. https://doi.org/10.3390/math10071202
Zhang F, Gao R, Huang Z, Jiang C, Chen Y, Zhang H. Complex Modified Projective Difference Function Synchronization of Coupled Complex Chaotic Systems for Secure Communication in WSNs. Mathematics. 2022; 10(7):1202. https://doi.org/10.3390/math10071202
Chicago/Turabian StyleZhang, Fangfang, Rui Gao, Zhe Huang, Cuimei Jiang, Yawen Chen, and Haibo Zhang. 2022. "Complex Modified Projective Difference Function Synchronization of Coupled Complex Chaotic Systems for Secure Communication in WSNs" Mathematics 10, no. 7: 1202. https://doi.org/10.3390/math10071202
APA StyleZhang, F., Gao, R., Huang, Z., Jiang, C., Chen, Y., & Zhang, H. (2022). Complex Modified Projective Difference Function Synchronization of Coupled Complex Chaotic Systems for Secure Communication in WSNs. Mathematics, 10(7), 1202. https://doi.org/10.3390/math10071202






