Impact of Variable Fluid Properties and Double Diffusive Cattaneo–Christov Model on Dissipative Non-Newtonian Fluid Flow Due to a Stretching Sheet
Abstract
1. Introduction
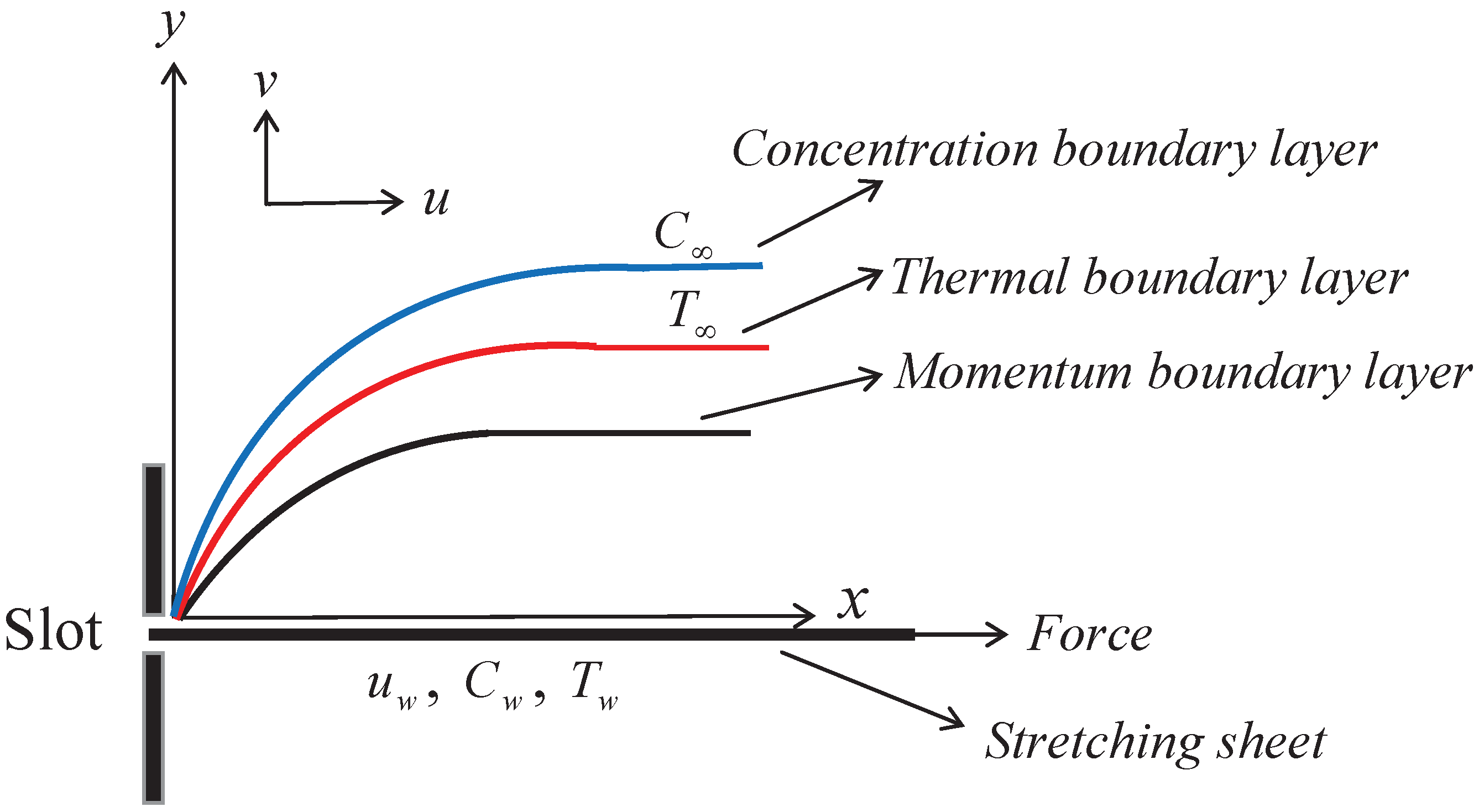
2. Fundamental Governing Equations
3. Solution Approach
4. Verification of Numerical Methodology
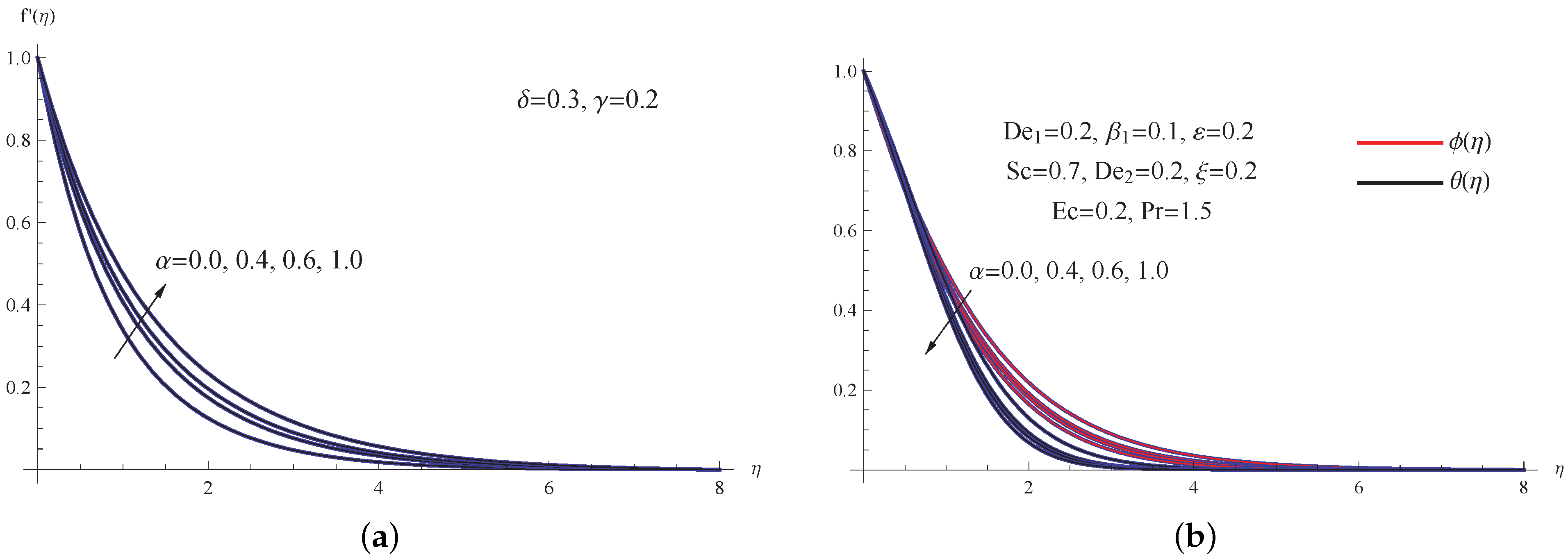
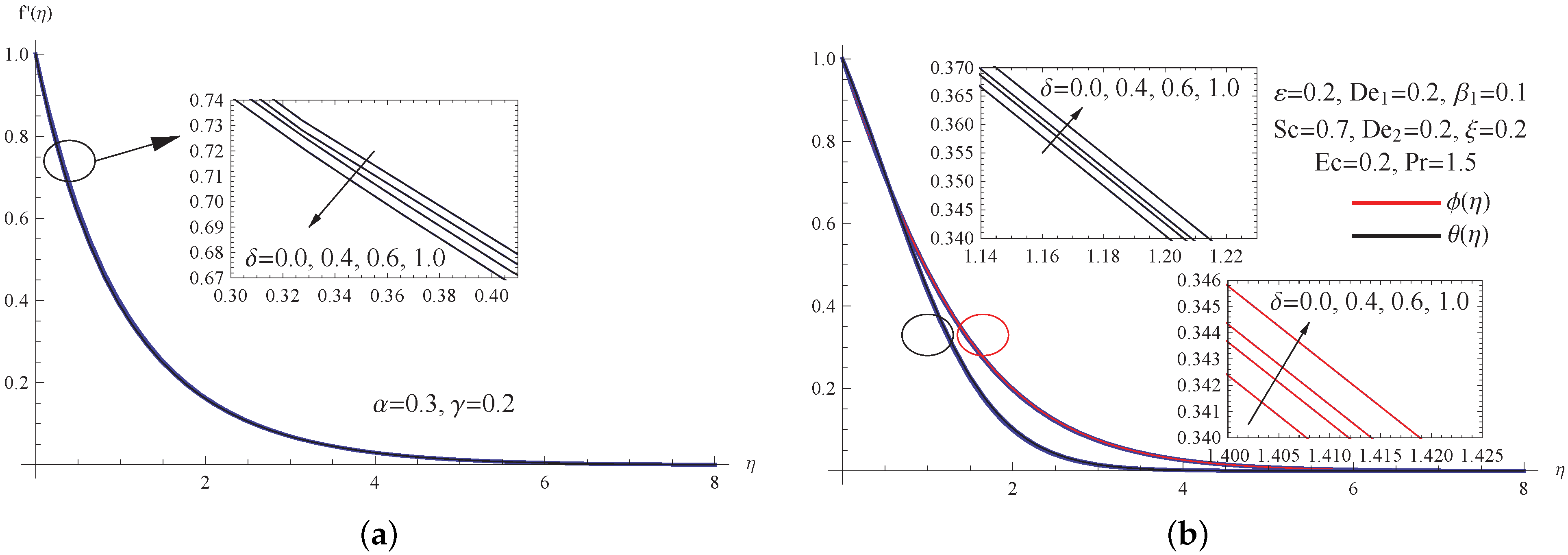
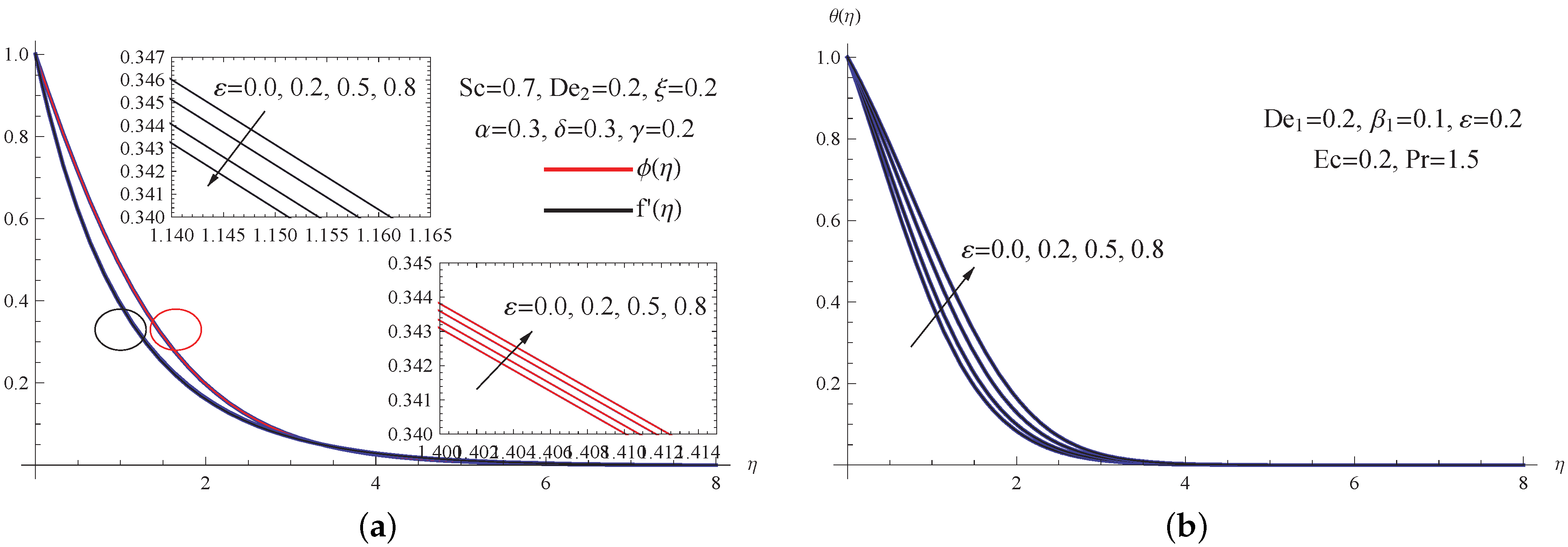
5. Outcomes with Discussion
6. Conclusions
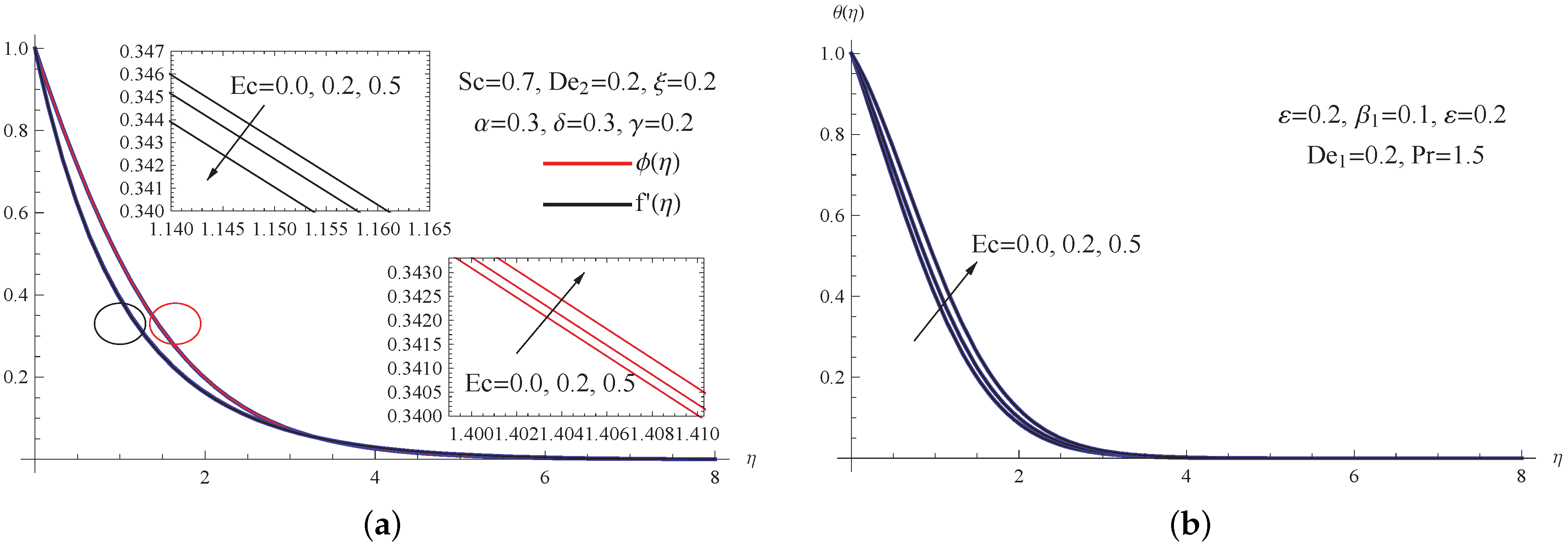
- The temperature distribution improves as the thermal conductivity parameter and the Eckert number improve, whereas the concentration distribution is affected by the chemical reaction parameter, which has a decreasing effect.
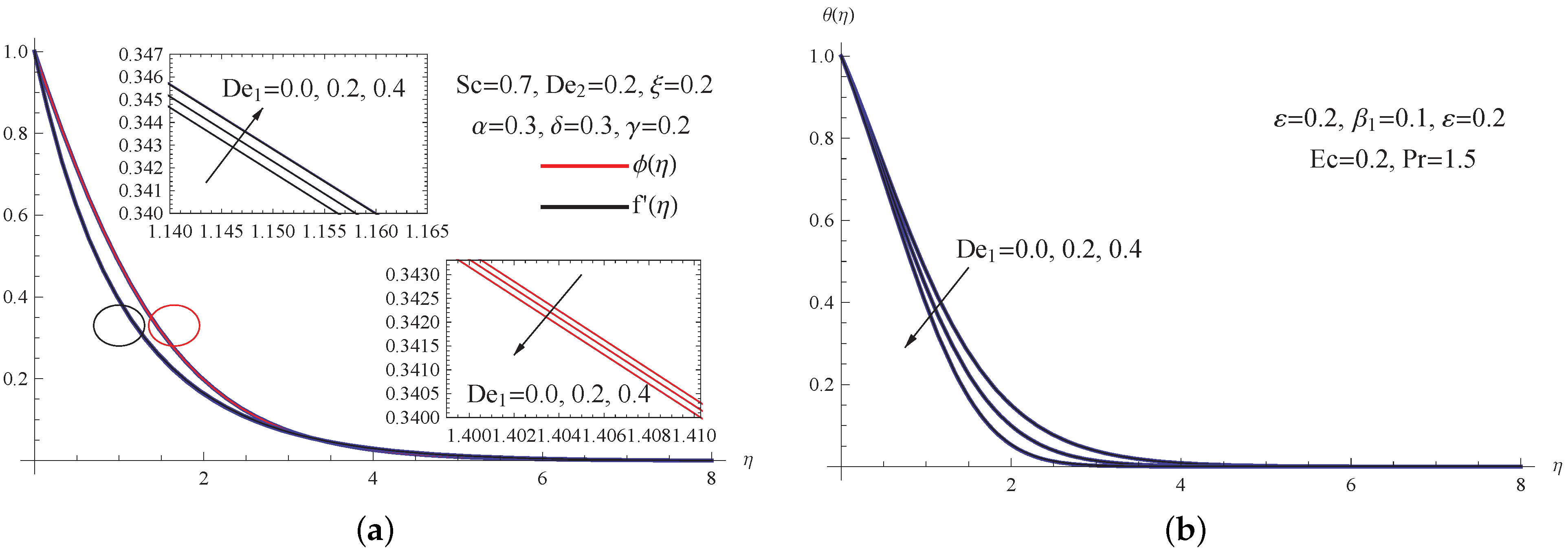
- The higher the viscosity parameter, the slower the fluid velocity becomes, and the lower the thermal Deborah number, the higher the thermal distribution becomes.
- The Nusselt number value diminishes for both higher values of thermal conductivity parameter and viscosity parameter.
- There is an increase in the Sherwood number with an increment in the chemical reaction parameter or with a decline in the viscosity parameter.
- The impact of diminishing the thermal Deborah number or expanding the thermal conductivity parameter reduces the speed profiles.
- In the future, we intend to expand on this research by looking at chemically reactive mixed convective non-Newtonian fluid flows, as well as heat and mass fluxes, in order to control the cooling process.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| a | velocity coefficient |
| c | Powell–Eyring parameter |
| specific heat at constant pressure | |
| C | nanoparticles concentration |
| skin friction coefficient | |
| surface nanoparticles concentration | |
| ambient nanoparticles concentration | |
| thermal Deborah number | |
| the mass Deborah number | |
| Eckret number | |
| f | dimensionless stream function |
| the rate of chemical reaction | |
| local Nusselt number | |
| Prandtl number | |
| Q | heat generation (absorption) coefficient |
| local Reynolds number | |
| Schmidt number | |
| T | fluid temperature |
| surface temperature | |
| ambient temperature | |
| u | velocity component in the direction |
| v | velocity component in the direction |
| Cartesian coordinates | |
| Greek symbols | |
| density of the fluid | |
| coefficient of viscosity | |
| kinematic viscosity | |
| dimensionless temperature | |
| dimensionless concentration | |
| relaxation time for heat flux | |
| relaxation time for mass flux | |
| similarity variable | |
| viscosity parameter | |
| thermal conductivity parameter | |
| chemical reaction parameter | |
| Powell–Eyring parameter | |
| the heat generation (absorption) parameter | |
| thermal conductivity | |
| Superscripts | |
| ′ | differentiation with respect to |
| ∞ | free stream condition |
| w | wall condition |
References
- Haliza, R.; Ishak, A.; Pop, I. Micropolar fluid flow towards a stretching/shrinking sheet in a porous medium with suction. Int. Commun. Heat Mass Trans. 2012, 39, 826–829. [Google Scholar]
- Abel, M.S.; Tawade, J.V.; Nandeppanavar, M.M. MHD flow and heat transfer for the upper-convected Maxwell fluid over a stretching sheet. Meccanica 2012, 47, 385–393. [Google Scholar]
- Megahed, A.M. Variable fluid properties and variable heat flux effects on the flow and heat transfer in a non-Newtonian Maxwell fluid over an unsteady stretching sheet with slip velocity. Chin. Phys. B 2013, 22, 484–489. [Google Scholar] [CrossRef]
- Sun, X.; Wang, S.; Zhao, M. Numerical solution of oscillatory flow of Maxwell fluid in a rectangular straight duct. Appl. Math. Mech. 2019, 40, 1647–1656. [Google Scholar] [CrossRef]
- Imran, M.A.; Sarwar, S.; Imran, M. Effects of slip on free convection flow of Casson fluid over an oscillating vertical plate. Bound. Value Probl. 2016, 2016, 30. [Google Scholar] [CrossRef][Green Version]
- Sharma, R.P.; Avinash, K.; Sandeep, N.; Makinde, O.D. Thermal radiation effect on non-Newtonian fluid flow over a stretched sheet of non-uniform thickness. Defect Diffus. Forum 2017, 377, 242–259. [Google Scholar] [CrossRef]
- Muhammad, B.; Samia, A. Flow and heat transfer analysis of Eyring-Powell fluid over stratified sheet with mixed convection. J. Egypt. Math. Soc. 2020, 28, 40. [Google Scholar]
- Megahed, A.M.; Abbas, W. Non-Newtonian Cross fluid flow through a porous medium with regard to the effect of chemical reaction and thermal stratification phenomenon. Case Stud. Therm. Eng. 2022, 29, 101715. [Google Scholar] [CrossRef]
- Cattaneo, C. Sulla conduzione del calore. Atti Semin. Mat. Fis. Univ. Modena Reggio Emilia 1948, 3, 83–101. [Google Scholar]
- Christov, C.I. On frame indifferent formulation of the Maxwell-Cattaneo model of finite-speed heat conduction. Mech. Res. Commun. 2009, 36, 481–486. [Google Scholar] [CrossRef]
- Hayat, T.; Khan, M.I.; Farooq, M.; Alsaedi, A.; Waqas, M.; Yasmeen, T. Impact of Cattaneo-Christov heat flux model in flow of variable thermal conductivity fluid over a variable thicked surface. Int. J. Heat Mass Trans. 2016, 99, 702–710. [Google Scholar] [CrossRef]
- Hayat, T.; Qayyum, S.; Shehzad, S.A.; Alsaedi, A. Chemical reaction and heat generation/absorption aspects in flow of Walters-B nanofluid with Cattaneo-Christov double-diffusion. Results Phys. 2017, 7, 4145–4152. [Google Scholar] [CrossRef]
- Sui, J.; Zheng, L.; Zhang, X. Boundary layer heat and mass transfer with Cattaneo-Christov double-diffusion in upper-convective Maxwell nanofluid past a stretching sheet with slip velocity. Int. J. Therm. Sci. 2016, 104, 461–468. [Google Scholar] [CrossRef]
- Shehzad, S.A.; Abbasi, F.M.; Hayat, T.; Ahmad, B. Cattaneo-Christov heat flux model for third-grade fluid flow towards exponentially stretching sheet. Appl. Math. Mech. 2016, 37, 761–768. [Google Scholar] [CrossRef]
- Li, J.; Zheng, L.; Liu, L. MHD viscoelastic flow and heat transfer over a vertical stretching sheet with Cattaneo-Christov heat flux effects. J. Mol. Liq. 2016, 221, 19–25. [Google Scholar] [CrossRef]
- Meraj, M.A.; Shehzad, S.A.; Hayat, T.; Abbasi, F.M.; Alsaedi, A. Darcy-Forchheimer flow of variable conductivity Jeffrey liquid with Cattaneo-Christov heat flux theory. Appl. Math. Mech. 2017, 38, 557–566. [Google Scholar] [CrossRef]
- Shehzad, S.A.; Hayat, T.; Alsaedi, A.; Meraj, M.A. Cattaneo-Christov heat and mass flux model for 3D hydromagnetic flow of chemically reactive Maxwell liquid. Appl. Math. Mech. 2017, 10, 1347–1356. [Google Scholar] [CrossRef]
- Prasad, K.V.; Vaidya, H.; Vajravelu, K.; Ramanjini, V. Analytical study of Cattaneo–Christov heat flux model for Williamson-nanofluid flow over a slender elastic sheet with variable thickness. J. Nanofluids 2018, 7, 583–594. [Google Scholar] [CrossRef]
- Ullah, K.S.; Ali, N.; Hayat, T.; Abbas, Z. Heat transfer analysis based on Cattaneo–Christov heat flux model and convective boundary conditions for flow over an oscillatory stretching surface. Therm. Sci. 2019, 23, 443–455. [Google Scholar] [CrossRef]
- Garia, R.; Rawat, S.K.; Kumar, M.; Yaseen, M. Hybrid nanofluid flow over two different geometries with Cattaneo–Christov heat flux model and heat generation: A model with correlation coefficient and probable error. Chin. J. Phys. 2021, 74, 421–439. [Google Scholar] [CrossRef]
- Christopher, A.J.; Magesh, N.; Gowda, R.J.P.; Kumar, R.N.; Kumar, R.S.V. Hybrid nanofluid flow over a stretched cylinder with the impact of homogeneous–heterogeneous reactions and Cattaneo–Christov heat flux: Series solution and numerical simulation. Heat Trans. 2021, 50, 3800–3821. [Google Scholar] [CrossRef]
- Abbaszadeh, M.; Dehghan, M.; Khodadadian, A.; Noii, N.; Heitzinger, C.; Wick, T. A reduced-order variational multiscale interpolating element free Galerkin technique based on proper orthogonal decomposition for solving Navier-Stokes equations coupled with a heat transfer equation: Nonstationary incompressible Boussinesq equations. J. Comput. Phys. 2021, 426, 109875. [Google Scholar] [CrossRef]
- Parvizi, M.; Khodadadian, A.; Eslahchi, M.R. Analysis of Ciarlet-Raviart mixed finite element methods for solving damped Boussinesq equation. J. Comput. Appl. Math. 2020, 379, 112818. [Google Scholar] [CrossRef]
- Rauf, A.; Abbas, Z.; Shehzad, S.A.; Alsaedi, A.; Hayat, T. Numerical simulation of chemically reactive Powell-Eyring liquid flow with double diffusive Cattaneo-Christov heat and mass flux theories. Appl. Math. Mech. 2018, 39, 467–476. [Google Scholar] [CrossRef]
- Megahed, A.M.; Reddy, M.G.; Abbas, W. Modeling of MHD fluid flow over an unsteady stretching sheet with thermal radiation, variable fluid properties and heat flux. Math. Comput. Simul. 2021, 185, 583–593. [Google Scholar] [CrossRef]
- Javed, T.; Ali, N.; Abbas, Z.; Sajid, M. Flow of an Eyring-Powellnon-Newtonian fluid over a stretching sheet. Chem. Eng. Commun. 2013, 200, 327–336. [Google Scholar] [CrossRef]


| Javed et al. [26] | Present Work | ||
|---|---|---|---|
| 0.0 | 0.0 | 1.0000 | 1.0000000000 |
| 0.2 | 0.0 | 1.0954 | 1.0953998521 |
| 0.4 | 0.0 | 1.1832 | 1.1831852914 |
| 0.2 | 0.0 | 1.0954 | 1.0953998521 |
| 0.2 | 0.1 | 1.0940 | 1.0940001201 |
| 0.2 | 0.2 | 1.0924 | 1.0923898767 |
| De1 | Ec | De2 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0.0 | 0.3 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.920887 | 0.468142 | 0.599312 |
| 0.4 | 0.3 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 1.112051 | 0.502697 | 0.622836 |
| 0.6 | 0.3 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 1.197817 | 0.513244 | 0.631776 |
| 1.0 | 0.3 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 1.354441 | 0.527314 | 0.646012 |
| 0.3 | 0.0 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 1.074721 | 0.497792 | 0.618709 |
| 0.3 | 0.4 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 1.064221 | 0.495515 | 0.617431 |
| 0.3 | 0.6 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 1.058640 | 0.494284 | 0.616745 |
| 0.3 | 1.0 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 1.046602 | 0.491591 | 0.615261 |
| 0.3 | 0.3 | 0.0 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 1.134321 | 0.508799 | 0.625702 |
| 0.3 | 0.3 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 1.064230 | 0.496106 | 0.617760 |
| 0.3 | 0.3 | 0.5 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.973111 | 0.476591 | 0.606035 |
| 0.3 | 0.3 | 0.8 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.888698 | 0.456668 | 0.594712 |
| 0.3 | 0.3 | 0.2 | 0.0 | 0.2 | 0.2 | 0.2 | 0.2 | 1.068531 | 0.567536 | 0.617941 |
| 0.3 | 0.3 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 1.066933 | 0.496106 | 0.617760 |
| 0.3 | 0.3 | 0.2 | 0.5 | 0.2 | 0.2 | 0.2 | 0.2 | 1.064971 | 0.420572 | 0.617541 |
| 0.3 | 0.3 | 0.2 | 0.8 | 0.2 | 0.2 | 0.2 | 0.2 | 1.063412 | 0.366929 | 0.617372 |
| 0.3 | 0.3 | 0.2 | 0.2 | 0.0 | 0.2 | 0.2 | 0.2 | 1.065840 | 0.465177 | 0.617651 |
| 0.3 | 0.3 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 1.066933 | 0.496106 | 0.617760 |
| 0.3 | 0.3 | 0.2 | 0.2 | 0.4 | 0.2 | 0.2 | 0.2 | 1.068043 | 0.528122 | 0.617781 |
| 0.3 | 0.3 | 0.2 | 0.2 | 0.2 | 0.0 | 0.2 | 0.2 | 1.068581 | 0.609484 | 0.617951 |
| 0.3 | 0.3 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 1.066933 | 0.496106 | 0.617760 |
| 0.3 | 0.3 | 0.2 | 0.2 | 0.2 | 0.5 | 0.2 | 0.2 | 1.064471 | 0.326569 | 0.617477 |
| 0.3 | 0.3 | 0.2 | 0.2 | 0.2 | 0.2 | 0.0 | 0.2 | 1.066930 | 0.496106 | 0.609967 |
| 0.3 | 0.3 | 0.2 | 0.2 | 0.2 | 0.2 | 0.5 | 0.2 | 1.066930 | 0.496106 | 0.631066 |
| 0.3 | 0.3 | 0.2 | 0.2 | 0.2 | 0.2 | 1.0 | 0.2 | 1.066930 | 0.496106 | 0.658297 |
| 0.3 | 0.3 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.0 | 1.066930 | 0.496106 | 0.481006 |
| 0.3 | 0.3 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 1.066930 | 0.496106 | 0.617760 |
| 0.3 | 0.3 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.5 | 1.066930 | 0.496106 | 0.775697 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khalil, K.M.; Soleiman, A.; Megahed, A.M.; Abbas, W. Impact of Variable Fluid Properties and Double Diffusive Cattaneo–Christov Model on Dissipative Non-Newtonian Fluid Flow Due to a Stretching Sheet. Mathematics 2022, 10, 1179. https://doi.org/10.3390/math10071179
Khalil KM, Soleiman A, Megahed AM, Abbas W. Impact of Variable Fluid Properties and Double Diffusive Cattaneo–Christov Model on Dissipative Non-Newtonian Fluid Flow Due to a Stretching Sheet. Mathematics. 2022; 10(7):1179. https://doi.org/10.3390/math10071179
Chicago/Turabian StyleKhalil, Khalil M., A. Soleiman, Ahmed M. Megahed, and W. Abbas. 2022. "Impact of Variable Fluid Properties and Double Diffusive Cattaneo–Christov Model on Dissipative Non-Newtonian Fluid Flow Due to a Stretching Sheet" Mathematics 10, no. 7: 1179. https://doi.org/10.3390/math10071179
APA StyleKhalil, K. M., Soleiman, A., Megahed, A. M., & Abbas, W. (2022). Impact of Variable Fluid Properties and Double Diffusive Cattaneo–Christov Model on Dissipative Non-Newtonian Fluid Flow Due to a Stretching Sheet. Mathematics, 10(7), 1179. https://doi.org/10.3390/math10071179






