Statistical Blending-Type Approximation by a Class of Operators That Includes Shape Parameters λ and α
Abstract
:1. Introduction
2. Preliminaries
3. Statistical Convergence of Univariate Blending -Bernstein Operators
4. Bivariate Operators
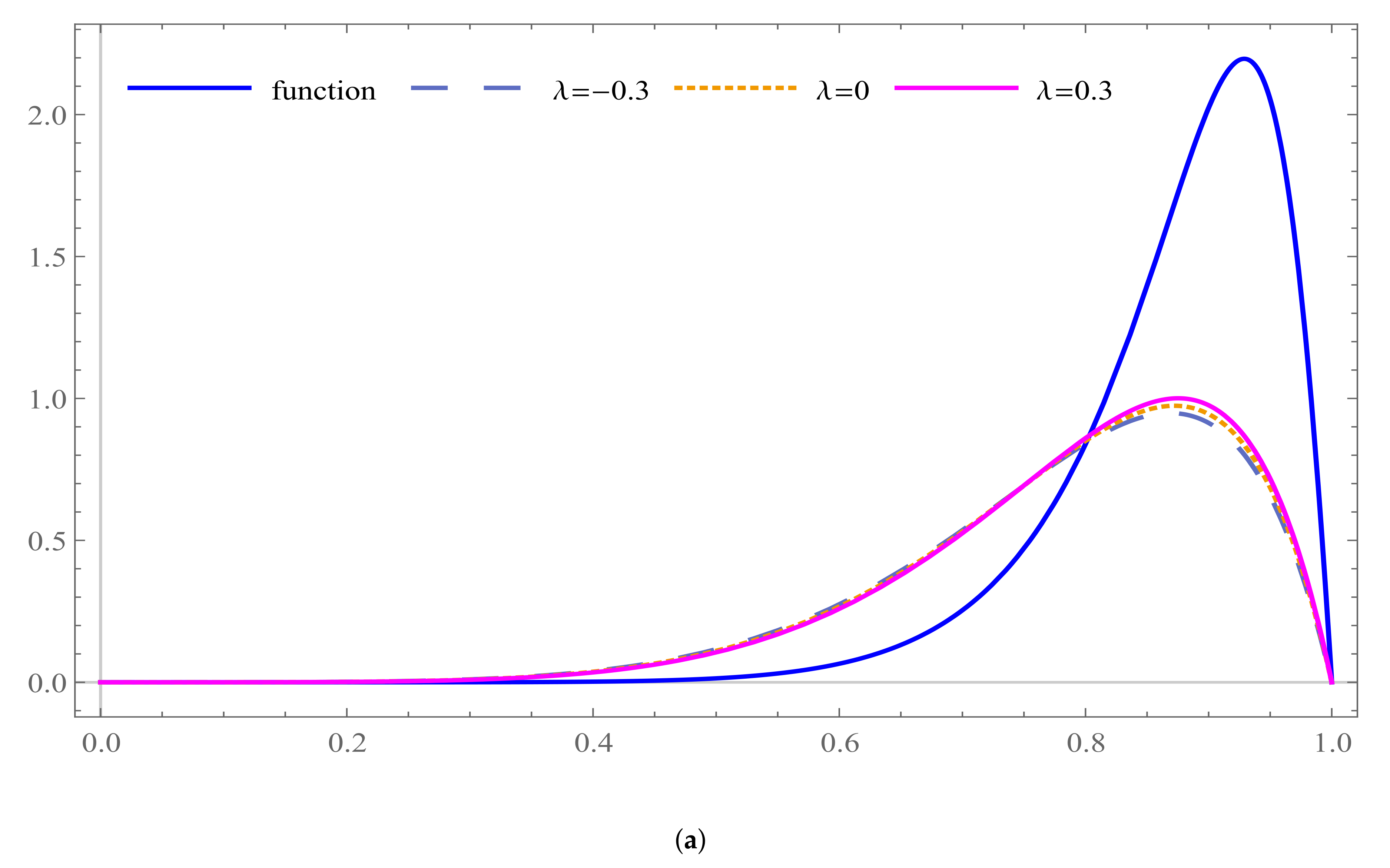
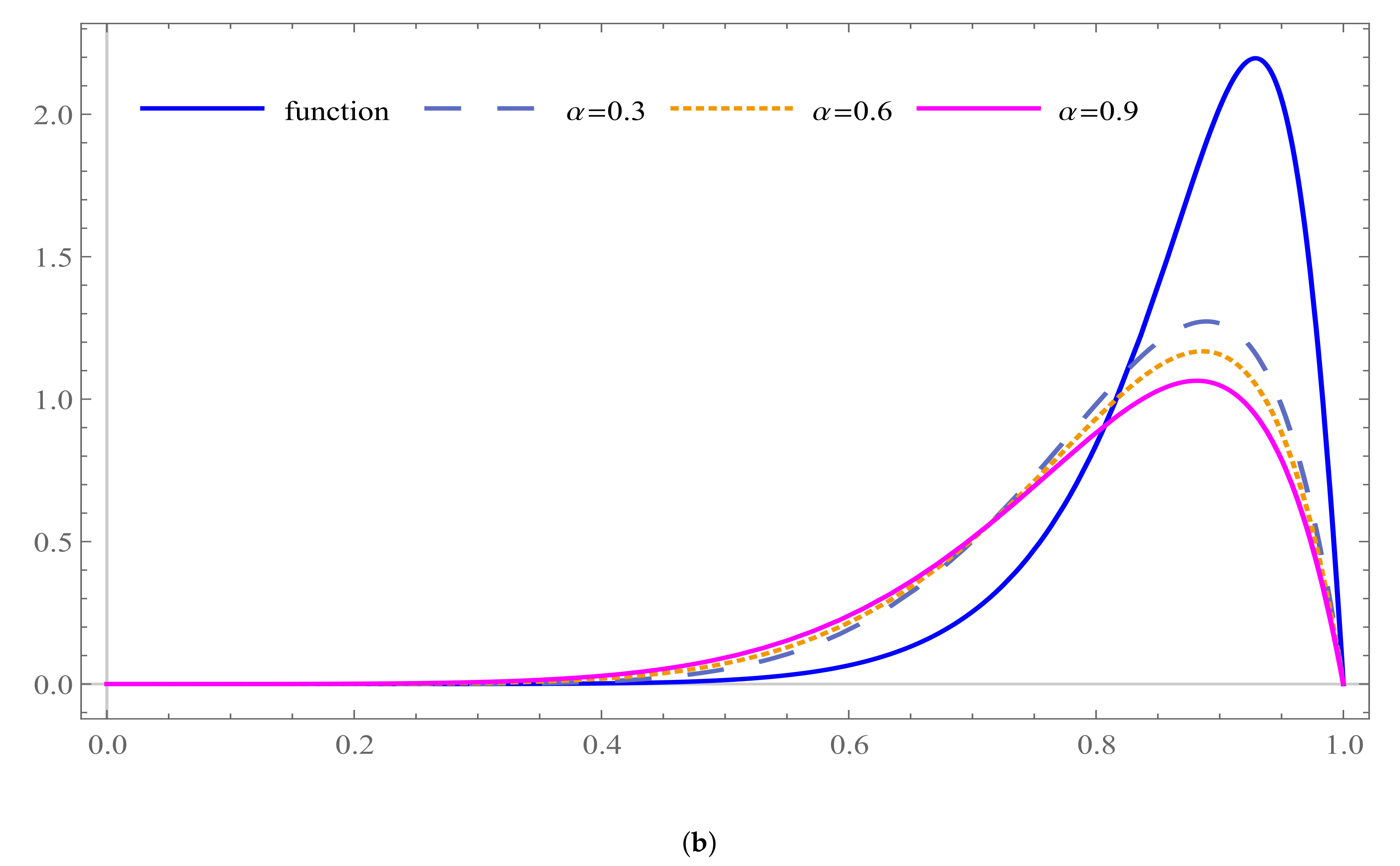
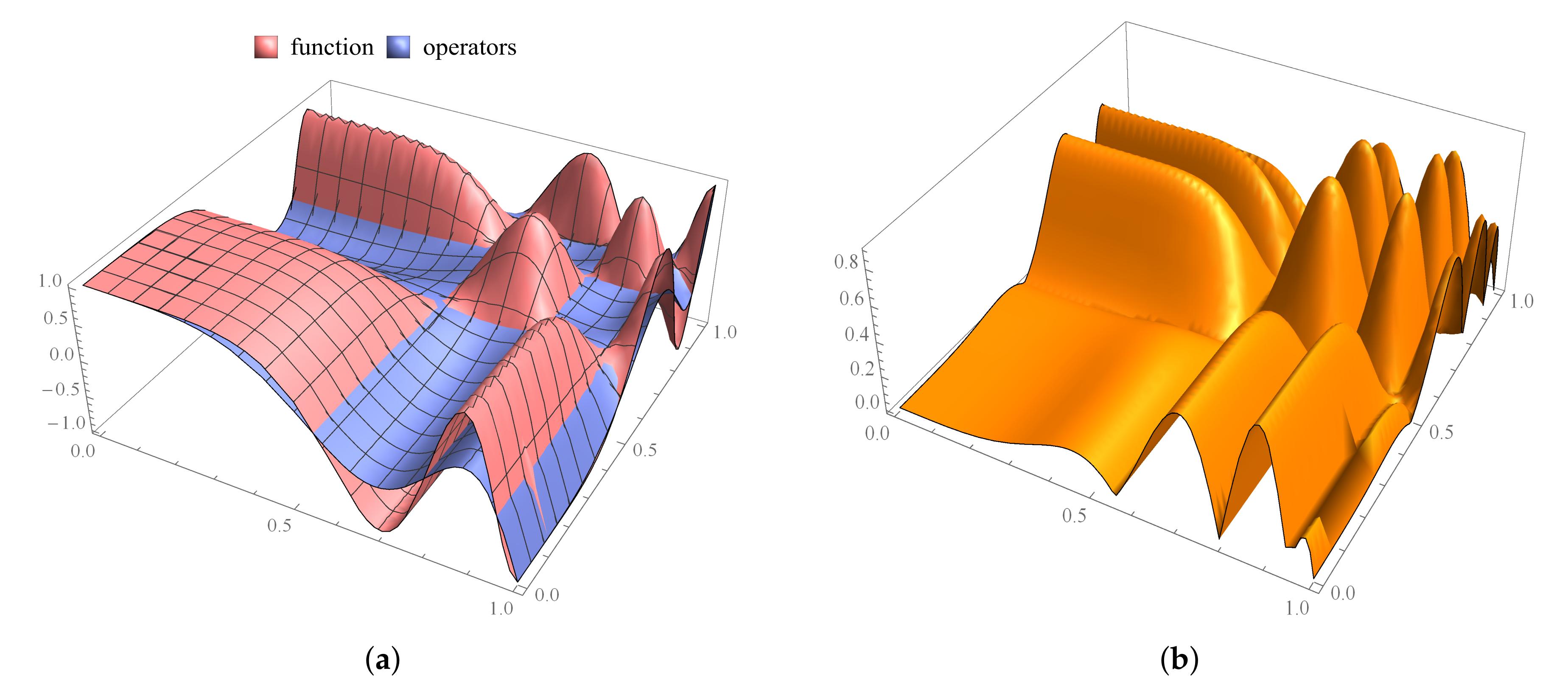
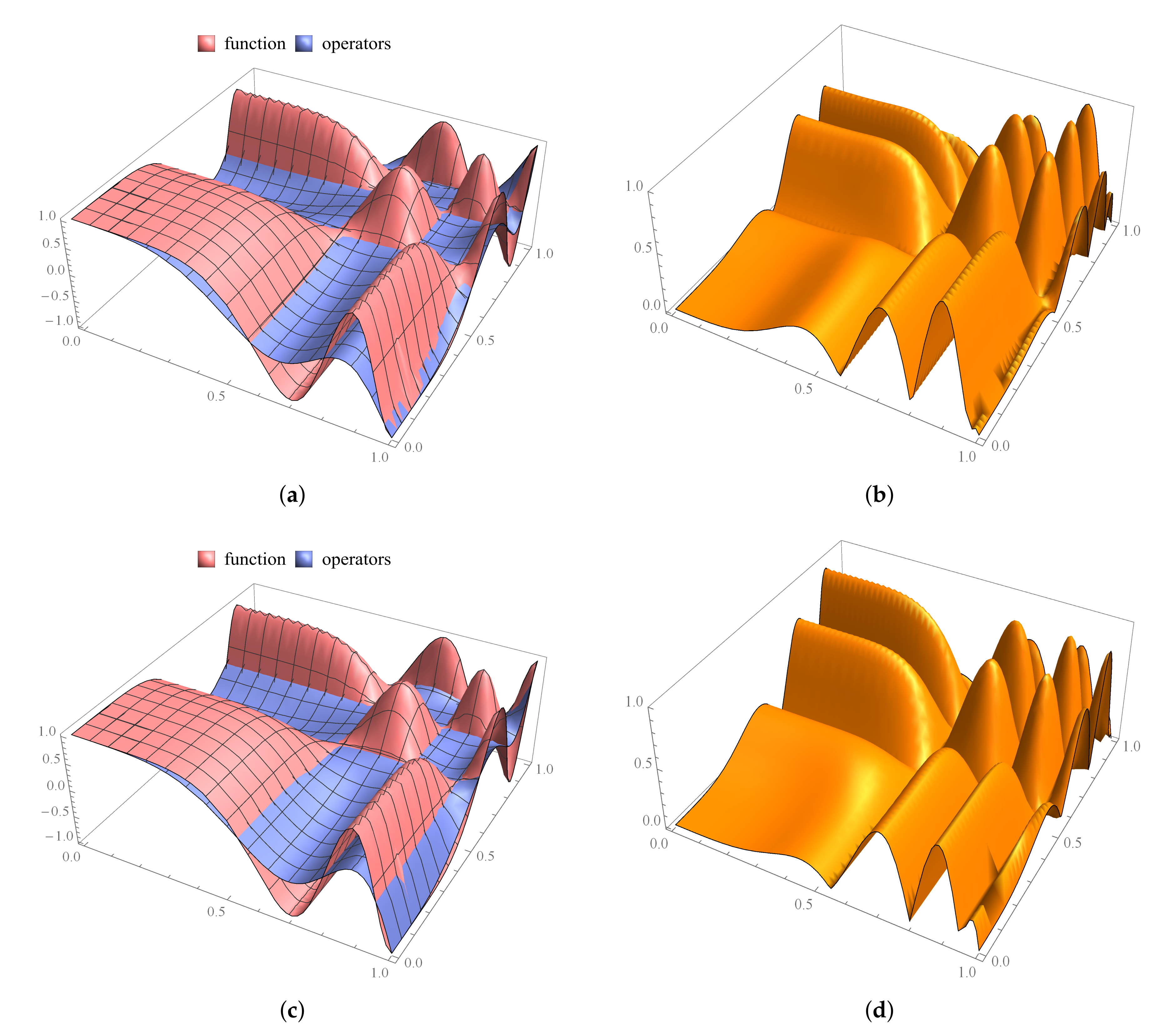
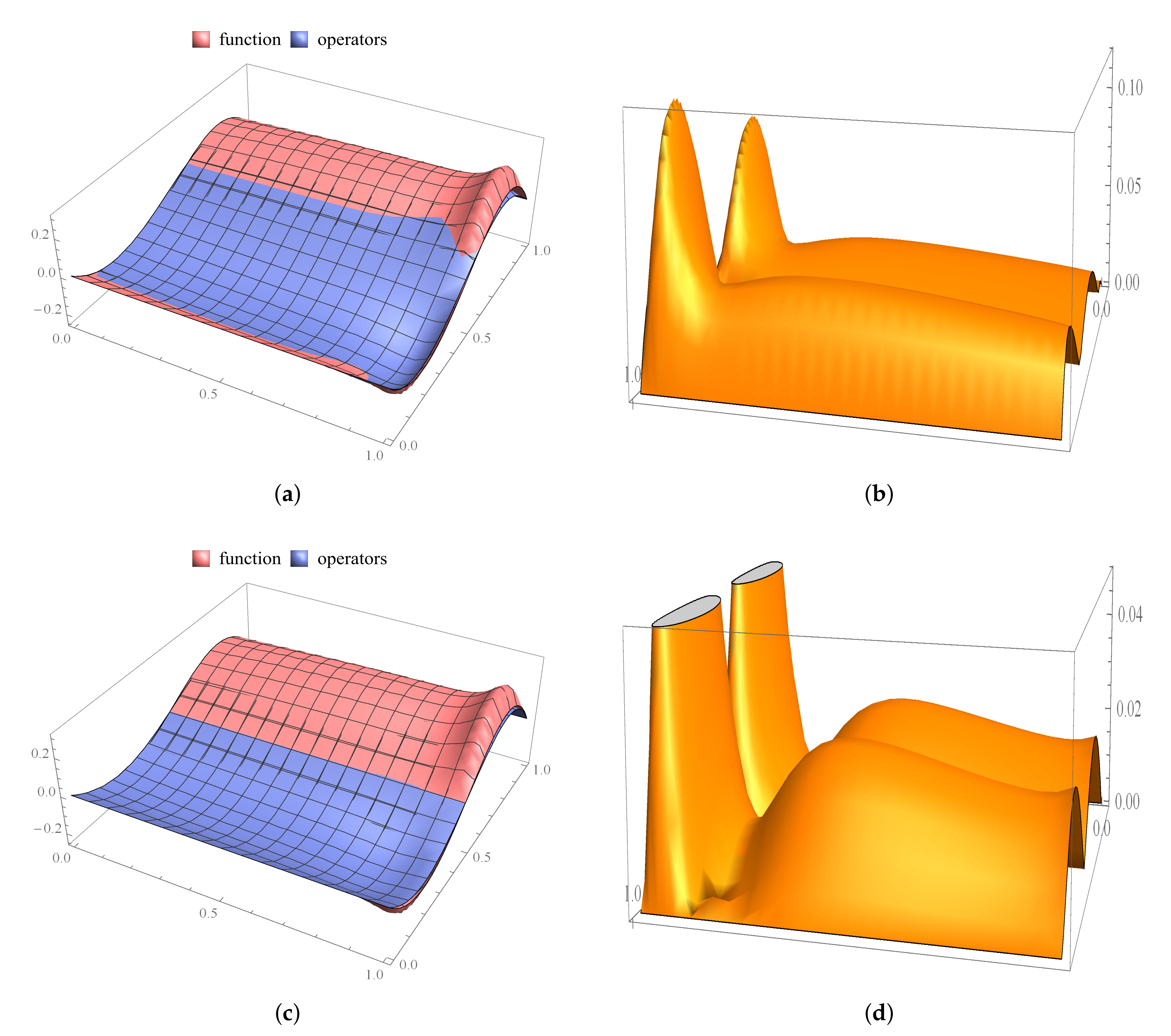
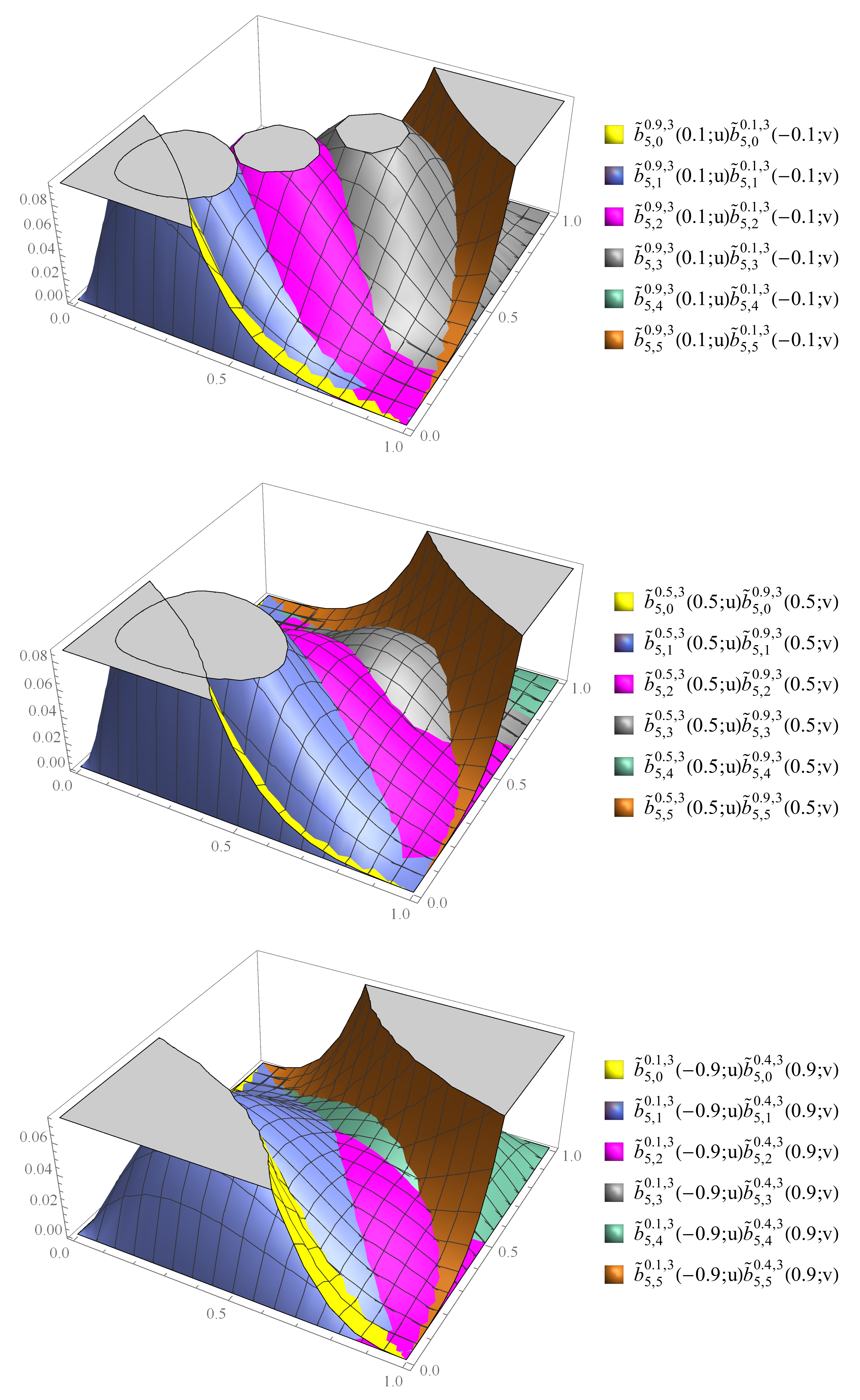
5. Graphical Results
Author Contributions
Funding
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Weierstrass, V.K. Ueber die analytische Darstellbarkeit sogennanter willkürlicher Functionen einer reellen Veranderlichep sp. Sitzungsberichte der Akademie zu Berlin. 1885, pp. 633–639 and 789–805. Available online: https://hat.net.technion.ac.il/files/2021/02/wei3.pdf (accessed on 1 February 2022).
- Bernstein, S. Dámonstration du tháorème de weirstrass. Foundeá sur le calcul des probabilitás. Commun. Soc. Math. Kharkow 1912, 13, 1–2. [Google Scholar]
- Usta, F.; Akyiğit, M.; Say, F.; Ansari, K.J. Bernstein operator method for approximate solution of singularly perturbed Volterra integral equations. J. Math. Anal. Appl. 2022, 507, 125828. [Google Scholar] [CrossRef]
- Usta, F. Bernstein approximation technique for numerical solution of Volterra integral equations of the third kind. Comput. Appl. Math. 2021, 40, 161. [Google Scholar] [CrossRef]
- Chen, X.; Tan, J.; Liu, Z.; Xie, J. Approximation of functions by a new family of generalized Bernstein operators. J. Math. Anal. Appl. 2017, 450, 244–261. [Google Scholar] [CrossRef]
- Mohiuddine, S.A.; Özger, F. Approximation of functions by Stancu variant of Bernstein-Kantorovich operators based on shape parameter alpha. Revista de la Real Academia de Ciebcias Exactas y Naturales Serie A Matemáticas 2020, 114, 70. [Google Scholar] [CrossRef]
- Mohiuddine, S.A.; Ahmad, N.; Özger, F.; Alotaibi, A.; Hazarika, B. Approximation by the Parametric Generalization of Baskakov-Kantorovich Operators Linking with Stancu Operators. Iran. J. Sci. Technol. Trans. Sci. 2021, 45, 593–605. [Google Scholar] [CrossRef]
- Özger, F.; Srivastava, H.M.; Mohiuddine, S.A. Approximation of functions by a new class of generalized Bernstein–Schurer operators. Revista de la Real Academia de Ciencias Exactas Físicas y Naturales Serie A Matemáticas 2020, 114, 173. [Google Scholar] [CrossRef]
- Ye, Z.; Long, X.; Zeng, X.M. Adjustment Algorithms for Bézier Curve and Surface. In Proceedings of the 2010 5th International Conference on Computer Science & Education, Hefei, China, 24–27 August 2010. [Google Scholar]
- Cai, Q.B.; Lian, B.-Y.; Zhou, G. Approximation properties of λ-Bernstein operators. J. Inequal. Appl. 2018, 2018, 61. [Google Scholar] [CrossRef]
- Aktuğlu, H.; Gezer, H.; Baytunç, E.; Atamert, M.S. Blending type α-Bernstein operators. submitted.
- Aktuğlu, H.; Yashar, Z.S. Approximation of functions by generalized parametric blending-type Bernstein operators. Iran. J. Sci. Technol. Trans. Sci. 2020, 44, 1495–1504. [Google Scholar] [CrossRef]
- Nasiruzzaman, M.; Rao, N.; Wazir, S.; Kumar, R. Approximation on parametric extension of Baskakov-Durrmeyer operators on weighted spaces. J. Inequal. Appl. 2019, 2019, 103. [Google Scholar] [CrossRef]
- Rao, N.; Nasiruzzaman, M.; Heshamuddin, M. Shadab, M. Approximation properties by modified Baskakov-Durrmeyer operators based on shape parameter α. Iran. J. Sci. Technol. Trans. Sci. 2021, 45, 1457–1465. [Google Scholar] [CrossRef]
- Mohiuddine, S.A.; Kajla, A.; Mursaleen, M.; Alghamdi, M. Blending type approximation by τ-Baskakov-Durrmeyer type hybrid operators. Adv. Differ. Equ. 2020, 2020, 467. [Google Scholar] [CrossRef]
- Rao, N.; Malik, P.; Rani, M. Blending type approximations by Kantorovich variant of α-Baskakov operators. Palest. J. Math. 2020, 9, 1–12. [Google Scholar]
- Sofyalıoğlu, M.; Kanat, K.; Çekim, B. Parametric generalization of the Meyer-König-Zeller operators. Chaos Solitons Fractals 2022, 152, 111417. [Google Scholar] [CrossRef]
- Sofyalıoğlu, M.; Kanat, K.; Çekim, B. Parametric generalization of the modified Bernstein operators. Filomat 2022, 2022, 36. [Google Scholar]
- Özger, F.; Demirci, K.; Yıldız, S. Approximation by Kantorovich variant of λ-Schurer operators and related numerical results. In Topics in Contemporary Mathematical Analysis and Applications; CRC Press: Boca Raton, FL, USA, 2021; pp. 77–94. ISBN 9780367532666. [Google Scholar]
- Özger, F. On new bezier bases with Schurer polnomials and Corresponding results in spproximation theory. Commun. Fac. Sci. Univ. Ank. Ser. A1 Math. Stat. 2020, 69, 376–393. [Google Scholar]
- Rahman, S.; Mursaleen, M.; Acu, A.M. Approximation properties of λ-Bernstein-Kantorovich operators with shifted knots. Math. Methods Appl. Sci. 2019, 42, 4042–4053. [Google Scholar] [CrossRef]
- Özger, F. Weighted statistical approximation properties of univariate and bivariate λ-Kantorovich operators. Filomat 2019, 33, 11. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Özger, F.; Mohiuddine, S.A. Construction of Stancu-type Bernstein operators based on Bézier bases with shape parameter λ. Symmetry 2019, 11, 316. [Google Scholar] [CrossRef] [Green Version]
- Aslan, R. Some approximation results on -Szász-Mirakjan-Kantorovich operators. Fundam. J. Math. Appl. 2021, 4, 150–158. [Google Scholar]
- Cai, Q.B.; Aslan, R. On a New Construction of Generalized q-Bernstein Polynomials Based on Shape Parameter λ. Symmetry 2021, 13, 1919. [Google Scholar] [CrossRef]
- Cai, Q.B.; Aslan, R. Note on a new construction of Kantorovich form q-Bernstein operators related to shape parameter λ. Comput. Model. Eng. Sci. 2021, 129, 1479–1493. [Google Scholar] [CrossRef]
- Rao, N.; Malik, P.; Rani, M. Generalized bivariate Baskakov Durrmeyer operators and associated GBS operators. Fiomat 2022, 36, 1–19. [Google Scholar]
- Mohiuddine, S.A. Approximation by bivariate generalized Bernstein–Schurer operators and associated GBS operators. Adv. Differ. Equ. 2020, 2020, 676. [Google Scholar] [CrossRef]
- Nasiruzzaman, M.; Rao, N.; Kumar, M.; Kumar, R. Approximation on bivariate parametric-extension of Baskakov-Durrmeyer-operators. Filomat 2021, 35, 2783–2800. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Ansari, K.; Özger, F.; Ödemiş Özger, Z. A link between approximation theory and summability methods via four-dimensional infinite matrices. Mathematics 2021, 9, 1895. [Google Scholar] [CrossRef]
- Özger, F. Applications of generalized weighted statistical convergence to approximation theorems for functions of one and two variables. Numer. Funct. Anal. Optim. 2020, 41, 1990–2006. [Google Scholar] [CrossRef]
- Gezer, H.; Aktuğlu, H.; Baytunç, E.; Atamert, M.S. Generalized blending type Bernstein operators based on the shape parameter λ. J. Inequal. Appl. 2022, 2022. [Google Scholar] [CrossRef]
- Kadak, U.; Özger, F. A numerical comparative study of generalized Bernstein-Kantorovich operators. Math. Found. Comput. 2021, 4, 311. [Google Scholar] [CrossRef]
- Özger, F.; Ansari, K.J. Statistical convergence of bivariate generalized Bernstein operators via four-dimensional infinite matrices. Filomat 2022, 36, 507–525. [Google Scholar] [CrossRef]
- Korovkin, P.P. Linear Operators and Approximation Theory; Hindustan Publishing Corporation: Delhi, India, 1960. [Google Scholar]
- Volkov, V.J. On the convergence of linear positive operators in the space of continuous functions of two variables. Doklakad Nauk SSSR 1957, 115, 17–19. (In Russian) [Google Scholar]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, Q.-B.; Ansari, K.J.; Temizer Ersoy, M.; Özger, F. Statistical Blending-Type Approximation by a Class of Operators That Includes Shape Parameters λ and α. Mathematics 2022, 10, 1149. https://doi.org/10.3390/math10071149
Cai Q-B, Ansari KJ, Temizer Ersoy M, Özger F. Statistical Blending-Type Approximation by a Class of Operators That Includes Shape Parameters λ and α. Mathematics. 2022; 10(7):1149. https://doi.org/10.3390/math10071149
Chicago/Turabian StyleCai, Qing-Bo, Khursheed J. Ansari, Merve Temizer Ersoy, and Faruk Özger. 2022. "Statistical Blending-Type Approximation by a Class of Operators That Includes Shape Parameters λ and α" Mathematics 10, no. 7: 1149. https://doi.org/10.3390/math10071149
APA StyleCai, Q.-B., Ansari, K. J., Temizer Ersoy, M., & Özger, F. (2022). Statistical Blending-Type Approximation by a Class of Operators That Includes Shape Parameters λ and α. Mathematics, 10(7), 1149. https://doi.org/10.3390/math10071149






