Contributions to Risk Assessment with Edgeworth–Sargan Density Expansions (I): Stability Testing
Abstract
:1. Introduction
2. A Simplified Case
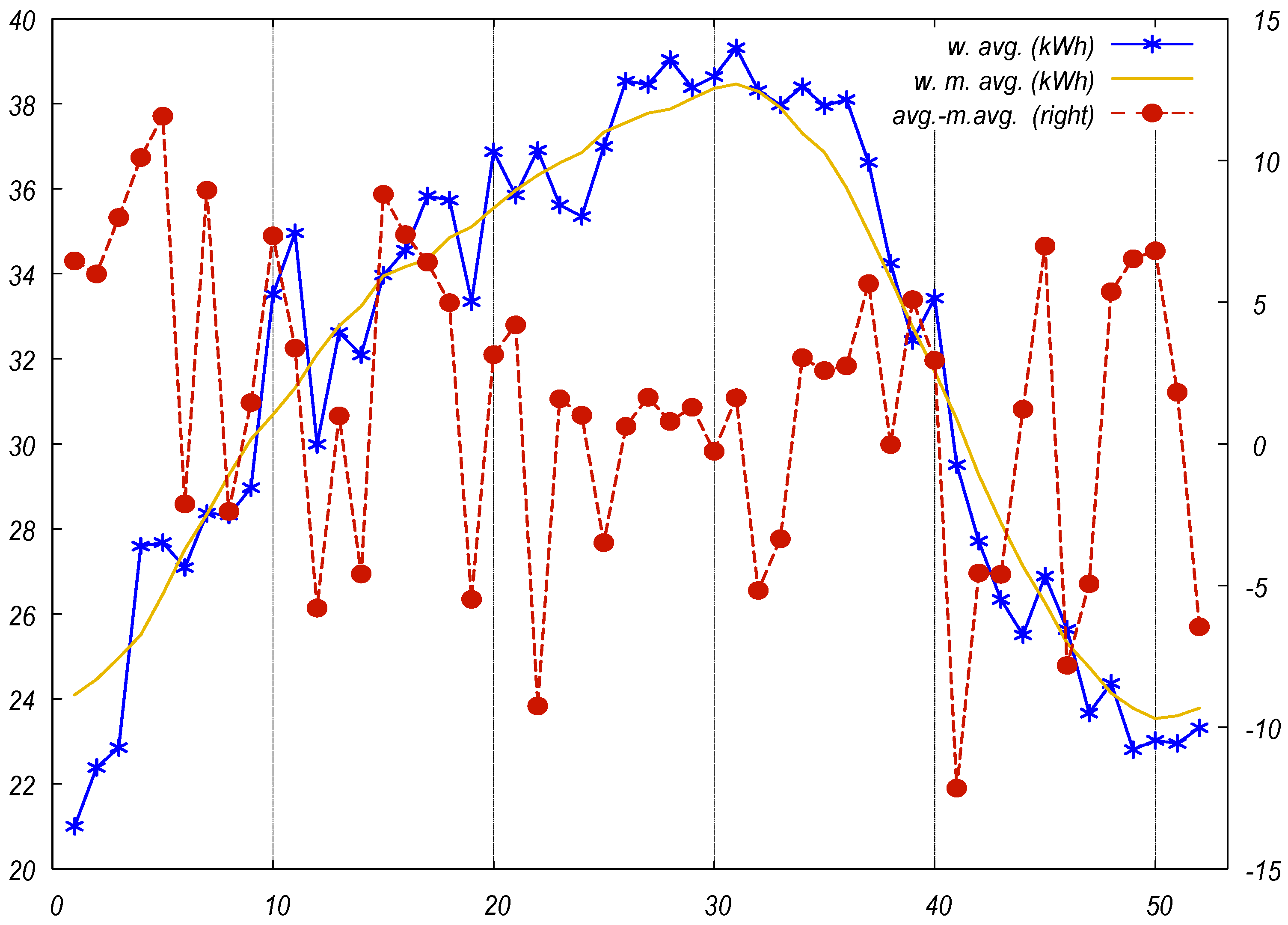
3. Empirical Results
4. Conclusions and Discussion
4.1. Results
4.2. Discussion and Implications
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Polar Coordinates and the Chi-Squared Distribution
Appendix A.1. Introduction
Appendix A.2. The Joint and Marginal Densities of
Appendix A.3. The Moments of
Appendix A.4. A Recursive Property of the Chi-Squared p.d.f.
Appendix B. Computational Aspects
Appendix B.1. Distribution Function of a Chi-Squared p.d.f.
Appendix B.2. Computing the Multinomial Theorem
Appendix B.3. Univariate Hermite Polynomials
Appendix B.4. The Operator
Appendix B.5. Computer Programs
Appendix C. Generalisation of the Test
Appendix C.1. General Derivation
Appendix C.2. List of Key Intermediate Results
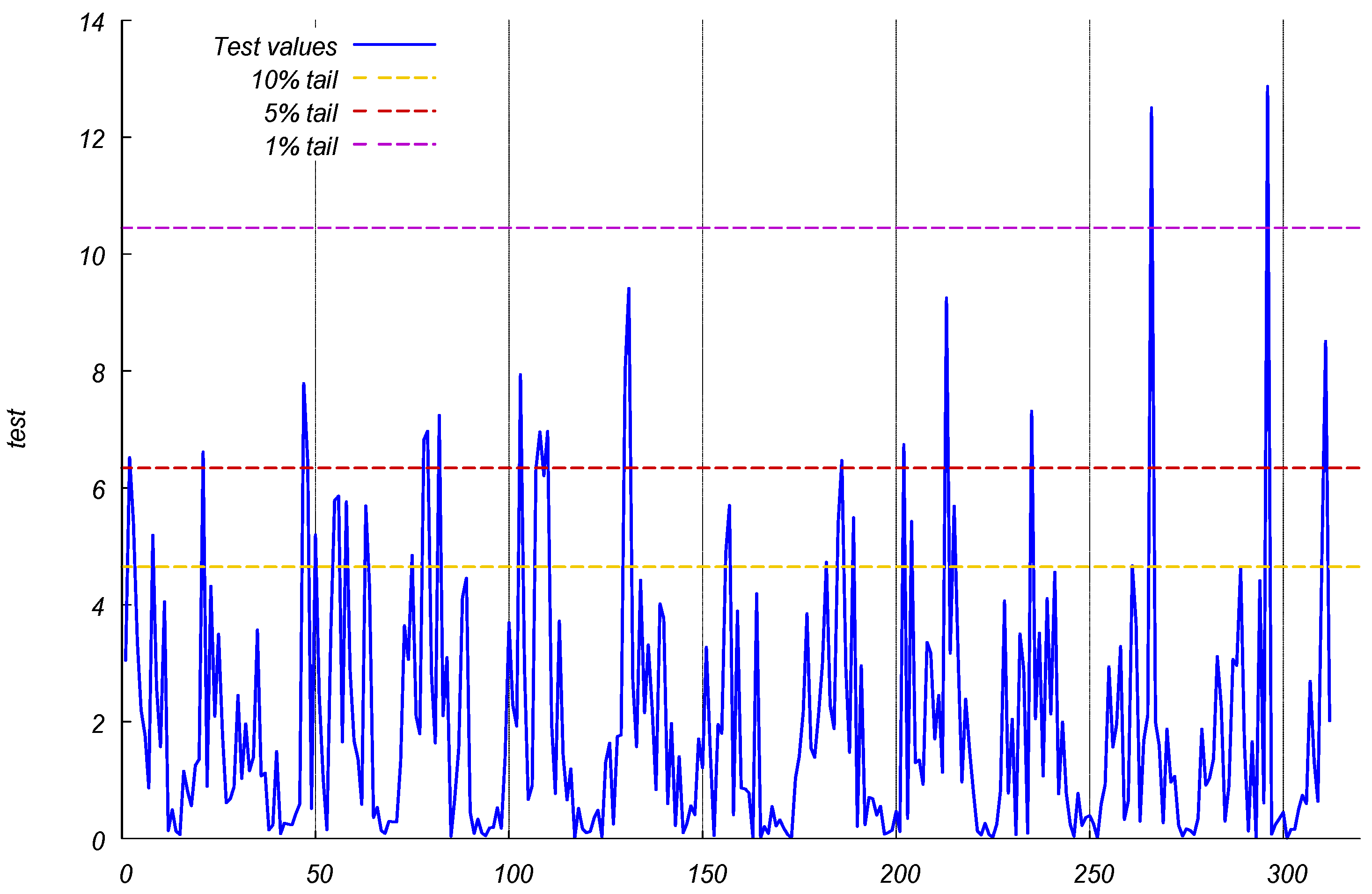
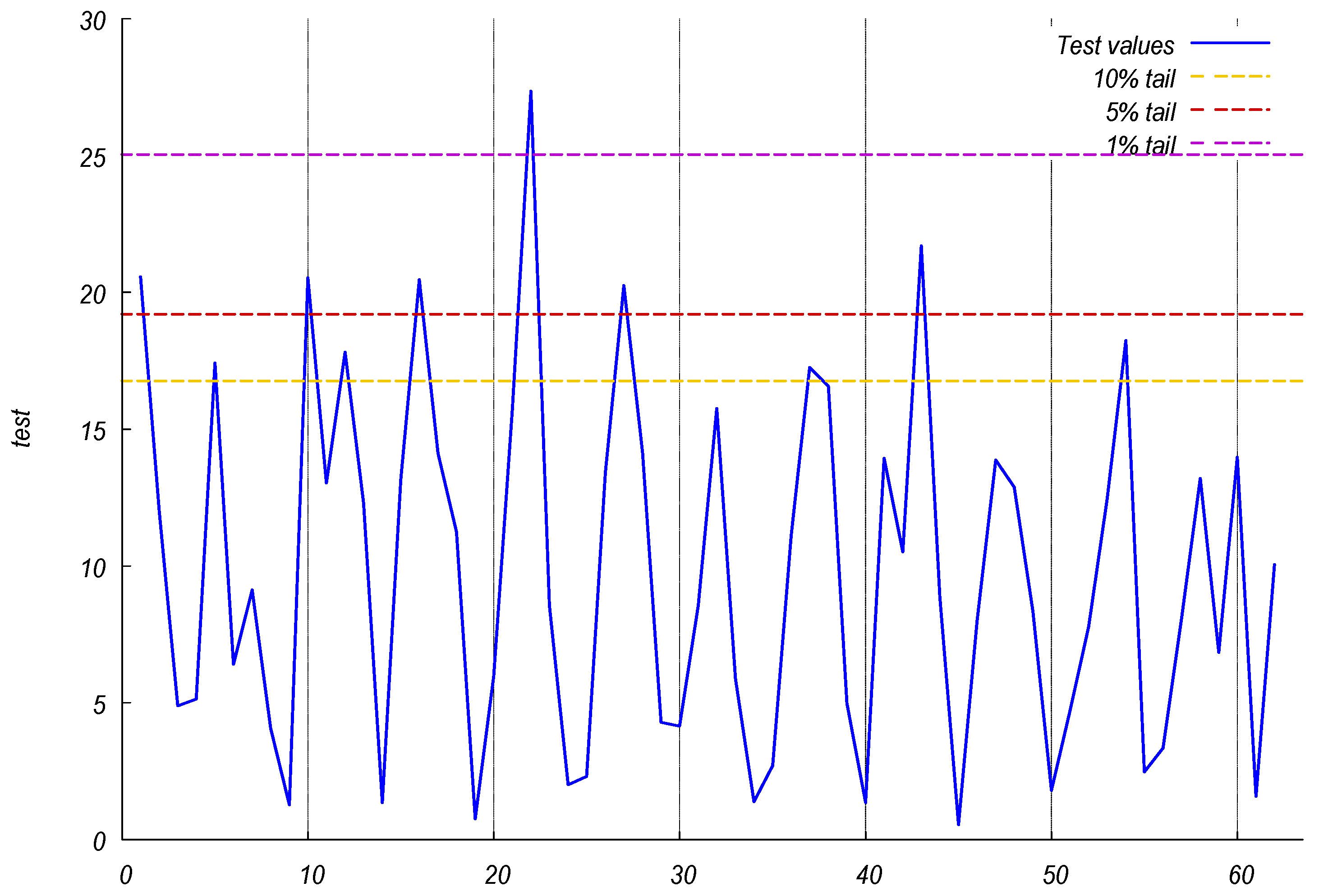
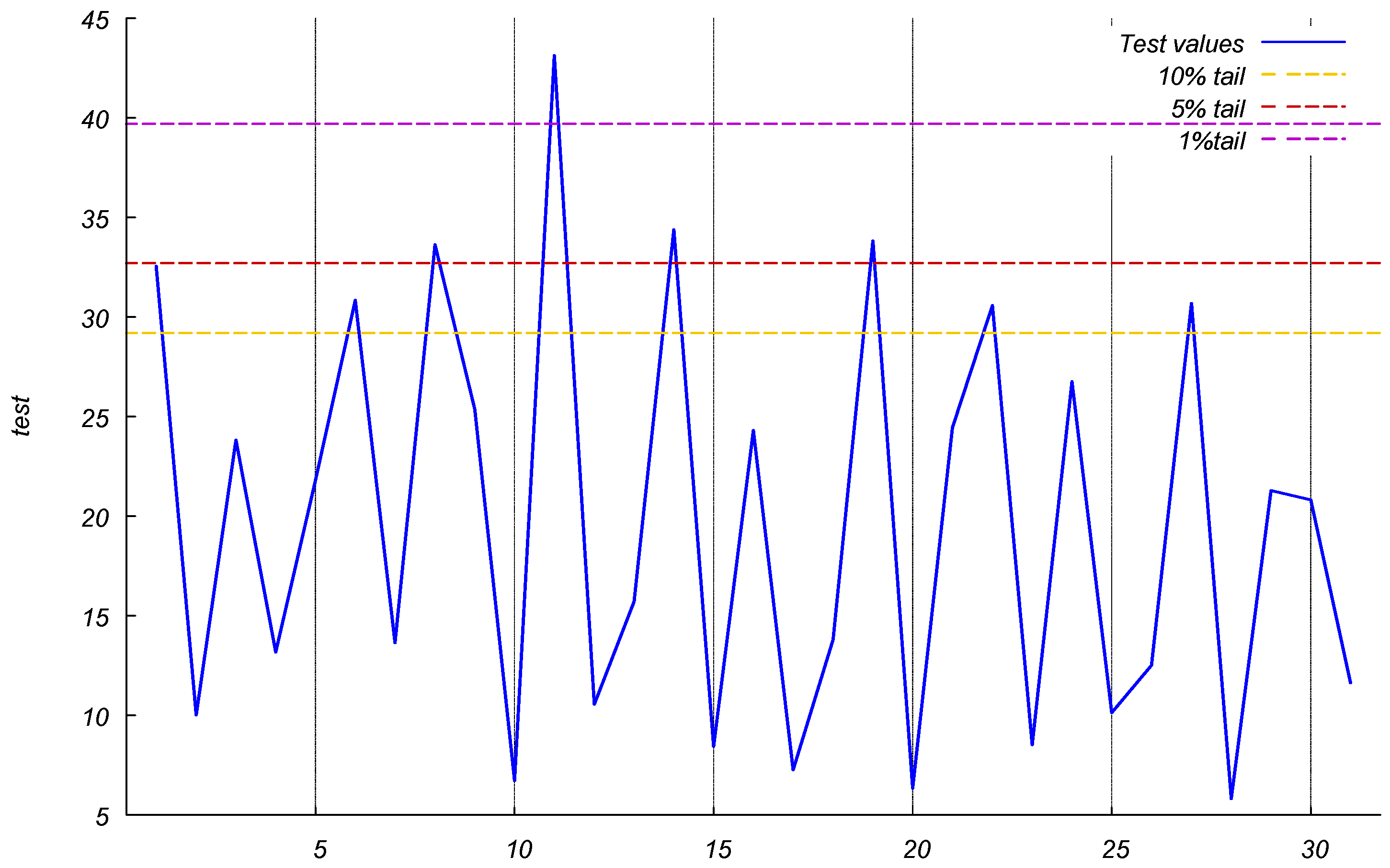
Appendix D. Additional Empirical Results
References
- European Commission. Available online: https://re.jrc.ec.europa.eu/pvg_tools/es/#MR (accessed on the 25 February 2022).
- Kendall, M.; Stuart, A. The Advanced Theory of Statistics, 4th ed.; Griffin & Co.: London, UK, 1977. [Google Scholar]
- Sargan, J.D. Econometric Estimators and the Edgeworth Approximation. Econometrica 1976, 44, 421–448. [Google Scholar] [CrossRef]
- Sargan, J.D. Some Approximations to the Distribution of Econometric Criteria which are Asymptotically Distributed as Chi-Squared. Econometrica 1980, 48, 1107–1138. [Google Scholar] [CrossRef]
- Gallant, R.; Nychka, D. Seminonparametric Maximum Likelihood Estimation. Econometrica 1987, 55, 363–390. [Google Scholar] [CrossRef] [Green Version]
- Gallant, R.; Tauchen, G. Seminonparametric Estimation of Conditionally Constrained Heterogeneous Processes: Asset Pricing Applications. Econometrica 1989, 57, 1091–1120. [Google Scholar] [CrossRef] [Green Version]
- Lee, T.; Tse, Y. Term structure of interest rates in the Singapore Asian dollar market. J. Appl. Econom. 1991, 5, 32–41. [Google Scholar] [CrossRef]
- Del Brio, E.B.; Mora-Valencia, A.; Perote, J. VaR Performance during the Subprime and Sovereign Debt Crises: An Application to Emerging Markets. Emerg. Mark. Rev. 2014, 20, 23–41. [Google Scholar] [CrossRef]
- Del Brio, E.B.; Mora-Valencia, A.; Perote, J. Expected shortfall assessment in, commodity (L)ETF portfolios with semi-nonparametric specifications. Eur. J. Financ. 2019, 25, 1746–1764. [Google Scholar] [CrossRef]
- León, Á.; Mencía, J.; Sentana, E. Parametric properties of semi-nonparametric distributions, with applications to option valuation. J. Bus. Econ. Stat. 2009, 27, 176–192. [Google Scholar] [CrossRef] [Green Version]
- Mauleón, I. Financial densities in emerging markets: An application of the Multivariate ES density. Emerg. Mark. Rev. 2003, 4, 197–223. [Google Scholar] [CrossRef]
- Mauleón, I. Modeling multivariate moments in European stock markets. Eur. J. Financ. 2006, 12, 241–263. [Google Scholar] [CrossRef]
- Mauleón, I.; Perote, J. Testing densities with financial data: An empirical comparison of the Edgeworth-Sargan density to the Student's t. Eur. J. Financ. 2000, 6, 225–239. [Google Scholar] [CrossRef]
- Mauleón, I. Assessing the value of Hermite densities for predictive distributions. J. Forecast. 2010, 29, 689–714. [Google Scholar] [CrossRef]
- Prucha, I.; Kelejian, H. The Structure of Simultaneous Equation Estimators: A Generalisation Towards Non-normal Disturbances. Econometrica 1984, 52, 721–737. [Google Scholar] [CrossRef]
- Hansen, B.E. Autoregressive Conditional Density Estimation. Int. Econ. Rev. 1994, 35, 705–730. [Google Scholar] [CrossRef]
- Adcock, C.J. Capital asset pricing for UK stocks under the multivariate skew-normal distribution. In Skew Elliptical Distributions and Their Applications: A Journey Beyond Normality; Genton, M., Ed.; Chapman and Hall: Boca Raton, FL, USA, 2004; pp. 191–204. [Google Scholar]
- Šúri, M.; Huld, T.A.; Dunlop, E.D.; Ossenbrink, H.A. Potential of solar electricity generation in the European Union member states and candidate countries. Solar Energy 2007, 81, 1295–1305. [Google Scholar] [CrossRef]
- Huld, T.; Müller, R.; Gambardella, A. A new solar radiation database for estimating PV performance in Europe and Africa. Sol. Energy 2012, 86, 1803–1815. [Google Scholar] [CrossRef]
- Silverman, B.W. Density Estimation for Statistics and Data Analysis; Chapman & Hall: London, UK, 1986. [Google Scholar]
- Batrancea, L.; Rathnaswamy, M.; Batrancea, I.; Nichita, A.; Rus, M.; Tulai, H.; Fatacean, G.; Masca, E.S.; Morar, I.D. Adjusted Net Savings of CEE and Baltic Nations in the Context of Sustainable Economic Growth: A Panel Data Analysis. J. Risk Financ. Manag. 2020, 13, 234. [Google Scholar] [CrossRef]
- Batrancea, L. An Econometric Approach Regarding the Impact of Fiscal Pressure on Equilibrium: Evidence from Electricity, Gas and Oil Companies Listed on the New York Stock Exchange. Mathematics 2021, 9, 630. [Google Scholar] [CrossRef]
- Matsumoto, M.; Nishimura, T. Mersenne twister: A 623-dimensionally equidistributed uniform pseudo-random number generator. ACM Trans. Modeling Comput. Simul. 1998, 8, 3–30. [Google Scholar] [CrossRef] [Green Version]
- Christoffersen, P.F. Evaluating interval forecasting. Int. Econ. Rev. 1998, 39, 841–862. [Google Scholar] [CrossRef]
- Wichura, M. Algorithm AS241: The Percentage Points of the Normal Distribution. Appl. Stat. 1988, 37, 477–484. [Google Scholar] [CrossRef]
- Greene, W. Econometric Analysis, 8th ed.; Pearson Prentice Hall: Upper Saddle River, NJ, USA, 2018. [Google Scholar]
- Mood, A.; Graybill, F.A.; Boes, D.C. Introduction to the Theory of Statistics, 3rd ed.; McGraw-Hill, Kogakusha: Tokyo, Japan, 1974. [Google Scholar]
- Abramowitz, M.; Stegun, I. Handbook of Mathematical Functions; Dover: New York, NY, USA, 1972. [Google Scholar]
- Gnu Regression, Econometrics and Time-Series Library. Available online: http://gretl.sourceforge.net/ (accessed on the 25 February 2022).
- Cottrell, A.; Luchetti, R. A Hansl Primer. 2015. Available online: http://gretl.sourceforge.net/ (accessed on the 25 February 2022).
- Janet, P.K. Gnuplot in Action: Understanding Data with Graphs, 2nd ed.; Manning Publications: Shelt Alan, NY, USA, 2016. [Google Scholar]
- Metcalf, M.; Reid, J. Fortran 90/95 Explained; Oxford University Press: Oxford, UK, 1996. [Google Scholar]

| Probability Intervals for the Stability Test (2, 5, 10 and 20 Weeks Ahead) | ||||
|---|---|---|---|---|
| ES and Chi-Squared Intervals (10%, 5%, 1% Upper Tail Probabilities) | ||||
| Deg. freedom | 2 | 5 | 10 | 20 |
| (A) 10% | ||||
| Chi-squared | 4.605 | 9.236 | 15.987 | 28.412 |
| ES | 4.650 | 9.627 | 16.758 | 29.175 |
| (B) 5% | ||||
| Chi-squared | 5.991 | 11.070 | 18.307 | 31.410 |
| ES | 6.341 | 11.793 | 19.203 | 32.678 |
| (C) 1% | ||||
| Chi-squared | 9.210 | 15.086 | 23.209 | 37.566 |
| ES | 10.448 | 16.559 | 25.034 | 39.683 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mauleón, I. Contributions to Risk Assessment with Edgeworth–Sargan Density Expansions (I): Stability Testing. Mathematics 2022, 10, 1074. https://doi.org/10.3390/math10071074
Mauleón I. Contributions to Risk Assessment with Edgeworth–Sargan Density Expansions (I): Stability Testing. Mathematics. 2022; 10(7):1074. https://doi.org/10.3390/math10071074
Chicago/Turabian StyleMauleón, Ignacio. 2022. "Contributions to Risk Assessment with Edgeworth–Sargan Density Expansions (I): Stability Testing" Mathematics 10, no. 7: 1074. https://doi.org/10.3390/math10071074
APA StyleMauleón, I. (2022). Contributions to Risk Assessment with Edgeworth–Sargan Density Expansions (I): Stability Testing. Mathematics, 10(7), 1074. https://doi.org/10.3390/math10071074





