Jointly Modeling Rating Responses and Times with Fuzzy Numbers: An Application to Psychometric Data
Abstract
:1. Introduction
2. Methodology
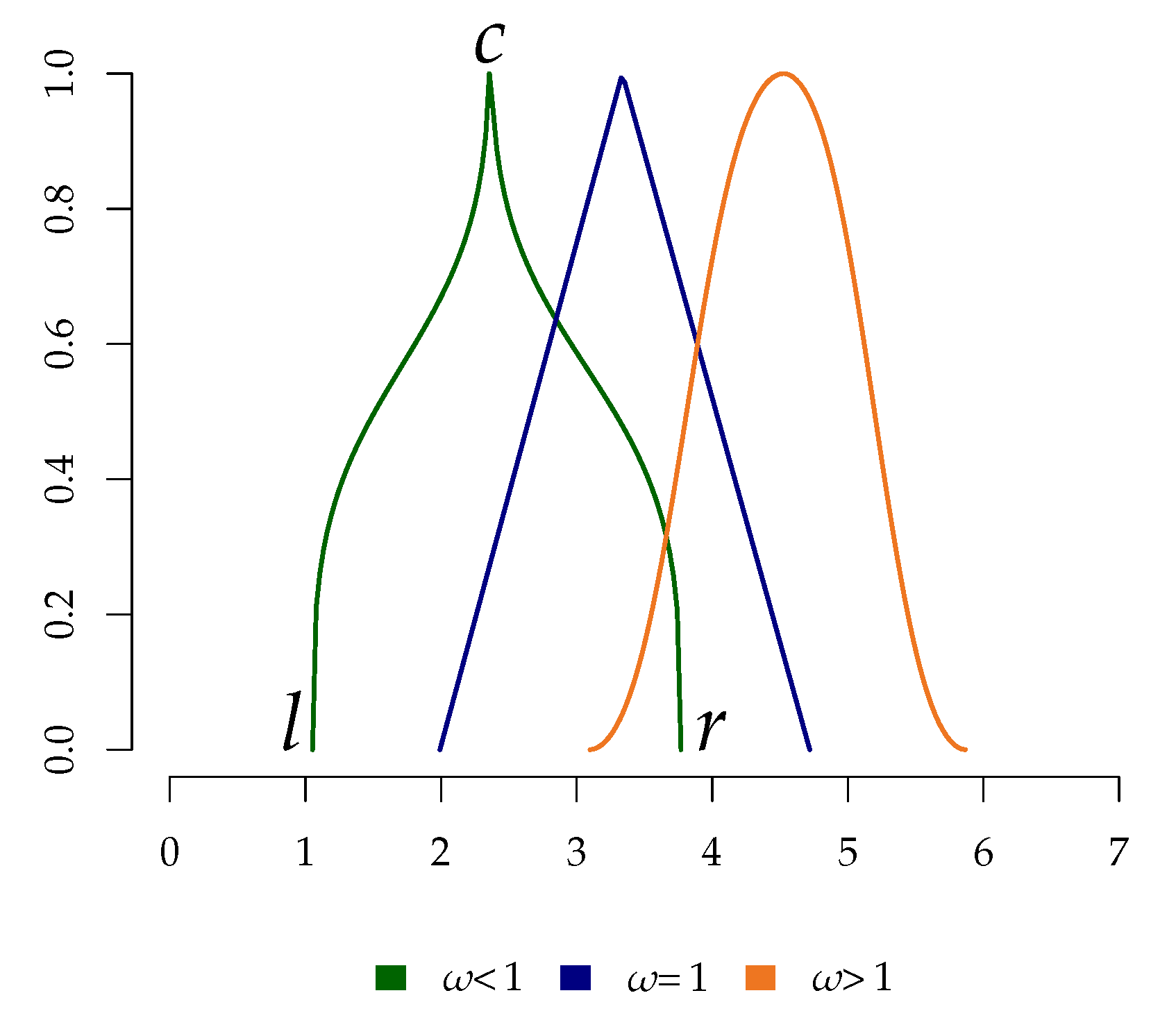
2.1. Fuzzy Numbers
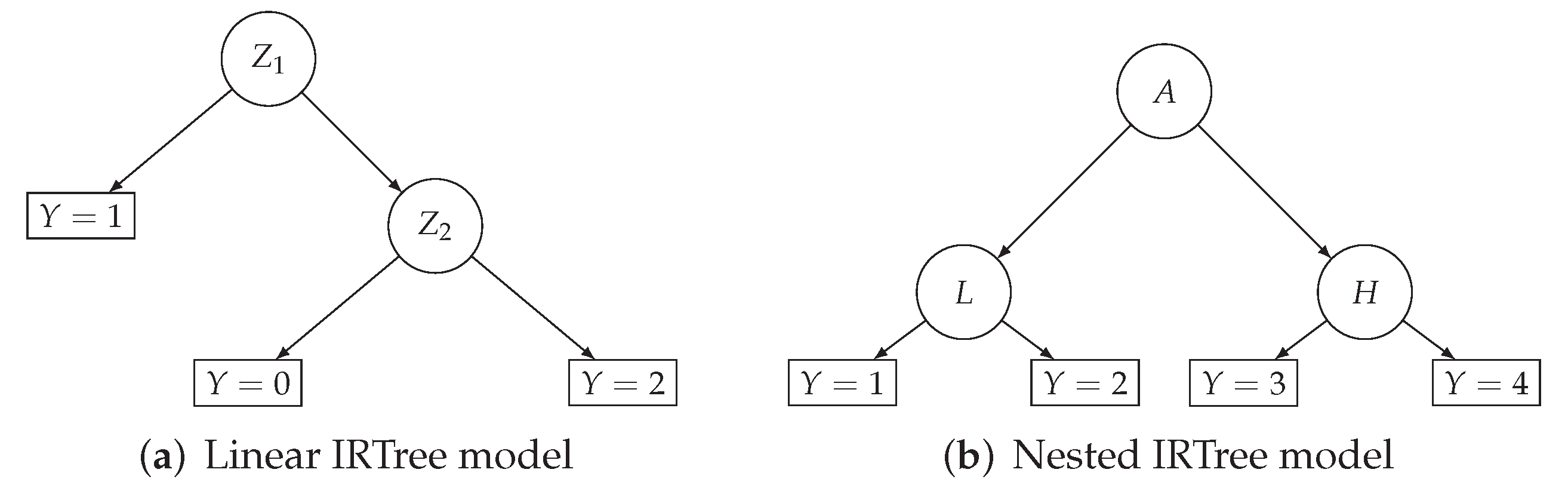
2.2. From IRTree to fIRTree
- Define and fit an IRTtree model to in order to obtain and
- Plug-in and into Equation (5) to obtain the estimated probability distribution
- Compute mode and precision of the fuzzy number via the following equalities:
- Compute left and right bounds using link equations:
- Compute the fuzzy membership function:
- Compute the intensification parameter:
2.3. Fuzzy Normal Linear Model with Crisp Predictors
3. Application
3.1. Data and Variables
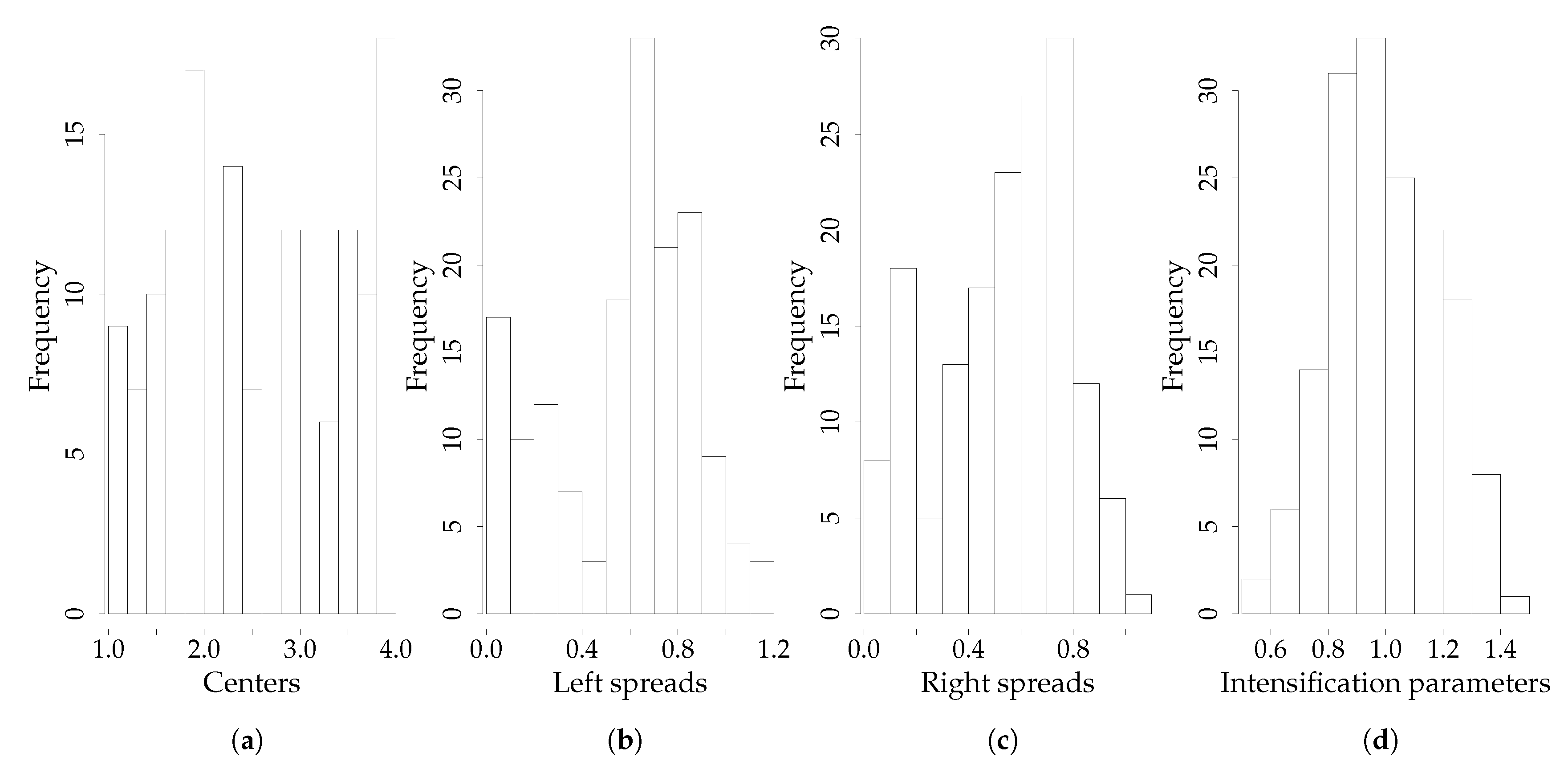
3.2. Data Analysis and Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Schwarz, N.; Oyserman, D. Asking questions about behavior: Cognition, communication, and questionnaire construction. Am. J. Eval. 2001, 22, 127–160. [Google Scholar] [CrossRef] [Green Version]
- Tourangeau, R.; Rips, L.J.; Rasinski, K. The Psychology of Survey Response; Cambridge University Press: Cambridge, MA, USA, 2000. [Google Scholar]
- Rosenbaum, P.J.; Valsiner, J. The un-making of a method: From rating scales to the study of psychological processes. Theory Psychol. 2011, 21, 47–65. [Google Scholar] [CrossRef]
- Calcagnì, A.; Lombardi, L. Modeling random and non-random decision uncertainty in ratings data: A fuzzy beta model. AStA Adv. Stat. Anal. 2022, 106, 145–173. [Google Scholar] [CrossRef]
- Hesketh, T.; Pryor, R.; Hesketh, B. An application of a computerized fuzzy graphic rating scale to the psychological measurement of individual differences. Int. J. Man-Mach. Stud. 1988, 29, 21–35. [Google Scholar] [CrossRef]
- de Sáa, S.D.L.R.; Gil, M.Á.; Gonzalez-Rodriguez, G.; López, M.T.; Lubiano, M.A. Fuzzy rating scale-based questionnaires and their statistical analysis. IEEE Trans. Fuzzy Syst. 2014, 23, 111–126. [Google Scholar] [CrossRef]
- Calcagnì, A.; Lombardi, L. Dynamic Fuzzy Rating Tracker (DYFRAT): A novel methodology for modeling real-time dynamic cognitive processes in rating scales. Appl. Soft Comput. 2014, 24, 948–961. [Google Scholar] [CrossRef]
- Li, Q. Indirect membership function assignment based on ordinal regression. J. Appl. Stat. 2016, 43, 441–460. [Google Scholar] [CrossRef]
- Lalla, M.; Facchinetti, G.; Mastroleo, G. Ordinal scales and fuzzy set systems to measure agreement: An application to the evaluation of teaching activity. Qual. Quant. 2005, 38, 577–601. [Google Scholar] [CrossRef]
- Yu, S.C.; Yu, M.N. Fuzzy partial credit scaling: A valid approach for scoring the Beck Depression Inventory. Soc. Behav. Personal. Int. J. 2007, 35, 1163–1172. [Google Scholar] [CrossRef]
- Costas, C.S.L.; Maranon, P.P.; Cabrera, J.A.H. Application of diffuse measurement to the evaluation of psychological structures. Qual. Quant. 1994, 28, 305–313. [Google Scholar] [CrossRef]
- Chen, P.Y.; Yao, G. Measuring quality of life with fuzzy numbers: In the perspectives of reliability, validity, measurement invariance, and feasibility. Qual. Life Res. 2015, 24, 781–785. [Google Scholar] [CrossRef] [PubMed]
- Calcagnì, A. fIRTree: An Item Response Theory modeling of fuzzy rating data. arXiv 2021, arXiv:2102.02025. [Google Scholar]
- Calcagnì, A.; Cao, N.; Rubaltelli, E.; Lombardi, L. A psychometric modeling approach to fuzzy rating data. Fuzzy Sets Syst. 2022; in press. [Google Scholar] [CrossRef]
- Boeck, P.D.; Partchev, I. IRTrees: Tree-Based Item Response Models of the GLMM Family. J. Stat. Soft. 2012, 48, 1–28. [Google Scholar] [CrossRef] [Green Version]
- Dombi, J.; Jónás, T. Flexible fuzzy numbers for likert scale-based evaluations. In International Workshop Soft Computing Applications; Springer: Berlin/Heidelberg, Germany, 2018; pp. 81–101. [Google Scholar]
- Kyllonen, P.C.; Zu, J. Use of response time for measuring cognitive ability. J. Intell. 2016, 4, 14. [Google Scholar] [CrossRef]
- Corral, N. The minimun inaccuracy fuzzy estimation: An extension of the maximum likelihood principle. Stochastica 1984, 8, 63–81. [Google Scholar]
- Kruse, R.; Borgelt, C.; Braune, C.; Mostaghim, S.; Steinbrecher, M. Fuzzy Data Analysis. In Computational Intelligence; Springer: Berlin/Heidelberg, Germany, 2016; pp. 431–456. [Google Scholar]
- Couso, I.; Borgelt, C.; Hullermeier, E.; Kruse, R. Fuzzy sets in data analysis: From statistical foundations to machine learning. IEEE Comput. Intell. Mag. 2019, 14, 31–44. [Google Scholar] [CrossRef]
- Chukhrova, N.; Johannssen, A. Fuzzy regression analysis: Systematic review and bibliography. Appl. Soft Comput. 2019, 84, 105708. [Google Scholar] [CrossRef]
- Couso, I.; Dubois, D. Statistical reasoning with set-valued information: Ontic vs. epistemic views. Int. J. Approx. Reason. 2014, 55, 1502–1518. [Google Scholar] [CrossRef]
- Gebhardt, J.; Gil, M.A.; Kruse, R. Fuzzy set-theoretic methods in statistics. In Fuzzy Sets in Decision Analysis, Operations Research and Statistics; Springer: Berlin/Heidelberg, Germany, 1998; pp. 311–347. [Google Scholar]
- Denœux, T. Maximum likelihood estimation from fuzzy data using the EM algorithm. Fuzzy Sets Syst. 2011, 183, 72–91. [Google Scholar] [CrossRef] [Green Version]
- Tóth, Z.E.; Jónás, T.; Dénes, R.V. Applying flexible fuzzy numbers for evaluating service features in healthcare–patients and employees in the focus. Total Qual. Manag. Bus. Excell. 2019, 30, S240–S254. [Google Scholar] [CrossRef]
- Nasibov, E.N.; Peker, S. On the nearest parametric approximation of a fuzzy number. Fuzzy Sets Syst. 2008, 159, 1365–1375. [Google Scholar] [CrossRef]
- Casey, M.M.; Tryon, W.W. Validating a double-press method for computer administration of personality inventory items. Psychol. Assess. 2001, 13, 521. [Google Scholar] [CrossRef]
- Mignault, A.; Marley, A.; Chaudhuri, A. Inverted-U effects generalize to the judgment of subjective properties of faces. Percept. Psychophys. 2008, 70, 1274–1288. [Google Scholar] [CrossRef] [PubMed]
- De Boeck, P.; Bakker, M.; Zwitser, R.; Nivard, M.; Hofman, A.; Tuerlinckx, F.; Partchev, I. The estimation of item response models with the lmer function from the lme4 package in R. J. Stat. Softw. 2011, 39, 1–28. [Google Scholar] [CrossRef] [Green Version]
- Jeon, M.; Boeck, P.D. A generalized item response tree model for psychological assessments. Behav. Res. Methods 2015, 48, 1070–1085. [Google Scholar] [CrossRef]
- Parkitny, L.; McAuley, J. The depression anxiety stress scale (DASS). J. Physiother. 2010, 56, 204. [Google Scholar] [CrossRef] [Green Version]
- Brooks, M.E.; Kristensen, K.; van Benthem, K.J.; Magnusson, A.; Berg, C.W.; Nielsen, A.; Skaug, H.J.; Maechler, M.; Bolker, B.M. glmmTMB Balances Speed and Flexibility Among Packages for Zero-inflated Generalized Linear Mixed Modeling. R J. 2017, 9, 378–400. [Google Scholar] [CrossRef] [Green Version]
- Gosling, S.D.; Rentfrow, P.J.; Swann, W.B., Jr. A very brief measure of the Big-Five personality domains. J. Res. Personal. 2003, 37, 504–528. [Google Scholar] [CrossRef]
- Lubiano, M.A.; García-Izquierdo, A.L.; Gil, M.Á. Fuzzy rating scales: Does internal consistency of a measurement scale benefit from coping with imprecision and individual differences in psychological rating? Inf. Sci. 2021, 550, 91–108. [Google Scholar] [CrossRef]
- Yan, T.; Tourangeau, R. Fast times and easy questions: The effects of age, experience and question complexity on web survey response times. Appl. Cogn. Psychol. Off. J. Soc. Appl. Res. Mem. Cogn. 2008, 22, 51–68. [Google Scholar] [CrossRef] [Green Version]
- Bjelland, I.; Krokstad, S.; Mykletun, A.; Dahl, A.A.; Tell, G.S.; Tambs, K. Does a higher educational level protect against anxiety and depression? The HUNT study. Soc. Sci. Med. 2008, 66, 1334–1345. [Google Scholar] [CrossRef] [PubMed]
- Koenig, H.G. Research on religion, spirituality, and mental health: A review. Can. J. Psychiatry 2009, 54, 283–291. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kotov, R.; Gamez, W.; Schmidt, F.; Watson, D. Linking “big” personality traits to anxiety, depressive, and substance use disorders: A meta-analysis. Psychol. Bull. 2010, 136, 768. [Google Scholar] [CrossRef]
- Veall, M.R.; Zimmermann, K.F. Evaluating Pseudo-R2’s for binary probit models. Qual. Quant. 1994, 28, 151–164. [Google Scholar] [CrossRef] [Green Version]
- De Boeck, P.; Jeon, M. An overview of models for response times and processes in cognitive tests. Front. Psychol. 2019, 10, 102. [Google Scholar] [CrossRef] [Green Version]


| Models | () | (1 − %) CI |
|---|---|---|
| Normal Linear Model | ||
| Residuals quantiles: Q1: −0.555, Med: −0.041, Q3: 0.611 | ||
| (Intercept) | 4.204 (0.211) | [3.788, 4.621] |
| religiousness (No vs. Yes) | −0.146 (0.135) | [−0.412, 0.120] |
| emotional_stability | −0.232 (0.029) | [−0.289, 0.174] |
| university (No vs. Yes) | −0.280 (0.119) | [−0.516, −0.044] |
| pseudo- | ||
| Log-Normal Model | ||
| Residuals quantiles: Q1: −0.298, Med: −0.060, Q3: 2.427 | ||
| (Intercept) | 0.138 (58.573) | [7.792, 8.336] |
| religiousness (No vs. Yes) | 0.256 (0.088) | [0.083, 0.429] |
| emotional_stability | 0.003 (0.019) | [−0.034, 0.041] |
| university (No vs. Yes) | 0.162 (0.078) | [0.008, 0.316] |
| pseudo- | ||
| Fuzzy Normal Linear Model | ||
| Residuals quantiles: Q1: −0.287, Med: 0.068, Q3: 0.737 | ||
| (Intercept) | 3.383 (0.259) | [2.870,3.894] |
| religiousness (No vs. Yes) | −0.169 (0.152) | [−0.469,0.130] |
| emotional_stability | −0.127 (0.034) | [−0.195, −0.060] |
| university (No vs. Yes) | −0.172 (0.134) | [−0.436, 0.093] |
| pseudo- |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, N.; Calcagnì, A. Jointly Modeling Rating Responses and Times with Fuzzy Numbers: An Application to Psychometric Data. Mathematics 2022, 10, 1025. https://doi.org/10.3390/math10071025
Cao N, Calcagnì A. Jointly Modeling Rating Responses and Times with Fuzzy Numbers: An Application to Psychometric Data. Mathematics. 2022; 10(7):1025. https://doi.org/10.3390/math10071025
Chicago/Turabian StyleCao, Niccolò, and Antonio Calcagnì. 2022. "Jointly Modeling Rating Responses and Times with Fuzzy Numbers: An Application to Psychometric Data" Mathematics 10, no. 7: 1025. https://doi.org/10.3390/math10071025
APA StyleCao, N., & Calcagnì, A. (2022). Jointly Modeling Rating Responses and Times with Fuzzy Numbers: An Application to Psychometric Data. Mathematics, 10(7), 1025. https://doi.org/10.3390/math10071025






