On a New Generalization of Bernstein-Type Rational Functions and Its Approximation
Abstract
1. Introduction
2. Approximation Results
3. Local and Global Approximation
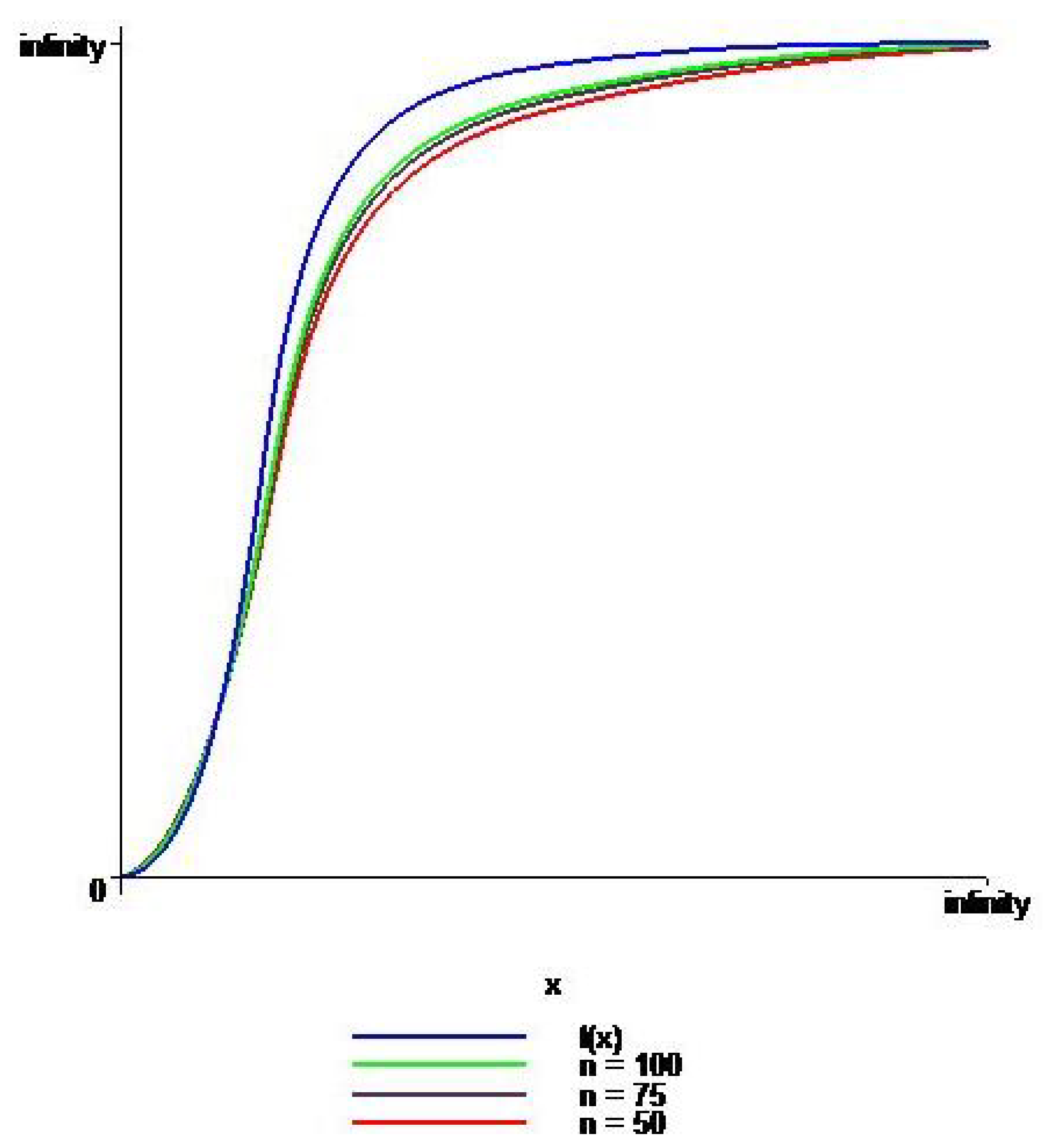
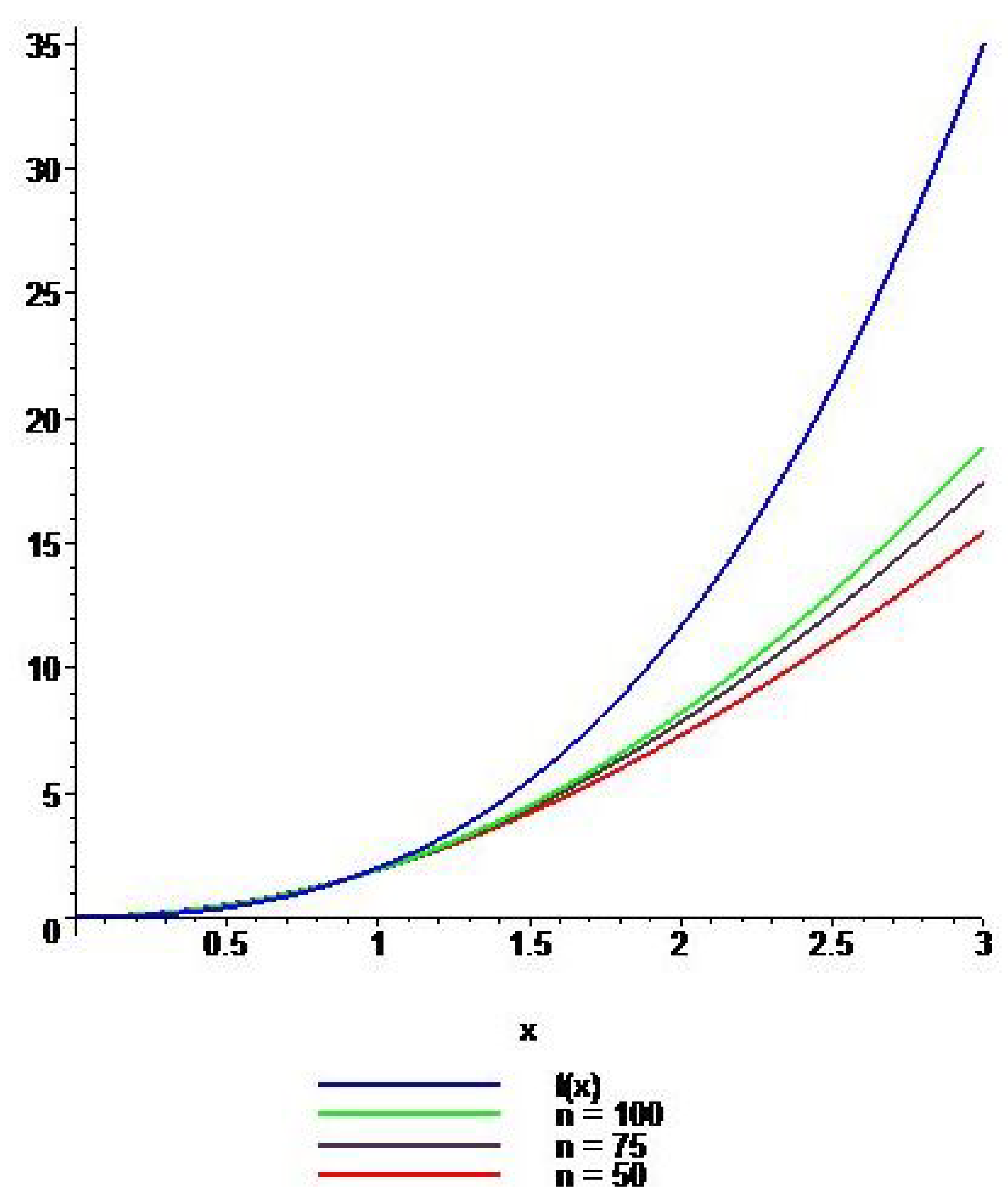
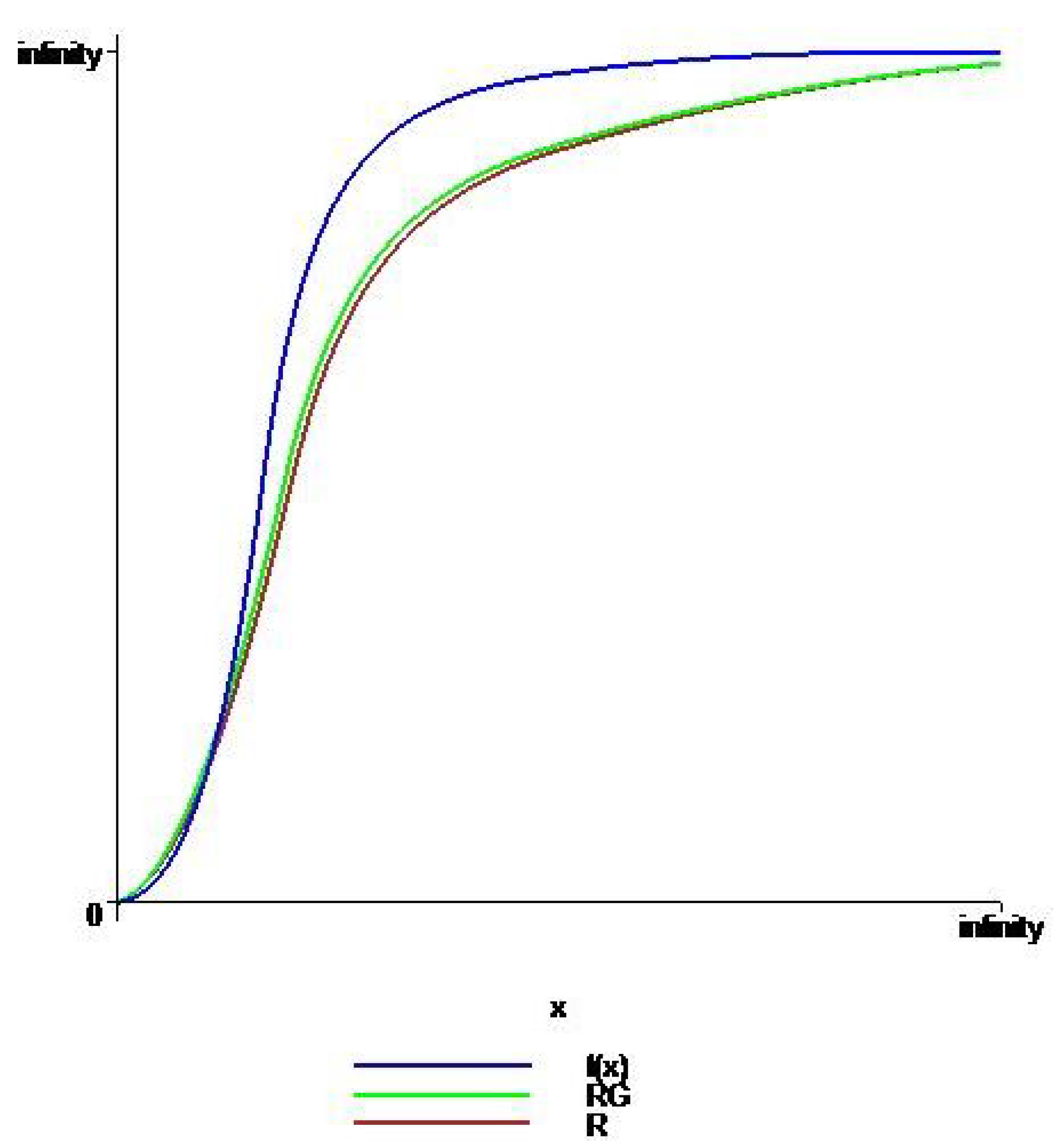
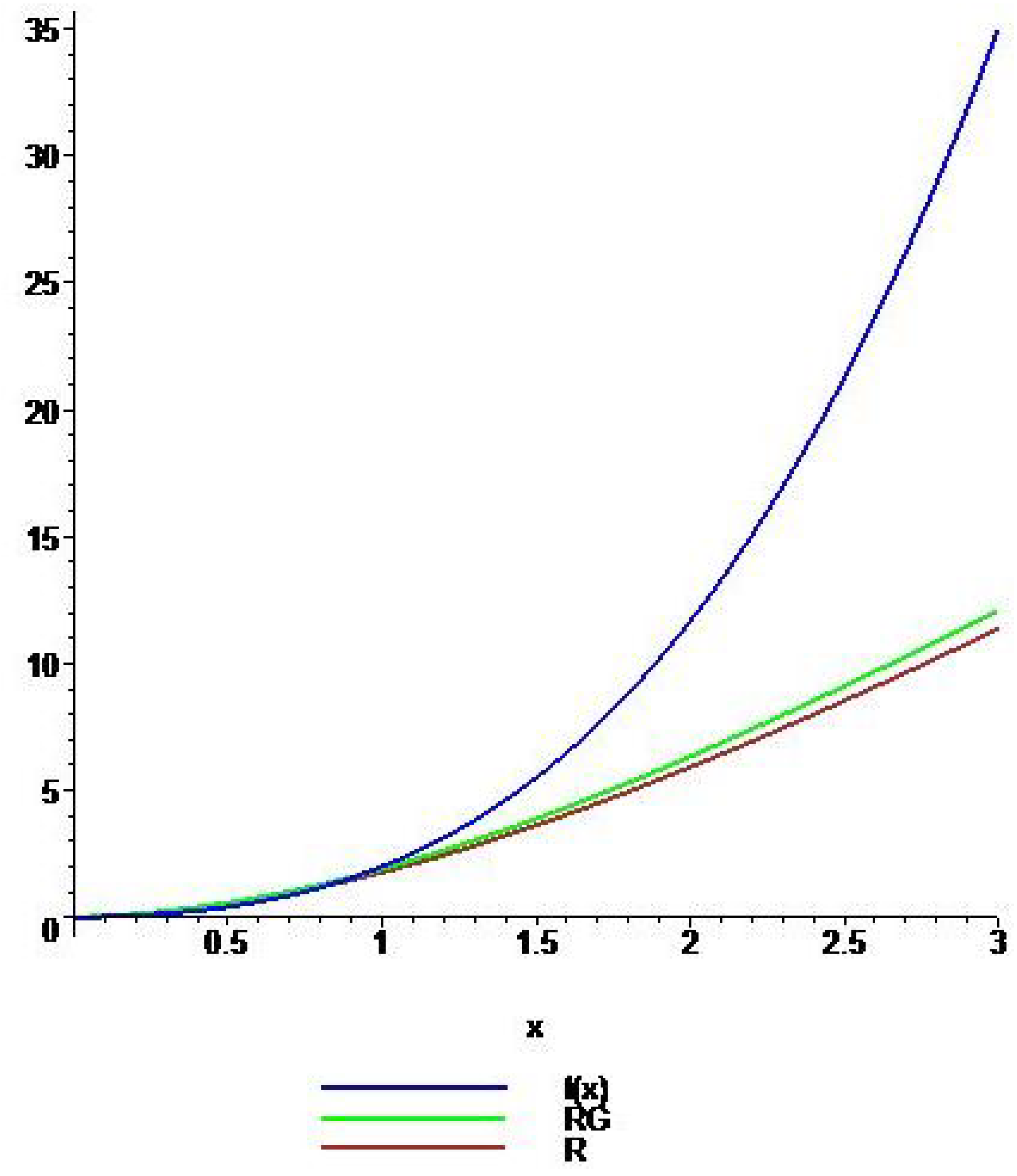
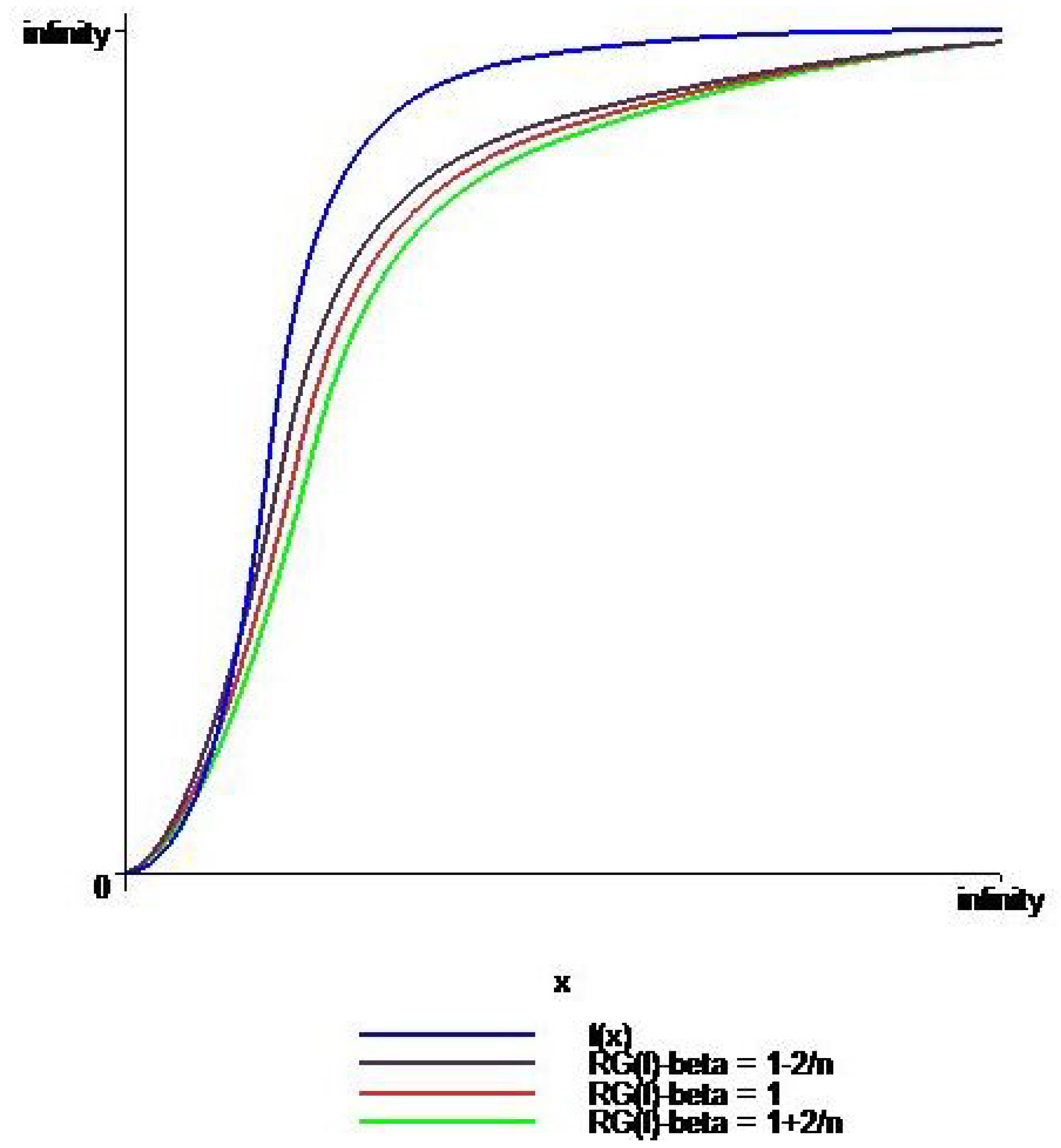
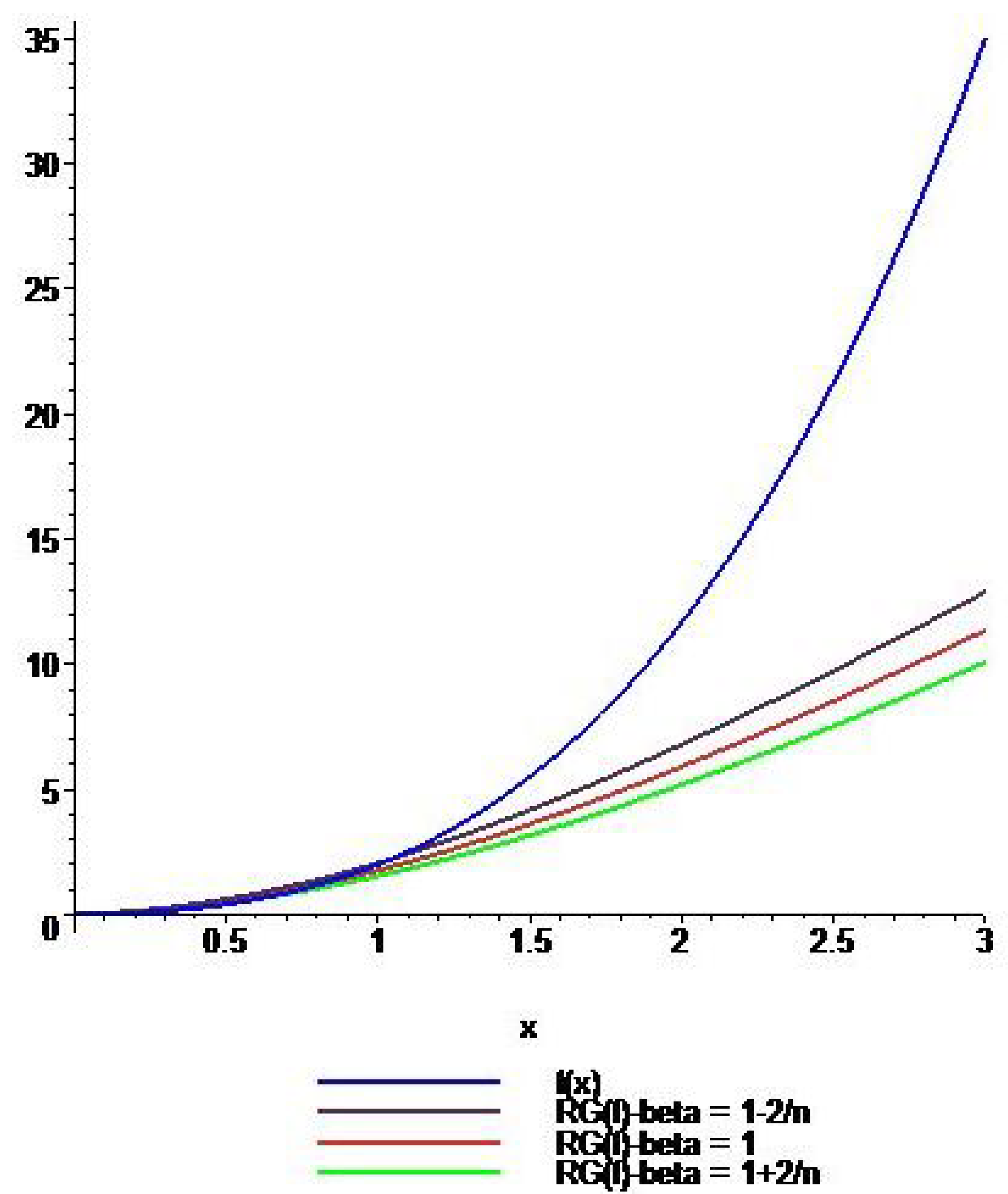
4. Graphical Comparison
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bernstein, S.N. Démonstration du théorème de Weierstrass fondée sur le calcul de probabilités. Commun. Soc. Math. Kharkow 2013, 13, 1–2. [Google Scholar]
- Balázs, K. Approximation by Bernstein type rational funstions. Acta Math. Acad. Sci. Hungar. 1975, 26, 123–134. [Google Scholar] [CrossRef]
- Balázs, K.; Szabados, J. Approximation by Bernstein type rational functions II. Acta Math. Acad. Sci. Hungar. 1982, 40, 331–337. [Google Scholar] [CrossRef]
- Balázs, K. Approximation by Bernstein type rational functions on the real axis. Acta Math. Hung. 1985, 46, 195–204. [Google Scholar] [CrossRef]
- Totik, V. Saturation for Bernstein type rational functions. Acta Math. Hung. 1984, 43, 219–250. [Google Scholar] [CrossRef]
- Abel, U.; Vecchia, B.D. Asymptotic approximation by the operators of K. Balázs and Szabados. Acta Sci. Math. 2000, 66, 137–145. [Google Scholar]
- Holhos, A. On the approximation by Balázs-Szabados operators. Mathematics 2021, 9, 1588. [Google Scholar] [CrossRef]
- İspir, N.; Atakut, Ç. Approximation by generalized Balázs type rational functions. Int. J. Comput. Numer. Anal. 2003, 4, 297–316. [Google Scholar]
- Agratini, O. On a class of Bernstein-type rational functions. Numer. Funct. Anal. Optim. 2020, 41, 483–494. [Google Scholar] [CrossRef]
- Gupta, V.; İspir, N. On Bézier variant of generalized Kantorovich type Balázs operators. Appl. Math. Lett. 2005, 18, 1053–1061. [Google Scholar] [CrossRef][Green Version]
- Gupta, V.; Lupaş, A. On the rate of approximation for the Bézier variant of Kantorovich-Balázs operators. Gen. Math. 2004, 1, 3–18. [Google Scholar] [CrossRef]
- Gupta, V.; Zeng, X.M. Rate of approximation fort he Bézier variant of Balázs Kantorovich operators. Math. Slovaca 2007, 57, 349–358. [Google Scholar] [CrossRef]
- Hamal, H.; Sabancıgil, P. Some approximation properties of new Kantorovich type q-analogue of Balázs-Szabados operators. J. Inequal. Appl. 2020, 2020, 159. [Google Scholar] [CrossRef]
- İspir, N.; Özkan, E.Y. Approximation properties of complex q-Balázs-Szabados operators in compact disks. J. Inequal. Appl. 2013, 2013, 361. [Google Scholar] [CrossRef]
- Özkan, E.Y.; İspir, N. Approximation by (p,q)-analogue of Balázs-Szabados operators. Filomat 2018, 32, 2257–2271. [Google Scholar] [CrossRef]
- Özkan, E.Y. Approximation properties of bivariate complex q-Balázs-Szabados operators of tensor product kind. J. Inequal. Appl. 2014, 2014, 20. [Google Scholar] [CrossRef][Green Version]
- Özkan, E.Y. Statistical approximation properties of q-Balázs-Szabados-Stancu operators. Filomat 2014, 28, 1943–1952. [Google Scholar] [CrossRef][Green Version]
- Özkan, E.Y. Approximation by complex bivariate Balázs-Szabados operators. Bull. Malays. Math. Sci. Soc. 2016, 39, 1–16. [Google Scholar] [CrossRef]
- Özkan, E.Y. Approximation properties of Kantorovich type q-Balázs-Szabados operators. Demonstr. Math. 2019, 52, 10–19. [Google Scholar] [CrossRef]
- Özkan, E.Y. Quantitative estimates for the tensor product (p,q)-Balázs-Szabados operators and associated Boolean sum operators. Filomat 2020, 34, 779–793. [Google Scholar] [CrossRef]
- Korovkin, P.P. On convergence of linear positive operators in the space of continuous functions. Dokl. Akad. Nauk. SSSR 1953, 90, 961–964. [Google Scholar]
- Devore, R.A.; Lorentz, G.G. Constructive Approximation: Polynomials and Splines Approximation; Springer: Berlin/Heidelberg, Germany, 1993. [Google Scholar]
- Butzer, P.L.; Berens, H. Semi-Groups of Operators and Approximation; Springer: New York, NY, USA, 1967. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Özkan, E.Y.; Aksoy, G. On a New Generalization of Bernstein-Type Rational Functions and Its Approximation. Mathematics 2022, 10, 973. https://doi.org/10.3390/math10060973
Özkan EY, Aksoy G. On a New Generalization of Bernstein-Type Rational Functions and Its Approximation. Mathematics. 2022; 10(6):973. https://doi.org/10.3390/math10060973
Chicago/Turabian StyleÖzkan, Esma Yıldız, and Gözde Aksoy. 2022. "On a New Generalization of Bernstein-Type Rational Functions and Its Approximation" Mathematics 10, no. 6: 973. https://doi.org/10.3390/math10060973
APA StyleÖzkan, E. Y., & Aksoy, G. (2022). On a New Generalization of Bernstein-Type Rational Functions and Its Approximation. Mathematics, 10(6), 973. https://doi.org/10.3390/math10060973





