Non-Isolated Resolving Sets of Corona Graphs with Some Regular Graphs

Abstract

Let G be a connected, simple, and finite graph. For an ordered set $W=\{w_1,w_2,\dots ,w_k\}\subseteq V\left(G\right)$ and a vertex v of G, the representation of v with respect to W is the k-vector $r\left(v\right|W)=(d_G(v,w_1),\dots ,d_G(v,w_k))$. The set W is called a resolving set of G, if every two vertices of G has a different representation. A resolving set containing a minimum number of vertices is called a basis of H. The number of elements in a basis of G is called the metric dimension of G and denoted by $dim\left(G\right)$. In this paper, we considered a resolving set W of G where the induced subgraph of G by W does not contain an isolated vertex. Such a resolving set is called a non-isolated resolving set. A non-isolated resolving set of G with minimum cardinality is called an $nr$-set of G. The cardinality of an $nr$-set of G is called the non-isolated resolving number of G, denoted by $nr\left(G\right)$. Let H be a graph. The corona product graph of G with H, denoted by $G\odot H$, is a graph obtained by taking one copy of G and $\left|V\right(G\left)\right|$ copies of H, namely $H^1,H^2,\dots ,H^{\left|V\right(G\left)\right|}$, such that the i-th vertex of G is adjacent to every vertex of $H^i$. If the degree of every vertex of H is k, then H is called a k-regular graph. In this paper, we determined $nr(G\odot H)$ where G is an arbitrary connected graph of order n at least two and H is a k-regular graph of order t with $k\in \{t-2,t-3\}$.

1. Introduction

Let G be a simple, finite, and connected graph with the vertex set $V\left(G\right)$ and the edge set $E\left(G\right)$. For u and v in $V\left(G\right)$, the distance between two different vertices u and v is the length of the shortest u - v path in G, denoted by $d_G(u,v)$. Let $W=\{w_1,w_2,\dots ,w_k\}$ be an ordered set of vertices of G. The representation of $v\in V\left(G\right)$ with respect to W is the k-vector $r\left(v\right|W)=(d_G(v,w_1),\dots ,d_G(v,w_k))$. If every two vertices of G has a different representation, then the set W is called a resolving set of G. A resolving set containing a minimum number of vertices is called a basis of G. The number of elements in a basis of G is called the metric dimension of G and denoted by $dim\left(G\right)$.

The metric dimension concept of a graph was first introduced by Slater [1] and Harary and Melter [2]. Since then, many results in the metric dimension have been obtained. Some of them can be seen in [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17]. A resolving set is needed to manage robotic navigation [18], to identify chemical compounds [19], and to optimize the placement of threat detection sensors [20].

Practically, we need a threat detection sensor that also has the function to check whether its neighbor sensor is malfunctioning or not. Hence, we need an optimization of the placement of threat detection sensors such that the location of each sensor must not be isolated. In 2015, Chitra and Arumugan [21] introduced the concept of a non-isolated resolving set. Let W be a subset of $V\left(H\right)$. A resolving set W is called a non-isolated resolving set, if the induced subgraph of H by W has no isolated vertex. A non-isolated resolving set of H with minimum cardinality is called an nr-set of H. The cardinality of an $nr$-set of H is called the non-isolated resolving number of H, denoted by $nr\left(H\right)$. Since a non-isolated resolving set is also a resolving set of a connected graph H of order n, we have:

$$1\le dim\left(H\right)\le nr\left(H\right)\le n-1.$$

(1)

Chitra and Arumugam [21] determined the non-isolated resolving number of some classes of graphs such as complete bipartite graphs, complete graphs, paths, and friendship graphs. The non-isolated resolving number of the graph depends on the structure of the graph. We can obtain a structure of a graph by using an operation between two graphs. Determining a relation, in terms of a non-isolated resolving number, between the original graph and the resulting graph under a graph operation is also interesting to be considered. Chitra and Arumugam also determined the non-isolated resolving number of the Cartesian product between a path and a path, a cycle, and a complete graph. In addition, they provided an upper bound for the non-isolated resolving number of the Cartesian product of a connected graph with a complete graph. In 2018, Hasibuan et al. [22] continued the investigation of the non-isolated resolving set of the Cartesian product of some graphs. They showed the non-isolated number of the Cartesian product between a path and some simple graphs, namely a complete graph, a cycle, a bipartite, and a friendship graph.

Now, we consider corona product graphs. Let G be a connected graph of order $n\ge 2$ and H be a graph of order $t\ge 2$. The corona product graph $G\odot H$ is a graph obtained by taking one copy of G and $\left|V\right(G\left)\right|$ copies of H, namely $H^1,H^2,\dots ,H^{\left|V\right(G\left)\right|}$, such that the i-th vertex of G is adjacent to every vertex of $H^i$. If the degree of every vertex of H is k, then H is said to be k-regular. Abidin et al. [23] studied the non-isolated resolving set of $G\odot H$ where H is a complete graph. Note that a simple and $(t-1)$-regular graph is isomorphic to a complete graph of order t.

In this paper, we determined $nr(G\odot H)$ where G is any connected graph of order at least two and H is a k-regular graph of order t for $k=t-2$ or $k=t-3$. From now on, we only consider finite and simple graphs. We also define $[a,b]=\{n\in Z|a\le n\le b\}$.

2. Non-Isolated Resolving Set of $\mathit{G}\odot {\mathit{H}}_{\mathit{t}}$ Where ${\mathit{H}}_{\mathit{t}}$ Is a $(\mathit{t}-\mathbf{2})$-Regular Graph

Let $H_t$ be a $(t-2)$-regular graph of order t. A subset M of $E\left(H_t\right)$ is called a matching in $H_t$ if no two of its elements are adjacent in $H_t$. If M is a matching in $H_t$ with the property that every vertex of $H_t$ is incident with an edge of M, then M is called a perfect matching in $H_t$ [24]. If $H_t$ is a $(t-2)$-regular graph of order $t\ge 2$, it is easy to check that t is an even positive integer and $H_t$ is isomorphic to a complete graph of order t minus a perfect matching in $H_t$. In this section, we determine a non-isolated resolving number of the corona product of a connected graph with a $(t-2)$-regular graph of order t.

Theorem 1.

Let n be a positive integer and t be an even integer at least two. If G is a connected graph of order n and $H_t$ is a $(t-2)$-regular graph of order t, then:

$$nr(G\odot H_t)=\left\{\begin{array}{cc}2n,\hfill & \mathrm{if}t=2;\hfill \\ {\displaystyle \frac{nt}{2}},\hfill & \mathrm{if}t\ge 4.\hfill \end{array}\right.$$

Proof. 

Let $V\left(G\right)=\{u_1,u_2,u_3,u_4,\cdots ,u_n\}$ and $t=2m$ for some positive integer m. By the definition of the corona product, for every $l\in [1,n]$, let $V\left(H_t^l\right)=\{v_1^l,v_2^l,\dots ,v_{2m}^l\}$ be the vertex set of $H_t^l$ such that $E\left(H_t^l\right)=\left\{v_i^l{v}_j^l\right|i$ and j in $[1,2m]$ with $i<j$ and $j\ne m+i\}$. Therefore, we can say that $V(G\odot H_t)=V\left(G\right)\cup {\bigcup }_{l=1}^{n}V\left(H_t^l\right)$ and $E(G\odot H_t)=E\left(G\right)\cup {\bigcup }_{l=1}^{n}E\left(H_t^l\right)\cup \left\{v_j^l{u}_l\right|l\in [1,n],j\in [1,2m]\}.$ We distinguish two cases.

Case 1. $m=1$:

First, we show that $nr(G\odot H_t)\le 2n$. We define $W_l=\{u_l,v_1^l\}$ for every $l\in [1,n]$. Let $W={\cup }_{l=1}^n{W}_l$. Since $u_l{v}_1^l\in E(G\odot H_t)$, there is no isolated vertex in W. Let x and y be two different vertices in $V(G\odot H_t)-W=\left\{v_2^l\right|l\in [1,n]\}$. Let $x=v_2^p$ and $y=v_2^q$ for some p and q in $[1,n]$ with $p\ne q$. Since $d_{G\odot H_t}(x,v_1^p)=2<d_{G\odot H_t}(y,v_1^p)$, we obtain $r\left(x\right|W_p)\ne r\left(y\right|W_p)$. Therefore, $r\left(x\right|W)\ne r(y\left|W\right)$.

Next, we show that $nr(G\odot H_t)\ge 2n$. Suppose that $W^{\prime }$ is an $nr$-set of $G\odot H_t$ with $|W^{\prime }|<2n$. For every $a\in [1,n]$, let $W_a^{\prime }=W^{\prime }\cap \{V\left(H_t^a\right)\cup \left\{u_a\right\}\}$. Since $|W^{\prime }|<2n$, there exists $b\in [1,n]$ such that $|W_b^{\prime }|\le 1$. Since $W_b^{\prime }$ does not contain an isolated vertex, there are two different vertices $v_1^b$ and $v_2^b$ in $V\left(H_t^b\right)-W^{\prime }$ satisfying $r\left(v_1^b\right|W^{\prime })=r\left(v_2^b\right|W^{\prime })$. Therefore, we obtain a contradiction.

Case 2.$m\ge 2$:

We show that $nr(G\odot H_t)\le nm$. For every $l\in [1,n]$, we define $W_l=\{v_1^l,v_2^l\dots ,v_m^l\}$. Since an induced subgraph of $G\odot H_t$ by $W_l$ is isomorphic to a complete graph on order m, it is easy to see that there is no isolated vertex in $W_l$. Let $W={\bigcup }_{l=1}^n{W}_l$. Let x and y be any two different vertices in $V\left(H_t\right)-W$. We consider four subcases.

Subcase 2.1.x and y in $V\left(H_t^p\right)$ for some $p\in [1,n]$:

Let $x=v_{m+a}^p$ and $y=v_{m+b}^p$ for some a and b in $[1,m]$ with $a\ne b$. Since $d_{G\odot H_t}(x,v_b^p)=1<d_{G\odot H_t}(y,v_b^p)$, we have $r\left(x\right|W_p)\ne r\left(y\right|W_p)$. Therefore, $r\left(x\right|W)\ne r(y\left|W\right)$.

Subcase 2.2.$x\in V\left(H_t^p\right)$ for some $p\in [1,n]$ and $y\in V\left(G\right)$:

Let $x=v_{m+a}^p$ for some $a\in [1,m]$ and $y=u_q$ for some $q\in [1,n]$. If $p=q$, then $d_{G\odot H_t}(x,v_a^p)=2>1=d_{G\odot H_t}(y,v_a^p)$. This means that $r\left(x\right|W_p)\ne r\left(y\right|W_p)$. If $p\ne q$, then there exists $v_c^p\in W_p-\left\{v_a^p\right\}$ such that $d_{G\odot H_t}(x,v_c^p)=1<d_{G\odot H_t}(y,v_c^p)$. This means that $r\left(x\right|W_p)\ne r\left(y\right|W_p)$. Therefore, $r\left(x\right|W)\ne r(y\left|W\right)$.

Subcase 2.3.$x\in V\left(H_t^p\right)$ and $y\in V\left(H_t^q\right)$ for some p and q in $[1,n]$ with $p\ne q$:

Let $x=v_{m+a}^p$ and $y=v_{m+b}^q$ for some a and b in $[1,m]$. Since $d_{G\odot H_t}(x,v_a^p)=2<d_{G\odot H_t}(y,v_a^p)$, we obtain $r\left(x\right|W_p)\ne r\left(y\right|W_p)$. Therefore, $r\left(x\right|W)\ne r(y\left|W\right)$.

Subcase 2.4.x and y in $V\left(G\right)$ with $x\ne y$:

Let $x=u_p$ and $y=u_q$ for some p and q in $[1,n]$ with $p\ne q$. Since $d_{G\odot H_t}(x,v_1^p)=1<d_{G\odot H_t}(y,v_1^p)$, we obtain $r\left(x\right|W_p)\ne r\left(y\right|W_p)$. Therefore, $r\left(x\right|W)\ne r(y\left|W\right)$.

Next, we show that $nr(G\odot H_t)\ge nm$. Suppose that $W^{\prime }$ is an $nr$-set of $G\odot H_t$ with $|W^{\prime }|<nm$. Then, there exists $p\in [1,n]$ such that $|W^{\prime }\cap V\left(H_t^p\right)|<m$. There exist two different vertices $v_a^p$ and $v_{a+m}^p$ for some $a\in [1,m]$ that are not in $W^{\prime }$. Note that for every $c\in [1,2m]-\{a,a+m\},$ we obtain $d_{G\odot H_t}(v_a^p,v_c^p)=1=d_{G\odot H_t}(v_{a+m}^p,v_c^p)$, and for every $z\in V(G\odot H_t)-V\left(H_l^p\right)$, we have $d_{G\odot H_t}(v_a^p,z)=d_{G\odot H_t}(v_{a+m}^p,z)$. Therefore, we have $r\left(v_a^p\right|W^{\prime })=r\left(v_{a+m}^p\right|W^{\prime })$. This is a contradiction. □

An illustration of Theorem 1 can be seen in Figure 1.

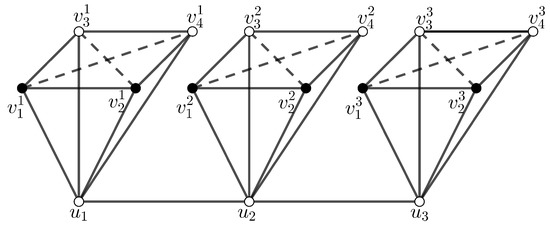
Figure 1. $P_3\odot K_4$ with its $nr$-set $W=\{v_1^1,v_2^1,v_1^2,v_2^2,v_1^3,v_2^3$}.

3. Non-Isolated Resolving Set of $\mathit{G}\odot {\mathit{H}}_{\mathit{t}}$ Where ${\mathit{H}}_{\mathit{t}}$ Is a $(\mathit{t}-\mathbf{3})$-Regular Graph

In this section, we investigate $nr(G\odot H_t)$ where $H_t$ is a $(t-3)$-regular graph for any $t\ge 3$. It is easy to check that $H_t$ is connected if and only if $t\ge 5$. Note that for a connected graph G, a graph $G\odot H_t$ is still connected for $t\in \{3,4\}$. In case $t\in [3,4]$, we show that $nr(G\odot H_t)$ only depends on the order of G, which can be seen in Section 3.3. In case $t\ge 5$, we prove that for most cases of $nr(G\odot H_t)$, it depends on $nr\left(H_t\right)$.

Now, assume $t\ge 5$. In Lemma 1, we show that $H_t$ is isomorphic to the join product of $B_{m_1},B_{m_2},\dots ,$ and $B_{m_q}$ for some $q\in [1,\lfloor \frac{t}{3}\rfloor ]$, where $B_{m_i}=K_{m_i}-E\left(C_{m_i}\right)$ with $K_{m_i}$ a complete graph of order $m_i$ and $C_{m_i}$ a cycle graph of order $m_i$. We recall the join product of $G_1$ and $G_2$, denoted by $G_1+G_2$, which is a graph with the vertex set $V(G_1+G_2)=V\left(G_1\right)\cup V\left(G_2\right)$ and the edge set $E(G_1+G_2)=E\left(G_1\right)\cup E\left(G_2\right)\cup \left\{uv\right|u\in V\left(G_1\right),v\in V\left(G_2\right)\}$. We also prove that for some cases $H_t$, $nr\left(H_t\right)$ depends on $nr\left(B_k\right)$ for every $k\in [1,q]$.

Lemma 1.

For an integer $t\ge 5$, let $H_t$ be a $(t-3)$-regular graph. Then, there exists $q\in [1,\lfloor \frac{t}{3}\rfloor ]$ such that $H_t=B_{m_1}+B_{m_2}+\dots +B_{m_q}$, where for every $i\in [1,q],B_{m_i}=K_{m_i}-E\left(C_{m_i}\right)$ with $m_i$ is an integer at least three and $m_1+\dots +m_q=t$.

Proof. 

Let $H_t$ be a $(t-3)$-regular graph. Let $3\le m_i\le t$ and $B_{m_i}$ be a complete graph of order $m_i$ minus a Hamiltonian cycle. It is shown that $H_t=B_{m_1}+B_{m_2}+\dots +B_{m_q}$ by using the following algorithm.

Input: a $(t-3)$-regular graph $H_t$ with t vertices:

1.

Let $i:=1$;

2.

Let $G_i=H_t$;

3.

Choose two non-adjacent vertices in $G_i$, say $v_1^i$ and $v_2^i$ and say another unlabeled vertex that is not adjacent to $v_2^i$ as $v_3^i$;

4.

Let $j:=3$;

5.

Let $v\ne v_{j-1}^i$ be a vertex that is not adjacent to $v_j^i$;

6.

If $v_j^i{v}_1^i\in E\left(G_i\right)$, then $v_{j+1}^i=v$, and define $j:=j+1$, then repeat Step 5. Otherwise, go to Step 7;

7.

Let $B_{m_i}$ be an induced subgraph of $G_i$ by $\{v_1^i,v_2^i,\dots ,v_j^i\}$;

8.

Define $G_{i+1}=G_i-B_{m_i}$;

9.

If $V\left(G_{i+1}\right)\ne \varnothing$, then define $i:=i+1$, and repeat Step 3. Otherwise, finish.

Let q be the last number i obtained from the above algorithm. We obtain $H_t=B_{m_1}+B_{m_2}+\dots +B_{m_q}$. □

Let us consider a graph $G\odot H_t$, where G is a connected graph of order n and $H_t$ is a $(t-3)$-regular graph. For $i\in [1,n]$, for every x and y in $V\left(H_t^i\right)$ and $z\notin V(G\odot H_t)-V\left(H_t^i\right)$, we have $d_{G\odot H_t}(x,z)=d_{G\odot H_t}(y,z)$, which implies any two vertices in $H_t^i$ are only resolved in $V\left(H_t^i\right)$. Therefore, it is necessary to determine $nr\left(H_t^i\right)$ for every $i\in [1,n]$. Note that $H_t^i$ is a $(t-3)$-regular graph.

Let $t\ge 5$ and $B_m\subseteq H_t$ such that $B_m=K_m-E\left(C_m\right)$ for some $m\in [3,t]$. It is easy to check that $B_m$ is connected if and only if $m\ge 5$. If $H_t$ is only thejoin of some $B_3$ or $B_4$, $H_t$ is still connected. This case of $H_t$ is investigated in Section 3.2. Now, we assume $m\ge 5$. Note that for every two vertices $v\in V\left(B_m\right)$ and $u\in V\left(H_t\right)-V\left(B_m\right)$, we obtain $vu\in E\left(H_t\right)$. Therefore, every two vertices x and y in $V\left(B_m\right)$ is not resolved by u. Therefore, an $nr$-set of $H_t$ must contain some vertices in $B_m$, which resolves $B_m$.

Lemma 2.

Let $H_t$ be a $(t-3)$-regular graph of order $t\ge 5$. Let W be an $nr$-set of $H_t$. Let $B_m\subseteq H_t$ where $B_m=K_m-E\left(C_m\right)$ for some $m\in [5,t]$:

 (i)

If $m=t$, then W is an $nr$-set of $B_t$;

 (ii)

If $m<t$, then $|W\cap V\left(B_m\right)|\ge dim\left(B_m\right)$.

Proof. 

(i)

Since $m=t$, we have $B_t=H_t$. Hence, W is also an $nr$-set of $B_t$;

(ii)

Since $H_t$ is a $(t-3)$-regular graph, by Lemma 1, there is $q\in [1,\lfloor \frac{t}{3}\rfloor ]$ such that $H_t=B_{m_1}+B_{m_2}+\dots +B_{m_q}$ where $B_{m_i}=K_{m_i}-E\left(C_{m_i}\right)$ and $m_1+\dots +m_q=t$. Let W be an $nr$-set of $H_t$ and $W_i=W\cap V\left(B_{m_i}\right)$ for every $i\in [1,q]$. Next, it is proven by contradiction. Suppose there is $j\in [1,q]$ such that $|W_j|<dim\left(B_{m_j}\right)$. As a consequence, there are two vertices u and v in $V\left(B_{m_j}\right)-W_j$ such that $r\left(u\right|W_j)=r\left(v\right|W_j)$. Since every $w\in W-W_j$ is adjacent to all vertices in $B_{m_j}$, we have $r\left(u\right|W)=r(v\left|W\right)$. We obtain a contradiction.

 □

In order to determine $nr\left(H_t\right)$, according to Lemma 2, we need to determine $dim(K_m-E\left(C_m\right))$ for some $m\in [5,t]$, which can be seen in Section 3.1. Note that $K_m-E\left(C_m\right)$ is a complete graph of order m minus a Hamiltonian cycle. In Section 3.2, we provide the non-isolated resolving number of $H_t$. Some results in Section 3.1 can be used to determine $nr\left(H_t\right)$. All results in Section 3.1 and Section 3.2 were used to determine $nr(G\odot H_t)$, which can be seen in Section 3.3.

3.1. Resolvability of a Complete Graph Minus a Hamiltonian Cycle

By Lemma 2, we need to determine a basis or an $nr$-set of $B_{m_i}$. It is easy to check that $B_m$ is connected when $m\ge 5$. We use a gap between two vertices to determine a (non-isolated) resolving set of $B_m$. Let Q be a subset of $V\left(B_m\right)$. Let u and v be two different vertices in Q. A gap of Q between u and v is defined as $V\left(P\right(u,v\left)\right)-\{u,v\}$ where $P(u,v)$ is a $u-v$ path in $C_m$, all inner vertices of which are not in Q. Note that every pair of vertices u and v in Q has at most two different gaps. The vertices u and v are called the end point of a gap of Q between u and v. If two different gaps of Q have a common end point, then those two gaps are called neighboring gaps. Therefore, if $\left|Q\right|=r$, then Q has r gaps, and some of the gaps may be empty. This technique was introduced in [25]. For illustration, let $Q=\{v_1,v_5,v_7,v_{10},v_{11},v_{14}\}$ as described in Figure 2. We have some gaps, namely $\{v_2,v_3,v_4\},\left\{v_6\right\},\{v_8,v_9\},\left\{\right\},\{v_{12},v_{13}\},$ and $\left\{v_{15}\right\}$.

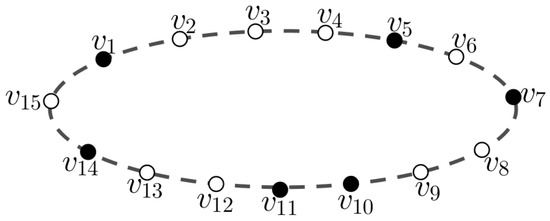
Figure 2. $B_{10}=K_{10}-E\left(C_{10}\right)$ with its $Q=\{v_1,v_5,v_7,v_{10},v_{11},v_{14}\}$.

Lemma 3.

Let $m\ge 5$ and $B_m=K_m-E\left(C_m\right)$. Then, W is a resolving set of $B_m$ if and only if W satisfies all the following properties:

 (i)

Every gap of W contains at most three vertices;

 (ii)

At most one gap of W contains three vertices;

 (iii)

If a gap of W contains at least two vertices, then its neighboring gaps contain at most one vertex.

Proof. 

Let $V\left(B_m\right)=\{v_1,v_2,\dots ,v_m\}$ such that $E\left(C_m\right)=\{v_1{v}_2,v_2{v}_3,\dots ,v_{m-1}{v}_m,v_m{v}_1\}$ and $v_1\in W$.

$(\to )$ Let W be a resolving set of $B_m$:

(i)

Suppose there is a gap of W containing four vertices $v_k,v_{k+1},v_{k+2},v_{k+3}$ for some $k\in [2,m-3]$. We obtain $r\left(v_{k+1}\right|W)=r\left(v_{k+2}\right|W)=(1,1,\dots ,1)$. We obtain a contradiction. Hence, every gap of W contains at most three vertices;

(ii)

Suppose there are two different gaps containing three vertices $v_k,v_{k+1},v_{k+2}$ and $v_l,v_{l+1},v_{l+2}$ for some k and l in $[2,m-2]$ with $k\ne l$. We obtain $r\left(v_{k+1}\right|W)=r\left(v_{l+1}\right|W)=(1,1,\dots ,1)$. This is a contradiction. Therefore, the number of gaps of W containing three vertices is at most one;

(iii)

Suppose there are five vertices $v_k,v_{k+1},v_{k+2},v_{k+3},v_{k+4}$ for some $k\in [2,m-4]$ such that $v_{k+2}$ is the only vertex of W. Since $d_{B_m}(v_{k+1},v_{k+2})=2=d_{B_m}(v_{k+3},v_{k+2})$ and for every $z\in W-\left\{v_{k+2}\right\},d_{B_m}(v_{k+1},z)=1=d_{B_m}(v_{k+3},z)$, we obtain $r\left(v_{k+1}\right|W)=r\left(v_{k+3}\right|W)$. This is a contradiction. We conclude that if A is a gap of W containing at least two vertices, then the neighboring gaps of A contain at most one vertex.

$(\leftarrow )$ Let W satisfy the three above properties. We show that W is a resolving set of $B_m$. Let v be any vertex in $V\left(B_m\right)-W$. We divide the proof into three cases as follows:

• v belongs to a gap of size one of W:
  Let $v_i$ and $v_{i+2}$ be the end points of a gap containing v. Then, the vertex v has a distance of two to both $v_i$ and $v_{i+2}$. Since $m\ge 5$, for every $u\in V\left(B_m\right)-\{v,v_i,v_{i+2}\}$, we have $d_{B_m}(u,v_i)=1$ or $d_{B_m}(u,v_{i+2})=1$. This implies $r\left(v\right|W)\ne r(u\left|W\right)$;
• v belongs to a gap of size two of W:
  Let $v_i$ and $v_{i+3}$ be the end points of a gap containing v. Without loss of generality, let $v=v_{i+1}$, then $d_{B_m}(v,v_i)=2$ and $d_{B_m}(v,v_{i+3})=1$. If there is $u\in V\left(B_m\right)-W$ with $u\ne v$ and $d_{B_m}(u,v_i)=2$ and $d_{B_m}(u,v_{i+3})=1$, then there is $w\in W-\left\{v_i\right\}$ such that $d_{B_m}(w,u)=2$ and $d_{B_m}(w,v)=1$. Therefore, for every $x\in V\left(B_m\right)-\left\{v\right\}$, we obtain $r\left(v\right|W)\ne r(x\left|W\right)$
• v belongs to a gap of size three of W:
  Let $v_i$ and $v_{i+4}$ be the end points of a gap containing v. Let $v=v_{i+2}$, then $r\left(v\right|W)=(1,1,1,\dots ,1)$. By Properties $\left(i\right)$ and $\left(ii\right)$ of Lemma 3, no other vertex of $B_m$ has this representation. Now, let $v=v_{i+1}$ or $v=v_{i+3}$. Without loss of generality, let $v=v_{i+1}$, then $d_{B_m}(v,v_i)=2$ and $d_{B_m}(v,v_{i+4})=1$. If there is $u\in \{V\left(B_m\right)-W\}$ with $u\ne v$, $d_{B_m}(u,v_i)=2$ and $d_{B_m}(u,v_{i+4})=1$, then there is $w\in W-\left\{v_i\right\}$ such that $d_{B_m}(w,u)=2$ and $d_{B_m}(w,v)=1$. Therefore, for every $x\in V\left(B_m\right)-\left\{v\right\}$, we obtain $r\left(v\right|W)\ne r(x\left|W\right)$.

We conclude that every vertex in $V\left(B_m\right)$ has a distinct representation with respect to W. Therefore, W is a resolving set of $B_m$. □

Now, we are ready to determine $dim(K_m-E\left(C_m\right))$ and $nr(K_m-E\left(C_m\right))$ where $m\ge 5$.

Theorem 2.

Let $m\ge 5$ and $B_m=K_m-E\left(C_m\right)$. Then:

$$nr\left(B_m\right)=dim\left(B_m\right)=\lfloor \frac{2m+2}{5}\rfloor .$$

Proof. 

First, we show that $dim\left(B_m\right)\ge \lfloor \frac{2m+2}{5}\rfloor$. Let W be a resolving set of $B_m$. Based on Properties $\left(i\right)–\left(iii\right)$ of Lemma 3, there is at most one gap of W that contains three vertices. Furthermore, at most $\lfloor \frac{\left|W\right|}{2}\rfloor -1$ gaps contain two vertices, and the rest of the gaps contain at most one vertex. Let us consider two cases below:

• $\left|W\right|=2p$ for some $p\in \mathbb{N}$:
  The number of vertices in all gaps of W is at most $3p+1$. Therefore, $m-2p\le 3p+1$. This implies that $\left|W\right|=2p\ge \lceil \frac{2}{5}m-\frac{2}{5}\rceil \ge \lfloor \frac{2m+2}{5}\rfloor$;
• $\left|W\right|=2p+1$ for some $p\in \mathbb{N}$:
  The number of vertices in all gaps of W is at most $3p+2$. Therefore, $m-2p-1\le 3p+2$. This means that $\left|W\right|=2p+1\ge \lceil \frac{2}{5}m-\frac{6}{5}+1\rceil \ge \lfloor \frac{2m+2}{5}\rfloor$.

For an upper bound, let $V\left(B_m\right)=\{v_1,\dots ,v_m\}$ such that $E\left(C_m\right)=\{v_1{v}_2,\dots ,v_{m-1}{v}_m,v_m{v}_1\}.$ We show that $dim\left(B_m\right)\le \lfloor \frac{2m+2}{5}\rfloor$. Let us consider five cases below:

• $m=0(mod 5)$:
  Therefore, $m=5l$ for some $l\in \mathbb{N}$. Thus, $\lfloor \frac{2m+2}{5}\rfloor =2l$. We define $W=\{v_{5j+1},v_{5j+4}|j\in [0,l-1]\}$. Note that W contains $2l$ vertices and satisfies Properties $\left(i\right)–\left(iii\right)$ of Lemma 3;
• $m=1(mod 5)$:
  Therefore, $m=5l+1$ for some $l\in \mathbb{N}$. Thus, $\lfloor \frac{2m+2}{5}\rfloor =2l$. For $l=1$, we define $W=\{v_1,v_5\}$. For $l\ge 2$, we define $W=\{v_{5j+1},v_{5j+4}|j\in [0,l-2]\}\cup \{v_{5l-4},v_{5l}\}$. Note that W contains $2l$ vertices and satisfies Properties $\left(i\right)–\left(iii\right)$ of Lemma 3;
• $m=2(mod 5)$:
  Therefore, $m=5l+2$ for some $l\in \mathbb{N}$. Thus, $\lfloor \frac{2m+2}{5}\rfloor =2l+1$. We define $W=\{v_{5j+1},v_{5j+4}|j\in [0,l-1]\}\cup \left\{v_{5l+1}\right\}$. Note that W contains $2l+1$ vertices and satisfies Properties $\left(i\right)–\left(iii\right)$ of Lemma 3;
• $m=3(mod 5)$:
  Therefore, $m=5l+3$ for some $l\in \mathbb{N}$. Thus, $\lfloor \frac{2m+2}{5}\rfloor =2l+1$. For $l=1$, we define $W=\{v_1,v_5,v_7\}$. For $l\ge 2$, we define $W=\{v_{5j+1},v_{5j+4}|j\in [0,l-2]\}\cup \{v_{5l-4},v_{5l},v_{5l+2}\}$. Note that W contains $2l+1$ vertices and satisfies Properties $\left(i\right)–\left(iii\right)$ of Lemma 3;
• $m=4(mod 5)$:
  Therefore, $m=5l+4$ for some $l\in \mathbb{N}$. Thus, $\lfloor \frac{2m+2}{5}\rfloor =2l+2$. We define $W=\{v_{5j+1},v_{5j+4}|j\in [0,l]\}$. Note that W contains $2l+2$ vertices and satisfies Properties $\left(i\right)–\left(iii\right)$ of Lemma 3.

Therefore, W with $\left|W\right|=\lfloor \frac{2m+2}{5}\rfloor$ is a resolving set of $B_m$. We obtain that $dim\left(B_m\right)=\lfloor \frac{2m+2}{5}\rfloor$. Next, it is easy to check that W does not contain an isolated vertex. Consequently, W is also a non-isolated resolving set. Hence, $nr\left(B_m\right)\le dim\left(B_m\right)$. By (1), we have $nr\left(B_m\right)\ge dim\left(B_m\right)$. We conclude that $nr\left(B_m\right)=dim\left(B_m\right)$. □

3.2. $nr$-Set of a $(t-3)$-Regular Graph

Let $H_t$ be a $(t-3)$-regular graph of order $t\ge 5$. By Lemma 1, a $(t-3)$-regular graph is isomorphic to $B_{m_1}+B_{m_2}+\dots +B_{m_q}$ for some $q\in [1,\lfloor \frac{t}{3}\rfloor ]$, where $B_{m_i}=K_{m_i}-E\left(C_{m_i}\right)$ and $m_i\ge 3$ for every $i\in [1,q]$. Let W be an $nr$-set of $H_t$. By Lemma 2 (i), if $q=1$, then W is an $nr$-set of $K_t-E\left(C_t\right)$. Note that an $nr$-set of $K_t-E\left(K_t\right)$ for any $t\ge 5$ was discussed in Section 3.1. If $H_t$ contains $B_{m_i}$ with $m_i\in [5,t-3]$, by Lemma 2 (ii), then $|W\cap V\left(B_m\right)|\ge dim\left(B_m\right)$. A basis of $B_{m_i}$ also was discussed in Section 3.1. Note that for $q\ge 2$, it is possible to have $B_3$ or $B_4$ in $H_t$. However, $B_m$ with $m\in \{3,4\}$ is a disconnected graph. In Lemma 4, we provide a property of an $nr$-set of $H_t$ that contains $B_3$ or $B_4$.

Lemma 4.

Let $H_t$ be a $(t-3)$-regular graph where $t\ge 6$. Let $B_m\subseteq H_t$ where $B_m=K_m-E\left(C_m\right)$ for some $m\in \{3,4\}$. Then, $B_m$ contributes at least two vertices in an $nr$-set of $H_t$.

Proof. 

Suppose there exists an $nr$-set $W^{\prime }$ of $H_t$ that contains at most one vertex of $B_m$. Note that for every $v\in V\left(B_m\right)$ and $z\in V\left(H_t\right)-V\left(B_m\right)$, there are two vertices x and y in $V\left(B_m\right)$ such that $d_{B_m}(x,v)=2=d_{B_m}(y,v)$ and $d_{B_m}(x,z)=1=d_{B_m}(y,z)$. Hence, $r\left(x\right|W^{\prime })=r\left(y\right|W^{\prime })$. We have a contradiction. □

Let $H_t=B_{m_1}+B_{m_2}+\dots +B_{m_q}$ with $3\le m_i\le m_{i+1}$ for every $i\in [1,q-1]$. We assume that $H_t$ contains b subgraphs that are isomorphic to $B_3$ or $B_4$. By Lemma 2 (ii) and Lemma 4, we have $nr\left(H_t\right)\ge 2b+dim\left(B_{m_{b+1}}\right)+dim\left(B_{m_{b+2}}\right)+\dots +dim\left(B_{m_q}\right)$. Let $S\subseteq V\left(H_t\right)$ and $S_i=S\cap V\left(B_{m_i}\right)$ for every $i\in [b+1,q]$. We define gaps of S in $H_t$ as the union of gaps of $S_{b+1},S_{b+2},\dots ,$ and $S_q$. In order to determine $nr\left(H_t\right)$, we also need to consider some necessary conditions for the $nr$-set of $H_t$, which can be seen in the following lemma.

Lemma 5.

Let $H_t$ be a $(t-3)$-regular graph of order $t\ge 5$. Let W be a non-isolated resolving set of $H_t$. Then, W satisfies the two conditions below:

 (i)

Every gap of W contains at most three vertices;

 (ii)

At most one gap of W contains three vertices.

Proof. 

Let W be a non-isolated resolving set of $H_t$. For every $i\in [1,q]$, let $V\left(B_{m_i}\right)=\left\{v_{h,i}\right|h\in [1,m_i]\}$ such that $E\left(C_{m_i}\right)=\{v_{1,i}{v}_{2,i},v_{2,i}{v}_{3,i},\dots ,v_{m_i-1,i}{v}_{m_i,i},v_{m_i,i}{v}_{1,i}\}$ and $v_{1,i}\in W$:

(i)

Suppose there is a gap of W containing four vertices $v_{k,i},v_{k+1,i},v_{k+2,i},v_{k+3,i}$ for some $k\in [2,m_i-3]$ and $i\in [1,q]$. We obtain $r\left(v_{k+1,i}\right|W)=r\left(v_{k+2,i}\right|W)=(1,1,\dots ,1)$. We obtain a contradiction. Hence, every gap of W contains at most three vertices;

(ii)

By considering Lemma 4, suppose there are two different gaps containing three vertices $v_{k,i},v_{k+1,i},$$v_{k+2,i}$ in $V\left(B_{m_i}\right)$ of $H_t$ and $v_{l,j},v_{l+1,j},v_{l+2,j}$ in $V\left(B_{m_j}\right)$ of $H_t$ for some $k\in [2,m_i-2]$ and $l\in [2,m_j-2]$ with $i\ne j$. We obtain $r\left(v_{k+1,i}\right|W)=r\left(v_{l+1,j}\right|W)=(1,1,\dots ,1)$. We have a contradiction. Hence, the number of gaps of W containing three vertices is at most one.

□

In order to determine an $nr$-set of $H_t$, by Lemma 5, we need to investigate the gap property for a basis of $B_{m_i}$, which can be seen in the lemma below.

Lemma 6.

Let $H_t$ be a $(t-3)$-regular graph of order $t\ge 5$. Let $B_m\subseteq H_t$ such that $B_m=K_m-E\left(C_m\right)$ for some $m\in [5,t]$, then every basis of $B_m$ has a gap containing at least three vertices if and only if $m=1$ or $3(mod 5)$.

Proof. 

Let $V\left(B_m\right)=\{v_1,v_2,\dots ,v_m\}$ such that $E\left(C_m\right)=\{v_1{v}_2,v_2{v}_3,\dots ,v_{m-1}{v}_m,v_m{v}_1\}$.

$(\to )$ Suppose $m\ne 1$ or $3(mod 5)$. We distinguish three cases as follows:

Case 1.$m=0(mod 5)$:

Let $m=5l$ for some integer l at least two. Thus, $\lfloor \frac{2m+2}{5}\rfloor =2l$. We define $W=\{v_{5j+1},v_{5j+4}|j\in [0,l-1]\}$.

Case 2.$m=2(mod 5)$:

Let $m=5l+2$ for some $l\in \mathbb{N}$. Thus, $\lfloor \frac{2m+2}{5}\rfloor =2l+1$. We define $W=\{v_{5j+1},v_{5j+4}|j\in [0,l-1]\}\cup \left\{v_{5l+1}\right\}$.

Case 3.$m=4(mod 5)$:

Let $m=5l+4$ for some $l\in \mathbb{N}$. Thus, $\lfloor \frac{2m+2}{5}\rfloor =2l+2$. We define $W=\{v_{5j+1},v_{5j+4}|j\in [0,l]\}$.

From all cases above, we have that every gap of W contains at most two vertices. By Lemma 3 and Theorem 2, we conclude that W is a basis of $B_m$.

$(\leftarrow )$ Suppose that every gap of the basis of $B_m$ contains at most two vertices. We have two cases:

Case 1.$m=1(mod 5)$:

Let $m=5l+1$ for some $l\in \mathbb{N}$. By using Theorem 2, we obtain $dim=2l$. By Properties $\left(iii\right)$ of Lemma 3, there are $\frac{dim\left(B_m\right)}{2}$ gaps that contain one vertex and at most $\frac{dim\left(B_m\right)}{2}$ gaps that contain two vertices. By Theorem 2, we obtain $\left|V\right(B_m\left)\right|\le 5l$, a contradiction with $m=5l+1$.

Case 2.$m=3(mod 5)$:

Let $m=5l+3$ for some $l\in \mathbb{N}$. By using Theorem 2, we obtain $dim=2l+1$. By Properties $\left(iii\right)$ of Lemma 3, there are $\frac{dim\left(B_m\right)+1}{2}$ gaps that contain one vertex and at most $\frac{dim\left(B_m\right)-1}{2}$ gaps that contain two vertices. By Theorem 2, we obtain $\left|V\right(B_m\left)\right|\le 5l+2$, a contradiction with $m=5l+3$. □

The lemma below is useful to determine the non-isolated number of $H_t$.

Lemma 7.

Let $H_t$ be a $(t-3)$-regular graph of order $t\ge 5$. Let $B_m\subseteq H_t$ such that $B_m=K_m-E\left(C_m\right)$ for some $m\in \{3,4\}$. There is an $nr$-set W of $H_t$ such that for every $v\in V\left(B_m\right)$, $r\left(v\right|W)\ne (1,1,\dots ,1)$.

Proof. 

Let $V\left(B_m\right)=\{v_1,v_2,\dots ,v_m\}$ such that $E\left(C_m\right)=\{v_1{v}_2,\dots ,v_{m-1}{v}_m,v_m{v}_1\}$. Let $S=\{v_1,v_m\}$. Let $S^{\prime }$ be an $nr$-set of $V\left(H_t\right)-V\left(B_m\right)$. We define $W=S\cup S^{\prime }$. We distinguish two cases as follows:

• For $m=3$, we have $r\left(v_1\right|S)=(0,2),r\left(v_2\right|S)=(2,2),$ and $r\left(v_3\right|S)=(2,0)$;
• For $m=4$, we have $r\left(v_1\right|S)=(0,2),r\left(v_2\right|S)=(2,1),r\left(v_3\right|S)=(1,2)$, and $r\left(v_4\right|S)=(2,0)$.

Therefore, for all $v\in V\left(B_m\right)$, we obtain $r\left(v\right|W)\ne (1,1,\dots ,1)$. □

In the next theorem, we provide the non-isolated resolving number of a $(t-3)$-regular graph where $t\ge 5$.

Theorem 3.

Let $H_t$ be a $(t-3)$-regular graph of order $t\ge 5$. Let $q\in [1,\lfloor \frac{t}{3}\rfloor ]$ such that $H_t=B_{m_1}+B_{m_2}+\dots +B_{m_q}$, where $B_{m_i}=K_{m_i}-E\left(C_{m_i}\right)$ and $3\le m_i\le m_{i+1}$, for every $i\in [1,q-1]$. Let b be the number of $B_3$ and $B_4$. Let d be the number of $B_g$ with $g=1$ or $3(mod 5)$ and $g\ge 6$. Then,

$$nr\left(H_t\right)=\left\{\begin{array}{cc}nr\left(B_t\right),\hfill & \mathrm{if}q=1;\hfill \\ 2b,\hfill & \mathrm{if}b=q\ge 2;\hfill \\ 2b+{\sum }_{i=b+1}^{q}nr\left(B_{m_i}\right),\hfill & \mathrm{if}q\ge 2,d\in \{0,1\},\mathrm{and}b<q;\hfill \\ 2b+{\sum }_{i=b+1}^{q}nr\left(B_{m_i}\right)+d-1,\hfill & \mathrm{if}q\ge 2,d\ge 2,\mathrm{and}b<q.\hfill \end{array}\right.$$

Proof. 

We divide the proof into four cases.

Case 1.$q=1$:

According to Lemma 1, we obtain $H_t=B_t$. Therefore, $nr\left(H_t\right)=nr\left(B_t\right)$.

Case 2.$b=q\ge 2$:

By Lemma 4, we only need to show that $nr\left(H_t\right)\le 2b$. For every $i\in [1,q]$, let $V\left(B_{m_i}\right)=\{v_{1,i},v_{2,i},\dots ,v_{m_i,i}\}$ such that $E\left(C_{m_i}\right)=\{v_{1,i}{v}_{2,i},\dots ,v_{m_i,i}{v}_{1,i}\}$. We define $W_i=\{v_{1,i},v_{m_i,i}\}$ of $H_t$. Let $W={\bigcup }_{i=1}^q{W}_i$. Note that $\left|W\right|=2q$ and W does not contain an isolated vertex. For $m_i=3$, we have $r\left(v_{2,i}\right|W_i)=(2,2)$. For $m_i=4$, we have $r\left(v_{2,i}\right|W_i)=(2,1)\ne (1,2)=r\left(v_{3,i}\right|W_i)$. Since $x\in V\left(B_{m_i}\right)$ is adjacent to $y\in V\left(B_{m_j}\right)$ with $i\ne j$, we have $r\left(x\right|W)\ne r(y\left|W\right)$. Therefore, $nr\left(H_t\right)=2q=2b$.

Case 3.$q\ge 2,d\in \{0,1\}$, and $b<q$:

Let W be a non-isolated resolving set of $H_t$. Let $W_i=W\cap B_{m_i}$ for every $i\in [1,q]$. By Lemma 4, we obtain $|W_j|\ge 2$ for every $j\in [1,b]$. Since $b<q$, we have $m_k\ge 5$ for every $k\in [b+1,q]$. By Lemma 2 (ii) and Theorem 2, we obtain $|W_k|\ge dim\left(B_{m_k}\right)=nr\left(B_{m_k}\right)$. Therefore, we obtain $nr\left(H_t\right)\ge 2b+{\sum }_{i=b+1}^{q}nr\left(B_{m_i}\right)$.

Next, for every $i\in [1,q]$, let $V\left(B_{m_i}\right)=\{v_{1,i},v_{2,i},\dots ,v_{m_i,i}\}$ such that $E\left(C_{m_i}\right)=\{v_{1,i}{v}_{2,i},\dots ,v_{m_i,i}{v}_{1,i}\}$. We construct a non-isolated resolving set of $H_t$ with $2b+{\sum }_{i=b+1}^{q}nr\left(B_{m_i}\right)$ elements. For every $k\in [1,b]$, let $W_k=\{v_{1,k},v_{m,k}\}$. For every $j\in [b+1,q]$, choose a basis $W_j$ of $B_{m_j}$ such that if $m_j=0,2,$ or $4(mod 5)$, then every gap of $W_j$ contains at most two vertices. We define $W={\cup }_{k=1}^b{W}_k\bigcup {\cup }_{j=b+1}^q{W}_j$.

We show that W is a non-isolated resolving set of $H_t$. Note that W does not contain an isolated vertex. For $m_k=3$, we have $r\left(v_{2,k}\right|W_k)=(2,2)$. For $m_k=4$, we have $r\left(v_{2,k}\right|W_k)=(2,1)\ne (1,2)=r\left(v_{3,k}\right|W_k)$. For every $m_j\ge 5$, since $W_j$ is a basis of $B_{m_j}$, every two different vertices x and y of $B_{m_j}$ satisfies $r\left(x\right|W_j)\ne r\left(y\right|W_j)$. Thus, for $i\in [1,q]$, every pair of distinct vertices x and y in $V\left(B_{m_i}\right)$ satisfies $r\left(x\right|W_i)\ne r\left(y\right|W_i)$.

Now, for distinct integers r and s in $[1,q]$, let us consider $x\in V\left(B_{m_r}\right)-W_r$ and $z\in V\left(B_{m_s}\right)-W_s$. If $r\in [1,b]$, or $m_r=0,2,$ or $4(mod 5)$ with $m_r\ge 5$, then there exists a vertex in $W_r$ that is not adjacent to x, which implies $r\left(x\right|W_r)\ne (1,1,\dots ,1)=r\left(z\right|W_r)$. If $m_r=1$ or $3(mod 5)$ with $m_r\ge 5$, then there exists a vertex in $W_s$ that is not adjacent to z, which implies $r\left(z\right|W_s)\ne (1,1,\dots ,1)=r\left(x\right|W_s)$. Therefore, we have $r\left(x\right|W)\ne r(z\left|W\right)$. We conclude that W is a non-isolated resolving set of $H_t$. Since $\left|W\right|=2b+{\sum }_{i=b+1}^{q}dim\left(B_{m_i}\right)$ and by considering Theorem 2, we obtain that $nr\left(H_t\right)\le 2b+{\sum }_{i=b+1}^{q}dim\left(B_{m_i}\right)=2b+{\sum }_{i=b+1}^{q}nr\left(B_{m_i}\right)$.

Case 4.$q\ge 2,d\ge 2$, and $b<q$:

Let W be a non-isolated resolving set of $H_t$. Let $W_i=W\cap B_{m_i}$ for every $i\in [1,q]$. By Lemma 4, we obtain $|W_j|\ge 2$ for every $j\in [1,b]$. Since $b<q$, we have $m_k\ge 5$ for every $k\in [b+1,q]$. By Lemma 2 (ii) and Theorem 2, we obtain $|W_k|\ge dim\left(B_{m_k}\right)=nr\left(B_{m_k}\right)$. Since there are $d\ge 2$ gaps containing three vertices, by Lemma 5 (ii), we have $nr\left(H_t\right)\ge 2b+{\sum }_{i=b+1}^{q}nr\left(B_{m_i}\right)+d-1$.

Next, for every $i\in [1,q]$, let $V\left(B_{m_i}\right)=\{v_{1,i},v_{2,i},\dots ,v_{m_i,i}\}$ such that $E\left(C_{m_i}\right)=\{v_{1,i}{v}_{2,i},\dots ,v_{m_i,i}{v}_{1,i}\}$. We construct a non-isolated resolving set of $H_t$ with $2b+{\sum }_{i=b+1}^{q}nr\left(B_{m_i}\right)+d-1$ elements. For every $k\in [1,b]$, let $W_k=\{v_{1,k},v_{m,k}\}$. For every $j\in [b+1,q]$, choose a basis $W_j$ of $B_{m_j}$ such that if $m_j=0,2,$ or $4(mod 5)$, then every gap of $W_j$ contains at most two vertices. For $j\in [b+1,q]$, if $m_j=1$ or $3(mod 5)$, then by Lemma 3.7, $W_j$ has a gap containing three vertices. For those $W_j$, without loss of generality, let $v_{1,j},v_{2,j},v_{3,j}$ be a gap of $W_j$ with three vertices. Let $A=\left\{v_{2,j}\right|j\in [b+1,q],m_j=1$ or $3(mod 5)\}$. Note that $\left|A\right|=d$. Let $\alpha =min\{j\in [b+1,q]|m_j=1$ or $3(mod 5)\}$, we define $A^{\prime }=A-\left\{v_{2,\alpha }\right\}$. We define $W={\cup }_{k=1}^b{W}_k\bigcup {\cup }_{j=b+1}^q{W}_j\cup A^{\prime }$.

We show that W is a non-isolated resolving set of $H_t$. Note that W does not contain an isolated vertex. For $m_k=3$, we have $r\left(v_{2,k}\right|W_k)=(2,2)$. For $m_k=4$, we have $r\left(v_{2,k}\right|W_k)=(2,1)\ne (1,2)=r\left(v_{3,k}\right|W_k)$. For every $m_j\ge 5$ with $j\in [b+1,q]$, since $W_j$ is a basis of $B_{m_j}$, every two different vertices x and y of $B_{m_j}$ satisfies $r\left(x\right|W_j)\ne r\left(y\right|W_j)$. Thus, for $i\in [1,q]$, for two distinct vertices x and y in $V\left(B_{m_i}\right)$, we obtain $r\left(x\right|W_i)\ne r\left(y\right|W_i)$.

Now, for distinct integers r and s in $[1,q]$, let us consider $x\in V\left(B_{m_r}\right)-W$ and $z\in V\left(B_{m_s}\right)-W$. If $r\in [1,b]$, or $m_r=0,2,$ or $4(mod 5)$ with $m_r\ge 5$, then there exists a vertex in $W_r$ that is not adjacent to x. Hence, $r\left(x\right|W_r)\ne (1,1,\dots ,1)=r\left(z\right|W_r)$. If $m_s=0,2,$ or $4(mod 5)$ with $m_s\ge 5$, then there exists a vertex in $W_s$ that is not adjacent to z, which implies $r\left(z\right|W_s)\ne (1,1,\dots ,1)=r\left(x\right|W_s)$. If $m_r=1$, or $3(mod 5)$ with $m_r\ge 5$ and $m_s=1$, or $3(mod 5)$ with $m_s\ge 5$, without loss of generality, and assuming $r<s$, then there exists a vertex in $W\cap V\left(B_{m_s}\right)$ that is not adjacent to z, which implies $r\left(z\right|W_s\cup \left\{v_{2,m_s}\right\})\ne (1,1,\dots ,1)=r\left(x\right|W_s\cup \left\{v_{2,m_s}\right\})$. Therefore, we have $r\left(x\right|W)\ne r(z\left|W\right)$. We conclude that W is a non-isolated resolving set of $H_t$. Since $\left|W\right|=2b+{\sum }_{i=b+1}^{q}dim\left(B_{m_i}\right)+d-1$ and by considering Theorem 2, we obtain that $nr\left(H_t\right)\le 2b+{\sum }_{i=b+1}^{q}dim\left(B_{m_i}\right)+d-1=2b+{\sum }_{i=b+1}^{q}nr\left(B_{m_i}\right)+d-1$. □

Some illustrations of Theorem 3 can be seen in some figures of $H_{32}$ below. An illustration of Theorem 3 of Case 1, Case 2, and Case 3 can be seen in Figure 3, Figure 4 and Figure 5, respectively. In those figures, we have $H_{32}$ as $B_{32},4B_3+5B_4$, and $B_3+B_4+B_{12}+B_{13}$, respectively. The black vertices represent the elements of a chosen $nr$-set. For Case 4, $H_{32}=2B_4+B_{11}+B_{13}$ with its $nr$-set in Figure 6. For every $j\in [1,4]$, let $W_j$ be an $nr$-set of $B_{m_j}$. There is one gap of $W_3$ containing three vertices, which are $v_{1,3},v_{2,3},v_{3,3}$, and there is one gap of $W_4$ containing three vertices, which are $v_{1,4},v_{2,4},v_{3,4}$. Note that vertices $v_{2,3}$ and $v_{2,4}$ have the same representation. Hence, we should add vertex $v_{2,3}$ to an $nr$-set of $H_{32}$.

Figure 3. $H_{32}=B_{32}$ with its $nr$-set.

Figure 4. $H_{32}=4B_3+5B_4$ with its $nr$-set.

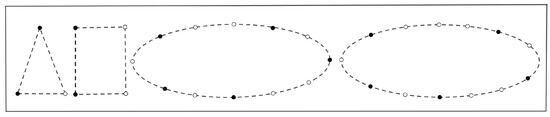
Figure 5. $H_{32}=B_3+B_4+B_{12}+B_{13}$ with its $nr$-set.

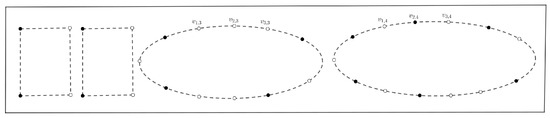
Figure 6. $H_{32}=2B_4+B_{11}+B_{13}$ with its $nr$-set.

3.3. $nr$-Set of $G\odot H_t$ Where $H_t$ Is a $(t-3)$-Regular Graph

Let $H_t$ be a $(t-3)$-regular graph of order $t\ge 3$. Note that $H_t$ is isomorphic to a complete graph $K_t$ minus the edge set of some disjoint cycles.

Theorem 4.

Let G be a connected graph of order $n\ge 2$ and $H_t$ be a $(t-3)$-regular graph of order $t\ge 3$. Then,

$$nr(G\odot H_t)=\left\{\begin{array}{cc}3n,\hfill & \mathrm{if}t=3\mathrm{or}t=4;\hfill \\ n\times nr\left(H_t\right),\hfill & \mathrm{if}t\ge 5.\hfill \end{array}\right.$$

Proof. 

Let $V\left(G\right)=\{u_1,u_2,\dots ,u_n\}$. For every $i\in [1,n]$, we define $H_t^i$ as a copy of $H_t$ in $G\odot H_t$ where all of its vertices are adjacent to $u_i$. Let $V\left(H_t^i\right)=\{v_1^i,v_2^i,\dots ,v_t^i\}$. We divide a proof into three cases.

Case 1.$t=3$:

First, we show that $nr(G\odot H_t)\le 3n$. For every $i\in [1,n]$, we define $W_i=\{v_1^i,v_2^i,u_i\}$. Let $W={\bigcup }_{i=1}^n{W}_i$. Note that $\left|W\right|=3n$. Since $u_i{v}_1^i$ and $u_i{v}_2^i$ in $E(G\odot H_t)$, W does not contain an isolated vertex. Next, we show that W is a resolving set of $G\odot H_t$. Let x and y be two distinct vertices in $V(G\odot H_t)-W$. Let $x=v_3^p$ and $y=v_3^q$ for some p and q in $[1,n]$ with $p\ne q$. Since $d_{G\odot H_t}(x,u_p)=1<d_{G\odot H_t}(y,u_p)$, this implies that $r\left(x\right|W)\ne r(y\left|W\right)$.

Now, we show that $nr(G\odot H_t)\ge 3n$. Suppose that $nr(G\odot H_t)\le 3n-1$. Let $W^{\prime }$ be an $nr$-set of $G\odot H_t$ and $W_i^{\prime }=W_i\cap V\left(H_t^i\right)$ for every $i\in [1,n]$. Then, there exists $j\in [1,n]$ such that $1\le \left|W_j^{\prime }\right|\le 2$. We have two subcases:

• If $u_j\in W_j^{\prime }$, then there exist two vertices x and y in $V\left(H_t^j\right)$ such that $d_{G\odot H_t}(x,u_j)=1=d_{G\odot H_t}(y,u_j)$. This implies that $r\left(x\right|W^{\prime })=r\left(y\right|W^{\prime })$, a contradiction;
• If $u_j\notin W_j^{\prime }$, then $W^{\prime }$ contains an isolated vertex, a contradiction.

Case 2.$t=4$:

Without loss of generality, let $E\left(H_t^i\right)=\{v_1^i{v}_3^i,v_2^i{v}_4^i\}$. First, we show that $nr(G\odot H_t)\le 3n$. For every $i\in [1,n]$, we define $W_i=\{v_1^i,v_2^i,u_i\}$. Let $W={\bigcup }_{i=1}^n{W}_i$. Note that $\left|W\right|=3n$. Since $u_i{v}_1^i,u_i{v}_2^i\in E(G\odot H_t)$, W does not contain an isolated vertex. Next, we show that W is a resolving set of $G\odot H_t$. Let x and y be two distinct vertices in $V(G\odot H_t)-W$. We have two subcases:

• x and y in $H_t^j$ for some $j\in [1,n]$:
  Let $x=v_3^j$ and $y=v_4^j$. Since $d_{G\odot H_t}(x,v_1^j)=1<d_{G\odot H_t}(y,v_1^j)$, we obtain $r\left(x\right|W)\ne r(y\left|W\right)$;
• $x\in H_t^j$ and $y\in H_t^k$ for some j and k in $[1,n]$ with $j\ne k$:
  Let $x=v_a^j$ and $y=v_b^k$ for some a and b in $\{3,4\}$. Since $d_{G\odot H_t}(x,u_j)=1<d_{G\odot H_t}(y,u_j)$, we obtain $r\left(x\right|W)\ne r(y\left|W\right)$.

Now, we show that $nr(G\odot H_t)\ge 3n$. Suppose that $nr(G\odot H_t)\le 3n-1$. Let $W^{\prime }$ be an $nr$-set of $G\odot H_t$ and $W_i^{\prime }=W_i\cap V\left(H_t^i\right)$ for every $i\in [1,n]$. Then, there exists $j\in [1,n]$ such that $|W_j^{\prime }|\le 2$. We have two subcases:

• If $u_j\in W_j^{\prime }$, then there exist two vertices x and y in $V\left(H_t^j\right)$ such that $d_{G\odot H_t}(x,u_j)=1=d_{G\odot H_t}(y,u_j)$. This implies that $r\left(x\right|W^{\prime })=r\left(y\right|W^{\prime })$, a contradiction;
• For $u_j\notin W_j^{\prime }$, if $W^{\prime }$ contains an isolated vertex, then we have a contradiction. Otherwise, then there exist two vertices x and y in $V\left(H_t^j\right)$ such that $d_{G\odot H_t}(x,z)=2=d_{G\odot H_t}(y,z)$ for every $z\in W_j^{\prime }$. This implies that $r\left(x\right|W^{\prime })=r\left(y\right|W^{\prime })$, a contradiction.

Case 3.$t\ge 5$:

We prove that $nr(G\odot H_t)\le n\left(nr\left(H_t\right)\right)$. For every $i\in [1,n]$, let $W_i$ be an $nr$-set of $H_t^i$. We define $W={\bigcup }_{i=1}^n{W}_i$. Note that there is no isolated vertex in W. Next, we show that every two distinct vertices in $G\odot H_t$ has a distinct representation with respect to W. Let x and y be different vertices in $V(G\odot H_t)-W$. We divide this into four subcases:

• x and y in $V\left(H_t^j\right)$ for some $j\in [1,n]$:
  Since $W_j$ is an $nr$-set of $H_t^j$, we have $r\left(x\right|W_j)\ne r\left(y\right|W_j)$. This means that $r\left(x\right|W)\ne r(y\left|W\right)$;
• $x\in V\left(H_t^j\right)$ and $y\in V\left(G\right)$ for some $j\in [1,n]$:
  If $y=u_j$, then for some $k\in [1,n]$ with $k\ne j$ and for any $z\in W_k$, we have $d_{G\odot H_t}(x,z)=d_{G\odot H_t}(y,z)+1$. If $y=u_k$, then for any $z\in W_k$, we have $d_{G\odot H_t}(x,z)=d_{G\odot H_t}(x,y)+d_{G\odot H_t}(y,z)$. Therefore, $r\left(x\right|W_k)\ne r\left(y\right|W_k)$, and this means that $r\left(x\right|W)\ne r(y\left|W\right)$;
• $x\in V\left(H_t^j\right)$ and $y\in V\left(H_t^k\right)$ for some j and k in $[1,n]$ with $j\ne k$:
  For any $z\in W_k$, we have $d_{G\odot H_t}(x,z)\ge 3,$ but $d_{G\odot H_t}(y,z)\le 2$. Therefore, $r\left(x\right|W_j)\ne r\left(y\right|W_j)$, so that $r\left(x\right|W)\ne r(y\left|W\right)$;
• x and y in $V\left(G\right)$:
  Let $x=u_j$ and $y=u_k$ for some j and k in $[1,n]$ with $j\ne k$. For any $z\in W_j$, we have $d_{G\odot H_t}(x,z)=1<d_{G\odot H_t}(y,z)$. Therefore $r\left(x\right|W_j)\ne r\left(y\right|W_j)$. This means that $r\left(x\right|W)\ne r(y\left|W\right)$.

Next, we show that $nr(G\odot H_t)\ge n\left(nr\left(H_t\right)\right)$. Suppose that $nr(G\odot H_t)\le n\left(nr\left(H_t\right)\right)-1$. Let $W^{\prime }$ be an $nr$-set of $G\odot H_t$. For every $i\in [1,n]$, let $W_i^{\prime }=W^{\prime }\cap V\left(H_t^i\right)$. Then, there exists $j\in [1,n]$ such that $|W_j^{\prime }|\le nr\left(H_t^j\right)-1$. Hence, there exist two vertices x and y in $V\left(H_t^j\right)$ such that $d_{G\odot H_t}(x,w)=d_{G\odot H_t}(y,w)$ for every $w\in W_j^{\prime }$. Since for every $v\in V(G\odot H_t)-V\left(H_t^j\right)$, we have $d_{G\odot H_t}(x,v)=d_{G\odot H_t}(y,v)$. Therefore, $r\left(x\right|W^{\prime })=r\left(y\right|W^{\prime })$. This is a contradiction. □

4. Conclusions

In this paper, we studied the non-isolated resolving number of the corona product $G\odot H$ where G is an arbitrary connected graph of order n at least two and H is a k-regular graph of order t with $k\in \{t-2,t-3\}$. We obtained that the non-isolated resolving number of $G\odot H$ is a function of $nr\left(H\right)$. We made the hypothesis that $nr(G\odot H)$ for any k-regular graph H is also a function of $nr\left(H\right)$.