Accurate Analytical Model and Evaluation of Wi-Fi Halow Based IoT Networks under a Rayleigh-Fading Channel with Capture
Abstract
:1. Introduction
- We model the channel access within a RAW slot under a Rayleigh fading channel with capture, considering the geometric distribution of stations around the AP.
- We develop a renewal theory based framework to model the contention within the RAW slot by deploying a counting process to track transmissions within the RAW slot period. We then evaluate the RAW slot throughput representing the channel usage ratio in delivering data frames during the RAW slot period.
- We derive the throughput of a RAW consisting of several RAW slots, which represents the channel usage ratio to deliver data frames during the overall RAW duration. We also evaluate the RAW performance in a no-capture channel scenario and derive the capture ratio in a given RAW configuration.
- We present a meticulous validation of the analytical findings through extensive simulations obtained via a discrete-event simulator developed with the MATLAB software. We henceforth carry out a discussion and analysis of several parameters affecting the performance of a RAW slot and a RAW consisting of several RAW slots.
2. Background
2.1. The IEEE 802.11ah RAW Mechanism
2.2. Related Work
3. System Model
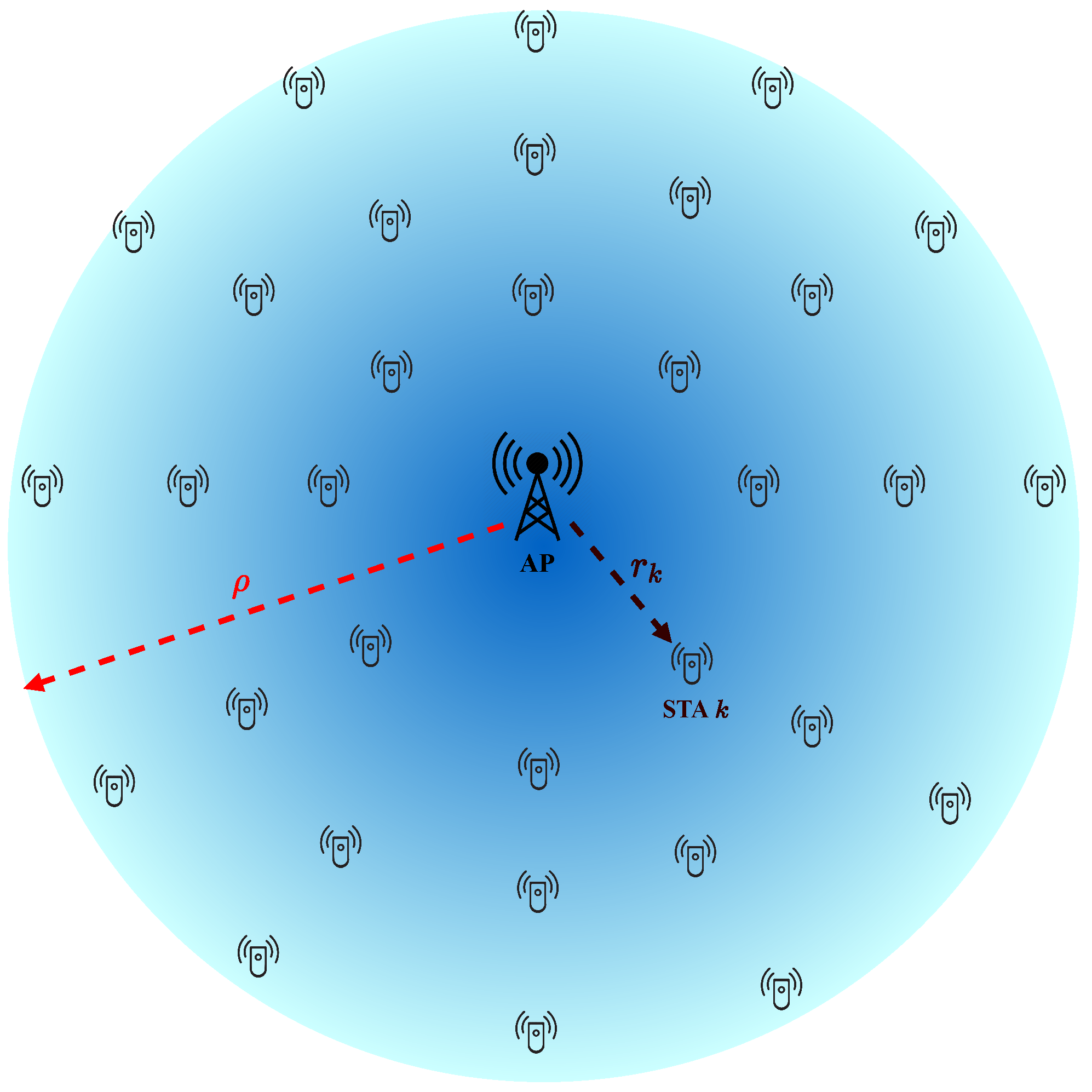
3.1. Scenario
3.2. Channel Model
- is the transmitted signal power.
- represents the deterministic path-loss law, where is the distance between the station k and the AP.
- is the path-loss exponent, and it depends on the propagation environment. For the convenience of analysis, we assume for the rest of this paper.
- A is a dimensionless constant in the path-loss law.
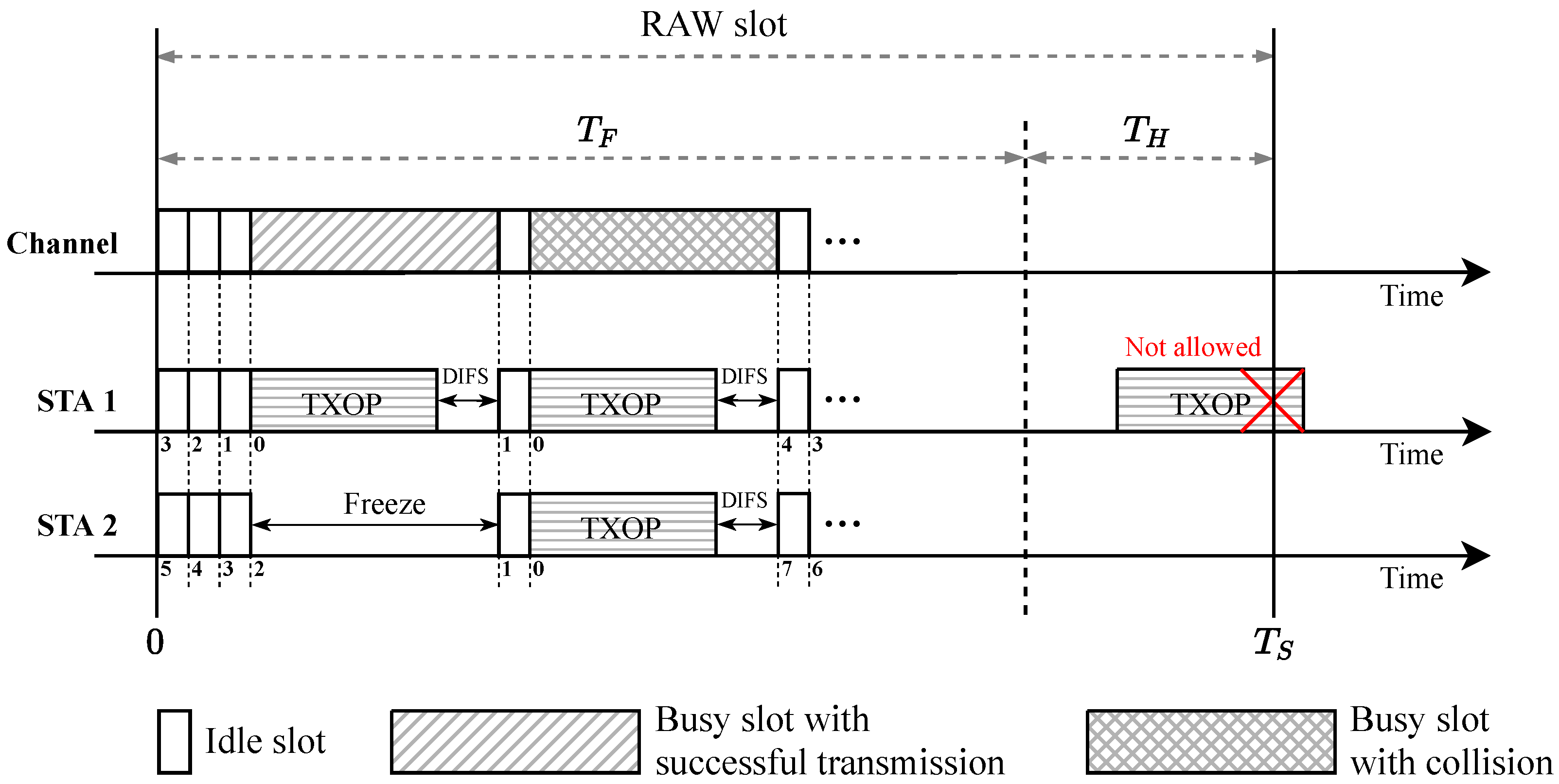
3.3. Capture Aware Channel Access
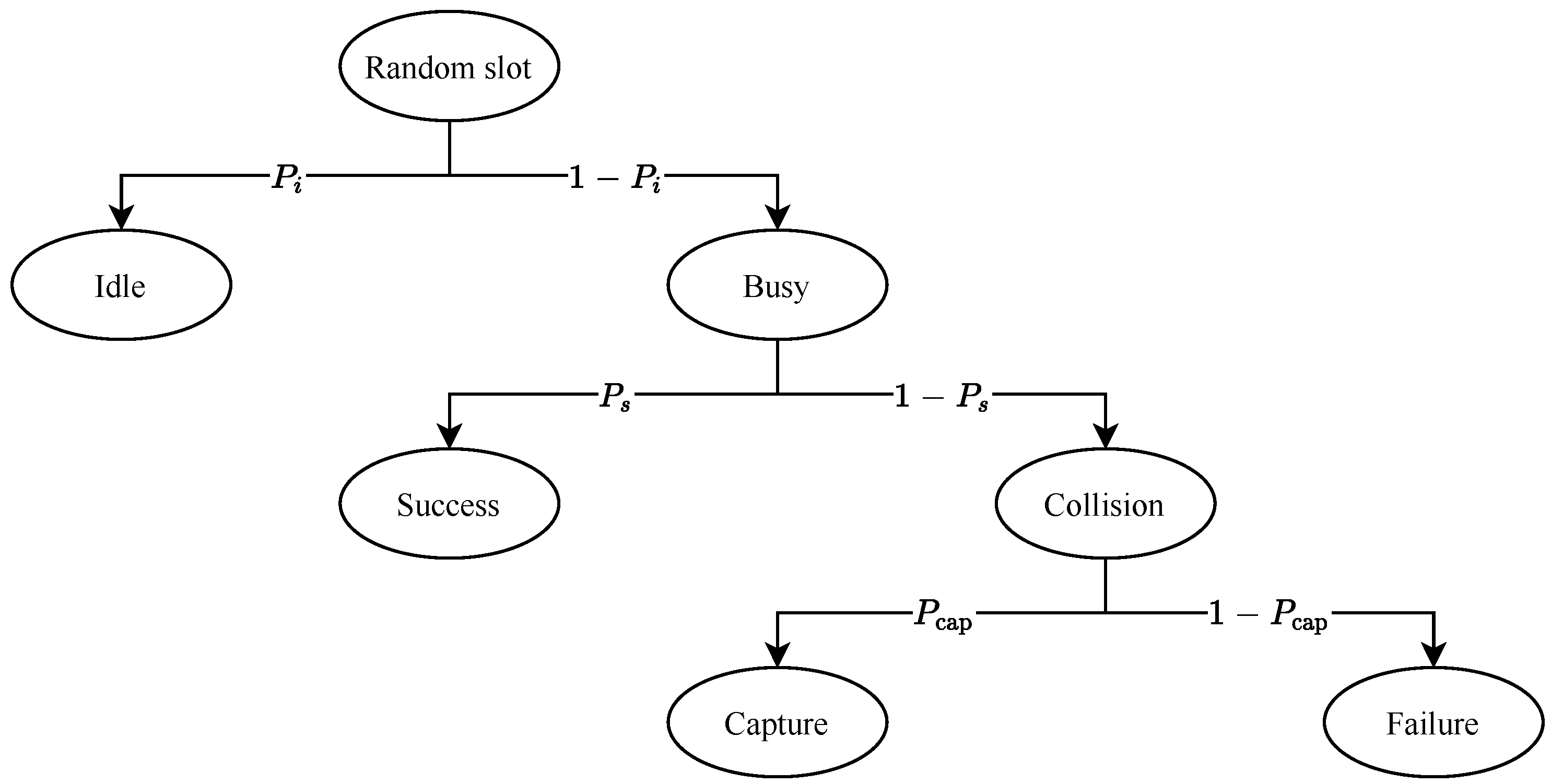
3.4. Channel Slot State
- Idle: When there are no ongoing transmissions in the slot. That is, all stations are listening to the medium while counting down their backoff counter. A randomly chosen slot is idle with probability .
- Success: When only one station transmits and its packet is delivered successfully. Given that this state is a subset of busy slots, a randomly chosen slot contains a successful single transmission with probability .
- Capture: When two or more stations transmit and the packet of one station is captured successfully from the collision. This type of slot is a subset of slots containing collisions, which are a subset of busy slots. Thus, a randomly chosen slot contains a collision with a capture with probability .
- Failure: When two or more stations transmit and no packet is captured. Given that this state is a subset of slots containing collisions, the probability that a randomly chosen slot contains a collision and no packet is captured is given by .
4. Analytical Model and Performance Evaluation
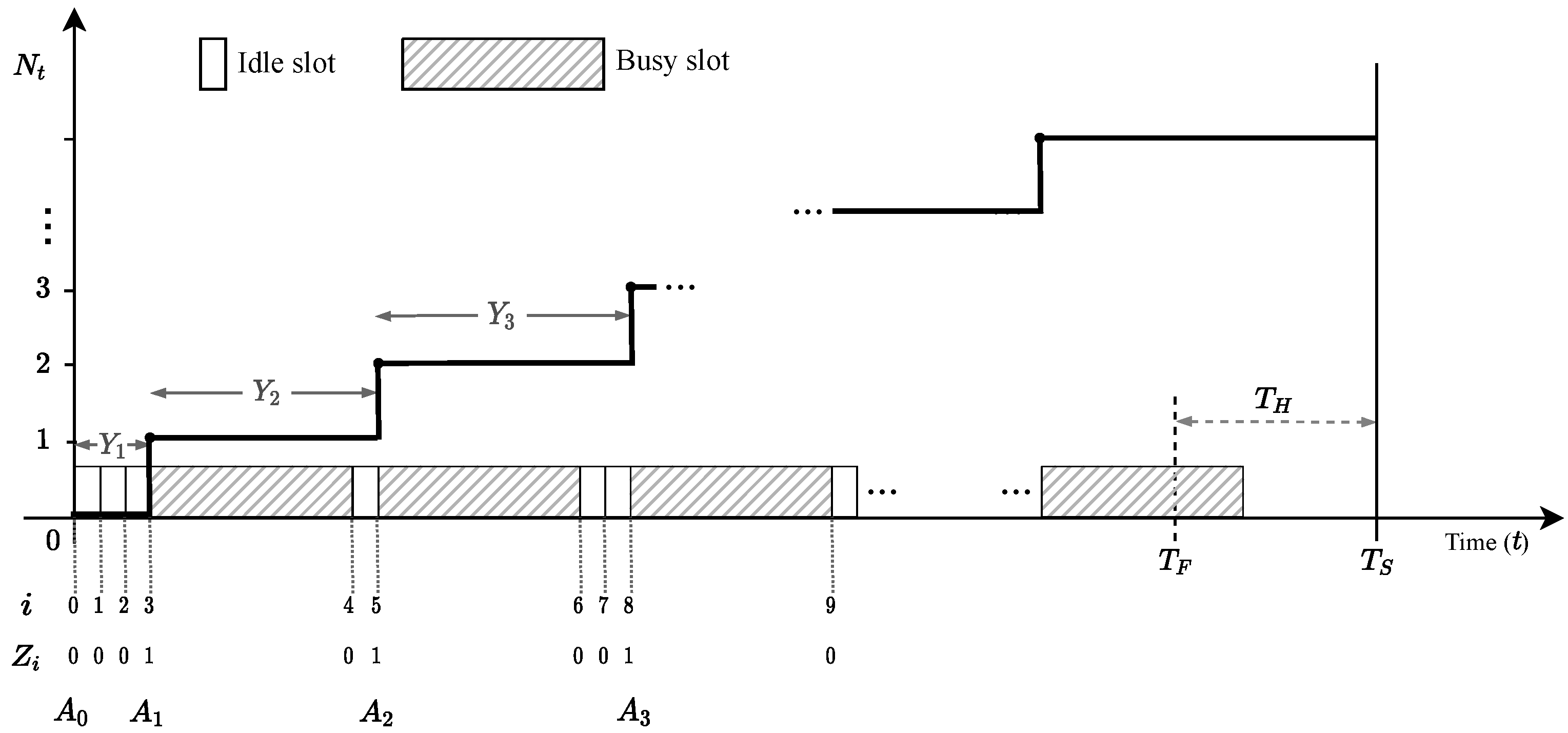
4.1. Stochastic Model
4.2. Evaluating a Single RAW Slot
4.3. Evaluating Several RAW Slots
5. Results and Discussion
5.1. RAW Slot
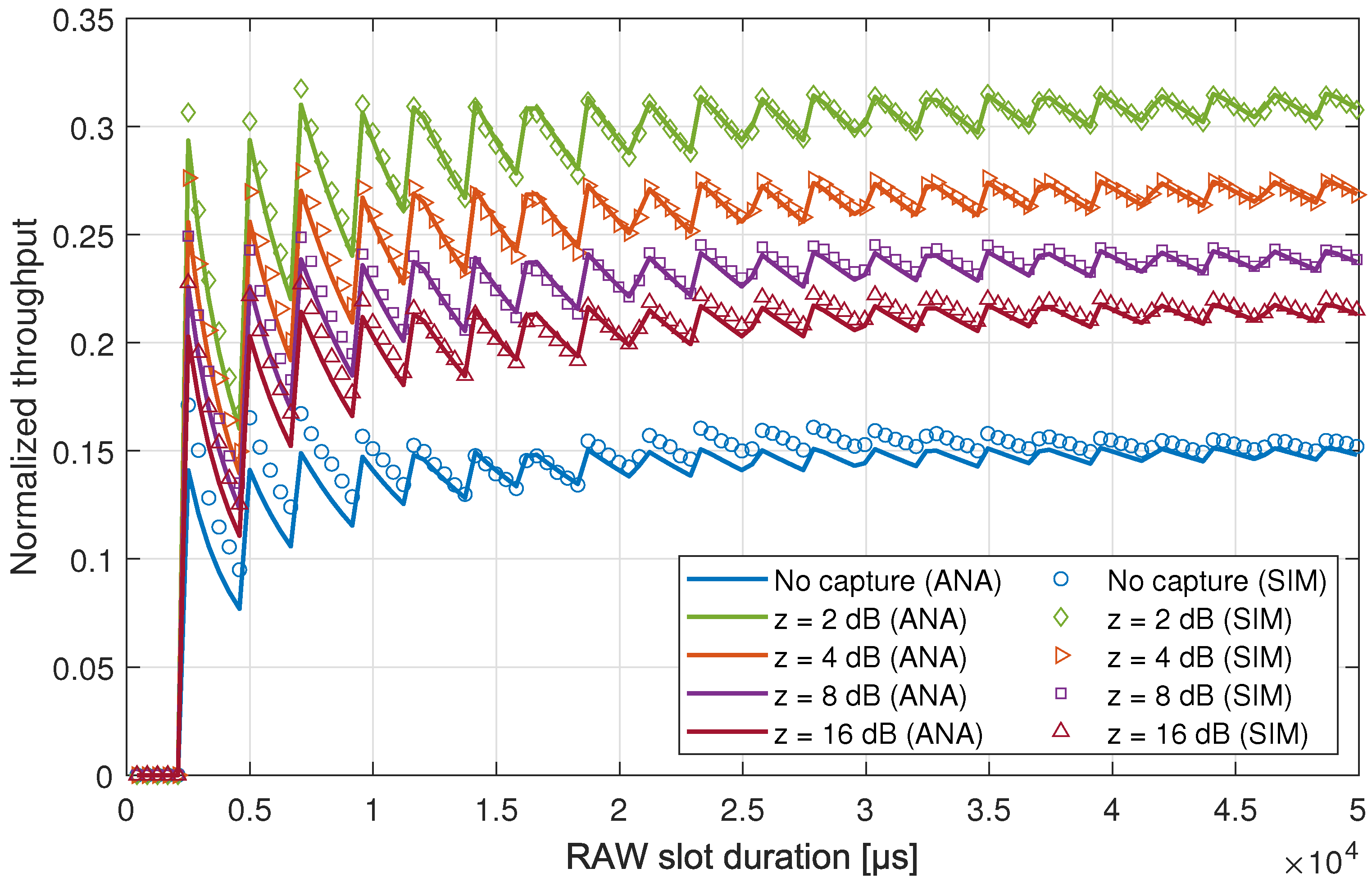
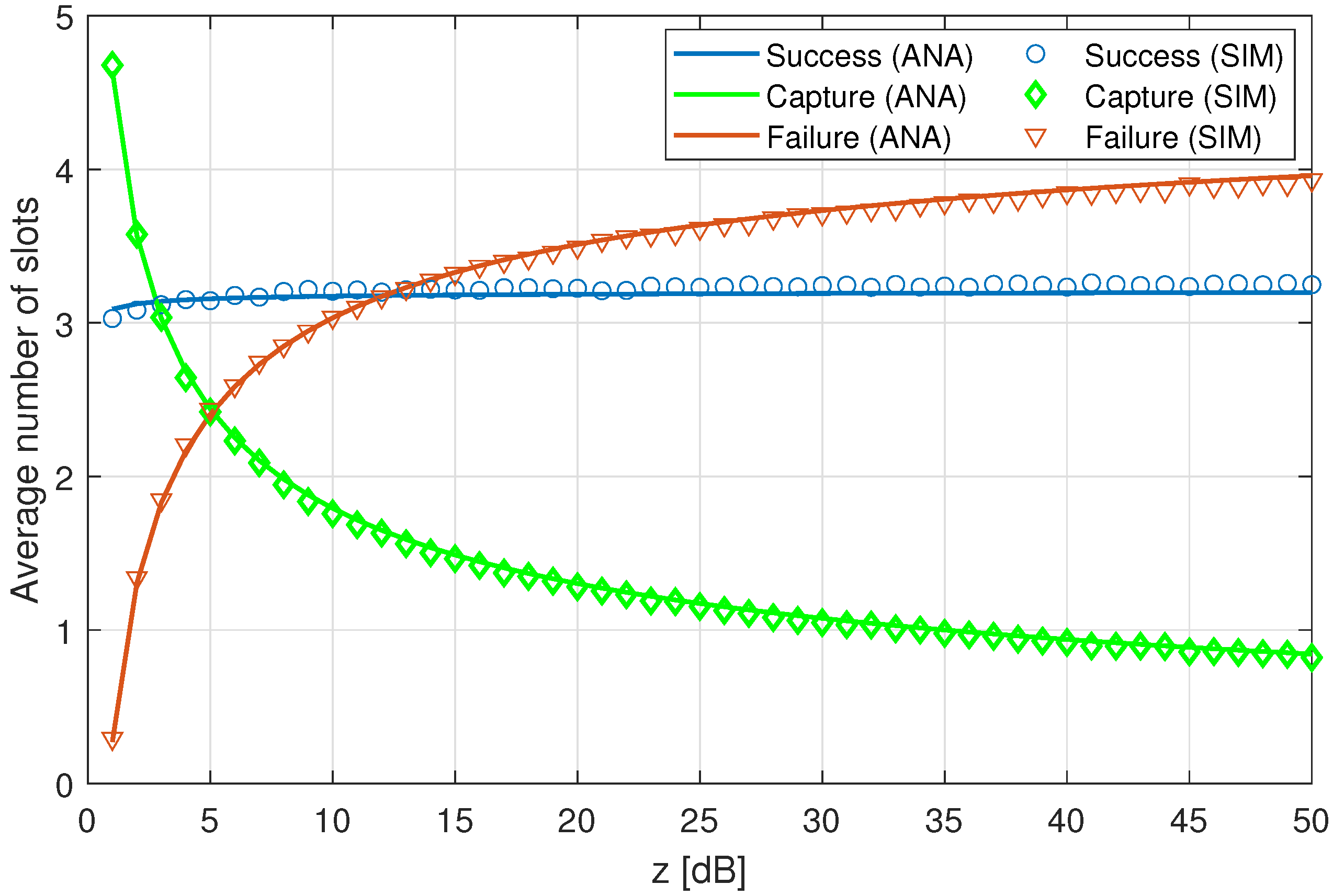
5.1.1. RAW Slot Period
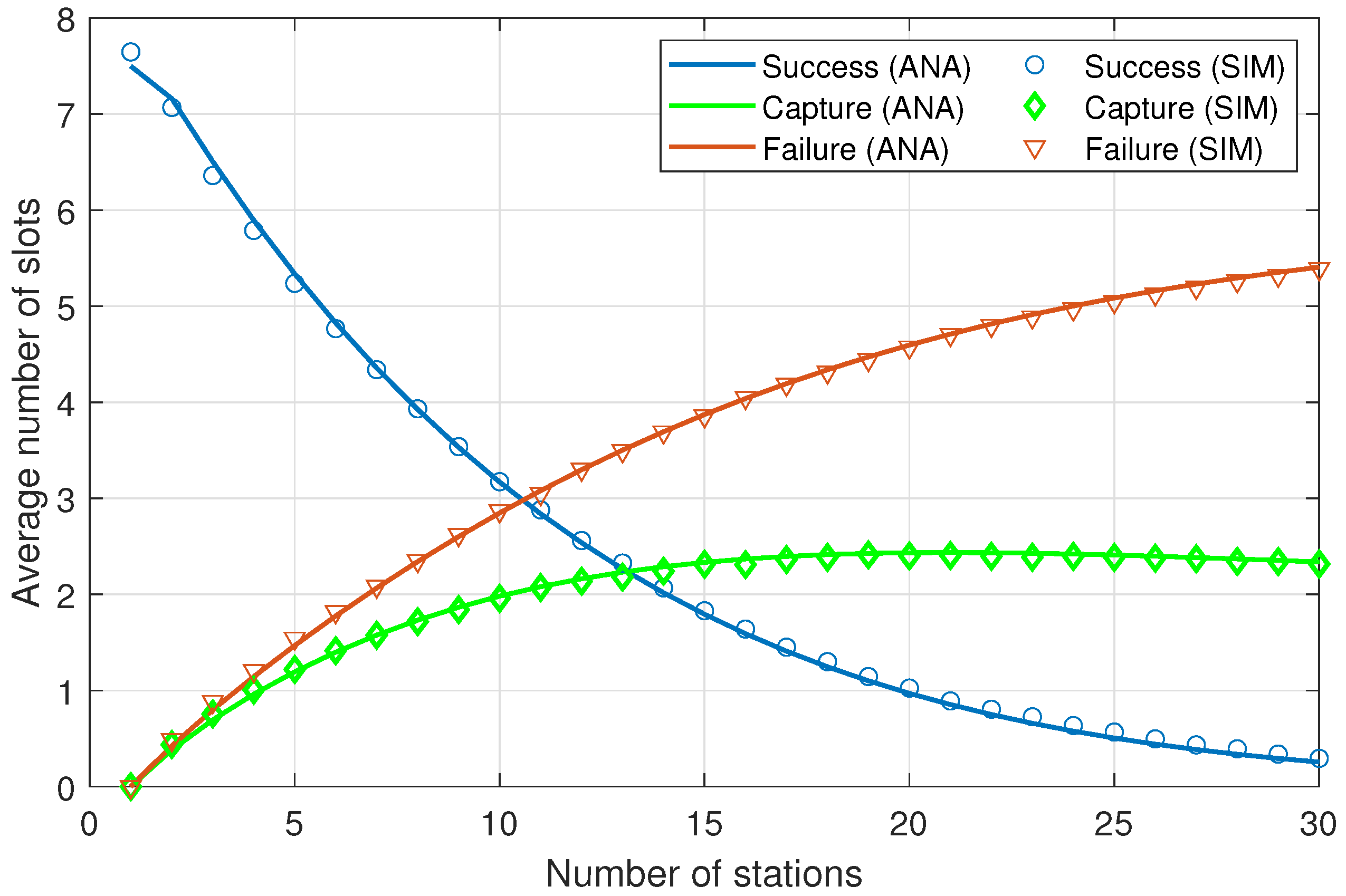
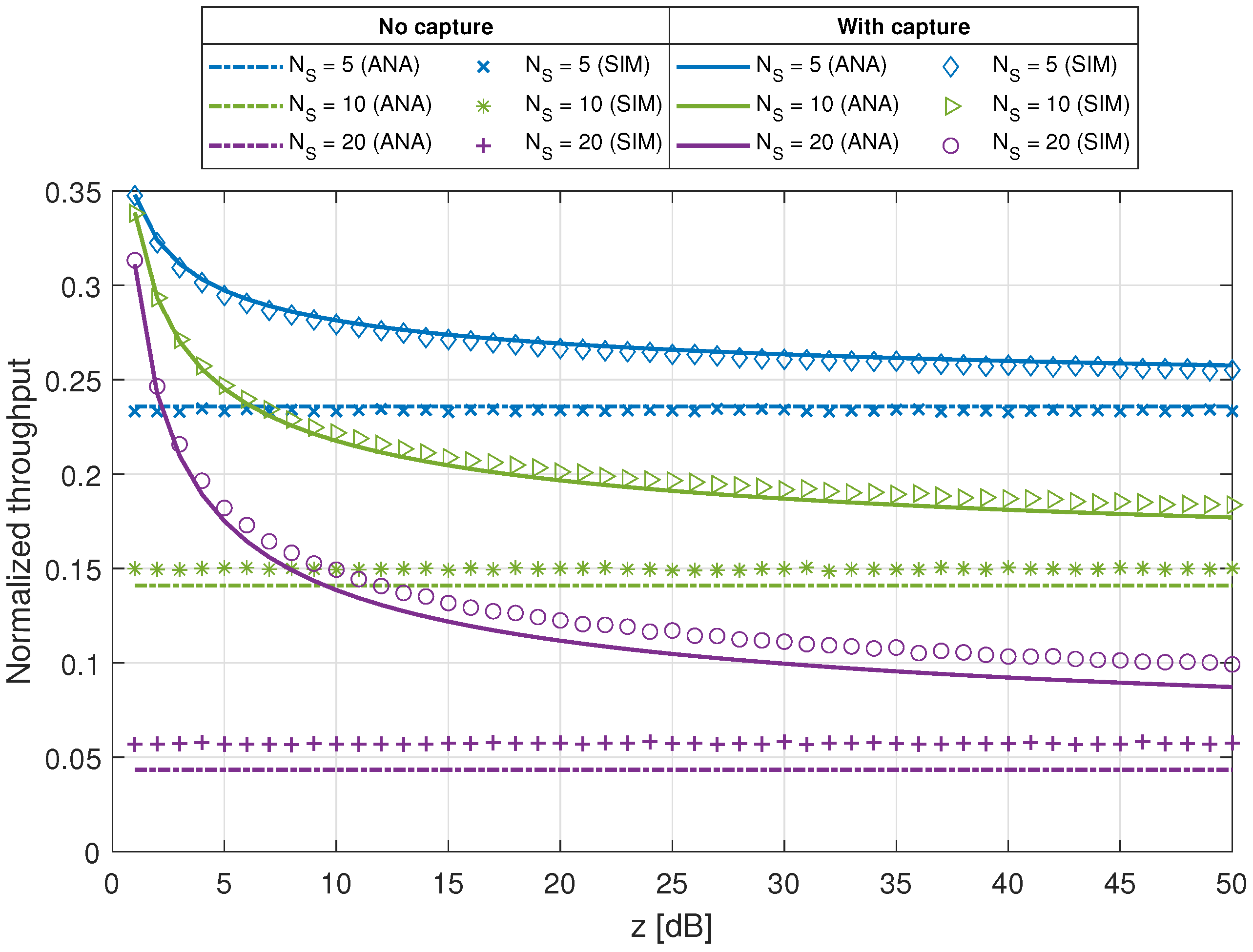
5.1.2. Contending Stations
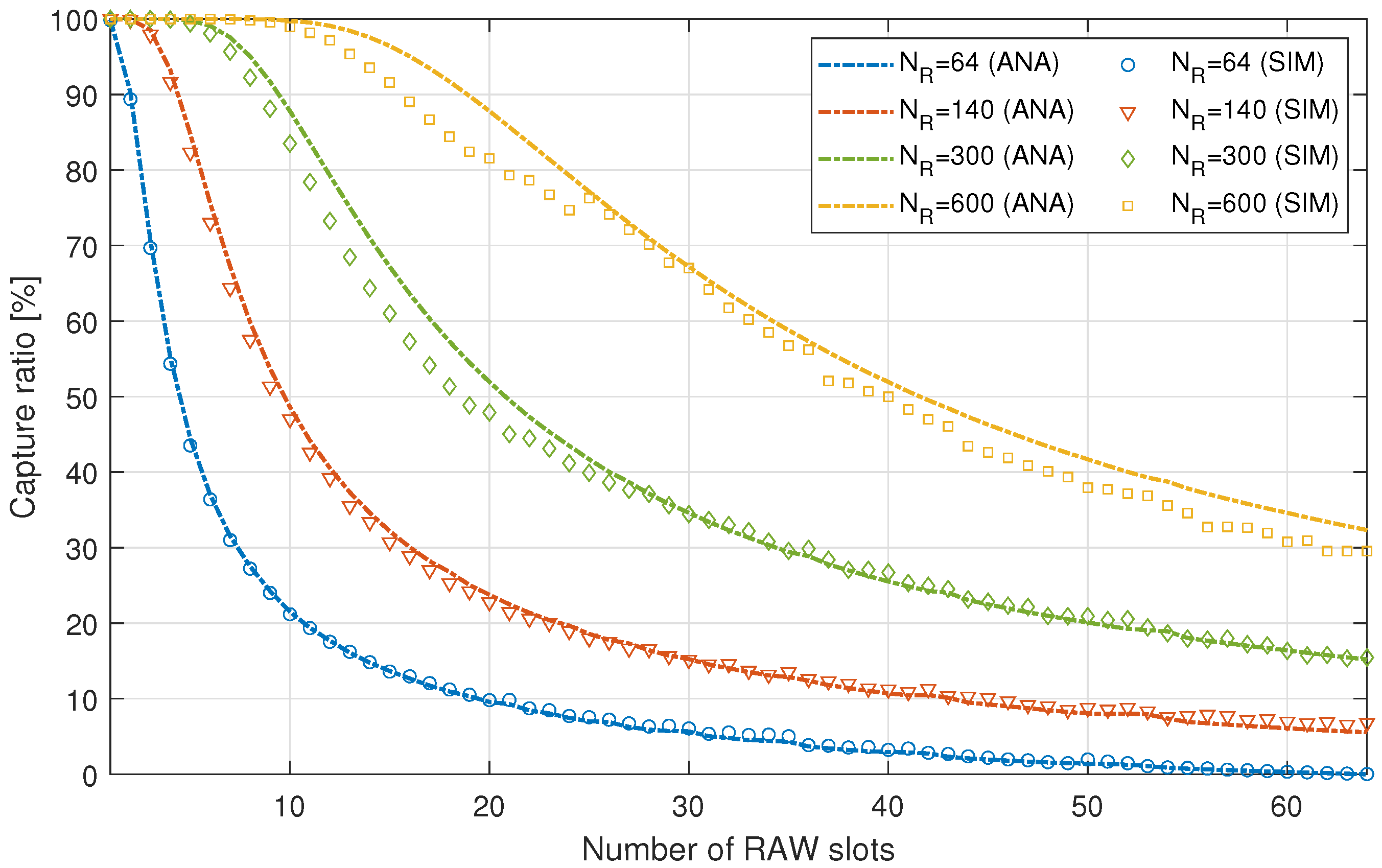
5.1.3. Capture Threshold
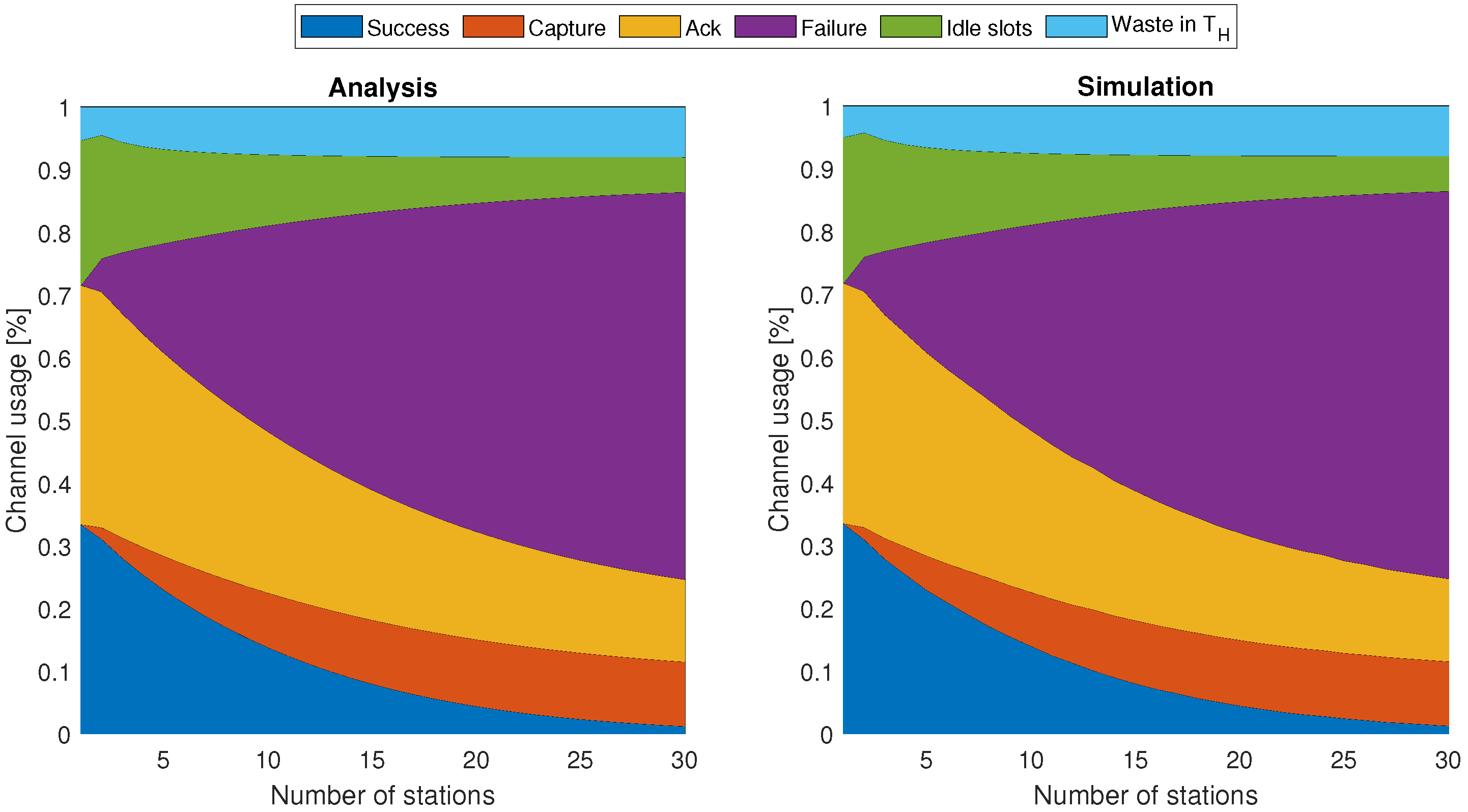
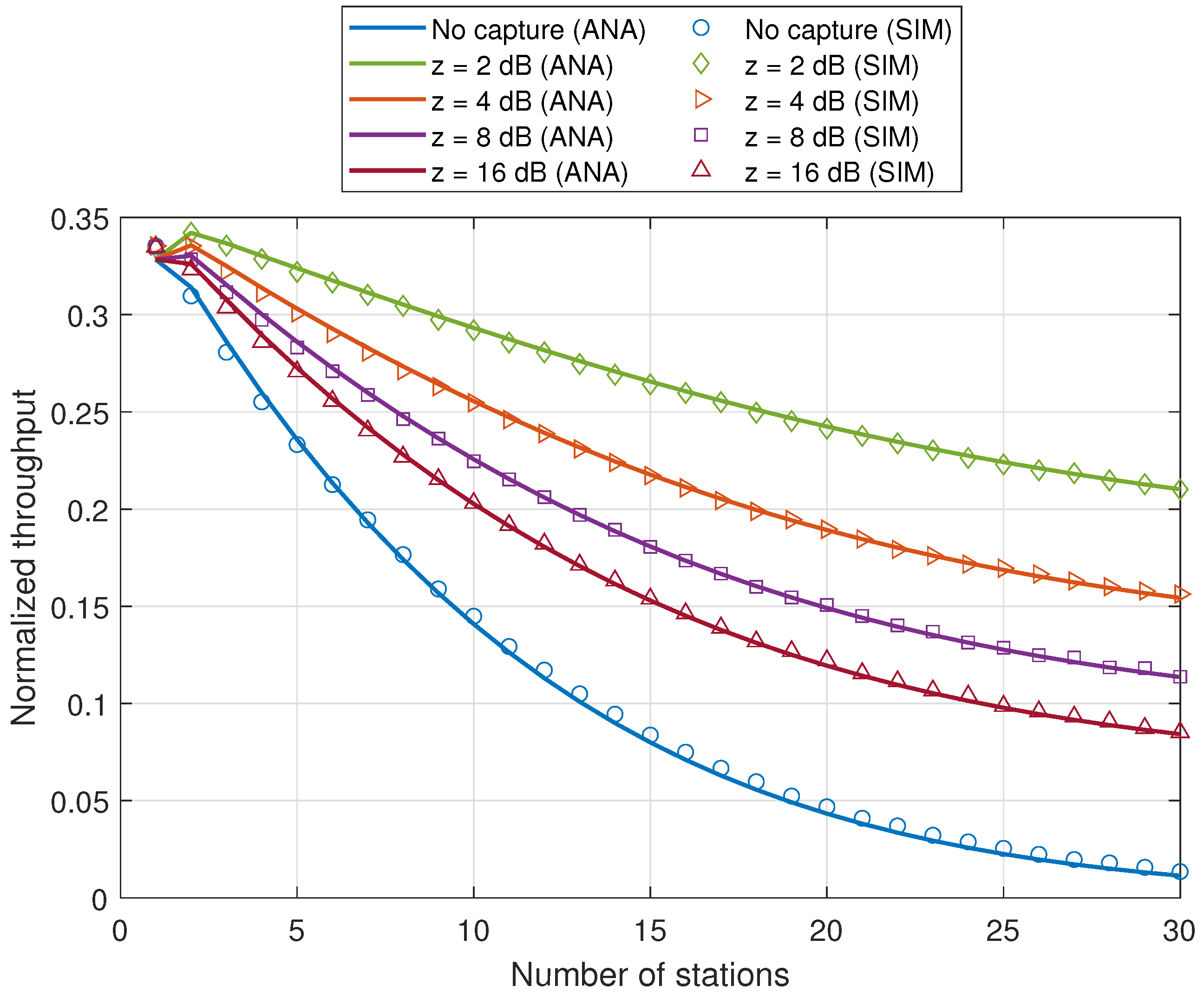
5.2. RAW Performance
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kassab, W.; Darabkh, K.A. A–Z survey of Internet of Things: Architectures, protocols, applications, recent advances, future directions and recommendations. J. Netw. Comput. Appl. 2020, 163, 102663. [Google Scholar] [CrossRef]
- Verma, P.K.; Verma, R.; Prakash, A.; Agrawal, A.; Naik, K.; Tripathi, R.; Alsabaan, M.; Khalifa, T.; Abdelkader, T.; Abogharaf, A. Machine-to-Machine (M2M) communications: A survey. J. Netw. Comput. Appl. 2016, 66, 83–105. [Google Scholar] [CrossRef]
- Tian, L.; Santi, S.; Seferagić, A.; Lan, J.; Famaey, J. Wi-Fi HaLow for the Internet of Things: An up-to-date survey on IEEE 802.11ah research. J. Netw. Comput. Appl. 2021, 182, 103036. [Google Scholar] [CrossRef]
- IEEE 802.11ah-2016; Standard for Information Technology—Telecommunications and Information Exchange between Systems—Local and Metropolitan Area Networks–Specific Requirements—Part 11: Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) Specifications Amendment 2: Sub 1 GHz License Exempt Operation. IEEE: Piscataway, NY, USA, 2017; pp. 1–594. [CrossRef]
- Khorov, E.; Lyakhov, A.; Krotov, A.; Guschin, A. A survey on IEEE 802.11ah: An enabling networking technology for smart cities. Comput. Commun. 2015, 58, 53–69. [Google Scholar] [CrossRef]
- Bianchi, G. Performance analysis of the IEEE 802.11 distributed coordination function. IEEE J. Sel. Areas Commun. 2000, 18, 535–547. [Google Scholar] [CrossRef]
- Taramit, H.; Barbosa, L.O.; Haqiq, A. Energy Efficiency Framework for Time-limited Contention in the IEEE 802.11ah Standard. In Proceedings of the 2021 IEEE Globecom Workshops (GC Wkshps), Madrid, Spain, 7–11 December 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Yang, Z.; Ghubaish, A.; Unal, D.; Jain, R. Factors Affecting the Performance of Sub-1 GHz IoT Wireless Networks. Wirel. Commun. Mob. Comput. 2021, 2021. [Google Scholar] [CrossRef]
- Liao, R.F.; Wen, H.; Wu, J.; Song, H.; Pan, F.; Dong, L. The Rayleigh fading channel prediction via deep learning. Wirel. Commun. Mob. Comput. 2018, 2018, 6497340. [Google Scholar] [CrossRef]
- Ahmed, N.; Rahman, H.; Hussain, M.I. A comparison of 802.11ah and 802.15.4 for IoT. ICT Express 2016, 2, 100–102. [Google Scholar] [CrossRef] [Green Version]
- Domazetović, B.; Kočan, E.; Mihovska, A. Performance evaluation of IEEE 802.11ah systems. In Proceedings of the 2016 24th Telecommunications Forum (TELFOR), Belgrade, Serbia, 22–23 November 2016; pp. 1–4. [Google Scholar] [CrossRef]
- Ba nos Gonzalez, V.; Afaqui, M.S.; López Aguilera, E.; García Villegas, E. IEEE 802.11ah: A Technology to Face the IoT Challenge. Sensors 2016, 16, 1960. [Google Scholar] [CrossRef] [Green Version]
- Šljivo, A.; Kerkhove, D.; Tian, L.; Famaey, J.; Munteanu, A.; Moerman, I.; Hoebeke, J.; De Poorter, E. Performance Evaluation of IEEE 802.11ah Networks With High-Throughput Bidirectional Traffic. Sensors 2018, 18, 325. [Google Scholar] [CrossRef] [Green Version]
- Raeesi, O.; Pirskanen, J.; Hazmi, A.; Levanen, T.; Valkama, M. Performance evaluation of IEEE 802.11ah and its restricted access window mechanism. In Proceedings of the 2014 IEEE International Conference on Communications Workshops (ICC), Sydney, Australia, 10–14 June 2014; pp. 460–466. [Google Scholar] [CrossRef]
- Santi, S.; Tian, L.; Khorov, E.; Famaey, J. Accurate Energy Modeling and Characterization of IEEE 802.11ah RAW and TWT. Sensors 2019, 19, 2614. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zazhigina, E.; Yusupov, R.; Khorov, E.; Lyakhov, A. Analytical Study of Periodic Restricted Access Window Mechanism for Short Slots. Electronics 2021, 10, 549. [Google Scholar] [CrossRef]
- Khorov, E.; Krotov, A.; Lyakhov, A.; Yusupov, R.; Condoluci, M.; Dohler, M.; Akyildiz, I. Enabling the Internet of Things with Wi-Fi halow—Performance evaluation of the restricted access window. IEEE Access 2019, 7, 127402–127415. [Google Scholar] [CrossRef]
- Khorov, E.; Lyakhov, A.; Nasedkin, I.; Yusupov, R.; Famaey, J.; Akyildiz, I.F. Fast and Reliable Alert Delivery in Mission-Critical Wi-Fi HaLow Sensor Networks. IEEE Access 2020, 8, 14302–14313. [Google Scholar] [CrossRef]
- Pahlavan, K. Understanding Communications Networks for Emerging Cybernetics Applications; River Publishers: Gistrup, Denmark, 2021. [Google Scholar]
- Daneshgaran, F.; Laddomada, M.; Mesiti, F.; Mondin, M. Unsaturated Throughput Analysis of IEEE 802.11 in Presence of Non Ideal Transmission Channel and Capture Effects. IEEE Trans. Wirel. Commun. 2008, 7, 1276–1286. [Google Scholar] [CrossRef] [Green Version]
- Daneshgaran, F.; Laddomada, M.; Mesiti, F.; Mondin, M.; Zanolo, M. Saturation throughput analysis of IEEE 802.11 in the presence of non ideal transmission channel and capture effects. IEEE Trans. Commun. 2008, 56, 1178–1188. [Google Scholar] [CrossRef] [Green Version]
- Sutton, G.J.; Liu, R.P.; Collings, I.B. Modelling IEEE 802.11 DCF Heterogeneous Networks with Rayleigh Fading and Capture. IEEE Trans. Commun. 2013, 61, 3336–3348. [Google Scholar] [CrossRef]
- Gallager, R.G. Stochastic Processes: Theory for Applications; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Ling, X.; Cheng, Y.; Mark, J.W.; Shen, X. A renewal theory based analytical model for the contention access period of IEEE 802.15. 4 MAC. IEEE Trans. Wirel. Commun. 2008, 7, 2340–2349. [Google Scholar] [CrossRef]
- Zhang, X. A new method for analyzing nonsaturated IEEE 802.11 DCF networks. IEEE Wirel. Commun. Lett. 2013, 2, 243–246. [Google Scholar] [CrossRef]
- Khairy, S.; Han, M.; Cai, L.X.; Cheng, Y.; Han, Z. A renewal theory based analytical model for multi-channel random access in IEEE 802.11 ac/ax. IEEE Trans. Mob. Comput. 2019, 18, 1000–1013. [Google Scholar] [CrossRef]
- Cocco, D.; Giona, M. Generalized Counting Processes in a Stochastic Environment. Mathematics 2021, 9, 2573. [Google Scholar] [CrossRef]
- Goldsmith, A. Wireless Communications; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Zheng, L.; Ni, M.; Cai, L.; Pan, J.; Ghosh, C.; Doppler, K. Performance Analysis of Group-Synchronized DCF for Dense IEEE 802.11 Networks. IEEE Trans. Wirel. Commun. 2014, 13, 6180–6192. [Google Scholar] [CrossRef] [Green Version]
- Tian, L.; Lopez-Aguilera, E.; Garcia-Villegas, E.; Mehari, M.T.; De Poorter, E.; Latré, S.; Famaey, J. Optimization-Oriented RAW Modeling of IEEE 802.11ah Heterogeneous Networks. IEEE Internet Things J. 2019, 6, 10597–10609. [Google Scholar] [CrossRef] [Green Version]




| Parameter | Value |
|---|---|
| Data rate | 1.95 Mbps |
| MacHeader | 272 bits |
| 1000 μs | |
| 80 μs | |
| 52 μs | |
| SIFS | 160 μs |
| DIFS | 264 μs |
| 8 | |
| 16 | |
| m | 1 |
| Payload | 160 bytes |
| 100 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Taramit, H.; Camacho-Escoto, J.J.; Gomez, J.; Orozco-Barbosa, L.; Haqiq, A. Accurate Analytical Model and Evaluation of Wi-Fi Halow Based IoT Networks under a Rayleigh-Fading Channel with Capture. Mathematics 2022, 10, 952. https://doi.org/10.3390/math10060952
Taramit H, Camacho-Escoto JJ, Gomez J, Orozco-Barbosa L, Haqiq A. Accurate Analytical Model and Evaluation of Wi-Fi Halow Based IoT Networks under a Rayleigh-Fading Channel with Capture. Mathematics. 2022; 10(6):952. https://doi.org/10.3390/math10060952
Chicago/Turabian StyleTaramit, Hamid, José Jaime Camacho-Escoto, Javier Gomez, Luis Orozco-Barbosa, and Abdelkrim Haqiq. 2022. "Accurate Analytical Model and Evaluation of Wi-Fi Halow Based IoT Networks under a Rayleigh-Fading Channel with Capture" Mathematics 10, no. 6: 952. https://doi.org/10.3390/math10060952
APA StyleTaramit, H., Camacho-Escoto, J. J., Gomez, J., Orozco-Barbosa, L., & Haqiq, A. (2022). Accurate Analytical Model and Evaluation of Wi-Fi Halow Based IoT Networks under a Rayleigh-Fading Channel with Capture. Mathematics, 10(6), 952. https://doi.org/10.3390/math10060952









