Efficient Generation of Roots of Power Residues Modulo Powers of Two

Abstract

We propose a characterization for the roots of power residues modulo powers of two. By this characterization, the remainder of dividing a root by a power of two is uniformly distributed in a set with two odd integers, while the quotient is uniformly distributed in an initial segment of positive integers. This property allows us to generate roots of power residues modulo powers of two efficiently.

1. Introduction and Preliminaries

Recent years have shown a significant interest in studying algorithmic problems related to higher-order residuosity. That is because higher-order residuosity may help design cryptographic systems at the binary stream level, while quadratic residuosity is usually limited to bit-by-bit data processing [1,2,3,4,5,6,7,8,9,10,11]. Unfortunately, the use of higher-order residuosity in cryptography faces several challenging problems related to the computation of higher-order residues. A lot of research has recently been dedicated to these kinds of problems [12,13,14,15,16,17].

In this paper, we focus on roots of power residues modulo powers of two. Given a positive integer n, nth roots of power residues modulo powers of two are solutions to the congruence

$$x^n\equiv amod{2}^e,$$

(1)

where a is an odd integer and $e\ge 1$. This congruence can be easily solved when $e=1$ or $e=2$ because in such a case, the multiplicative group ${\mathbb{Z}}_{2^e}^{\ast }$ of integers modulo 2^e has primitive roots. For instance, when $e=2$, $g=3$ is a primitive root modulo $2^2$. Thus, solving (1) comes down to finding solutions to the linear congruence

$$ny\equiv in{d}_g(a)mod2,$$

(2)

where $in{d}_g\left(a\right)$ is the index of a with respect to g [18,19]. The congruence (2) has solutions if and only if the gcd of n and 2, denoted $(n,2)$, divides $in{d}_g\left(a\right)$. Moreover, if it has solutions, then it has $(n,2)$ solutions in ${\mathbb{Z}}_{2^2}^{\ast }$. Two cases are now to be considered:

• n is odd. In this case, $(n,2)=1$ and so the congruence (2) has exactly one solution in ${\mathbb{Z}}_{2^2}^{\ast }$, no matter a;
• n is even. In this case, the congruence (2) has solutions if and only if $in{d}_g\left(a\right)=0$, which is equivalent to saying that $a\equiv 1mod{2}^2$. Moreover, if the congruence has solutions, then it has exactly two solutions in ${\mathbb{Z}}_{2^2}^{\ast }$, namely 1 and 3.

Solving (1) when $e>2$ is harder mainly because ${\mathbb{Z}}_{2^e}^{\ast }$ does not have primitive roots. When n is odd, the unique solution modulo $2^2$ can be lifted to 2^e in exactly one way. Thus, for n odd, the congruence (1) always has a unique solution in ${\mathbb{Z}}_{2^e}^{\ast }$.

The case when n is even contrasts sharply with the case when n is odd. It can be shown in this case [20,21] that the congruence (1) is solvable if and only if $a\equiv 1mod{2}^{d+2}$, where $2^d=(n,2^{e-2})$. Moreover, if the congruence is solvable, then it has $2^{d+1}$ solutions in ${\mathbb{Z}}_{2^e}^{\ast }$. This result gives information about the solvability of (1) when n is even, but it does not say anything about the form of the solutions or how to obtain them. Nor does its proof in [21] provide a characterization of the solutions.

• Contribution

In this paper, we provide a characterization of the solutions to $x^n\equiv amod{2}^{d+\ell }$, where $n=2^{d}k$, $d\ge 1$, k is odd, and $\ell \ge 2$. More precisely, we show that each solution to this congruence can be written in the form $u+2^{\ell }q$, where u is uniformly distributed in a set with exactly two odd integers less than $2^{\ell }$, while q is uniformly distributed between 0 and $2^d-1$. Moreover, we show that u can be obtained recursively from one of the two integers in the set $\{1,3\}$. This characterization leads to a reasonably efficient algorithm to generate random solutions for the above congruence:

• Choose randomly an integer $u_2$ from the set $\{1,3\}$;
• Apply the recursive procedure to $u_2$ in $\ell -2$ steps to get an integer $u_{\ell }$;
• Randomly generate q between 0 and $2^d-1$;
• Return the solution $u_{\ell }+2^{\ell }q$.

• Preliminaries

We recall some basic notation and terminology on elementary number theory that we are going to use in the paper. For details, the reader is referred to [18,19].

The set of integers is denoted by $\mathbb{Z}$. For two positive integers a and b, $C_a^b$ stands for the number of combinations of a taken by b.

The gcd of two integers a and b is denoted $(a,b)$. a and b are called co-prime if $(a,b)=1$. If m is another integer, then a and b are called congruent modulo m, which are denoted $a\equiv bmodm$ or $a{\equiv }_{m}b$, if m divides $a-b$. The remainder of the integer division of a by m, assuming $m\ne 0$, is denoted $amodm$.

Given a positive integer m, ${\mathbb{Z}}_m$ stands for $\{0,\dots ,m-1\}$ and ${\mathbb{Z}}_m^{\ast }=\{a\in {\mathbb{Z}}_n\mid (a,m)=1\}$. The cardinality of ${\mathbb{Z}}_m^{\ast }$ is $\varphi \left(m\right)$, where $\varphi$ is Euler’s totient function. As a multiplicative group, ${\mathbb{Z}}_m^{\ast }$ is cyclic if and only if m is 2, 4, $p^e$, or $2p^e$ for some prime $p\ge 3$ and $e\ge 1$. When ${\mathbb{Z}}_m^{\ast }$ is cyclic, it has generators (also called primitive roots), and each integer $a\in {\mathbb{Z}}_m^{\ast }$ can be written as $g^{i}modm$ for any generator g and some unique $0\le i<\varphi \left(m\right)$ that depends on g. The integer i is called the index of a with respect to g modulo m, which is denoted $in{d}_q\left(a\right)modm$.

Let f be a polynomial with integer coefficients, p be a prime, and $e>1$. If $a\in {\mathbb{Z}}_{p^e}$ is a solution to the congruence

$$f(x)\equiv 0mod{p}^e$$

(3)

then $r=amod{p}^{e-1}$ is a solution to the congruence

$$f(x)\equiv 0mod{p}^{e-1}$$

(4)

When a solution $r\in {\mathbb{Z}}_{p^{e-1}}$ to (4) gives rise to a solution a to (3) such that $r=amod{p}^{e-1}$, we say that r is lifted from $p^{e-1}$ to $p^e$. The theorem below provides the lifting criteria.

Theorem 1

(Hensel’s Lemma, [18,19]). Let $p\ge 2$ be a prime integer, $e>1$, and $r\in {\mathbb{Z}}_{p^{e-1}}$ be a solution to (4). Then, the following properties hold:

1. 

If $f^{\prime }\left(r\right)\not\equiv 0modp$, where $f^{\prime }$ is the formal derivative of f, then r can be lifted from $p^{e-1}$ to $p^e$ in a unique way $a=r+q{p}^{e-1}$, where q is the unique solution modulo p to the linear congruence;

$$q{f}^{\prime }(r)+\frac{f(r)}{p^{e-1}}\equiv 0modp$$

(5)

2. 

If $f^{\prime }\left(r\right)\equiv 0modp$ and $f\left(r\right)\equiv 0mod{p}^e$, then r can be lifted from $p^{e-1}$ to $p^e$ in exactly p distinct ways $a_i=r+i{p}^{e-1}$, for all $0\le i<p$;

3. 

If $f^{\prime }\left(r\right)\equiv 0modp$ and $f\left(r\right)\not\equiv 0mod{p}^e$, then r cannot be lifted from $p^{e-1}$ to $p^e$.

An integer a co-prime with m is an nth residue modulo m, where $n\ge 2$, if the congruence $x^n\equiv amodm$ is solvable. When solvable, any solution to this congruence will be called an nth root of a modulo m.

2. Characterization Results

Let $n=2^{d}k$ be an even integer, a be an odd integer, and $e\ge 2$, where $d,k\ge 1$. In the study of the solutions to the congruence (1), we will distinguish two important cases: the first case is the one in which $e\le d+2$, and the second is the one in which $e>d+2$.

Before entering into the treatment of the two cases, we present a technical result.

Lemma 1.

Let $n=2^{d}k$ be an even integer, where $d,k\ge 1$. Then, for any $1\le i<n$, $2^{d+\lfloor (i-1)/2\rfloor +1}$ divides $C_n^i{2}^i$, where $\lfloor ·\rfloor$ stands for the floor function.

Proof. 

Recall from [22] (Chapter 1, §15) that the highest power of a prime p that divides $i!$, where $i\ge 1$, is given by

$$⌊\frac{i}{p}⌋+⌊\frac{i}{p^2}⌋+\cdots$$

Taken $p=2$ and assuming that $2^t\le i<2^{t+1}$ for some $t\ge 1$, we obtain

$$\begin{array}{ccc}⌊\frac{i}{2}⌋+⌊\frac{i}{2^2}⌋+\cdots \hfill & =& ⌊\frac{i}{2}⌋+⌊\frac{i}{2^2}⌋+\cdots +⌊\frac{i}{2^t}⌋\hfill \\ & \le & i{\sum }_{j=1}^t\frac{1}{2^j}\hfill \\ & =& i-\frac{i}{2^t}\hfill \\ & \le & i-1\hfill \end{array}$$

Now, given $1\le i<n$, we have

$$C_n^i{2}^i=\frac{n(n-1)\cdots (n-i+1)}{1\cdots i}{2}^i$$

Let $i!=2^{s}a$, where a is odd. According to the above result, $s\le i-1$.

The factors $(n-2)$, $(n-4)$, and so on are all even. There are $\lfloor (i-1)/2\rfloor$ such factors. As $n=2^{d}k$, we conclude that $2^{d+\lfloor (i-1)/2\rfloor +1}$ must divide $C_n^i{2}^i$. □

The following lemma completely treats the first case.

Lemma 2.

Let a be an odd integer and $n=2^{d}k$ be an even integer, where $d,k\ge 1$. Then, for any $0\le \ell \le d$, the following two properties hold:

1. 

The congruence

$$x^n\equiv amod{2}^{\ell +2};$$

(6)

is solvable in $\mathbb{Z}$ if and only if $a\equiv 1mod{2}^{\ell +2}$;

2. 

If the congruence (6) is solvable, then it has $2^{\ell +1}$ solutions in ${\mathbb{Z}}_{2^{\ell +2}}^{\ast }$, namely all the odd integers in this set.

The standard proof of Lemma 2 is based on the fact that any odd integer r fulfills the congruence

$$r^{2^{\ell }}\equiv 1mod{2}^{\ell +2},$$

for any $\ell \ge 1$ (remark that we can only get $r^{2^{\ell }}\equiv 1mod{2}^{\ell +1}$ by Euler’s theorem). This fact was first noticed in [21] and can be easily proved by mathematical induction. According to this fact, the congruence (6) is solvable if and only if $a\equiv 1mod{2}^{\ell +2}$ and, when it is solvable, any odd integer is a solution to it.

We can also prove Lemma 2 by using Hensel’s Lemma. For the sake of uniformity and completeness with the second case that we discuss further, we attach in Appendix A a proof of this type for Lemma 2.

We now turn to the second case mentioned at the beginning of the section.

Theorem 2.

Let a be an odd integer and $n=2^{d}k$ be an even integer, where $d\ge 1$ and k is odd. Then, for any $\ell \ge 2$, the following two properties hold:

1. 

The congruence

$$x^n\equiv amod{2}^{d+\ell }$$

(7)

is solvable in $\mathbb{Z}$ if and only if $a\equiv 1mod{2}^{d+2}$.

2. 

If the congruence (7) is solvable, then there exists a set $U^{\ell }$ with exactly two odd integers less than $2^{\ell }$ such that the set of solutions in ${\mathbb{Z}}_{2^{d+\ell }}^{\ast }$ to the congruence (7) is

$$\{u+2^{\ell }q\mid u\in U^{\ell },0\le q<2^d\}$$

and has the cardinality $2^{d+1}$.

Proof. 

The congruence (7) is solvable if and only if the congruence $x^n\equiv amod{2}^{d+2}$ is solvable and at least one of its solutions can be lifted from $2^{d+2}$ to $2^{d+\ell }$. According to Lemma 2, the congruence $x^n\equiv amod{2}^{d+2}$ is solvable if and only if $a\equiv 1mod{2}^{d+2}$. We will further show that, when $x^n\equiv amod{2}^{d+2}$ is solvable, half of its solutions can be lifted, in consecutive steps, from $2^{d+2}$ to $2^{d+\ell }$.

For the sake of clarity, we denote by $C^{\ell }$ the set of solution in ${\mathbb{Z}}_{2^{d+\ell }}^{\ast }$ to the congruence (7). According to the division theorem, for any $r\in C^{\ell }$, there exist unique u and q such that $r=u+2^{\ell }q$, $0<u<2^{\ell }$, and $q\ge 0$. Moreover, u must be odd. We further use the following notation:

• $U^{\ell }$—the set of remainders u of the solutions $r\in C^{\ell }$, as defined above;
• $C^{\ell }\left(u\right)$—the set of all $r\in C^{\ell }$ such that the remainder of dividing r by $2^{\ell }$ is u;
• $C_0^{\ell }\left(u\right)$—the set of all $r\in C^{\ell }\left(u\right)$ such that the quotient of dividing r by $2^{\ell }$ is even;
• $C_1^{\ell }\left(u\right)$—the set of all $r\in C^{\ell }\left(u\right)$ such that the quotient of dividing r by $2^{\ell }$ is odd.

We are now ready to prove by mathematical induction on $\ell \ge 2$ the following properties:

(P₁)

The set $U^{\ell }$ contains exactly two odd integers and $C^{\ell }=\{u+2^{\ell }q\mid u\in U^{\ell },0\le q<2^{\ell }\}$. As a result, $|C^{\ell }|=2^{\ell +1}$;

(P₂)

$|C_0^{\ell }\left(u\right)|=|C_1^{\ell }\left(u\right)|=2^{d-1}$, for any $u\in U^{\ell }$;

(P₃)

For any $u\in U^{\ell }$ and depending on it, either all solutions in $C_0^{\ell }\left(u\right)$ or all solutions in $C_1^{\ell }\left(u\right)$ fulfill the lifting requirement from $2^{d+\ell }$ to $2^{d+\ell +1}$. Then, $C^{\ell +1}$ is obtained by lifting all solutions r that fulfill the lifting requirement in exactly two ways, namely r and $r+2^{d+\ell }$.

Base step:$\ell =2$. According to Lemma 2, the solutions to $x^n\equiv amod{2}^{d+2}$ are all the integers in ${\mathbb{Z}}_{2^{d+2}}^{\ast }$. According to the division theorem, each of them can be written as $r=u+2^{2}q$, where $u\in U^2=\{1,3\}$ and $0\le q<2^d$. Then, we can easily show that the properties $\left(P_1\right)$ and $\left(P_2\right)$ are true.

We focus now on the property $\left(P_3\right)$. Let $f\left(x\right)=x^n-a$. We remark that $f^{\prime }\left(x\right)=n{x}^{n-1}\equiv 0mod2$ and, therefore, according to Hensel’s Lemma, a solution $r\in C^2$ can be lifted from $2^{d+2}$ to $2^{d+3}$ if and only if $f\left(r\right)\equiv 0mod{2}^{d+3}$. The last condition is equivalent to $r^n\equiv amod{2}^{d+3}$.

Let $r=u+2^{2}q\in C^2$, where $u\in U^2$ and $0\le q<2^d$. Then,

$$\begin{array}{ccc}{r}^n\hfill & =& {(u+2^{2}q)}^n\hfill \\ & =& u^n+C_n^1{u}^{n-1}{2}^{2}q+C_n^2{u}^{n-2}{2}^4{q}^2+\cdots +C_n^n{2}^{2n}{q}^n\hfill \\ & =& u^n+2^{d+2}k{u}^{n-1}q+C_n^2{u}^{n-2}{2}^4{q}^2+\cdots +C_n^n{2}^{2n}{q}^n\hfill \end{array}$$

Now, remark that k and u are odd and $2^{d+3}$ divides $C_n^i{2}^{2i}$, for all $i\ge 2$ (Lemma 1). Therefore,

$$r^n\equiv \left\{\begin{array}{cc}{u}^{n}mod{2}^{d+3},\hfill & \mathrm{if}r\in C_0^2(u)\hfill \\ (u^n+2^{d+2})mod{2}^{d+3},\hfill & \mathrm{if}r\in C_1^2(u)\hfill \end{array}\right.$$

It remains now to investigate the relationship between $u^n$ and a modulo $2^{d+3}$. Looking back to the binomial expansion of $r^n$, we conclude that $r^n\equiv u^{n}mod{2}^{d+2}$. As $r^n\equiv amod{2}^{d+2}$ (because $r\in C^2$), we obtain $u^n\equiv amod{2}^{d+2}$. Combining this with $a\equiv 1mod{2}^{d+2}$, we get

$$a=1+b{2}^{d+2}+\beta 2^{d+3},$$

for some $b\in \{0,1\}$ and integer $\beta \ge 0$, and

$$u^n=1+c{2}^{d+2}+\gamma 2^{d+3},$$

for some $c\in \{0,1\}$ and integer $\gamma \ge 0$.

Two cases are to be considered now:

• $b=c$. In such a case, $u^n\equiv amod{2}^{d+3}$. As $r^n\equiv u^{n}mod{2}^{d+3}$ for all $r\in C_0^2\left(u\right)$, we obtain $r^n\equiv amod{2}^{d+3}$ for all $r\in C_0^2\left(u\right)$. This means that all $r\in C_0^2\left(u\right)$ fulfill the lifting requirement from $2^{d+2}$ to $2^{d+3}$;
• $b\ne c$. This is equivalent to $b\equiv c+1mod2$, and therefore, $u^n+1\equiv amod{2}^{d+3}$. As in the previous case, we obtain $r^n\equiv amod{2}^{d+3}$ for all $r\in C_1^2\left(u\right)$ and so, all solutions in $C_1^2\left(u\right)$ can be lifted from $2^{d+2}$ to $2^{d+3}$.

One has also to remark that if a solution in $C_0^2\left(u\right)$ can be lifted from $2^{d+2}$ to $2^{d+3}$, then no solution in $C_1^2\left(u\right)$ can be lifted from $2^{d+2}$ to $2^{d+3}$, and vice versa. Moreover, the lifting requirement above is depended on u.

According to Hensel’s Lemma, a solution r is lifted to $2^{d+3}$ in exactly two ways, r and $r+2^{d+2}$. Thus, the property $\left(P_3\right)$ is proved.

Inductive step: Assume that the three properties hold for $\ell \ge 2$ and we prove them for $\ell +1$. The elements of the set $C^{\ell +1}$ are obtained by lifting the elements of either $C_0^{\ell }\left(u\right)$ or $C_1^{\ell }\left(u\right)$, depending on $u\in U^{\ell }$, from $2^{d+\ell }$ to $2^{d+\ell +1}$.

If $r=u+2^{\ell }q\in C_0^{\ell }\left(u\right)$, then

$$r=u+2^{\ell +1}{q}^{\prime }$$

and

$$r+2^{d+\ell }=u+2^{\ell +1}(q^{\prime }+2^{d-1}),$$

where $q=2q^{\prime }$, $0\le q^{\prime }<2^{d-1}$. Therefore, if $C_0^{\ell }\left(u\right)$ is lifted to $2^{d+\ell +1}$, then $u\in U^{\ell +1}$ and $C^{\ell +1}$ will include all the integers $u+2^{\ell +1}q$ with and even q, $0\le q<2^d$.

If $r=u+2^{\ell }q\in C_1^{\ell }\left(u\right)$, then

$$r=u+2^{\ell }+2^{\ell +1}{q}^{\prime }$$

and

$$r+2^{d+\ell }=u+2^{\ell }+2^{\ell +1}(q^{\prime }+2^{d-1}),$$

where $q=1+2q^{\prime }$, $0\le q^{\prime }<2^{d-1}$. Therefore, if $C_1^{\ell }\left(u\right)$ is lifted to $2^{d+\ell +1}$, then $u+2^{\ell }\in U^{\ell +1}$ and $C^{\ell +1}$ will include all the integers $u+2^{\ell +1}q$ with an odd q, $0\le q<2^d$.

These show that $\left(P_1\right)$ and $\left(P_2\right)$ hold. The property $\left(P_3\right)$ is proven in a quite similar way as in the base step of the induction, and so it is omitted.

As the three properties $\left(P_1\right)$, $\left(P_2\right)$, and $\left(P_3\right)$ hold, we conclude that the theorem holds. □

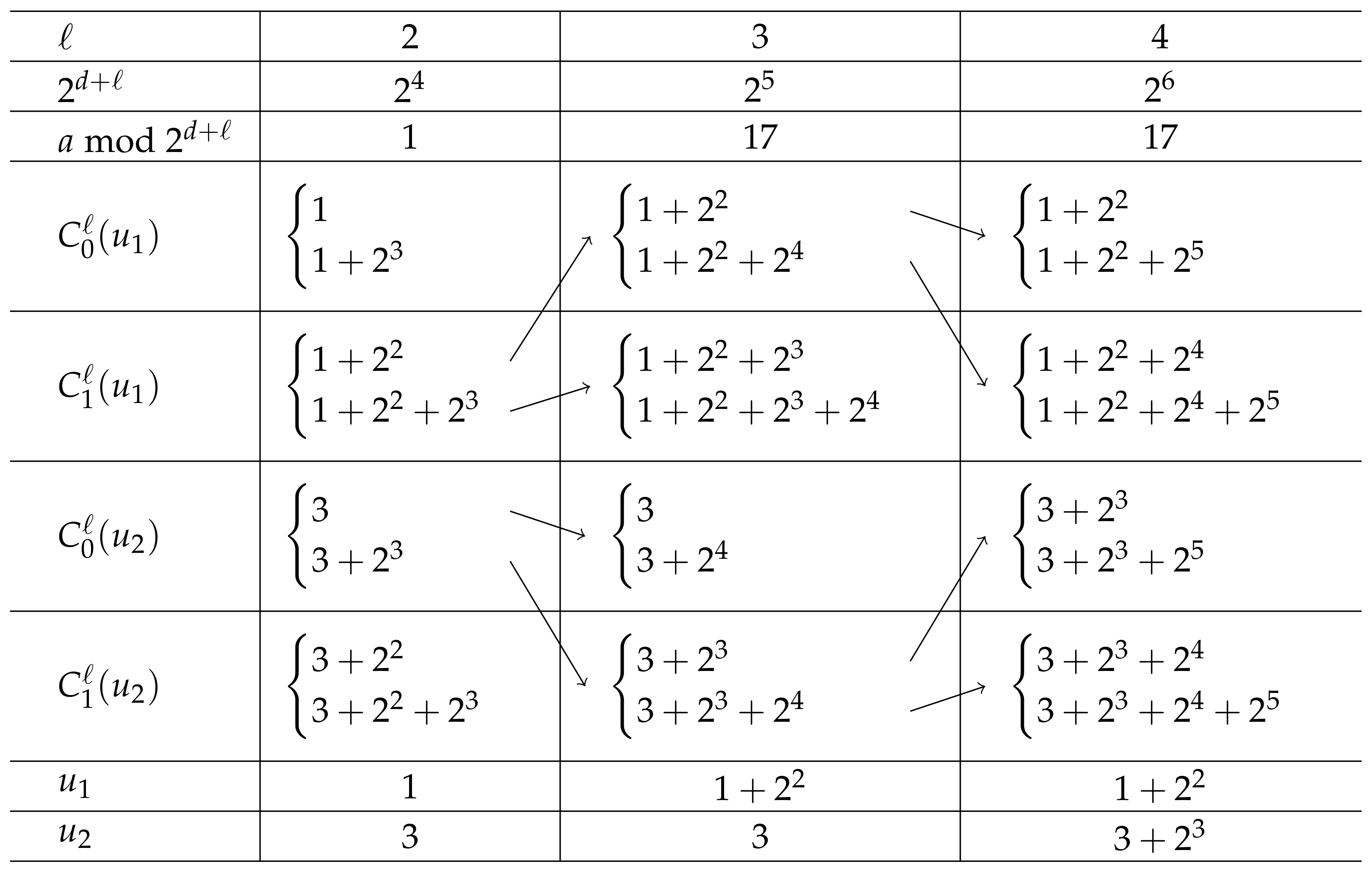
Example 1.

Assume that we want to lift the solutions to the congruence $x^{12}\equiv 81mod{2}^4$ to $2^5$ and $2^6$. In this case, $n=2^2·3$, $d=2$, $a=81$, and $\ell \in \{2,3,4\}$.

As $a\equiv 1mod{2}^4$, the congruence has $2^3$ solutions in ${\mathbb{Z}}_{2^4}^{\ast }$. These solutions can be obtained as shown by Lemma 2. They can be lifted to $2^5$ and $2^6$ by the procedure shown in the proof of Theorem 2. The process is illustrated in Figure 1.

Figure 1. Lifting the solutions to $x^{12}\equiv 81mod{2}^4$.

3. Computational Aspects

Let $n=2^{d}k$ be an even integer, $0\le \ell \le d$, and let a be an odd integer such that $a\equiv 1mod{2}^{\ell +2}$, where $d,k\ge 1$. Finding solutions to the congruence (6) is easy. According to Lemma 2, any odd integer between 0 and $2^{\ell +2}-1$ is a solution to this congruence, and therefore, what we have to do is to generate integers in this interval. If a random integer in this interval is odd, then it is a solution to the congruence. Otherwise, we may increment or decrement it by one to get a solution.

Let us consider now $n=2^{d}k$, $\ell >2$, and $a\in {\mathbb{Z}}_{2^{d+\ell }}^{\ast }$ such that $d\ge 1$, $k\ge 1$ is odd, and $a\equiv 1mod{2}^{d+2}$. The proof of Theorem 2 leads to an efficient algorithm to generate solutions to the congruence (7). The algorithm is based on the following remarks:

1.

Each solution r has the form $r=u+2^{\ell }q$, where $u\in U^{\ell }$ and $0\le q<2^d$;

2.

To compute r comes down to compute u. This can be efficiently done in a recursive way starting with some $u_2\in U^2=\{1,3\}$ and updating it by

$$u_{i+1}=\left\{\begin{array}{cc}{u}_i,\hfill & \mathrm{if}{u}_i^n[d+i]=a[d+i]\hfill \\ u_i+2^i,\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

for all $2\le i<\ell$ ($x[d+i]$ denotes the $(d+i)$th bit in the binary representation of x);

3.

When $u_{\ell }$ is reached, randomly choose $q\leftarrow [0,2^d)$ and return $r=u_{\ell }+2^{\ell }q$.

The algorithm is presented below.

The correctness of Algorithm 1 follows from the proof of Theorem 2. As one can see, the most complex operation is the modular exponentiation $u^{n}mod{2}^{d+i+1}$. This step can be optimized by using Euler’s theorem. Namely:

• Compute $s=kmod{2}^i$;

  Algorithm 1 Generating a random solution to $x^n\equiv amod{2}^{d+\ell }$

  Input:$n=2^{d}k$ with $d\ge 1$ and $k\ge 1$ odd, $\ell >2$, a with $a\equiv 1mod{2}^{d+2}$

  Output: a random solution r to $x^n\equiv amod{2}^{d+\ell }$

  $u\leftarrow \{1,3\}$

  for $i:=2$ to $\ell -1$ do

  $v:=u^{n}mod{2}^{d+i+1}$

  if $v[d+i]\ne a[d+i]$ then

  $u:=u+2^i$

  end if

  end for

  $q\leftarrow [0,2^d)$

  $r:=u+2^{\ell }q$

• Compute $v=u^{2^{d}s}mod{2}^{d+i+1}$.

The correctness of this is based on the fact that if $k=s+2^{i}q$, where $0<s<2^i$, then

$$\begin{array}{ccc}{u}^{2^{d}k}\hfill & \equiv & u^{2^{d}s}{u}_i^{2^{d+i}q}mod{2}^{d+i+1}\hfill \\ & \equiv & u^{2^{d}s}mod{2}^{d+i+1}\hfill \end{array}$$

due to the Euler’s theorem, according to which $u^{2^{d+i}}\equiv 1mod{2}^{d+i+1}$.

The extraction of the bits of the binary representations of a and $u^n$, and also the addition and multiplication by powers of two, are very efficient operations that can be neglected.

Hensel’s lifting procedure is a general methodology for lifting solutions to polynomial congruences. Algorithm 1 should be seen as a practical streamlining of the lifting process, reducing the number of operations and the size of the operands. More precisely:

• By Hensel’s lifting, we start with an odd integer $r_2$ in the interval $[0,2^{d+2})$ and try to lift it in consecutive steps to $2^{d+\ell }$;
• Assume that we have obtained $r_i$ in the interval $[0,2^{d+i})$, where $2\le i<\ell$. If the lifting requirement for $r_i$ is fulfilled, then $r_i$ is lifted to $2^{d+i+1}$ in one of the two possible ways. Otherwise, we go back to $r_{i-1}$ and lift it again in the second possible way if it has not been tried yet. If both lifting possibilities have been tried, then we go back to $r_{i-2}$. Thus, we are faced with a backtracking process that can be very expensive. For instance, let us look to the table in Figure 1. The solution $r_2=3+2^3$ in the second column is lifted to $r_3=3+2^3$ and then to $r_4=3+2^3+2^5$. However, $r_4$ cannot be lifted further and so, we have to go back to $r_3$. Even the second lifting possibility for $r_3$ will not be able to lift further. As a result, we go back to $r_2$;
• Algorithm 1 completely avoids the backtracking process above;
• Hensel’s lifting procedure exponentiates integers in ${\mathbb{Z}}_{2^{d+i}}^{\ast }$ to see if they can be lifted from $2^{d+i}$ to $2^{d+i+1}$. Algorithm 1 exponentiates only two residues modulo $2^i$ to get all solution modulo $2^{d+i+1}$.

Our discussion above shows that the complexity of Algorihm 1 is $\mathcal{O}\left({log}^{3}n\right)$, while the complexity of Hensel’s lifting can be estimated to:

• Best case: $\mathcal{O}(\ell {log}^{3}n)$, where ℓ is the parameter in Algorithm 1;
• Worst case: $\mathcal{O}(\ell ({\sum }_{i=1}^{\ell }{s}_i){log}^{3}n)$, where $s_i$ is the maximum number of backtraking possibilities at the ith lifting.

4. Conclusions

We have proposed a characterization for the roots of power residues modulo powers of two. Namely, by this characterization, each solution to $x^n\equiv amod{2}^{d+\ell }$, where $n=2^{d}k$, $d\ge 1$, $k\ge 1$ is odd, and $\ell \ge 2$ can be written in the form $u_{\ell }+2^{\ell }q$, where $u_{\ell }$ is uniformly distributed in a set with two integers les than $2^{\ell }$ and q is uniformly distributed between 0 and $2^d-1$. Moreover, we have also obtained a recurrence relation for $u_{\ell }$, starting from some $u_2\in \{1,3\}$.

This characterization leads to a reasonably efficient algorithm to generate random solutions for the above congruence. Finding a way to efficiently compute $u_{i+1}^{n}mod{2}^{d+i+2}$ from $u_i^{n}mod{2}^{d+i+1}$, where $2\le i<\ell$, would lead to a great improvement of Algorithm 1.