Abstract
A Galerkin/POD reduced-order model from eigenfunctions of non-converged time evolution transitory states in a problem of Rayleigh–Bénard is presented. The problem is modeled in a rectangular box with the incompressible momentum equations coupled with an energy equation depending on the Rayleigh number R as a bifurcation parameter. From the numerical solution and stability analysis of the system for a single value of the bifurcation parameter, the whole bifurcation diagram in an interval of values of R is obtained. Three different bifurcation points and four types of solutions are obtained with small errors. The computing time is drastically reduced with this methodology.
Keywords:
reduced-order models; proper orthogonal decomposition; spectral methods; Rayleigh–Bénard instability; geophysical flows MSC:
35B32; 35B35; 65N35; 76D05; 76E06
1. Introduction
The study of bifurcation and instability phenomena is of great interest because it is a mechanism that explains many physical and engineering processes. These processes are modeled by partial differential equations which are solved numerically. Bifurcation problems require solving the partial differential equations for many values of the parameters. This requires a huge computing time using standard numerical solvers [1,2,3]. A way to avoid this is the use of reduced-order models, i.e., reduced basis [4,5,6,7,8,9,10] or proper orthogonal decomposition (POD) [11,12,13,14,15,16,17,18,19,20] models. Reduced models are based on the fact that, for dissipative evolution equations, a finite low-dimensional manifold contains the long-term behavior of the system [21,22,23,24,25]. These ideas have been applied in practical contexts, such as aerodynamics [11,26,27], haemodynamics [28], naval industry [29], technologies of measurement [30], or energy efficiency [31], among many others.
The Rayleigh–Bénard convection is a bifurcation problem where a two-dimensional horizontal fluid layer is uniformly heated from the lower plate. To model this problem, we use the continuity equation, the two-dimensional Navier–Stokes equations, and the heat equation, where the Boussinesq approximation is considered. The conductive quiescent state becomes unstable for a critical vertical temperature gradient, measured by the Rayleigh number R [32]. Beyond this threshold, a convective motion sets in. This state suffers transitions as the value of R is further increased. Some industrial setups concerning the use of Rayleigh–Bénard convection equations can be found in [33,34,35,36,37,38,39,40]. Reduced-order models based on POD usually operate in two phases: (1) an off-line phase, where proper bases for the problem unknowns are computed from snapshots, and (2) an on-line phase, where the original partial differential equations are projected over the aforementioned bases. The POD technique has been used extensively to produce reduced-order models for fluid flows [12,14,15,16,17,18,19,20,22,41,42,43] or convective flows [8,13,44,45]. Regarding the off-line phase, there are different types of snapshots that can be considered: solutions at different values of the bifurcation parameter [44], unconverged numerical solutions for a unique value of R [25,46], or other variants of the method [47,48,49]. In Ref. [50], a Rayleigh–Bénard problem was analyzed, and the bifurcation diagram was calculated with a Legendre collocation method. In this work, the same problem is solved with a new Galerkin/POD method. Eigenfunctions of the linear stability analysis of unconverged states of a time evolution scheme for a single value of the bifurcation parameter are used as snapshots of the POD method. The method achievements are: the stationary solutions are recovered for all the different values of the parameters in an interval, the linear stability analysis is solved for all these stationary solutions, and the bifurcation points, as well as the whole bifurcation diagram, are obtained. A previous work used unconverged states of a time evolution scheme for a single value of the parameter as snapshots [46]; in that case, only the stationary solutions in the interval were obtained.
The advantage of non-converged states over other types of snapshots is that, by solving the equations for a single value of the parameter, it is possible to reproduce the different solutions of the problem for many values of the parameter. Other reduced-order methods calculate the complete bifurcation diagram using solutions in different values of the parameter as snapshots [44]. This problem was also studied in Ref. [51], with a reduced basis method selecting steady states at various values of the parameter R, ordered in a greedy way. These procedures have a higher computational cost than the proposed methodology.
2. Formulation of the Problem
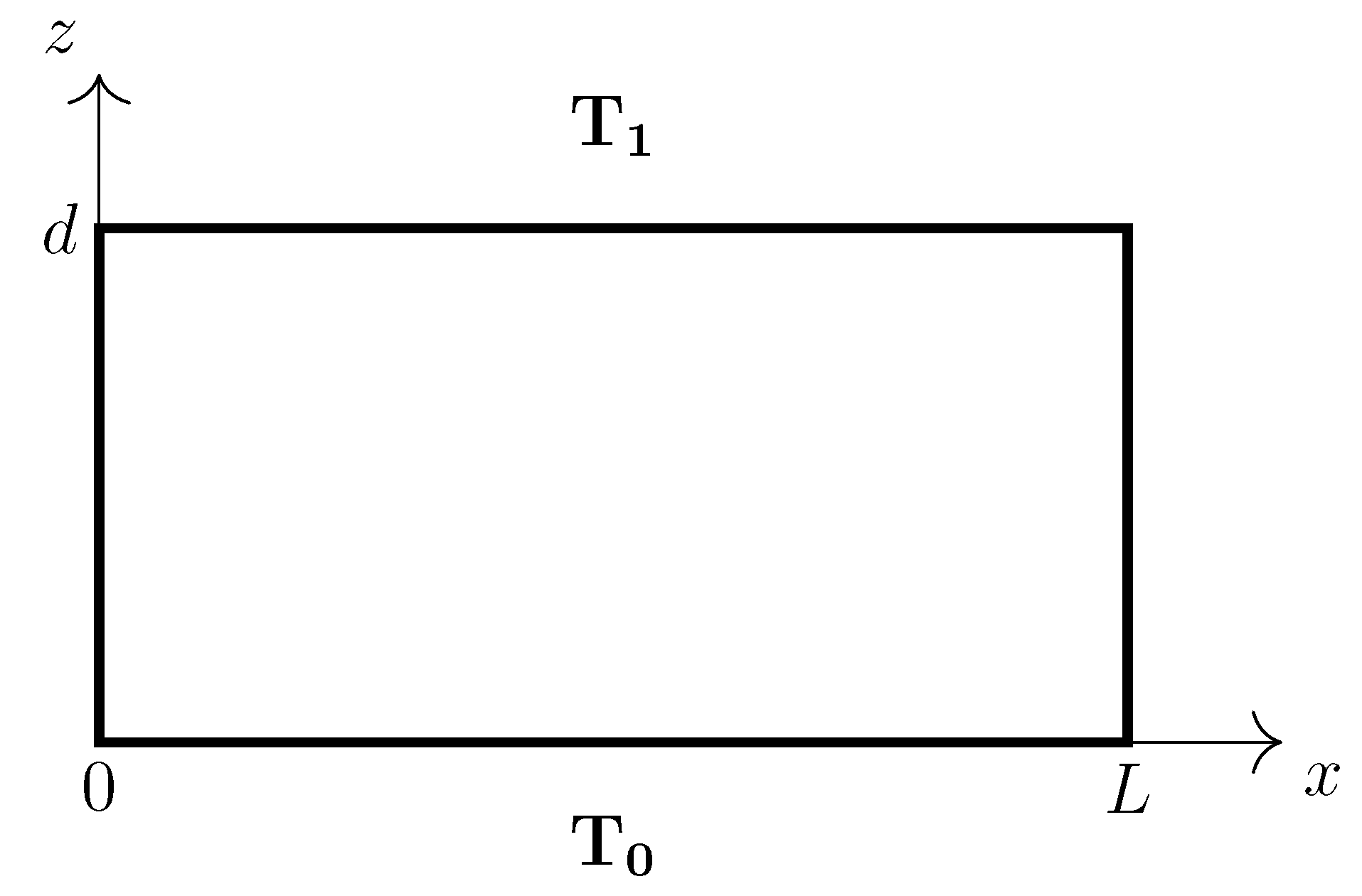
A two-dimensional fluid layer is contained in a rectangle of depth d and length L (see Figure 1). At the lower solid plate, a temperature is considered, and at the upper non-deformable free surface, the temperature is . Then, the temperature difference between both plates is . The lateral boundaries are impenetrable, non-deformable, and exhibit zero heat-flux. In a Cartesian coordinate system, the horizontal and vertical coordinates x and z, the time t, and the velocity , the pressure P, and the temperature fields are adimensionalized, according to Ref. [46], , , , , , and , where primes denote dimensionless quantities, is the density of the fluid at temperature , k is the constant thermal diffusivity, and is the constant viscosity. Dropping primes, the dimensionless velocity, temperature, and pressure fields satisfy the following equations:
where , , is the upwards vertical unit vector, is the Prandtl number, is the Rayleigh number, is the thermal expansion coefficient, and g is the acceleration of the gravity. The boundary conditions (bc) are:
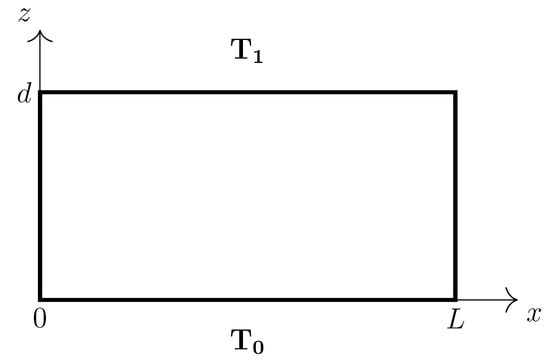
Figure 1.
Sketch of the domain and thermal conditions.
Equations (1)–(3) are the continuity, momentum, and energy conservation equations, in which the Boussinesq approximation is considered in order to simplify the problem, as in Refs. [46,50]. Problem (1)–(5) has a simple conductive solution , , and . The Prandtl number is considered infinite, as in geophysical models of Refs. [50,52,53]; then, the left-hand side of Equation (2) is neglected. Rescaling the problem, as in Ref. [46], and , and dropping the primes, Problem (1)–(5) is rewritten as follows:
together with bc:
Stationary Solutions and Linear Stability Analysis
There exist several stationary solutions for this problem [54]. We denote with superscript b a stationary solution . The linear stability of this solution is studied through the perturbation:
where the tilde refers to the perturbation fields [50,55]. To quantify , , , and , Expression (11) is introduced into (6)–(8), together with (9) and (10). As a result, the following equations are obtained:
where the second-order term in the third equation will be neglected because we are interested in linear stability. Noticing that is a stationary solution, and removing the tildes to simplify notation, the perturbation fields and satisfy the following eigenvalue problem:
with bc (9) and (10).
The eigenvalues and their corresponding eigenfunctions depend on the stationary solution and, therefore, on the Rayleigh number R. We denote as the largest real part of all the eigenvalues . To determine the stability of the stationary solution, we study the sign of . If , the stationary solution is stable. If , the solution is unstable. In this context, we first name the eigenfunction of the stationary solution the eigenfunction related to .
3. The POD Reduced-Order Method
One of the solutions of Problem (6)–(10) is the trivial one, with the fields equal to zero, named the conductive solution, denoted by . This solution is stationary and exists for any value of R. We fix a value of the Rayleigh number . We solve the linear stability analysis Problem (12)–(14) with bc (9) and (10) for the conductive numerical solution with a standard numerical method. A linear combination of the two eigenfunctions associated with the eigenvalues with a maximum real part is the initial condition to obtain a different non-trivial steady solution, solving Problem (6)–(10) with a standard time evolution discretization. This procedure generates some transitory numerical states before convergence . We are taking the transitory states such that . The linear stability analysis for those transitory states is numerically performed, and the first eigenfunctions for these states are the snapshots for the POD analysis. Thus, we obtain K snapshots , where i denotes the time step. This procedure is summarized in Algorithm 1 below.
| Algorithm 1: Calculation of the snapshots. |
|
These snapshots construct, in columns, the corresponding snapshot matrices, , for the first and the second components of the velocity field, the temperature, and the pressure fields, , and , whose columns are the velocity, temperature, and pressure snapshots, respectively. Once these matrices are obtained, we proceed to calculate the modified snapshot matrices , and in terms of the snapshots, as is defined in Algorithm 2 below. These matrices are not the usual correlation matrices used in other works, and it has been proved they are more efficient [46]. We obtain the singular values , and the corresponding eigenvectors , of the modified snapshot matrices. If the singular values decay quickly to zero, this means that the model reduction approach will be worth implementing.
Algorithm 2 describes, for the thermal snapshots , the numerical method applied to compute , and their corresponding POD modes. The procedure is similar for the hydrodynamic fields.
| Algorithm 2: Computation of and POD modes. |
|
In this algorithm, is the size of the mesh grid of the space numerical discretization and is the diagonal matrix whose elements define the discretized scalar product in .
Remarks:
- In practice, matrices and are not considered and Algorithm 2 is not applied to the pressure field because the pressure field disappears from the variational formulation used to solve the problem; see the next section.
- The POD bases for velocity fields and are computed, separately, following Algorithm 2. Below, we refer to the POD basis for the velocity field as . Each element of , , is obtained concatenating vertically the corresponding elements in and , and and .
3.1. The POD/Galerkin Projection Procedure for the Stationary Problem
A Galerkin method is developed to solve the stationary Problem (6)–(10), where the temporal derivative is disregarded. The unknown fields are expanded in the orthonormalized POD bases calculated following Algorithm 2.
The variational form of the stationary problem can be written as follows [51]:
The non-linearity is solved with a Newton procedure, and the velocity and temperature fields are expanded into the POD modes: and . We note that the pressure field disappears from the variational formulation of Equation (7) because the POD modes are incompressible and the normal components of the velocity POD modes vanish at the boundaries [16].
3.2. Linear Stability Analysis of POD/Galerkin Solutions
Let us explain the POD/Galerkin method developed to solve the eigenvalue Problem (12)–(14) together with its corresponding boundary conditions. It is based on the POD modes , and associated with the stationary solutions, as is calculated in Algorithm 2.
The variational form of the eigenvalue problem can be written as follows [56]:
where the velocity and temperature fields that we seek are expanded into the POD modes: and . As in Section 3.1, the pressure field disappears from the variational formulation of Equation (13) because the POD modes are incompressible and the normal components of the velocity POD modes vanish at the boundaries [16]. and are the orthonormalized POD bases for the velocity and temperature fields, where I and J are the number of unsaturated POD modes for each field.
The eigenvalue problem in its variational form (17) and (18) becomes a algebraic eigenvalue problem as follows:
where , and is the identity matrix of size J. The matrix is . Problem (19) has eigenvalues . As explained in Section 2, we are interested in studying the sign of the real part of the eigenvalue with largest real part, . If , the solution is unstable; otherwise, the solution is stable.
4. Numerical Results
A Legendre collocation method is used as a space discretization. Two different Legendre grids are considered, one with 18 nodes in the x-direction and 14 nodes in the z-direction, and another with 36 nodes in the x-direction and 14 nodes in the z-direction. Thus, the maximum number of grid points is . The integrals in Equations (15)–(18) and the usual scalar product are performed with the Legendre–Gauss–Lobatto quadrature formulas [57]. Then, is the diagonal matrix whose elements are the Legendre–Gauss–Lobatto weights. These expansions have good convergence properties [55]. The time evolution scheme is a finite-differences Euler implicit. We consider an aspect ratio , as in Refs. [50,51], and the parameter R takes values in the interval .
4.1. First Bifurcation
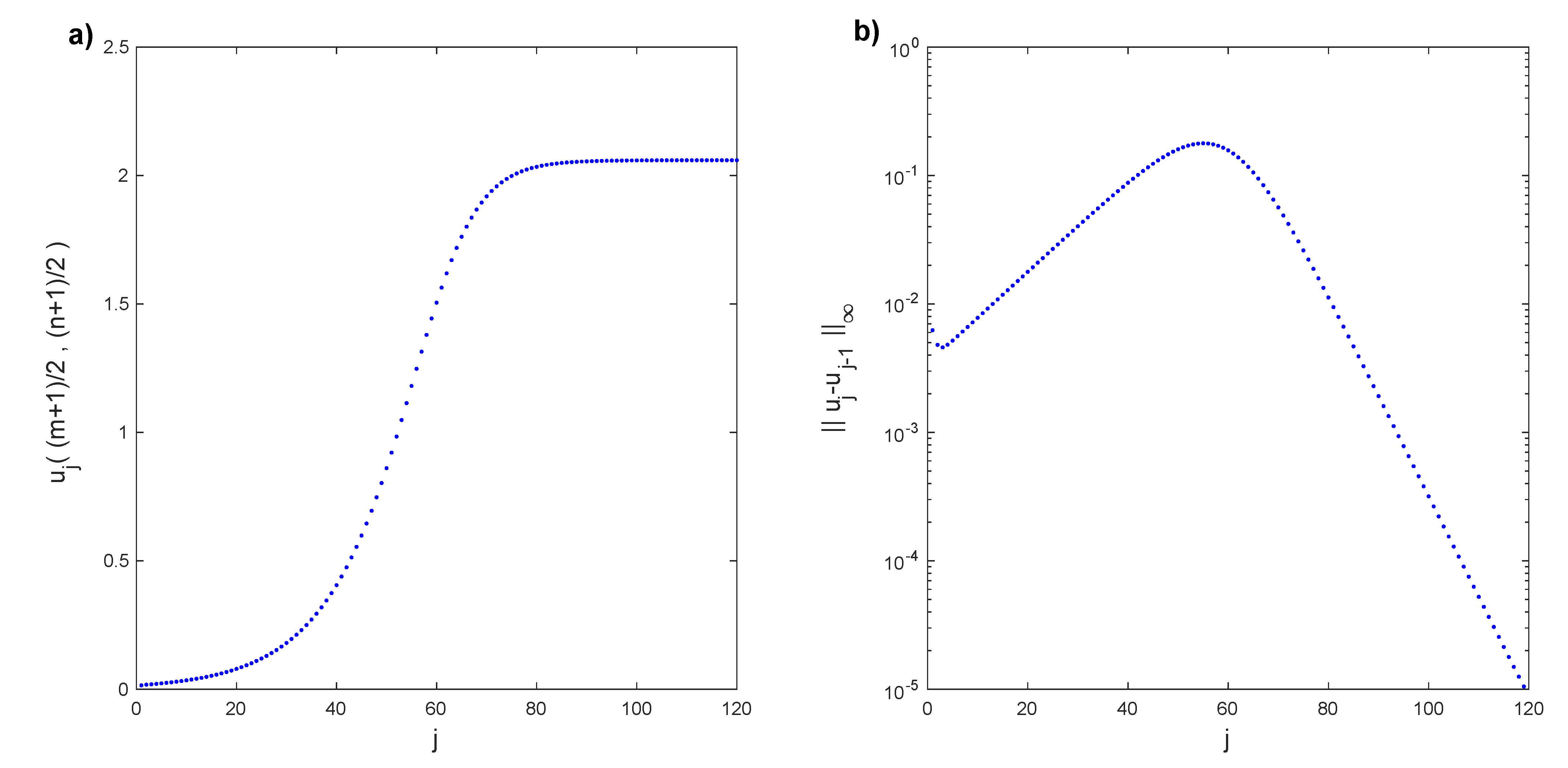
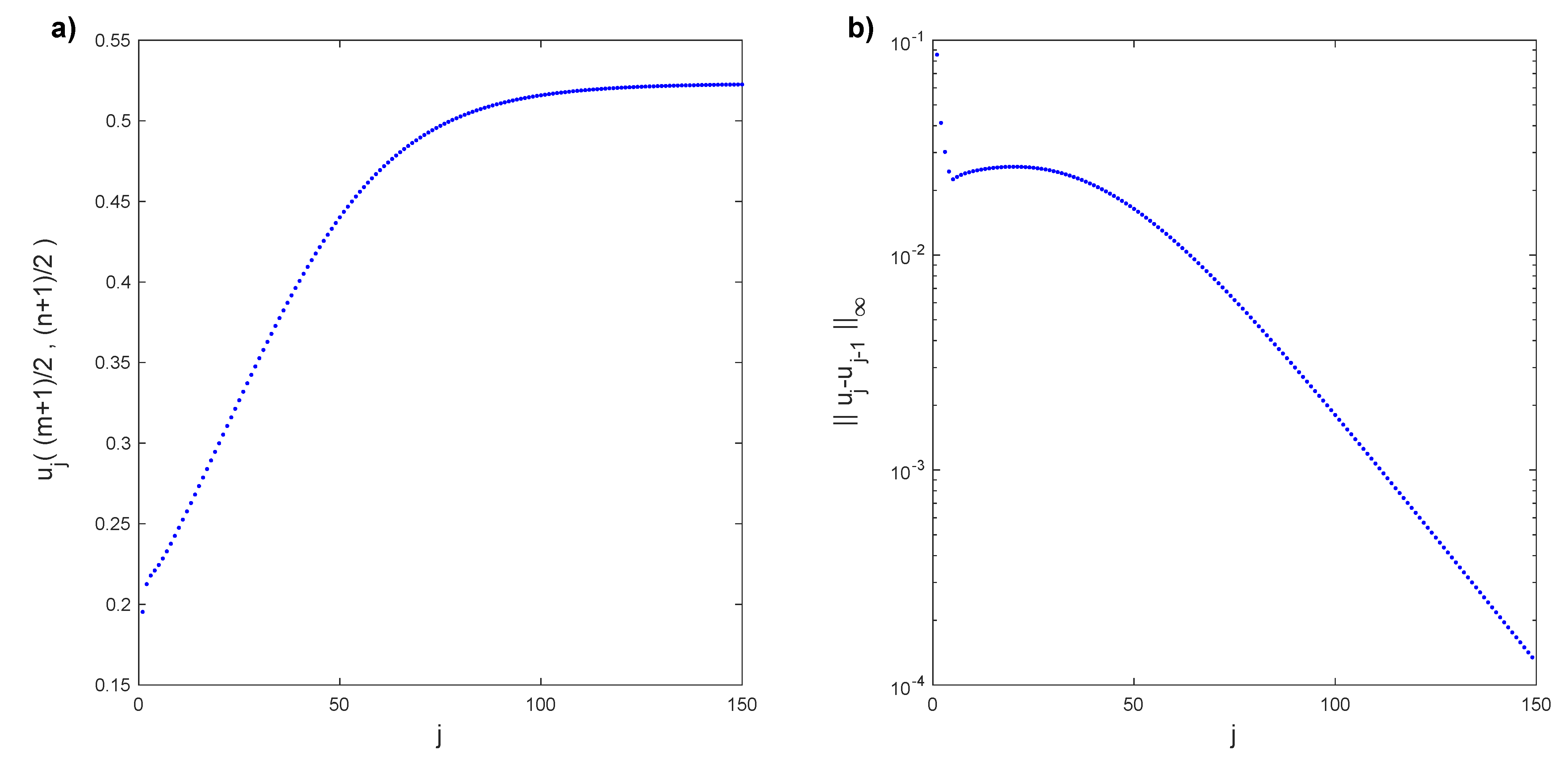
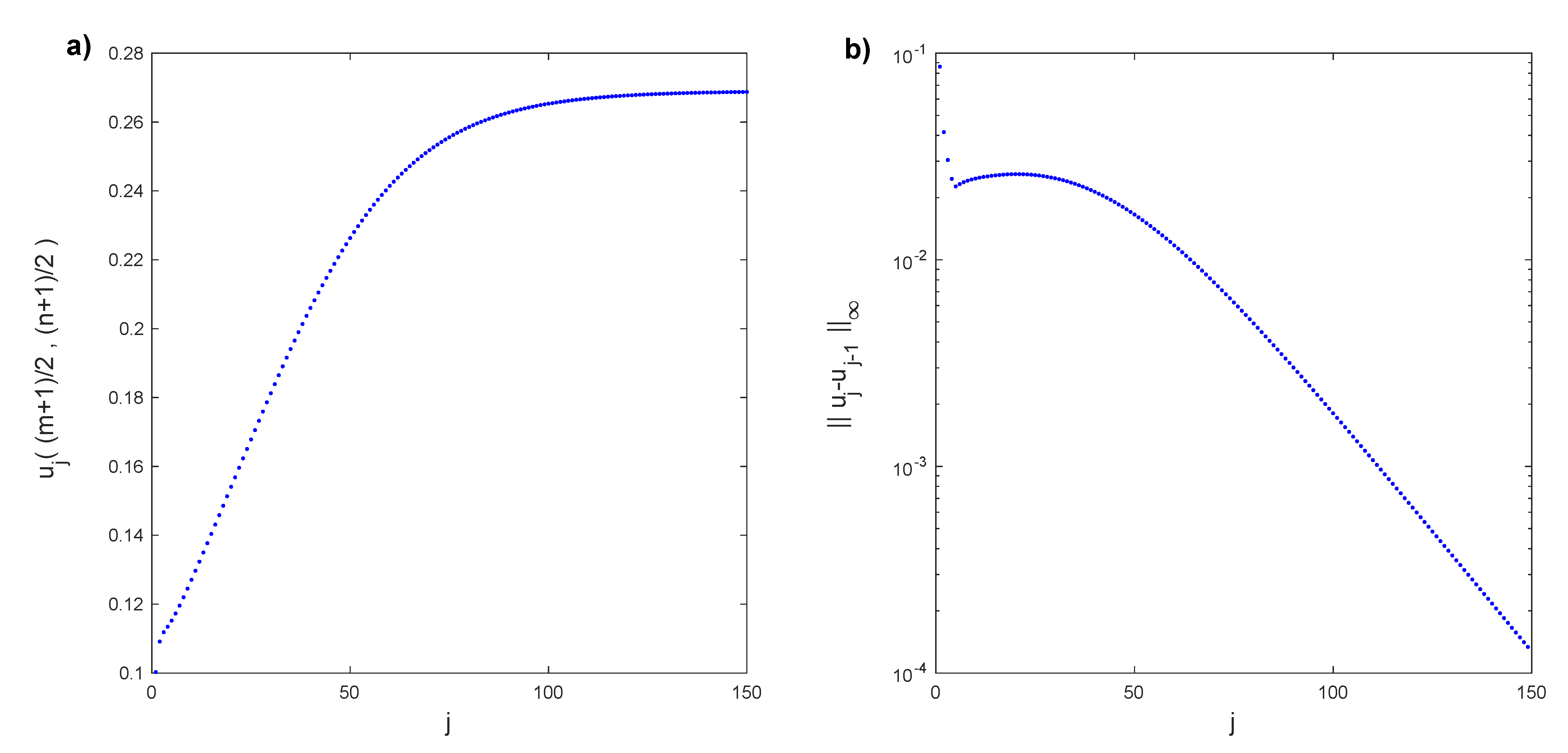
The exhibited reduced-order model is applied to find a first bifurcation point. The following numerical results were obtained with a grid of Legendre–Gauss–Lobatto nodes. First, we follow Algorithm 1 for the Rayleigh number . We solve the linear stability analysis Problem (12)–(14) with bc (9) and (10) for the conductive solution with a Legendre collocation method. A linear combination of the two eigenfunctions associated with the eigenvalues with a maximum real part is the initial condition to obtain the solution , solving Problem (6)–(10) with the time evolution discretization. This procedure generates some transitory numerical states before convergence . We are initially taking the transitory states , such that . A total of 66 transitory states meet this condition; however, we only consider the first 21, so . In Figure 2a, the horizontal component of the velocity in the middle of the cell , depending on the transitory time step, is plotted. We observe that the transitory states converge to the solution . In Figure 2b, the infinity norm of the difference between two consecutive transitory states of the horizontal component of the velocity field is displayed. As expected, these differences tend to zero. Isotherms of the transitory states at temporal steps , and can be seen in Figure 3. These transitory states are far from the converged solution.
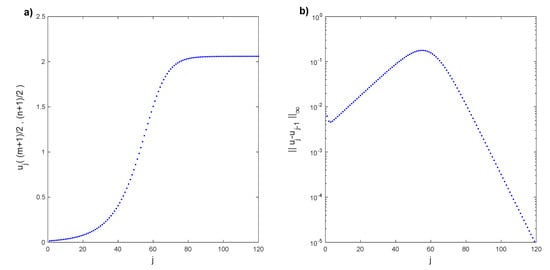
Figure 2.
(a) Horizontal component of the velocity transitory field , , , converging to for . (b) Infinity norm of the difference between consecutive transitory states of the horizontal component of the velocity field.
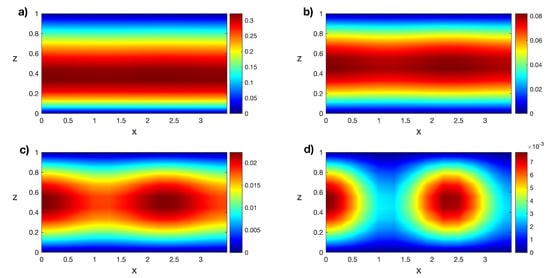
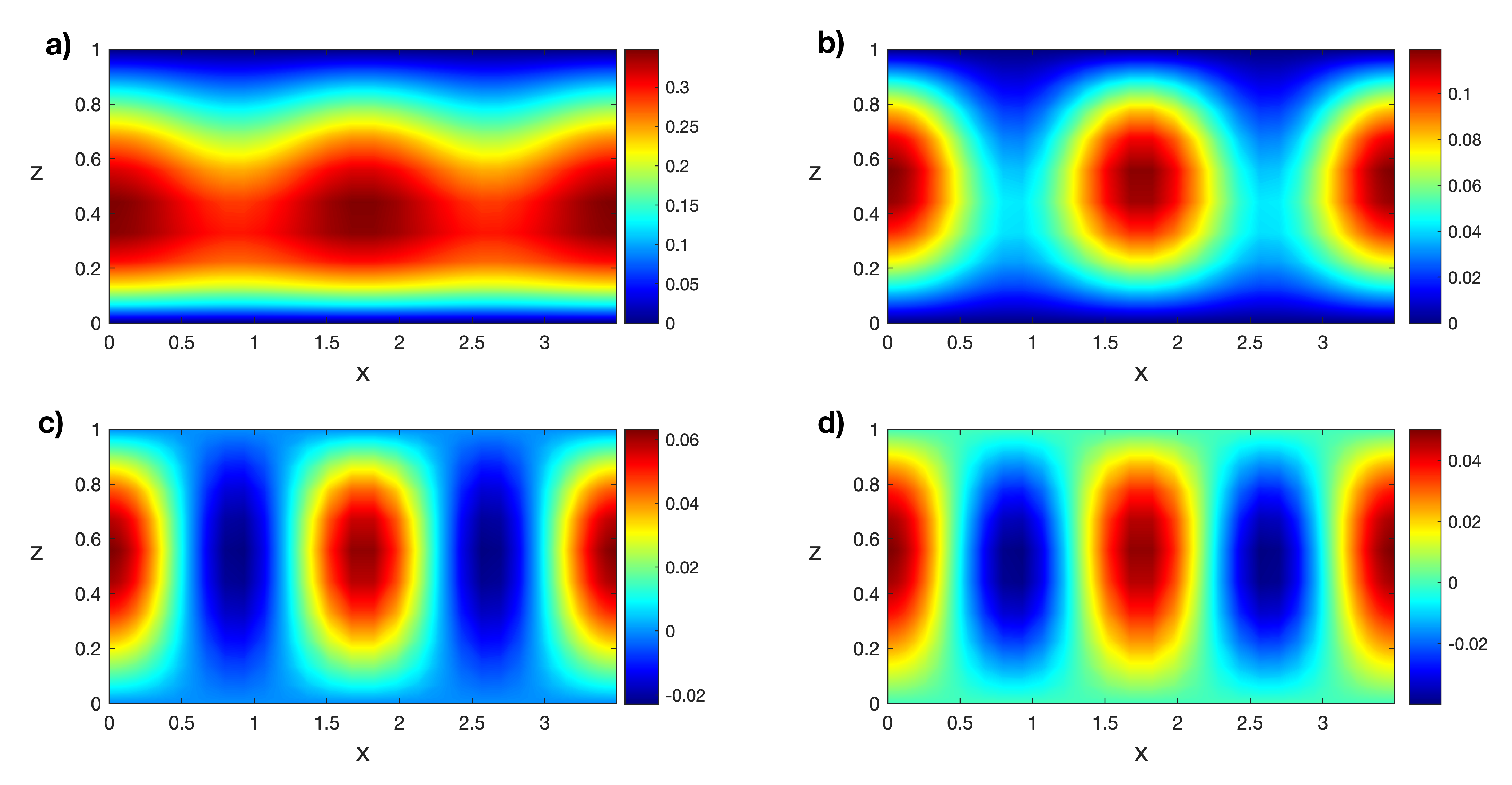
Figure 3.
Isotherms of the transitory states for at (a) , (b) , (c) , and (d) . Results obtained with a spatial numerical grid of Legendre–Gauss–Lobatto nodes.
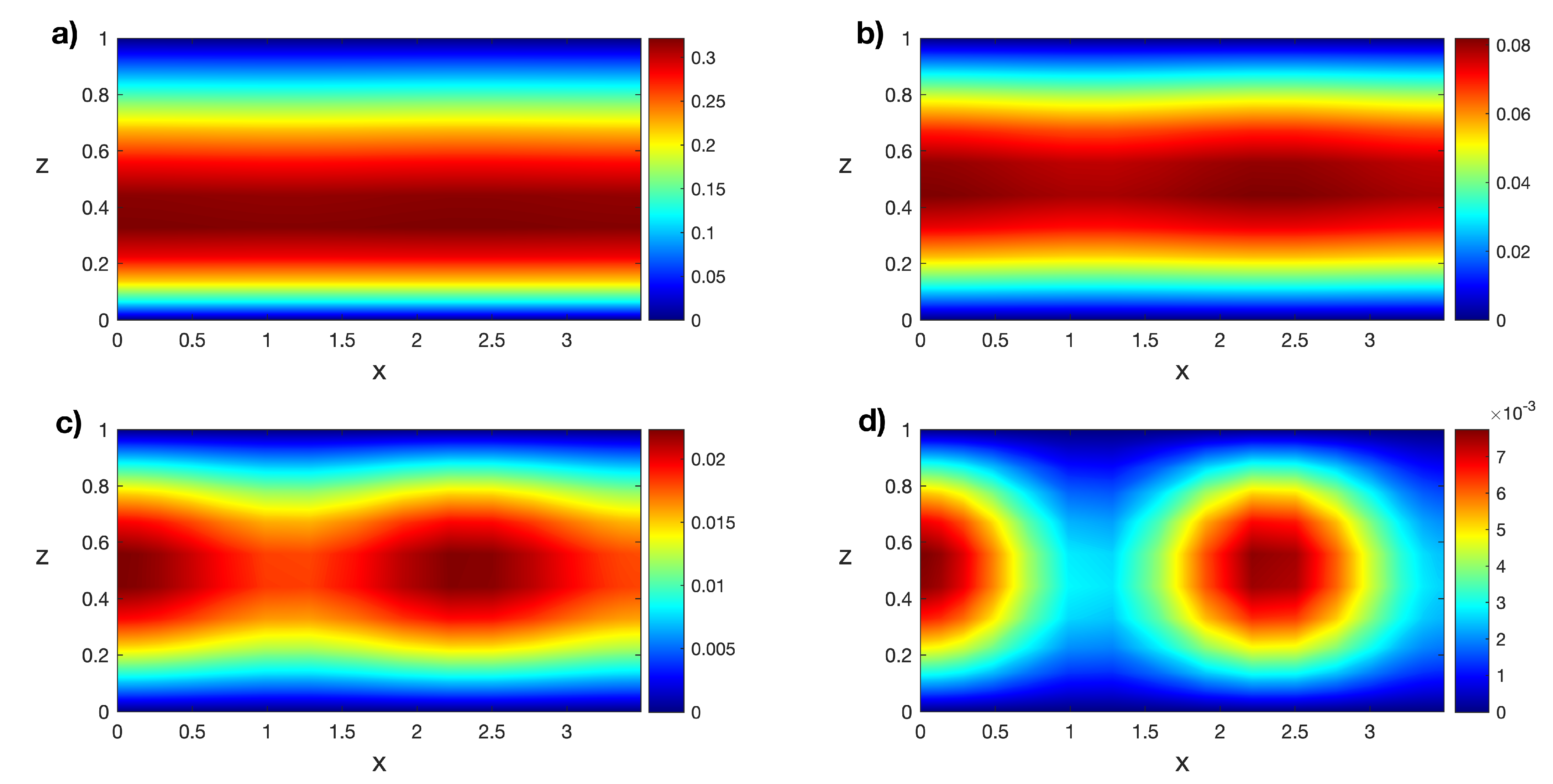
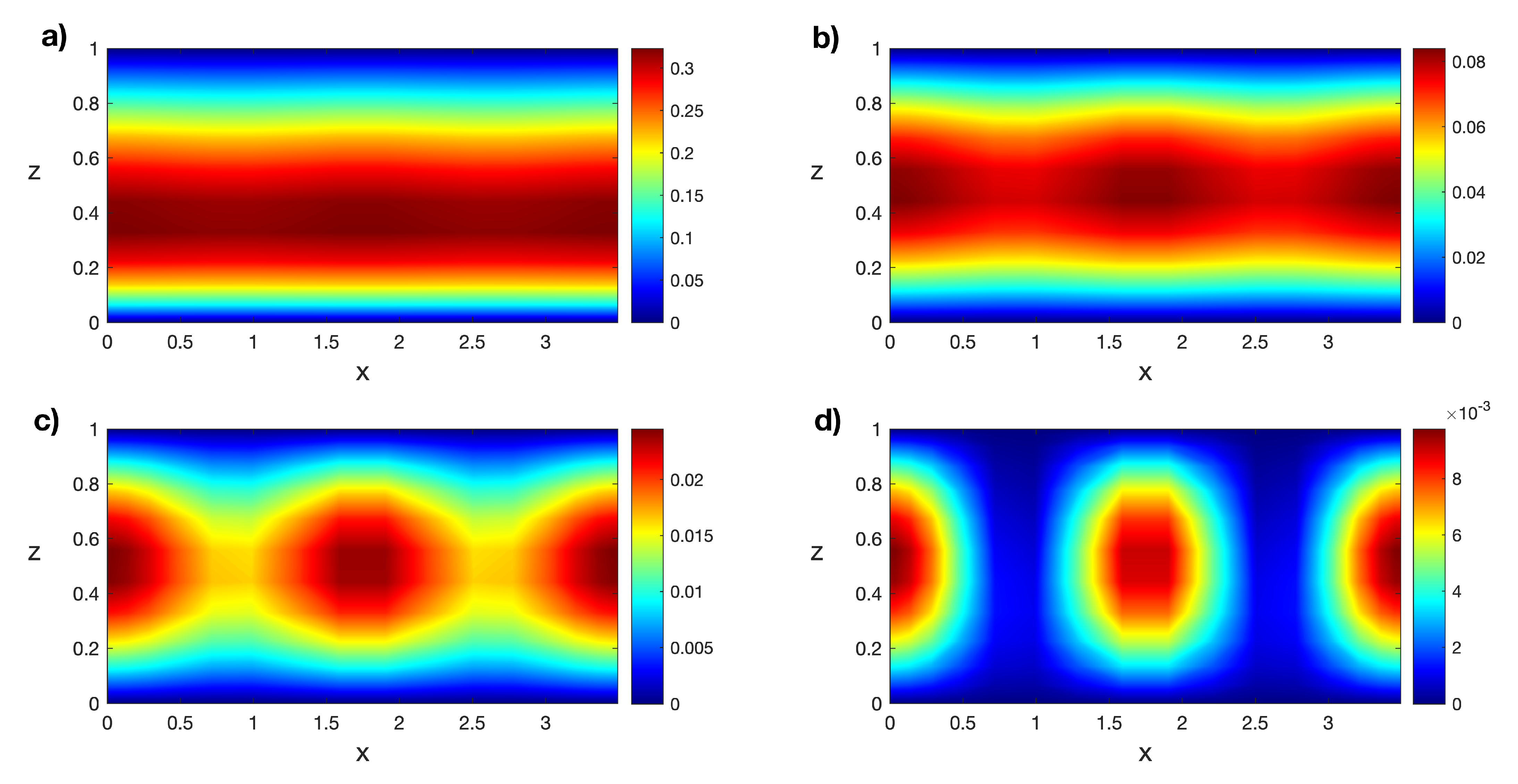
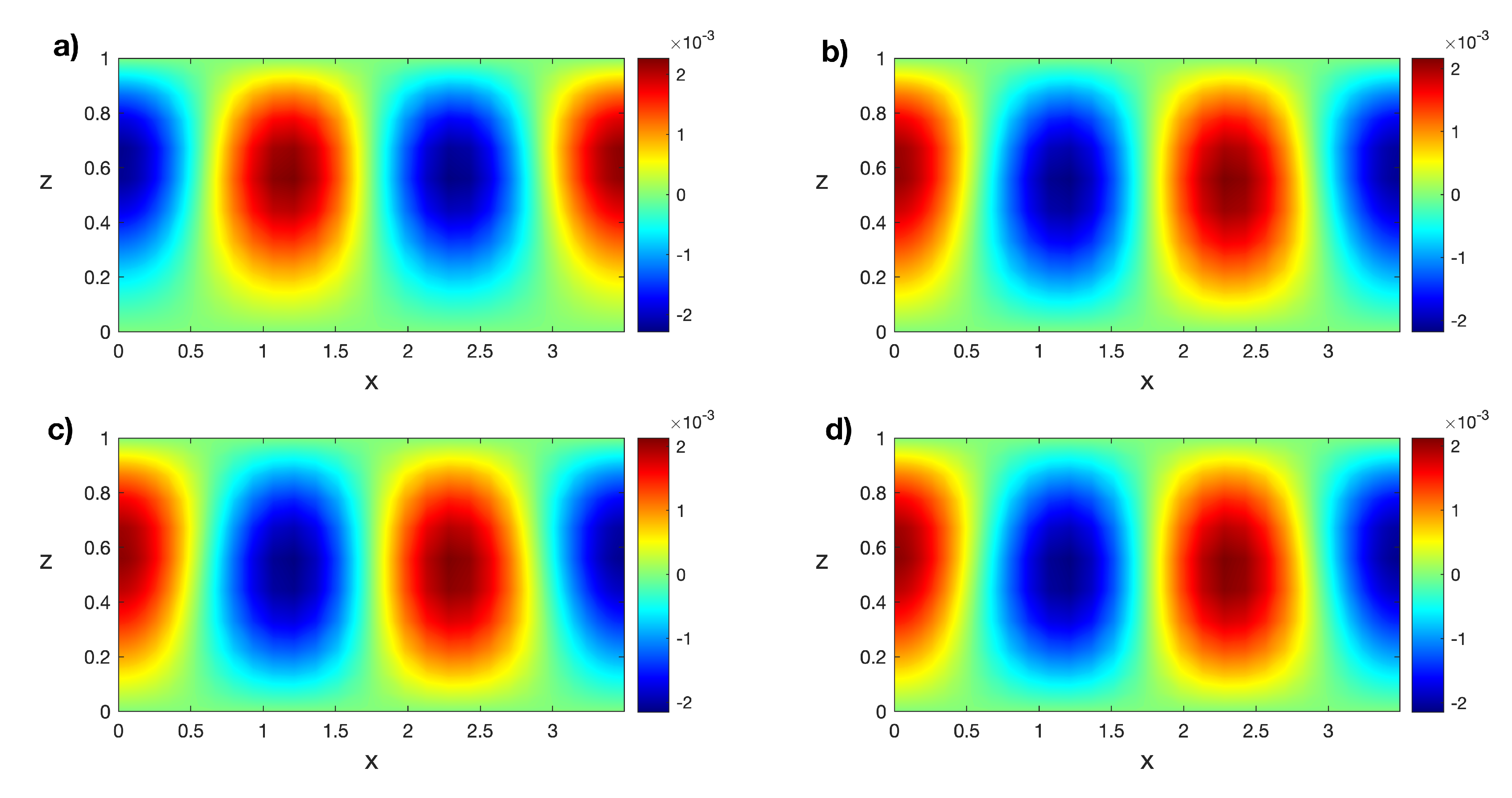
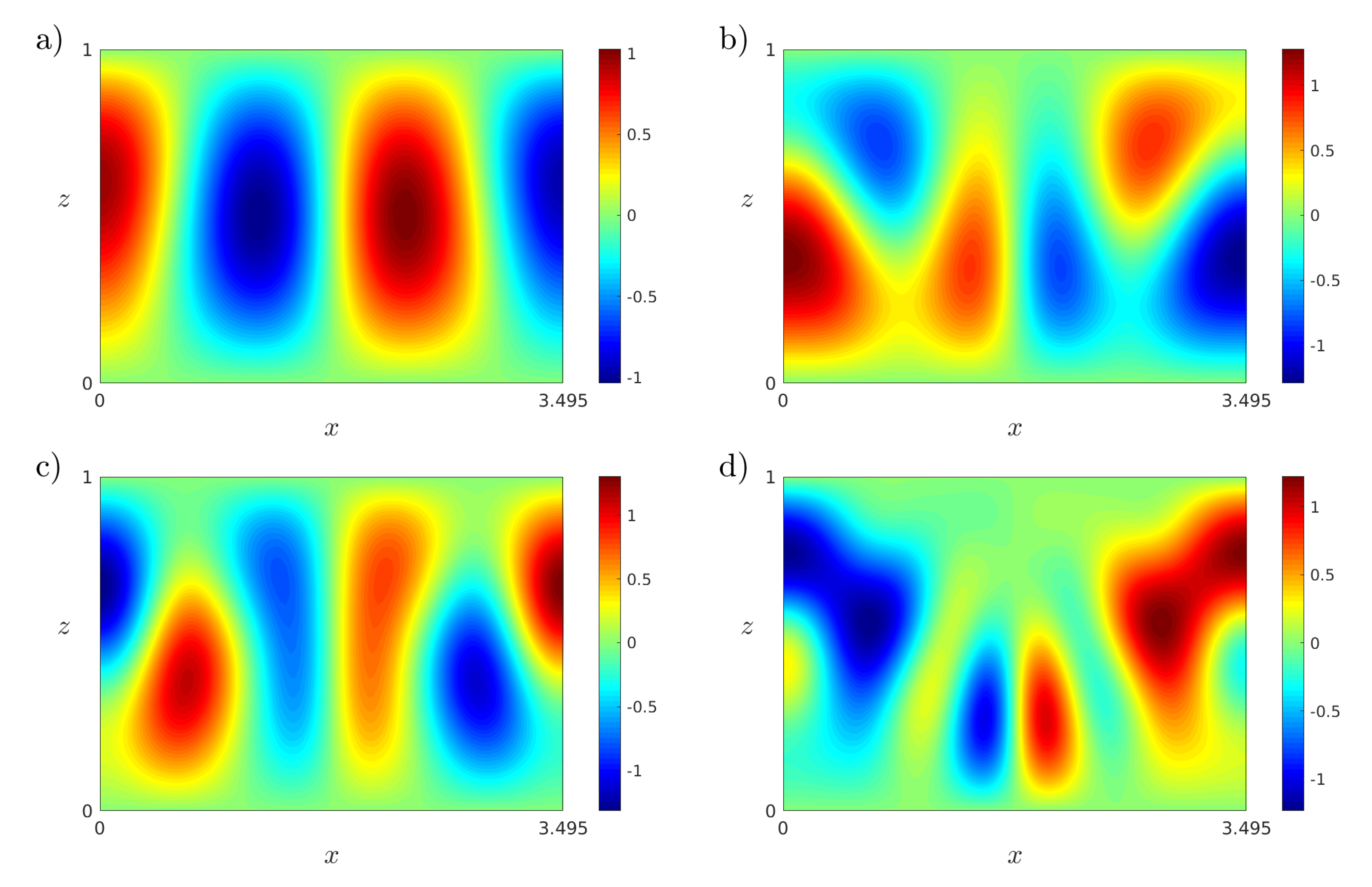
The linear stability analysis for the transitory states is numerically performed, and the first eigenfunctions for these states are the snapshots for the POD analysis. Therefore, a set of numerical snapshots, , is obtained, such that i is the temporal step. Figure 4 shows isotherms of the first eigenfunctions of the transitory states in Figure 3. It can be observed that some eigenfunctions are very similar because the transitory states are close in time.
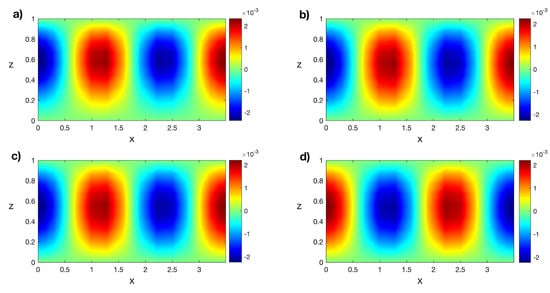
Figure 4.
Isotherms of the first eigenfunctions of the transitory states for at (a) , (b) , (c) , and (d) . Results obtained with a spatial numerical grid of Legendre–Gauss–Lobatto nodes.
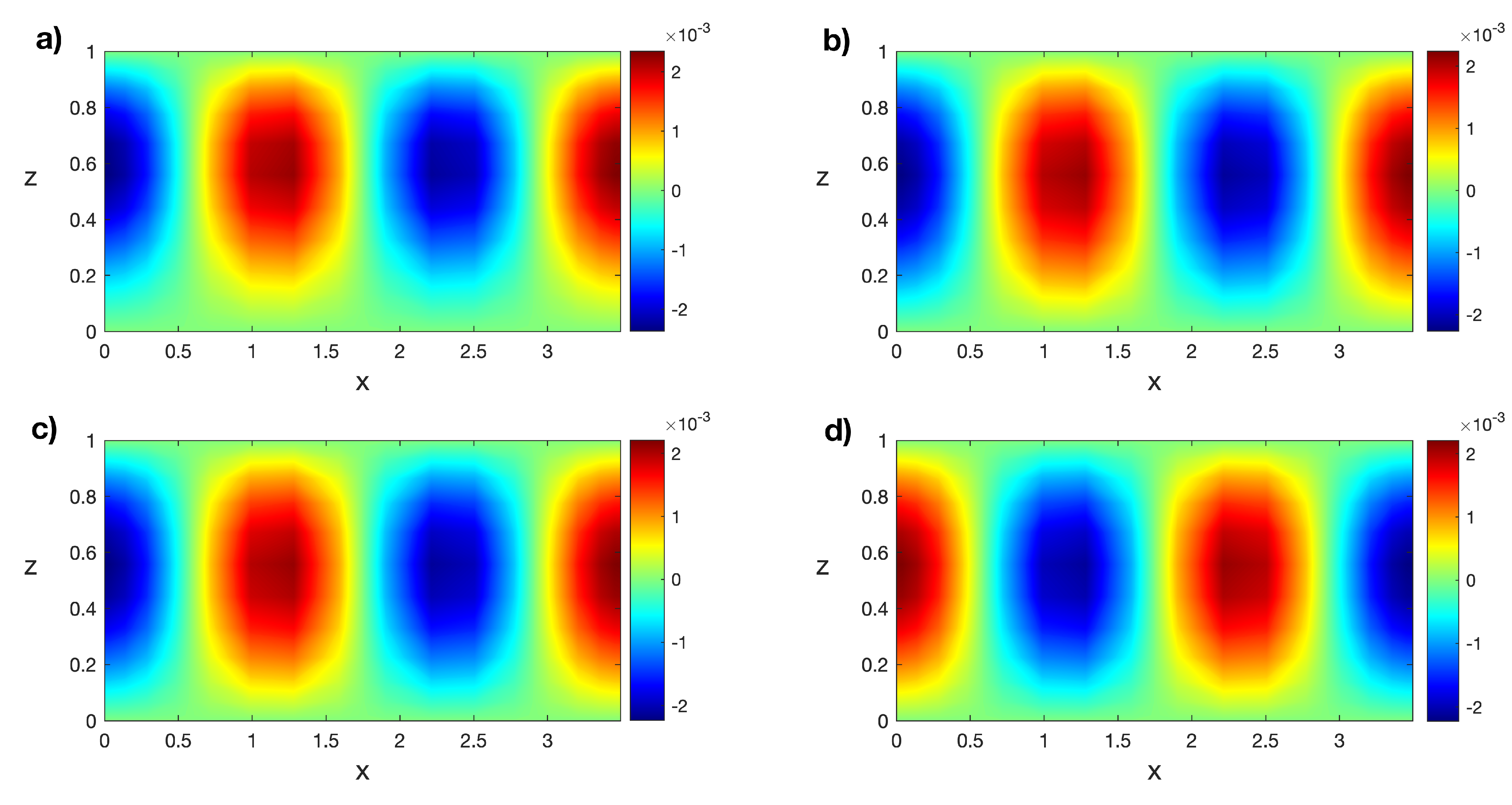
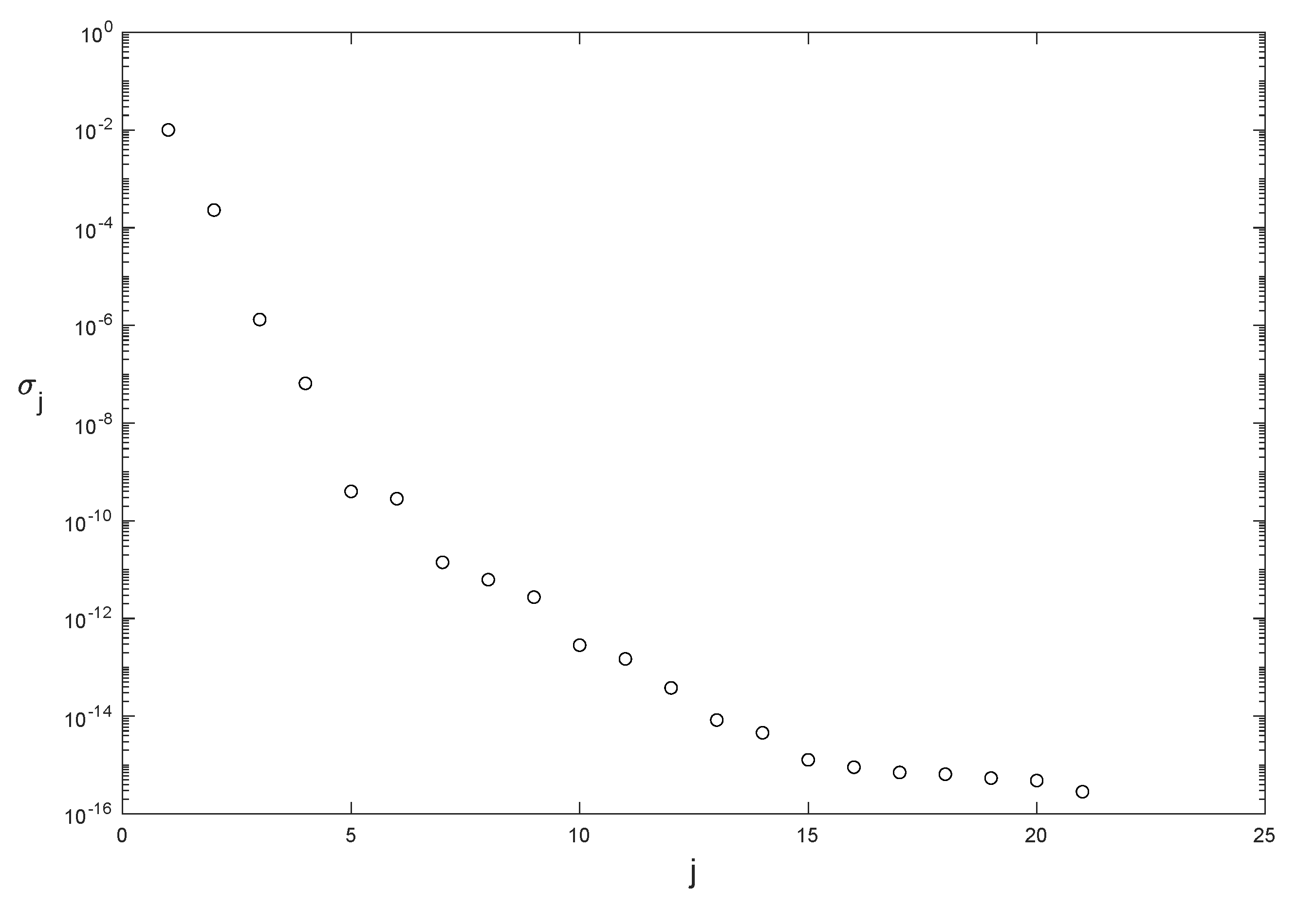
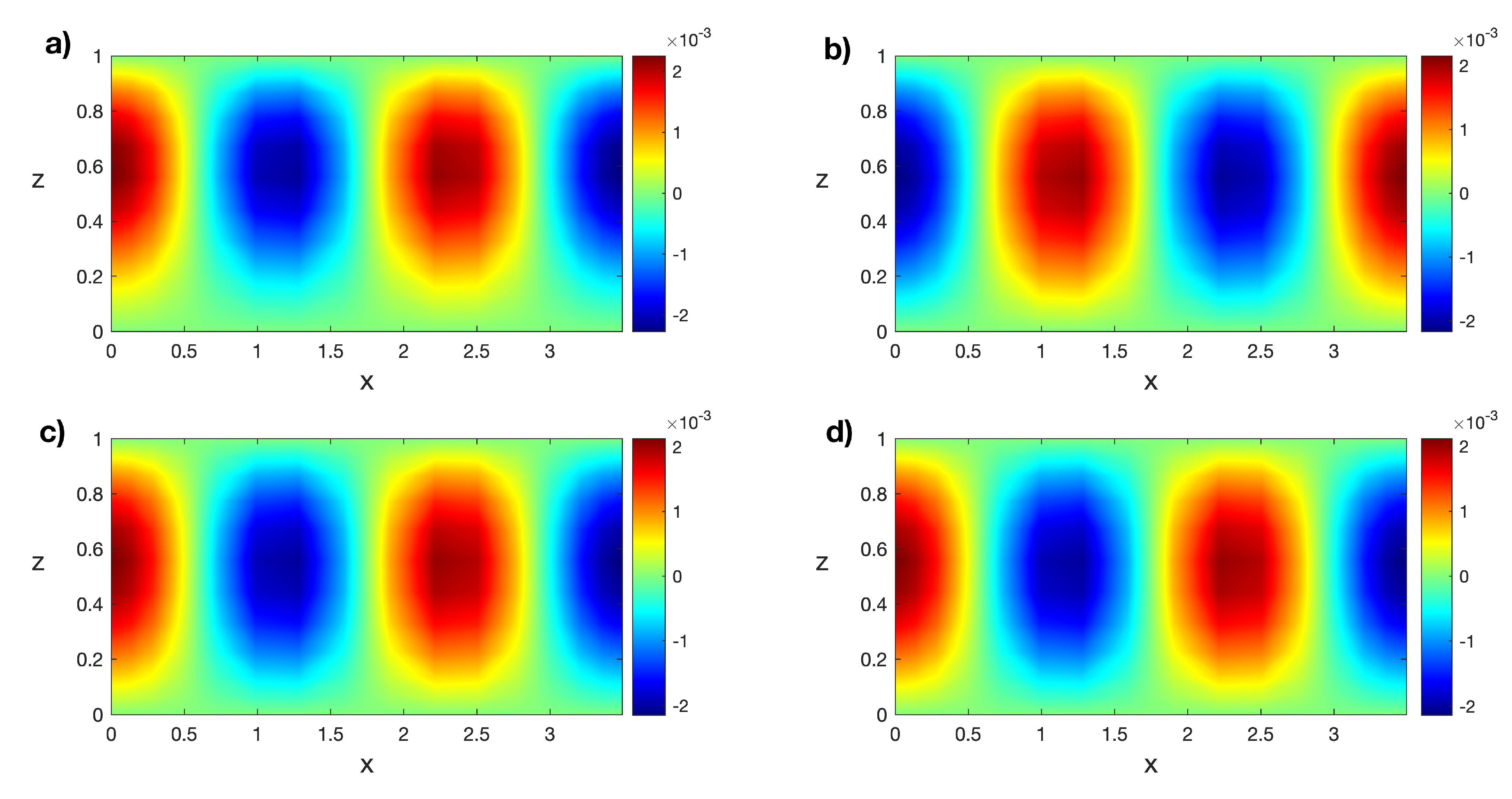
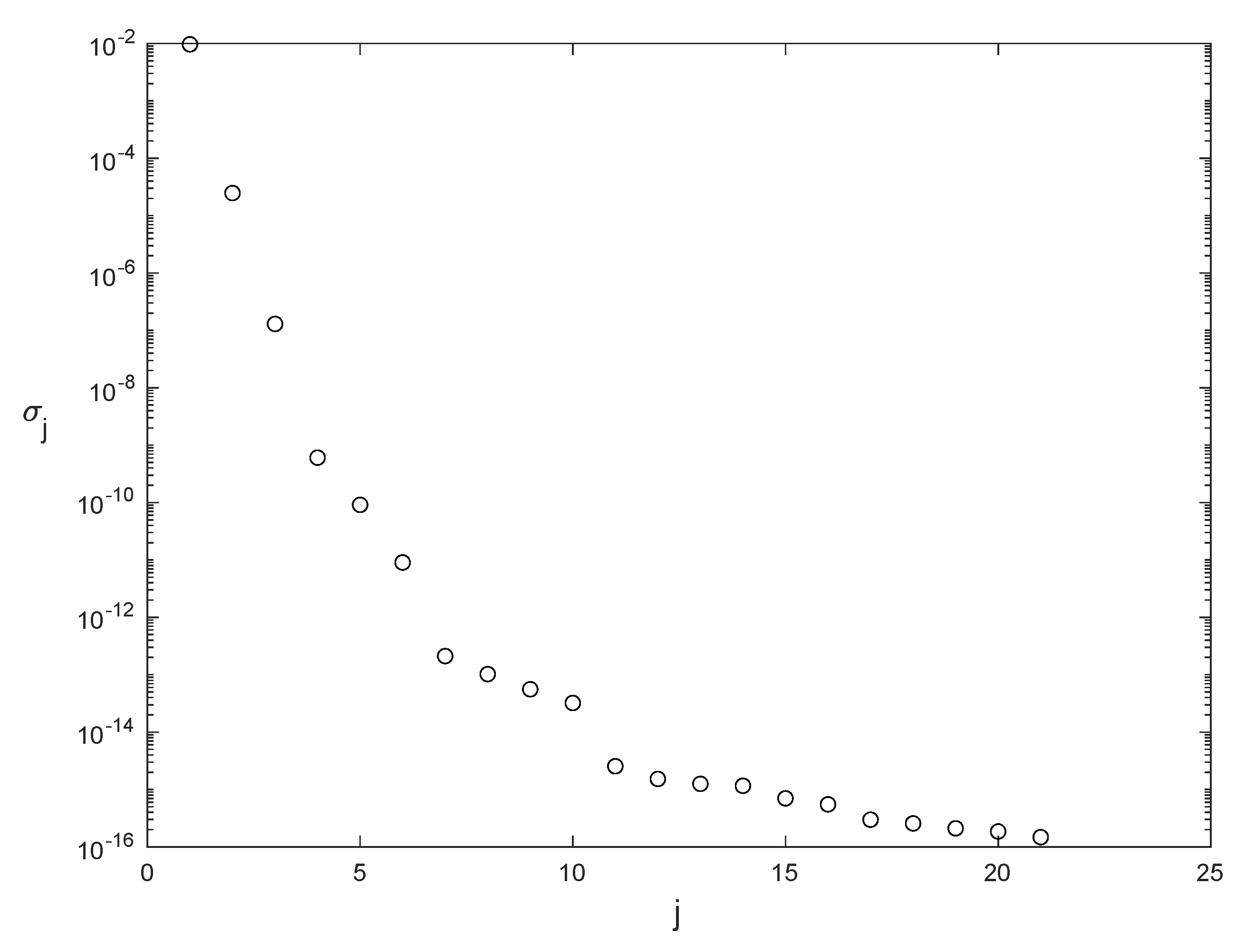
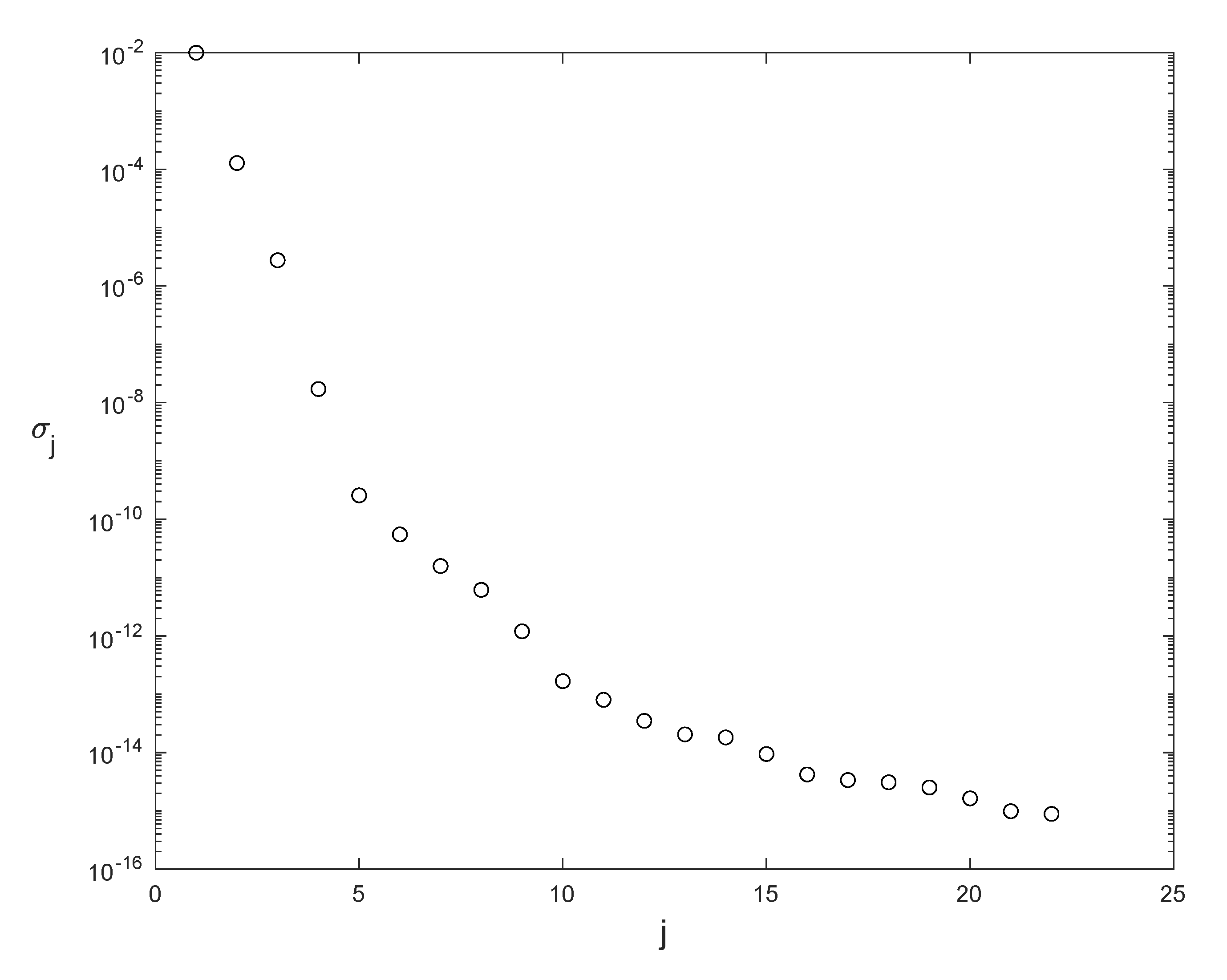
Algorithm 2 is followed to calculate the modified snapshot matrices, , the singular values and eigenvectors for those matrices, and the resulting POD bases. The singular values for the modified snapshot matrix are plotted in Figure 5. The number of unsaturated modes for temperature is , and for velocity is . We observe that the singular values rapidly decay to zero, so the POD analysis is reliable. The thermal POD modes, computed at , corresponding with the first four singular values , and 4, are represented in Figure 6. The complexity of the modes increases as the singular values decrease.
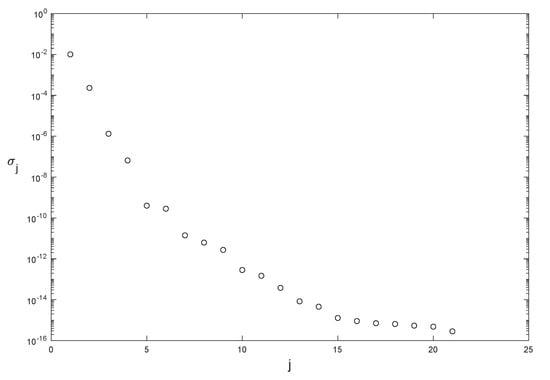
Figure 5.
Singular values of the thermal modified snapshot matrix .
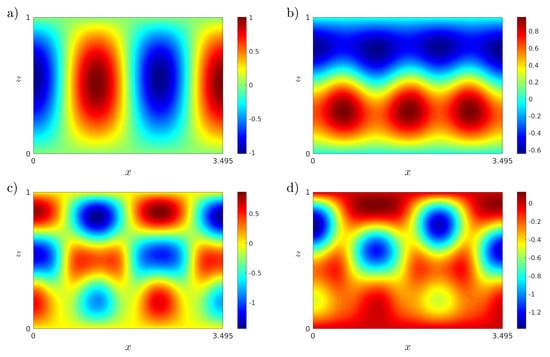
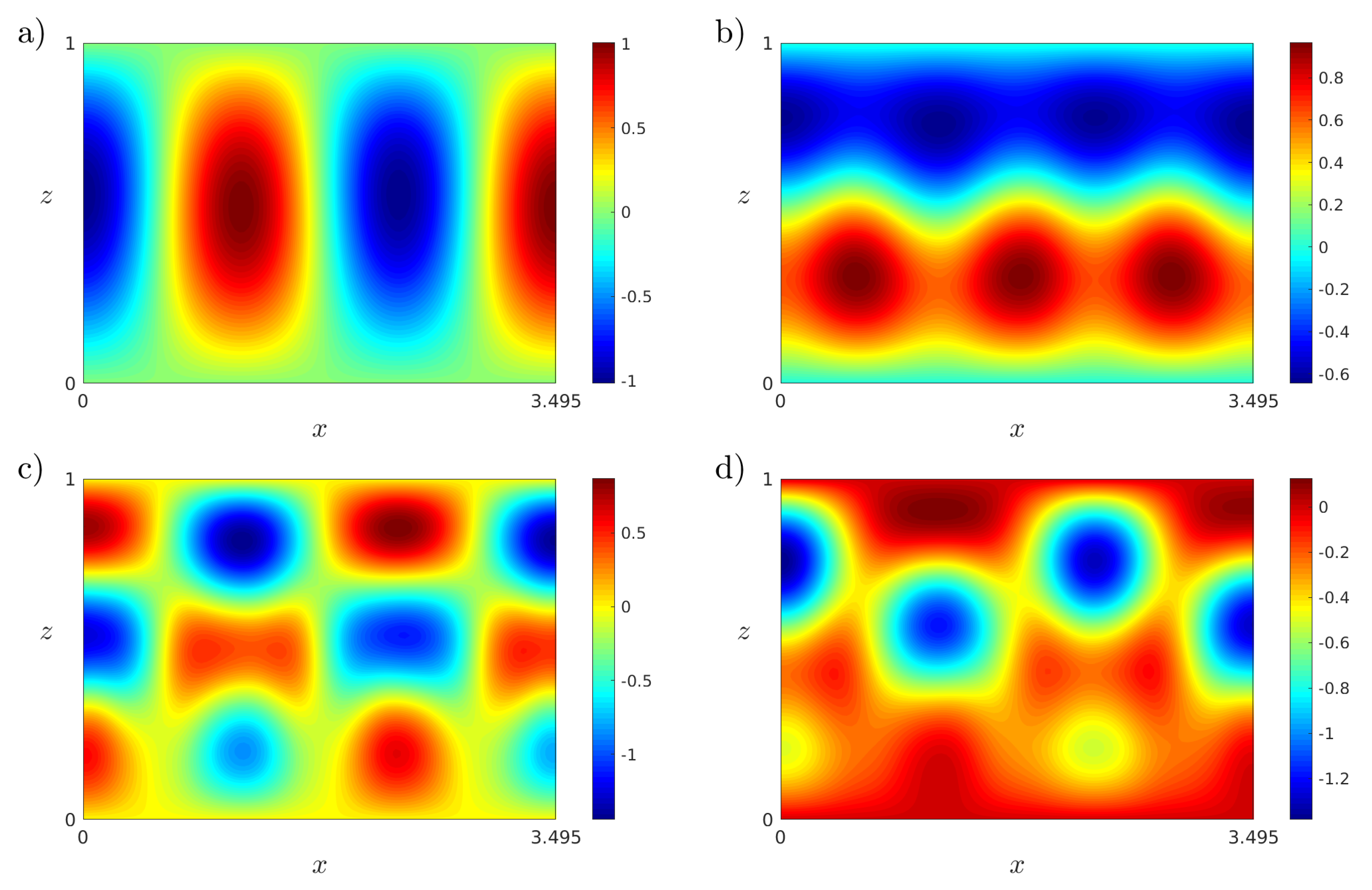
Figure 6.
(a–d) Isotherms of the first four thermal POD modes in computed at . Results obtained with a spatial numerical grid of Legendre–Gauss–Lobatto nodes.
Validation and Results
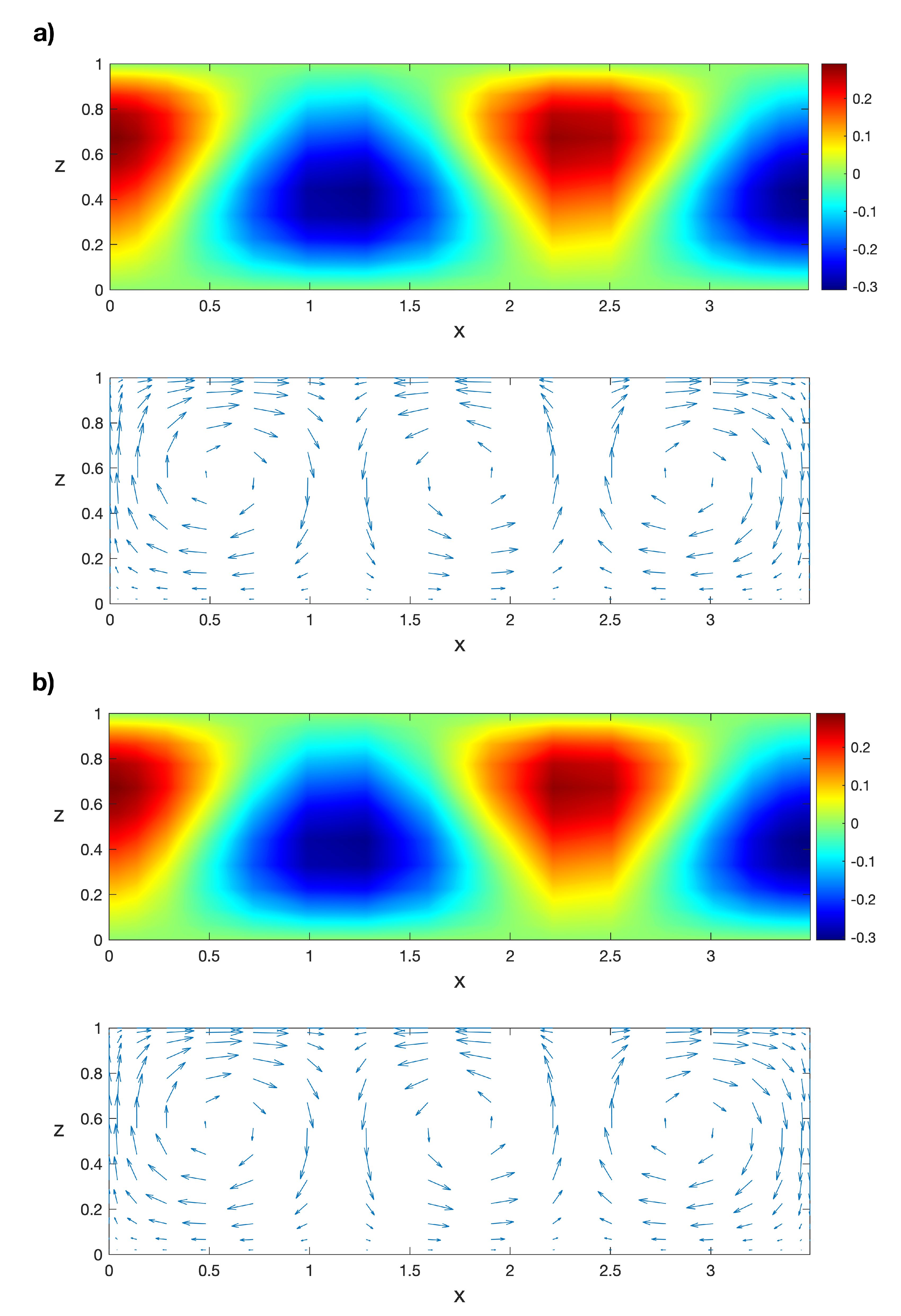
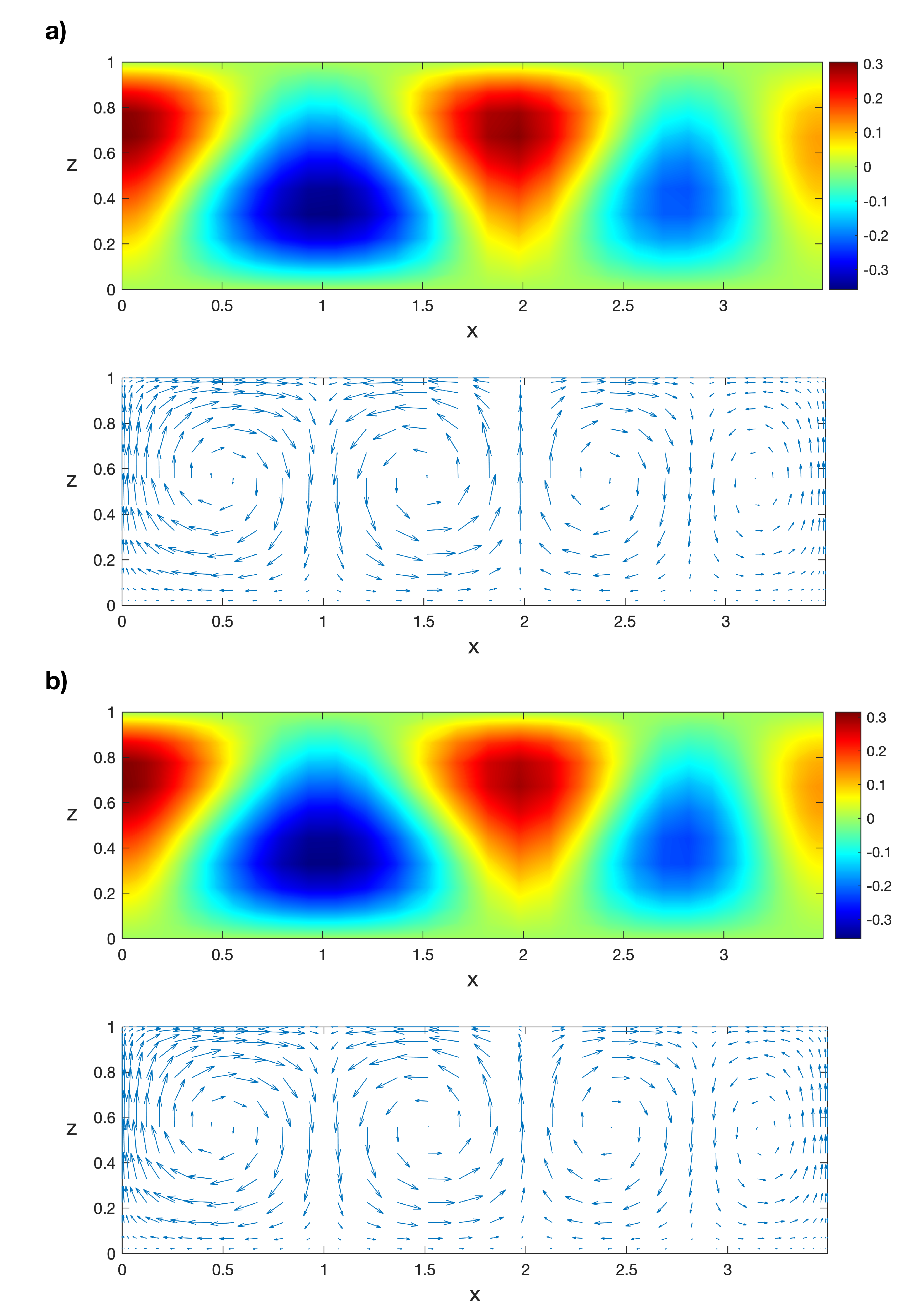
Now, we solve Problem (6)–(10) for values of the Rayleigh number in the interval with the POD/Galerkin method and with Legendre collocation. For instance, the isotherms and the velocity field of the POD solution for can be seen in Figure 7a. The same solution obtained with Legendre collocation is shown in Figure 7b, as in Ref. [50]. The norm of the difference between both solutions is order . Now, we solve the Galerkin/POD linear stability Problem (17) and (18) for . The first eigenfunction of the solution , computed with the POD method, can be seen in Figure 8a. The norm of the horizontal component of the velocity field for the solutions in the interval can be seen in Figure 9a; the continuous line has been obtained with Legendre collocation and the dashed line with POD. The difference between both solutions is order . Finally, a linear stability analysis for those stationary solutions has been performed with the POD method. A plot of the real part of the eigenvalue with the largest real part, , can be seen in Figure 9b; the continuous line has been obtained with Legendre collocation and the dashed line with POD. The relative difference between both values of is plotted in Figure 10; it is order , except at the bifurcation point , where we divide by a value near zero. The POD stability analysis in Figure 9b shows that is negative in the interval, so solutions are stable for any value of R in the interval .
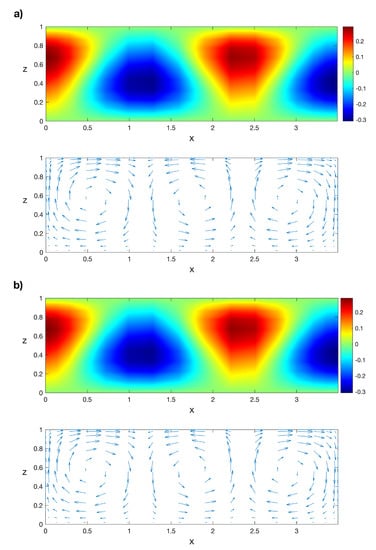
Figure 7.
(a) Isotherms and velocity field of the POD solution at and (b) the respective isotherms and velocity field computed with Legendre collocation. Results obtained with a spatial numerical grid of Legendre–Gauss–Lobatto nodes.
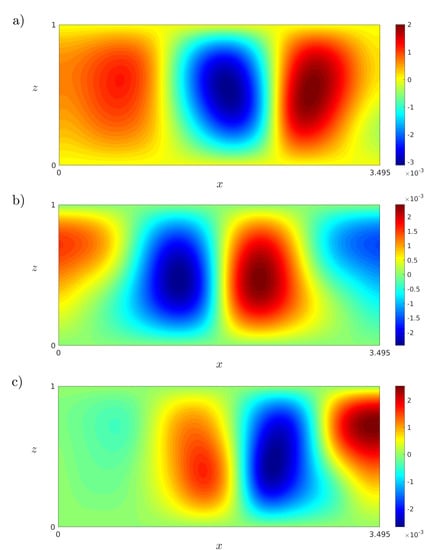
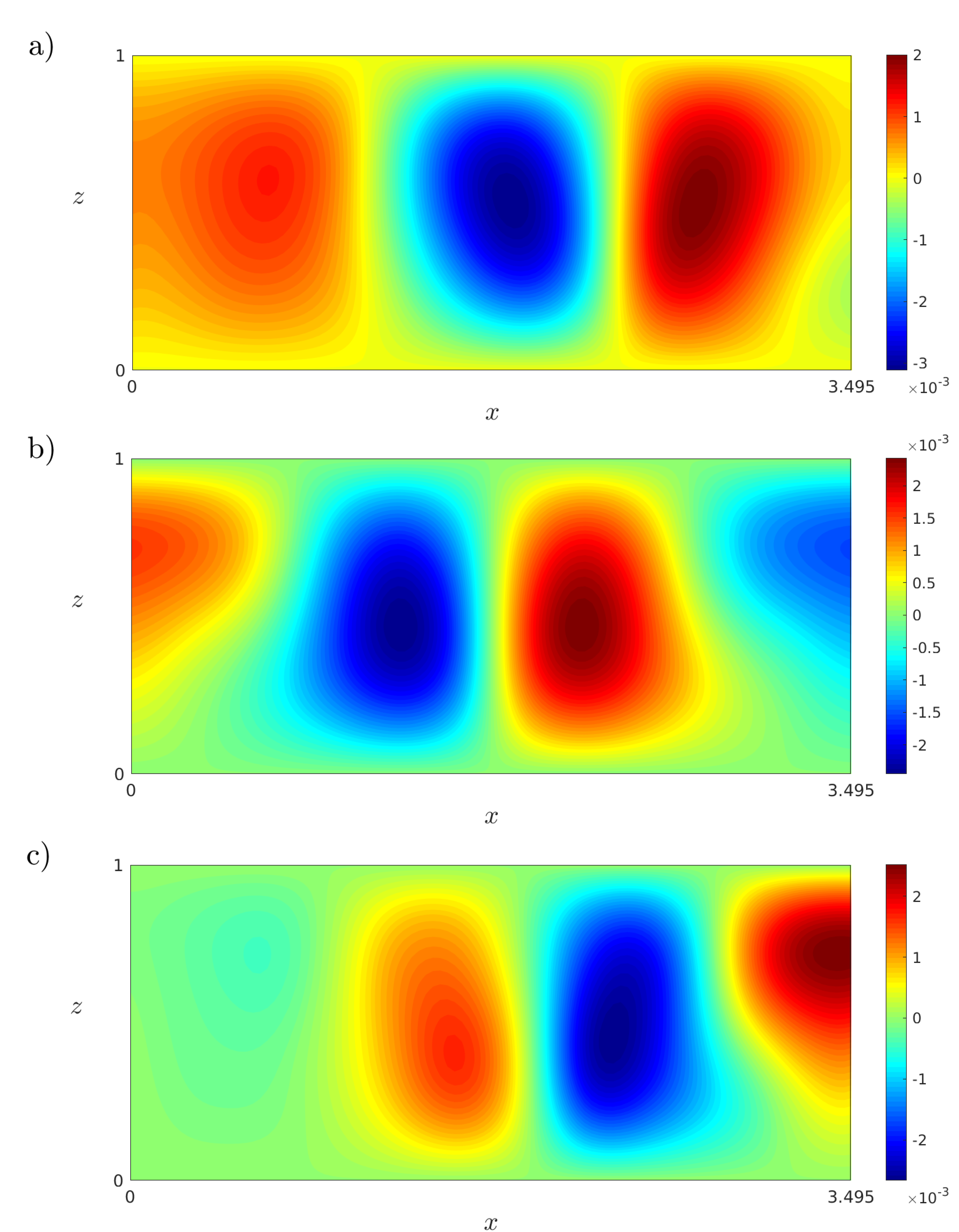
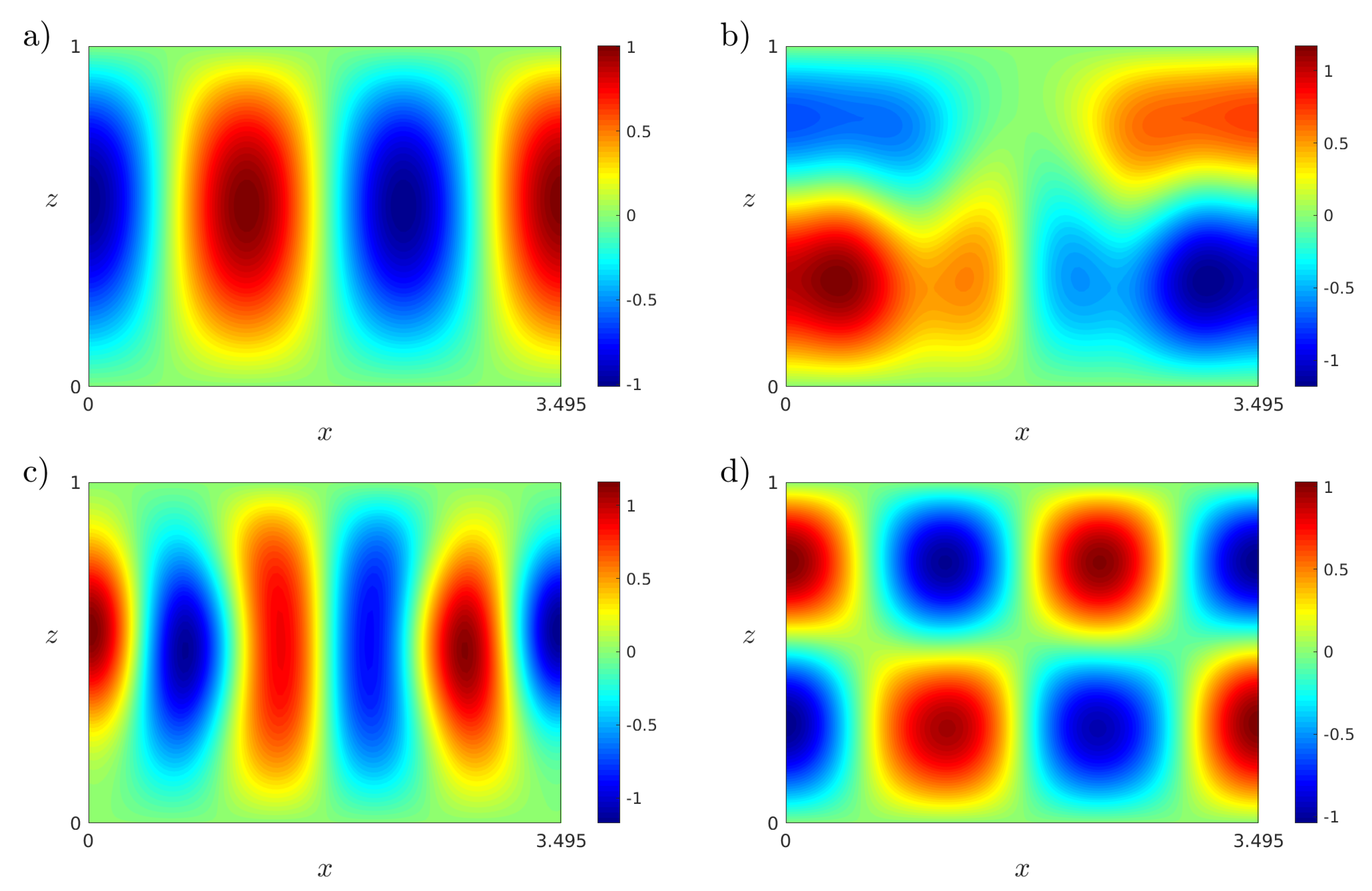
Figure 8.
(a) Isotherms of the first eigenfunction for solution at . (b) Isotherms of the first eigenfunction for solution at . (c) Isotherms of the first eigenfunction for solution at . All results were obtained with the POD method.
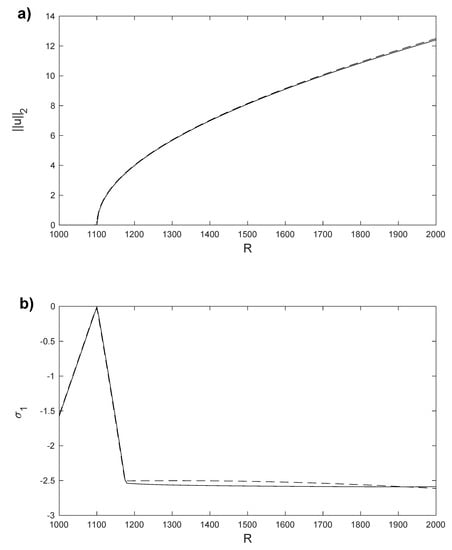
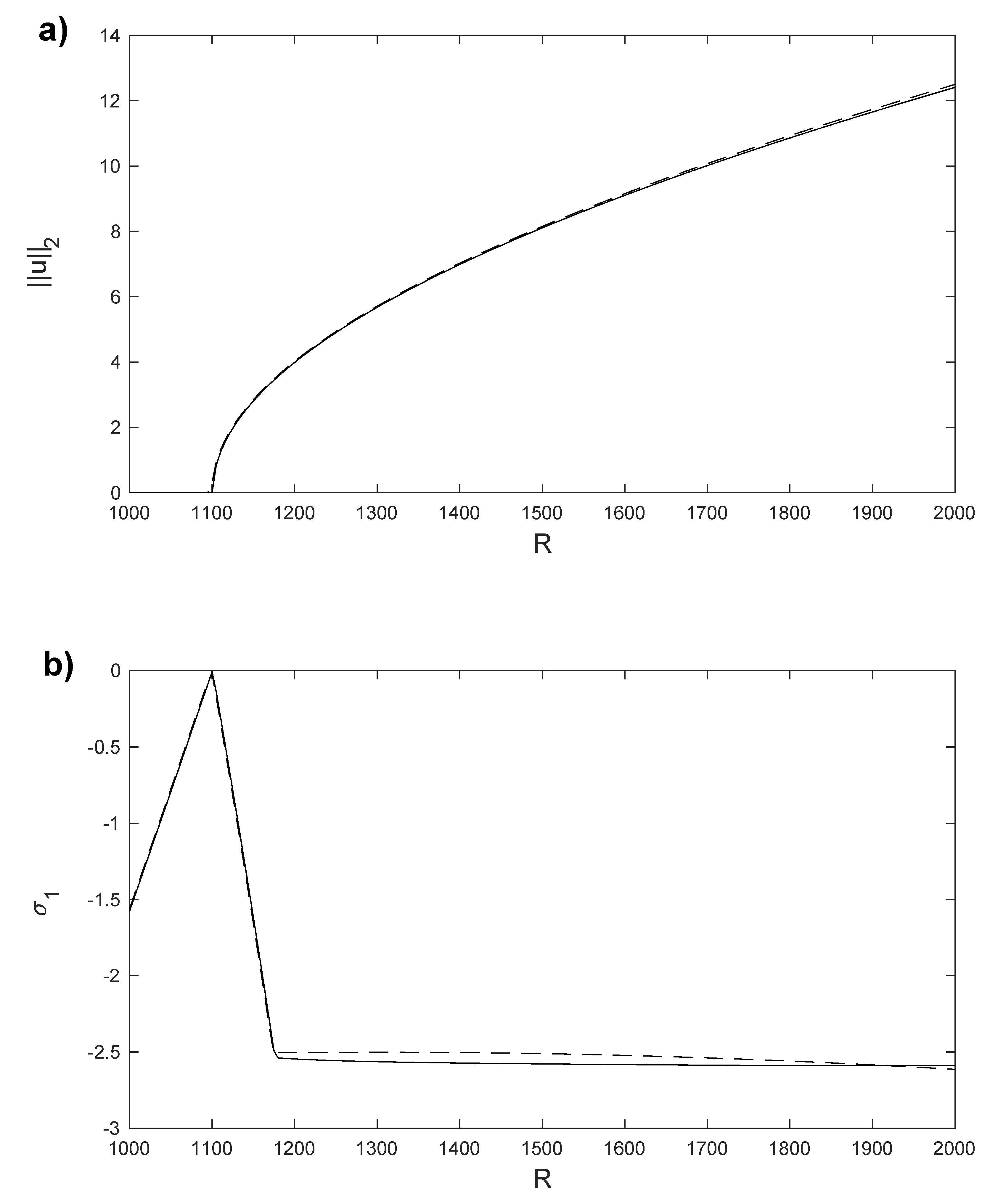
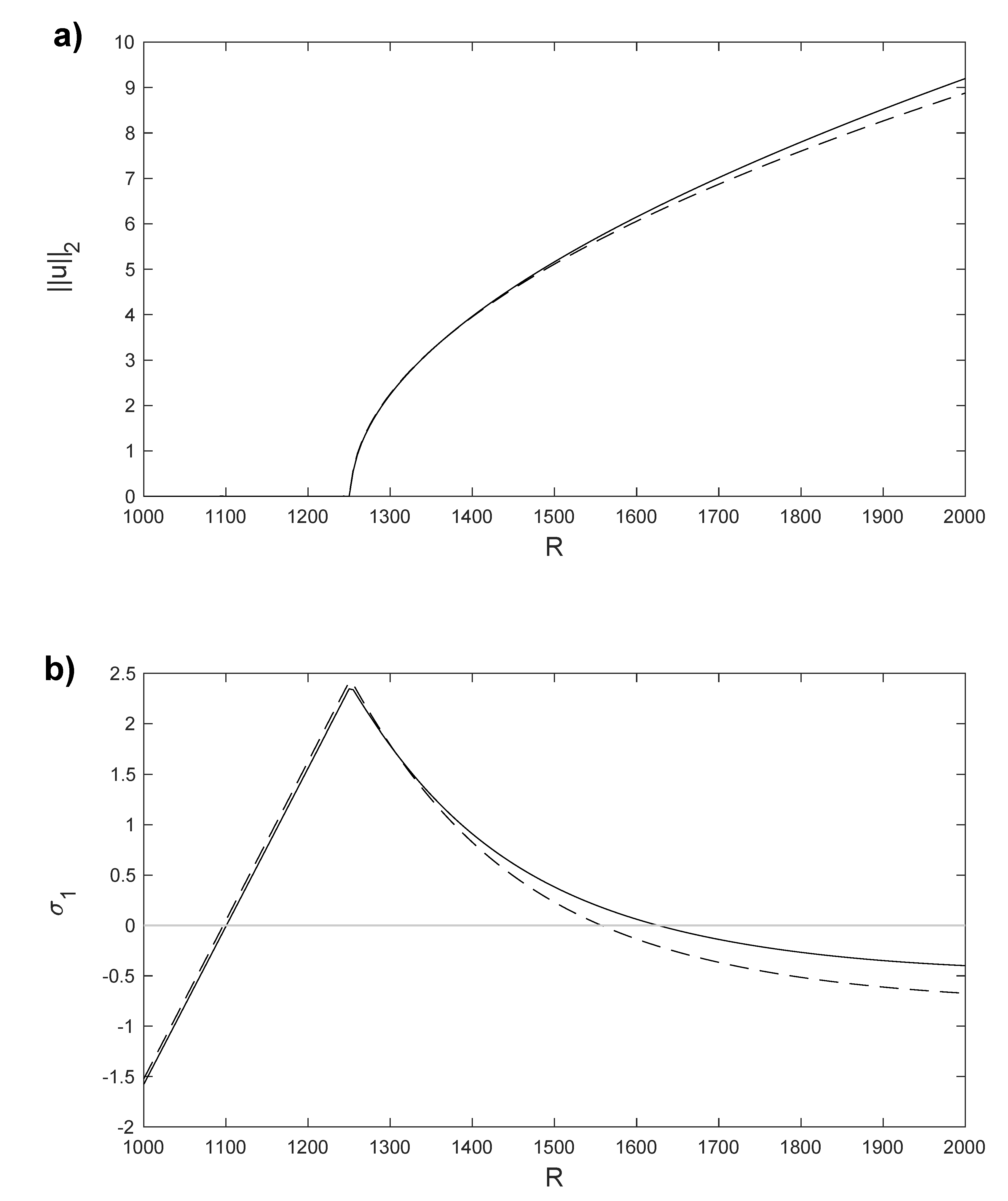
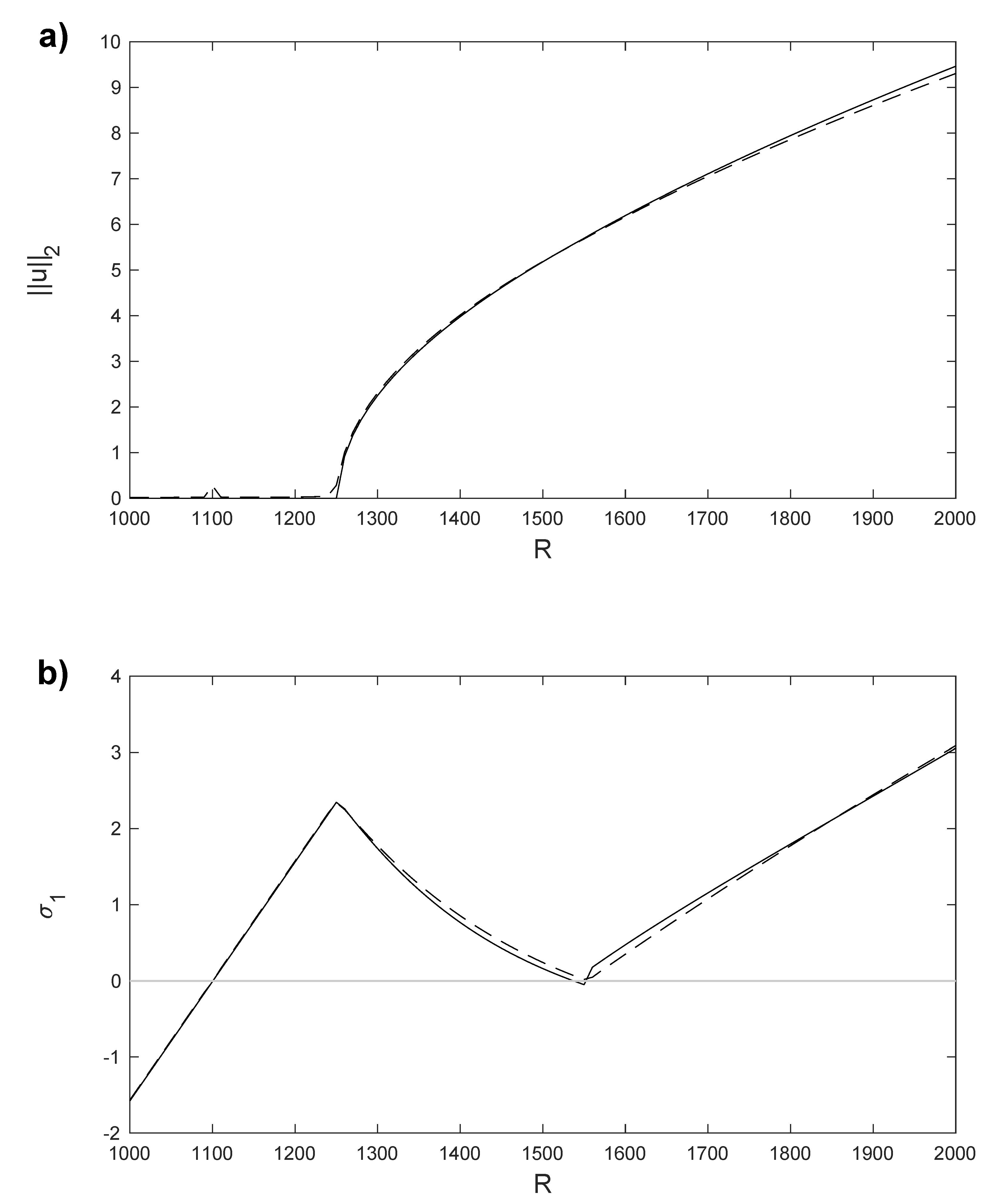
Figure 9.
(a) norm of the horizontal velocity component, u, for the stationary solutions and , obtained with Legendre collocation (solid line) and with the POD method (dashed line). (b) for the stationary solutions and obtained with Legendre collocation (solid line) and with the POD method (dashed line). Results computed in a spatial numerical grid of Legendre–Gauss–Lobatto nodes.
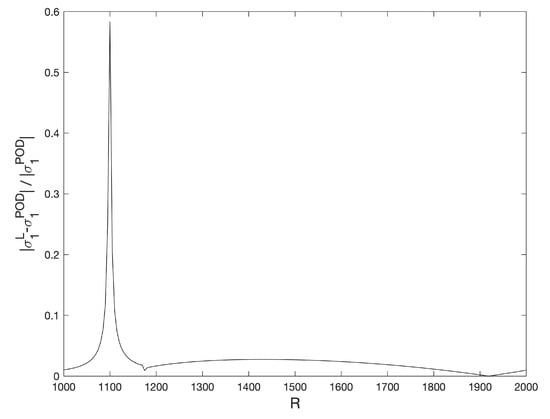
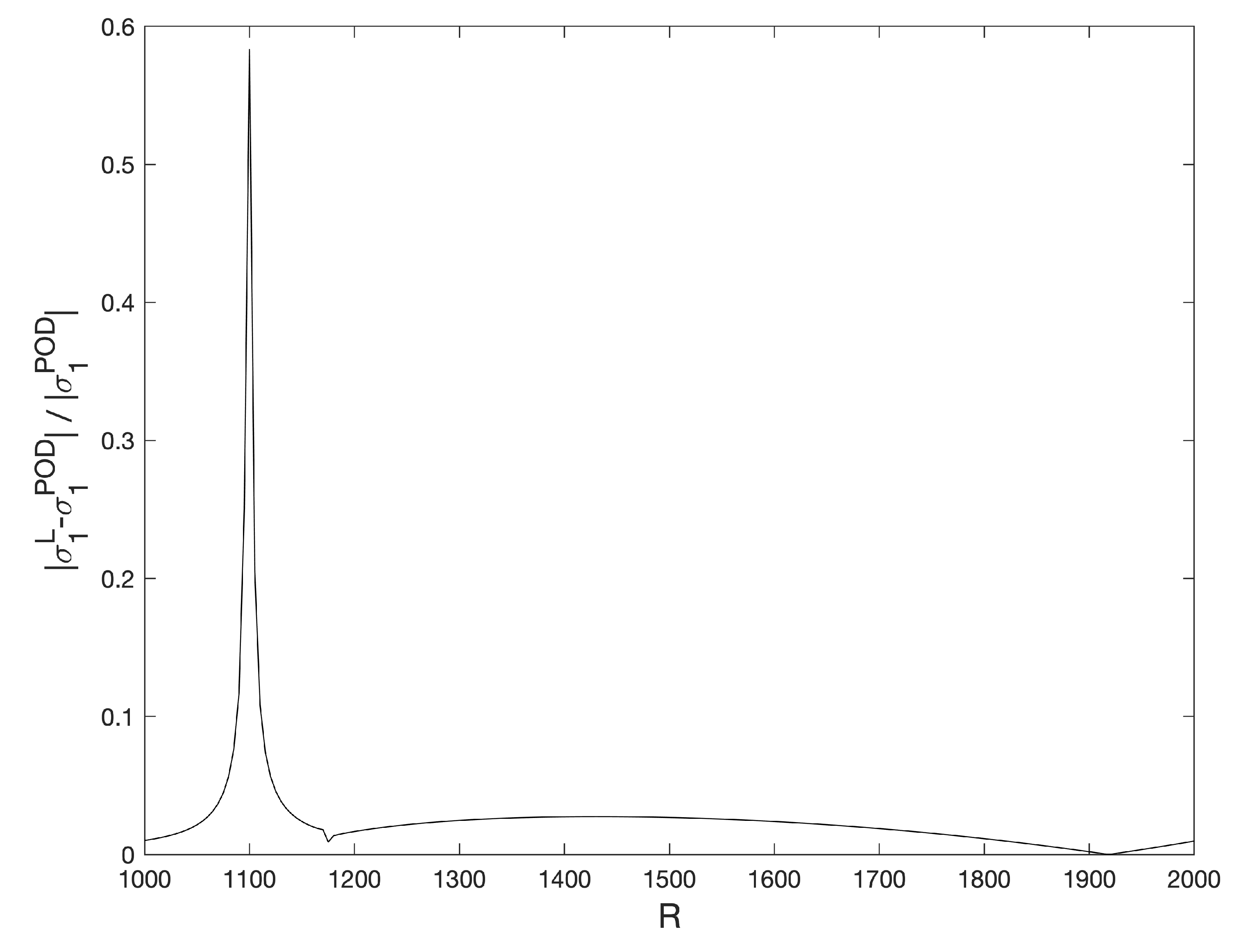
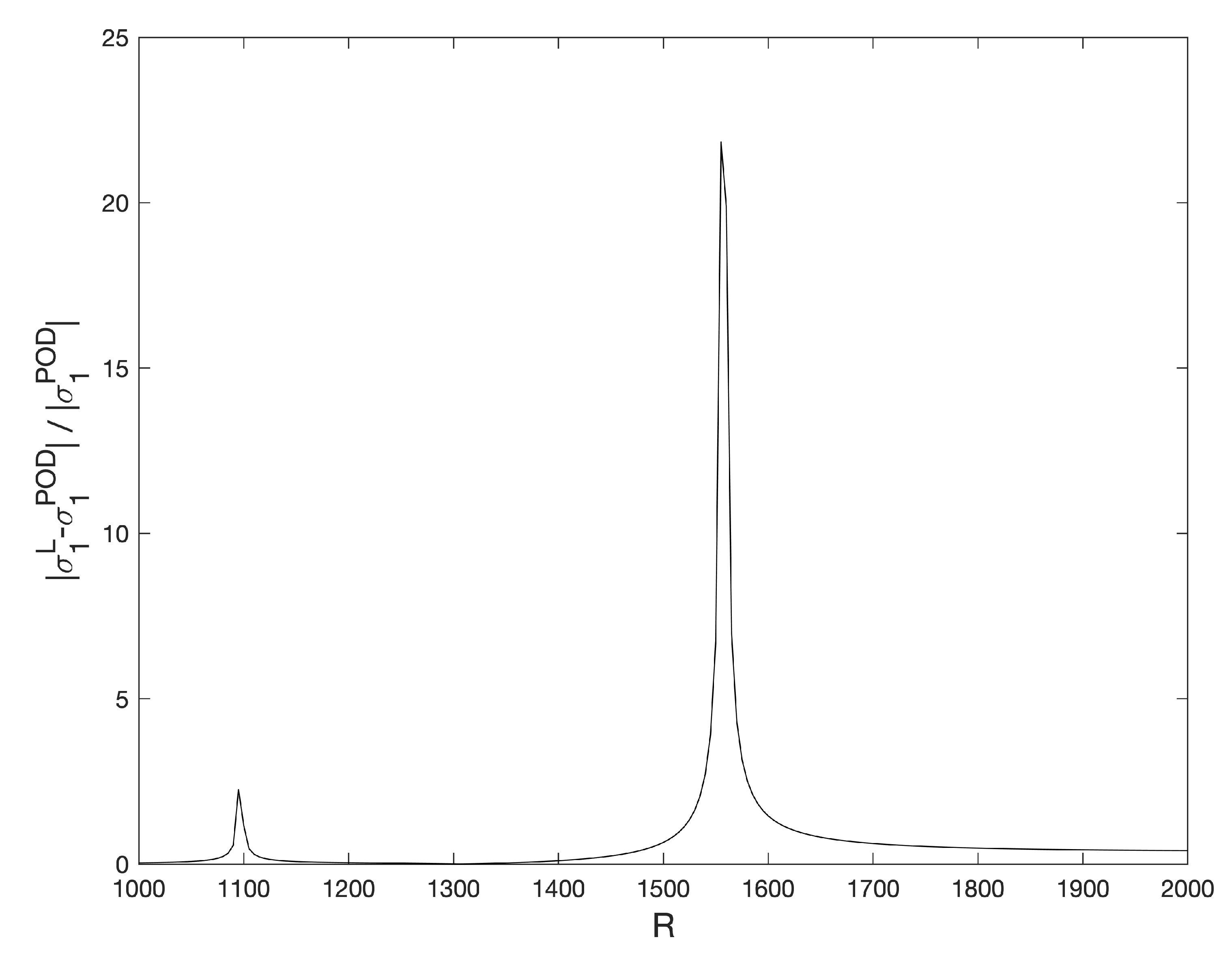
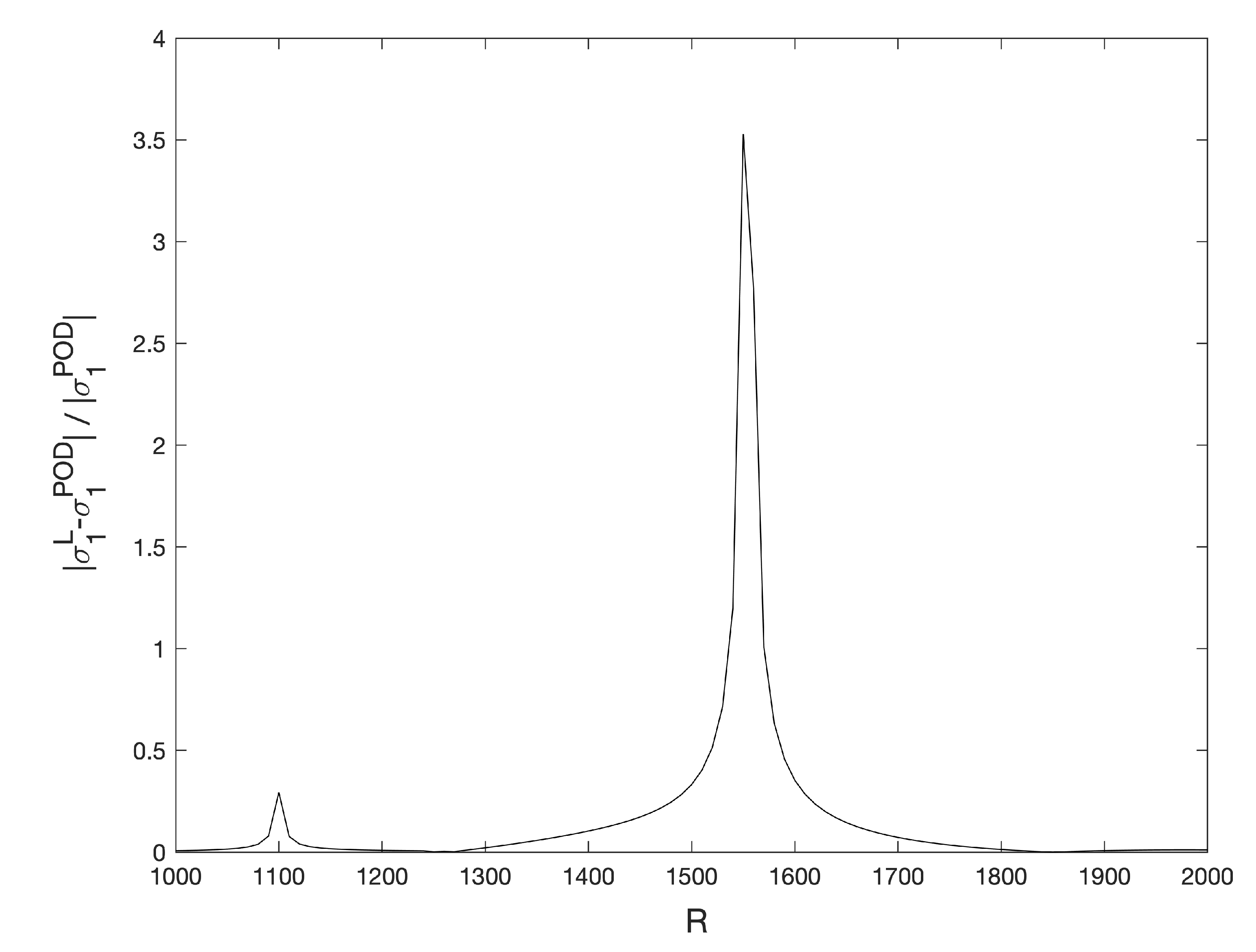
Figure 10.
Relative differences of for the stationary solutions , computed with a Legendre standard collocation method and the POD method.
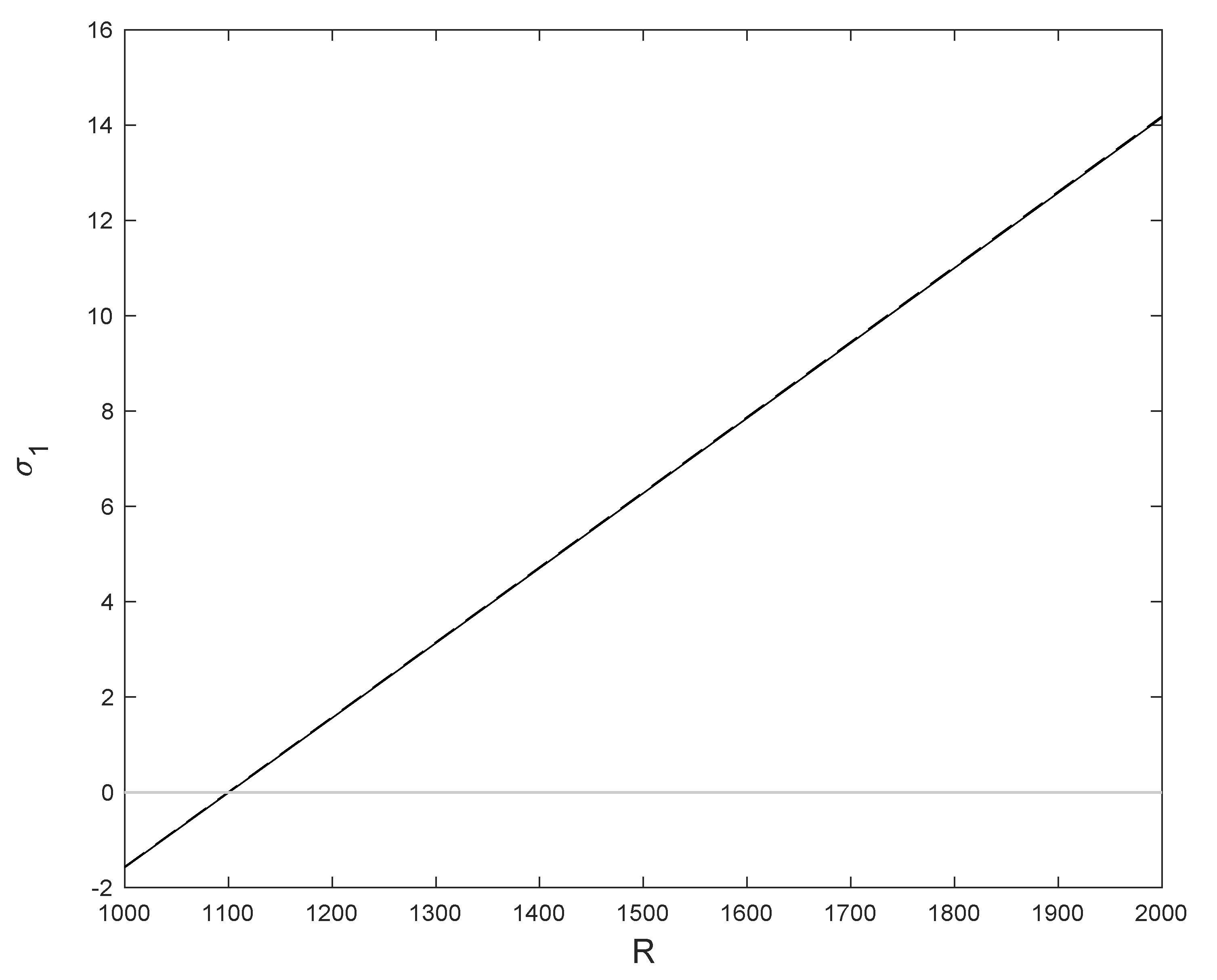
The POD method is applied to perform the linear stability analysis of the conductive solutions . A plot of can be seen in Figure 11; the continuous line has been obtained with Legendre collocation and the dashed line with POD. The relative difference between both values of is plotted in Figure 12; it is order , except at the bifurcation point , where we divide by a value near zero. The POD stability analysis in Figure 11 shows that is negative for and positive for . Then, the conductive solutions are stable for and unstable for . We observe that, at , an exchange of stability takes place; a stable branch of solutions, , emerges while the conductive branch, , becomes unstable. These results coincide with those from Ref. [50], obtained with Legendre collocation.
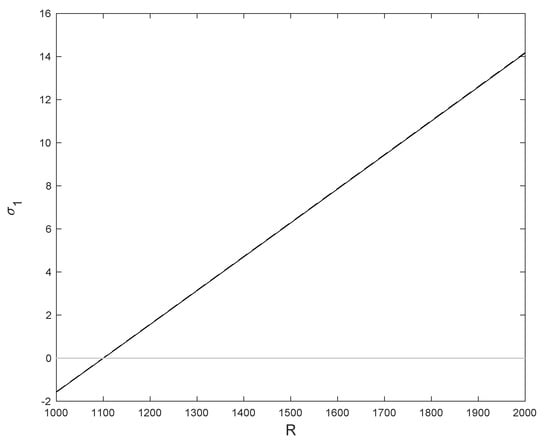
Figure 11.
for the stationary solutions , obtained with Legendre collocation (solid line) and with the POD method (dashed line). Results computed in a spatial numerical grid of Legendre–Gauss–Lobatto nodes.
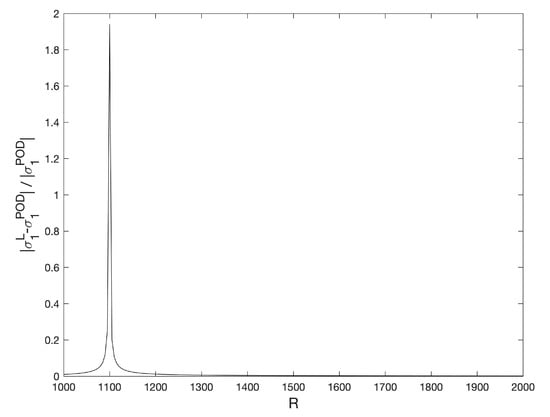
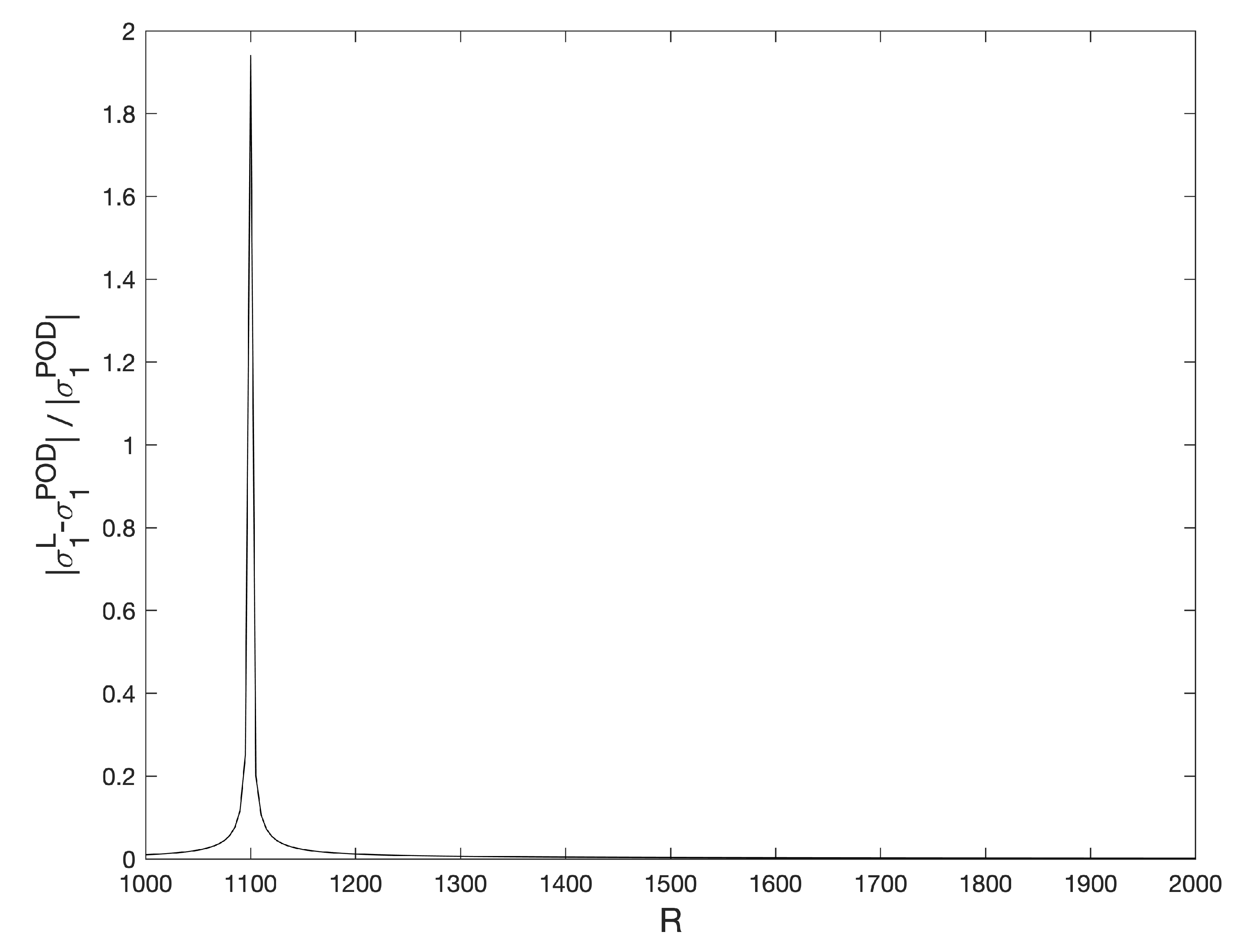
Figure 12.
Relative differences of for the stationary solutions , computed with a Legendre standard collocation method and the POD method. Results obtained with a spatial numerical grid of Legendre–Gauss–Lobatto nodes.
Note that, with the information obtained in just a single value of the Rayleigh number, , the bifurcation diagram for and solutions, , and its linear stability has been computed. Indeed, only 21 transitory states and their corresponding eigenfunctions have been considered at . The number of thermal POD modes is , and the number of hydrodynamic POD modes is .
4.2. Second Bifurcation
Now, the presented reduced-order method is applied to calculate a second bifurcation point. The following numerical results were obtained with a grid of Legendre–Gauss–Lobatto nodes. First, we follow Algorithm 1 for the value of the Rayleigh number . We solve the linear stability analysis Problem (12)–(14) with bc (9) and (10) for the conductive solution, , with a Legendre collocation method. A linear combination of the two eigenfunctions corresponding to the eigenvalues with the largest real part is the initial condition to obtain the steady solution with the time evolution discretization. This procedure generates some transitory numerical states before convergence . We are taking the transitory states such that . A total of 64 transitory states meet this condition. The first 13 are disregarded. Half of the remaining states have been taken, namely, the even ones. Then, . In Figure 13a, the horizontal component of the velocity in the middle of the cell , depending on the transitory time step, is plotted. We observe that the transitory states converge to the solution . In Figure 13b, the infinity norm of the difference between two consecutive transitory states of the horizontal component of the velocity field is displayed. As expected, these differences tend to zero. Isotherms of the transitory states at temporal steps , and can be seen in Figure 14. The exhibited transitory states are far from the converged solution.
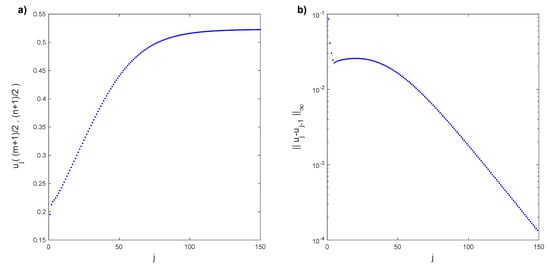
Figure 13.
(a) Horizontal component of the velocity transitory field , , , converging to for . (b) Infinity norm of the difference between consecutive transitory states of the horizontal component of the velocity field.
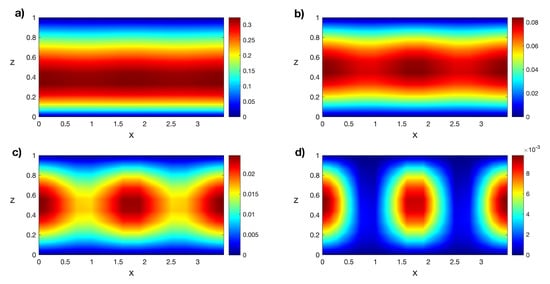
Figure 14.
Isotherms of the transitory states for at (a) , (b) , (c) , and (d) . Results obtained with a spatial numerical grid of Legendre–Gauss–Lobatto nodes.
The linear stability analysis for the transitory states is numerically performed, and the first eigenfunctions for these states are the snapshots for the POD analysis: . Figure 15 shows isotherms of the first eigenfunctions of the transitory states in Figure 14. Some eigenfunctions are similar because the transitory states are close in time.
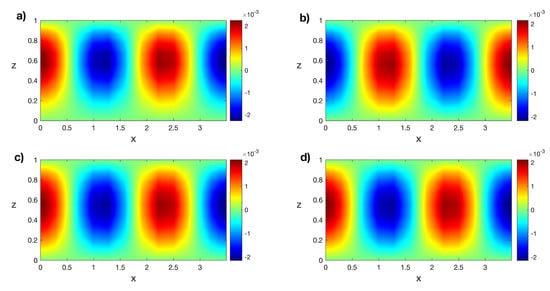
Figure 15.
Isotherms of the first eigenfunctions of the transitory states for at (a) , (b) , (c) , and (d) . Results obtained with a spatial numerical grid of Legendre–Gauss–Lobatto nodes.
As in Section 4.1, Algorithm 2 is followed to calculate the modified snapshot matrices , the singular values and eigenvectors for those matrices, and the resulting POD bases. The singular values for the modified snapshot matrix are plotted in Figure 16. The number of unsaturated modes for temperature is , and for velocity is . We observe that the singular values rapidly decay to zero, so the POD analysis is reliable. The thermal POD modes, computed at , corresponding with the first four singular values , and 4, are represented in Figure 17. The complexity of the modes increases as the singular values decrease.
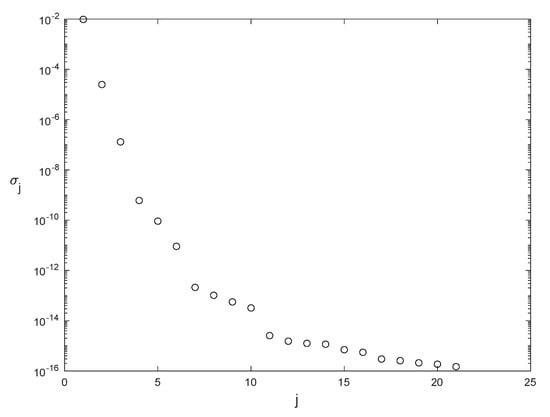
Figure 16.
Singular values of the thermal modified snapshot matrix .
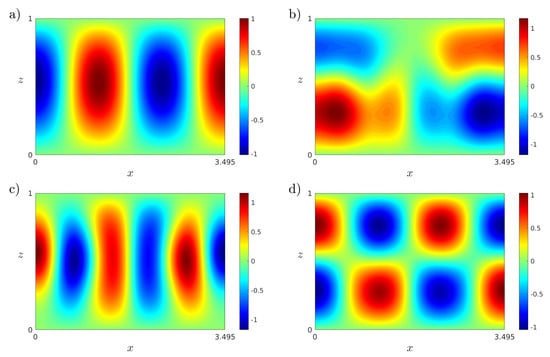
Figure 17.
(a–d) Isotherms of the first four thermal POD modes in computed at . Results obtained with a spatial numerical grid of Legendre–Gauss–Lobatto nodes.
Validation and Results
Now, we solve Problem (6)–(10) for values of the Rayleigh number in the interval with the POD/Galerkin method and with Legendre collocation. For instance, the isotherms and the velocity field of the POD solution for can be seen in Figure 18a. The same solution obtained with Legendre collocation is shown in Figure 18b, as in Ref. [50]. The norm of the difference between both solutions is order . Then, we solve the Galerkin/POD linear stability Problem (17) and (18) for . The first eigenfunction of the solution , computed with the POD method, can be seen in Figure 8b. The norm of the horizontal component of the velocity field for these solutions in the interval is displayed in Figure 19a; the continuous line has been obtained with Legendre collocation and the dashed line with POD. The difference between both solutions is order . Finally, a linear stability analysis for those stationary solutions is performed with the POD method. A plot of can be seen in Figure 19b; the continuous line has been obtained with Legendre collocation and the dashed line with POD. The relative difference between both values of is plotted in Figure 20; it is order , except at the bifurcation points and , where we divide by a value near zero. In this case, the computed eigenvalue shown in Figure 19b, , corresponds to the stability of in the interval , and to the stability of in the interval . As we already calculated, is stable for values of and unstable for . At , a new solution emerges from . This solution is unstable in the interval because is positive in this interval for this solution; this solution is stable for because is negative there. These results coincide with those in Ref. [50], obtained with Legendre collocation.
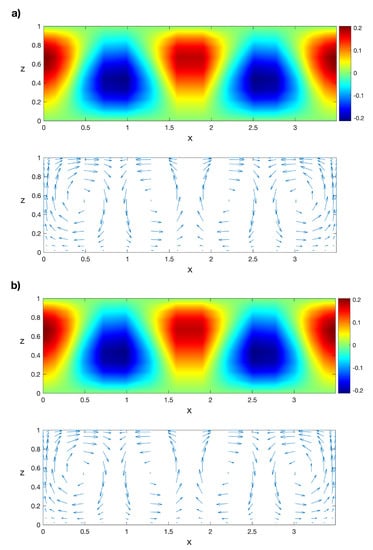
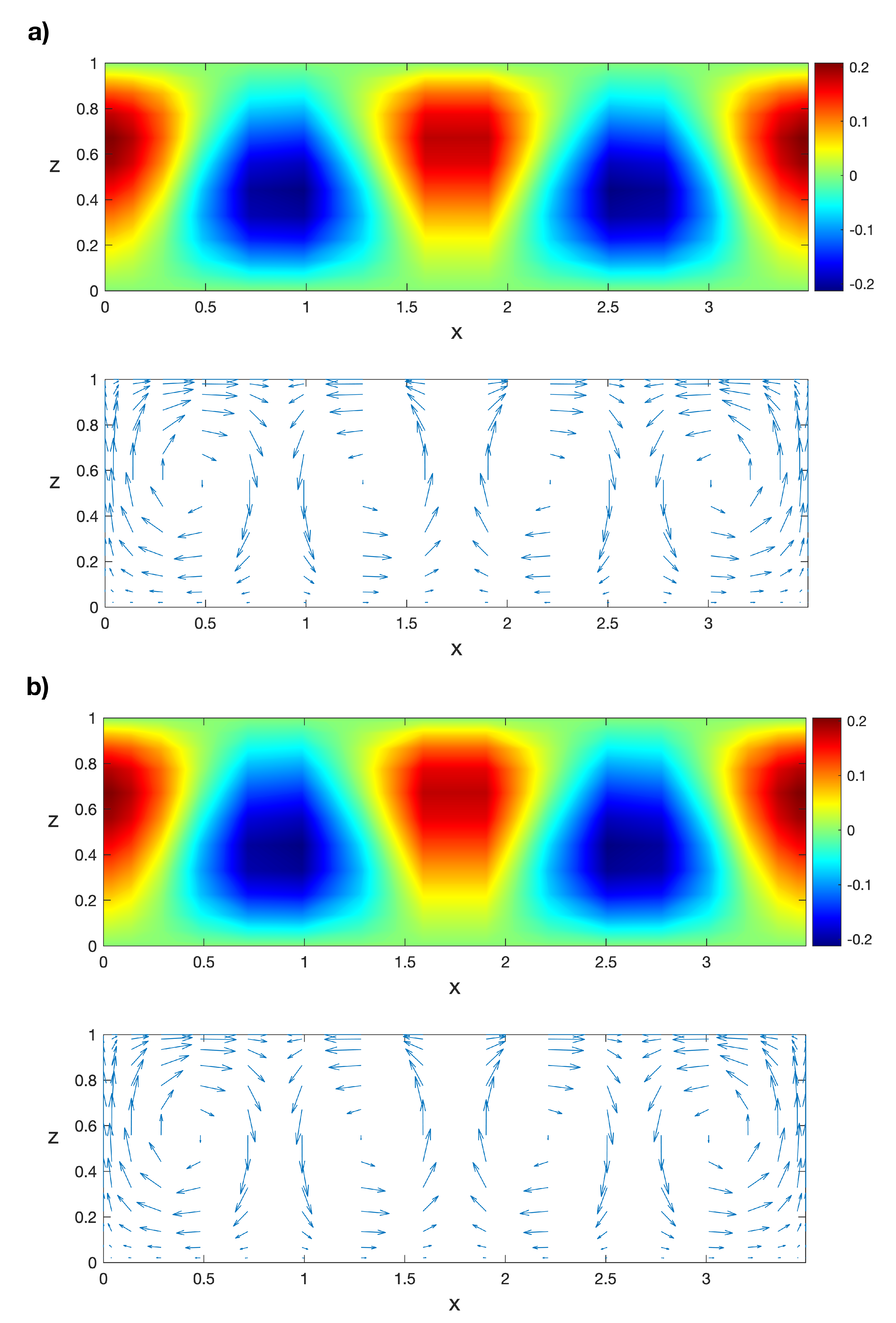
Figure 18.
(a) Isotherms and velocity field of the POD solution for and (b) the respective isotherms and velocity field computed with Legendre collocation. Results obtained with a spatial numerical grid of Legendre–Gauss–Lobatto nodes.
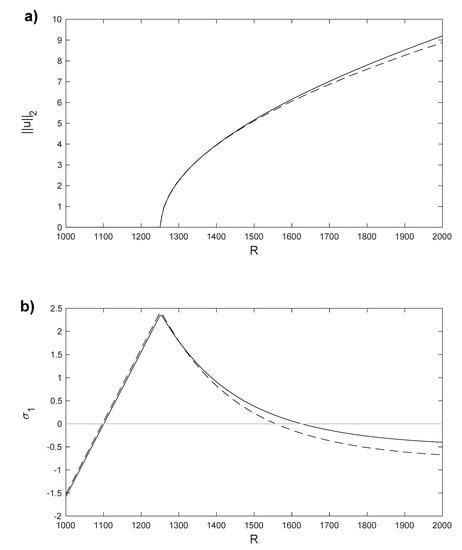
Figure 19.
(a) norm of the horizontal velocity component, u, for the stationary solutions and , obtained with Legendre collocation (solid line) and with the POD method (dashed line). (b) for the stationary solutions and , obtained with Legendre collocation (solid line) and with the POD method (dashed line). Results computed in a spatial numerical grid of Legendre–Gauss–Lobatto nodes.
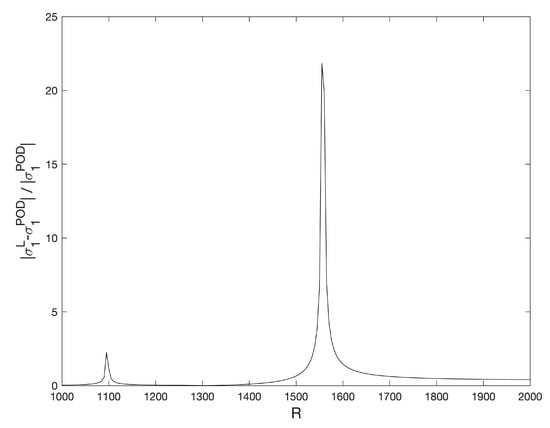
Figure 20.
Relative differences of for the stationary solutions computed with a Legendre standard collocation method and the POD method. Results obtained with a spatial numerical grid of Legendre–Gauss–Lobatto nodes.
As in Section 4.1, we remark that, with the information obtained in just a single value of the Rayleigh number, , the bifurcation diagram for and solutions, , and its linear stability has been computed. Only 26 transitory states and their corresponding eigenfunctions have been considered at . The number of thermal POD modes is , and the number of hydrodynamic POD modes is .
4.3. Third Bifurcation
Finally, the presented reduced-order method is applied to calculate a third bifurcation point. The following numerical results were obtained with a grid of Legendre–Gauss–Lobatto nodes. This time, a finer numerical discretization was required to capture the bifurcation point. We follow Algorithm 1 for the value of the Rayleigh number . We solve the linear stability analysis Problem (12)–(14) with bc (9) and (10) for the conductive solution, , with a Legendre collocation method. A linear combination of the two eigenfunctions corresponding to the eigenvalues with the largest real part is the initial condition to obtain the steady solution with the time evolution discretization. This procedure generates some transitory numerical states before convergence . We are taking the transitory states such that . A total of 41 transitory states meet this condition. Only the last 21 are considered, so . In Figure 21a, the horizontal component of the velocity in the middle of the cell , depending on the transitory time step, is plotted. We observe that the transitory states converge to the steady solution . In Figure 21b, the infinity norm of the difference between two consecutive transitory states of the horizontal component of the velocity field is displayed. Again, these differences tend to zero. Isotherms of the transitory states at temporal steps , and can be seen in Figure 22. The exhibited transitory states are far from the converged solution.
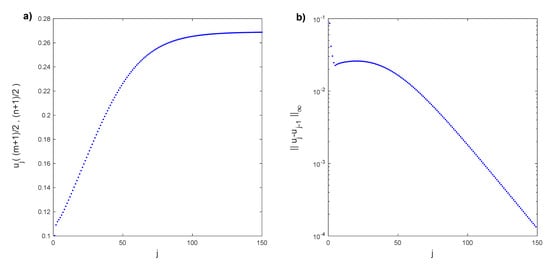
Figure 21.
(a) Horizontal component of the velocity transitory field , , , converging to for . (b) Infinity norm of the difference between consecutive transitory states of the horizontal component of the velocity field.
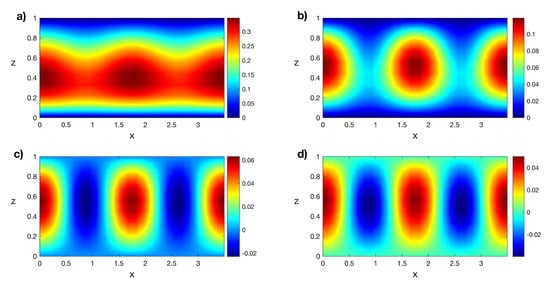
Figure 22.
Isotherms of the transitory states for at (a) , (b) , (c) , and (d) . Results obtained with a spatial numerical grid of Legendre–Gauss–Lobatto nodes.
The linear stability analysis for the transitory states is numerically performed, and the first eigenfunctions for these states are the snapshots for the POD analysis: , where i is the temporal step. Figure 23 shows isotherms of the first eigenfunctions of the transitory states in Figure 22. Some eigenfunctions are very similar because the transitory states are close in time.
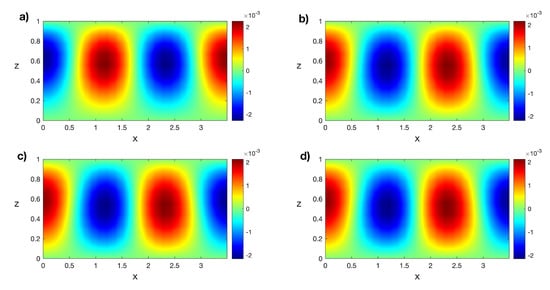
Figure 23.
Isotherms of the first eigenfunctions of the transitory states for at (a) , (b) , (c) , and (d) . Results obtained with a spatial numerical grid of Legendre–Gauss–Lobatto nodes.
As in previous subsections, Algorithm 2 is followed to calculate the modified snapshot matrices: , the singular values and eigenvectors for those matrices, and the resulting POD bases. The singular values for the modified snapshot matrix are plotted in Figure 24. The number of unsaturated modes for temperature is and for velocity is . We observe that the singular values rapidly decay to zero, so the POD analysis is reliable. The thermal POD modes, computed at , corresponding with the first four singular values , and 4, are represented in Figure 25. The complexity of the modes increases as the singular values decrease.
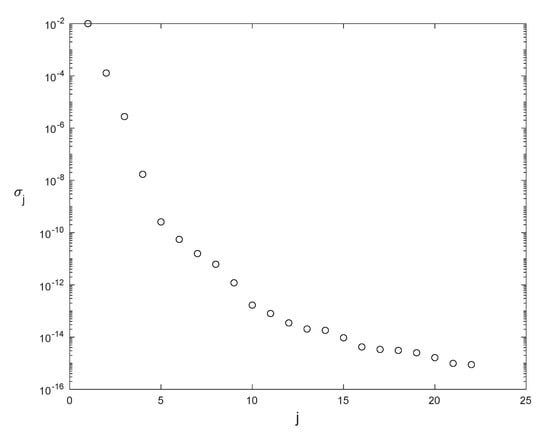
Figure 24.
Singular values of the thermal modified snapshots matrix .
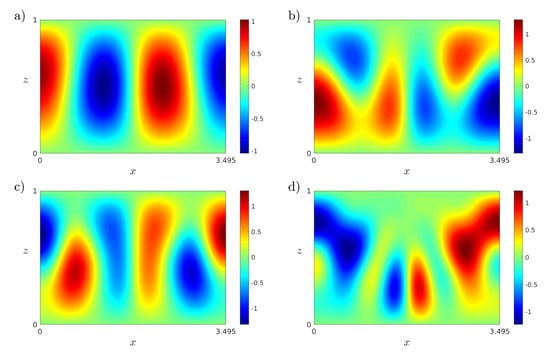
Figure 25.
(a–d) Isotherms of the first four thermal POD modes in , computed at . Results obtained with a spatial numerical grid of Legendre–Gauss–Lobatto nodes.
Validation and Results
Now, we solve Problem (6)–(10) for values of the Rayleigh number in the interval with the POD/Galerkin method and with Legendre collocation. For instance, the isotherms and the velocity field of the POD solution for can be seen in Figure 26a. The same solution, obtained with Legendre collocation, is shown in Figure 26b, as in Ref. [50]. The norm of the difference between both solutions is order . Then, we solve the Galerkin/POD linear stability Problem (17) and (18) for . The first eigenfunction of the solution , computed with the POD method, can be seen in Figure 8c. The norm of the horizontal component of the velocity field for this solution in the interval can be seen in Figure 27a; the continuous line has been obtained with Legendre collocation and the dashed line with POD. The difference between both solutions is order . Finally, the POD method is applied to perform the linear stability analysis. The corresponding plot of can be seen in Figure 27b; the continuous line has been obtained with Legendre collocation and the dashed line with POD. The relative difference between both values of is plotted in Figure 28; it is order , except at the bifurcation points and , where we divide by a value near zero. The computed eigenvalue shown in Figure 27b, , corresponds to the stability of in the interval , the stability of in the interval , and the stability of in the interval . As we already calculated, is stable for values of and unstable for . At , solution appears from . These solutions are unstable in the interval because is positive in this interval for these solutions and it is stable for , as can be seen in Figure 19b. Solution emerges from at . These solutions are unstable for because is positive there. These results coincide with those in Ref. [50].
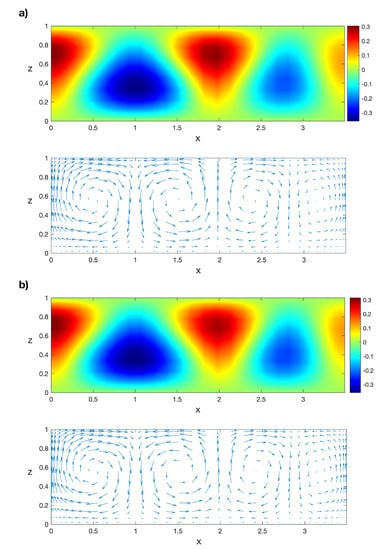
Figure 26.
(a) Isotherms and velocity field of the POD solution for , and (b) the respective isotherms and velocity field computed with Legendre collocation. Results obtained with a spatial numerical grid of Legendre–Gauss–Lobatto nodes.
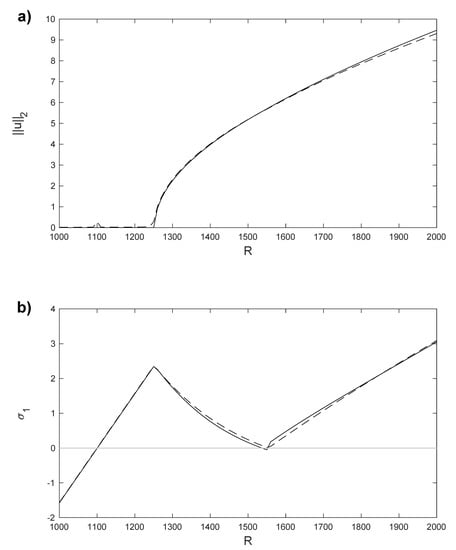
Figure 27.
(a) norm of the horizontal velocity component, u, for the stationary solutions , , and , obtained with Legendre collocation (solid line) and with the POD method (dashed line). (b) for the stationary solutions , , and , obtained with Legendre collocation (solid line) and with the POD method (dashed line). Results computed in a spatial numerical grid of Legendre–Gauss–Lobatto nodes.
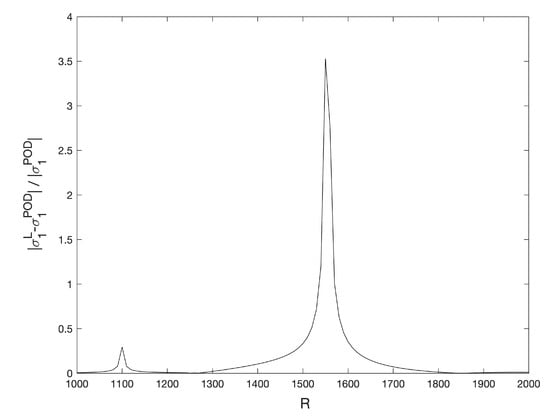
Figure 28.
Relative differences of for the stationary solutions , computed with Legendre collocation and with the POD method. Results obtained with a spatial numerical grid of Legendre–Gauss–Lobatto nodes.
As in previous subsections, it should be noted that, with the information obtained in just a single value of the Rayleigh number, , the bifurcation diagram for , , and solutions, , and its linear stability has been computed. Only 21 transitory states and their corresponding eigenfunctions have been considered at . The number of thermal POD modes is , and the number of hydrodynamic POD modes is .
4.4. Bifurcation Diagram
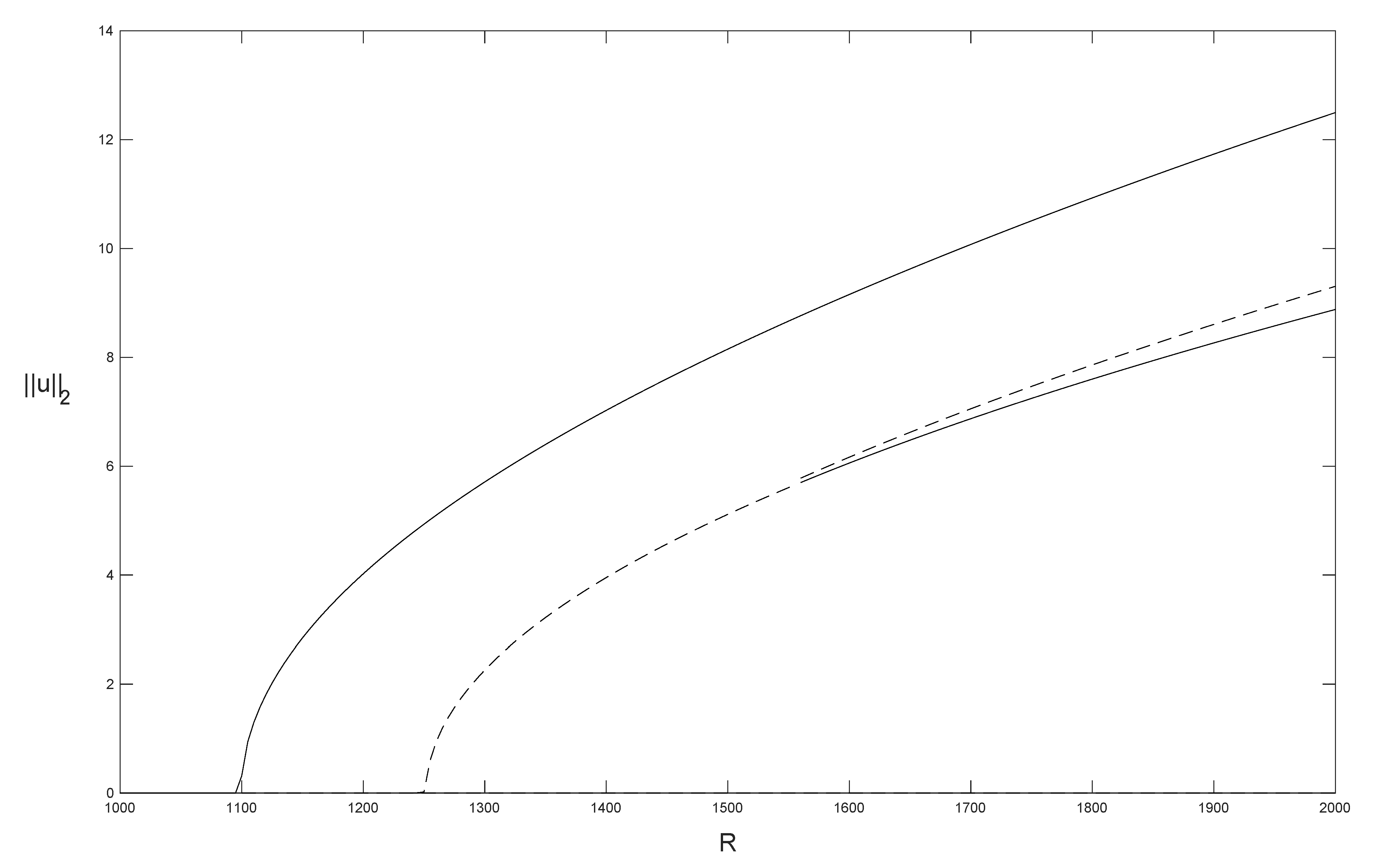
The different branches of solutions and bifurcations are summarized in the bifurcation diagram (Figure 29) obtained with the POD method. The bifurcation digram represents the norm of the component u of the velocity field as function of the parameter R (horizontal axis). The horizontal line represents the conductive solution ; the velocity field for the conductive solution is zero (in particular u). The branches of stable stationary solutions are marked with solid lines and the unstable solutions with dashed lines. The conductive stationary solution constitutes the conductive branch of solutions, , which exhibits two pitchfork bifurcations as R increases in . The first takes place at , where loses its stability and a new branch of solutions, , emerges. These solutions are stable for any value of R in the interval . The second is a pitchfork bifurcation at that produces a branch of solutions emerging from at this critical threshold . At , a subcritical pitchfork bifurcation occurs. Solutions emerge from . Solutions are unstable for , but at higher values, they become stable. Solutions are unstable for . These results coincide with those in Refs. [46,50].
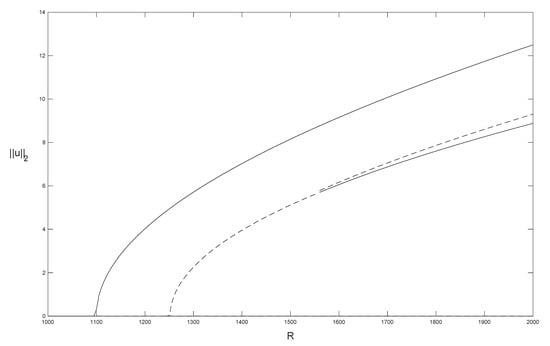
Figure 29.
Bifurcation diagram in which the norm of u, , is shown versus R, . The critical Rayleigh numbers (first supercritical pitchfork bifurcation), (secondary bifurcation), and (subcritical pitchfork bifurcation) are captured. Solid line represents stable solutions. Dashed line represents unstable solutions.
4.5. Computational Cost
Now, we approximate the number of operations considering only products at each step of the algorithms. We name , , : number of time steps computed by the standard time evolution solver, : number of values of R for which the problem is solved, and : number of Newton iterations for solving the variational problem. We consider first the number of operations for the calculation of a single branch of solutions. The maximum values considered are , , , , , , , and .
Algorithm 1 requires operations, in the maximum case . Algorithm 2 needs operations, in the maximum case . The calculation of the POD/Galerkin solutions and their linear stability requires operations, in the maximum case . A detailed analysis of the computational cost of Algorithm 1, Algorithm 2 and the calculation of the POD/Galerkin solutions and their linear stability is displayed below.
Breakdown of the computational cost of Algorithm 1:
- Step 5: Solve, numerically, the linear stability analysis for K transitory states:.
Breakdown of the computational cost of Algorithm 2:
- Step 3: Construct the matrices , and from thermal and hydrodynamic snapshots: ;
- Step 4: Apply a SVD decomposition to , and to obtain their eigenvectors and singular values: ;
- Step 5: Obtain the thermal and hydrodynamic POD modes related to J and I unsaturated singular values, , , and , as linear combinations of thermal and hydrodynamic snapshots: ;
- Step 6: Orthonormalize the bases , , and by applying a Gram–Schmidt method: .
Computational cost of the calculation of the POD/Galerkin solutions and their linear stability:
- ;
- ;
The cost of the off-line calculation is . The cost of the on-line calculation is . The calculation of a branch of the bifurcation diagram with the standard method is and with the POD method is . In our case, the reduction goes from to . However, taking into account the on-line and the off-line, the POD computational cost is , in our case . The Legendre collocation method calculates 201 solutions in the interval of R, , by steps of five with a computational cost of 0.0279 h in a 3.6-GHz Intel Core i9 microprocessor. The calculation of the eigenvalues for those solutions takes 1.862 h. Therefore, the total computational cost for the Legendre collocation method is 1.8899 h. Regarding the POD method, the off-line computational cost, including the snapshots, the singular values decomposition, the POD bases, and the stability calculation is 0.2008 h. The on-line computational cost of the POD solutions and the corresponding eigenvalue problem with the same interval and steps is 0.4344 s, or h. Then, the total computational cost for the POD method is 0.2009 h. We obtain a reduction in the CPU time of a factor of 9.4, i.e., , as previously estimated in the computational cost. Taking into account only the on-line computational cost, the factor of reduction is 15619, i.e., , as was seen in the computational cost.
5. Conclusions
A Galerkin/POD reduced-order model from eigenfunctions of non-converged time evolution states in a Rayleigh–Bénard problem is presented. This convection problem is modeled in a rectangular domain with a heat equation coupled with the incompressible Navier–Stokes equations, depending on the Rayleigh number R as a bifurcation parameter. This problem is solved with a time evolution Legendre collocation method for a value of the Rayleigh number. The eigenfunctions of the linear stability analysis of the non-converged states are the snapshots of the POD analysis. From a single value of the bifurcation parameter, the whole bifurcation diagram in an interval of values of R is obtained. Three different bifurcation points and four types of solutions are obtained with small errors. The calculations use less than 30 modes, so the matrices for the eigenvalue problem solved with the POD method are very small, and the computational cost is drastically reduced, by a factor of .
Author Contributions
All authors contributed equally to this work. All authors have read and agreed to the published version of the manuscript.
Funding
Partial funding for this work was provided by the Research Grants PID2019-109652GB-I00 (MICINN, Spanish Government), and 2021-GRIN-30985 and 2020-GRIN-28738 (Universidad de Castilla-La Mancha), which include ERDF funds.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Canuto, C.; Hussaini, M.; Quarteroni, A.; Zang, T. Spectral Methods in Fluid Dynamics; Springer: New York, NY, USA, 1988. [Google Scholar]
- Strikwerda, J. Finite Difference Schemes and Partial Differential; Wadsworth and Brooks: Pacific Grove, CA, USA, 1989. [Google Scholar]
- Zienkiewicz, O. The Finite Element Method in Engineering Science; McGraw-Hill: New York, NY, USA, 1971. [Google Scholar]
- Veroy, K.; Prud’homme, C.; Rovas, D.; Patera, A. A Posteriori Error Bounds for Reduced-Basis Approximation of Parametrized Noncoercive and Nonlinear Elliptic Partial Differential Equations. In Proceedings of the 16th AIAA Computational Fluid Dynamics Conference, Orlando, FL, USA, 23–26 June 2003; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2012. [Google Scholar] [CrossRef]
- Barrett, G.R. On the reduced basis method. Z. Angew. Math. Mech. 1995, 75, 543–549. [Google Scholar] [CrossRef]
- Rozza, G.; Huynh, D.B.P.; Patera, A.T. Reduced Basis Approximation and a Posteriori Error Estimation for Affinely Parametrized Elliptic Coercive Partial Differential Equations. Arch. Comput. Methods Eng. 2007, 15, 229–275. [Google Scholar] [CrossRef]
- Prud’homme, C.; Rovas, D.V.; Veroy, K.; Machiels, L.; Maday, Y.; Patera, A.T.; Turinici, G. Reliable Real-Time Solution of Parametrized Partial Differential Equations: Reduced-Basis Output Bound Methods. J. Fluids Eng. 2001, 124, 70–80. [Google Scholar] [CrossRef]
- Deparis, S.; Rozza, G. Reduced basis method for multi-parameter-dependent steady Navier-Stokes equations: Applications to natural convection in a cavity. J. Comp. Phys. 2009, 228, 4359–4378. [Google Scholar] [CrossRef]
- Manzoni, A. An efficient computational framework for reduced basis approximation and a posteriori error estimation of parametrized Navier-Stokes flows. ESAIM Math. Model. Numer. Anal. 2014, 48, 1199–1226. [Google Scholar] [CrossRef]
- Noor, A.; Balch, C.; Shibut, M. Reduction methods for non-linear steadystate thermal analysis. Int. J. Numer. Methods Eng. 1984, 20, 1323–1348. [Google Scholar] [CrossRef]
- LeGresley, P.; Alonso, J. Investigation of non-linear projection for POD based reduced order models for aerodynamics. J. Dyn. Differ. Equ. 1991, 3, 491–514. [Google Scholar]
- Lumley, J. Coherent Structures in Turbulence. In Transition and Turbulence; Meyer, R.E., Ed.; Academic Press: Cambridge, MA, USA, 1981; pp. 215–242. [Google Scholar] [CrossRef]
- Bache, E.; Vega, J.; Velazquez, A. Model reduction in the back step fluid-thermal problem with variable geometry. Int. J. Therm. Sci. 2010, 49, 2376–2384. [Google Scholar] [CrossRef]
- Terragni, F.; Valero, E.; Vega, J.M. Local POD Plus Galerkin Projection in the Unsteady Lid-Driven Cavity Problem. SIAM J. Sci. Comput. 2011, 33, 3538–3561. [Google Scholar] [CrossRef]
- Rempfer, D. Low-dimensional modeling and numerical simulation of transition in simple shear flows. Annu. Rev. Fluid Mech. 2003, 35, 229–265. [Google Scholar] [CrossRef]
- Lassila, T.; Manzoni, A.; Quarteroni, A.; Rozza, G. Model Order Reduction in Fluid Dynamics: Challenges and Perspectives. In Reduced Order Methods for Modeling and Computational Reduction; Quarteroni, A., Rozza, G., Eds.; MS&A—Modeling, Simulation and Applications; Springer: Cham, Switzerland, 2014; pp. 235–273. [Google Scholar] [CrossRef]
- Couplet, M.; Basdevant, C.; Sagaut, P. Calibrated reduced-order POD-Galerkin system for fluid flow modelling. J. Comput. Phys. 2005, 207, 192–220. [Google Scholar] [CrossRef]
- Sirisup, S.; Karniadakis, G.E. Stability and accuracy of periodic flow solutions obtained by a POD-penalty method. Phys. D 2005, 202, 218–237. [Google Scholar] [CrossRef]
- Sirisup, S.; Karniadakis, G.E.; Xiu, D.; Kevrekidis, I.G. Equation-free/Galerkin-free POD-assisted computation of incompressible flows. J. Comput. Phys. 2005, 207, 568–587. [Google Scholar] [CrossRef]
- Siegel, S.G.; Seidel, J.; Fagley, C.; Luchtenburg, D.M.; Cohen, K.; Mclaughlin, T. Low-dimensional modelling of a transient cylinder wake using double proper orthogonal decomposition. J. Fluid Mech. 2008, 610, 1–42. [Google Scholar] [CrossRef]
- Foias, C.; Sell, G.R.; Temam, R. Inertial manifolds for nonlinear evolutionary equations. J. Differ. Equ. 1988, 73, 309–353. [Google Scholar] [CrossRef]
- Jolly, M. Bifurcation computations on an approximate inertial manifold for the 2D Navier-Stokes equations. Phys. D 1993, 63, 8–20. [Google Scholar] [CrossRef]
- Robinson, J. Computing inertial manifolds. Discret. Cont. Dyn. Syst. 2002, 8, 815–833. [Google Scholar] [CrossRef]
- Foias, C.; Nicolaenko, B.; Sell, G.R.; Temam, R. Inertial manifolds for the Kuramoto-Sivashinsky equation and an estimate of their lowest dimension. J. Math. Pures Appl. 1988, 67, 197–226. [Google Scholar]
- Promislow, K.; Temam, R. Localization and approximation of attractors for the Ginzburg-Landau equation. J. Dyn. Differ. Equ. 1991, 3, 491–514. [Google Scholar] [CrossRef]
- Alonso, D.; Vega, J.M.; Velazquez, A. Reduced-Order Model for Viscous Aerodynamic Flow Past an Airfoil. AIAA J. 2010, 48, 1946–1958. [Google Scholar] [CrossRef]
- Braconnier, T.; Ferrier, M.; Jouhaud, J.C.; Montagnac, M.; Sagaut, P. Towards an adaptive POD/SVD surrogate model for aeronautic design. Comput. Fluids 2011, 40, 195–209. [Google Scholar] [CrossRef]
- Ballarin, F.; Faggiano, E.; Ippolito, S.; Manzoni, A.; Quarteroni, A.; Rozza, G.; Scrofani, R. Fast simulations of patient-specific haemodynamics of coronary artery bypass grafts based on a POD–Galerkin method and a vascular shape parametrization. J. Comput. Phys. 2016, 315, 609–628. [Google Scholar] [CrossRef]
- Demo, N.; Tezzele, M.; Gustin, G.; Lavini, G.; Rozza, G. Shape Optimization by means of Proper Orthogonal Decomposition and Dynamic Mode Decomposition. In Technology and Science for the Ships of the Future: Proceedings of NAV 2018: 19th International Conference on Ship & Maritime Research; IOS Press: Trieste, Italy, 2018. [Google Scholar] [CrossRef]
- Ghosh, R.; Joshi, Y. Proper Orthogonal Decomposition-Based Modeling Framework for Improving Spatial Resolution of Measured Temperature Data. IEEE Trans. Compon. Packag. Manuf. Technol. 2014, 4, 848–858. [Google Scholar] [CrossRef]
- Samadiani, E. Reduced Order Modeling Based Energy Efficient and Adaptable Design. In Energy Efficient Thermal Management of Data Centers; Joshi, Y., Kumar, P., Eds.; Springer: Boston, MA, USA, 2012. [Google Scholar]
- Bénard, H. Les tourbillons cèllulaires dansune nappe liquide. Rev. Gen. Sci. Pures Appl. Bull. Assoc. 2010, 11, 1261–1271. [Google Scholar]
- Bejan, A. Convection Heat Transfer; Wiley: Hoboken, NJ, USA, 2013. [Google Scholar]
- Zahra El Fatnani, F.; Guyomar, D.; Belhora, F.; Mazroui, M.; Boughaleb, Y.; Hajjaji, A. A new concept to harvest thermal energy using pyroeletric effect and Rayleigh-Benard convections. Eur. Phys. J. Plus 2016, 131, 252. [Google Scholar] [CrossRef]
- Owen, J.M.; Tang, H.; Lock, G.D. Buoyancy-Induced Heat Transfer inside Compressor Rotors: Overview of Theoretical Models. Aerospace 2018, 5, 32. [Google Scholar] [CrossRef]
- Müller, G. Convection and Inhomogeneities in Crystal Growth from the Melt. In Crystal Growth from the Melt; Müller, G., Ed.; Springer: Berlin/Heidelberg, Germany, 1988; pp. 1–136. [Google Scholar] [CrossRef]
- Kumar, A.; Roy, S. Effect of three-dimensional melt pool convection on process characteristics during laser cladding. Comput. Mater. Sci. 2009, 46, 495–506. [Google Scholar] [CrossRef]
- Xu, F.; Xu, S.; Passe, U.; Ganapathysubramanian, B. Computational study of natural ventilation in a sustainable building with complex geometry. Sustain. Energy Technol. Assess. 2021, 45, 101153. [Google Scholar] [CrossRef]
- Maatki, C. Three-Dimensional Numerical Study of the Effect of Protective Barrier on the Dispersion of the Contaminant in a Building. Mathematics 2021, 9, 1125. [Google Scholar] [CrossRef]
- Giroux-Julien, S.; Vareilles, J.; Menezo, C.; Pabiou, H.; Fossa, M.; Leonardi, E. Natural Convection In a Nonuniformly Heated Channel Investigation with application to Photovoltaic Façades. Comput. Therm. Sci. 2009, 1, 231–258. [Google Scholar] [CrossRef]
- Kunisch, K.; Volkwein, S. Galerkin Proper Orthogonal Decomposition Methods for a General Equation in Fluid Dynamics. SIAM J. Numer. Anal. 2002, 40, 492–515. [Google Scholar] [CrossRef]
- Novo, J.; Rubino, S. Error Analysis of Proper Orthogonal Decomposition Stabilized Methods for Incompressible Flows. SIAM J. Numer. Anal. 2021, 59, 334–369. [Google Scholar] [CrossRef]
- Fresca, S.; Manzoni, A. Real-Time Simulation of Parameter-Dependent Fluid Flows through Deep Learning-Based Reduced Order Models. Fluids 2021, 6, 259. [Google Scholar] [CrossRef]
- Pla, F.; Herrero, H. Reduced Basis method applied to eigenvalue problems from convection. Int. J. Bifurcat. Chaos 2019, 29, 1950028. [Google Scholar] [CrossRef]
- Georgaka, S.; Stabile, G.; Star, K.; Rozza, G.; Bluck, M.J. A hybrid reduced order method for modelling turbulent heat transfer problems. Comput. Fluids 2020, 208, 104615. [Google Scholar] [CrossRef]
- Pla, F.; Herrero, H.; Vega, J.M. A flexible symmetry-preserving Galerkin/POD reduced order model applied to a convective instability problem. Comput. Fluids 2015, 119, 162–175. [Google Scholar] [CrossRef]
- Dumon, A.; Allery, C.; Ammar, A. Proper general decomposition (PGD) for the resolution of Navier–Stokes equations. J. Comp. Phys. 2011, 230, 1387–1407. [Google Scholar] [CrossRef][Green Version]
- Chinesta, F.; Ladeveze, P.; Cueto, E. A Short Review on Model Order Reduction Based on Proper Generalized Decomposition. Arch. Comput. Methods Eng. 2011, 18, 395–404. [Google Scholar] [CrossRef]
- Burkardt, J.; Gunzburger, M.; Lee, H.C. POD and CVT-based reduced-order modeling of Navier–Stokes flows. Comput. Meth. Appl. Mech. Eng. 2006, 196, 337–355. [Google Scholar] [CrossRef]
- Pla, F.; Mancho, A.; Herrero, H. Bifurcation phenomena in a convection problem with temperature dependent viscosity at low aspect ratio. Phys. Nonlinear Phenom. 2009, 238, 572–580. [Google Scholar] [CrossRef]
- Herrero, H.; Maday, Y.; Pla, F. RB (Reduced Basis) applied to RB (Rayleigh-Bénard). Comput. Methods Appl. Mech. Eng. 2013, 261–262, 132–141. [Google Scholar] [CrossRef]
- Moresi, L.; Solomatov, V. Numerical investigation of 2D convection with extremely large viscosity variations. Phys. Fluids 1995, 7, 2154–2162. [Google Scholar] [CrossRef]
- Davies, G.F. Dynamic Earth. Plates, Plumes and Mantle Convection; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Lorca, S.; Boldrini, J. The initial value problem for a generalized Boussinesq model: Regularity and global existence of strong solutions. Mat. Contemp. 1996, 11, 71–94. [Google Scholar] [CrossRef]
- Pla, F.; Herrero, H.; Lafitte, O. Theoretical and numerical study of a thermal convection problem with temperature-dependent viscosity in an infinite layer. Phys. Nonlinear Phenom. 2010, 239, 1108–1119. [Google Scholar] [CrossRef]
- Herrero, H.; Maday, Y.; Pla, F. Reduced basis method applied to a convective stability problem. J. Math. Ind. 2018, 8. [Google Scholar] [CrossRef]
- Bernardi, C.; Maday, Y. Approximations Spectrales de Problèmes aux Limites Elliptiques; Springer: New York, NY, USA, 1991. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).