An Implementation of Image Secret Sharing Scheme Based on Matrix Operations

Abstract

The image secret sharing scheme shares a secret image as multiple shadows. The secret image can be recovered from shadow images that meet a threshold number. However, traditional image secret sharing schemes generally reuse the Lagrange’s interpolation in the recovery stage to obtain the polynomial in the sharing stage. Since the coefficients of the polynomial are the pixel values of the secret image, it is able to recover the secret image. This paper presents an implementation of the image secret sharing scheme based on matrix operations. Different from the traditional image secret sharing scheme, this paper does not use the method of Lagrange’s interpolation in the recovery stage, but first identifies the participants as elements to generate a matrix and calculates its inverse matrix. By repeating the matrix multiplication, the polynomial coefficients of the sharing stage are quickly derived, and then the secret image is recovered. By theoretical analysis and the experimental results, the implementation of secret image sharing based on matrix operation is higher than Lagrange’s interpolation in terms of efficiency.

1. Introduction

Secret sharing is an important research direction in the field of modern cryptography. The use of a secret sharing scheme to transmit or save the secret information can prevent excessive concentration of power on the one hand, and ensure the integrity, reliability and security of secret information on the other. Only when the attacker has a certain number of shared keys is it possible to recover the original secret information correctly, so the recovery of the original secret information is very difficult. Moreover, when some shared keys are lost or damaged due to subjective or objective factors, the remaining participants can still jointly recover the secret information through the shared keys they hold. Thus, the secret sharing technology has a wide range of applications in data security, key management, bank network management and other aspects.

A secret sharing scheme with a threshold of (k, n) means sharing a secret message into n shares, where any k or more shares can recover the secret. Shamir [1] first introduced this concept in 1979, in which a secret message is embedded as a constant term of a polynomial of order k − 1, and random numbers are used for the other coefficients of the polynomial. Thien and Lin [2] proposed an image secret sharing scheme, (k, n)-SIS, based on Shamir’s scheme in 2002. K secret pixels are used at a time embedded into the coefficients of a (k − 1) order polynomial in their scheme. In 2004, Lin and Tsai [3] used a steganography approach to embed the shadow image in [2] in a steganographic image, which improves the security of the scheme and has verifiable functionality. In 2007, Yang et al. [4], based on [3], used a hash function instead of parity to rearrange the positions of shared bits and authentication bits to improve the authentication capability and quality of steganographic images. Polynomial based image secret sharing schemes have attracted a lot of attention, and new secret sharing algorithms based on polynomial sharing schemes have been developed.

The concept of an image secret sharing scheme with essential participants, like (t, s, k, n)-ESIS, was first proposed in 2013 by Li et al. [5]. It was designed to address the inconsistent power of participants in the practical application of image secret sharing schemes. Essential participants have higher levels of power than non-essential participants when performing image restoration. This concept has since been implemented by many researchers in different ways [6,7,8,9,10], such as polynomial differentiation in (k, n)-SIS to obtain new polynomials [8]. Considering that a dynamic threshold k has a greater role in some cases, Yuan et al. first proposed a polynomial-based image secret sharing scheme with variable thresholds in 2016 [11]. Liu has improved on this by allowing the threshold to be varied over a range of values [12].

In recent years, image secret sharing schemes with new functions have been researched. In 2016, Maroti Deshmukh et al. proposed a (n, n)-Multi Secret Image Sharing Scheme [13], which uses Boolean XOR and Modular Arithmetic to share n secret images as n shares. This idea has since been continuously improved. [14,15,16,17,18,19] In response to the verifiability of participant identity and shadow, researchers also proposed a verifiable ISS on the polynomial-based ISS [20,21,22,23]. In 2017, Adnan Gutub et al. proposed a counting-based secret sharing technique for multimedia applications [24]. By performing parallel counting on binary secret information, the sharing and recovery of secret information can be achieved quickly. This method provides a new idea for fast sharing of binary images.

For polynomial-based image secret sharing, it often uses Lagrange’s interpolation when performing secret image recovery to reconstruct one polynomial and thus obtain the grayscale values of the original secret image. A simple way to implement Lagrange’s interpolation and construct the polynomial is by solving a linear system of equations. Many researchers just simply adopted this method in the revealing process of the SIS scheme [1,2,3,5,8,10,11,12,16,17,19,22,23]. In practice, many secret image pixels and a large amount of data require solving many linear systems until all pixels are recovered. This requires a large amount of computation, which shows the disadvantage of low efficiency when encrypting larger images. Actually, these linear systems are only different in their constant terms. They have the same coefficient matrix and the coefficient matrix is invertible. This coefficient matrix is only determined by IDs of the participants involved in the revealing process.

This paper proposes a more efficient implementation method of SIS based on matrix operation: using matrix multiplication instead of Lagrange’s interpolation based on the properties of polynomial coefficients. This not only greatly reduces the computational complexity but also improves the efficiency of secret image recovery.

The structure of this article is as follows. The classical secret image sharing scheme proposed by Thien and Lin is reviewed in Section 2. In Section 3, the implementation of the SIS scheme based on a matrix operation is proposed, and Section 4 shows the advantages of our method in efficiency compared with the SIS scheme with Lagrange’s interpolation by experiments. Finally, concise conclusions are formulated in Section 5.

2. Thien and Lin’s Secret Image Sharing Scheme

2.1. Secret Sharing Stage

In Thien and Lin’s image secret sharing scheme, the threshold is k, the number of participants is n, and the participant identifiers are id₁, id₂, … , id_n. The secret image to be shared is S and its number of pixels is w. The allocator first takes n distinct non-zero elements (id₁, id₂, … , id_n) in the finite field as identifiers for the n participants. id₁, id₂, … , id_i and its correspondence with each participant is public. The allocator takes the grayscale value of the first to kth pixels in S as the value of a₀, a₁, … , a_k−1, forming the polynomial:

$$f(x)=(a_0+a_{1}x+a_2{x}^2+\cdots +a_{(k-1)}{x}^{(k-1)})modp$$

(1)

The allocator generates n secrets to share with n participants based on each participant’s identifier as the first pixel Sⁱ₁ of each shadow image Sⁱ₁

$$S^i{}_1=f(i{d}_i),i=1,\cdots ,n$$

(2)

The allocator then repeats the above operation for the kth + 1st to 2kth pixel in S as the value of a₀, a₁, …, a_k−1 to obtain Sⁱ₂, i = 1, … , n. And so on until all pixels in S have been secretly shared to obtain Sⁱ_w/k, i = 1, … , n.

The specific algorithm of Thien and Lin’s image secret sharing scheme is described in Algorithm 1.

Algorithm 1 Thien and Lin’s secret image sharing scheme

Input: S, id1, id2, … , idn Output: S1, S2, … , Sn

Step1: Let j = 1 Step2: The k pixels from k(j−1) + 1 to k(j−1) + k are selected in S and assigned to a0, a1, …, ak−1 Step3: Construct the polynomial (1) where p > 0 Step4: Calculate Sij = f(idi), i = 1, … , n. Step5: If j < w/k, let j = j + 1 and skip to Step2; if j < w/k, skip to Step6. Step6: Using Sij, j = 1, … ,w/k as the pixel gray value of image Si and obtain the shadow image Si, i = 1, … , n.

2.2. Secret Recovery Stage

In Thien and Lin’s image secret recovery scheme [2], secret recovery is performed using k shadow images S¹, S², … , Sⁿ, id₁, id₂, … , id_n are known, taking the first pixel of each shadow image S¹, S², … , Sⁿ.

From the Lagrange’s interpolation formula,

$$f\left(x\right)={\displaystyle \sum _{i=1}^{k}f\left(x_i\right){\displaystyle \prod _{h\ne i}^{1\le h\le k}\frac{\left(x-x_h\right)}{\left(x_i-x_h\right)}}}$$

(3)

we have,

$$f\left(x\right)={\displaystyle \sum _{i=1}^k{S}^i{}_1{\displaystyle \prod _{h\ne i}^{1\le h\le k}\frac{\left(x-i{d}_h\right)}{\left(i{d}_i-i{d}_h\right)}}}$$

(4)

The grayscale value of the first to kth pixel of the secret message as a secret image (a₀, a₁, … , a_k−1) can be obtained according to the coefficient of f (x). Take the second pixel of each shadow image (S¹₂, S²₂, … , S^k₂) for Lagrange’s interpolation.

$$f\left(x\right)={\displaystyle \sum _{i=1}^k{S}^i{}_2{\displaystyle \prod _{h\ne i}^{1\le h\le k}\frac{\left(x-i{d}_h\right)}{\left(i{d}_i-i{d}_h\right)}}}$$

(5)

From the coefficients of f (x), obtain a₀, a₁, … , a_k−1 as the kth + 1st to 2kth pixels in the secret image. Hence, the above process is repeated until all pixels in S have been recovered to obtain the secret image S.

The specific algorithm of Thien and Lin’s image secret recovery scheme is described in Algorithm 2.

Algorithm 2 Thien and Lin’s secret image recovery scheme

Input: id1, id2, …, idk; S1, S2, …, Sk. Output: S

Step1: Denote the jth pixel gray value of Si as Sij and let j = 1. Step2: Substitute id1, id2, … , idk and S1j, S2j, … , Skj into the Lagrange’s interpolation polynomial (4). Step3: Take the coefficient a0, a1, … , ak−1 of f (x), let Sk(j−1) + 1 = a0, Sk(j−1) + 2 = a1, … , Sk(j−1) + k = ak−1. Step4: If j < w/k, let j = j + 1 and skip to Step2; if j = w/k, then skip to Step5. Step5: Get the secret image S

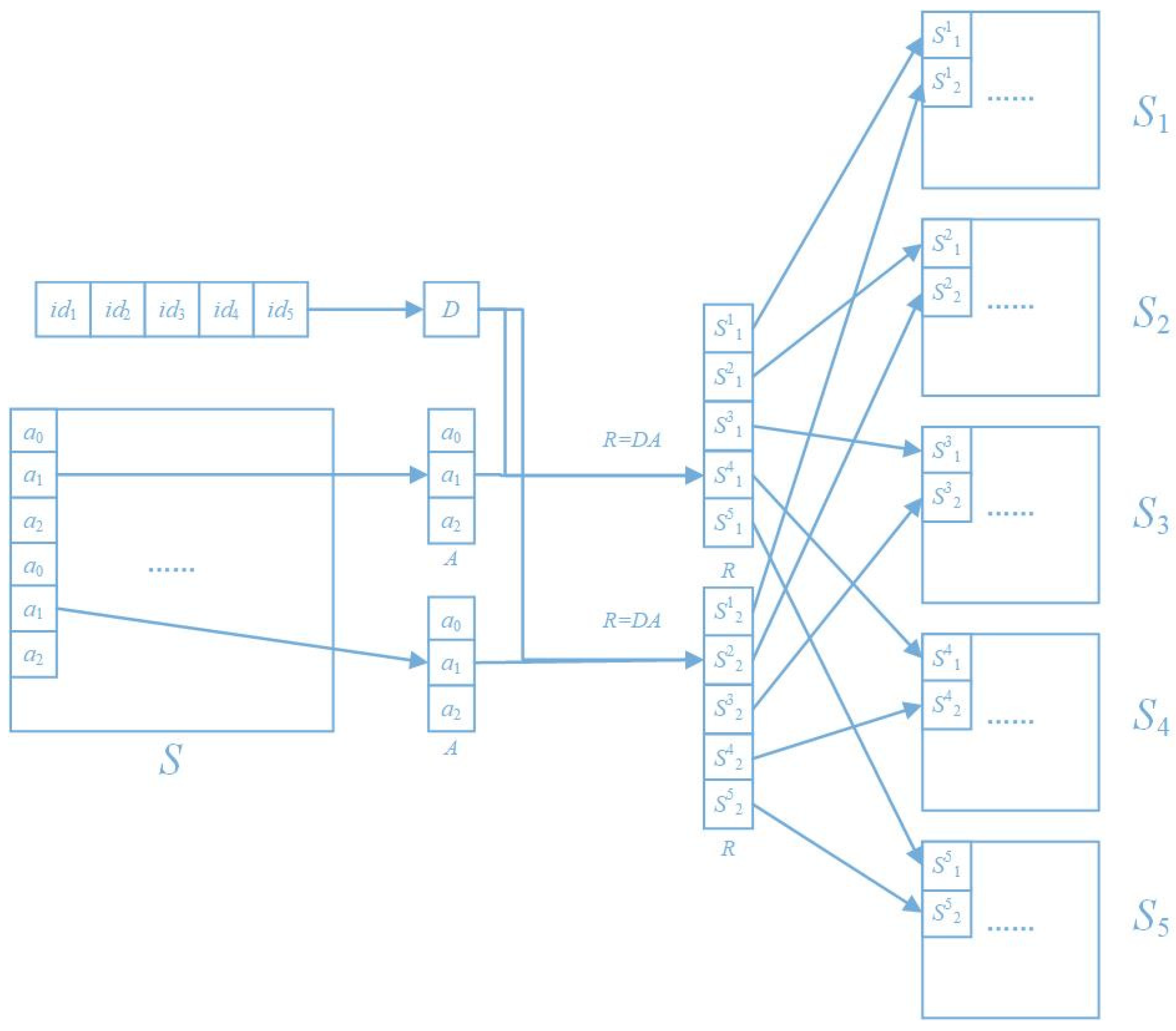
3. Implementation of SIS with Matrix Operation

3.1. Motivation

An image secret sharing scheme is a technique to share a secret image among a group of participants. In a polynomial-based SIS scheme, the shadows are generated by polynomials, and the secret pixels are derived from the coefficients of a Lagrange interpolating polynomial. Actually, to determine the coefficients of a Lagrange interpolating polynomial, we need to solve linear equations. In a real life application, sometimes the secret image has a large size with a high resolution, such as the CT and MR medical image, and a confidential image in military or in commerce. Therefore, in the revealing process, we need to repeatedly solve linear equations many times. This operation is inefficient, since solving linear equations has computation complexity O(n³). Therefore, improving the efficiency of the secret sharing scheme is crucial for the practical application of image secret sharing.

In the case of Thien and Lin’s experiments, due to the large number of pixels in the secret image, the sharing and recovery of the image secret was done in many iterations. The id value in each operation is the same, in particular during the secret image recovery stage, each time the same id value is substituted into the Lagrange’s interpolation polynomial calculation. Optimization and improvement are attempted for this property.

First, in the image secret sharing process as shown in Algorithm 1, Step2, Step3 constructs f(x) = (a₀ + a₁x + a_{2 ×} ² +…+ a_(k−1)x^(k−1))modp and computes Sⁱ_j = f(id_i) separately at i = 1, … , n. This process is equivalent to calculating:

$$\{\begin{array}{c}{a}_0+a_{1}i{d}_1+a_{2}i{d}_1^2+\cdots +a_{k-1}i{d}_1^{k-1}=S^1{}_j\\ a_0+a_{1}i{d}_2+a_{2}i{d}_2^2+\cdots +a_{k-1}i{d}_2^{k-1}=S^2{}_j\\ ⋮\\ a_0+a_{1}i{d}_n+a_{2}i{d}_n^2+\cdots +a_{k-1}i{d}_n^{k-1}=S^n{}_j\end{array}$$

(6)

Equation (6) can be rewritten in the form of the product of matrices in linear algebraic terms:

$$\left(\begin{array}{ccccc}1& i{d}_1& i{d}_1^2& \cdots & i{d}_1^{k-1}\\ 1& i{d}_2& i{d}_2^2& \cdots & i{d}_2^{k-1}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 1& i{d}_n& i{d}_n^2& \cdots & i{d}_n^{k-1}\end{array}\right)\left(\begin{array}{c}{a}_0\\ a_1\\ ⋮\\ a_{k-1}\end{array}\right)=\left(\begin{array}{c}{S}^1{}_j\\ S^2{}_j\\ ⋮\\ S^n{}_j\end{array}\right)$$

(7)

Denote that,

$$D=\left(\begin{array}{ccccc}1& i{d}_1& i{d}_1^2& \cdots & i{d}_1^{k-1}\\ 1& i{d}_2& i{d}_2^2& \cdots & i{d}_2^{k-1}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 1& i{d}_n& i{d}_n^2& \cdots & i{d}_n^{k-1}\end{array}\right)$$

(8)

$$A={\left(\begin{array}{cccc}{a}_0& a_1& \cdots & a_{k-1}\end{array}\right)}^T$$

(9)

$$R={\left(\begin{array}{cccc}{S}^1{}_j& S^2{}_j& \cdots & S^n{}_j\end{array}\right)}^T$$

(10)

The formula (7) can be written as: DA = R.

In the image secret recovery process shown in Algorithm 2, Step2 and Step3 substitute id₁, id₂, … , id_k and S¹_j, S²_j, … , S^k_j into a Lagrange’s interpolation polynomial, and the obtained coefficients a₀, a₁, … , a_k−1 of function f (x) are used as the pixel values of the secret image S. The purpose of this process is to solve for the value of a₀, a₁, … , a_k−1.

Solving for the value of a₀, a₁, … , a_k−1 in terms of linear algebra means solving for the matrix A. If any k rows are taken out of the matrix D to form a new matrix F, the pixel values involved in the recovery form a new vector G. Then we have FA = G. Calculate the inverse matrix F⁻¹ of F, both sides of the equation FA = G are simultaneously multiplied left by F⁻¹ to obtain F⁻¹FA = F⁻¹G. Thus, we get A = F⁻¹G and a₀, a₁, … , a_k−1.

This paper provides a procedure for solving F⁻¹ in [25] is as follows:

Step1: Construct e₁, e₂, e₃ as shown (11) below.

Step2: Solve the system of linear equations separately to obtain x₁, x₂, … , x_k.

Step3: Get F⁻¹ = (x₁, x₂, … , x_k).

$$e_1={\left(\begin{array}{cccc}1& 0& \cdots & 0\end{array}\right)}^T,e_2={\left(\begin{array}{cccc}0& 1& \cdots & 0\end{array}\right)}^T,\cdots ,e_k={\left(\begin{array}{cccc}0& 0& \cdots & 1\end{array}\right)}^T$$

(11)

$$F{x}_1=e_1,F{x}_2=e_2,\cdots ,F{x}_k=e_k$$

(12)

The following scheme is proposed after the theoretical derivation of the feasibility of matrix operations (see Section 3.2).

3.2. Agrithm of Secret Image Sharing Scheme with Matrix Operatio n

The implementation method of matrix operation-based image secret sharing scheme proposed in this paper is as follows: the allocator substitutes id₁, id₂, … , id_n into the (8) construction matrix D, and the grayscale values of the first to kth pixels in S are substituted as the values of a₀, a₁, … , a_k−1 to form the vector A as shown in (9). The allocator calculates R = DA to obtain the vector R as shown. The allocator can generate n secret messages to share with n participants based on each participant’s identifier as the first pixel of each shadow image Sⁱ: Sⁱ₁.

The allocator then repeats the above operation by using the grayscale values of the kth + 1st to 2kth pixels in S as the value of a₀, a₁, … , a_k−1 to obtain Sⁱ₂, i = 1, … , n. Until all pixels in S have been shared to obtain Sⁱ_w/k, i = 1, … , n. Thus, get the shadow image S₁, S₂, … , S_n.

The proposed algorithm of secret image sharing based on matrix operation (ISSMO) is shown in Algorithm 3. When n = 5, k = 3, the schematic diagram of the sharing process is shown in Figure 1.

Algorithm 3 Image secret sharing algorithm based on matrix operations

Input: S; id1, id2, … , idn Output: S1, S2, … , Sk

Step1: Construct matrix D from (8). Step2: Let j = 1 Step3: Select the k pixels from k(j−1) + 1 to k(j−1) + k in S and assign a0, a1, … , ak−1 to each pixel Step4: Construct the column vector A and calculate R = DA. Step5: Get S1j, S2j, … , Snj Step6: If j < w/k, let j = j + 1 and jump to Step3; if j = w/k, skip to Step7. Step7: The shadow image S1, S2, … , Sn is obtained by using Si1, Si2, … , Siw/k as the pixel grayscale value of image Si

When using k shadow images S¹, S², … , S^k for secret recovery, its corresponding participant identifiers id₁, id₂, … , id_n are known. First, the matrix F is obtained by taking the k rows corresponding to id₁, id₂, … , id_k in the matrix D.

$$F=\left(\begin{array}{ccccc}1& i{d}_1& i{d}_1^2& \cdots & i{d}_1^{k-1}\\ 1& i{d}_2& i{d}_2^2& \cdots & i{d}_2^{k-1}\\ 1& i{d}_3& i{d}_3^1& \cdots & i{d}_3^{k-1}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 1& i{d}_k& i{d}_k^2& \cdots & i{d}_k^{k-1}\end{array}\right)$$

(13)

Next, follow the method mentioned in Section 3.1 to derive F⁻¹. Take the first pixel S¹₁, S²₁, … , S^k₁ of each shadow image to form the vector

$$G={\left(\begin{array}{cccc}{S}^1{}_1& S^2{}_1& \cdots & S^k{}_1\end{array}\right)}^T$$

(14)

Then calculate A = G⁻¹R to get the column vector A. From the coefficients of A, we can get the secret information a₀, a₁, … , a_k−1, as the gray value of k pixels from 1 to k of the secret image.

Next, the second pixel S¹₂, S²₂, … , S^k₂ of each shadow image is taken to form the vector G = (S¹₂, S²₂, … , S^k₂)^T, and A = F⁻¹G is calculated to obtain the column vector A. From the coefficients of A, the secret information a₀, a₁, … , a_k−1, as the grayscale values of kth + 1st to 2kth pixels of the secret image, is obtained. The above process is repeated until all pixels of S are secretly recovered and obtain the secret image S.

In this paper, the proposed image secret sharing algorithm based on matrix operations is shown in Algorithm 4. A schematic diagram of the recovery process is shown in Figure 2. We assume that the identities of the participants involved in recovery are id₁, id₂, and id₃.

Algorithm 4 Image secret recovery algorithm based on matrix operations

Input: id1, id2, …, idk, S1, S2, … , Sk Output: S

Step1: The matrix F is obtained by taking out the k rows corresponding to id1, id2, … , idk in the matrix D. Step2: Calculate the inverse matrix F−1 of F according to the method in Section 3.1. Motivation Step3: Denote the jth pixel gray value of Si as Sij and let j = 1. Step4: Construct G = (S1j, S2j, … , Skj)T and compute A = F−1G to obtain the column vector A. Step5: Get a0, a1, … , ak−1 from (9), let Sk(j−1) + 1 = a0, Sk(j−1) + 2 = a0, … , Sk(j−1) + k = ak−1 Step6: If j < w/k, then let j = j + 1 and skip to Step4; if j = w/k, skip to Step7. Step7: Obtain S by using S1, S2, … , Sw. as the pixel gray value of the image S.

3.3. Example of (3, 3)-SIS

This section will assign id₁ = 1, id₂ = 2, id₃ = 3 to each participant’s identity without loss of generality under the finite fields GF (2⁸) and GF (251), respectively. Share a set of secret pixels through an image secret sharing scheme with threshold conditions: k = 3, n = 3. The shared secret pixel grayscale values are: 25, 156, 7, 210, 54, 134.The secret image recovery algorithm based on matrix operations is shown more specifically by the following example.

3.3.1. Example of (3, 3)-SIS Scheme in GF (2⁸)

In the SISMO sharing process, first construct matrix D according to the value of each participant’s identity.

$$D=\left(\begin{array}{ccc}1& 1& 1\\ 1& 2& 4\\ 1& 3& 9\end{array}\right)$$

(15)

Construct the column vector A₁ = (25 156 7)^T using the first three numbers in the secret message. Through R₁ = DA₁ to get the column vector R₁.

$$R_1=D{A}_1=\left(\begin{array}{ccc}1& 1& 1\\ 1& 2& 4\\ 1& 3& 9\end{array}\right)\left(\begin{array}{c}25\\ 156\\ 7\end{array}\right)=\left(\begin{array}{c}130\\ 32\\ 187\end{array}\right)$$

(16)

The first element of the three shadow images S¹₁ = 130, S²₁ = 32, S³₁ = 187 can be obtained according to the elements of the vector R. Then use the last three numbers in the secret message to construct the column vector A₂ = (210 54 134)^T, and R₂ is obtained by calculate R₂ = DA₂.

In the recovery process, first construct the matrix F according to the formula.

$$F=\left(\begin{array}{ccc}1& 1& 1\\ 1& 2& 4\\ 1& 3& 9\end{array}\right)$$

(17)

Then construct e₁, e₂, e₃.

$$e_1={\left(\begin{array}{ccc}1& 0& 0\end{array}\right)}^T,e_2={\left(\begin{array}{ccc}0& 1& 0\end{array}\right)}^T,e_3={\left(\begin{array}{ccc}0& 0& 1\end{array}\right)}^T$$

(18)

Solve the linear equations Fx₁ = e₁, Fx₂ = e₂, … , Fx_k = e_k separately as follows.

$$\begin{array}{l} \left(\begin{array}{ccc}1& 1& 1\\ 1& 2& 4\\ 1& 3& 9\end{array}\right)\left(\begin{array}{c}{x}_{1,1}\\ x_{1,2}\\ x_{1,3}\end{array}\right)=\left(\begin{array}{c}1\\ 0\\ 0\end{array}\right)\\ \left(\begin{array}{ccc}1& 1& 1\\ 1& 2& 4\\ 1& 3& 9\end{array}\right)\left(\begin{array}{c}{x}_{2,1}\\ x_{2,2}\\ x_{2,3}\end{array}\right)=\left(\begin{array}{c}0\\ 1\\ 0\end{array}\right)\\ \left(\begin{array}{ccc}1& 1& 1\\ 1& 2& 4\\ 1& 3& 9\end{array}\right)\left(\begin{array}{c}{x}_{3,1}\\ x_{3,2}\\ x_{3,3}\end{array}\right)=\left(\begin{array}{c}0\\ 0\\ 1\end{array}\right)\end{array}$$

(19)

Get x₁, x₂, x₃ and calculate F⁻¹ as follows.

$$x_1=\left(\begin{array}{c}1\\ 122\\ 122\end{array}\right),x_2=\left(\begin{array}{c}1\\ 245\\ 244\end{array}\right),x_3=\left(\begin{array}{c}1\\ 143\\ 142\end{array}\right)$$

(20)

$$F^{-1}=\left(x_1 x_2 x_3\right)=\left(\begin{array}{ccc}1& 1& 1\\ 122& 245& 143\\ 122& 244& 142\end{array}\right)$$

(21)

The next step is to construct G₁ = (130 32 187)^T and calculate A₁ = F⁻¹G₁.

$$A_1=F^{-1}{G}_1=\left(\begin{array}{ccc}3& 248& 1\\ 123& 4& 124\\ 126& 250& 126\end{array}\right)\left(\begin{array}{c}130\\ 32\\ 187\end{array}\right)=\left(\begin{array}{c}25\\ 156\\ 7\end{array}\right)$$

(22)

The first three numbers of the secret information are known. Next is to build G₂ = (98 156 44)^T and calculate A₂ = F⁻¹G₂.

$$A_2=F^{-1}{G}_2=\left(\begin{array}{ccc}3& 248& 1\\ 123& 4& 124\\ 126& 250& 126\end{array}\right)\left(\begin{array}{c}98\\ 156\\ 44\end{array}\right)=\left(\begin{array}{c}210\\ 54\\ 134\end{array}\right)$$

(23)

So far, the complete secret information is obtained: 25, 156, 7, 210, 54, 134.

3.3.2. Example of (3, 3)-SIS Scheme in GF (251)

In the secret sharing process, first construct the matrix D as shown,

$$D=\left(\begin{array}{ccc}1& 1& 1\\ 1& 2& 4\\ 1& 3& 9\end{array}\right)$$

(24)

Then construct the column vector A₃ = (25 156 7) ^T, calculate R₃ as follows and get the first pixel of the three shadow images: S¹₁ = 188, S²₁ = 114, S³₁ = 54.

$$R_3=D{A}_3=\left(\begin{array}{ccc}1& 1& 1\\ 1& 2& 4\\ 1& 3& 9\end{array}\right)\left(\begin{array}{c}25\\ 156\\ 7\end{array}\right)=\left(\begin{array}{c}188\\ 114\\ 54\end{array}\right)$$

(25)

Next, construct the column vector A₄ = (210 54 134) ^T and calculate R₄ according to the following formula, S¹₂ = 147, S²₂ = 101, S³₂ = 72, we can get S₁ = (188 147) ^T, S₂ = (144 101) ^T, S₃ = (54 72) ^T,

$$R_4=D{A}_4=\left(\begin{array}{ccc}1& 1& 1\\ 1& 2& 4\\ 1& 3& 9\end{array}\right)\left(\begin{array}{c}210\\ 54\\ 134\end{array}\right)=\left(\begin{array}{c}147\\ 101\\ 72\end{array}\right)$$

(26)

In the recovery process, first construct the matrix F and e₁, e₂, e₃ as shown in the formulas:

$$F=\left(\begin{array}{ccc}1& 1& 1\\ 1& 2& 4\\ 1& 3& 9\end{array}\right)$$

(27)

$$e_1={\left(\begin{array}{ccc}1& 0& 0\end{array}\right)}^T,e_2={\left(\begin{array}{ccc}0& 1& 0\end{array}\right)}^T,e_3={\left(\begin{array}{ccc}0& 0& 1\end{array}\right)}^T$$

(28)

Solve the linear equations Fx₁ = e₁, Fx₂ = e₂, … , Fx_k = e_k separately as shown:

$$\begin{array}{l} \left(\begin{array}{ccc}1& 1& 1\\ 1& 2& 4\\ 1& 3& 9\end{array}\right)\left(\begin{array}{c}{x}_{1,1}\\ x_{1,2}\\ x_{1,3}\end{array}\right)=\left(\begin{array}{c}1\\ 0\\ 0\end{array}\right)\\ \left(\begin{array}{ccc}1& 1& 1\\ 1& 2& 4\\ 1& 3& 9\end{array}\right)\left(\begin{array}{c}{x}_{2,1}\\ x_{2,2}\\ x_{2,3}\end{array}\right)=\left(\begin{array}{c}0\\ 1\\ 0\end{array}\right)\\ \left(\begin{array}{ccc}1& 1& 1\\ 1& 2& 4\\ 1& 3& 9\end{array}\right)\left(\begin{array}{c}{x}_{3,1}\\ x_{3,2}\\ x_{3,3}\end{array}\right)=\left(\begin{array}{c}0\\ 0\\ 1\end{array}\right)\end{array}$$

(29)

Get x₁, x₂, x₃ and F⁻¹ as shown:

$$x_1=\left(\begin{array}{c}3\\ 123\\ 126\end{array}\right),x_2=\left(\begin{array}{c}248\\ 4\\ 250\end{array}\right),x_3=\left(\begin{array}{c}1\\ 124\\ 126\end{array}\right)$$

(30)

$$F^{-1}=(x_1 x_2{x}_3)=\left(\begin{array}{ccc}3& 248& 1\\ 123& 4& 124\\ 126& 250& 126\end{array}\right)$$

(31)

Then construct G₃ = (118 114 54)^T and calculate A₃, construct G₄ = (147 101 72)^T and calculate A₄ as follows:

$$A_3=F^{-1}{G}_3=\left(\begin{array}{ccc}3& 248& 1\\ 123& 4& 124\\ 126& 250& 126\end{array}\right)\left(\begin{array}{c}118\\ 114\\ 54\end{array}\right)=\left(\begin{array}{c}25\\ 156\\ 7\end{array}\right)$$

(32)

Finally, the secret information: 25, 156, 7, 210, 54, 134 is obtained. Thus it can be seen that the restoration process is more effective compared with the original secret information.

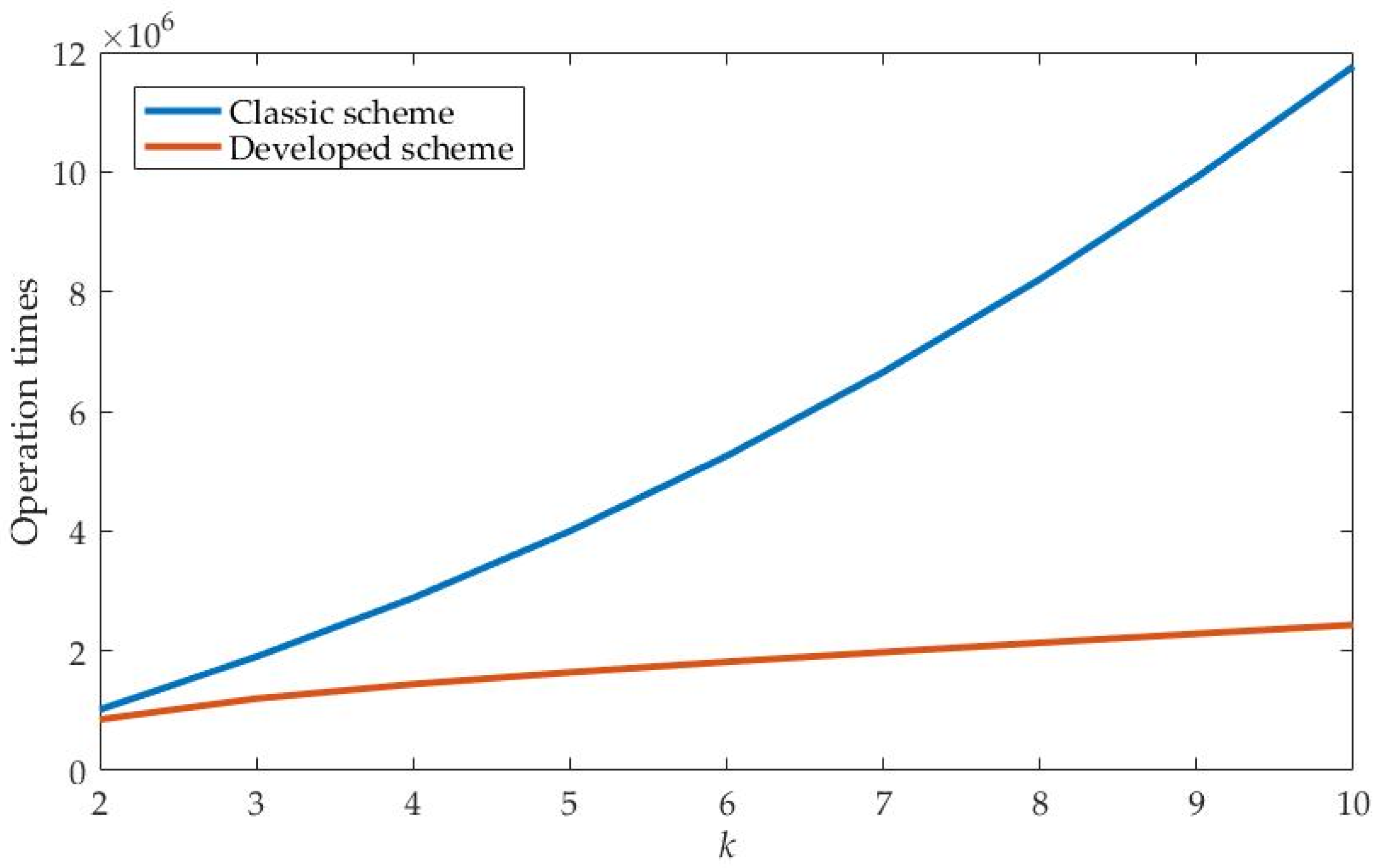
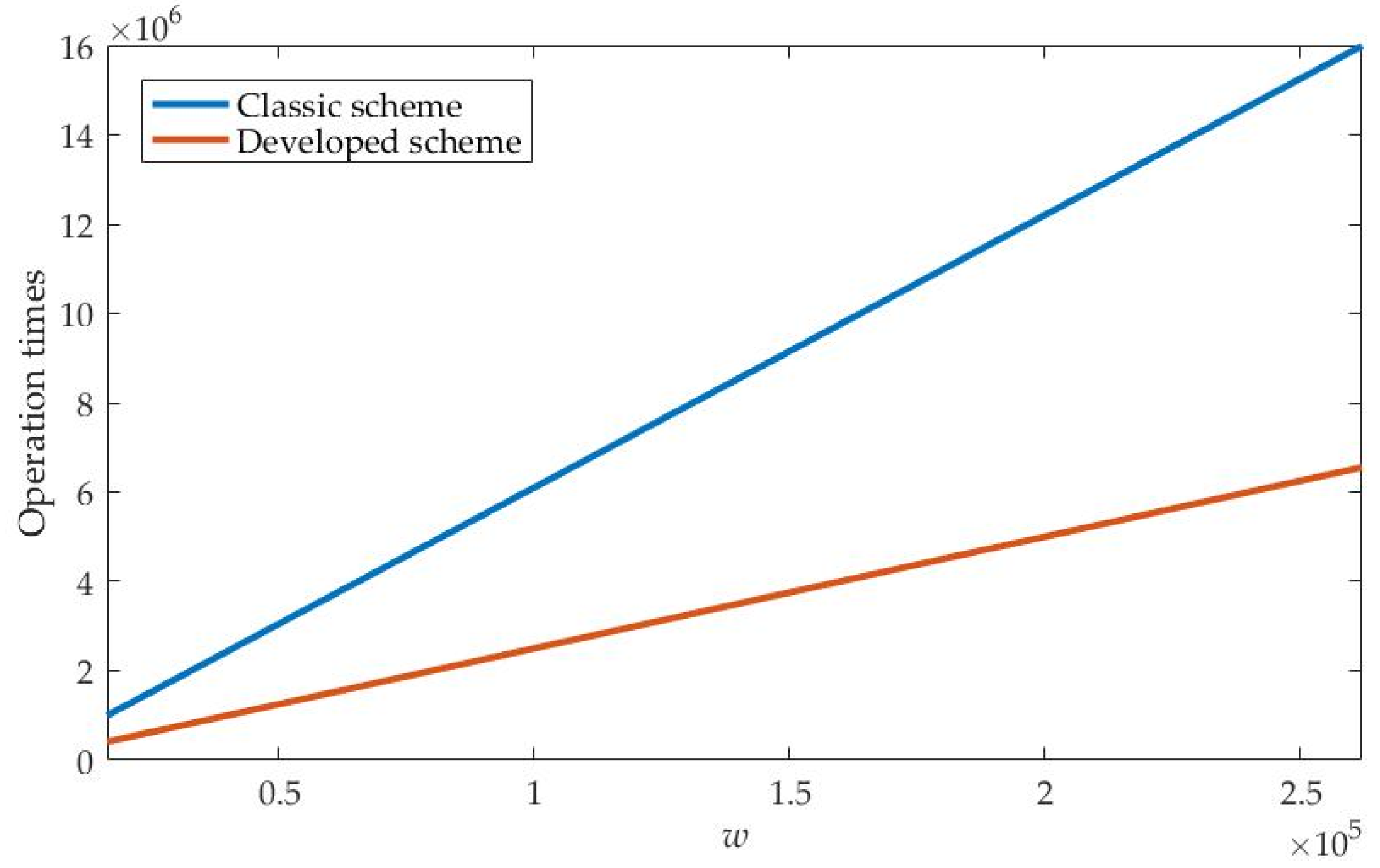
3.4. Computational Efficiency Analysis

The complicated step of the calculation in this scheme is to construct the matrix D and calculate D⁻¹. Since id₁, id₂, … , id_n and its correspondence with P₁, P₂, … , P_n are public in the secret sharing process, the process of constructing the matrix D and calculating D⁻¹ only needs to be done before recovering the first set of pixels. In this way, the process of recovering all secret pixels afterwards only needs to be performed to calculate A = D⁻¹S, which greatly reduced the computation complexity of the secret recovery. In this section, the efficiency of the two algorithms is analyzed in terms of the number of operations (+, −, ×, ÷) required by the two schemes.

3.4.1. Efficiency Analysis of Thien and Lin’s (k, n)-SIS Scheme

In Thien and Lin’s image secret sharing process, as described in Algorithm 1, no operation occurred in Step1 to Step3 and it takes place in Step4, the calculation of a polynomial of degree k−1 is performed. The number of operations that have occurred is:

$$O_1{S}_1=\frac{1}{2}n{k}^2+\frac{1}{2}nk-n$$

(33)

Step5 makes a judgment and loops Step1 to Stpe4 for w/k times; no operation occurs in Step6. After collating the above steps, the number of operations occurred during the secret sharing of images of Thien and Lin is obtained as:

$$O_{1}S=\frac{w}{k}{O}_1{S}_1=\frac{1}{2}wnk+\frac{1}{2}wn-wn{k}^{-1}$$

(34)

In Thien and Lin’s image secret recovery process Algorithm 2, no operation occurs in Step1. Step2 involves the calculation of Lagrange’s interpolation polynomials, which is equivalent to constructing a linear equation system first, and then solving it. The number of operations that occurred in this step is:

$$O_1{R}_1=\left(\frac{1}{2}{\mathrm{k}}^3+\frac{1}{2}{k}^2\right)+\left(\frac{2}{3}{k}^3+\frac{1}{2}{k}^2-\frac{7}{6}k\right)=\frac{7}{6}{k}^3+k^2-\frac{7}{6}k$$

(35)

No operation occurred in Step3, Step1~Step3 are looped for w/k times after the judgment of Step4. Collating all the steps, the number of operations occurred during the Thien and Lin’s image secret recovery process is:

$$O_{1}R=\frac{w}{k}{O}_1{R}_1=\frac{7}{6}w{k}^2+wk-\frac{7}{6}w$$

(36)

Integrating the number of operations of the sharing process with the recovery process, the total number of operations occurring in Thien and Lin’s image secret sharing scheme is:

$$O_1=O_{1}S+O_{1}R=\frac{7}{6}w{k}^2+\left(\frac{1}{2}n+1\right)wk+\frac{1}{2}wn-\frac{7}{6}w-wn{k}^{-1}$$

(37)

3.4.2. Efficiency Analysis of (k, n)-SIS Scheme Based on Matrix Operations

In Algorithm 3, a secret sharing process for images based on matrix operations, the number of operations that occur in Step1 is:

$$O_2{S}_1=\frac{1}{2}n{k}^2-\frac{3}{2}nk+n$$

(38)

No operation occurs in Step2 and Step3 and one matrix multiplication operation occurs in Step4. Since it is a matrix of n rows and k columns multiplied by a column vector of k rows, the number of addition operations that occur is:

$$O_2{S}_2=2nk-2n$$

(39)

No operation occurred in step5 and Step7, and Step6 made a judgment and cycled Step3 to Step5 w/k times. In summary, the total number of operations that occurred in Algorithm 3, a secret sharing process for images based on matrix operations, is:

$$O_{2}S=O_2{S}_1+\frac{w}{k}{O}_2{S}_2=\frac{1}{2}n{k}^2-\frac{3}{2}nk+2wn+n-2wn{k}^{-1}$$

(40)

And in the matrix operation-based image secret recovery process Algorithm 4, the number of operations occurring in Step1 is:

$$O_2{R}_1=\frac{1}{2}{k}^3-\frac{3}{2}{k}^2+k$$

(41)

In Step2, the process of solving the system of linear equations is performed k times and the total number of operations performed is:

$$O_2{R}_2=\frac{2}{3}{k}^4+\frac{1}{2}{k}^3-\frac{7}{6}{k}^2$$

(42)

No operation occurs in Step3. The number of operations that occur in Step4 is:

$$O_2{R}_3=2k^2-k$$

(43)

In Step5, no operation occurred. Step6 made a judgment and looped Step4 and Step5 w/k times. No operation occurred in Step7. To sum up, the total number of operations occurred in Algorithm 4 of the image secret recovery process based on matrix operations is:

$$O_{2}R=O_2{R}_1+O_2{R}_2+\frac{w}{k}{O}_2{R}_3=\frac{2}{3}{k}^4+k^3-\frac{8}{3}{k}^2+\left(1+2w\right)k-w$$

(44)

By integrating the number of operations of the sharing process with the recovery process, the total number of operations occurring in the implementation of image secret sharing scheme based on matrix operations is:

$$\begin{array}{l}{O}_2=O_{2}S+O_{2}R\\ =\frac{2}{3}{k}^4+k^3+\left(\frac{n}{2}-\frac{8}{3}\right)k^2+\left(2w-\frac{3}{2}n+1\right)k+2wn-w+n-wn{k}^{-1}\end{array}$$

(45)

3.4.3. Operation Time Comparison

In this paper, the number of operations of the classical secret sharing scheme compared with the secret sharing scheme proposed in this paper is plotted using MATLAB 2016a. Figure 3 shows the image of the number of operations performed by the two different schemes varying with the value of k, where w = 256 × 256, n = 10, and k is taken from 2 to 10.

And Figure 4 shows the images of the number of operations performed by the two schemes with different w when w is taken from 128 × 128 to 512 × 512 and k = 5, n = 10.

According to the comparison of operation times as shown in Figure 3 and Figure 4, the number of operations of the implementation method proposed in this paper is smaller than that of Thien and Lin’s image secret sharing scheme in the range of threshold values from 2 to 10 and secret image sizes from 128 × 128 to 512 × 512. Moreover, the difference between the number of operations of both methods is proportional to the threshold and secret image size.

4. Experiments and Comparisons

4.1. Feasibility Experiment of the Implementation Proposed in This Paper

The implementation of image secret sharing scheme based on matrix operations proposed in this paper was programmed using MATLAB 2016a. The (5, 7)-secret sharing is performed on the original image Figure 5a with image size 256 × 256 pixels, and the values of id₁, id₂, … , id₇ are: id_i = i, i = 1, … , 7.

The shadow images obtained from the experiment are shown in Figure 5b. The secret image is recovered according to the matrix operation-based image secret recovery algorithm, and the recovered image obtained is shown in Figure 5c. Comparing the recovered Figure 5a with Figure 5c shows that the image secret sharing scheme based on matrix operation proposed in this paper is effective.

4.2. Comparison Experiment of Computing Efficiency under Different Thresholds

In this experiment, a 256 × 256 size image is used for secret sharing, and the same shares are selected for secret sharing using two different implementation methods: Thien and Lin’s image secret sharing scheme based on Lagrange’s polynomials, and the implementation of image secret sharing scheme based on matrix operations for secret sharing and recovery. The running times of the two schemes are calculated separately.

The experiment used MATLAB2016 for programming, and selected GF(2⁸) as the finite field. The irreducible polynomial used in the operation is x⁸ + x⁴ + x³ + x² + x+1.The running time is recorded when the threshold is k = 2, 3, 4, 5 respectively, as shown in the following

Table 1. Running time with different threshold in GF(2⁸).

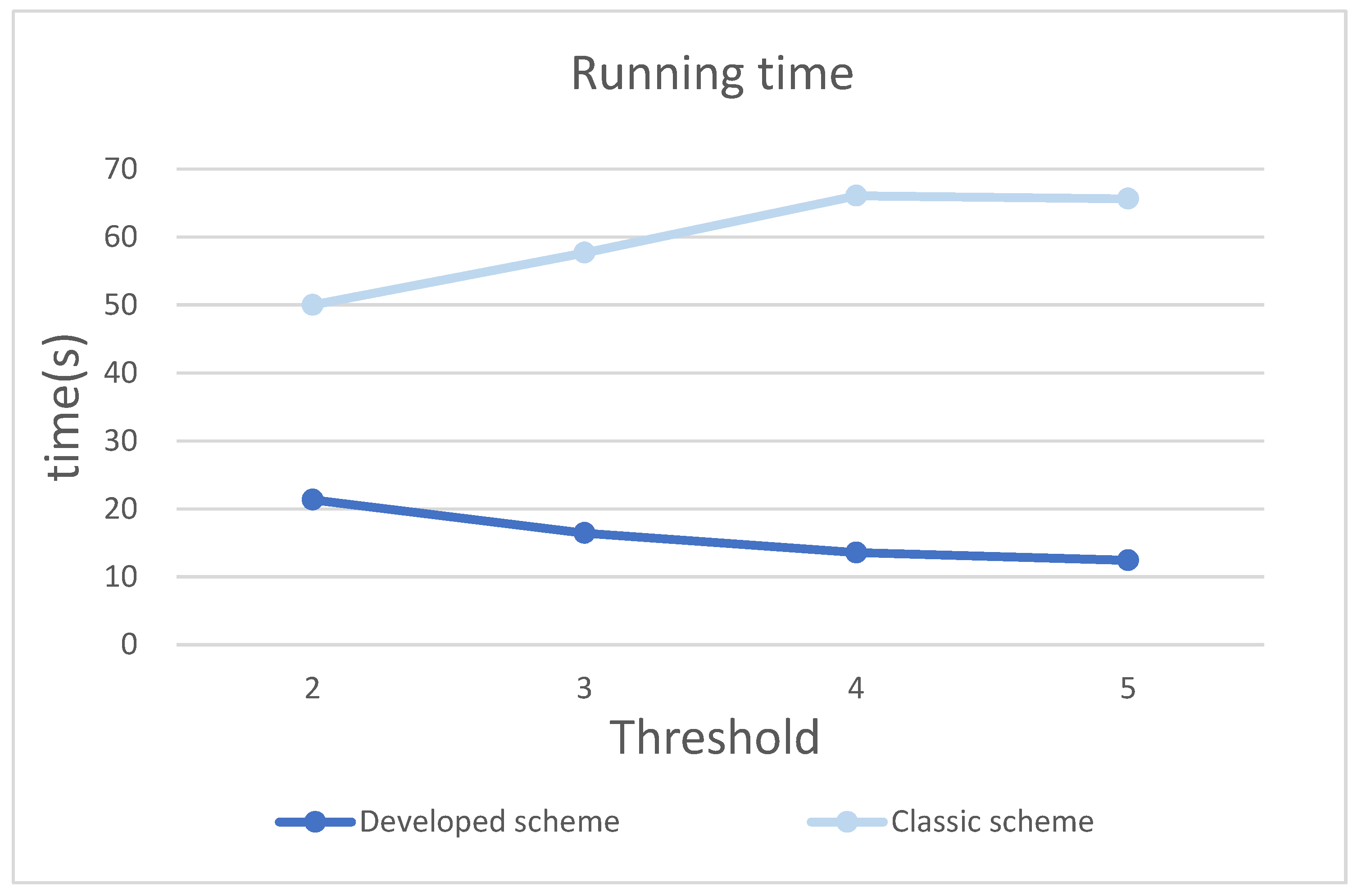
	Threshold k = 2	Threshold k = 3	Threshold k = 4	Threshold k = 5
Developed scheme Running time (second)	21.3185	16.4230	13.5538	12.4131
Classic scheme Running time (second)	50.0028	57.6745	66.0707	65.6301

, and the comparison of the running time is shown in Figure 6.

Under the finite field GF(251), the running times for threshold values of k = 2, 3, 4, 5 are recorded respectively as shown in the following

Table 2. Running time in different threshold in GF(251).

	Threshold k = 2	Threshold k = 3	Threshold k = 4	Threshold k = 5
Developed scheme Running time (second)	0.3453	0.2960	0.2448	0.2524
Classic scheme Running time (second)	0.4062	0.3633	0.3287	0.3622

, and the running time comparison graphs are shown in Figure 7.

4.3. Comparison Experiments of Computing Efficiency under Secret Image Recovery of Different Sizes

This experiment used images of different sizes for secret sharing. The same shares are selected to perform (5, 5) secret sharing and recovery using two different secret sharing schemes: the classical Thien and Lin’s image secret sharing scheme (Classic scheme), and the matrix operation-based secret sharing scheme (Developed scheme) proposed in this paper, and the running times of the two are calculated separately.

The experiments were programmed using MATLAB2016 with the finite field selection GF(2⁸). The irreducible polynomial used in the operation is x⁸ + x⁴ + x³ + x² + x+1.The running times when the secret image size is 128 × 128, 192 × 192, 256 × 256, 384 × 384, 512 × 512 are recorded respectively as shown in the following

Table 3. Running times with different sizes in GF(2⁸).

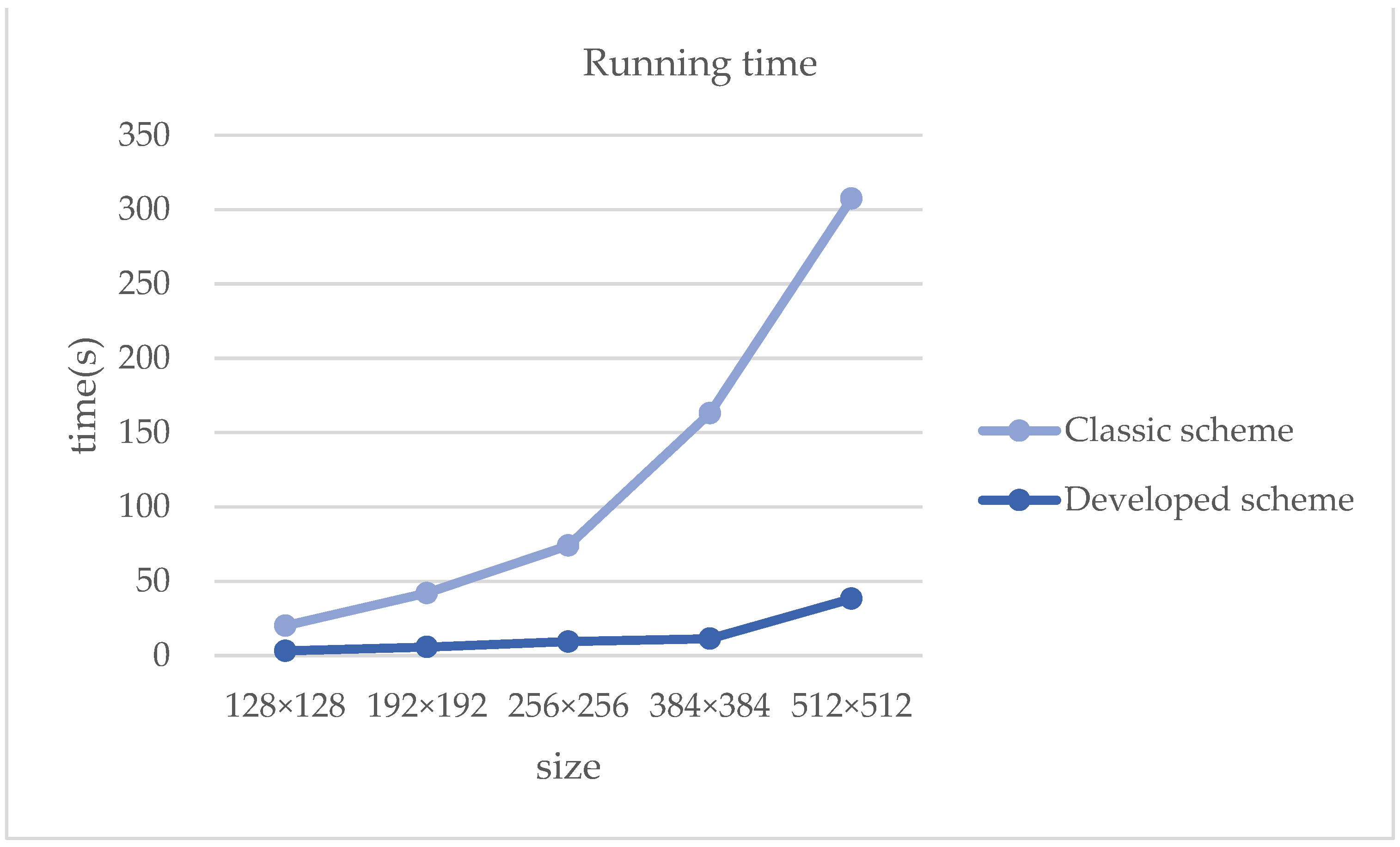
	Secret Image Size 128 × 128	Secret Image Size 192 × 192	Secret Image Size 256 × 256	Secret Image Size 384 × 384	Secret Image Size 512 × 512
Developed scheme Running time (second)	3.1263	5.7193	9.3425	11.3432	38.2335
Classic scheme Running time (second)	16.9145	36.3079	64.6712	151.6507	269.1568

, and the running time comparison graphs are shown in Figure 8.

Under the finite field GF(251), the running time when the recording size is 128 × 128, 192 × 192, 256 × 256, 384 × 384, 512 × 512 is shown in the following

Table 4. Running times with different sizes in GF(251).

	Secret Image Size 128 × 128	Secret Image Size 192 × 192	Secret Image Size 256 × 256	Secret Image Size 384 × 384	Secret Image Size 512 × 512
Developed scheme Running time (second)	0.1517	0.1778	0.2208	0.3558	0.5600
Classic scheme Running time (second)	0.2008	0.2203	0.4060	0.5803	0.9693

, and the running time comparison chart is shown in Figure 9.

4.4. Analysis of Experimental Results

A comparison of the operation times of the two schemes under GF(251) and GF(2⁸) finite fields with different thresholds k is shown respectively in Section 4.2. Section 4.3 shows the comparison of the computation time of the two schemes under two finite fields (GF(251) and GF(2⁸)) with different secret image sizes. Experiments show that the operation time of the matrix operation-based secret image sharing scheme proposed in this paper is smaller than that of the polynomial interpolation-based secret image sharing scheme. And the time difference between the two schemes is proportional to the threshold value k and the size of the secret image. The experimental results are consistent with the theoretical results in Section 3.4.

5. Conclusions

Thien and Lin’s ISS scheme uses Lagrange’s interpolation polynomials in the secret reconstruction process, which requires a lot of calculations in practice, which affects the efficiency of the schemes. This paper proposes an implementation method of a secret sharing scheme based on matrix operations instead of the traditional polynomial calculation method to reduce the number of operations in the revealing process. Compared with Lagrange’s interpolation, the proposed implementation method has better performance through theoretical analysis, which is also confirmed by experimental results. The implementation in this paper is still valid for general polynomial based secret sharing schemes, and may have better results for image secret sharing schemes with different functions. For example, for an image secret sharing scheme with essential participants, the implementation of this paper may provide new ideas for building essential participants. This direction still deserves further research.