Cost-Sensitive Broad Learning System for Imbalanced Classification and Its Medical Application
Abstract
:1. Introduction
- A cost-sensitive BLS framework, CS-BLS, is proposed to improve the performance of standard BLS on imbalanced classification problems;
- Four CS-BLS approaches are proposed, and each approach adopts a different penalty factor calculation method based on inverse class frequency or effective numbers;
- A systemic experimental study on the CS-BLS is conducted, in which two commonly used datasets with different imbalanced ratios and a clinical ultrasound image diagnosis dataset are utilized.
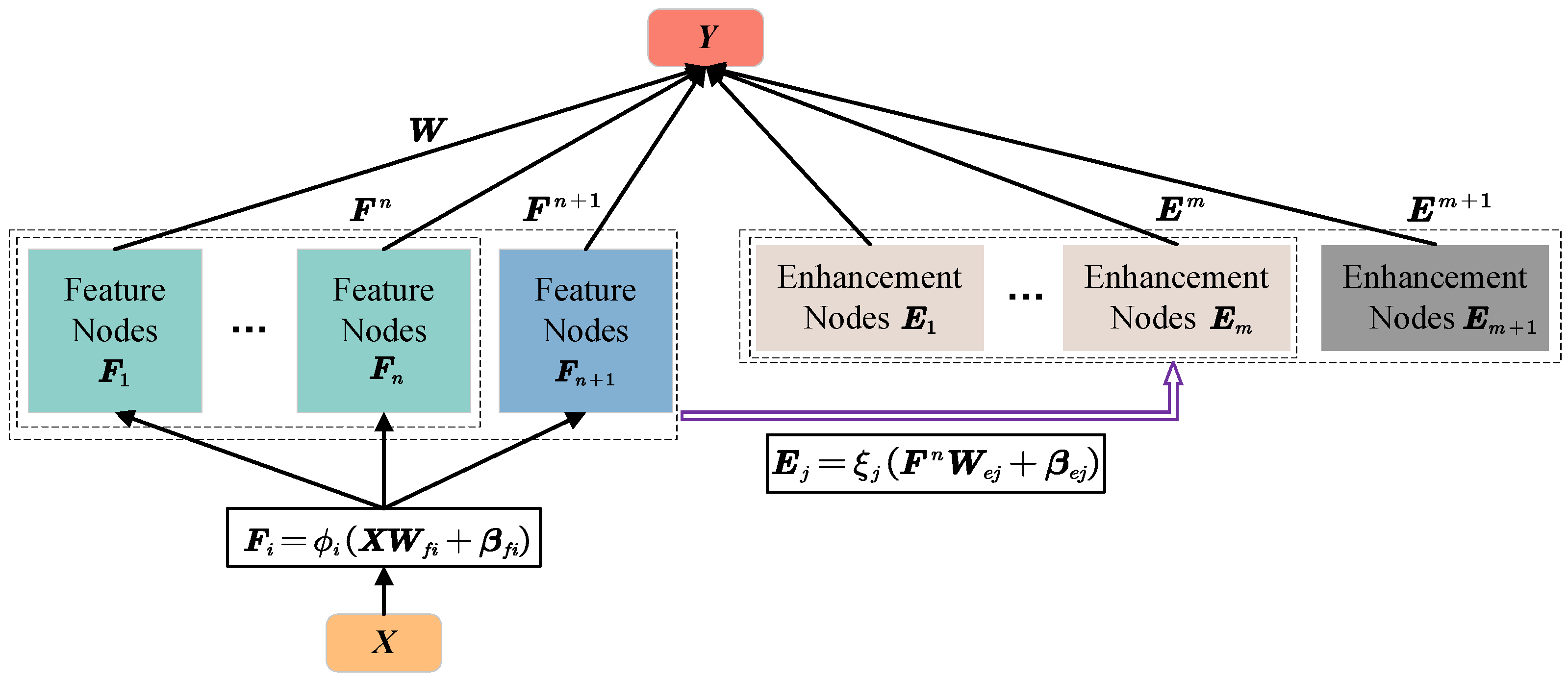
2. Proposed Method
2.1. Cost-Sensitive Broad Learning System (CS-BLS)
2.2. Methods for Calculating Weighted Penalty Factors
2.2.1. Calculation Methods Based on Inverse Class Frequency
2.2.2. Calculation Methods Based on Effective Numbers
3. Experiments and Results
3.1. Evaluation Metrics
3.2. Experiments on Imbalanced MNIST
- (1)
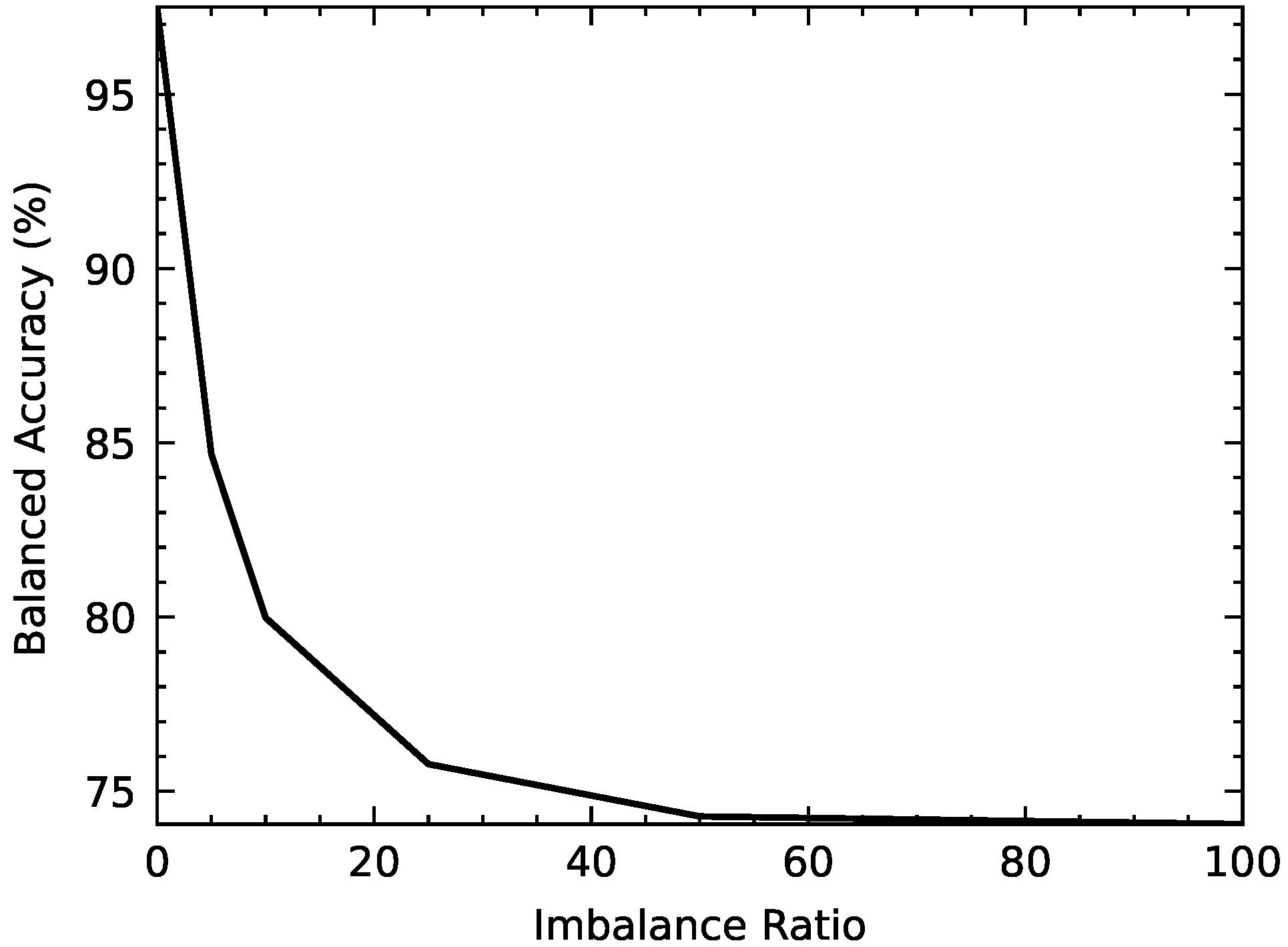
- Comparison of the standard BLS under different imbalance ratios demonstrates that the performance of the standard BLS gradually decreases as IR increases. Taking B_ACC as an example, it drops from 84.66% (IR = 5) to 74.06% (IR = 100). The other evaluation metrics of standard BLS, as shown in Figure 5, have the same trend as the increase of IR.
- (2)
- The proposed CS-BLS methods have better performance than the standard BLS on different values of IR. Taking B_ACC and MCC as examples, on average, the B_ACC of the proposed four CS-BLS methods is higher than the standard BLS by 12.30% (5.68–15.74%), and the MCC of the CS-BLS methods and the BLS are 0.8774 (0.8285–0.8974) and 0.7453 (0.7163–0.8312), respectively. The other evaluation metrics of the CS-BLS methods and the BLS show the same pattern as B_ACC and MCC. The results demonstrate the superiority of the CS-BLS methods over the standard BLS in handling imbalanced data.
- (3)
- It can be found that the performance of different CS-BLS methods is relatively close, and no unique CS-BLS method can achieve the best performance for all the metrics and imbalance ratios.
- (1)
- In general, the performance of the CS-BLS has improved as the number of feature nodes and enhancement nodes increases to a finite number. Taking B_ACC as an example again, the average B_ACC of the CS-BLS methods increases from 85.56% (84.29–86.69%) on the broad structure (20, 5, 100) to 90.02% (88.38–90.82%) on the broad structure (50, 15, 500). However, the performance of BLS is quite stable at a relatively low value (74.36% on average).
- (2)
- The proposed CS-BLS has better performance than the standard BLS on each compared broad structure. Taking B_ACC and MCC as examples, on average, the B_ACC of the proposed CS-BLS methods is higher than the standard BLS by 14.31% (11.32–15.74%), and the MCC values of the CS-BLS methods and BLS are 0.8760 (0.8416–0.8904) and 0.7234 (0.7222–0.7239), respectively. The other evaluation metrics of the CS-BLS methods and the BLS show the same pattern as B_ACC and MCC.
- (3)
- With different broad structures, the performance of the four CS-BLS methods is quite close with a slight variance.
3.3. Experiments on Imbalanced Small NORB
- (1)
- The results demonstrate that the performance of the standard BLS gradually decreases as IR increases. Taking B_ACC as an example, it drops from 74.91% (IR = 5) to 62.78% (IR = 100). The other evaluation metrics of standard BLS, as shown in Figure 7, have the same trend as the increase of IR.
- (2)
- The proposed CS-BLS methods have better performance than the standard BLS on different values of IR. Taking B_ACC and MCC as examples, on average, the B_ACC of the proposed CS-BLS methods is higher than the standard BLS by 12.62% (5.24–17.07%), and the MCC of the CS-BLS and BLS are 0.7350 (0.6222–0.8195) and 0.5869 (0.5552–0.6906), respectively. The other evaluation metrics of the CS-BLS and the BLS show the same pattern as B_ACC and MCC.
- (3)
- The performance of the four different CS-BLS methods is relatively close, and no unique CS-BLS method can achieve the best performance for all the mentioned imbalance ratios.
- (1)
- In general, the performance of the CS-BLS has improved as the number of feature nodes and enhancement nodes increases to a finite number. Taking B_ACC as an example again, the average B_ACC of the CS-BLS increases from 63.25% (59.67–67.12%) on broad structure (20, 5, 100) to 79.74% (77.45–82.18%) on broad structure (50, 15, 200). However, the performance of BLS is quite stable at a relatively low value (61.88% on average).
- (2)
- The proposed CS-BLS methods have better performance than the standard BLS on each compared broad structure. Taking B_ACC and MCC as examples, the average B_ACC of the proposed CS-BLS methods is higher than the standard BLS by 14.12% (6.92–16.97%), and the MCC of the CS-BLS (on average) and BLS are 0.7060 (0.5574–0.7502) and 0.5449 (0.4750–0.5658), respectively. The other evaluation metrics of the CS-BLS and the BLS show the same pattern as B_ACC and MCC.
- (3)
- With different broad structures, the performance of the four CS-BLS methods is quite close with a slight variance.
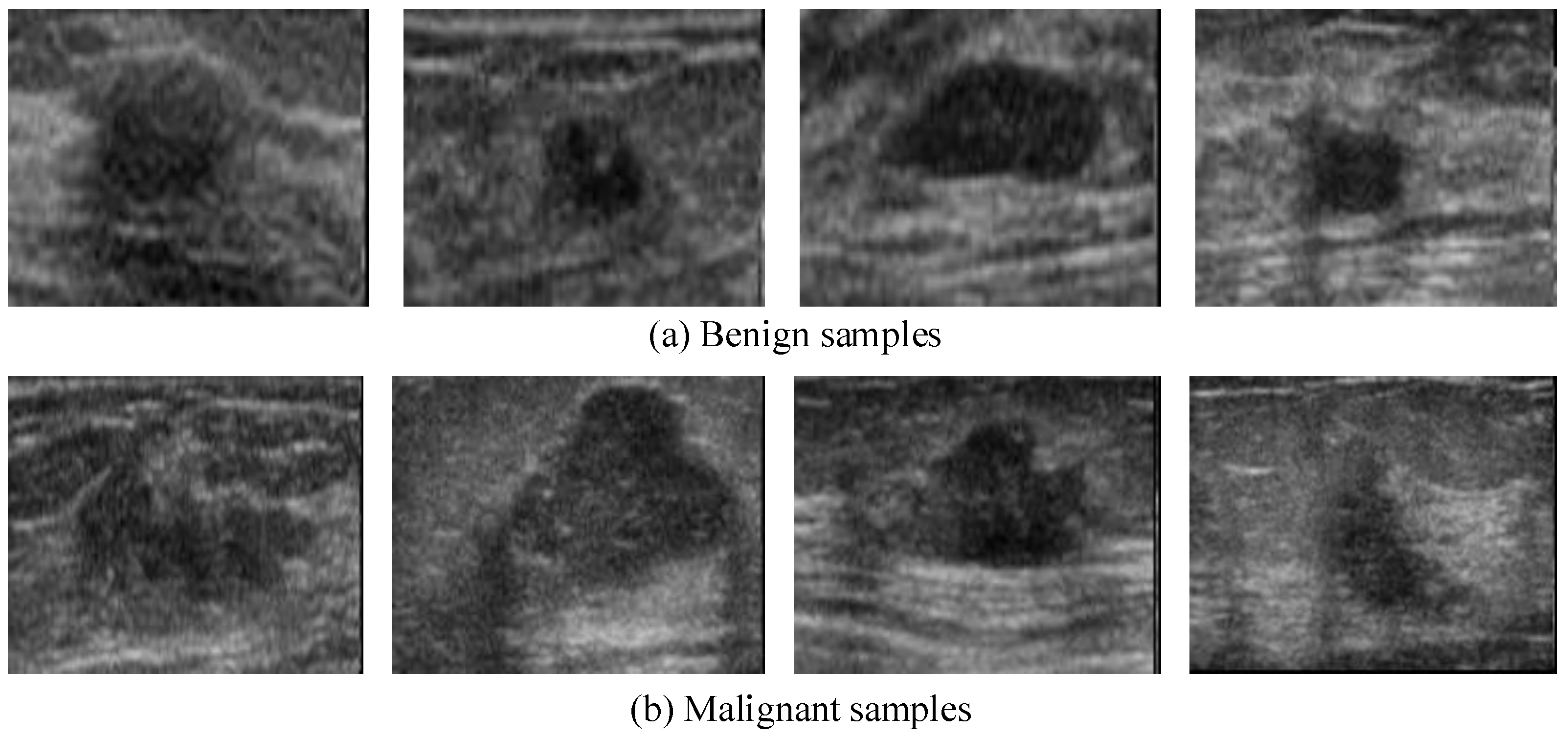
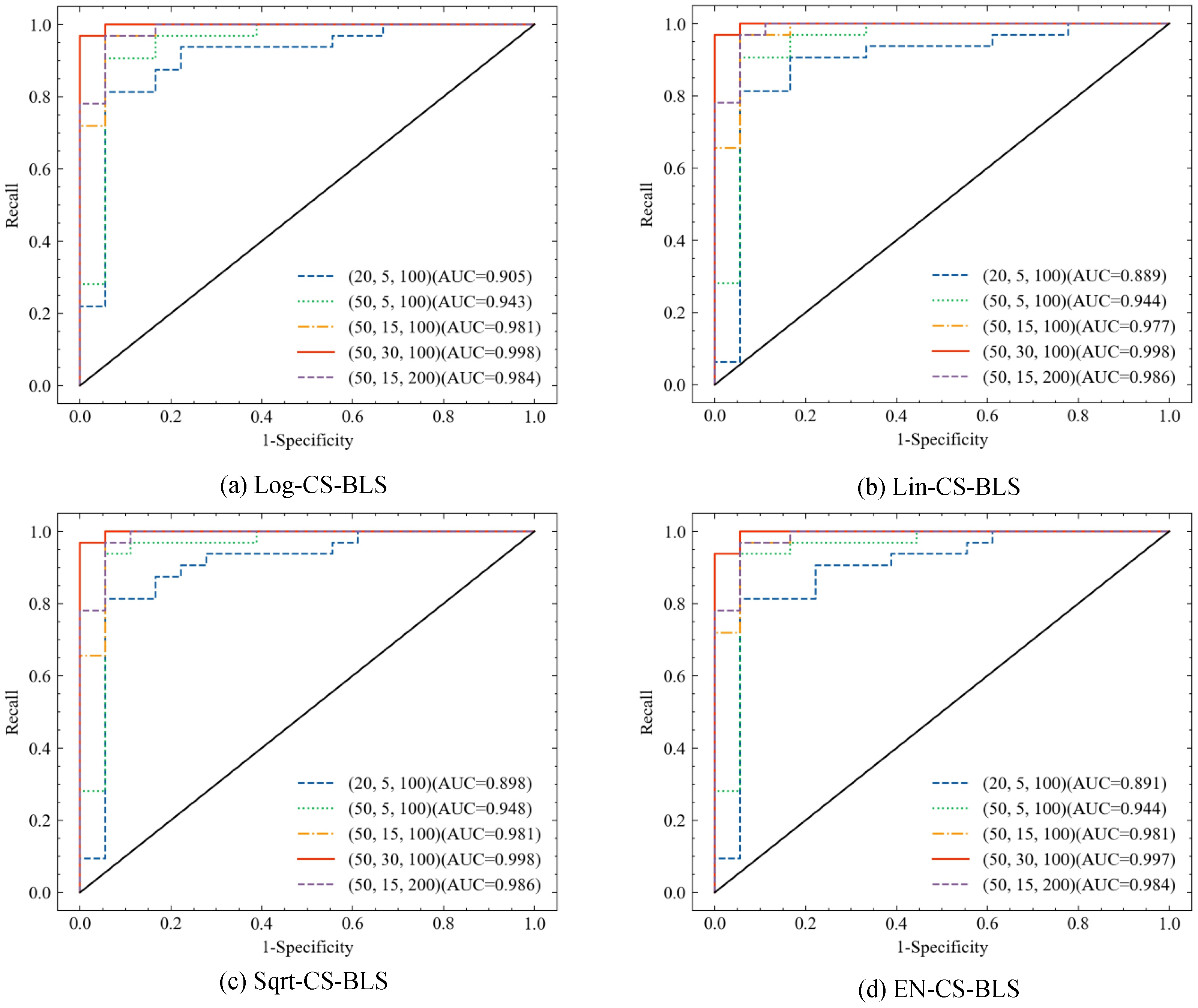
3.4. Experiments on Breast Ultrasound Cancer Diagnosis
- (1)
- In general, the performance of the CS-BLS is improved as the number of hidden nodes increases to a finite number. Taking B_ACC as an example again, the average B_ACC of the CS-BLS increases from 85.00% (82.00–86.00%) on broad structure (20, 5, 100) to 96.50% (96.00–98.00%) on broad structure (50, 30, 100). The other evaluation metrics show the same pattern with B_ACC.
- (2)
- With different broad structures, the performance of the four CS-BLS methods is quite close with little variance.
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, C.L.P.; Liu, Z. Broad learning system: An effective and efficient incremental learning system without the need for deep architecture. IEEE Trans. Neural Netw. Learn. Syst. 2017, 29, 10–24. [Google Scholar] [CrossRef]
- Pao, Y.H.; Park, G.H.; Sobajic, D.J. Learning and generalization characteristics of the random vector functional-link net. Neurocomputing 1994, 6, 163–180. [Google Scholar] [CrossRef]
- Wong, P.K.; Yao, L.; Yan, T.; Choi, I.C.; Yu, H.H.; Hu, Y. Broad learning system stacking with multi-scale attention for the diagnosis of gastric intestinal metaplasia. Biomed. Signal Process. Control 2022, 73, 103476. [Google Scholar] [CrossRef]
- Jiang, S.B.; Wong, P.K.; Guan, R.; Liang, Y.; Li, J. An efficient fault diagnostic method for three-phase induction motors based on incremental broad learning and non-negative matrix factorization. IEEE Access 2019, 7, 17780–17790. [Google Scholar] [CrossRef]
- Huang, H.; Zhang, T.; Yang, C.; Chen, C.P. Motor learning and generalization using broad learning adaptive neural control. IEEE Trans. Ind. Electron. 2019, 67, 8608–8617. [Google Scholar] [CrossRef]
- Xu, L.; Chen, C.L.P.; Han, R. Sparse Bayesian Broad Learning System for Probabilistic Estimation of Prediction. IEEE Access 2020, 8, 56267–56280. [Google Scholar] [CrossRef]
- Feng, S.; Chen, C.P. Broad learning system for control of nonlinear dynamic systems. In Proceedings of the 2018 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Miyazaki, Japan, 7–10 October 2018; pp. 2230–2235. [Google Scholar]
- Huang, C.; Huang, X.; Fang, Y.; Xu, J.; Qu, Y.; Zhai, P.; Fan, L.; Yin, H.; Xu, Y.; Li, J. Sample imbalance disease classification model based on association rule feature selection. Pattern Recognit. Lett. 2020, 133, 280–286. [Google Scholar] [CrossRef]
- Gao, X.; Chen, Z.; Tang, S.; Zhang, Y.; Li, J. Adaptive weighted imbalance learning with application to abnormal activity recognition. Neurocomputing 2016, 173, 1927–1935. [Google Scholar] [CrossRef]
- Zhao, B.; Zhang, X.; Li, H.; Yang, Z. Intelligent fault diagnosis of rolling bearings based on normalized CNN considering data imbalance and variable working conditions. Knowl.-Based Syst. 2020, 199, 105971. [Google Scholar] [CrossRef]
- Somasundaram, A.; Reddy, S. Parallel and incremental credit card fraud detection model to handle concept drift and data imbalance. Neural Comput. Appl. 2019, 31, 3–14. [Google Scholar] [CrossRef]
- Rodrigues, P.S. Breast Ultrasound Image. Mendeley Data 2018. [Google Scholar] [CrossRef]
- Kaur, H.; Pannu, H.S.; Malhi, A.K. A Systematic Review on Imbalanced Data Challenges in Machine Learning: Applications and Solutions. ACM Comput. Surv. 2019, 52, 1–36. [Google Scholar] [CrossRef] [Green Version]
- Leevy, J.L.; Khoshgoftaar, T.M.; Bauder, R.A.; Seliya, N. A survey on addressing high-class imbalance in big data. J. Big Data 2018, 5, 42. [Google Scholar] [CrossRef]
- Johnson, J.M.; Khoshgoftaar, T.M. Survey on deep learning with class imbalance. J. Big Data 2019, 6, 27. [Google Scholar] [CrossRef]
- Vitter, J.S. Random sampling with a reservoir. ACM Trans. Math. Softw. 1985, 11, 37–57. [Google Scholar] [CrossRef] [Green Version]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Chen, S.; He, H.; Garcia, E.A. RAMOBoost: Ranked minority oversampling in boosting. IEEE Trans. Neural Netw. 2010, 21, 1624–1642. [Google Scholar] [CrossRef]
- He, H.; Bai, Y.; Garcia, E.A.; Li, S. ADASYN: Adaptive synthetic sampling approach for imbalanced learning. In Proceedings of the 2008 IEEE International Joint Conference on Neural Networks, Hong Kong, China, 1–8 June 2008; pp. 1322–1328. [Google Scholar]
- Han, H.; Wang, W.Y.; Mao, B.H. Borderline-SMOTE: A new over-sampling method in imbalanced data sets learning. In Proceedings of the International Conference on Intelligent Computing (ICIC), Hefei, China, 23–25 August 2005; pp. 878–887. [Google Scholar]
- Barua, S.; Islam, M.M.; Yao, X.; Murase, K. MWMOTE–Majority weighted minority oversampling technique for imbalanced data set learning. IEEE Trans. Knowl. Data Eng. 2012, 26, 405–425. [Google Scholar] [CrossRef]
- Lin, W.C.; Tsai, C.F.; Hu, Y.H.; Jhang, J.S. Clustering-based undersampling in class-imbalanced data. Inf. Sci. 2017, 409, 17–26. [Google Scholar] [CrossRef]
- Barandela, R.; Rangel, E.; Sánchez, J.S.; Ferri, F.J. Restricted decontamination for the imbalanced training sample problem. In Proceedings of the Iberoamerican Congress on Pattern Recognition, Havana, Cuba, 26–29 November 2003; pp. 424–431. [Google Scholar]
- Zheng, Y.D.; Liu, Z.; Lu, T.; Wang, L. Dynamic sampling networks for efficient action recognition in videos. IEEE Trans. Image Process. 2020, 29, 7970–7983. [Google Scholar] [CrossRef]
- Fu, B.; He, J.; Zhang, Z.; Qiao, Y. Dynamic Sampling Network for Semantic Segmentation. In Proceedings of the AAAI Conference on Artificial Intelligence (AAAI), Midtown, NY, USA, 7–12 February 2020; Volume 34, pp. 10794–10801. [Google Scholar]
- Zong, W.; Huang, G.B.; Chen, Y. Weighted extreme learning machine for imbalance learning. Neurocomputing 2013, 101, 229–242. [Google Scholar] [CrossRef]
- Krawczyk, B.; Woźniak, M.; Schaefer, G. Cost-sensitive decision tree ensembles for effective imbalanced classification. Appl. Soft Comput. 2014, 14, 554–562. [Google Scholar] [CrossRef] [Green Version]
- Aurelio, Y.S.; de Almeida, G.M.; de Castro, C.L.; Braga, A.P. Learning from imbalanced data sets with weighted cross-entropy function. Neural Process. Lett. 2019, 50, 1937–1949. [Google Scholar] [CrossRef]
- Wong, M.L.; Seng, K.; Wong, P.K. Cost-sensitive ensemble of stacked denoising autoencoders for class imbalance problems in business domain. Expert Syst. Appl. 2020, 141, 112918. [Google Scholar] [CrossRef]
- Wang, S.; Liu, W.; Wu, J.; Cao, L.; Meng, Q.; Kennedy, P.J. Training deep neural networks on imbalanced data sets. In Proceedings of the 2016 International Joint Conference on Neural Networks (IJCNN), Vancouver, BC, Canada, 24–29 July 2016; pp. 4368–4374. [Google Scholar]
- Lin, T.Y.; Goyal, P.; Girshick, R.; He, K.; Dollár, P. Focal loss for dense object detection. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2980–2988. [Google Scholar]
- Liu, X.Y.; Wu, J.; Zhou, Z.H. Exploratory undersampling for class-imbalance learning. IEEE Trans. Syst. Man Cybern. Cybern. 2008, 39, 539–550. [Google Scholar]
- Chawla, N.V.; Lazarevic, A.; Hall, L.O.; Bowyer, K.W. SMOTEBoost: Improving prediction of the minority class in boosting. In Proceedings of the European Conference on Principles of Data Mining and Knowledge Discovery (PKDD), Cavtat-Dubrovnik, Croatia, 22–26 September 2003; pp. 107–119. [Google Scholar]
- Havaei, M.; Davy, A.; Warde-Farley, D.; Biard, A.; Courville, A.; Bengio, Y.; Pal, C.; Jodoin, P.M.; Larochelle, H. Brain tumor segmentation with deep neural networks. Med. Image Anal. 2017, 35, 18–31. [Google Scholar] [CrossRef] [Green Version]
- Malakar, S.; Ghosh, M.; Bhowmik, S.; Sarkar, R.; Nasipuri, M. A GA based hierarchical feature selection approach for handwritten word recognition. Neural Comput. Appl. 2020, 32, 2533–2552. [Google Scholar] [CrossRef]
- Bacanin, N.; Stoean, R.; Zivkovic, M.; Petrovic, A.; Rashid, T.A.; Bezdan, T. Performance of a novel chaotic firefly algorithm with enhanced exploration for tackling global optimization problems: Application for dropout regularization. Mathematics 2021, 9, 2705. [Google Scholar] [CrossRef]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef] [Green Version]
- Zhang, T.L.; Chen, R.; Yang, X.; Guo, S. Rich feature combination for cost-based broad learning system. IEEE Access 2018, 7, 160–172. [Google Scholar] [CrossRef]
- Chu, F.; Liang, T.; Chen, C.P.; Wang, X.; Ma, X. Weighted broad learning system and its application in nonlinear industrial process modeling. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 3017–3031. [Google Scholar] [CrossRef]
- Zhang, T.; Li, Y.; Chen, R. Evolutionary-Based Weighted Broad Learning System for Imbalanced Learning. In Proceedings of the 2019 IEEE 14th International Conference on Intelligent Systems and Knowledge Engineering (ISKE), Dalian, China, 14–16 November 2019; pp. 607–615. [Google Scholar]
- Gan, M.; Zhu, H.T.; Chen, G.Y.; Chen, C.P. Weighted generalized cross-validation-based regularization for broad learning system. IEEE Trans. Cybern. 2020, 1–9. [Google Scholar] [CrossRef]
- Yang, K.; Yu, Z.; Chen, C.P.; Cao, W.; You, J.J.; San Wong, H. Incremental Weighted Ensemble Broad Learning System For Imbalanced Data. IEEE Trans. Knowl. Data Eng. 2021. [Google Scholar] [CrossRef]
- Zheng, Y.; Chen, B.; Wang, S.; Wang, W. Broad Learning System Based on Maximum Correntropy Criterion. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 3083–3097. [Google Scholar] [CrossRef]
- Chen, G.; Choi, W.; Yu, X.; Han, T.; Chandraker, M. Learning efficient object detection models with knowledge distillation. In Proceedings of the 31st International Conference on Neural Information Processing Systems (NIPS), Long Beach, CA, USA, 4–9 December 2017; pp. 742–751. [Google Scholar]
- Lertnattee, V.; Theeramunkong, T. Analysis of inverse class frequency in centroid-based text classification. In Proceedings of the IEEE International Symposium on Communications and Information Technology (ISCIT), Sapporo, Japan, 26–29 October 2004; Volume 2, pp. 1171–1176. [Google Scholar]
- Cui, Y.; Jia, M.; Lin, T.Y.; Song, Y.; Belongie, S. Class-balanced loss based on effective number of samples. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 9268–9277. [Google Scholar]
- Sung, H.; Ferlay, J.; Siegel, R.L.; Laversanne, M.; Soerjomataram, I.; Jemal, A.; Bray, F. Global cancer statistics 2020: GLOBOCAN estimates of incidence and mortality worldwide for 36 cancers in 185 countries. CA Cancer J. Clin. 2021, 71, 209–249. [Google Scholar] [CrossRef]
- Cronin, K.A.; Lake, A.J.; Scott, S.; Sherman, R.L.; Noone, A.M.; Howlader, N.; Henley, S.J.; Anderson, R.N.; Firth, A.U.; Ma, J.; et al. Annual Report to the Nation on the Status of Cancer, Part I: National Cancer Statistics. Cancer 2018, 124, 2785–2800. [Google Scholar] [CrossRef] [Green Version]
- Chen, M.; Shi, X.; Zhang, Y.; Wu, D.; Guizani, M. Deep feature learning for medical image analysis with convolutional autoencoder neural network. IEEE Trans. Big Data 2017, 7, 750–758. [Google Scholar] [CrossRef]
- Kermany, D.S.; Goldbaum, M.; Cai, W.; Valentim, C.C.S.; Liang, H.; Baxter, S.L.; Mckeown, A.; Yang, G.; Wu, X.; Yan, F. Identifying Medical Diagnoses and Treatable Diseases by Image-Based Deep Learning. Cell 2018, 172, 1122–1131. [Google Scholar] [CrossRef]




| Hyperparameter | Value |
|---|---|
| Imbalance ratio (IR) | 5, 10, 25, 50, 100, 250, 500, 1500 |
| Weight decay | 0.0005 |
| Learning rate | 0.001 |
| Maximum epoch | 100 |
| Broad structure | (20, 5, 100), (50, 5, 100), (50, 15, 100), (50, 30, 100), (50, 15, 200) |
| Nonlinear activation function | tanh |
| Structure | Method | B_ACC | MCC | F-Score | Recall | Precision | AUC |
|---|---|---|---|---|---|---|---|
| (20, 5, 100) | BLS | 74.24% | 0.7222 | 0.7110 | 74.25% | 70.32% | 0.9766 |
| Log-CS-BLS | 84.29% | 0.8276 | 0.8445 | 84.29% | 85.31% | 0.9869 | |
| Lin-CS-BLS | 86.47% | 0.8517 | 0.8667 | 86.47% | 86.59% | 0.9877 | |
| Sqr-CS-BLS | 84.78% | 0.8331 | 0.8504 | 84.78% | 85.54% | 0.9865 | |
| EN-CS-BLS | 86.69% | 0.8541 | 0.8690 | 86.69% | 87.00% | 0.9880 | |
| (50, 5, 100) | BLS | 74.55% | 0.7251 | 0.7134 | 74.54% | 70.10% | 0.9765 |
| Log-CS-BLS | 88.60% | 0.8743 | 0.8871 | 88.60% | 88.79% | 0.9907 | |
| Lin-CS-BLS | 88.14% | 0.8697 | 0.8820 | 88.14% | 88.33% | 0.9901 | |
| Sqr-CS-BLS | 88.40% | 0.8722 | 0.8850 | 88.40% | 88.69% | 0.9905 | |
| EN-CS-BLS | 88.99% | 0.8794 | 0.8905 | 88.99% | 89.15% | 0.9909 | |
| (50, 15, 100) | BLS | 74.32% | 0.7230 | 0.7118 | 74.32% | 70.23% | 0.9760 |
| Log-CS-BLS | 89.57% | 0.8852 | 0.8969 | 89.57% | 89.72% | 0.9915 | |
| Lin-CS-BLS | 88.72% | 0.8774 | 0.8891 | 88.72% | 89.17% | 0.9909 | |
| Sqr-CS-BLS | 89.83% | 0.8884 | 0.8994 | 89.83% | 89.90% | 0.9916 | |
| EN-CS-BLS | 89.97% | 0.8913 | 0.9011 | 89.97% | 90.23% | 0.9917 | |
| (50, 30, 100) | BLS | 74.41% | 0.7239 | 0.7126 | 74.41% | 70.17% | 0.9757 |
| Log-CS-BLS | 89.74% | 0.8885 | 0.8984 | 89.74% | 90.11% | 0.9926 | |
| Lin-CS-BLS | 88.38% | 0.8733 | 0.8856 | 88.38% | 89.01% | 0.9912 | |
| Sqr-CS-BLS | 89.23% | 0.8821 | 0.8937 | 89.23% | 89.49% | 0.9914 | |
| EN-CS-BLS | 87.72% | 0.8671 | 0.8795 | 87.72% | 88.57% | 0.9903 | |
| (50, 15, 200) | BLS | 74.31% | 0.7230 | 0.7119 | 74.31% | 70.27% | 0.9760 |
| Log-CS-BLS | 89.72% | 0.8868 | 0.8981 | 89.72% | 89.78% | 0.9919 | |
| Lin-CS-BLS | 89.10% | 0.8806 | 0.8914 | 89.10% | 89.31% | 0.9913 | |
| Sqr-CS-BLS | 89.28% | 0.8820 | 0.8942 | 89.28% | 89.47% | 0.9917 | |
| EN-CS-BLS | 88.83% | 0.8785 | 0.8893 | 88.83% | 89.21% | 0.9915 |
| Structure | Method | B_ACC | MCC | F-Score | Recall | Precision | AUC |
|---|---|---|---|---|---|---|---|
| (20, 5, 100) | BLS | 56.33% | 0.4750 | 0.5051 | 56.33% | 47.93% | 0.8597 |
| Log-CS-BLS | 59.67% | 0.5204 | 0.5560 | 58.85% | 73.43% | 0.9175 | |
| Lin-CS-BLS | 66.75% | 0.5946 | 0.6658 | 66.59% | 72.09% | 0.9252 | |
| Sqr-CS-BLS | 59.47% | 0.5156 | 0.5669 | 58.71% | 71.12% | 0.9175 | |
| EN-CS-BLS | 67.12% | 0.5991 | 0.6701 | 66.91% | 72.86% | 0.9255 | |
| (50, 5, 100) | BLS | 63.07% | 0.5604 | 0.5653 | 63.07% | 52.40% | 0.9125 |
| Log-CS-BLS | 76.87% | 0.7165 | 0.7631 | 77.18% | 78.37% | 0.9530 | |
| Lin-CS-BLS | 77.16% | 0.7146 | 0.7716 | 77.08% | 77.43% | 0.9525 | |
| Sqr-CS-BLS | 78.40% | 0.7340 | 0.7822 | 78.68% | 79.66% | 0.9528 | |
| EN-CS-BLS | 76.34% | 0.7063 | 0.7647 | 76.19% | 77.93% | 0.9508 | |
| (50, 15, 100) | BLS | 62.80% | 0.5563 | 0.5602 | 62.80% | 51.53% | 0.9161 |
| Log-CS-BLS | 80.41% | 0.7573 | 0.7996 | 80.32% | 80.62% | 0.9581 | |
| Lin-CS-BLS | 75.35% | 0.6960 | 0.7496 | 75.15% | 76.51% | 0.9464 | |
| Sqr-CS-BLS | 78.81% | 0.7418 | 0.7843 | 78.81% | 80.81% | 0.9562 | |
| EN-CS-BLS | 77.04% | 0.7171 | 0.7695 | 77.11% | 78.67% | 0.9537 | |
| (50, 30, 100) | BLS | 63.51% | 0.5658 | 0.5664 | 63.51% | 52.10% | 0.9165 |
| Log-CS-BLS | 85.31% | 0.8176 | 0.8515 | 85.18% | 85.66% | 0.9710 | |
| Lin-CS-BLS | 74.53% | 0.6900 | 0.7414 | 74.05% | 77.74% | 0.9561 | |
| Sqr-CS-BLS | 80.49% | 0.7598 | 0.7957 | 80.05% | 81.08% | 0.9691 | |
| EN-CS-BLS | 76.01% | 0.7037 | 0.7581 | 75.66% | 77.48% | 0.9519 | |
| (50, 15, 200) | BLS | 62.77% | 0.5560 | 0.5599 | 62.77% | 51.50% | 0.9165 |
| Log-CS-BLS | 79.88% | 0.7502 | 0.7964 | 79.70% | 80.28% | 0.9594 | |
| Lin-CS-BLS | 77.45% | 0.7249 | 0.7644 | 77.40% | 78.51% | 0.9583 | |
| Sqr-CS-BLS | 82.18% | 0.7803 | 0.8217 | 82.12% | 83.35% | 0.9649 | |
| EN-CS-BLS | 79.47% | 0.7453 | 0.7910 | 79.32% | 79.76% | 0.9591 |
| Structure | Method | B_ACC | MCC | F-Score | Recall | Precision |
|---|---|---|---|---|---|---|
| (20, 5, 100) | BLS | 78.00% | 0.5618 | 0.7726 | 79.17% | 77.05% |
| Log-CS-BLS | 86.00% | 0.7290 | 0.8553 | 87.85% | 85.10% | |
| Lin-CS-BLS | 86.00% | 0.7290 | 0.8553 | 87.85% | 85.10% | |
| Sqr-CS-BLS | 86.00% | 0.7005 | 0.8498 | 85.42% | 84.63% | |
| EN-CS-BLS | 82.00% | 0.6281 | 0.8108 | 82.29% | 80.54% | |
| (50, 5, 100) | BLS | 82.00% | 0.6003 | 0.7896 | 77.43% | 82.85% |
| Log-CS-BLS | 88.00% | 0.7622 | 0.8750 | 89.41% | 86.85% | |
| Lin-CS-BLS | 86.00% | 0.7290 | 0.8553 | 87.85% | 85.10% | |
| Sqr-CS-BLS | 92.00% | 0.8335 | 0.9151 | 92.53% | 90.83% | |
| EN-CS-BLS | 92.00% | 0.8335 | 0.9151 | 92.53% | 90.83% | |
| (50, 15, 100) | BLS | 86.00% | 0.7005 | 0.8498 | 85.42% | 84.63% |
| Log-CS-BLS | 92.00% | 0.8335 | 0.9151 | 92.53% | 90.83% | |
| Lin-CS-BLS | 92.00% | 0.8335 | 0.9151 | 92.53% | 90.83% | |
| Sqr-CS-BLS | 96.00% | 0.9132 | 0.9566 | 95.66% | 95.66% | |
| EN-CS-BLS | 92.00% | 0.8335 | 0.9151 | 92.53% | 90.83% | |
| (50, 30, 100) | BLS | 84.00% | 0.6528 | 0.8264 | 82.64% | 82.64% |
| Log-CS-BLS | 96.00% | 0.9186 | 0.9576 | 96.88% | 95.00% | |
| Lin-CS-BLS | 98.00% | 0.9580 | 0.9785 | 98.44% | 97.37% | |
| Sqr-CS-BLS | 96.00% | 0.9132 | 0.9566 | 95.66% | 95.66% | |
| EN-CS-BLS | 96.00% | 0.9132 | 0.9566 | 95.66% | 95.66% | |
| (50, 15, 200) | BLS | 88.00% | 0.7396 | 0.8698 | 86.98% | 86.98% |
| Log-CS-BLS | 92.00% | 0.8335 | 0.9151 | 92.53% | 90.83% | |
| Lin-CS-BLS | 94.00% | 0.8722 | 0.9356 | 94.10% | 93.12% | |
| Sqr-CS-BLS | 94.00% | 0.8722 | 0.9356 | 94.10% | 93.12% | |
| EN-CS-BLS | 96.00% | 0.9132 | 0.9566 | 95.66% | 95.66% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, L.; Wong, P.K.; Zhao, B.; Wang, Z.; Lei, L.; Wang, X.; Hu, Y. Cost-Sensitive Broad Learning System for Imbalanced Classification and Its Medical Application. Mathematics 2022, 10, 829. https://doi.org/10.3390/math10050829
Yao L, Wong PK, Zhao B, Wang Z, Lei L, Wang X, Hu Y. Cost-Sensitive Broad Learning System for Imbalanced Classification and Its Medical Application. Mathematics. 2022; 10(5):829. https://doi.org/10.3390/math10050829
Chicago/Turabian StyleYao, Liang, Pak Kin Wong, Baoliang Zhao, Ziwen Wang, Long Lei, Xiaozheng Wang, and Ying Hu. 2022. "Cost-Sensitive Broad Learning System for Imbalanced Classification and Its Medical Application" Mathematics 10, no. 5: 829. https://doi.org/10.3390/math10050829
APA StyleYao, L., Wong, P. K., Zhao, B., Wang, Z., Lei, L., Wang, X., & Hu, Y. (2022). Cost-Sensitive Broad Learning System for Imbalanced Classification and Its Medical Application. Mathematics, 10(5), 829. https://doi.org/10.3390/math10050829






