Abstract
Security and privacy issues with IoT edge devices hinder the application of IoT technology in many applications. Applying cryptographic protocols to edge devices is the perfect solution to security issues. Implementing these protocols on edge devices represents a significant challenge due to their limited resources. Finite-field multiplication is the core operation for most cryptographic protocols, and its efficient implementation has a remarkable impact on their performance. This article offers an efficient low-area and low-power one-dimensional bit-parallel systolic implementation for field multiplication in () based on an irreducible all-one polynomial (AOP). We represented the adopted multiplication algorithm in the bit-level form to be able to extract its dependency graph (DG). We choose to apply specific scheduling and projection vectors to the DG to extract the bit-parallel systolic multiplier structure. In contrast with most of the previously published parallel structures, the proposed one has an area complexity of the order compared to the area complexity of the order of for most parallel multiplier structures. The complexity analysis of the proposed multiplier structure shows that it exhibits a meaningful reduction in area compared to most of the compared parallel multipliers. To confirm the results of the complexity analysis, we performed an ASIC implementation of the proposed and the existing efficient multiplier structures using an ASIC CMOS library. The obtained ASIC synthesis report shows that the proposed multiplier structure displays significant savings in terms of its area, power consumption, area-delay product (ADP), and power-delay product (PDP). It offers average savings in space of nearly 33.7%, average savings in power consumption of 39.3%, average savings in ADP of 24.8%, and savings in PDP of 31.2% compared to the competitive existing multiplier structures. The achieved results make the proposed multiplier structure more suitable for utilization in resource-constrained devices such as IoT edge devices, smart cards, and other compact embedded devices.
Keywords:
IoT edge devices; cybersecurity; systolic multipliers; physical security; compact embedded devices; parallel computing; cryptography MSC:
68W10; 68M25
1. Introduction
The internet of things currently plays a crucial role in our daily life. These devices can be used in many fields, such as healthcare, automobiles, entertainment, industrial appliances, agriculture, and in homes. The main goal of the IoT network is to collect data and transfer these data to the cloud for further analysis and decision-making. Since most of the applications using IoT technology are sensitive ones, the data collected by IoT devices should be protected throughout all the layers of the IoT network. Due to the limited resources of most IoT edge devices, implementing security mechanisms on these devices represents a great challenge. Therefore, many efforts have been made to solve this challenging problem. Many security protocols have been proposed to be suitable for implementation on resource-constrained IoT edge devices. Furthermore, cryptographic algorithms such as elliptic curve cryptography (ECC) are optimized to be suitable for implementation on these devices. Most of the optimized algorithms depend mainly on finite-field arithmetic operations, namely, finite-field multiplication. Field multiplication is the core operation of the other field operations, such as inversion, division, and exponentiation [1]. Therefore, it has attracted great interest in order to help in implementing compact and highly efficient cryptographic algorithms [2,3,4,5,6,7,8,9,10,11,12].
1.1. Literature Review
We can perform finite-field multiplication on different bases, such as a polynomial basis (PB), a normal basis (NB), and a dual basis (DB) [13]. PB multiplication is comparatively simple and does not require basis conversion, as the others do. The need for base conversion increases the hardware complexity of the multipliers. As a result, PB multipliers are widely employed in a variety of cryptographic techniques.
Due to the simplicity and efficiency of their implementation in hardware, several hardware algorithms and structures for PB multiplication for fields formed by trinomials and pentanomials have been proposed in the literature [14,15,16,17,18]. When compared to trinomials and pentanomial-based multipliers, all-one polynomials (AOP) represent a special class that can be employed for simpler and more efficient implementation. As a result, the AOP-based element representation is predicted to find use in efficient hardware implementations of elliptic curve cryptosystems and error control coding [19]. Although irreducible AOPs are not as common as irreducible trinomials or pentanomials, finding the AOP bases for creating finite fields is not difficult [19]. Efficient structures for finite-field multiplication for AOP-formed fields have been offered in the literature [19,20,21].
To obtain an efficient VLSI implementation for finite-field multipliers, we should offer hardware structures that have regular modules with local interconnections such as systolic arrays. The main building blocks of the systolic array are processing elements (PEs). The PEs perform a specific task and can be organized in one-dimensional or two-dimensional space. The systolic multiplier structures can be arranged in bit-parallel [4,5,8,22,23,24,25,26,27] or bit-serial systolic structures [2,28,29]. Bit-parallel systolic architectures are well known for their significant area cost and high power consumption. On the other hand, they act effectively to execute the tasks that have been assigned to them. Bit-serial systolic architectures show significant savings in area and power consumption, but with a high degradation in their execution speed.
In the literature, many authors have tried to offer efficient implementations of bit-parallel systolic multipliers over the binary extension field Most of them tried to use a specific irreducible polynomial to build their structures. In 2001, Lee et al. [22,23] offered a bit-parallel systolic multiplier structure based on the equally spaced and AOP polynomials. In 2005, Lee et al. [24] suggested a mapping approach transforming the bit-parallel systolic multiplier based on AOP into one that is based on trinomials to decrease its complexity. In 2008, Lee et al. [25] used Toeplitz matrix-vector representation to decrease the complexity of the recommended Montgomery-based bit-parallel multiplier. In 2015, Sarmadi [26] offered a bit-parallel systolic multiplier with low hardware complexity and high throughput. The recommended multiplier is based on the Montgomery algorithm that used trinomials as a reduction polynomial. In 2018, Mathe [27] adopted an interleaving multiplication algorithm over the binary extension field to implement a bit-parallel systolic multiplier with low hardware complexity.
1.2. Paper Contribution
In this paper, we offer a low-space bit-parallel systolic implementation for finite-field multiplication. The multiplication operation is performed over and based on the irreducible all-one polynomial (AOP). We present the adopted multiplication algorithm, offered by [19], in the bit-level form in order to extract its dependency graph (DG). The DG will help us to extract the proposed low-complexity bit-parallel systolic multiplier structure by choosing the proper time-scheduling and node-projection functions. The multiplier structure offered here shows an area complexity of the order of , which differentiates it from most of the previously reported ones, which have an area complexity of the order of . Therefore, the proposed structure achieves a remarkable reduction in area complexity and power consumption. The reduction in the area does not lead to a deterioration in the performance of the recommended multiplier structure, and it shows almost the same timing delays as the previously reported ones. Furthermore, it has a regular systolic structure with local communication between the constituting PEs, making it suitable for VLSI implementation. Local interconnection between the PEs reduces the wire delays and hence improves the whole performance of the multiplier structure. Due to the significant savings in terms of area and power consumption of the recommended multiplier structure, it is more suited to be used in resource-constrained IoT edge devices or compact embedded devices.
1.3. Paper Organization
The layout of this paper can be summarized as follows: Section 2 presents the mathematical formulation of the adopted multiplication algorithm and its representation in bit-level form. Section 3 explains the developed DG of the adopted algorithm. Section 4 describes the methodology used to extract the recommended bit-parallel systolic multiplier structure. Section 5 presents the complexity analysis of the proposed multiplier and of the existing efficient structures. Furthermore, it provides a performance evaluation of the suggested multiplier design and other competitive designs based on ASIC synthesis. Conclusions are provided in Section 6.
2. Formulation of the Finite Field Multiplication Algorithm
Suppose the irreducible polynomial of degree n defines the finite field over the binary extension field . We can represent in the polynomial form as follows:
where . Let represent the root of the irreducible polynomial . Therefore, the set of polynomial bases can be used to represent the field elements.
Suppose E and H are any two field elements in . They can be represented in the polynomial form of degree as:
where .
The multiplication of E and H over can be performed as follows:
We can expand Equation (4) to have a recurrence relation of multiplication as follows:
where is a polynomial of degree n and can be represented as:
where and for .
By expanding the polynomial of (6) and multiplying by , we can obtain
Since is a root of , this leads to = 0. Therefore, from Equation (1) we can obtain
When polynomial is an AOP, we can write Equation (8) as:
If we multiply both sides of Equatin (9) by , we can obtain:
We note based on Equation (11) that the cyclic-shift-left operation of polynomial K will produce the partially-reduced polynomial of polynomial . Similarly, the cyclic-shift-left operation of polynomial will produce the partially-reduced polynomial of polynomial . In general, cyclic-shift-left of polynomial will produce the partially-reduced polynomial of polynomial . We can mathematically express this cyclic-shift-left operation as:
where and represent the cyclic-shift-left operation. Equation (12) can help us to rewrite Equation (5) as:
where .
Alternately, we can express Equation (13) as:
where V is the sum of polynomials of degree n that can be represented as:
where .
The polynomial in Equation (15) can be represented as:
By replacing in Equation (16) with the expansion given in Equation (9), we obtain the reduced form of polynomial (polynomial of degree ) as:
Assuming that j represents the bit position in a binary string that represents any polynomial, we can express Equations (12) and (15) in the bit-level form as shown in Equations (18) and (19), respectively:
where , , , and 0 .
Furthermore, the reduced form of the product polynomial D, given in Equation (17), can be represented in the bit-level form as:
where 0 .
3. Dependency Graph
The two iterative equations, Equations (18) and (19), describe the iterative part of the finite-field multiplication algorithm. The two indices i and j define the iterations. Following the technique of [30], it is possible to develop a dependance graph (DG) in the two-dimensional integer domain . Figure 1 shows the DG for the case in which . The nodes of the DG symbolize the operations represented by Equations (18) and (19). Based on the construction rules of [30], signals of are represented by vertical lines. Signals are represented by horizontal lines. Signals are represented by diagonal lines. signal is generated from the last column nodes and assigned to the nodes in the first column. As described in the reduction step of the algorithm, Equation (20), the resulting signals , , from the bottom row are added, using XOR gates, with the most significant signal used to generate the final product bits , .
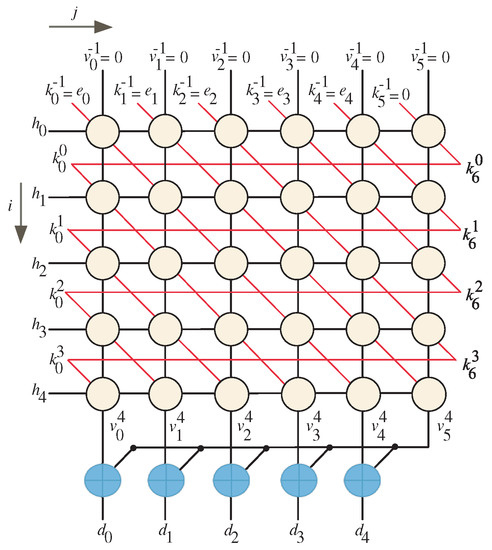
Figure 1.
DG of the adopted algorithm for .
The algorithm inputs , are represented in the DG as the vertical and diagonal inputs to the nodes at the top row. On the other hand, the reduced product output , , results from the bottom row after adding the outputs of the least significant bits of , , with the most significant bit output resulting from the right bottom node. Since the addition is conducted in the binary field, , it can be performed using two input XOR gates (blue nodes) as displayed in Figure 1.
4. Extraction of the Bit-Parallel Systolic Multiplier Architecture
In this section we discuss the scheduling and node projection methodologies proposed in [30,31,32] and used to extract the bit-parallel systolic array structure from the adopted finite-field multiplication algorithm.
4.1. Scheduling Function
Each node in the DG of Figure 1 is expressed as a point . Data scheduling is determined through the timing function using a scheduling vector , which assign a time value to each node based on a scheduling function, defined as follows:
where u is a scalar value added to the previous function to avoid allocating negative time values to any node of the DG. In our case, choosing will assign only positive values to the DG nodes shown in Figure 1.
There are restrictions on the possible values of the scheduling vector. For example, iterations in Equation (19) for variable dictate that point must be executed after point , i.e.,
Using the value of , we can write the above equation as:
Another timing limitation is obtained using the iterations in Equation (18), which dictate that must be executed after point , i.e.,
Using the value of , we can write the above equation as:
Inequalities (23) and (25) allow us to choose valid scheduling vectors. As one choice of a valid scheduling vector, we could have the scheduling vector , given as:
This choice of scheduling vector results in the associated DG shown in Figure 2. The input signals and are fed in parallel (i.e., at the same time) and output signals are obtained in parallel after n clock cycles.
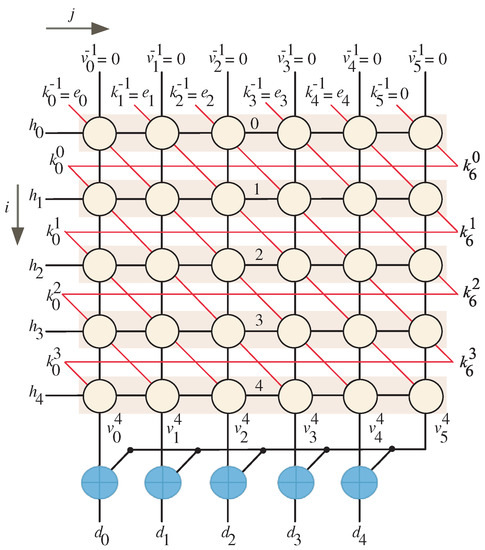
Figure 2.
Scheduling time for .
4.2. Projection Function
According to [30], the projection function maps many DG nodes or points to one processing element . The resulting processing elements are connected to constitute the systolic array. The projection function can be expressed as follows:
where symbolizes a projection matrix. To extract the projection matrix, we should first find a projection vector , which is the null space of . According to the discussion provided in [30], the following restriction should be applied to the projection vector:
This constraint ensures that each PE executes the allocated tasks at different clock periods. This multiplexing results in better PE utilization.
Using the limitations placed on , Equation (28), and the scheduling vector , the suitable projection vector resulting in the bit-parallel systolic array is supplied by:
Since is the null space of the projection matrix , it can be presented as:
4.3. Extraction of the Bit-Parallel Systolic Multiplier Structure
By inserting the scheduling vector and projection matrix into Equations (21) and (27), we can obtain the time scheduling and node projection functions for every DG node or point, . The resultant functions are expressed as:
The bit-parallel systolic multiplier structure, resulting from applying the previously-derived scheduling and projection functions to the points (nodes) of the DG, is shown in Figure 3. The systolic structure is composed of regular PEs. Figure 4 shows the logical details of the PEs. In contrast with most of the previously published parallel systolic designs that have area complexities of the order of , the proposed systolic multiplier has an area complexity of the order of . In addition, as with most previously published parallel systolic structures, the final product output from the systolic array is available after a latency of n clock cycles. As a result, the offered systolic multiplier structure surpasses them in terms of area complexity while also having a comparable latency.
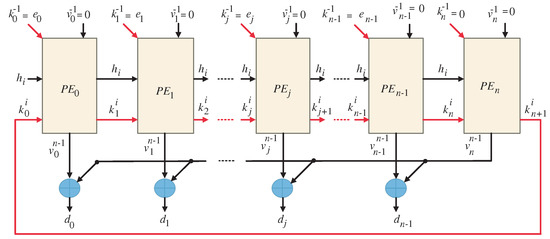
Figure 3.
Bit-parallel systolic multiplier structure.
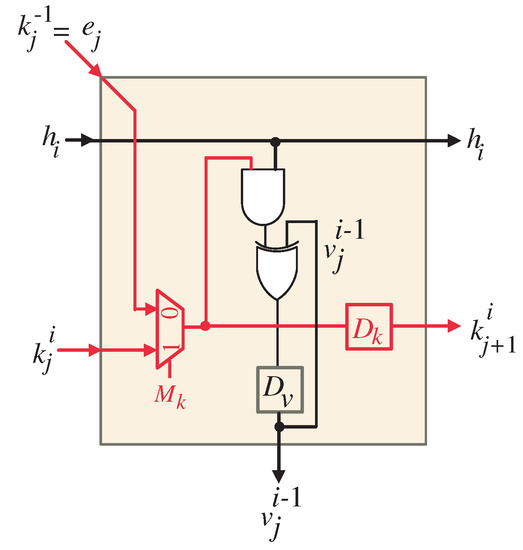
Figure 4.
Logic diagram of PE. symbolizes a D-Latch.
By investigating Figure 3 and Figure 4, we can describe the structure of the bit-parallel systolic multiplier as follows. The input bits of K and are assigned to each PE. Since the initial values of input V ( ) have zero values, they can be generated by clearing the latches before the PEs start the execution process. The resulting internal bits of K and are pipelined through the latches between the PEs. In addition, the resulting internal bits of V and are produced locally inside each PE. The last PE (PE) generates the bits of that were assigned to at the first PE (PE). Input bits are fed in series, one bit at each time step, and pass through all the PEs. After n clock cycles, the resultant bits of V and , will be available in parallel at the outputs of all the PEs. These bits are logically XORed with the most significant bit to generate the final product bits ; .
The operation of the explored bit-parallel systolic multiplier structure is explained as follows.
- Throughout the initial clock period, MUXes are deactivated () to pass the input bits of K and , to be localized in each PE. Furthermore, the latches, in each PE, are cleared to initialize the signal with zero values. The input bit is fed to all PEs in this clock period.
- Throughout the subsequent clock periods, the PEs generate the internal bit values of and , and . Furthermore, input bits of and are fed in a bit sequence to all PEs.
- In the last clock period (clock period n), the XOR gates shown in Figure 3 generate the resultant output bits of the product d, . They are produced in parallel, as displayed in the figure.
5. Results and Discussion
This section presents an estimate for the area and time complexities, as well as the power consumption, of the offered one-dimensional bit-parallel systolic multiplier and the existing efficient systolic multiplier structures presented in [4,26,27,33,34,35,36], as well as the competitive sequential multiplier structures presented in [37]. The multiplier systolic structures proposed in [4,26,27,33,34,37] are based on trinomials, whereas the multiplier systolic structures proposed in [35,36] are based on AOPs. As displayed in Figure 3, the proposed systolic structure consists of regular PEsand each PE consists of AND gates, XOR gates, MUXes, and Latches. For the reduction process to obtain the final product results, the output of the first n PEs is added to the most significant bit resulting from the last PE () using n XOR gates. Therefore, the total number of utilized XOR gates should be . As we discussed above, the proposed multiplier produces the output results after a latency of n clock cycles. By investigating the PE logic details, we can estimate the critical path delay (CPD) of the proposed multiplier as the sum of the delays of the AND gate (), XOR gate (), and 2-to-1 MUXes (). Table 1 lists the gate counts, latch counts, latency in the number of cycles, and the cycle period (CPD) of the suggested bit-parallel systolic multiplier design, in addition to the existing systolic designs presented in [4,26,27,33,34,35,36] and the competitive sequential multiplier structure presented in [37]. As can be noted from Table 1, the proposed multiplier design consumes significantly less AND gates and MUXes compared to the recently published systolic multiplier structure of Ibrahim [34]. Furthermore, it has almost the same number of XOR gates and latches compared to that structure. We can also note that the proposed systolic design saves more AND gates and latches compared to the competitive design of Chen [36] and has the same number of XOR gates and MUXes. Moreover, the proposed multiplier consumes less area compared to all the remaining multiplier structures, as they require a significant number of gates compared to the proposed one. Table 1 also shows that the systolic multiplier structure of Kim [4] has the lowest latency compared to all the other designs, including the proposed one, and it has a cycle period (CPD) that is comparable to the multiplier designs of Sarmadi [26], Know [35], Chen [36] and which is shorterthan those of the other multiplier structures. The proposed systolic design has a comparable latency and cycle period (CPD) to the other remaining designs.

Table 1.
Area and time-complexities of the proposed and the existing effective multipliers.
Based on the above qualitative analysis, we note that the multiplier structure of Chen [36] is the most competitive one in relation to the proposed multiplier structure. Therefore, we chose this structure for quantitative comparisons with our proposed structure. To validate and evaluate the performance of the offered systolic multiplier structure and the competitive multiplier structure of Chen [36], we described both multiplier structures using the VHDL hardware description language and synthesized the obtained code using the Synopsis design compiler with the Nangate (1.5 nm, 0.8 V) open-cell library. Before synthesizing them, the multiplier designs were verified using ModelSim tools for functional verification. The power consumption was evaluated at a frequency of 10 MHz.
Table 2 shows the estimated area, delay, power consumption, the computed area-delay product (ADP), and power delay product (PDP) for AOP field sizes of and . It also shows the savings in terms of area, power consumption, ADP, and PDP of the developed bit-parallel systolic multiplier structure and the existing competitive design [36]. Considering the results obtained in Table 2, we can observe the following:

Table 2.
Performance evaluation of various multiplier structures for and .
- The proposed systolic multiplier structure shows significant savings in area and power consumption over the competitive design presented by Chen [36]. The average savings of area for and are 30.9% and 33.7%, respectively. Furthermore, the table shows that the achievable average reductions in power consumption, for and , of the developed multiplier structure over the multiplier structure of Chen [36] are 37.1% and 39.3%, respectively.
- The developed systolic structure shows a significant reduction in area-delay product (ADP) and power-delay product (PDP) over the competitive systolic design presented by Chen [36]. The average reductions of ADP at and are equivalent to 18.3% and 24.8%, respectively. Furthermore, the achievable average reductions of PDP offered by our proposed multiplier structure over the competitive design for and represent savings of 25.6% and 31.2%, respectively.
As can be seen from the obtained results, the proposed bit-parallel systolic multiplier showed the lowest area and power consumption. These achievable results make the proposed multiplier structure more suitable for utilization in resource-constrained devices such as IoT edge devices, smart cards, and other compact embedded devices. The savings in terms of area and power consumption of the proposed design are attributed to the significant reductions in AND gate counts and latches of the proposed systolic structure compared to competitive multiplier designs. Due to the regularity of the proposed multiplier structure and the local communication between the PEs, the wiring complexity is minimized, making a limited contribution to the overall space consumed by the proposed systolic multiplier compared to the other multiplier structures.
6. Summary and Conclusions
In this paper we have presented a low-area and low-power one-dimensional bit-parallel systolic implementation for field multiplication in () based on the irreducible all-one polynomial. The adopted algorithm is a regular iterative algorithm and can be represented by means of a dependency graph. By assigning proper scheduling and node projection functions to each node of the DG, we obtained an efficient bit-parallel systolic multiplier structure. The extracted parallel structure has an area complexity of the order of , which distinguishes it from most of the previously published parallel structures, which have an area complexity of the order of . Furthermore, it has a regular systolic array structure with local interconnection between its PEs, making it more suitable for ASIC implementation. The complexity analysis of the proposed multiplier structure shows that it exhibits a meaningful reduction in the number of gate counts and latches compared to most of the compared parallel multipliers. To verify the results of the complexity analysis, we synthesized the proposed structure and one of the existing efficient multiplier structures, based on an ASIC CMOS library, to evaluate their performance. The estimated ASIC results show that the proposed bit-parallel systolic multiplier demonstrated significant savings in area and power consumption, the area-delay product, and the power delay-product. These achievable results make the proposed multiplier structure more suitable for utilization in resource-constrained devices such as IoT edge devices, smart cards, and all other compact embedded devices. In our future work, we will incorporate the proposed multiplier structure into an ECC cryptographic processing unit to calculate the overall savings in area and the energy consumed by the entire system.
Author Contributions
Conceptualization, A.I. and F.G.; methodology, A.I. and F.G.; software, A.I. and W.N.; validation, Y.B. and U.T.; formal analysis, A.I. and W.N.; investigation, A.I.; resources, A.I. and T.A.; data curation, A.I. and Y.B.; writing—original draft preparation, A.I. and F.G.; writing—review and editing, A.I. and Y.B.; visualization, A.I. and U.T.; supervision, A.I.; project administration, A.I. and F.G.; funding acquisition, A.I. All authors have read and agreed to the published version of the manuscript.
Funding
Deputyship for Research & Innovation, Ministry of Education in Saudi Arabia, project number (IF-PSAU-2021/01/17867).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors extend their appreciation to the Deputyship for Research & Innovation, Ministry of Education in Saudi Arabia for funding this research work through project number (IF-PSAU-2021/01/17867).
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| IoT | Internet of Things |
| ADP | Area-Delay Product |
| PDP | Power-Delay Product |
| ASIC | Application-Specific Integrated Circuit |
| ECC | Elliptic Curve Cryptography |
| DG | Dependency Graph |
| AOP | All-One Polynomial |
| VLSI | Very Large Scale Integrated Circuit |
| CSL | Cyclic-Shift-Left |
| CPD | Critical Path Delay |
References
- Chen, C.C.; Lee, C.Y.; Lu, E.H. Scalable and Systolic Montgomery Multipliers Over GF(2m). IEICE Trans. Fundam. 2008, E91-A, 1763–1771. [Google Scholar] [CrossRef]
- Chiou, C.W.; Lee, C.Y.; Deng, A.W.; Lin, J.M. Concurrent error detection in Montgomery multiplication over GF(2m). IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 2006, E89-A, 566–574. [Google Scholar] [CrossRef]
- Huang, W.T.; Chang, C.; Chiou, C.; Chou, F. Concurrent error detection and correction in a polynomial basis multiplier over GF(2m). IET Inf. Secur. 2010, 4, 111–124. [Google Scholar] [CrossRef]
- Kim, K.W.; Jeon, J.C. Polynomial Basis Multiplier Using Cellular Systolic Architecture. IETE J. Res. 2014, 60, 194–199. [Google Scholar] [CrossRef]
- Choi, S.; Lee, K. Efficient systolic modular multiplier/squarer for fast exponentiation over GF(2m). IEICE Electron. Express 2015, 12, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Reyhani-Masoleh, A. A new bit-serial architecture for field multiplication using polynomial bases. In Proceedings of the 7th International Workshop Cryptographic Hardware Embedded Systems (CHES 2008), Edinburgh, UK, 29 August–1 September 2008; pp. 300–314. [Google Scholar]
- Abdulrahman, E.A.H.; Reyhani-Masoleh, A. High-Speed Hybrid-Double Multiplication Architectures Using New Serial-Out Bit-Level Mastrovito Multipliers. IEEE Trans. Comput. 2016, 65, 1734–1747. [Google Scholar] [CrossRef]
- Kim, K.W.; Jeon, J.C. A semi-systolic Montgomery multiplier over GF(2m). IEICE Electron. Express 2015, 12, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Ibrahim, A. Novel Bit-Serial Semi-Systolic Array Structure for Simultaneously Computing Field Multiplication and Squaring. IEICE Electron. Express 2019, 16, 20190600. [Google Scholar] [CrossRef] [Green Version]
- Kim, K.W.; Lee, J.D. Efficient unified semi-systolic arrays for multiplication and squaring over GF(2m). Electron. Express 2017, 14, 1–10. [Google Scholar]
- Kim, K.W.; Kim, S.H. Efficient bit-parallel systolic architecture for multiplication and squaring over GF(2m). IEICE Electron. Express 2018, 15, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Ibrahim, A. Efficient Parallel and Serial Systolic Structures for Multiplication and Squaring Over GF (2m). Can. J. Electr. Comput. Eng. 2019, 42, 114–120. [Google Scholar] [CrossRef]
- Roman, S. Field Theory, 2nd ed.; Springer: New York, NY, USA, 1983. [Google Scholar]
- Pillutla, S.R.; Boppana, L. Area-efficient low-latency polynomial basis finite field GF(2m) systolic multiplier for a class of trinomials. Microelectron. J. 2020, 97, 104709. [Google Scholar] [CrossRef]
- Imana, J.L. LFSR-Based Bit-Serial GF(2m) Multipliers Using Irreducible Trinomials. IEEE Trans. Comput. 2020, 70, 156–162. [Google Scholar]
- Pillutla, S.R.; Boppana, L. Low-latency area-efficient systolic bit-parallel GF(2m) multiplier for a narrow class of trinomials. Microelectron. J. 2021, 117, 105275. [Google Scholar] [CrossRef]
- Li, Y.; Cui, X.; Zhang, Y. An Efficient CRT-based Bit-parallel Multiplier for Special Pentanomials. IEEE Trans. Comput. 2021, 71, 736–742. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Y.; He, W. Fast hybrid Karatsuba multiplier for type II pentanomials. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2020, 28, 2459–2463. [Google Scholar] [CrossRef]
- Meher, P.K.; Lou, X. Low-Latency, Low-Area, and Scalable Systolic-Like Modular Multipliers for GF(2m) Based on Irreducible All-One Polynomials. IEEE Trans. Circuits Syst. I Regul. Pap. 2016, 64, 399–408. [Google Scholar] [CrossRef]
- Mohaghegh, S.; Yemiscoglu, G.; Muhtaroglu, A. Low-power and area-efficient finite field multiplier architecture based on irreducible all-one polynomials. In Proceedings of the 2020 IEEE International Symposium on Circuits and Systems (ISCAS), Seville, Spain, 12–14 October 2020; pp. 1–5. [Google Scholar]
- Zhang, Y.; Li, Y. Efficient Hybrid GF(2m) Multiplier for All-One Polynomial Using Varied Karatsuba Algorithm. IEICE Trans. Fundam. Electron. Comput. Sci. 2021, 104, 636–639. [Google Scholar] [CrossRef]
- Lee, C.Y.; Lu, E.H.; Lee, J.Y. Bit-Parallel Systolic Multipliers for GF(2m) Fields Defined by All-One and Equally-Spaced Polynomials. IEEE Trans. Comput. 2001, 50, 358–393. [Google Scholar]
- Lee, C.Y.; Lu, E.H.; Sun, L.F. Low-Complexity Bit-Parallel Systolic Architecture for Computing AB2+C in a Class of Finite Field GF(2m). IEEE Trans. Circuits Syst. II 2001, 50, 519–523. [Google Scholar]
- Lee, C.Y.; Chiou, C.W. Efficient Design of Low-Complexity Bit-Parallel Systolic Hankel Multipliers to Implement Multiplication in Normal and Dual Bases of GF(2m). IEICE Trans. Fund. Electron. Comm. Comp. Sci. 2005, E88-A, 3169–3179. [Google Scholar] [CrossRef]
- Lee, C.Y. Low-latency bit-pararallel systolic multiplier for irreducible xm+xn+1 with GCD(m,n)=1. IEICE Trans. Fund. Electron. Commun. Comp. Sci. 2008, 55, 828–837. [Google Scholar]
- Bayat-Sarmadi, S.; Farmani, M. High-Throughput Low-Complexity Systolic Montgomery Multiplication Over GF(2m) Based on Trinomials. IEEE Trans. Circuits Syst. II 2015, 62, 377–381. [Google Scholar] [CrossRef]
- Mathe, S.E.; Boppana, L. Bit-parallel systolic multiplier over GF(2m) for irreducible trinomials with ASIC and FPGA implementations. IET Circuits Desvices Syst. 2018, 12, 315–325. [Google Scholar] [CrossRef]
- Zhou, B.B. A New Bit Serial Systolic Multiplier over GF(2m). IEEE Trans. Comput. 1988, 37, 749–751. [Google Scholar] [CrossRef]
- Fenn, S.T.J.; Taylor, D.; Benaissa, M. A Dual Basis Bit Serial Systolic Multiplier for GF(2m). Integr. VLSI J 1995, 18, 139–149. [Google Scholar] [CrossRef]
- Gebali, F. Algorithms and Parallel Computers; John Wiley: New York, NY, USA, 2011. [Google Scholar]
- Ibrahim, A.; Gebali, F. Scalable and Unified Digit-Serial Processor Array Architecture for Multiplication and Inversion over GF(2m). IEEE Trans. Circuits Syst. I Regul. Pap. 2017, 22, 2894–2906. [Google Scholar] [CrossRef]
- Ibrahim, A.; Alsomani, T.; Gebali, F. New Systolic Array Architecture for Finite Field Inversion. IEEE Can. J. Electr. Comput. Eng. 2017, 40, 23–30. [Google Scholar] [CrossRef]
- Chiou, C.W.; Lin, J.M.; Lee, C.Y.; Ma, C.T. Novel Mastrovito Multiplier over GF(2m) Using Trinomial. In Proceedings of the 2011 5th International Conference on Genetic and Evolutionary Computing (ICGEC), Kitakyushu, Japan, 29 August–1 September 2011; pp. 237–242. [Google Scholar]
- Ibrahim, A.; Gebali, F.; Bouteraa, Y.; Tariq, U.; Ahanger, T.; Alnowaiser, K. Compact Bit-Parallel Systolic Multiplier Over GF(2m). IEEE Can. J. Electron. Comput. Eng. 2021, 44, 199–205. [Google Scholar] [CrossRef]
- Kwon, S.; Kim, C.H.; Hong, C.P. A linear systolic array for multiplication in GF (2m) for high speed cryptographic processors. In International Conference on Computational Science and Its Applications; Springer: Berlin/Heidelberg, Germany, 2004; pp. 106–116. [Google Scholar]
- Chen, Z.H.; Jing, M.H.; Chen, J.H.; Chang, Y. New viewpoint of bit-serial/parallel normal basis multipliers using irreducible all-one polynomial. In Proceedings of the 2006 IEEE International Symposium on Circuits and Systems, Kos, Greece, 21–24 May 2006; p. 4. [Google Scholar]
- Mathe, S.E.; Boppana, L. Design and Implementation of a Sequential Polynomial Basis Multiplier over GF(2m). KSII Trans. Internet Inf. Syst. 2017, 11, 2680–2700. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).