Graph-Informed Neural Networks for Regressions on Graph-Structured Data
Abstract
1. Introduction
2. Mathematical Formulation of the Graph-Informed Layers
- Given a vector of weights associated with the vertices V, the defined filter of the matrix is obtained by multiplying the i-th row of by the weight , i.e.,where is the diagonal matrix with a diagonal that corresponds to vector ;
- Given the layer activation function , we denote by the element-wise application of f;
- is the vector of biases.
- denotes the input feature of node , for each ;
- is the set of indices j, such that there exists an incoming edge ;
- is the bias corresponding to node ;
- is the output feature associated to , computed by the filter (see Figure 1).
2.1. Generalization to K Input Node Features
- is the input matrix (i.e., the output of the previous layer) and denotes the vector in obtained by concatenating the columns of X;
- Given the matrix , the defined filter of , whose columns are the vectors of weights associated with the k-th input feature of the graph’s vertices, the matrix is defined as
2.2. Generalization to F Output Node Features
- We define the filter of , the tensor , given by the concatenation along the third dimension of the weight matrices , corresponding to the F output features of the nodes. Each column of is the basic filter describing the contribution of the k-th input feature to the computation of the l-th output feature of the nodes, for each , and ;
- The tensor is defined as the concatenation along the second dimension (i.e., the column dimension) of the matrices , such thatfor each . Before the concatenation, the matrices are reshaped as tensors in (see Figure 2);
- the operation is a tensor–vector product (see Remark 2);
- is the matrix of the biases, i.e., each column is the bias vector corresponding to the l-th output feature of the nodes.
2.3. Additional Properties for GI Layers
3. Numerical Tests
3.1. The Maximum-Flow Problem
- The two nodes , , are defined as the source and the sink of the network, respectively;
- c is a real-valued non-negative function defined on the edges, , assigning to each edge a capacity .
- The capacity condition: for each , it holds ;
- The conservation condition: for each , the amount of flow entering v must be equal to the amount of flow leaving v, i.e.,where is the subset of the incoming edges of v, and is the subset of outcoming edges of v;
- The amount of flow leaving the source s must be greater than, or equal to, the one entering s, i.e., .
3.1.1. The Stochastic Maximum-Flow Problem
- The two nodes , , are defined as the source and the sink of the network, respectively;
- p is a real-valued non-negative probability distribution for the edge capacities of the network.
- is a vector whose is sampled from p;
- The function c is such that , for each .
3.2. The Maximum-Flow Regression Problem
3.2.1. Line Graphs for the Exploitation of GINN Models
- The vertices of L are the edges of G;
- Two vertices in L are adjacent if the corresponding edges in G share at least one vertex.
3.3. Maximum-Flow Numerical Experiments
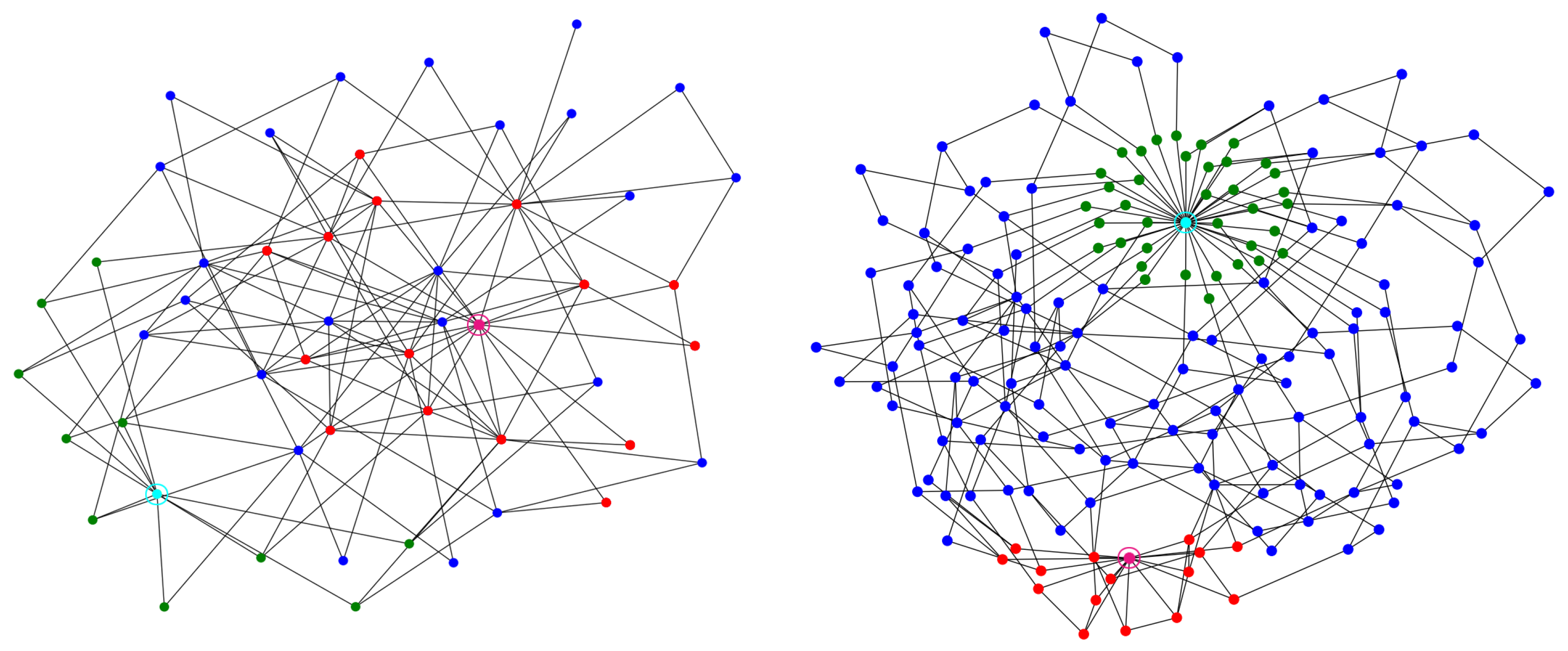
- . The graph of characterizes a flow network built on an extended Barabási–Albert (BA) model graph [34,35]. Put simply, an extended BA model graph is a random graph generated using a preferential attachment criterion. This family of graphs describes a very common behavior in many natural and human systems, where few nodes are characterized by a higher degree if they are compared to the other nodes of the network.In particular, we generate an extended BA undirected graph using the NetworkX Python module [36] (function extended_barabasi_albert_graph, input arguments , and ); then, we denote t (the sink of the network) as the node with the highest betweenness centrality [37] and we add a new node s (the source of the network) connected to the 10 nodes with smallest closeness centrality [38,39]. With these operations, we obtain a graph of 51 nodes and edges, where the source s is connected to the 10 nodes and the sink t is connected to the nodes (see Figure 3-left).In the end, since, in real-world applications, truncated normal distributions seem to be very common (see Remark 7), in order to simulate a rather general maximum-flow regression problem, we chose a truncated normal distribution between 0 and 10, with a mean of 0, and a standard deviation of , as a probability distribution p for the edge capacities (see Section 3.1.1); i.e.,
- . The graph of characterizes a flow network built on an Erdos-Rényi (ER) model graph [40,41]. Put simply, an ER model graph is a random graph generated with a fixed number of nodes, where the edge has a fixed probability of being created. This family of graphs is typically used to prove and/or find new properties that hold for almost all the graphs; for this reason, we consider a stochastic flow network based on an ER graph in our experiments.In particular, we generate an ER undirected graph using the NetworkX Python module [36] (function fast_gnp_random_graph, input arguments ) and we select its largest connected component (in terms of the number of vertices). Then, we add to two new nodes: a node s (the source of the network) connected to all the nodes with degree equal to 1, and a node t (the sink of the network) connected to the 15 most distant nodes from s. With these operations, we obtain a graph of 171 nodes and edges, where the source s is connected to 37 nodes and the sink t is connected to nodes (see Figure 3-right).In the end, we chose the truncated normal distribution (20) as the probability distribution p for the edge capacities.
- , , and ;
- , , and ;
3.3.1. NN Architectures, Hyper-Parameters, and Training
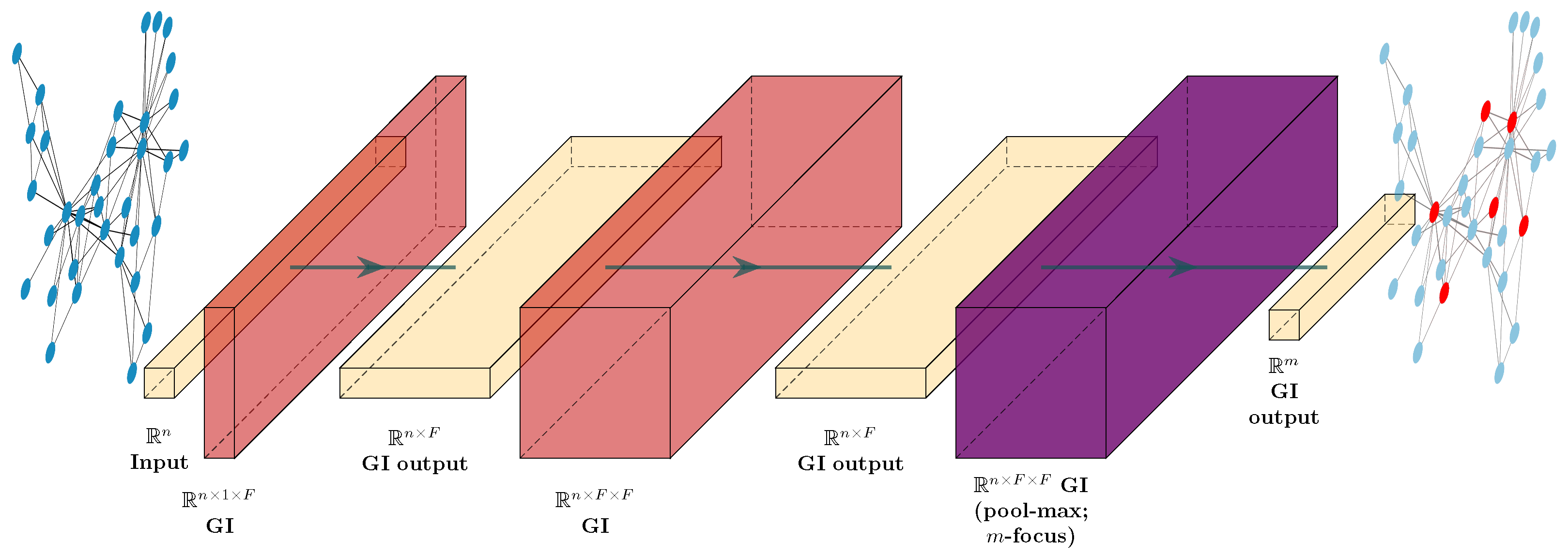
- MLP Archetype: The NN architecture is characterized by one input layer , , hidden layers with a nonlinear activation function f, and one output layer with a linear activation function. The output layer is characterized by m units, while all the other layers are characterized by n units. Finally, we apply a batch normalization [43] before the activation function for each hidden layer . See Figure 4.
- GINN Archetype: The NN architecture is characterized by one input layer of n units, hidden GI layers with a nonlinear activation function f, and one output layer with a linear activation function. All the GI layers are built with respect to the adjacency matrix of the line graph of the network (see Section 3.2.1) and they are characterized by filters (i.e., output features). Then, the number of input features K of the GI layer is , if , and , if . As for the MLP archetype, we apply a batch normalization before the activation function of each hidden layer. Finally, the output layer is characterized by a pooling operation and by the application of a mask (see Section 2.3) to focus on the m units corresponding to the m target flows. See Figure 5.
- MLP archetype. and . We do not use deeper MLPs to avoid the so-called degradation problem [44], i.e., the problem in which increasing the number of hidden layers causes the performance of an NN to saturate and degrade rapidly.
- GINN archetype., , and pooling operations in (only if ); for and for . In particular, we select these values of H because they are a discrete interval around the value , also including cases near, or equal to, the minimum and maximum values and , respectively.
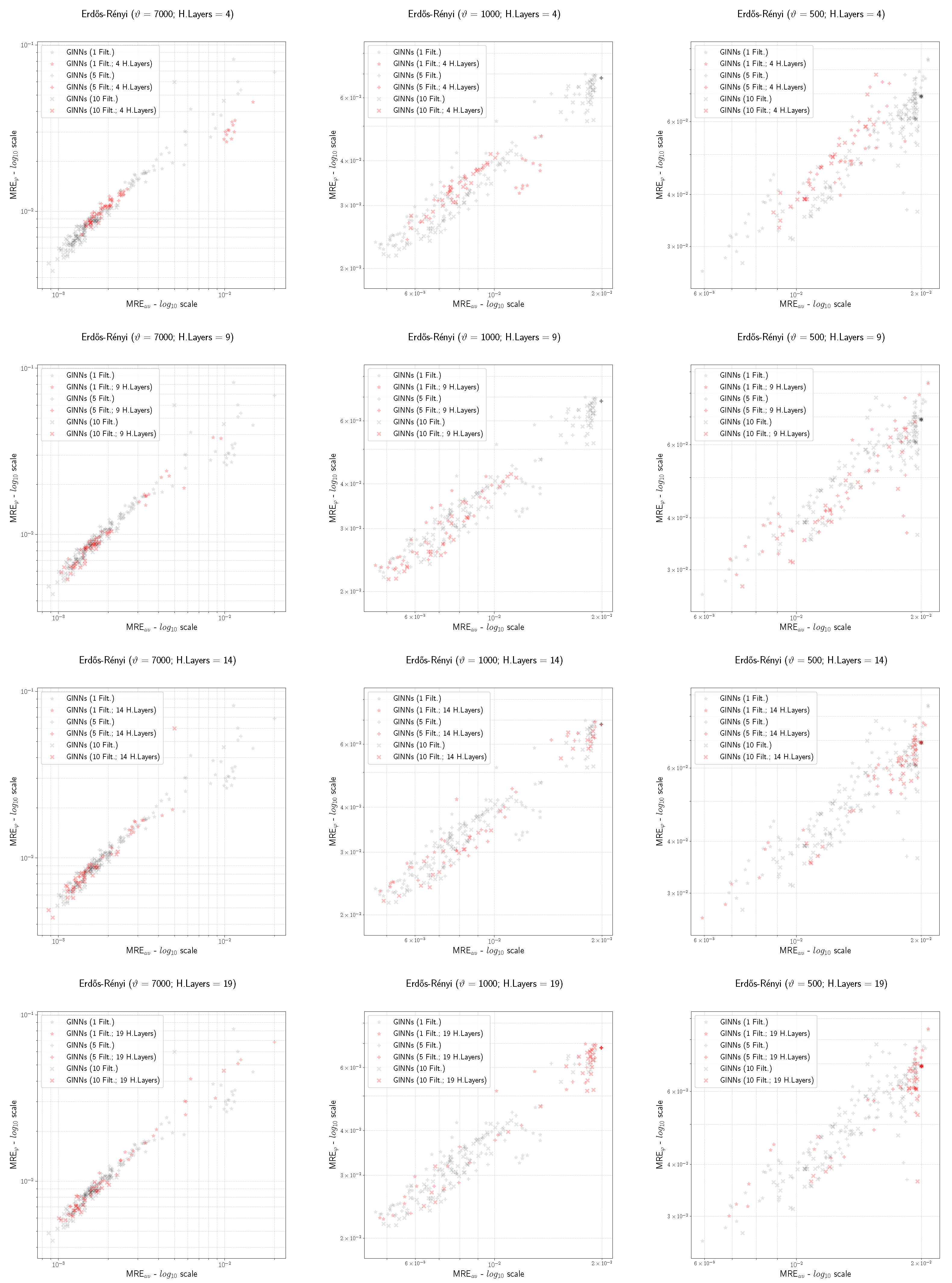
3.3.2. Performance Analysis of Maximum-Flow Regression
- (1)
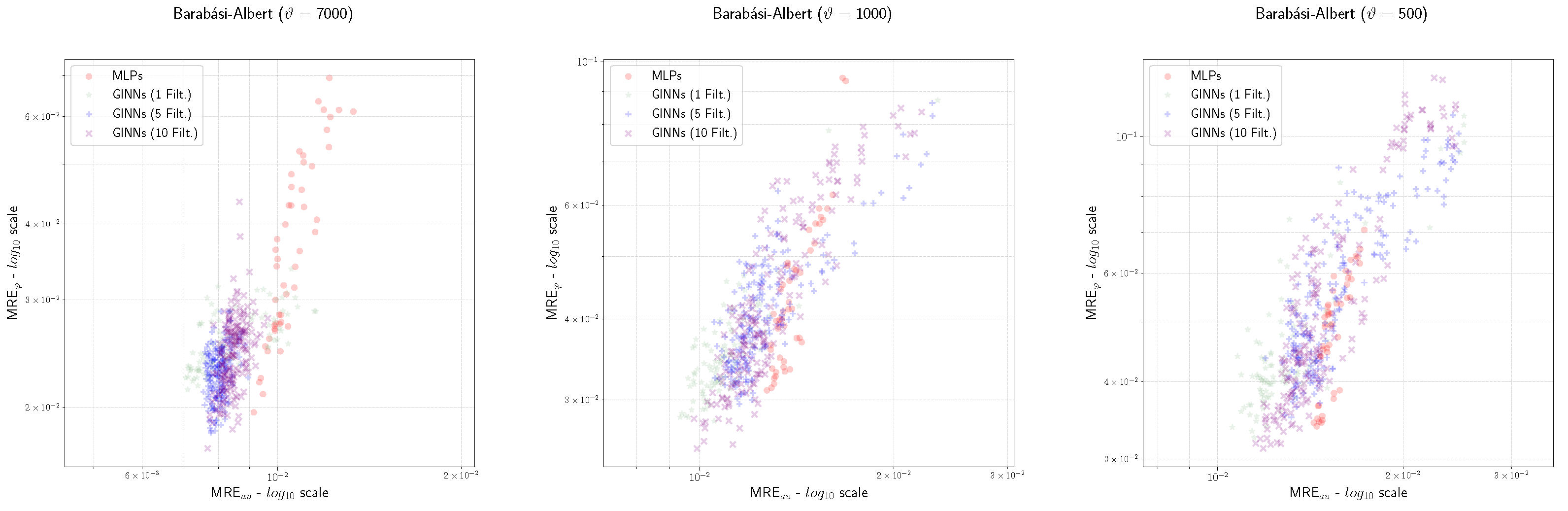
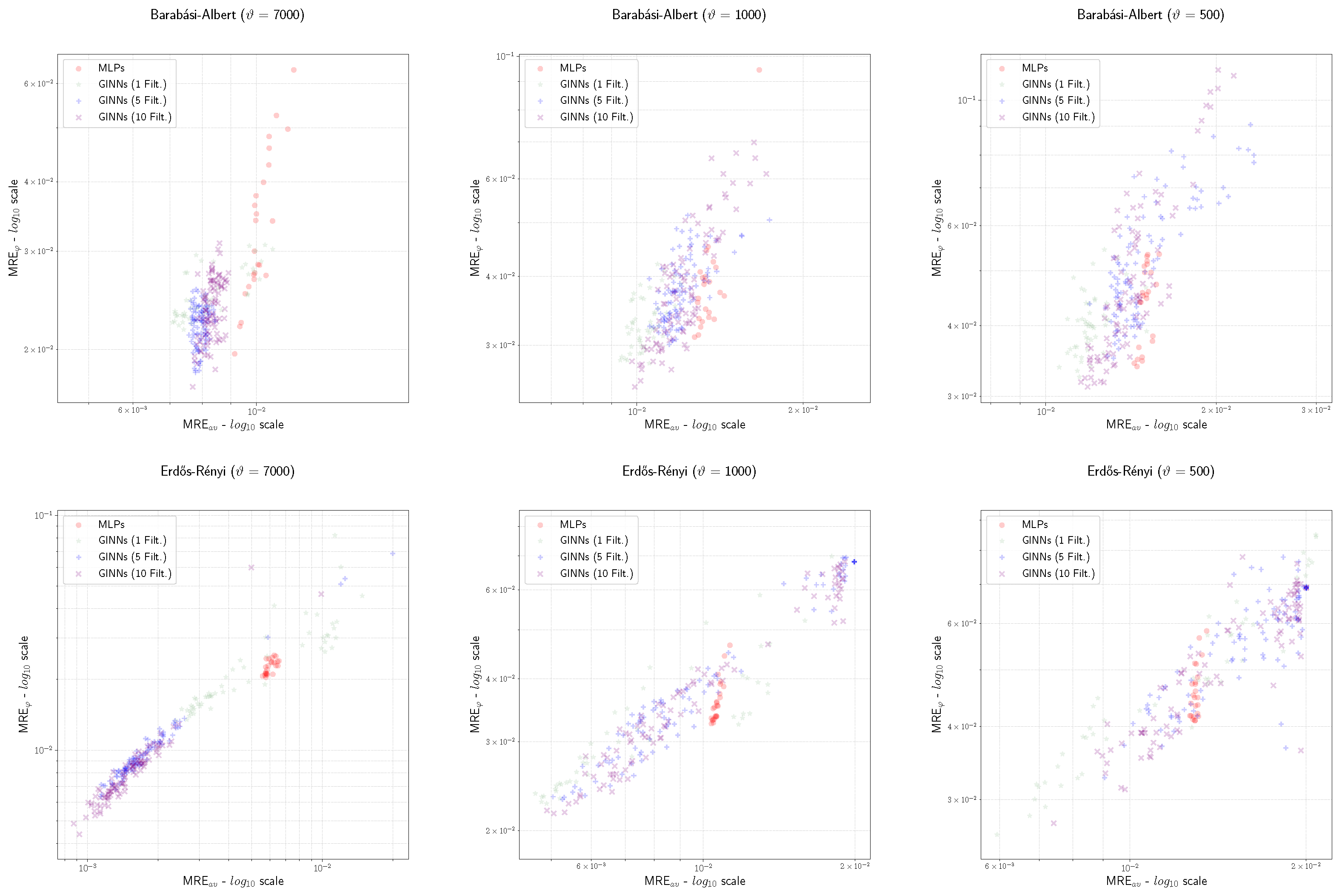
- The MRE of the GINNs is generally smaller than the MLPs, and this effect increases with ;
- (2)
- The MRE of the GINNs is almost always smaller than the MLPs, and this effect seems to be almost stable while varying ;
- (3)
- Looking at the hyper-parameter F, we observe that the cases with generally perform better with fewer training samples (i.e., ) while the cases with generally perform better with . This phenomenon suggests that increasing the number of filters can improve the quality of the training, even if a clear rule for the best choice of F is not apparent.
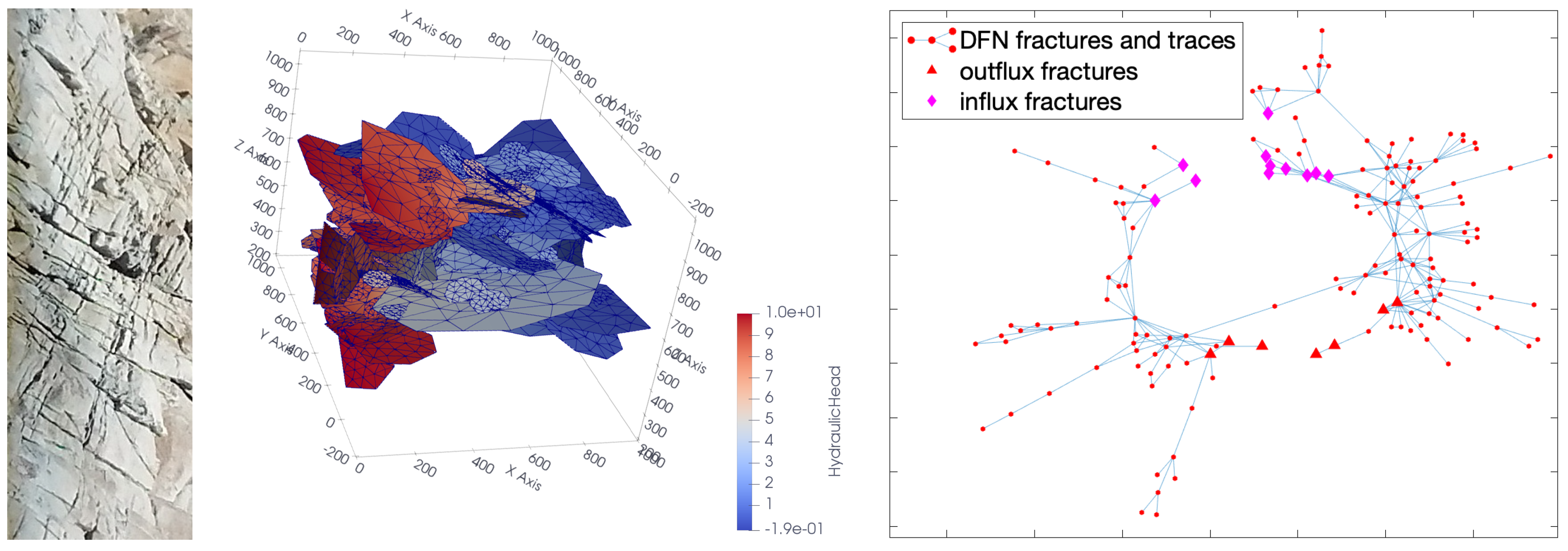
3.4. GINNs for Flux Regression in Discrete Fracture Networks
3.4.1. The DFN Model and the Flux-Regression Task in DFNs
3.4.2. Performance Analysis of DFN Flux Regression
- (number of training and validation data);
- (mini-batch size);
- The relu activation function is not considered in the experiments;
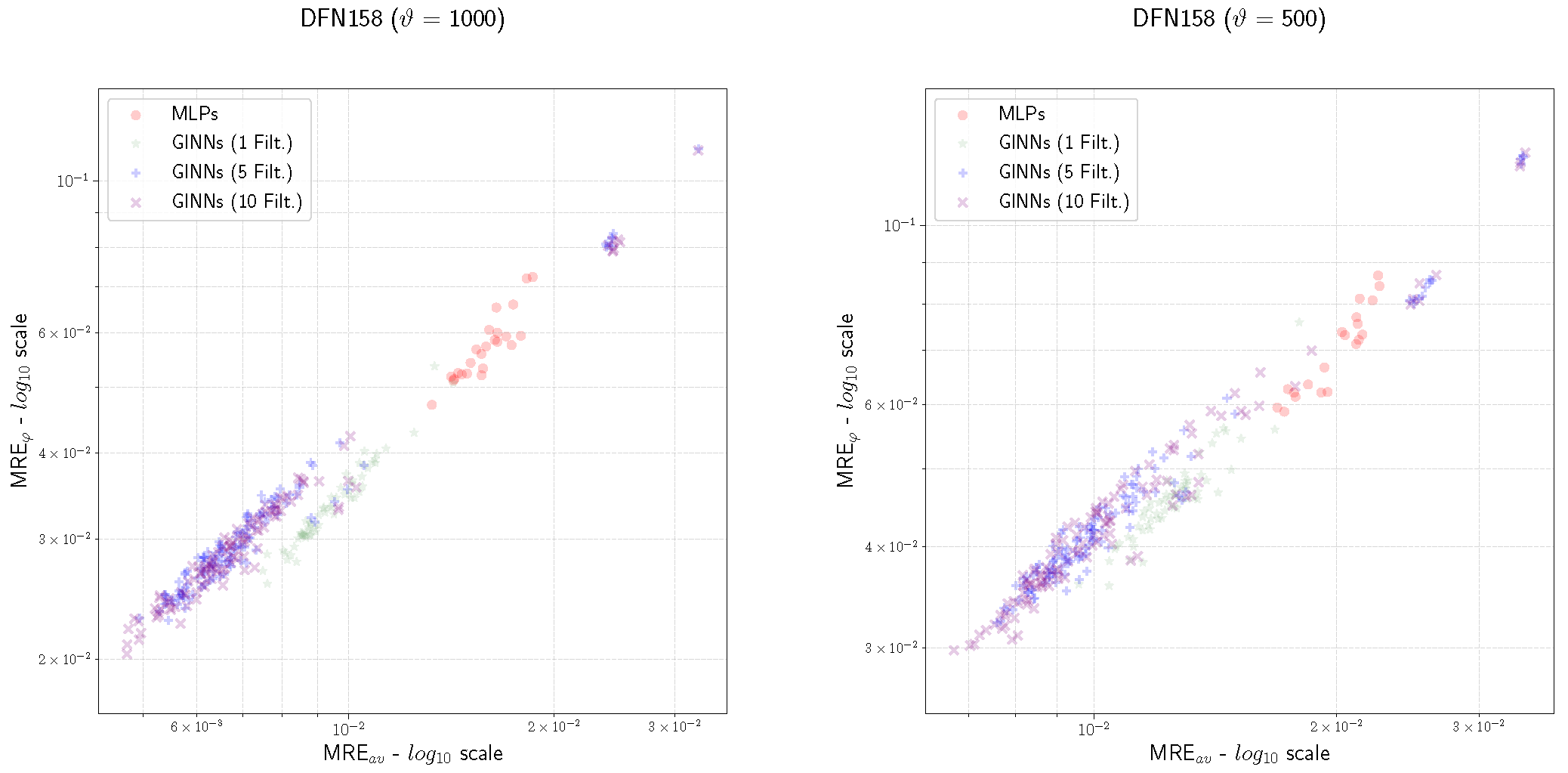
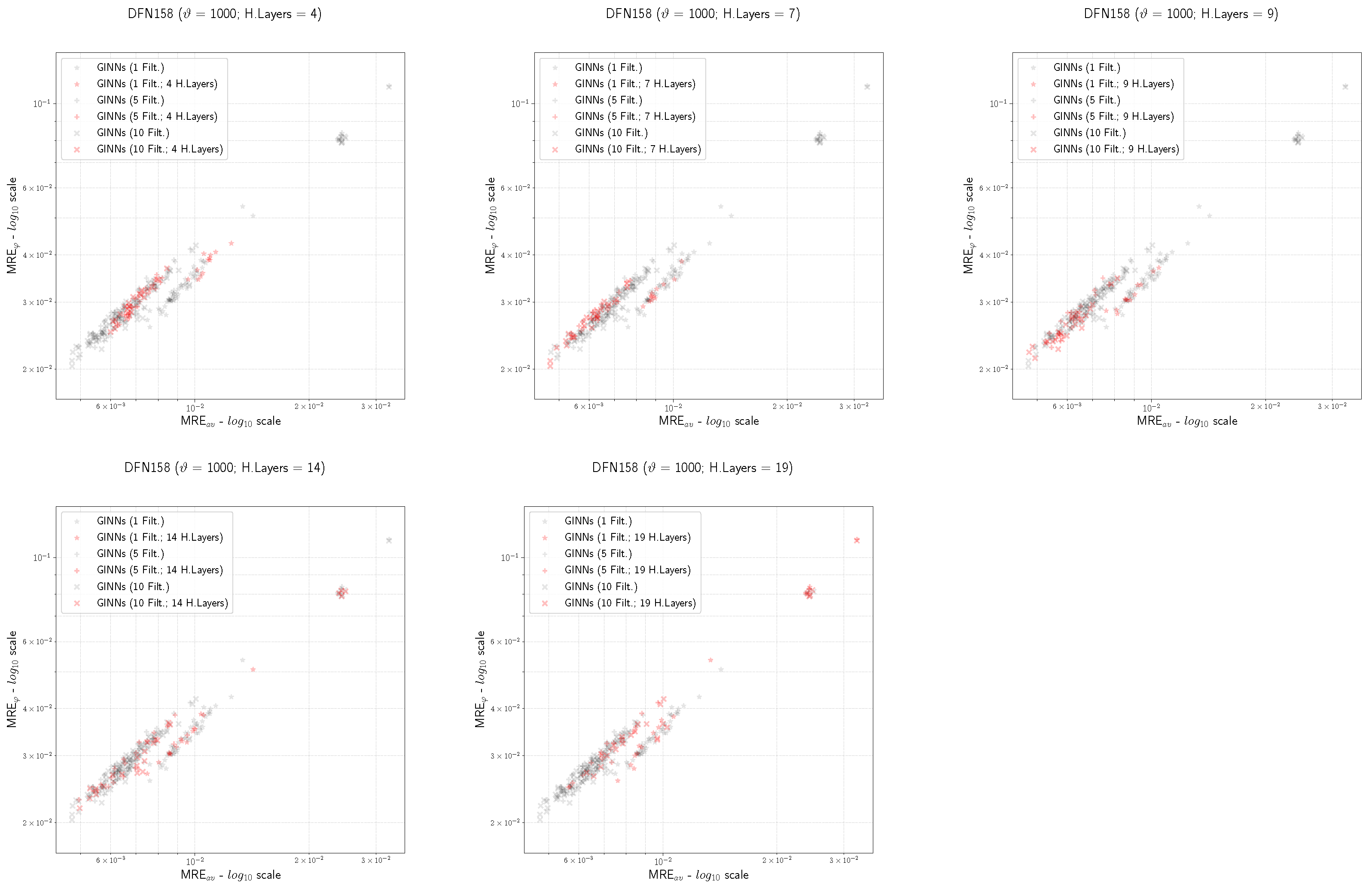
- For the GINN models, we consider the depth parameter values . The rationale behind this choice is that it is a set of values around 8, which is the number of deterministic fractures that, on average, represent an inlet-outlet flow path for DFN158 (in the absence of a value equivalent to that cannot be easily computed for DFN158);
- The GI layers are built with respect to the adjacency matrix A of DFN158; indeed, we do not need to introduce the line graph of the network since the features (i.e., the transmissivities) are assigned to the nodes of the graph and not to the edges.
- Both the MRE and the MRE of the GINNs are almost always smaller than the ones of the MLPs, independently of ;
- Looking at the filter hyper-parameter F, we observe that the GINN performances are better as F increases (from , to , to ).
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BA | Barabási–Albert |
| CNN | Convolutional Neural Network |
| CwD | Circulation with Demand |
| DCNN | Diffusion-Convolutional Neural Networks |
| DFN | Discrete Fracture Network |
| DL | Deep Learning |
| ER | Erdos–Rényi |
| FC | Fully-Connected |
| GCN | Graph Convolutional Network |
| GI | Graph-Informed |
| GINN | Graph-Informed Neural Network |
| GNN | Graph Neural Network |
| ML | Machine Learning |
| MLP | Multi-Layer Perceptron |
| MRE | Mean Relative Error |
| MRE | Edge-Wise Average MRE |
| MRE | MRE on the Predicted Maxflow/Outflow |
| MSE | Mean Square Error |
| NIM | Network Interdiction Model |
| NN | Neural Network |
| UQ | Uncertainty Quantification |
Appendix A. Multi-Sets
- Equality: is equal to () if and , for each .
- Inclusion: is included in () if and , for each . Analogously, is included in, or equal to, () if and , for each .
- Intersection: the intersection of and () is a multi-set , such that and , for each .
- Union: the union of and () is a multi-set , such that and , for each .
- Sum: the sum of and () is a multi-set , such that and , for each .
- Difference: the difference of and () is a multi-set , such that .
References
- Brandes, U.; Erlebach, T. (Eds.) Network Analysis—Methodological Foundations; Theoretical Computer Science and General Issues; Springer: Berlin/Heidelberg, Germay, 2005; Volume 3418. [Google Scholar] [CrossRef]
- Gori, M.; Monfardini, G.; Scarselli, F. A new model for learning in graph domains. In Proceedings of the 2005 IEEE International Joint Conference on Neural Networks, Montreal, QC, Canada, 31 July–4 August 2005; Volume 2, pp. 729–734. [Google Scholar] [CrossRef]
- Micheli, A. Neural Network for Graphs: A Contextual Constructive Approach. IEEE Trans. Neural Netw. 2009, 20, 498–511. [Google Scholar] [CrossRef]
- Scarselli, F.; Gori, M.; Tsoi, A.C.; Hagenbuchner, M.; Monfardini, G. The Graph Neural Network Model. IEEE Trans. Neural Netw. 2009, 20, 61–80. [Google Scholar] [CrossRef]
- Wu, Z.; Pan, S.; Chen, F.; Long, G.; Zhang, C.; Yu, P.S. A Comprehensive Survey on Graph Neural Networks. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 4–24. [Google Scholar] [CrossRef]
- Bruna, J.; Zaremba, W.; Szlam, A.; LeCun, Y. Spectral networks and locally connected networks on graphs. In Proceedings of the International Conference on Learning Representations, Banff, AB, Canada, 14–16 April 2014. [Google Scholar]
- Defferrard, M.; Bresson, X.; Vandergheynst, P. Convolutional neural networks on graphs with fast localized spectral filtering. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: Red Hook, NY, USA, 2016; Volume 29, pp. 3844–3852. [Google Scholar]
- Kipf, T.; Welling, M. Semi-supervised classification with graph convolutional networks. In Proceedings of the International Conference on Learning Representations, Toulon, France, 24–26 April 2017. [Google Scholar]
- Hamilton, W.; Ying, Z.; Leskovec, J. Advances in Neural Information Processing Systems; Curran Associates, Inc.: Red Hook, NY, USA, 2017; Volume 30. [Google Scholar]
- Monti, F.; Boscaini, D.; Masci, J.; Rodolà, E.; Svoboda, J.; Bronstein, M.M. Geometric deep learning on graphs and manifolds using mixture model CNNs. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 5115–5124. [Google Scholar]
- Niepert, M.; Ahmed, M.; Kutzkov, K. Learning Convolutional Neural Networks for Graphs. In Proceedings of the 33rd International Conference on Machine Learning, New York, NY, USA, 20–22 June 2016; Volume 48, pp. 2014–2023. [Google Scholar]
- Gao, H.; Wang, Z.; Ji, S. Large-Scale Learnable Graph Convolutional Networks. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, London, UK, 19–23 August 2018. [Google Scholar] [CrossRef]
- Li, Q.; Han, Z.; Wu, X.M. Deeper Insights Into Graph Convolutional Networks for Semi-Supervised Learning. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; Volume 32. [Google Scholar]
- Kleinberg, J.; Tardos, E. Algorithm Design; Addison-Wesley: Boston, MA, USA, 2005. [Google Scholar]
- Dimitrov, N.B.; Morton, D.P. Interdiction Models and Applications. In Handbook of Operations Research for Homeland Security; Herrmann, J.W., Ed.; Springer: New York, NY, USA, 2013; pp. 73–103. [Google Scholar] [CrossRef]
- Berrone, S.; Della Santa, F.; Pieraccini, S.; Vaccarino, F. Machine learning for flux regression in discrete fracture networks. GEM-Int. J. Geomath. 2021, 12, 9. [Google Scholar] [CrossRef]
- Berrone, S.; Della Santa, F. Performance Analysis of Multi-Task Deep Learning Models for Flux Regression in Discrete Fracture Networks. Geosciences 2021, 11, 131. [Google Scholar] [CrossRef]
- Berrone, S.; Della Santa, F.; Mastropietro, A.; Pieraccini, S.; Vaccarino, F. Discrete Fracture Network insights by eXplainable AI. Machine Learning and the Physical Sciences. In Proceedings of the Workshop at the 34th Conference on Neural Information Processing Systems (NeurIPS), Neural Information Processing Systems Foundation, Virtual, 6–7 December 2002; Available online: https://ml4physicalsciences.github.io/2020/ (accessed on 1 February 2022).
- Berrone, S.; Della Santa, F.; Mastropietro, A.; Pieraccini, S.; Vaccarino, F. Layer-wise relevance propagation for backbone identification in discrete fracture networks. J. Comput. Sci. 2021, 55, 101458. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Atwood, J.; Towsley, D. Diffusion-Convolutional Neural Networks. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: Red Hook, NY, USA, 2016; Volume 29, pp. 1993–2001. [Google Scholar]
- Donon, B.; Donnot, B.; Guyon, I.; Marot, A. Graph Neural Solver for Power Systems. In Proceedings of the International Joint Conference on Neural Networks, Budapest, Hungary, 14–19 July 2019; pp. 1–8. [Google Scholar] [CrossRef]
- Donon, B.; Clément, R.; Donnot, B.; Marot, A.; Guyon, I.; Schoenauer, M. Neural networks for power flow: Graph neural solver. Electr. Power Syst. Res. 2020, 189, 106547. [Google Scholar] [CrossRef]
- Raissi, M.; Karniadakis, G.E. Hidden physics models: Machine learning of nonlinear partial differential equations. J. Comput. Phys. 2018, 357, 125–141. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis; George, E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Ding, S. The α-maximum flow model with uncertain capacities. Appl. Math. Model. 2015, 39, 2056–2063. [Google Scholar] [CrossRef]
- Malhotra, V.; Kumar, M.; Maheshwari, S. An O(|V|3) algorithm for finding maximum flows in networks. Inf. Process. Lett. 1978, 7, 277–278. [Google Scholar] [CrossRef]
- Goldberg, A.V.; Tarjan, R.E. A New Approach to the Maximum-Flow Problem. J. ACM 1988, 35, 921–940. [Google Scholar] [CrossRef]
- Cheriyan, J.; Maheshwari, S.N. Analysis of preflow. In Foundations of Software Technology and Theoretical Computer Science; Nori, K.V., Kumar, S., Eds.; Springer: Berlin/Heidelberg, Germay, 1988; pp. 30–48. [Google Scholar]
- King, V.; Rao, S.; Tarjan, R. A Faster Deterministic Maximum Flow Algorithm. J. Algorithms 1994, 17, 447–474. [Google Scholar] [CrossRef]
- Goldberg, A.V.; Rao, S. Beyond the Flow Decomposition Barrier. J. ACM 1998, 45, 783–797. [Google Scholar] [CrossRef]
- Golumbic, M.C. (Ed.) Algorithmic Graph Theory and Perfect Graphs; Academic Press: Cambridge, MA, USA, 1980. [Google Scholar]
- Degiorgi, D.G.; Simon, K. A dynamic algorithm for line graph recognition. In Graph-Theoretic Concepts in Computer Science; Nagl, M., Ed.; Springer: Berlin/Heidelberg, Germay, 1995; pp. 37–48. [Google Scholar] [CrossRef]
- Barabási, A.L.; Albert, R. Emergence of Scaling in Random Networks. Science 1999, 286, 509–512. [Google Scholar] [CrossRef]
- Albert, R.; Barabási, A.L. Topology of Evolving Networks: Local Events and Universality. Phys. Rev. Lett. 2000, 85, 5234–5237. [Google Scholar] [CrossRef]
- Hagberg, A.A.; Schult, D.A.; Swart, P.J. Exploring Network Structure, Dynamics, and Function using NetworkX. In Proceedings of the 7th Python in Science Conference, Pasadena, CA, USA, 19–24 August 2008; Varoquaux, G., Vaught, T., Millman, J., Eds.; pp. 11–15. [Google Scholar]
- Freeman, L.C. A Set of Measures of Centrality Based on Betweenness. Sociometry 1977, 40, 35–41. [Google Scholar] [CrossRef]
- Bavelas, A. Communication Patterns in Task-Oriented Groups. J. Acoust. Soc. Am. 1950, 22, 725–730. [Google Scholar] [CrossRef]
- Sabidussi, G. The centrality index of a graph. Psychometrika 1966, 31, 581–603. [Google Scholar] [CrossRef]
- Erdős, P.; Rényi, A. On Random Graphs. Publ. Math. 1959, 6, 290–297. [Google Scholar]
- Gilbert, E.N. Random Graphs. Ann. Math. Stat. 1959, 30, 1141–1144. [Google Scholar] [CrossRef]
- Reilly, W. Highway Capacity Manual; Transport Research Board: Washington, DC, USA, 2000. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. In Proceedings of the 32nd International Conference on International Conference on Machine Learning, ICML’15, Lille, France, 7–9 July 2015; Volume 37, pp. 448–456. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Glorot, X.; Bengio, Y. Understanding the difficulty of training deep feedforward neural networks. J. Mach. Learn. Res. 2010, 9, 249–256. [Google Scholar]
- Kingma, D.P.; Ba, J.L. Adam: A method for stochastic optimization. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015—Conference Track Proceedings, San Diego, CA, USA, 7–9 May 2015; pp. 1–15. [Google Scholar]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems, 2015. Software. Available online: tensorflow.org (accessed on 1 February 2022).
- Adler, P. Fractures and Fracture Networks; Kluwer Academic: Dordrecht, The Netherlands, 1999. [Google Scholar]
- Cammarata, G.; Fidelibus, C.; Cravero, M.; Barla, G. The Hydro-Mechanically Coupled Response of Rock Fractures. Rock Mech. Rock Eng. 2007, 40, 41–61. [Google Scholar] [CrossRef]
- Fidelibus, C.; Cammarata, G.; Cravero, M. Hydraulic characterization of fractured rocks. In Rock Mechanics: New Research; Abbie, M., Bedford, J.S., Eds.; Nova Science Publishers Inc.: New York, NY, USA, 2009. [Google Scholar]
- Hyman, J.D.; Hagberg, A.; Osthus, D.; Srinivasan, S.; Viswanathan, H.; Srinivasan, G. Identifying Backbones in Three-Dimensional Discrete Fracture Networks: A Bipartite Graph-Based Approach. Multiscale Model. Simul. 2018, 16, 1948–1968. [Google Scholar] [CrossRef]
- Sanchez-Vila, X.; Guadagnini, A.; Carrera, J. Representative hydraulic conductivities in saturated grqundwater flow. Rev. Geophys. 2006, 44, 1–46. [Google Scholar] [CrossRef]
- Svensk Kärnbränslehantering, A.B. Data Report for the Safety Assessment, SR-Site; Technical Report TR-10-52; SKB: Stockholm, Sweden, 2010. [Google Scholar]
- Hyman, J.D.; Aldrich, G.; Viswanathan, H.; Makedonska, N.; Karra, S. Fracture size and transmissivity correlations: Implications for transport simulations in sparse three-dimensional discrete fracture networks following a truncated power law distribution of fracture size. Water Resour. Res. 2016, 52, 6472–6489. [Google Scholar] [CrossRef]
- Berrone, S.; Pieraccini, S.; Scialò, S. A PDE-constrained optimization formulation for discrete fracture network flows. SIAM J. Sci. Comput. 2013, 35, B487–B510. [Google Scholar] [CrossRef]
- Berrone, S.; Pieraccini, S.; Scialò, S. On simulations of discrete fracture network flows with an optimization-based extended finite element method. SIAM J. Sci. Comput. 2013, 35, A908–A935. [Google Scholar] [CrossRef][Green Version]
- Berrone, S.; Pieraccini, S.; Scialò, S. An optimization approach for large scale simulations of discrete fracture network flows. J. Comput. Phys. 2014, 256, 838–853. [Google Scholar] [CrossRef][Green Version]
- Srinivasan, S.; Karra, S.; Hyman, J.; Viswanathan, H.; Srinivasan, G. Model reduction for fractured porous media: A machine learning approach for identifying main flow pathways. Comput. Geosci. 2019, 23, 617–629. [Google Scholar] [CrossRef]
- Blizard, W.D. Multiset theory. Notre Dame J. Form. Log. 1989, 30, 36–66. [Google Scholar] [CrossRef]
- Hein, J.L. Discrete Mathematics; Jones & Bartlett Publishers: Burlington, MA, USA, 2003. [Google Scholar]






| GINNs | MLPs | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Rank | MRE | Pool. | Init. | Rank | MRE | ||||||||
| 7000 | 1/528 | 0.00707 | 9 | 1 | elu | 64 | - | G.Norm. | 446/528 | 0.00914 | 3 | swish | 32 |
| 2/528 | 0.00712 | 9 | 1 | elu | 128 | - | Norm. | 453/528 | 0.00934 | 3 | swish | 64 | |
| 3/528 | 0.00713 | 9 | 1 | elu | 32 | - | Norm | 455/528 | 0.00939 | 4 | swish | 32 | |
| 1000 | 1/528 | 0.00933 | 9 | 1 | softplus | 32 | - | G.Norm. | 338/528 | 0.01272 | 5 | softplus | 32 |
| 2/528 | 0.00940 | 7 | 1 | elu | 32 | - | Norm. | 353/528 | 0.01289 | 4 | elu | 32 | |
| 3/528 | 0.00952 | 7 | 1 | elu | 32 | - | G.Norm. | 357/528 | 0.01292 | 5 | elu | 32 | |
| 500 | 1/528 | 0.01056 | 7 | 1 | softplus | 32 | - | Norm. | 263/528 | 0.01433 | 5 | softplus | 32 |
| 2/528 | 0.01077 | 5 | 1 | relu | 32 | - | G.Norm. | 279/528 | 0.01448 | 5 | softplus | 64 | |
| 3/528 | 0.01092 | 7 | 1 | softplus | 32 | - | G.Norm. | 284/528 | 0.01452 | 4 | softplus | 32 | |
| GINNs | MLPs | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Rank | MRE | Pool. | Init. | Rank | MRE | ||||||||
| 7000 | 1/528 | 0.00087 | 14 | 10 | softplus | 32 | max | G.Norm. | 442/528 | 0.00557 | 2 | elu | 32 |
| 2/528 | 0.00092 | 14 | 10 | softplus | 32 | mean | G.Norm. | 445/528 | 0.00571 | 5 | softplus | 64 | |
| 3/528 | 0.00099 | 12 | 10 | softplus | 32 | mean | G.Norm | 446/528 | 0.00573 | 5 | elu | 32 | |
| 1000 | 1/528 | 0.00465 | 9 | 1 | elu | 32 | - | G.Norm. | 263/528 | 0.01038 | 3 | softplus | 32 |
| 2/528 | 0.00478 | 19 | 1 | elu | 32 | - | G.Norm. | 264/528 | 0.01038 | 2 | swish | 32 | |
| 3/528 | 0.00479 | 14 | 1 | softplus | 32 | - | Norm. | 267/528 | 0.01043 | 3 | softplus | 64 | |
| 500 | 1/528 | 0.00593 | 14 | 1 | elu | 32 | - | G.Norm. | 114/528 | 0.01266 | 2 | swish | 32 |
| 2/528 | 0.00674 | 14 | 1 | softplus | 32 | - | G.Norm. | 118/528 | 0.01272 | 2 | swish | 64 | |
| 3/528 | 0.00688 | 19 | 1 | softplus | 32 | - | G.Norm. | 119/528 | 0.01272 | 5 | softplus | 32 | |
| Avg. Time per Epoch (s) | ||
|---|---|---|
| GINNs | MLPs | |
| Mean | 1.099 | 0.565 |
| Std | 1.359 | 0.292 |
| 25th perc. | 0.318 | 0.380 |
| 50th perc. | 0.567 | 0.431 |
| 75th perc. | 1.296 | 0.632 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Berrone, S.; Della Santa, F.; Mastropietro, A.; Pieraccini, S.; Vaccarino, F. Graph-Informed Neural Networks for Regressions on Graph-Structured Data. Mathematics 2022, 10, 786. https://doi.org/10.3390/math10050786
Berrone S, Della Santa F, Mastropietro A, Pieraccini S, Vaccarino F. Graph-Informed Neural Networks for Regressions on Graph-Structured Data. Mathematics. 2022; 10(5):786. https://doi.org/10.3390/math10050786
Chicago/Turabian StyleBerrone, Stefano, Francesco Della Santa, Antonio Mastropietro, Sandra Pieraccini, and Francesco Vaccarino. 2022. "Graph-Informed Neural Networks for Regressions on Graph-Structured Data" Mathematics 10, no. 5: 786. https://doi.org/10.3390/math10050786
APA StyleBerrone, S., Della Santa, F., Mastropietro, A., Pieraccini, S., & Vaccarino, F. (2022). Graph-Informed Neural Networks for Regressions on Graph-Structured Data. Mathematics, 10(5), 786. https://doi.org/10.3390/math10050786







