Abstract
A secret sharing scheme allocates to each participant a share of a secret in such a way that authorized subsets of participants can reconstruct the secret, while shares of unauthorized subsets of participants provide no useful information about the secret. For positive integers with , an –threshold essential secret sharing scheme is an algorithm that decomposes a secret S into n shares, s of which are essential, in a way that authorized subsets are precisely those with at least t members, at least r of whom are essential. This work proposes a lossless linear algebraic –threshold essential secret image sharing scheme that decomposes the secret, S, into equally-sized shares, each of size the size of S. For each block, B, of S, the scheme assigns to the n participants distinct signature vectors in the vector space , where is a suitable positive integer, typically between 2 and 5, inclusive. These signature vectors must adhere to some admissibility conditions in order to satisfy the secret sharing threshold properties. The decomposition of B into n shares is obtained by partitioning B into t vectors, then computing the share of the jth participant (), as a linear combination of these parts with coefficients from the signature . The presented simulations showcase the effectiveness and robustness of the proposed scheme against standard statistical and security attacks. They further demonstrate its superiority with respect to existing schemes.
Keywords:
secret sharing; threshold secret sharing; essential secret sharing; secret image sharing; admissible tracks; chaos MSC:
94A62, 94A60
1. Introduction
A –threshold secret sharing scheme is any approach that decomposes a secret S into n shares such that any collection of at least t shares can reconstruct the secret S, while any collection of less than t shares does not provide any useful information about S. Most existing secret sharing schemes are based on polynomial interpolation [1], hyperplane geometry [2], and the Chinese remainder theorem [3]. In a –threshold secret sharing scheme, referred to as a –SS scheme, each participant () receives a share , where all shares enjoy the same importance. Thus, the secret can be recovered when any t participants present their shares. In a –SS scheme, no participant has a privilege over another, and any subset consisting of t or more participants is an authorized set for reconstructing the secret, S. However, some applications may require allowing privileged (or essential) participants. For example, in a banking application, a bank manager would be considered an essential participant among a group of bank employees sharing a bank safe password. In such a scenario, a set of participants is authorized to recover the secret whenever it has the required size, and it includes the required number of essential participants. This motivates the definition of an essential secret sharing scheme: if are positive integers, then an –essential threshold secret sharing scheme, or an –ESS scheme for short, is any method of decomposing a secret, S, into s essential and non-essential shares, such that any set of at least t shares which contains at least r essential shares is able to reconstruct S; while any set of shares with fewer than t shares or with fewer than r essential shares is unable to reveal any useful information about S. With n participants, s of whom are essential participants, an –ESS scheme allocates each of the s essential shares to an essential participant and each of the non-essential shares to a non-essential participant.
In the last two decades, the widespread use of digital images has led scientists and engineers in developing secret image sharing techniques for decomposing secret images into shares. In a secret image sharing setting, shares are often referred to as shadow images. A number of –threshold secret image sharing schemes based on different techniques such as polynomial interpolation, hyperplane geometry, the Chinese remainder theorem, and matrix theory have been published by researchers [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18]. Since these schemes do not possess the essentiality condition, all participants have the same importance in the reconstruction phase. However, some applications require the presence of essential participants. Thus, –threshold essential secret image sharing schemes, –ESIS schemes for short, have grasped the attention of researchers [19,20,21,22,23,24]. However, some of these –ESIS schemes suffer from at least one of the following drawbacks: (i) the non-essential shadow images and essential shadow images are of different sizes; (ii) the concatenation of sub-shadow images. These are reviewed in more detail in the present paper.
In [19,20], the proposed –ESIS schemes are based on polynomial interpolation. Li et al. [21] proposed an –ESIS scheme based on derivative polynomial and Birkhoff interpolation. While this scheme solves the issues of unequal size of shadows and concatenation of sub-shadows in the schemes of [19,20], it generates shadow images of size the size of the secret. Hence, its individual and total shadow sizes are larger than those of [19,20]. In [22], a three-layered structure –ESIS scheme based on the Lagrange interpolation is proposed that can generate equal-sized essential and non-essential shadow images. However, this property is achieved only when the parameters are properly chosen. Li et al. [23] proposed an –ESIS scheme, with , while this scheme solves problems such as generating shadow images of different sizes, concatenation of sub-shadows and the use of multiple secret image sharing schemes, the requirement restricts application of this scheme. In [24], an –ESIS scheme using a derivative polynomial is proposed, which generates equally sized shadow images. It also removes the concatenation operation in the sharing phase.
Kanso et al. [25] proposed a lossless linear algebraic –SIS scheme, referred to as KGA throughout this work, that for each secret block, B, associates to the i-th participant () a vector, , where is a chosen positive integer and must satisfy some admissibility conditions. The vector, , is called the signature of the i-th participant (for the secret block at hand). The i-th share is then constructed as a linear combination of the t vectors from the secret block, B, with coefficients from . In this paper, we extend KGA to propose a lossless –threshold essential secret image sharing scheme. The proposed scheme has the following properties:
- It is a linear algebraic scheme.
- It decomposes the secret S into equally-sized shares each of size .
- It requires no concatenation in the share generation phase.
- It does not require multiple secret image sharing schemes.
If denote the n participants, then we assume without loss of generality that are the essential participants and are the non-essential participants; meanwhile, similarly to KGA, the main frame of work in the proposed scheme is to assign a signature vector, , to each participant, , to satisfy the different threshold properties, which now include the essentiality of the shares allocated to ; one needs to modify the admissibility conditions of the signature vectors. More specifically, the essential signatures, , need to be linearly independent, while the non-essential signatures, , need to span a –dimensional space, and every of them must form a basis for this space. In addition to these “threshold” constraints, the signature vectors need to satisfy further conditions that guarantee security of the proposed scheme. These are defined in detail in the following sections.
Simulations demonstrate the efficiency of the proposed scheme. They also show its robustness against well-known statistical and security attacks. Moreover, in comparison with existing schemes, the proposed scheme is shown to have superior performance over existing schemes.
We can summarize the main contributions as follows:
- The proposed ESIS scheme is lossless. Therefore, it can be used for sharing any type of digital content including textual data.
- The scheme does not require multiple secret image sharing schemes.
- It requires no concatenation operation in the sharing phase.
- The scheme generates equally sized and similarly structured shadow images, thus making essential and non-essential shares indistinguishable to an intruder.
- The scheme has a preprocessing phase independent of the secret image. The signatures, , can be generated in advance if the length of S is known. There is a work-around to avoid high storage cost if the signatures are to be computed in advance.
- The proposed scheme is competitive with existing ESIS schemes.
The paper is organized as follows: Section 2 provides a brief description of the KGA scheme [25]. In Section 3, we present a detailed description of the proposed –ESIS scheme. Section 4 is devoted to experimental results and security analysis. In Section 5, we compare the performance of the proposed scheme with existing ones. Some concluding remarks are given in Section 6.
2. Background
KGA is a –SIS scheme proposed in [25] which uses admissible matrices with entries in the field , for some positive integer , to generate shadow images for sharing a secret image. Admissible matrices are defined and studied in [26,27].
Definition 1
([27]). An matrix X, where , is said to be t–admissible if it satisfies the following properties:
- Every submatrix of X is non-singular.
- Every submatrix of X is non-singular.
All computations in KGA are performed in the field for some chosen positive integer, . With the number of participants, n, and the threshold, t, known, KGA produces for each secret block, B, an admissible matrix X, whose rows are assigned to the participants as signature vectors. This step is independent of the secret image. Now, for a given secret image, the first step in KGA is to obtain a matrix representation, Q, in of the secret image. To this end, the preprocessing phase concatenates the entries (bytes) of the secret image in groups of bytes each, to produce -bit values which correspond to elements of . The secret image is padded if necessary, and shuffled, then reshaped to populate the matrix Q of t rows in a column-first order. Columns of the matrix Q are then divided into groups of m (where m is a parameter) each to form blocks. Shares are generated for each block, B, as explained in the following, and then block shares of each participant are concatenated and converted back to bytes to produce their shadow image. If , then the ith share of any block, B, of the secret is defined to be the i-th row of the matrix , where X is an admissible matrix. Therefore, Y constitutes all the shares.
More specifically, given blocks , the shadow images of the proposed scheme are obtained using -distinct admissible matrices. In [25], admissible matrices are constructed using a 3-dimensional chaotic cat map [28], defined by
where
with being positive integers. Given an initial condition with entries in , iterated applications of Equation (1) generate a sequence of 3-tuples with pseudorandom entries in .
On the basis of the admissibility condition on the matrices X, the lossless recovery of S is straight forward in the presence of any t shares.
3. The Proposed Scheme
In this work, we extend the KGA –SIS scheme to propose an –ESIS scheme. Similarly to KGA, all computations are in the field , where . We use a fixed correspondence, as follows:
to move between the field and the group , where with .
The main framework and the preprocessing of the proposed scheme are as in KGA: the shares of a secret block, B, of S are defined to be the rows of the matrix
where B represents a block of the secret, X is an admissible matrix, and Y constitutes the shares. To achieve the required essentiality properties, the definition of admissibility (hence the generation of the signatures matrix X) needs to be modified.
Suppose that some rows of Y and their corresponding rows of X are presented in order to recover the secret block, B. Let and denote the submatrices of Y and X consisting of the provided rows. If , then the linear system has a unique solution (note that this system is consistent since is a solution). On the other hand, if , then this system is under-determined, hence it has infinitely many solutions. This means that we need to design the signature vectors (rows of X) in a way that signature vectors of any unauthorized set of participants for recovery of the secret constitute a submatrix with rank less than t, while submatrices of X corresponding to authorized sets have rank t. This can be achieved by making sure that the essential signatures are linearly independent, while the non-essential signatures span a –dimensional space. This means that to obtain a submatrix of X with rank t, we may use at most non-essential signatures, thus we need at least r essential signatures. To make sure that any non-essential participants can cooperate together with at least r essential participants, we need to also require that every non-essential signature vectors are linearly independent. Moreover, if (respectively, ) denotes the subspace of spanned by the essential (respectively non-essential) signature vectors, then we must have to assure no overlap between essential and non-essential signatures. This is achieved by requiring the vectors to be linearly independent.
3.1. The Preprocessing Phase
Let P denote the matrix of intensity values of the secret image. Given the parameters and m, the preprocessing phase of the proposed –ESIS scheme generates blocks of the secret according to Algorithm 1.
| Algorithm 1: Preprocessing of the secret image |
| Data: Matrix P and parameters and m |
| Result: Blocks |
| 1 reshape P into a 1-dimensional array |
| 2 pad so that its length equals for some integer |
| 3 shuffle the entries of using a pseudorandom number generator |
| 4 concatenate every consecutive entries of into a single entry |
| 5 reshape into a matrix |
| 6 Partition Q into blocks , each of size |
| 7 Return |
3.2. The Construction of Shadow Images
The proposed –ESIS scheme shares each block (), using an admissible matrix . In [25], admissible matrices are generated from the 3-dimensional cat map defined in (1). In this work, we modify the admissible matrix generation algorithm proposed in [25] to satisfy the admissibility properties of the proposed –ESIS scheme. Algorithm 2 presents the procedure for generating admissible matrices. The algorithm generates linearly independent vectors in , as in KGA [25]. The first s vectors are associated with the essential participants , and the remaining vectors are associated with the non-essential participants . The scheme then generates vectors , as linear combinations of the vectors , and associates them with the remaining non-essential participants .
Upon generation of the admissible matrices , the shadow images can be produced as follows. Given secret blocks, , the corresponding share matrices, , can be obtained by computing the following:
The row vectors of , namely constitute the shares corresponding to block . More precisely, each (for and ) constitutes a share block of the shadow image associated with essential participant , whereas each share (for and ) constitutes a share block of the shadow image associated with non-essential participant . Algorithm 3 outlines the procedure for generating the shadow images .
| Algorithm 2: Generation of admissible matrices |
| Data: Parameters and m of the scheme |
| Data: Cat matrix A and initial state |
| Result: Admissible matrices |
 |
| Algorithm 3: Generation of shadow images |
| Data: Admissible matrices |
| Data: Blocks |
| Result: Shadow images |
| 1for to γdo |
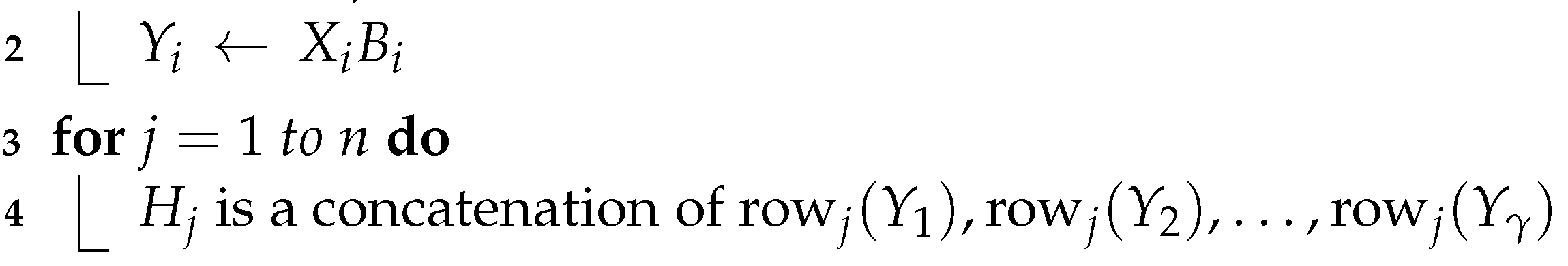 |
| 5 Convert each element of to an integer via the correspondence of Equation (3) |
| 6 Break each integer value of to bytes |
| 7 Shuffle according to some pseudorandom sequences , respectively, generated using Equation (1), where each sequence has length |
| 8 Reshape into rectangular arrays for presentation as images |
| 9 Return |
| 10 End |
3.3. Reconstruction of the Secret Image
Suppose that t shadow images , from which r shadow images are essential, are submitted to a central authority holding the secret key. The procedure for the construction of the secret image is as follows:
- Use the secret key to generate the sequences .
- Apply the inverse of the permutations , which sort , respectively, on to unshuffle them.
- For each sequence resulting from the preceding step, group every bytes into an integer and convert it to an element in using Equation (3).
- Divide each resulting sequence into blocks each of length m.
- Construct matrices , where (for and ) consists of the i–th blocks of the j–th sequence obtained in the preceding step. That is, each consists of rows of the matrix generated in Algorithm 3.
- Use the secret key to generate the matrices . Let be the submatrix of , induced by the rows .
- Since (for ), and by the admissibility of X, is non-singular. Thus, we obtain .
- Once all the blocks are obtained, we can reverse Algorithm 1 to obtain the secret image P.
It is evident that if at most of the t presented shadow images are essential, then from the construction of the admissible matrices , the matrices are singular matrices. In such case, the scheme fails to reconstruct the secret image. In Section 4, we investigate the security of the proposed scheme, and analyze the security level of the aforementioned scenario.
The security of the proposed scheme depends on keeping the shadow images secure. The dealer has various means to deliver the shadow images to the intended participant, such as (1) a secure channel, (2) an encryption scheme, and (3) a steganographic scheme.
4. Performance Analysis
This section is devoted to showcase the performance of the proposed –ESIS scheme. We present simulation results to demonstrate robustness of the proposed scheme against statistical and security attacks. In all simulations, we set the number of bytes per value , hence the scheme is tested in the field . For the cat map of Equation (1), we use the coefficient matrix
which is obtained by setting . The largest eigenvalue of A is , which guarantees the chaotic behavior of the cat map.
We study the performance of the proposed secret image sharing scheme using two standard test images: the grayscale image Elaine, and the color image Lena. Both test images are presented in Figure 1. Further parameters of the tests are presented in Table 1.

Figure 1.
The grayscale secret image Elaine (left) and the color secret image Lena (right).

Table 1.
Image information and test parameters.
Figure 2 presents the six shadow images corresponding to the image Elaine, each of size . The essential shadow images are and , whereas the remaining ones are the non-essential shadow images. Similarly, Figure 3 presents the five RGB shadow images corresponding to the image Lena, each of size . The essential shadow images are and , whereas the remaining ones are the non-essential shadow images.

Figure 2.
The shadow images corresponding to the test image Elaine. (Top): the essential shadow images , and . (Bottom): the non-essential shadow images , and .
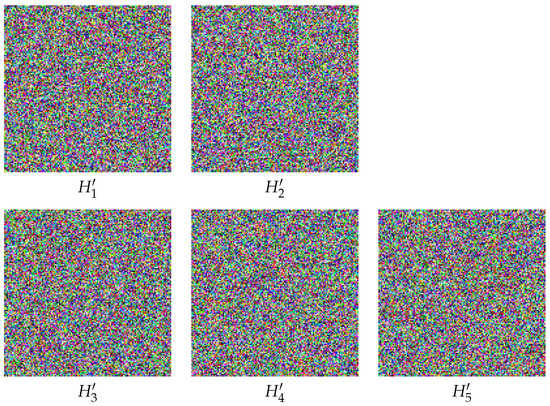
Figure 3.
The color shadow images of test image Lena. (Top): the essential shadow images and . (Bottom): the non-essential shadow images , and .
One way to deliver the shadow images to the intended participants is using a steganographic scheme, such as that proposed in [29]. Suppose that the host image is the one presented in Figure 4 (left). The stego image carrying the shadow image presented in Figure 2 is depicted in Figure 4 (right). It is evident that one cannot distinguish between the host image and the stego image (for further details the reader is referred to [29]).

Figure 4.
The host image (left), and the stego image carrying (right).
4.1. Statistical Analysis
The proposed –ESIS scheme is an extension of the scheme proposed in [25], where the shadow images are all essential. Therefore, the shadow images are expected to be random-looking [25]. In this section, we present histogram analysis, correlation coefficient analysis, and entropy analysis of shadow images generated by the proposed –ESIS scheme. For further details about these tests, the reader is referred to [25]. Furthermore, we evaluated the randomness of the shadow images using one of the most common used test suites, namely the statistical test suite proposed in [30].
Figure 5 shows that the histograms of sample non-essential shadow image corresponding to the Elaine image and an essential shadow image corresponding to the Lena Image. It is evident that one cannot deduce any useful information about the secret image from the histogram of its corresponding shadow image. The histograms of the other shadow images possess similar behavior—hence, we omit them.
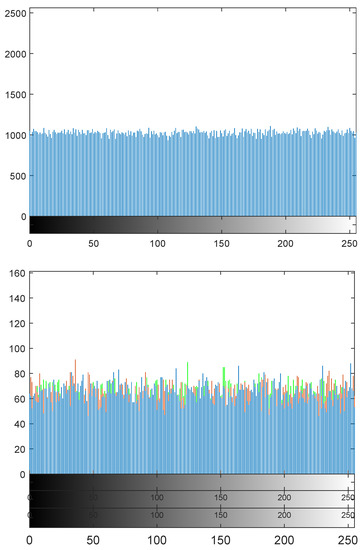
Figure 5.
(Top): histogram of a non-essential shadow image of Elaine. (Bottom): histogram of an essential shadow image of Lena.
Table 2 presents the correlation coefficients between 10,000 random pairs of adjacent pixels in the horizontal, vertical, and diagonal directions of the test image Elaine and that of the 6 shadow images. On the other hand, Table 3 presents the correlation coefficients between Lena and that of the five shadow images. It can be concluded from the obtained values, which are close to 0, that the shadow images are almost free of any correlation.

Table 2.
Correlation coefficients of adjacent pixels in the test image Elaine and the six shadow images.

Table 3.
Correlation coefficients of adjacent pixels in the test image Lena and the five shadow images.
Table 4 and Table 5 display the information entropy measures [31] of each test image and its shadow images. The fact that the resulting measures are close to 8 indicates the unpredictability of the shadow images.

Table 4.
Information entropy of the test image Elaine and the six shadow images.

Table 5.
Information entropy of the test image Lena and the five shadow images.
To further evaluate the randomness of the shadow images, we subject the shadow images to the statistical test suite (STS) [30]. For a given secret key, the scheme generates six shadow images for the test image Elaine. We repeat this generation for 15 different initial conditions of the chaotic cat map of Equation (1), resulting in 90 shadow images of the length of 2,097,152 bits each. The STS processes each shadow image as a single binary sequence. The test results presented in Table 6 demonstrate the randomness of the shadow images. For further details about the STS results we refer the reader to [30]). Analysis of 100 similarly generated shadow images of the test image Lena produces similar results, presented in Table 6.

Table 6.
Randomness analysis of shadow images using the NIST statistical test suite.
In addition to the STS results presented in Table 6, which confirm the randomness of shadow images generated by the proposed –ESIS scheme, we show that there is no similarity between any pair of shadow images. The number of pixels change rate (NPCR) and the unified average changing intensity (UACI) [32] are two of the most used measures to analyze similarity between a pair of images. Figure 6 (top) reports the NPCR and UACI measures for all possible pairs () of shadow images corresponding to the test image Elaine, and Figure 6 (bottom) reports the same for all possible pairs () of shadow images corresponding to the test image Lena. Each point in Figure 6 corresponds to a pair of NPCR and UACI measures for a pair of shadow images. It is evident that the reported measures are close to the ideal NPCR and UACI measures reported in [32], which are and , respectively. We conclude that the shadow images looks random in comparison with each other.
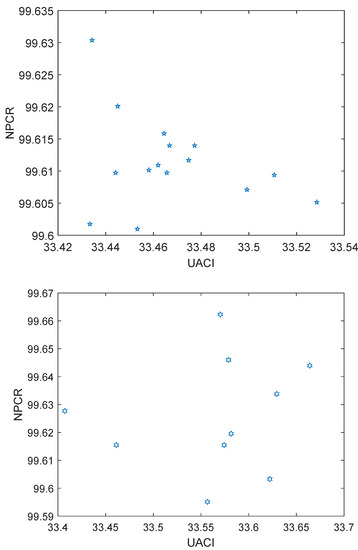
Figure 6.
The NPCR and UACI measures of pairs of shadow images. (Top): pairs corresponding to the test image Elaine. (Bottom): pairs corresponding to the test image Lena.
The statistical results demonstrate the excellent randomness properties of the shadow images generated by the proposed –ESIS scheme.
4.2. Speed
Testing admissibility of the signature matrices X (Algorithm 2) is the bottle-neck of the proposed –ESIS scheme. However, such matrices do not depend on the content of the secret image and can be generated independently of it. Indeed the number of admissible matrices needed for sharing a secret, S, depends on the size of S, but one can generate a large number of signature matrices in advance, and only generate more when needed. On the other hand, to avoid the cost of storing these signature matrices, we can record only the number of times the main for-loop in Algorithm 2 is executed to produce an admissible signature matrix. It is demonstrated in [25] that with probability higher than , the first randomly generated matrix X is indeed admissible. Hence the majority of the stored numbers equal 1, and the list can be compressed if needed.
As an example, with initial condition
all admissible matrices for sharing the secret image Elaine are generated in the first attempt. The running time for generating the six shares corresponding to the secret image Elaine, using MATLAB R2016a on a desktop machine with an Intel® Core™ i7-3520 processor and 8 GB of memory running Widows 10, was s.
4.3. Security Analysis
Similar to the scheme proposed in [25], the proposed –ESIS scheme is highly sensitive to its initial conditions and control parameters. Thus, it is highly sensitive to its secret key (for further details please see [25]). The secret key, K, of the proposed –ESIS scheme consists of
- (i)
- initial conditions and control parameters of the pseudorandom generator used for shuffling the secret image;
- (ii)
- initial conditions and control parameters of the 3-dimensional cat map used in generation of admissible matrices;
- (iii)
- initial conditions and control parameters of the pseudorandom generators used to generate the sequences .
Note that when the 3-dimensional cat map of Equation (1) is used as the pseudorandom generator, the initial conditions, , consist of three double-precision real numbers and the control parameters, , are six integers. In this case, only the initial conditions of the maps used for (i) and (ii) above contribute six double-precision numbers to K. Thus, with a 64-bit double precision of , the size of the key space of K is at least , which is large enough to render exhaustive search attacks impractical.
To assess the security of reconstruction of the secret, let us assume that essential shares are present. This unauthorized set cannot derive any useful information about the secret image. It is shown in [25], that the probability for recovering a single secret block of the secret image is about , where and is the block size of the secret. When this attack is impractical. Furthermore, if shares are present, r from which are essential shares, then once again no useful information can be derived about the secret image. The probability for recovering a single secret block of the secret image is about .
4.4. Error-Resilient Capability
The error-resilient capability of the proposed –ESIS scheme follows from that in [25]. Figure 7 depicts the recovered (filtered) test images of Elaine obtained from an authorized set of four shadow images one of which is (i) cropped by (left), and (ii) subjected to salt and pepper noise with ratio (right).

Figure 7.
The recovered test image Elaine obtained from an authorized set of four shadow images one of which is (i) cropped by (left), and (ii) subjected to salt and pepper noise with ratio (right).
5. Comparison with Existing Work
This section shows the performance of the proposed –ESIS scheme with respect to some existing ones, such as those presented in [20,21,22,24,33,34]. A number of –ESIS schemes have drawbacks caused by (i) generation of unequal-sized shadow images, and (ii) concatenation of sub-shadow images. These drawbacks result in security vulnerability and complication in the reconstruction of the secret image. Hence it is important for an –ESIS scheme to overcome these drawbacks. In Table 7, we give a summary of the schemes under comparison with respect to these drawbacks. Some of the schemes that overcome these drawbacks are further compared in terms of size of shadow images in Table 8. This table also reports whether the secret image is reconstructed with no distortion.

Table 7.
Comparison in terms of essential and non-essential shadow images sizes, and concatenation of sub-shadow images.

Table 8.
Size of shadow images, and the quality of the reconstructed secret image.
On the basis of the reported results, the superiority of the proposed scheme over existing schemes is evident.
6. Concluding Remarks
This work proposes a lossless linear algebraic –threshold essential secret image sharing scheme that generates equally-sized shadow images, each of size , where L is the length of the given secret image, S. For sharing a block of the secret, the proposed scheme associates distinct admissible signature vectors in the vector space, , to the essential participants and non-essential participants. Simulations demonstrate the effectiveness and robustness of the proposed scheme against standard statistical and security attacks. Furthermore, they show its superiority in comparison with existing schemes.
Author Contributions
Conceptualization, M.G., A.K. and A.A.; Formal analysis, M.G., A.K. and A.A.; Methodology, M.G., A.K. and A.A.; Software, M.G., A.K. and A.A.; Writing—original draft, A.K.; Writing—review—editing, M.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors are thankful to the anonymous referees for their helpful comments.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Shamir, A. How to share a secret. Commun. ACM 1979, 22, 612–613. [Google Scholar] [CrossRef]
- Blakley, G.R. Safeguarding cryptographic keys. In Proceedings of the IEEE 1979 International Workshop on Managing Requirements Knowledge (MARK), New York, NY, USA, 4–7 June 1979; pp. 313–318. [Google Scholar]
- Mignotte, M. How to share a secret. In Workshop on Cryptography; Springer: Berlin/Heidelberg, Germany, 1982; pp. 371–375. [Google Scholar]
- Thien, C.-C.; Lin, J.-C. Secret image sharing. Comput. Graph. 2002, 26, 765–770. [Google Scholar] [CrossRef]
- Lin, C.-C.; Tsai, W.-H. Secret image sharing with steganography and authentication. J. Syst. Softw. 2004, 73, 405–414. [Google Scholar] [CrossRef]
- Bai, L. A reliable (k, n) image secret sharing scheme. In Proceedings of the 2006 2nd IEEE International Symposium on Dependable, Autonomic and Secure Computing, Indianapolis, IN, USA, 29 September–1 October 2006; pp. 31–36. [Google Scholar]
- del Rey, A.M. A matrix-based secret sharing scheme for images. In Iberoamerican Congress on Pattern Recognition; Springer: Berlin/Heidelberg, Germany, 2008; pp. 635–642. [Google Scholar]
- Ulutas, M.; Nabiyev, V.V.; Ulutas, G. Improvements in geometry-based secret image sharing approach with steganography. Math. Probl. Eng. 2009, 2009, 187874. [Google Scholar] [CrossRef]
- Hu, W.-T.; Li, M.-C.; Guo, C.; Ren, Y.-Z. Reversible secret image sharing with steganography and dynamic embedding. Secur. Commun. Netw. 2012, 5, 1267–1276. [Google Scholar] [CrossRef]
- El-Latif, A.A.A.; Yan, X.; Li, L.; Wang, N.; Peng, J.-L.; Niu, X. A new meaningful secret sharing scheme based on random grids, error diffusion and chaotic encryption. Opt. Laser Technol. 2013, 54, 389–400. [Google Scholar] [CrossRef]
- Wu, K.-S. A secret image sharing scheme for light images. EURASIP J. Adv. Signal Process. 2013, 2013, 49. [Google Scholar] [CrossRef]
- Zarepour-Ahmadabadi, J.; Ahmadabadi, M.S.; Latif, A. An adaptive secret image sharing with a new bitwise steganographic property. Inf. Sci. 2016, 369, 467–480. [Google Scholar] [CrossRef]
- Kanso, A.; Ghebleh, M. An efficient (t,n)–threshold secret image sharing scheme. Multimed. Tools Appl. 2017, 76, 16369–16388. [Google Scholar] [CrossRef]
- Deng, X.; Wen, W.; Shi, Z. Threshold multi-secret sharing scheme based on phase-shifting interferometry. Opt. Commun. 2017, 387, 409–414. [Google Scholar] [CrossRef]
- Kabirirad, S.; Eslami, Z. A (t, n)-multi secret image sharing scheme based on boolean operations. J. Vis. Commun. Image Represent. 2018, 57, 39–47. [Google Scholar] [CrossRef]
- Ghebleh, M.; Kanso, A. A novel secret image sharing scheme using large primes. Multimed. Tools Appl. 2018, 77, 11903–11923. [Google Scholar] [CrossRef]
- Ding, W.; Liu, K.; Yan, X.; Wang, H.; Liu, L.; Gong, Q. An image secret sharing method based on matrix theory. Symmetry 2018, 10, 530. [Google Scholar] [CrossRef]
- Kanso, A.; Ghebleh, M. An efficient lossless secret sharing scheme for medical images. J. Vis. Commun. Image Represent. 2018, 56, 245–255. [Google Scholar] [CrossRef]
- Li, P.; Yang, C.-N.; Wu, C.-C.; Kong, Q.; Ma, Y. Essential secret image sharing scheme with different importance of shadows. J. Vis. Commun. Image Represent. 2013, 24, 1106–1114. [Google Scholar] [CrossRef]
- Yang, C.-N.; Li, P.; Wu, C.-C.; Cai, S.-R. Reducing shadow size in essential secret image sharing by conjunctive hierarchical approach. Signal Process. Image Commun. 2015, 31, 1–9. [Google Scholar] [CrossRef]
- Li, P.; Yang, C.-N.; Zhou, Z. Essential secret image sharing scheme with the same size of shadows. Digit. Signal Process. 2016, 50, 51–60. [Google Scholar] [CrossRef]
- Chen, C.-C. Essential secret image sharing scheme with equal-sized shadows generation. J. Vis. Commun. Image Represent. 2018, 52, 143–150. [Google Scholar] [CrossRef]
- Li, P.; Liu, Z.; Yang, C.-N. A construction method of (t,k,n)-essential secret image sharing scheme. Signal Process. Image Commun. 2018, 65, 210–220. [Google Scholar] [CrossRef]
- Wu, Z.; Liu, Y.-N.; Wang, D.; Yang, C.-N. An efficient essential secret image sharing scheme using derivative polynomial. Symmetry 2019, 11, 69. [Google Scholar] [CrossRef]
- Kanso, A.; Ghebleh, M.; Alazemi, A. A lossless linear algebraic secret image sharing scheme. Informatica 2020, 31, 499–522. [Google Scholar] [CrossRef]
- Schinzel, A.; Spież, S.; Urbanowicz, J. Admissible tracks in shamir’s scheme. Finite Fields Their Appl. 2010, 16, 449–462. [Google Scholar] [CrossRef][Green Version]
- Spież, S.; Srebrny, M.; Urbanowicz, J. Remarks on the classical threshold secret sharing schemes. Fundam. Inform. 2012, 114, 345–357. [Google Scholar] [CrossRef]
- Chen, G.; Mao, Y.; Chui, C.K. A symmetric image encryption scheme based on 3D chaotic cat maps. Chaos Solitons Fractals 2004, 21, 749–761. [Google Scholar] [CrossRef]
- Ghebleh, M.; Kanso, A. A robust chaotic algorithm for digital image steganography. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 1898–1907. [Google Scholar] [CrossRef]
- Bassham, L.E., III; Rukhin, A.L.; Soto, J.; Nechvatal, J.R.; Smid, M.E.; Barker, E.B.; Leigh, S.D.; Levenson, M.; Vangel, M.; Banks, D.L.; et al. Sp 800-22 rev. 1a. A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications; 2010. Available online: https://nvlpubs.nist.gov/nistpubs/legacy/sp/nistspecialpublication800-22r1a.pdf (accessed on 18 January 2022).
- Shannon, C.E. Prediction and entropy of printed English. Bell Syst. Tech. J. 1951, 30, 50–64. [Google Scholar] [CrossRef]
- Wu, Y.; Noonan, J.P.; Agaian, S. NPCR and UACI randomness tests for image encryption. Cyber J. Multidiscip. J. Sci. Technol. J. Sel. Areas Telecommun. (JSAT) 2011, 1, 31–38. [Google Scholar]
- Chen, C.-C.; Chen, S.-C. Two-layered structure for optimally essential secret image sharing scheme. J. Vis. Commun. Image Represent. 2016, 38, 595–601. [Google Scholar] [CrossRef]
- Chen, C.-C.; Tsai, Y.-H. An expandable essential secret image sharing structure. J. Inf. Hiding Multimed. Signal Process 2016, 7, 135–144. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
