What Group Theory Can Do for You: From Magmas to Abstract Thinking in School Mathematics
Abstract
:1. Introduction
2. The New Math Era: A Brief Historical Overview
3. Historical and Contemporary Ideas on Teaching Abstract Algebra
3.1. Educational Key Findings of the ‘New Math’ Era
- Algebraic structures must not be introduced in a formal way or independent of tangible models. The axiomatic nature can be discussed if an opportunity presents itself, but it is of secondary importance.
- Mathematical terms may only be introduced if they can be demonstrated or illustrated on the basis of already existing terms.
- The goal of abstraction is only possible if the underlying concepts have been studied thoroughly.
3.1.1. No Axiomatic Group Theory
3.1.2. Magmas Instead of Groups
- How many models in the direct mathematical periphery tap the algebraic structure? In other words, which structures draw the most from visual demonstrations?
- Which of those algebraic structures in 1. allow for an adequate (in relation to school mathematics), deductive approach as well as an exploratory approach?
- Dihedral groups but also the groups of symmetries of rectangles, rhombuses, rhomboids, kites, etc.
- Frieze groups
- Cyclic groups
- The additive groups of , and
- The multiplicative groups of , , etc.
- The orthogonal groups
3.1.3. Interim Conclusions
3.2. Educational Key Findings in Contemporary Research
3.2.1. Linear Equations and Familiar Number Sets
3.2.2. Geometrical Aspects of Group Theory
3.2.3. Properties of Binary Operations
3.2.4. Interim Conclusions
4. Design Principles and Structure of a New Teaching Concept
“Abstraction is not the first stage, but the last stage, in a mathematical development.” [p. 98]
4.1. Realistic Mathematical Education (RME)
- Level 1: An algebraic property emerges implicitly in the student’s intuitive activity with an example structure.
- Level 2: The property appears explicitly in the student’s general description of his or her activity with the structure.
- Level 3: The student repurposes the property as a lens to classify other structures.
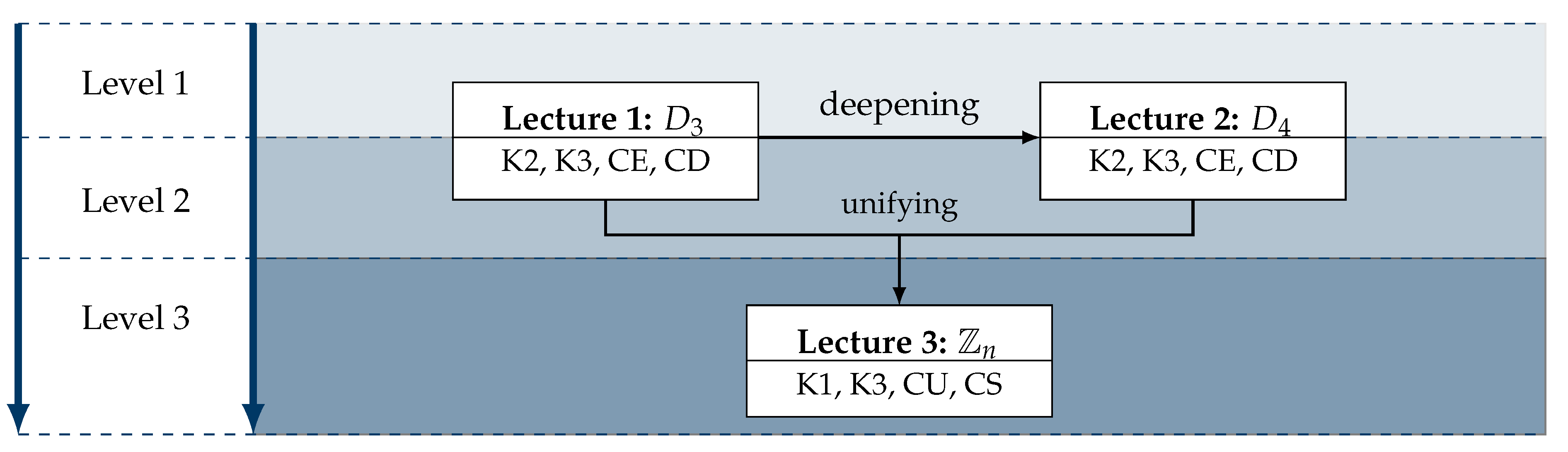
4.2. The EDUS-System
- Extending (CE) the context in which a set of existing understandings are situated. For our concept, this is incorporated by considering geometrical transformations of the equilateral triangle and the square.
- Deepening (CD) the level of existing understandings of a certain, single mathematical object. For our concept, this is incorporated by deepening the understanding of the object map and inverse map.
- Unifying (CU) existing understandings that were previously unrelated by the student under a specific overarching mathematical object. For our concept, this is incorporated by unifying the understandings of number sets and the properties of binary operations defined on them.
- Strengthening (CS) the links between existing understandings of more than one mathematical object. For our concept, this is incorporated by looking at similarities of the different sets and deriving the magma structure from those observations.
4.3. Connecting Abstract Algebra to Algebraic Thinking
- generalizing mathematical structures (cf. CE, K1, K2, K3)
- exploring and symbolizing functional relationships (cf. CU, K2)
- building mathematical arguments that reflect more generalized forms (cf. CE, K3)
- reasoning about abstract quantities (cf. CS, K1)
- generalized arithmetic (cf. CE, K1, K3)
- functional thinking (cf. CU, K2)
- application of generalizations as a modeling language (cf. CS, K1, K3).
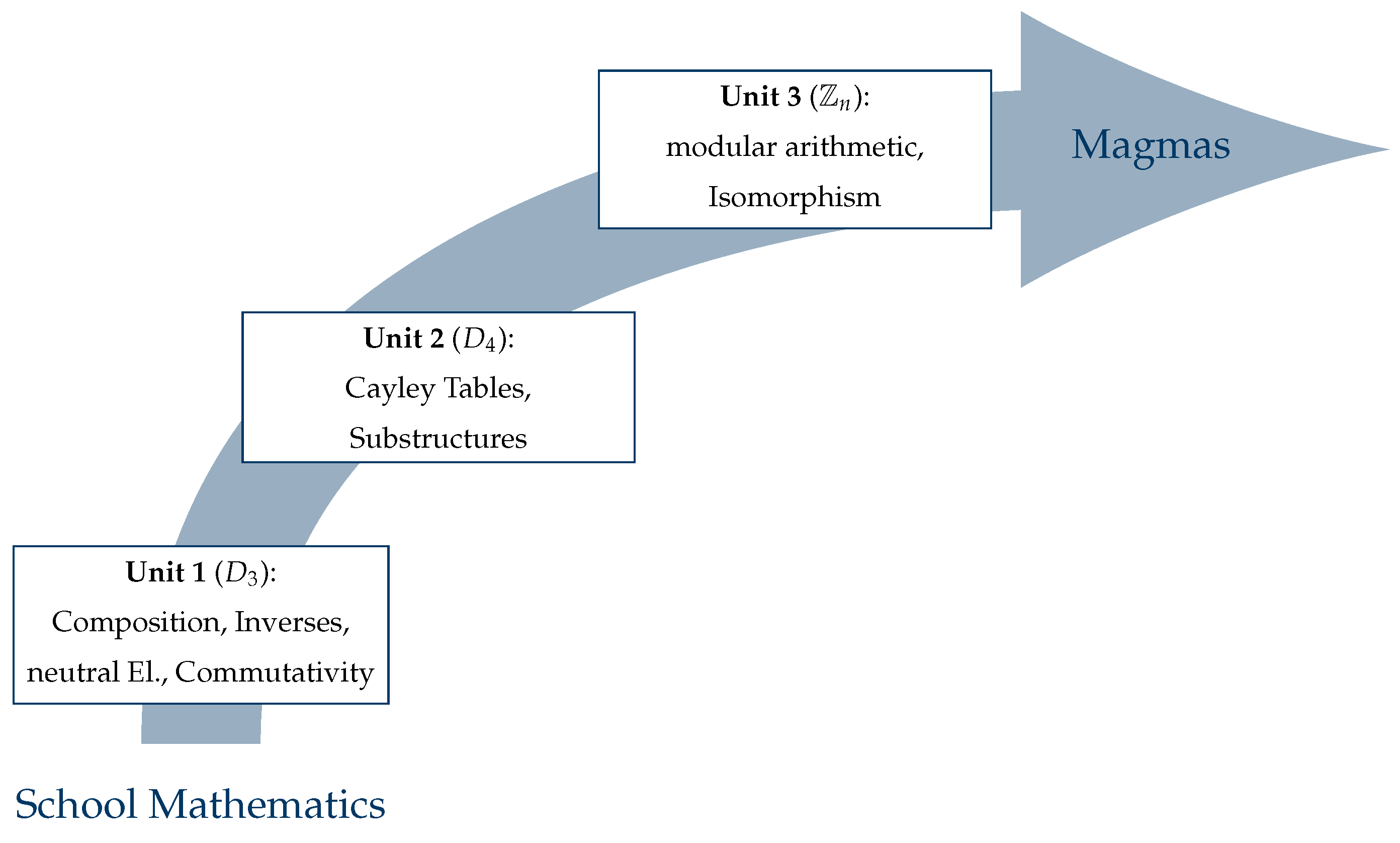
5. The Hildesheim Teaching Concept of Abstract Algebra
5.1. Unit 1: Introducing the Dihedral Group
5.1.1. Exploring the Transformations
5.1.2. Describing the Transformations
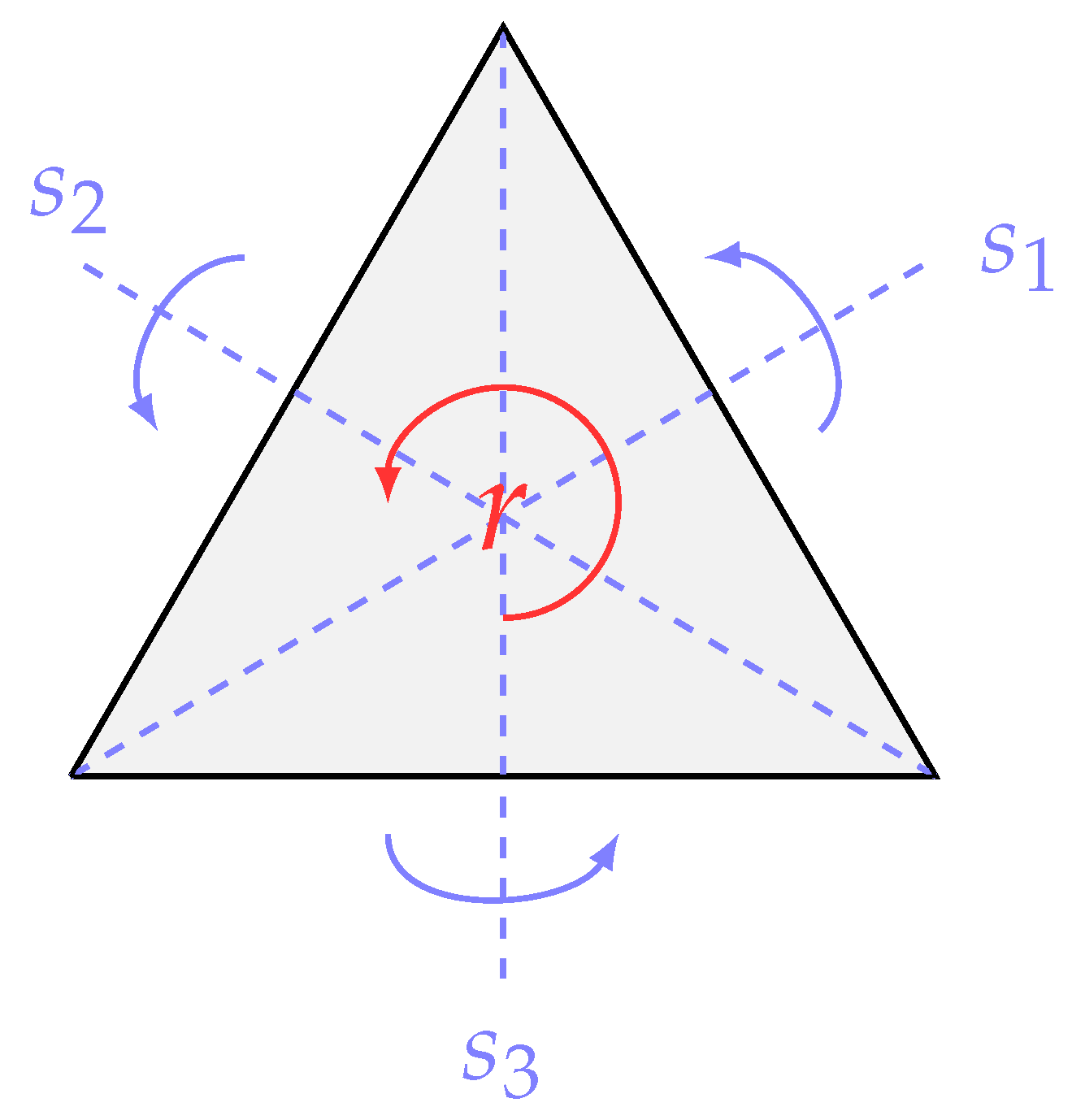
5.1.3. Exploring the Composition
- The (for students) somewhat unintuitive definition of composition, and
- compositions involving reflections.
5.1.4. Exploring the Group Structure of
- try out all six possible by drawing the transformations as seen in Figure 6,
- try out all six possible physically by taking the glass triangle or
- note that one can reverse the reflection and thus compute .
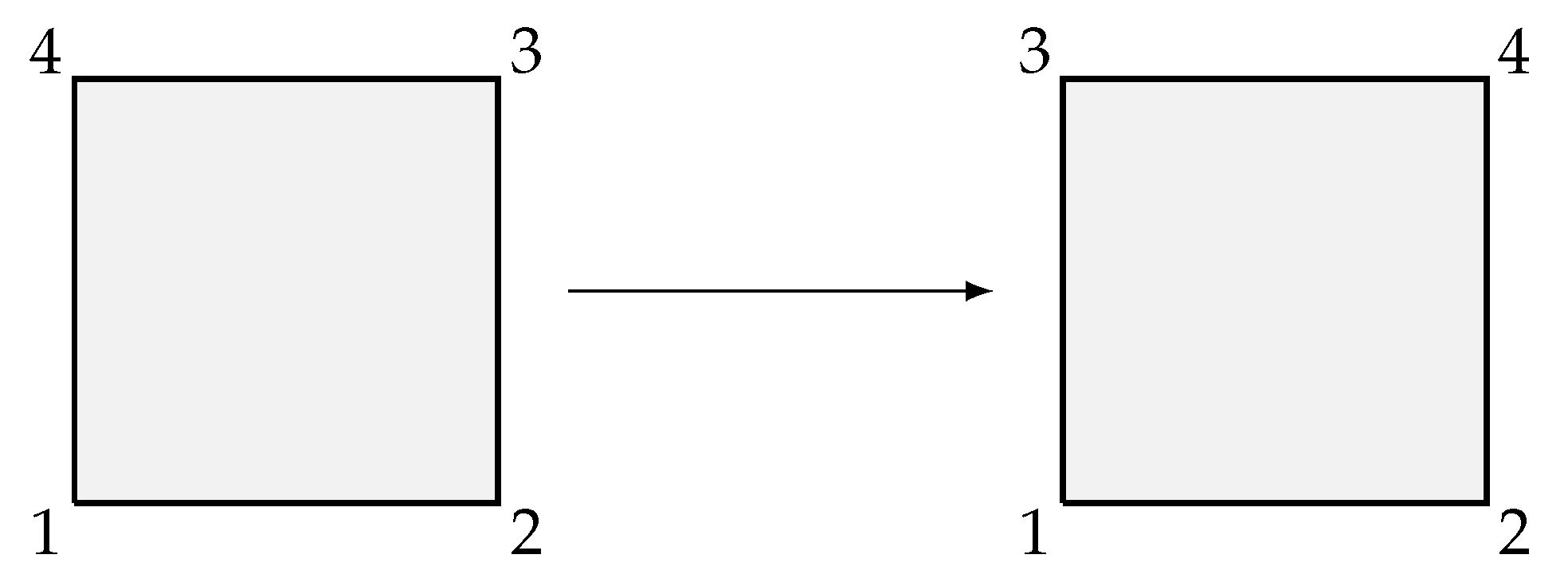
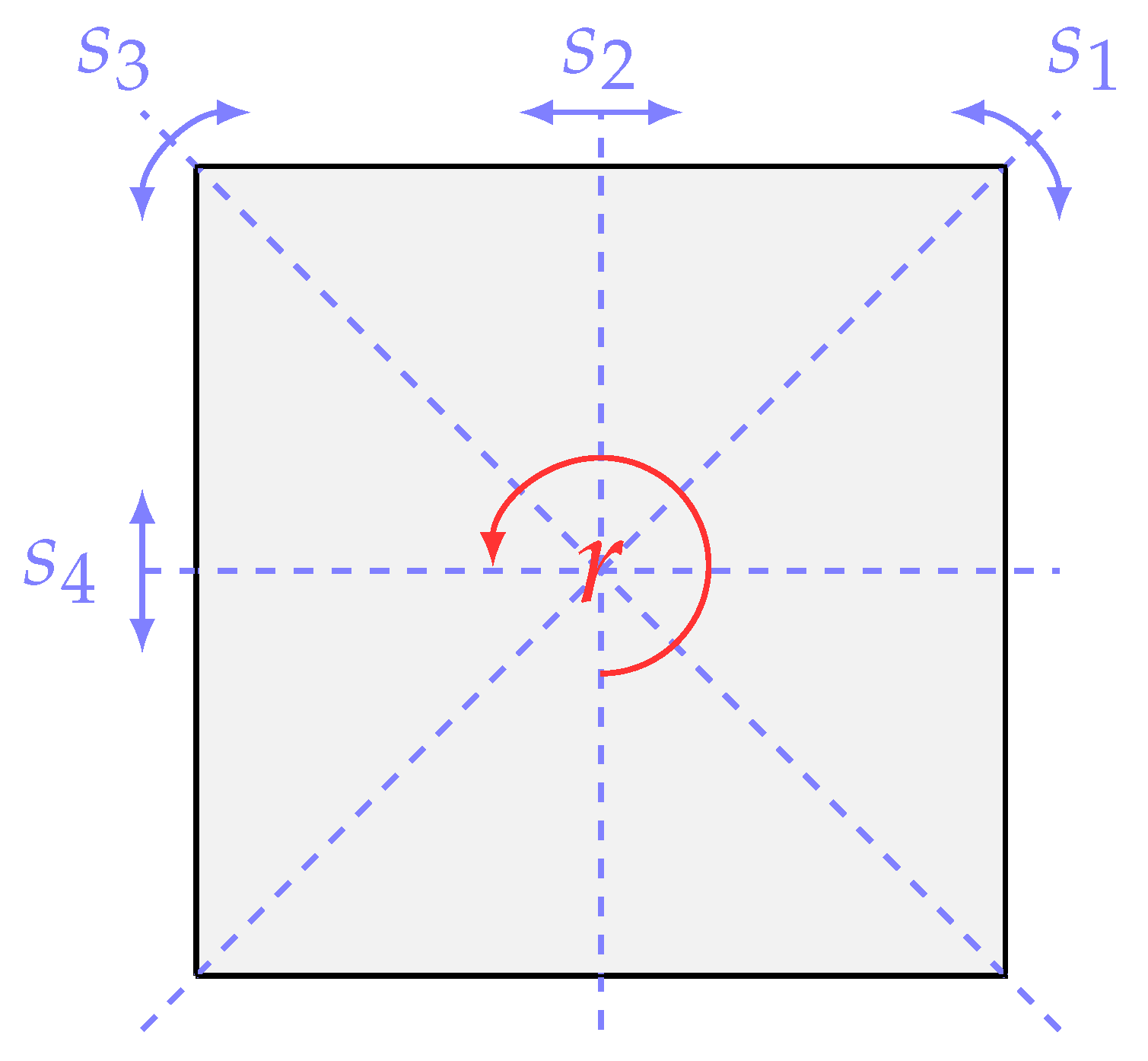
5.2. Unit 2: Introducing the Dihedral Group
5.2.1. Cayley Tables
5.2.2. Exploring the Transformations
5.2.3. Exploring a Substructure
5.3. Unit 3: Introducing the Cyclic Groups
5.3.1. Exploring Residue Classes
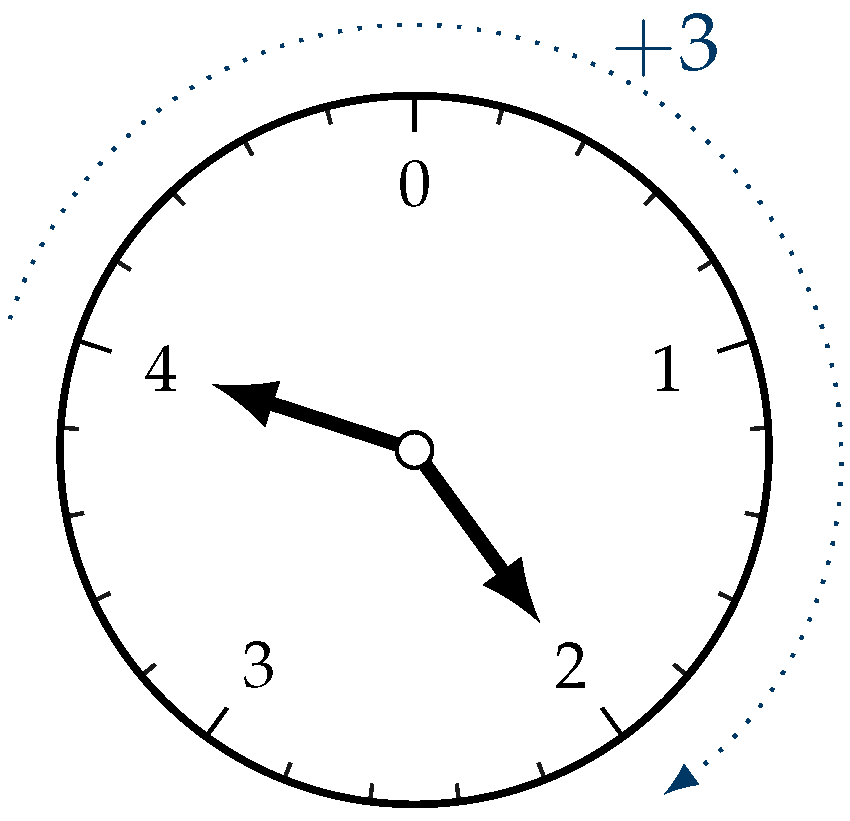
- Let’s imagine waiting at a station for a train. It is already late, 10:00 p.m. to be precise, and according to the schedule the train will not arrive before 01:00 a.m. A quick mental calculation tells us we need to wait for three more hours, since .
- Then we remember that we have to study for a test. Today is 26 November, and the test is precisely in two weeks. Another mental calculation tells us that because November has 30 days, the test will be on 10 December, since .
5.3.2. Establishing the Addition of Residue Classes
5.3.3. Modular Arithmetic
- The equation has only one solution when viewed in but two solutions when viewed in .
- The equation has no solution when viewed in but one solution when viewed in .
5.3.4. Generalizing the Findings
6. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wasserman, N.H. Introducing Algebraic Structures through Solving Equations: Vertical Content Knowledge for K-12 Mathematics Teachers. PRIMUS 2014, 24, 191–214. [Google Scholar] [CrossRef]
- McCrory, R.; Floden, R.; Ferrini-Mundy, J.; Reckase, M.D.; Senk, S.L. Knowledge of Algebra for Teaching: A Framework of Knowledge and Practices. J. Res. Math. Educ. 2012, 43, 584–615. [Google Scholar] [CrossRef]
- Even, R. The relevance of advanced mathematics studies to expertise in secondary school mathematics teaching: Practitioners’ views. ZDM Math. Educ. 2011, 43, 941–950. [Google Scholar] [CrossRef]
- Veith, J.M.; Bitzenbauer, P. Two Challenging Concepts in Mathematics Education: Subject-Specific Thoughts on the Complex Unit and Angles. Eur. J. Sci. Math. Educ. 2021, 9, 244–251. [Google Scholar] [CrossRef]
- Shamash, J.; Barabash, M.; Even, R. From Equations to Structures: Modes of Relevance of Abstract Algebra to School Mathematics as Viewed by Teacher Educators and Teachers. In Connecting Abstract Algebra to Secondary Mathematics, for Secondary Mathematics Teachers; Springer: Cham, Switzerland, 2018; pp. 241–262. [Google Scholar]
- Burn, R. What Are the Fundamental Concepts of Group Theory? Educ. Stud. Math. 1996, 31, 371–377. [Google Scholar] [CrossRef]
- Freudenthal, H. What groups mean in mathematics and what they should mean in mathematical education. In Developments in Mathematical Education; Howson, A.G., Ed.; Cambridge University Press: Cambridgeshire, UK, 1973; pp. 101–114. [Google Scholar]
- Wasserman, N.H. Abstract Algebra for Algebra Teaching: Influencing School Mathematics Instruction. Can. J. Sci. Math. Technol. Educ. 2016, 16, 28–47. [Google Scholar] [CrossRef]
- Eisenberg, T.A. Begle revisited: Teacher knowledge and student achievement in algebra. J. Res. Math. Educ. 1977, 8, 216–222. [Google Scholar] [CrossRef]
- Wasserman, N.H.; Galarza, P. Exploring an Instructional Model for Designing Modules for Secondary Mathematics Teachers in an Abstract Algebra Course. In Connecting Abstract Algebra to Secondary Mathematics, for Secondary Mathematics Teachers; Springer: Cham, Switzerland, 2018; pp. 335–361. [Google Scholar]
- Hunkler, R.F. Achievement of Sixth-Grade Pupils in Modern Mathematics as Related to Their Teachers’ Mathematics Preparation. Ph.D. Thesis, The Agricultural and Mechanical College of Texas, College Station, TX, USA, 1968. [Google Scholar]
- Hurst, D. The Relationship between Certain Teacher-Related Variables and Student Achievement in Third Grade Arithmetic. Ph.D. Thesis, Oklahoma State University, Stillwater, OK, USA, 1967. [Google Scholar]
- Norris, F.R. Pupil Achievement as a Function of an Inservice Training Program on Mathematics Concepts for Sixth Grade Teachers. Ph.D. Thesis, George Peabody College for Teachers, Nashville, TN, USA, 1969. [Google Scholar]
- Wasserman, N.H. Exploring Advanced Mathematics Courses and Content for Secondary Mathematics Teachers. In Connecting Abstract Algebra to Secondary Mathematics, for Secondary Mathematics Teachers; Springer: Cham, Switzerland, 2018; pp. 1–15. [Google Scholar]
- Rouse, W.M. A Study of the Correlation between the Academic Preparation of Teachers of Mathematics and the Mathematics Achievement of Their Students in Kindergarten through Grade Eight. Ph.D. Thesis, Michigan State University, East Lansing, MI, USA, 1967. [Google Scholar]
- Copel, W.D.; Doyle, W. Laboratory skill training and student teacher classroom performance. J. Exp. Educ. 1973, 42, 16–21. [Google Scholar] [CrossRef]
- Hamann, T. Die “Mengenlehre” im Anfangsunterricht: Historische Darstellung einer Gescheiterten Unterrichtsreform in der Bundesrepublik Deutschland. Ph.D Thesis, University of Hildesheim, Hildesheim, Germany, 2017. [Google Scholar]
- Rappaport, D. The New Math and Its Aftermath. Sch. Sci. Math. 1976, 7, 563–570. [Google Scholar] [CrossRef]
- Royaumont Seminar. New Thinking in School Mathematics; OECD Publications Center: Paris, France, 1961. [Google Scholar]
- OECD. Synopsis für moderne Schulmathematik; Diesterweg: Berlin, Germany, 1966. [Google Scholar]
- Kline, M. Why Johnny Can’t Add; Random House Inc.: New York, NY, USA, 1973. [Google Scholar]
- Smith, J.P. Foreshadowing Ideas in Abstract Algebra: Reflections from the Secondary School Mathematics Curriculum Improvement Study. In Connecting Abstract Algebra to Secondary Mathematics, for Secondary Mathematics Teachers; Springer: Cham, Switzerland, 2018; pp. 103–124. [Google Scholar]
- Wilfried, N. Die moderne Algebra und ihre Stellung im heutigen Mathematikunterricht. Didaktik Mathematik 1977, 3, 236–241. [Google Scholar]
- Dubinski, E.; Dautermann, J.; Leron, U.; Zazkis, R. A Reaction To Burn’s “What are the Fundamental Concepts of Group Theory?”. Educ. Stud. Math. 1997, 34, 249–253. [Google Scholar] [CrossRef]
- Liermann, H. Die Behandlung von Restklassengruppen und -ringen im Oberstufenunterricht der Gymnasien. Der Mathematikunterricht 1966, 2, 95–104. [Google Scholar]
- Kropp, G. Der Bildungswert der Mathematik in neuer Sicht und die Bildungsaufgabe des Mathematikunterrichts. Der Mathematikunterricht 1965, 4, 5–17. [Google Scholar]
- Griesel, H. Die Leitlinie Menge–Struktur im gegenwärtigen Mathematikunterricht. Mathematikunterricht 1965, 1, 40–53. [Google Scholar]
- Quadling, D.A. The use of the axiomatic method in secondary teaching. Math. Gaz. 1966, 50, 259–275. [Google Scholar] [CrossRef]
- Freudenthal, H. Was ist Axiomatik und welchen bildenden Wert kann sie haben? Mathematikunterricht 1963, 4, 5–29. [Google Scholar]
- Meschkowski, H. Definitionen in der Schulmathematik. Mathematikunterricht 1965, 4, 94–108. [Google Scholar]
- Servais, W.; Varga, T. Treatment of the Axiomatic Method in Class. In Teaching School Mathematics; Penguin Books: London, UK, 1971; pp. 124–150. [Google Scholar]
- Howson, A.G. The Role of axioms in contemporary mathematics and in mathematical education. In Developments in Mathematical Education; Cambridge University Press: Cambridgeshire, UK, 1973; pp. 262–271. [Google Scholar]
- Steiner, H. Menge, Struktur, Abbildung als Leitbegriffe für den modernen mathematischen Unterricht. Mathematikunterricht 1965, 1, 5–19. [Google Scholar]
- Steiner, H. Einfache Verknüpfungsgebilde als Vorfeld der Gruppentheorie. Mathematikunterricht 1966, 2, 5–18. [Google Scholar]
- Dieudonne, J. Vortrag auf der 27. Tagung zur Pflege des Zusammenhangs von Universität und Höherer Schule in Münster. Didaktik Mathematik 1962, 4, 171–183. [Google Scholar]
- Leppig, M. Beispiele zum Rechnen in endlichen Gruppen. Mathematikunterricht 1966, 2, 39–49. [Google Scholar]
- Kirsch, A. Über die enaktive Repräsentation von Abbildungen, insbesondere Permutationen. Didaktik Mathematik 1965, 3, 169–194. [Google Scholar]
- Wasserman, N.H. Connecting Abstract Algebra to Secondary Mathematics, for Secondary Mathematics Teachers; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Selden, A.; Selden, J. Errors and misconceptions in college level theorem proving. Proc. Second. Int. Semin. Misconceptions Educ. Strateg. Sci. Math. 1987, 3, 457–470. [Google Scholar]
- Weber, K.; Larsen, S. Teaching and Learning Group Theory. In Making The Connection; Carlson, M.P., Rasmussen, C., Eds.; Mathematical Association of America: Washington, DC, USA, 2008; pp. 139–151. [Google Scholar]
- Zbiek, R.M.; Heid, M.K. Making Connections from the Secondary Classroom to the Abstract Algebra Course: A Mathematical Activity Approach. In Connecting Abstract Algebra to Secondary Mathematics, for Secondary Mathematics Teachers; Springer: Cham, Switzerland, 2018; pp. 189–209. [Google Scholar]
- Baldinger, E.E. Learning Mathematical Practices to Connect Abstract Algebra to High School Algebra. In Connecting Abstract Algebra to Secondary Mathematics, for Secondary Mathematics Teachers; Springer: Cham, Switzerland, 2018; pp. 211–239. [Google Scholar]
- Suominen, A.L. Abstract Algebra and Secondary School Mathematics Connections as Discussed by Mathematicians and Mathematics Educators. In Connecting Abstract Algebra to Secondary Mathematics, for Secondary Mathematics Teachers; Springer: Cham, Switzerland, 2018; pp. 149–173. [Google Scholar]
- Melhuish, K.; Fagan, J. Connecting the Group Theory Concept Assessment to Core Concepts at the Secondary Level. In Connecting Abstract Algebra to Secondary Mathematics, for Secondary Mathematics Teachers; Springer: Cham, Switzerland, 2018; pp. 19–45. [Google Scholar]
- Wasserman, N.H. Making Sense of Abstract Algebra: Exploring Secondary Teachers’ Understandings of Inverse Functions in Relation to Its Group Structure. Math. Think. Learn. 2017, 19, 181–201. [Google Scholar] [CrossRef]
- Brown, A.; DeVries, D.J.; Dubinskiy, E.; Thomas, K. Learning Binary Operations, Groups, and Subgroups. J. Math. Behav. 1997, 16, 187–239. [Google Scholar] [CrossRef]
- Larsen, S. Making Sense of Abstract Algebra: Reinventing the concepts of group and isomorphism: The case of Jessica and Sandra. J. Math. Behav. 2009, 28, 119–137. [Google Scholar] [CrossRef]
- Lee, Y.; Heid, M.K. Developing a Structural Perspective and Its Role in Connecting School Algebra and Abstract Algebra: A Factorization Example. In Connecting Abstract Algebra to Secondary Mathematics, for Secondary Mathematics Teachers; Springer: Cham, Switzerland, 2018; pp. 291–318. [Google Scholar]
- Van den Heuvel-Panhuizen, M.; Drijvers, P. Connecting the Group Theory Concept Assessment to Core Concepts at the Secondary Level. In Encyclopedia of Mathematics Education; Springer: Cham, Switzerland, 2020. [Google Scholar]
- Cook, J.P. Monster-Barring as a Catalyst for Bridging Secondary Algebra to Abstract Algebra. In Connecting Abstract Algebra to Secondary Mathematics, for Secondary Mathematics Teachers; Springer: Cham, Switzerland, 2018; pp. 47–70. [Google Scholar]
- Blanton, M.L.; Stephens, A.; Knuth, E.; Gardiner, A.M.; Isler-Baykal, I.; Kim, J.-S. The Development of Children’s Algebraic Thinking: The Impact of a Comprehensive Early Algebra Intervention in Third Grade. J. Res. Math. Educ. 2015, 46, 39–87. [Google Scholar] [CrossRef]
- Kaput, J. What is algebra? What is algebraic reasoning? In Algebra in the Early Grades; Kaput, J., Carraher, D.W., Blanton, M.L., Eds.; Routledge: New York, NY, USA, 2008; pp. 5–17. [Google Scholar]
- Carraher, D.W.; Martinez, M.V.; Schliemann, A.D. Early algebra and mathematical generalization. ZDM Math. Educ. 2007, 40, 3–22. [Google Scholar]
- Papic, M. An Early Mathematical Patterning Assessment: Identifying young Australian Indigenous children’s patterning skills. Math. Educ. Res. J. 2015, 27, 519–534. [Google Scholar] [CrossRef]
- Pincheira, N.; Alsina, A. Teachers’ Mathematics Knowledge for Teaching Early Algebra: A Systematic Review from the MKT Perspective. Mathematics 2021, 9, 2590. [Google Scholar] [CrossRef]
- Kirsch, A. Elementare Zahlbereichserweiterungen und der Gruppenbegriff. Der Mathematikunterricht 1966, 2, 50–66. [Google Scholar]
- Dubinskiy, E.; Dautermann, J.; Leron, U.; Zazkis, R. On learning fundamental concepts of group theory. Educ. Stud. Math. 1994, 27, 267–305. [Google Scholar] [CrossRef]
- Hyman, B. Understanding School Mathematics in Terms of Linear Measure and Discrete Real Additive Groups. In Connecting Abstract Algebra to Secondary Mathematics, for Secondary Mathematics Teachers; Springer: Cham, Switzerland, 2018; pp. 125–147. [Google Scholar]
- Alvarez, J.M.; White, D. Making Mathematical Connections Between Abstract Algebra and Secondary Mathematics Explicit: Implications for Curriculum, Research, and Faculty Professional Development. In Connecting Abstract Algebra to Secondary Mathematics, for Secondary Mathematics Teachers; Springer: Cham, Switzerland, 2018; pp. 175–185. [Google Scholar]
- Ticknor, C.S. Situated learning in an abstract algebra classroom. Educ. Stud. Math. 2012, 81, 307–323. [Google Scholar] [CrossRef]
- Hart, E. Analysis of the proof-writing performance of expert and novice students in elementary group theory. In Research Issues in Undergraduate Mathematics Learning: Preliminary Analyses and Reports; Mathematical Association of America: Washington, DC, USA, 1994; pp. 49–62. [Google Scholar]
- Jung, W. Probing acceptance: A technique for investigating learning difficulties. In Research in Physics Learning. Theoretical Issues and Empirical Studies; Duit, R., Goldberg, F., Niedderer, H., Eds.; IPN: Kiel, Germany, 1992; pp. 278–295. [Google Scholar]
- Anderson, T.; Shattuck, J. Design-Based Research: A Decade of Progress in Education Research? Educ. Res. 2012, 41, 16–25. [Google Scholar] [CrossRef] [Green Version]

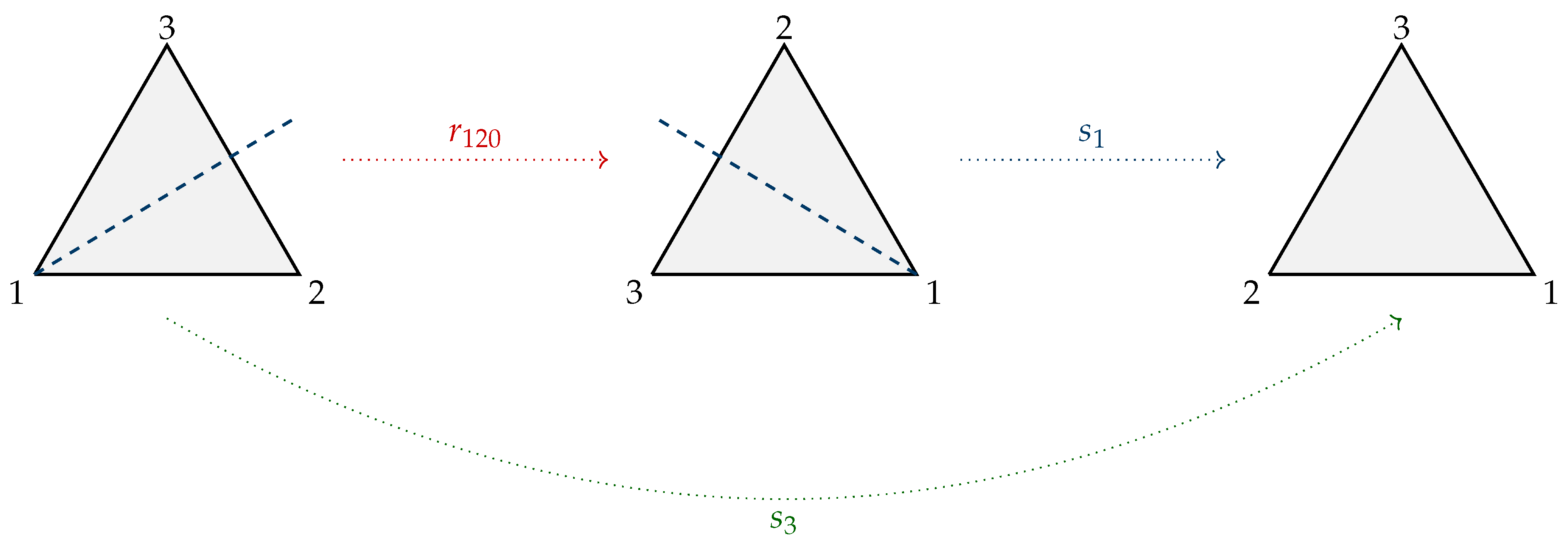
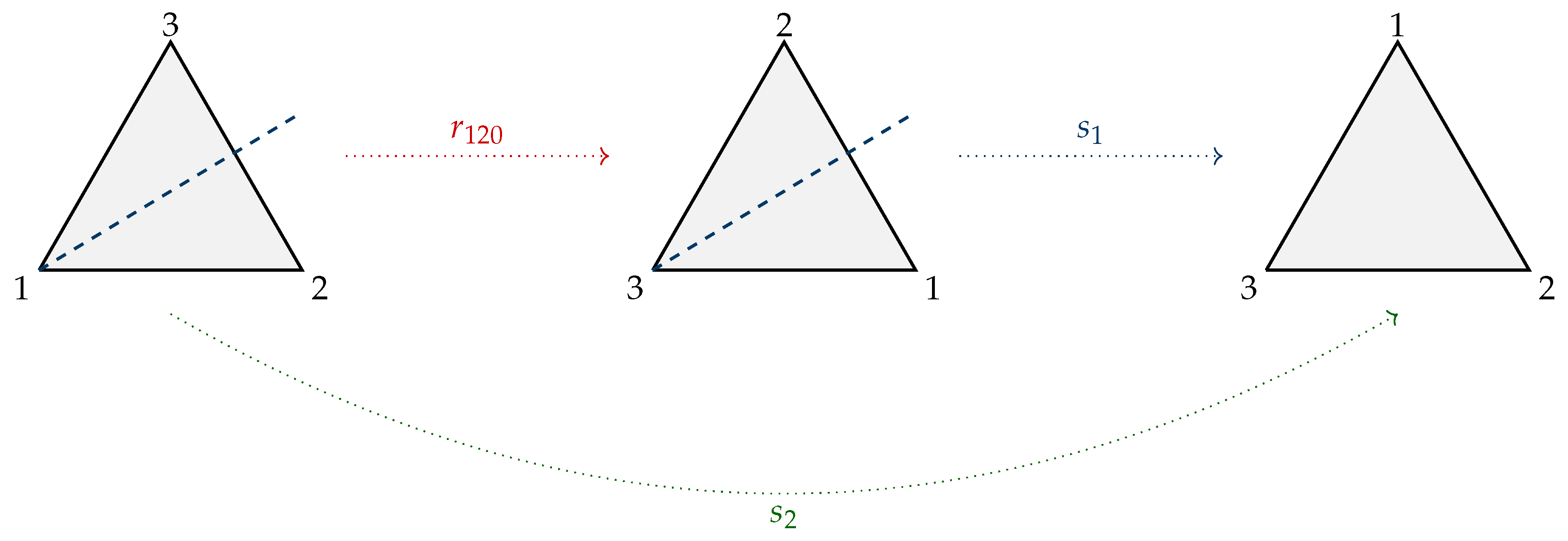
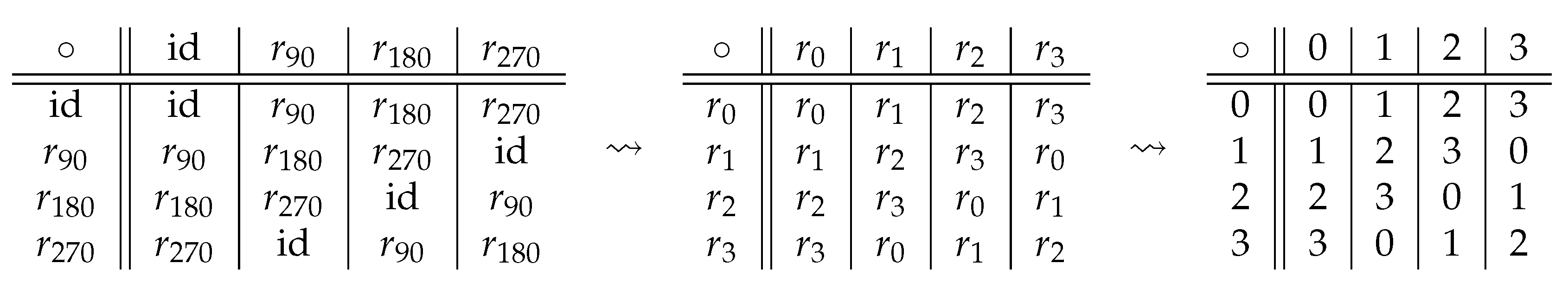
| Key Finding | References |
|---|---|
| No axiomatic group theory | [7,24,29] |
| Magmas instead of groups | [33,34,35] |
| Best groups for introducution are , and | [27,36,37] |
| Key Finding | Abbreviation | References |
|---|---|---|
| Solving Equations, working with familiar number sets (, , , ) | K1 | [1,5,39,40] |
| Symmetries, experimenting, engaging physically | K2 | [1,6,24,40,42,46,47] |
| Properties of binary operations | K3 | [1,44,45] |
| Key Finding | Suggested Contents |
|---|---|
| K1 | Modular Arithmetic, Cyclic Groups |
| K2 | Dihedral Groups |
| K3 | Comparing , etc. |
| Mapping | Description |
|---|---|
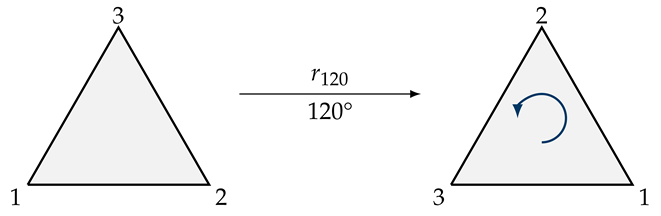 | Rotating the triangle counter-clockwise by . We will denote this mapping with the symbol . |
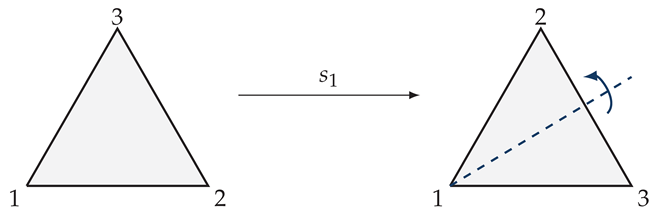 | Reflecting the triangle on the angle bisector through vertex 1. We will denote this mapping with the symbol . |
| ⋮ | ⋮ |
| Transformation | id | |||||
| Reverse Transformation | id |
| ∘ | id | |||||
| id | id | |||||
| id | ||||||
| id | ||||||
| id | ||||||
| id | ||||||
| id |
| Transformation | id | |||||||
| Construction |
| ∘ | id | |||||||
| id | id | |||||||
| id | ||||||||
| id | ||||||||
| id | ||||||||
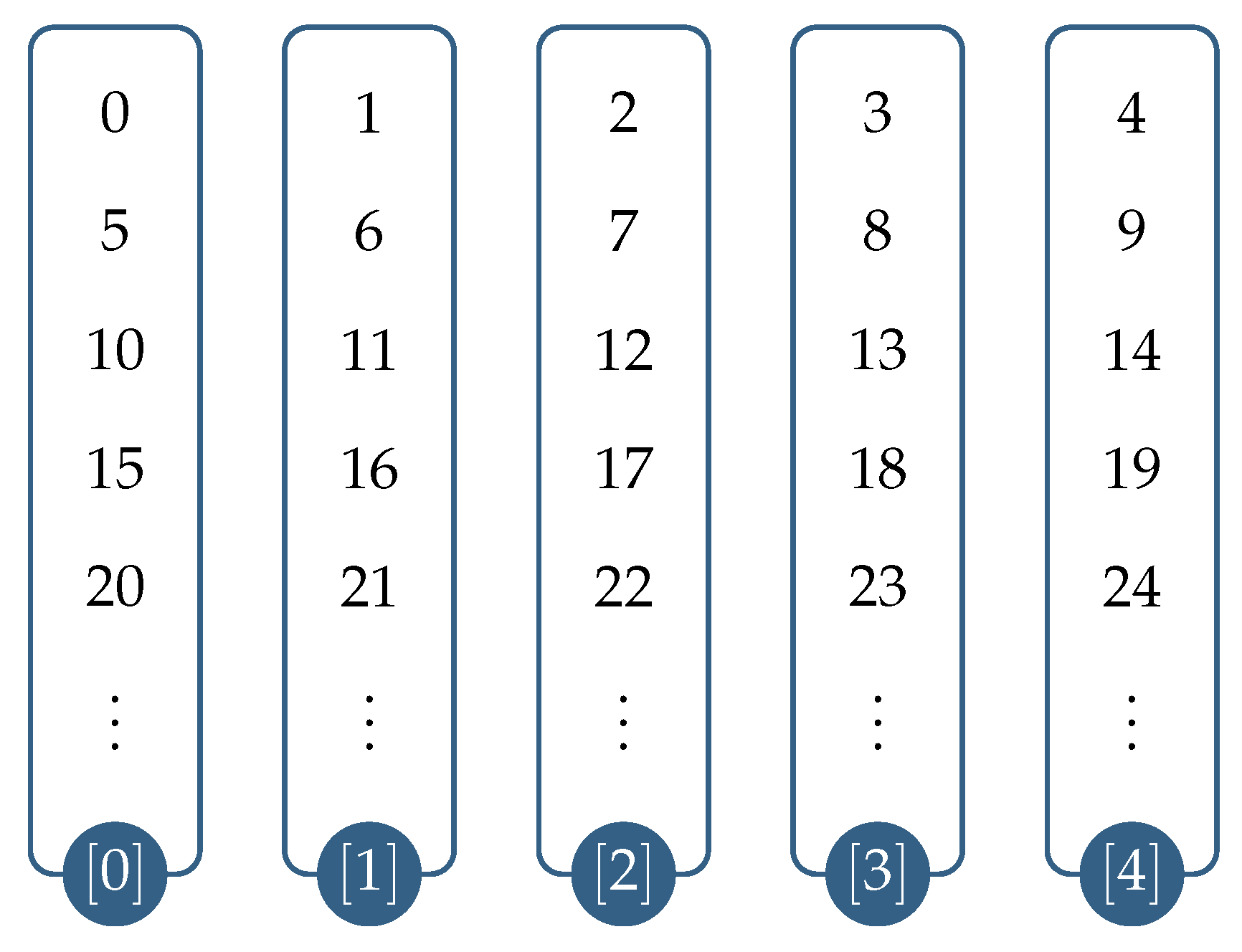
| ⊕ | 0 | 1 | 2 | 3 | 4 |
| 0 | 0 | 1 | 2 | 3 | 4 |
| 1 | 1 | 2 | 3 | 4 | 0 |
| 2 | 2 | 3 | 4 | 0 | 1 |
| 3 | 3 | 4 | 0 | 1 | 2 |
| 4 | 4 | 0 | 1 | 2 | 3 |
| Residue Class | |||||
| Inverse Class |
| ⊕ | 0 | 1 | 2 | 3 |
| 0 | 0 | 1 | 2 | 3 |
| 1 | 1 | 2 | 3 | 0 |
| 2 | 2 | 3 | 0 | 1 |
| 3 | 3 | 0 | 1 | 2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Veith, J.M.; Bitzenbauer, P. What Group Theory Can Do for You: From Magmas to Abstract Thinking in School Mathematics. Mathematics 2022, 10, 703. https://doi.org/10.3390/math10050703
Veith JM, Bitzenbauer P. What Group Theory Can Do for You: From Magmas to Abstract Thinking in School Mathematics. Mathematics. 2022; 10(5):703. https://doi.org/10.3390/math10050703
Chicago/Turabian StyleVeith, Joaquin Marc, and Philipp Bitzenbauer. 2022. "What Group Theory Can Do for You: From Magmas to Abstract Thinking in School Mathematics" Mathematics 10, no. 5: 703. https://doi.org/10.3390/math10050703
APA StyleVeith, J. M., & Bitzenbauer, P. (2022). What Group Theory Can Do for You: From Magmas to Abstract Thinking in School Mathematics. Mathematics, 10(5), 703. https://doi.org/10.3390/math10050703






