Free Vibration of FG-CNTRCs Nano-Plates/Shells with Temperature-Dependent Properties

Abstract

This article presents a mathematical continuum model to analyze the free vibration response of cross-ply carbon-nanotube-reinforced composite laminated nanoplates and nanoshells, including microstructure and length scale effects. Different shell geometries, such as plate (infinite radii), spherical, cylindrical, hyperbolic-paraboloid and elliptical-paraboloid are considered in the analysis. By employing Hamilton’s variational principle, the equations of motion are derived based on hyperbolic sine function shear deformation theory. Then, the derived equations are solved analytically using the Galerkin approach. Two types of material distribution are proposed. Higher-order nonlocal strain gradient theory is employed to capture influences of shear deformation, length scale parameter (nonlocal) and material/microstructurescale parameter (gradient). Temperature-dependent material properties are considered. The validation of the proposed mathematical model is presented. Detailed parametric analyses are carried out to highlight the effects of the carbon nanotubes (CNT) distribution pattern, the thickness stretching, the geometry of the plate/shell, the boundary conditions, the total number of layers, the length scale and the material scale parameters, on the vibrational frequencies of CNTRC laminated nanoplates and nanoshells.

1. Introduction

Carbon nanotubes (CNTs) discovered in 1991 by Iijima, are graphite sheets rolled to cylindrical geometry with 1 nm diameter and lengths up to micrometres [1]. Because of their extraordinary properties, they have received significant interest in many areas, including materials science, engineering, chemistry, and physics, and in applications involving nanoelectronics, nanosensors, and nanodevices [2]. Composite multilayer beam, plate, and shell are basic structures used in various applications, such as in the defense, aviation, turbomachinery and shipbuilding industries. The broad range of applications of composite shells have led academics to investigate the performance of these structures, which are made of different materials and subjected to numerous dynamic loads [3].

Many researchers have considered the mechanical responses of functionally graded, carbon-nanotube-reinforced composite (FG-CNTRC) using macroscale continuum theories. The vibration response of FG-CNTRC plate and beams have been studied by the finite element method [4,5], the state-space Levy method [6], the velocity feedback control method [7], Navier’s solution technique [8], generalized differential quadrature [9,10,11], mesh-free solution [12], and the three-step direct iterative scheme [13]. Shen and Zhang [14] investigated the thermal buckling/postbuckling behavior of FG-CNTRC plates subjected to in-plane temperature variation. Tang and Dai [15] examined the influence of hygrothermal conditions on the nonlinear dynamic response of FG-CNTRC plate with different CNT distributions. In an analysis of free vibration of FG-CNTRC shell structures, Kiani et al. [16] and Miao et al. [17] exploited numerical Chebyshev–Ritz methodology and Donnell’s kinematic. Mohandes and Ghasemi [18] studied the free vibration of FG-CNTRC shell based on Love’s first approximation shell theory. Bisheh et al. [19] illustrated the coupling effects of piezoelectricity, temperature, and moisture on the free vibration of smart FG-CNTRC cylindrical shells. Babaei [20] studied the frequency response of pre/post buckled FG-CNTRC pipes rested on nonlinear elastic foundation under thermal loads. Punera and Kant [21] developed a 2D kinematic model to investigate the static and dynamic response of FG-CNTRC sandwich cylindrical panels. Shahmohammadi et al. [22] assessed the impact of agglomeration of CNTs on the vibration of FG-CNTRC panels with constant and variable thickness using a finite element and isogeometric finite strip method. Sobhani et al. [23] studied the free vibration of sandwich FG-CNTRC-joined conical-cylindrical-conical shells in the framework of Donnell’s approach and generalized differential quadrature method.

When the dimensions of a structure become comparable to the size of its material micro-structure, size effects that are missed by classical continuum theories are observed. Therefore, to envisage the mechanical responses of structure up to micro and nano size accurately, advanced and modified continuum model theories have been applied, such as, nonlocal elasticity [24,25,26,27,28,29], couple stress theory [30,31], strain gradient theory [32], surface elasticity theory [33], the energy equivalent method [34], doublet mechanics [35], and quantum mechanics [36,37].

Nonlocal strain gradient theory (NLSGT) is considered one of the most widely used theories to study the size-dependent behavior of nanostructures [38]. Based on NLSGT, many studies have considered the development of nanoplate. Shahsavari et al. [39] studied the damped vibration of a graphene sheet using the NLSGT Kirchhoff plate model in a hygrothermal environment. Arefi et al. [40] studied the bending response of a sandwich porous NLSGT nanoplate integrated with piezomagnetic face-sheets. Daikh et al. [41] investigated the stability of sandwich FG-CNTRC curved nanobeams exposed to the thermal environment. Daikh et al. [42,43] exploited the quasi-3D shear deformation in a bending analysis of sandwich sigmoid FG nanoplates and FG-CNTRC nanoplates using nonlocal strain gradient theory.

For nanoshell analysis, Ansari et al. [44] presented the impact of size-dependent strain gradient theory on the thermo-mechanical vibration and instability of conveying fluid FG nanoshells. Rouhi et al. [45] investigated the vibrations of nanoshells based on surface stress elasticity. Farajpour et al. [46] examined the vibration and buckling smart control of microtubules using piezoelectric nonlocal nanoshells under electric voltage in a thermal environment. Jouneghani et al. [47] investigated the micro and nano mechanical behavior of orthotropic, doubly curved shell based on first-order shear deformation theory. Kachapi et al. [48] presented nonlinear dynamics and stability analysis of a piezo-visco-elastic nanoshell resonator with electrostatic and harmonic actuation. Al-Furjan et al. [49] studied the dynamic buckling of carbon nanocones, under magnetic and thermal loads, via nonlocal viscoelastic strain gradient theory. Aminipour et al. [50] investigated the size-dependent wave propagation of FG doubly curved nonlocal nanoshells based on higher-order shear deformation theory. Zhu et al. [51] developed a new approach for the smart control of size-dependent, nonlinear, free vibration of viscoelastic orthotropic piezoelectric doubly curved nanoshells. Xu et al. [52] studied the forced vibration response of doubly curved NLSGT nanoshells including different shape panels.

For FG nanoshell, Razavi et al. [53] predicted the vibration of FG piezoelectric cylindrical nanoshell based on consistent couple stress theory. Faleh et al. [54] illustrated the forced vibration response of a porous FG nanoshell by employing a two-parameter, non-classical elasticity theory. Dindarloo and Li [55] studied the 3D vibrational response of FG-CNTRC doubly curved, nonlocal nanoshells, based on a new higher-order shear deformation theory. Karami et al. [56] studied the free vibration of doubly curved NLSGT nanoshells in which the material properties are temperature and porosity dependent. Cao et al. [57] evaluated the effects of multi-directional FGMs on the natural frequency of doubly curved, nonlocal Eringen’s nanoshells, using Navier admissible functions. Tran et al. [58] extended four-unknown, higher-order shear deformation nonlocal theory to study the bending, buckling and free vibration of FG porous nanoshell resting on an elastic foundation. Twinkle and Pitchaimani [59] developed a semi-analytical, nonlocal model to investigate the static stability and vibration behavior of FG-CNTRC nano cylinders under non-uniform edge loads.

This manuscript aims, for the first time, to investigate the impact of the length scale, as well as the microstructure, on the natural frequencies of sandwich FG-CNTRC nonlocal strain gradient of nanoshell, using kinematic higher-order hyperbolic shear function. Two types of material distribution and four gradations (UN, X, O, and V) are proposed and presented in Section 2. The problem formulation, constitutive equations, variational statement, and equations of motion are derived in Section 3 and Section 4. The analytical solution of the governing equations of motion is derived in Section 5. The accuracy of the developed procedure is verified and discussed in Section 6. In Section 7, detailed parametric studies are performed and discussed to highlight the effect of the CNT distribution pattern, the thickness and the stretching, the geometry of the plate/shell, the boundary conditions, the total number of layers, the length scale and material scale parameters, on the natural frequencies. The conclusion and main points are summarized in Section 8.

2. Material and Geometrical Modeling

A rectangular multilayer shell in the Cartesian coordinate system, (x, y, z) is shown in Figure 1. The shell has a curved length, a, width, b, and thickness h. The principal radii of curvature of the mid-plane in x is R_x, and R_y in the y direction. The shell is reinforced by single wall carbon nanotubes (SWCNTs). All sheets of the shell have the same thickness. Four different patterns of CNT distribution are presented in this study, which are a uniform distribution UD and three functionally graded distributions, FG-X FG-V and FG-O. Two types of cross-ply multilayer CNTRC shells are proposed.

Figure 1. Material properties, geometry and coordinate system (a) and gradation type (b).

2.1. CNTRC Structure Type (A): CNTRC(A)

In Type (A), each layer has self-distribution (UD, X, O or V) (as shown in Figure 2). The effective material properties of CNT-reinforced composite shell are obtained based on a micromechanical model following [60].

Figure 2. The geometry of multilayer structure (a) and their types (b).

UD distribution pattern:

$$V_{cnt}=V_{cnt}^{*}$$

(1)

FG-X distribution Pattern:

$$\begin{array}{c}{V}_{cnt}=2{\left(\frac{\left|2\left|z\right|-\left|z_{\left(k-1\right)}+z_{\left(k\right)}\right|\right|}{z_{\left(k\right)}-z_{\left(k-1\right)}}\right)}^p{V}_{cnt}^{*}\end{array}$$

(2)

FG-O distribution Pattern:

$$V_{cnt}=2\left(1-{\left(\frac{\left|2\left|z\right|-\left|z_{\left(k-1\right)}+z_{\left(k\right)}\right|\right|}{z_{\left(k\right)}-z_{\left(k-1\right)}}\right)}^p\right)V_{cnt}^{*}$$

(3)

FG-V distribution Pattern:

$$V_{cnt}=2{\left(\frac{1}{2}-\left(\frac{2z-z_{\left(k\right)}-z_{\left(k-1\right)}}{2\left(z_{\left(k\right)}-z_{\left(k-1\right)}\right)}\right)\right)}^p{V}_{cnt}^{*}$$

(4)

$V_{cnt} \mathrm{and} V_{cnt}^{*}$ refer, respectively, to the volume fraction and the total volume fraction of CNTs, p is the inhomogeneity material graduation index, $k$ denotes the layer number.

2.2. CNTRC Structure Type (B): CNTRC(B)

In this type, the distribution of CNTs is applied along the total thickness (see Figure 2). The effective material properties of CNTRC shell are defined as

FG-X distribution Pattern:

$$V_{cnt}=2{\left(\frac{2\left|z\right|}{h}\right)}^p{V}_{cnt}^{*}$$

(5)

FG-O distribution Pattern:

$$V_{cnt}=2{\left(1-\frac{2\left|z\right|}{h}\right)}^p{V}_{cnt}^{*}$$

(6)

FG-V distribution Pattern:

$$V_{cnt}={\left(1+\frac{2z}{h}\right)}^p{V}_{cnt}^{*}$$

(7)

3. Kinematics and Kinetics Relations

Within this section, the kinematics and kinetics relations are presented. Hyperbolic sine function shear deformation theory is applied in this analysis to satisfy the zero-shear stress at the free outer boundaries. Based on the higher-order hyperbolic shear function, the displacement field is given as, [61]

$$\begin{array}{c}u\left(x,y,z,t\right)=\left(1+\frac{z}{R_x}\right)u_0-z\frac{\partial w_0}{\partial x}+f\left(z\right){\psi }_x\\ v\left(x,y,z,t\right)=\left(1+\frac{z}{R_y}\right)v_0-z\frac{\partial w_0}{\partial y}+f\left(z\right){\psi }_y\\ w\left(x,y,z,t\right)=w_0\end{array}$$

(8)

The displacements of the midplane of the composite plate are $u_0$, $v_0$, and $w_0$, whereas ${\psi }_x$ and ${\psi }_y$ are the rotations of the transverse normal at the middle surface z = 0. The proposed hyperbolic sine shape function, $f\left(z\right)$ can be written as

$$f\left(z\right)=h\sinh \left(\frac{z}{h}\right)-\frac{3z^3}{2h^2}$$

(9)

The strain displacement relations can be obtained by derivative of the displacements as

$$\begin{gathered} \left\{\begin{array}{c}{\epsilon }_{xx}\\ {\epsilon }_{yy}\\ {\gamma }_{xy}\end{array}\right\}=\left\{\begin{array}{c}{\epsilon }_{xx}^0\\ {\epsilon }_{yy}^0\\ {\gamma }_{xy}^0\end{array}\right\}+z\left\{\begin{array}{c}{\epsilon }_{xx}^1\\ {\epsilon }_{yy}^1\\ {\gamma }_{xy}^1\end{array}\right\}+f\left(z\right)\left\{\begin{array}{c}{\epsilon }_{xx}^2\\ {\epsilon }_{yy}^2\\ {\gamma }_{xy}^2\end{array}\right\} \\ {\epsilon }_{zz}=0, \left\{\begin{array}{c}{\gamma }_{yz}\\ {\gamma }_{xz}\end{array}\right\}=\frac{\mathrm{d}f\left(z\right)}{\mathrm{d}z}\left\{\begin{array}{c}{\gamma }_{yz}^0\\ {\gamma }_{xz}^0\end{array}\right\}, \end{gathered}$$

(10)

where ε_xx, ε_yy, γ_xy, are, respectively, the normal and shear strain component, while ${\epsilon }_{xx}^0, {\epsilon }_{yy}^0, {\gamma }_{xy}^0$, ${\epsilon }_{xx}^2, {\epsilon }_{yy}^2, {\gamma }_{xy}^2, {\gamma }_{yz}^0, \mathrm{and} {\gamma }_{xz}^0$ are related to the midplane displacement and rotaion deriviatives and rotation as follows:

$$\begin{gathered} \left\{\begin{array}{c}{\epsilon }_{xx}^0\\ {\epsilon }_{yy}^0\\ {\gamma }_{xy}^0\end{array}\right\}=\left\{\begin{array}{c}\frac{\partial u_0}{\partial x}+\frac{w_0}{R_x}\\ \frac{\partial v_0}{\partial y}+\frac{w_0}{R_y}\\ \frac{\partial v_0}{\partial x}+\frac{\partial u_0}{\partial y}\end{array}\right\}, \left\{\begin{array}{c}{\epsilon }_{xx}^1\\ {\epsilon }_{yy}^1\\ {\gamma }_{xy}^1\end{array}\right\}=-\left\{\begin{array}{c}\frac{{\partial }^2{w}_0}{\partial x^2}\\ \frac{{\partial }^2{w}_0}{\partial y^2}\\ 2\frac{{\partial }^2{w}_0}{\partial x\partial y}\end{array}\right\}, \\ \begin{array}{c} \\ \left\{\begin{array}{c}{\epsilon }_{xx}^2\\ {\epsilon }_{yy}^2\\ {\gamma }_{xy}^2\end{array}\right\}=\left\{\begin{array}{c}\frac{\partial {\phi }_1}{\partial x}\\ \frac{\partial {\phi }_2}{\partial y}\\ \frac{\partial {\phi }_2}{\partial x}+\frac{\partial {\phi }_1}{\partial y}\end{array}\right\}, \left\{\begin{array}{c}{\gamma }_{yz}^0\\ {\gamma }_{xz}^0\end{array}\right\}=\left\{\begin{array}{c}{\phi }_x\\ {\phi }_y\end{array}\right\}.\end{array} \end{gathered}$$

(11)

The stresses relations of kth layer accounting for both nonlocal elastic stress field and the strain gradient stress field, can be written as [38]

$$\left[1-\mu {\nabla }^2\right]{\left\{\begin{array}{c}{\sigma }_{xx}\\ {\sigma }_{yy}\\ \begin{array}{c}\begin{array}{c}{\tau }_{yz}\\ {\tau }_{xz}\end{array}\\ {\tau }_{xy}\end{array}\end{array}\right\}}^{\left(k\right)}=\left[1-\lambda {\nabla }^2\right]\left[\begin{array}{cc}\begin{array}{cc}\begin{array}{ccc}{\overline{Q}}_{11}^k& {\overline{Q}}_{12}^k& 0\\ {\overline{Q}}_{12}^k& {\overline{Q}}_{22}^k& 0\\ \begin{array}{c}0\\ 0\\ 0\end{array}& \begin{array}{c}0\\ 0\\ 0\end{array}& \begin{array}{c}{\overline{Q}}_{44}^k\\ 0\\ 0\end{array}\end{array}& \begin{array}{c}0\\ 0\\ \begin{array}{c}0\\ {\overline{Q}}_{55}^k\\ 0\end{array}\end{array}\end{array}& \begin{array}{c}0\\ 0\\ \begin{array}{c}0\\ 0\\ {\overline{Q}}_{66}^k\end{array}\end{array}\end{array}\right]{\left\{\begin{array}{c}{\epsilon }_{xx}\\ {\epsilon }_{yy}\\ \begin{array}{c}\begin{array}{c}{\gamma }_{yz}\\ {\gamma }_{xz}\end{array}\\ {\gamma }_{xy}\end{array}\end{array}\right\}}^{\left(k\right)}$$

(12)

Here, $\mu$ denote the nonlocal parameter and $\lambda$ is the length scale parameter and ${\nabla }^2$ denotes the Laplacian operator [62]. The transformed material constants ${\overline{Q}}_{ij}^k$ are expressed as:

$$\begin{array}{c}{\overline{Q}}_{11}^k=Q_{11}co{s}^4{\theta }_k+2\left(Q_{12}+2Q_{66}\right)si{n}^2{\theta }_{k}co{s}^2{\theta }_k+Q_{22}si{n}^4{\theta }_k\\ {\overline{Q}}_{12}^k=\left(Q_{11}+Q_{22}-4Q_{66}\right)si{n}^2{\theta }_{k}co{s}^2{\theta }_k+Q_{12}\left(si{n}^4{\theta }_k+co{s}^4{\theta }_k\right)\\ {\overline{Q}}_{22}^k=Q_{11}si{n}^4{\theta }_k+2\left(Q_{12}+2Q_{66}\right)si{n}^2{\theta }_{k}co{s}^2{\theta }_k+Q_{22}co{s}^4{\theta }_k\\ {\overline{Q}}_{66}^k=\left(Q_{11}+Q_{22}-2Q_{12}-2Q_{66}\right)si{n}^2{\theta }_{k}co{s}^2{\theta }_k+Q_{66}\left(si{n}^4{\theta }_k+co{s}^4{\theta }_k\right)\\ {\overline{Q}}_{44}^k=Q_{44}co{s}^2{\theta }_k+Q_{55}si{n}^2{\theta }_k\\ {\overline{Q}}_{55}^k=Q_{55}co{s}^2{\theta }_k+Q_{44}si{n}^2{\theta }_k\end{array}$$

(13)

where ${\theta }_k$ is the lamination angle $\left({\theta }_k=0°, 90°\right)$ and

$$\begin{array}{c}{Q}_{11}=\frac{E_{11}}{1-{\nu }_{12}{\nu }_{21}}, Q_{22}=\frac{E_{22}}{1-{\nu }_{12}{\nu }_{21}}, Q_{12}=\frac{{\nu }_{12}{E}_{22}}{1-{\nu }_{12}{\nu }_{21}},\\ Q_{44}=G_{23}, Q_{55}=G_{13}, Q_{66}=G_{12}\end{array}$$

(14)

The stress relations, moment and additional moment resultants can be obtained by integration of Equation (12), which will result

$$\left[1-\mu {\nabla }^2\right]\left\{\begin{array}{c}\left\{N\right\}\\ \left\{M\right\}\\ \left\{P\right\}\end{array}\right\}=\left[1-\lambda {\nabla }^2\right]\left[\begin{array}{ccc}\left[A\right]& \left[B\right]& \left[C\right]\\ \left[B\right]& \left[D\right]& \left[F\right]\\ \left[C\right]& \left[F\right]& \left[H\right]\end{array}\right]\left\{\begin{array}{c}\left\{{\epsilon }^0\right\}\\ \left\{{\epsilon }^1\right\}\\ \left\{{\epsilon }^2\right\}\end{array}\right\}$$

(15)

$$\left[1-\mu {\nabla }^2\right]\left\{\begin{array}{c}{R}_{yz}\\ R_{xz}\end{array}\right\}=\left[1-\lambda {\nabla }^2\right]\left[\begin{array}{cc}{J}_{44}& J_{45}\\ J_{45}& J_{55}\end{array}\right]\left\{\begin{array}{c}{\gamma }_{yz}^0\\ {\gamma }_{xz}^0\end{array}\right\}$$

(16)

where

$$\begin{array}{c}\left\{N\right\}={\left\{\begin{array}{ccc}{N}_{xx}& N_{yy}& N_{xy}\end{array}\right\}}^T, \left\{M\right\}={\left\{\begin{array}{ccc}{M}_{xx}& M_{yy}& M_{xy}\end{array}\right\}}^T, \left\{P\right\}={\left\{\begin{array}{ccc}{P}_{xx}& P_{yy}& P_{xy}\end{array}\right\}}^T\\ \left\{{\epsilon }^0\right\}={\left\{\begin{array}{ccc}{\epsilon }_{xx}^0& {\epsilon }_{yy}^0& {\gamma }_{xy}^0\end{array}\right\}}^T, \left\{{\epsilon }^1\right\}={\left\{\begin{array}{ccc}{\epsilon }_{xx}^1& {\epsilon }_{yy}^1& {\gamma }_{xy}^1\end{array}\right\}}^T, \left\{{\epsilon }^2\right\}={\left\{\begin{array}{ccc}{\epsilon }_{xx}^2& {\epsilon }_{yy}^2& {\gamma }_{xy}^2\end{array}\right\}}^T\end{array}$$

(17)

The coefficients $A_{ij}$, $B_{ij}$, $D_{ij}$, $C_{ij}$, $F_{ij}$ and $H_{ij}$ can be defined as

$$\begin{array}{c}\left\{A_{ij}, B_{ij}, D_{ij}, C_{ij},F_{ij},H_{ij}\right\}={\displaystyle {\displaystyle \sum }_{n=1}^n}\underset{h_{n-1}}{\overset{h_n}{{\displaystyle \int }}}{Q}_{ij}{}^{\left(n\right)}\left\{1, z,z^2,f\left(z\right),zf\left(z\right),f{\left(z\right)}^2\right\}\mathrm{d}z, \left(i,j=1,2,6\right)\\ J_{ii}={\displaystyle {\displaystyle \sum }_{n=1}^n}\underset{h_{n-1}}{\overset{h_n}{{\displaystyle \int }}}{Q}_{ii}{}^{\left(n\right)}{\left[\frac{\mathrm{d}f\left(z\right)}{\mathrm{d}z}\right]}^2\mathrm{d}z,\left(i=4,5\right)\end{array}$$

(18)

4. Dynamic Equations of Motion

To derive the equations of motion of the CNTRC shell, Hamilton’s principle is utilized:

$${{\displaystyle \int }}_{t_2}^{t_1}\delta \left(U-T+V\right)dt=0$$

(19)

The virtual strain energy of the CNTRC shell, $\delta \left(U\right)$ can be determined as

$$\delta U_p=\frac{1}{2}{{\displaystyle \int }}_V\left[{\sigma }_{xx}^{\left(k\right)}\delta {\epsilon }_{xx}+{\sigma }_{yy}^{\left(k\right)}\delta {\epsilon }_{xx}+{\sigma }_{xy}^{\left(k\right)}\delta {\gamma }_{xy}+{\sigma }_{xz}^{\left(k\right)}\delta {\gamma }_{xz}+{\sigma }_{yz}^{\left(k\right)}\delta {\gamma }_{yz}\right]\mathrm{d}V$$

(20)

At any moment, the virtual kinetic energy of the CNTRC shell, $\delta T$ can be stated as

$$\delta T=\frac{1}{2}{{\displaystyle \int }}_0^L{{\displaystyle \int }}_A\rho \left(\dot{u}\delta \dot{u}+\dot{v}\delta \dot{v}+\dot{w}\delta \dot{w}\right)dAdx$$

(21)

$$\begin{array}{c}\begin{array}{c}\delta T={{\displaystyle \int }}_V\{I_0\left({\dot{u}}_0\delta {\dot{u}}_0+{\dot{v}}_0\delta {\dot{v}}_0+{\dot{w}}_0\delta {\dot{w}}_0\right)+I_1\left(\frac{\partial {\dot{w}}_0}{\partial x}\delta {\dot{u}}_0+\frac{\partial {\dot{w}}_0}{\partial y}\delta {\dot{v}}_0+{\dot{u}}_0\frac{\partial \delta {\dot{w}}_0}{\partial x}{\dot{+v}}_0\frac{\partial \delta {\dot{w}}_0}{\partial y}\right)\#\end{array}\\ +I_2\left(\frac{\partial {\dot{w}}_0}{\partial x}\frac{\partial \delta {\dot{w}}_0}{\partial x}+\frac{\partial {\dot{w}}_0}{\partial y}\frac{\partial \delta {\dot{w}}_0}{\partial y}\right)+I_3\left({\dot{\phi }}_x\delta {\dot{u}}_0+{\dot{u}}_0\delta {\dot{\phi }}_x+{\dot{\phi }}_y\delta {\dot{v}}_0+{\dot{v}}_0\delta {\dot{\phi }}_y\right)\\ +I_4\left({\dot{\phi }}_x\frac{\partial \delta {\dot{w}}_0}{\partial x}+\frac{\partial {\dot{w}}_0}{\partial x}\delta {\dot{\phi }}_x+{\dot{\phi }}_y\frac{\partial \delta {\dot{w}}_0}{\partial y}+\frac{\partial {\dot{w}}_0}{\partial y}\delta {\dot{\phi }}_y\right)+I_5\left({\dot{\phi }}_x\delta {\dot{\phi }}_x+{\dot{\phi }}_y\delta {\dot{\phi }}_y\right)\}\mathrm{d}x\mathrm{d}y\mathrm{d}z\end{array}$$

(22)

where

$$\left\{I_0, I_1, I_2, I_3,I_4,I_5\right\}={\displaystyle \sum }_{n=1}^k\rho \left(z\right)\left\{1, z,z^2,\Phi \left(z\right),z\Phi \left(z\right),{\left(\Phi \left(z\right)\right)}^2\right\}dz$$

(23)

Neglecting the effect of the external applied load, insertion of Equations (20) and (22), into Equation (19), the equilibrium equations for CNTRC shells can be obtained as follows:

$$\begin{array}{c}[1-\mu {\nabla }^2][A_{11}\frac{{\partial }^2{u}_0}{\partial x^2}+A_{66}\frac{{\partial }^2{u}_0}{\partial y^2}+(A_{12}+A_{66})\frac{{\partial }^2{v}_0}{\partial x\partial y}+(\frac{A_{11}}{R_x}+\frac{A_{12}}{R_y})\frac{\partial w_0}{\partial x}-B_{11}\frac{{\partial }^3{w}_0}{\partial x^3}\\ -(B_{12}+2B_{66})\frac{{\partial }^3{w}_0}{\partial x\partial y^2}+B_{11}^S\frac{{\partial }^2{\psi }_x}{\partial x^2}+B_{66}^S\frac{{\partial }^2{\psi }_x}{\partial y^2}+(B_{12}^S+B_{66}^S)\frac{{\partial }^2{\psi }_y}{\partial x\partial y}]\\ =[1-\lambda {\nabla }^2][(I_0+2\frac{I_1}{R_x}+\frac{I_3}{R_y{}^2})\frac{{\partial }^2{u}_0}{\partial t^2}-(I_1+\frac{I_2}{R_x})\frac{{\partial }^2{w}_0}{\partial x\partial t^2}+(I_3+\frac{I_4}{R_x})\frac{{\partial }^2{\psi }_x}{\partial t^2}]\end{array}$$

(24)

$$\begin{array}{c}[1-\mu {\nabla }^2][(A_{12}+A_{66})\frac{{\partial }^2{u}_0}{\partial x\partial y}+A_{22}\frac{{\partial }^2{v}_0}{\partial y^2}+A_{66}\frac{{\partial }^2{v}_0}{\partial x^2}-(B_{11}+2B_{66})\frac{{\partial }^3{w}_0}{\partial x^2\partial y}-B_{22}\frac{{\partial }^3{w}_0}{\partial y^3}\\ +(\frac{A_{12}}{R_x}+\frac{A_{22}}{R_y})\frac{\partial w_0}{\partial x}+(B_{12}^S+B_{66}^S)\frac{{\partial }^2{\psi }_x}{\partial x\partial y}+B_{22}^S\frac{{\partial }^2{\psi }_y}{\partial y^2}+B_{66}^S\frac{{\partial }^2{\psi }_y}{\partial x^2}]\\ =[1-\lambda {\nabla }^2][(I_0+2\frac{I_1}{R_y}+\frac{I_2}{R_y{}^2})\frac{{\partial }^2{v}_0}{\partial t^2}-(I_1+\frac{I_2}{R_y})\frac{{\partial }^3{w}_0}{\partial y\partial t^2}+(I_3+\frac{I_4}{R_y})\frac{{\partial }^2{\psi }_y}{\partial t^2}]\end{array}$$

(25)

$$\begin{array}{c}[1-\mu {\nabla }^2][B_{11}\frac{{\partial }^3{u}_0}{\partial x^3}+(B_{12}+2B_{66})\frac{{\partial }^3{u}_0}{\partial x\partial y^2}-(\frac{A_{11}}{R_x}+\frac{A_{12}}{R_y})\frac{\partial u_0}{\partial x}+(B_{12}+2B_{66})\frac{{\partial }^3{v}_0}{\partial x^2\partial y}+B_{22}\frac{{\partial }^3{v}_0}{\partial y^3}\\ -(\frac{A_{12}}{R_x}+\frac{A_{22}}{R_y})\frac{\partial v_0}{\partial y}+(\frac{2B_{11}}{R_x}+\frac{2B_{12}}{R_y})\frac{{\partial }^2{w}_0}{\partial x^2}-D_{11}\frac{{\partial }^4{w}_0}{\partial x^4}-(2D_{12}+4D_{66})\frac{{\partial }^4{w}_0}{\partial x^2\partial y^2}--D_{22}\frac{{\partial }^4{w}_0}{\partial y^4}\\ +(\frac{2B_{12}}{R_x}+\frac{2B_{22}}{R_y})\frac{{\partial }^2{w}_0}{\partial y^2}-(\frac{A_{11}}{R_x{}^2}+2\frac{A_{12}}{R_x{R}_y}+\frac{A_{22}}{R_y{}^2})w_0+D_{11}^S\frac{{\partial }^3{\psi }_x}{\partial x^3}+(D_{12}^S+2D_{66}^S)\frac{{\partial }^3{\psi }_x}{\partial x\partial y^2}\\ -(\frac{B_{11}^S}{R_x}+\frac{B_{12}^S}{R_y})\frac{\partial {\psi }_x}{\partial x}+(D_{12}^S+2D_{66}^S)\frac{{\partial }^3{\psi }_y}{\partial x^2\partial y}+D_{22}^S\frac{{\partial }^3{\psi }_y}{\partial y^3}-(\frac{B_{12}^S}{R_x}+\frac{B_{22}^S}{R_y})\frac{\partial {\psi }_y}{\partial y}]\\ =[1-\lambda {\nabla }^2][I_0\frac{{\partial }^2{w}_0}{\partial t^2}+(I_1+\frac{I_2}{R_x})\frac{{\partial }^3{u}_0}{\partial x\partial t^2}+(I_1+\frac{I_2}{R_y})\frac{{\partial }^3{v}_0}{\partial y\partial t^2}\\ -I_2(\frac{{\partial }^4{w}_0}{\partial x^2\partial t^2}+\frac{{\partial }^4{w}_0}{\partial y^2\partial t^2})+I_4(\frac{{\partial }^3{\psi }_x}{\partial x\partial t^2}+\frac{{\partial }^3{\psi }_y}{\partial y\partial t^2})]\end{array}$$

(26)

$$\begin{array}{c}[1-\mu {\nabla }^2][B_{11}^S\frac{{\partial }^2{u}_0}{\partial x^2}+B_{66}^S\frac{{\partial }^2{u}_0}{\partial y^2}+(B_{12}^S+B_{66}^S)\frac{{\partial }^2{v}_0}{\partial x\partial y}\frac{\partial u_0}{\partial x}-D_{11}^S\frac{{\partial }^3{w}_0}{\partial x^3}-(D_{12}^S+2D_{66}^S)\frac{{\partial }^3{w}_0}{\partial x\partial y^2}\\ +(\frac{B_{11}^S}{R_x}+\frac{B_{12}^S}{R_y})\frac{\partial w_0}{\partial x}+F_{11}^S\frac{{\partial }^2{\psi }_x}{\partial x^2}+F_{66}^S\frac{{\partial }^2{\psi }_x}{\partial y^2}-A_{44}^S{\psi }_x+(F_{12}^S+F_{66}^S)\frac{{\partial }^2{\psi }_y}{\partial x\partial y}]\\ =[1-\lambda {\nabla }^2][(I_3+\frac{I_4}{R_x})\frac{{\partial }^2{u}_0}{\partial t^2}-I_4\frac{{\partial }^3{w}_0}{\partial x\partial t^2}+I_5\frac{{\partial }^2{\psi }_x}{\partial t^2}]\end{array}$$

(27)

$$\begin{array}{c}[1-\mu {\nabla }^2][(B_{12}^S+B_{66}^S)\frac{{\partial }^2{u}_0}{\partial x\partial y}+B_{11}^S\frac{{\partial }^2{v}_0}{\partial y^2}+B_{66}^S\frac{{\partial }^2{v}_0}{\partial x^2}-(D_{12}^S+2D_{66}^S)\frac{{\partial }^3{w}_0}{\partial x^2\partial y}-D_{22}^S\frac{{\partial }^3{w}_0}{\partial y^3}\\ +(\frac{B_{12}^S}{R_x}+\frac{B_{22}^S}{R_y})\frac{\partial w_0}{\partial x}+(F_{12}^S+F_{66}^S)\frac{{\partial }^2{\psi }_x}{\partial x\partial y}+F_{11}^S\frac{{\partial }^2{\psi }_y}{\partial y^2}+F_{66}^S\frac{{\partial }^2{\psi }_y}{\partial x^2}-A_{44}^S{\psi }_y]\\ =[1-\lambda {\nabla }^2][(I_3+\frac{I_4}{R_y})\frac{{\partial }^2{v}_0}{\partial t^2}-I_4\frac{{\partial }^3{w}_0}{\partial y\partial t^2}+I_5\frac{{\partial }^2{\psi }_y}{\partial t^2}]\end{array}$$

(28)

5. Analytical Solution

Within this section, closed forms are presented for the eigen value problem of the free vibration of the CNTRC shells considering different boundary conditions including: simple-simple (SSSS), clamped-clamped (CCCC), clamped-simple-clamped-simple (CSCS), clamped-clamped-simple-simple (CCSS), clamped-simple-simple-simple (CSSS), clamped-clamped-clamped-simple (CCCS). The Galerkin approach is employed to provide accurate closed-form solutions. Based on the Galerkin technique, the expressions for generalized displacements are as follows:

$$\begin{array}{c}\left\{u_0,{\psi }_x\right\}={\displaystyle {\displaystyle \sum }_{m=1}^{\infty }}{\displaystyle {\displaystyle \sum }_{n=1}^{\infty }}\left\{U_{mn},X_{mn}\right\}\frac{\partial X_m\left(x\right)}{\partial x}{Y}_n\left(y\right)e^{i\omega t}\\ \left\{v_0,{\psi }_y\right\}={\displaystyle {\displaystyle \sum }_{m=1}^{\infty }}{\displaystyle {\displaystyle \sum }_{n=1}^{\infty }}\left\{V_{mn},Z_{mn}\right\}{X}_m\left(x\right)\frac{\partial Y_n\left(y\right)}{\partial y}{e}^{i\omega t}\\ w_0={\displaystyle {\displaystyle \sum }_{m=1}^{\infty }}{\displaystyle {\displaystyle \sum }_{n=1}^{\infty }}{W}_{mn}{X}_m\left(x\right)Y_n\left(y\right)e^{i\omega t}\end{array}$$

(29)

$U_{mn}$, $V_{mn}$, $X_{mn}$ and $Z_{mn}$ are arbitrary parameters. The functions $X_m\left(x\right)$ and $Y_n\left(y\right)$ that satisfy the above boundary conditions are given in Table 1.

Table 1. The admissible functions $X_m\left(x\right)$ and $Y_n\left(y\right)$.

BCs.	$\mathbf{The} \mathbf{Functions} {\mathit{X}}_{\mathit{m}}$$\mathbf{and} {\mathit{Y}}_{\mathit{n}}$
	$X_m\left(x\right)$	$Y_n\left(y\right)$
SSSS	$\sin \left(\alpha x\right)$	$\sin \left(\beta y\right)$
CCCC	${\sin }^2\left(\alpha x\right)$	${\sin }^2\left(\beta y\right)$
CSCS	$\sin \left(\alpha x\right)\left[\cos \left(\alpha x\right)-1\right]$	$\sin \left(\beta y\right)\left[\cos \left(\beta y\right)-1\right]$
CCSS	${\sin }^2\left(\alpha x\right)$	$\sin \left(\beta y\right)$
CSSS	$\sin \left(\alpha x\right)\left[\cos \left(\alpha x\right)-1\right]$	$\sin \left(\beta y\right)$
CCCS	${\sin }^2\left(\alpha x\right)$	$\sin \left(\beta y\right)\left[\cos \left(\beta y\right)-1\right]$

Where $\lambda =m\pi /a$, $\mu =n\pi /b$. $m$ and $n$ are mode numbers. By substituting Equation (29) in Equations (24)–(28), one obtains

$$\begin{gathered} \left[{\left[K\right]}_{5\times 5}-{\omega }_{nm}^2{\left[M\right]}_{5\times 5}\right]\{\Delta \}=0 \\ \left[K\right]=\left[\begin{array}{c}\begin{array}{ccc}{K}_{11}& K_{12}& \begin{array}{ccc}{K}_{13}& K_{14}& K_{15}\end{array}\end{array}\\ \begin{array}{ccc}{K}_{12}& K_{22}& \begin{array}{ccc}{K}_{23}& K_{24}& K_{25}\end{array}\end{array}\\ \begin{array}{c}\begin{array}{ccc}{K}_{13}& K_{23}& \begin{array}{ccc}{K}_{33}& K_{34}& K_{35}\end{array}\end{array}\\ \begin{array}{ccc}{K}_{14}& K_{24}& \begin{array}{ccc}{K}_{34}& K_{44}& K_{45}\end{array}\end{array}\\ \begin{array}{ccc}{K}_{15}& K_{25}& \begin{array}{ccc}{K}_{35}& K_{45}& K_{55}\end{array}\end{array}\end{array}\end{array}\right], \left[M\right]=\left[\begin{array}{c}\begin{array}{ccc}{M}_{11}& M_{12}& \begin{array}{ccc}{M}_{13}& M_{14}& M_{15}\end{array}\end{array}\\ \begin{array}{ccc}{M}_{21}& M_{22}& \begin{array}{ccc}{M}_{23}& M_{24}& M_{25}\end{array}\end{array}\\ \begin{array}{c}\begin{array}{ccc}{M}_{13}& M_{23}& \begin{array}{ccc}{M}_{33}& M_{34}& M_{35}\end{array}\end{array}\\ \begin{array}{ccc}{M}_{14}& M_{24}& \begin{array}{ccc}{M}_{34}& M_{44}& M_{45}\end{array}\end{array}\\ \begin{array}{ccc}{M}_{15}& M_{25}& \begin{array}{ccc}{M}_{35}& M_{45}& M_{55}\end{array}\end{array}\end{array}\end{array}\right] \end{gathered}$$

(30)

where ${\omega }^2 \mathrm{and} \{\Delta \}$ are, respectively, the eigen values and the eigen vectors. $\left[K\right] \mathrm{and} \left[M\right]$ are, respectively, the rigidity and mass matrices. The elements $K_{ij}$ and $M_{ij}$ of the matrix [K] and [M] are given in Appendix A.

6. Verification of the Developed Procedure

The accuracy of the proposed procedure will be checked in this section. The developed procedure is applied to obtain results for the free vibration of functionally graded plates and shells. For the straight plate, the radii of curvature are $R_x/a=R_y/b=\infty$, and $R_x/a=R_y/b=5$ for the spherical shell, $R_x/a=5$ and $R_y/b=\infty$ for the cylindrical shell, $R_x/a=5$ and $R_y/b=-5$ for the hyperbolic-paraboloid shell, $R_x/a=5$ and $R_y/b=7.5$ for the elliptical-paraboloid shell (see Figure 3). The obtained results are compared with those generated in the literature using various solution techniques, as shown in Figure 4. The material characteristics used for verification are as follows: alumina (AlO₂) as ceramic with material properties; ($E_c=380 \mathrm{GPa}$, ${\rho }_c=3800 \mathrm{kg}/{\mathrm{m}}^3$) and aluminium (Al) as metal with the following characteristics: ($E_m=70 \mathrm{GPa}$, ${\rho }_c=2707 \mathrm{kg}/{\mathrm{m}}^3$). Poisson’s ratio is taken as $\upsilon =0.3$. Comparison between results shows good agreement verifiying the accuracy of the developed procedure.

Figure 3. Forms of various plate/shells.

Figure 4. Variation of the non-dimensional frequency parameter $\left(\tilde{\omega }=\omega h\sqrt{{\rho }_c/E_c}\right)$ with the material gradation index, P for simply supported Al/Al₂O₃ functionally graded square plates and doubly curved shells (a = b = 10 h, m = n = 1).

7. Results and Discussions

Considering a CNTRC nanoshell in a high-temperature medium. The temperature field is assumed to be uniform over the nanoshell. The (10,10) single-walled carbon nanotubes (SWCNT) are utilized as reinforcements. The effective temperature-dependent material properties of the CNTs are given as the following expression [62]

$$P=P_0\left(P_{-1}{T}^{-1}+1+P_{1}T+P_2{T}^2+P_3{T}^3\right)$$

(31)

Here, $T=T_0+\Delta T$, where $T_0$ is the ambient temperature $\left(T_0=300K\right)$ and $\Delta T$ is the temperature difference. $P_0$, $P_1$, $P_2$, and $P_3$ are the temperature coefficients given in Table 2.

Table 2. Temperature-dependent coefficients of CNT material properties.

	${\mathit{P}}_0$	${\mathit{P}}_{-1}$	${\mathit{P}}_1$	${\mathit{P}}_2$	${\mathit{P}}_3$
$E_{11}^{cnt}\left[\mathrm{TPa}\right]$	6.3998	0	−6.77898 × 10−4	1.16097 × 10−6	−6.96636 × 10−10
$E_{22}^{cnt}\left[\mathrm{TPa}\right]$	8.02155	0	−6.75726 × 10−4	1.15626 × 10−6	−6.93444 × 10−10
$G_{12}^{cnt}\left[\mathrm{TPa}\right]$	1.40755	0	2.46968 × 10−3	−4.94831 × 10−6	3.18224 × 10−9
${\rho }^{cnt}$	1400	0	0	0	0
${\nu }_{12}^{cnt}$	0.175	0	0	0	0

Young’s modulus of the polymeric matrix (PmPV) is dependent on the temperature and can be expressed as:

$$E_m\left[\mathrm{GPa}\right]=\left(3.51-0.0047T\right)$$

(32)

The Poisson ratio and the mass density are independent of the temperature and given as: $v_m=0.34$ and ${\rho }_m=1150\mathrm{kg}/{\mathrm{m}}^3$, respectively.

To standardize and simplify calculations, the normalized parameters for the vibration analyses of CNTRC shells are described using the following forms:

$$\overline{\omega }=\omega h\sqrt{\frac{{\rho }_m}{E_m}}$$

(33)

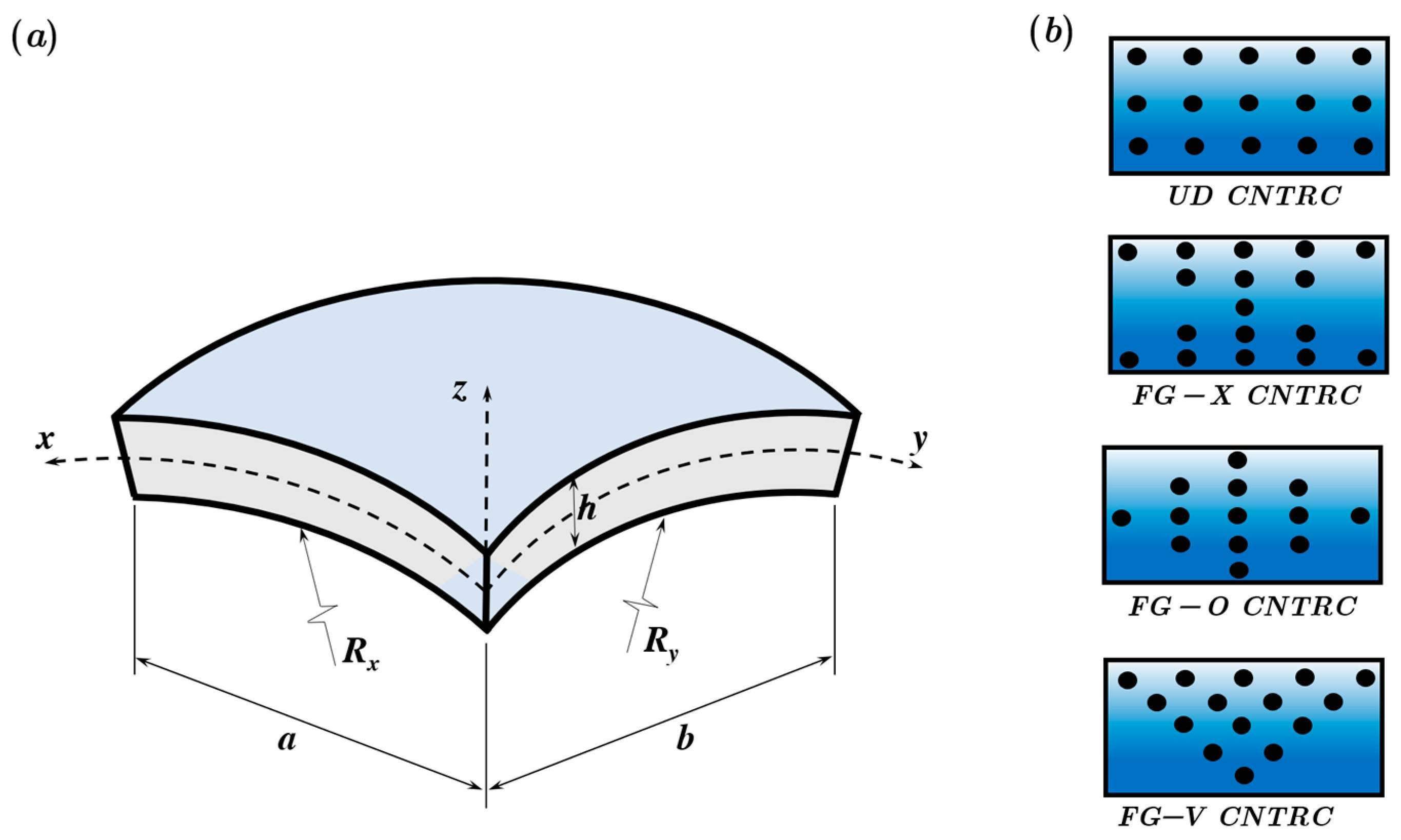
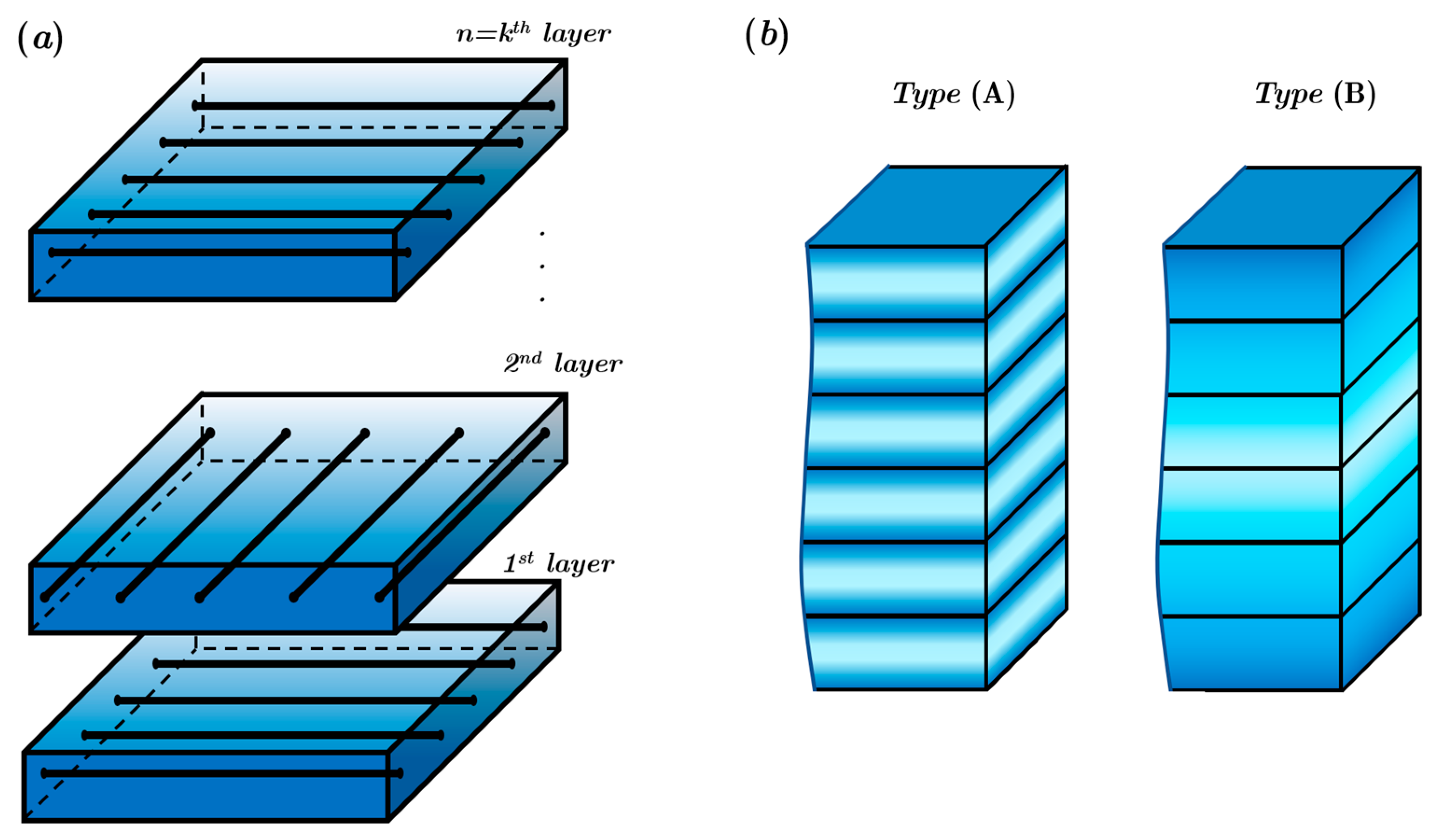
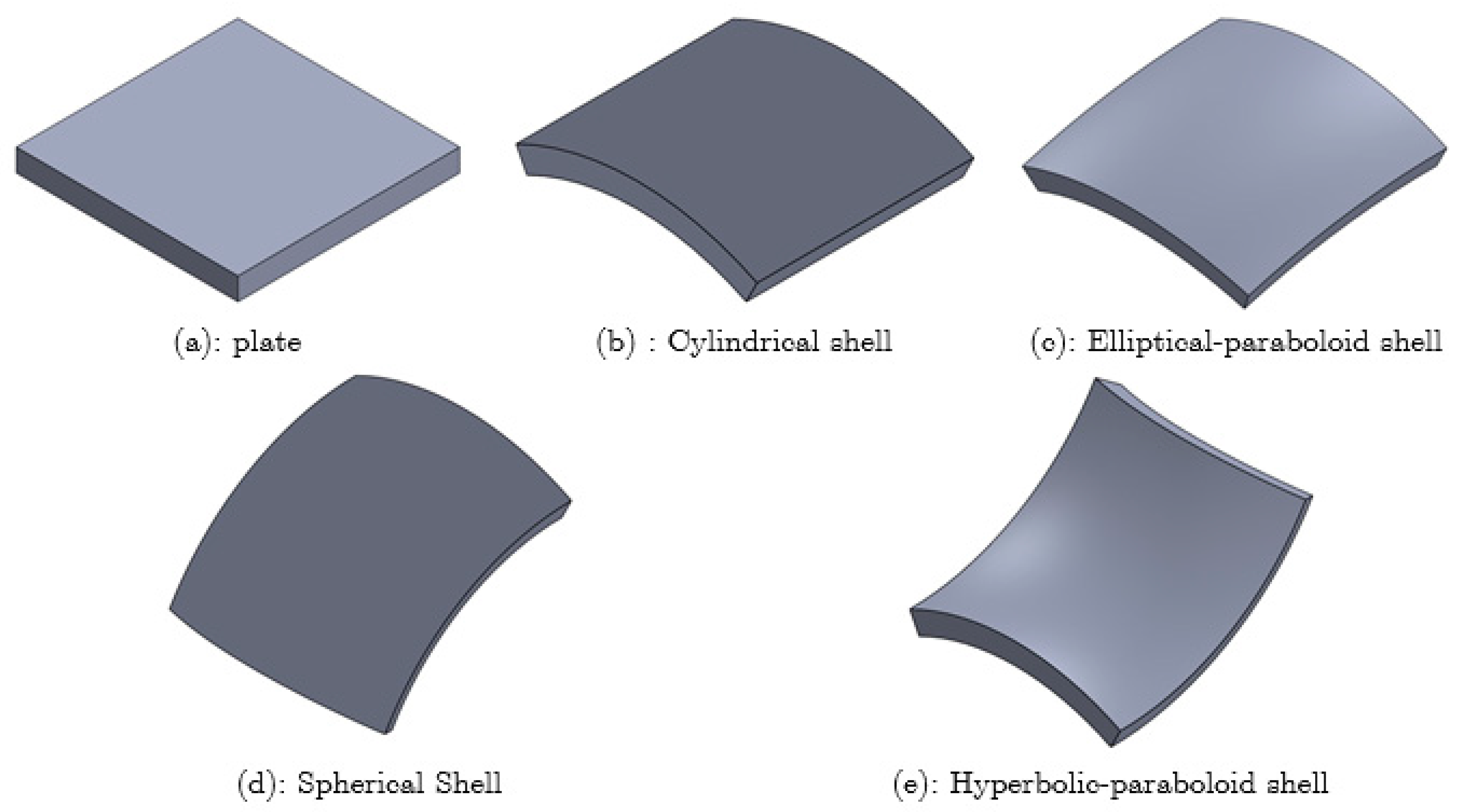
In the following study, a parametric analysis of the vibration of CNTRC shells was carried out. As mentioned in the previous section, two types of laminated shells are proposed: CNTRC(A) and CNTRC(B). For the straight plate, the radii of curvature are $R_x/a=R_y/b=\infty$, and $R_x/a=R_y/b=5$ for the spherical shell, $R_x/a=5$ and $R_y/b=\infty$ for the cylindrical shell, $R_x/a=5$ and $R_y/b=-5$ for the hyperbolic-paraboloid shell, $R_x/a=5$ and $R_y/b=7.5$ for the elliptical-paraboloid shell (Figure 3).

The effect of CNTRC type and CNT distribution patterns on the dimensionless frequency of CNTRC shells for various inhomogeneity material index p is illustrated in Table 3. Increase in the material parameter p leads to decrement in dimensionless frequencies.

Table 3. Effect of CNTRC type and CNT distribution pattern on the dimensionless frequency of CNTRC shells for various inhomogeneity material index p (SSSS, N = 10, $b/a=1$, $a/h=10$, $V_{cnt}=0.17, T=300\mathrm{K}$ ).

	p	CNTRC(A)			CNTRC(B)
		FG-X	FG-O	FG-V	FG-X	FG-O	FG-V
Plate	0.2	0.2225	0.1328	0.2223	0.2275	0.2140	0.1826
	0.5	0.2076	0.1659	0.2072	0.2185	0.1863	0.1756
	1	0.1900	0.1890	0.1893	0.2078	0.1526	0.1689
	2	0.1674	0.2071	0.1665	0.1913	0.1147	0.1681
	5	0.1355	0.2225	0.1348	0.1506	0.0856	0.2026
Cylindrical shell	0.2	0.2228	0.1334	0.2226	0.2278	0.2142	0.1831
	0.5	0.2079	0.1664	0.2075	0.2188	0.1867	0.1764
	1	0.1903	0.1894	0.1896	0.2082	0.1530	0.1702
	2	0.1678	0.2075	0.1668	0.1918	0.1154	0.1697
	5	0.1361	0.2228	0.1351	0.1516	0.0866	0.2054
Spherical shell	0.2	0.2389	0.1377	0.2387	0.2473	0.2241	0.1922
	0.5	0.2212	0.1735	0.2207	0.2389	0.1908	0.1854
	1	0.2005	0.1996	0.1997	0.2282	0.1551	0.1811
	2	0.1749	0.2207	0.1738	0.2103	0.1181	0.1857
	5	0.1404	0.2389	0.1391	0.1633	0.0902	0.1680
Elliptical paraboloid shell	0.2	0.2341	0.1362	0.2338	0.2414	0.2210	0.1893
	0.5	0.2171	0.1712	0.2166	0.2330	0.1894	0.1825
	1	0.1973	0.1964	0.1966	0.2224	0.1543	0.1777
	2	0.1726	0.2166	0.1716	0.2052	0.1171	0.1814
	5	0.1389	0.2340	0.1377	0.1607	0.0888	0.2109
Hyperbolic paraboloidal shell	0.2	0.2020	0.1295	0.2018	0.2015	0.2030	0.1727
	0.5	0.1913	0.1584	0.1908	0.1910	0.1829	0.1660
	1	0.1780	0.1770	0.1773	0.1787	0.1518	0.1567
	2	0.1599	0.1908	0.1590	0.1618	0.1141	0.1424
	5	0.1323	0.2021	0.1315	0.1253	0.0848

In Table 4, we analyse the impact of the number of layers and CNT distribution patterns on the dimensionless frequency of CNTRC shells. In general, increase in the number of layers leads to increment in the dimensionless frequency and the stiffness of the plate. The FG–X CNTRC(B) shells have the highest values of dimensionless frequencies.

Table 4. Effect of CNTRC type and CNT distribution pattern on the dimensionless frequency of CNTRC shells for various number of layers N (SSSS, p = 1, $b/a=1$, $a/h=10$, $V_{cnt}=0.17, T=300 \mathrm{K}$ ).

	N	UD	CNTRC(A)			CNTRC(B)
			FG-X	FG-O	FG-V	FG-X	FG-O	FG-V
Plate	2	0.1291	0.1469	0.1075	0.1168	0.1208	0.1116	0.1236
	4	0.1784	0.1820	0.1758	0.1774	0.1751	0.1525	0.1598
	6	0.1854	0.1873	0.1846	0.1853	0.1986	0.1525	0.1659
	8	0.1878	0.1891	0.1876	0.1880	0.2046	0.1526	0.1680
	10	0.1889	0.1900	0.1890	0.1893	0.2078	0.1526	0.1689
Cylindrical shell	2	0.1302	0.1479	0.1088	0.1171	0.1222	0.1127	0.1248
	4	0.1790	0.1826	0.1764	0.1778	0.1760	0.1530	0.1611
	6	0.1859	0.1878	0.1851	0.1857	0.1992	0.1530	0.1671
	8	0.1882	0.1895	0.1880	0.1883	0.2051	0.1530	0.1692
	10	0.1893	0.1903	0.1894	0.1896	0.2082	0.1530	0.1702
Spherical shell	2	0.0962	0.1360		0.0600		0.0986	0.1042
	4	0.1976	0.2010	0.1949	0.1964	0.1957	0.1523	0.1832
	6	0.2007	0.2024	0.1999	0.2004	0.2261	0.1557	0.1833
	8	0.2003	0.2015	0.2001	0.2003	0.2288	0.1547	0.1821
	10	0.1995	0.2005	0.1996	0.1997	0.2282	0.1551	0.1811
Elliptical paraboloid shell	2	0.1258	0.1521	0.0900	0.1051	0.0919	0.1127	0.1278
	4	0.1932	0.1965	0.1905	0.1919	0.1967	0.1525	0.1778
	6	0.1965	0.1983	0.1957	0.1962	0.2195	0.1547	0.1788
	8	0.1967	0.1979	0.1964	0.1967	0.2223	0.1540	0.1783
	10	0.1963	0.1973	0.1964	0.1966	0.2224	0.1543	0.1777
Hyperbolic paraboloidal shell	2							0.1261
	4	0.1407	0.1459	0.1375	0.1401		0.1544	0.1150
	6	0.1636	0.1661	0.1629	0.1638	0.1428	0.1512	0.1421
	8	0.1723	0.1739	0.1722	0.1727	0.1650	0.1523	0.1518
	10	0.1768	0.1780	0.1770	0.1773	0.1787	0.1518	0.1567

In Table 5, the influence of a change in temperature on the dimensionless frequency of different types and patterns of simply supported CNTRC shells is investigated. The stiffness of the CNTRC shell reduces with increase in temperature.

Table 5. Effect of temperature on the dimensionless frequency of CNTRC shells (SSSS, p = 1, N = 10, $b/a=1$, $a/h=10$, $V_{cnt}=0.17$ ).

	T (K)	UD	CNTRC(A)			CNTRC(B)
			FG-X	FG-O	FG-V	FG-X	FG-O	FG-V
Plate	300	0.1889	0.1900	0.1890	0.1893	0.2078	0.1526	0.1689
	400	0.1781	0.1792	0.1782	0.1785	0.1942	0.1449	0.1598
	500	0.1639	0.1649	0.1640	0.1643	0.1764	0.1353	0.1482
	600	0.1415	0.1425	0.1416	0.1419	0.1492	0.1201	0.1302
Cylindrical shell	300	0.1893	0.1903	0.1894	0.1896	0.2082	0.1530	0.1702
	400	0.1784	0.1794	0.1785	0.1787	0.1945	0.1453	0.1607
	500	0.1640	0.1651	0.1642	0.1644	0.1766	0.1355	0.1488
	600	0.1415	0.1426	0.1417	0.1420	0.1493	0.1202	0.1304
Spherical shell	300	0.1995	0.2005	0.1996	0.1997	0.2282	0.1551	0.1811
	400	0.1901	0.1910	0.1901	0.1903	0.2177	0.1470	0.1727
	500	0.1783	0.1792	0.1783	0.1786	0.2048	0.1369	0.1629
	600	0.1610	0.1618	0.1610	0.1613	0.1870	0.1213	0.1493
Elliptical paraboloid shell	300	0.1963	0.1973	0.1964	0.1966	0.2224	0.1543	0.1777
	400	0.1865	0.1875	0.1866	0.1868	0.2111	0.1464	0.1691
	500	0.1740	0.1749	0.1741	0.1743	0.1969	0.1364	0.1588
	600	0.1553	0.1562	0.1554	0.1556	0.1768	0.1209	0.1440
Hyperbolic paraboloidal shell	300	0.1768	0.1780	0.1770	0.1773	0.1787	0.1518	0.1567
	400	0.1635	0.1648	0.1638	0.1641	0.1589	0.1442	0.1450
	500	0.1449	0.1463	0.1452	0.1456	0.1295	0.1345	0.1288
	600	0.1131	0.1147	0.1135	0.1140	0.0721	0.1192	0.1007

The action of the geometric parameters (a/h and b/a) on the dimensionless frequency of various types of simply supported spherical CNTRC shells is shown in Table 6. It is observed that the frequencies increase by increasing both the thickness ratio a/h and the aspect ratio b/a.

Table 6. Effect of geometric parameters a/h and b/a on the dimensionless frequency of spherical CNTRC shells for various boundary conditions (p = 1, N = 10, $b/a=1$, $a/h=10$, $V_{cnt}=0.17, T=300 \mathrm{K}$ ).

BCs.	b/a	CNTRC(A)			CNTRC(B)
		a/h = 5	a/h = 10	a/h = 5	a/h = 10	a/h = 20
SSSS	0.5	1.2295	0.4619	1.4675	0.5401	0.1787
	1	0.5809	0.2005	0.6491	0.2282	0.0680
	2	0.4032	0.1411	0.4248	0.1557	0.0478
	3	0.3810	0.1353	0.3962	0.1487	0.0460
CCCC	0.5	1.6638	0.6732	1.9208	0.7527	0.2988
	1	0.8340	0.3475	0.8983	0.3725	0.1426
	2	0.6021	0.2538	0.6153	0.2640	0.1035
	3	0.5639	0.2410	0.5693	0.2488	0.0990
CCSS	0.5	1.2904	0.4994	1.5164	0.5722	0.1973
	1	0.7010	0.2775	0.7531	0.2974	0.1088
	2	0.5644	0.2395	0.5727	0.2474	0.0979
	3	0.5497	0.2365	0.5526	0.2435	0.0972
CSCS	0.5	1.7117	0.6842	2.0023	0.7765	0.2932
	1	0.8497	0.3362	0.9255	0.3677	0.1293
	2	0.6049	0.2420	0.6229	0.2564	0.0927
	3	0.5674	0.2309	0.5764	0.2428	0.0889
CSSS	0.5	1.2944	0.4965	1.5209	0.5712	0.1935
	1	0.7075	0.2712	0.7615	0.2947	0.1009
	2	0.5714	0.2312	0.5829	0.2434	0.0888
	3	0.5563	0.2278	0.5627	0.2391	0.0878
CCCS	0.5	1.0441	0.4284	1.1680	0.4690	0.1782
	1	0.5788	0.2533	0.5894	0.2610	0.1088
	2	0.4539	0.2146	0.4401	0.2171	0.0957
	3	0.4502	0.2110	0.4406	0.2143	0.0938

Table 7 presents the impact of the nonlocal and length scale parameters on the dimensionless frequency of simply supported spherical nanoshell. It is clear that the value of the frequency reduces by decreasing the length scale parameter and increasing the nonlocal parameter.

Table 7. Effect of nonlocal and length scale parameters on the dimensionless frequency of spherical nanoshell (SSSS, p = 1, N = 10, $b/a=1$, $a/h=10$, $V_{cnt}=0.17$ ).

$\mathit{\mu }$	$\mathit{\lambda }$	UD	CNTRC(A)			CNTRC(B)
			FG-X	FG-O	FG-V	FG-X	FG-O	FG-V
0	0	0.1995	0.2005	0.1996	0.1997	0.2282	0.1551	0.1811
	0.5	0.2196	0.2206	0.2197	0.2189	0.2466	0.1786	0.2116
	1	0.2421	0.2431	0.2422	0.2408	0.2671	0.2048	0.2408
	1.5	0.2656	0.2665	0.2657	0.2639	0.2886	0.2317	0.2687
	2	0.2894	0.2902	0.2893	0.2872	0.3103	0.2583	0.2952
0.5	0	0.1904	0.1913	0.1904	0.1905	0.2177	0.1480	0.1727
	0.5	0.2095	0.2104	0.2096	0.2089	0.2353	0.1704	0.2018
	1	0.2310	0.2319	0.2311	0.2298	0.2548	0.1954	0.2297
	1.5	0.2534	0.2543	0.2534	0.2518	0.2753	0.2210	0.2563
	2	0.2761	0.2768	0.2760	0.2740	0.2961	0.2465	0.2816
1	0	0.1823	0.1832	0.1824	0.1825	0.2086	0.1418	0.1655
	0.5	0.2007	0.2016	0.2008	0.2001	0.2254	0.1633	0.1933
	1	0.2213	0.2221	0.2213	0.2201	0.2441	0.1872	0.2201
	1.5	0.2428	0.2436	0.2428	0.2412	0.2637	0.2117	0.2455
	2	0.2644	0.2652	0.2644	0.2625	0.2836	0.2361	0.2698
1.5	0	0.1753	0.1761	0.1753	0.1754	0.2005	0.1363	0.1590
	0.5	0.1929	0.1938	0.1930	0.1923	0.2166	0.1569	0.1858
	1	0.2127	0.2135	0.2127	0.2116	0.2346	0.1799	0.2115
	1.5	0.2333	0.2341	0.2334	0.2318	0.2535	0.2035	0.2360
	2	0.2542	0.2549	0.2541	0.2523	0.2726	0.2269	0.2593
2	0	0.1690	0.1698	0.1690	0.1691	0.1933	0.1314	0.1533
	0.5	0.1860	0.1868	0.1860	0.1854	0.2088	0.1513	0.1791
	1	0.2050	0.2058	0.2051	0.2039	0.2262	0.1734	0.2039
	1.5	0.2249	0.2257	0.2249	0.2234	0.2443	0.1962	0.2275
	2	0.2450	0.2457	0.2450	0.2432	0.2628	0.2187	0.2500

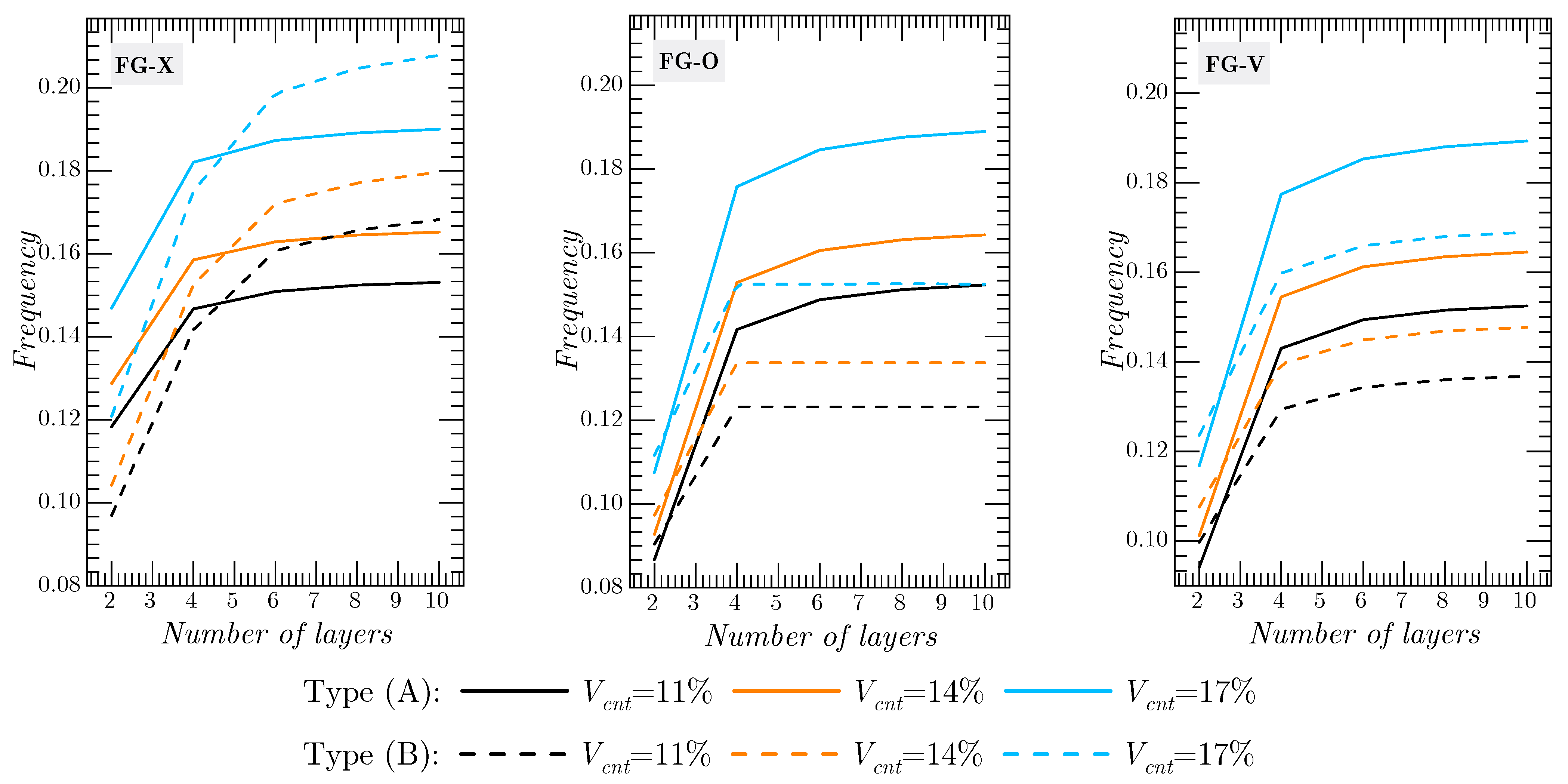
To understand the impact of the number of layers and to view the advantages of the proposed structure, Figure 5 is presented. Clearly, as shown in these figures, increase in the number of layers produces a stiffer structure. Comparing the two structure types, the CNTRC structure Type (B) in distribution FG-X has the highest stiffness, and therefore an increment in the dimensionless frequency. In addition, as is known, increase in the volume fraction $V_{cnt}^{*}$ increases the rigidity of the structure regardless of the CNTRC type and the CNT distribution. The use of more than two layers in the case of FG–O CNTRC(B) barely changes the frequency values, whatever the volume fraction.

Figure 5. Effect of the number of layers N on dimensionless frequencies of various CNTRC plate types $\left(SSSS,p=1, T=300K\right)$.

In Figure 6, we plotted the dimensionless frequencies of two types of simply supported CNTRC plates with FG-X distribution as a function of the number of layers and the inhomogeneity material parameter p. Through these curves, we can clearly see that the material parameter p has a significant effect on the CNTRC(B) plates, more so than the CNTRC(A).

Figure 6. Effect of number of layers N and power-law index p on the dimensionless frequencies of CNTRC plates $\left(FG-X,SSSS, V_{cnt}^{*}=0.17, T=300K\right)$.

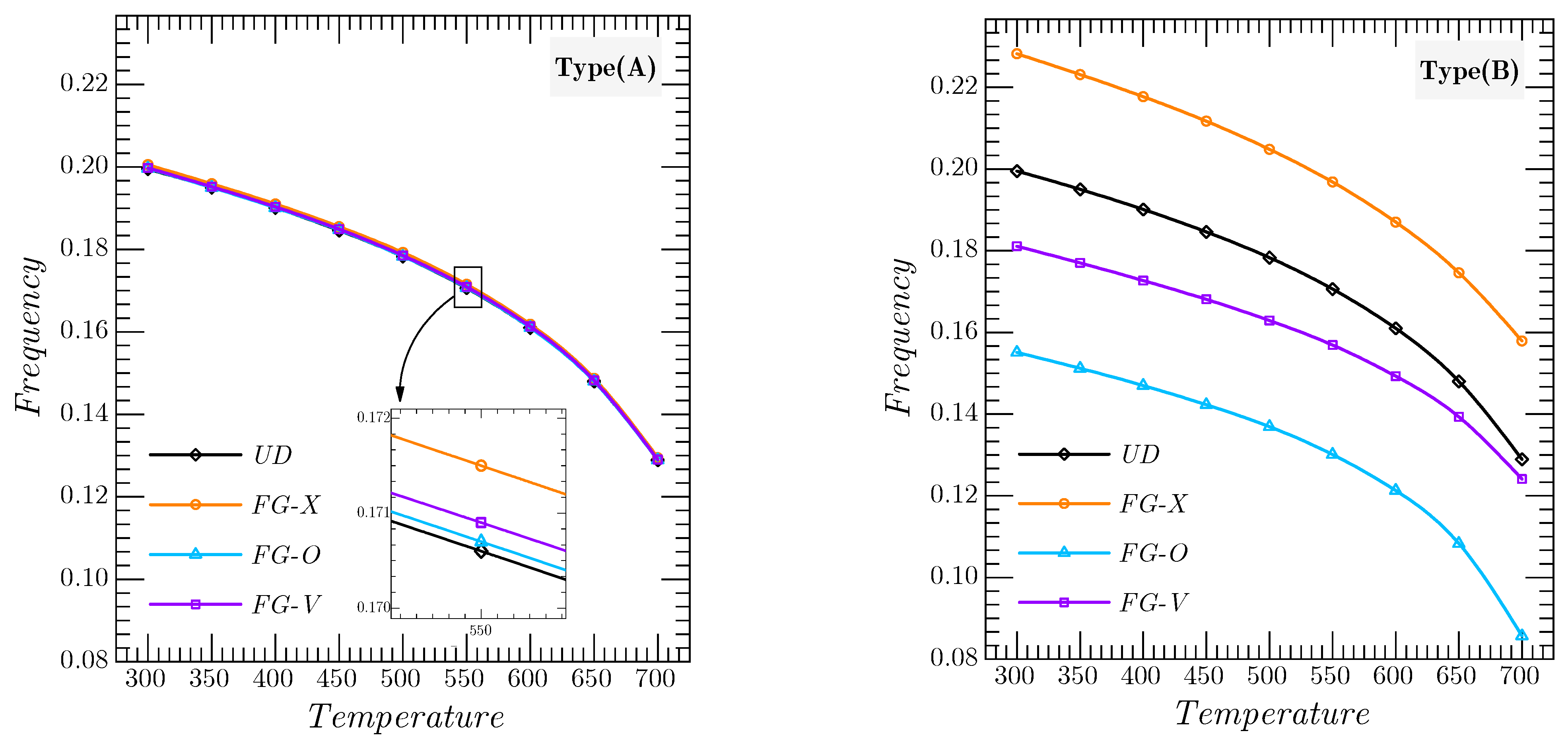
High temperature reduces the stiffness of the structure by affecting the material properties. Figure 7 presents an examination of the impact of the thermal environment on the vibrational response of the two types of simply supported spherical CNTRC shell for various CNT distribution patterns. Because of the even distribution of CNTs in each layer (10 layers) of CNTRC(A) structures, we obtained similar results, and, therefore, we conclude that the CNT distribution pattern has almost no influence on the mechanical response, unlike the CNTRC(B) shell. In addition, increase in the temperature leads to a decrement in the rigidity of the CNTRC shell, and thus, the dimensionless frequency decreases.

Figure 7. Effect of temperature on the dimensionless frequency of spherical CNTRC shell $\left(SSSS,R_x/a=R_y/b=5,N=10 V_{cnt}^{*}=0.17,p=1 \right)$.

In Figure 8, we show the radii of curvature $\left(R_x/a\right)$ on the dimensionless frequencies of CNTRC(B) shells by fixing the radii of curvature $R_y/b$ at inf, 5 and −5. In the case of the cylindrical shell and the elliptical-paraboloid shells (R/b = inf, 5), the augmentation of the radii of curvature $R_x/a$ leads to a decrement in frequencies for the values $R_x/a\le 5$, whatever the CNT distribution pattern is, and then the results are almost constant.

Figure 8. Effect of temperature on the dimensionless frequency of various shell types $\left(Type\left(B\right), SSSS,N=10 V_{cnt}^{*}=0.17,p=1 \right).$

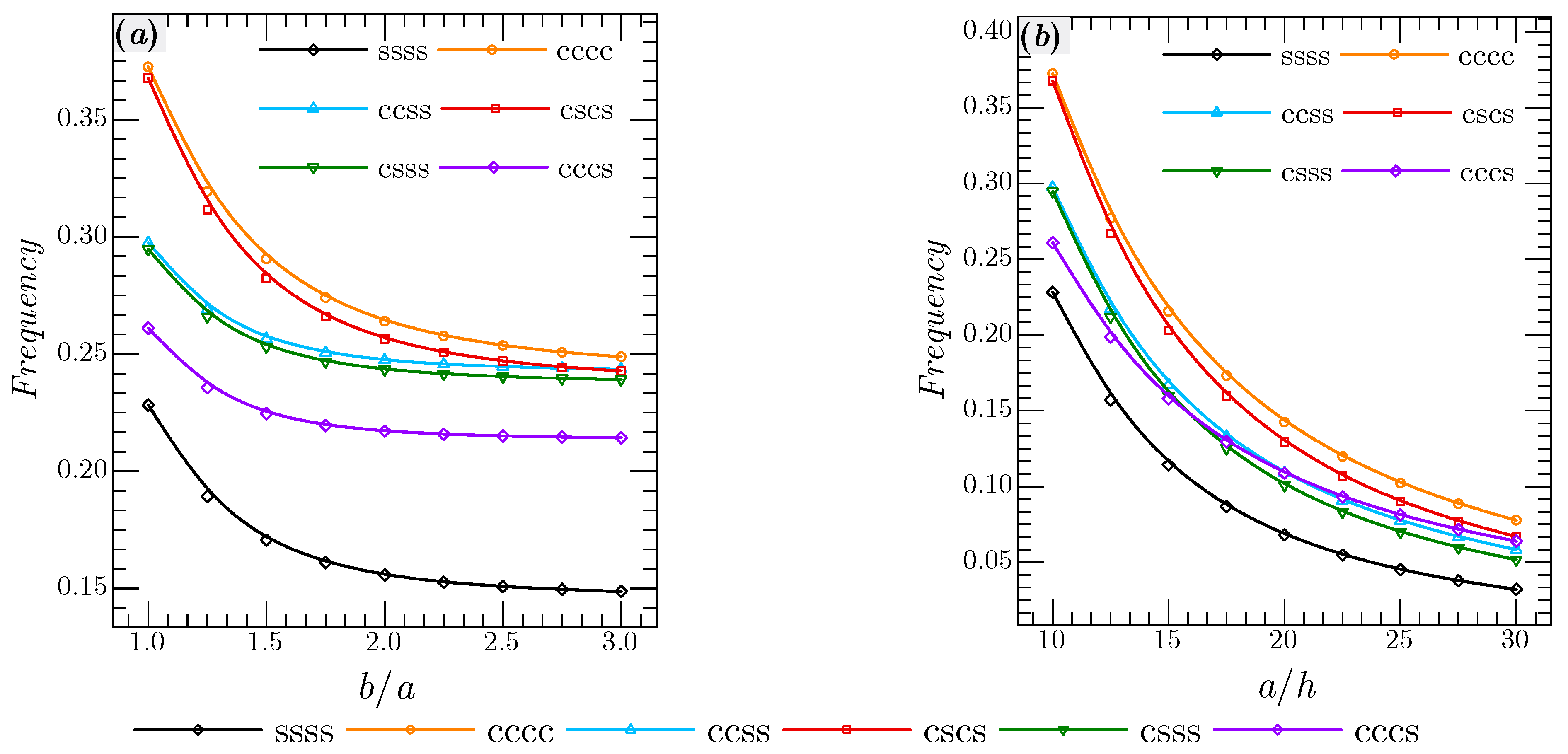
The impact of various boundary conditions and the geometry of the CNTRC(B) plate (b/a and a/h) on the frequencies is plotted in Figure 9. The dimensionless frequencies decrease with decrease in the thickness ratio a/h. For the aspect ratio b/a effect, the frequencies decrease critically for values $b/a\le 2$. In addition, the fully clamped shells have the highest values of frequency, while the lowest values are for the simply supported one.

Figure 9. Effect of geometry parameters b/a (shown in (a)) and a/h (shown in (b)) on the dimensionless frequency of spherical shell for various boundary conditions $\left(Type\left(B\right), FG-X, N=10 V_{cnt}^{*}=0.17,p=1 \right)$.

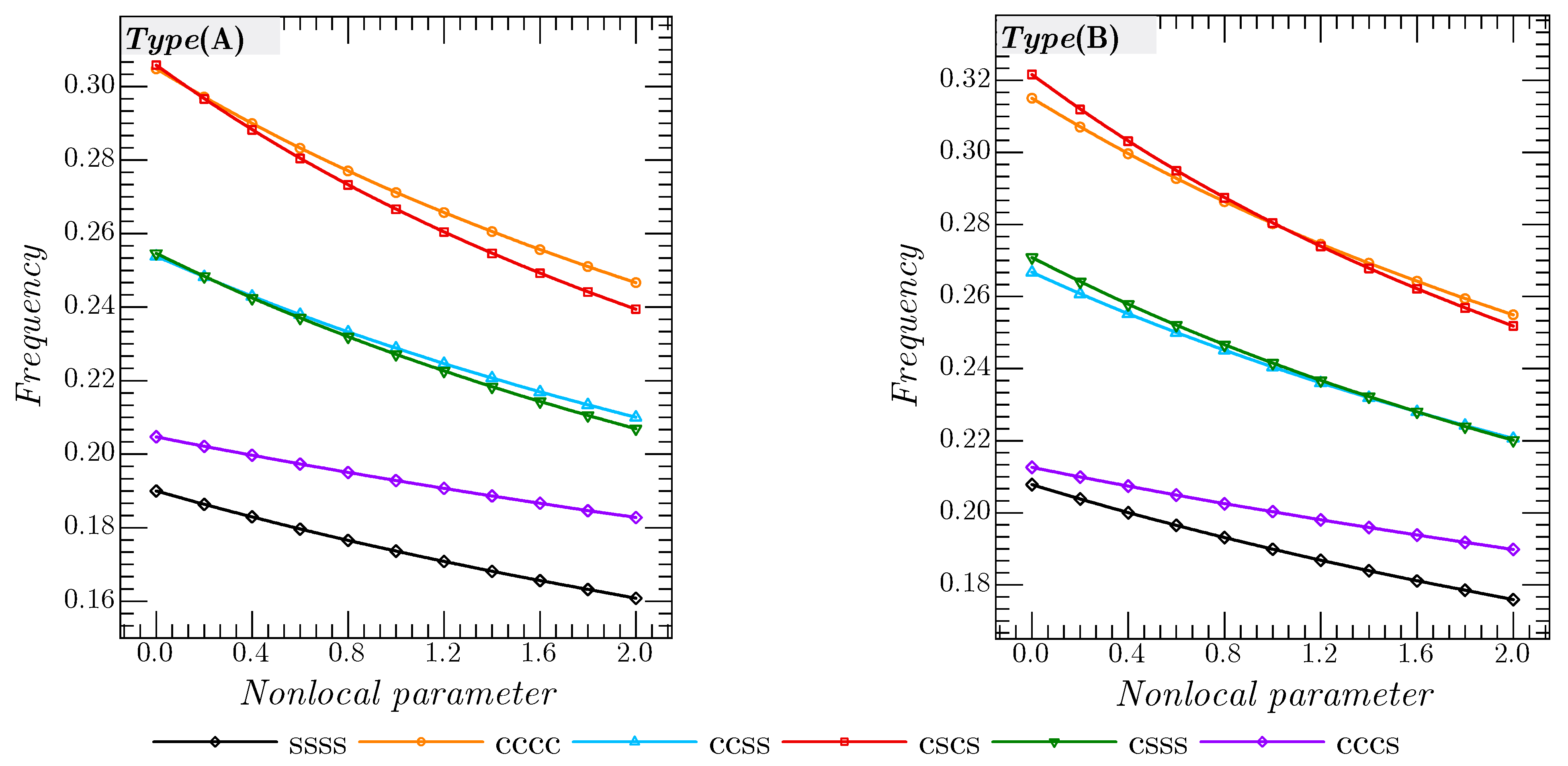
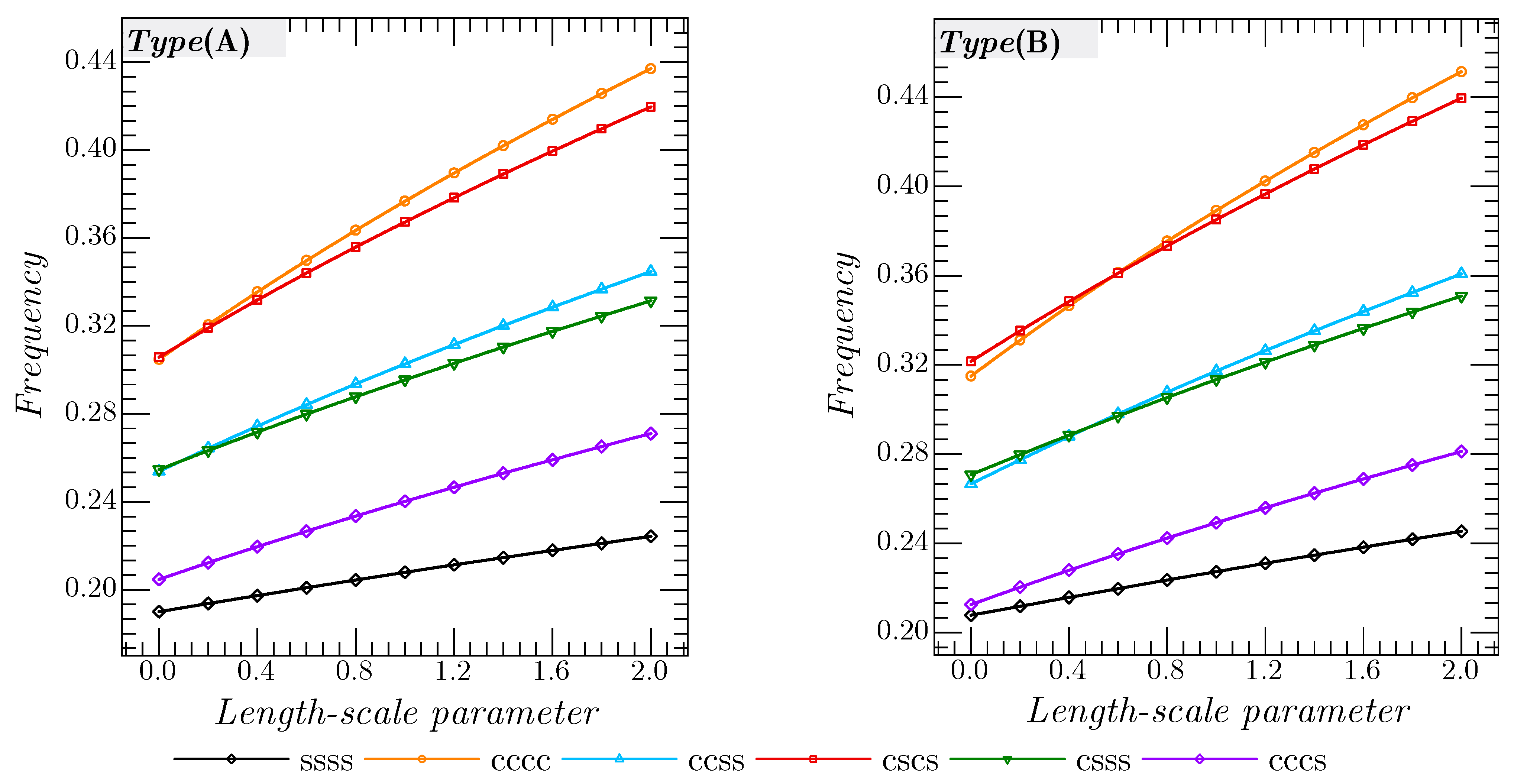
To show the nonlocality effect on the dimensionless frequency of the two types of CNTRC spherical shell for various boundary conditions, Figure 10 curves are plotted. The nonlocal parameter μ is changed from 0 to 2. Regardless of either the CNTRC type or the boundary conditions, it is seen from this figure that the inclusion of the nonlocal parameter reduces the plate stiffness, and therefore decreases the dimensionless frequencies. Unlike the nonlocal parameter effect, in Figure 11, it is observed that the dimensionless frequency decreases with increase in the length-scale parameter.

Figure 10. Effect of nonlocal parameter on the dimensionless frequency of spherical shell for various boundary conditions $\left(FG-X, N=10, V_{cnt}^{*}=0.17,p=1,\lambda =0 \right)$.

Figure 11. Effect of length-scale parameter on the dimensionless frequency of spherical shell for various boundary conditions $\left(FG-X, N=10 V_{cnt}^{*}=0.17,p=1,\mu =0 \right)$.

8. Conclusions

This paper presents a modified mathematical continuum model to investigate the free vibration response of FG-CNTRC nanoshell with temperature-dependent material properties. The length scale and microstructure influences are employed in the model by using nonlocal strain gradient theory. The Galerkin approach is implemented to solve the system of equations and obtain the analytical solution. Numerical studies are performed to present the CNT distribution pattern, the thickness stretching, the geometry of the plate/shell, boundary conditions, the total number of layers, the length scale and material scale parameters on the vibrational frequencies of CNTRC laminated nanoplates and nanoshells. The main findings can be summarized as: -

• Increase in the material gradation parameter p leads to decrement in dimensionless frequencies.
• The material parameter p has a significant effect on the CNTRC(B) plates, more than the CNTRC(A).
• Increase in the volume fraction $V_{cnt}^{*}$ increases the rigidity of the structure regardless of the CNTRC type and the CNT distribution
• Increase in the number of layers leads to increment in the dimensionless frequency and the stiffness of the plate. The FG–X CNTRC(B) shells have the highest values of dimensionless frequencies.
• Based on the geometric parameters, the frequencies increase by increasing both the thickness ratio a/h and the aspect ratio b/a. For the aspect ratio b/a effect, the frequencies decrease critically for values of $b/a\le 2$.
• In the case of the cylindrical shell, the elliptical-paraboloid shells (R/b = inf, 5), the augmentation of the radii of curvature $R_x/a$ leads to a decrement in frequencies for the values $R_x/a\le 5$ whatever the CNT distribution pattern is, and then the results are almost constant.
• The fully clamped shells have the highest values of frequency, while the lowest values are for the simply supported one.
• For size-length and microstructure scales, the value of the frequency reduces by decreasing the length scale parameter and increasing the nonlocal parameter.