An Intelligent Expert Combination Weighting Scheme for Group Decision Making in Railway Reconstruction

Abstract

The intuitionistic fuzzy entropy has been widely used in measuring the uncertainty of intuitionistic fuzzy sets. In view of some counterintuitive phenomena of the existing intuitionistic fuzzy entropies, this article proposes an improved intuitionistic fuzzy entropy based on the cotangent function, which not only considers the deviation between membership and non-membership, but also expresses the hesitancy degree of decision makers. The analyses and comparison of the data show that the improved entropy is reasonable. Then, a new IF similarity measure whose value is an IF number is proposed. The intuitionistic fuzzy entropy and similarity measure are applied to the study of the expert weight in group decision making. Based on the research of the existing expert clustering and weighting methods, we summarize an intelligent expert combination weighting scheme. Through the new intuitionistic fuzzy similarity, the decision matrix is transformed into a similarity matrix, and through the analysis of threshold change rate and the design of risk parameters, reasonable expert clustering results are obtained. On this basis, each category is weighted; the experts in the category are weighted by entropy weight theory, and the total weight of experts is determined by synthesizing the two weights. This scheme provides a new method in determining the weight of experts objectively and reasonably. Finally, the method is applied to the evaluation of railway reconstruction scheme, and an example shows the feasibility of the method.

1. Introduction

With the characteristics of high speed, large volume, low energy consumption, little pollution, safety and reliability, railway transportation has become the main transportation mode in the modern transportation system in China (see Figure 1 and Figure 2) [1,2,3] and plays an important role in the development of the national economy.

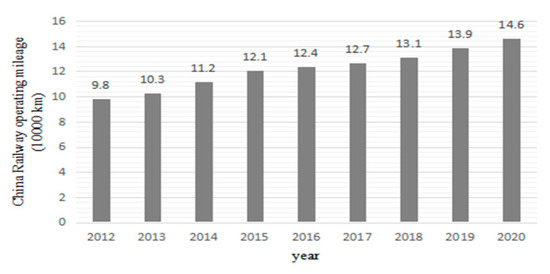
Figure 1. Business mileage of China’s railways.

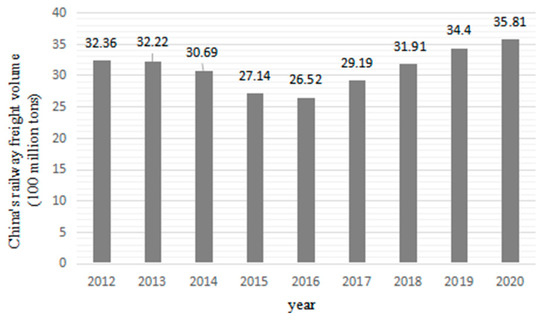
Figure 2. Total railway freight volume in China.

As an important national infrastructure and popular means of transportation, railway is the backbone of China’s comprehensive transportation system. With the continuous acceleration of China’s urbanization process and the urban expansion, railway construction has entered a period of rapid development, and the railway plays an increasingly important role in people’s choice of travel mode (see Figure 3) [1,4].

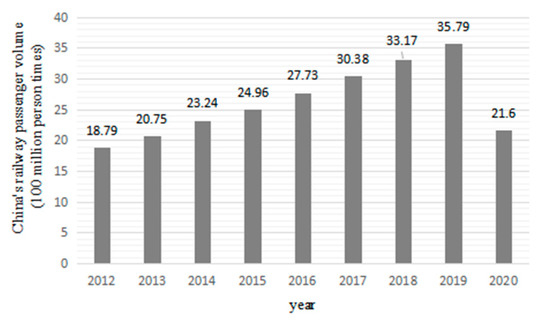
Figure 3. China railway passenger volume.

With regard to railway reconstruction, due to the huge investment and complex factors [5,6,7], it is necessary to compare and select various construction schemes in order to optimize the scheme with more reasonable technology and economy. Therefore, the use of scientific evaluation methods is very important. At present, the method of expert scoring and evaluation with the help of fuzzy theory has been more common, but the expert scoring is more or less subjective. This paper proposes an intelligent expert combination weighting method to optimize the scheme.

The rest of this paper is structured as follows. Section 2 introduces the related work of this study. Section 3 introduces the preparatory knowledge. Section 4 puts forward the weighted scheme of intelligent expert combination. Section 5 introduces the risk factors of the railway reconstruction project and uses the method proposed in the fourth section to optimize the railway reconstruction scheme. Finally, Section 6 summarizes the whole paper.

2. The Related Work

Fuzziness, as developed in [8], is a kind of uncertainty that often appears in human decision-making problems. Fuzzy set theory deals with uncertainties happening in daily life successfully. The membership degrees can be effectively decided by a fuzzy set. However, in real-life situations, the non-membership degrees should be considered in many cases as well. Thus, Atanassov [9] introduced the concept of an intuitionistic fuzzy (IF) set that considers both membership and non-membership degrees. IF set has been implemented in numerous areas due to its ability to handle uncertain information more effectively [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24]. Tao et al. [10] provided an insight with an alternative queuing method and intuitionistic fuzzy set into dynamic group MCDM, which ranked the alternatives based on preference relation. Intuitionistic fuzzy sets based on the weighted average were adopted for aggregating individual suggestions of decision makers by Singh et al. [11]. Chaira [12] suggested a novel clustering approach for segmenting lesions/tumors in mammogram images using Atanassov’s intuitionistic fuzzy set theory. Jiang et al. [13] studied a novel three-way group investment decision model under an intuitionistic fuzzy multi-attribute group decision-making environment. Wang et al. [14] put forward a novel three-way multi-attribute decision-making model in light of a probabilistic dominance relation with intuitionistic fuzzy sets. Wan and Dong [15] developed a new intuitionistic fuzzy best-worst method for multi-criteria decision making. Kumar et al. [16] formulated an intuitionistic fuzzy set theory-based, bias-corrected intuitionistic fuzzy c-means with spatial neighborhood information method for MRI image segmentation. In addition, intuitionistic fuzzy sets are extended to various forms and applied to practical problems. Senapati and Yager [17,18,19] proposed Fermatean fuzzy sets and introduced four new weighted aggregated operators, as well as defined basic operations over the Fermatean fuzzy sets. Ashraf et al. [20] introduced a new version of the picture fuzzy set, so-called spherical fuzzy sets (SFS), and discussed some operational rules. Khan et al. [21] introduced a method to solve decision-making problems using an adjustable weighted soft discernibility matrix in a generalized picture fuzzy soft set. Riaz and Hashmi [22] introduced the novel concept of the linear Diophantine fuzzy set (LDFS) with the addition of reference parameters.

Shannon used probability theory as a mathematical tool to measure information. He defined information as something that eliminates uncertainty, thus connecting information with uncertainty. Taking entropy as a measure of the uncertainty of information state, Shannon put forward the concept of information entropy. De Luca and Termini [25] studied the measurement of fuzziness of fuzzy sets, extended probabilistic information entropy to non-probabilistic information entropy and proposed axioms that fuzzy information entropy must satisfy. Szmidt and Kacprzyk [26] extended the axioms of De Luca and Termini and extended fuzzy information entropy to IF information entropy. Some scholars have conducted in-depth research in this aspect and constructed IF entropy formulae from different angles and applied it to the fields of multi-attribute decision making and pattern recognition [27,28,29,30,31,32,33,34]. Whether these entropy formulas can reasonably measure the uncertainty of IF sets is directly related to the rationality of their application. In this paper, some entropy formulas in existing literature are classified, and their advantages and disadvantages are analyzed with data. On this basis, a new IF entropy is constructed that not only considers the deviation between membership and non-membership but also includes the hesitancy in the entropy measure. The rationality of entropy is fully explained by data analysis and comparison.

In recent years, the decision-making problem with IF information has attracted many scholars’ attention [35]. Due to the complexity and uncertainty of pragmatic problems, expert group decision-making method is commonly used in decision-making problems. Expert group decision making can fully gather the experience and knowledge of various experts, making the decision-making results more scientific and reasonable. However, in the actual evaluation, experts in group decision making are influenced by numerous factors, such as knowledge structure, understanding of scheme, interest correlation and so on. They often hold different views and attitudes. How to determine the weight of experts and effectively aggregate the decision-making information of experts with different preferences has become the focus of scholars [36,37,38,39,40,41].

In traditional group decision making, the expert weighting method usually uses the consistency ratio of the judgment matrix to construct the weight coefficient, which lacks the attention to the overall consistency of group decision-making objectives. In order to surmount the shortcomings of the traditional method, a cluster analysis method is often used to realize the expert weighting in group decision making. The basic principle of expert cluster analysis is to measure the similarity degree of expert evaluation opinions according to certain standards and cluster experts based on the similarity degree. He and Lei [36] extended fuzzy C-means clustering to IF C-means clustering and proposed a clustering algorithm based on IF sets. Zhang et al. [37] and He et al. [38] proposed the concept of IF similarity, whose value is an IF number; they also constructed the IF similarity matrix, the IF equivalent matrix and its $\lambda$- cut matrix and gave a clustering method based on the IF similarity matrix. Wang et al. [39] proposed a new method of an IF similar matrix, avoided the tedious process of calculating an IF equivalent matrix and used the membership degrees of elements in an IF similar matrix to cluster. Zhou et al. [40] conducted cluster analysis on experts according to the principle of entropy, used information similarity coefficients to measure the similarity degrees of expert opinions and then classified the experts.

The above clustering methods have the following problems when clustering IF information.

(1)

In reference [36], the clustering results of IF sets are expressed in real numbers, which does not accord with the characteristics of IF sets.

(2)

After obtaining the IF similarity matrix, the method proposed in reference [37,38] also needs to test whether it is an IF equivalent matrix. If not, it needs a lot of iterative operations until it becomes an IF equivalent matrix, which requires a large amount of calculation.

(3)

Reference [39] reduced the amount of calculation, but after obtaining the IF similarity matrix, only membership degree is used for clustering, ignoring non-membership degree and hesitation degree, which will inevitably cause the loss of information.

(4)

In literature [40], there is no analysis on the value of the clustering threshold. The value directly affects the clustering results, so the rationality of the value is particularly important.

Considering the above situation, this paper proposes a method of clustering and weighting experts based on IF entropy. According to the evaluation information of IF numbers given by experts, a new IF similarity measure is constructed, whose value is an IF number. Then the decision matrix is transformed into a similar matrix. By analyzing the change rate of the threshold and designing the risk parameters, the decision maker can choose the appropriate clustering threshold and risk parameters so as to obtain the reasonable expert clustering results, and based on this result, experts are weighted between categories. It can make more experts in a category, so that the weight of the category is greater, which reflects the important principle of the minority obeying the majority in group decision making. Using the new IF entropy proposed in this paper, the experts in the same category with clear logic and an accurate evaluation can get a larger weight. The total weight of experts is determined by synthesizing the weight between categories and within categories. Finally, the IF weighted aggregation operator is used to aggregate weighted experts and their IF information, and the alternatives are optimized and sorted.

3. Preliminaries

In the following part, we introduce some basic concepts, which will be used in the next sections.

Definition 1

([9]). Let $X$ be a given universal set. An IF set is an object having the form $A=\{<x_i,{\mu }_A(x_i),{\nu }_A(x_i)>|x_i\in X\}$ where the function ${\mu }_A:X\to [0,1]$ defines the degree of membership, and ${\nu }_A:X\to [0,1]$ defines the degree of non-membership of the element $x_i\in X$, respectively, and for every $x_i\in X$, it holds that $0\le {\mu }_A(x_i)+{\nu }_A(x_i)\le 1$. Furthermore, for any IF set $A$ and $x_i\in X$, ${\pi }_A(x_i)=1-{\mu }_A(x_i)-{\nu }_A(x_i)$ is called the hesitancy degree of $x_i$. All IF sets on $X$ are denoted as $IFSs(X)$.

For simplicity, Xu and Chen [41] denoted$\alpha =({\mu }_{\alpha },{\nu }_{\alpha })$as an IF number (IFN), where${\mu }_{\alpha }$and${\nu }_{\alpha }$are the degree of membership and the degree of non-membership of the element$\alpha \in X$to$A$, respectively.

The basic operational laws of IF set defined by Atanassov [9] are introduced as follows:

Definition 2

([9]). Let $A=\{<x_i,{\mu }_A(x_i),{\nu }_A(x_i)>|x_i\in X\}$ and $B=\{<x_i,{\mu }_B(x_i),$${\nu }_B(x_i)>|x_i\in X\}$ be two IF sets; then,

(1) 

$A\subseteq B$if and only if${\mu }_A(x_i)\le {\mu }_B(x_i)$and${\nu }_A(x_i)\ge {\nu }_B(x_i)$for all$x_i\in X;$

(2) 

$A=B$if and only if$A\subseteq B$and$B\subseteq A$;

(3) 

The complementary set of$A$, denoted by$A^C$, is$A^C=\{<x_i,{\nu }_A(x_i),$ $>|x_i\in X\}$

(4) 

$A^n=\{<x_i,{[{\mu }_A(x_i)]}^n,{[{\nu }_A(x_i)]}^n>|x_i\in X\}$;

(5) 

$A\prec B$called$A$less fuzzy than$B$, i.e., for$\forall x_i\in X$

• if${\mu }_B(x_i)\le {\nu }_B(x_i)$, then${\mu }_A(x_i)\le {\mu }_B(x_i)$,${\nu }_A(x_i)\ge {\nu }_B(x_i)$;
• if${\mu }_B(x_i)\ge {\nu }_B(x_i)$, then${\mu }_A(x_i)\ge {\mu }_B(x_i)$,${\nu }_A(x_i)\le {\nu }_B(x_i)$.

Definition 3

([9]). Let $A=\{<x_i,{\mu }_A(x_i),{\nu }_A(x_i)>|x_i\in X\}$ and $B=\{<x_i,{\mu }_B(x_i),$ ${\nu }_B(x_i)>|x_i\in X\}$ be two IF sets and $\omega ={({\omega }_1,{\omega }_2,\cdots ,{\omega }_n)}^{{\rm T}}$ be the weight vector of the element $x_i$$(i=1,2,\cdots ,n)$, where ${\omega }_j\ge 0$ and ${\displaystyle \sum _{j=1}^n{\omega }_j}=1$. The weighted Hamming distance for $A$ and $B$ is defined as follows:

$$d(A,B)=\frac{1}{2}{\displaystyle \sum _{i=1}^n{\omega }_i(|{\mu }_A(x_i)-{\mu }_B(x_i)|+|{\nu }_A(x_i)-{\nu }_B(x_i)|+|{\pi }_A(x_i)-{\pi }_B(x_i)|)}.$$

Definition 4

([26]). A map $E:IFSs(X)\to [0,1]$ is called the IF entropy if it satisfies the following properties:

(1) 

$E(A)=0$if and only if$A$is a crisp set;

(2) 

$E(A)=1$if and only if${\mu }_A(x_i)={\nu }_A(x_i),\forall x_i\in X$;

(3) 

$E(A)=E(A^C)$;

(4) 

If$A\prec B$, then$E(A)\prec E(B)$.

Definition 5

([37]). Let $z_{ij}(i=1,2,\cdots ,m;j=1,2,\cdots ,n)$ be a collection of IFNs, and the matrix $Z={(z_{ij})}_{m\times n}$ is called an IF matrix.

Definition 6

([37]). Let $\psi :IFSs(X)\times IFSs(X)\to IFNs$ and $C_1,C_2,C_3$ be three IF sets. $\psi (C_1,C_2)$ is called an IF similarity measure of $C_1$ and $C_2$ if it satisfies the following properties:

(1) 

$\psi (C_1,C_2)$is an IFN;

(2) 

$\psi (C_1,C_2)=<1,0>$if and only if$C_1=C_2$;

(3) 

$\psi (C_1,C_2)$=$\psi (C_2,C_1)$;

(4) 

If$C_1\subseteq C_2\subseteq C_3$, then$\psi (C_1,C_3)\subseteq \psi (C_1,C_2)$, and$\psi (C_1,C_3)\subseteq \psi (C_2,C_3)$.

Definition 7

([42]). The membership degree ${\mu }_i(x_j)$ is expressed as ${\mu }_{ij}$, and the non-membership degree ${\nu }_i(x_j)$ is expressed as ${\nu }_{ij}$. If an IF matrix $Z={(a_{ij})}_{m\times n}$ where $a_{ij}=<{\mu }_{ij},v_{ij}>$ satisfies the following conditions:

(1) 

Reflexivity:$a_{ii}=<1,0>,i=1,2,\cdots ,m.$

(2) 

Symmetry:$a_{ij}=a_{ji},i=1,2,\cdots ,m,j=1,2,\cdots ,n.$

then $Z$ is called an IF similarity matrix.

In order to compare the magnitudes of two IF sets, Xu and Yager [43] introduced the score and accuracy functions for IF sets and gave a simple comparison law as follows:

Definition 8

([43]). Let $A=<\mu ,\nu >$ be an IFN; the score function $M(A)$ and accuracy function $\Delta (A)$ of $A$ can be defined, respectively, as follows:

$$\{\begin{array}{l}M(A)=\mu -\nu \\ \Delta (A)=\mu +\nu \end{array}$$

(1)

Obviously,$M(A)\in [-1,1],\Delta (A)\in [0,1]$.

Based on the score and accuracy functions, a comparison law for IF set is introduced as below:

Let$A_j$and$A_k$be two IF sets,$M(A_j)$and$M(A_k)$be the scores of$A_j$and$A_k$, respectively, and$\Delta (A_j)$and$\Delta (A_k)$be the accuracy degrees of$A_j$and$A_k$, respectively; then,

(1) 

If$M(A_j)>M(A_k)$, then$A_j>A_k$.

(2) 

If$M(A_j)=M(A_k)$, then$\{\begin{array}{l}\Delta (A_j)=\Delta (A_k)\Rightarrow A_j=A_k\\ \Delta (A_j)<\Delta (A_k)\Rightarrow A_j<A_k\\ \Delta (A_j)>\Delta (A_k)\Rightarrow A_j>A_k\end{array}$.

The weighted aggregation operator for an IF set developed by Xu and Yager [43] is presented as follows:

Definition 9

([43]). Let $A_j=<{\mu }_j,{\nu }_j>(j=1,2,\cdots ,n)$ be a collection of IF sets, and $\omega ={({\omega }_1,{\omega }_2,\cdots ,{\omega }_n)}^{{\rm T}}$ be the weight vector of $A_j(j=1,2,\cdots ,n)$, where ${\omega }_j$ indicates the importance degree of $A_j$, satisfying ${\omega }_j\ge 0(j=1,2,\cdots ,n)$ and ${\displaystyle \sum _{j=1}^n{\omega }_j}=1$, and let $f_{\omega }^A:F^n\to F$. If

$$f_{\omega }^A(A_1,A_2,\cdots ,A_n)={\displaystyle \sum _{j=1}^n{\omega }_j{A}_j}=<1-{\displaystyle \prod _{j=1}^n{(1-{\mu }_j)}^{{\omega }_j}},{\displaystyle \prod _{j=1}^n{\nu }_j{}^{{\omega }_j}}>$$

(2)

then the function $f_{\omega }^A$ is called the IF weighted aggregation operator.

4. Our Proposed Intelligent Expert Combination Weighting Scheme

4.1. A New IF Entropy

The uncertainty of IF sets is embodied in fuzziness and intuitionism. Fuzziness is determined by the difference between membership and non-membership. Intuitionism is determined by its hesitation. Therefore, entropy is used as a tool to describe the uncertainty of IF sets; the difference between membership and non-membership and their hesitation should be considered at the same time. Only in this way can the degree of uncertainty be reflected more fully. Next, we will classify the existing entropy formulas according to whether they describe the fuzziness and intuitiveness of IF sets. In addition, the motivation behind the origination of fuzzy and non-standard fuzzy models is their intimacy with human thinking. Therefore, if an entropy measure does not meet some cognitive aspect, we call it a counterintuitive case.

In this section, suppose that $A=\left\{<x_i,{\mu }_A(x_i),{\nu }_A(x_i)>|x_i\in X,i=1,2,\cdots ,n\right\}$ is an IF set.

(1) The entropy measure only describes the fuzziness of IF sets. For example, the IF entropy measure of Ye [27] is

$$E_Y(A)=\frac{1}{n}{\displaystyle \sum _{i=1}^n[(\sqrt{2}\cos \frac{{\mu }_A(x_i)-{\nu }_A(x_i)}{4}\pi -1)}\times \frac{1}{\sqrt{2}-1}]$$

The IF entropy measure of Zeng and Li [28] is

$$E_Z(A)=1-\frac{1}{n}{\displaystyle \sum _{i=1}^n|}{\mu }_A(x_i)-{\nu }_A(x_i)|.$$

The IF entropy measure of Zhang and Jiang [29] is

$$\begin{array}{ll}{E}_{ZJ}(A)=-\frac{1}{n}{\displaystyle \sum _{i=1}^n}& {\displaystyle [\frac{{\mu }_A(x_i)+1-{\nu }_A(x_i)}{2}{\log }_2(\frac{{\mu }_A(x_i)+1-{\nu }_A(x_i)}{2})}\\ & +\frac{{\nu }_A(x_i)+1-{\mu }_A(x_i)}{2}{\log }_2(\frac{{\nu }_A(x_i)+1-{\mu }_A(x_i)}{2})].\end{array}$$

The exponential IF entropy measure of Verma and Sharma [30] is

$$\begin{array}{ll}{E}_{VS}(A)=\frac{1}{n(\sqrt{e}-1)}& {\displaystyle \sum _{i=1}^n[(\frac{{\mu }_A(x_i)+1-{\nu }_A(x_i)}{2}{e}^{1-\frac{{\mu }_A(x_i)+1-{\nu }_A(x_i)}{2}}}\\ & +\frac{{\nu }_A(x_i)+1-{\mu }_A(x_i)}{2}{e}^{1-\frac{{\nu }_A(x_i)+1-{\mu }_A(x_i)}{2}}-1)].\end{array}$$

Example 1.

Let$A_1=\left\{<x,0.3,0.4>|x\in X\right\}$and$A_2=\left\{<x,0.2,0.3>|x\in X\right\}$be two IF sets. Calculate the entropy of$A_1$and$A_2$with the entropy formulae$E_Y$,$E_Z$,$E_{ZJ}$and$E_{VS}$.

According to the above formulae, the results are as follows:

• $E_Y(A_1)=E_Y(A_2)=0.9895$, $E_Z(A_1)=E_Z(A_2)=0.9$,
• $E_{ZJ}(A_1)=E_{ZJ}(A_2)=0.9928$, $E_{VS}(A_1)=E_{VS}(A_2)=0.9905$.

It can be seen that$x$belongs to IF sets$A_1$and$A_2$; the absolute value of deviation between membership and non-membership is equal; and the hesitation degree increases, so the uncertainty of$A_1$is smaller than$A_2$. However, the entropy formulae$E_Y$,$E_Z$,$E_{ZJ}$and$E_{VS}$calculated the entropy of two IF sets as equal. In fact, for any IF sets$\tilde{A}=\left\{<x_i,{\mu }_{\tilde{A}}(x_i),{\nu }_{\tilde{A}}(x_i)>|x_i\in X\right\}$and$\tilde{B}=\{<x_i,{\mu }_{\tilde{B}}(x_i),{\nu }_{\tilde{B}}(x_i)>|x_i\in X\}$if${\mu }_{\tilde{A}}(x_i)-{\nu }_{\tilde{A}}(x_i)$for all$x_i\in X$, then any entropy formula$E$above is adopted, and all of them have$E(\tilde{A})=E(\tilde{B})$. These are counterintuitive situations.

(2) The entropy measure only describes the intuitionism of IF sets.

For example, we show the IF entropy measure of Burillo and Bustince [31]:

$$E_{B_1}(A)={\displaystyle \sum _{i=1}^n[1-({\mu }_A}(x_i)+{\nu }_A(x_i))]={\displaystyle \sum _{i=1}^n{\pi }_A}(x_i)$$

$$E_{B_2}(A)={\displaystyle \sum _{i=1}^n[1-({\mu }_A}(x_i)+{\nu }_A(x_i){)}^{\lambda }],\lambda =2,3,\cdots ,\infty ;$$

$$E_{B_3}(A)={\displaystyle \sum _{i=1}^n[1-({\mu }_A}(x_i)+{\nu }_A(x_i))]e^{[1-({\mu }_A(x_i)+{\nu }_A(x_i))]};$$

$$E_{B_4}(A)={\displaystyle \sum _{i=1}^n[1-({\mu }_A}(x_i)+{\nu }_A(x_i))]\sin (\frac{\pi }{2}({\mu }_A(x_i)+{\nu }_A(x_i)));$$

Example 2.

Let$A_3=\left\{<x,0.09,0.41>|x\in X\right\}$and$A_4=\left\{<x,0.18,0.32>|x\in X\right\}$be two IF sets. Calculate the entropy of$A_3$and$A_4$with the entropy formula$E_{B_1}$.

From Formula$E_{B_1}$, we can get the following results:$E_{B_1}(A_3)=E_{B_1}(A_4)=0.5$. For IF sets$A_3$and$A_4$, the hesitancy degree of element$x$is equal, but the absolute value of the deviation between the membership degree and non-membership degree of$A_3$is greater than that of$A_4$, so the uncertainty of$A_3$is obviously smaller than that of$A_4$. However, the entropy formulae$E_{B_1}$,$E_{B_2}$,$E_{B_3}$and$E_{B_4}$calculated the entropy of two IF sets as equal, which is inconsistent with people’s intuition. In fact, for any IF sets$\tilde{A}=\left\{<x_i,{\mu }_{\tilde{A}}(x_i),{\nu }_{\tilde{A}}(x_i)>|x_i\in X\right\}$and$\tilde{B}=\left\{<x_i,{\mu }_{\tilde{B}}(x_i),{\nu }_{\tilde{B}}(x_i)>|x_i\in X\right\}$, if$|{\mu }_{\tilde{A}}(x_i)+{\nu }_{\tilde{A}}(x_i)|=|{\mu }_{\tilde{B}}(x_i)+{\nu }_{\tilde{B}}(x_i)|$for all$x_i\in X$, then any entropy formula$E$above is adopted, and all of them have$E(\tilde{A})=E(\tilde{B})$.

(3) The entropy measure includes both the fuzziness and intuitionism of IF sets. However, some situations cannot be well distinguished.

For example, we show the IF entropy measure of Wang and Wang [32]:

$$E_W(A)=\frac{1}{n}{\displaystyle \sum _{i=1}^n\cot (\frac{\pi }{4}+\frac{|{\mu }_A(x_i)-{\nu }_A(x_i)|}{4(1+{\pi }_A(x_i))}\pi )}$$

The IF entropy measure of Wei et al. [33] is the following:

$$\begin{array}{l}\\ E_{WG}(A)=\frac{1}{n}{\displaystyle \sum _{i=1}^n\cos (\frac{{\mu }_A(x_i)-{\nu }_A(x_i)}{2(1+{\pi }_A(x_i))}\pi )}\end{array}$$

Example 3.

Let$A_5=\left\{<x,0.2,0.5>|x\in X\right\}$and$A_6=\left\{<x,0.4,0.04>|x\in X\right\}$be two IF sets. Obviously, the fuzziness of$A_5$is greater than that of$A_6$. Calculate the entropies of$A_5$and$A_6$with the entropy formulae$E_W$and$E_{WG}$.

We can get the following results:

$$E_W(A_5)=E_W(A_6)=0.6903, E_{WG}(A_5)=E_{WG}(A_6)=0.9350$$

which are counterintuitive.

For example, the IF entropy measure of Liu and Ren [34] is

$$E_{LR}(A)=\frac{1}{n}{\displaystyle \sum _{i=1}^n\cos \frac{{\mu }_A{}^2(x_i)-{\nu }_A{}^2(x_i)}{2}\pi }$$

Example 4.

Let$A_7=\left\{<x,0.2,0.4>|x\in X\right\}$and$A_8=\left\{<x,0.4272,0.25>|x\in X\right\}$be two IF sets. Obviously, the fuzzinesses of$A_7$and$A_8$are not equal. However, calculating the entropy of$A_7$and$A_8$with the entropy formula$E_{LR},$we have$E_{LR}\left(A_7\right)=E_{LR}\left(A_8\right)=0.9823$.

Motivation: we can see that some existing cosine and cotangent function-based entropy measures have no ability to discriminate some IF sets, and there are counterintuitive phenomena, such as the cases of Example 1 to 4. In this paper, we are also devoted to the development of IF entropy measures. We propose a new intuitionistic fuzzy entropy based on a cotangent function, which is an improvement of Wang’s entropy [32], as follows:

$$\begin{array}{l}{E}_{RZ}(A)=\frac{1}{n}{\displaystyle \sum _{i=1}^n\cot (\frac{\pi }{4}+\frac{|{\mu }_A(x_i)-{\nu }_A(x_i)|}{4+{\pi }_A(x_i)}\pi )}\\ \end{array}$$

(3)

which not only considers the deviation between membership and non-membership degrees ${\mu }_A(x_i)-{\nu }_A(x_i)$, but also considers the hesitancy degree ${\pi }_A(x_i)$ of the IF set.

Theorem 1.

The measure given by Equation (3) is an IF entropy.

Proof. 

To prove the measure $E_{RZ}(A)$ given by Equation (3) is an IF entropy, we only need to prove it satisfies the properties in Definition 4. Obviously, for every $x_i$, we have:

$$0\le \frac{|{\mu }_A(x_i)-{\nu }_A(x_i)|}{4+{\pi }_A(x_i)}\pi \le \frac{\pi }{4},$$

then

$$0\le \cot (\frac{\pi }{4}+\frac{|{\mu }_A(x_i)-{\nu }_A(x_i)|}{4+{\pi }_A(x_i)}\pi )\le 1$$

Thus, we have $0\le E_{RZ}(A)\le 1$.

(i) Let $A$ be a crisp set, i.e., for $\forall x_i\in X$, we have ${\mu }_A(x_i)=1,{\nu }_A(x_i)=0$ or ${\mu }_A(x_i)=0,{\nu }_A(x_i)=1$. It is obvious that $E_{RZ}(A)=0$.

If $E_{RZ}(A)=0$, i.e., $E_{RZ}(A)=\frac{1}{n}{\displaystyle \sum _{i=1}^n\cot (\frac{\pi }{4}+\frac{|{\mu }_A(x_i)-{\nu }_A(x_i)|}{4+{\pi }_A(x_i)}\pi )}=0$, then $\forall x_i\in X$, we have ${\displaystyle \sum _{i=1}^n\cot (\frac{\pi }{4}+\frac{|{\mu }_A(x_i)-{\nu }_A(x_i)|}{4+{\pi }_A(x_i)}\pi )}=0$.

Thus $\frac{|{\mu }_A(x_i)-{\nu }_A(x_i)|}{4+{\pi }_A(x_i)}=\frac{1}{4}$, amd then we have ${\mu }_A(x_i)=1$ ${\nu }_A(x_i)=0$ or ${\mu }_A(x_i)=0,{\nu }_A(x_i)=1$. Therefore, $A$ is a crisp set.

(ii) Let ${\mu }_A(x_i)={\nu }_A(x_i)$,$\forall x_i\in X$; according to Equation (3), we have $E_{RZ}(A)=\frac{1}{n}{\displaystyle \sum _{i=1}^n\cot (\frac{\pi }{4})=1}$.

Now we assume that $E_{RZ}(A)=1$; then for all $x_i\in X$, we have: $\cot (\frac{\pi }{4}+\frac{|{\mu }_A(x_i)-{\nu }_A(x_i)|}{4+{\pi }_A(x_i)}\pi )=1$, then $|{\mu }_A(x_i)-{\nu }_A(x_i)|=0$, and we can obtain the conclusion ${\mu }_A(x_i)={\nu }_A(x_i)$ for all $x_i\in X$.

(iii) By $A^C=\{<x_i,{\nu }_A(x_i),{\mu }_A(x_i)>|x_i\in X\}$ and Equation (3), we have:

$$E_{RZ}(A^C)=\frac{1}{n}{\displaystyle \sum _{i=1}^n\cot (\frac{\pi }{4}+\frac{|{\nu }_A(x_i)-{\mu }_A(x_i)|}{4+{\pi }_A(x_i)}\pi )}=E_{RZ}(A).$$

(iv) Construct the function:

$$f(x,y)=\cot (\frac{\pi }{4}+\frac{|x-y|}{5-(x+y)}\pi ), \mathrm{where}x,y\in [0,1].$$

Now, when $x\le y$, we have $f(x,y)=\cot (\frac{\pi }{4}+\frac{y-x}{5-(x+y)}\pi )$; we need to prove that the function $f(x,y)$ is increasing with $x$ and decreasing with $y$.

We can easily derive the partial derivatives of $f(x,y)$ to $x$ and to $y$, respectively:

$$\frac{\partial f}{\partial x}=-{\csc }^2(\frac{\pi }{4}+\frac{y-x}{5-(x+y)}\pi )·\frac{(2y-5)\pi }{{[5-(x+y)]}^2}$$

$$\frac{\partial f}{\partial y}=-{\csc }^2(\frac{\pi }{4}+\frac{y-x}{5-(x+y)}\pi )·\frac{(5-2x)\pi }{{[5-(x+y)]}^2}$$

When $x\le y$, we have $\frac{\partial f}{\partial x}\ge 0,\frac{\partial f}{\partial y}\le 0$; then, $f(x,y)$ is increasing with $x$ and decreasing with $y$; thus, when ${\mu }_B(x_i)\le {\nu }_B(x_i)$ and ${\mu }_A(x_i)\le {\mu }_B(x_i),{\nu }_A(x_i)\ge {\nu }_B(x_i)$ are satisfied, we have $f({\mu }_A(x_i),{\nu }_A(x_i))\le f({\mu }_B(x_i),{\nu }_B(x_i))$.

So $\cot (\frac{\pi }{4}+\frac{|{\mu }_A(x_i)-{\nu }_A(x_i)|}{4+{\pi }_A(x_i)}\pi )\le \cot (\frac{\pi }{4}+\frac{|{\mu }_B(x_i)-{\nu }_B(x_i)|}{4+{\pi }_B(x_i)}\pi ),$ that is, $E_{RZ}(A)\prec E_{RZ}(B)$ holds.

Similarly, we can prove that when $x\ge y$, $\frac{\partial f}{\partial x}\le 0,\frac{\partial f}{\partial y}\ge 0$, then $f(x,y)$ is decreasing with $x$ and increasing with $y$, thus when ${\mu }_B(x_i)\ge {\nu }_B(x_i)$ and ${\mu }_A(x_i)\ge {\mu }_B(x_i),$ ${\nu }_A(x_i)\le {\nu }_B(x_i)$ is satisfied, so we have $f({\mu }_A(x_i),{\nu }_A(x_i))\le f({\mu }_B(x_i),{\nu }_B(x_i))$.

Therefore, if $A\prec B$, we have $\frac{1}{n}{\displaystyle \sum _{i=1}^{n}f({\mu }_A(x_i),{\nu }_A(x_i))}\le \frac{1}{n}{\displaystyle \sum _{i=1}^{n}f({\mu }_B(x_i),{\nu }_B(x_i))}$, i.e., $E_{RZ}(A)\prec E_{RZ}(B)$. □

From Equation (3), the entropies of $A_1,A_2,A_3,A_4,A_5,A_6,A_7 \mathrm{and} A_8$ in Examples 1 to 4 can be obtained as follows:

$$\begin{gathered} E_{RZ}(A_1)=0.8634,E_{RZ}(A_2)=0.8694,E_{RZ}(A_1)\prec E_{RZ}(A_2). \\ {E}_{RZ}(A_3)=0.6298,E_{RZ}(A_4)=0.8215,E_{RZ}(A_3)\prec E_{RZ}(A_4). \\ {E}_{RZ}(A_5)=0.6356,E_{RZ}(A_6)=0.5959,E_{RZ}(A_5)\succ E_{RZ}(A_6). \\ {E}_{RZ}(A_7)=0.7486,E_{RZ}(A_5)=0.7707,E_{RZ}(A_7)\prec E_{RZ}(A_8). \end{gathered}$$

The calculation results are in agreement with our intuition.

According to the above examples, we see that the proposed entropy measure has a better performance than the entropy measures $E_Y,E_Z,E_{ZJ},E_{VS},E_{B_1},E_W,E_{WG},E_{LR}$. Furthermore, the new entropy measure considers the two aspects of the IF set (i.e., the uncertainty depicted by the derivation of membership and non-membership and the hesitancy degree reflected by the hesitation degree of the IF set), and thus the proposed entropy measure is a good entropy measure formula of the IF set.

4.2. Clustering Method of Group Decision Experts

For group decision-making problems, suppose that $X=\{x_1,x_2,\cdots ,x_m\}$ is a set of $m$ schemes, and $O=\{O_1,O_2,\cdots ,O_n\}$ is a set of $n$ decision makers. The evaluation values decision makers $O_j\in O$ to schemes $x_k\in X$ are expressed by IF number $<{\mu }_j(x_k),{\nu }_j(x_k)>$, where ${\mu }_j(x_k)$ and ${\nu }_j(x_k)$ are the membership (satisfaction) and non-membership (dissatisfaction) degrees of the decision maker $O_j\in O$ to the scheme $x_k\in X$ with respect to the fuzzy concept so that they satisfy the conditions $0\le {\mu }_j(x_k)\le 1,0\le {\nu }_j(x_k)\le 1$ and $0\le {\mu }_j(x_k)+{\nu }_j(x_k)\le 1$ ($j=1,2,\cdots ,n$; $k=1,2,\cdots ,m$).

Thus, a group decision-making problem can be expressed by the decision matrix $O={[<{\mu }_{kj},{\nu }_{kj}>]}_{m\times n}$ as follows:

$$O={[<{\mu }_{kj},{\nu }_{kj}>]}_{m\times n}=\begin{array}{l}\begin{array}{ccccccccccc}\begin{array}{cccccccccccccccccc}& & & & & O_1& & & & & & & O_2& & & & \cdots & \end{array}& & & O_n& & & & & & & \end{array}\\ \begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_m\end{array}{\left[\begin{array}{cccc}<{\mu }_{11},{\nu }_{11}>& <{\mu }_{12},{\nu }_{12}>& \cdots & <{\mu }_{1n},{\nu }_{1n}>\\ <{\mu }_{21},{\nu }_{21}>& <{\mu }_{22},{\nu }_{22}>& \cdots & <{\mu }_{2n},{\nu }_{2n}>\\ & \cdots & \cdots & \\ <{\mu }_{m1},{\nu }_{m1}>& <{\mu }_{m2},{\nu }_{m2}>& \cdots & <{\mu }_{mn},{\nu }_{mn}>\end{array}\right]}_{m\times n}\end{array}$$

4.2.1. A New IF Similarity Measure

To measure the similarities among any form of data is an important topic [44,45]. The measures used to find the resemblance between data is called a similarity measure. It has different applications in classification, medical diagnosis, pattern recognition, data mining, clustering [46], decision making and image processing. Khan et al. [47] proposed a newly similarity measure for a q-rung orthopair fuzzy set based on a cosine and cotangent function. Chen and Chang [48] proposed a new similarity measure between Atanassov’s intuitionistic fuzzy sets (AIFSs) based on transformation techniques and applied the proposed similarity measure between AIFSs to deal with pattern recognition problems. Beliakov et al. [49] presented a new approach for defining similarity measures for AIFSs and applied it to image segmentation. Lohani et al. [50] presented a novel probabilistic similarity measure (PSM) for AIFSs and developed the novel probabilistic λ-cutting algorithm for clustering. Liu et al. [51] proposed a new intuitionistic fuzzy similarity measure, introduced it into intuitionistic fuzzy decision system and proposed an intuitionistic fuzzy three branch decision method based on intuitionistic fuzzy similarity. Mei [52] constructed a similarity model between intuitionistic fuzzy sets and applied it to dynamic intuitionistic fuzzy multi-attribute decision making.

At present, most of the existing similarity measures are expressed in real numbers, which is not in line with the characteristics of intuitionistic fuzzy sets. In this section, we define a new IF similarity measure whose value is an IF number.

For any two experts $O_j$ and $O_k$, let

$$X_p(O_j,O_k)=\sqrt[p]{{\displaystyle \sum _{i=1}^m{w}_i{({\nu }_{ij}-{\nu }_{ik})}^p}}\mathrm{and}{M}_p(O_j,O_k)=\sqrt[p]{{\displaystyle \sum _{i=1}^m{w}_i{({\mu }_{ij}-{\mu }_{ik})}^p}},$$

where $w_i$ is the weight of scheme $x_i$ for all $i\in \{1,2,\cdots ,m\}$ and ${\displaystyle \sum _{i=1}^m{w}_i}=1$ and $p\ge 1$ is a parameter.

Let

$${\overline{\mu }}_{jk}=1-\max \{X_p(O_j,O_k),M_p(O_j,O_k)\},$$

$${\overline{\nu }}_{jk}=\min \{X_p(O_j,O_k),M_p(O_j,O_k)\}$$

Theorem 2.

Let$O_j$and$O_k$be two IF sets; then,

$$\psi (O_j,O_k)=<{\overline{\mu }}_{jk},{\overline{\nu }}_{jk}>$$

(4)

is the IF similarity measure of$O_j$and$O_k$.

Proof. 

To prove the measure given by Equation (4) is an IF similarity measure of $O_j$ and $O_k$, we only need to prove that it satisfies the properties in Definition 6.

First, we prove that $\psi (O_j,O_k)$ is the form of an IFN.

Because $0\le X_p(O_j,O_k)=\sqrt[p]{{\displaystyle \sum _{i=1}^m{w}_i{({\nu }_{ij}-{\nu }_{ik})}^p}}\le 1$ and $0\le M_p(O_j,O_k)=\sqrt[p]{{\displaystyle \sum _{i=1}^m{w}_i{({\mu }_{ij}-{\mu }_{ik})}^p}}\le 1$, so $0\le 1-\max \{X_p(O_j,O_k),M_p(O_j,O_k)\}\le 1$,$0\le \min \{X_p(O_j,O_k),M_p(O_j,O_k)\}\le 1$ and ${\overline{\mu }}_{jk}+{\overline{\nu }}_{jk}\le 1$. This proves that $\psi (O_j,O_k)$ is the form of an IFN.

Let $\psi (O_j,O_k)=<{\overline{\mu }}_{jk},{\overline{\nu }}_{jk}>=<1,0>$; we have

$${\overline{\mu }}_{jk}=1-\max \{X_p(O_j,O_k),M_p(O_j,O_k)\}=1$$

And ${\overline{\nu }}_{jk}=\min \{X_p(O_j,O_k),M_p(O_j,O_k)\}=0$, so $X_p(O_j,O_k)=M_p(O_j,O_k)$. Because of the arbitrariness of $w_i$, we get ${\mu }_{ij}={\mu }_{ik}$ and ${\nu }_{ij}={\nu }_{ik}$ for all $i\in \{1,2,\cdots ,m\}$, that is, $O_j=O_k$.

Now we assume that $O_j=O_k$; then for all $i\in \{1,2,\cdots ,m\}$, we have ${\mu }_{ij}={\mu }_{ik},{\nu }_{ij}={\nu }_{ik}$; we can obtain $X_p(O_j,O_k)=M_p(O_j,O_k)=0$ and ${\overline{\mu }}_{jk}=1-\max \{X_p(O_j,O_k),M_p(O_j,O_k)\}=1$,${\overline{\nu }}_{jk}=\min \{X_p(O_j,O_k),M_p(O_j,O_k)\}=0$, that is, $\psi (O_j,O_k)=<1,0>$.

Property 3 clearly holds.

If $O_1\subseteq O_2\subseteq O_3$, i.e.,${\mu }_{i1}\le {\mu }_{i2}\le {\mu }_{i3},$${\nu }_{i1}\ge {\nu }_{i2}\ge {\nu }_{i3}$ for all $i\in \{1,2,\cdots ,m\}$,then ${({\mu }_{i1}-{\mu }_{i2})}^p\le {({\mu }_{i1}-{\mu }_{i3})}^p,{({\nu }_{i1}-{\nu }_{i2})}^p\le {({\nu }_{i1}-{\nu }_{i3})}^p$ for all $i\in \{1,2,\cdots ,m\}$.

We have $X_p(O_1,O_2)\le X_p(O_1,O_3)$ and $M_p(O_1,O_2)\le M_p(O_1,O_3)$; therefore,${\overline{\mu }}_{12}\ge {\overline{\mu }}_{13}$, and ${\overline{\nu }}_{12}\le {\overline{\nu }}_{13}$, that is,$\psi (O_1,O_3)\subseteq \psi (O_1,O_2)$. Similarly, it can be proved that $\psi (O_1,O_3)\subseteq \psi (O_2,O_3)$.

This theorem is proved. □

For IF similarity measure Equation (4), since each scheme is equal, this paper takes $p=2,w_i=\frac{1}{m}$ for all $i\in \{1,2,\cdots ,m\}$. Using this formula, the IF decision matrix $O={[<{\mu }_{kj},{\nu }_{kj}>]}_{m\times n}$ can be transformed into the IF similar matrix $Z={(z_{jk})}_{n\times n}$, where $z_{jk}=\psi (O_j,O_k)=<{\overline{\mu }}_{jk},{\overline{\nu }}_{jk}>$ is an IFN.

The IF decision matrix can be transformed into the IF similarity matrix $Z={(z_{jk})}_{n\times n}$ by using the IF similarity formula proposed in this paper, where $z_{jk}=\psi (O_j,O_k)=<{\overline{\mu }}_{jk},{\overline{\nu }}_{jk}>$ is an IFN.

People’s pursuit of risk varies from person to person. Let $\beta \in [0,1]$ be the risk factor; then the IF similarity matrix $Z={(z_{jk})}_{n\times n}$ can be transformed into a real matrix $R={(r_{jk})}_{n\times n}$ where $r_{jk}={\overline{\mu }}_{jk}+\beta (1-{\overline{\mu }}_{jk}-{\overline{\nu }}_{jk})$.

$$R={(r_{jk})}_{n\times n}=\left[\begin{array}{cccc}{r}_{11}& r_{12}& \cdots & r_{1n}\\ r_{21}& r_{22}& \cdots & r_{2n}\\ & \cdots & \cdots & \\ r_{n1}& r_{n2}& \cdots & r_{nn}\end{array}\right]$$

4.2.2. Threshold Change Rate Analysis Method

The method of Zhou et al. [40] is adopted in this section.

Let the clustering threshold $\theta ={\theta }_t$, where ${\theta }_t\in [0,1]$. If

$$r_{jk}\ge {\theta }_t,j\ne k$$

(5)

then elements $O_k$ and $O_j$ are considered to have the same properties. The closer the threshold is to 1, the finer the classification is.

In Zhou et al. [40], the selection of the optimal clustering threshold ${\theta }_i$ can be deter-mined by analyzing the change rate $C_i$ of ${\theta }_i$. The rate of change $C_i$ is given as follows:

$$C_i=\frac{{\theta }_{i-1}-{\theta }_i}{n_i-n_{i-1}}$$

(6)

where $i$ is the clustering times of $\theta$ from large to small, $n_i$ and $n_{i-1}$ are the number of objects in the $i$-th and $(i-1)$-th clustering, respectively, and ${\theta }_i$ and ${\theta }_{i-1}$ are the thresholds for the $i$-th and $(i-1)$-th clustering, respectively. If

$$C_i=\underset{j}{\max }\left\{C_j\right\}$$

(7)

then the threshold value of $i$ clustering is the best.

It can be seen from Equation (5) that the greater the change rate $C_i$ of the clustering threshold $\theta$ is, the greater the difference between the corresponding two clusters and the more obvious the boundary between classes. When $C_i$ is the maximum value, its corresponding $\theta$ is the optimal clustering threshold value, which can make the difference between the clusters obtained by the $i$-th clustering to be the largest, thus realizing the purpose and significance of classification.

4.3. Analysis of Group Decision Making Expert Group Weighting

In group decision-making problems, because each expert has a different specialty, experience and preference, their evaluation information should be treated differently. In order to reflect the status and importance of each expert in decision making, it is of great significance to determine the expert weight reasonably.

Two aspects need to be considered in expert weight, namely, the weight between categories and the weight within categories. The weight between categories mainly considers the number of experts in the category of experts. For the category with large capacity, the evaluation results given by experts represent the opinions of most experts, so the corresponding categories should be given a larger weight, which reflects the principle that the minority is subordinate to the majority, while the category with smaller capacity should be given a smaller weight.

Suppose that $n$ experts are divided into $t$ categories; the number of experts in the $i$ category is ${\phi }_i({\phi }_i\le n)$; and the weights between the expert categories ${\lambda }_i$ are as follows:

$${\lambda }_i=\frac{{\phi }_i{}^2}{{\displaystyle \sum _{k=1}^t{\phi }_t{}^2}},k=1,2,\cdots ,t.$$

(8)

The weight of experts within the category can be measured by the information contained in an IF evaluation value given by experts. Entropy is a measure of information uncertainty and information quantity. If the entropy of the evaluation information given by an expert is smaller, the uncertainty of the evaluation information is smaller, which means that the logic of the expert is clearer; the amount of information provided is greater; and the role of the expert in the comprehensive evaluation is greater, so the expert should be given more weight. Therefore, the weight of experts within the category can be measured by IF entropy.

The evaluation vector of expert $k$ is $O_k=(<{\mu }_k(x_1),{\nu }_k(x_1)>,\cdots ,<{\mu }_k(x_5),{\nu }_k(x_5)>).$

The IF entropy corresponding to Equation (1) is expressed as follows:

$$E(k)=\frac{1}{5}{\displaystyle \sum _{i=1}^5\cot (\frac{\pi }{4}+\frac{|{\mu }_k(x_i)-{\nu }_k(x_i)|}{4+{\pi }_k(x_i)}\pi )}$$

(9)

The internal weight $a_{ik}$ of the $k$ expert in category $i$ is as follows:

$$a_{ik}=\frac{1-E(k)}{{\displaystyle \sum _{i=1}^{\phi (i)}[1-E(i)]}}$$

(10)

By linear weighting ${\lambda }_i$ and $a_{ik}$, the total weight of experts ${\omega }_k$ is obtained:

$${\omega }_k={\lambda }_i·a_{ik},k=1,2,\cdots ,n.$$

(11)

4.4. Intelligent Expert Combination Weighting Algorithm

A cluster analysis method is often used to realize the expert weighting in group decision making. The basic principle of expert cluster analysis is to measure the similarity degree of expert evaluation opinions according to certain standards and cluster experts based on the similarity degree. In short, Figure 4 shows the general scheme of the expert clustering method.

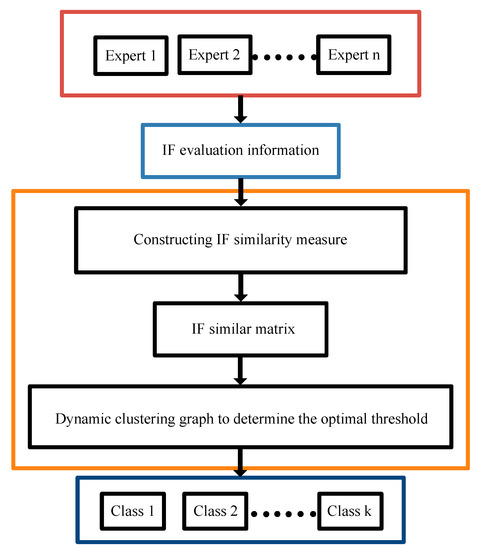
Figure 4. The general scheme of expert clustering method.

To sum up, this paper proposes an expert combination weighting scheme for group decision making, and obtains the following algorithm, which we call the intelligent expert combination weighting algorithm (see Algorithm 1).

Algorithm 1. Intelligent expert combination weighting algorithm

Input the IF decision matrix $O={[<{\mu }_{ij},{\nu }_{ij}>]}_{n\times m}$ given by experts where

$I=\{1,2,\cdots ,n\} \mathrm{and}J=\{1,2,\cdots ,m\}.$

1: For $j\in I$ implement.

2: For $k\in I$ implement.

3: For $i\in J$ implement.

4: The IF similarity measure between experts $\psi (O_j,O_k)=<{\overline{\mu }}_{jk},{\overline{\nu }}_{jk}>$ is calculated according to formula (4).

5: End for

6: Let $z_{jk}=\psi (O_j,O_k)=<{\overline{\mu }}_{jk},{\overline{\nu }}_{jk}>.$

7: End for

8: End for

9: The IF decision matrix $O={[<{\mu }_{ij},{\nu }_{ij}>]}_{n\times m}$ is transformed into the similarity matrix $Z={(z_{jk})}_{n\times n}.$

10: By selecting the risk factor β, the IF similarity matrix $Z={(z_{jk})}_{n\times n}$ is transformed into the real matrix $R={(r_{jk})}_{n\times n} .$

11: According to the real matrix $R={(r_{jk})}_{n\times n}$, the dynamic clustering graph is drawn, and the optimal clustering threshold is determined by Formulae (6) and (7). According to this threshold, experts are classified into L categories.

12: For $l\in L$ implement.

13: Using Formula (8), the weight of experts between categories λl is determined.

14: For $k\in I$ implement.

15: Using Formula (8), the weight of experts between categories alk is determined.

16: Formula (11) is used to determine the total weight of experts. ωk is calculated.

17: End for.

18: End for.

19: For $i\in J$ implement.

20: For $k\in I$ implement.

21: The weighted operator (2) of IF sets is used to aggregate expert IF group decision-making information.

22: End for.

23: According to definition 8, the scores and accuracy values of each scheme xi are obtained.

24: End for.

25: return The results of the ranking of schemes xi.

5. Performance Analysis

The railway is an important national infrastructure and livelihood project. It is a resource-saving and environment-friendly mode of transportation. In recent years, China’s railway development has made remarkable achievements, but compared with the needs of economic and social development, other modes of transportation and advanced foreign railway technique, the railway in China is still a weak part of the whole transportation system [53,54]. In order to further accelerate railway construction, expand the scale of railway network and improve the layout structure and quality, the state promulgated the medium and long term railway network plan, which puts forward a series of railway plans, including the plan for railway reconstruction.

The railway reconstruction project is carried out under a series of communication, coordination and cooperation efforts, and the complex work is arranged in a limited work area, so it has encountered many unexpected challenges, such as carelessness or inadequate planning, which may lead to accidents and cause significant damage to life, assets, environment and society. According to literature [55], we can conclude that there are about seven types of risks in railway reconstruction projects, including financial and economic risks, contract and legal risks, subcontractor related risks, operation and safety risks, political and social risks, design risks and force majeure risks.

It is assumed that nine experts $O_i(i=1,2,\cdots ,9)$ form a decision-making group to rank five alternatives $x_j(j=1,2,3,4,5)$ from the seven evaluation attributes above. Evaluation alternatives always contain ambiguity and diversity of meaning. In addition, in terms of qualitative attributes, human assessment is subjective and therefore inaccurate. In this case, an IF set is very advantageous; it can describe the decision process more accurately. IF sets are used in this study. After expert investigation and statistical analysis, we can get the satisfaction degree ${\mu }_{ij}$ and dissatisfaction ${\nu }_{ij}$ given by each expert $O_i(i=1,2,\cdots ,9)$ for each scheme $x_j(j=1,2,3,4,5)$. The specific data are given in Table 1.

Table 1. Expert evaluation information on the program.

Expert	${\mathit{x}}_{\mathbf{1}}$	${\mathit{x}}_{\mathbf{2}}$	${\mathit{x}}_{\mathbf{3}}$	${\mathit{x}}_{\mathbf{4}}$	${\mathit{x}}_{\mathbf{5}}$
$O_1$	<0.43,0.45>	<0.24,0.70>	<0.57,0.40>	<0.29,0.55>	<0.25,0.60>
$O_2$	<0.58,0.30>	<0.37,0.52>	<0.30,0.50>	<0.55,0.35>	<0.35,0.50>
$O_3$	<0.31,0.61>	<0.74,0.22>	<0.70,0.25>	<0.50,0.40>	<0.70,0.20>
$O_4$	<0.44,0.45>	<0.31,0.60>	<0.56,0.40>	<0.31,0.52>	<0.24,0.60>
$O_5$	<0.31,0.60>	<0.70,0.20>	<0.75,0.20>	<0.60,0.30>	<0.68,0.20>
$O_6$	<0.70,0.20>	<0.58,0.32>	<0.52,0.40>	<0.20,0.70>	<0.60,0.30>
$O_7$	<0.38,0.52>	<0.72,0.21>	<0.68,0.22>	<0.61,0.30>	<0.70,0.22>
$O_8$	<0.41,0.40>	<0.28,0.60>	<0.55,0.35>	<0.30,0.55>	<0.26,0.60>
$O_9$	<0.56,0.34>	<0.40,0.50>	<0.30,0.40>	<0.71,0.10>	<0.38,0.45>

The calculation steps of the proposed method are given as follows:

Step 1. According to Equation (4), the IF similarity matrix $Z$ is obtained as follows:

$$Z=\begin{array}{l}[\begin{array}{ccccc}<1,0>& <0.805,0.152>& <0.675,0.304>& <0.953,0.033>& <0.672,0.327>\\ & <1,0>& <0.685,0.261>& <0.821,0.125>& <0.685,0.274>\\ & & <1,0>& <0.694,0.271>& <0.946,0.051>\\ & & & <1,0>& <0.689,0.294>\\ & & & & <1,0>\\ & & & & \\ & & & & \\ & & & & \\ & & & & \end{array}\end{array}$$

$$\begin{array}{cccc}<0.746,0.253>& <0.668,0.311>& <0.945,0.023>& <0.752,0.235>\\ <0.758,0.211>& <0.706,0.246>& <0.816,0.133>& <0.876,0.075>\\ <0.751,0.245>& <0.938,0.060>& <0.691,0.276>& <0.689,0.255>\\ <0.762,0.229>& <0.688,0.276>& <0.966,0.022>& <0.768,0.210>\\ <0.722,0.277>& <0.954,0.038>& <0.686,0.298>& <0.698,0.245>\\ <1,0>& <0.745,0.250>& <0.755,0.216>& <0.705,0.286>\\ & <1,0>& <0.683,0.279>& <0.720,0.220>\\ & & <1,0>& <0.763,0.220>\\ & & & <1,0>\end{array}]$$

Step 2. By selecting the risk factor $\beta =0.5$, i.e., moderate risk, the real matrix $R$ is obtained.

$$R=\left[\begin{array}{ccccccccc}1& 0.827& 0.686& 0.96& 0.673& 0.747& 0.679& 0.961& 0.759\\ & 1& 0.712& 0.848& 0.706& 0.774& 0.73& 0.842& 0.901\\ & & 1& 0.712& 0.948& 0.753& 0.939& 0.708& 0.717\\ & & & 1& 0.700& 0.767& 0.706& 0.972& 0.779\\ & & & & 1& 0.723& 0.958& 0.694& 0.727\\ & & & & & 1& 0.748& 0.770& 0.710\\ & & & & & & 1& 0.702& 0.75\\ & & & & & & & 1& 0.772\\ & & & & & & & & 1\end{array}\right]$$

Step 3. According to Equation (5), let $i$ take all the values in turn to get a series of classifications, and then draw a dynamic clustering graph according to Equations (5) and (6), as shown in Figure 5.

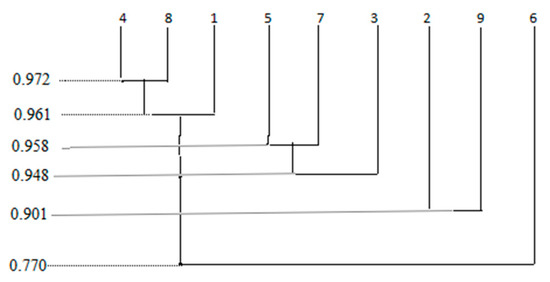
Figure 5. Dynamic clustering graph.

According to Equation (6), we have

$$\begin{gathered} C_1=\frac{1-0.972}{2-0}=0.014, C_2=\frac{0.972-0.961}{3-2}=0.011, C_3=\frac{0.961-0.958}{5-3}=0.0015, \\ {C}_4=\frac{0.958-0.948}{6-5}=0.01,C_5=\frac{0.948-0.901}{8-6}=0.0235,C_6=\frac{0.901-0.770}{9-8}=0.131. \end{gathered}$$

Since it is meaningless for each expert to become a category or all experts to be classified into one category, we do not consider $C_6$; then, we have $C_5=\max \{C_1,C_2,C_3,C_4,C_5\}$.

Therefore, taking $\theta =0.891$ as the optimal clustering threshold, the clustering result is the most reasonable and consistent with the actual situation, and the clustering results are shown in Figure 6. We can see that the corresponding clustering results are as follows:

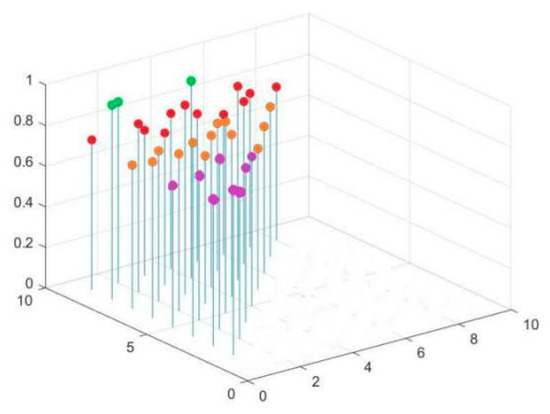
Figure 6. Clustering results.

{(1 4 8), (3 5 7), (2 9), (6)}

Step 4. According to Equation (8), the weight of experts between categories is as follows:

$${\lambda }_1=0.3913,{\lambda }_2=0.3913,{\lambda }_3=0.1739,{\lambda }_4=0.0435.$$

Step 5. According to Equation (9), the entropy vector of the expert group is obtained as follows:

(0.6868, 0.7405, 0.5538, 0.7364, 0.4995, 0.5935, 0.5507, 0.7159, 0.7339)

According to Equation (10), the weight of experts within the category is shown in Table 2.

Table 2. The weight of experts within the category.

Category	The Weight of Experts within the Category
Category 1	$a_{11}=0.3638,a_{14}=0.3062,$$a_{18}=0.330$
Category 2	$a_{23}=0.3196,$$a_{25}=0.3585,a_{27}=0.3219$
Category 3	$a_{32}=0.4937,$$a_{39}=0.4303$
Category 4	$a_{46}=1$

Step 6. We weight ${\lambda }_i$ and $a_{ik}$ linearly to get the total weight vector ${\omega }_k$ of experts as follows:

(0.1424, 0.0859, 0.1251, 0.1198, 0.1403, 0.0435, 0.1260, 0.1291, 0.0748).

Step 7. According to the total weight of nine experts, the weighted aggregation operator given by Equation (2) is used to aggregate the expert information, and the comprehensive evaluation vector is obtained as follows:

(0.3616, 0.4504), (0.5226, 0.3878), (0.5932, 0.3218), (0.4749, 0.3853), (0.4972, 0.3718).

According to Equation (1), the scores and accuracy values of the comprehensive evaluation vector are calculated as follows:

$$\begin{gathered} M(x_1)=-0.089,M(x_2)=0.1348,M(x_3)=0.2714,M(x_4)=0.0896,M(x_5)=0.1254. \\ \Delta (x_1)=0.812, \Delta (x_2)=0.9104, \Delta (x_3)=0.915, \Delta (x_4)=0.8602,\Delta (x_5)=0.869 \end{gathered}$$

Therefore, the priority of the five alternatives is $x_3\succ x_2\succ x_5\succ x_4\succ x_1$, and the optimal one is $x_3$.

6. Conclusions and Future Work

This article listed some counterintuitive phenomena of some existing intuitionistic fuzzy entropies. We defined an improved intuitionistic fuzzy entropy based on a cotangent function and a new IF similarity measure whose value is an IF number, applied them to the expert weight problem of group decision making and put forward the expert weight combination weighting scheme. Finally, this method was applied to a railway reconstruction case to illustrate the effectiveness of the method.

In the future, we will apply the expert weight combination weighting scheme proposed in this paper to situations in real life. We will also formulate this kind of entropy measure and similarity measures for an interval-valued IF set [56], Fermat fuzzy set, spherical fuzzy set, t-spherical fuzzy set, picture fuzzy set, single valued neutrosophic set [55,57], Plithogenic set [58] and linear fuzzy set.

While studying the theoretical method, this paper used numerical examples rather than the actual production data, which is the limitation of this paper. In the future research, we will apply the expert weight combination weighting scheme proposed in this paper to practical production problems.