Sobolev-Slobodeckij Spaces on Compact Manifolds, Revisited

Abstract

In this manuscript, we present a coherent rigorous overview of the main properties of Sobolev-Slobodeckij spaces of sections of vector bundles on compact manifolds; results of this type are scattered through the literature and can be difficult to find. A special emphasis has been put on spaces with noninteger smoothness order, and a special attention has been paid to the peculiar fact that for a general nonsmooth domain $\Omega$ in ${\mathbb{R}}^n$, $0<t<1$, and $1<p<\infty$, it is not necessarily true that $W^{1,p}(\Omega )\hookrightarrow W^{t,p}(\Omega )$. This has dire consequences in the multiplication properties of Sobolev-Slobodeckij spaces and subsequently in the study of Sobolev spaces on manifolds. We focus on establishing certain fundamental properties of Sobolev-Slobodeckij spaces that are particularly useful in better understanding the behavior of elliptic differential operators on compact manifolds. In particular, by introducing notions such as “geometrically Lipschitz atlases” we build a general framework for developing multiplication theorems, embedding results, etc. for Sobolev-Slobodeckij spaces on compact manifolds. To the authors’ knowledge, some of the proofs, especially those that are pertinent to the properties of Sobolev-Slobodeckij spaces of sections of general vector bundles, cannot be found in the literature in the generality appearing here.

1. Introduction

Suppose $s\in \mathbb{R}$ and $p\in (1,\infty )$. With each nonempty open set $\Omega$ in ${\mathbb{R}}^n$ we can associate a complete normed function space denoted by $W^{s,p}(\Omega )$ called the Sobolev-Slobodeckij space with smoothness degree s and integrability degree p. Similarly, given a compact smooth manifold M and a vector bundle E over M, there are several ways to define the normed spaces $W^{s,p}(M)$ and more generally $W^{s,p}(E)$. The main goal of this manuscript is to review these various definitions and rigorously study the key properties of these spaces. Some of the properties that we are interested in are as follows:

• Density of smooth functions
• Completeness, separability, reflexivity
• Embedding properties
• Behavior under differentiation
• Being closed under multiplication by smooth functions:

  $$u\in W^{s,p},\phi \mathrm{is}\mathrm{smooth}\stackrel{?}{⟹}\phi u\in W^{s,p}$$
• Invariance under change of coordinates:

  $$u\in W^{s,p},T \mathrm{is} a \mathrm{diffeomorphism}\stackrel{?}{⟹}u\circ T\in W^{s,p}$$
• Invariance under composition by a smooth function:

  $$u\in W^{s,p},F \mathrm{is} \mathrm{smooth}\stackrel{?}{⟹}F(u)\in W^{s,p}$$

As we shall see, there are several ways to define $W^{s,p}(E)$. In particular, ${\parallel u\parallel }_{W^{s,p}(E)}$ can be defined using the components of the local representations of u with respect to a fixed augmented total trivialization atlas $\Lambda$, or it can be defined using the notion of connection in E. Here are some of the questions that we have studied in this paper regarding this issue:

• Are the different characterizations that exist in the literature equivalent? If not, what is the relationship between the various characterizations of Sobolev-Slobodeckij spaces on M?
• In particular, does the corresponding space depend on the chosen atlas (more precisely the chosen augmented total trivialization atlas) used in the definition?
• Suppose $f\in W^{s,p}(M)$. Does this imply that the local representation of f with respect to each chart $(U_{\alpha },{\phi }_{\alpha })$ is in $W^{s,p}({\phi }_{\alpha }(U_{\alpha }))$? If g is a metric on M and $g\in W^{s,p}$, can we conclude that $g_{ij}\circ {\phi }_{\alpha }^{-1}\in W^{s,p}({\phi }_{\alpha }(U_{\alpha }))$?
• Suppose that $P:C^{\infty }(M)\to C^{\infty }(M)$ is a linear differential operator. Is it possible to gain information about the mapping properties of P by studying the mapping properties of its local representations with respect to charts in a given atlas? For example, suppose that the local representations of P with respect to each chart $(U_{\alpha },{\phi }_{\alpha })$ in an atlas is continuous from $W^{s,p}({\phi }_{\alpha }(U_{\alpha }))$ to $W^{\tilde{s},\tilde{p}}({\phi }_{\alpha }(U_{\alpha }))$. Is it possible to extend P to a continuous linear map from $W^{s,p}(M)$ to $W^{\tilde{s},\tilde{p}}(M)$?

To further motivate the questions that are studied in this paper and the study of the key properties mentioned above, let us consider a concrete example. For any two sets A and B, let $\mathrm{Func}(A,B)$ denote the collection of all functions from A to B. Consider the differential operator

$${\mathrm{div}}_g:C^{\infty }(TM)\to \mathrm{Func}(M,\mathbb{R}),{\mathrm{div}}_{g}X=(\mathrm{tr}\circ {\mathrm{sharp}}_g\circ \nabla \circ {\mathrm{flat}}_g)X,$$

on a compact Riemannian manifold $(M,g)$ with $g\in W^{s,p}$. Let $\{(U_{\alpha },{\phi }_{\alpha })\}$ be a smooth atlas for M. It can be shown that for each $\alpha$

$$({\mathrm{div}}_{g}X)\circ {\phi }_{\alpha }^{-1}=\sum _{j=1}^n\frac{1}{\sqrt{\det g_{\alpha }}}\frac{\partial }{\partial x^j}\left[(\sqrt{\det g_{\alpha }})(X^j\circ {\phi }_{\alpha }^{-1})\right],$$

where $g_{\alpha }(x)$ is the matrix whose $(i,j)$-entry is $(g_{ij}\circ {\phi }_{\alpha }^{-1})(x)$. As it will be discussed in detail in Section 10, we call $Q^{\alpha }:C^{\infty }({\phi }_{\alpha }(U_{\alpha }),{\mathbb{R}}^n)\to \mathrm{Func}({\phi }_{\alpha }(U_{\alpha }),\mathbb{R})$ defined by

$$Q^{\alpha }(Y)=\sum _{j=1}^n\underset{Q_j^{\alpha }(Y^j)}{\underbrace{\frac{1}{\sqrt{\det g_{\alpha }}}\frac{\partial }{\partial x^j}\left[(\sqrt{\det g_{\alpha }})(Y^j)\right]}}$$

the local representation of ${\mathrm{div}}_g$ with respect to the local chart $(U_{\alpha },{\phi }_{\alpha })$. Let us say we can prove that for each $\alpha$ and j, $Q_j^{\alpha }$ maps $W_0^{e,q}({\phi }_{\alpha }(U_{\alpha }))$ to $W^{e-1,q}({\phi }_{\alpha }(U_{\alpha }))$. Can we conclude that ${\mathrm{div}}_g$ maps $W^{e,q}(TM)$ to $W^{e-1,q}(M)$? Furthermore, how can we find exponents e and q such that

$$Q_j^{\alpha }:W_0^{e,q}({\phi }_{\alpha }(U_{\alpha }))\to W^{e-1,q}({\phi }_{\alpha }(U_{\alpha }))$$

is a well-defined continuous map? We will see how the properties we mentioned above play a key role in answering these questions.

Since $W^{0,p}(\Omega )=L^p(\Omega )$, Sobolev-Slobodeckij spaces can be viewed as a generalization of classical Lebesgue spaces. Of course, unlike Lebesgue spaces, some of the key properties of $W^{s,p}(\Omega )$ (for $s\ne 0$) depend on the geometry of the boundary of $\Omega$. Indeed, to thoroughly study the properties of $W^{s,p}(\Omega )$ one should consider the following cases independently:

(1)

$\Omega ={\mathbb{R}}^n$

(2)

$\Omega$ is an arbitrary open subset of ${\mathbb{R}}^n$ $\left\{\begin{array}{c}2a)\mathrm{bounded}\hfill \\ 2b)\mathrm{unbounded}\hfill \end{array}\right.$

(3)

$\Omega$ is an open subset of ${\mathbb{R}}^n$ with smooth boundary $\left\{\begin{array}{c}3a)\mathrm{bounded}\hfill \\ 3b)\mathrm{unbounded}\hfill \end{array}\right.$

Let us mention here four facts to highlight the dependence on domain and some atypical behaviors of certain fractional Sobolev spaces. Let $s\in (0,\infty )$ and $p\in (1,\infty )$.

• Fact 1:

  $$\begin{array}{c}\hfill \forall j\frac{\partial }{\partial x^j}:W^{s,p}({\mathbb{R}}^n)\to W^{s-1,p}({\mathbb{R}}^n)\end{array}$$

  is a well-defined bounded linear operator.
• Fact 2: If we further assume that $s\ne \frac{1}{p}$ and $\Omega$ has smooth boundary then

  $$\forall j\frac{\partial }{\partial x^j}:W^{s,p}(\Omega )\to W^{s-1,p}(\Omega )$$

  is a well-defined bounded linear operator.
• Fact 3: If $\tilde{s}\le s$, then

  $$\begin{array}{c}\hfill W^{s,p}({\mathbb{R}}^n)\hookrightarrow W^{\tilde{s},p}({\mathbb{R}}^n).\end{array}$$
• Fact 4: If $\Omega$ does NOT have Lipschitz boundary, then it is NOT necessarily true that

  $$\begin{array}{c}\hfill W^{1,p}(\Omega )\hookrightarrow W^{\tilde{s},p}(\Omega )\end{array}$$

  for $0<\tilde{s}<1$.

Let M be an n-dimensional compact smooth manifold and let $\{(U_{\alpha },{\phi }_{\alpha })\}$ be a smooth atlas for M. As we will see, the properties of Sobolev-Slobodeckij spaces of sections of vector bundles on M are closely related to the properties of spaces of locally Sobolev-Slobodeckij functions on domains in ${\mathbb{R}}^n$. Primarily we will be interested in the properties of $W^{s,p}({\phi }_{\alpha }(U_{\alpha }))$ and $W_{loc}^{s,p}({\phi }_{\alpha }(U_{\alpha }))$. Furthermore, when we want to patch things together consistently and move from “local” to “global”, we will need to consider spaces $W^{s,p}({\phi }_{\alpha }(U_{\alpha }\cap U_{\beta }))$ and $W^{s,p}({\phi }_{\beta }(U_{\alpha }\cap U_{\beta }))$. However, as we pointed out earlier, some of the properties of $W^{s,p}(\Omega )$ depend heavily on the geometry of the boundary of $\Omega$. Considering that the intersection of two Lipschitz domains is not necessarily a Lipschitz domain, we need to consider the following question:

• Is it possible to find an atlas such that the image of each coordinate domain in the atlas (and the image of the intersection of any two coordinate domains in the atlas) under the corresponding coordinate map is either the entire ${\mathbb{R}}^n$ or a nonempty bounded set with smooth boundary? Furthermore, if we define the Sobolev spaces using such an atlas, will the results be independent of the chosen atlas?

This manuscript is an attempt to collect some results concerning these questions and certain other fundamental questions similar to the ones stated above, and we pay special attention to spaces with noninteger smoothness order and to general sections of vector bundles. There are a number of standard sources for properties of integer order Sobolev spaces of functions and related elliptic operators on domains in ${\mathbb{R}}^n$ (cf. [1,2,3]), real order Sobolev spaces of functions [4,5,6,7,8], Sobolev spaces of functions on manifolds [9,10,11,12], and Sobolev spaces of sections of vector bundles on manifolds [13,14]. However, most of these works focus on spaces of functions rather than general sections, and in many cases the focus is on integer order spaces. This paper should be viewed as a part of our efforts to build a more complete foundation for the study and use of Sobolev-Slobodeckij spaces on manifolds through a sequence of related manuscripts [15,16,17,18].

Outline of Paper. In Section 2, we summarize some of the basic notation and conventions used throughout the paper. In Section 3, we will review a number of basic constructions in linear algebra that are essential in the study of function spaces of generalized sections of vector bundles. In Section 4 we will recall some useful tools from analysis and topology. In particular, a concise overview of some of the main properties of topological vector spaces is presented in this section. Section 5 deals with reviewing some results we need from differential geometry. The main purpose of this section is to set the notation, definitions, and conventions straight. This section also includes some less well-known facts about topics such as higher order covariant derivatives in the context of vector bundles. In Section 6 we collect the results that we need from the theory of generalized functions on Euclidean spaces and vector bundles. Section 7 is concerned with various definitions and properties of Sobolev spaces that are needed for developing a coherent theory of such spaces on the vector bundles. In Section 8 and Section 9 we introduce Lebesgue spaces and Sobolev–Slobodeckij spaces of sections of vector bundles and we present a rigorous account of their various properties. Finally in Section 10 we study the continuity of certain differential operators between Sobolev spaces of sections of vector bundles. Although the purpose of Section 3 through Section 7 is to give a quick overview of the prerequisites that are needed to understand the proofs of the results in later sections and set the notation straight, as it was pointed out earlier, several theorems and proofs that appear in these sections cannot be found elsewhere in the generality that are stated here.

2. Notation and Conventions

Throughout this paper, $\mathbb{R}$ denotes the set of real numbers, $\mathbb{N}$ denotes the set of positive integers, and ${\mathbb{N}}_0$ denotes the set of nonnegative integers. For any nonnegative real number s, the integer part of s is denoted by $\lfloor s\rfloor$. The letter n is a positive integer and stands for the dimension of the space.

$\Omega$ is a nonempty open set in ${\mathbb{R}}^n$. The collection of all compact subsets of $\Omega$ will be denoted by $\mathcal{K}(\Omega )$. Lipschitz domain in ${\mathbb{R}}^n$ refers to a nonempty bounded open set in ${\mathbb{R}}^n$ with Lipschitz continuous boundary.

Each element of ${\mathbb{N}}_0^n$ is called a multi-index. For a multi-index $\alpha =({\alpha }_1,\dots ,{\alpha }_n)\in {\mathbb{N}}_0^n$, we let

• $|\alpha |:={\alpha }_1+\dots +{\alpha }_n$;
• $\alpha !:={\alpha }_1!\dots {\alpha }_n!$.

If $\alpha ,\beta \in {\mathbb{N}}_0^n$, we say $\beta \le \alpha$ provided that ${\beta }_i\le {\alpha }_i$ for all $1\le i\le n$. If $\beta \le \alpha$, we let

$$\left(\genfrac{}{}{0pt}{}{\alpha }{\beta }\right):=\frac{\alpha !}{\beta !(\alpha -\beta )!}=\left(\genfrac{}{}{0pt}{}{{\alpha }_1}{{\beta }_1}\right)\dots \left(\genfrac{}{}{0pt}{}{{\alpha }_n}{{\beta }_n}\right).$$

Suppose that $\alpha \in {\mathbb{N}}_0^n$. For sufficiently smooth functions $u:\Omega \to \mathbb{R}$ (or for any distribution u) we define the $\alpha$th order partial derivative of u as follows:

$${\partial }^{\alpha }u:=\frac{{\partial }^{|\alpha |}u}{\partial x_1^{{\alpha }_1}\dots \partial x_n^{{\alpha }_n}}.$$

We use the notation $A⪯B$ to mean $A\le cB$, where c is a positive constant that does not depend on the non-fixed parameters appearing in A and B. We write $A\simeq B$ if $A⪯B$ and $B⪯A$.

For any nonempty set X and $r\in \mathbb{N}$, $X^{\times r}$ stands for ${\underbrace{X\times \dots \times X}}_{r\mathrm{times}}$.

For any two nonempty sets X and Y, $\mathrm{Func}(X,Y)$ denotes the collection of all functions from X to Y.

We write $L(X,Y)$ for the space of all continuous linear maps from the normed space X to the normed space Y. $L(X,\mathbb{R})$ is called the (topological) dual of X and is denoted by $X^{*}$. We use the notation $X\hookrightarrow Y$ to mean $X\subseteq Y$ and the inclusion map is continuous.

$\mathrm{GL}(n,\mathbb{R})$ is the set of all $n\times n$ invertible matrices with real entries. Note that $\mathrm{GL}(n,\mathbb{R})$ can be identified with an open subset of ${\mathbb{R}}^{n^2}$ and so it can be viewed as a smooth manifold (more precisely, $\mathrm{GL}(n,\mathbb{R})$ is a Lie group).

Throughout this manuscript, all manifolds are assumed to be smooth, Hausdorff, and second-countable.

Let M be an n-dimensional compact smooth manifold. The tangent space of the manifold M at point $p\in M$ is denoted by $T_{p}M$, and the cotangent space by $T_p^{*}M$. If $(U,\phi =(x^i))$ is a local coordinate chart and $p\in U$, we denote the corresponding coordinate basis for $T_{p}M$ by ${\partial }_i{|}_p$ while $\frac{\partial }{\partial x^i}{|}_x$ denotes the basis for the tangent space to ${\mathbb{R}}^n$ at $x=\phi (p)\in {\mathbb{R}}^n$; that is,

$${\phi }_{*}{\partial }_i=\frac{\partial }{\partial x^i}.$$

Note that for any smooth function $f:M\to \mathbb{R}$ we have

$$({\partial }_{i}f)\circ {\phi }^{-1}=\frac{\partial }{\partial x^i}(f\circ {\phi }^{-1}).$$

The vector space of all k-covariant, l-contravariant tensors on $T_{p}M$ is denoted by $T_l^k(T_{p}M)$. So, each element of $T_l^k(T_{p}M)$ is a multilinear map of the form

$$F:\underset{l\mathrm{copies}}{\underbrace{T_p^{*}M\times \cdots \times T_p^{*}M}}\times \underset{k\mathrm{copies}}{\underbrace{T_{p}M\times \cdots \times T_{p}M}}\to \mathbb{R}.$$

We are primarily interested in the vector bundle of $\left(\genfrac{}{}{0pt}{}{k}{l}\right)$-tensors on M whose total space is

$$T_l^k(M)=\underset{p\in M}{⨆}{T}_l^k(T_{p}M).$$

A section of this bundle is called a $\left(\genfrac{}{}{0pt}{}{k}{l}\right)$-tensor field. We set $T^{k}M:=T_0^k(M)$. $TM$ denotes the tangent bundle of M and $T^{*}M$ is the cotangent bundle of M. We set

$${\tau }_l^k(M)=C^{\infty }(M,T_l^k(M))=\mathrm{collection} \mathrm{of} \mathrm{smooth} \left(\genfrac{}{}{0pt}{}{k}{l}\right)\text{-}\mathrm{tensor} \mathrm{fields} \mathrm{on} M$$

and

$$\chi (M)=C^{\infty }(M,TM)=\mathrm{the}\mathrm{collection}\mathrm{of}\mathrm{smooth}\mathrm{vector}\mathrm{fields}\mathrm{on}M.$$

A symmetric positive definite section of $T^{2}M$ is called a Riemannian metric on M. If M is equipped with a Riemannian metric g, the combination $(M,g)$ will be referred to as a Riemannian manifold. If there is no possibility of confusion, we may write $⟨X,Y⟩$ instead of $g(X,Y)$. The norm induced by g on each tangent space will be denoted by ${\parallel .\parallel }_g$. We say that g is smooth (or the Riemannian manifold is smooth) if $g\in C^{\infty }(M,T^{2}M)$.

d denotes the exterior derivative and $\mathrm{grad}:C^{\infty }(M)\to C^{\infty }(M,TM)$ denotes the gradient operator which is defined by $g(\mathrm{grad}f,X)=df(X)$ for all $f\in C^{\infty }(M)$ and $X\in C^{\infty }(M,TM)$.

Given a metric g on M, one can define the musical isomorphisms as follows:

$$\begin{array}{cc}\hfill {\mathrm{flat}}_g:T_{p}M& \to T_p^{*}M\hfill \\ \hfill X& \mapsto X^{♭}:=g(X,·),\hfill \\ \hfill {\mathrm{sharp}}_g:T_p^{*}M& \to T_{p}M\hfill \\ \hfill \psi & \mapsto {\psi }^{♯}:={\mathrm{flat}}_g^{-1}(\psi ).\hfill \end{array}$$

Using ${\mathrm{sharp}}_g$ we can define the $\left(\genfrac{}{}{0pt}{}{0}{2}\right)$-tensor field $g^{-1}$ (which is called the inverse metric tensor) as follows

$$g^{-1}({\psi }_1,{\psi }_2):=g({\mathrm{sharp}}_g({\psi }_1),{\mathrm{sharp}}_g({\psi }_2)).$$

Let $\{E_i\}$ be a local frame on an open subset $U\subset M$ and $\{{\eta }^i\}$ be the corresponding dual coframe. So we can write $X=X^i{E}_i$ and $\psi ={\psi }_i{\eta }^i$. It is standard practice to denote the ith component of ${\mathrm{flat}}_{g}X$ by $X_i$ and the ith component of ${\mathrm{sharp}}_g(\psi )$ by ${\psi }^i$:

$${\mathrm{flat}}_{g}X=X_i{\eta }^i,{\mathrm{sharp}}_g\psi ={\psi }^i{E}_i.$$

It is easy to show that

$$X_i=g_{ij}{X}^j,{\psi }^i=g^{ij}{\psi }_j,$$

where $g_{ij}=g(E_i,E_j)$ and $g^{ij}=g^{-1}({\eta }^i,{\eta }^j)$. It is said that ${\mathrm{flat}}_{g}X$ is obtained from X by lowering an index and ${\mathrm{sharp}}_g\psi$ is obtained from $\psi$ by raising an index.

3. Review of Some Results from Linear Algebra

In this section, we summarize a collection of definitions and results from linear algebra that play an important role in our study of function spaces and differential operators on manifolds.

There are several ways to construct new vector spaces from old ones: subspaces, products, direct sums, quotients, etc. The ones that are particularly important for the study of Sobolev spaces of sections of vector bundles are the vector space of linear maps between two given vector spaces, the tensor product of vector spaces, and the vector space of all densities on a given vector space which we briefly review here in order to set the notation straight.

• Let V and W be two vector spaces. The collection of all linear maps from V to W is a new vector space which we denote by $\mathrm{Hom}(V,W)$. In particular, $\mathrm{Hom}(V,\mathbb{R})$ is the (algebraic) dual of V. If V and W are finite-dimensional, then $\mathrm{Hom}(V,W)$ is a vector space whose dimension is equal to the product of dimensions of V and W. Indeed, if we choose a basis for V and a basis for W, then $\mathrm{Hom}(V,W)$ is isomorphic with the space of matrices with $\dim W$ rows and $\dim V$ columns.
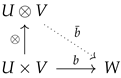
• Let U and V be two vector spaces. Roughly speaking, the tensor product of U and V (denoted by $U\otimes V$) is the unique vector space (up to isomorphism of vector spaces) such that for any vector space W, $\mathrm{Hom}(U\otimes V,W)$ is isomorphic to the collection of bilinear maps from $U\times V$ to W. Informally, $U\otimes V$ consists of finite linear combinations of symbols $u\otimes v$, where $u\in U$ and $v\in V$. It is assumed that these symbols satisfy the following identities:

  $$\begin{array}{cc}\hfill & (u_1+u_2)\otimes v-u_1\otimes v-u_2\otimes v=0,\hfill \\ \hfill & u\otimes (v_1+v_2)-u\otimes v_1-u\otimes v_2=0,\hfill \\ \hfill & \alpha (u\otimes v)-(\alpha u)\otimes v=0,\hfill \\ \hfill & \alpha (u\otimes v)-u\otimes (\alpha v)=0,\hfill \end{array}$$

  for all $u,u_1,u_2\in U$, $v,v_1,v_2\in V$ and $\alpha \in \mathbb{R}$. These identities simply say that the map

  $$\otimes :U\times V\to U\otimes V,(u,v)\mapsto u\otimes v,$$

  is a bilinear map. The image of this map spans $U\otimes V$.
  Definition 1.

  Let U and V be two vector spaces. Tensor product is a vector space $U\otimes V$ together with a bilinear map $\otimes :U\times V\to U\otimes V,(u,v)\mapsto u\otimes v$ such that given any vector space W and any bilinear map $b:U\times V\to W$, there is a unique linear map $\overline{b}:U\otimes V\to W$ with $\overline{b}(u\otimes v)=b(u,v)$. That is, the following diagram commutes:

  

  For us, the most useful property of the tensor product of finite dimensional vector spaces is the following property:

  $$\mathrm{Hom}(V,W)\cong V^{*}\otimes W.$$

  Indeed, the following map is an isomorphism of vector spaces:

  $$F:V^{*}\otimes W\to \mathrm{Hom}(V,W),\underset{\mathrm{an}\mathrm{element}\mathrm{of}\mathrm{Hom}(V,W)}{\underbrace{F(v^{*}\otimes w)}}(v)=\underset{a\mathrm{real}\mathrm{number}}{\underbrace{[v^{*}(v)]}}w.$$

  It is useful to obtain an expression for the inverse of F too. That is, given $T\in \mathrm{Hom}(V,W)$, we want to find an expression for the corresponding element of $V^{*}\otimes W$. To this end, let ${\{e_i\}}_{1\le i\le n}$ be a basis for V and ${\{e^i\}}_{1\le i\le n}$ denote the corresponding dual basis. Let ${\{s_a\}}_{1\le a\le r}$ be a basis for W. Then $\{e^i\otimes s_b\}$ is a basis for $V^{*}\otimes W$. Suppose ${\sum }_{i,a}{R}_i^a{e}^i\otimes s_a$ is the element of $V^{*}\otimes W$ that corresponds to T. We have

  $$\begin{array}{cc}\hfill F(\sum _{i,a}{R}_i^a{e}^i\otimes s_a)=T& ⟹\forall u\in V\sum _{i,a}{R}_i^{a}F[e^i\otimes s_a](u)=T(u)\hfill \\ \hfill & ⟹\forall u\in V\sum _{i,a}{R}_i^a{e}^i(u)s_a=T(u).\hfill \end{array}$$

  In particular, for all $1\le j\le n$,

  $$T(e_j)=\sum _{i,a}{R}_i^a\underset{{\delta }_j^i}{\underbrace{e^i(e_j)}}{s}_a=\sum _a{R}_j^a{s}_a.$$

  That is, $R_i^a$ is the entry in the ath row and ith column of the matrix of the linear transformation T.
• Let V be an n-dimensional vector space. A density on V is a function $\mu :\underset{n\mathrm{copies}}{\underbrace{V\times \dots \times V}}\to \mathbb{R}$ with the property that

  $$\mu (T{v}_1,\dots ,T{v}_n)=|\det T|\mu (v_1,\dots ,v_n),$$

  for all $T\in \mathrm{Hom}(V,V)$.
  We denote the collection of all densities on V by $\mathcal{D}(V)$. It can be shown that $\mathcal{D}(V)$ is a one dimensional vector space under the obvious vector space operations. Indeed, if $(e_1,\dots ,e_n)$ is a basis for V, then each element $\mu \in \mathcal{D}(V)$ is uniquely determined by its value at $(e_1,\dots ,e_n)$ because for any $(v_1,\dots ,v_n)\in V^{\times n}$, we have $\mu (v_1,\dots ,v_n)=|\det T|\mu (e_1,\dots ,e_n)$ where $T:V\to V$ is the linear transformation defined by $T(e_i)=v_i$ for all $1\le i\le n$. Thus

  $$F:\mathcal{D}(V)\to \mathbb{R},F(\mu )=\mu (e_1,\dots ,e_n),$$

  will be an isomorphism of vector spaces.
  Moreover, if $\omega \in {\Lambda }^n(V)$ where ${\Lambda }^n(V)$ is the collection of all alternating covariant n-tensors, then $|\omega |$ belongs to $\mathcal{D}(V)$. Thus, if $\omega$ is any nonzero element of ${\Lambda }^n(V)$, then $\{|\omega |\}$ will be a basis for $\mathcal{D}(V)$ ([19], p. 428).

4. Review of Some Results from Analysis and Topology

4.1. Euclidean Space

Let $\Omega$ be a nonempty open set in ${\mathbb{R}}^n$ and $m\in {\mathbb{N}}_0$. Here is a list of several useful function spaces on $\Omega$:

$$\begin{array}{l}C(\Omega )=\{f:\Omega \to \mathbb{R}:f\mathrm{is}\mathrm{continuous}\}\hfill \\ C^m(\Omega )=\{f:\Omega \to \mathbb{R}:\forall |\alpha |\le m{\partial }^{\alpha }f\in C(\Omega )\}(C^0(\Omega )=C(\Omega ))\hfill \\ BC(\Omega )=\{f:\Omega \to \mathbb{R}:f\mathrm{is}\mathrm{continuous}\mathrm{and}\mathrm{bounded}\mathrm{on}\Omega \}\hfill \\ B{C}^m(\Omega )=\{f\in C^m(\Omega ):\forall |\alpha |\le m{\partial }^{\alpha }f\mathrm{is}\mathrm{bounded}\mathrm{on}\Omega \}\hfill \\ BC(\overline{\Omega })=\{f:\Omega \to \mathbb{R}:f\in \mathit{BC}(\Omega )\mathrm{and}f\mathrm{is}\mathrm{uniformly}\mathrm{continuous}\mathrm{on}\Omega \}\hfill \\ B{C}^m(\overline{\Omega })=\{f:\Omega \to \mathbb{R}:f\in {\mathit{BC}}^m(\Omega ),\forall |\alpha |\le m{\partial }^{\alpha }f\mathrm{is}\mathrm{uniformly}\mathrm{continuous}\mathrm{on}\Omega \}\hfill \\ C^{\infty }(\Omega )=\bigcap _{m\in {\mathbb{N}}_0}{C}^m(\Omega ),B{C}^{\infty }(\Omega )=\bigcap _{m\in {\mathbb{N}}_0}B{C}^m(\Omega ),B{C}^{\infty }(\overline{\Omega })=\bigcap _{m\in {\mathbb{N}}_0}B{C}^m(\overline{\Omega })\hfill \end{array}$$

Remark 1

([1]). If $g:\Omega \to \mathbb{R}$ is in $BC(\overline{\Omega })$, then it possesses a unique, bounded, continuous extension to the closure $\overline{\Omega }$ of Ω.

Notation: 

Let $\Omega$ be a nonempty open set in ${\mathbb{R}}^n$. The collection of all compact sets in $\Omega$ is denoted by $\mathcal{K}(\Omega )$. If $f:\Omega \to \mathbb{R}$ is a function, the support of f is denoted by $\mathrm{supp}f$. Notice that, in some references $\mathrm{supp}f$ is defined as the closure of $\{x\in \Omega :f(x)\ne 0\}$ in $\Omega$, while in certain other references it is defined as the closure of $\{x\in \Omega :f(x)\ne 0\}$ in ${\mathbb{R}}^n$. Of course, if we are concerned with functions whose support is inside an element of $\mathcal{K}(\Omega )$, then the two definitions agree. For the sake of definiteness, in this manuscript we always use the former interpretation of support. Furthermore, support of a distribution will be discussed in Section 6.

Remark 2.

If $\mathcal{F}(\Omega )$ is any function space on Ω and $K\in \mathcal{K}(\Omega )$, then ${\mathcal{F}}_K(\Omega )$ denotes the collection of elements in $\mathcal{F}(\Omega )$ whose support is inside K. Furthermore,

$${\mathcal{F}}_c(\Omega )={\mathcal{F}}_{comp}(\Omega )=\bigcup _{K\in \mathcal{K}(\Omega )}{\mathcal{F}}_K(\Omega ).$$

Let $0<\lambda \le 1$. A function $F:\Omega \subseteq {\mathbb{R}}^n\to {\mathbb{R}}^k$ is called λ-Holder continuous if there exists a constant L such that

$$|F(x)-F(y)|\le {L|x-y|}^{\lambda }\forall x,y\in \Omega .$$

Clearly, a $\lambda$-Holder continuous function on $\Omega$ is uniformly continuous on $\Omega$. 1-Holder continuous functions are also called Lipschitz continuous functions or simply Lipschitz functions. We define

$$\begin{array}{cc}\hfill B{C}^{m,\lambda }(\Omega )& =\{f:\Omega \to \mathbb{R}:\forall |\alpha |\le m{\partial }^{\alpha }f\mathrm{is}\lambda -\mathrm{Holder}\mathrm{continuous}\mathrm{and}\mathrm{bounded}\}\hfill \\ \hfill & =\{f\in B{C}^m(\Omega ):\forall |\alpha |\le m{\partial }^{\alpha }f\mathrm{is}\lambda -\mathrm{Holder}\mathrm{continuous}\}\hfill \\ \hfill & =\{f\in B{C}^m(\overline{\Omega }):\forall |\alpha |\le m{\partial }^{\alpha }f\mathrm{is}\lambda -\mathrm{Holder}\mathrm{continuous}\}\hfill \end{array}$$

and $B{C}^{\infty ,\lambda }(\Omega ):={\bigcap }_{m\in {\mathbb{N}}_0}B{C}^{m,\lambda }(\Omega )$.

Remark 3.

Let $F:\Omega \subseteq {\mathbb{R}}^n\to {\mathbb{R}}^k$ ($F=(F^1,\cdots ,F^k)$). Then

$$\begin{array}{c}\hfill F \mathit{is} \mathit{Lipschitz}⟺\forall 1\le i\le k{F}^i \mathit{is} \mathit{Lipschitz}.\end{array}$$

Indeed, for each i

$$|F^i(x)-F^i(y)|\le \sqrt{\sum _{j=1}^k{|F^j(x)-F^j(y)|}^2}=|F(x)-F(y)|\le L|x-y|,$$

which shows that if F is Lipschitz so will be its components. Furthermore, if for each i, there exists $L_i$ such that

$$|F^i(x)-F^i(y)|\le L_i|x-y|,$$

then

$$\sum _{j=1}^k|F^j(x)-F^j{(y)|}^2\le n{L}^2{|x-y|}^2,$$

where $L=max\{L_1,\cdots ,L_k\}$. This proves that if each component of F is Lipschitz so is F itself.

Theorem 1

([20]). Let Ω be a nonempty open set in ${\mathbb{R}}^n$ and let $K\in \mathcal{K}(\Omega )$. There is a function $\psi \in C_c^{\infty }(\Omega )$ taking values in $[0,1]$ such that $\psi =1$ on a neighborhood of K.

Theorem 2

(Exhaustion by Compact Sets [20]). Let Ω be a nonempty open subset of ${\mathbb{R}}^n$. There exists a sequence of compact subsets ${(K_j)}_{j\in \mathbb{N}}$ such that ${\cup }_{j\in \mathbb{N}}{\mathring{K}}_j=\Omega$ and

$$K_1\subseteq {\mathring{K}}_2\subseteq K_2\subseteq \cdots \subseteq {\mathring{K}}_j\subseteq K_j\subseteq \cdots .$$

Moreover, as a direct consequence, if K is any compact subset of the open set Ω, then there exists an open set V such that $K\subseteq V\subseteq \overline{V}\subseteq \Omega$.

Theorem 3

([20]). Let Ω be a nonempty open subset of ${\mathbb{R}}^n$. Let ${\{K_j\}}_{j\in \mathbb{N}}$ be an exhaustion of Ω by compact sets. Define

$$V_0={\mathring{K}}_4,\forall j\in \mathbb{N}{V}_j={\mathring{K}}_{j+4}\setminus K_j.$$

Then

(1) 

Each $V_j$ is an open bounded set and $\Omega ={\cup }_j{V}_j$;

(2) 

The cover ${\{V_j\}}_{j\in {\mathbb{N}}_0}$ is locally finite in Ω, that is, each compact subset of Ω has nonempty intersection with only a finite number of the $V_j$’s;

(3) 

There is a family of functions ${\psi }_j\in C_c^{\infty }(\Omega )$ taking values in $[0,1]$ such that $\mathit{supp}{\psi }_j\subseteq V_j$ and

$$\sum _{j\in {\mathbb{N}}_0}{\psi }_j(x)=1\mathit{for} \mathit{all}x\in \Omega .$$

Theorem 4

([21], p. 74). Suppose Ω is an open set in ${\mathbb{R}}^n$ and $G:\Omega \to G(\Omega )\subseteq {\mathbb{R}}^n$ is a $C^1$-diffeomorphism (i.e., G and $G^{-1}$ are both $C^1$ maps). If f is a Lebesgue measurable function on $G(\Omega )$, then $f\circ G$ is Lebesgue measurable on Ω. If $f\ge 0$ or $f\in L^1(G(\Omega ))$, then

$${\int }_{G(\Omega )}f(x)dx={\int }_{\Omega }f\circ G(x)|\det G^{\prime }(x)|dx.$$

Theorem 5

([21], p. 79). If f is a nonnegative measurable function on ${\mathbb{R}}^n$ such that $f(x)=g(|x|)$ for some function g on $(0,\infty )$, then

$$\int f(x)dx=\sigma (S^{n-1}){\int }_0^{\infty }g(r)r^{n-1}dr,$$

where $\sigma (S^{n-1})$ is the surface area of $(n-1)$-sphere.

Theorem 6

([22], Section 12.11). Suppose U is an open set in ${\mathbb{R}}^n$ and $f:U\to \mathbb{R}$ is differentiable. Let x and y be two points in U and suppose the line segment joining x and y is contained in U. Then there exists a point z on the line joining x to y such that

$$f(y)-f(x)=\nabla f(z).(y-x).$$

As a consequence, if U is convex and all first order partial derivatives of f are bounded, then f is Lipschitz on U.

Warning: 

Suppose $f\in B{C}^{\infty }(U)$. By the above item, if U is convex, then f is Lipschitz. However, if U is not convex, then f is not necessarily Lipschitz. For example, let $U={\cup }_{n=0}^{\infty }(n,n+1)$ and define

$$f:U\to \mathbb{R},f(x)={(-1)}^n,\forall x\in (n,n+1).$$

Clearly, all derivatives of U are equal to zero, so $f\in B{C}^{\infty }(U)$. However, f is not uniformly continuous and thus it is not Lipschitz. Indeed, for any $1>\delta >0$, we can let $x=2-\delta /4$ and $y=2+\delta /4$. Clearly $|x-y|<\delta$, however, $|f(x)-f(y)|=2$.

Of course, if $f\in C_c^1(U)$, then f can be extended by zero to a function in $C_c^1({\mathbb{R}}^n)$. Since ${\mathbb{R}}^n$ is convex, we may conclude that the extension by zero of f is Lipschitz which implies that $f:U\to \mathbb{R}$ is Lipschitz. As a consequence, $C_c^1(U)\subseteq B{C}^{0,1}(U)$ and $C_c^{\infty }(U)\subseteq B{C}^{\infty ,1}(U)$. Furthermore, Theorem 60 and the following theorem provide useful information regarding this issue.

Theorem 7.

Let $U\subseteq {\mathbb{R}}^n$ and $V\subseteq {\mathbb{R}}^k$ be two nonempty open sets and let $T:U\to V$ $(T=(T^1,\dots ,T^k))$ be a $C^1$ map (that is, for each $1\le i\le k$, $T^i\in C^1(U)$). Suppose $B\subseteq U$ is a bounded set such that $B\subseteq \overline{B}\subseteq U$. Then $T:B\to V$ is Lipschitz.

Proof. 

By Remark 3 it is enough to show that each $T^i$ is Lipschitz on B. Fix a function $\phi \in C_c^{\infty }({\mathbb{R}}^n)$ such that $\phi =1$ on $\overline{B}$ and $\phi =0$ on ${\mathbb{R}}^n\setminus U$. Then $\phi T^i$ can be viewed as an element of $C_c^1({\mathbb{R}}^n)$. Therefore, it is Lipschitz (${\mathbb{R}}^n$ is convex) and there exists a constant L, which may depend on $\phi$, B and $T^i$, such that

$$|\phi T^i(x)-\phi T^i(y)|\le L|x-y|\forall x,y\in {\mathbb{R}}^n.$$

Since $\phi =1$ on $\overline{B}$, it follows that

$$|T^i(x)-T^i(y)|\le L|x-y|\forall x,y\in B.$$

□

4.2. Normed Spaces

Theorem 8.

Let X and Y be normed spaces. Let A be a dense subspace of X and B be a dense subspace of Y. Then

• $A\times B$ is dense in $X\times Y$;
• If $T:A\times B\to \mathbb{R}$ is a continuous bilinear map, then T has a unique extension to a continuous bilinear operator $\tilde{T}:X\times Y\to \mathbb{R}$.

Theorem 9

([1]). Let X be a normed space and let M be a closed vector subspace of X.

(1) 

If X is reflexive, then X is a Banach space.

(2) 

X is reflexive if and only if $X^{*}$ is reflexive.

(3) 

If $X^{*}$ is separable, then X is separable.

(4) 

If X is reflexive and separable, then so is $X^{*}$.

(5) 

If X is a reflexive Banach space, then so is M.

(6) 

If X is a separable Banach space, then so is M.

Moreover, if $X_1,\dots ,X_r$ are reflexive Banach spaces, then $X_1\times \dots \times X_r$ equipped with the norm

$$\parallel (x_1,\dots ,x_r)\parallel =\parallel x_1{\parallel }_{X_1}+\dots +{\parallel x_r\parallel }_{X_r}$$

is also a reflexive Banach space.

4.3. Topological Vector Spaces

There are different, generally nonequivalent, ways to define topological vector spaces. The conventions in this section mainly follow Rudin’s functional analysis [23]. Statements in this section are either taken from Rudin’s functional analysis, Grubb’s distributions and operators [20], excellent presentation of Reus [24], and Treves’ topological vector spaces [25] or are direct consequences of statements in the aforementioned references. Therefore we will not give the proofs.

Definition 2.

A topological vector space is a vector space X together with a topology τ with the following properties:

(i) 

For all $x\in X$, the singleton $\{x\}$ is a closed set.

(ii) 

The maps

$$\begin{array}{cc}\hfill & (x,y)\mapsto x+y(\mathit{from}X\times X\mathit{into}X),\hfill \\ \hfill & (\lambda ,x)\mapsto \lambda x(\mathit{from}\mathbb{R}\times X\mathit{into}X),\hfill \end{array}$$

are continuous where $X\times X$ and $\mathbb{R}\times X$ are equipped with the product topology.

Definition 3.

Suppose $(X,\tau )$ is a topological vector space and $Y\subseteq X$.

• Y is said to be convex if for all $y_1,y_2\in Y$ and $t\in (0,1)$ it is true that $t{y}_1+(1-t)y_2\in Y$.
• Y is said to be balanced if for all $y\in Y$ and $|\lambda |\le 1$ it holds that $\lambda y\in Y$. In particular, any balanced set contains the origin.
• We say Y is bounded if for any neighborhood U of the origin (i.e., any open set containing the origin), there exits $t>0$ such that $Y\subseteq tU$.

Theorem 10

(Important Properties of Topological Vector Spaces).

• Every topological vector space is Hausdorff.
• If $(X,\tau )$ is a topological vector space, then

  (1) 

  For all $a\in X$: $E\in \tau ⟺a+E\in \tau$ (that is, τ is translation invariant);

  (2) 

  For all $\lambda \in \mathbb{R}\setminus \{0\}$: $E\in \tau ⟺\lambda E\in \tau$ (that is, τ is scale invariant);

  (3) 

  If $A\subseteq X$ is convex and $x\in X$, then so is $A+x$;

  (4) 

  If ${\{A_i\}}_{i\in I}$ is a family of convex subsets of X, then ${\cap }_{i\in I}{A}_i$ is convex.

Note: 

Some authors do not include condition (i) in the definition of topological vector spaces. In that case, a topological vector space will not necessarily be Hausdorff.

Definition 4.

Let $(X,\tau )$ be a topological space.

• A collection $\mathcal{B}\subseteq \tau$ is said to be a basis for τ, if every element of τ is a union of elements in $\mathcal{B}$.
• Let $p\in X$. If $\gamma \subseteq \tau$ is such that each element of γ contains p and every neighborhood of p (i.e., every open set containing p) contains at least one element of γ, then we say γ is a local base at p . If X is a vector space, then the local base γ is said to be convex if each element of γ is a convex set.
• $(X,\tau )$ is called first-countable if each point has a countable local base.
• $(X,\tau )$ is called second-countable if there is a countable basis for τ.

Theorem 11.

Let $(X,\tau )$ be a topological space and suppose for all $x\in X$, ${\gamma }_x$ is a local base at x. Then $\mathcal{B}={\cup }_{x\in X}{\gamma }_x$ is a basis for τ.

Theorem 12.

Let X be a vector space and suppose τ is a translation invariant topology on X. Then for all $x_1,x_2\in X$, the collection ${\gamma }_{x_1}$ is a local base at $x_1$ if and only if the collection ${\{A+(x_2-x_1)\}}_{A\in {\gamma }_{x_1}}$ is a local base at $x_2$.

Remark 4.

Let X be a vector space and suppose τ is a translation invariant topology on X. As a direct consequence of the previous theorems the topology τ is uniquely determined by giving a local base ${\gamma }_{x_0}$ at some point $x_0\in X$.

Definition 5.

Let $(X,\tau )$ be a topological vector space. X is said to be metrizable if there exists a metric $d:X\times X\to [0,\infty )$ whose induced topology is τ. In this case we say that the metric d is compatible with the topology τ.

Theorem 13.

Let $(X,\tau )$ be a topological vector space.

• X is metrizable $⟺$ there exists a metric d on X such that for all $x\in X$, ${\{B(x,\frac{1}{n})\}}_{n\in \mathbb{N}}$ is a local base at x.
• A metric d on X is compatible with τ$⟺$ for all $x\in X$, ${\{B(x,\frac{1}{n})\}}_{n\in \mathbb{N}}$ is a local base at x. ($B(x,\frac{1}{n})$ is the open ball of radius $\frac{1}{n}$ centered at x).

Definition 6.

Let X be a vector space and d be a metric on X. d is said to be translation invariant provided that

$$\forall x,y,a\in Xd(x+a,y+a)=d(x,y).$$

Remark 5.

Let $(X,\tau )$ be a topological vector space and suppose d is a translation invariant metric on X. Then the following statements are equivalent:

(1) 

For all $x\in X$, ${\{B(x,\frac{1}{n})\}}_{n\in \mathbb{N}}$ is a local base at x.

(2) 

There exists $x_0\in X$ such that ${\{B(x_0,\frac{1}{n})\}}_{n\in \mathbb{N}}$ is a local base at $x_0$.

Therefore, d is compatible with τ if and only if ${\{B(0,\frac{1}{n})\}}_{n\in \mathbb{N}}$ is a local base at the origin.

Theorem 14.

Let $(X,\tau )$ be a topological vector space. Then $(X,\tau )$ is metrizable if and only if it has a countable local base at the origin. Moreover, if $(X,\tau )$ is metrizable, then one can find a translation invariant metric that is compatible with τ.

Definition 7.

Let $(X,\tau )$ be a topological vector space and let $\{x_n\}$ be a sequence in X.

• We say that $\{x_n\}$ converges to a point $x\in X$ provided that

  $$\forall U\in \tau ,x\in U\exists N\forall n\ge N{x}_n\in U.$$
• We say that $\{x_n\}$ is a Cauchy sequence provided that

  $$\forall U\in \tau ,0\in U\exists N\forall m,n\ge N{x}_n-x_m\in U.$$

Theorem 15.

Let $(X,\tau )$ be a topological vector space, $\{x_n\}$ be a sequence in X, and $x,y\in X$. Additionally, suppose γ is a local base at the origin. The following statements are equivalent:

(1) 

$x_n\to x$;

(2) 

$(x_n-x)\to 0$;

(3) 

$x_n+y\to x+y$;

(4) 

$\forall V\in \gamma \exists N\forall n\ge N{x}_n-x\in V$.

Moreover, $\{x_n\}$ is a Cauchy sequence if and only if

$$\forall V\in \gamma \exists N\forall n,m\ge N{x}_n-x_m\in V.$$

Remark 6.

In contrast with properties like continuity of a function and convergence of a sequence which depend only on the topology of the space, the property of being a Cauchy sequence is not a topological property. Indeed, it is easy to construct examples of two metrics $d_1$ and $d_2$ on a vector space X that induce the same topology (i.e., the metrics are equivalent) but have different collection of Cauchy sequences. However, it can be shown that if $d_1$ and $d_2$ are two translation invariant metrics that induce the same topology on X, then the Cauchy sequences of $(X,d_1)$ will be exactly the same as the Cauchy sequences of $(X,d_2)$.

Theorem 16.

Let $(X,\tau )$ be a metrizable topological vector space and d be a translation invariant metric on X that is compatible with τ. Let $\{x_n\}$ be a sequence in X. The following statements are equivalent:

(1) 

$\{x_n\}$ is a Cauchy sequence in the topological vector space $(X,\tau )$.

(2) 

$\{x_n\}$ is a Cauchy sequence in the metric space $(X,d)$.

Definition 8.

Let $(X,\tau )$ be a topological vector space. We say $(X,\tau )$ is locally convex if it has a convex local base at the origin.

Note that, as a consequence of Theorems 10 and 12, the following statements are equivalent:

(1)

$(X,\tau )$ is a locally convex topological vector space.

(2)

There exists $p\in X$ with a convex local base at p.

(3)

For every $p\in X$ there exists a convex local base at p.

Definition 9.

Let $(X,\tau )$ be a metrizable locally convex topological vector space. Let d be a translation invariant metric on X that is compatible with τ. We say that X is complete if and only if the metric space $(X,d)$ is a complete metric space. A complete metrizable locally convex topological vector space is called a Frechet space.

Remark 7.

Our previous remark about Cauchy sequences shows that the above definition of completeness is independent of the chosen translation invariant metric d. Indeed one can show that the locally convex topological vector space $(X,\tau )$ is complete in the above sense if and only if every Cauchy net in $(X,\tau )$ is convergent.

Theorem 17

([26], p. 63). A linear continuous bijective mapping of a Frechet space X onto a Frechet space Y has a continuous linear inverse.

Definition 10.

A seminorm on a vector space X is a real-valued function $p:X\to \mathbb{R}$ such that

(i) 

$\forall x,y\in Xp(x+y)\le p(x)+p(y)$

(ii) 

$\forall x\in X\forall \alpha \in \mathbb{R}p(\alpha x)=|\alpha |p(x)$

If $\mathcal{P}$ is a family of seminorms on X, then we say $\mathcal{P}$ is separating provided that for all $x\ne 0$ there exists at least one $p\in \mathcal{P}$ such that $p(x)\ne 0$ (that is, if $p(x)=0$ for all $p\in \mathcal{P}$, then $x=0$).

Remark 8.

It follows from conditions (i) and (ii) that if $p:X\to \mathbb{R}$ is a seminorm, then $p(x)\ge 0$ for all $x\in X$.

Theorem 18.

Suppose $\mathcal{P}$ is a separating family of seminorms on a vector space X. For all $p\in \mathcal{P}$ and $n\in \mathbb{N}$ let

$$V(p,n):=\{x\in X:p(x)<\frac{1}{n}\}.$$

Furthermore, let γ be the collection of all finite intersections of $V(p,n)$’s. That is,

$$A\in \gamma ⟺\exists k\in \mathbb{N},\exists p_1,\dots ,p_k\in \mathcal{P},\exists n_1,\dots ,n_k\in \mathbb{N}\mathit{such} \mathit{that}A={\cap }_{i=1}^{k}V(p_i,n_i)$$

Then each element of γ is a convex balanced subset of X. Moreover, there exists a unique topology τ on X that satisfies both of the following properties:

(1) 

τ is translation invariant (that is, if $U\in \tau$ and $a\in X$, then $a+U\in \tau$).

(2) 

γ is a local base at the origin for τ.

This unique topology is called the natural topology induced by the family of seminorms $\mathcal{P}$. Furthermore, if X is equipped with the natural topology τ, then

(i) 

$(X,\tau )$ is a locally convex topological vector space,

(ii) 

every $p\in \mathcal{P}$ is a continuous function from X to $\mathbb{R}$.

Theorem 19.

Suppose $\mathcal{P}$ is a separating family of seminorms on a vector space X. Let τ be the natural topology induced by $\mathcal{P}$. Then

(1) 

τ is the smallest topology on X that is translation invariant and with respect to which every $p\in \mathcal{P}$ is continuous,

(2) 

τ is the smallest topology on X with respect to which addition is continuous and every $p\in \mathcal{P}$ is continuous.

Theorem 20.

Let X and Y be two vector spaces and suppose $\mathcal{P}$ and $\mathcal{Q}$ are two separating families of seminorms on X and Y, respectively. Equip X and Y with the corresponding natural topologies.

(1) 

A sequence $x_n$ converges to x in X if and only if for all $p\in \mathcal{P}$, $p(x_n-x)\to 0$.

(2) 

A linear operator $T:X\to Y$ is continuous if and only if

$$\forall q\in \mathcal{Q}\exists c>0,k\in \mathbb{N},p_1,\dots ,p_k\in \mathcal{P}\mathit{such} \mathit{that}\forall x\in X|q\circ T(x)|\le c\underset{1\le i\le k}{max}{p}_i(x).$$

(3) 

A linear operator $T:X\to \mathbb{R}$ is continuous if and only if

$$\exists c>0,k\in \mathbb{N},p_1,\dots ,p_k\in \mathcal{P}\mathit{such} \mathit{that}\forall x\in X|T(x)|\le c\underset{1\le i\le k}{max}{p}_i(x).$$

Theorem 21.

Let X be a Frechet space and let Y be a topological vector space. When T is a linear map of X into Y, the following two properties are equivalent:

(1) 

T is continuous.

(2) 

$x_n\to 0$ in X⟹$T{x}_n\to 0$ in Y.

Theorem 22.

Let $\mathcal{P}={\{p_k\}}_{k\in \mathbb{N}}$ be a countable separating family of seminorms on a vector space X. Let τ be the corresponding natural topology. Then the locally convex topological vector space $(X,\tau )$ is metrizable and the following translation invariant metric on X is compatible with τ:

$$d(x,y)=\sum _{k=1}^{\infty }\frac{1}{2^k}\frac{p_k(x-y)}{1+p_k(x-y)}.$$

Let $(X,\tau )$ be a locally convex topological vector space. Consider the topological dual of X,

$$X^{*}:=\{f:X\to \mathbb{R}:f \mathrm{is} \mathrm{linear} \mathrm{and} \mathrm{continuous}\}.$$

There are several ways to topologize $X^{*}$: the weak${}^{*}$ topology, the topology of convex compact convergence, the topology of compact convergence, and the strong topology (see [25], Chapter 19). Here we describe the weak${}^{*}$ topology and the strong topology on $X^{*}$.

Definition 11.

Let $(X,\tau )$ be a locally convex topological vector space.

• The weak${}^{*}$ topology on $X^{*}$ is the natural topology induced by the separating family of seminorms ${\{p_x\}}_{x\in X}$ where

  $$\forall x\in X{p}_x:X^{*}\to \mathbb{R},p_x(f):=|f(x)|.$$

  A sequence $\{f_m\}$ converges to f in $X^{*}$ with respect to the weak${}^{*}$ topology if and only if $f_m(x)\to f(x)$ in $\mathbb{R}$ for all $x\in X$.
• The strong topology on $X^{*}$ is the natural topology induced by the separating family of seminorms ${\{p_B\}}_{B\subseteq X\mathit{bounded}}$ where for any bounded subset B of X

  $$p_B:X^{*}\to \mathbb{R}{p}_B(f):=sup\{|f(x)|:x\in B\}.$$

  (It can be shown that for any bounded subset B of X and $f\in X^{*}$, $f(B)$ is a bounded subset of $\mathbb{R}$.)

Remark 9.

(1) 

If X is a normed space, then the topology induced by the norm

$$\forall f\in X^{*}{\parallel f\parallel }_{op}=\underset{{\parallel x\parallel }_X=1}{sup}|f(x)|$$

on $X^{*}$ is the same as the strong topology on $X^{*}$ ([25], p. 198).

(2) 

In this manuscript, we always consider the topological dual of a locally convex topological vector space with the strong topology. Of course, it is worth mentioning that for many of the spaces that we will consider (including $X=\mathcal{E}(\Omega )$ or $X=D(\Omega )$ where Ω is an open subset of ${\mathbb{R}}^n$) a sequence in $X^{*}$ converges with respect to the weak${}^{*}$ topology if and only if it converges with respect to the strong topology (for more details on this see the definition and properties of Montel spaces in Section 34.4, page 356 of [25]).

The following theorem, which is easy to prove, will later be used in the proof of completeness of Sobolev spaces of sections of vector bundles.

Theorem 23

([24], p. 160). If X and Y are topological vector spaces and $I:X\to Y$ and $P:Y\to X$ are continuous linear maps such that $P\circ I=i{d}_X$, then $I:X\to I(X)\subseteq Y$ is a linear topological isomorphism and $I(X)$ is closed in Y.

Now we briefly review the relationship between the dual of a product of topological vector spaces and the product of the dual spaces. This will play an important role in our discussion of local representations of distributions in vector bundles in later sections.

Let $X_1,\dots ,X_r$ be topological vector spaces. Recall that the product topology on $X_1\times \dots \times X_r$ is the smallest topology such that the projection maps

$${\pi }_k:X_1\times \dots \times X_r\to X_k,{\pi }_k(x_1,\dots ,x_r)=x_k,$$

are continuous for all $1\le k\le r$. It can be shown that if each $X_k$ is a locally convex topological vector space whose topology is induced by a family of seminorms ${\mathcal{P}}_k$, then $X_1\times \dots \times X_r$ equipped with the product topology is a locally convex topological vector space whose topology is induced by the following family of seminorms

$$\{p_1\circ {\pi }_1+\dots +p_r\circ {\pi }_r:p_k\in {\mathcal{P}}_k\forall 1\le k\le r\}.$$

Theorem 24

([24], p. 164). Let $X_1,\dots ,X_r$ be locally convex topological vector spaces. Equip $X_1\times \dots \times X_r$ and $X_1^{*}\times \dots \times X_r^{*}$ with the product topology. The mapping $\tilde{L}:X_1^{*}\times \dots \times X_r^{*}\to {(X_1\times \dots \times X_r)}^{*}$ defined by

$$\tilde{L}(u_1,\dots ,u_r)=u_1\circ {\pi }_1+\dots +u_r\circ {\pi }_r$$

is a linear topological isomorphism. Its inverse is

$$L(v)=(v\circ i_1,\dots ,v\circ i_r),$$

where for all $1\le k\le r$, $i_k:X_k\to X_1\times \dots \times X_r$ is defined by

$$i_k(z)=(0,\dots ,0,\underset{k^{\mathrm{th}} \mathit{position}}{\underbrace{z}},0,\dots ,0).$$

The notion of adjoint operator, which frequently appears in the future sections, is introduced in the following theorem.

Theorem 25

([24], p. 163). Let X and Y be locally convex topological vector spaces and suppose $T:X\to Y$ is a continuous linear map. Then

(1) 

The map

$$T^{*}:Y^{*}\to X^{*}{⟨T^{*}y,x⟩}_{X^{*}\times X}={⟨y,Tx⟩}_{Y^{*}\times Y},$$

is well-defined, linear, and continuous. ($T^{*}$ is called the adjoint of T).

(2) 

If $T(X)$ is dense in Y, then $T^{*}:Y^{*}\to X^{*}$ is injective.

Remark 10.

In the subsequent sections we will focus heavily on certain function spaces on domains Ω in the Euclidean space. For approximation purposes, it is always desirable to have $D(\Omega )(=C_c^{\infty }(\Omega ))$ as a dense subspace of our function spaces. However, there is another, may be more profound, reason for being interested in having $D(\Omega )$ as a dense subspace. It is important to note that we would like to use the term “function spaces” for topological vector spaces that can be continuously embedded in $D^{\prime }(\Omega )$ (see Section 6 for the definition of $D^{\prime }(\Omega )$) so that concepts such as differentiation will be meaningful for the elements of our function spaces. Given a function space $A(\Omega )$ it is usually helpful to consider its dual too. In order to be able to view the dual of $A(\Omega )$ as a function space we need to ensure that ${[A(\Omega )]}^{*}$ can be viewed as a subspace of $D^{\prime }(\Omega )$. To this end, according to the above theorem, it is enough to ensure that the identity map from $D(\Omega )$ to $A(\Omega )$ is continuous with dense image in $A(\Omega )$.

Let us consider more closely two special cases of Theorem 25.

(1)

Suppose Y is a normed space and H is a dense subspace of Y. Clearly, the identity map $i:H\to Y$ is continuous with dense image. Therefore, $i^{*}:Y^{*}\to H^{*}$ (${F\mapsto F|}_H$) is continuous and injective. Furthermore, by the Hahn–Banach theorem for all $\phi \in H^{*}$ there exists $F\in Y^{*}$ such that ${F|}_H=\phi$ and ${\parallel F\parallel }_{Y^{*}}={\parallel \phi \parallel }_{H^{*}}$. So the above map is indeed bijective and $Y^{*}$ and $H^{*}$ are isometrically isomorphic. As an important example, let $\Omega$ be a nonempty open set in ${\mathbb{R}}^n$, $s\ge 0$, and $1<p<\infty$. Consider the space $W_0^{s,p}(\Omega )$ (see Section 7 for the definition of $W_0^{s,p}(\Omega )$). $C_c^{\infty }(\Omega )$ is a dense subspace of $W_0^{s,p}(\Omega )$. Therefore, $W^{-s,p^{\prime }}(\Omega ):={[W_0^{s,p}(\Omega )]}^{*}$ is isometrically isomorphic to $[(C_c^{\infty }{(\Omega ),\parallel .\parallel }_{s,p}{)]}^{*}$. In particular, if $F\in W^{-s,p^{\prime }}(\Omega )$, then

$${\parallel F\parallel }_{W^{-s,p^{\prime }}(\Omega )}=\underset{0\neg \equiv \psi \in C_c^{\infty }(\Omega )}{sup}\frac{|F(\psi )|}{{\parallel \psi \parallel }_{s,p}}.$$

(2)

Suppose $(Y,\parallel .{\parallel }_Y)$ is a normed space, $(X,\tau )$ is a locally convex topological vector space, $X\subseteq Y$, and the identity map $i:(X,\tau )\to (Y,\parallel .{\parallel }_Y)$ is continuous with dense image. So $i^{*}:Y^{*}\to X^{*}$ (${F\mapsto F|}_X$) is continuous and injective and can be used to identify $Y^{*}$ with a subspace of $X^{*}$.

• Question: Exactly what elements of $X^{*}$ are in the image of $i^{*}$? That is, which elements of $X^{*}$ “belong to” $Y^{*}$?
• Answer: $\phi \in X^{*}$ belongs to the image of $i^{*}$ if and only if $\phi :(X,\parallel .{\parallel }_Y)\to \mathbb{R}$ is continuous, that is, $\phi \in X^{*}$ belongs to the image of $i^{*}$ if and only if ${sup}_{x\in X\setminus \{0\}}\frac{|\phi (x)|}{{\parallel x\parallel }_Y}<\infty$.

So, an element $\phi \in X^{*}$ can be considered as an element of $Y^{*}$ if and only if

$$\underset{x\in X\setminus \{0\}}{sup}\frac{|\phi (x)|}{{\parallel x\parallel }_Y}<\infty .$$

Furthermore, if we denote the unique corresponding element in $Y^{*}$ by $\tilde{\phi }$ (normally we identify $\phi$ and $\tilde{\phi }$ and we use the same notation for both) then since X is dense in Y

$$\parallel \tilde{\phi }{\parallel }_{Y^{*}}=\underset{y\in Y\setminus \{0\}}{sup}\frac{|\tilde{\phi }(y)|}{{\parallel y\parallel }_Y}=\underset{x\in X\setminus \{0\}}{sup}\frac{|\phi (x)|}{{\parallel x\parallel }_Y}<\infty .$$

Remark 11.

To sum up, given an element $\phi \in X^{*}$ in order to show that φ can be considered as an element of $Y^{*}$ we just need to show that ${sup}_{x\in X\setminus \{0\}}\frac{|\phi (x)|}{{\parallel x\parallel }_Y}<\infty$ and in that case, norm of φ as an element of $Y^{*}$ is ${sup}_{x\in X\setminus \{0\}}\frac{|\phi (x)|}{{\parallel x\parallel }_Y}$. However, it is important to notice that if $F:Y\to \mathbb{R}$ is a linear map, X is a dense subspace of Y, and ${F|}_X{:(X,\parallel .\parallel }_Y)\to \mathbb{R}$ is bounded, that does NOT imply that $F\in Y^{*}$. It just shows that there exists $G\in Y^{*}$ such that ${G|}_X{=F|}_X$.

We conclude this section by a quick review of the inductive limit topology.

Definition 12.

Let X be a vector space and let ${\{X_{\alpha }\}}_{\alpha \in I}$ be a family of vector subspaces of X with the property that

• For each $\alpha \in I$, $X_{\alpha }$ is equipped with a topology that makes it a locally convex topological vector space, and
• ${\bigcup }_{\alpha \in I}{X}_{\alpha }=X$.

The inductive limit topology on X with respect to the family ${\{X_{\alpha }\}}_{\alpha \in I}$ is defined to be the largest topology with respect to which

(1) 

X is a locally convex topological vector space;

(2) 

All the inclusions $X_{\alpha }\subseteq X$ are continuous.

Theorem 26

([24], p. 161). Let X be a vector space equipped with the inductive limit topology with respect to $\{X_{\alpha }\}$ as described above. If Y is a locally convex vector space, then a linear map $T:X\to Y$ is continuous if and only if ${T|}_{X_{\alpha }}:X_{\alpha }\to Y$ is continuous for all $\alpha \in I$.

Theorem 27

([24], p. 162). Let X be a vector space equipped with the inductive limit topology with respect to $\{X_{\alpha }\}$ as described above. A convex subset W of X is a neighborhood of the origin (i.e., an open set containing the origin) in X if and only if for all α, the set $W\cap X_{\alpha }$ is a neighborhood of the origin in $X_{\alpha }$.

Theorem 28

([24], p. 165). Let X be a vector space and let ${\{X_j\}}_{j\in {\mathbb{N}}_0}$ be a nested family of vector subspaces of X:

$$X_0⊊X_1⊊\dots ⊊X_j⊊\dots .$$

Suppose each $X_j$ is equipped with a topology that makes it a locally convex topological vector space. Equip X with the inductive limit topology with respect to $\{X_j\}$. Then the following topologies on $X^{\times r}$ are equivalent (=they are the same):

(1) 

The product topology;

(2) 

The inductive limit topology with respect to the family $\{X_j^{\times r}\}$ (For each j, $X_j^{\times r}$ is equipped with the product topology).

As a consequence, if Y is a locally convex vector space, then a linear map $T:X^{\times r}\to Y$ is continuous if and only if ${T|}_{X_j^{\times r}}:X_j^{\times r}\to Y$ is continuous for all $j\in {\mathbb{N}}_0$.

5. Review of Some Results from Differential Geometry

The main purpose of this section is to set the notation and terminology straight. To this end we cite the definitions of several basic terms and a number of basic properties that we will frequently use. The main reference for the majority of the definitions is one of the invaluable books by John M. Lee [19].

5.1. Smooth Manifolds

Suppose M is a topological space. We say that M is a topological manifold of dimension n if it is Hausdorff, second-countable, and locally Euclidean in the sense that each point of M has a neighborhood that is homeomorphic to an open subset of ${\mathbb{R}}^n$. It is easy to see that the following statements are equivalent ([19], p. 3):

(1)

Each point of M has a neighborhood that is homeomorphic to an open subset of ${\mathbb{R}}^n$.

(2)

Each point of M has a neighborhood that is homeomorphic to an open ball in ${\mathbb{R}}^n$.

(3)

Each point of M has a neighborhood that is homeomorphic to ${\mathbb{R}}^n$.

By a coordinate chart (or just chart) on M we mean a pair $(U,\phi )$, where U is an open subset of M and $\phi :U\to \widehat{U}$ is a homeomorphism from U to an open subset $\widehat{U}=\phi (U)\subseteq {\mathbb{R}}^n$. U is called a coordinate domain or a coordinate neighborhood of each of its points and $\phi$ is called a coordinate map. An atlas for M is a collection of charts whose domains cover M. Two charts $(U,\phi )$ and $(V,\psi )$ are said to be smoothly compatible if either $U\cap V=\varnothing$ or the transition map $\psi \circ {\phi }^{-1}$ is a $C^{\infty }$-diffeomorphism. An atlas $\mathcal{A}$ is called a smooth atlas if any two charts in $\mathcal{A}$ are smoothly compatible with each other. A smooth atlas $\mathcal{A}$ on M is maximal if it is not properly contained in any larger smooth atlas. A smooth structure on M is a maximal smooth atlas. A smooth manifold is a pair $(M,\mathcal{A})$, where M is a topological manifold and $\mathcal{A}$ is a smooth structure on M. Any chart $(U,\phi )$ contained in the given maximal smooth atlas is called a smooth chart. If M and N are two smooth manifolds, a map $F:M\to N$ is said to be a smooth $(C^{\infty })$ map if for every $p\in M$, there exist smooth charts $(U,\phi )$ containing p and $(V,\psi )$ containing $F(p)$ such that $F(U)\subseteq V$ and $\psi \circ F\circ {\phi }^{-1}\in C^{\infty }(\phi (U))$. It can be shown that if F is smooth, then its restriction to every open subset of M is smooth. Furthermore, if every $p\in M$ has a neighborhood U such that ${F|}_U$ is smooth, then F is smooth.

Remark 12.

• Sometimes we use the shorthand notation $M^n$ to indicate that M is n-dimensional.
• Clearly, if $(U,\phi )$ is a chart in a maximal smooth atlas and V is an open subset of U, then $(V,\psi )$ where ${\psi =\phi |}_V$ is also a smooth chart (i.e., it belongs to the same maximal atlas).
• Every smooth atlas $\mathcal{A}$ for M is contained in a unique maximal smooth atlas, called the smooth structure determined by $\mathcal{A}$.
• If M is a compact smooth manifold, then there exists a smooth atlas with finitely many elements that determines the smooth structure of M (this is immediate from the definition of compactness).

Definition 13.

• We say that a smooth atlas for a smooth manifold M is a geometrically Lipschitz (GL) smooth atlas if the image of each coordinate domain in the atlas under the corresponding coordinate map is a nonempty bounded open set with Lipschitz boundary.
• We say that a smooth atlas for a smooth manifold $M^n$ is a generalized geometrically Lipschitz (GGL) smooth atlas if the image of each coordinate domain in the atlas under the corresponding coordinate map is the entire ${\mathbb{R}}^n$ or a nonempty bounded open set with Lipschitz boundary.
• We say that a smooth atlas for a smooth manifold $M^n$ is a nice smooth atlas if the image of each coordinate domain in the atlas under the corresponding coordinate map is a ball in ${\mathbb{R}}^n$.
• We say that a smooth atlas for a smooth manifold $M^n$ is a super nice smooth atlas if the image of each coordinate domain in the atlas under the corresponding coordinate map is the entire ${\mathbb{R}}^n$.
• We say that two smooth atlases ${\{(U_{\alpha },{\phi }_{\alpha })\}}_{\alpha \in I}$ and ${\{({\tilde{U}}_{\beta },{\tilde{\phi }}_{\beta })\}}_{\beta \in J}$ for a smooth manifold $M^n$ are geometrically Lipschitz compatible (GLC) smooth atlases provided that each atlas is GGL and moreover for all $\alpha \in I$ and $\beta \in J$ with $U_{\alpha }\cap {\tilde{U}}_{\beta }\ne \varnothing$, ${\phi }_{\alpha }(U_{\alpha }\cap {\tilde{U}}_{\beta })$ and ${\tilde{\phi }}_{\beta }(U_{\alpha }\cap {\tilde{U}}_{\beta })$ are nonempty bounded open sets with Lipschitz boundary or the entire ${\mathbb{R}}^n$.

Clearly, every super nice smooth atlas is also a GGL smooth atlas; every nice smooth atlas is also a GL smooth atlas, and every GL smooth atlas is also a GGL smooth atlas. Furthermore, note that two arbitrary GL smooth atlases are not necessarily GLC smooth atlases because the intersection of two Lipschitz domains is not necessarily Lipschitz (see, e.g., [27], pp. 115–117).

Given a smooth atlas $\{(U_{\alpha },{\phi }_{\alpha })\}$ for a compact smooth manifold M, it is not necessarily possible to construct a new atlas $\{(U_{\alpha },{\tilde{\phi }}_{\alpha })\}$ such that this new atlas is nice; for instance if $U_{\alpha }$ is not connected we cannot find ${\tilde{\phi }}_{\alpha }$ such that ${\tilde{\phi }}_{\alpha }(U_{\alpha })={\mathbb{R}}^n$ (or any ball in ${\mathbb{R}}^n$). However, as the following lemma states, it is always possible to find a refinement that is nice.

Lemma 1.

Suppose ${\{(U_{\alpha },{\phi }_{\alpha })\}}_{1\le \alpha \le N}$ is a smooth atlas for a compact smooth manifold M. Then there exists a finite open cover ${\{V_{\beta }\}}_{1\le \beta \le L}$ of M such that

$$\forall \beta \exists 1\le \alpha (\beta )\le Ns.t.V_{\beta }\subseteq U_{\alpha (\beta )},{\phi }_{\alpha (\beta )}(V_{\beta })isaballin{\mathbb{R}}^n.$$

Therefore, ${\{(V_{\beta },{\phi }_{\alpha (\beta )}{|}_{V_{\beta }})\}}_{1\le \beta \le L}$ is a nice smooth atlas.

Proof. 

For each $1\le \alpha \le N$ and $p\in U_{\alpha }$, there exists $r_{\alpha p}>0$ such that $B_{r_{\alpha p}}({\phi }_{\alpha }(p))\subseteq {\phi }_{\alpha }(U_{\alpha })$. Let $V_{\alpha p}:={\phi }_{\alpha }^{-1}(B_{r_{\alpha p}}({\phi }_{\alpha }(p)))$. ${\bigcup }_{1\le \alpha \le N}{\bigcup }_{p\in U_{\alpha }}{V}_{\alpha p}$ is an open cover of M and so it has a finite subcover $\{V_{{\alpha }_1{p}_1},\dots ,V_{{\alpha }_L{p}_L}\}$. Let $V_{\beta }=V_{{\alpha }_{\beta }{p}_{\beta }}$. Clearly, $V_{\beta }\subseteq U_{{\alpha }_{\beta }}$ and ${\phi }_{{\alpha }_{\beta }}(V_{\beta })$ is a ball in ${\mathbb{R}}^n$.  □

Remark 13.

Every open ball in ${\mathbb{R}}^n$ is $C^{\infty }$-diffeomorphic to ${\mathbb{R}}^n$. Furthermore, compositions of diffeomorphisms is a diffeomorphism. Therefore, existence of a finite nice smooth atlas on a compact smooth manifold, which is guaranteed by the above lemma, implies the existence of a finite super nice smooth atlas.

Lemma 2.

Let M be a compact smooth manifold. Let ${\{U_{\alpha }\}}_{1\le \alpha \le N}$ be an open cover of M. Suppose C is a closed set in M (so C is compact) which is contained in $U_{\beta }$ for some $1\le \beta \le N$. Then there exists an open cover ${\{A_{\alpha }\}}_{1\le \alpha \le N}$ of M such that $C\subseteq A_{\beta }\subseteq {\overline{A}}_{\beta }\subseteq U_{\beta }$ and $A_{\alpha }\subseteq {\overline{A}}_{\alpha }\subseteq U_{\alpha }$ for all $\alpha \ne \beta$.

Proof. 

Without loss of generality we may assume that $\beta =1$. For each $1\le \alpha \le N$ and $p\in U_{\alpha }$, there exists $r_{\alpha p}>0$ such that $B_{2r_{\alpha p}}({\phi }_{\alpha }(p))\subseteq {\phi }_{\alpha }(U_{\alpha })$. Let $V_{\alpha p}:={\phi }_{\alpha }^{-1}(B_{r_{\alpha p}}({\phi }_{\alpha }(p)))$. Clearly, $p\in V_{\alpha p}\subseteq {\overline{V}}_{\alpha p}\subseteq U_{\alpha }$. Since M is compact, the open cover ${\bigcup }_{1\le \alpha \le N}{\bigcup }_{p\in U_{\alpha }}{V}_{\alpha p}$ of M has a finite subcover $\mathcal{A}$. For each $1\le \alpha \le N$ let $E_{\alpha }=\{p\in U_{\alpha }:V_{\alpha p}\in \mathcal{A}\}$ and

$$I_1=\{\alpha :E_{\alpha }\ne \varnothing \}.$$

If $\alpha \in I_1$, we let $W_{\alpha }={\bigcup }_{p\in E_{\alpha }}{V}_{\alpha p}$. For $\alpha \notin I_1$ choose one point $p\in U_{\alpha }$ and let $W_{\alpha }=V_{\alpha p}$.

C is compact so ${\phi }_1(C)$ is a compact set inside the open set ${\phi }_1(U_1)$. Therefore, there exists an open set B such that

$${\phi }_1(C)\subseteq B\subseteq \overline{B}\subseteq {\phi }_1(U_1).$$

Let $W={\phi }_1^{-1}(B)$. Clearly, $C\subseteq W\subseteq \overline{W}\subseteq U_{\alpha }$. Now Let

$$\begin{array}{cc}\hfill & A_1=W\bigcup W_1,\hfill \\ \hfill & A_{\alpha }=W_{\alpha }\forall \alpha >1.\hfill \end{array}$$

Clearly, $A_1$ contains W which contains C. Furthermore, union of $A_{\alpha }$’s contains ${\bigcup }_{\alpha =1}^N{\bigcup }_{p\in E_{\alpha }}{V}_{\alpha p}$ which is equal to M. Closure of a union of sets is a subset of the union of closures of those sets. Therefore, for each $\alpha$, ${\overline{A}}_{\alpha }\subseteq U_{\alpha }$.  □

Theorem 29

(Exhaustion by Compact Sets for Manifolds). Let M be a smooth manifold. There exists a sequence of compact subsets ${(K_j)}_{j\in \mathbb{N}}$ such that ${\cup }_{j\in \mathbb{N}}{\mathring{K}}_j=M$, ${\mathring{K}}_{j+1}\backslash K_j\ne \varnothing$ for all j and

$$K_1\subseteq {\mathring{K}}_2\subseteq K_2\subseteq \dots \subseteq {\mathring{K}}_j\subseteq K_j\subseteq \dots .$$

Definition 14.

A $C^{\infty }$ partition of unity on a smooth manifold is a collection of nonnegative $C^{\infty }$ functions ${\{{\psi }_{\alpha }:M\to \mathbb{R}\}}_{\alpha \in A}$ such that

(i) 

The collection of supports, ${\{supp{\psi }_{\alpha }\}}_{\alpha \in A}$ is locally finite in the sense that every point in M has a neighborhood that intersects only finitely many of the sets in ${\{supp{\psi }_{\alpha }\}}_{\alpha \in A}$.

(ii) 

${\sum }_{\alpha \in A}{\psi }_{\alpha }=1$.

Given an open cover ${\{U_{\alpha }\}}_{\alpha \in A}$ of M, we say that a partition of unity ${\{{\psi }_{\alpha }\}}_{\alpha \in A}$ is subordinate to the open cover ${\{U_{\alpha }\}}_{\alpha \in A}$ if $supp{\psi }_{\alpha }\subseteq U_{\alpha }$ for every $\alpha \in A$.

Theorem 30

([28], p. 146). Let M be a compact smooth manifold and ${\{U_{\alpha }\}}_{\alpha \in A}$ an open cover of M. There exists a $C^{\infty }$ partition of unity ${\{{\psi }_{\alpha }\}}_{\alpha \in A}$ subordinate to ${\{U_{\alpha }\}}_{\alpha \in A}$ (notice that the index sets are the same).

Theorem 31

([28], p. 347). Let ${\{U_{\alpha }\}}_{\alpha \in A}$ be an open cover of a smooth manifold M.

(i) 

There is a $C^{\infty }$ partition of unity ${\{{\phi }_k\}}_{k=1}^{\infty }$ with every ${\phi }_k$ having compact support such that for each k, $supp{\phi }_k\subseteq U_{\alpha }$ for some $\alpha \in A$.

(ii) 

If we do not require compact support, then there is a $C^{\infty }$ partition of unity ${\{{\psi }_{\alpha }\}}_{\alpha \in A}$ subordinate to ${\{U_{\alpha }\}}_{\alpha \in A}$.

Remark 14.

Let M be a compact smooth manifold. Suppose ${\{U_{\alpha }\}}_{\alpha \in A}$ is an open cover of M and ${\{{\psi }_{\alpha }\}}_{\alpha \in A}$ is a partition of unity subordiante to ${\{U_{\alpha }\}}_{\alpha \in A}$.

◦

For all $m\in \mathbb{N}$, $\{{\tilde{\psi }}_{\alpha }=\frac{{\psi }_{\alpha }^m}{{\sum }_{\alpha \in A}{\psi }_{\alpha }^m}\}$ is another partition of unity subordinate to ${\{U_{\alpha }\}}_{\alpha \in A}$.

◦

If ${\{V_{\beta }\}}_{\beta \in B}$ is an open cover of M and $\{{\xi }_{\beta }\}$ is a partition of unity subordinate to ${\{V_{\beta }\}}_{\beta \in B}$, then ${\{{\psi }_{\alpha }{\xi }_{\beta }\}}_{(\alpha ,\beta )\in A\times B}$ is a partition of unity subordinate to the open cover ${\{U_{\alpha }\cap V_{\beta }\}}_{(\alpha ,\beta )\in A\times B}$.

Lemma 3.

Let M be a compact smooth manifold. Suppose ${\{U_{\alpha }\}}_{1\le \alpha \le N}$ is an open cover of M. Suppose C is a closed set in M (so C is compact) which is contained in $U_{\beta }$ for some $1\le \beta \le N$. Then there exists a partition of unity ${\{{\psi }_{\alpha }\}}_{1\le \alpha \le N}$ subordinate to ${\{U_{\alpha }\}}_{1\le \alpha \le N}$ such that ${\psi }_{\beta }=1$ on C.

Proof. 

We follow the argument in [29]. Without loss of generality we may assume $\beta =1$. We can construct a partition of unity with the desired property as follows: Let $A_{\alpha }$ be a collection of open sets that covers M and such that $C\subseteq A_1\subseteq {\overline{A}}_1\subseteq U_1$ and for $\alpha >1$, $A_{\alpha }\subseteq {\overline{A}}_{\alpha }\subseteq U_{\alpha }$ (see Lemma 2). Let ${\eta }_{\alpha }\in C_c^{\infty }(U_{\alpha })$ be such that $0\le {\eta }_{\alpha }\le 1$ and ${\eta }_{\alpha }=1$ on a neighborhood of ${\overline{A}}_{\alpha }$. Of course ${\sum }_{\alpha =1}^N{\eta }_{\alpha }$ is not necessarily equal to 1 for all $x\in M$. However, if we define ${\psi }_1={\eta }_1$ and for $\alpha >1$

$${\psi }_{\alpha }={\eta }_{\alpha }(1-{\eta }_1)\dots (1-{\eta }_{\alpha -1}),$$

by induction one can easily show that for $1\le l\le N$

$$1-\sum _{\alpha =1}^l{\psi }_{\alpha }=(1-{\eta }_1)\dots (1-{\eta }_l).$$

In particular,

$$1-\sum _{\alpha =1}^N{\psi }_{\alpha }=(1-{\eta }_1)\dots (1-{\eta }_N)=0,$$

since for each $x\in M$ there exists $\alpha$ such that $x\in A_{\alpha }$ and so ${\eta }_{\alpha }(x)=1$. Consequently, ${\sum }_{\alpha =1}^N{\psi }_{\alpha }=1$.  □

5.2. Vector Bundles, Basic Definitions

Let M be a smooth manifold. A (smooth real) vector bundle of rank r over M is a smooth manifold E together with a surjective smooth map $\pi :E\to M$ such that

(1)

For each $x\in M$, $E_x={\pi }^{-1}(x)$ is an r-dimensional (real) vector space;

(2)

For each $x\in M$, there exists a neighborhood U of x in M and a smooth map $\rho =({\rho }^1,\dots ,{\rho }^r)$ from ${E|}_U:={\pi }^{-1}(U)$ onto ${\mathbb{R}}^r$ such that

• For every $x\in U$, ${\rho |}_{E_x}:E_x\to {\mathbb{R}}^r$ is an isomorphism of vector spaces,
• $\mathsf{\Phi }=(\pi {|}_{E_U},\rho ):E_U\to U\times {\mathbb{R}}^r$ is a diffeomorphism.

We denote the projection onto the last r components by ${\pi }^{\prime }$. So ${\pi }^{\prime }\circ \mathsf{\Phi }=\rho$. The expressions “E is a vector bundle over M”, or “$E\to M$ is a vector bundle”, or “$\pi :E\to M$ is a vector bundle” are all considered to be equivalent in this manuscript.

If $\pi :E\to M$ is a vector bundle of rank r, U is an open set in M, $\rho :E_U={\pi }^{-1}(U)\to {\mathbb{R}}^r$ and $\mathsf{\Phi }=(\pi {|}_{E_U},\rho ):E_U\to U\times {\mathbb{R}}^r$ satisfy the properties stated in item (2), then we refer to both $\mathsf{\Phi }:E_U\to U\times {\mathbb{R}}^r$ and $\rho :E_U\to {\mathbb{R}}^r$ as a (smooth) local trivialization of E over U (it will be clear from the context which one we are referring to). We say that ${E|}_U$ is trivial. The pair $(U,\rho )$ (or $(U,\mathsf{\Phi })$) is sometimes called a vector bundle chart. It is easy to see that if $(U,\rho )$ is a vector bundle chart and $\varnothing \ne V\subseteq U$ is open, then $(V,\rho {|}_{E_V})$ is also a vector bundle chart for E. Moreover, if V is any nonempty open subset of M, then $E_V$ is a vector bundle over the manifold V. We say that a triple $(U,\phi ,\rho )$ is a total trivialization triple of the vector bundle $\pi :E\to M$ provided that $(U,\phi )$ is a smooth coordinate chart and $\rho =({\rho }^1,\cdots ,{\rho }^r):E_U\to {\mathbb{R}}^r$ is a trivialization of E over U. A collection $\{(U_{\alpha },{\phi }_{\alpha },{\rho }_{\alpha })\}$ is called a total trivialization atlas for the vector bundle $E\to M$ provided that for each $\alpha$, $(U_{\alpha },{\phi }_{\alpha },{\rho }_{\alpha })$ is a total trivialization triple and $\{(U_{\alpha },{\phi }_{\alpha })\}$ is a smooth atlas for M.

Lemma 4

([19], p. 252). Let $\pi :E\to M$ be a smooth vector bundle of rank r over M. Suppose $\mathsf{\Phi }:{\pi }^{-1}(U)\to U\times {\mathbb{R}}^r$ and $\mathsf{\Psi }:{\pi }^{-1}(V)\to V\times {\mathbb{R}}^r$ are two smooth local trivializations of E with $U\cap V\ne \varnothing$. There exists a smooth map $\tau :U\cap V\to \mathrm{GL}(r,\mathbb{R})$ such that the composition

$$\mathsf{\Phi }\circ {\mathsf{\Psi }}^{-1}:(U\cap V)\times {\mathbb{R}}^r\to (U\cap V)\times {\mathbb{R}}^r$$

has the form

$$\mathsf{\Phi }\circ {\mathsf{\Psi }}^{-1}(p,v)=(p,\tau (p)v).$$

Remark 15.

Let E be a vector bundle over an n-dimensional smooth manifold M. Suppose ${\{(U_{\alpha },{\phi }_{\alpha },{\rho }_{\alpha })\}}_{\alpha \in I}$ is a total trivialization atlas for the vector bundle $\pi :E\to M$. Then for each $\alpha \in I$, the mapping

$$\begin{array}{c}\hfill E_{U_{\alpha }}={\pi }^{-1}(U_{\alpha })\to {\phi }_{\alpha }(U_{\alpha })\times {\mathbb{R}}^r\subseteq {\mathbb{R}}^{n+r},s\mapsto \left({\phi }_{\alpha }(\pi (s)),{\rho }_{\alpha }(s)\right)\end{array}$$

will be a coordinate map for the manifold E over the coordinate domain $E_{U_{\alpha }}$. The collection ${\{\left(E_{U_{\alpha }},({\phi }_{\alpha }\circ \pi ,{\rho }_{\alpha })\right)\}}_{\alpha \in I}$ will be a smooth atlas for the manifold E.

The following statements show that any vector bundle has a total trivialization atlas.

Lemma 5

([30], p. 77). Let E be a vector bundle over an n-dimensional smooth manifold M (M does not need to be compact). Then M can be covered by $n+1$ open sets $V_0,\dots ,V_n$ where the restriction ${E|}_{V_i}$ is trivial.

Theorem 32.

Let E be a vector bundle of rank r over an n-dimensional smooth manifold M. Then $E\to M$ has a total trivialization atlas. In particular, if M is compact, then it has a total trivialization atlas that consists of only finitely many total trivialization triples.

Proof. 

Let $V_0,\dots ,V_n$ be an open cover of M such that E is trivial over $V_{\beta }$ with the mapping ${\rho }_{\beta }:E_{V_{\beta }}\to {\mathbb{R}}^r$. Let ${\{(U_{\alpha },{\phi }_{\alpha })\}}_{\alpha \in I}$ be a smooth atlas for M (if M is compact, the index set I can be chosen to be finite). For all $\alpha \in I$ and $0\le \beta \le n$ let $W_{\alpha \beta }=U_{\alpha }\cap V_{\beta }$. Let $J=\{(\alpha ,\beta ):W_{\alpha \beta }\ne \varnothing \}$. Clearly, ${\{(W_{\alpha \beta },{\phi }_{\alpha \beta },{\rho }_{\alpha \beta })\}}_{(\alpha ,\beta )\in J}$ where ${\phi }_{\alpha \beta }={\phi }_{\alpha }{|}_{W_{\alpha \beta }}$ and ${\rho }_{\alpha \beta }={\rho }_{\beta }{|}_{{\pi }^{-1}(W_{\alpha \beta })}$ is a total trivialization atlas for $E\to M$.  □

Definition 15.

• We say that a total trivialization triple $(U,\phi ,\rho )$ is geometrically Lipschitz (GL) provided that $\phi (U)$ is a nonempty bounded open set with Lipschitz boundary. A total trivialization atlas is called geometrically Lipschitz if each of its total trivialization triples is GL.
• We say that a total trivialization triple $(U,\phi ,\rho )$ is nice provided that $\phi (U)$ is equal to a ball in ${\mathbb{R}}^n$. A total trivialization atlas is called nice if each of its total trivialization triples is nice.
• We say that a total trivialization triple $(U,\phi ,\rho )$ is super nice provided that $\phi (U)$ is equal to ${\mathbb{R}}^n$. A total trivialization atlas is called super nice if each of its total trivialization triples is super nice.
• A total trivialization atlas is called generalized geometrically Lipschitz (GGL) if each of its total trivialization triples is GL or super nice.
• We say that two total trivialization atlases ${\{(U_{\alpha },{\phi }_{\alpha },{\rho }_{\alpha })\}}_{\alpha \in I}$ and ${\{({\tilde{U}}_{\beta },{\tilde{\phi }}_{\beta },{\tilde{\rho }}_{\beta })\}}_{\beta \in J}$ are geometrically Lipschitz compatible (GLC) if the corresponding atlases ${\{(U_{\alpha },{\phi }_{\alpha })\}}_{\alpha \in I}$ and ${\{({\tilde{U}}_{\beta },{\tilde{\phi }}_{\beta })\}}_{\beta \in J}$ are GLC.

Theorem 33.

Let E be a vector bundle of rank r over an n-dimensional compact smooth manifold M. Then E has a nice total trivialization atlas (and a super nice total trivialization atlas) that consists of only finitely many total trivialization triples.

Proof. 

By Theorem 32, $E\to M$ has a finite total trivialization atlas $\{(U_{\alpha },{\phi }_{\alpha },{\rho }_{\alpha })\}$. By Lemma 1 (and Remark 13) there exists a finite open cover ${\{V_{\beta }\}}_{1\le \beta \le L}$ of M such that

$$\begin{array}{c}\forall \beta \exists 1\le \alpha (\beta )\le Ns.t.V_{\beta }\subseteq U_{\alpha (\beta )},{\phi }_{\alpha (\beta )}(V_{\beta })\mathrm{is} \mathrm{a} \mathrm{ball} \mathrm{in} {\mathbb{R}}^n\hfill \\ (\mathrm{or}\forall \beta \exists 1\le \alpha (\beta )\le N\mathrm{s}.\mathrm{t}.V_{\beta }\subseteq U_{\alpha (\beta )},{\phi }_{\alpha (\beta )}(V_{\beta })={\mathbb{R}}^n),\hfill \end{array}$$

and thus ${\{(V_{\beta },{\phi }_{\alpha (\beta )}{|}_{V_{\beta }})\}}_{1\le \beta \le L}$ is a nice (resp. super nice) smooth atlas. Now, clearly, $\{(V_{\beta },{\phi }_{\alpha (\beta )}{|}_{V_{\beta }},{\rho }_{\alpha (\beta )}{|}_{E_{V_{\beta }}}{)\}}_{1\le \beta \le L}$ is a nice (resp. super nice) total trivialization atlas.  □

Theorem 34.

Let E be a vector bundle of rank r over an n-dimensional compact smooth manifold M. Then E admits a finite total trivialization atlas that is GL compatible with itself. In fact, there exists a total trivialization atlas ${\{(U_{\alpha },{\phi }_{\alpha },{\rho }_{\alpha })\}}_{1\le \alpha \le N}$ such that

• For all $1\le \alpha \le N$, ${\phi }_{\alpha }(U_{\alpha })$ is bounded with Lipschitz continuous boundary;
• For all $1\le \alpha ,\beta \le N$, $U_{\alpha }\cap U_{\beta }$ is either empty or else ${\phi }_{\alpha }(U_{\alpha }\cap U_{\beta })$ and ${\phi }_{\beta }(U_{\alpha }\cap U_{\beta })$ are bounded with Lipschitz continuous boundary.

Proof. 

The proof of this theorem is based on the argument presented in the proof of Lemma 3.1 in [31]. Equip M with a smooth Riemannian metric g. Let $r_{inj}$ denote the injectivity radius of M which is strictly positive because M is compact. Let $V_0,\dots ,V_n$ be an open cover of M such that E is trivial over $V_{\beta }$ with the mapping ${\rho }_{\beta }:E_{V_{\beta }}\to {\mathbb{R}}^r$. For every $x\in M$ choose $0\le i(x)\le n$ such that $x\in V_{i(x)}$. For all $x\in M$ let $r_x$ be a positive number less than $\frac{r_{inj}}{2}$ such that ${\exp }_x(B_{r_x})\subseteq V_{i(x)}$ where $B_{r_x}$ denotes the open ball in $T_{x}M$ of radius $r_x$ (with respect to the inner product induced by the Riemannian metric g) and ${\exp }_x:T_{x}M\to M$ denotes the exponential map at x. For every $x\in M$ define the normal coordinate chart centered at x, $(U_x,{\phi }_x)$, as follows:

$$U_x={\exp }_x(B_{r_x}),{\phi }_x:={\lambda }_x^{-1}\circ {\exp }_x^{-1}:U_x\to {\mathbb{R}}^n,$$

where ${\lambda }_x:{\mathbb{R}}^n\to T_{x}M$ is an isomorphism defined by ${\lambda }_x(y^1,\dots ,y^n)=y^i{E}_{ix}$; Here ${\{E_{ix}\}}_{i=1}^n$ is a an arbitrary but fixed orthonormal basis for $T_{x}M$. It is well-known that (see, e.g., [32])

• ${\phi }_x(x)=(0,\dots ,0)$;
• $g_{ij}(x)={\delta }_{ij}$ where $g_{ij}$ denotes the components of the metric with respect to the normal coordinate chart $(U_x,{\phi }_x)$;
• $E_{ix}={\mathsf{\partial }}_i{|}_x$ where ${\{{\mathsf{\partial }}_i\}}_{1\le i\le n}$ is the coordinate basis induced by $(U_x,{\phi }_x)$.

As a consequence of the previous items, it is easy to show that if $X\in T_{x}M$$(X=X^i{\mathsf{\partial }}_i{|}_x)$, then the Euclidean norm of X will be equal to the norm of X with respect to the metric g, that is, ${|X|}_g={|X|}_{\overline{g}}$ where

$${|X|}_{\overline{g}}=\sqrt{{(X^1)}^2+\dots +{(X^n)}^2}{|X|}_g=\sqrt{g(X,X)}.$$

Consequently, for every $x\in M$, ${\phi }_x(U_x)$ will be a ball in the Euclidean space, in particular, ${\{(U_x,{\phi }_x)\}}_{x\in M}$ is a GL atlas. The proof of Lemma 3.1 in [31] in part shows that the atlas ${\{(U_x,{\phi }_x)\}}_{x\in M}$ is GL compatible with itself. Since M is compact there exists $x_1,\dots ,x_N\in M$ such that ${\{U_{x_j}\}}_{1\le j\le N}$ also covers M.

Now, clearly, ${\{(U_{x_j},{\phi }_{x_j},{\rho }_{i(x_j)}{|}_{U_{x_j}})\}}_{1\le j\le N}$ is a total trivialization atlas for E that is GL compatible with itself.  □

Corollary 1.

Let E be a vector bundle of rank r over an n-dimensional compact smooth manifold M. Then E admits a finite super nice total trivialization atlas that is GL compatible with itself.

Proof. 

Let ${\{(U_{\alpha },{\phi }_{\alpha },{\rho }_{\alpha })\}}_{1\le \alpha \le N}$ be the total trivialization atlas that was constructed above. For each $\alpha$, ${\phi }_{\alpha }(U_{\alpha })$ is a ball in the Euclidean space and so it is diffeomorphic to ${\mathbb{R}}^n$; let ${\xi }_{\alpha }:{\phi }_{\alpha }(U_{\alpha })\to {\mathbb{R}}^n$ be such a diffeomorphism. We let ${\tilde{\phi }}_{\alpha }:={\xi }_{\alpha }\circ {\phi }_{\alpha }:U_{\alpha }\to {\mathbb{R}}^n$. A composition of diffeomorphisms is a diffeomorphism, so for all $1\le \alpha ,\beta \le N$, ${\tilde{\phi }}_{\alpha }\circ {\tilde{\phi }}_{\beta }^{-1}:{\tilde{\phi }}_{\beta }(U_{\alpha }\cap U_{\beta })\to {\tilde{\phi }}_{\alpha }(U_{\alpha }\cap U_{\beta })$ is a diffeomorphism. So ${\{(U_{\alpha },{\tilde{\phi }}_{\alpha },{\rho }_{\alpha })\}}_{1\le \alpha \le N}$ is clearly a smooth super nice total trivialization atlas. Moreover, if $1\le \alpha ,\beta \le N$ are such that $U_{\alpha }\cap U_{\beta }$ is nonempty, then ${\tilde{\phi }}_{\alpha }(U_{\alpha }\cap U_{\beta })$ is ${\mathbb{R}}^n$ or a bounded open set with Lipschitz continuous boundary. The reason is that ${\tilde{\phi }}_{\alpha }={\xi }_{\alpha }\circ {\phi }_{\alpha }$, and ${\phi }_{\alpha }(U_{\alpha }\cap U_{\beta })$ is ${\mathbb{R}}^n$ or Lipschitz, ${\xi }_{\alpha }$ is a diffeomorphism and being equal to ${\mathbb{R}}^n$ or Lipschitz is a property that is preserved under diffeomorphisms. Therefore, ${\{(U_{\alpha },{\tilde{\phi }}_{\alpha },{\rho }_{\alpha })\}}_{1\le \alpha \le N}$ is a finite super nice total trivialization atlas that is GL compatible with itself.  □

A section of E is a map $u:M\to E$ such that $\pi \circ u=I{d}_M$. The collection of all sections of E is denoted by $\Gamma (M,E)$. A section $u\in \Gamma (M,E)$ is said to be smooth if it is smooth as a map from the smooth manifold M to the smooth manifold E. The collection of all smooth sections of $E\to M$ is denoted by $C^{\infty }(M,E)$. Note that if ${\{(U_{\alpha },{\phi }_{\alpha },{\rho }_{\alpha })\}}_{\alpha \in I}$ is a total trivialization atlas for the vector bundle $\pi :E\to M$ of rank r, then for $u\in \Gamma (M,E)$ we have $u\in C^{\infty }(M,E)$ if and only if for all $\alpha \in I$, the local representation of u with respect to the coordinate charts $(U_{\alpha },{\phi }_{\alpha })$ and $\left(E_{U_{\alpha }},({\phi }_{\alpha }\circ \pi ,{\rho }_{\alpha })\right)$ is smooth, that is,

$$\begin{array}{cc}\hfill u\in C^{\infty }(M,E)& ⟺\forall \alpha \in Ix\mapsto \left({\phi }_{\alpha }\circ \pi \circ u\circ {\phi }_{\alpha }^{-1},{\rho }_{\alpha }\circ u\circ {\phi }_{\alpha }^{-1}\right)\mathrm{is}\mathrm{smooth}\hfill \\ \hfill & ⟺\forall \alpha \in Ix\mapsto \left(x,{\rho }_{\alpha }\circ u\circ {\phi }_{\alpha }^{-1}\right)\mathrm{is}\mathrm{smooth}\hfill \\ \hfill & ⟺\forall \alpha \in Ix\mapsto {\rho }_{\alpha }\circ u\circ {\phi }_{\alpha }^{-1}\mathrm{is}\mathrm{smooth}\hfill \\ \hfill & ⟺\forall \alpha \in I,\forall 1\le l\le r{\rho }_{\alpha }^l\circ u\circ {\phi }_{\alpha }^{-1}\in C^{\infty }({\phi }_{\alpha }(U_{\alpha })).\hfill \end{array}$$

A local section of E over an open set $U\subseteq M$ is a map $u:U\to E$ where u has the property that $\pi \circ u=I{d}_U$ (that is, u is a section of the vector bundle $E_U\to U$). We denote the collection of all local sections on U by $\Gamma (U,E)$ or $\Gamma (U,E_U)$.

Remark 16.

As a consequence of ${\rho |}_{E_x}:E_x\to {\mathbb{R}}^r$ being an isomorphism, if u is a section of ${E|}_U\to U$ and $f:U\to \mathbb{R}$ is a function, then $\rho (fu)=f\rho (u)$. In particular, $\rho (0)=0$.

Given a total trivialization triple $(U,\phi ,\rho )$ we have the following commutative diagram:

If s is a section of ${E|}_U\to U$, then by definition the pushforward of s by ${\rho }^j$ (the jth component of $\rho$) is a section of $\phi (U)\times \mathbb{R}\to \phi (U)$ which is defined by

$${\rho }_{*}^j(s)={\rho }^j\circ s\circ {\phi }^{-1}(\mathrm{i}.\mathrm{e}.,z\in \phi (U)\mapsto (z,{\rho }^j\circ s\circ {\phi }^{-1}(z))).$$

Let $E\to M$ be a vector bundle of rank r and $U\subseteq M$ be an open set. A (smooth) local frame for E over U is an ordered r-tuple $(s_1,\dots ,s_r)$ of (smooth) local sections over U such that for each $x\in U$, $(s_1(x),\dots ,s_r(x))$ is a basis for $E_x$. Given any vector bundle chart $(V,\rho )$, we can define the associated (smooth) local frame on V as follows:

$$\forall 1\le l\le r\forall x\in V{s}_l{(x)=\rho |}_{E_x}^{-1}(e_l),$$

where $(e_1,\cdots ,e_r)$ is the standard basis of ${\mathbb{R}}^r$. The following theorem states the converse of this observation is also true.

Theorem 35

([19], p. 258). Let $E\to M$ be a vector bundle of rank r and let $(s_1,\dots ,s_r)$ be a smooth local frame over an open set $U\subseteq M$. Then $(U,\rho )$ is a vector bundle chart where the map $\rho :E_U\to {\mathbb{R}}^r$ is defined by

$$\forall x\in U,\forall u\in E_x\rho (u)=u^1{e}_1+\dots +u^r{e}_r,$$

where $u=u^1{s}_1(x)+\dots +u^r{s}_r(x)$.

Theorem 36

([19], p. 260). Let $E\to M$ be a vector bundle of rank r and let $(s_1,\dots ,s_r)$ be a smooth local frame over an open set $U\subseteq M$. If $f\in \Gamma (M,E)$, then f is smooth on U if and only if its component functions with respect to $(s_1,\dots ,s_r)$ are smooth.

A (smooth) fiber metric on a vector bundle E is a (smooth) function which assigns to each $x\in M$ an inner product

$${⟨.,.⟩}_E:E_x\times E_x\to \mathbb{R}.$$

Note that the smoothness of the fiber metric means that for all $u,v\in C^{\infty }(M,E)$ the mapping

$$M\to \mathbb{R},x\mapsto {⟨u(x),v(x)⟩}_E$$

is smooth. One can show that every (smooth) vector bundle can be equipped with a (smooth) fiber metric ([33], p. 72).

Remark 17.

If $(M,g)$ is a Riemannian manifold, then g can be viewed as a fiber metric on the tangent bundle. The metric g induces fiber metrics on all tensor bundles; it can be shown that ([32]) if $(M,g)$ is a Riemannian manifold, then there exists a unique inner product on each fiber of $T_l^k(M)$ with the property that for all $x\in M$, if $\{e_i\}$ is an orthonormal basis of $T_{x}M$ with dual basis $\{{\eta }^i\}$, then the corresponding basis of $T_l^k(T_{x}M)$ is orthonormal. We denote this inner product by ${⟨.,.⟩}_F$ and the corresponding norm by ${|.|}_F$. If A and B are two tensor fields, then with respect to any local coordinate system

$${⟨A,B⟩}_F=g^{i_1{r}_1}\dots g^{i_k{r}_k}{g}_{j_1{s}_1}\dots g_{j_l{s}_l}{A}_{i_1\dots i_k}^{j_1\dots j_l}{B}_{r_1\dots r_k}^{s_1\dots s_l}.$$

Theorem 37.

Let $\pi :E\to M$ be a vector bundle with rank r equipped with a fiber metric ${⟨.,.⟩}_E$. Then given any total trivialization triple $(U,\phi ,\rho )$, there exists a smooth map $\tilde{\rho }:E_U\to {\mathbb{R}}^r$ such that with respect to the new total trivialization triple $(U,\phi ,\tilde{\rho })$ the fiber metric trivializes on U, that is,

$$\forall x\in U\forall u,v\in E_x{⟨u,v⟩}_E=u^1{v}^1+\dots +u^r{v}^r,$$

where for each $1\le l\le r$, $u^l$ and $v^l$ denote the lth components of u and v, respectively, (with respect to the local frame associated with the bundle chart $(U,\tilde{\rho })$).

Proof. 

Let $(t_1,\dots ,t_r)$ be the local frame on U associated with the vector bundle chart $(U,\rho )$. That is,

$$\forall x\in U,\forall 1\le l\le r{t}_l{(x)=\rho |}_{E_x}^{-1}(e_l).$$

Now, we apply the Gram–Schmidt algorithm to the local frame $(t_1,\dots ,t_r)$ to construct an orthonormal frame $(s_1,\dots ,s_r)$ where

$$\forall 1\le l\le r{s}_l=\frac{t_l-{\sum }_{j=1}^{l-1}{⟨t_l,s_j⟩}_E{s}_j}{|t_l-{\sum }_{j=1}^{l-1}{⟨t_l,s_j⟩}_E{s}_j|}.$$

$s_l:U\to E$ is smooth because

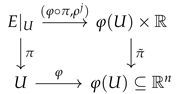
(1)

Smooth local sections over U form a module over the ring $C^{\infty }(U)$;

(2)

The function $x\mapsto {⟨t_l(x),s_j(x)⟩}_E$ from U to $\mathbb{R}$ is smooth;

(3)

Since $\mathrm{Span}\{s_1,\dots ,s_{l-1}\}=\mathrm{Span}\{t_1,\dots ,t_{l-1}\}$, $t_l-{\sum }_{j=1}^{l-1}{⟨t_l,s_j⟩}_E{s}_j$ is nonzero on U and $x\mapsto |t_l(x)-{\sum }_{j=1}^{l-1}{⟨t_l(x),s_j(x)⟩}_E{s}_j(x)|$ as a function from U to $\mathbb{R}$ is nonzero on U and it is a composition of smooth functions.

Thus, for each l, $s_l$ is a linear combination of elements of the $C^{\infty }(U)$-module of smooth local sections over U, and so it is a smooth local section over U. Now, we let $(U,\tilde{\rho })$ be the associated vector bundle chart described in Theorem 35. For all $x\in U$ and for all $u,v\in E_x$ we have

$${⟨u,v⟩}_E={⟨u^l{s}_l,v^j{s}_j⟩}_E=u^l{v}^j{⟨s_l,s_j⟩}_E=u^l{v}^j{\delta }_{lj}=u^1{v}^1+\dots +u^r{v}^r.$$

  □

Corollary 2.

As a consequence of Theorem 37, Theorem 34, and Theorem 33 every vector bundle on a compact manifold equipped with a fiber metric admits a nice finite total trivialization atlas (and a super nice finite total trivialization atlas and a finite total trivialization atlas that is GL compatible with itself) such that the fiber metric is trivialized with respect to each total trivialization triple in the atlas.

5.3. Standard Total Trivialization Triples

Let $M^n$ be a smooth manifold and $\pi :E\to M$ be a vector bundle of rank r. For certain vector bundles there are standard methods to associate with any given smooth coordinate chart $(U,\phi =(x^i))$ a total trivialization triple $(U,\phi ,\rho )$. We call such a total trivialization triple the standard total trivialization associated with $(U,\phi )$. Usually this is done by first associating with $(U,\phi )$ a local frame for $E_U$ and then applying Theorem 35 to construct a total trivialization triple.

• $E=T_l^k(M)$: The collection of the following tensor fields on U forms a local frame for $E_U$ associated with $(U,\phi =(x^i))$.

  $$\frac{\mathsf{\partial }}{\mathsf{\partial }{x}^{i_1}}\otimes \dots \otimes \frac{\mathsf{\partial }}{\mathsf{\partial }{x}^{i_l}}\otimes d{x}^{j_1}\otimes \dots \otimes d{x}^{j_k}.$$

  So, given any atlas $\{(U_{\alpha },{\phi }_{\alpha })\}$ of a manifold $M^n$, there is a corresponding total trivialization atlas for the tensor bundle $T_l^k(M)$, namely $\{(U_{\alpha },{\phi }_{\alpha },{\rho }_{\alpha })\}$ where for each $\alpha$, ${\rho }_{\alpha }$ has $n^{k+l}$ components which we denote by ${({\rho }_{\alpha })}_{i_1\dots i_k}^{j_1\dots j_l}$. For all $F\in \Gamma (M,T_l^k(M))$, we have

  $${({\rho }_{\alpha })}_{i_1\dots i_k}^{j_1\dots j_l}(F)={(F_{\alpha })}_{i_1\dots i_k}^{j_1\dots j_l}.$$

  Here ${(F_{\alpha })}_{i_1\dots i_k}^{j_1\dots j_l}$ denotes the components of F with respect to the standard frame for $T_l^k{U}_{\alpha }$ described above. When there is no possibility of confusion, we may write $F_{i_1\dots i_k}^{j_1\dots j_l}$ instead of ${(F_{\alpha })}_{i_1\dots i_k}^{j_1\dots j_l}$.
• $E={\Lambda }^k(M)$: This is the bundle whose fiber over each $x\in M$ consists of alternating covariant tensors of order k. The collection of the following forms on U form a local frame for $E_U$ associated with $(U,\phi =(x^i))$

  $$d{x}^{j_1}\wedge \dots \wedge d{x}^{j_k}((j_1,\dots ,j_k)\mathrm{is}\mathrm{increasing}).$$
• $E=\mathcal{D}(M)$ (the density bundle): The density bundle over M is the vector bundle whose fiber over each $x\in M$ is $\mathcal{D}(T_{x}M)$. More precisely, if we let

  $$\mathcal{D}(M)=\coprod _{x\in M}\mathcal{D}(T_{x}M),$$

  then $\mathcal{D}(M)$ is a smooth vector bundle of rank 1 over M ([19], p. 429). Indeed, for every smooth chart $(U,\phi =(x^i))$, $|d{x}^1\wedge \dots \wedge d{x}^n|$ on U is a local frame for ${\mathcal{D}(M)|}_U$. We denote the corresponding trivialization by ${\rho }_{\mathcal{D},\phi }$, that is, given $\mu \in \mathcal{D}(T_{y}M)$, there exists a number a such that

  $$\mu =a(|d{x}^1\wedge \dots \wedge d{x}^n{|}_y)$$

  and ${\rho }_{\mathcal{D},\phi }$ sends $\mu$ to a. Sometimes we write $\mathcal{D}$ instead of $\mathcal{D}(M)$ if M is clear from the context. Furthermore, when there is no possibility of confusion we may write ${\rho }_{\mathcal{D}}$ instead of ${\rho }_{\mathcal{D},\phi }$.

Remark 18

(Integration of densities on manifolds). Elements of $C_c(M,\mathcal{D})$ can be integrated over M. Indeed, for $\mu \in C_c(M,\mathcal{D})$ we may consider two cases

• Case 1: There exists a smooth chart $(U,\phi )$ such that $supp\mu \subseteq U$.

  $${\int }_M\mu :={\int }_{\phi (U)}{\rho }_{\mathcal{D},\phi }\circ \mu \circ {\phi }^{-1}dV.$$
• Case 2: If μ is an arbitrary element of $C_c(M,\mathcal{D})$, then we consider a smooth atlas ${\{(U_{\alpha },{\phi }_{\alpha })\}}_{\alpha \in I}$ and a partition of unity ${\{{\psi }_{\alpha }\}}_{\alpha \in I}$ subordinate to $\{U_{\alpha }\}$ and we let

  $${\int }_M\mu :=\sum _{\alpha \in I}{\int }_M{\psi }_{\alpha }\mu .$$

It can be shown that the above definitions are independent of the choices (charts and partition of unity) involved ([19], pp. 431–432).

5.4. Constructing New Bundles from Old Ones

5.4.1. Hom Bundle, Dual Bundle, Functional Dual Bundle

• The construction $\mathrm{Hom}(.,.)$ can be applied fiberwise to a pair of vector bundles E and $\tilde{E}$ over a manifold M to give a new vector bundle denoted by $\mathrm{Hom}(E,\tilde{E})$. The fiber of $\mathrm{Hom}(E,\tilde{E})$ at any given point $p\in M$ is the vector space $\mathrm{Hom}(E_p,{\tilde{E}}_p)$. Clearly, if $\mathrm{rank}E=r$ and $\mathrm{rank}\tilde{E}=\tilde{r}$, then $\mathrm{rank}\mathrm{Hom}(E,\tilde{E})=r\tilde{r}$.
  If $\{(U_{\alpha },{\phi }_{\alpha },{\rho }_{\alpha })\}$ and $\{(U_{\alpha },{\phi }_{\alpha },{\tilde{\rho }}_{\alpha })\}$ are total trivialization atlases for the vector bundles $\pi :E\to M$ and $\tilde{\pi }:\tilde{E}\to M$, respectively, then $\{U_{\alpha },{\phi }_{\alpha },{\widehat{\rho }}_{\alpha }\}$ will be a total trivialization atlas for ${\pi }_{\mathrm{Hom}}:\mathrm{Hom}(E,\tilde{E})\to M$ where ${\widehat{\rho }}_{\alpha }:{\pi }_{\mathrm{Hom}}^{-1}(U_{\alpha })\to \mathrm{Hom}({\mathbb{R}}^r,{\mathbb{R}}^{\tilde{r}})\cong {\mathbb{R}}^{r\tilde{r}}$ is defined as follows: for $p\in U_{\alpha }$, $A_p\in \mathrm{Hom}(E_p,{\tilde{E}}_p)$ is mapped to $[{\tilde{\rho }}_{\alpha }{|}_{{\tilde{E}}_p}]\circ A\circ {[{\rho }_{\alpha }{|}_{E_p}]}^{-1}$.
• Let $\pi :E\to M$ be a vector bundle. The dual bundle $E^{*}$ is defined by $E^{*}=\mathrm{Hom}(E,\tilde{E}=M\times \mathbb{R})$.
• Let $\pi :E\to M$ be a vector bundle and let $\mathcal{D}$ denote the density bundle of M. The functional dual bundle $E^{\vee }$ is defined by $E^{\vee }=\mathrm{Hom}(E,\mathcal{D})$ (see [24]). Let us describe explicitly what the standard total trivialization triples of this bundle are. Let $(U,\phi ,\rho )$ be a total trivialization triple for E. We can associate with this triple the total trivialization triple $(U,\phi ,{\rho }^{\vee })$ for $E^{\vee }$ where ${\rho }^{\vee }:E_U^{\vee }\to {\mathbb{R}}^r$ is defined as follows: for $p\in U$, $L_p\in \mathrm{Hom}(E_p,{\mathcal{D}}_p)$ is mapped to ${\rho }_{\mathcal{D},\phi }\circ L_p\circ {(\rho {|}_{E_p})}^{-1}\in {({\mathbb{R}}^r)}^{*}\simeq {\mathbb{R}}^r$. Note that ${({\mathbb{R}}^r)}^{*}\simeq {\mathbb{R}}^r$ under the following isomorphism

  $${({\mathbb{R}}^r)}^{*}\to {\mathbb{R}}^r,u\mapsto u(e_1)e_1+\dots +u(e_r)e_r.$$

  That is, u as an element of ${\mathbb{R}}^r$ is the vector whose components are $(u(e_1),\dots ,u(e_r))$. In particular, if $z=z_1{e}_1+\dots +z_r{e}_r$ is an arbitrary vector in ${\mathbb{R}}^r$, then

  $$u(z)=u(z_1{e}_1+\dots +z_r{e}_r)=z_{1}u(e_1)+\dots +z_{r}u(e_r)=z·u,$$

  where on the LHS u is viewed as an element of ${({\mathbb{R}}^r)}^{*}$ and on the RHS u is viewed as an element of ${\mathbb{R}}^r$.
  In short, ${\rho }^{\vee }:E_U^{\vee }\to {\mathbb{R}}^r$ is given by

  $$\forall 1\le l\le r{({\rho }^{\vee })}^l(L_p)=\left({\rho }_{\mathcal{D},\phi }\circ L_p\circ {(\rho {|}_{E_p})}^{-1}\right)(e_l).$$

5.4.2. Tensor Product of Bundles

Let $\pi :E\to M$ and $\tilde{\pi }:\tilde{E}\to M$ be two vector bundles. Then $E\otimes \tilde{E}$ is a new vector bundle whose fiber at $p\in M$ is $E_p\otimes {\tilde{E}}_p$. If $\{(U_{\alpha },{\phi }_{\alpha },{\rho }_{\alpha })\}$ and $\{(U_{\alpha },{\phi }_{\alpha },{\tilde{\rho }}_{\alpha })\}$ are total trivialization atlases for the vector bundles $\pi :E\to M$ and $\tilde{\pi }:\tilde{E}\to M$, respectively, then $\{(U_{\alpha },{\phi }_{\alpha },{\widehat{\rho }}_{\alpha }))\}$ will be a total trivialization atlas for ${\pi }_{\mathrm{tensor}}:E\otimes \tilde{E}\to M$ where ${\widehat{\rho }}_{\alpha }:{\pi }_{\mathrm{tensor}}^{-1}(U_{\alpha })\to ({\mathbb{R}}^r\otimes {\mathbb{R}}^{\tilde{r}})\cong {\mathbb{R}}^{r\tilde{r}}$ is defined as follows: for $p\in U_{\alpha }$, $a_p\otimes {\tilde{a}}_p\in E_p\otimes {\tilde{E}}_p$ is mapped to ${\rho }_{\alpha }{{|}_{E_p}(a_p)\otimes {\tilde{\rho }}_{\alpha }|}_{{\tilde{E}}_p}({\tilde{a}}_p)$.

It can be shown that $\mathrm{Hom}(E,\tilde{E})\cong E^{*}\otimes \tilde{E}$ (isomorphism of vector bundles over M).

Remark 19

(Fiber Metric on Tensor Product). Consider the inner product spaces $(U,{⟨.,.⟩}_U)$ and $(V,{⟨.,.⟩}_V)$. We can turn the tensor product of U and V, $U\otimes V$ into an inner product space by defining

$${⟨u_1\otimes v_1,u_2\otimes v_2⟩}_{U\otimes V}={⟨u_1,u_2⟩}_U{⟨v_1,v_2⟩}_V,$$

and extending by linearity. As a consequence, if E is a vector bundle (on a Riemannian manifold $(M,g)$) equipped with a fiber metric ${⟨.,.⟩}_E$, then there is a natural fiber metric on the bundle ${(T^{*}M)}^{\otimes k}$ and subsequently on the bundle ${(T^{*}M)}^{\otimes k}\otimes E$. If $F=F_{i_1\dots i_k}^{a}d{x}^{i_1}\otimes \dots \otimes d{x}^{i_k}\otimes s_a$ and $G=G_{j_1\dots j_k}^{b}d{x}^{j_1}\otimes \dots \otimes d{x}^{j_k}\otimes s_b$ are two local sections of this bundle on a domain U of a total trivialization triple, then at any point in U we have

$$\begin{array}{cc}\hfill {⟨F,G⟩}_{{(T^{*}M)}^{\otimes k}\otimes E}& =F_{i_1\cdots i_k}^a{G}_{j_1\dots j_k}^b{⟨d{x}^{i_1},d{x}^{j_1}⟩}_{T^{*}M}\dots {⟨d{x}^{i_k},d{x}^{j_k}⟩}_{T^{*}M}{⟨s_a,s_b⟩}_E\hfill \\ \hfill & =g^{i_1{j}_1}\dots g^{i_k{j}_k}{h}_{ab}{F}_{i_1\dots i_k}^a{G}_{j_1\dots j_k}^b,\hfill \end{array}$$

where $h_{ab}:={⟨s_a,s_b⟩}_E$ (here ${\{s_a={\rho }^{-1}(e_a)\}}_{1\le a\le r}$ is a local frame for E over U.${\{e_a\}}_{1\le a\le r}$ is the standard basis for ${\mathbb{R}}^r$ where $r=rankE$).

5.5. Connection on Vector Bundles, Covariant Derivative

5.5.1. Basic Definitions

Let $\pi :E\to M$ be a vector bundle.

Definition 16.

A connection in E is a map

$$\nabla :C^{\infty }(M,TM)\times C^{\infty }(M,E)\to C^{\infty }(M,E),(X,u)\mapsto {\nabla }_{X}u$$

satisfying the following properties:

(1) 

${\nabla }_{X}u$ is linear over $C^{\infty }(M)$ in X

$$\forall f,g\in C^{\infty }(M){\nabla }_{f{X}_1+g{X}_2}u=f{\nabla }_{X_1}u+g{\nabla }_{X_2}u.$$

(2) 

${\nabla }_{X}u$ is linear over $\mathbb{R}$ in u:

$$\forall a,b\in \mathbb{R}{\nabla }_X(a{u}_1+b{u}_2)=a{\nabla }_X{u}_1+b{\nabla }_X{u}_2.$$

(3) 

∇ satisfies the following product rule

$$\forall f\in C^{\infty }(M){\nabla }_X(fu)=f{\nabla }_{X}u+(Xf)u.$$

A metric connection in a real vector bundle E with a fiber metric is a connection ∇ such that

$$\forall X\in C^{\infty }(M,TM),\forall u,v\in C^{\infty }(M,E)X{⟨u,v⟩}_E={⟨{\nabla }_{X}u,v⟩}_E+{⟨u,{\nabla }_{X}v⟩}_E.$$

Here is a list of useful facts about connections:

• ([34], p. 183) Using a partition of unity, one can show that any real vector bundle with a smooth fiber metric admits a metric connection;
• ([19], p. 50) If ∇ is a connection in a bundle E, $X\in C^{\infty }(M,TM)$, $u\in C^{\infty }(M,E)$, and $p\in M$, then ${\nabla }_X{u|}_p$ depends only on the values of u in a neighborhood of p and the value of X at p. More precisely, if $u=\tilde{u}$ on a neighborhood of p and $X_p={\tilde{X}}_p$, then ${\nabla }_{X}u{{|}_p={\nabla }_{\tilde{X}}\tilde{u}|}_p$;
• ([19], p. 53) If ∇ is a connection in $TM$, then there exists a unique connection in each tensor bundle $T_l^k(M)$, also denoted by ∇, such that the following conditions are satisfied:

  (1)

  On the tangent bundle, ∇ agrees with the given connection.

  (2)

  On $T^0(M)$, ∇ is given by ordinary differentiation of functions, that is, for all real-valued smooth functions $f:M\to \mathbb{R}$: ${\nabla }_{X}f=Xf$.

  (3)

  ${\nabla }_X(F\otimes G)=({\nabla }_{X}F)\otimes G+F\otimes ({\nabla }_{X}G)$.

  (4)

  If $\mathrm{tr}$ denotes the trace on any pair of indices, then ${\nabla }_X(\mathrm{tr}F)=\mathrm{tr}({\nabla }_{X}F)$.

  This connection satisfies the following additional property: for any $T\in C^{\infty }(M,T_l^k(M))$, vector fields $Y_i$, and differential 1-forms ${\omega }^j$,

  $$\begin{array}{cc}\hfill ({\nabla }_{X}T)({\omega }^1,\cdots ,& {\omega }^l,Y_1,\cdots ,Y_k)=X(T({\omega }^1,\cdots ,{\omega }^l,Y_1,\cdots ,Y_k))\hfill \\ \hfill & -\sum _{j=1}^{l}T({\omega }^1,\cdots ,{\nabla }_X{\omega }^j,\cdots ,{\omega }^l,Y_1,\cdots ,Y_k)\hfill \\ \hfill & -\sum _{i=1}^{k}T({\omega }^1,\cdots ,{\omega }^l,Y_1,\cdots ,{\nabla }_X{Y}_i,\cdots ,Y_k).\hfill \end{array}$$

Definition 17.

Let ∇ be a connection in $\pi :E\to M$. We define the corresponding covariant derivative on E, also denoted ∇, as follows

$$\nabla :C^{\infty }(M,E)\to C^{\infty }(M,Hom(TM,E))\cong C^{\infty }(M,T^{*}M\otimes E),u\mapsto \nabla u$$

where for all $p\in M$, $\nabla u(p):T_{p}M\to E_p$ is defined by

$$X_p\mapsto {\nabla }_X{u|}_p,$$

where X on the RHS is any smooth vector field whose value at p is $X_p$.

Remark 20.

Let ∇ be a connection in $TM$. As it was discussed ∇ induces a connection in any tensor bundle $E=T_l^k(M)$, also denoted by ∇. Some authors (including Lee in [19], p. 53) define the corresponding covariant derivative on $E=T_l^k(M)$ as follows:

$$\nabla :C^{\infty }(M,T_l^k(M))\to C^{\infty }(M,T_l^{k+1}(M)),F\mapsto \nabla F$$

where

$$\nabla F({\omega }^1,\dots ,{\omega }^l,Y_1,\dots ,Y_k,X)=({\nabla }_{X}F)({\omega }^1,\dots ,{\omega }^l,Y_1,\dots ,Y_k).$$

This definition agrees with the previous definition of covariant derivative that we had for general vector bundles because

$$T^{*}M\otimes T_l^{k}M\cong T^{*}M\otimes \underset{kfactors}{\underbrace{T^{*}M\otimes \dots \otimes T^{*}M}}\otimes \underset{lfactors}{\underbrace{TM\otimes \dots \otimes TM}}\cong T_l^{k+1}M.$$

Therefore,

$$C^{\infty }(M,Hom(TM,T_l^{k}M))\cong C^{\infty }(M,T^{*}M\otimes T_l^{k}M)\cong C^{\infty }(M,T_l^{k+1}M).$$

More concretely, we have the following one-to-one correspondence between $C^{\infty }(M,Hom(TM,T_l^{k}M))$ and $C^{\infty }(M,T_l^{k+1}M)$:

(1) 

Given $u\in C^{\infty }(M,T_l^{k+1}M)$, the corresponding element $\tilde{u}\in C^{\infty }(M,Hom(TM,T_l^{k}M))$ is given by

$$\forall p\in M\tilde{u}(p):T_{p}M\to T_l^k(T_{p}M),X\mapsto u(p)(\dots ,\dots ,X).$$

(2) 

Given $\tilde{u}\in C^{\infty }(M,Hom(TM,T_l^{k}M))$, the corresponding element $u\in C^{\infty }(M,T_l^{k+1}M)$ is given by

$$\forall p\in Mu(p)({\omega }^1,\dots ,{\omega }^l,Y_1,\dots ,Y_k,X)=[\tilde{u}(p)(X)]({\omega }^1,\dots ,{\omega }^l,Y_1,\dots ,Y_k).$$

5.5.2. Covariant Derivative on Tensor Product of Bundles

If E an $\tilde{E}$ are vector bundles over M with covariant derivatives ${\nabla }^E:C^{\infty }(M,E)\to C^{\infty }(M,T^{*}M\otimes E)$ and ${\nabla }^{\tilde{E}}:C^{\infty }(M,\tilde{E})\to C^{\infty }(M,T^{*}M\otimes \tilde{E})$, respectively, then there is a uniquely determined covariant derivative ([14], p. 87)

$${\nabla }^{E\otimes \tilde{E}}:C^{\infty }(M,E\otimes \tilde{E})\to C^{\infty }(M,T^{*}M\otimes E\otimes \tilde{E})$$

such that

$${\nabla }^{E\otimes \tilde{E}}(u\otimes \tilde{u})={\nabla }^{E}u\otimes \tilde{u}+{\nabla }^{\tilde{E}}\tilde{u}\otimes u.$$

The above sum makes sense because of the following isomorphisms:

$$(T^{*}M\otimes E)\otimes \tilde{E}\cong T^{*}M\otimes E\otimes \tilde{E}\cong T^{*}M\otimes \tilde{E}\otimes E\cong (T^{*}M\otimes \tilde{E})\otimes E.$$

Remark 21.

Recall that for tensor fields covariant derivative can be considered as a map from $C^{\infty }(M,T_l^{k}M)\to C^{\infty }(M,T_l^{k+1}M)$. Using this, we can give a second description of covariant derivative on $E\otimes \tilde{E}$ when $E=T_l^{k}M$. In this new description we have

$${\nabla }^{T_l^{k}M\otimes \tilde{E}}:C^{\infty }(M,T_l^{k}M\otimes \tilde{E})\to C^{\infty }(M,T_l^{k+1}M\otimes \tilde{E}).$$

Indeed, for $F\in C^{\infty }(M,T_l^{k}M)$ and $u\in C^{\infty }(M,\tilde{E})$

$${\nabla }^{T_l^{k}M\otimes \tilde{E}}(F\otimes u)=\underset{T_l^{k+1}M}{\underbrace{({\nabla }^{T_l^{k}M}F)}}\otimes u+\underset{T_l^{k+1}M\otimes \tilde{E}}{\underbrace{\underset{T_l^{k}M}{\underbrace{F}}\otimes \underset{T^{*}M\otimes \tilde{E}}{\underbrace{{\nabla }^{E_{˜}}u}}}}.$$

In particular, if $f\in C^{\infty }(M)$ and $u\in C^{\infty }(M,E)$ we have ${\nabla }^E(fu)\in C^{\infty }(M,T^{*}M\otimes E)$ and it is equal to

$${\nabla }^E(fu)=df\otimes u+f{\nabla }^{E}u.$$

5.5.3. Higher Order Covariant Derivatives

Let $\pi :E\to M$ be a vector bundle. Let ${\nabla }^E$ be a connection in E and ∇ be a connection in $TM$ which induces a connection in $T^{*}M$. We have the following chain

$$\begin{array}{cc}\hfill C^{\infty }(M,E)\stackrel{{\nabla }^E}{\to }{C}^{\infty }(M,T^{*}M\otimes E)& \stackrel{{\nabla }^{T^{*}M\otimes E}}{\to }{C}^{\infty }(M,{(T^{*}M)}^{\otimes 2}\otimes E)\stackrel{{\nabla }^{{(T^{*}M)}^{\otimes 2}\otimes E}}{\to }\hfill \\ \hfill & \cdots \stackrel{{\nabla }^{{(T^{*}M)}^{\otimes (k-1)}\otimes E}}{\to }{C}^{\infty }(M,{(T^{*}M)}^{\otimes k}\otimes E)\stackrel{{\nabla }^{{(T^{*}M)}^{\otimes k}\otimes E}}{\to }\cdots .\hfill \end{array}$$

In what follows we denote all the maps in the above chain by ${\nabla }^E$. That is, for any $k\in {\mathbb{N}}_0$ we consider ${\nabla }^E$ as a map from $C^{\infty }(M,{(T^{*}M)}^{\otimes k}\otimes E)$ to $C^{\infty }(M,{(T^{*}M)}^{\otimes (k+1)}\otimes E)$. So,

$${({\nabla }^E)}^k:C^{\infty }(M,E)\to C^{\infty }(M,{(T^{*}M)}^{\otimes k}\otimes E).$$

As an example, let us consider ${({\nabla }^E)}^k(fu)$ where $f\in C^{\infty }(M)$ and $u\in C^{\infty }(M,E)$. We have

$$\begin{array}{cc}\hfill & {\nabla }^E(fu)=df\otimes u+f{\nabla }^{E}u.\hfill \\ \hfill & {({\nabla }^E)}^2(fu)={\nabla }^{T^{*}M\otimes E}\left[df\otimes u+f{\nabla }^{E}u\right]\hfill \\ \hfill & =[{\nabla }^{T^{*}M}(df)\otimes u+df\otimes {\nabla }^{E}u]+[df\otimes {\nabla }^{E}u+f{({\nabla }^E)}^{2}u]\hfill \\ \hfill & =\sum _{j=0}^2\left(\genfrac{}{}{0pt}{}{2}{j}\right){({\nabla }^{T^{*}M})}^{j}f\otimes {({\nabla }^E)}^{2-j}u.\hfill \end{array}$$

In general, we can show by induction that

$${({\nabla }^E)}^k(fu)=\sum _{j=0}^k\left(\genfrac{}{}{0pt}{}{k}{j}\right){({\nabla }^{T^{*}M})}^{j}f\otimes {({\nabla }^E)}^{k-j}u.$$

where ${({\nabla }^{T^{*}M})}^0=Id$. Here ${({\nabla }^{T^{*}M})}^{j}f$ should be interpreted as applying ∇ (in the sense described in Remark 20) j times; so ${({\nabla }^{T^{*}M})}^{j}f$ at each point is an element of $T_0^{j}M={(T^{*}M)}^{\otimes j}$.

5.5.4. Three Useful Rules, Two Important Observations

Let $\pi :E\to M$ and $\tilde{\pi }:\tilde{E}\to M$ be two vector bundles over M with ranks r and $\tilde{r}$, respectively. Let ∇ be a connection in $TM$ (which automatically induces a connection in all tensor bundles), ${\nabla }^E$ be a connection in E and ${\nabla }^{\tilde{E}}$ be a connection in $\tilde{E}$. Let $(U,\phi ,\rho )$ be a total trivialization triple for E.

(1)

${\{{\mathsf{\partial }}_i={\phi }_{*}^{-1}\frac{\mathsf{\partial }}{\mathsf{\partial }{x}^i}\}}_{1\le i\le n}$ is a coordinate frame for $TM$ over U.

(2)

${\{s_a={\rho }^{-1}(e_a)\}}_{1\le a\le r}$ is a local frame for E over U (${\{e_a\}}_{1\le a\le r}$ is the standard basis for ${\mathbb{R}}^r$ where $r=\mathrm{rank}E$).

(3)

Christoffel Symbols for ∇ on $(U,\phi ,\rho )$: ${\nabla }_{{\mathsf{\partial }}_i}{\mathsf{\partial }}_j={\Gamma }_{ij}^k{\mathsf{\partial }}_k$.

(4)

Christoffel Symbols for ${\nabla }^E$ on $(U,\phi ,\rho )$: ${\nabla }_{{\mathsf{\partial }}_i}{s}_a={({\Gamma }_E)}_{ia}^b{s}_b$.

Furthermore, recall that for any 1-form $\omega$,

$${\nabla }_X\omega =(X^i{\mathsf{\partial }}_i{\omega }_k-X^i{\omega }_j{\Gamma }_{ik}^j)d{x}^k.$$

Therefore,

$${\nabla }_{{\mathsf{\partial }}_i}d{x}^j=-{\Gamma }_{ik}^{j}d{x}^k.$$

• Rule 1: For all $u\in C^{\infty }(M,E)$

  $${\nabla }^{E}u=d{x}^i\otimes {\nabla }_{{\mathsf{\partial }}_i}^{E}u\mathrm{on}U.$$
  The reason is as follows: Recall that for all $p\in M$, ${\nabla }^{E}u(p)\in T^{*}M\otimes E$. Since $\{d{x}^i\otimes s_a\}$ is a local frame for $T^{*}M\otimes E$ on U we have

  $${\nabla }^{E}u=R_i^{a}d{x}^i\otimes s_a=d{x}^i\otimes (R_i^a{s}_a).$$

  According to what was discussed in the study of the isomorphism $\mathrm{Hom}(V,W)\cong V^{*}\otimes W$ in Section 3 we know that at any point $p\in M$, $R_i^a$ is the element in column i and row a of the matrix of ${\nabla }^{E}u(p)$ as an element of $\mathrm{Hom}(T_{p}M,E_p)$. Therefore,

  $${\nabla }_{{\mathsf{\partial }}_i}^{E}u=R_i^a{s}_a.$$

  Consequently, we have ${\nabla }^{E}u=d{x}^i\otimes (R_i^a{s}_a)=d{x}^i\otimes {\nabla }_{{\mathsf{\partial }}_i}^{E}u$.
• Rule 2: For all $v_1\in C^{\infty }(M,E)$ and $v_2\in C^{\infty }(M,\tilde{E})$

  $${\nabla }_{{\mathsf{\partial }}_j}^{E\otimes \tilde{E}}(v_1\otimes v_2)=({\nabla }_{{\mathsf{\partial }}_j}^E{v}_1)\otimes v_2+v_1\otimes ({\nabla }_{{\mathsf{\partial }}_j}^{\tilde{E}}{v}_2).$$
• Rule 3: For all $u\in C^{\infty }(M,E)$ and $f\in C^{\infty }(M)$

  $${\nabla }^E(fu)=f{\nabla }^{E}u+df\otimes u.$$

The following two examples are taken from [35].

• Example 1: Let $u\in C^{\infty }(M,E)$. On U we may write $u=u^a{s}_a$. We have

  $$\begin{array}{cc}\hfill {\nabla }^{E}u& ={\nabla }^E(u^a{s}_a)\stackrel{\mathrm{Rule}3}{=}{u}^a{\nabla }^E{s}_a+d{u}^a\otimes s_a=u^a{\nabla }^E{s}_a+({\mathsf{\partial }}_i{u}^{a}d{x}^i)\otimes s_a\hfill \\ \hfill & \stackrel{\mathrm{Rule}1}{=}{u}^{a}d{x}^i\otimes {\nabla }_{{\mathsf{\partial }}_i}^E{s}_a+({\mathsf{\partial }}_i{u}^{a}d{x}^i)\otimes s_a\hfill \\ \hfill & =u^{a}d{x}^i\otimes \left({({\Gamma }_E)}_{ia}^b{s}_b\right)+({\mathsf{\partial }}_i{u}^{a}d{x}^i)\otimes s_a=d{x}^i\otimes \left(u^a{({\Gamma }_E)}_{ia}^b{s}_b\right)+d{x}^i\otimes ({\mathsf{\partial }}_i{u}^a{s}_a)\hfill \\ \hfill & =d{x}^i\otimes \left(u^b{({\Gamma }_E)}_{ib}^a{s}_a\right)+d{x}^i\otimes ({\mathsf{\partial }}_i{u}^a{s}_a)\hfill \\ \hfill & =[{\mathsf{\partial }}_i{u}^a+{({\Gamma }_E)}_{ib}^a{u}^b]d{x}^i\otimes s_a.\hfill \end{array}$$

  That is, ${\nabla }^{E}u={({\nabla }^{E}u)}_i^{a}d{x}^i\otimes s_a$ where

  $${({\nabla }^{E}u)}_i^a={\mathsf{\partial }}_i{u}^a+{({\Gamma }_E)}_{ib}^a{u}^b.$$
• Example 2: Let $u\in C^{\infty }(M,E)$. On U we may write $u=u^a{s}_a$. We have

  $$\begin{array}{cc}\hfill {({\nabla }^E)}^{2}u& ={\nabla }^{T^{*}M\otimes E}\left([{\mathsf{\partial }}_i{u}^a+{({\Gamma }_E)}_{ib}^a{u}^b]d{x}^i\otimes s_a\right)\hfill \\ \hfill & \stackrel{\mathrm{Rule}3}{=}[{\mathsf{\partial }}_i{u}^a+{({\Gamma }_E)}_{ib}^a{u}^b]{\nabla }^{T^{*}M\otimes E}(d{x}^i\otimes s_a)+d[{\mathsf{\partial }}_i{u}^a+{({\Gamma }_E)}_{ib}^a{u}^b]\otimes (d{x}^i\otimes s_a)\hfill \\ \hfill & \stackrel{\mathrm{Rule}1}{=}[{\mathsf{\partial }}_i{u}^a+{({\Gamma }_E)}_{ib}^a{u}^b]d{x}^j\otimes {\nabla }_{{\mathsf{\partial }}_j}^{T^{*}M\otimes E}(d{x}^i\otimes s_a)+d[{\mathsf{\partial }}_i{u}^a+{({\Gamma }_E)}_{ib}^a{u}^b]\otimes (d{x}^i\otimes s_a)\hfill \\ \hfill & \stackrel{\mathrm{Def}.\mathrm{of}d}{=}[{\mathsf{\partial }}_i{u}^a+{({\Gamma }_E)}_{ib}^a{u}^b]d{x}^j\otimes {\nabla }_{{\mathsf{\partial }}_j}^{T^{*}M\otimes E}(d{x}^i\otimes s_a)+{\mathsf{\partial }}_j[{\mathsf{\partial }}_i{u}^a+{({\Gamma }_E)}_{ib}^a{u}^b]d{x}^j\otimes d{x}^i\otimes s_a\hfill \\ \hfill & \stackrel{\mathrm{Rule}2}{=}[{\mathsf{\partial }}_i{u}^a+{({\Gamma }_E)}_{ib}^a{u}^b]d{x}^j\otimes \left[{\nabla }_{{\mathsf{\partial }}_j}^{T^{*}M}d{x}^i\otimes s_a+d{x}^i\otimes {\nabla }_{{\mathsf{\partial }}_j}^E{s}_a\right]+{\mathsf{\partial }}_j[{\mathsf{\partial }}_i{u}^a+{({\Gamma }_E)}_{ib}^a{u}^b]d{x}^j\otimes d{x}^i\otimes s_a\hfill \\ \hfill & =[{\mathsf{\partial }}_i{u}^a+{({\Gamma }_E)}_{ib}^a{u}^b]d{x}^j\otimes \left[-{\Gamma }_{jk}^{i}d{x}^k\otimes s_a+d{x}^i\otimes {({\Gamma }_E)}_{ja}^c{s}_c\right]+{\mathsf{\partial }}_j[{\mathsf{\partial }}_i{u}^a+{({\Gamma }_E)}_{ib}^a{u}^b]d{x}^j\otimes d{x}^i\otimes s_a\hfill \\ \hfill & \stackrel{i\leftrightarrow k\mathrm{in}\mathrm{the}\mathrm{first}\mathrm{summand}}{=}[{\mathsf{\partial }}_k{u}^a+{({\Gamma }_E)}_{kb}^a{u}^b]d{x}^j\otimes \left[-{\Gamma }_{ji}^{k}d{x}^i\otimes s_a+d{x}^k\otimes {({\Gamma }_E)}_{ja}^c{s}_c\right]+{\mathsf{\partial }}_j[{\mathsf{\partial }}_i{u}^a+{({\Gamma }_E)}_{ib}^a{u}^b]d{x}^j\otimes d{x}^i\otimes s_a\hfill \\ \hfill & =\{{\mathsf{\partial }}_j[{\mathsf{\partial }}_i{u}^a+{({\Gamma }_E)}_{ib}^a{u}^b]-{\Gamma }_{ji}^k[{\mathsf{\partial }}_k{u}^a+{({\Gamma }_E)}_{kb}^a{u}^b]\}d{x}^j\otimes d{x}^i\otimes s_a+[{\mathsf{\partial }}_k{u}^a+{({\Gamma }_E)}_{kb}^a{u}^b]{({\Gamma }_E)}_{ja}^{c}d{x}^j\otimes d{x}^k\otimes s_c\hfill \\ \hfill & \stackrel{i\leftrightarrow k\mathrm{in}\mathrm{the}\mathrm{last}\mathrm{summand}}{=}\{{\mathsf{\partial }}_j[{\mathsf{\partial }}_i{u}^a+{({\Gamma }_E)}_{ib}^a{u}^b]-{\Gamma }_{ji}^k[{\mathsf{\partial }}_k{u}^a+{({\Gamma }_E)}_{kb}^a{u}^b]\}d{x}^j\otimes d{x}^i\otimes s_a\hfill \\ \hfill & +[{\mathsf{\partial }}_i{u}^a+{({\Gamma }_E)}_{ib}^a{u}^b]{({\Gamma }_E)}_{ja}^{c}d{x}^j\otimes d{x}^i\otimes s_c\hfill \\ \hfill & \stackrel{c\leftrightarrow a\mathrm{in}\mathrm{the}\mathrm{last}\mathrm{summand}}{=}\{{\mathsf{\partial }}_j[{\mathsf{\partial }}_i{u}^a+{({\Gamma }_E)}_{ib}^a{u}^b]-{\Gamma }_{ji}^k[{\mathsf{\partial }}_k{u}^a+{({\Gamma }_E)}_{kb}^a{u}^b]\}d{x}^j\otimes d{x}^i\otimes s_a\hfill \\ \hfill & +[{\mathsf{\partial }}_i{u}^c+{({\Gamma }_E)}_{ib}^c{u}^b]{({\Gamma }_E)}_{jc}^{a}d{x}^j\otimes d{x}^i\otimes s_a.\hfill \end{array}$$

Considering the above examples we make the following two useful observations that can be proved by induction.

• Observation 1: In general ${({\nabla }^E)}^{k}u={\left({({\nabla }^E)}^{k}u\right)}_{i_1\dots i_k}^{a}d{x}^{i_1}\otimes \dots \otimes d{x}^{i_k}\otimes s_a$$(1\le a\le r,1\le i_1,\dots ,i_k\le n)$ where $({({\nabla }^E)}^{k}u{)}_{i_1\dots i_k}^a\circ {\phi }^{-1}$ is a linear combination of $u^1\circ {\phi }^{-1},\dots ,u^r\circ {\phi }^{-1}$ and their partial derivatives up to order k and the coefficients are polynomials in terms of Christoffel symbols (of the linear connection on M and connection in E) and their derivatives (on a compact manifold these coefficients are uniformly bounded provided that the metric and the fiber metric are smooth). That is,

  $${({({\nabla }^E)}^{k}u)}_{i_1\dots i_k}^a\circ {\phi }^{-1}=\sum _{|\eta |\le k}\sum _{l=1}^r{C}_{\eta l}{\mathsf{\partial }}^{\eta }(u^l\circ {\phi }^{-1}),$$

  where for each $\eta$ and l, $C_{\eta l}$ is a polynomial in terms of Christoffel symbols (of the linear connection on M and connection in E) and their derivatives.
• Observation 2: The highest order term in $({({\nabla }^E)}^{k}u{)}_{i_1\dots i_k}^a\circ {\phi }^{-1}$ is $\frac{\mathsf{\partial }}{x^{i_1}}\dots \frac{\mathsf{\partial }}{x^{i_k}}(u^a\circ {\phi }^{-1})$; that is,

  $$\begin{array}{c}\hfill ({({\nabla }^E)}^{k}u{)}_{i_1\dots i_k}^a\circ {\phi }^{-1}=\frac{\mathsf{\partial }}{\mathsf{\partial }{x}^{i_1}}\dots \frac{\mathsf{\partial }}{\mathsf{\partial }{x}^{i_k}}(u^a\circ {\phi }^{-1})+\dots \end{array}$$

  where extra terms contain derivatives of order at most $k-1$ of $u^l\circ {\phi }^{-1}$$(1\le l\le r)$:

  $${({({\nabla }^E)}^{k}u)}_{i_1\dots i_k}^a\circ {\phi }^{-1}=\frac{{\mathsf{\partial }}^k}{\mathsf{\partial }{x}^{i_1}\dots \mathsf{\partial }{x}^{i_k}}(u^a\circ {\phi }^{-1})+\sum _{|\eta |<k}\sum _{l=1}^r{C}_{\eta l}{\mathsf{\partial }}^{\eta }(u^l\circ {\phi }^{-1}).$$

6. Some Results from the Theory of Generalized Functions

In this section, we collect some results from the theory of distributions that will be needed for our definition of function spaces on manifolds. Our main reference for this part is the exquisite exposition by Marcel De Reus [24].

6.1. Distributions on Domains in Euclidean Space

Let $\Omega$ be a nonempty open set in ${\mathbb{R}}^n$.

(1)

Recall that

• $\mathcal{K}(\Omega )$ is the collection of all compact subsets of $\Omega$.
• $C^{\infty }(\Omega )$ = the collection of all infinitely differentiable (real-valued) functions on $\Omega$.
• For all $K\in \mathcal{K}(\Omega )$, $C_K^{\infty }(\Omega )=\{\phi \in C^{\infty }(\Omega ):\mathrm{supp}\phi \subseteq K\}$.
• $C_c^{\infty }(\Omega )={\bigcup }_{K\in \mathcal{K}(\Omega )}{C}_K^{\infty }(\Omega )=\{\phi \in C^{\infty }(\Omega ):\mathrm{supp}\phi \mathrm{is}\mathrm{compact}\mathrm{in}\Omega \}$.

(2)

For all $\phi \in C^{\infty }(\Omega )$, $j\in \mathbb{N}$ and $K\in \mathcal{K}(\Omega )$ we define

$${\parallel \phi \parallel }_{j,K}:=sup\{|{\mathsf{\partial }}^{\alpha }\phi (x)|:|\alpha |\le j,x\in K\}.$$

(3)

For all $j\in \mathbb{N}$ and $K\in \mathcal{K}(\Omega )$, ${\parallel .\parallel }_{j,K}$ is a seminorm on $C^{\infty }(\Omega )$. We define $\mathcal{E}(\Omega )$ to be $C^{\infty }(\Omega )$ equipped with the natural topology induced by the separating family of seminorms ${\{\parallel .\parallel }_{j,K}{\}}_{j\in \mathbb{N},K\in \mathcal{K}(\Omega )}$. It can be shown that $\mathcal{E}(\Omega )$ is a Frechet space.

(4)

For all $K\in \mathcal{K}(\Omega )$ we define ${\mathcal{E}}_K(\Omega )$ to be $C_K^{\infty }(\Omega )$ equipped with the subspace topology. This subspace topology on $C_K^{\infty }(\Omega )$ is the natural topology induced by the separating family of seminorms ${\{\parallel .\parallel }_{j,K}{\}}_{j\in \mathbb{N}}$. Since $C_K^{\infty }(\Omega )$ is a closed subset of the Frechet space $\mathcal{E}(\Omega )$, ${\mathcal{E}}_K(\Omega )$ is also a Frechet space.

(5)

We define $D(\Omega )={\bigcup }_{K\in \mathcal{K}(\Omega )}{\mathcal{E}}_K(\Omega )$ equipped with the inductive limit topology with respect to the family of vector subspaces ${\{{\mathcal{E}}_K(\Omega )\}}_{K\in \mathcal{K}(\Omega )}$. It can be shown that if ${\{K_j\}}_{j\in {\mathbb{N}}_0}$ is an exhaustion by compacts sets of $\Omega$, then the inductive limit topology on $D(\Omega )$ with respect to the family ${\{{\mathcal{E}}_{K_j}\}}_{j\in {\mathbb{N}}_0}$ is exactly the same as the inductive limit topology with respect to ${\{{\mathcal{E}}_K(\Omega )\}}_{K\in \mathcal{K}(\Omega )}$.

Remark 22.

Let us mention a trivial but extremely useful consequence of the above description of the inductive limit topology on $D(\Omega )$. Suppose Y is a topological space and the mapping $T:Y\to D(\Omega )$ is such that $T(Y)\subseteq {\mathcal{E}}_K(\Omega )$ for some $K\in \mathcal{K}(\Omega )$. Since ${\mathcal{E}}_K(\Omega )\hookrightarrow D(\Omega )$, if $T:Y\to {\mathcal{E}}_K(\Omega )$ is continuous, then $T:Y\to D(\Omega )$ will be continuous.

Theorem 38

(Convergence and Continuity for $\mathcal{E}(\Omega )$). Let Ω be a nonempty open set in ${\mathbb{R}}^n$. Let Y be a topological vector space whose topology is induced by a separating family of seminorms $\mathcal{Q}$.

(1) 

A sequence $\{{\phi }_m\}$ converges to φ in $\mathcal{E}(\Omega )$ if and only if $\parallel {\phi }_m{-\phi \parallel }_{j,K}\to 0$ for all $j\in \mathbb{N}$ and $K\in \mathcal{K}(\Omega )$.

(2) 

Suppose $T:\mathcal{E}(\Omega )\to Y$ is a linear map. Then the following is equivalent

• T is continuous.
• For every $q\in \mathcal{Q}$, there exist $j\in \mathbb{N}$ and $K\in \mathcal{K}(\Omega )$, and $C>0$ such that

  $$\forall \phi \in \mathcal{E}(\Omega )q(T(\phi ))\le {C\parallel \phi \parallel }_{j,K}.$$
• If ${\phi }_m\to 0$ in $\mathcal{E}(\Omega )$, then $T({\phi }_m)\to 0$ in Y.

(3) 

In particular, a linear map $T:\mathcal{E}(\Omega )\to \mathbb{R}$ is continuous if and only if there exist $j\in \mathbb{N}$ and $K\in \mathcal{K}(\Omega )$, and $C>0$ such that

$$\forall \phi \in \mathcal{E}(\Omega )|T(\phi )|\le {C\parallel \phi \parallel }_{j,K}.$$

(4) 

A linear map $T:Y\to \mathcal{E}(\Omega )$ is continuous if and only if

$$\forall j\in \mathbb{N},\forall K\in \mathcal{K}(\Omega )\exists C>0,k\in \mathbb{N},q_1,\dots ,q_k\in \mathcal{Q}such that \forall y{\parallel T(y)\parallel }_{j,K}\le C\underset{1\le i\le k}{max}{q}_i(y).$$

Theorem 39

(Convergence and Continuity for ${\mathcal{E}}_K(\Omega )$). Let Ω be a nonempty open set in ${\mathbb{R}}^n$ and $K\in \mathcal{K}(\Omega )$. Let Y be a topological vector space whose topology is induced by a separating family of seminorms $\mathcal{Q}$.

(1) 

A sequence $\{{\phi }_m\}$ converges to φ in ${\mathcal{E}}_K(\Omega )$ if and only if $\parallel {\phi }_m{-\phi \parallel }_{j,K}\to 0$ for all $j\in \mathbb{N}$.

(2) 

Suppose $T:{\mathcal{E}}_K(\Omega )\to Y$ is a linear map. Then the following is equivalent:

• T is continuous.
• For every $q\in \mathcal{Q}$, there exists $j\in \mathbb{N}$ and $C>0$ such that

  $$\forall \phi \in {\mathcal{E}}_K(\Omega )q(T(\phi ))\le C{\parallel \phi \parallel }_{j,K}.$$
• If ${\phi }_m\to 0$ in ${\mathcal{E}}_K(\Omega )$, then $T({\phi }_m)\to 0$ in Y.

Theorem 40

(Convergence and Continuity for $D(\Omega )$). Let Ω be a nonempty open set in ${\mathbb{R}}^n$. Let Y be a topological vector space whose topology is induced by a separating family of seminorms $\mathcal{Q}$.

(1) 

A sequence $\{{\phi }_m\}$ converges to φ in $D(\Omega )$ if and only if there is a $K\in \mathcal{K}(\Omega )$ such that $supp{\phi }_m\subseteq K$ and ${\phi }_m\to \phi$ in ${\mathcal{E}}_K(\Omega )$.

(2) 

Suppose $T:D(\Omega )\to Y$ is a linear map. Then the following is equivalent

• T is continuous.
• For all $K\in \mathcal{K}(\Omega )$, $T:{\mathcal{E}}_K(\Omega )\to Y$ is continuous.
• For every $q\in \mathcal{Q}$ and $K\in \mathcal{K}(\Omega )$, there exists $j\in \mathbb{N}$ and $C>0$ such that

  $$\forall \phi \in {\mathcal{E}}_K(\Omega )q(T(\phi ))\le C{\parallel \phi \parallel }_{j,K}.$$
• If ${\phi }_m\to 0$ in $D(\Omega )$, then $T({\phi }_m)\to 0$ in Y.

(3) 

In particular, a linear map $T:D(\Omega )\to \mathbb{R}$ is continuous if and only if for every $K\in \mathcal{K}(\Omega )$, there exists $j\in \mathbb{N}$ and $C>0$ such that

$$\forall \phi \in {\mathcal{E}}_K(\Omega )|T(\phi )|\le {C\parallel \phi \parallel }_{j,K}.$$

Remark 23.

Let Ω be a nonempty open set in ${\mathbb{R}}^n$. Here are two immediate consequences of the previous theorems and remark:

(1) 

The identity map

$$i_{D,\mathcal{E}}:D(\Omega )\to \mathcal{E}(\Omega )$$

is continuous (that is, $D(\Omega )\hookrightarrow \mathcal{E}(\Omega )$ ).

(2) 

If $T:\mathcal{E}(\Omega )\to \mathcal{E}(\Omega )$ is a continuous linear map such that $supp(T\phi )\subseteq supp\phi$ for all $\phi \in \mathcal{E}(\Omega )$ (i.e., T is a local continuous linear map), then T restricts to a continuous linear map from $D(\Omega )$ to $D(\Omega )$. Indeed, the assumption $supp(T\phi )\subseteq supp\phi$ implies that $T(D(\Omega ))\subseteq D(\Omega )$. Moreover, $T:D(\Omega )\to D(\Omega )$ is continuous if and only if for $K\in \mathcal{K}(\Omega )$$T:{\mathcal{E}}_K(\Omega )\to D(\Omega )$ is continuous. Since $T({\mathcal{E}}_K(\Omega ))\subseteq {\mathcal{E}}_K(\Omega )$, this map is continuous if and only if $T:{\mathcal{E}}_K(\Omega )\to {\mathcal{E}}_K(\Omega )$ is continuous (see Remark 22). However, since the topology of ${\mathcal{E}}_K(\Omega )$ is the induced topology from $\mathcal{E}(\Omega )$, the continuity of the preceding map follows from the continuity of $T:\mathcal{E}(\Omega )\to \mathcal{E}(\Omega )$.

Theorem 41.

Let Ω be a nonempty open set in ${\mathbb{R}}^n$. Let Y be a topological vector space whose topology is induced by a separating family of seminorms $\mathcal{Q}$. Suppose $T:{[D(\Omega )]}^{\times r}\to Y$ is a linear map. The following are equivalent: (product spaces are equipped with the product topology)

(1) 

$T:{[D(\Omega )]}^{\times r}\to Y$ is continuous.

(2) 

For all $K\in \mathcal{K}(\Omega )$, $T:{[{\mathcal{E}}_K(\Omega )]}^{\times r}\to Y$ is continuous.

(3) 

For all $q\in \mathcal{Q}$ and $K\in \mathcal{K}(\Omega )$, there exists $j_1,\dots ,j_l\in \mathbb{N}$ such that

$$\forall ({\phi }_1,\dots ,{\phi }_r)\in {[{\mathcal{E}}_K(\Omega )]}^{\times r}|q\circ T({\phi }_1,\dots ,{\phi }_r)|\le C(\parallel {\phi }_1{\parallel }_{j_1,K}+\dots +\parallel {\phi }_r{\parallel }_{j_r,K}).$$

Theorem 42.

Let Ω be a nonempty open set in ${\mathbb{R}}^n$.

(1) 

A set $B\subseteq D(\Omega )$ is bounded if and only if there exists $K\in \mathcal{K}(\Omega )$ such that B is a bounded subset of ${\mathcal{E}}_K(\Omega )$ which is in turn equivalent to the following statement:

$$\forall j\in \mathbb{N}\exists r_j\ge 0suchthat\forall \phi \in B{\parallel \phi \parallel }_{j,K}\le r_j.$$

(2) 

If $\{{\phi }_m\}$ is a Cauchy sequence in $D(\Omega )$, then it converges to a function $\phi \in D(\Omega )$. We say $D(\Omega )$ is sequentially complete.

Remark 24.

Topological spaces whose topology is determined by knowing the convergent sequences and their limits exhibit nice properties and are of particular interest. Let us recall a number of useful definitions related to this topic:

• Let X be a topological space and let $E\subseteq X$. The sequential closure of E, denoted $scl(E)$ is defined as follows:

  $$scl(E)=\{x\in X:thereisasequence\{x_n\}inEsuchthat{x}_n\to x\}.$$

  Clearly, $scl(E)$ is contained in the closure if E.
• A topological space X is called a Frechet-Urysohn space if for every $E\subseteq X$ the sequential closure of E is equal to the closure of E.
• A subset E of a topological space X is said to be sequentially closed if $E=scl(E)$.
• A topological space X is said to be sequential if for every $E\subseteq X$, E is closed if and only if E is sequentially closed. If X is a sequential topological space and Y is any topological space, then a map $f:X\to Y$ is continuous if and only if

  $$\underset{n\to \infty }{lim}f(x_n)=f(\underset{n\to \infty }{lim}{x}_n)$$

  for each convergent sequence $\{x_n\}$ in X.

The following implications hold for a topological space X:

$$Xismetrizable\to Xisfirst\text{-}countable\to XisFrechet\text{-}Urysohn\to Xissequential$$

As it was stated, $\mathcal{E}$ and ${\mathcal{E}}_K$ (For all $K\in \mathcal{K}(\Omega )$) are Frechet and subsequently they are metrizable. However, it can be shown that $D(\Omega )$ is not first-countable and subsequently it is not metrizable. In fact, although according to Theorem 40, the elements of the dual of $D(\Omega )$ can be determined by knowing the convergent sequences in $D(\Omega )$, it can be proved that $D(\Omega )$ is not sequential.

Definition 18.

Let Ω be a nonempty open set in ${\mathbb{R}}^n$. The topological dual of $D(\Omega )$, denoted $D^{\prime }(\Omega )$ $(D^{\prime }(\Omega )={[D(\Omega )]}^{*})$, is called the space of distributions on Ω. Each element of $D^{\prime }(\Omega )$ is called a distribution on Ω.

Remark 25.

Every function $f\in L_{loc}^1(\Omega )$ defines a distribution $u_f\in D^{\prime }(\Omega )$ as follows:

$$\forall \phi \in D(\Omega )u_f(\phi ):={\int }_{\Omega }f\phi dx.$$

(1)

In particular, every function $\phi \in \mathcal{E}(\Omega )$ defines a distribution $u_{\phi }$. It can be shown that the map $j:\mathcal{E}(\Omega )\to D^{\prime }(\Omega )$ which sends φ to $u_{\phi }$ is an injective linear continuous map ([24], p. 11). Therefore, we can identify $\mathcal{E}(\Omega )$ with a subspace of $D^{\prime }(\Omega )$.

Remark 26.

Let $\Omega \subseteq {\mathbb{R}}^n$ be a nonempty open set. Recall that $f:\Omega \to \mathbb{R}$ is locally integrable ($f\in L_{loc}^1(\Omega )$) if it satisfies any of the following equivalent conditions:

(1) 

$f\in L^1(K)$ for all $K\in \mathcal{K}(\Omega )$.

(2) 

For all $\phi \in C_c^{\infty }(\Omega )$, $f\phi \in L^1(\Omega )$.

(3) 

For every nonempty open set $V\subseteq \Omega$ such that $\overline{V}$ is compact and contained in Ω, $f\in L^1(V)$.

(It can be shown that every locally integrable function is measurable ([36], p. 70)).

As a consequence, if we define ${Func}_{reg}(\Omega )$ to be the set

$$\{f:\Omega \to \mathbb{R}:u_f:D(\Omega )\to \mathbb{R}definedbyEquation(1)iswell\text{-}definedandcontinuous\},$$

then ${Func}_{reg}(\Omega )=L_{loc}^1(\Omega )$.

Definition 19

(Calculus Rules for Distributions). Let Ω be a nonempty open set in ${\mathbb{R}}^n$. Let $u\in D^{\prime }(\Omega )$.

• For all $\phi \in C^{\infty }(\Omega )$, $\phi u$ is defined by

  $$\forall \psi \in C_c^{\infty }(\Omega )[\phi u](\psi ):=u(\phi \psi ).$$
  It can be shown that $\phi u\in D^{\prime }(\Omega )$.
• For all multiindices α, ${\mathsf{\partial }}^{\alpha }u$ is defined by

  $$\forall \psi \in C_c^{\infty }(\Omega )[{\mathsf{\partial }}^{\alpha }u](\psi )={(-1)}^{|\alpha |}u({\mathsf{\partial }}^{\alpha }\psi ).$$
  It can be shown that ${\mathsf{\partial }}^{\alpha }u\in D^{\prime }(\Omega )$.

Furthermore, it is possible to make sense of “change of coordinates” for distributions. Let $\Omega$ and ${\Omega }^{\prime }$ be two open sets in ${\mathbb{R}}^n$. Suppose $T:\Omega \to {\Omega }^{\prime }$ is a $C^{\infty }$ diffeomorphism. T can be used to move any function on $\Omega$ to a function on ${\Omega }^{\prime }$ and vice versa.

$$\begin{array}{cc}\hfill & T^{*}:\mathrm{Func}({\Omega }^{\prime },\mathbb{R})\to \mathrm{Func}(\Omega ,\mathbb{R}),T^{*}(f)=f\circ T,\hfill \\ \hfill & T_{*}:\mathrm{Func}(\Omega ,\mathbb{R})\to \mathrm{Func}({\Omega }^{\prime },\mathbb{R}),T_{*}(f)=f\circ T^{-1}.\hfill \end{array}$$

$T^{*}f$ is called the pullback of the function f under the mapping T and $T_{*}f$ is called the pushforward of the function f under the mapping T. Clearly, $T^{*}$ and $T_{*}$ are inverses of each other and $T_{*}={(T^{-1})}^{*}$. One can show that $T_{*}$ sends functions in $L_{loc}^1(\Omega )$ to $L_{loc}^1({\Omega }^{\prime })$ and furthermore $T_{*}$ restricts to linear topological isomorphisms $T_{*}:\mathcal{E}(\Omega )\to \mathcal{E}({\Omega }^{\prime })$ and $T_{*}:D(\Omega )\to D({\Omega }^{\prime })$. Note that for all $f\in L_{loc}^1(\Omega )$ and $\phi \in C_c^{\infty }({\Omega }^{\prime })$

$$\begin{array}{cc}\hfill <u_{T_{*}f},\phi {>}_{D^{\prime }({\Omega }^{\prime })\times D({\Omega }^{\prime })}& ={\int }_{{\Omega }^{\prime }}(T_{*}f)(y)\phi (y)dy={\int }_{{\Omega }^{\prime }}(f\circ T^{-1})(y)\phi (y)dy\hfill \\ \hfill & \stackrel{x=T^{-1}(y)}{=}{\int }_{\Omega }f(x)\phi (T(x))|\det T^{\prime }(x)|dx\hfill \\ \hfill & =<u_f,|\det T^{\prime }(x)|\phi (T(x)){>}_{D^{\prime }(\Omega )\times D(\Omega )}.\hfill \end{array}$$

The above observation motivates us to define the pushforward of any distribution $u\in D^{\prime }(\Omega )$ as follows:

$$\forall \phi \in D({\Omega }^{\prime }){⟨T_{*}u,\phi ⟩}_{D^{\prime }({\Omega }^{\prime })\times D({\Omega }^{\prime })}:=⟨u,|\det T^{\prime }(x){|\phi (T(x))⟩}_{D^{\prime }(\Omega )\times D(\Omega )}.$$

It can be shown that $T_{*}u:D({\Omega }^{\prime })\to \mathbb{R}$ is continuous and so it is in fact an element of $D^{\prime }({\Omega }^{\prime })$. Similarly, the pullback $T^{*}:D^{\prime }({\Omega }^{\prime })\to D^{\prime }(\Omega )$ is defined by

$$\forall \phi \in D(\Omega ){⟨T^{*}u,\phi ⟩}_{D^{\prime }(\Omega )\times D(\Omega )}:=⟨u,|\det {(T^{-1})}^{\prime }(y){|\phi (T^{-1}(y))⟩}_{D^{\prime }({\Omega }^{\prime })\times D({\Omega }^{\prime })}.$$

It can be shown that $T^{*}u:D(\Omega )\to \mathbb{R}$ is continuous and so it is in fact an element of $D^{\prime }(\Omega )$.

Definition 20

(Extension by Zero of a Function). Let Ω be an open subset of ${\mathbb{R}}^n$ and V be an open susbset of Ω. We define the linear map ${ext}_{V,\Omega }^0:Func(V,\mathbb{R})\to Func(\Omega ,\mathbb{R})$ as follows:

$${ext}_{V,\Omega }^0(f)(x)=\left\{\begin{array}{c}f(x)ifx\in V\hfill \\ 0ifx\in \Omega \backslash V\hfill \end{array}\right..$$

${ext}_{V,\Omega }^0$ restricts to a continuous linear map $D(V)\to D(\Omega )$.

Definition 21

(Restriction of a Distribution). Let Ω be an open subset of ${\mathbb{R}}^n$ and V be an open susbset of Ω. We define the restriction map ${res}_{\Omega ,V}:D^{\prime }(\Omega )\to D^{\prime }(V)$ as follows:

$${⟨{res}_{\Omega ,V}u,\phi ⟩}_{D^{\prime }(V)\times D(V)}:={⟨u,{ext}_{V,\Omega }^0\phi ⟩}_{D^{\prime }(\Omega )\times D(\Omega )}.$$

This is well-defined; indeed, ${res}_{\Omega ,V}:D^{\prime }(\Omega )\to D^{\prime }(V)$ is a continuous linear map as it is the adjoint of the continuous map ${ext}_{V,\Omega }^0:D(V)\to D(\Omega )$. Given $u\in D^{\prime }(\Omega )$, we sometimes write ${u|}_V$ instead of ${res}_{\Omega ,V}u$.

Remark 27.

It is easy to see that the restriction of the map ${res}_{\Omega ,V}:D^{\prime }(\Omega )\to D^{\prime }(V)$ to $\mathcal{E}(\Omega )$ agrees with the usual restriction of smooth functions.

Definition 22

(Support of a Distribution). Let Ω be a nonempty open set in ${\mathbb{R}}^n$. Let $u\in D^{\prime }(\Omega )$.

• We say u is equal to zero on some open subset V of Ω if ${u|}_V=0$.
• Let ${\{V_i\}}_{i\in I}$ be the collection of all open subsets of Ω such that u is equal to zero on $V_i$. Let $V={\bigcup }_{i\in I}{V}_i$. The support of u is defined as follows:

  $$suppu:=\Omega \backslash V.$$

  Note that $suppu$ is closed in Ω but it is not necessarily closed in ${\mathbb{R}}^n$.

Theorem 43

(Properties of the Support [20,23,24]). Let Ω and ${\Omega }^{\prime }$ be nonempty open sets in ${\mathbb{R}}^n$.

• If $f\in L_{loc}^1(\Omega )$, then $suppf=supp{u}_f$.
• For all $u\in D^{\prime }(\Omega )$, $u=0$ on $\Omega \backslash suppu$.
• Let $u\in D^{\prime }(\Omega )$. If $\phi \in D(\Omega )$ vanishes on an open neighborhood of $suppu$, then $u(\phi )=0$.
• For every closed subset A of Ω and every $u\in D^{\prime }(\Omega )$, we have $suppu\subseteq A$ if and only if $u(\phi )=0$ for every $\phi \in D(\Omega )$ with $supp\phi \subseteq \Omega \backslash A$.
• For every $u\in D^{\prime }(\Omega )$ and $\psi \in \mathcal{E}(\Omega )$, $supp(\psi u)\subseteq supp(\psi )\cap supp(u)$.
• Let $u,v\in D^{\prime }(\Omega )$. If there exists a nonempty open subset U of Ω such that $suppu\subseteq U$ and $suppv\subseteq U$ and

  $${⟨u{|}_U,\phi ⟩}_{D^{\prime }(U)\times D(U)}={⟨v{|}_U,\phi ⟩}_{D^{\prime }(U)\times D(U)}\forall \phi \in C_c^{\infty }(U),$$

  then $u=v$ as elements of $D^{\prime }(\Omega )$.
• Let $u,v\in D^{\prime }(\Omega )$. Then $supp(u+v)\subseteq suppu\cup suppv$.
• Let $\{u_i\}$ be a sequence in $D^{\prime }(\Omega )$, $u\in D(\Omega )$, and $K\in \mathcal{K}(\Omega )$ such that $u_i\to u$ in $D^{\prime }(\Omega )$ and $supp{u}_i\subseteq K$ for all i. Then also $suppu\subseteq K$.
• For every $u\in D^{\prime }(\Omega )$ and $\alpha \in {\mathbb{N}}_0^n$, $supp({\mathsf{\partial }}^{\alpha }u)\subseteq supp(u)$.
• If $T:\Omega \to {\Omega }^{\prime }$ is a diffeomorphism, then $supp(T_{*}u)=T(suppu)$. In particular, if u has compact support, then so has $T_{*}u$.

Considering the eighth item in the above theorem, an interesting question that one may ask is the following: Let $\{u_i\}$ be a sequence in $D(\Omega )$ such that $u_i\to u$ in $D^{\prime }(\Omega )$, and suppose there exists $K\in \mathcal{K}(\Omega )$ such that $\mathrm{supp}u\subseteq K$. Does the fact that the limiting distribution has compact support imply that there exists a compact set $\tilde{K}$ such that $\mathrm{supp}{u}_i\subseteq \tilde{K}$ for all i? The answer is negative. For example, for each $i\in \mathbb{N}$ let $u_i\in D(\mathbb{R})$ be a nonnegative function such that $u_i=0$ outside the interval $(i,i+1)$ and ${\int }_i^{i+1}{u}_{i}dx=\frac{1}{i}$. Clearly, $u_i\to 0$ in $L^1(\mathbb{R})$ and so $u_i\to 0$ in $D^{\prime }(\mathbb{R})$. However, there is no compact set $\tilde{K}$ such that $\mathrm{supp}{u}_i\subseteq \tilde{K}$ for all i.

Theorem 44

([24], pp. 10 and 20). Let Ω be a nonempty open set in ${\mathbb{R}}^n$. Let ${\mathcal{E}}^{\prime }(\Omega )$ denote the topological dual of $\mathcal{E}(\Omega )$ equipped with the strong topology. Then

• The map that sends $u\in {\mathcal{E}}^{\prime }(\Omega )$ to ${u|}_{D(\Omega )}$ is an injective continuous linear map from ${\mathcal{E}}^{\prime }(\Omega )$ into $D^{\prime }(\Omega )$.
• The image of the above map consists precisely of those $u\in D^{\prime }(\Omega )$ for which $suppu$ is compact.

Due to the above theorem we may identify ${\mathcal{E}}^{\prime }(\Omega )$ with distributions on $\Omega$ with compact support.

Definition 23

(Extension by Zero of Distributions With Compact Support). Let Ω be a nonempty open set in ${\mathbb{R}}^n$ and V be a nonempty open subset of Ω. We define the linear map ${ext}_{V,\Omega }^0:{\mathcal{E}}^{\prime }(V)\to {\mathcal{E}}^{\prime }(\Omega )$ as the adjoint of the continuous linear map ${res}_{\Omega ,V}:\mathcal{E}(\Omega )\to \mathcal{E}(V)$; that is,

$${⟨{ext}_{V,\Omega }^{0}u,\phi ⟩}_{{\mathcal{E}}^{\prime }(\Omega )\times \mathcal{E}(\Omega )}:={⟨u,\phi {|}_V⟩}_{{\mathcal{E}}^{\prime }(V)\times \mathcal{E}(V)}.$$

Suppose ${\Omega }^{\prime }$ and $\Omega$ are two nonempty open sets in ${\mathbb{R}}^n$ such that ${\Omega }^{\prime }\subseteq \Omega$ and $K\in \mathcal{K}({\Omega }^{\prime })$. One can easily show that:

• For all $u\in {\mathcal{E}}_K({\Omega }^{\prime })$, ${\mathrm{res}}_{{\mathbb{R}}^n,\Omega }\circ {\mathrm{ext}}_{{\Omega }^{\prime },{\mathbb{R}}^n}^{0}u={\mathrm{ext}}_{{\Omega }^{\prime },\Omega }^{0}u$.
• For all $u\in {\mathcal{E}}_K({\Omega }^{\prime })$, ${\mathrm{ext}}_{\Omega ,{\mathbb{R}}^n}^0\circ {\mathrm{ext}}_{{\Omega }^{\prime },\Omega }^{0}u={\mathrm{ext}}_{{\Omega }^{\prime },{\mathbb{R}}^n}^{0}u$.
• For all $u\in {\mathcal{E}}_K(\Omega )$, ${\mathrm{ext}}_{{\Omega }^{\prime },\Omega }^0\circ {\mathrm{res}}_{\Omega ,{\Omega }^{\prime }}u=u$.

We summarize the important topological properties of the spaces of test functions and distributions in Table 1 below.

Table 1. Topological properties of the spaces of test functions.

	$\mathit{D}(\mathsf{\Omega })$	$\mathcal{E}(\mathsf{\Omega })$	${\mathit{D}}^{\prime }(\mathsf{\Omega })$ Strong	${\mathcal{E}}^{\prime }(\mathsf{\Omega })$ Strong	${\mathit{D}}^{\prime }(\mathsf{\Omega })$ Weak	${\mathcal{E}}^{\prime }(\mathsf{\Omega })$ Weak
Sequential	No	Yes	No	No	No	No
First-Countable	No	Yes	No	No	No	No
Metrizable	No	Yes	No	No	No	No
Second-Countable	No	Yes	No	No	No	No
Sequentially Complete	Yes	Yes	Yes	Yes	Yes	Yes
Complete	Yes	Yes	Yes	Yes	No	No

6.2. Distributions on Vector Bundles

6.2.1. Basic Definitions, Notation

Let $M^n$ be a smooth manifold (M is not necessarily compact). Let $\pi :E\to M$ be a vector bundle of rank r.

(1)

$\mathcal{E}(M,E)$ is defined as $C^{\infty }(M,E)$ equipped with the locally convex topology induced by the following family of seminorms: let ${\{(U_{\alpha },{\phi }_{\alpha },{\rho }_{\alpha })\}}_{\alpha \in I}$ be a total trivialization atlas. Then for every $\alpha \in I$, $1\le l\le r$, and $f\in C^{\infty }(M,E)$, ${\tilde{f}}_{\alpha }^l:={\rho }_{\alpha }^l\circ f\circ {\phi }_{\alpha }^{-1}$ is an element of $C^{\infty }({\phi }_{\alpha }(U_{\alpha }))$. For every 4-tuple $(l,\alpha ,j,K)$ with $1\le l\le r$, $\alpha \in I$, $j\in \mathbb{N}$, K a compact subset of $U_{\alpha }$ (i.e., $K\in \mathcal{K}(U_{\alpha })$) we define

$${\parallel .\parallel }_{l,\alpha ,j,K}:C^{\infty }(M,E)\to \mathbb{R},f\mapsto {\parallel {\rho }_{\alpha }^l\circ f\circ {\phi }_{\alpha }^{-1}\parallel }_{j,{\phi }_{\alpha }(K)}.$$

It is easy to check that ${\parallel .\parallel }_{l,\alpha ,j,K}$ is a seminorm on $C^{\infty }(M,E)$ and the locally convex topology induced by the above family of seminorms does not depend on the choice of the total trivialization atlas. Sometimes we may write ${\parallel .\parallel }_{l,{\phi }_{\alpha },j,K}$ instead of ${\parallel .\parallel }_{l,\alpha ,j,K}$.

(2)

For any compact subset $K\subseteq M$ we define

$${\mathcal{E}}_K(M,E):=\{f\in \mathcal{E}(M,E):\mathrm{supp}f\subseteq K\}$$

equipped with the subspace topology.

(3)

$D(M,E):=C_c^{\infty }(M,E)={\cup }_{K\in \mathcal{K}(M)}{\mathcal{E}}_K(M,E)$ (union over all compact subsets of M) equipped with the inductive limit topology with respect to the family ${\{{\mathcal{E}}_K(M,E)\}}_{K\in \mathcal{K}(M)}$. Clearly, if M is compact, then $D(M,E)=\mathcal{E}(M,E)$ (as topological vector spaces).

Remark 28.

• If for each $\alpha \in I$, ${\{K_m^{\alpha }\}}_{m\in \mathbb{N}}$ is an exhaustion by compact sets of $U_{\alpha }$, then the topology induced by the family of seminorms

  $$\{\parallel .{\parallel }_{l,\alpha ,j,K_m^{\alpha }}:1\le l\le r,\alpha \in I,j\in \mathbb{N},m\in \mathbb{N}\}$$

  on $C^{\infty }(M,E)$ is the same as the topology of $\mathcal{E}(M,E)$. This together with the fact that every manifold has a countable total trivialization atlas shows that the topology of $\mathcal{E}(M,E)$ is induced by a countable family of seminorms. So $\mathcal{E}(M,E)$ is metrizable.
• If ${\{K_j\}}_{j\in \mathbb{N}}$ is an exhuastion by compact sets of M, then the inductive limit topology on $C_c^{\infty }(M,E)$ with respect to the family $\{{\mathcal{E}}_{K_j}(M,E)\}$ is the same as the topology on $D(M,E)$.

Definition 24.

The space of distributions on the vector bundle E, denoted $D^{\prime }(M,E)$, is defined as the topological dual of $D(M,E^{\vee })$. That is,

$$D^{\prime }(M,E)={[D(M,E^{\vee })]}^{*}.$$

As usual we equip the dual space with the strong topology. Recall that $E^{\vee }$ denotes the bundle $Hom(E,\mathcal{D}(M))$ where $\mathcal{D}(M)$ is the density bundle of M.

Remark 29.

The reason that space of distributions on the vector bundle E is defined as the dual of $D(M,E^{\vee })$ rather than the dual of the seemingly natural choice $D(M,E)$ is well explained in [24,37]. Of course, there are other nonequivalent ways to make sense of distributions on vector bundles (see [37] for a detailed discussion). Furthermore, see Lemma 13 where it is proved that Riemannian density can be used to identify $D^{\prime }(M,E)$ with ${[D(M,E)]}^{*}$.

Remark 30.

Let U and V be nonempty open sets in M with $V\subseteq U$.

• As in the Euclidean case, the linear map ${ext}_{V,U}^0:\Gamma (V,E_V^{\vee })\to \Gamma (U,E_U^{\vee })$ defined by

  $${ext}_{V,U}^{0}f(x)=\left\{\begin{array}{c}f(x)x\in V\hfill \\ 0x\in U\backslash V\hfill \end{array}\right.$$

  restricts to a continuous linear map from $D(V,E_V^{\vee })$ to $D(U,E_U^{\vee })$.
• As in the Euclidean case, the restriction map ${res}_{U,V}:D^{\prime }(U,E_U)\to D^{\prime }(V,E_V)$ is defined as the adjoint of $ex{t}_{V,U}^0$:

  $${⟨{res}_{U,V}u,\phi ⟩}_{D^{\prime }(V,E_V)\times D(V,E_V^{\vee })}={⟨u,{ext}_{V,U}^0\phi ⟩}_{D^{\prime }(U,E_U)\times D(U,E_U^{\vee })}.$$
• Support of a distribution $u\in D^{\prime }(M,E)$ is defined in the exact same way as for distributions in the Euclidean space. It can be shown that

  (1) 

  ([24], p. 105) If $u\in D^{\prime }(M,E)$ and $\phi \in D(M,E^{\vee })$ vanishes on an open neighborhood of $suppu$, then $u(\phi )=0$.

  (2) 

  ([24], p. 104) For every closed subset A of M and every $u\in D^{\prime }(M,E)$, we have $suppu\subseteq A$ if and only if $u(\phi )=0$ for every $\phi \in D(M,E^{\vee })$ with $supp\phi \subseteq M\backslash A$.

The strength of the theory of distributions in the Euclidean case is largely due to the fact that it is possible to identify a huge class of ordinary functions with distributions. A question that arises is that whether there is a natural way to identify regular sections of E (i.e., elements of $\Gamma (M,E)$) with distributions. The following theorem provides a partial answer to this question. Recall that compactly supported continuous sections of the density bundle can be integrated over M.

Theorem 45.

Every $f\in \mathcal{E}(M,E)$ defines the following continuous map:

$$u_f:D(M,E^{\vee })\to \mathbb{R},\psi \mapsto {\int }_M[\psi ,f],$$

(2)

where the pairing $[\psi ,f]$ defines a compactly supported continuous section of the density bundle:

$$\forall x\in M[\psi ,f](x):=[\psi (x)][f(x)](\psi (x)\in Hom(E_x,D_x)evaluatedatf(x)\in E_x).$$

In general, we define ${\Gamma }_{reg}(M,E)$ as the set

$$\{f\in \Gamma (M,E):u_f\mathrm{defined}\mathrm{by}\mathrm{Equation}(2)\mathrm{is} \text{well-defined} \mathrm{and}\mathrm{continuous}\}.$$

Compare this with the definition of ${\mathrm{Func}}_{reg}(\Omega )$ in Remark 26. Theorem 45 tells us that $\mathcal{E}(M,E)$ is contained in ${\Gamma }_{reg}(M,E)$. If $u\in D^{\prime }(M,E)$ is such that $u=u_f$ for some $f\in {\Gamma }_{reg}(M,E)$, then we say that u is a regular distribution.

Now, let $(U,\phi ,\rho )$ be a total trivialization triple for E and let $(U,\phi ,{\rho }_{\mathcal{D}})$ and $(U,\phi ,{\rho }^{\vee })$ be the corresponding standard total trivialization triples for $\mathcal{D}(M)$ and $E^{\vee }$, respectively. The local representation of the pairing $[\psi ,f]$ has a very simple expression in terms of the local representations of f and $\psi$:

$$\begin{array}{cc}\hfill & f\in {\Gamma }_{reg}(M,E)⟹({\tilde{f}}^1,\dots ,{\tilde{f}}^r):=(f^1\circ {\phi }^{-1},\dots ,f^r\circ {\phi }^{-1}):=\rho \circ f\circ {\phi }^{-1}\in {[\mathrm{Func}(\phi (U),\mathbb{R})]}^{\times r}\hfill \\ \hfill & ({\tilde{f}}^1,\dots ,{\tilde{f}}^r)\mathrm{is}\mathrm{the}\mathrm{local}\mathrm{representation}\mathrm{of}f.\hfill \\ \hfill & \psi \in D(M,E^{\vee })⟹({\tilde{\psi }}^1,\dots ,{\tilde{\psi }}^r):=({\psi }^1\circ {\phi }^{-1},\dots ,{\psi }^r\circ {\phi }^{-1}):={\rho }^{\vee }\circ \psi \circ {\phi }^{-1}\in {[\mathrm{Func}(\phi (U),\mathbb{R})]}^{\times r}\hfill \\ \hfill & ({\tilde{\psi }}^1,\dots ,{\tilde{\psi }}^r)\mathrm{is}\mathrm{the}\mathrm{local}\mathrm{representation}\mathrm{of}\psi .\hfill \end{array}$$

Our claim is that the local representation of $[\psi ,f]$ (that is, ${\rho }_{\mathcal{D}}\circ [\psi ,f]\circ {\phi }^{-1}$) is equal to the Euclidean dot product of the local representations of f and $\psi$:

$${\rho }_{\mathcal{D}}\circ [\psi ,f]\circ {\phi }^{-1}=\sum _i{\tilde{f}}^i{\tilde{\psi }}^i.$$

The reason is as follows: Let $y\in \phi (U)$ and $x={\phi }^{-1}(y)$

$$\begin{array}{c}[{\rho }_{\mathcal{D}}\circ [\psi ,f]\circ {\phi }^{-1}](y)={\rho }_{\mathcal{D}}\left([\psi (x)][f(x)]\right)={\rho }_{\mathcal{D}}\left([\psi (x)][{(\rho {|}_{E_x})}^{-1}({\tilde{f}}^1(y),\dots ,{\tilde{f}}^r(y))]\right)\hfill \\ =[{\rho }_{\mathcal{D}}\circ \psi (x)\circ {(\rho {|}_{E_x})}^{-1}]({\tilde{f}}^1(y),\dots ,{\tilde{f}}^r(y))\hfill \\ =[{\rho }^{\vee }(\psi (x))][({\tilde{f}}^1(y),\dots ,{\tilde{f}}^r(y))]\mathrm{the}\mathrm{left}\mathrm{bracket}\mathrm{is}\mathrm{applied}\mathrm{to}\mathrm{the}\mathrm{right}\mathrm{bracket}\hfill \\ ={\rho }^{\vee }(\psi (x))·({\tilde{f}}^1(y),\dots ,{\tilde{f}}^r(y))\mathrm{dot}\mathrm{product}!{\rho }^{\vee }(\psi (x))\mathrm{viewed}\mathrm{as}\mathrm{an}\mathrm{element}\mathrm{of}{\mathbb{R}}^r\hfill \\ =({\tilde{\psi }}^1(y),\dots ,{\tilde{\psi }}^r(y))·({\tilde{f}}^1(y),\dots ,{\tilde{f}}^r(y)).\hfill \end{array}$$

6.2.2. Local Representation of Distributions

Let $(U,\phi ,\rho )$ be a total trivialization triple for $\pi :E\to M$. We know that each $f\in \Gamma (M,E)$ can locally be represented by r components ${\tilde{f}}^1,\dots ,{\tilde{f}}^r$ defined by

$$\forall 1\le l\le r{\tilde{f}}^l:\phi (U)\to \mathbb{R},{\tilde{f}}^l={\rho }^l\circ f\circ {\phi }^{-1}.$$

These components play a crucial role in our study of Sobolev spaces. Now the question is that whether we can similarly use the total trivialization triple $(U,\phi ,\rho )$ to locally associate with each distribution $u\in D^{\prime }(M,E)$, r components ${\tilde{u}}^1,\dots ,{\tilde{u}}^r$ belonging to $D^{\prime }(\phi (U))$. That is, we want to see whether we can define a nice map

$$D^{\prime }(U,E_U)={[D(U,E_U^{\vee })]}^{*}\to \underset{r\mathrm{times}}{\underbrace{D^{\prime }(\phi (U))\times \dots \times D^{\prime }(\phi (U))}}.$$

(Note that according to Remark 30, if $u\in D^{\prime }(M,E)$, then ${u|}_U\in D^{\prime }(U,E_U)$.) Such a map, in particular, will be important when we want to make sense of Sobolev spaces with negative exponents of sections of vector bundles. Furthermore, it would be desirable to ensure that if u is a regular distribution then the components of u as a distribution agree with the components obtained when u is viewed as an element of $\Gamma (M,E)$.

We begin with the following map at the level of compactly supported smooth functions:

$${\tilde{T}}_{E^{\vee },U,\phi }:D(U,E_U^{\vee })\to {[D(\phi (U))]}^{\times r},\xi \to {\rho }^{\vee }\circ \xi \circ {\phi }^{-1}=({({\rho }^{\vee })}^1\circ \xi \circ {\phi }^{-1},\dots ,{({\rho }^{\vee })}^r\circ \xi \circ {\phi }^{-1}).$$

Note that ${\tilde{T}}_{E^{\vee },U,\phi }$ has the property that for all $\psi \in C^{\infty }(U)$ and $\xi \in D(U,E_U^{\vee })$

$${\tilde{T}}_{E^{\vee },U,\phi }(\psi \xi )=(\psi \circ {\phi }^{-1}){\tilde{T}}_{E^{\vee },U,\phi }(\xi ).$$

Theorem 46.

The map ${\tilde{T}}_{E^{\vee },U,\phi }:D(U,E_U^{\vee })\to {[D(\phi (U))]}^{\times r}$ is a linear topological isomorphism (${[D(\phi (U))]}^{\times r}$ is equipped with the product topology).

Proof. 

Clearly, ${\tilde{T}}_{E^{\vee },U,\phi }$ is linear. Furthermore, the map ${\tilde{T}}_{E^{\vee },U,\phi }$ is bijective. Indeed, the inverse of ${\tilde{T}}_{E^{\vee },U,\phi }$ (which we denote by $T_{E^{\vee },U,\phi }$) is given by

$$\begin{array}{cc}\hfill & T_{E^{\vee },U,\phi }:{[D(\phi (U))]}^{\times r}\to D(U,E_U^{\vee })\hfill \\ \hfill & \forall x\in U{T}_{E^{\vee },U,\phi }({\xi }_1,\dots ,{\xi }_r)(x)={\left({\rho }^{\vee }{|}_{E_x^{\vee }}\right)}^{-1}\circ ({\xi }_1,\dots ,{\xi }_r)\circ \phi (x).\hfill \end{array}$$

Now, we show that ${\tilde{T}}_{E^{\vee },U,\phi }:D(U,E_U^{\vee })\to {[D(\phi (U))]}^{\times r}$ is continuous. To this end, it is enough to prove that for each $1\le l\le r$ the map

$${\pi }^l\circ {\tilde{T}}_{E^{\vee },U,\phi }:D(U,E_U^{\vee })\to D(\phi (U)),\xi \mapsto {({\rho }^{\vee })}^l\circ \xi \circ {\phi }^{-1}$$

is continuous. The topology on $D(U,E_U^{\vee })$ is the inductive limit topology with respect to ${\{{\mathcal{E}}_K(U,E_U^{\vee })\}}_{K\in \mathcal{K}(U)}$, so it is enough to show that for each $K\in \mathcal{K}(U)$, ${\pi }^l\circ {\tilde{T}}_{E^{\vee },U,\phi }:{\mathcal{E}}_K(U,E_U^{\vee })\to D(\phi (U))$ is continuous. Note that ${\pi }^l\circ {\tilde{T}}_{E^{\vee },U,\phi }[{\mathcal{E}}_K(U,E_U^{\vee })]\subseteq {\mathcal{E}}_{\phi (K)}(\phi (U))$. Considering that ${\mathcal{E}}_{\phi (K)}(\phi (U))\hookrightarrow D(\phi (U))$, it is enough to show that

$${\pi }^l\circ {\tilde{T}}_{E^{\vee },U,\phi }:{\mathcal{E}}_K(U,E_U^{\vee })\to {\mathcal{E}}_{\phi (K)}(\phi (U))$$

is continuous. For all $\xi \in {\mathcal{E}}_K(U,E_U^{\vee })$ and $j\in \mathbb{N}$ we have

$$\parallel {\pi }^l\circ {\tilde{T}}_{E^{\vee },U,\phi }{(\xi )\parallel }_{j,\phi (K)}=\parallel {({\rho }^{\vee })}^l\circ \xi \circ {\phi }^{-1}{\parallel }_{j,\phi (K)}={\parallel \xi \parallel }_{l,\phi ,j,K},$$

which implies the continuity (note that even an inequality in place of the last equality would have been enough to prove the continuity). It remains to prove the continuity of $T_{E^{\vee },U,\phi }:{[D(\phi (U))]}^{\times r}\to D(U,E_U^{\vee })$. By Theorem 41 it is enough to show that for all $K\in \mathcal{K}(\phi (U))$, $T_{E^{\vee },U,\phi }:{[{\mathcal{E}}_K(\phi (U))]}^{\times r}\to D(U,E_U^{\vee })$ is continuous. It is clear that $T_{E^{\vee },U,\phi }({[{\mathcal{E}}_K(\phi (U))]}^{\times r})\subseteq {\mathcal{E}}_{{\phi }^{-1}(K)}(U,E_U^{\vee })$. Since ${\mathcal{E}}_{{\phi }^{-1}(K)}(U,E_U^{\vee })\hookrightarrow D(U,E_U^{\vee })$, it is sufficient to show that $T_{E^{\vee },U,\phi }:{[{\mathcal{E}}_K(\phi (U))]}^{\times r}\to {\mathcal{E}}_{{\phi }^{-1}(K)}(U,E_U^{\vee })$ is continuous. To this end, by Theorem 41, we just need to show that for all $j\in \mathbb{N}$ and $1\le l\le r$ there exists $j_1,\dots ,j_r$ such that

$$\parallel T_{E^{\vee },U,\phi }({\xi }_1,\dots ,{\xi }_r){\parallel }_{l,\phi ,j,{\phi }^{-1}(K)}\le C(\parallel {\xi }_1{\parallel }_{j_1,K}+\dots \parallel {\xi }_r{\parallel }_{j_r,K}).$$

However, this obviously holds because

$$\parallel T_{E^{\vee },U,\phi }({\xi }_1,\dots ,{\xi }_r){\parallel }_{l,\phi ,j,{\phi }^{-1}(K)}={\parallel {\xi }_l\parallel }_{j,K}.$$

  □

The adjoint of $T_{E^{\vee },U,\phi }$ is

$$\begin{array}{cc}\hfill & T_{E^{\vee },U,\phi }^{*}:{[D(U,E_U^{\vee })]}^{*}\to {\left({[D(\phi (U))]}^{\times r}\right)}^{*}\hfill \\ \hfill & ⟨T_{E^{\vee },U,\phi }^{*}u,({\xi }_1,\dots ,{\xi }_r)⟩=⟨u,T_{E^{\vee },U,\phi }({\xi }_1,\dots ,{\xi }_r)⟩.\hfill \end{array}$$

Note that, since $T_{E^{\vee },U,\phi }$ is a linear topological isomorphism, $T_{E^{\vee },U,\phi }^{*}$ is also a linear topological isomorphism (and in particular it is bijective). For every $u\in {[D(U,E_U^{\vee })]}^{*}$, $T_{E^{\vee },U,\phi }^{*}u$ is in ${\left({[D(\phi (U))]}^{\times r}\right)}^{*}$; we can combine this with the bijective map

$$L:{\left({[D(\phi (U))]}^{\times r}\right)}^{*}\to {[D^{\prime }(\phi (U))]}^{\times r},L(v)=(v\circ i_1,\dots ,v\circ i_r)$$

(see Theorem 24) to send $u\in {[D(U,E_U^{\vee })]}^{*}$ into an element of ${[D^{\prime }(\phi (U))]}^{\times r}$:

$$L(T_{E^{\vee },U,\phi }^{*}u)=((T_{E^{\vee },U,\phi }^{*}u)\circ i_1,\dots ,(T_{E^{\vee },U,\phi }^{*}u)\circ i_r),$$

where for all $1\le l\le r$, $(T_{E^{\vee },U,\phi }^{*}u)\circ i_l\in D^{\prime }(\phi (U))$ is given by

$$\begin{array}{cc}\hfill ((T_{E^{\vee },U,\phi }^{*}u)\circ i_l)(\xi )& =(T_{E^{\vee },U,\phi }^{*}u)(i_l(\xi ))=(T_{E^{\vee },U,\phi }^{*}u)(0,\dots ,0,\underset{l\mathrm{th}\mathrm{position}}{\underbrace{\xi }},0,\cdots ,0)\hfill \\ \hfill & =⟨u,T_{E^{\vee },U,\phi }(0,\dots ,0,\underset{l\mathrm{th}\mathrm{position}}{\underbrace{\xi }},0,\dots ,0)⟩.\hfill \end{array}$$

If we define $g_{l,\xi ,U,\phi }\in D(U,E_U^{\vee })$ by

$$\begin{array}{cc}\hfill g_{l,\xi ,U,\phi }(x)& =T_{E^{\vee },U,\phi }(0,\dots ,0,\underset{l\mathrm{th}\mathrm{position}}{\underbrace{\xi }},0,\dots ,0)(x)\hfill \\ \hfill & ={\left({\rho }^{\vee }{|}_{E_x^{\vee }}\right)}^{-1}\circ (0,\dots ,0,\underset{l\mathrm{th}\mathrm{position}}{\underbrace{\xi }},0,\cdots ,0)\circ \phi (x),\hfill \end{array}$$

then we may write

$${⟨(T_{E^{\vee },U,\phi }^{*}u)\circ i_l,\xi ⟩}_{D^{\prime }(\phi (U))\times D(\phi (U))}={⟨u,g_{l,\xi ,U,\phi }⟩}_{{[D(U,E_U^{\vee })]}^{*}\times D(U,E_U^{\vee })}.$$

Summary: We can associate with $u\in D^{\prime }(U,E_U)={(D(U,E_U^{\vee }))}^{*}$ the following r distributions in $D^{\prime }(\phi (U))$:

$$\forall 1\le l\le r{\tilde{u}}^l=T_{E^{\vee },U,\phi }^{*}u\circ i_l,$$

that is,

$$\forall \xi \in D(\phi (U))⟨{\tilde{u}}^l,\xi ⟩=⟨u,g_{l,\xi ,U,\phi }⟩,$$

where $g_{l,\xi ,U,\phi }\in D(U,E_U^{\vee })$ is defined by

$${\left({\rho }^{\vee }{|}_{E_x^{\vee }}\right)}^{-1}\circ (0,\dots ,0,\underset{l\mathrm{th}\mathrm{position}}{\underbrace{\xi }},0,\dots ,0)\circ \phi (x).$$

In particular,

$${\rho }^{\vee }\circ g_{l,\xi ,U,\phi }\circ {\phi }^{-1}=(0,\dots ,0,\underset{l\mathrm{th}\mathrm{position}}{\underbrace{\xi }},0,\dots ,0),$$

and so ${({\rho }^{\vee }\circ g_{l,\xi ,U,\phi }\circ {\phi }^{-1})}^l=\xi$.

Let us give a name to the composition of L with $T_{E^{\vee },U,\phi }^{*}$ that we used above. We set $H_{E^{\vee },U,\phi }:=L\circ T_{E^{\vee },U,\phi }^{*}$:

$$H_{E^{\vee },U,\phi }:{[D(U,E_U^{\vee })]}^{*}\to {(D^{\prime }(\phi (U)))}^{\times r},u\mapsto L(T_{E^{\vee },U,\phi }^{*}u)=({\tilde{u}}^1,\dots ,{\tilde{u}}^r).$$

Remark 31.

Here we make three observations about the mapping $H_{E^{\vee },U,\phi }$.

(1) 

For every $u\in {[D(U,E_U^{\vee })]}^{*}$

$$supp{[H_{E^{\vee },U,\phi }u]}^l=supp{\tilde{u}}^l\subseteq \phi (suppu).$$

Indeed, let $A=\phi (suppu)$. By Theorem 43, it is enough to show that if $\eta \in D(\phi (U))$ is such that $supp\eta \subseteq \phi (U)\backslash A$, then ${\tilde{u}}^l(\eta )=0$. Note that

$$\begin{array}{c}\hfill ⟨{\tilde{u}}^l,\eta ⟩=⟨u,g_{l,\eta ,U,\phi }⟩.\end{array}$$

So, by Remark 30 we just need to show that $g_{l,\eta ,U,\phi }=0$ on an open neighborhood of $suppu$. Let $K=supp\eta$. Clearly, $U\backslash {\phi }^{-1}(K)$ is an open neighborhood of $suppu$. We will show that $g_{l,\eta ,U,\phi }$ vanishes on this open neighborhood. Note that

$$g_{l,\eta ,U,\phi }(x)={({\rho }^{\vee }{|}_{E_x^{\vee }})}^{-1}(0,\dots ,0,\underset{lthposition}{\underbrace{\eta \circ \phi (x)}},0,\dots ,0).$$

Since ${\rho }^{\vee }{|}_{E_x^{\vee }}$ is an isomorphism and $\eta =0$ on $\phi (U)\backslash K$, we conclude that $g_{l,\eta ,U,\phi }=0$ on ${\phi }^{-1}(\phi (U)\backslash K)=U\backslash {\phi }^{-1}(K)$.

(2) 

Clearly, $H_{E^{\vee },U,\phi }:D^{\prime }(U,E_U)\to {[D^{\prime }(\phi (U))]}^{\times r}$ preserves addition. Moreover, if $f\in C^{\infty }(U)$ and $u\in D^{\prime }(U,E_U)$, then $H_{E^{\vee },U,\phi }(fu)=(f\circ {\phi }^{-1})H_{E^{\vee },U,\phi }(u)$. Recall that $H=L\circ T_{E^{\vee },U,\phi }^{*}$.

$$\begin{array}{cc}\hfill ⟨T_{E^{\vee },U,\phi }^{*}(fu),({\xi }_1,\dots ,{\xi }_r)⟩& =⟨fu,T_{E^{\vee },U,\phi }({\xi }_1,\dots ,{\xi }_r)⟩\hfill \\ \hfill & =⟨u,f{T}_{E^{\vee },U,\phi }({\xi }_1,\dots ,{\xi }_r)⟩\hfill \\ \hfill & =⟨u,T_{E^{\vee },U,\phi }[(f\circ {\phi }^{-1})({\xi }_1,\dots ,{\xi }_r)]⟩\hfill \\ \hfill & =⟨T_{E^{\vee },U,\phi }^{*}u,(f\circ {\phi }^{-1})({\xi }_1,\dots ,{\xi }_r)⟩\hfill \\ \hfill & =⟨(f\circ {\phi }^{-1})T_{E^{\vee },U,\phi }^{*}u,({\xi }_1,\dots ,{\xi }_r)⟩\hfill \end{array}$$

(The third equality follows directly from the definition of $T_{E^{\vee },U,\phi }$.) Therefore,

$$T_{E^{\vee },U,\phi }^{*}(fu)=(f\circ {\phi }^{-1})T_{E^{\vee },U,\phi }^{*}u.$$

The fact that $L((f\circ {\phi }^{-1})T_{E^{\vee },U,\phi }^{*}u)=(f\circ {\phi }^{-1})L(T_{E^{\vee },U,\phi }^{*}u)$ is an immediate consequence of the definition of L.

(3) 

Since $T_{E^{\vee },U,\phi }$ and L are both linear topological isomorphisms, $H_{E^{\vee },U,\phi }^{-1}={(L\circ T_{E^{\vee },U,\phi }^{*})}^{-1}:{(D^{\prime }(\phi (U)))}^{\times r}\to D^{*}(U,E_U^{\vee })$ is also a linear topological isomorphism. It is useful for our later considerations to find an explicit formula for this map. Note that

$$\begin{array}{cc}\hfill H_{E^{\vee },U,\phi }^{-1}& ={(L\circ T_{E^{\vee },U,\phi }^{*})}^{-1}={(T_{E^{\vee },U,\phi }^{*})}^{-1}\circ L^{-1}={(T_{E^{\vee },U,\phi }^{-1})}^{*}\circ L^{-1}\hfill \\ \hfill & ={({\tilde{T}}_{E^{\vee },U,\phi })}^{*}\circ L^{-1}={({\tilde{T}}_{E^{\vee },U,\phi })}^{*}\circ \tilde{L}.\hfill \end{array}$$

Recall that

$$\begin{array}{cc}\hfill & \tilde{L}:{[D^{*}(\phi (U))]}^{\times r}\to {[{(D(\phi (U)))}^{\times r}]}^{*},(v^1,\dots ,v^r)\mapsto v^1\circ {\pi }_1+\dots +v^r\circ {\pi }_r,\hfill \\ \hfill & {\tilde{T}}_{E^{\vee },U,\phi }^{*}:{[{(D(\phi (U)))}^{\times r}]}^{*}\to D^{*}(U,E_U^{\vee }).\hfill \end{array}$$

Therefore, for all $\xi \in D(U,E_U^{\vee })$

$$\begin{array}{cc}\hfill H_{E^{\vee },U,\phi }^{-1}(v^1,\dots ,v^r)(\xi )& =⟨{\tilde{T}}_{E^{\vee },U,\phi }^{*}(v^1\circ {\pi }_1+\dots +v^r\circ {\pi }_r),\xi ⟩\hfill \\ \hfill & =⟨(v^1\circ {\pi }_1+\dots +v^r\circ {\pi }_r),\tilde{T}\xi ⟩\hfill \\ \hfill & =⟨(v^1\circ {\pi }_1+\dots +v^r\circ {\pi }_r),({({\rho }^{\vee })}^1\circ \xi \circ {\phi }^{-1},\dots ,{({\rho }^{\vee })}^r\circ \xi \circ {\phi }^{-1})⟩\hfill \\ \hfill & =\sum _i{v}^i[{({\rho }^{\vee })}^i\circ \xi \circ {\phi }^{-1}].\hfill \end{array}$$

Remark 32.

Suppose $u\in D^{\prime }(M,E)$ is a regular distribution, that is, $u=u_f$ where $f\in {\Gamma }_{reg}(M,E)$. We want to see whether the local components of such a distribution agree with its components as an element of $\Gamma (M,E)$. With respect to the total trivialization triple $(U,\phi ,\rho )$ we have

(1) 

$f\mapsto ({\tilde{f}}^1,\dots ,{\tilde{f}}^r),{\tilde{f}}^l={\rho }^l\circ f\circ {\phi }^{-1}$,

(2) 

$u_f\mapsto ({\widetilde{u_f}}^1,\dots ,{\widetilde{u_f}}^l)$.

The question is whether $u_{{\tilde{f}}^l}={\widetilde{u_f}}^l$? Here we will show that the answer is positive. Indeed, for all $\xi \in D(\phi (U))$ we have

$$\begin{array}{cc}\hfill ⟨{\widetilde{u_f}}^l,\xi ⟩& =⟨u_f,g_{l,\xi ,U,\phi }⟩={\int }_M[g_{l,\xi ,U,\phi },f]={\int }_{\phi (U)}\sum _i{({\tilde{g}}_{l,\xi ,U,\phi })}^i{\tilde{f}}^{i}dV={\int }_{\phi (U)}{({\tilde{g}}_{l,\xi ,U,\phi })}^l{\tilde{f}}^{l}dV\hfill \\ \hfill & ={\int }_{\phi (U)}{\tilde{f}}^l\xi dV=⟨u_{{\tilde{f}}^l},\xi ⟩.\hfill \end{array}$$

Note that the above calculation in fact shows that the restriction of $H_{E^{\vee },U,\phi }$ to $D(U,E_U)$ is ${\tilde{T}}_{E,U,\phi }$.

7. Spaces of Sobolev and Locally Sobolev Functions in ${\mathbb{R}}^{\mathit{n}}$

In this section, we present a brief overview of the basic definitions and properties related to Sobolev spaces on Euclidean spaces.

7.1. Basic Definitions

Definition 25.

Let $s\ge 0$ and $p\in [1,\infty ]$. The Sobolev–Slobodeckij space $W^{s,p}({\mathbb{R}}^n)$ is defined as follows:

• If $s=k\in {\mathbb{N}}_0$, $p\in [1,\infty ]$,

  $$W^{k,p}({\mathbb{R}}^n)=\{u\in L^p({\mathbb{R}}^n){:\parallel u\parallel }_{W^{k,p}({\mathbb{R}}^n)}:=\sum _{|\nu |\le k}\parallel {\partial }^{\nu }u{\parallel }_p<\infty \}.$$
• If $s=\theta \in (0,1)$, $p\in [1,\infty )$,

  $$W^{\theta ,p}({\mathbb{R}}^n)=\{u\in L^p({\mathbb{R}}^n){:|u|}_{W^{\theta ,p}({\mathbb{R}}^n)}:={\left(\int {\int }_{{\mathbb{R}}^n\times {\mathbb{R}}^n}\frac{{|u(x)-u(y)|}^p}{{|x-y|}^{n+\theta p}}dxdy\right)}^{\frac{1}{p}}<\infty \}.$$
• If $s=\theta \in (0,1)$, $p=\infty$,

  $$W^{\theta ,\infty }({\mathbb{R}}^n)=\{u\in L^{\infty }({\mathbb{R}}^n){:|u|}_{W^{\theta ,\infty }({\mathbb{R}}^n)}:=\underset{x,y\in {\mathbb{R}}^n,x\ne y}{ess\; sup}\frac{|u(x)-u(y)|}{{|x-y|}^{\theta }}<\infty \}.$$
• If $s=k+\theta ,k\in {\mathbb{N}}_0,\theta \in (0,1)$, $p\in [1,\infty ]$,

  $$W^{s,p}({\mathbb{R}}^n)=\{u\in W^{k,p}({\mathbb{R}}^n){:\parallel u\parallel }_{W^{s,p}({\mathbb{R}}^n)}:={\parallel u\parallel }_{W^{k,p}({\mathbb{R}}^n)}+\sum _{|\nu |=k}|{\partial }^{\nu }u{|}_{W^{\theta ,p}({\mathbb{R}}^n)}<\infty \}.$$

Remark 33.

Clearly, for all $s\ge 0$, $W^{s,p}({\mathbb{R}}^n)\subseteq L^p({\mathbb{R}}^n)$. Recall that $L^p({\mathbb{R}}^n)\subseteq L_{loc}^1({\mathbb{R}}^n)\subseteq D^{\prime }({\mathbb{R}}^n)$. So, we may consider elements of $W^{s,p}({\mathbb{R}}^n)$ as distributions in $D^{\prime }({\mathbb{R}}^n)$. Indeed, for $s\ge 0$, $p\in (1,\infty )$, and $u\in D^{\prime }({\mathbb{R}}^n)$ we define

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\parallel u\parallel }_{W^{s,p}({\mathbb{R}}^n)}:={\parallel f\parallel }_{W^{s,p}({\mathbb{R}}^n)}\hfill & \mathit{if}u=u_f\mathit{for\; some}f\in L^p({\mathbb{R}}^n)\hfill \\ {\parallel u\parallel }_{W^{s,p}({\mathbb{R}}^n)}:=\infty \hfill & \mathit{otherwise}\hfill \end{array}\right..\end{array}$$

As a consequence, we may write

$$W^{s,p}({\mathbb{R}}^n)=\{u\in D^{\prime }({\mathbb{R}}^n){:\parallel u\parallel }_{W^{s,p}({\mathbb{R}}^n)}<\infty \}.$$

Remark 34.

Let us make some observations that will be helpful in the proof of a number of important theorems. Let A be a nonempty measurable set in ${\mathbb{R}}^n$.

(1) 

We may write:

$$\begin{array}{cc}\hfill & \int {\int }_{{\mathbb{R}}^n\times {\mathbb{R}}^n}\frac{|{\partial }^{\nu }u(x)-{\partial }^{\nu }{u(y)|}^p}{{|x-y|}^{n+\theta p}}dxdy\hfill \\ \hfill & =\int {\int }_{A\times A}\dots dxdy+{\int }_A{\int }_{{\mathbb{R}}^n\backslash A}\dots dxdy+{\int }_{{\mathbb{R}}^n\backslash A}{\int }_A\dots dxdy+{\int }_{{\mathbb{R}}^n\backslash A}{\int }_{{\mathbb{R}}^n\backslash A}\dots dxdy.\hfill \end{array}$$

In particular, if $\mathit{supp}u\subseteq A$, then the last integral vanishes and the sum of the two middle integrals will be equal to $2{\int }_A{\int }_{{\mathbb{R}}^n\backslash A}\frac{|{\partial }^{\nu }{u(x)|}^p}{{|x-y|}^{n+\theta p}}dydx$. Therefore, in this case

$$\begin{array}{cc}\hfill & \int {\int }_{{\mathbb{R}}^n\times {\mathbb{R}}^n}\frac{|{\partial }^{\nu }u(x)-{\partial }^{\nu }{u(y)|}^p}{{|x-y|}^{n+\theta p}}dxdy=\hfill \\ \hfill & \int {\int }_{A\times A}\frac{|{\partial }^{\nu }u(x)-{\partial }^{\nu }{u(y)|}^p}{{|x-y|}^{n+\theta p}}dxdy+2{\int }_A{\int }_{{\mathbb{R}}^n\backslash A}\frac{|{\partial }^{\nu }{u(x)|}^p}{{|x-y|}^{n+\theta p}}dydx.\hfill \end{array}$$

(2) 

If A is open, $K\subseteq A$ is compact and $\alpha >n$, then there exists a number C such that for all $x\in K$ we have

$${\int }_{{\mathbb{R}}^n\backslash A}\frac{1}{{|x-y|}^{\alpha }}dy\le C.$$

(C may depend on A, K, n, and α but is independent of x.) The reason is as follows: Let $R=\frac{1}{2}\mathit{dist}(K,A^c)>0$. Clearly, for all $x\in K$, the ball $B_R(x)$ is inside A. Therefore, for all $x\in K$, ${\mathbb{R}}^n\backslash A\subseteq {\mathbb{R}}^n\backslash B_R(x)$ which implies that for all $x\in K$

$${\int }_{{\mathbb{R}}^n\backslash A}\frac{1}{{|x-y|}^{\alpha }}dy\le {\int }_{{\mathbb{R}}^n\backslash B_R(x)}\frac{1}{{|x-y|}^{\alpha }}dy\stackrel{z=y-x}{=}{\int }_{{\mathbb{R}}^n\backslash B_R(0)}\frac{1}{{|z|}^{\alpha }}dz=\sigma (S^{n-1}){\int }_R^{\infty }\frac{1}{r^{\alpha }}{r}^{n-1}dr,$$

which converges because $\alpha >n$. We can let $C=\sigma (S^{n-1}){\int }_R^{\infty }\frac{1}{r^{\alpha }}{r}^{n-1}dr$.

(3) 

If A is bounded and $\alpha <n$, then there exists a number C such that for all $x\in A$

$${\int }_A\frac{1}{{|x-y|}^{\alpha }}dy\le C.$$

(C depends on A, n, and α but is independent of x.) The reason is as follows: Since A is bounded there exists $R>0$ such that for all $x,y\in A$ we have $|x-y|<R$. So, for all $x\in A$

$${\int }_A\frac{1}{{|x-y|}^{\alpha }}dy\le \sigma (S^{n-1}){\int }_0^R\frac{1}{r^{\alpha }}{r}^{n-1}dr,$$

which converges because $\alpha <n$.

Theorem 47.

Let $s\ge 0$ and $p\in (1,\infty )$. $C_c^{\infty }({\mathbb{R}}^n)$ is dense in $W^{s,p}({\mathbb{R}}^n)$. In fact, the identity map $i_{D,W}:D({\mathbb{R}}^n)\to W^{s,p}({\mathbb{R}}^n)$ is a linear continuous map with dense image.

Proof. 

The fact that $C_c^{\infty }({\mathbb{R}}^n)$ is dense in $W^{s,p}({\mathbb{R}}^n)$ follows from Theorem 7.38 and Lemma 7.44 in [38] combined with Remark 39. Linearity of $i_{D,W}$ is obvious. It remains to prove that this map is continuous. By Theorem 40 it is enough to show that

$$\forall K\in \mathcal{K}({\mathbb{R}}^n),\forall \phi \in {\mathcal{E}}_K({\mathbb{R}}^n)\exists j\in {\mathbb{N}s.t.\parallel \phi \parallel }_{W^{s,p}({\mathbb{R}}^n)}⪯{\parallel \phi \parallel }_{j,K}.$$

Let $s=m+\theta$ where $m\in {\mathbb{N}}_0$ and $\theta \in [0,1)$. If $\theta \ne 0$, by definition ${\parallel \phi \parallel }_{W^{s,p}({\mathbb{R}}^n)}={\parallel \phi \parallel }_{W^{m,p}({\mathbb{R}}^n)}+{\sum }_{|\nu |=m}{|{\partial }^{\nu }\phi |}_{W^{\theta ,p}({\mathbb{R}}^n)}$. It is enough to show that each summand can be bounded by a constant multiple of ${\parallel \phi \parallel }_{j,K}$ for some j.

• Step 1: If $\theta =0$,

  $$\begin{array}{cc}\hfill {\parallel \phi \parallel }_{W^{m,p}({\mathbb{R}}^n)}& =\sum _{|\nu |\le m}\parallel {\partial }^{\nu }{\phi \parallel }_{L^p({\mathbb{R}}^n)}=\sum _{|\nu |\le m}{\parallel {\partial }^{\nu }\phi \parallel }_{L^p(K)}\hfill \\ \hfill & =\sum _{|\nu |\le m}{(\parallel \phi \parallel }_{m,K}{|K|}^{\frac{1}{p}}{)⪯\parallel \phi \parallel }_{m,K},\hfill \end{array}$$

  where the implicit constant depends on m, p, and K but is independent of $\phi$.
• Step 2: Let A be an open ball that contains K (in particular, A is bounded). As it was pointed out in Remark 34 we may write

  $$\begin{array}{cc}\hfill & \int {\int }_{{\mathbb{R}}^n\times {\mathbb{R}}^n}\frac{|{\partial }^{\nu }\phi (x)-{\partial }^{\nu }{\phi (y)|}^p}{{|x-y|}^{n+\theta p}}dxdy=\hfill \\ \hfill & \int {\int }_{A\times A}\frac{|{\partial }^{\nu }\phi (x)-{\partial }^{\nu }{\phi (y)|}^p}{{|x-y|}^{n+\theta p}}dxdy+2{\int }_A{\int }_{{\mathbb{R}}^n\backslash A}\frac{|{\partial }^{\nu }{\phi (x)|}^p}{{|x-y|}^{n+\theta p}}dydx.\hfill \end{array}$$

  First note that ${\mathbb{R}}^n$ is a convex open set; so by Theorem 6 every function $f\in {\mathcal{E}}_K({\mathbb{R}}^n)$ is Lipschitz; indeed, for all $x,y\in {\mathbb{R}}^n$ we have $|f(x)-f(y)|⪯{\parallel f\parallel }_{1,K}\parallel x-y\parallel$. Hence

  $$\begin{array}{cc}\hfill \int {\int }_{A\times A}\frac{|{\partial }^{\nu }\phi (x)-{\partial }^{\nu }{\phi (y)|}^p}{{|x-y|}^{n+\theta p}}dxdy& \le {\int }_A{\parallel {\partial }^{\nu }\phi \parallel }_{1,K}^p{\int }_A\frac{{|x-y|}^p}{{|x-y|}^{n+\theta p}}dydx\hfill \\ \hfill & ={\int }_A{\parallel {\partial }^{\nu }\phi \parallel }_{1,K}^p{\int }_A\frac{1}{{|x-y|}^{n+(\theta -1)p}}dydx.\hfill \end{array}$$

  By part 3 of Remark 34 ${\int }_A\frac{1}{{|x-y|}^{n+(\theta -1)p}}dy$ is bounded by a constant independent of x; also, clearly, $\parallel {\partial }^{\nu }{\phi \parallel }_{1,K}\le {\parallel \phi \parallel }_{m+1,K}$. Considering that $|A|$ is finite we get

  $$\int {\int }_{A\times A}\frac{|{\partial }^{\nu }\phi (x)-{\partial }^{\nu }{\phi (y)|}^p}{{|x-y|}^{n+\theta p}}dxdy⪯{\parallel \phi \parallel }_{m+1,K}^p.$$

  Finally, for the remaining integral we have

  $$\begin{array}{c}\hfill {\int }_A{\int }_{{\mathbb{R}}^n\backslash A}\frac{|{\partial }^{\nu }{\phi (x)|}^p}{{|x-y|}^{n+\theta p}}dydx={\int }_K{\int }_{{\mathbb{R}}^n\backslash A}\frac{|{\partial }^{\nu }{\phi (x)|}^p}{{|x-y|}^{n+\theta p}}dydx,\end{array}$$

  because the inner integral is zero for $x\notin K$. Now, we can write

  $$\begin{array}{c}\hfill {\int }_K{\int }_{{\mathbb{R}}^n\backslash A}\frac{|{\partial }^{\nu }{\phi (x)|}^p}{{|x-y|}^{n+\theta p}}dydx⪯{\int }_K{\parallel \phi \parallel }_{m,K}^p{\int }_{{\mathbb{R}}^n\backslash A}\frac{1}{{|x-y|}^{n+\theta p}}dydx.\end{array}$$

  By part 2 of Remark 34 for all $x\in K$, the inner integral is bounded by a constant. Since $|K|$ is finite we conclude that

  $${\int }_A{\int }_{{\mathbb{R}}^n\backslash A}\frac{|{\partial }^{\nu }{\phi (x)|}^p}{{|x-y|}^{n+\theta p}}dydx⪯{\parallel \phi \parallel }_{m,K}^p.$$

Hence

$${\parallel u\parallel }_{W^{s,p}({\mathbb{R}}^n)}⪯{\parallel \phi \parallel }_{m+1,K}.$$

 □

Definition 26.

Let $s>0$ and $p\in (1,\infty )$. We define

$$W^{-s,p^{\prime }}({\mathbb{R}}^n)={(W^{s,p}({\mathbb{R}}^n))}^{*}(\frac{1}{p}+\frac{1}{p^{\prime }}=1).$$

Remark 35.

Note that since the identity map from $D({\mathbb{R}}^n)$ to $W^{s,p}({\mathbb{R}}^n)$ is continuous with dense image, the dual space $W^{-s,p^{\prime }}({\mathbb{R}}^n)$ can be viewed as a subspace of $D^{\prime }({\mathbb{R}}^n)$. Indeed, by Theorem 25 the adjoint of the identity map, $i_{D,W}^{*}:W^{-s,p^{\prime }}({\mathbb{R}}^n)\to D^{\prime }({\mathbb{R}}^n)$ is an injective linear continuous map and we can use this map to identify $W^{-s,p^{\prime }}({\mathbb{R}}^n)$ with a subspace of $D^{\prime }({\mathbb{R}}^n)$. It is a direct consequence of the definition of adjoint that for all $u\in W^{-s,p^{\prime }}({\mathbb{R}}^n)$, $i_{D,W}^{*}{u=u|}_{D({\mathbb{R}}^n)}$. So, by identifying $u:W^{s,p}({\mathbb{R}}^n)\to \mathbb{R}$ with ${u|}_{D({\mathbb{R}}^n)}:D({\mathbb{R}}^n)\to \mathbb{R}$, we can view $W^{-s,p^{\prime }}({\mathbb{R}}^n)$ as a subspace of $D^{\prime }({\mathbb{R}}^n)$.

Remark 36.

• It is a direct consequence of the contents of pp. 88 and 178 of [8] that for $m\in \mathbb{Z}$ and $1<p<\infty$

  $$W^{m,p}({\mathbb{R}}^n)=H_p^m({\mathbb{R}}^n)=F_{p,2}^m({\mathbb{R}}^n).$$
• It is a direct consequence of the contents of pp. 38, 51, 90 and 178 of [8] that for $s\notin \mathbb{Z}$ and $1<p<\infty$

  $$W^{s,p}({\mathbb{R}}^n)=B_{p,p}^s({\mathbb{R}}^n).$$

Theorem 48.

For all $s\in \mathbb{R}$ and $1<p<\infty$, $W^{s,p}({\mathbb{R}}^n)$ is reflexive.

Proof. 

See the proof of Theorem 64. Additionally, see [39], Section 2.6, p. 198. □

Note that by definition for all $s>0$ we have ${[W^{s,p}({\mathbb{R}}^n)]}^{*}=W^{-s,p^{\prime }}({\mathbb{R}}^n)$. Now, since $W^{s,p}({\mathbb{R}}^n)$ is reflexive, ${[W^{-s,p^{\prime }}({\mathbb{R}}^n)]}^{*}$ is isometrically isomorphic to $W^{s,p}({\mathbb{R}}^n)$ and so they can be identified with one another. Thus, for all $s\in \mathbb{R}$ and $1<p<\infty$ we may write

$${[W^{s,p}({\mathbb{R}}^n)]}^{*}=W^{-s,p^{\prime }}({\mathbb{R}}^n).$$

Let $s\ge 0$ and $p\in (1,\infty )$. Every function $\phi \in C_c^{\infty }({\mathbb{R}}^n)$ defines a linear functional $L_{\phi }:W^{s,p}({\mathbb{R}}^n)\to \mathbb{R}$ defined by

$$L_{\phi }(u)={\int }_{{\mathbb{R}}^n}u\phi dx.$$

$L_{\phi }$ is continuous because by Holder’s inequality

$$|L_{\phi }(u)|=|{\int }_{{\mathbb{R}}^n}{u\phi dx|\le \parallel u\parallel }_{L^p({\mathbb{R}}^n)}{\parallel \phi \parallel }_{L^{p^{\prime }}({\mathbb{R}}^n)}\le {\parallel \phi \parallel }_{L^{p^{\prime }}({\mathbb{R}}^n)}{\parallel u\parallel }_{W^{s,p}({\mathbb{R}}^n)}.$$

Furthermore, the map $L:C_c^{\infty }({\mathbb{R}}^n)\to W^{-s,p^{\prime }}({\mathbb{R}}^n)$ which maps $\phi$ to $L_{\phi }$ is injective because

$$\begin{array}{c}\hfill L_{\phi }=L_{\psi }\to \forall u\in W^{s,p}({\mathbb{R}}^n){\int }_{{\mathbb{R}}^n}u(\phi -\psi )dx=0\to {\int }_{{\mathbb{R}}^n}{|\phi -\psi |}^{2}dx=0\to \phi =\psi .\end{array}$$

Thus, we may identify $\phi$ with $L_{\phi }$ and consider $C_c^{\infty }({\mathbb{R}}^n)$ as a subspace of $W^{-s,p^{\prime }}({\mathbb{R}}^n)$.

Theorem 49.

For all $s>0$ and $p\in (1,\infty )$, $C_c^{\infty }({\mathbb{R}}^n)$ is dense in $W^{-s,p^{\prime }}({\mathbb{R}}^n)$.

Proof. 

The proof given in p. 65 of [1] for the density of $L^{p^{\prime }}$ in the integer order Sobolev space $W^{-m,p^{\prime }}$, which is based on reflexivity of Sobolev spaces, works equally well for establishing the density of $C_c^{\infty }({\mathbb{R}}^n)$ in $W^{-s,p^{\prime }}({\mathbb{R}}^n)$. □

Remark 37.

As a consequence of the above theorems, for all $s\in \mathbb{R}$ and $p\in (1,\infty )$, $W^{s,p}({\mathbb{R}}^n)$ can be considered as a subspace of $D^{\prime }({\mathbb{R}}^n)$. See Theorem 25 and the discussion thereafter for further insights. Additionally, see Remark 45.

Next we list several definitions pertinent to Sobolev spaces on open subsets of ${\mathbb{R}}^n$.

Definition 27.

Let Ω be a nonempty open set in ${\mathbb{R}}^n$. Let $s\in \mathbb{R}$ and $p\in (1,\infty )$.

(1) 

• If $s=k\in {\mathbb{N}}_0$,

  $$W^{k,p}(\Omega )=\{u\in L^p{(\Omega ):\parallel u\parallel }_{W^{k,p}(\Omega )}:=\sum _{|\nu |\le k}\parallel {\partial }^{\nu }u{\parallel }_{L^p(\Omega )}<\infty \}.$$
• If $s=\theta \in (0,1)$,

  $$W^{\theta ,p}(\Omega )=\{u\in L^p{(\Omega ):|u|}_{W^{\theta ,p}(\Omega )}:={\left(\int {\int }_{\Omega \times \Omega }\frac{{|u(x)-u(y)|}^p}{{|x-y|}^{n+\theta p}}dxdy\right)}^{\frac{1}{p}}<\infty \}.$$
• If $s=k+\theta ,k\in {\mathbb{N}}_0,\theta \in (0,1)$,

  $$W^{s,p}(\Omega )=\{u\in W^{k,p}{(\Omega ):\parallel u\parallel }_{W^{s,p}(\Omega )}:={\parallel u\parallel }_{W^{k,p}(\Omega )}+\sum _{|\nu |=k}|{\partial }^{\nu }u{|}_{W^{\theta ,p}(\Omega )}<\infty \}.$$
• If $s<0$,

  $$W^{s,p}(\Omega )={(W_0^{-s,p^{\prime }}(\Omega ))}^{*}(\frac{1}{p}+\frac{1}{p^{\prime }}=1),$$

  where for all $e\ge 0$ and $1<q<\infty$, $W_0^{e,q}(\Omega )$ is defined as the closure of $C_c^{\infty }(\Omega )$ in $W^{e,q}(\Omega )$.

(2) 

$W^{s,p}(\overline{\Omega })$ is defined as the restriction of $W^{s,p}({\mathbb{R}}^n)$ to Ω. That is, $W^{s,p}(\overline{\Omega })$ is the collection of all $u\in D^{\prime }(\Omega )$ such that there is a $v\in W^{s,p}({\mathbb{R}}^n)$ with ${v|}_{\Omega }=u$. Here ${v|}_{\Omega }$ should be interpreted as the restriction of a distribution in $D^{\prime }({\mathbb{R}}^n)$ to a distribution in $D^{\prime }(\Omega )$. $W^{s,p}(\overline{\Omega })$ is equipped with the following norm:

$${\parallel u\parallel }_{W^{s,p}(\overline{\Omega })}=\underset{v\in W^{s,p}({\mathbb{R}}^n){,v|}_{\Omega }=u}{inf}{\parallel v\parallel }_{W^{s,p}({\mathbb{R}}^n)}.$$

(3) 

$${\tilde{W}}^{s,p}(\overline{\Omega })=\{u\in W^{s,p}({\mathbb{R}}^n):\mathit{supp}u\subseteq \overline{\Omega }\}.$$

${\tilde{W}}^{s,p}(\overline{\Omega })$ is equipped with the norm ${\parallel u\parallel }_{{\tilde{W}}^{s,p}(\overline{\Omega })}={\parallel u\parallel }_{W^{s,p}({\mathbb{R}}^n)}$.

(4) 

$${\tilde{W}}^{s,p}(\Omega )=\{u=v{|}_{\Omega },v\in {\tilde{W}}^{s,p}(\overline{\Omega })\}.$$

(3)

Again ${v|}_{\Omega }$ should be interpreted as the restriction of an element in $D^{\prime }({\mathbb{R}}^n)$ to $D^{\prime }(\Omega )$. So ${\tilde{W}}^{s,p}(\Omega )$ is a subspace of $D^{\prime }(\Omega )$. This space is equipped with the norm ${\parallel u\parallel }_{{\tilde{W}}^{s,p}}=inf{\parallel v\parallel }_{W^{s,p}({\mathbb{R}}^n)}$ where the infimum is taken over all v that satisfy the equality in Equation (3). Note that two elements $v_1$ and $v_2$ of ${\tilde{W}}^{s,p}(\overline{\Omega })$ restrict to the same element in $D^{\prime }(\Omega )$ if and only if $\mathit{supp}(v_1-v_2)\subseteq \partial \Omega$. Therefore,

$${\tilde{W}}^{s,p}(\Omega )=\frac{{\tilde{W}}^{s,p}(\overline{\Omega })}{\{v\in W^{s,p}({\mathbb{R}}^n):\mathit{supp}v\subseteq \partial \Omega \}}.$$

(5) 

For $s\ge 0$ we define

$$W_{00}^{s,p}(\Omega )=\{u\in W^{s,p}(\Omega ):{\mathit{ext}}_{\Omega ,{\mathbb{R}}^n}^{0}u\in W^{s,p}({\mathbb{R}}^n)\}.$$

We equip this space with the norm

$${\parallel u\parallel }_{W_{00}^{s,p}(\Omega )}:={\parallel {\mathit{ext}}_{\Omega ,{\mathbb{R}}^n}^{0}u\parallel }_{W^{s,p}({\mathbb{R}}^n)}.$$

Note that previously we defined the operator ${\mathit{ext}}_{\Omega ,{\mathbb{R}}^n}^0$ only for distributions with compact support and functions; this is why the values of s are restricted to be nonnegative in this definition.

(6) 

For all $K\in \mathcal{K}(\Omega )$ we define

$$W_K^{s,p}(\Omega )=\{u\in W^{s,p}(\Omega ):\mathit{supp}u\subseteq K\},$$

with ${\parallel u\parallel }_{W_K^{s,p}(\Omega )}:={\parallel u\parallel }_{W^{s,p}(\Omega )}$.

(7) 

$$W_{comp}^{s,p}(\Omega )=\bigcup _{K\in \mathcal{K}(\Omega )}{W}_K^{s,p}(\Omega ).$$

This space is normally equipped with the inductive limit topology with respect to the family ${\{W_K^{s,p}(\Omega )\}}_{K\in \mathcal{K}(\Omega )}$. However, in these notes we always consider $W_{comp}^{s,p}(\Omega )$ as a normed space equipped with the norm induced from $W^{s,p}(\Omega )$.

Remark 38.

Each of these definitions has its advantages and disadvantages. For example, the way we defined the spaces $W^{s,p}(\Omega )$ is well suited for using duality arguments while proving the usual embedding theorems for these spaces on an arbitrary open set Ω is not trivial; on the other hand, duality arguments do not work as well for spaces $W^{s,p}(\overline{\Omega })$ but the embedding results for these spaces on an arbitrary open set Ω automatically follow from the corresponding results on ${\mathbb{R}}^n$. Various authors adopt different definitions for Sobolev spaces on domains based on the applications in which they are interested. Unfortunately, the notation used in the literature for the various spaces introduced above are not uniform. First note that it is a direct consequence of Remark 36 and the definitions of $B_{p,q}^s(\Omega )$, $H_p^s(\Omega )$ and $F_{p,q}^s(\Omega )$ in [39] p. 310 and [40] that

$$W^{s,p}(\overline{\Omega })=\left\{\begin{array}{c}{F}_{p,2}^s(\Omega )=H_p^s(\Omega )\mathit{if}s\in \mathbb{Z}\hfill \\ B_{p,p}^s(\Omega )\mathit{if}s\notin \mathbb{Z}\hfill \end{array}\right..$$

With this in mind, we have Table 2 which displays the connection between the notation used in this work with the notation in a number of well-known references.

Table 2. Connection to notation employed in previous literature.

This Manuscript	Triebel [39]	Triebel [40]	Grisvard [5]	Bhattacharyya [4]
$W^{s,p}(\Omega )$			$W_p^s(\Omega )$	$W^{s,p}(\Omega )$
$W^{s,p}(\overline{\Omega })$	$W_p^s(\Omega )$	$W_p^s(\Omega )$	$W_p^s(\overline{\Omega })$	$W^{s,p}(\overline{\Omega })$
${\tilde{W}}^{s,p}(\overline{\Omega })$	${\tilde{W}}_p^s(\Omega )$	${\tilde{W}}_p^s(\overline{\Omega })$
${\tilde{W}}^{s,p}(\Omega )$		${\tilde{W}}_p^s(\Omega )$
$W_{00}^{s,p}(\Omega )$			${\tilde{W}}_p^s(\Omega )$	$W_{00}^{s,p}(\Omega )$

Remark 39.

• Note that

  $$\begin{array}{cc}\hfill {\parallel u\parallel }_{W^{k,p}(\Omega )}& +\sum _{|\nu |=k}|{\partial }^{\nu }{u|}_{W^{\theta ,p}(\Omega )}\le {\parallel u\parallel }_{W^{k,p}(\Omega )}+\sum _{|\nu |=k}{\parallel {\partial }^{\nu }u\parallel }_{W^{\theta ,p}(\Omega )}\hfill \\ \hfill & ={\parallel u\parallel }_{W^{k,p}(\Omega )}+\sum _{|\nu |=k}\left(\parallel {\partial }^{\nu }{u\parallel }_{L^p(\Omega )}+{|{\partial }^{\nu }u|}_{W^{\theta ,p}(\Omega )}\right)\hfill \\ \hfill & ⪯{\parallel u\parallel }_{W^{k,p}(\Omega )}+\sum _{|\nu |=k}{|{\partial }^{\nu }u|}_{W^{\theta ,p}(\Omega )}(\mathit{since}\sum _{|\nu |=k}\parallel {\partial }^{\nu }{u\parallel }_{L^p(\Omega )}\le {\parallel u\parallel }_{W^{k,p}(\Omega )}).\hfill \end{array}$$

  Therefore, the following is an equivalent norm on $W^{s,p}(\Omega )$

  $${\parallel u\parallel }_{W^{s,p}(\Omega )}:={\parallel u\parallel }_{W^{k,p}(\Omega )}+\sum _{|\alpha |=k}{\parallel {\partial }^{\alpha }u\parallel }_{W^{\theta ,p}(\Omega )}.$$
• For $p\in (1,\infty )$ and $a,b>0$ we have ${(a^p+b^p)}^{\frac{1}{p}}\simeq a+b$; indeed,

  $$a^p+b^p\le {(a+b)}^p\le {(2max\{a,b\})}^p\le 2^p(a^p+b^p).$$

  More generally, if $a_1,\dots ,a_m$ are nonnegative numbers, then ${(a_1^p+\dots +a_m^p)}^{\frac{1}{p}}\simeq a_1+\dots +a_m$. Therefore, for any nonempty open set Ω in ${\mathbb{R}}^n$, $s>0$, the following expressions are both equivalent to the original norm on $W^{s,p}(\Omega )$

  $$\begin{array}{cc}\hfill & {\parallel u\parallel }_{W^{s,p}(\Omega )}:={\left[{\parallel u\parallel }_{W^{k,p}(\Omega )}^p+\sum _{|\nu |=k}{|{\partial }^{\nu }u|}_{W^{\theta ,p}(\Omega )}^p\right]}^{\frac{1}{p}},\hfill \\ \hfill & {\parallel u\parallel }_{W^{s,p}(\Omega )}:={\left[{\parallel u\parallel }_{W^{k,p}(\Omega )}^p+\sum _{|\nu |=k}{\parallel {\partial }^{\nu }u\parallel }_{W^{\theta ,p}(\Omega )}^p\right]}^{\frac{1}{p}},\hfill \end{array}$$

  where $s=k+\theta ,k\in {\mathbb{N}}_0,\theta \in (0,1)$.

7.2. Properties of Sobolev Spaces on the Whole Space ${\mathbb{R}}^n$

Theorem 50

(Embedding Theorem I, [39], Section 2.8.1). Suppose $1<p\le q<\infty$ and $-\infty <t\le s<\infty$ satisfy $s-\frac{n}{p}\ge t-\frac{n}{q}$. Then $W^{s,p}({\mathbb{R}}^n)\hookrightarrow W^{t,q}({\mathbb{R}}^n)$. In particular, $W^{s,p}({\mathbb{R}}^n)\hookrightarrow W^{t,p}({\mathbb{R}}^n)$.

Theorem 51

(Multiplication by smooth functions, [12], p. 203). Let $s\in \mathbb{R}$, $1<p<\infty$, and $\phi \in B{C}^{\infty }({\mathbb{R}}^n)$. Then the linear map

$$m_{\phi }:W^{s,p}({\mathbb{R}}^n)\to W^{s,p}({\mathbb{R}}^n),u\mapsto \phi u$$

is well-defined and bounded.

A detailed study of the following multiplication theorems can be found in [18].

Theorem 52.

Let $s_i,s$ and $1\le p,p_i<\infty$ ($i=1,2$) be real numbers satisfying

(i) 

$s_i\ge s\ge 0$,

(ii) 

$s\in {\mathbb{N}}_0$,

(iii) 

$s_i-s\ge n({\displaystyle \frac{1}{p_i}}-{\displaystyle \frac{1}{p}})$,

(iv) 

$s_1+s_2-s>n({\displaystyle \frac{1}{p_1}}+{\displaystyle \frac{1}{p_2}}-{\displaystyle \frac{1}{p}})\ge 0$,

where the strictness of the inequalities in items (iii) and (iv) can be interchanged.

If $u\in W^{s_1,p_1}({\mathbb{R}}^n)$ and $v\in W^{s_2,p_2}({\mathbb{R}}^n)$, then $uv\in W^{s,p}({\mathbb{R}}^n)$ and moreover the pointwise multiplication of functions is a continuous bilinear map

$$W^{s_1,p_1}({\mathbb{R}}^n)\times W^{s_2,p_2}({\mathbb{R}}^n)\to W^{s,p}({\mathbb{R}}^n).$$

Theorem 53

(Multiplication theorem for Sobolev spaces on the whole space, nonnegative exponents). Assume $s_i,s$ and $1\le p_i\le p<\infty$ ($i=1,2$) are real numbers satisfying

(i) 

$s_i\ge s$,

(ii) 

$s\ge 0$,

(iii) 

$s_i-s\ge n({\displaystyle \frac{1}{p_i}}-{\displaystyle \frac{1}{p}})$,

(iv) 

$s_1+s_2-s>n({\displaystyle \frac{1}{p_1}}+{\displaystyle \frac{1}{p_2}}-{\displaystyle \frac{1}{p}})$.

If $u\in W^{s_1,p_1}({\mathbb{R}}^n)$ and $v\in W^{s_2,p_2}({\mathbb{R}}^n)$, then $uv\in W^{s,p}({\mathbb{R}}^n)$ and moreover the pointwise multiplication of functions is a continuous bilinear map

$$W^{s_1,p_1}({\mathbb{R}}^n)\times W^{s_2,p_2}({\mathbb{R}}^n)\to W^{s,p}({\mathbb{R}}^n).$$

Theorem 54

(Multiplication theorem for Sobolev spaces on the whole space, negative exponents I). Assume $s_i,s$ and $1<p_i\le p<\infty$ ($i=1,2$) are real numbers satisfying

(i) 

$s_i\ge s$,

(ii) 

$min\{s_1,s_2\}<0$,

(iii) 

$s_i-s\ge n({\displaystyle \frac{1}{p_i}}-{\displaystyle \frac{1}{p}})$,

(iv) 

$s_1+s_2-s>n({\displaystyle \frac{1}{p_1}}+{\displaystyle \frac{1}{p_2}}-{\displaystyle \frac{1}{p}})$,

(v) 

$s_1+s_2\ge n({\displaystyle \frac{1}{p_1}}+{\displaystyle \frac{1}{p_2}}-1)\ge 0$.

Then the pointwise multiplication of smooth functions extends uniquely to a continuous bilinear map

$$W^{s_1,p_1}({\mathbb{R}}^n)\times W^{s_2,p_2}({\mathbb{R}}^n)\to W^{s,p}({\mathbb{R}}^n).$$

Theorem 55

(Multiplication theorem for Sobolev spaces on the whole space, negative exponents II). Assume $s_i,s$ and $1<p,p_i<\infty$ ($i=1,2$) are real numbers satisfying

(i) 

$s_i\ge s$,

(ii) 

$min\{s_1,s_2\}\ge 0$ and $s<0$,

(iii) 

$s_i-s\ge n({\displaystyle \frac{1}{p_i}}-{\displaystyle \frac{1}{p}})$,

(iv) 

$s_1+s_2-s>n({\displaystyle \frac{1}{p_1}}+{\displaystyle \frac{1}{p_2}}-{\displaystyle \frac{1}{p}})\ge 0$,

(v) 

$s_1+s_2>n({\displaystyle \frac{1}{p_1}}+{\displaystyle \frac{1}{p_2}}-1)$ (the inequality is strict).

Then the pointwise multiplication of smooth functions extends uniquely to a continuous bilinear map

$$W^{s_1,p_1}({\mathbb{R}}^n)\times W^{s_2,p_2}({\mathbb{R}}^n)\to W^{s,p}({\mathbb{R}}^n).$$

Remark 40.

Let us discuss further how we should interpret multiplication in the case where negative exponents are involved. Suppose for instance $s_1<0$ ($s_2$ may be positive or negative). A moment’s thought shows that the relation

$$W^{s_1,p_1}({\mathbb{R}}^n)\times W^{s_2,p_2}({\mathbb{R}}^n)\hookrightarrow W^{s,p}({\mathbb{R}}^n)$$

in the above theorems can be interpreted as follows: for all $u\in W^{s_1,p_1}({\mathbb{R}}^n)$ and $v\in W^{s_2,p_2}({\mathbb{R}}^n)$, if $\{{\phi }_i\}$ in $C^{\infty }({\mathbb{R}}^n)\cap W^{s_1,p_1}({\mathbb{R}}^n)$ is any sequence such that ${\phi }_i\to u$ in $W^{s_1,p_1}({\mathbb{R}}^n)$, then

(1) 

For all i, ${\phi }_{i}v\in W^{s,p}({\mathbb{R}}^n)$ (multiplication of a smooth function and a distribution);

(2) 

${\phi }_{i}v$ converges to some element g in $W^{s,p}({\mathbb{R}}^n)$ as $i\to \infty$;

(3) 

${\parallel g\parallel }_{W^{s,p}({\mathbb{R}}^n)}⪯{\parallel u\parallel }_{W^{s_1,p_1}({\mathbb{R}}^n)}{\parallel v\parallel }_{W^{s_2,p_2}({\mathbb{R}}^n)}$ where the implicit constant does not depend on u and v;

(4) 

$g\in W^{s,p}({\mathbb{R}}^n)$ is independent of the sequence $\{{\phi }_i\}$ and can be regarded as the product of u and v.

In particular, ${\phi }_{i}v\to uv$ in $D^{\prime }({\mathbb{R}}^n)$ and for all $\psi \in C_c^{\infty }({\mathbb{R}}^n)$

$${⟨uv,\psi ⟩}_{D^{\prime }({\mathbb{R}}^n)\times D({\mathbb{R}}^n)}=\underset{i\to \infty }{lim}{⟨{\phi }_{i}v,\psi ⟩}_{D^{\prime }({\mathbb{R}}^n)\times D({\mathbb{R}}^n)}={⟨v,{\phi }_i\psi ⟩}_{D^{\prime }({\mathbb{R}}^n)\times D({\mathbb{R}}^n)}.$$

7.3. Properties of Sobolev Spaces on Smooth Bounded Domains

In this section, we assume that $\Omega$ is an open bounded set in ${\mathbb{R}}^n$ with smooth boundary unless a weaker assumption is stated. First we list some facts that can be useful in understanding the relationship between various definitions of Sobolev spaces on domains.

• ([4], p. 584) [Theorem 8.10.13 and its proof] Suppose $s>0$ and $1<p<\infty$. Then $W^{s,p}(\Omega )=W^{s,p}(\overline{\Omega })$ in the sense of equivalent normed spaces.
• ([40], pp. 481 and 494) For $s>\frac{1}{p}-1$, ${\tilde{W}}^{s,p}(\overline{\Omega })={\tilde{W}}^{s,p}(\Omega )$. That is, for $s>\frac{1}{p}-1$

  $$\{v\in W^{s,p}({\mathbb{R}}^n):\mathrm{supp}v\subseteq \partial \Omega \}=\{0\}.$$
• Let $s>0$ and $1<p<\infty$. Then for $s\ne \frac{1}{p},1+\frac{1}{p},2+\frac{1}{p},\dots$ (that is, when the fractional part of s is not equal to $\frac{1}{p}$) we have

  (1)

  ([4], p. 592) [Theorem 8.10.20] $W_{00}^{s,p}(\Omega )=W_0^{s,p}(\Omega )$ in the sense of equivalent normed spaces.

  (2)

  $${\mathrm{ext}}_{\Omega ,{\mathbb{R}}^n}^0:\left(C_c^{\infty }(\Omega ),{\parallel .\parallel }_{s,p}\right)\to W^{s,p}({\mathbb{R}}^n)$$

  is a well-defined bounded linear operator.

  (3)

  $${\mathrm{res}}_{{\mathbb{R}}^n,\Omega }:W^{-s,p^{\prime }}({\mathbb{R}}^n)\to W^{-s,p^{\prime }}(\Omega ){u\mapsto u|}_{\Omega }$$

  is a well-defined bounded linear operator.

Note that the connection between items (2) and (3) above can be seen as follows: Let $u\in W^{-s,p^{\prime }}({\mathbb{R}}^n)$. ${\mathrm{res}}_{{\mathbb{R}}^n,\Omega }u\in W^{-s,p^{\prime }}(\Omega )$ if and only if ${u|}_{\Omega }{:(D(\Omega ),\parallel .\parallel }_{s,p})\to \mathbb{R}$ is continuous, that is, if

$$\underset{0\ne \phi \in D(\Omega )}{sup}\frac{|{⟨u{|}_{\Omega },\phi ⟩}_{D^{\prime }(\Omega )\times D(\Omega )}|}{{\parallel \phi \parallel }_{W^{s,p}(\Omega )}}<\infty .$$

We have

$$\begin{array}{cc}\hfill |{⟨u{|}_{\Omega },\phi ⟩}_{D^{\prime }(\Omega )\times D(\Omega )}|& =|{⟨u,{\mathrm{ext}}_{\Omega ,{\mathbb{R}}^n}^0\phi ⟩}_{D^{\prime }({\mathbb{R}}^n)\times D({\mathbb{R}}^n)}|=|{⟨u,{\mathrm{ext}}_{\Omega ,{\mathbb{R}}^n}^0\phi ⟩}_{W^{-s,p^{\prime }}({\mathbb{R}}^n)\times W_0^{s,p}({\mathbb{R}}^n)}|\hfill \\ \hfill & ⪯{\parallel u\parallel }_{W^{-s,p^{\prime }}({\mathbb{R}}^n)}{\parallel {\mathrm{ext}}_{\Omega ,{\mathbb{R}}^n}^0\phi \parallel }_{W_0^{s,p}({\mathbb{R}}^n)}.\hfill \end{array}$$

So, the desired inequality holds if one can show that for all $\phi \in D(\Omega )$, $\parallel {\mathrm{ext}}_{\Omega ,{\mathbb{R}}^n}^0{\phi \parallel }_{W_0^{s,p}({\mathbb{R}}^n)}⪯{\parallel \phi \parallel }_{W^{s,p}(\Omega )}$.

Next we recall some facts about extension operators and embedding properties of Sobolev spaces. The existence of extension operator can be helpful in transferring known results for Sobolev spaces defined on ${\mathbb{R}}^n$ to Sobolev spaces defined on bounded domains.

Theorem 56

(Extension Property I [4], p. 584). Let $\Omega \subset {\mathbb{R}}^n$ be a bounded open set with Lipschitz continuous boundary. Then for all $s>0$ and for $1\le p<\infty$, there exists a continuous linear extension operator $P:W^{s,p}(\Omega )\hookrightarrow W^{s,p}({\mathbb{R}}^n)$ such that ${(Pu)|}_{\Omega }=u$ and ${\parallel Pu\parallel }_{W^{s,p}({\mathbb{R}}^n)}\le C{\parallel u\parallel }_{W^{s,p}(\Omega )}$ for some constant C that may depend on s, p, and Ω but is independent of u.

The next theorem states that the claim of Theorem 56 holds for all values of s (positive and negative) if we replace $W^{s,p}(\Omega )$ with $W^{s,p}(\overline{\Omega })$.

Theorem 57

(Extension Property II [40], p. 487, [8], p. 201). Let $\Omega \subset {\mathbb{R}}^n$ be a bounded open set with Lipschitz continuous boundary, $p\in (1,\infty )$ and $s\in \mathbb{R}$. Let $R:W^{s,p}({\mathbb{R}}^n)\to W^{s,p}(\overline{\Omega })$ be the restriction operator $(R(u)=u{|}_{\Omega })$. Then there exists a continuous linear operator $S:W^{s,p}(\overline{\Omega })\to W^{s,p}({\mathbb{R}}^n)$ such that $R\circ S=Id$.

Corollary 3.

One can easily show that the results of Sobolev multiplication theorems in the previous section (Theorems 52–55) hold also for Sobolev spaces on any Lipschitz domain as long as all the Sobolev spaces involved satisfy $W^{e,q}(\Omega )=W^{e,q}(\overline{\Omega })$ (and so, in particular, existence of an extension operator is guaranteed). Indeed, if $P_1:W^{s_1,p_1}(\Omega )\to W^{s_1,p_1}({\mathbb{R}}^n)$ and $P_2:W^{s_2,p_2}(\Omega )\to W^{s_2,p_2}({\mathbb{R}}^n)$ are extension operators, then $(P_{1}u)(P_{2}v){|}_{\Omega }=uv$ and therefore,

$$\begin{array}{cc}\hfill {\parallel uv\parallel }_{W^{s,p}(\Omega )}={\parallel uv\parallel }_{W^{s,p}(\overline{\Omega })}\le {\parallel (P_{1}u)(P_{2}v)\parallel }_{W^{s,p}({\mathbb{R}}^n)}& ⪯\parallel P_1{u\parallel }_{W^{s_1,p_1}({\mathbb{R}}^n)}{\parallel P_{2}v\parallel }_{W^{s_2,p_2}({\mathbb{R}}^n)}\hfill \\ \hfill & ⪯{\parallel u\parallel }_{W^{s_1,p_1}(\Omega )}{\parallel v\parallel }_{W^{s_2,p_2}(\Omega )}.\hfill \end{array}$$

Remark 41.

In the above Corollary, we presumed that $(P_{1}u)(P_{2}v){|}_{\Omega }=uv$. Clearly, if $s_1$ and $s_2$ are both nonnegative, the equality holds. However, what if at least one of the exponents, say $s_1$, is negative? In order to prove this equality, we may proceed as follows: let $\{{\phi }_i\}$ be a sequence in $C^{\infty }({\mathbb{R}}^n)\cap W^{s_1,p_1}({\mathbb{R}}^n)$ such that ${\phi }_i\to P_{1}u$ in $W^{s_1,p_1}({\mathbb{R}}^n)$. By assumption $W^{s_1,p_1}(\Omega )=W^{s_1,p_1}(\overline{\Omega })$, therefore the restriction operator is continuous and $\{{\phi }_i{|}_{\Omega }\}$ is a sequence in $C^{\infty }(\Omega )\cap W^{s_1,p_1}(\Omega )$ that converges to u in $W^{s_1,p_1}(\Omega )$. For all $\psi \in C_c^{\infty }(\Omega )$ we have

$$\begin{array}{cc}\hfill {⟨[(P_{1}u)(P_{2}v)]{|}_{\Omega },\psi ⟩}_{D^{\prime }(\Omega )\times D(\Omega )}& ={⟨(P_{1}u)(P_{2}v),{\mathit{ext}}_{\Omega ,{\mathbb{R}}^n}^0\psi ⟩}_{D^{\prime }({\mathbb{R}}^n)\times D({\mathbb{R}}^n)}\hfill \\ \hfill & \stackrel{\mathit{Remark}\mathit{40}}{=}\underset{i\to \infty }{lim}{⟨{\phi }_i(P_{2}v),{\mathit{ext}}_{\Omega ,{\mathbb{R}}^n}^0\psi ⟩}_{D^{\prime }({\mathbb{R}}^n)\times D({\mathbb{R}}^n)}\hfill \\ \hfill & =\underset{i\to \infty }{lim}{⟨(P_{2}v),{\phi }_i{\mathit{ext}}_{\Omega ,{\mathbb{R}}^n}^0\psi ⟩}_{D^{\prime }({\mathbb{R}}^n)\times D({\mathbb{R}}^n)}\hfill \\ \hfill & =\underset{i\to \infty }{lim}{⟨(P_{2}v),{\mathit{ext}}_{\Omega ,{\mathbb{R}}^n}^0({\phi }_i{|}_{\Omega }\psi )⟩}_{D^{\prime }({\mathbb{R}}^n)\times D({\mathbb{R}}^n)}\hfill \\ \hfill & =\underset{i\to \infty }{lim}⟨(P_{2}v){|}_{\Omega },{\phi }_i{{|}_{\Omega }\psi ⟩}_{D^{\prime }(\Omega )\times D(\Omega )}\hfill \\ \hfill & =\underset{i\to \infty }{lim}{⟨{\phi }_i{|}_{\Omega }v,\psi ⟩}_{D^{\prime }(\Omega )\times D(\Omega )}\hfill \\ \hfill & ={⟨uv,\psi ⟩}_{D^{\prime }(\Omega )\times D(\Omega )}.\hfill \end{array}$$

Theorem 58

(Embedding Theorem II [5]). Let Ω be a nonempty bounded open subset of ${\mathbb{R}}^n$ with Lipschitz continuous boundary or $\Omega ={\mathbb{R}}^n$. If $sp>n$, then $W^{s,p}(\Omega )\hookrightarrow L^{\infty }(\Omega )\cap C^0(\Omega )$ and $W^{s,p}(\Omega )$ is a Banach algebra.

Theorem 59

(Embedding Theorem III [18]). Let Ω be a nonempty bounded open subset of ${\mathbb{R}}^n$ with Lipschitz continuous boundary. Suppose $1\le p,q<\infty$ (p does NOT need to be less than or equal to q) and $0\le t\le s$ satisfy $s-\frac{n}{p}\ge t-\frac{n}{q}$. If $s\notin {\mathbb{N}}_0$, additionally assume that $s\ne t$. Then $W^{s,p}(\Omega )\hookrightarrow W^{t,q}(\Omega )$. In particular, $W^{s,p}(\Omega )\hookrightarrow W^{t,p}(\Omega )$.

Theorem 60.

Let Ω be a nonempty bounded open subset of ${\mathbb{R}}^n$ with Lipschitz continuous boundary. Then $u:\Omega \to \mathbb{R}$ is Lipschitz continuous if and only if $u\in W^{1,\infty }(\Omega )$. In particular, every function in $B{C}^1(\Omega )$ is Lipschitz continuous.

Proof. 

The above theorem is proved in Chapter 5 of [2] for open sets with $C^1$ boundary. The exact same proof works for open sets with Lipschitz continuous boundary. □

The following theorem (and its corollary) will play an important role in our study of Sobolev spaces on manifolds.

Theorem 61

(Multiplication by smooth functions). Let Ω be a nonempty bounded open set in ${\mathbb{R}}^n$ with Lipschitz continuous boundary.

(1) 

Let $k\in {\mathbb{N}}_0$ and $1<p<\infty$. If $\phi \in B{C}^k(\Omega )$, then the linear map $W^{k,p}(\Omega )\to W^{k,p}(\Omega )$ defined by $u\mapsto \phi u$ is well-defined and bounded.

(2) 

Let $s\in (0,\infty )$ and $1<p<\infty$. If $\phi \in B{C}^{\lfloor s\rfloor ,1}(\Omega )$ (all partial derivatives of φ up to and including order $\lfloor s\rfloor$ exist and are bounded and Lipschitz continuous), then the linear map $W^{s,p}(\Omega )\to W^{s,p}(\Omega )$ defined by $u\mapsto \phi u$ is well-defined and bounded.

(3) 

Let $s\in (-\infty ,0)$ and $1<p<\infty$. If $\phi \in B{C}^{\infty ,1}(\Omega )$, then the linear map $W^{s,p}(\Omega )\to W^{s,p}(\Omega )$ defined by $u\mapsto \phi u$ is well-defined and bounded.

Note: According to Theorem 60, when Ω is an open bounded set with Lipschitz continuous boundary, every function in $B{C}^1(\Omega )$ is Lipschitz continuous. As a consequence, $B{C}^{\infty ,1}(\Omega )=B{C}^{\infty }(\Omega )$. Of course, as it was discussed after Theorem 6, for a general bounded open set Ω whose boundary is not Lipschitz, functions in $B{C}^{\infty }(\Omega )$ are not necessarily Lipschitz.

Proof. 

• Step 1:$s=k\in {\mathbb{N}}_0$. The claim is proved in ([29], p. 995).
• Step 2:$0<s<1$. The proof in p. 194 of [41], with obvious modifications, shows the validity of the claim for the case where $s\in (0,1)$.
• Step 3:$1<s\notin \mathbb{N}$. In this case we can proceed as follows: Let $k=\lfloor s\rfloor$, $\theta =s-k$.

  $$\begin{array}{cc}\hfill {\parallel \phi u\parallel }_{s,p}& \stackrel{\mathrm{Remark\; 39}}{=}{\parallel \phi u\parallel }_{k,p}+\sum _{|\nu |=k}{\parallel {\partial }^{\nu }(\phi u)\parallel }_{\theta ,p}\hfill \\ \hfill & ⪯{\parallel \phi u\parallel }_{k,p}+\sum _{|\nu |=k}\sum _{\beta \le \nu }{\parallel {\partial }^{\nu -\beta }\phi {\partial }^{\beta }u\parallel }_{\theta ,p}\hfill \\ \hfill & ⪯{\parallel u\parallel }_{k,p}+\sum _{|\nu |=k}\sum _{\beta \le \nu }{\parallel {\partial }^{\beta }u\parallel }_{\theta ,p}(\mathrm{by}\mathrm{steps}1\mathrm{and}2;\mathrm{the}\mathrm{implicit}\mathrm{constant}\mathrm{may}\mathrm{depend}\mathrm{on}\phi )\hfill \\ \hfill & ={\parallel u\parallel }_{s,p}+\sum _{|\nu |=k}\sum _{\beta <\nu }{\parallel {\partial }^{\beta }u\parallel }_{\theta ,p}\hfill \\ \hfill & ⪯{\parallel u\parallel }_{s,p}+\sum _{|\nu |=k}\sum _{\beta <\nu }{\parallel u\parallel }_{\theta +|\beta |,p}({\partial }^{\beta }:W^{\theta +|\beta |,p}(\Omega )\to W^{\theta ,p}(\Omega )\mathrm{is}\mathrm{continuous})\hfill \\ \hfill & ⪯{\parallel u\parallel }_{s,p}+\sum _{|\nu |=k}\sum _{\beta <\nu }{\parallel u\parallel }_{s,p}(\theta +|\beta |<s\Rightarrow W^{s,p}(\Omega )\hookrightarrow W^{\theta +|\beta |,p}(\Omega ))\hfill \\ \hfill & ⪯{\parallel u\parallel }_{s,p}.\hfill \end{array}$$

  Note that the embedding $W^{s,p}(\Omega )\hookrightarrow W^{\theta +|\beta |,p}(\Omega )$ is valid due to the extra assumption that $\Omega$ is bounded with Lipschitz continuous boundary (see Theorem 68 and Remark 42).
• Step 4:$s<0$. For this case we use a duality argument. Note that since $\phi \in C^{\infty }(\Omega )$, $\phi u$ is defined as an element of $D^{\prime }(\Omega )$. Furthermore, recall that $W^{s,p}(\Omega )$ is isometrically isomorphic to $[C_c^{\infty }{(\Omega ),\parallel .\parallel }_{-s,p^{\prime }}{]}^{*}$ (see the discussion after Remark 10). So, in order to prove the claim, it is enough to show that multiplication by $\phi$ is a well-defined continuous operator from $W^{s,p}(\Omega )$ to $A=[C_c^{\infty }{(\Omega ),\parallel .\parallel }_{-s,p^{\prime }}{]}^{*}$. We have

  $$\begin{array}{cc}\hfill {\parallel \phi u\parallel }_A& =\underset{v\in C_c^{\infty }\backslash \{0\}}{sup}\frac{{|⟨\phi u,v⟩}_{D^{\prime }(\Omega )\times D(\Omega )}|}{{\parallel v\parallel }_{-s,p^{\prime }}}=\underset{v\in C_c^{\infty }\backslash \{0\}}{sup}\frac{{|⟨u,\phi v⟩}_{D^{\prime }(\Omega )\times D(\Omega )}|}{{\parallel v\parallel }_{-s,p^{\prime }}}\hfill \\ \hfill & \stackrel{\mathrm{Remark\; 45}}{=}\underset{v\in C_c^{\infty }\backslash \{0\}}{sup}\frac{{|⟨u,\phi v⟩}_{W^{s,p}(\Omega )\times W_0^{-s,p^{\prime }}(\Omega )}|}{{\parallel v\parallel }_{-s,p^{\prime }}}\hfill \\ \hfill & \le \underset{v\in C_c^{\infty }\backslash \{0\}}{sup}\frac{{\parallel u\parallel }_{s,p}{\parallel \phi v\parallel }_{-s,p^{\prime }}}{{\parallel v\parallel }_{-s,p^{\prime }}}⪯\underset{v\in C_c^{\infty }\backslash \{0\}}{sup}\frac{{\parallel u\parallel }_{s,p}{\parallel v\parallel }_{-s,p^{\prime }}}{{\parallel v\parallel }_{-s,p^{\prime }}}={\parallel u\parallel }_{s,p}.\hfill \end{array}$$

□

Corollary 4.

Let Ω be a nonempty bounded open set in ${\mathbb{R}}^n$ with Lipschitz continuous boundary. Let $K\in \mathcal{K}(\Omega )$. Suppose $s\in \mathbb{R}$ and $p\in (1,\infty )$. If $\phi \in C^{\infty }(\Omega )$, then the linear map $W_K^{s,p}(\Omega )\to W_K^{s,p}(\Omega )$ defined by $u\mapsto \phi u$ is well-defined and bounded.

Proof. 

Let U be an open set such that $K\subset U\subseteq \overline{U}\subseteq \Omega$. Let $\psi \in C_c^{\infty }(\Omega )$ be such that $\psi =1$ on K and $\psi =0$ outside U. Clearly $\psi \phi \in C_c^{\infty }(\Omega )$ and thus $\psi \phi \in B{C}^{\infty ,1}(\Omega )$ (see the paragraph above Theorem 7). So, it follows from Theorem 61 that ${\parallel \psi \phi u\parallel }_{s,p}⪯{\parallel u\parallel }_{s,p}$ where the implicit constant in particular may depend on $\phi$ and $\psi$. Now the claim follows from the obvious observation that for all $u\in W_K^{s,p}(\Omega )$, we have $\psi \phi u=\phi u$. □

Theorem 62.

Let $\Omega ={\mathbb{R}}^n$ or Ω be a nonempty bounded open set in ${\mathbb{R}}^n$ with Lipschitz continuous boundary. Let $K\subseteq \Omega$ be compact, $s\in \mathbb{R}$ and $p\in (1,\infty )$. Then

(1) 

$W_K^{s,p}(\Omega )\subseteq W_0^{s,p}(\Omega )$. That is, every element of $W_K^{s,p}(\Omega )$ is a limit of a sequence in $C_c^{\infty }(\Omega )$;

(2) 

if $K\subseteq V\subseteq K^{\prime }\subseteq \Omega$ where and $K^{\prime }$ is compact and V is open, then for every $u\in W_K^{s,p}(\Omega )$, there exists a sequence in $C_{K^{\prime }}^{\infty }(\Omega )$ that converges to u in $W^{s,p}(\Omega )$.

Proof. 

(1)

Let $u\in W_K^{s,p}(\Omega )$. By Theorems 65 and 66, there exists a sequence $\{{\phi }_i\}$ in $C^{\infty }(\Omega )$ such that ${\phi }_i\to u$ in $W^{s,p}(\Omega )$. Let $\psi \in C_c^{\infty }(\Omega )$ be such that $\psi =1$ on K. Since $C_c^{\infty }(\Omega )\subseteq B{C}^{\infty ,1}(\Omega )$, it follows from Theorems 51 and 61 that $\psi {\phi }_i\to \psi u$ in $W^{s,p}(\Omega )$. This proves the claim because $\psi {\phi }_i\in C_c^{\infty }(\Omega )$ and $\psi u=u$.

(2)

In the above argument, choose $\psi \in C_c^{\infty }(\Omega )$ such that $\psi =1$ on K and $\psi =0$ outside V.

□

Theorem 63

(([40], p. 496), ([39], pp. 317, 330, and 332)). Let Ω be a bounded Lipschitz domain in ${\mathbb{R}}^n$. Suppose $1<p<\infty$, $0\le s<\frac{1}{p}$. Then $C_c^{\infty }(\Omega )$ is dense in $W^{s,p}(\Omega )$ (thus $W^{s,p}(\Omega )=W_0^{s,p}(\Omega )$).

7.4. Properties of Sobolev Spaces on General Domains

In this section, $\Omega$ and ${\Omega }^{\prime }$ are arbitrary nonempty open sets in ${\mathbb{R}}^n$. We begin with some facts about the relationship between various Sobolev spaces defined on bounded domains.

• Suppose $s\ge 0$ and ${\Omega }^{\prime }\subseteq \Omega$. Then for all $u\in W^{s,p}(\Omega )$, we have ${\mathrm{res}}_{\Omega ,{\Omega }^{\prime }}u\in W^{s,p}({\Omega }^{\prime })$. Moreover, $\parallel {\mathrm{res}}_{\Omega ,{\Omega }^{\prime }}{u\parallel }_{W^{s,p}({\Omega }^{\prime })}\le {\parallel u\parallel }_{W^{s,p}(\Omega )}$. Indeed, if we let $s=k+\theta$

  $$\begin{array}{cc}\hfill {\parallel u\parallel }_{W^{s,p}({\Omega }^{\prime })}& ={\parallel u\parallel }_{W^{k,p}({\Omega }^{\prime })}+\sum _{|\nu |=k}{\left(\int {\int }_{{\Omega }^{\prime }\times {\Omega }^{\prime }}\frac{|{\partial }^{\nu }u(x)-{\partial }^{\nu }{u(y)|}^p}{{|x-y|}^{n+\theta p}}dxdy\right)}^{\frac{1}{p}}\hfill \\ \hfill & =\sum _{|\alpha |\le k}{\parallel {\partial }^{\alpha }u\parallel }_{L^p({\Omega }^{\prime })}+\sum _{|\nu |=k}{\left(\int {\int }_{{\Omega }^{\prime }\times {\Omega }^{\prime }}\frac{|{\partial }^{\nu }u(x)-{\partial }^{\nu }{u(y)|}^p}{{|x-y|}^{n+\theta p}}dxdy\right)}^{\frac{1}{p}}\hfill \\ \hfill & \le \sum _{|\alpha |\le k}\parallel {\partial }^{\alpha }{u\parallel }_{L^p(\Omega )}+\sum _{|\nu |=k}{\left(\int {\int }_{\Omega \times \Omega }\frac{|{\partial }^{\nu }u(x)-{\partial }^{\nu }{u(y)|}^p}{{|x-y|}^{n+\theta p}}dxdy\right)}^{\frac{1}{p}}={\parallel u\parallel }_{W^{s,p}(\Omega )}.\hfill \end{array}$$

  So, ${\mathrm{res}}_{\Omega ,{\Omega }^{\prime }}:W^{s,p}(\Omega )\to W^{s,p}({\Omega }^{\prime })$ is a continuous linear map. Furthermore, as a consequence, for every real number $s\ge 0$

  $$W^{s,p}(\overline{\Omega })\hookrightarrow W^{s,p}(\Omega ).$$

  Indeed, if $u\in W^{s,p}(\overline{\Omega })$, then there exists $v\in W^{s,p}({\mathbb{R}}^n)$ such that ${\mathrm{res}}_{{\mathbb{R}}^n,\Omega }v=u$ and thus $u\in W^{s,p}(\Omega )$. Moreover, for every such v, ${\parallel u\parallel }_{W^{s,p}(\Omega )}=\parallel {\mathrm{res}}_{{\mathbb{R}}^n,\Omega }{v\parallel }_{W^{s,p}(\Omega )}\le {\parallel v\parallel }_{W^{s,p}({\mathbb{R}}^n)}$. This implies that

  $${\parallel u\parallel }_{W^{s,p}(\Omega )}\le \underset{v\in W^{s,p}({\mathbb{R}}^n){,v|}_{\Omega }=u}{inf}{\parallel v\parallel }_{W^{s,p}({\mathbb{R}}^n)}={\parallel u\parallel }_{W^{s,p}(\overline{\Omega })}.$$
• Clearly, for all $s\ge 0$

  $$W_{00}^{s,p}(\Omega )\hookrightarrow W^{s,p}(\overline{\Omega }).$$
• For every integer $m>0$ ([5], p. 18)

  $$W_0^{m,p}(\Omega )\subseteq W_{00}^{m,p}(\Omega )\subseteq W^{m,p}(\overline{\Omega })\subseteq W^{m,p}(\Omega ).$$
• Suppose $s\ge 0$. Clearly, the restriction map ${\mathrm{res}}_{{\mathbb{R}}^n,\Omega }:W^{s,p}({\mathbb{R}}^n)\to W^{s,p}(\overline{\Omega })$ is a continuous linear map. This combined with the fact that $C_c^{\infty }({\mathbb{R}}^n)$ is dense in $W^{s,p}({\mathbb{R}}^n)$ implies that $C_c^{\infty }(\overline{\Omega }):={\mathrm{res}}_{{\mathbb{R}}^n,\Omega }(C_c^{\infty }({\mathbb{R}}^n))$ is dense in $W^{s,p}(\overline{\Omega })$ for all $s\ge 0$.
• ${\tilde{W}}^{s,p}(\overline{\Omega })$ is a closed subspace of $W^{s,p}({\mathbb{R}}^n)$. Closed subspaces of reflexive spaces are reflexive, hence ${\tilde{W}}^{s,p}(\overline{\Omega })$ is a reflexive space.

Theorem 64.

Let Ω be a nonempty open set in ${\mathbb{R}}^n$ and $1<p<\infty$.

(1) 

For all $s\ge 0$, $W^{s,p}(\Omega )$ is reflexive.

(2) 

For all $s\ge 0$, $W_0^{s,p}(\Omega )$ is reflexive.

(3) 

For all $s<0$, $W^{s,p}(\Omega )$ is reflexive.

Proof. 

(1)

The proof for $s\in {\mathbb{N}}_0$ can be found in [1]. Let $s=k+\theta$ where $k\in {\mathbb{N}}_0$ and $0<\theta <1$. Let

$$r=\mathrm{card}\{\nu \in {\mathbb{N}}_0^n:|\nu |=k\}.$$

Define $P:W^{s,p}(\Omega )\to W^{k,p}(\Omega )\times {[L^p(\Omega \times \Omega )]}^{\times r}$ by

$$P(u)=(u,{\left(\frac{|{\partial }^{\nu }u(x)-{\partial }^{\nu }u(y)|}{{|x-y|}^{\frac{n}{p}+\theta }}\right)}_{|\nu |=k}).$$

The space $W^{k,p}(\Omega )\times {[L^p(\Omega \times \Omega )]}^{\times r}$ equipped with the norm

$$\parallel (f,v_1,\dots ,v_r){\parallel :=\parallel f\parallel }_{W^{k,p}(\Omega )}+\parallel v_1{\parallel }_{L^p(\Omega \times \Omega )}+\dots +{\parallel v_r\parallel }_{L^p(\Omega \times \Omega )}$$

is a product of reflexive spaces and so it is reflexive (see Theorem 9). Clearly, the operator P is an isometry from $W^{s,p}(\Omega )$ to $W^{k,p}(\Omega )\times {[L^p(\Omega \times \Omega )]}^{\times r}$. Since $W^{s,p}(\Omega )$ is a Banach space, $P(W^{s,p}(\Omega ))$ is a closed subspace of the reflexive space $W^{k,p}(\Omega )\times {[L^p(\Omega \times \Omega )]}^{\times r}$ and thus it is reflexive. Hence $W^{s,p}(\Omega )$ itself is reflexive.

(2)

$W_0^{s,p}(\Omega )$ is the closure of $C_c^{\infty }(\Omega )$ in $W^{s,p}(\Omega )$. Closed subspaces of reflexive spaces are reflexive. Therefore, $W_0^{s,p}(\Omega )$ is reflexive.

(3)

A normed space X is reflexive if and only if $X^{*}$ is reflexive (see Theorem 9). Since for $s<0$ we have $W^{s,p}(\Omega )={[W_0^{-s,p^{\prime }}(\Omega )]}^{*}$, the reflexivity of $W^{s,p}(\Omega )$ follows from the reflexivity of $W_0^{-s,p^{\prime }}(\Omega )$.

□

Theorem 65.

For all $s<0$ and $1<p<\infty$, $C_c^{\infty }(\Omega )$ is dense in $W^{s,p}(\Omega )$.

Proof. 

The proof of the density of $L^p$ in $W^{m,p}$ in p. 65 of [1] for integer order Sobolev spaces, which is based on the reflexivity of $W_0^{-m,p^{\prime }}(\Omega )$, works in the exact same way for establishing the density of $C_c^{\infty }(\Omega )$ in $W^{s,p}(\Omega )$. □

Theorem 66

(Meyers-Serrin). For all $s\ge 0$ and $p\in (1,\infty )$, $C^{\infty }(\Omega )\cap W^{s,p}(\Omega )$ is dense in $W^{s,p}(\Omega )$.

Next we consider extension by zero and its properties.

Lemma 6

([4], p. 201). Let Ω be a nonempty open set in ${\mathbb{R}}^n$ and $u\in W_0^{m,p}(\Omega )$ where $m\in {\mathbb{N}}_0$ and $1<p<\infty$. Then

(1) 

$\forall |\alpha |\le m$, ${\partial }^{\alpha }\tilde{u}=\widetilde{({\partial }^{\alpha }u)}$ as elements of $D^{\prime }({\mathbb{R}}^n)$,

(2) 

$\tilde{u}\in W^{m,p}({\mathbb{R}}^n)$ with $\parallel \tilde{u}{\parallel }_{W^{m,p}({\mathbb{R}}^n)}={\parallel u\parallel }_{W^{m,p}(\Omega )}$.

Here, $\tilde{u}:={\mathit{ext}}_{\Omega ,{\mathbb{R}}^n}^{0}u$ and $\widetilde{({\partial }^{\alpha }u)}:={\mathit{ext}}_{\Omega ,{\mathbb{R}}^n}^0({\partial }^{\alpha }u)$.

Lemma 7

([6], p. 546). Let Ω be a nonempty open set in ${\mathbb{R}}^n$, $K\in \mathcal{K}(\Omega )$, $u\in W_K^{s,p}(\Omega )$ where $s\in (0,1)$ and $1<p<\infty$. Then ${\mathit{ext}}_{\Omega ,{\mathbb{R}}^n}^{0}u\in W^{s,p}({\mathbb{R}}^n)$ and

$$\parallel {\mathit{ext}}_{\Omega ,{\mathbb{R}}^n}^0{\parallel }_{W^{s,p}({\mathbb{R}}^n)}⪯{\parallel u\parallel }_{W^{s,p}(\Omega )},$$

where the implicit constant depends on $n,p,s,K$ and Ω.

Theorem 67

(Extension by Zero). Let $s\ge 0$ and $p\in (1,\infty )$. Let Ω be a nonempty open set in ${\mathbb{R}}^n$ and let $K\in \mathcal{K}(\Omega )$. Suppose $u\in W_K^{s,p}(\Omega )$. Then

(1) 

${\mathit{ext}}_{\Omega ,{\mathbb{R}}^n}^{0}u\in W^{s,p}({\mathbb{R}}^n)$. Indeed, $\parallel {\mathit{ext}}_{\Omega ,{\mathbb{R}}^n}^0{u\parallel }_{W^{s,p}({\mathbb{R}}^n)}⪯{\parallel u\parallel }_{W^{s,p}(\Omega )}$ where the implicit constant may depend on $s,p,n,K,\Omega$ but it is independent of $u\in W_K^{s,p}(\Omega )$.

(2) 

Moreover,

$$\parallel {\mathit{ext}}_{\Omega ,{\mathbb{R}}^n}^0{u\parallel }_{W^{s,p}({\mathbb{R}}^n)}\ge {\parallel u\parallel }_{W^{s,p}(\Omega )}.$$

In short, $\parallel {\mathit{ext}}_{\Omega ,{\mathbb{R}}^n}^0{u\parallel }_{W^{s,p}({\mathbb{R}}^n)}\simeq {\parallel u\parallel }_{W^{s,p}(\Omega )}$.

Proof. 

Let $\tilde{u}={\mathit{ext}}_{\Omega ,{\mathbb{R}}^n}^{0}u$. If $s\in {\mathbb{N}}_0$, then both items follow from Lemma 6. So, let $s=m+\theta$ where $m\in {\mathbb{N}}_0$ and $\theta \in (0,1)$. We have

$$\begin{array}{cc}\hfill \parallel \tilde{u}{\parallel }_{W^{s,p}({\mathbb{R}}^n)}& =\parallel \tilde{u}{\parallel }_{W^{m,p}({\mathbb{R}}^n)}+\sum _{|\nu |=m}{|{\partial }^{\nu }\tilde{u}|}_{W^{\theta ,p}({\mathbb{R}}^n)}\hfill \\ \hfill & \stackrel{\mathrm{Lemma\; 6}}{=}{\parallel u\parallel }_{W^{m,p}(\Omega )}+\sum _{|\nu |=m}{|\widetilde{{\partial }^{\nu }u}|}_{W^{\theta ,p}({\mathbb{R}}^n)}\hfill \\ \hfill & \stackrel{\mathrm{Lemma\; 7}}{⪯}{\parallel u\parallel }_{W^{m,p}(\Omega )}+\sum _{|\nu |=m}{\parallel {\partial }^{\nu }u\parallel }_{W^{\theta ,p}(\Omega )}\hfill \\ \hfill & ⪯{\parallel u\parallel }_{W^{s,p}(\Omega )}.\hfill \end{array}$$

The fact that $\parallel \tilde{u}{\parallel }_{W^{s,p}({\mathbb{R}}^n)}\ge {\parallel u\parallel }_{W^{s,p}(\Omega )}$ is a direct consequence of the decomposition stated in item 1 of Remark 34. □

Corollary 5.

Let $s\ge 0$ and $p\in (1,\infty )$. Let Ω and ${\Omega }^{\prime }$ be nonempty open sets in ${\mathbb{R}}^n$ with ${\Omega }^{\prime }\subseteq \Omega$ and let $K\in \mathcal{K}({\Omega }^{\prime })$. Suppose $u\in W_K^{s,p}({\Omega }^{\prime })$. Then

(1) 

${\mathit{ext}}_{{\Omega }^{\prime },\Omega }^{0}u\in W^{s,p}(\Omega )$,

(2) 

$\parallel {\mathit{ext}}_{{\Omega }^{\prime },\Omega }^0{u\parallel }_{W^{s,p}(\Omega )}\simeq {\parallel u\parallel }_{W^{s,p}({\Omega }^{\prime })}$.

Proof. 

$$\begin{array}{c}\hfill u\in W_K^{s,p}({\Omega }^{\prime })⟹{\mathrm{ext}}_{{\Omega }^{\prime },{\mathbb{R}}^n}^{0}u\in W^{s,p}({\mathbb{R}}^n)⟹{\mathrm{ext}}_{{\Omega }^{\prime },{\mathbb{R}}^n}^0{u|}_{\Omega }\in W^{s,p}(\overline{\Omega }).\end{array}$$

As we know, $W^{s,p}(\overline{\Omega })\hookrightarrow W^{s,p}(\Omega )$. Furthermore, it is easy to see that ${\mathrm{ext}}_{{\Omega }^{\prime },{\mathbb{R}}^n}^0{u|}_{\Omega }={\mathrm{ext}}_{{\Omega }^{\prime },\Omega }^{0}u$. Therefore, ${\mathrm{ext}}_{{\Omega }^{\prime },\Omega }^{0}u\in W^{s,p}(\Omega )$. Moreover,

$$\parallel {\mathrm{ext}}_{{\Omega }^{\prime },\Omega }^0{u\parallel }_{W^{s,p}(\Omega )}\simeq \parallel {\mathrm{ext}}_{\Omega ,{\mathbb{R}}^n}^0\circ {\mathrm{ext}}_{{\Omega }^{\prime },\Omega }^0{u\parallel }_{W^{s,p}({\mathbb{R}}^n)}=\parallel {\mathrm{ext}}_{{\Omega }^{\prime },{\mathbb{R}}^n}^0{u\parallel }_{W^{s,p}({\mathbb{R}}^n)}\simeq {\parallel u\parallel }_{W^{s,p}({\Omega }^{\prime })}.$$

 □

Extension by zero for Sobolev spaces with negative exponents will be discussed in Theorem 71.

Theorem 68

(Embedding Theorem IV). Let $\Omega \subseteq {\mathbb{R}}^n$ be an arbitrary nonempty open set.

(1) 

Suppose $1\le p\le q<\infty$ and $0\le t\le s$ satisfy $s-\frac{n}{p}\ge t-\frac{n}{q}$. Then $W^{s,p}(\overline{\Omega })\hookrightarrow W^{t,q}(\overline{\Omega })$.

(2) 

Suppose $1\le p\le q<\infty$ and $0\le t\le s$ satisfy $s-\frac{n}{p}\ge t-\frac{n}{q}$. Then $W_K^{s,p}(\Omega )\hookrightarrow W_K^{t,q}(\Omega )$ for all $K\in \mathcal{K}(\Omega )$.

(3) 

For all $k_1,k_2\in {\mathbb{N}}_0$ with $k_1\le k_2$ and $1<p<\infty$, $W^{k_2,p}(\Omega )\hookrightarrow W^{k_1,p}(\Omega )$.

(4) 

If $0\le t\le s<1$ and $1<p<\infty$, then $W^{s,p}(\Omega )\hookrightarrow W^{t,p}(\Omega )$.

(5) 

If $0\le t\le s<\infty$ are such that $\lfloor s\rfloor =\lfloor t\rfloor$ and $1<p<\infty$, then $W^{s,p}(\Omega )\hookrightarrow W^{t,p}(\Omega )$.

(6) 

If $0\le t\le s<\infty$, $t\in {\mathbb{N}}_0$, and $1<p<\infty$, then $W^{s,p}(\Omega )\hookrightarrow W^{t,p}(\Omega )$.

Proof. 

(1)

This item can be found in ([39], Section 4.6.1).

(2)

For all $u\in W_K^{s,p}(\Omega )$ we have

$$\begin{array}{c}\hfill {\parallel u\parallel }_{W^{t,q}(\Omega )}\simeq \parallel {\mathrm{ext}}_{\Omega ,{\mathbb{R}}^n}^0{u\parallel }_{W^{t,q}({\mathbb{R}}^n)}⪯\parallel {\mathrm{ext}}_{\Omega ,{\mathbb{R}}^n}^0{u\parallel }_{W^{s,p}({\mathbb{R}}^n)}\simeq {\parallel u\parallel }_{W^{s,p}(\Omega )}.\end{array}$$

(3)

This item is a direct consequence of the definition of integer order Sobolev spaces.

(4)

Proof can be found in [6], p. 524.

(5)

This is a direct consequence of the previous two items.

(6)

This is true because $W^{s,p}(\Omega )\hookrightarrow W^{\lfloor s\rfloor ,p}(\Omega )\hookrightarrow W^{t,p}(\Omega )$.

□

Remark 42.

For an arbitrary open set Ω in ${\mathbb{R}}^n$ and $0<t<1$, the embedding $W^{1,p}(\Omega )\hookrightarrow W^{t,p}(\Omega )$ does NOT necessarily hold (see, e.g., [6], Section 9). Of course, as it was discussed, under the extra assumption that Ω is Lipschitz, the latter embedding holds true. So, if $\lfloor s\rfloor \ne \lfloor t\rfloor$ and $t\notin {\mathbb{N}}_0$, then in order to ensure that $W^{s,p}(\Omega )\hookrightarrow W^{t,p}(\Omega )$ we need to assume some sort of regularity for the domain Ω (for instance it is enough to assume Ω is Lipschitz).

Theorem 69

(Multiplication by smooth functions). Let Ω be any nonempty open set in ${\mathbb{R}}^n$. Let $p\in (1,\infty )$.

(1) 

If $0\le s<1$ and $\phi \in B{C}^{0,1}(\Omega )$ (that is, φ is bounded and φ is Lipschitz), then

$$m_{\phi }:W^{s,p}(\Omega )\to W^{s,p}(\Omega ),u\mapsto \phi u$$

is a well-defined bounded linear map.

(2) 

If $k\in {\mathbb{N}}_0$ and $\phi \in B{C}^k(\Omega )$, then

$$m_{\phi }:W^{k,p}(\Omega )\to W^{k,p}(\Omega ),u\mapsto \phi u$$

is a well-defined bounded linear map.

(3) 

If $-1<s<0$ and $\phi \in B{C}^{\infty ,1}(\Omega )$ or $s\in {\mathbb{Z}}^{-}$ and $\phi \in B{C}^{\infty }(\Omega )$, then

$$m_{\phi }:W^{s,p}(\Omega )\to W^{s,p}(\Omega ),u\mapsto \phi u$$

is a well-defined bounded linear map ($\phi u$ is interpreted as the product of a smooth function and a distribution).

Proof. 

(1)

Proof can be found in [6], p. 547.

(2)

Proof can be found in [29], p. 995.

(3)

The duality argument in Step 4 of the proof of Theorem 61 works for this item too.

□

Remark 43.

Suppose $\phi \in B{C}^{\infty ,1}(\Omega )$. Note that the above theorem says nothing about the boundedness of the mapping $m_{\phi }:W^{s,p}(\Omega )\to W^{s,p}(\Omega )$ in the case where s is noninteger such that $|s|>1$. Of course, if we assume Ω is Lipschitz, then the continuity of $m_{\phi }$ follows from Theorem 61. It is important to note that the proof of that theorem for the case $s>1$ (noninteger) uses the embedding $W^{k+\theta ,p}(\Omega )\hookrightarrow W^{k^{\prime }+\theta ,p}(\Omega )$ with $k^{\prime }<k$ which as we discussed does not hold for an arbitrary open set Ω. The proof for the case $s<-1$ (noninteger) uses duality to transfer the problem to $s>1$ and thus again we need the extra assumption of regularity of the boundary of Ω.

Theorem 70.

Let Ω be a nonempty open set in ${\mathbb{R}}^n$, $K\in \mathcal{K}(\Omega )$, $p\in (1,\infty )$, and $-1<s<0$ or $s\in {\mathbb{Z}}^{-}$ or $s\in [0,\infty )$. If $\phi \in C^{\infty }(\Omega )$, then the linear map

$$W_K^{s,p}(\Omega )\to W_K^{s,p}(\Omega ),u\mapsto \phi u$$

is well-defined and bounded.

Proof. 

There exists $\psi \in C_c^{\infty }(\Omega )$ such that $\psi =1$ on K. Clearly $\psi \phi \in C_c^{\infty }(\Omega )$ and if $u\in W_K^{s,p}(\Omega )$, $\psi \phi u=\phi u$ on $\Omega$. Thus without loss of generality we may assume that $\phi \in C_c^{\infty }(\Omega )$. Since $C_c^{\infty }(\Omega )\subseteq B{C}^{\infty }(\Omega )$ and $C_c^{\infty }(\Omega )\subseteq B{C}^{\infty ,1}(\Omega )$, the cases where $-1<s<0$ or $s\in {\mathbb{Z}}^{-}$ follow from Theorem 69. For $s\ge 0$, the proof of Theorem 61 works for this theorem as well. The only place in that proof that the regularity of the boundary of $\Omega$ was used was for the validity of the embedding $W^{s,p}(\Omega )\hookrightarrow W^{\theta +|\beta |,p}(\Omega )$. However, as we know (see Theorem 68), this embedding holds for Sobolev spaces with support in a fixed compact set inside $\Omega$ for a general open set $\Omega$, that is, for $W_K^{s,p}(\Omega )\hookrightarrow W_K^{\theta +|\beta |,p}(\Omega )$ to be true we do not need to assume $\Omega$ is Lipschitz. □

Remark 44.

Note that our proofs for $s<0$ are based on duality. As a result, it seems that for the case where s is a noninteger less than $-1$ we cannot have a multiplication by smooth functions result for $W_K^{s,p}(\Omega )$ similar to the one stated in the above theorem (note that there is no fixed compact set K such that every $v\in C_c^{\infty }(\Omega )$ has compact support in K. Thus, the technique used in Step 4 of the proof of Theorem 61 does not work in this case).

Theorem 71.

Let $s<0$ and $p\in (1,\infty )$. Let Ω and ${\Omega }^{\prime }$ be nonempty open sets in ${\mathbb{R}}^n$ with ${\Omega }^{\prime }\subseteq \Omega$ and let $K\in \mathcal{K}({\Omega }^{\prime })$. Suppose $u\in W_K^{s,p}({\Omega }^{\prime })$. Then

(1) 

If ${\mathit{ext}}_{{\Omega }^{\prime },\Omega }^{0}u\in W^{s,p}(\Omega )$, then ${\parallel u\parallel }_{W^{s,p}({\Omega }^{\prime })}⪯{\parallel {\mathit{ext}}_{{\Omega }^{\prime },\Omega }^{0}u\parallel }_{W^{s,p}(\Omega )}$ (the implicit constant may depend on K).

(2) 

If $s\in (-\infty ,-1]\cap \mathbb{Z}$ or $-1<s<0$, then ${\mathit{ext}}_{{\Omega }^{\prime },\Omega }^{0}u\in W^{s,p}(\Omega )$ and $\parallel {\mathit{ext}}_{{\Omega }^{\prime },\Omega }^0{u\parallel }_{W^{s,p}(\Omega )}\simeq {\parallel u\parallel }_{W^{s,p}({\Omega }^{\prime })}$. This result holds for all $s<0$ if we further assume that Ω is Lipschitz or $\Omega ={\mathbb{R}}^n$.

Proof. 

To be completely rigorous, let $i_{D,W}:D({\Omega }^{\prime })\to W_0^{-s,p^{\prime }}({\Omega }^{\prime })$ be the identity map and let $i_{D,W}^{*}:W^{s,p}({\Omega }^{\prime })\to D^{\prime }({\Omega }^{\prime })$ be its dual with which we identify $W^{s,p}({\Omega }^{\prime })$ with a subspace of $D^{\prime }({\Omega }^{\prime })$. Previously we defined $ex{t}_{{\Omega }^{\prime },\Omega }^0$ for distributions with compact support in ${\Omega }^{\prime }$. For any $u\in W_K^{s,p}({\Omega }^{\prime })$ we let

$${\mathrm{ext}}_{{\Omega }^{\prime },\Omega }^{0}u:={\mathrm{ext}}_{{\Omega }^{\prime },\Omega }^0\circ i_{D,W}^{*}u,$$

which by definition will be an element of $D^{\prime }(\Omega )$. Note that (see Remark 45 and the discussion right after Remark 10)

$$\begin{array}{cc}\hfill & \parallel {\mathrm{ext}}_{{\Omega }^{\prime },\Omega }^0{u\parallel }_{W^{s,p}(\Omega )}=\underset{0\ne \psi \in D(\Omega )}{sup}\frac{|{⟨{\mathrm{ext}}_{{\Omega }^{\prime },\Omega }^{0}u,\psi ⟩}_{D^{\prime }(\Omega )\times D(\Omega )}|}{{\parallel \psi \parallel }_{W^{-s,p^{\prime }}(\Omega )}}\hfill \\ \hfill & {\parallel u\parallel }_{W^{s,p}({\Omega }^{\prime })}=\underset{0\ne \phi \in D({\Omega }^{\prime })}{sup}\frac{{|⟨u,\phi ⟩}_{D^{\prime }({\Omega }^{\prime })\times D({\Omega }^{\prime })}|}{{\parallel \phi \parallel }_{W^{-s,p^{\prime }}({\Omega }^{\prime })}}.\hfill \end{array}$$

So, in order to prove the first item we just need to show that

$$\forall 0\ne \phi \in D({\Omega }^{\prime })\exists \psi \in D(\Omega )\mathrm{s}.\mathrm{t}.\frac{{|⟨u,\phi ⟩}_{D^{\prime }({\Omega }^{\prime })\times D({\Omega }^{\prime })}|}{{\parallel \phi \parallel }_{W^{-s,p^{\prime }}({\Omega }^{\prime })}}⪯\frac{|{⟨{\mathrm{ext}}_{{\Omega }^{\prime },\Omega }^{0}u,\psi ⟩}_{D^{\prime }(\Omega )\times D(\Omega )}|}{{\parallel \psi \parallel }_{W^{-s,p^{\prime }}(\Omega )}}.$$

Let $\phi \in D({\Omega }^{\prime })$. Define $\psi ={\mathit{ext}}_{{\Omega }^{\prime },\Omega }^0\phi$. Clearly, $\psi \in D(\Omega )$ and $\psi =\phi$ on ${\Omega }^{\prime }$. Therefore,

$${⟨{\mathit{ext}}_{{\Omega }^{\prime },\Omega }^{0}u,\psi ⟩}_{D^{\prime }(\Omega )\times D(\Omega )}={⟨u,\psi {|}_{{\Omega }^{\prime }}⟩}_{D^{\prime }({\Omega }^{\prime })\times D({\Omega }^{\prime })}={⟨u,\phi ⟩}_{D^{\prime }({\Omega }^{\prime })\times D({\Omega }^{\prime })}.$$

Moreover, since $-s>0$

$${\parallel \psi \parallel }_{W^{-s,p^{\prime }}(\Omega )}=\parallel {\mathrm{ext}}_{{\Omega }^{\prime },\Omega }^0{\phi \parallel }_{W^{-s,p^{\prime }}(\Omega )}⪯{\parallel \phi \parallel }_{W^{-s,p^{\prime }}({\Omega }^{\prime })}.$$

This completes the proof of the first item. For the second item we just need to prove that under the given hypotheses

$$\forall 0\ne \psi \in D(\Omega )\exists \phi \in D({\Omega }^{\prime })\mathrm{s}.\mathrm{t}.\frac{|{⟨{\mathrm{ext}}_{{\Omega }^{\prime },\Omega }^{0}u,\psi ⟩}_{D^{\prime }(\Omega )\times D(\Omega )}|}{{\parallel \psi \parallel }_{W^{-s,p^{\prime }}(\Omega )}}⪯\frac{{|⟨u,\phi ⟩}_{D^{\prime }({\Omega }^{\prime })\times D({\Omega }^{\prime })}|}{{\parallel \phi \parallel }_{W^{-s,p^{\prime }}({\Omega }^{\prime })}}.$$

To this end suppose $\psi \in D(\Omega )$. Choose a compact set $\tilde{K}$ such that $K\subset \mathring{\tilde{K}}\subset \tilde{K}\subset {\Omega }^{\prime }$. Fix $\chi \in D(\Omega )$ such that $\chi =1$ on $\tilde{K}$ and $\mathrm{supp}\chi \subset {\Omega }^{\prime }$. Clearly, $\psi =\chi \psi$ on a neighborhood of K and if we set ${\phi =\chi \psi |}_{{\Omega }^{\prime }}$, then $\phi \in D({\Omega }^{\prime })$. Therefore,

$${⟨{\mathrm{ext}}_{{\Omega }^{\prime },\Omega }^{0}u,\psi ⟩}_{D^{\prime }(\Omega )\times D(\Omega )}={⟨{\mathrm{ext}}_{{\Omega }^{\prime },\Omega }^{0}u,\chi \psi ⟩}_{D^{\prime }(\Omega )\times D(\Omega )}={⟨u,\chi \psi {|}_{{\Omega }^{\prime }}⟩}_{D^{\prime }({\Omega }^{\prime })\times D({\Omega }^{\prime })}={⟨u,\phi ⟩}_{D^{\prime }({\Omega }^{\prime })\times D({\Omega }^{\prime })}.$$

Furthermore, since $-s>0$, we have

$${\parallel \phi \parallel }_{W^{-s,p^{\prime }}({\Omega }^{\prime })}\le \parallel {\mathrm{ext}}_{{\Omega }^{\prime },\Omega }^0{\phi \parallel }_{W^{-s,p^{\prime }}(\Omega )}={\parallel \chi \psi \parallel }_{W^{-s,p^{\prime }}(\Omega )}⪯{\parallel \psi \parallel }_{W^{-s,p^{\prime }}(\Omega )}.$$

The latter inequality is the place where we used the assumption that $s\in (-\infty ,-1]\cap \mathbb{Z}$ or $-1<s<0$ or $\Omega$ is Lipschitz or $\Omega ={\mathbb{R}}^n$. This completes the proof of the second item. □

Corollary 6.

Let $p\in (1,\infty )$. Let Ω and ${\Omega }^{\prime }$ be nonempty open sets in ${\mathbb{R}}^n$ with ${\Omega }^{\prime }\subseteq \Omega$ and let $K\in \mathcal{K}({\Omega }^{\prime })$. Suppose $u\in W_K^{s,p}(\Omega )$. It follows from Corollary 5 and Theorem 71 that

• If $s\in \mathbb{R}$ is not a noninteger less than $-1$, then

  $${\parallel u\parallel }_{W^{s,p}(\Omega )}\simeq {\parallel u\parallel }_{W^{s,p}({\Omega }^{\prime })},$$
• If Ω is Lipschitz or $\Omega ={\mathbb{R}}^n$, then for all $s\in \mathbb{R}$

  $${\parallel u\parallel }_{W^{s,p}(\Omega )}\simeq {\parallel u\parallel }_{W^{s,p}({\Omega }^{\prime })}.$$

Note that on the right hand sides of the above expressions, u stands for ${\mathit{res}}_{\Omega ,{\Omega }^{\prime }}u$. Clearly, ${\mathit{ext}}_{{\Omega }^{\prime },\Omega }^0\circ {\mathit{res}}_{\Omega ,{\Omega }^{\prime }}u=u$.

Theorem 72.

Let Ω be any nonempty open set in ${\mathbb{R}}^n$, $K\subseteq \Omega$ be compact, $s>0$, and $p\in (1,\infty )$. Then the following norms on $W_K^{s,p}(\Omega )$ are equivalent:

$$\begin{array}{cc}\hfill & {\parallel u\parallel }_{W^{s,p}(\Omega )}:={\parallel u\parallel }_{W^{k,p}(\Omega )}+\sum _{|\nu |=k}{|{\partial }^{\nu }u|}_{W^{\theta ,p}(\Omega )},\hfill \\ \hfill & {[u]}_{W^{s,p}(\Omega )}:={\parallel u\parallel }_{W^{k,p}(\Omega )}+\sum _{1\le |\nu |\le k}{|{\partial }^{\nu }u|}_{W^{\theta ,p}(\Omega )},\hfill \end{array}$$

where $s=k+\theta ,k\in {\mathbb{N}}_0,\theta \in (0,1)$. Moreover, if we further assume Ω is Lipschitz, then the above norms are equivalent on $W^{s,p}(\Omega )$.

Proof. 

Clearly, for all $u\in W^{s,p}(\Omega )$, ${\parallel u\parallel }_{W^{s,p}(\Omega )}\le {[u]}_{W^{s,p}(\Omega )}$. So, it is enough to show that there is a constant $C>0$ such that for all $u\in W_K^{s,p}(\Omega )$ (or $u\in W^{s,p}(\Omega )$ if $\Omega$ is Lipschitz)

$${[u]}_{W^{s,p}(\Omega )}\le C{\parallel u\parallel }_{W^{s,p}(\Omega )}.$$

For each $1\le i\le k$ we have

$$\sum _{|\nu |=i}|{\partial }^{\nu }{u|}_{W^{\theta ,p}(\Omega )}={\parallel u\parallel }_{W^{i+\theta ,p}(\Omega )}-{\parallel u\parallel }_{W^{i,p}(\Omega )}.$$

Thus

$$\begin{array}{cc}\hfill {[u]}_{W^{s,p}(\Omega )}& ={\parallel u\parallel }_{W^{s,p}(\Omega )}+\sum _{1\le i<k}\sum _{|\nu |=i}{|{\partial }^{\nu }u|}_{W^{\theta ,p}(\Omega )}\hfill \\ \hfill & ={\parallel u\parallel }_{W^{s,p}(\Omega )}+\sum _{1\le i<k}\left({\parallel u\parallel }_{W^{i+\theta ,p}(\Omega )}-{\parallel u\parallel }_{W^{i,p}(\Omega )}\right).\hfill \end{array}$$

Therefore, it is enough to show that there exists a constant $C\ge 1$ such that

$$\sum _{1\le i<k}{\parallel u\parallel }_{W^{i+\theta ,p}(\Omega )}\le {(C-1)\parallel u\parallel }_{W^{s,p}(\Omega )}+\sum _{1\le i<k}{\parallel u\parallel }_{W^{i,p}(\Omega )}.$$

By Theorem 68, for each $1\le i<k$, $W_K^{s,p}(\Omega )\hookrightarrow W_K^{i+\theta ,p}(\Omega )$ (also, we have $W^{s,p}(\Omega )\hookrightarrow W^{i+\theta ,p}(\Omega )$ with the extra assumption that $\Omega$ is Lipschitz); so there is a constant $C_i$ such that ${\parallel u\parallel }_{W^{i+\theta ,p}(\Omega )}\le C_i{\parallel u\parallel }_{W^{s,p}(\Omega )}$. Clearly with $C=1+{\sum }_{i=1}^{k-1}{C}_i$ the desired inequality holds. □

Remark 45.

Let $s\ge 0$ and $1<p<\infty$. Here we summarize the connection between Sobolev spaces and space of distributions.

(1) 

Question 1: What does it mean to say $u\in D^{\prime }(\Omega )$ belongs to $W^{-s,p^{\prime }}(\Omega )$?

Answer:

$$\begin{array}{cc}\hfill & u\in D^{\prime }(\Omega )\mathit{is\; in}{W}^{-s,p^{\prime }}(\Omega )⟺u:(D(\Omega ),\parallel .{\parallel }_{s,p})\to \mathbb{R}\mathit{is\; continuous}\hfill \\ \hfill & ⟺u:D(\Omega )\to \mathbb{R}\mathit{has\; a\; unique\; continuous\; extension\; to}\widehat{u}:W_0^{s,p}(\Omega )\to \mathbb{R}\hfill \end{array}$$

(2) 

Question 2: How should we interpret $W^{-s,p^{\prime }}(\Omega )\subseteq D^{\prime }(\Omega )$?

Answer: $i:D(\Omega )\to W_0^{s,p}(\Omega )$ is continuous with dense image. Therefore, $i^{*}:W^{-s,p^{\prime }}(\Omega )\to D^{\prime }(\Omega )$ is an injective continuous linear map. If $u\in W^{-s,p^{\prime }}(\Omega )$, then $i^{*}u\in D^{\prime }(\Omega )$ and

$${⟨i^{*}u,\phi ⟩}_{D^{\prime }(\Omega )\times D(\Omega )}={⟨u,i\phi ⟩}_{W^{-s,p^{\prime }}(\Omega )\times W_0^{s,p}(\Omega )}={⟨u,\phi ⟩}_{W^{-s,p^{\prime }}(\Omega )\times W_0^{s,p}(\Omega )}.$$

So, $i^{*}{u=u|}_{D(\Omega )}$ and if we identify with $i^{*}u$ with u we can write

$${⟨u,\phi ⟩}_{D^{\prime }(\Omega )\times D(\Omega )}={⟨u,\phi ⟩}_{W^{-s,p^{\prime }}(\Omega )\times W_0^{s,p}(\Omega )},{\parallel u\parallel }_{W^{-s,p^{\prime }}(\Omega )}=\underset{0\ne \phi \in C_c^{\infty }(\Omega )}{sup}\frac{{|⟨u,\phi ⟩}_{D^{\prime }(\Omega )\times D(\Omega )}|}{{\parallel \phi \parallel }_{W^{s,p}(\Omega )}}.$$

(3) 

Question 3: How should we interpret $W^{s,p}(\Omega )\subseteq D^{\prime }(\Omega )$?

Answer: It is a direct consequence of the definition of $W^{s,p}(\Omega )$ that $W^{s,p}(\Omega )\hookrightarrow L^p(\Omega )$ for any open set Ω. So, any $f\in W^{s,p}(\Omega )$ can be identified with the regular distribution $u_f\in D^{\prime }(\Omega )$ where

$$⟨u_f,\phi ⟩=\int f\phi \forall \phi \in D(\Omega ).$$

(4) 

Question 4: What does it mean to say $u\in D^{\prime }(\Omega )$ belongs to $W^{s,p}(\Omega )$?

Answer: It means there exists $f\in W^{s,p}(\Omega )$ such that $u=u_f$.

Remark 46.

Let Ω be a nonempty open set in ${\mathbb{R}}^n$ and $f,g\in C_c^{\infty }(\Omega )$. Suppose $s\in \mathbb{R}$ and $p\in (1,\infty )$.

• If $s\ge 0$, then

  $${\parallel f\parallel }_{W^{-s,p^{\prime }}(\Omega )}=\underset{0\ne \phi \in C_c^{\infty }(\Omega )}{sup}\frac{{|⟨f,\phi ⟩}_{D^{\prime }(\Omega )\times D(\Omega )}|}{{\parallel \phi \parallel }_{W^{s,p}(\Omega )}}=\underset{0\ne \phi \in C_c^{\infty }(\Omega )}{sup}\frac{|{\int }_{\Omega }f\phi dx|}{{\parallel \phi \parallel }_{W^{s,p}(\Omega )}}.$$

  So, for all $\phi \in C_c^{\infty }(\Omega )$

  $$|{\int }_{\Omega }{f\phi dx|\le \parallel f\parallel }_{W^{-s,p^{\prime }}(\Omega )}{\parallel \phi \parallel }_{W^{s,p}(\Omega )}.$$

  In particular, for g, we have

  $$|{\int }_{\Omega }{fgdx|\le \parallel f\parallel }_{W^{-s,p^{\prime }}(\Omega )}{\parallel g\parallel }_{W^{s,p}(\Omega )}.$$
• If $s<0$, we may replace the roles of f and g, and also $(s,p)$ and $(-s,p^{\prime })$ in the above argument to get the exact same inequality: $|{\int }_{\Omega }{fgdx|\le \parallel f\parallel }_{W^{-s,p^{\prime }}(\Omega )}{\parallel g\parallel }_{W^{s,p}(\Omega )}$.

7.5. Invariance under Change of Coordinates, Composition

Theorem 73

([12], Section 4.3). Let $s\in \mathbb{R}$ and $1<p<\infty$. Suppose that $T:{\mathbb{R}}^n\to {\mathbb{R}}^n$ is a $C^{\infty }$-diffeomorphism (i.e., T is bijective and T and $T^{-1}$ are $C^{\infty }$) with the property that the partial derivatives (of any order) of the components of T are bounded on ${\mathbb{R}}^n$ (the bound may depend on the order of the partial derivative) and ${inf}_{{\mathbb{R}}^n}|\mathit{det}{T}^{\prime }|>0$. Then the linear map

$$W^{s,p}({\mathbb{R}}^n)\to W^{s,p}({\mathbb{R}}^n),u\mapsto u\circ T$$

is well-defined and is bounded.

Now, let U and V be two nonempty open sets in ${\mathbb{R}}^n$. Suppose $T:U\to V$ is a bijective map. Similar to [1] we say T is k-smooth if all the components of T belong to $B{C}^k(U)$ and all the components of $T^{-1}$ belong to $B{C}^k(V)$.

Remark 47.

It is useful to note that if T is 1-smooth, then

$$\underset{U}{inf}|\mathit{det}{T}^{\prime }|>0\mathit{and}\underset{V}{inf}|\mathit{det}{(T^{-1})}^{\prime }|>0.$$

Indeed, since the first order partial derivatives of the components of T and $T^{-1}$ are bounded, there exist postive numbers M and $\tilde{M}$ such that for all $x\in U$ and $y\in V$

$$|\mathit{det}{T}^{\prime }(x)|<M,|\mathit{det}{(T^{-1})}^{\prime }(y)|<\tilde{M}.$$

Since $|\mathit{det}{T}^{\prime }(x)|\times |\mathit{det}{(T^{-1})}^{\prime }(T(x))|=1$, we can conclude that for all $x\in U$ and $y\in V$

$$|\mathit{det}{T}^{\prime }(x)|>\frac{1}{\tilde{M}},|\mathit{det}{(T^{-1})}^{\prime }(y)|>\frac{1}{M},$$

which proves the claim.

Remark 48.

Furthermore, it is interesting to note that, as a consequence of the inverse function theorem, if $T:U\to V$ is a bijective map that is $C^k$ ($k\in \mathbb{N}$) with the property that $\mathit{det}{T}^{\prime }(x)\ne 0$ for all $x\in U$, then the inverse of T will be $C^k$ as well, that is, T will automatically be a $C^k$-diffeomorphism (see, e.g., Appendix C in [19] for more details).

Remark 49.

Note that since we do not assume that U and V are necessarily convex or Lipschitz, the continuity and boundedness of the partial derivatives of the components of T do not imply that the components of T are Lipschitz. (see the “Warning” immediately after Theorem 6).

Theorem 74

(([29], p. 1003), ([1], pp. 77–78 )). Let $p\in (1,\infty )$ and $k\in \mathbb{N}$. Suppose that U and V are nonempty open subsets of ${\mathbb{R}}^n$.

(1) 

If $T:U\to V$ is a 1-smooth map, then the map

$$L^p(V)\to L^p(U),u\mapsto u\circ T$$

is well-defined and is bounded.

(2) 

If $T:U\to V$ is a k-smooth map, then the map

$$W^{k,p}(V)\to W^{k,p}(U),u\mapsto u\circ T$$

is well-defined and is bounded.

Theorem 75.

Let $p\in (1,\infty )$ and $k\in {\mathbb{Z}}^{-}$ (k is a negative integer). Suppose that U and V are nonempty open subsets of ${\mathbb{R}}^n$, and $T:U\to V$ is ∞-smooth. Then the map

$$W^{k,p}(V)\to W^{k,p}(U),u\mapsto u\circ T$$

is well-defined and is bounded.

Proof. 

By definition we have ($T^{*}u$ denotes the pullback of u by T)

$$\begin{array}{cc}\hfill \parallel T^{*}{u\parallel }_{W^{k,p}(U)}& =\underset{\phi \in C_c^{\infty }(U)}{sup}\frac{|{⟨T^{*}u,\phi ⟩}_{D^{\prime }(U)\times D(U)}|}{{\parallel \phi \parallel }_{W^{-k,p^{\prime }}(U)}}\hfill \\ \hfill & =\underset{\phi \in C_c^{\infty }(U)}{sup}\frac{|⟨u,|\det {(T^{-1})}^{\prime }|\phi \circ T^{-1}{⟩}_{D^{\prime }(V)\times D(V)}|}{{\parallel \phi \parallel }_{W^{-k,p^{\prime }}(U)}}\hfill \\ \hfill & ⪯\underset{\phi \in C_c^{\infty }(U)}{sup}\frac{{\parallel u\parallel }_{W^{k,p}(V)}\parallel |\det {(T^{-1})}^{\prime }{|\phi \circ T^{-1}\parallel }_{W^{-k,p^{\prime }}(V)}}{{\parallel \phi \parallel }_{W^{-k,p^{\prime }}(U)}}\hfill \\ \hfill & \stackrel{|\det {(T^{-1})}^{\prime }|\in B{C}^{\infty }}{⪯}\underset{\phi \in C_c^{\infty }(U)}{sup}\frac{{\parallel u\parallel }_{W^{k,p}(V)}{\parallel \phi \circ T^{-1}\parallel }_{W^{-k,p^{\prime }}(V)}}{{\parallel \phi \parallel }_{W^{-k,p^{\prime }}(U)}}.\hfill \end{array}$$

Since $-k$ is a positive integer, by Theorem 74 we have $\parallel \phi \circ T^{-1}{\parallel }_{W^{-k,p^{\prime }}(V)}⪯{\parallel \phi \parallel }_{W^{-k,p^{\prime }}(U)}$. Consequently,

$$\parallel T^{*}{u\parallel }_{W^{k,p}(U)}⪯{\parallel u\parallel }_{W^{k,p}(V)}.$$

 □

Theorem 76.

Let $p\in (1,\infty )$ and $0<s<1$. Suppose that U and V are nonempty open subsets of ${\mathbb{R}}^n$, $T:U\to V$ is 1-smooth, and T is Lipschitz continuous on U. Then the map

$$W^{s,p}(V)\to W^{s,p}(U),u\mapsto u\circ T$$

is well-defined and is bounded.

Proof. 

Note that

$${\parallel u\circ T\parallel }_{W^{s,p}(U)}={\parallel u\circ T\parallel }_{L^p(U)}{+|u\circ T|}_{W^{s,p}(U)}\stackrel{Theorem74}{⪯}{\parallel u\parallel }_{L^p(V)}+{|u\circ T|}_{W^{s,p}(U)}.$$

So, it is enough to show that ${|u\circ T|}_{W^{s,p}(U)}⪯{|u|}_{W^{s,p}(V)}$.

$$\begin{array}{cc}\hfill {|u\circ T|}_{W^{s,p}(U)}& ={\left(\int {\int }_{U\times U}\frac{{|(u\circ T)(x)-(u\circ T)(y)|}^p}{{|x-y|}^{n+sp}}dxdy\right)}^{\frac{1}{p}}\hfill \\ \hfill & \stackrel{\stackrel{z=T(x)}{w=T(y)}}{⪯}{\left(\int {\int }_{V\times V}\frac{{|u(z)-u(w)|}^p}{|T^{-1}(z)-T^{-1}{(w)|}^{n+sp}}\frac{1}{|\det T^{\prime }(x)|}\frac{1}{|\det T^{\prime }(y)|}dzdw\right)}^{\frac{1}{p}}\hfill \\ \hfill & ⪯{\left(\int {\int }_{V\times V}\frac{{|u(z)-u(w)|}^p}{|T^{-1}(z)-T^{-1}{(w)|}^{n+sp}}dzdw\right)}^{\frac{1}{p}}.\hfill \end{array}$$

T is Lipschitz continuous on U; so, there exists a constant $C>0$ such that

$$|T(x)-T(y)|\le C|x-y|⟹|z-w|\le C|T^{-1}(z)-T^{-1}(w)|.$$

Therefore,

$${|u\circ T|}_{W^{s,p}(U)}⪯{\left(\int {\int }_{V\times V}\frac{{|u(z)-u(w)|}^p}{{|z-w|}^{n+sp}}dzdw\right)}^{\frac{1}{p}}={|u|}_{W^{s,p}(V)}.$$

 □

Theorem 77.

Let $p\in (1,\infty )$ and $-1<s<0$. Suppose that U and V are nonempty open subsets of ${\mathbb{R}}^n$, $T:U\to V$ is ∞-smooth, $T^{-1}$ is Lipschitz continuous on V, and $|\mathit{det}{(T^{-1})}^{\prime }|$ is in $B{C}^{0,1}(V)$. Then the map

$$W^{s,p}(V)\to W^{s,p}(U),u\mapsto u\circ T$$

is well-defined and is bounded.

Proof. 

The proof of Theorem 75, with obvious modifications, shows the validity of the above claim. □

Remark 50.

In the previous theorem, by assumption, the first order partial derivatives of the components of $T^{-1}$ are continuous and bounded. Furthermore, it is true that absolute value of a Lipschitz continuous function and the sum and product of bounded Lipschitz continuous functions will be Lipschitz continuous. Consequently, in order to ensure that $|\mathit{det}{(T^{-1})}^{\prime }|$ is in $B{C}^{0,1}(V)$, it is enough to make sure that the first order partial derivatives of the components of $T^{-1}$ are bounded and Lipschitz continuous.

Theorem 78.

Let $s=k+\theta$ where $k\in \mathbb{N}$, $\theta \in (0,1)$, and let $p\in (1,\infty )$. Suppose that U and V are two nonempty open sets in ${\mathbb{R}}^n$. Let $T:U\to V$ be a Lipschitz continuous k-smooth map on U such that the partial derivatives up to and including order k of all the components of T are Lipschitz continuous on U as well. Then

(1) 

For each $K\in \mathcal{K}(V)$ the linear map

$$T^{*}:W_K^{s,p}(V)\to W_{T^{-1}(K)}^{s,p}(U),u\mapsto u\circ T$$

is well-defined and is bounded.

(2) 

If we further assume that V is Lipschitz (and so U is Lipschitz), the linear map

$$T^{*}:W^{s,p}(V)\to W^{s,p}(U),u\mapsto u\circ T$$

is well-defined and is bounded.

Note: When U is a Lipschitz domain, the fact that T is k-smooth automatically implies that all the partial derivatives of the components of T up to and including order $k-1$ are Lipschitz continuous (see Theorem 60). So in this case, the only extra assumption, in addition to T being k-smooth, is that the partial derivatives of the components of T of order k are Lipschitz continuous on U.

Proof. 

Recall that $C^{\infty }(V)\cap W^{s,p}(V)$ is dense in $W^{s,p}(V)$. Our proof consists of two steps: in the first step we addditionally assume that $u\in C^{\infty }(V)$. Then in the second step we prove the validity of the claim for $u\in W_K^{s,p}(V)$ (or $u\in W^{s,p}(V)$ with the assumption that V is Lipschitz).

• Step 1: We have

  $$\begin{array}{cc}\hfill {\parallel u\circ T\parallel }_{W^{s,p}(U)}& ={\parallel u\circ T\parallel }_{W^{k,p}(U)}+\sum _{|\nu |=k}{|{\partial }^{\nu }(u\circ T)|}_{W^{\theta ,p}(U)}\hfill \\ \hfill & \stackrel{\mathrm{Theorem\; 74}}{⪯}{\parallel u\parallel }_{W^{k,p}(V)}+\sum _{|\nu |=k}{|{\partial }^{\nu }(u\circ T)|}_{W^{\theta ,p}(U)}.\hfill \end{array}$$

  Since u and T are both $C^k$, it can be proved by induction that (see, e.g., [1])

  $${\partial }^{\nu }(u\circ T)(x)=\sum _{\beta \le \nu ,1\le |\beta |}{M}_{\nu \beta }(x)[({\partial }^{\beta }u)\circ T](x),$$

  where $M_{\nu \beta }(x)$ are polynomials of degree at most $|\beta |$ in derivatives of order at most $|\nu |$ of the components of T. In particular, $M_{\nu \beta }\in B{C}^{0,1}(U)$. Therefore,

  $$\begin{array}{cc}\hfill |{\partial }^{\nu }& {(u\circ T)|}_{W^{\theta ,p}(U)}\le \parallel {\partial }^{\nu }{(u\circ T)\parallel }_{W^{\theta ,p}(U)}={\parallel \sum _{\beta \le \nu ,1\le |\beta |}{M}_{\nu \beta }(x)[({\partial }^{\beta }u)\circ T](x)\parallel }_{W^{\theta ,p}(U)}\hfill \\ \hfill & \stackrel{\mathrm{Theorem\; 69}}{⪯}\sum _{\beta \le \nu ,1\le |\beta |}\parallel ({\partial }^{\beta }u){\circ T\parallel }_{W^{\theta ,p}(U)}=\sum _{\beta \le \nu ,1\le |\beta |}\parallel ({\partial }^{\beta }u){\circ T\parallel }_{L^p(U)}+{|({\partial }^{\beta }u)\circ T|}_{W^{\theta ,p}(U)}\hfill \\ \hfill & \stackrel{\mathrm{Theorems\; 74\; and\; 76}}{⪯}\sum _{\beta \le \nu ,1\le |\beta |}\parallel {\partial }^{\beta }{u\parallel }_{L^p(V)}+|{\partial }^{\beta }{u|}_{W^{\theta ,p}(V)}\le {\parallel u\parallel }_{W^{k,p}(V)}+\sum _{\beta \le \nu ,1\le |\beta |}{|{\partial }^{\beta }u|}_{W^{\theta ,p}(V)}.\hfill \end{array}$$
  (The fact that ${\partial }^{\beta }u$ belongs to $W^{\theta ,p}(V)\hookrightarrow L^p(V)$ is a consequence of the definition of the Slobodeckij norm combined with our embedding theorems for Sobolev spaces of functions with fixed compact support in an arbitrary domain or embedding theorems for Sobolev spaces of functions on a Lipschitz domain). Hence

  $$\begin{array}{cc}\hfill {\parallel u\circ T\parallel }_{W^{s,p}(U)}& ⪯{\parallel u\parallel }_{W^{k,p}(V)}+\sum _{1\le |\nu |\le k}\sum _{\beta \le \nu ,1\le |\beta |}{|{\partial }^{\beta }u|}_{W^{\theta ,p}(V)}\hfill \\ \hfill & ⪯{\parallel u\parallel }_{W^{k,p}(V)}+\sum _{1\le |\alpha |\le k}|{\partial }^{\alpha }{u|}_{W^{\theta ,p}(V)}\stackrel{Theorem72}{\simeq }{\parallel u\parallel }_{W^{s,p}(V)}.\hfill \end{array}$$

  Note that the last equivalence is due to the assumption that $u\in W_K^{s,p}(V)$ (or $u\in W^{s,p}(V)$ with V being Lipschitz).
• Step 2: Now suppose u is an arbitrary element of $W_K^{s,p}(V)$ (or $W^{s,p}(V)$ with V being Lipschitz). There exists a sequence ${\{u_m\}}_{m\ge 1}$ in $C^{\infty }(V)$ such that $u_m\to u$ in $W^{s,p}(V)$. In particular, $\{u_m\}$ is Cauchy. By the previous steps we have

  $$\parallel T^{*}{u}_m-T^{*}{u}_l{\parallel }_{W^{s,p}(U)}⪯{\parallel u_m-u_l\parallel }_{W^{s,p}(V)}\to 0(\mathrm{as}m,l\to \infty ).$$

  Therefore, $\{T^{*}{u}_m\}$ is a Cauchy sequence in the Banach space $W^{s,p}(U)$ and subsequently there exists $v\in W^{s,p}(U)$ such that $T^{*}{u}_m\to v$ as $m\to \infty$. It remains to show that $v=T^{*}u$ as elements of $W^{s,p}(U)$. As a direct consequence of the definition of $W^{s,p}$-norm $(s\ge 0)$ we have

  $$\begin{array}{cc}\hfill & \parallel T^{*}{u}_m{-v\parallel }_{L^p(U)}\le {\parallel T^{*}{u}_m-v\parallel }_{W^{s,p}(U)}\to 0,\hfill \\ \hfill & \parallel u_m{-u\parallel }_{L^p(V)}\le {\parallel u_m-u\parallel }_{W^{s,p}(V)}\to 0.\hfill \end{array}$$
  Note that by Theorem 74, $u_m\to u$ in $L^p(V)$ implies that $T^{*}{u}_m\to T^{*}u$ in $L^p(U)$. Thus $T^{*}u=v$ as elements of $L^p(U)$ and hence as elements of $W^{s,p}(U)$.

□

Theorem 79.

Let $p\in (1,\infty )$ and $s<-1$ be a noninteger number. Suppose that U and V are two nonempty Lipschitz open sets in ${\mathbb{R}}^n$ and $T:U\to V$ is a ∞-smooth map. Then the linear map

$$T^{*}:W^{s,p}(V)\to W^{s,p}(U),u\mapsto u\circ T$$

is well-defined and is bounded.

Note: Since V is a Lipschitz domain, the fact that T is ∞-smooth automatically implies that $T^{-1}$ and all the partial derivatives of the components of $T^{-1}$ are Lipschitz continuous (see Theorem 60).

Proof. 

The proof is completely analogous to the proof of Theorem 75. We have

$$\begin{array}{cc}\hfill \parallel T^{*}{u\parallel }_{W^{s,p}(U)}& =\underset{\phi \in C_c^{\infty }(U)}{sup}\frac{|{⟨T^{*}u,\phi ⟩}_{D^{\prime }(U)\times D(U)}|}{{\parallel \phi \parallel }_{W^{-s,p^{\prime }}(U)}}\hfill \\ \hfill & =\underset{\phi \in C_c^{\infty }(U)}{sup}\frac{|⟨u,|\mathit{det}{(T^{-1})}^{\prime }|\phi \circ T^{-1}{⟩}_{D^{\prime }(V)\times D(V)}|}{{\parallel \phi \parallel }_{W^{-s,p^{\prime }}(U)}}\hfill \\ \hfill & ⪯\frac{{\parallel u\parallel }_{W^{s,p}(V)}\parallel |\mathit{det}{(T^{-1})}^{\prime }{|\phi \circ T^{-1}\parallel }_{W^{-s,p^{\prime }}(V)}}{{\parallel \phi \parallel }_{W^{-s,p^{\prime }}(U)}}\hfill \\ \hfill & \stackrel{|\mathit{det}{(T^{-1})}^{\prime }|\in B{C}^{\infty }(V)}{⪯}\frac{{\parallel u\parallel }_{W^{s,p}(V)}{\parallel \phi \circ T^{-1}\parallel }_{W^{-s,p^{\prime }}(V)}}{{\parallel \phi \parallel }_{W^{-s,p^{\prime }}(U)}}.\hfill \end{array}$$

Since $-s>0$, it follows from the hypotheses of this theorem and the result of Theorem 78 that $\parallel \phi \circ T^{-1}{\parallel }_{W^{-s,p^{\prime }}(V)}⪯{\parallel \phi \parallel }_{W^{-s,p^{\prime }}(U)}$. Consequently,

$$\parallel T^{*}{u\parallel }_{W^{s,p}(U)}⪯{\parallel u\parallel }_{W^{s,p}(V)}.$$

 □

Lemma 8.

Let U and V be two nonempty open sets in ${\mathbb{R}}^n$. Suppose $T:U\to V$ ($T=(T^1,\dots ,T^n)$) is a $C^{k+1}$-diffeomorphism for some $k\in {\mathbb{N}}_0$ and let $B\subseteq U$ be a nonempty bounded open set such that $B\subseteq \overline{B}\subseteq U$. Then

(1) 

$T:B\to T(B)$ is a $(k+1)$-smooth map.

(2) 

$T:B\to T(B)$ and $T^{-1}:T(B)\to B$ are Lipschitz (the Lipschitz constant may depend on B).

(3) 

For all $1\le i\le n$ and $|\alpha |\le k$, ${\partial }^{\alpha }{T}^i\in B{C}^{k,1}(B)$ and ${\partial }^{\alpha }{(T^{-1})}^i\in B{C}^{k,1}(T(B))$.

Proof. 

Item 1 is true because $\overline{B}$ is compact and so $T(\overline{B})$ is compact and continuous functions are bounded on compact sets. Items 2 and 3 are direct consequences of Theorem 7. □

Theorem 80.

Let $s\in \mathbb{R}$ and $p\in (1,\infty )$. Suppose that U and V are two nonempty open sets in ${\mathbb{R}}^n$ and $T:U\to V$ is a $C^{\infty }$-diffeomorphism (if $s\ge 0$ it is enough to assume T is a $C^{\lfloor s\rfloor +1}$-diffeomorphism). Let $B\subseteq U$ be a nonempty bounded open set such that $B\subseteq \overline{B}\subseteq U$. Let $u\in W^{s,p}(V)$ be such that $\mathit{supp}u\subseteq T(B)$ (note that if $\mathit{supp}u$ is compact in V, then such a B exists).

(1) 

If s is NOT a noninteger less than $-1$, then

$${\parallel u\circ T\parallel }_{W^{s,p}(U)}⪯{\parallel u\parallel }_{W^{s,p}(V)}.$$

(The implicit constant may depend on B but otherwise is independent of u.)

(2) 

If U and V are Lipschitz or ${\mathbb{R}}^n$, then the above result holds for all $s\in \mathbb{R}$.

Proof. 

If s is an integer or $-1<s<1$, or if U and V are Lipschitz or ${\mathbb{R}}^n$ and $s\in \mathbb{R}$ then as a consequence of the above lemma and the preceding theorems we may write

$$\begin{array}{c}\hfill {\parallel u\circ T\parallel }_{W^{s,p}(U)}\stackrel{\mathrm{Corollary\; 6}}{\simeq }{\parallel u\circ T\parallel }_{W^{s,p}(B)}⪯{\parallel u\parallel }_{W^{s,p}(T(B))}\stackrel{\mathrm{Corollary\; 6}}{\simeq }{\parallel u\parallel }_{W^{s,p}(V)}.\end{array}$$

For general U and V, if $s=k+\theta$, we let $\widehat{B}$ be an open set such that $\overline{\widehat{B}}$ is a compact subset of U and $\overline{B}\subseteq \widehat{B}$. We can apply the previous lemma to $\widehat{B}$ and write

$$\begin{array}{c}\hfill {\parallel u\circ T\parallel }_{W^{s,p}(U)}\stackrel{\mathrm{Corollary\; 6}}{\simeq }{\parallel u\circ T\parallel }_{W_{\overline{B}}^{s,p}(\widehat{B})}\stackrel{\mathrm{Theorem\; 78}}{⪯}{\parallel u\parallel }_{W_{T(\overline{B})}^{s,p}(T(\widehat{B}))}\stackrel{\mathrm{Corollary\; 6}}{\simeq }{\parallel u\parallel }_{W^{s,p}(V)}.\end{array}$$

 □

Theorem 81

([42]). Let $s\in [1,\infty )$, $1<p<\infty$, and let

$$\begin{array}{c}\hfill m=\left\{\begin{array}{cc}\hfill & s,\mathit{if}s\mathit{is\; an\; integer}\hfill \\ \hfill & \lfloor s\rfloor +1,\mathit{otherwise}\hfill \end{array}\right..\end{array}$$

If $F\in C^m(\mathbb{R})$ is such that $F(0)=0$ and $F,F^{\prime },\dots ,F^{(m)}\in L^{\infty }(\mathbb{R})$ (in particular, note that every $F\in C_c^{\infty }(\mathbb{R})$ with $F(0)=0$ satisfies these conditions), then the map $u\mapsto F(u)$ is well-defined and continuous from $W^{s,p}({\mathbb{R}}^n)\cap W^{1,sp}({\mathbb{R}}^n)$ into $W^{s,p}({\mathbb{R}}^n)$.

Corollary 7.

Let s, p, and F be as in the previous theorem. Moreover, suppose $sp>n$. Then the map $u\mapsto F(u)$ is well-defined and continuous from $W^{s,p}({\mathbb{R}}^n)$ into $W^{s,p}({\mathbb{R}}^n)$. The reason is that when $sp>n$, we have $W^{s,p}({\mathbb{R}}^n)\hookrightarrow W^{1,sp}({\mathbb{R}}^n)$.

7.6. Differentiation

Theorem 82

(([4], pp. 598–605), ([5], Section 1.4)). Let $s\in \mathbb{R}$, $1<p<\infty$, and $\alpha \in {\mathbb{N}}_0^n$. Suppose Ω is a nonempty open set in ${\mathbb{R}}^n$. Then

(1) 

The linear operator ${\partial }^{\alpha }:W^{s,p}({\mathbb{R}}^n)\to W^{s-|\alpha |,p}({\mathbb{R}}^n)$ is well-defined and bounded.

(2) 

For $s<0$, the linear operator ${\partial }^{\alpha }:W^{s,p}(\Omega )\to W^{s-|\alpha |,p}(\Omega )$ is well-defined and bounded.

(3) 

For $s\ge 0$ and $|\alpha |\le s$, the linear operator ${\partial }^{\alpha }:W^{s,p}(\Omega )\to W^{s-|\alpha |,p}(\Omega )$ is well-defined and bounded.

(4) 

If Ω is bounded with Lipschitz continuous boundary, and if $s\ge 0$, $s-\frac{1}{p}\ne \mathit{integer}$ (i.e., the fractional part of s is not equal to $\frac{1}{p}$), then the linear operator ${\partial }^{\alpha }:W^{s,p}(\Omega )\to W^{s-|\alpha |,p}(\Omega )$ for $|\alpha |>s$ is well-defined and bounded.

Remark 51.

Comparing the first and last items of the previous theorem, we see that not all the properties of Sobolev–Slobodeckij spaces on ${\mathbb{R}}^n$ are fully inherited by Sobolev–Slobodeckij spaces on bounded domains even when the domain has Lipschitz continuous boundary (note that the above difference is related to the more fundamental fact that for $s>0$, even when Ω is Lipschitz, $C_c^{\infty }(\Omega )$ is not necessarily dense in $W^{s,p}(\Omega )$ and subsequently $W^{-s,p^{\prime }}(\Omega )$ is defined as the dual of $W_0^{s,p}(\Omega )$ rather than the dual of $W^{s,p}(\Omega )$ itself). For this reason, when working with Sobolev spaces on manifolds, we prefer super nice atlases (i.e., we prefer to work with coordinate charts whose image under the coordinate map is the entire ${\mathbb{R}}^n$). The next best choice would be GGL or GL atlases.

7.7. Spaces of Locally Sobolev Functions

Material of this section are taken from our manuscript on the properties of locally Sobolev-Slobodeckij functions [17].

Definition 28.

Let $s\in \mathbb{R}$, $1<p<\infty$. Let Ω be a nonempty open set in ${\mathbb{R}}^n$. We define

$$\begin{array}{c}\hfill W_{loc}^{s,p}(\Omega ):=\{u\in D^{\prime }(\Omega ):\forall \phi \in C_c^{\infty }(\Omega )\phi u\in W^{s,p}(\Omega )\}.\end{array}$$

$W_{loc}^{s,p}(\Omega )$ is equipped with the natural topology induced by the separating family of seminorms ${\{|.|}_{\phi }{\}}_{\phi \in C_c^{\infty }(\Omega )}\}$ where

$$\forall u\in W_{loc}^{s,p}(\Omega )\phi \in C_c^{\infty }{(\Omega )|u|}_{\phi }:={\parallel \phi u\parallel }_{W^{s,p}(\Omega )}.$$

Theorem 83.

Let $s\in \mathbb{R}$, $1<p<\infty$, and $\alpha \in {\mathbb{N}}_0^n$. Suppose Ω is a nonempty bounded open set in ${\mathbb{R}}^n$ with Lipschitz continuous boundary. Then

(1) 

The linear operator ${\partial }^{\alpha }:W_{loc}^{s,p}({\mathbb{R}}^n)\to W_{loc}^{s-|\alpha |,p}({\mathbb{R}}^n)$ is well-defined and continuous.

(2) 

For $s<0$, the linear operator ${\partial }^{\alpha }:W_{loc}^{s,p}(\Omega )\to W_{loc}^{s-|\alpha |,p}(\Omega )$ is well-defined and continuous.

(3) 

For $s\ge 0$ and $|\alpha |\le s$, the linear operator ${\partial }^{\alpha }:W_{loc}^{s,p}(\Omega )\to W_{loc}^{s-|\alpha |,p}(\Omega )$ is well-defined and continuous.

(4) 

If $s\ge 0$, $s-\frac{1}{p}\ne \mathit{integer}$ (i.e., the fractional part of s is not equal to $\frac{1}{p}$), then the linear operator ${\partial }^{\alpha }:W_{loc}^{s,p}(\Omega )\to W_{loc}^{s-|\alpha |,p}(\Omega )$ for $|\alpha |>s$ is well-defined and continuous.

The following statements play a key role in our study of Sobolev spaces on Riemannian manifolds with rough metrics.

Theorem 84.

Let Ω be a nonempty bounded open set in ${\mathbb{R}}^n$ with Lipschitz continuous boundary or $\Omega ={\mathbb{R}}^n$. Suppose $u\in W_{loc}^{s,p}(\Omega )$ where $sp>n$. Then u has a continuous version.

Lemma 9.

Let $\Omega ={\mathbb{R}}^n$ or Ω be a bounded open set in ${\mathbb{R}}^n$ with Lipschitz continuous boundary. Suppose $s_1,s_2,s\in \mathbb{R}$ and $1<p_1,p_2,p<\infty$ are such that

$$W^{s_1,p_1}(\Omega )\times W^{s_2,p_2}(\Omega )\hookrightarrow W^{s,p}(\Omega ).$$

Then

(1) 

$W_{loc}^{s_1,p_1}(\Omega )\times W_{loc}^{s_2,p_2}(\Omega )\hookrightarrow W_{loc}^{s,p}(\Omega )$,

(2) 

For all $K\in \mathcal{K}(\Omega )$, $W_{loc}^{s_1,p_1}(\Omega )\times W_K^{s_2,p_2}(\Omega )\hookrightarrow W^{s,p}(\Omega )$. In particular, if $f\in W_{loc}^{s_1,p_1}(\Omega )$, then the mapping $u\mapsto fu$ is a well-defined continuous linear map from $W_K^{s_2,p_2}(\Omega )$ to $W^{s,p}(\Omega )$.

Remark 52.

It can be shown that the locally Sobolev spaces on Ω are metrizable, so the continuity of the mapping

$$W_{loc}^{s_1,p_1}(\Omega )\times W_{loc}^{s_2,p_2}(\Omega )\to W_{loc}^{s,p}(\Omega ),(u,v)\mapsto uv$$

in the above lemma can be interpreted as follows: if $u_i\to u$ in $W_{loc}^{s_1,p_1}(\Omega )$ and $v_i\to v$ in $W_{loc}^{s_2,p_2}(\Omega )$, then $u_i{v}_i\to uv$ in $W_{loc}^{s,p}(\Omega )$. Furthermore, since $W_K^{s_2,p_2}(\Omega )$ is considered as a normed subspace of $W^{s_2,p_2}(\Omega )$, we have a similar interpretation of the continuity of the mapping in item 2.

Lemma 10.

Let $\Omega ={\mathbb{R}}^n$ or let Ω be a nonempty bounded open set in ${\mathbb{R}}^n$ with Lipschitz continuous boundary. Let $s\in \mathbb{R}$ and $p\in (1,\infty )$ be such that $sp>n$. Let $B:\Omega \to \mathrm{GL}(k,\mathbb{R})$. Suppose for all $x\in \Omega$ and $1\le i,j\le k$, $B_{ij}(x)\in W_{loc}^{s,p}(\Omega )$. Then

(1) 

$\mathit{det}B\in W_{loc}^{s,p}(\Omega )$.

(2) 

Moreover, if for each $m\in \mathbb{N}$$B_m:\Omega \to \mathit{GL}(k,\mathbb{R})$ and for all $1\le i,j\le k$ ${(B_m)}_{ij}\to B_{ij}$ in $W_{loc}^{s,p}(\Omega )$, then $\mathit{det}{B}_m\to \mathit{det}B$ in $W_{loc}^{s,p}(\Omega )$.

Theorem 85.

Let $\Omega ={\mathbb{R}}^n$ or let Ω be a nonempty bounded open set in ${\mathbb{R}}^n$ with Lipschitz continuous boundary. Let $s\ge 1$ and $p\in (1,\infty )$ be such that $sp>n$.

(1) 

Suppose that $u\in W_{loc}^{s,p}(\Omega )$ and that $u(x)\in I$ for all $x\in \Omega$ where I is some interval in $\mathbb{R}$. If $F:I\to \mathbb{R}$ is a smooth function, then $F(u)\in W_{loc}^{s,p}(\Omega )$.

(2) 

Suppose that $u_m\to u$ in $W_{loc}^{s,p}(\Omega )$ and that for all $m\ge 1$ and $x\in \Omega$, $u_m(x),u(x)\in I$ where I is some open interval in $\mathbb{R}$. If $F:I\to \mathbb{R}$ is a smooth function, then $F(u_m)\to F(u)$ in $W_{loc}^{s,p}(\Omega )$.

(3) 

If $F:\mathbb{R}\to \mathbb{R}$ is a smooth function, then the map taking u to $F(u)$ is continuous from $W_{loc}^{s,p}(\Omega )$ to $W_{loc}^{s,p}(\Omega )$.

8. Lebesgue Spaces on Compact Manifolds

Let $M^n$ be a compact smooth manifold and $E\to M$ be a smooth vector bundle of rank r.

Definition 29.

A collection ${\{(U_{\alpha },{\phi }_{\alpha },{\rho }_{\alpha },{\psi }_{\alpha })\}}_{1\le \alpha \le N}$ of 4-tuples is called an augmented total trivialization atlas for $E\to M$ provided that ${\{(U_{\alpha },{\phi }_{\alpha },{\rho }_{\alpha })\}}_{1\le \alpha \le N}$ is a total trivialization atlas for $E\to M$ and $\{{\psi }_{\alpha }\}$ is a partition of unity subordinate to the open cover $\{U_{\alpha }\}$.

Let ${\{(U_{\alpha },{\phi }_{\alpha },{\rho }_{\alpha },{\psi }_{\alpha })\}}_{1\le \alpha \le N}$ be an augmented total trivialization atlas for $E\to M$. Let g be a continuous Riemannian metric on M and ${⟨.,.⟩}_E$ be a fiber metric on E (we denote the corresponding norm by ${|.|}_E$). Suppose $1\le q<\infty$.

(1)

Definition A: The space $L^q(M,E)$ is the completion of $C^{\infty }(M,E)$ with respect to the following norm:

$${\parallel u\parallel }_{L^q(M,E)}:=\sum _{\alpha =1}^N\sum _{l=1}^r{\parallel {\rho }_{\alpha }^l\circ ({\psi }_{\alpha }u)\circ {\phi }_{\alpha }^{-1}\parallel }_{L^q({\phi }_{\alpha }(U_{\alpha }))}.$$

Note that for this definition to make sense it is not necessary to have metric on M or fiber metric on E.

(2)

Definition B: The space $L^q(M,E)$ is the completion of $C^{\infty }(M,E)$ with respect to the following norm:

$${|u|}_{L^q(M,E)}:={\left({\int }_M{|u|}_E^{q}d{V}_g\right)}^{\frac{1}{q}}.$$

(3)

Definition C: The metric g defines a measure on M. Define the following equivalence relation on $\Gamma (M,E)$:

$$u\sim v⟺u=va.e.$$

We define

$$L^q(M,E):=\frac{\{u\in \Gamma (M,E):\parallel u{\parallel }_{L^q(M,E)}^q:={\int }_M|u{|}_E^{q}d{V}_g<\infty \}}{\sim }.$$

For $q=\infty$ we define

$$L^{\infty }(M,E):=\frac{\{u\in \Gamma (M,E):\parallel u{\parallel }_{L^{\infty }(M,E)}:=\mathrm{esssup}|u{|}_E<\infty \}}{\sim }.$$

Note: We may define negligible sets (sets of measure zero) on a compact manifold using charts (see Chapter 6 in [43]); it can be shown that this definition is independent of the charts and equivalent to the one that is obtained using the metric g. So, it is meaningful to write $u=va.e$ even without using a metric.

Theorem 86.

Definition A is equivalent to Definition B (i.e., the norms are equivalent).

Proof. 

Our proof consists of four steps:

• Step 1: In the next section it will be proved that different total trivialization atlases and partitions of unity result in equivalent norms (note that $L^q=W^{0,q}$). Therefore, without loss of generality we may assume that ${\{(U_{\alpha },{\phi }_{\alpha },{\rho }_{\alpha })\}}_{1\le \alpha \le N}$ is a total trivialization atlas that trivializes the fiber metric ${⟨.,.⟩}_E$ (see Theorem 37 and Corollary 2). So, on any bundle chart $(U,\phi ,\rho )$ and for any section u we have

  $${|u|}_E^2\circ {\phi }^{-1}={⟨u,u⟩}_E\circ {\phi }^{-1}=\sum _{l=1}^r{({\rho }^l\circ u\circ {\phi }^{-1})}^2.$$
• Step 2: In this step we show that if there is $1\le \beta \le N$ such that $\mathrm{supp}u\subseteq U_{\beta }$, then

  $${|u|}_{L^q(M,E)}^q={\int }_M{|u|}_E^{q}d{V}_g\simeq \sum _{l=1}^r{\parallel {\rho }_{\beta }^l\circ u\circ {\phi }_{\beta }^{-1}\parallel }_{L^q({\phi }_{\beta }(U_{\beta }))}^q.$$
  We have

  $$\begin{array}{cc}\hfill {\int }_M{|u|}_E^{q}d{V}_g& ={\int }_{{\phi }_{\beta }(U_{\beta })}{(|u|}_E\circ {\phi }_{\beta }^{-1}{)}^q\sqrt{det(g_{ij}\circ {\phi }_{\beta }^{-1})(x)}d{x}^1\dots d{x}^n\hfill \\ \hfill & \simeq {\int }_{{\phi }_{\beta }(U_{\beta })}{(|u|}_E\circ {\phi }_{\beta }^{-1}{)}^{q}d{x}^1\dots d{x}^n(\sqrt{det(g_{\mathit{ij}}\circ {\phi }_{\beta }^{-1})(x)}\mathrm{is\; bounded\; by\; positive\; constants})\hfill \\ \hfill & ={\int }_{{\phi }_{\beta }(U_{\beta })}{\left(\sqrt{\sum _{l=1}^r{({\rho }_{\beta }^l\circ u\circ {\phi }_{\beta }^{-1})}^2}\right)}^{q}d{x}^1\dots d{x}^n\hfill \\ \hfill & \simeq {\int }_{{\phi }_{\beta }(U_{\beta })}[\sum _{l=1}^r|{\rho }_{\beta }^l\circ u\circ {\phi }_{\beta }^{-1}{|]}^{q}d{x}^1\dots d{x}^n(\sqrt{\sum a_l^2}\simeq \sum |a_l|)\hfill \\ \hfill & \simeq {\int }_{{\phi }_{\beta }(U_{\beta })}\sum _{l=1}^r{|{\rho }_{\beta }^l\circ u\circ {\phi }_{\beta }^{-1}|}^{q}d{x}^1\dots d{x}^n({(\sum a_l)}^q\simeq \sum a_l^q)\hfill \\ \hfill & =\sum _{l=1}^r{\int }_{{\phi }_{\beta }(U_{\beta })}|{\rho }_{\beta }^l\circ u\circ {\phi }_{\beta }^{-1}{|}^{q}d{x}^1\dots d{x}^n=\sum _{l=1}^r{\parallel {\rho }_{\beta }^l\circ u\circ {\phi }_{\beta }^{-1}\parallel }_{L^q({\phi }_{\beta }(U_{\beta }))}^q.\hfill \end{array}$$
• Step 3: In this step we will prove that for all $u\in C^{\infty }(M,E)$

  $${|u|}_{L^q(M,E)}^q\simeq \sum _{\alpha }{|{\psi }_{\alpha }u|}_{L^q(M,E)}^q.$$
  We have

  $$\begin{array}{cc}\hfill {|u|}_{L^q(M,E)}^q& ={\int }_M{|u|}_E^{q}d{V}_g=\sum _{\alpha }{\int }_M\frac{{\psi }_{\alpha }^q}{{\sum }_{\beta }{\psi }_{\beta }^q}{|u|}_E^{q}d{V}_g(\{\frac{{\psi }_{\alpha }^q}{{\sum }_{\beta }{\psi }_{\beta }^q}\}\mathrm{is\; partition\; of\; unity\; subordinate\; to}\{U_{\alpha }\})\hfill \\ \hfill & \simeq \sum _{\alpha }{\int }_{U_{\alpha }}{\psi }_{\alpha }^q{|u|}_E^{q}d{V}_g(\frac{1}{{\sum }_{\beta }{\psi }_{\beta }^q}\mathrm{is\; bounded\; by\; positive\; constants})\hfill \\ \hfill & =\sum _{\alpha }{\int }_{U_{\alpha }}|{\psi }_{\alpha }{u|}_E^{q}d{V}_g=\sum _{\alpha }{\int }_M{|{\psi }_{\alpha }u|}_E^{q}d{V}_g\hfill \\ \hfill & =\sum _{\alpha }{|{\psi }_{\alpha }u|}_{L^q(M,E)}^q.\hfill \end{array}$$
• Step 4: Let u be an arbitrary element of $C^{\infty }(M,E)$. We have

  $$\begin{array}{c}\hfill {|u|}_{L^q(M,E)}^q\stackrel{\mathrm{Step}3}{\simeq }\sum _{\alpha }|{\psi }_{\alpha }{u|}_{L^q(M,E)}^q\stackrel{\mathrm{Step}2}{\simeq }\sum _{\alpha }\sum _l\parallel {\rho }_{\alpha }^l\circ ({\psi }_{\alpha }u)\circ {\phi }_{\alpha }^{-1}{\parallel }_{L^q({\phi }_{\alpha }(U_{\alpha }))}^q\simeq {\parallel u\parallel }_{L^q(M,E)}^q.\end{array}$$

□

9. Sobolev Spaces on Compact Manifolds and Alternative Characterizations

9.1. The Definition

Let $M^n$ be a compact smooth manifold. Let $\pi :E\to M$ be a smooth vector bundle of rank r. Let $\Lambda ={\{(U_{\alpha },{\phi }_{\alpha },{\rho }_{\alpha },{\psi }_{\alpha })\}}_{1\le \alpha \le N}$ be an augmented total trivialization atlas for $E\to M$. For each $1\le \alpha \le N$, let $H_{\alpha }$ denote the map $H_{E^{\vee },U_{\alpha },{\phi }_{\alpha }}$ which was introduced in Section 6.

Definition 30.

$$W^{e,q}(M,E;\Lambda )=\{u\in D^{\prime }{(M,E):\parallel u\parallel }_{W^{e,q}(M,E;\Lambda )}=\sum _{\alpha =1}^N\sum _{l=1}^r\parallel {[H_{\alpha }({\psi }_{\alpha }u)]}^l{\parallel }_{W^{e,q}({\phi }_{\alpha }(U_{\alpha }))}<\infty \}.$$

Remark 53.

(1) 

If $u\in W^{e,q}(M,E;\Lambda )$ is a regular distribution, it follows from Remark 32 that

$${\parallel u\parallel }_{W^{e,q}(M,E;\Lambda )}=\sum _{\alpha =1}^N\sum _{l=1}^r{\parallel {({\rho }_{\alpha })}^l\circ ({\psi }_{\alpha }u)\circ {\phi }_{\alpha }^{-1}\parallel }_{W^{e,q}({\phi }_{\alpha }(U_{\alpha }))}.$$

(2) 

It is clear that the collection of functions from M to $\mathbb{R}$ can be identified with sections of the vector bundle $E=M\times \mathbb{R}$. For this reason $W^{e,q}(M;\Lambda )$ is defined as $W^{e,q}(M,M\times \mathbb{R};\Lambda )$. Note that in this case, for each α, ${\rho }_{\alpha }$ is the identity map. So, we may consider an augmented total trivialization atlas Λ as a collection of 3-tuples ${\{(U_{\alpha },{\phi }_{\alpha },{\psi }_{\alpha })\}}_{1\le \alpha \le N}$. In particular, if $u\in W^{e,q}(M;\Lambda )$ is a regular distribution, then

$${\parallel u\parallel }_{W^{e,q}(M;\Lambda )}=\sum _{\alpha =1}^N{\parallel ({\psi }_{\alpha }u)\circ {\phi }_{\alpha }^{-1}\parallel }_{W^{e,q}({\phi }_{\alpha }(U_{\alpha }))}.$$

(3) 

Sometimes, when the underlying manifold M and the augmented total trivialization atlas are clear from the context (or when they are irrelevant), we may write $W^{e,q}(E)$ instead of $W^{e,q}(M,E;\Lambda )$. In particular, for tensor bundles, we may write $W^{e,q}(T_l^{k}M)$ instead of $W^{e,q}(M,T_l^{k}M;\Lambda )$.

Remark 54.

Here is a list of some alternative, not necessarily equivalent, characterizations of Sobolev spaces.

(1) 

Suppose $e\ge 0$.

$$W^{e,q}(M,E;\Lambda )=\{u\in L^q{(M,E):\parallel u\parallel }_{W^{e,q}(M,E;\Lambda )}=\sum _{\alpha =1}^N\sum _{l=1}^r\parallel {({\rho }_{\alpha })}^l\circ ({\psi }_{\alpha }u)\circ {\phi }_{\alpha }^{-1}{\parallel }_{W^{e,q}({\phi }_{\alpha }(U_{\alpha }))}<\infty \}.$$

(2) 

$$W^{e,q}(M,E;\Lambda )=\{u\in D^{\prime }{(M,E):\parallel u\parallel }_{W^{e,q}(M,E;\Lambda )}=\sum _{\alpha =1}^N\sum _{l=1}^r\parallel {\mathrm{ext}}_{{\phi }_{\alpha }(U_{\alpha }),{\mathbb{R}}^n}^0{[H_{\alpha }({\psi }_{\alpha }u)]}^l{\parallel }_{W^{e,q}({\mathbb{R}}^n)}<\infty \}.$$

(3) 

$$W^{e,q}(M,E;\Lambda )=\{u\in D^{\prime }(M,E):{[H_{\alpha }(u{|}_{U_{\alpha }})]}^l\in W_{loc}^{e,q}({\phi }_{\alpha }(U_{\alpha })),\forall 1\le \alpha \le N,\forall 1\le l\le r\}.$$

(4) 

$W^{e,q}(M,E;\Lambda )$ is the completion of $C^{\infty }(M,E)$ with respect to the norm

$${\parallel u\parallel }_{W^{e,q}(M,E;\Lambda )}=\sum _{\alpha =1}^N\sum _{l=1}^r{\parallel {({\rho }_{\alpha })}^l\circ ({\psi }_{\alpha }u)\circ {\phi }_{\alpha }^{-1}\parallel }_{W^{e,q}({\phi }_{\alpha }(U_{\alpha }))}.$$

(5) 

• Let g be a smooth Riemannian metric (i.e., a fiber metric on $TM$). So, $g^{-1}$ is a fiber metric on $T^{*}M$.
• Let ${⟨.,.⟩}_E$ be a smooth fiber metric on E.
• Let ${\nabla }^E$ be a metric connection in the vector bundle $\pi :E\to M$.

For $k\in {\mathbb{N}}_0$, $W^{k,q}(M,E;g,{\nabla }^E)$ is the completion of $C^{\infty }(M,E)$ with respect to the following norm:

$${\parallel u\parallel }_{W^{k,q}(M,E;g,{\nabla }^E)}={\left(\sum _{i=0}^k{|{({\nabla }^E)}^{i}u|}_{L^q}^q\right)}^{\frac{1}{q}}={\left(\sum _{i=0}^k{\int }_M{|\underset{i\mathrm{times}}{\underbrace{{\nabla }^E\dots {\nabla }^E}}u|}_{{(T^{*}M)}^{\otimes i}\otimes E}^{q}d{V}_g\right)}^{\frac{1}{q}}.$$

In particular, if we denote the Levi Civita connection corresponding to the smooth Riemannian metric g by ∇, then $W^{k,q}(M;g)$ is the completion of $C^{\infty }(M)$ with respect to the following norm

$$\begin{array}{cc}\hfill & {\parallel u\parallel }_{W^{k,q}(M;g)}={\left(\sum _{i=0}^k{|{\nabla }^{i}u|}_{L^q}^q\right)}^{\frac{1}{q}}={\left(\sum _{i=0}^k{\int }_M{|\underset{i\mathrm{times}}{\underbrace{\nabla \dots \nabla }}u|}_{T^{i}M}^{q}d{V}_g\right)}^{\frac{1}{q}}.\hfill \end{array}$$

In the subsequent discussions we will study the relation between each of these alternative descriptions of Sobolev spaces and Definition 30.

Remark 55.

As it is discussed for example in [18], Sobolev-Slobodeckij spaces on ${\mathbb{R}}^n$ with noninteger smoothness degree can be defined using real interpolation. Indeed, for $s\in \mathbb{R}\backslash \mathbb{Z}$ and $\theta =s-\lfloor s\rfloor$,

$$W^{s,p}({\mathbb{R}}^n)={\left(W^{\lfloor s\rfloor ,p}({\mathbb{R}}^n),W^{\lfloor s\rfloor +1,p}({\mathbb{R}}^n)\right)}_{\theta ,p}.$$

One may use any of the previously mentioned descriptions to define $W^{k,q}(M,E)$ for $k\in \mathbb{Z}$, and then use real interpolation to define $W^{e,q}(M,E)$ for $e\notin \mathbb{Z}$. We postpone the study of this approach to an independent manuscript with focus on the role of interpolation theory in investigation of Bessel potential spaces and Sobolev–Slobodeckij spaces on compact manifolds.

An important question is whether our definition of Sobolev spaces (as topological spaces) depends on the augmented total trivialization atlas $\Lambda$. We will answer this question at 3 levels. Although each level can be considered as a generalization of the preceding level, the proofs will be independent of each other. The following theorems show that at least when e is not a noninteger less than $-1$, the space $W^{e,q}(M,E;\Lambda )$ and its topology are independent of the choice of augmented total trivialization atlas.

Remark 56.

In the following theorems, by the equivalence of two norms ${\parallel .\parallel }_1$ and ${\parallel .\parallel }_2$ we mean there exist constants $C_1$ and $C_2$ such that

$$C_1{\parallel .\parallel }_1\le {\parallel .\parallel }_2\le C_2{\parallel .\parallel }_1,$$

where $C_1$ and $C_2$ may depend on

$$n,e,q,{\phi }_{\alpha },U_{\alpha },{\tilde{\phi }}_{\beta },{\tilde{U}}_{\beta },{\psi }_{\alpha },{\tilde{\psi }}_{\beta }.$$

Theorem 87

(Equivalence of norms for functions). Let $e\in \mathbb{R}$ and $q\in (1,\infty )$. Let $\Lambda ={\{(U_{\alpha },{\phi }_{\alpha },{\psi }_{\alpha })\}}_{1\le \alpha \le N}$ and $\mathsf{{\rm Y}}={\{({\tilde{U}}_{\beta },{\tilde{\phi }}_{\beta },{\tilde{\psi }}_{\beta })\}}_{1\le \beta \le \tilde{N}}$ be two augmented total trivialization atlases for the trivial bundle $M\times \mathbb{R}\to M$. Furthermore, let $\mathcal{W}$ be any vector subspace of $W^{e,q}(M;\mathsf{{\rm Y}})$ whose elements are regular distributions (e.g., $C^{\infty }(M)$).

(1) 

If e is not a noninteger less than $-1$, then W is a subspace of $W^{e,q}(M;\Lambda )$ as well, and the norms produced by Λ and Υ are equivalent on $\mathcal{W}$.

(2) 

If e is a noninteger less than $-1$, further assume that the total trivialization atlases corresponding to Λ and Υ are GLC. Then W is a subspace of $W^{e,q}(M;\Lambda )$ as well, and the norms produced by Λ and Υ are equivalent on $\mathcal{W}$.

Proof. 

Let $u\in {\Gamma }_{reg}(M)$. Our goal is to show that the following expressions are comparable:

$$\begin{array}{cc}\hfill & \sum _{\alpha =1}^N{\parallel ({\psi }_{\alpha }u)\circ {\phi }_{\alpha }^{-1}\parallel }_{W^{e,q}({\phi }_{\alpha }(U_{\alpha }))},\hfill \\ \hfill & \sum _{\beta =1}^{\tilde{N}}{\parallel ({\tilde{\psi }}_{\beta }u)\circ {\tilde{\phi }}_{\beta }^{-1}\parallel }_{W^{e,q}({\tilde{\phi }}_{\beta }({\tilde{U}}_{\beta }))}.\hfill \end{array}$$

To this end it suffices to show that for each $1\le \alpha \le N$

$$\parallel ({\psi }_{\alpha }u)\circ {\phi }_{\alpha }^{-1}{\parallel }_{W^{e,q}({\phi }_{\alpha }(U_{\alpha }))}⪯\sum _{\beta =1}^{\tilde{N}}{\parallel ({\tilde{\psi }}_{\beta }u)\circ {\tilde{\phi }}_{\beta }^{-1}\parallel }_{W^{e,q}({\tilde{\phi }}_{\beta }({\tilde{U}}_{\beta }))}.$$

We have

$$\begin{array}{cc}\hfill \parallel ({\psi }_{\alpha }u)\circ {\phi }_{\alpha }^{-1}{\parallel }_{W^{e,q}({\phi }_{\alpha }(U_{\alpha }))}& =\parallel \sum _{\beta =1}^{\tilde{N}}{\tilde{\psi }}_{\beta }({\psi }_{\alpha }u)\circ {\phi }_{\alpha }^{-1}{\parallel }_{W^{e,q}({\phi }_{\alpha }(U_{\alpha }))}\hfill \\ \hfill & \le \sum _{\beta =1}^{\tilde{N}}{\parallel {\tilde{\psi }}_{\beta }({\psi }_{\alpha }u)\circ {\phi }_{\alpha }^{-1}\parallel }_{W^{e,q}({\phi }_{\alpha }(U_{\alpha }))}\hfill \\ \hfill & \simeq \sum _{\beta =1}^{\tilde{N}}{\parallel ({\tilde{\psi }}_{\beta }{\psi }_{\alpha }u)\circ {\phi }_{\alpha }^{-1}\parallel }_{W^{e,q}({\phi }_{\alpha }(U_{\alpha }\cap {\tilde{U}}_{\beta }))}.\hfill \end{array}$$

The last equality follows from Corollary 6 because $({\tilde{\psi }}_{\beta }{\psi }_{\alpha }u)\circ {\phi }_{\alpha }^{-1}$ has support in the compact set ${\phi }_{\alpha }(\mathrm{supp}{\psi }_{\alpha }\cap \mathrm{supp}{\tilde{\psi }}_{\beta })\subseteq {\phi }_{\alpha }(U_{\alpha }\cap {\tilde{U}}_{\beta })$. Note that here we used the assumption that if e is a noninteger less than $-1$, then ${\phi }_{\alpha }(U_{\alpha })$ is Lipschitz or the entire ${\mathbb{R}}^n$. Clearly,

$$\sum _{\beta =1}^{\tilde{N}}\parallel ({\tilde{\psi }}_{\beta }{\psi }_{\alpha }u)\circ {\phi }_{\alpha }^{-1}{\parallel }_{W^{e,q}({\phi }_{\alpha }(U_{\alpha }\cap {\tilde{U}}_{\beta }))}=\sum _{\beta =1}^{\tilde{N}}{\parallel ({\tilde{\psi }}_{\beta }{\psi }_{\alpha }u)\circ {\tilde{\phi }}_{\beta }^{-1}\circ {\tilde{\phi }}_{\beta }\circ {\phi }_{\alpha }^{-1}\parallel }_{W^{e,q}({\phi }_{\alpha }(U_{\alpha }\cap {\tilde{U}}_{\beta }))}.$$

Since ${\tilde{\phi }}_{\beta }\circ {\phi }_{\alpha }^{-1}:{\phi }_{\alpha }(U_{\alpha }\cap {\tilde{U}}_{\beta })\to {\tilde{\phi }}_{\beta }(U_{\alpha }\cap {\tilde{U}}_{\beta })$ is a $C^{\infty }$-diffeomorphism and $({\tilde{\psi }}_{\beta }{\psi }_{\alpha }u)\circ {\tilde{\phi }}_{\beta }^{-1}$ has compact support in the compact set ${\tilde{\phi }}_{\beta }(\mathrm{supp}{\psi }_{\alpha }\cap \mathrm{supp}{\tilde{\psi }}_{\beta })\subseteq {\tilde{\phi }}_{\beta }(U_{\alpha }\cap {\tilde{U}}_{\beta })$, it follows from Theorem 80 that

$$\sum _{\beta =1}^{\tilde{N}}\parallel ({\tilde{\psi }}_{\beta }{\psi }_{\alpha }u)\circ {\tilde{\phi }}_{\beta }^{-1}\circ {\tilde{\phi }}_{\beta }\circ {\phi }_{\alpha }^{-1}{\parallel }_{W^{e,q}({\phi }_{\alpha }(U_{\alpha }\cap {\tilde{U}}_{\beta }))}⪯\sum _{\beta =1}^{\tilde{N}}{\parallel ({\tilde{\psi }}_{\beta }{\psi }_{\alpha }u)\circ {\tilde{\phi }}_{\beta }^{-1}\parallel }_{W^{e,q}({\tilde{\phi }}_{\beta }(U_{\alpha }\cap {\tilde{U}}_{\beta }))}.$$

Note that here we used the assumption that if e is a noninteger less than $-1$, then the two total trivialization atlases are GL compatible. As a direct consequence of Corollary 5 and Theorem 71 we have

$$\begin{array}{cc}\hfill \parallel ({\tilde{\psi }}_{\beta }{\psi }_{\alpha }u)\circ {\tilde{\phi }}_{\beta }^{-1}{\parallel }_{W^{e,q}({\tilde{\phi }}_{\beta }(U_{\alpha }\cap {\tilde{U}}_{\beta }))}& \simeq \parallel ({\tilde{\psi }}_{\beta }{\psi }_{\alpha }u)\circ {\tilde{\phi }}_{\beta }^{-1}{\parallel }_{W^{e,q}({\tilde{\phi }}_{\beta }({\tilde{U}}_{\beta }))}\hfill \\ \hfill & =\parallel ({\psi }_{\alpha }\circ {\tilde{\phi }}_{\beta }^{-1})[({\tilde{\psi }}_{\beta }u)\circ {\tilde{\phi }}_{\beta }^{-1}]{\parallel }_{W^{e,q}({\tilde{\phi }}_{\beta }({\tilde{U}}_{\beta }))}.\hfill \end{array}$$

Now, note that ${\psi }_{\alpha }\circ {\tilde{\phi }}_{\beta }^{-1}\in C^{\infty }({\tilde{\phi }}_{\beta }({\tilde{U}}_{\beta }))$ and $({\tilde{\psi }}_{\beta }u)\circ {\tilde{\phi }}_{\beta }^{-1}$ has support in the compact set ${\tilde{\phi }}_{\beta }(\mathrm{supp}{\tilde{\psi }}_{\beta })$. Therefore, by Theorem 70 (for the case where e is not a noninteger less than $-1$) and Corollary 4 (for the case where e is a noninteger less than $-1$) we have

$$\parallel ({\psi }_{\alpha }\circ {\tilde{\phi }}_{\beta }^{-1})[({\tilde{\psi }}_{\beta }u)\circ {\tilde{\phi }}_{\beta }^{-1}]{\parallel }_{W^{e,q}({\tilde{\phi }}_{\beta }({\tilde{U}}_{\beta }))}⪯{\parallel ({\tilde{\psi }}_{\beta }u)\circ {\tilde{\phi }}_{\beta }^{-1}\parallel }_{W^{e,q}({\tilde{\phi }}_{\beta }({\tilde{U}}_{\beta }))}.$$

Hence

$$\parallel ({\psi }_{\alpha }u)\circ {\phi }_{\alpha }^{-1}{\parallel }_{W^{e,q}({\phi }_{\alpha }(U_{\alpha }))}⪯\sum _{\beta =1}^{\tilde{N}}{\parallel ({\tilde{\psi }}_{\beta }u)\circ {\tilde{\phi }}_{\beta }^{-1}\parallel }_{W^{e,q}({\tilde{\phi }}_{\beta }({\tilde{U}}_{\beta }))}.$$

□

Theorem 88

(Equivalence of norms for regular sections). Let $e\in \mathbb{R}$ and $q\in (1,\infty )$. Let $\Lambda ={\{(U_{\alpha },{\phi }_{\alpha },{\rho }_{\alpha },{\psi }_{\alpha })\}}_{1\le \alpha \le N}$ and $\mathsf{{\rm Y}}={\{({\tilde{U}}_{\beta },{\tilde{\phi }}_{\beta },{\tilde{\rho }}_{\beta },{\tilde{\psi }}_{\beta })\}}_{1\le \beta \le \tilde{N}}$ be two augmented total trivialization atlases for the vector bundle $E\to M$. Furthermore, let $\mathcal{W}$ be any vector subspace of $W^{e,q}(M,E;\mathsf{{\rm Y}})$ whose elements are regular distributions (e.g., $C^{\infty }(M,E)$).

(1) 

If e is not a noninteger less than $-1$, then W is a subspace of $W^{e,q}(M,E;\Lambda )$ as well, and the norms produced by Λ and Υ are equivalent on $\mathcal{W}$.

(2) 

If e is a noninteger less than $-1$, further assume that the total trivialization atlases corresponding to Λ and Υ are GLC. Then W is a subspace of $W^{e,q}(M,E;\Lambda )$ as well, and the norms produced by Λ and Υ are equivalent on $\mathcal{W}$.

Proof. 

Let $u\in {\Gamma }_{reg}(M,E)$. Our goal is to show that the following expressions are comparable:

$$\begin{array}{cc}\hfill & \sum _{\alpha =1}^N\sum _{l=1}^r{\parallel {\rho }_{\alpha }^l\circ ({\psi }_{\alpha }u)\circ {\phi }_{\alpha }^{-1}\parallel }_{W^{e,q}({\phi }_{\alpha }(U_{\alpha }))},\hfill \\ \hfill & \sum _{\beta =1}^{\tilde{N}}\sum _{l=1}^r{\parallel {\tilde{\rho }}_{\beta }^l\circ ({\tilde{\psi }}_{\beta }u)\circ {\tilde{\phi }}_{\beta }^{-1}\parallel }_{W^{e,q}({\tilde{\phi }}_{\beta }({\tilde{U}}_{\beta }))}.\hfill \end{array}$$

To this end, it is enough to show that for each $1\le \alpha \le N$ and $1\le l\le r$

$$\parallel {\rho }_{\alpha }^l\circ ({\psi }_{\alpha }u)\circ {\phi }_{\alpha }^{-1}{\parallel }_{W^{e,q}({\phi }_{\alpha }(U_{\alpha }))}⪯\sum _{\beta =1}^{\tilde{N}}\sum _{t=1}^r{\parallel {\tilde{\rho }}_{\beta }^t\circ ({\tilde{\psi }}_{\beta }u)\circ {\tilde{\phi }}_{\beta }^{-1}\parallel }_{W^{e,q}({\tilde{\phi }}_{\beta }({\tilde{U}}_{\beta }))}.$$

We have

$$\begin{array}{cc}\hfill \parallel {\rho }_{\alpha }^l\circ ({\psi }_{\alpha }u)\circ {\phi }_{\alpha }^{-1}{\parallel }_{W^{e,q}({\phi }_{\alpha }(U_{\alpha }))}& =\parallel {\rho }_{\alpha }^l\circ (\sum _{\beta =1}^{\tilde{N}}{\tilde{\psi }}_{\beta }{\psi }_{\alpha }u)\circ {\phi }_{\alpha }^{-1}{\parallel }_{W^{e,q}({\phi }_{\alpha }(U_{\alpha }))}\hfill \\ \hfill & \le \sum _{\beta =1}^{\tilde{N}}{\parallel {\rho }_{\alpha }^l\circ ({\tilde{\psi }}_{\beta }{\psi }_{\alpha }u)\circ {\phi }_{\alpha }^{-1}\parallel }_{W^{e,q}({\phi }_{\alpha }(U_{\alpha }))}\hfill \\ \hfill & \simeq \sum _{\beta =1}^{\tilde{N}}{\parallel {\rho }_{\alpha }^l\circ ({\tilde{\psi }}_{\beta }{\psi }_{\alpha }u)\circ {\phi }_{\alpha }^{-1}\parallel }_{W^{e,q}({\phi }_{\alpha }(U_{\alpha }\cap {\tilde{U}}_{\beta }))}.\hfill \end{array}$$

The last equality follows from Corollary 6 because ${\rho }_{\alpha }^l\circ ({\tilde{\psi }}_{\beta }{\psi }_{\alpha }u)\circ {\phi }_{\alpha }^{-1}$ has support in the compact set ${\phi }_{\alpha }(\mathrm{supp}{\psi }_{\alpha }\cap \mathrm{supp}{\tilde{\psi }}_{\beta })\subseteq {\phi }_{\alpha }(U_{\alpha }\cap {\tilde{U}}_{\beta })$. Note that here we used the assumption that if e is a noninteger less than $-1$, then ${\phi }_{\alpha }(U_{\alpha })$ is either Lipschitz or equal to the entire ${\mathbb{R}}^n$. Note that

$$\begin{array}{cc}\hfill \sum _{\beta =1}^{\tilde{N}}\parallel {\rho }_{\alpha }^l\circ ({\tilde{\psi }}_{\beta }{\psi }_{\alpha }u)& \circ {\phi }_{\alpha }^{-1}{\parallel }_{W^{e,q}({\phi }_{\alpha }(U_{\alpha }\cap {\tilde{U}}_{\beta }))}\hfill \\ \hfill & =\sum _{\beta =1}^{\tilde{N}}{\parallel {\rho }_{\alpha }^l\circ ({\tilde{\psi }}_{\beta }{\psi }_{\alpha }u)\circ {\tilde{\phi }}_{\beta }^{-1}\circ {\tilde{\phi }}_{\beta }\circ {\phi }_{\alpha }^{-1}\parallel }_{W^{e,q}({\phi }_{\alpha }(U_{\alpha }\cap {\tilde{U}}_{\beta }))}\hfill \\ \hfill & \stackrel{\mathrm{Theorem} 80}{⪯}\sum _{\beta =1}^{\tilde{N}}{\parallel {\rho }_{\alpha }^l\circ ({\tilde{\psi }}_{\beta }{\psi }_{\alpha }u)\circ {\tilde{\phi }}_{\beta }^{-1}\parallel }_{W^{e,q}({\tilde{\phi }}_{\beta }(U_{\alpha }\cap {\tilde{U}}_{\beta }))}\hfill \\ \hfill & =\sum _{\beta =1}^{\tilde{N}}{\parallel ({\psi }_{\alpha }\circ {\tilde{\phi }}_{\beta }^{-1})[{\rho }_{\alpha }^l\circ ({\tilde{\psi }}_{\beta }u)\circ {\tilde{\phi }}_{\beta }^{-1}]\parallel }_{W^{e,q}({\tilde{\phi }}_{\beta }(U_{\alpha }\cap {\tilde{U}}_{\beta }))}\hfill \\ \hfill & =\sum _{\beta =1}^{\tilde{N}}{\parallel ({\psi }_{\alpha }\circ {\tilde{\phi }}_{\beta }^{-1})\left[{\pi }_l\circ \underset{{\rho }_{\alpha }}{\underbrace{{\pi }^{\prime }\circ {\Phi }_{\alpha }}}\circ ({\tilde{\psi }}_{\beta }u)\circ {\tilde{\phi }}_{\beta }^{-1}\right]\parallel }_{W^{e,q}({\tilde{\phi }}_{\beta }(U_{\alpha }\cap {\tilde{U}}_{\beta }))}\hfill \\ \hfill & =\sum _{\beta =1}^{\tilde{N}}{\parallel ({\psi }_{\alpha }\circ {\tilde{\phi }}_{\beta }^{-1})\left[{\pi }_l\circ {\pi }^{\prime }\circ {\Phi }_{\alpha }\circ {\Phi }_{\beta }^{-1}\circ {\Phi }_{\beta }\circ ({\tilde{\psi }}_{\beta }u)\circ {\tilde{\phi }}_{\beta }^{-1}\right]\parallel }_{W^{e,q}({\tilde{\phi }}_{\beta }(U_{\alpha }\cap {\tilde{U}}_{\beta }))}.\hfill \end{array}$$

Let $v_{\beta }:{\tilde{\phi }}_{\beta }({\tilde{U}}_{\beta })\to E$ be defined by $v_{\beta }(x)=({\tilde{\psi }}_{\beta }u)\circ {\tilde{\phi }}_{\beta }^{-1}$. Clearly $\pi (v_{\beta }(x))={\tilde{\phi }}_{\beta }^{-1}(x)$. Therefore,

$${\Phi }_{\beta }(v_{\beta }(x))=\left(\pi (v_{\beta }(x)),{\tilde{\rho }}_{\beta }(v_{\beta }(x))\right)=\left({\tilde{\phi }}_{\beta }^{-1}(x),{\tilde{\rho }}_{\beta }(v_{\beta }(x))\right).$$

For all $x\in {\tilde{\phi }}_{\beta }(U_{\alpha }\cap {\tilde{U}}_{\beta })$ we have

$$\begin{array}{cc}\hfill {\pi }^{\prime }& \circ {\Phi }_{\alpha }\circ {\Phi }_{\beta }^{-1}\left({\Phi }_{\beta }(v_{\beta }(x))\right)\hfill \\ \hfill & ={\pi }^{\prime }\circ {\Phi }_{\alpha }\circ {\Phi }_{\beta }^{-1}\left({\tilde{\phi }}_{\beta }^{-1}(x),{\tilde{\rho }}_{\beta }(v_{\beta }(x))\right)\hfill \\ \hfill & \stackrel{\mathrm{Lemma} 4}{=}{\pi }^{\prime }\circ \left({\tilde{\phi }}_{\beta }^{-1}(x),{\tau }_{\alpha \beta }({\tilde{\phi }}_{\beta }^{-1}(x)){\tilde{\rho }}_{\beta }(v_{\beta }(x))\right)\hfill \\ \hfill & =\underset{\mathrm{an}r\times r\mathrm{matrix}}{\underbrace{{\tau }_{\alpha \beta }({\tilde{\phi }}_{\beta }^{-1}(x))}}{\tilde{\rho }}_{\beta }(v_{\beta }(x)).\hfill \end{array}$$

Let $A_{\alpha \beta }={\tau }_{\alpha \beta }\circ {\tilde{\phi }}_{\beta }^{-1}$ on ${\tilde{\phi }}_{\beta }(U_{\alpha }\cap {\tilde{U}}_{\beta })$. So, we can write

$$\begin{array}{cc}\hfill \parallel {\rho }_{\alpha }^l& \circ ({\psi }_{\alpha }u)\circ {\phi }_{\alpha }^{-1}{\parallel }_{W^{e,q}({\tilde{\phi }}_{\beta }(U_{\alpha }\cap {\tilde{U}}_{\beta }))}\hfill \\ \hfill & ⪯\sum _{\beta =1}^{\tilde{N}}{\parallel ({\psi }_{\alpha }\circ {\tilde{\phi }}_{\beta }^{-1})(x)\left[{\pi }_l\circ A_{\alpha \beta }(x){\tilde{\rho }}_{\beta }(v_{\beta }(x))\right]\parallel }_{W^{e,q}({\tilde{\phi }}_{\beta }(U_{\alpha }\cap {\tilde{U}}_{\beta }))}\hfill \\ \hfill & =\sum _{\beta =1}^{\tilde{N}}{\parallel ({\psi }_{\alpha }\circ {\tilde{\phi }}_{\beta }^{-1})(x)\left[\sum _{t=1}^r{(A_{\alpha \beta }(x))}_{lt}{\tilde{\rho }}_{\beta }^t(v_{\beta }(x))\right]\parallel }_{W^{e,q}({\tilde{\phi }}_{\beta }(U_{\alpha }\cap {\tilde{U}}_{\beta }))}\hfill \\ \hfill & \le \sum _{\beta =1}^{\tilde{N}}\sum _{t=1}^r{\parallel ({\psi }_{\alpha }\circ {\tilde{\phi }}_{\beta }^{-1})(x){(A_{\alpha \beta }(x))}_{lt}{\tilde{\rho }}_{\beta }^t(v_{\beta }(x))\parallel }_{W^{e,q}({\tilde{\phi }}_{\beta }(U_{\alpha }\cap {\tilde{U}}_{\beta }))}.\hfill \end{array}$$

Now, note that ${(A_{\alpha \beta }(x))}_{lt}$ are in $C^{\infty }({\tilde{\phi }}_{\beta }(U_{\alpha }\cap {\tilde{U}}_{\beta }))$ and $({\psi }_{\alpha }\circ {\tilde{\phi }}_{\beta }^{-1})(x){\tilde{\rho }}_{\beta }^t(v_{\beta }(x))$ has support inside the compact set ${\tilde{\phi }}_{\beta }(\mathrm{supp}\widetilde{{\psi }_{\beta }}\cap \mathrm{supp}{\psi }_{\alpha })$. Therefore, by Theorem 70 (for the case where e is not a noninteger less than $-1$) and Corollary 4 (for the case where e is a noninteger less than $-1$), we have

$$\sum _{t=1}^r\parallel ({\psi }_{\alpha }\circ {\tilde{\phi }}_{\beta }^{-1})(x){(A_{\alpha \beta }(x))}_{lt}{\tilde{\rho }}_{\beta }^t(v_{\beta }(x)){\parallel }_{W^{e,q}({\tilde{\phi }}_{\beta }(U_{\alpha }\cap {\tilde{U}}_{\beta }))}⪯\sum _{t=1}^r{\parallel ({\psi }_{\alpha }\circ {\tilde{\phi }}_{\beta }^{-1})(x){\tilde{\rho }}_{\beta }^t(v_{\beta }(x))\parallel }_{W^{e,q}({\tilde{\phi }}_{\beta }(U_{\alpha }\cap {\tilde{U}}_{\beta }))}.$$

Therefore,

$$\begin{array}{cc}\hfill \parallel {\rho }_{\alpha }^l& \circ ({\psi }_{\alpha }u)\circ {\phi }_{\alpha }^{-1}{\parallel }_{W^{e,q}({\phi }_{\alpha }(U_{\alpha }))}\hfill \\ \hfill & ⪯\sum _{\beta =1}^{\tilde{N}}\sum _{t=1}^r{\parallel ({\psi }_{\alpha }\circ {\tilde{\phi }}_{\beta }^{-1})(x){\tilde{\rho }}_{\beta }^t(v_{\beta }(x))\parallel }_{W^{e,q}({\tilde{\phi }}_{\beta }(U_{\alpha }\cap {\tilde{U}}_{\beta }))}\hfill \\ \hfill & \simeq \sum _{\beta =1}^{\tilde{N}}\sum _{t=1}^r{\parallel ({\psi }_{\alpha }\circ {\tilde{\phi }}_{\beta }^{-1})(x){\tilde{\rho }}_{\beta }^t(v_{\beta }(x))\parallel }_{W^{e,q}({\tilde{\phi }}_{\beta }({\tilde{U}}_{\beta }))}\hfill \\ \hfill & (\mathrm{Here}\mathrm{we}\mathrm{used}\mathrm{Corollary}5\mathrm{and}\mathrm{Theorem}71)\hfill \\ \hfill & ⪯\sum _{\beta =1}^{\tilde{N}}\sum _{t=1}^r{\parallel {\tilde{\rho }}_{\beta }^t(v_{\beta }(x))\parallel }_{W^{e,q}({\tilde{\phi }}_{\beta }({\tilde{U}}_{\beta }))}\hfill \\ \hfill & (\mathrm{Here}\mathrm{we}\mathrm{used}\mathrm{Theorem}70\mathrm{and}\mathrm{Corollary}4)\hfill \\ \hfill & =\sum _{\beta =1}^{\tilde{N}}\sum _{t=1}^r{\parallel {\tilde{\rho }}_{\beta }^t\circ ({\tilde{\psi }}_{\beta }u)\circ {\tilde{\phi }}_{\beta }^{-1}\parallel }_{W^{e,q}({\tilde{\phi }}_{\beta }({\tilde{U}}_{\beta }))}.\hfill \end{array}$$

□

Theorem 89

(Equivalence of norms for distributional sections). Let $e\in \mathbb{R}$ and $q\in (1,\infty )$. Let $\Lambda ={\{(U_{\alpha },{\phi }_{\alpha },{\rho }_{\alpha },{\psi }_{\alpha })\}}_{1\le \alpha \le N}$ and $\mathsf{{\rm Y}}={\{({\tilde{U}}_{\beta },{\tilde{\phi }}_{\beta },{\tilde{\rho }}_{\beta },{\tilde{\psi }}_{\beta })\}}_{1\le \beta \le \tilde{N}}$ be two augmented total trivialization atlases for the vector bundle $E\to M$.

(1) 

If e is not a noninteger less than $-1$, then $W^{e,q}(M,E;\Lambda )$ and $W^{e,q}(M,E;\mathsf{{\rm Y}})$ are equivalent normed spaces.

(2) 

If e is a noninteger less than $-1$, further assume that the total trivialization atlases corresponding to Λ and Υ are GLC. Then $W^{e,q}(M,E;\Lambda )$ and $W^{e,q}(M,E;\mathsf{{\rm Y}})$ are equivalent normed spaces.

Proof. 

Let $u\in D^{\prime }(M,E)$. We want to show the following expressions are comparable:

$$\begin{array}{cc}\hfill & \sum _{\alpha =1}^N\sum _{l=1}^r{\parallel {[H_{\alpha }({\psi }_{\alpha }u)]}^l\parallel }_{W^{e,q}({\phi }_{\alpha }(U_{\alpha }))},\hfill \\ \hfill & \sum _{\beta =1}^{\tilde{N}}\sum _{i=1}^r{\parallel {[{\tilde{H}}_{\beta }({\tilde{\psi }}_{\beta }u)]}^i\parallel }_{W^{e,q}({\tilde{\phi }}_{\beta }({\tilde{U}}_{\beta }))}.\hfill \end{array}$$

To this end it is enough to show that for each $1\le \alpha \le N$ and $1\le l\le r$

$$\parallel {[H_{\alpha }({\psi }_{\alpha }u)]}^l{\parallel }_{W^{e,q}({\phi }_{\alpha }(U_{\alpha }))}⪯\sum _{\beta =1}^{\tilde{N}}\sum _{i=1}^r{\parallel {[{\tilde{H}}_{\beta }({\tilde{\psi }}_{\beta }u)]}^i\parallel }_{W^{e,q}({\tilde{\phi }}_{\beta }({\tilde{U}}_{\beta }))}.$$

We have

$${[H_{\alpha }({\psi }_{\alpha }u)]}^l={[H_{\alpha }(\sum _{\beta =1}^{\tilde{N}}{\tilde{\psi }}_{\beta }{\psi }_{\alpha }u)]}^l\stackrel{\mathrm{Remark}31}{=}\sum _{\beta =1}^{\tilde{N}}{[H_{\alpha }({\tilde{\psi }}_{\beta }{\psi }_{\alpha }u)]}^l.$$

In what follows we will prove that

$${[H_{\alpha }({\tilde{\psi }}_{\beta }{\psi }_{\alpha }u)]}^l=\sum _{i=1}^r\left({(A_{\alpha \beta })}_{il}{[{\tilde{H}}_{\beta }({\tilde{\psi }}_{\beta }{\psi }_{\alpha }u)]}^i\right)\circ {\tilde{\phi }}_{\beta }\circ {\phi }_{\alpha }^{-1},$$

(4)

for some functions ${(A_{\alpha \beta })}_{il},(1\le i\le r)$ in $C^{\infty }({\tilde{\phi }}_{\beta }(U_{\alpha }\cap {\tilde{U}}_{\beta }))$. For now let us assume the validity of Equation (4) to prove the claim.

$$\begin{array}{cc}\hfill \parallel [H_{\alpha }({\psi }_{\alpha }u)& {]}^l{\parallel }_{W^{e,q}({\phi }_{\alpha }(U_{\alpha }))}={\parallel \sum _{\beta =1}^{\tilde{N}}{[H_{\alpha }({\tilde{\psi }}_{\beta }{\psi }_{\alpha }u)]}^l\parallel }_{W^{e,q}({\phi }_{\alpha }(U_{\alpha }))}\hfill \\ \hfill & \le \sum _{\beta =1}^{\tilde{N}}{\parallel {[H_{\alpha }({\tilde{\psi }}_{\beta }{\psi }_{\alpha }u)]}^l\parallel }_{W^{e,q}({\phi }_{\alpha }(U_{\alpha }))}\hfill \\ \hfill & \stackrel{\mathrm{Corollary}6}{\simeq }\sum _{\beta =1}^{\tilde{N}}{\parallel {[H_{\alpha }({\tilde{\psi }}_{\beta }{\psi }_{\alpha }u)]}^l\parallel }_{W^{e,q}({\phi }_{\alpha }(U_{\alpha }\cap {\tilde{U}}_{\beta }))}\hfill \\ \hfill & (\mathrm{note} \mathrm{that} \mathrm{by} \mathrm{Remark} 31 {[H_{\alpha }({\tilde{\psi }}_{\beta }{\psi }_{\alpha }u)]}^l \mathrm{has} \mathrm{support} \mathrm{in} \mathrm{the} \mathrm{compact} \mathrm{set} {\phi }_{\alpha }(\mathrm{supp}{\psi }_{\alpha }\cap \mathrm{supp}{\tilde{\psi }}_{\beta }))\hfill \\ \hfill & =\sum _{\beta =1}^{\tilde{N}}{\parallel \sum _{i=1}^r\left({(A_{\alpha \beta })}_{il}{[{\tilde{H}}_{\beta }({\tilde{\psi }}_{\beta }{\psi }_{\alpha }u)]}^i\right)\circ {\tilde{\phi }}_{\beta }\circ {\phi }_{\alpha }^{-1}\parallel }_{W^{e,q}({\phi }_{\alpha }(U_{\alpha }\cap {\tilde{U}}_{\beta }))}\hfill \\ \hfill & \le \sum _{\beta =1}^{\tilde{N}}\sum _{i=1}^r{\parallel \left({(A_{\alpha \beta })}_{il}{[{\tilde{H}}_{\beta }({\tilde{\psi }}_{\beta }{\psi }_{\alpha }u)]}^i\right)\circ {\tilde{\phi }}_{\beta }\circ {\phi }_{\alpha }^{-1}\parallel }_{W^{e,q}({\phi }_{\alpha }(U_{\alpha }\cap {\tilde{U}}_{\beta }))}\hfill \\ \hfill & \stackrel{\mathrm{Theorem}80}{⪯}\sum _{\beta =1}^{\tilde{N}}\sum _{i=1}^r{\parallel {(A_{\alpha \beta })}_{il}{[{\tilde{H}}_{\beta }({\tilde{\psi }}_{\beta }{\psi }_{\alpha }u)]}^i\parallel }_{W^{e,q}({\tilde{\phi }}_{\beta }(U_{\alpha }\cap {\tilde{U}}_{\beta }))}\hfill \\ \hfill & =\sum _{\beta =1}^{\tilde{N}}\sum _{i=1}^r{\parallel {(A_{\alpha \beta })}_{il}({\psi }_{\alpha }\circ {\tilde{\phi }}_{\beta }^{-1}){[{\tilde{H}}_{\beta }({\tilde{\psi }}_{\beta }u)]}^i\parallel }_{W^{e,q}({\tilde{\phi }}_{\beta }(U_{\alpha }\cap {\tilde{U}}_{\beta }))}\hfill \\ \hfill & ⪯\sum _{\beta =1}^{\tilde{N}}\sum _{i=1}^r{\parallel ({\psi }_{\alpha }\circ {\tilde{\phi }}_{\beta }^{-1}){[{\tilde{H}}_{\beta }({\tilde{\psi }}_{\beta }u)]}^i\parallel }_{W^{e,q}({\tilde{\phi }}_{\beta }(U_{\alpha }\cap {\tilde{U}}_{\beta }))}\hfill \\ \hfill & \simeq \sum _{\beta =1}^{\tilde{N}}\sum _{i=1}^r{\parallel ({\psi }_{\alpha }\circ {\tilde{\phi }}_{\beta }^{-1}){[{\tilde{H}}_{\beta }({\tilde{\psi }}_{\beta }u)]}^i\parallel }_{W^{e,q}({\tilde{\phi }}_{\beta }({\tilde{U}}_{\beta }))}\hfill \\ \hfill & (\mathrm{Here}\mathrm{we}\mathrm{used}\mathrm{Corollary}\mathrm{and}\mathrm{Theorem})\hfill \\ \hfill & ⪯\sum _{\beta =1}^{\tilde{N}}\sum _{i=1}^r{\parallel {[{\tilde{H}}_{\beta }({\tilde{\psi }}_{\beta }u)]}^i\parallel }_{W^{e,q}({\tilde{\phi }}_{\beta }({\tilde{U}}_{\beta }))}\hfill \\ \hfill & (\mathrm{Here}\mathrm{we}\mathrm{used}\mathrm{Theorem}70\mathrm{and}\mathrm{Corollary}4).\hfill \end{array}$$

So, it remains to prove Equation (4). Since $\mathrm{supp}{[H_{\alpha }({\tilde{\psi }}_{\beta }{\psi }_{\alpha }u)]}^l$ is inside the compact set ${\phi }_{\alpha }(\mathrm{supp}{\psi }_{\alpha }\cap \mathrm{supp}{\tilde{\psi }}_{\beta })\subseteq {\phi }_{\alpha }(U_{\alpha }\cap {\tilde{U}}_{\beta })$, it is enough to consider the action of ${[H_{\alpha }({\tilde{\psi }}_{\beta }{\psi }_{\alpha }u)]}^l$ on elements of $C_c^{\infty }({\phi }_{\alpha }(U_{\alpha }\cap {\tilde{U}}_{\beta }))$. ${\tilde{\phi }}_{\beta }\circ {\phi }_{\alpha }^{-1}:{\phi }_{\alpha }(U_{\alpha }\cap {\tilde{U}}_{\beta })\to {\tilde{\phi }}_{\beta }(U_{\alpha }\cap {\tilde{U}}_{\beta })$ is a $C^{\infty }$-diffeomorphism. Therefore, the map

$$C_c^{\infty }[{\tilde{\phi }}_{\beta }(U_{\alpha }\cap {\tilde{U}}_{\beta })]\to C_c^{\infty }[{\phi }_{\alpha }(U_{\alpha }\cap {\tilde{U}}_{\beta })],\eta \mapsto \eta \circ {\tilde{\phi }}_{\beta }\circ {\phi }_{\alpha }^{-1}$$

is bijective. In particular, an arbitrary element of $C_c^{\infty }[{\phi }_{\alpha }(U_{\alpha }\cap {\tilde{U}}_{\beta })]$ has the form $\eta \circ {\tilde{\phi }}_{\beta }\circ {\phi }_{\alpha }^{-1}$ where $\eta$ is an element of $C_c^{\infty }[{\tilde{\phi }}_{\beta }(U_{\alpha }\cap {\tilde{U}}_{\beta })]$.

For all $\eta \in C_c^{\infty }[{\tilde{\phi }}_{\beta }(U_{\alpha }\cap {\tilde{U}}_{\beta })]$ we have (see Section 6.2.2)

$$⟨{[H_{\alpha }({\tilde{\psi }}_{\beta }{\psi }_{\alpha }u)]}^l,\eta \circ {\tilde{\phi }}_{\beta }\circ {\phi }_{\alpha }^{-1}⟩=⟨{\tilde{\psi }}_{\beta }{\psi }_{\alpha }u,g_{l,\eta \circ {\tilde{\phi }}_{\beta }\circ {\phi }_{\alpha }^{-1}}^{\alpha }⟩,$$

(5)

where $g_{l,\eta \circ {\tilde{\phi }}_{\beta }\circ {\phi }_{\alpha }^{-1}}^{\alpha }$ stands for $g_{l,\eta \circ {\tilde{\phi }}_{\beta }\circ {\phi }_{\alpha }^{-1},U_{\alpha },{\phi }_{\alpha }}$.

For all $y\in {\phi }_{\alpha }(U_{\alpha }\cap {\tilde{U}}_{\beta })$ we have $(x={\phi }_{\alpha }^{-1}(y))$

$$\begin{array}{cc}\hfill & {\rho }_{\alpha }^{\vee }{|}_{E_x^{\vee }}\circ g_{l,\eta \circ {\tilde{\phi }}_{\beta }\circ {\phi }_{\alpha }^{-1}}^{\alpha }\circ \underset{x}{\underbrace{{\phi }_{\alpha }^{-1}(y)}}=(0,\dots ,0,\underset{l\mathrm{th}\mathrm{position}}{\underbrace{\eta \circ {\tilde{\phi }}_{\beta }\circ {\phi }_{\alpha }^{-1}(y)}},0,\dots ,0),\hfill \\ \hfill & {\tilde{\rho }}_{\beta }^{\vee }\circ {\tilde{g}}_{l,\eta }^{\beta }\circ \underset{x}{\underbrace{{\tilde{\phi }}_{\beta }^{-1}({\tilde{\phi }}_{\beta }\circ {\phi }_{\alpha }^{-1}(y))}}=(0,\dots ,0,\underset{l\mathrm{th}\mathrm{position}}{\underbrace{\eta \circ {\tilde{\phi }}_{\beta }\circ {\phi }_{\alpha }^{-1}(y)}},0,\dots ,0).\hfill \end{array}$$

Therefore, for all $y\in {\phi }_{\alpha }(U_{\alpha }\cap {\tilde{U}}_{\beta })$

$${\rho }_{\alpha }^{\vee }{|}_{E_x^{\vee }}\circ g_{l,\eta \circ {\tilde{\phi }}_{\beta }\circ {\phi }_{\alpha }^{-1}}^{\alpha }\circ {\phi }_{\alpha }^{-1}(y)={\tilde{\rho }}_{\beta }^{\vee }\circ {\tilde{g}}_{l,\eta }^{\beta }\circ {\phi }_{\alpha }^{-1}(y),$$

which implies that on $U_{\alpha }\cap {\tilde{U}}_{\beta }$

$$g_{l,\eta \circ {\tilde{\phi }}_{\beta }\circ {\phi }_{\alpha }^{-1}}^{\alpha }={[{\rho }_{\alpha }^{\vee }{|}_{E_x^{\vee }}]}^{-1}\circ [{\tilde{\rho }}_{\beta }^{\vee }{|}_{E_x^{\vee }}]\circ {\tilde{g}}_{l,\eta }^{\beta }.$$

(6)

It follows from Lemma 4 that for all $a\in E_x^{\vee }$

$$[{\tilde{\rho }}_{\beta }^{\vee }{|}_{E_x^{\vee }}]\circ {[{\rho }_{\alpha }^{\vee }{|}_{E_x^{\vee }}]}^{-1}\circ [{\tilde{\rho }}_{\beta }^{\vee }{|}_{E_x^{\vee }}](a)=\underset{r\times r}{\underbrace{{\tau }^{\tilde{\beta }\alpha }(x)}}({\tilde{\rho }}_{\beta }^{\vee }{|}_{E_x^{\vee }}(a)).$$

That is,

$${[{\rho }_{\alpha }^{\vee }{|}_{E_x^{\vee }}]}^{-1}\circ [{\tilde{\rho }}_{\beta }^{\vee }{|}_{E_x^{\vee }}](a)={[{\tilde{\rho }}_{\beta }^{\vee }{|}_{E_x^{\vee }}]}^{-1}[{\tau }^{\tilde{\beta }\alpha }(x)({\tilde{\rho }}_{\beta }^{\vee }{|}_{E_x^{\vee }}(a))].$$

For $a={\tilde{g}}_{l,\eta }^{\beta }(x)$ we have

$${\tilde{\rho }}_{\beta }^{\vee }{{|}_{E_x^{\vee }}(a)={\tilde{\rho }}_{\beta }^{\vee }|}_{E_x^{\vee }}({\tilde{g}}_{l,\eta }^{\beta }(x))=(0,\dots ,0,\underset{l\mathrm{th}\mathrm{position}}{\underbrace{\eta \circ {\tilde{\phi }}_{\beta }(x)}},0,\dots ,0).$$

So,

$$\begin{array}{cc}\hfill {[{\rho }_{\alpha }^{\vee }{|}_{E_x^{\vee }}]}^{-1}\circ [{\tilde{\rho }}_{\beta }^{\vee }{|}_{E_x^{\vee }}]\circ {\tilde{g}}_{l,\eta }^{\beta }& ={[{\tilde{\rho }}_{\beta }^{\vee }{|}_{E_x^{\vee }}]}^{-1}[{\tau }^{\tilde{\beta }\alpha }(x)({\tilde{\rho }}_{\beta }^{\vee }{|}_{E_x^{\vee }}({\tilde{g}}_{l,\eta }^{\beta }(x)))]={[{\tilde{\rho }}_{\beta }^{\vee }{|}_{E_x^{\vee }}]}^{-1}\left((\eta \circ {\tilde{\phi }}_{\beta })\left[\begin{array}{c}{\tau }_{1l}^{\tilde{\beta }\alpha }\\ ⋮\\ {\tau }_{rl}^{\tilde{\beta }\alpha }\end{array}\right]\right)\hfill \\ \hfill & ={[{\tilde{\rho }}_{\beta }^{\vee }{|}_{E_x^{\vee }}]}^{-1}\left(\left[\begin{array}{c}(\eta \circ {\tilde{\phi }}_{\beta }){\tau }_{1l}^{\tilde{\beta }\alpha }\\ 0\\ ⋮\\ 0\end{array}\right]+\cdots +\left[\begin{array}{c}0\\ ⋮\\ 0\\ (\eta \circ {\tilde{\phi }}_{\beta }){\tau }_{rl}^{\tilde{\beta }\alpha }\end{array}\right]\right)\hfill \\ \hfill & ={\tilde{g}}_{1,({\tau }_{1l}^{\tilde{\beta }\alpha }\circ {\tilde{\phi }}_{\beta }^{-1})\eta }^{\beta }+\cdots +{\tilde{g}}_{r,({\tau }_{rl}^{\tilde{\beta }\alpha }\circ {\tilde{\phi }}_{\beta }^{-1})\eta }^{\beta }.\hfill \end{array}$$

(7)

It follows from (5)–(7) that for all $\eta \in C_c^{\infty }[{\tilde{\phi }}_{\beta }(U_{\alpha }\cap {\tilde{U}}_{\beta })]$

$$\begin{array}{cc}\hfill ⟨[& H_{\alpha }({\tilde{\psi }}_{\beta }{\psi }_{\alpha }u){]}^l,\eta \circ {\tilde{\phi }}_{\beta }\circ {\phi }_{\alpha }^{-1}⟩=⟨{\tilde{\psi }}_{\beta }{\psi }_{\alpha }u,{[{\rho }_{\alpha }^{\vee }{|}_{E_x^{\vee }}]}^{-1}\circ [{\tilde{\rho }}_{\beta }^{\vee }{|}_{E_x^{\vee }}]\circ {\tilde{g}}_{l,\eta }^{\beta }⟩\hfill \\ \hfill & =⟨{\tilde{\psi }}_{\beta }{\psi }_{\alpha }u,\sum _{i=1}^r{\tilde{g}}_{i,({\tau }_{il}^{\tilde{\beta }\alpha }\circ {\tilde{\phi }}_{\beta }^{-1})\eta }^{\beta }⟩\hfill \\ \hfill & =\sum _{i=1}^r⟨{[{\tilde{H}}_{\beta }({\tilde{\psi }}_{\beta }{\psi }_{\alpha }u)]}^i,({\tau }_{il}^{\tilde{\beta }\alpha }\circ {\tilde{\phi }}_{\beta }^{-1})\eta ⟩\hfill \\ \hfill & =\sum _{i=1}^r⟨({\tau }_{il}^{\tilde{\beta }\alpha }\circ {\tilde{\phi }}_{\beta }^{-1}){[{\tilde{H}}_{\beta }({\tilde{\psi }}_{\beta }{\psi }_{\alpha }u)]}^i,\eta ⟩\hfill \\ \hfill & =\sum _{i=1}^r⟨({\tau }_{il}^{\tilde{\beta }\alpha }\circ {\tilde{\phi }}_{\beta }^{-1}){[{\tilde{H}}_{\beta }({\tilde{\psi }}_{\beta }{\psi }_{\alpha }u)]}^i,\eta \circ {\tilde{\phi }}_{\beta }\circ {\phi }_{\alpha }^{-1}\circ ({\phi }_{\alpha }\circ {\tilde{\phi }}_{\beta }^{-1})⟩\hfill \\ \hfill & =\sum _{i=1}^r⟨\frac{1}{\det ({\phi }_{\alpha }\circ {\tilde{\phi }}_{\beta }^{-1})}({\tau }_{il}^{\tilde{\beta }\alpha }\circ {\tilde{\phi }}_{\beta }^{-1}){[{\tilde{H}}_{\beta }({\tilde{\psi }}_{\beta }{\psi }_{\alpha }u)]}^i\circ {\tilde{\phi }}_{\beta }\circ {\phi }_{\alpha }^{-1},\eta \circ {\tilde{\phi }}_{\beta }\circ {\phi }_{\alpha }^{-1}⟩.\hfill \end{array}$$

For the last equality we used the following identity

$$⟨\frac{1}{\det T^{-1}}(u\circ T),\phi ⟩=⟨u,\phi \circ T^{-1}⟩.$$

Hence

$${[H_{\alpha }({\tilde{\psi }}_{\beta }{\psi }_{\alpha }u)]}^l=\sum _{i=1}^r\frac{1}{\det ({\phi }_{\alpha }\circ {\tilde{\phi }}_{\beta }^{-1})}({\tau }_{il}^{\tilde{\beta }\alpha }\circ {\tilde{\phi }}_{\beta }^{-1}){[{\tilde{H}}_{\beta }({\tilde{\psi }}_{\beta }{\psi }_{\alpha }u)]}^i\circ {\tilde{\phi }}_{\beta }\circ {\phi }_{\alpha }^{-1},$$

and consequently letting

$${(A_{\alpha \beta })}_{il}=\frac{1}{\det ({\phi }_{\alpha }\circ {\tilde{\phi }}_{\beta }^{-1})}({\tau }_{il}^{\tilde{\beta }\alpha }\circ {\tilde{\phi }}_{\beta }^{-1})$$

leads to (4). □

Remark 57.

Note that the above theorems establish the full independence of $W^{e,q}(M,E;\Lambda )$ from Λ at least when e is not a noninteger less than $-1$. So, it is justified to write $W^{e,q}(M,E)$ instead of $W^{e,q}(M,E;\Lambda )$ at least when e is not a noninteger less than $-1$. Additionally, see Remark 61.

9.2. The Properties

9.2.1. Multiplication Properties

Theorem 90.

Let $M^n$ be a compact smooth manifold and $E\to M$ be a vector bundle with rank r. Let $\Lambda ={\{(U_{\alpha },{\phi }_{\alpha },{\rho }_{\alpha },{\psi }_{\alpha })\}}_{1\le \alpha \le N}$ be an augmented total trivialization atlas for E. Suppose $e\in \mathbb{R}$, $q\in (1,\infty )$, $\eta \in C^{\infty }(M)$. If e is a noninteger less than $-1$, further assume that the total trivialization atlas of Λ is GGL. Then the linear map

$$m_{\eta }:W^{e,q}(M,E;\Lambda )\to W^{e,q}(M,E;\Lambda ),u\mapsto \eta u$$

is well-defined and bounded.

Proof. 

$$\begin{array}{cc}\hfill {\parallel \eta u\parallel }_{W^{e,q}(M,E;\Lambda )}:& =\sum _{\alpha =1}^N\sum _{l=1}^r{\parallel {(H_{\alpha }({\psi }_{\alpha }\eta u))}^l\parallel }_{W^{e,q}({\phi }_{\alpha }(U_{\alpha }))}\hfill \\ \hfill & \stackrel{\mathrm{Remark}31}{=}\sum _{\alpha =1}^N\sum _{l=1}^r{\parallel (\eta \circ {\phi }_{\alpha }^{-1}){(H_{\alpha }({\psi }_{\alpha }u))}^l\parallel }_{W^{e,q}({\phi }_{\alpha }(U_{\alpha }))}\hfill \\ \hfill & ⪯\sum _{\alpha =1}^N\sum _{l=1}^r\parallel {(H_{\alpha }({\psi }_{\alpha }u))}^l{\parallel }_{W^{e,q}({\phi }_{\alpha }(U_{\alpha }))}={\parallel u\parallel }_{W^{e,q}(M,E;\Lambda )}.\hfill \end{array}$$

For the case where e is not a noninteger less than $-1$, the last inequality follows from Theorem 70. If e is a noninteger less than $-1$, then by assumption ${\phi }_{\alpha }(U_{\alpha })$ is either entire ${\mathbb{R}}^n$ or is Lipschitz, and the last inequality is due to Theorem 51 and Corollary 4. □

Theorem 91.

Let $M^n$ be a compact smooth manifold and $E\to M$ be a vector bundle with rank r. Let Λ be an augmented total trivialization atlas for E. Let $s_1,s_2,s\in \mathbb{R}$ and $p_1,p_2,p\in (1,\infty )$. If any of $s_1$, $s_2$, or s is a noninteger less than $-1$, further assume that the total trivialization atlas of Λ is GL compatible with itself.

(1) 

If $s_1$, $s_2$, and s are not nonintegers less than $-1$, and if $W^{s_1,p_1}({\mathbb{R}}^n)\times W^{s_2,p_2}({\mathbb{R}}^n)\hookrightarrow W^{s,p}({\mathbb{R}}^n)$, then

$$W^{s_1,p_1}(M;\Lambda )\times W^{s_2,p_2}(M,E;\Lambda )\hookrightarrow W^{s,p}(M,E;\Lambda ).$$

(2) 

If $s_1$, $s_2$, and s are not nonintegers less than $-1$, and if $W^{s_1,p_1}(\Omega )\times W^{s_2,p_2}(\Omega )\hookrightarrow W^{s,p}(\Omega )$, for any open ball Ω, then

$$W^{s_1,p_1}(M;\Lambda )\times W^{s_2,p_2}(M,E;\Lambda )\hookrightarrow W^{s,p}(M,E;\Lambda ).$$

(3) 

If any of $s_1$, $s_2$, or s is a noninteger less than $-1$, and if $W^{s_1,p_1}(\Omega )\times W^{s_2,p_2}(\Omega )\hookrightarrow W^{s,p}(\Omega )$ for $\Omega ={\mathbb{R}}^n$ and for any bounded open set Ω with Lipschitz continuous boundary, then

$$W^{s_1,p_1}(M;\Lambda )\times W^{s_2,p_2}(M,E;\Lambda )\hookrightarrow W^{s,p}(M,E;\Lambda ).$$

Proof. 

(1)

Let ${\Lambda }_1={\{(U_{\alpha },{\phi }_{\alpha },{\rho }_{\alpha },{\psi }_{\alpha })\}}_{1\le \alpha \le N}$ be any augmented total trivialization atlas which is super nice. Let ${\Lambda }_2={\{(U_{\alpha },{\phi }_{\alpha },{\rho }_{\alpha },{\tilde{\psi }}_{\alpha })\}}_{1\le \alpha \le N}$ where for each $1\le \alpha \le N$, ${\tilde{\psi }}_{\alpha }=\frac{{\psi }_{\alpha }^2}{{\sum }_{\beta =1}^N{\psi }_{\beta }^2}$. Note that $\frac{1}{{\sum }_{\beta =1}^N{\psi }_{\beta }^2}\circ {\phi }_{\alpha }^{-1}\in B{C}^{\infty }({\phi }_{\alpha }(U_{\alpha }))$. For $f\in W^{s_1,p_1}(M;\Lambda )$ and $u\in W^{s_2,p_2}(M,E;\Lambda )$ we have

$$\begin{array}{cc}\hfill {\parallel fu\parallel }_{W^{s,p}(M,E;\Lambda )}& \simeq {\parallel fu\parallel }_{W^{s,p}(M,E;{\Lambda }_2)}=\sum _{\alpha =1}^N\sum _{j=1}^r{\parallel {[H_{\alpha }({\tilde{\psi }}_{\alpha }(fu))]}^j\parallel }_{W^{s,p}({\phi }_{\alpha }(U_{\alpha }))}\hfill \\ \hfill & ⪯\sum _{\alpha =1}^N\sum _{j=1}^r{\parallel (({\psi }_{\alpha }f)\circ {\phi }_{\alpha }^{-1}){[H_{\alpha }({\psi }_{\alpha }u)]}^j\parallel }_{W^{s,p}({\phi }_{\alpha }(U_{\alpha }))}\hfill \\ \hfill & ⪯\left(\sum _{\alpha =1}^N{\parallel ({\psi }_{\alpha }f)\circ {\phi }_{\alpha }^{-1}\parallel }_{W^{s_1,p_1}({\phi }_{\alpha }(U_{\alpha }))}\right)\left(\sum _{\alpha =1}^N\sum _{j=1}^r{\parallel {[H_{\alpha }({\psi }_{\alpha }u)]}^j\parallel }_{W^{s_2,p_2}({\phi }_{\alpha }(U_{\alpha }))}\right)\hfill \\ \hfill & ={\parallel f\parallel }_{W^{s_1,p_1}(M;{\Lambda }_1)}{\parallel u\parallel }_{W^{s_2,p_2}(M,E;{\Lambda }_1)}\simeq {\parallel f\parallel }_{W^{s_1,p_1}(M;\Lambda )}{\parallel u\parallel }_{W^{s_2,p_2}(M,E;\Lambda )}.\hfill \end{array}$$

(2)

We can use the exact same argument as item 1. Just choose ${\Lambda }_1$ to be “nice” instead of “super nice”.

(3)

The exact same argument as item 1 works. Just choose ${\Lambda }_1=\Lambda$. (The equality ${\parallel fu\parallel }_{W^{s,p}(M,E;\Lambda )}\simeq {\parallel fu\parallel }_{W^{s,p}(M,E;{\Lambda }_2)}$ holds due to the assumption that $\Lambda ={\Lambda }_1$ is GL compatible with itself.)

□

Remark 58.

Suppose e is a noninteger less than $-1$ and $q\in (1,\infty )$. We will prove that if Λ and $\tilde{\Lambda }$ are two augmented total trivialization atlases and each of Λ and $\tilde{\Lambda }$ is GL compatible with itself, then $W^{e,q}(M,E;\Lambda )=W^{e,q}(M,E;\tilde{\Lambda })$ (see Remark 61). Considering this and the fact that we can choose ${\Lambda }_1$ to be super nice (or nice) and GL compatible with itself (see Theorem 34 and Corollary 1), we can remove the assumption “$s_1$, $s_2$, and s are not nonintegers less than $-1$” from part 1 and part 2 of the preceding theorem.

9.2.2. Embedding Properties

Theorem 92.

Let $M^n$ be a compact smooth manifold. Let $\pi :E\to M$ be a smooth vector bundle of rank r over M. Let Λ be an augmented total trivialization atlas for E. Let $e_1,e_2\in \mathbb{R}$ and $q_1,q_2\in (1,\infty )$. If any of $e_1$ or $e_2$ is a noninteger less than $-1$, further assume that the total trivialization atlas in Λ is GGL.

(1) 

If $e_1$ and $e_2$ are not nonintegers less than $-1$ and if $W^{e_1,q_1}({\mathbb{R}}^n)\hookrightarrow W^{e_2,q_2}({\mathbb{R}}^n)$, then $W^{e_1,q_1}(M,E;\Lambda )\hookrightarrow W^{e_2,q_2}(M,E;\Lambda )$.

(2) 

If $e_1$ and $e_2$ are not nonintegers less than $-1$ and if $W^{e_1,q_1}(\Omega )\hookrightarrow W^{e_2,q_2}(\Omega )$ for all open balls $\Omega \subseteq {\mathbb{R}}^n$, then $W^{e_1,q_1}(M,E;\Lambda )\hookrightarrow W^{e_2,q_2}(M,E;\Lambda )$.

(3) 

If any of $e_1$ or $e_2$ is a noninteger less than $-1$ and if $W^{e_1,q_1}(\Omega )\hookrightarrow W^{e_2,q_2}(\Omega )$ for $\Omega ={\mathbb{R}}^n$ and for any bounded domain $\Omega \subseteq {\mathbb{R}}^n$ with Lipschitz continuous boundary, then $W^{e_1,q_1}(M,E;\Lambda )\hookrightarrow W^{e_2,q_2}(M,E;\Lambda )$.

Proof. 

(1)

Let ${\Lambda }_1={\{(U_{\alpha },{\phi }_{\alpha },{\rho }_{\alpha },{\psi }_{\alpha })\}}_{1\le \alpha \le N}$ be any augmented total trivialization atlas for E which is super nice. We have

$$\begin{array}{cc}\hfill {\parallel u\parallel }_{W^{e_2,q_2}(M,E;\Lambda )}& \simeq {\parallel u\parallel }_{W^{e_2,q_2}(M,E;{\Lambda }_1)}=\sum _{\alpha =1}^N\sum _{l=1}^r{\parallel {[H_{\alpha }({\psi }_{\alpha }u)]}^l\parallel }_{W^{e_2,q_2}({\phi }_{\alpha }(U_{\alpha }))}\hfill \\ \hfill & ⪯\sum _{\alpha =1}^N\sum _{l=1}^r{\parallel {[H_{\alpha }({\psi }_{\alpha }u)]}^l\parallel }_{W^{e_1,q_1}({\phi }_{\alpha }(U_{\alpha }))}\hfill \\ \hfill & ={\parallel u\parallel }_{W^{e_1,q_1}(M,E;{\Lambda }_1)}\simeq {\parallel u\parallel }_{W^{e_1,q_1}(M,E;\Lambda )}.\hfill \end{array}$$

(2)

We can use the exact same argument as item 1. Just choose ${\Lambda }_1$ to be “nice” instead of “super nice”.

(3)

The exact same argument as item 1 works. Just choose ${\Lambda }_1=\Lambda$.

□

Remark 59.

If we further assume that Λ is GL compatible with itself, then we can remove the assumption “$e_1$ and $e_2$ are not nonintegers less than $-1$” from part 1 and part 2 of the preceding theorem. (see the explanation in Remark 58).

Theorem 93.

Let $M^n$ be a compact smooth manifold. Let $\pi :E\to M$ be a smooth vector bundle of rank r over M equipped with fiber metric ${⟨.,.⟩}_E$ (so it is meaningful to talk about $L^{\infty }(M,E)$). Suppose $s\in \mathbb{R}$ and $p\in (1,\infty )$ are such that $sp>n$. Then $W^{s,p}(M,E)\hookrightarrow L^{\infty }(M,E)$. Moreover, every element u in $W^{s,p}(M,E)$ has a continuous version (note that since s is not a noninteger less than $-1$, the choice of the augmented total trivialization atlas is immaterial).

Proof. 

Let ${\{(U_{\alpha },{\phi }_{\alpha },{\rho }_{\alpha })\}}_{1\le \alpha \le N}$ be a nice total trivialization atlas for $E\to M$ that trivializes the fiber metric. Let ${\{{\psi }_{\alpha }\}}_{1\le \alpha \le N}$ be a partition of unity subordinate to $\{U_{\alpha }\}$. We need to show that for every $u\in W^{s,p}(M,E)$

$${|u|}_{L^{\infty }(M,E)}⪯{\parallel u\parallel }_{W^{s,p}(M,E)}.$$

Note that since $s>0$, $W^{s,p}(M,E)\hookrightarrow L^p(M,E)$ and we can treat u as an ordinary section of E. We prove the above inequality in two steps:

•

Step 1: Suppose there exists $1\le \beta \le N$ such that $\mathrm{supp}u\subseteq U_{\beta }$. We have

$$\begin{array}{cc}\hfill {|u|}_{L^{\infty }(M,E)}& =\underset{x\in M}{ess\; sup}{|u|}_E=\underset{x\in U_{\beta }}{ess\; sup}{|u|}_E\hfill \\ \hfill & =\underset{y\in {\phi }_{\beta }(U_{\beta })}{ess\; sup}\sqrt{{\sum }_{l=1}^r{|{\rho }_{\beta }^l\circ u\circ {\phi }_{\beta }^{-1}|}^2}(\mathrm{by} \mathrm{assumption} \mathrm{the} \mathrm{triples} \mathrm{trivialize} \mathrm{the} \mathrm{metric})\hfill \\ \hfill & \le \underset{y\in {\phi }_{\beta }(U_{\beta })}{ess\; sup}\sum _{l=1}^r|{\rho }_{\beta }^l\circ u\circ {\phi }_{\beta }^{-1}|\le \sum _{l=1}^r\underset{y\in {\phi }_{\beta }(U_{\beta })}{ess\; sup}|{\rho }_{\beta }^l\circ u\circ {\phi }_{\beta }^{-1}|\hfill \\ \hfill & =\sum _{l=1}^r{\parallel {\rho }_{\beta }^l\circ u\circ {\phi }_{\beta }^{-1}\parallel }_{L^{\infty }({\phi }_{\beta }(U_{\beta }))}\hfill \\ \hfill & ⪯\sum _{l=1}^r{\parallel {\rho }_{\beta }^l\circ u\circ {\phi }_{\beta }^{-1}\parallel }_{W^{s,p}({\phi }_{\beta }(U_{\beta }))}(\mathit{sp}>n\mathrm{so}{W}^{s,p}({\phi }_{\beta }(U_{\beta }))\hookrightarrow L^{\infty }({\phi }_{\beta }(U_{\beta }))).\hfill \end{array}$$

•

Step 2: Now, suppose u is an arbitrary element of $W^{s,p}(M,E)$. We have

$$\begin{array}{cc}\hfill {|u|}_{L^{\infty }(M,E)}& =|\sum _{\alpha =1}^N{\psi }_{\alpha }{u|}_{L^{\infty }(M,E)}\le \sum _{\alpha =1}^N{|{\psi }_{\alpha }u|}_{L^{\infty }(M,E)}\hfill \\ \hfill & \stackrel{\mathrm{Step}1}{⪯}\sum _{\alpha =1}^N\sum _{l=1}^r\parallel {\rho }_{\alpha }^l\circ {\psi }_{\alpha }u\circ {\phi }_{\alpha }^{-1}{\parallel }_{W^{s,p}({\phi }_{\alpha }(U_{\alpha }))}\simeq {\parallel u\parallel }_{W^{s,p}(M,E)}.\hfill \end{array}$$

Next we prove that every element u of $W^{s,p}(M,E)$ has a continuous version. Note that for all $x\in U_{\alpha }$

$${\psi }_{\alpha }u(x)={\Phi }_{\alpha }^{-1}(x,{\rho }_{\alpha }^1\circ {\psi }_{\alpha }u,\dots ,{\rho }_{\alpha }^r\circ {\psi }_{\alpha }u).$$

Furthermore, for all $1\le l\le r$ and $1\le \alpha \le N$ we have

$${\rho }_{\alpha }^l\circ {\psi }_{\alpha }u\circ {\phi }_{\alpha }^{-1}\in W^{s,p}({\phi }_{\alpha }(U_{\alpha })).$$

Therefore, ${\rho }_{\alpha }^l\circ {\psi }_{\alpha }u\circ {\phi }_{\alpha }^{-1}$ has a continuous version which we denote by $v_{\alpha }^l$. Suppose $A_{\alpha }^l$ is the set of measure zero on which $v_{\alpha }^l\ne {\rho }_{\alpha }^l\circ {\psi }_{\alpha }u\circ {\phi }_{\alpha }^{-1}$. Let $A_{\alpha }={\cup }_{1\le l\le r}{A}_{\alpha }^l$. Clearly, $A_{\alpha }$ is a set of measure zero. Since ${\phi }_{\alpha }:U_{\alpha }\to {\phi }_{\alpha }(U_{\alpha })$ is a diffeomorphism, $B_{\alpha }:={\phi }_{\alpha }^{-1}(A_{\alpha })$ is a set of measure zero in $U_{\alpha }$ (In general, if M and N are smooth n-manifolds, $F:M\to N$ is a smooth map, and $A\subseteq M$ is a subset of measure zero, then $F(A)$ has measure zero in N. See p. 128 in [19]).

Clearly,

$$(x,v_{\alpha }^1\circ {\phi }_{\alpha },\dots ,v_{\alpha }^r\circ {\phi }_{\alpha })=(x,{\rho }_{\alpha }^1\circ {\psi }_{\alpha }u,\dots ,{\rho }_{\alpha }^r\circ {\psi }_{\alpha }u).$$

on $U_{\alpha }\backslash B_{\alpha }$. So,

$$w_{\alpha }:={\Phi }_{\alpha }^{-1}(x,v_{\alpha }^1\circ {\phi }_{\alpha },\dots ,v_{\alpha }^r\circ {\phi }_{\alpha })={\Phi }_{\alpha }^{-1}(x,{\rho }_{\alpha }^1\circ {\psi }_{\alpha }u,\dots ,{\rho }_{\alpha }^r\circ {\psi }_{\alpha }u)={\psi }_{\alpha }u$$

on $U_{\alpha }\backslash B_{\alpha }$. Note that $w_{\alpha }:U_{\alpha }\to E$ is a composition of continuous functions and so it is continuous on $U_{\alpha }$. Let ${\xi }_{\alpha }\in C_c^{\infty }(U_{\alpha })$ be such that ${\xi }_{\alpha }=1$ on $\mathrm{supp}{\psi }_{\alpha }$. So ${\xi }_{\alpha }{w}_{\alpha }={\psi }_{\alpha }u$ on $M\backslash B_{\alpha }$. Consequently, if we let $w={\sum }_{\alpha =1}^N{\xi }_{\alpha }{w}_{\alpha }$, then w is a continuous function that agrees with $u={\sum }_{\alpha =1}^N{\psi }_{\alpha }u$ on $M\backslash B$ where $B={\cup }_{1\le \alpha \le N}{B}_{\alpha }$. □

9.2.3. Observations concerning the Local Representation of Sobolev Functions

Let $M^n$ be a compact smooth manifold. Let $E\to M$ be a smooth vector bundle of rank r over M. As it was discussed in Section 6, given a total trivialization triple $(U_{\alpha },{\phi }_{\alpha },{\rho }_{\alpha })$, we can associate with every $u\in D^{\prime }(M,E)$ and every $f\in \Gamma (M,E)$, a local representation with respect to $(U_{\alpha },{\phi }_{\alpha },{\rho }_{\alpha })$:

$$\begin{array}{cc}\hfill & u\mapsto ({\tilde{u}}^1,\dots ,{\tilde{u}}^r)\in {[D^{\prime }({\phi }_{\alpha }(U_{\alpha }))]}^{\times r},{\tilde{u}}^l={[H_{\alpha }(u{|}_{U_{\alpha }})]}^l,\hfill \\ \hfill & f\mapsto ({\tilde{f}}^1,\dots ,{\tilde{f}}^r)\in {[\mathrm{Func}({\phi }_{\alpha }(U_{\alpha }),\mathbb{R})]}^{\times r},{\tilde{f}}^l={\rho }_{\alpha }^l\circ (f{|}_{U_{\alpha }})\circ {\phi }_{\alpha }^{-1},\hfill \end{array}$$

and of course, as it was pointed out in Remark 32, the two representations agree when u is a regular distribution. The goal of this section is to list some useful facts about the local representations of elements of Sobolev spaces. In what follows, when there is no possibility of confusion, we may write $H_{\alpha }(u)$ instead of $H_{\alpha }(u{|}_{U_{\alpha }})$, or ${\rho }_{\alpha }^l\circ f\circ {\phi }_{\alpha }^{-1}$ instead of ${\rho }_{\alpha }^l\circ (f{|}_{U_{\alpha }})\circ {\phi }_{\alpha }^{-1}$.

Theorem 94.

Let $M^n$ be a compact smooth manifold and $E\to M$ be a vector bundle of rank r. Suppose $\Lambda ={\{(U_{\alpha },{\phi }_{\alpha },{\rho }_{\alpha },{\psi }_{\alpha })\}}_{\alpha =1}^N$ is an augmented total trivialization atlas for $E\to M$. Let $u\in D^{\prime }(M,E)$, $e\in \mathbb{R}$, and $q\in (1,\infty )$. If for all $1\le \alpha \le N$ and $1\le j\le r$, ${[H_{\alpha }(u)]}^j\in W_{loc}^{e,q}({\phi }_{\alpha }(U_{\alpha }))$, then $u\in W^{e,q}(M,E;\Lambda )$.

Proof. 

$$\begin{array}{cc}\hfill {\parallel u\parallel }_{W^{e,q}(M,E;\Lambda )}& =\sum _{\alpha =1}^N\sum _{j=1}^r{\parallel {[H_{\alpha }({\psi }_{\alpha }u)]}^j\parallel }_{W^{e,q}({\phi }_{\alpha }(U_{\alpha }))}\hfill \\ \hfill & =\sum _{\alpha =1}^N\sum _{j=1}^r{\parallel ({\psi }_{\alpha }\circ {\phi }_{\alpha }^{-1})·({[H_{\alpha }(u)]}^j)\parallel }_{W^{e,q}({\phi }_{\alpha }(U_{\alpha }))}.\hfill \end{array}$$

Now, note that ${\psi }_{\alpha }\circ {\phi }_{\alpha }^{-1}:{\phi }_{\alpha }(U_{\alpha })\to \mathbb{R}$ is smooth with compact support (its support is in the compact set ${\phi }_{\alpha }(\mathrm{supp}{\psi }_{\alpha })$). Therefore, it follows from the assumption that each term on the right hand side of the above equality is finite. □

Remark 60.

Note that, as opposed to what is claimed in some references, it is NOT true in general that if $u\in W^{e,q}(M,E;\Lambda )$, then the components of the local representations of u will be in the corresponding Euclidean Sobolev space; that is, $u\in W^{e,q}(M,E;\Lambda )$ does not imply that for all $1\le \alpha \le N$ and $1\le j\le r$, ${[H_{\alpha }(u)]}^j\in W^{e,q}({\phi }_{\alpha }(U_{\alpha }))$. Consider the following example:

$M=S^1$, $e=0$, $q=1$, and $f:M\to \mathbb{R}$ defined by $f\equiv 1$. Clearly $f\in W^{0,1}(M)=L^1(S^1)$. Now, consider the atlas $\mathcal{A}=\{(U_1,{\phi }_1),(U_2,{\phi }_2)\}$ where

$$\begin{array}{cc}\hfill & U_1=S^1\backslash \{(0,1)\},{\phi }_1(x,y)=\frac{x}{1-y},\hfill \\ \hfill & U_2=S^1\backslash \{(0,-1)\},{\phi }_2(x,y)=\frac{x}{1+y}(\mathit{stereographic} \mathit{projection}).\hfill \end{array}$$

Clearly, $f\circ {\phi }_1^{-1}=f\circ {\phi }_2^{-1}=1$ and ${\phi }_1(U_1)={\phi }_2(U_2)=\mathbb{R}$. So, $f\circ {\phi }_1^{-1}$ and $f\circ {\phi }_2^{-1}$ do not belong to $L^1({\phi }_1(U_1))$ or $L^1({\phi }_2(U_2))$.

However, the following theorem holds true.

Theorem 95.

Let $M^n$ be a compact smooth manifold and $E\to M$ be a vector bundle of rank r. Let $e\in \mathbb{R}$ and $q\in (1,\infty )$. Suppose $\Lambda ={\{(U_{\alpha },{\phi }_{\alpha },{\rho }_{\alpha },{\psi }_{\alpha })\}}_{\alpha =1}^N$ is an augmented total trivialization atlas for $E\to M$. If e is a noninteger less than $-1$ further assume that Λ is GL compatible with itself. Let $u\in W^{e,q}(M,E;\Lambda )$ be such that $\mathrm{supp}u\subseteq V\subseteq \overline{V}\subseteq U_{\beta }$ for some open set V and some $1\le \beta \le N$. Then for all $1\le i\le r$, ${[H_{\beta }(u)]}^i\in W^{e,q}({\phi }_{\beta }(U_{\beta }))$. Indeed,

$$\parallel {[H_{\beta }(u)]}^i{\parallel }_{W^{e,q}({\phi }_{\beta }(U_{\beta }))}\le {\parallel u\parallel }_{W^{e,q}(M,E;\Lambda )}.$$

Proof. 

Let ${\Lambda }_1={\{(U_{\alpha },{\phi }_{\alpha },{\rho }_{\alpha },{\tilde{\psi }}_{\alpha })\}}_{\alpha =1}^N$ where ${\{{\tilde{\psi }}_{\alpha }\}}_{1\le \alpha \le N}$ is a partition of unity subordinate to the cover ${\{U_{\alpha }\}}_{1\le \alpha \le N}$ such that ${\tilde{\psi }}_{\beta }=1$ on a neighborhood of $\overline{V}$ (see Lemma 3). We have

$$\begin{array}{cc}\hfill \parallel {[H_{\beta }(u)]}^i{\parallel }_{W^{e,q}({\phi }_{\beta }(U_{\beta }))}& =\parallel {[H_{\beta }({\tilde{\psi }}_{\beta }u)]}^i{\parallel }_{W^{e,q}({\phi }_{\beta }(U_{\beta }))}\hfill \\ \hfill & \le \sum _{\alpha =1}^N\sum _{j=1}^r{\parallel {[H_{\alpha }({\tilde{\psi }}_{\alpha }u)]}^j\parallel }_{W^{e,q}({\phi }_{\alpha }(U_{\alpha }))}\hfill \\ \hfill & ={\parallel u\parallel }_{W^{e,q}(M,E;{\Lambda }_1)}\simeq {\parallel u\parallel }_{W^{e,q}(M,E;\Lambda )}.\hfill \end{array}$$

□

Corollary 8.

Let $M^n$ be a compact smooth manifold and $E\to M$ be a vector bundle of rank r. Let $e\in \mathbb{R}$ and $q\in (1,\infty )$. Suppose $\Lambda ={\{(U_{\alpha },{\phi }_{\alpha },{\rho }_{\alpha },{\psi }_{\alpha })\}}_{\alpha =1}^N$ is an augmented total trivialization atlas for $E\to M$. If e is a noninteger less than $-1$ further assume that Λ is GL compatible with itself. If $u\in W^{e,q}(M,E;\Lambda )$, then for all $1\le \alpha \le N$ and $1\le i\le r$, ${[H_{\alpha }(u)]}^i$ (i.e., each component of the local representation of u with respect to $(U_{\alpha },{\phi }_{\alpha },{\rho }_{\alpha })$) belongs to $W_{loc}^{e,q}({\phi }_{\alpha }(U_{\alpha }))$. Moreover, if $\xi \in C_c^{\infty }({\phi }_{\alpha }(U_{\alpha }))$, then

$$\parallel \xi {[H_{\alpha }(u)]}^i{\parallel }_{W^{e,q}({\phi }_{\alpha }(U_{\alpha }))}⪯{\parallel u\parallel }_{W^{e,q}(M,E;\Lambda )},$$

where the implicit constant may depend on ξ.

Proof. 

Define $G:M\to \mathbb{R}$ by

$$G(p)=\left\{\begin{array}{cc}\hfill \xi \circ {\phi }_{\alpha }\hfill & \mathrm{if}p\in U_{\alpha }\hfill \\ \hfill 0\hfill & \mathrm{if}p\notin U_{\alpha }\hfill \end{array}\right..$$

Clearly, $G\in C^{\infty }(M)$. So, by Theorem 90, $Gu\in W^{e,q}(M,E;\Lambda )$. Furthermore, since $\xi \in C_c^{\infty }({\phi }_{\alpha }(U_{\alpha }))$, there exists a compact set K such that

$$\mathrm{supp}\xi \subseteq \mathring{K}\subseteq K\subseteq {\phi }_{\alpha }(U_{\alpha }).$$

Consequently, there exists an open set $V_{\alpha }$ (e.g., $V_{\alpha }={\phi }_{\alpha }^{-1}(\mathring{K})$) such that

$$\mathrm{supp}(Gu)\subseteq \mathrm{supp}(\xi \circ {\phi }_{\alpha })\subseteq V_{\alpha }\subseteq {\overline{V}}_{\alpha }\subseteq U_{\alpha }.$$

So, by Theorem 95, ${[H_{\alpha }(Gu)]}^i\in W^{e,q}({\phi }_{\alpha }(U_{\alpha }))$ and

$$\begin{array}{c}\hfill \parallel {[H_{\alpha }(Gu)]}^i{\parallel }_{W^{e,q}({\phi }_{\alpha }(U_{\alpha }))}⪯{\parallel Gu\parallel }_{W^{e,q}(M,E;\Lambda )}⪯{\parallel u\parallel }_{W^{e,q}(M,E;\Lambda )}.\end{array}$$

Now, we just need to notice that on ${\phi }_{\alpha }(U_{\alpha })$,

$${[H_{\alpha }(Gu)]}^i=(G\circ {\phi }_{\alpha }^{-1}){[H_{\alpha }(u)]}^i=\xi {[H_{\alpha }(u)]}^i.$$

□

9.2.4. Observations concerning the Riemannian Metric

The Sobolev spaces that appear in this section all have nonnegative smoothness exponents; therefore, the choice of the augmented total trivialization atlas is immaterial and will not appear in the notation.

Corollary 9.

Let $(M^n,g)$ be a compact Riemannian manifold with $g\in W^{s,p}(T^{2}M)$, $sp>n$. Let ${\{(U_{\alpha },{\phi }_{\alpha },{\rho }_{\alpha })\}}_{1\le \alpha \le N}$ be a standard total trivialization atlas for $T^{2}M\to M$. Fix some α and denote the components of the metric with respect to $(U_{\alpha },{\phi }_{\alpha },{\rho }_{\alpha })$ by $g_{ij}:U_{\alpha }\to \mathbb{R}$ $(g_{ij}={({\rho }_{\alpha })}_{ij}\circ g)$. As an immediate consequence of Corollary 8 we have

$$\begin{array}{c}\hfill g_{ij}\circ {\phi }_{\alpha }^{-1}\in W_{loc}^{s,p}({\phi }_{\alpha }(U_{\alpha })).\end{array}$$

Theorem 96.

Let $(M^n,g)$ be a compact Riemannian manifold with $g\in W^{s,p}(T^{2}M)$, $sp>n$, $s\ge 1$. Let ${\{(U_{\alpha },{\phi }_{\alpha },{\rho }_{\alpha })\}}_{1\le \alpha \le N}$ be a GGL standard total trivialization atlas for $T^{2}M\to M$. Fix some α and denote the components of the metric with respect to $(U_{\alpha },{\phi }_{\alpha },{\rho }_{\alpha })$ by $g_{ij}:U_{\alpha }\to \mathbb{R}$ $(g_{ij}={({\rho }_{\alpha })}_{ij}\circ g)$. Then

(1) 

$\det g_{\alpha }\in W_{loc}^{s,p}({\phi }_{\alpha }(U_{\alpha }))$ where $g_{\alpha }(x)$ is the matrix whose $(i,j)$-entry is $g_{ij}\circ {\phi }_{\alpha }^{-1}$,

(2) 

$\sqrt{\det g}\circ {\phi }_{\alpha }^{-1}=\sqrt{\det g_{\alpha }}\in W_{loc}^{s,p}({\phi }_{\alpha }(U_{\alpha }))$,

(3) 

$\frac{1}{\sqrt{\det g}\circ {\phi }_{\alpha }^{-1}}\in W_{loc}^{s,p}({\phi }_{\alpha }(U_{\alpha }))$.

Proof. 

(1)

By Corollary 8, $g_{ij}\circ {\phi }_{\alpha }^{-1}$ is in $W_{loc}^{s,p}({\phi }_{\alpha }(U_{\alpha }))$. So, it follows from Lemma 10 that $\det g_{\alpha }\in W_{loc}^{s,p}({\phi }_{\alpha }(U_{\alpha }))$.

(2)

This is a direct consequence of item 1 and Theorem 85.

(3)

This is a direct consequence of item 1 and Theorem 85.

□

Theorem 97.

Let $(M^n,g)$ be a compact Riemannian manifold with $g\in W^{s,p}(T^{2}M)$, $sp>n$, $s\ge 1$. Then the inverse metric tensor $g^{-1}$ (which is a $\left(\genfrac{}{}{0pt}{}{0}{2}\right)$ tensor field) is in $W^{s,p}(T_{2}M)$.

Proof. 

Let ${\{(U_{\alpha },{\phi }_{\alpha },{\rho }_{\alpha })\}}_{1\le \alpha \le N}$ be a GGL standard total trivialization atlas for $T^{2}M\to M$. Let ${\{{\psi }_{\alpha }\}}_{1\le \alpha \le N}$ be a partition of unity subordinate to ${\{U_{\alpha }\}}_{1\le \alpha \le N}$. We have

$$\parallel g^{-1}{\parallel }_{W^{s,p}(T_{2}M)}=\sum _{\alpha =1}^N\sum _{i,j}{\parallel {\psi }_{\alpha }{g}^{ij}\circ {\phi }_{\alpha }^{-1}\parallel }_{W^{s,p}({\phi }_{\alpha }(U_{\alpha }))}.$$

So, it is enough to show that for all $i,j$ and $\alpha$, $g^{ij}\circ {\phi }_{\alpha }^{-1}$ is in $W_{loc}^{s,p}({\phi }_{\alpha }(U_{\alpha }))$. Let $B=(B_{ij})$ where $B_{ij}=g_{ij}\circ {\phi }_{\alpha }^{-1}$. By assumption, $g\in W^{s,p}(T^{2}M)$; it follows from Corollary 8 that $B_{ij}\in W_{loc}^{s,p}({\phi }_{\alpha }(U_{\alpha }))$. Our goal is to show that the entries of the inverse of B are in $W_{loc}^{s,p}({\phi }_{\alpha }(U_{\alpha }))$. Recall that

$${(B^{-1})}_{ij}=\frac{{(-1)}^{i+j}}{\det B}{M}_{ij},$$

where $M_{ij}$ is the determinant of the $(n-1)\times (n-1)$ matrix formed by removing the jth row and ith column of B. Since the entries of B are in $W_{loc}^{s,p}({\phi }_{\alpha }(U_{\alpha }))$, it follows from Lemma 10 and Theorem 85 that $\frac{1}{\det B}$ and $M_{ij}$ are in $W_{loc}^{s,p}({\phi }_{\alpha }(U_{\alpha }))$. Furthermore, $sp>n$, so $W_{loc}^{s,p}({\phi }_{\alpha }(U_{\alpha }))$ is closed under multiplication. Consequently, ${(B^{-1})}_{ij}$ is in $W_{loc}^{s,p}({\phi }_{\alpha }(U_{\alpha }))$. □

Corollary 10.

Let $(M^n,g)$ be a compact Riemannian manifold with $g\in W^{s,p}(T^{2}M)$, $sp>n$, $s\ge 1$. ${\{(U_{\alpha },{\phi }_{\alpha })\}}_{1\le \alpha \le N}$ be a GGL smooth atlas for M. Denote the standard components of the inverse metric with respect to this chart by $g^{ij}:U_{\alpha }\to \mathbb{R}$. As an immediate consequence of Theorem 97 and Corollary 8 we have

$$\begin{array}{c}\hfill g^{ij}\circ {\phi }_{\alpha }^{-1}\in W_{loc}^{s,p}({\phi }_{\alpha }(U_{\alpha })).\end{array}$$

Furthermore, since

$$\begin{array}{c}\hfill {\Gamma }_{ij}^k\circ {\phi }_{\alpha }^{-1}=\frac{1}{2}{g}^{kl}({\partial }_i{g}_{jl}+{\partial }_j{g}_{il}-{\partial }_l{g}_{ij})\circ {\phi }_{\alpha }^{-1},\end{array}$$

it follows from Corollary 9, Lemma 9, Theorem 83, and the fact that $W^{s,p}({\phi }_{\alpha }(U_{\alpha }))\times W^{s-1,p}({\phi }_{\alpha }(U_{\alpha }))\hookrightarrow W^{s-1,p}({\phi }_{\alpha }(U_{\alpha }))$ that

$${\Gamma }_{ij}^k\circ {\phi }_{\alpha }^{-1}\in W_{loc}^{s-1,p}({\phi }_{\alpha }(U_{\alpha })).$$

9.2.5. A Useful Isomorphism

Let $M^n$ be a compact smooth manifold and $E\to M$ be a vector bundle of rank r. Let $e\in \mathbb{R}$ and $q\in (1,\infty )$. Suppose $\Lambda ={\{(U_{\alpha },{\phi }_{\alpha },{\rho }_{\alpha },{\psi }_{\alpha })\}}_{\alpha =1}^N$ is an augmented total trivialization atlas for $E\to M$. Given a closed subset $A\subseteq M$, $W_A^{e,q}(M,E;\Lambda )$ is defined to be the subspace of $W^{e,q}(M,E;\Lambda )$ consisting of $u\in W^{e,q}(M,E;\Lambda )$ with $\mathrm{supp}u\subseteq A$. Fix $1\le \beta \le N$ and suppose $K\subseteq U_{\beta }$ is compact. Then each element of $W_K^{e,q}(M,E;\Lambda )$ can be identified with an element of $D^{\prime }(U_{\beta },E_{U_{\beta }})$ under the injective map $u\in W_K^{e,q}(M,E;\Lambda )\subseteq D^{\prime }{(M,E)\mapsto u|}_U\in D^{\prime }(U_{\beta },E_{U_{\beta }})$. So, we can restrict the domain of $H_{\beta }:{[D(U_{\beta },E_{U_{\beta }}^{\vee })]}^{*}\to {(D^{\prime }({\phi }_{\beta }(U_{\beta })))}^{\times r}$ to $W_K^{e,q}(M,E;\Lambda )$ which associates with each element $u\in W_K^{e,q}(M,E;\Lambda )$, the r components of $H_{\beta }(u)=({\tilde{u}}_{\beta }^1,\cdots ,{\tilde{u}}_{\beta }^r)$ (here $H_{\beta }$ stands for $H_{E^{\vee },U_{\beta },{\phi }_{\beta }}$).

Lemma 11.

Consider the above setting and further assume that if e is a noninteger less than $-1$, then the total trivialization atlas in Λ is GL compatible with itself. Then the linear topological isomorphism $H_{\beta }:{[D(U_{\beta },E_{U_{\beta }}^{\vee })]}^{*}=D^{\prime }(U_{\beta },E_{U_{\beta }})\to {(D^{\prime }({\phi }_{\beta }(U_{\beta })))}^{\times r}$ restricts to a linear topological isomorphism

$${\widehat{H}}_{\beta }:W_K^{e,q}(M,E;\Lambda )\to {[W_{{\phi }_{\beta }(K)}^{e,q}({\phi }_{\beta }(U_{\beta }))]}^{\times r}.$$

Proof. 

In order to simplify the notation we will use $(U,\phi ,\rho )$, H, $\widehat{H}$, and ${\tilde{u}}^l$ instead of $(U_{\beta },{\phi }_{\beta },{\rho }_{\beta })$, $H_{\beta }$, ${\widehat{H}}_{\beta }$, and ${\tilde{u}}_{\beta }^l$. In order to prove this claim, we proceed as follows:

(1)

First we show that $\mathrm{supp}{\tilde{u}}^l\subseteq \phi (K)$.

(2)

Next we show that if $u\in W_K^{e,q}(M,E;\Lambda )$, then ${\parallel u\parallel }_{W^{e,q}(M,E;\Lambda )}\simeq {\sum }_{l=1}^r{\parallel {\tilde{u}}^l\parallel }_{W^{e,q}(\phi (U))}$ which proves that:

(i)

${\tilde{u}}^l$ is indeed an element of $W^{e,q}(\phi (U))$;

(ii)

$\widehat{H}$ is continuous.

Note that (i) together with the fact that $\mathrm{supp}{\tilde{u}}^l\subseteq \phi (K)$ shows that ${\tilde{u}}^l$ is indeed an element of $W_{\phi (K)}^{e,q}(\phi (U))$ so $\widehat{H}$ is well-defined.

(3)

We prove that $\widehat{H}$ is injective.

(4)

In order to prove that $\widehat{H}$ is surjective we use our explicit formula for $H^{-1}$ (see Remark 31).

Note that the fact that $\widehat{H}$ is bijective combined with the equality ${\parallel u\parallel }_{W^{e,q}(M,E;\Lambda )}\simeq {\sum }_{l=1}^r{\parallel {\tilde{u}}^l\parallel }_{W^{e,q}(\phi (U))}$ implies that ${\widehat{H}}^{-1}$ is continuous as well.

Here are the proofs:

(1)

This item is a direct consequence of item 1 in Remark 31.

(2)

Define the augmented total trivialization atlas ${\Lambda }_1$ by ${\Lambda }_1={\{(U_{\alpha },{\phi }_{\alpha },{\rho }_{\alpha },{\tilde{\psi }}_{\alpha })\}}_{\alpha =1}^N$ where ${\{{\tilde{\psi }}_{\alpha }\}}_{1\le \alpha \le N}$ is a partition of unity subordinate to ${\{U_{\alpha }\}}_{1\le \alpha \le N}$ such that ${\tilde{\psi }}_{\beta }=1$ on a neighborhood of K. Note that for each $\alpha$, ${\tilde{\psi }}_{\alpha }\ge 0$ and ${\sum }_{\alpha =1}^N{\tilde{\psi }}_{\alpha }=1$. Thus, the assumption ${\tilde{\psi }}_{\beta }=1$ on K implies that ${\tilde{\psi }}_{\alpha }=0$ on K for all $\alpha \ne \beta$. We have

$$\begin{array}{cc}\hfill {\parallel u\parallel }_{W^{e,q}(M,E;\Lambda )}& \simeq {\parallel u\parallel }_{W^{e,q}(M,E;{\Lambda }_1)}\simeq \sum _{\alpha =1}^N\sum _{l=1}^r{\parallel {(H_{\alpha }({\tilde{\psi }}_{\alpha }u))}^l\parallel }_{W^{e,q}({\phi }_{\alpha }(U_{\alpha }))}\hfill \\ \hfill & =\sum _{l=1}^r\parallel {(H({\tilde{\psi }}_{\beta }u))}^l{\parallel }_{W^{e,q}({\phi }_{\alpha }(U_{\alpha }))}=\sum _{l=1}^r{\parallel {[H(u)]}^l\parallel }_{W^{e,q}({\phi }_{\alpha }(U_{\alpha }))}.\hfill \end{array}$$

Note that $\mathrm{supp}u\subseteq K$ and ${\tilde{\psi }}_{\beta }=1$ on K, so ${\tilde{\psi }}_{\beta }{u=u|}_U$ as elements of $D^{\prime }(U,E_U)$. Therefore, $H({\tilde{\psi }}_{\beta }u)=H(u)=({\tilde{u}}^1,\dots ,{\tilde{u}}^r)$.

(3)

$\widehat{H}$ is injective because it is a restriction of the injective map H.

(4)

Let $(v^1,\dots ,v^r)\in {[W_{\phi (K)}^{e,q}(\phi (U))]}^{\times r}$. Our goal is to show that $H^{-1}(v^1,\dots ,v^r)\in W_K^{e,q}(M,E;\Lambda )\simeq W_K^{e,q}(M,E;{\Lambda }_1)$ (this implies that $\widehat{H}$ is surjective). By Remark 31, for all $\xi \in D(U,E_U^{\vee })$

$$\begin{array}{c}\hfill H^{-1}(v^1,\dots ,v^r)(\xi )=\sum _i{v}^i[{({\rho }^{\vee })}^i\circ \xi \circ {\phi }^{-1}].\end{array}$$

First note it follows from Remark 30 that $\mathrm{supp}{H}^{-1}(v^1,\dots ,v^r)\subseteq K$; indeed, if $\mathrm{supp}\xi \subseteq U\backslash K$, then $\xi \circ {\phi }^{-1}=0$ on $\phi (K)$. So, ${({\rho }^{\vee })}^i\circ \xi \circ {\phi }^{-1}=0$ on $\phi (K)$. That is, $\mathrm{supp}[{({\rho }^{\vee })}^i\circ \xi \circ {\phi }^{-1}]\subseteq \phi (U)\backslash \phi (K)$. Thus, for all i, $v^i[{({\rho }^{\vee })}^i\circ \xi \circ {\phi }^{-1}]=0$ (because, by assumption, $\mathrm{supp}{v}^i\subseteq \phi (K)$). This shows that if $\mathrm{supp}\xi \subseteq U\backslash K$, then $H^{-1}(v^1,\dots ,v^r)(\xi )=0$. Consequently, $\mathrm{supp}{H}^{-1}(v^1,\dots ,v^r)\subseteq K$.

Furthermore, we have

$$\parallel H^{-1}(v^1,\dots ,v^r){\parallel }_{W^{e,q}(M,E;{\Lambda }_1)}\simeq \sum _{l=1}^r{\parallel v^l\parallel }_{W^{e,q}(\phi (U))}<\infty .$$

So, $H^{-1}(v^1,\cdots ,v^r)\in W^{e,q}(M,E;\Lambda )$.

□

It is clear that $u\in W^{e,q}(M,E;\Lambda )$ if and only if for all $\alpha$, ${\psi }_{\alpha }u\in W_{K_{\alpha }}^{e,q}(M,E;\Lambda )$ where $K_{\alpha }$ can be taken as any compact set such that $\mathrm{supp}{\psi }_{\alpha }\subseteq K_{\alpha }\subseteq U_{\alpha }$. In fact as a direct consequence of the definition of Sobolev spaces and the above mentioned isomorphism we have

$$\begin{array}{cc}\hfill u\in W^{e,q}(M,E;\Lambda )& ⟺\forall 1\le \alpha \le N{H}_{\alpha }({\psi }_{\alpha }u)\in {[W_{{\phi }_{\alpha }(\mathrm{supp}{\psi }_{\alpha })}^{e,q}({\phi }_{\alpha }(U_{\alpha }))]}^{\times r}\hfill \\ \hfill & ⟺\forall 1\le \alpha \le N{\psi }_{\alpha }u\in W_{\mathrm{supp}{\psi }_{\alpha }}^{e,q}(M,E;\Lambda )\hfill \end{array}$$

9.2.6. Completeness; Density of Smooth Functions

Our proofs for completeness of Sobolev spaces and density of smooth functions are based on the ideas presented in [24].

Lemma 12.

Let $M^n$ be a compact smooth manifold and $E\to M$ be a vector bundle of rank r. Let $e\in \mathbb{R}$ and $q\in (1,\infty )$. Suppose $\Lambda ={\{(U_{\alpha },{\phi }_{\alpha },{\rho }_{\alpha },{\psi }_{\alpha })\}}_{\alpha =1}^N$ is an augmented total trivialization atlas for $E\to M$. If e is a noninteger less than $-1$ further assume that Λ is GL compatible with itself. Let $K_{\alpha }$ be a compact subset of $U_{\alpha }$ that contains the support of ${\psi }_{\alpha }$. Let $S:W^{e,q}(M,E;\Lambda )\to {\prod }_{\alpha =1}^N{W}_{K_{\alpha }}^{e,q}(M,E;\Lambda )$ be the linear map defined by $S(u)=({\psi }_{1}u,\dots ,{\psi }_{N}u)$. Then $S:W^{e,q}(M,E;\Lambda )\to S(W^{e,q}(M,E;\Lambda ))\subseteq {\prod }_{\alpha =1}^N{W}_{K_{\alpha }}^{e,q}(M,E;\Lambda )$ is a linear topological isomorphism. Moreover, $S(W^{e,q}(M,E;\Lambda ))$ is closed in ${\prod }_{\alpha =1}^N{W}_{K_{\alpha }}^{e,q}(M,E;\Lambda )$.

Proof. 

Each component of S is continuous (see Theorem 90), therefore S is continuous. Define $P:{\prod }_{\alpha =1}^N{W}_{K_{\alpha }}^{e,q}(M,E)\to W^{e,q}(M,E)$ by

$$P(v_1,\dots ,v_N)=\sum _i{v}_i.$$

Clearly, P is continuous. Furthermore, $P\circ S=id$. Now the claim follows from Theorem 23. □

Theorem 98.

Let $M^n$ be a compact smooth manifold and $E\to M$ be a vector bundle of rank r. Let $e\in \mathbb{R}$ and $q\in (1,\infty )$. Suppose $\Lambda ={\{(U_{\alpha },{\phi }_{\alpha },{\rho }_{\alpha },{\psi }_{\alpha })\}}_{\alpha =1}^N$ is an augmented total trivialization atlas for $E\to M$. If e is a noninteger less than $-1$ further assume that Λ is GL compatible with itself. Then $W^{e,q}(M,E;\Lambda )$ is a Banach space.

Proof. 

According to Lemma 11, for each $1\le \alpha \le N$, $W_{K_{\alpha }}^{e,q}(M,E;\Lambda )$ is isomorphic to the Banach space ${[W_{{\phi }_{\alpha }(K_{\alpha })}^{e,q}({\phi }_{\alpha }(U_{\alpha }))]}^{\times r}$. So ${\prod }_{\alpha =1}^N{W}_{K_{\alpha }}^{e,q}(M,E;\Lambda )$ is a Banach space. A closed subspace of a Banach space is Banach. Therefore, $S(W^{e,q}(M,E;\Lambda ))$ is a Banach space. Since S is a linear topological isomorphism onto its image, $W^{e,q}(M,E;\Lambda )$ is also a Banach space. □

Theorem 99.

Let $M^n$ be a compact smooth manifold and $E\to M$ be a vector bundle of rank r. Let $e\in \mathbb{R}$ and $q\in (1,\infty )$. Suppose $\Lambda ={\{(U_{\alpha },{\phi }_{\alpha },{\rho }_{\alpha },{\psi }_{\alpha })\}}_{\alpha =1}^N$ is an augmented total trivialization atlas for $E\to M$. If e is a noninteger less than $-1$ further assume that Λ is GL compatible with itself. Then $D(M,E)$ is dense in $W^{e,q}(M,E;\Lambda )$.

Proof. 

Let $K_{\alpha }=\mathrm{supp}{\psi }_{\alpha }$. For each $1\le \alpha \le N$, let $V_{\alpha }$ be an open set such that

$$K_{\alpha }\subseteq V_{\alpha }\subseteq {\overline{V}}_{\alpha }\subseteq U_{\alpha }.$$

Suppose $u\in W^{e,q}(M,E;\Lambda )$ and let $u_{\alpha }={\psi }_{\alpha }u$. Clearly, $\mathrm{supp}{u}_{\alpha }\subseteq K_{\alpha }$. Furthermore, according to Lemma 11, for each $\alpha$ there exists a linear topological isomorphism

$${\widehat{H}}_{\alpha }:W_{{\overline{V}}_{\alpha }}^{e,q}(M,E)\to {[W_{{\phi }_{\alpha }({\overline{V}}_{\alpha })}^{e,q}({\phi }_{\alpha }(U_{\alpha }))]}^{\times r}.$$

Note that ${\widehat{H}}_{\alpha }(u_{\alpha })\in {[W_{{\phi }_{\alpha }(K_{\alpha })}^{e,q}({\phi }_{\alpha }(U_{\alpha }))]}^{\times r}$. Therefore, by Lemma 62 there exists a sequence $\{{({\eta }_{\alpha })}_i\}$ in ${[C_{{\phi }_{\alpha }({\overline{V}}_{\alpha })}^{\infty }({\phi }_{\alpha }(U_{\alpha }))]}^{\times r}$ (of course we view each component of ${({\eta }_{\alpha })}_i$ as a distribution) that converges to ${\widehat{H}}_{\alpha }(u_{\alpha })$ in $W^{e,q}$ norm as $i\to \infty$. Since ${\widehat{H}}_{\alpha }$ is a linear topological isomorphism, we can conclude that

$${\widehat{H}}_{\alpha }^{-1}({({\eta }_{\alpha })}_i)\to u_{\alpha },(\mathrm{in}{W}_{{\overline{V}}_{\alpha }}^{e,q}(M,E;\Lambda )\mathrm{as}i\to \infty ).$$

(Note that if a sequence converges in $W_A^{e,q}(M,E;\Lambda )$ where A is a closed subset of M, it also obviously converges in $W^{e,q}(M,E;\Lambda )$.) Let ${\xi }_i={\sum }_{\alpha =1}^N{\widehat{H}}_{\alpha }^{-1}({({\eta }_{\alpha })}_i)$. This sum makes sense because, as we will shortly prove, each summand is in $C_c^{\infty }(U_{\alpha },E_{\alpha })$ and so by extension by zero can be viewed as an element of $C^{\infty }(M,E)$. Clearly ${\xi }_i\to {\sum }_{\alpha }{u}_{\alpha }=u$ in $W^{e,q}(M,E;\Lambda )$. It remains to show that for each i, ${\xi }_i$ is in $C^{\infty }(M,E)$. To this end, it suffices to show that if $\chi =({\chi }^1,\dots ,{\chi }^r)\in {[C_c^{\infty }({\phi }_{\alpha }(U_{\alpha }))]}^{\times r}$, then ${\widehat{H}}_{\alpha }^{-1}(\chi )$ is in $C_c^{\infty }(U_{\alpha },E_{\alpha })$ and so can be considered as an element of $C^{\infty }(M,E)$ (by extension by zero). Note that ${\widehat{H}}_{\alpha }^{-1}(\chi )$ is compactly supported in $U_{\alpha }$ because by definition of ${\widehat{H}}_{\alpha }$ any distribution in the codomain of ${\widehat{H}}_{\alpha }^{-1}$ has compact support in ${\overline{V}}_{\alpha }$. So, we just need to prove the smoothness of ${\widehat{H}}_{\alpha }^{-1}(\chi )$. That is, we need to show that there is a smooth section $f\in C^{\infty }(U_{\alpha },E_{U_{\alpha }})$ such that $u_f={\widehat{H}}_{\alpha }^{-1}(\chi )$. It seems that the natural candidate for $f(x)$ should be ${({\rho }_{\alpha }{|}_{E_x})}^{-1}\circ \chi \circ {\phi }_{\alpha }(x)$. In fact, if we define f by this formula, then ${\widehat{H}}_{\alpha }(u_f)=H_{\alpha }(u_f)$ and by Remark 32 $H_{\alpha }(u_f)$ is a distribution that corresponds to the regular function $({\tilde{f}}^1,\dots ,{\tilde{f}}^r)={\rho }_{\alpha }\circ f\circ {\phi }_{\alpha }^{-1}$. Obviously,

$${\rho }_{\alpha }\circ f\circ {\phi }_{\alpha }^{-1}{|}_{{\phi }_{\alpha }(x)}={\rho }_{\alpha }\circ {({\rho }_{\alpha }{|}_{E_x})}^{-1}\circ \chi \circ {\phi }_{\alpha }\circ {\phi }_{\alpha }^{-1}{{|}_{{\phi }_{\alpha }(x)}=\chi |}_{{\phi }_{\alpha }(x)}.$$

So, the regular section $f(x)={\rho }_{\alpha }{|}_{E_x}^{-1}\circ \chi \circ {\phi }_{\alpha }(x)$ corresponds to ${\widehat{H}}_{\alpha }^{-1}(\chi )$ and we just need to show that f is smooth; this is true because f is a composition of smooth functions. Indeed,

$$f(x)={\rho }_{\alpha }{|}_{E_x}^{-1}\circ \chi \circ {\phi }_{\alpha }(x)={\Phi }_{\alpha }^{-1}(x,\chi \circ {\phi }_{\alpha }(x))⟹f={\Phi }_{\alpha }^{-1}\circ (Id,\chi \circ {\phi }_{\alpha }),$$

and all the maps involved in the above expression are smooth. □

9.2.7. Dual of Sobolev Spaces

Lemma 13.

Let $M^n$ be a compact smooth manifold and let $\pi :E\to M$ be a vector bundle of rank r equipped with a fiber metric ${⟨.,.⟩}_E$. Let $e\in \mathbb{R}$ and $q\in (1,\infty )$. Suppose $\Lambda ={\{(U_{\alpha },{\phi }_{\alpha },{\rho }_{\alpha },{\psi }_{\alpha })\}}_{\alpha =1}^N$ is an augmented total trivialization atlas for $E\to M$ which trivializes the fiber metric. If e is a noninteger less than $-1$ further assume that the total trivialization atlas in Λ is GGL.

Fix a positive smooth density μ on M (for instance we can equip M with a smooth Riemannian metric and consider the corresponding Riemannian density). Let $T:D(M,E)\to D(M,E^{\vee })$ be the map that sends ξ to $T_{\xi }$ where $T_{\xi }$ is defined by

$$\forall x\in M{T}_{\xi }(x):E_x\to {\mathcal{D}}_x,a\mapsto {⟨a,\xi (x)⟩}_E\mu (x).$$

Then T is a linear bijective continuous map. Moreover, $T:(C^{\infty }{(M,E),\parallel .\parallel }_{W^{e,q}(M,E;\Lambda )})\to (C^{\infty }(M,E^{\vee }){,\parallel .\parallel }_{W^{e,q}(M,E^{\vee };{\Lambda }^{\vee })})$ is a topological isomorphism.

Note: Since M is compact, $D(M,E)$ and $D(M,E^{\vee })$ are Frechet spaces. So, by Theorem 17, the continuity of the bijective linear map $T:D(M,E)\to D(M,E^{\vee })$ implies the continuity of its inverse. That is, $T:D(M,E)\to D(M,E^{\vee })$ is a linear topological isomorphism. As a consequence, the adjoint of T is a well-defined bijective continuous map that can be used to identify $D^{\prime }(M,E)={[D(M,E^{\vee })]}^{*}$ with ${[D(M,E)]}^{*}$.

Proof. 

The fact that T is linear is obvious.

•

Tis one-to-one: Suppose $\xi \in D(M,E)$ is such that $T_{\xi }=0$. Then

$$\begin{array}{cc}\hfill \forall x\in M{T}_{\xi }(x)=0& ⟹\forall x\in M,\forall a\in E_x[T_{\xi }(x)](a)=0\hfill \\ \hfill & ⟹\forall x\in M,\forall a\in E_x{⟨a,\xi (x)⟩}_E=0\hfill \\ \hfill & ⟹\forall x\in M{⟨\xi (x),\xi (x)⟩}_E=0⟹\forall x\in M\xi (x)=0.\hfill \end{array}$$

•

Tis onto: Let $u\in D(M,E^{\vee })$. Our goal is to show that there exists $\xi \in D(M,E)$ such that $u=T_{\xi }$. Note that

$$\forall x\in Mu(x)=T_{\xi }(x)⟺\forall x\in M\forall a\in E_x{⟨a,\xi (x)⟩}_E\mu (x)=[u(x)](a).$$

Since ${\mathcal{D}}_x$ is 1-dimensional and both $\mu (x)$ (which is a positive smooth density) and $[u(x)][a]$ belong to ${\mathcal{D}}_x,$, there exists a number $b(x,a)$ such that

$$[u(x)](a)=b(x,a)\mu (x).$$

So, we need to show that there exists $\xi \in D(M,E)$ such that

$$\forall x\in M\forall a\in E_x{⟨a,\xi (x)⟩}_E=b(x,a).$$

The above equality uniquely defines a functional on $E_x$ which gives us a unique element $\xi (x)\in E_x$ by the Riesz representation theorem. It remains to prove that $\xi$ is smooth. To this end, we will show that for each $\alpha$, ${\xi |}_{U_{\alpha }}$ is smooth. Let $(s_1,\dots ,s_r)$ be a smooth orthonormal frame for $E_{U_{\alpha }}$.

$$\forall x\in U_{\alpha }\xi (x)={\xi }^1(x)s_1(x)+\dots +{\xi }^r(x)s_r(x).$$

It suffices to show that ${\xi }^1,\dots ,{\xi }^r$ are smooth functions (see Theorem 36). We have

$${\xi }^i(x)={⟨\xi (x),s_i(x)⟩}_E.$$

It follows from the definition of $\xi (x)$ that

$$[u(x)][s_i(x)]={⟨s_i(x),\xi (x)⟩}_E\mu (x).$$

Therefore, ${\xi }^i(x)$ satisfies the following equality

$$[u(x)][s_i(x)]={\xi }^i(x)\mu (x).$$

That is, if we define a section of $\mathcal{D}\to U_{\alpha }$ by

$$[u,s_i]:U_{\alpha }\to \mathcal{D},x\mapsto [u(x)][s_i(x)],$$

then ${\xi }^i$ is the component of this section with respect to the smooth frame $\{\mu (x)\}$ on $U_{\alpha }$. The smoothness of ${\xi }^i$ follows from the fact that if N is any manifold, $E\to N$ is a vector bundle and u and v are in $\mathcal{E}(N,E^{\vee })$ and $\mathcal{E}(N,E)$, respectively, then $[u,v]$ is in $\mathcal{E}(N,\mathcal{D})$; indeed, the local representation of $[u,v]$ is ${\sum }_l{\tilde{u}}^l{\tilde{v}}^l$ which is a smooth function because ${\tilde{u}}^l$ and ${\tilde{v}}^l$ are smooth functions.

•

$T:D(M,E)\to D(M,E^{\vee })$ is continuous:

We make use of Theorem 20. Recall that

(1)

The topology on $D(M,E)$ is induced by the seminorms:

$$\forall 1\le l\le r,\forall 1\le \alpha \le N,\forall k\in \mathbb{N},\forall K\subseteq U_{\alpha }(\mathrm{compact})p_{l,\alpha ,k,K}(\xi )={\parallel {\rho }_{\alpha }^l\circ \xi \circ {\phi }_{\alpha }^{-1}\parallel }_{{\phi }_{\alpha }(K),k}.$$

(2)

The topology on $D(M,E^{\vee })$ is induced by the seminorms:

$$\forall 1\le l\le r,\forall 1\le \alpha \le N,\forall k\in \mathbb{N},\forall K\subseteq U_{\alpha }(\mathrm{compact})q_{l,\alpha ,k,K}(\eta )={\parallel {({\rho }_{\alpha }^{\vee })}^l\circ \eta \circ {\phi }_{\alpha }^{-1}\parallel }_{{\phi }_{\alpha }(K),k}.$$

For all $\xi \in D(M,E)$ we have

$$\begin{array}{c}\hfill q_{l,\alpha ,k,K}(T_{\xi })=\parallel {({\rho }_{\alpha }^{\vee })}^l\circ T_{\xi }\circ {\phi }_{\alpha }^{-1}{\parallel }_{{\phi }_{\alpha }(K),k}={\parallel ({\rho }_{\mathcal{D},{\phi }_{\alpha }})\circ (T_{\xi }\circ {\phi }_{\alpha }^{-1})\circ \underset{s_l(x)}{\underbrace{{({\rho }_{\alpha }{|}_{E_x})}^{-1}(e_l)}}\parallel }_{{\phi }_{\alpha }(K),k},\end{array}$$

where $(e_1,\dots ,e_r)$ is the standard basis for ${\mathbb{R}}^r$. Let $y={\phi }_{\alpha }(x)$. Note that

$$[T_{\xi }({\phi }_{\alpha }^{-1}(y))][s_l(x)]={⟨s_l(x),\xi (x)⟩}_E\mu (x).$$

Therefore, if we define the smooth function $f_{\alpha }$ on $U_{\alpha }$ by $\mu (x)=f_{\alpha }(x)|d{x}^1\wedge \dots \wedge d{x}^n|$, then

$$({\rho }_{\mathcal{D},{\phi }_{\alpha }})\circ (T_{\xi }\circ {\phi }_{\alpha }^{-1})\circ s_l(x)={⟨s_l(x),\xi (x)⟩}_E{f}_{\alpha }(x)={\xi }^l(x)f_{\alpha }(x)=({\rho }_{\alpha }^l\circ \xi \circ {\phi }_{\alpha }^{-1}(y))(f_{\alpha }\circ {\phi }_{\alpha }^{-1}(y)).$$

(8)

So, if we let

$$C=\underset{y\in {\phi }_{\alpha }(K),|\beta |\le k}{max}|{\partial }^{\beta }(f_{\alpha }\circ {\phi }_{\alpha }^{-1}(y))|,$$

then

$$q_{l,\alpha ,k,K}(T_{\xi })=\parallel ({\rho }_{\alpha }^l\circ \xi \circ {\phi }_{\alpha }^{-1}(y))(f_{\alpha }\circ {\phi }_{\alpha }^{-1}(y)){\parallel }_{{\phi }_{\alpha }(K),k}\le C\parallel {\rho }_{\alpha }^l\circ \xi \circ {\phi }_{\alpha }^{-1}(y){)\parallel }_{{\phi }_{\alpha }(K),k}=C{p}_{l,\alpha ,k,K}(\xi ).$$

•

$T:(C^{\infty }{(M,E),\parallel .\parallel }_{e,q})\to (C^{\infty }(M,E^{\vee }){,\parallel .\parallel }_{e,q})$ is a topological isomorphism:

$${\parallel \xi \parallel }_{W^{e,q}(M,E;\Lambda )}=\sum _{\alpha =1}^N\sum _{l=1}^r{\parallel {\rho }_{\alpha }^l\circ {\psi }_{\alpha }\xi \circ {\phi }_{\alpha }^{-1}\parallel }_{W^{e,q}({\phi }_{\alpha }(U_{\alpha }))},$$

$$\begin{array}{cc}\hfill \parallel T_{\xi }{\parallel }_{W^{e,q}(M,E^{\vee };{\Lambda }^{\vee })}& =\sum _{\alpha =1}^N\sum _{l=1}^r{\parallel {({\rho }_{\alpha }^{\vee })}^l\circ {\psi }_{\alpha }{T}_{\xi }\circ {\phi }_{\alpha }^{-1}\parallel }_{W^{e,q}({\phi }_{\alpha }(U_{\alpha }))}.\hfill \end{array}$$

By Equation (8), we have

$${({\rho }_{\alpha }^{\vee })}^l\circ {\psi }_{\alpha }{T}_{\xi }\circ {\phi }_{\alpha }^{-1}={\rho }_{\mathcal{D},{\phi }_{\alpha }}\circ ({\psi }_{\alpha }{T}_{\xi }\circ {\phi }_{\alpha }^{-1})\circ s_l(x)=({\rho }_{\alpha }^l\circ {\psi }_{\alpha }\xi \circ {\phi }_{\alpha }^{-1})(f_{\alpha }\circ {\phi }_{\alpha }^{-1}).$$

Therefore,

$$\parallel T_{\xi }{\parallel }_{W^{e,q}(M,E^{\vee };{\Lambda }^{\vee })}=\sum _{\alpha =1}^N\sum _{l=1}^r{\parallel ({\rho }_{\alpha }^l\circ {\psi }_{\alpha }\xi \circ {\phi }_{\alpha }^{-1})(f_{\alpha }\circ {\phi }_{\alpha }^{-1})\parallel }_{W^{e,q}({\phi }_{\alpha }(U_{\alpha }))}.$$

Now, we just need to notice that $f_{\alpha }\circ {\phi }_{\alpha }^{-1}$ is a positive function and belongs to $C^{\infty }({\phi }_{\alpha }(U_{\alpha }))$ (so $\frac{1}{f_{\alpha }\circ {\phi }_{\alpha }^{-1}}$ is also smooth) and ${\rho }_{\alpha }^l\circ {\psi }_{\alpha }\xi \circ {\phi }_{\alpha }^{-1}$ has support in the compact set ${\phi }_{\alpha }(\mathrm{supp}({\psi }_{\alpha }))$ to conclude that

$${\parallel \xi \parallel }_{W^{e,q}(M,E;\Lambda )}\simeq {\parallel T_{\xi }\parallel }_{W^{e,q}(M,E^{\vee };{\Lambda }^{\vee })}.$$

□

Lemma 14.

Let $M^n$ be a compact smooth manifold and let $\pi :E\to M$ be a vector bundle of rank r equipped with a fiber metric ${⟨.,.⟩}_E$. Let $e\in \mathbb{R}$ and $q\in (1,\infty )$. Suppose $\Lambda ={\{(U_{\alpha },{\phi }_{\alpha },{\rho }_{\alpha },{\psi }_{\alpha })\}}_{\alpha =1}^N$ is an augmented total trivialization atlas for $E\to M$. If e is a noninteger less than $-1$ further assume that the total trivialization atlas in Λ is GGL. Then $D(M,E)\hookrightarrow W^{e,q}(M,E)\hookrightarrow D^{\prime }(M,E)$.

Proof. 

We refer to [24] for discussion about the case where $e\in \mathbb{Z}$. For $e\in \mathbb{R}\backslash \mathbb{Z}$ we have

$$\begin{array}{cc}\hfill & W^{e,q}(M,E;\Lambda )\hookrightarrow W^{\lfloor e\rfloor ,q}(M,E;\Lambda )\hookrightarrow D^{\prime }(M,E),\hfill \\ \hfill & D(M,E)\hookrightarrow W^{\lfloor e\rfloor +1,q}(M,E;\Lambda )\hookrightarrow W^{e,q}(M,E;\Lambda ).\hfill \end{array}$$

□

Theorem 100.

Let $M^n$ be a compact smooth manifold and let $\pi :E\to M$ be a vector bundle of rank r equipped with a fiber metric ${⟨.,.⟩}_E$. Let $e\in \mathbb{R}$ and $q\in (1,\infty )$. Suppose $\Lambda ={\{(U_{\alpha },{\phi }_{\alpha },{\rho }_{\alpha },{\psi }_{\alpha })\}}_{\alpha =1}^N$ is an augmented total trivialization atlas for $E\to M$ which trivializes the fiber metric. If e is a noninteger whose magnitude is greater than 1 further assume that the total trivialization atlas in Λ is GL compatible with itself. Fix a positive smooth density μ on M.

Consider the $L^2$ inner product on $D(M,E)$ defined by

$${⟨u,v⟩}_2={\int }_M{⟨u,v⟩}_E\mu .$$

Then

(i) 

${⟨.,.⟩}_2$ extends uniquely to a continuous bilinear pairing ${⟨.,.⟩}_2:W^{-e,q^{\prime }}(M,E;\Lambda )\times W^{e,q}(M,E;\Lambda )\to \mathbb{R}$ (We are using the same notation (i.e., ${⟨.,.⟩}_2$) for the extended bilinear map!)

(ii) 

The map $S:W^{-e,q^{\prime }}(M,E;\Lambda )\to {[W^{e,q}(M,E;\Lambda )]}^{*}$ defined by $S(u)=l_u$ where

$$l_u:W^{e,q}(M,E;\Lambda )\to \mathbb{R},l_u(v)={⟨u,v⟩}_2$$

is a well-defined topological isomorphism.

In particular, ${[W^{e,q}(M,E;\Lambda )]}^{*}$ can be identified with $W^{-e,q^{\prime }}(M,E;\Lambda )$.

Proof. 

(1)

By Theorem 8, in order to prove (i) it is enough to show that

$${⟨.,.⟩}_2:(C^{\infty }{(M,E),\parallel .\parallel }_{-e,q^{\prime }})\times (C^{\infty }{(M,E),\parallel .\parallel }_{e,q})\to \mathbb{R}$$

is a continuous bilinear map. Denote the corresponding standard trivialization map for the density bundle $\mathcal{D}\to M$ by ${\rho }_{\mathcal{D},{\phi }_{\alpha }}$. Let ${\Lambda }_1={\{(U_{\alpha },{\phi }_{\alpha },{\rho }_{\alpha },{\tilde{\psi }}_{\alpha })\}}_{\alpha =1}^N$ be an augmented total trivialization atlas for E where ${\tilde{\psi }}_{\alpha }=\frac{{\psi }_{\alpha }^3}{{\sum }_{\beta =1}^N{\psi }_{\beta }^3}$. Note that $\frac{1}{{\sum }_{\beta =1}^N{\psi }_{\beta }^3}\circ {\phi }_{\alpha }^{-1}\in B{C}^{\infty }({\phi }_{\alpha }(U_{\alpha }))$. Let $K_{\alpha }=\mathrm{supp}{\psi }_{\alpha }$. Recall that on $U_{\alpha }$ we may write $\mu =h_{\alpha }|d{x}^1\wedge \cdots \wedge d{x}^n|$ where $h_{\alpha }={\rho }_{\mathcal{D},{\phi }_{\alpha }}\circ \mu$ is smooth. Moreover, for any continuous function $f:M\to \mathbb{R}$,

$$\begin{array}{cc}\hfill {\int }_{M}f\mu & =\sum _{\alpha =1}^N{\int }_M{\tilde{\psi }}_{\alpha }f\mu \hfill \\ \hfill & =\sum _{\alpha =1}^N{\int }_{{\phi }_{\alpha }(U_{\alpha })}{({\phi }_{\alpha }^{-1})}^{*}({\tilde{\psi }}_{\alpha }f\mu )\hfill \\ \hfill & =\sum _{\alpha =1}^N{\int }_{{\phi }_{\alpha }(U_{\alpha })}({\tilde{\psi }}_{\alpha }f\circ {\phi }_{\alpha }^{-1}){({\phi }_{\alpha }^{-1})}^{*}\mu \hfill \\ \hfill & =\sum _{\alpha =1}^N{\int }_{{\phi }_{\alpha }(U_{\alpha })}({\tilde{\psi }}_{\alpha }f\circ {\phi }_{\alpha }^{-1})(h_{\alpha }\circ {\phi }_{\alpha }^{-1})dV\hfill \\ \hfill & ⪯\sum _{\alpha =1}^N{\int }_{{\phi }_{\alpha }(U_{\alpha })}({\psi }_{\alpha }^{2}f\circ {\phi }_{\alpha }^{-1})({\psi }_{\alpha }{h}_{\alpha }\circ {\phi }_{\alpha }^{-1})dV(\frac{1}{{\sum }_{\beta =1}^N{\psi }_{\beta }^3}\circ {\phi }_{\alpha }^{-1}\in {\mathit{BC}}^{\infty }({\phi }_{\alpha }(U_{\alpha }))).\hfill \end{array}$$

Therefore, we have

$$\begin{array}{cc}\hfill |{\int }_M{⟨u,v⟩}_E\mu |& =|\sum _{\alpha =1}^N{\int }_M{\tilde{\psi }}_{\alpha }{⟨u,v⟩}_E\mu |\hfill \\ \hfill & ⪯|\sum _{\alpha =1}^N{\int }_{{\phi }_{\alpha }(U_{\alpha })}({\psi }_{\alpha }^2{⟨u,v⟩}_E\circ {\phi }_{\alpha }^{-1})({\psi }_{\alpha }{h}_{\alpha }\circ {\phi }_{\alpha }^{-1})dV|.\hfill \end{array}$$

Since by assumption the total trivialization atlas in $\Lambda$ trivializes the metric, we get

$$\begin{array}{cc}\hfill & |{\int }_M{⟨u,v⟩}_E\mu |⪯\sum _{\alpha =1}^N\sum _{i=1}^r|{\int }_{{\phi }_{\alpha }(U_{\alpha })}({\psi }_{\alpha }\circ {\phi }_{\alpha }^{-1}{\tilde{u}}_i)({\psi }_{\alpha }\circ {\phi }_{\alpha }^{-1}{\tilde{v}}_i)({\psi }_{\alpha }{h}_{\alpha }\circ {\phi }_{\alpha }^{-1})dV|\hfill \\ \hfill & \stackrel{\mathrm{Remark}46}{⪯}\sum _{\alpha =1}^N\sum _{i=1}^r\parallel ({\psi }_{\alpha }\circ {\phi }_{\alpha }^{-1}{\tilde{u}}_i){\parallel }_{W^{-e,q^{\prime }}({\phi }_{\alpha }(U_{\alpha }))}{\parallel ({\psi }_{\alpha }\circ {\phi }_{\alpha }^{-1}{\tilde{v}}_i)({\psi }_{\alpha }{h}_{\alpha }\circ {\phi }_{\alpha }^{-1})\parallel }_{W^{e,q}({\phi }_{\alpha }(U_{\alpha }))}\hfill \\ \hfill & ⪯\sum _{\alpha =1}^N\sum _{i=1}^r\parallel ({\psi }_{\alpha }\circ {\phi }_{\alpha }^{-1}{\tilde{u}}_i){\parallel }_{W^{-e,q^{\prime }}({\phi }_{\alpha }(U_{\alpha }))}{\parallel ({\psi }_{\alpha }\circ {\phi }_{\alpha }^{-1}{\tilde{v}}_i)\parallel }_{W^{e,q}({\phi }_{\alpha }(U_{\alpha }))}\hfill \\ \hfill & ⪯\left[\sum _{\alpha =1}^N\sum _{i=1}^r{\parallel ({\psi }_{\alpha }\circ {\phi }_{\alpha }^{-1}{\tilde{u}}_i)\parallel }_{W^{-e,q^{\prime }}({\phi }_{\alpha }(U_{\alpha }))}\right]\left[\sum _{\alpha =1}^N\sum _{i=1}^r{\parallel ({\psi }_{\alpha }\circ {\phi }_{\alpha }^{-1}{\tilde{v}}_i)\parallel }_{W^{e,q}({\phi }_{\alpha }(U_{\alpha }))}\right]\hfill \\ \hfill & ={\parallel u\parallel }_{W^{-e,q^{\prime }}(M,E;\Lambda )}{\parallel v\parallel }_{W^{e,q}(M,E;\Lambda )}.\hfill \end{array}$$

(2)

For each $u\in W^{-e,q^{\prime }}(M,E;\Lambda )$, $l_u$ is continuous because ${⟨.,.⟩}_2$ is continuous. So, S is well-defined.

(3)

S is a continuous linear map because

$$\begin{array}{cc}\hfill \forall u\in W^{-e,q^{\prime }}(M,E;\Lambda )& {\parallel S(u)\parallel }_{{(W^{e,q}(M,E;\Lambda ))}^{*}}=\underset{0\ne v\in W^{e,q}(M,E;\Lambda )}{sup}\frac{|S(u)v|}{{\parallel v\parallel }_{W^{e,q}(M,E;\Lambda )}}\hfill \\ \hfill & =\underset{0\ne v\in W^{e,q}(M,E;\Lambda )}{sup}\frac{{|⟨u,v⟩}_2|}{{\parallel v\parallel }_{W^{e,q}(M,E;\Lambda )}}\le C{\parallel u\parallel }_{W^{-e,q^{\prime }}(M,E;\Lambda )},\hfill \end{array}$$

where C is the norm of the continuous bilinear form ${⟨.,.⟩}_2$.

(4)

S is injective: suppose $u\in W^{-e,q^{\prime }}(M,E;\Lambda )$ is such that $S(u)=0$, then

$$\forall v\in W^{e,q}(M,E;\Lambda )l_u(v)={⟨u,v⟩}_2=0.$$

We need to show that $u=0$.

•

Step 1: For $\xi$ and $\eta$ in $D(M,E)$ we have

$${⟨\xi ,\eta ⟩}_2={⟨u_{\xi },T\eta ⟩}_{{[D(M,E^{\vee })]}^{*}\times D(M,E^{\vee })},$$

where T is the map introduced in Lemma 13 (note that if we identify $D(M,E)$ with a subset of ${[D(M,E^{\vee })]}^{*}$, then we may write $\xi$ instead of $u_{\xi }$ on the right hand side of the above equality). The reason is as follows:

$$\begin{array}{cc}\hfill {⟨u_{\xi },T\eta ⟩}_{{[D(M,E^{\vee })]}^{*}\times D(M,E^{\vee })}& ={\int }_M[T_{\eta }(x)][\xi (x)](\mathrm{by}\mathrm{definition}\mathrm{of}{u}_{\xi }).\hfill \end{array}$$

Recall that by definition of $T_{\eta }$ we have

$$\forall x\in M\forall a\in E_x[T_{\eta }(x)][a]={⟨a,\eta (x)⟩}_E\mu .$$

In particular,

$$[T_{\eta }(x)][{\xi }_{(}x)]={⟨\xi (x),\eta (x)⟩}_E\mu .$$

Therefore,

$${⟨u_{\xi },T\eta ⟩}_{{[D(M,E^{\vee })]}^{*}\times D(M,E^{\vee })}={\int }_M{⟨\xi (x),\eta (x)⟩}_E\mu ={⟨\xi ,\eta ⟩}_2.$$

•

Step 2: For $w\in W^{-e,q^{\prime }}(M,E;\Lambda )$ and $\eta \in D(M,E)\subseteq W^{e,q}(M,E;\Lambda )$ we have

$${⟨w,\eta ⟩}_2={⟨w,T\eta ⟩}_{{[D(M,E^{\vee })]}^{*}\times D(M,E^{\vee })}.$$

Indeed, let $\{{\xi }_m\}$ be a sequence in $D(M,E)$ that converges to w in $W^{-e,q^{\prime }}(M,E;\Lambda )$. Note that $W^{-e,q^{\prime }}(M,E;\Lambda )\hookrightarrow {[D(M,E^{\vee })]}^{*}$, so the sequence converges to w in ${[D(M,E^{\vee })]}^{*}$ as well. By what was proved in the first step, for all m

$${⟨{\xi }_m,\eta ⟩}_2={⟨{\xi }_m,T\eta ⟩}_{{[D(M,E^{\vee })]}^{*}\times D(M,E^{\vee })}.$$

Taking the limit as $m\to \infty$ proves the claim.

•

Step 3: Finally note that for all $v\in D(M,E)\subseteq W^{e,q}(M,E;\Lambda )$

$${⟨T^{*}u,v⟩}_{{[D(M,E)]}^{*}\times D(M,E)}={⟨u,Tv⟩}_{{[D(M,E^{\vee })]}^{*}\times D(M,E^{\vee })}={⟨u,v⟩}_2=0.$$

Therefore, $T^{*}u=0$ as an element of ${[D(M,E)]}^{*}$. T is a continuous bijective map, so $T^{*}$ is injective. It follows that $u=0$ as an element of ${[D(M,E^{\vee })]}^{*}$ and so $u=0$ as an element of $W^{-e,q^{\prime }}(M,E;\Lambda )$.

(5)

S is surjective. Let $F\in {[W^{e,q}(M,E;\Lambda )]}^{*}$. We need to show that there is an element $u\in W^{-e,q^{\prime }}(M,E;\Lambda )$ such that $S(u)=F$. Since $D(M,E)$ is dense in $W^{e,q}(M,E;\Lambda )$, it is enough to show that there exists an element $u\in W^{-e,q^{\prime }}(M,E;\Lambda )$ with the property that

$$\forall \xi \in D(M,E)F(\xi )={⟨u,\xi ⟩}_2.$$

Note that, according to what was proved in Step 2,

$${⟨u,\xi ⟩}_2={⟨u,T\xi ⟩}_{{[D(M,E^{\vee })]}^{*}\times D(M,E^{\vee })}={⟨T^{*}u,\xi ⟩}_{{[D(M,E)]}^{*}\times D(M,E)}.$$

So, we need to show that there exists an element $u\in W^{-e,q^{\prime }}(M,E;\Lambda )$ such that

$$\forall \xi \in D(M,E)F(\xi )={⟨T^{*}u,\xi ⟩}_{{[D(M,E)]}^{*}\times D(M,E)}.$$

Since $D(M,E)\hookrightarrow W^{e,q}(M,E;\Lambda )$, ${F|}_{D(M,E)}$ is an element of ${[D(M,E)]}^{*}$. We let

$$u:={[T^{-1}]}^{*}(F{|}_{D(M,E)})\in {[D(M,E^{\vee })]}^{*}.$$

Clearly, u satisfies the desired equality (note that ${[T^{-1}]}^{*}={[T^{*}]}^{-1}$). So, we just need to show that u is indeed an element of $W^{-e,q^{\prime }}(M,E;\Lambda )$. Note that

$$u\in W^{-e,q^{\prime }}(M,E;\Lambda )⟺\forall 1\le \alpha \le N{H}_{\alpha }({\psi }_{\alpha }u)\in {[W_{{\phi }_{\alpha }(\mathrm{supp}{\psi }_{\alpha })}^{-e,q^{\prime }}({\phi }_{\alpha }(U_{\alpha }))]}^{\times r}.$$

Since $\mathrm{supp}({\psi }_{\alpha }u)\subseteq \mathrm{supp}{\psi }_{\alpha }$, it follows from Remark 31 that

$$\forall 1\le l\le r\mathrm{supp}({[H_{\alpha }({\psi }_{\alpha }u)]}^l)\subset {\phi }_{\alpha }(\mathrm{supp}{\psi }_{\alpha }).$$

It remains to prove that ${[H_{\alpha }({\psi }_{\alpha }u)]}^l\in W^{-e,q^{\prime }}({\phi }_{\alpha }(U_{\alpha }))$. Note that

$$\begin{array}{cc}\hfill & \mathrm{for}e\ge 0{[W_0^{e,q}({\phi }_{\alpha }(U_{\alpha }))]}^{*}=W^{-e,q^{\prime }}({\phi }_{\alpha }(U_{\alpha })),\hfill \\ \hfill & \mathrm{for}e<0{[W_0^{e,q}({\phi }_{\alpha }(U_{\alpha }))]}^{*}={[W^{e,q}({\phi }_{\alpha }(U_{\alpha }))]}^{*}=W_0^{-e,q^{\prime }}({\phi }_{\alpha }(U_{\alpha }))\subseteq W^{-e,q^{\prime }}({\phi }_{\alpha }(U_{\alpha })).\hfill \end{array}$$

Consequently, for all e

$${[W_0^{e,q}({\phi }_{\alpha }(U_{\alpha }))]}^{*}\subseteq W^{-e,q^{\prime }}({\phi }_{\alpha }(U_{\alpha })).$$

Therefore, it is enough to show that

$${[H_{\alpha }({\psi }_{\alpha }u)]}^l\in {[W_0^{e,q}({\phi }_{\alpha }(U_{\alpha }))]}^{*}.$$

To this end, we need to prove that

$${[H_{\alpha }({\psi }_{\alpha }u)]}^l:(C_c^{\infty }({\phi }_{\alpha }(U_{\alpha })){,\parallel .\parallel }_{e,q})\to \mathbb{R}$$

is continuous. For all $\xi \in C_c^{\infty }({\phi }_{\alpha }(U_{\alpha }))$ we have

$$\begin{array}{cc}\hfill {[H_{\alpha }({\psi }_{\alpha }u)]}^l(\xi )& ={⟨{\psi }_{\alpha }u,g_{l,\xi ,U_{\alpha },{\phi }_{\alpha }}⟩}_{{[D(U_{\alpha },E_{U_{\alpha }}^{\vee })]}^{*}\times D(U_{\alpha },E_{U_{\alpha }}^{\vee })}={⟨u,{\psi }_{\alpha }{g}_{l,\xi ,U_{\alpha },{\phi }_{\alpha }}⟩}_{{[D(M,E^{\vee })]}^{*}\times D(M,E^{\vee })}\hfill \\ \hfill & ={⟨{[T^{-1}]}^{*}F{|}_{D(M,E)},{\psi }_{\alpha }{g}_{l,\xi ,U_{\alpha },{\phi }_{\alpha }}⟩}_{{[D(M,E^{\vee })]}^{*}\times D(M,E^{\vee })}\hfill \\ \hfill & ={⟨F{|}_{D(M,E)},T^{-1}({\psi }_{\alpha }{g}_{l,\xi ,U_{\alpha },{\phi }_{\alpha }})⟩}_{D^{*}(M,E)\times D(M,E)}=F(T^{-1}({\psi }_{\alpha }{g}_{l,\xi ,U_{\alpha },{\phi }_{\alpha }})).\hfill \end{array}$$

Thus, ${[H_{\alpha }({\psi }_{\alpha }u)]}^l$ is the composition of the following maps:

$$\begin{array}{cc}\hfill & (C_c^{\infty }({\phi }_{\alpha }(U_{\alpha })){,\parallel .\parallel }_{e,q})\to {[W_{{\phi }_{\alpha }(\mathrm{supp}{\psi }_{\alpha })}^{e,q}({\phi }_{\alpha }(U_{\alpha }))]}^{\times r}\cap {[C_c^{\infty }({\phi }_{\alpha }(U_{\alpha }))]}^{\times r}\to W_{\mathrm{supp}{\psi }_{\alpha }}^{e,q}(M,E^{\vee };{\Lambda }^{\vee })\cap C^{\infty }(M,E^{\vee })\hfill \\ \hfill & \to (C^{\infty }(M,E),\parallel {\parallel }_{e,q})\to \mathbb{R}\hfill \\ \hfill & \\ \hfill & \xi \mapsto (0,\cdots ,0,\underset{l\mathrm{th}\mathrm{position}}{\underbrace{({\psi }_{\alpha }\circ {\phi }_{\alpha }^{-1})\xi }},0,\dots ,0)\mapsto H_{E^{\vee },U_{\alpha },{\phi }_{\alpha }}^{-1}(0,\dots ,0,({\psi }_{\alpha }\circ {\phi }_{\alpha }^{-1})\xi ,0,\cdots ,0)={\psi }_{\alpha }{g}_{l,\xi ,U_{\alpha },{\phi }_{\alpha }}\hfill \\ \hfill & \mapsto T^{-1}({\psi }_{\alpha }{g}_{l,\xi ,U_{\alpha },{\phi }_{\alpha }})\mapsto F(T^{-1}({\psi }_{\alpha }{g}_{l,\xi ,U_{\alpha },{\phi }_{\alpha }})),\hfill \end{array}$$

which is a composition of continuous maps.

(6)

$S:W^{-e,q^{\prime }}(M,E;\Lambda )\to {[W^{e,q}(M,E;\Lambda )]}^{*}$ is a continuous bijective map, so by the Banach isomorphism theorem, it is a topological isomorphism.

□

Remark 61.

(1) 

The result of Theorem 100 remains valid even if $\Lambda =\{(U_{\alpha },{\phi }_{\alpha },{\rho }_{\alpha },{\psi }_{\alpha })\}$ does not trivialize the fiber metric. Indeed, if e is not a noninteger whose magnitude is greater than 1, then the Sobolev spaces $W^{e,q}$ and $W^{-e,q^{\prime }}$ are independent of the choice of augmented total trivialization atlas. If e is a noninteger whose magnitude is greater than 1, then by Theorem 37 there exists an augmented total trivialization atlas $\tilde{\Lambda }=\{(U_{\alpha },{\phi }_{\alpha },{\tilde{\rho }}_{\alpha },{\psi }_{\alpha })\}$ that trivializes the metric and has the same base atlas as Λ (so it is GL compatible with Λ because by assumption Λ is GL compatible with itself). So, we can replace Λ by $\tilde{\Lambda }$.

(2) 

Let Λ be an augmented total trivialization atlas that is GL compatible with itself. Let e be a noninteger less than $-1$ and $q\in (1,\infty )$. By Theorem 100 and the above observation, $W^{e,q}(M,E;\Lambda )$ is topologically isomorphic to ${[W^{-e,q^{\prime }}(M,E;\Lambda )]}^{*}$. However, the space $W^{-e,q^{\prime }}(M,E;\Lambda )$ is independent of Λ. So, we may conclude that even when e is a noninteger less than $-1$, the space $W^{e,q}(M,E;\Lambda )$ is independent of the choice of the augmented total trivialization atlas as long as the corresponding total trivialization atlas is GL compatible with itself.

9.3. On the Relationship between Various Characterizations

Here we discuss the relationship between the characterizations of Sobolev spaces given in Remark 54 and our original definition (Definition 30).

(1)

Suppose $e\ge 0$.

$$W^{e,q}(M,E;\Lambda )=\{u\in L^q{(M,E):\parallel u\parallel }_{W^{e,q}(M,E;\Lambda )}=\sum _{\alpha =1}^N\sum _{l=1}^r\parallel {({\rho }_{\alpha })}^l\circ ({\psi }_{\alpha }u)\circ {\phi }_{\alpha }^{-1}{\parallel }_{W^{e,q}({\phi }_{\alpha }(U_{\alpha }))}<\infty \}.$$

As a direct consequence of Theorem 92, for $e\ge 0$, $W^{e,q}(M,E;\Lambda )\hookrightarrow L^q(M,E)$ with the original definition of $W^{e,q}(M,E;\Lambda )$. Therefore, the above characterization is completely consistent with the original definition.

(2)

$$W^{e,q}(M,E;\Lambda )=\{u\in D^{\prime }{(M,E):\parallel u\parallel }_{W^{e,q}(M,E;\Lambda )}=\sum _{\alpha =1}^N\sum _{l=1}^r\parallel {\mathrm{ext}}_{{\phi }_{\alpha }(U_{\alpha }),{\mathbb{R}}^n}^0{[H_{\alpha }({\psi }_{\alpha }u)]}^l{\parallel }_{W^{e,q}({\mathbb{R}}^n)}<\infty \}.$$

It follows from Corollary 6 that

•

If e is not a noninteger less than $-1$, then

$$\parallel {[H_{\alpha }({\psi }_{\alpha }u)]}^l{\parallel }_{W^{e,q}({\phi }_{\alpha }(U_{\alpha }))}\simeq {\parallel {\mathrm{ext}}_{{\phi }_{\alpha }(U_{\alpha }),{\mathbb{R}}^n}^0{[H_{\alpha }({\psi }_{\alpha }u)]}^l\parallel }_{W^{e,q}({\mathbb{R}}^n)},$$

•

If e is a noninteger less than $-1$ and ${\phi }_{\alpha }(U_{\alpha })$ is ${\mathbb{R}}^n$ or a bounded open set with Lipschitz continuous boundary, then again the above equality holds.

Therefore, when e is not a noninteger less than $-1$, the above characterization completely agrees with the original definition. If e is a noninteger less than $-1$ and the total trivialization atlas corresponding to $\Lambda$ is GGL, then again the two definitions agree.

(3)

$$W^{e,q}(M,E;\Lambda )=\{u\in D^{\prime }(M,E):{[H_{\alpha }(u{|}_{U_{\alpha }})]}^l\in W_{loc}^{e,q}({\phi }_{\alpha }(U_{\alpha })),\forall 1\le \alpha \le N,\forall 1\le l\le r\}.$$

It follows immediately from Theorem 94 and Corollary 8 that the above characterization of the set of Sobolev functions is equivalent to the set given in the original definition provided we assume that if e is a noninteger less than $-1$, then $\Lambda$ is GL compatible with itself.

(4)

$W^{e,q}(M,E;\Lambda )$ is the completion of $C^{\infty }(M,E)$ with respect to the norm

$${\parallel u\parallel }_{W^{e,q}(M,E;\Lambda )}=\sum _{\alpha =1}^N\sum _{l=1}^r{\parallel {({\rho }_{\alpha })}^l\circ ({\psi }_{\alpha }u)\circ {\phi }_{\alpha }^{-1}\parallel }_{W^{e,q}({\phi }_{\alpha }(U_{\alpha }))}.$$

It follows from Theorem 99 that if e is not a noninteger less than $-1$ the above characterization of Sobolev spaces is equivalent to the original definition. Furthermore, if e is a noninteger less than $-1$ and $\Lambda$ is GL compatible with itself, the two characterizations are equivalent.

Now, we will focus on proving the equivalence of the original definition and the fifth characterization of Sobolev spaces. In what follows instead of ${\parallel .\parallel }_{W^{k,q}(M,E;g,{\nabla }^E)}$ we just write ${|.|}_{W^{k,q}(M,E)}$. Furthermore, note that since k is a nonnegative integer, the choice of the augmented total trivialization atlas in Definition 30 is immaterial. Our proof follows the argument presented in [44] and is based on the following five facts:

•

Fact 1: Let $u\in C^{\infty }(M,E)$ be such that $\mathrm{supp}u\subseteq U_{\beta }$ for some $1\le \beta \le N$. Then

$${|u|}_{L^q(M,E)}^q={\int }_M{|u|}_E^{q}d{V}_g\simeq \sum _l{\parallel \underset{u^l}{\underbrace{{\rho }_{\beta }^l\circ u}}\circ {\phi }_{\beta }^{-1}\parallel }_{L^q({\phi }_{\beta }(U_{\beta }))}^q.$$

•

Fact 2: Let $u\in C^{\infty }(M,E)$ be such that $\mathrm{supp}u\subseteq U_{\beta }$ for some $1\le \beta \le N$. Then

$${|u|}_{W^{k,q}(M,E)}^q\simeq \sum _{s=0}^k\sum _{a=1}^r\sum _{1\le j_1,\dots ,j_s\le n}{\parallel {\left({({\nabla }^E)}^{s}u\right)}_{j_1\dots j_s}^a\circ {\phi }_{\beta }^{-1}\parallel }_{L^q({\phi }_{\beta }(U_{\beta }))}^q.$$

Proof. 

$$\begin{array}{cc}\hfill {|u|}_{W^{k,q}(M,E)}^q& \simeq \sum _{s=0}^k{|{({\nabla }^E)}^{s}u|}_{L^q(M,{(T^{*}M)}^{\otimes i}\otimes E)}^q\hfill \\ \hfill & \stackrel{\mathrm{Fact}1}{\simeq }\sum _{s=0}^k\sum _{a=1}^r\sum _{1\le j_1,\dots ,j_s\le n}{\parallel \underset{\mathrm{components}w.r.t(U_{\beta },{\phi }_{\beta },{\rho }_{\beta })}{\underbrace{{\left({({\nabla }^E)}^{s}u\right)}_{j_1\dots j_s}^a}}\circ {\phi }_{\beta }^{-1}\parallel }_{L^q({\phi }_{\beta }(U_{\beta }))}^q.\hfill \end{array}$$

□

•

Fact 3: Let $u\in C^{\infty }(M,E)$ be such that $\mathrm{supp}u\subseteq U_{\beta }$ for some $1\le \beta \le N$. Then

$${\parallel u\parallel }_{W^{e,q}(M,E)}\simeq \sum _{l=1}^r{\parallel {\rho }_{\beta }^l\circ u\circ {\phi }_{\beta }^{-1}\parallel }_{W^{e,q}({\phi }_{\beta }(U_{\beta }))}.$$

Proof. 

Let $\{{\psi }_{\alpha }\}$ be a partition of unity such that ${\psi }_{\beta }=1$ on $\mathrm{supp}u$ (note that since elements of a partition of unity are nonnegative and their sum is equal to 1, we can conclude that if $\alpha \ne \beta$ then ${\psi }_{\alpha }=0$ on $\mathrm{supp}u$). We have

$$\begin{array}{cc}\hfill {\parallel u\parallel }_{W^{e,q}(M,E)}& \simeq \sum _{\alpha =1}^N\sum _{l=1}^r{\parallel {\rho }_{\alpha }^l\circ ({\psi }_{\alpha }u)\circ {\phi }_{\alpha }^{-1}\parallel }_{W^{e,q}({\phi }_{\alpha }(U_{\alpha }))}\hfill \\ \hfill & =\sum _{l=1}^r\parallel {\rho }_{\beta }^l\circ ({\psi }_{\beta }u)\circ {\phi }_{\beta }^{-1}{\parallel }_{W^{e,q}({\phi }_{\beta }(U_{\beta }))}=\sum _{l=1}^r{\parallel {\rho }_{\beta }^l\circ u\circ {\phi }_{\beta }^{-1}\parallel }_{W^{e,q}({\phi }_{\beta }(U_{\beta }))}.\hfill \end{array}$$

□

•

Fact 4: Let $u\in C^{\infty }(M,E)$. Then for any multi-index $\gamma$ and all $1\le l\le r$ we have (on any total trivialization triple $(U,\phi ,\rho )$):

$$|{\partial }^{\gamma }[{\rho }^l\circ u\circ {\phi }^{-1}]|⪯\sum _{s\le |\gamma |}\underset{\mathrm{sum}\mathrm{over}\mathrm{all}\mathrm{components}\mathrm{of}{({\nabla }^E)}^{s}u}{\underbrace{{\sum }_{a=1}^r{\sum }_{1\le j_1,\cdots ,j_s\le n}}}|{\left({({\nabla }^E)}^{s}u\right)}_{j_1\cdots j_s}^a\circ {\phi }^{-1}|.$$

Proof. 

For any multi-index $\gamma =({\gamma }_1,\dots ,{\gamma }_n)$ we define $\mathrm{seq}\gamma$ to be the following list of numbers:

$$\mathrm{seq}\gamma =\underset{{\gamma }_1\mathrm{times}}{\underbrace{1\dots 1}}\underset{{\gamma }_2\mathrm{times}}{\underbrace{2\cdots 2}}\dots \underset{{\gamma }_n\mathrm{times}}{\underbrace{n\dots n}}.$$

Note that there are exactly $|\gamma |={\gamma }_1+\dots +{\gamma }_n$ numbers in $\mathrm{seq}\gamma$. By Observation 2 in Section 5.5.4 we have

$${\left({({\nabla }^E)}^{|\gamma |}u\right)}_{\mathrm{seq}\gamma }^l\circ {\phi }^{-1}={\partial }^{\gamma }[{\rho }^l\circ u\circ {\phi }^{-1}]+\sum _{a=1}^r\sum _{\alpha :|\alpha |<|\gamma |}{C}_{\alpha a}{\partial }^{\alpha }[{\rho }^a\circ u\circ {\phi }^{-1}].$$

Thus

$$\begin{array}{cc}\hfill & {\partial }^{\gamma }[{\rho }^l\circ u\circ {\phi }^{-1}]={\left({({\nabla }^E)}^{|\gamma |}u\right)}_{\mathrm{seq}\gamma }^l\circ {\phi }^{-1}-\sum _{a=1}^r\sum _{\alpha :|\alpha |<|\gamma |}{C}_{\alpha a}{\partial }^{\alpha }[{\rho }^a\circ u\circ {\phi }^{-1}],\hfill \\ \hfill & {\partial }^{\alpha }[{\rho }^a\circ u\circ {\phi }^{-1}]={\left({({\nabla }^E)}^{|\alpha |}u\right)}_{\mathrm{seq}\alpha }^a\circ {\phi }^{-1}-\sum _{b=1}^r\sum _{\beta :|\beta |<|\alpha |}{C}_{\beta b}{\partial }^{\beta }[{\rho }^b\circ u\circ {\phi }^{-1}],\hfill \\ \hfill & ⋮\hfill \end{array}$$

where the coefficients $C_{\alpha a}$, $C_{\beta b}$, etc. are polynomials in terms of christoffel symbols and the metric and so they are all bounded on the compact manifold M. Consequently,

$$|{\partial }^{\gamma }[{\rho }^l\circ u\circ {\phi }^{-1}]|⪯\sum _{s\le |\gamma |}\underset{\mathrm{sum}\mathrm{over}\mathrm{all}\mathrm{components}\mathrm{of}{({\nabla }^E)}^{s}u}{\underbrace{{\sum }_{a=1}^r{\sum }_{1\le j_1,\cdots ,j_s\le n}}}|{\left({({\nabla }^E)}^{s}u\right)}_{j_1\dots j_s}^a\circ {\phi }_{\beta }^{-1}|.$$

□

•

Fact 5: Let $f\in C^{\infty }(M,E)$ and $u\in W^{k,q}(M,\tilde{E})$ where $\tilde{E}$ is another vector bundle over M. Then

$${\parallel f\otimes u\parallel }_{W^{k,q}(M,E\otimes \tilde{E})}⪯{\parallel u\parallel }_{W^{k,q}(M,\tilde{E})},$$

where the implicit constant may depend on f but it does not depend on u.

Proof. 

Let ${\{(U_{\alpha },{\phi }_{\alpha },{\rho }_{\alpha })\}}_{1\le \alpha \le N}$ and ${\{(U_{\alpha },{\phi }_{\alpha },{\tilde{\rho }}_{\alpha })\}}_{1\le \alpha \le N}$ be total trivialization atlases for E and $\tilde{E}$, respectively. Let ${\{s_{\alpha ,a}={\rho }_{\alpha }^{-1}(e_a)\}}_{a=1}^r$ be the corresponding local frame for E on $U_{\alpha }$ and ${\{t_{\alpha ,b}={\tilde{\rho }}_{\alpha }^{-1}(e_b)\}}_{b=1}^{\tilde{r}}$ be the corresponding local frame for $\tilde{E}$ on $U_{\alpha }$. Let $G:\{1,\dots ,r\}\times \{1,\dots ,\tilde{r}\}\to \{1,\dots ,r\tilde{r}\}$ be an arbitrary but fixed bijective function. Then $\{(U_{\alpha },{\phi }_{\alpha },{\widehat{\rho }}_{\alpha })\}$ is a total trivialization atlas for $E\otimes \tilde{E}$ where

$${\widehat{\rho }}_{\alpha }(s_{\alpha ,a}\otimes t_{\alpha ,b})=e_{G(a,b)}(\mathrm{as}\mathrm{an}\mathrm{element}\mathrm{of}{\mathbb{R}}^{r\tilde{r}}),$$

and it is extended by linearity to the $E\otimes \tilde{E}{|}_{U_{\alpha }}$. Now we have

$$\begin{array}{cc}\hfill {\parallel f\otimes u\parallel }_{W^{k,q}(M,E\otimes \tilde{E})}& =\sum _{\alpha =1}^N\sum _{a=1}^r\sum _{b=1}^{\tilde{r}}{\parallel {\widehat{\rho }}_{\alpha }^{a,b}\circ ({\psi }_{\alpha }f\otimes u)\circ {\phi }_{\alpha }^{-1}\parallel }_{W^{k,q}({\phi }_{\alpha }(U_{\alpha }))}\hfill \\ \hfill & =\sum _{\alpha =1}^N\sum _{a=1}^r\sum _{b=1}^{\tilde{r}}{\parallel ({\psi }_{\alpha }\circ {\phi }_{\alpha }^{-1})(f_{\alpha }^a\circ {\phi }_{\alpha }^{-1})(u_{\alpha }^b\circ {\phi }_{\alpha }^{-1})\parallel }_{W^{k,q}({\phi }_{\alpha }(U_{\alpha }))},\hfill \end{array}$$

where $f=f_{\alpha }^a{s}_{\alpha ,a}$ and $u=u_{\alpha }^b{t}_{\alpha ,b}$ on $U_{\alpha }$. Clearly $f_{\alpha }^a\circ {\phi }_{\alpha }^{-1}\in C^{\infty }({\phi }_{\alpha }(U_{\alpha }))$. Therefore,

$$\begin{array}{c}\hfill {\parallel f\otimes u\parallel }_{W^{k,q}(M,E\otimes \tilde{E})}⪯\sum _{\alpha =1}^N\sum _{b=1}^{\tilde{r}}\parallel ({\psi }_{\alpha }\circ {\phi }_{\alpha }^{-1})(u_{\alpha }^b\circ {\phi }_{\alpha }^{-1}){\parallel }_{W^{k,q}({\phi }_{\alpha }(U_{\alpha }))}\simeq {\parallel u\parallel }_{W^{k,q}(M,\tilde{E})}.\end{array}$$

□

•

Part I: First we prove that ${\parallel u\parallel }_{W^{k,q}(M,E)}⪯{|u|}_{W^{k,q}(M,E)}$.

(1)

Case 1: Suppose there exists $1\le \beta \le N$ such that $\mathrm{supp}u\subseteq U_{\beta }$. We have

$$\begin{array}{cc}\hfill {\parallel u\parallel }_{W^{k,q}(M,E)}^q& \stackrel{\mathrm{Fact}3}{\simeq }\sum _{l=1}^r\parallel {\rho }_{\beta }^l\circ u\circ {\phi }_{\beta }^{-1}{\parallel }_{W^{k,q}({\phi }_{\beta }(U_{\beta }))}^q\simeq \sum _{l=1}^r\sum _{|\gamma |\le k}{\parallel {\partial }^{\gamma }({\rho }_{\beta }^l\circ u\circ {\phi }_{\beta }^{-1})\parallel }_{L^q({\phi }_{\beta }(U_{\beta }))}^q\hfill \\ \hfill & \stackrel{\mathrm{Fact}4}{⪯}\sum _{l=1}^r\sum _{|\gamma |\le k}\sum _{s\le |\gamma |}\sum _{a=1}^r\sum _{1\le j_1,\dots ,j_s\le n}{\parallel {\left({({\nabla }^E)}^{s}u\right)}_{j_1\dots j_s}^a\circ {\phi }_{\beta }^{-1}\parallel }_{L^q({\phi }_{\beta }(U_{\beta }))}^q\hfill \\ \hfill & ⪯\sum _{s=0}^k\sum _{a=1}^r\sum _{1\le j_1,\dots ,j_s\le n}{\parallel {\left({({\nabla }^E)}^{s}u\right)}_{j_1\dots j_s}^a\circ {\phi }_{\beta }^{-1}\parallel }_{L^q({\phi }_{\beta }(U_{\beta }))}^q\hfill \\ \hfill & \stackrel{\mathrm{Fact}2}{\simeq }{|u|}_{W^{k,q}(M,E)}^q.\hfill \end{array}$$

(2)

Case 2: Now let u be an arbitrary element of $C^{\infty }(M,E)$. We have

$$\begin{array}{cc}\hfill {\parallel u\parallel }_{W^{k,q}(M,E)}& =\parallel \sum _{\alpha =1}^N{\psi }_{\alpha }{u\parallel }_{W^{k,q}(M,E)}\le \sum _{\alpha =1}^N{\parallel {\psi }_{\alpha }u\parallel }_{W^{k,q}(M,E)}\hfill \\ \hfill & ⪯\sum _{\alpha =1}^N{|{\psi }_{\alpha }u|}_{W^{k,q}(M,E)}(\mathrm{by}\mathrm{what}\mathrm{was}\mathrm{proved}\mathrm{in}\mathrm{Case}1)\hfill \\ \hfill & ⪯\sum _{\alpha =1}^N{|u|}_{W^{k,q}(M,E)}\simeq {|u|}_{W^{k,q}(M,E)}.\hfill \end{array}$$

We note that the last inequality holds because

$$\begin{array}{cc}\hfill |{\psi }_{\alpha }{u|}_{W^{k,q}(M,E)}^q& =\sum _{i=0}^k{\parallel {({\nabla }^E)}^i({\psi }_{\alpha }u)\parallel }_{L^q(M,{(T^{*}M)}^{\otimes i}\otimes E)}^q\hfill \\ \hfill & =\sum _{i=0}^k{\parallel \sum _{j=0}^i\left(\genfrac{}{}{0pt}{}{i}{j}\right){\nabla }^j{\psi }_{\alpha }\otimes {({\nabla }^E)}^{i-j}u\parallel }_{L^q(M,{(T^{*}M)}^{\otimes i}\otimes E)}^q\hfill \\ \hfill & \stackrel{\mathrm{Fact}5}{⪯}\sum _{i=0}^k\sum _{j=0}^i{\parallel {({\nabla }^E)}^{i-j}u\parallel }_{L^q(M,{(T^{*}M)}^{\otimes (i-j)}\otimes E)}^q\hfill \\ \hfill & ⪯\sum _{s=0}^k\parallel {({\nabla }^E)}^s{u\parallel }_{L^q(M,{(T^{*}M)}^{\otimes s}\otimes E)}^q\simeq {|u|}_{W^{k,q}(M,E)}^q.\hfill \end{array}$$

•

Part II: Now we show that ${|u|}_{W^{k,q}(M,E)}⪯{\parallel u\parallel }_{W^{k,q}(M,E)}$.

(1)

Case 1: Suppose there exists $1\le \beta \le N$ such that $\mathrm{supp}u\subseteq U_{\beta }$.

$$\begin{array}{cc}\hfill & {|u|}_{W^{k,q}(M,E)}^q\stackrel{\mathrm{Fact}2}{\simeq }\sum _{s=0}^k\sum _{a=1}^r\sum _{1\le j_1,\dots ,j_s\le n}{\parallel {\left({({\nabla }^E)}^{s}u\right)}_{j_1\dots j_s}^a\circ {\phi }_{\beta }^{-1}\parallel }_{L^q({\phi }_{\beta }(U_{\beta }))}^q\hfill \\ \hfill & \stackrel{\mathrm{Observation}1\mathrm{in}\mathrm{5.5.4}}{=}\sum _{s=0}^k\sum _{a=1}^r\sum _{1\le j_1,\dots ,j_s\le n}{\parallel \sum _{|\eta |\le s}\sum _{l=1}^r{(C_{\eta l})}_{j_1\dots j_s}^a{\partial }^{\eta }(\underset{{\rho }_{\beta }^l\circ u}{\underbrace{u^l}}\circ {\phi }_{\beta }^{-1})\parallel }_{L^q({\phi }_{\beta }(U_{\beta }))}^q\hfill \\ \hfill & ⪯\sum _{l=1}^r\sum _{|\eta |\le k}\parallel {\partial }^{\eta }(u^l\circ {\phi }_{\beta }^{-1}){\parallel }_{L^q({\phi }_{\beta }(U_{\beta }))}^q=\sum _{l=1}^r{\parallel u^l\circ {\phi }_{\beta }^{-1}\parallel }_{W^{k,q}({\phi }_{\beta }(U_{\beta }))}^q\hfill \\ \hfill & \simeq {\parallel u\parallel }_{W^{k,q}(M,E)}^q.\hfill \end{array}$$

(2)

Case 2: Now let u be an arbitrary element of $C^{\infty }(M,E)$.

$$\begin{array}{cc}\hfill {|u|}_{W^{k,q}(M,E)}& =|\sum _{\alpha =1}^N{\psi }_{\alpha }{u|}_{W^{k,q}(M,E)}\le \sum _{\alpha =1}^N{|{\psi }_{\alpha }u|}_{W^{k,q}(M,E)}\hfill \\ \hfill & \stackrel{\mathrm{Case}1}{⪯}\sum _{\alpha =1}^N\parallel {\psi }_{\alpha }{u\parallel }_{W^{k,q}(M,E)}\stackrel{\mathrm{Fact}3}{\simeq }\sum _{\alpha =1}^N\sum _{l=1}^r{\parallel {\rho }_{\alpha }^l\circ ({\psi }_{\alpha }u)\circ {\phi }_{\alpha }^{-1}\parallel }_{W^{k,q}({\phi }_{\alpha }(U_{\alpha }))}\hfill \\ \hfill & \simeq {\parallel u\parallel }_{W^{k,q}(M,E)}.\hfill \end{array}$$

10. Some Results on Differential Operators

Let $M^n$ be a compact smooth manifold. Let E and $\tilde{E}$ be two vector bundles over M of ranks r and $\tilde{r}$, respectively. A linear operator $P:C^{\infty }(M,E)\to \Gamma (M,\tilde{E})$ is called local if

$$\forall u\in C^{\infty }(M,E)\mathrm{supp}Pu\subseteq \mathrm{supp}u.$$

If P is a local operator, then it is possible to have a well-defined notion of restriction of P to open sets $U\subseteq M$, that is, if $P:C^{\infty }(M,E)\to \Gamma (M,\tilde{E})$ is local and $U\subseteq M$ is open, then we can define a map

$${P|}_U:C^{\infty }(U,E_U)\to \Gamma (U,{\tilde{E}}_U)$$

with the property that

$$\forall u\in C^{\infty }(M,E)(Pu){{|}_U=P|}_U(u{|}_U).$$

Indeed, suppose $u,\tilde{u}\in C^{\infty }(M,E)$ agree on U, then as a result of P being local we have

$$\mathrm{supp}(Pu-P\tilde{u})\subseteq \mathrm{supp}(u-\tilde{u})\subseteq M\backslash U.$$

Therefore, if ${u|}_U=\tilde{u}{|}_U$, then ${(Pu)|}_U=(P\tilde{u}){|}_U$. Thus, if $v\in C^{\infty }(U,E_U)$ and $x\in U$, we can define $(P{|}_U)(v)(x)$ as follows: choose any $u\in C^{\infty }(M,E)$ such that $u=v$ on a neighborhood of x and then let $(P{|}_U)(v)(x)=(Pu)(x)$.

Recall that for any nonempty set V, $\mathrm{Func}(V,{\mathbb{R}}^t)$ denotes the vector space of all functions from V to ${\mathbb{R}}^t$. By the local representation of P with respect to the total trivialization triples $(U,\phi ,\rho )$ of E and $(U,\phi ,\tilde{\rho })$ of $\tilde{E}$ we mean the linear transformation $Q:C^{\infty }(\phi (U),{\mathbb{R}}^r)\to \mathrm{Func}(\phi (U),{\mathbb{R}}^{\tilde{r}})$ defined by

$$Q(f)=\tilde{\rho }\circ P({\rho }^{-1}\circ f\circ \phi )\circ {\phi }^{-1}.$$

Note that ${\rho }^{-1}\circ f\circ \phi$ is a section of $E_U\to U$. Furthermore, note that for all $u\in C^{\infty }(M,E)$

$$\tilde{\rho }\circ (P(u{|}_U))\circ {\phi }^{-1}=Q(\rho \circ (u{|}_U)\circ {\phi }^{-1}).$$

(9)

Let us denote the components of $f\in C^{\infty }(\phi (U),{\mathbb{R}}^r)$ by $(f^1,\dots ,f^r)$. Then we can write $Q(f^1,\cdots ,f^r)=(h^1,\dots ,h^{\tilde{r}})$ where for all $1\le k\le \tilde{r}$

$$h^k={\pi }_k\circ Q(f^1,\dots ,f^r)\stackrel{Q\mathrm{is}\mathrm{linear}}{=}{\pi }_k\circ Q(f^1,0,\dots ,0)+\dots +{\pi }_k\circ Q(0,\dots ,0,f^r).$$

So, if for each $1\le k\le \tilde{r}$ and $1\le i\le r$ we define $Q_{ki}:C^{\infty }(\phi (U),\mathbb{R})\to \mathrm{Func}(\phi (U),\mathbb{R})$ by

$$Q_{ki}(g)={\pi }_k\circ Q(0,\dots ,0,\underset{\mathrm{ith}\mathrm{position}}{\underbrace{g}},0,\dots ,0),$$

then we have

$$Q(f^1,\dots ,f^r)=(\sum _{i=1}^r{Q}_{1i}(f^i),\dots ,\sum _{i=1}^r{Q}_{\tilde{r}i}(f^i)).$$

In particular, note that the sth component of $\tilde{\rho }\circ Pu\circ {\phi }^{-1}$, that is ${\tilde{\rho }}^s\circ Pu\circ {\phi }^{-1}$, is equal to the sth component of $Q({\rho }^1\circ u\circ {\phi }^{-1},\cdots ,{\rho }^r\circ u\circ {\phi }^{-1})$ (see Equation (9)) which is equal to

$$\sum _{i=1}^r{Q}_{si}({\rho }^i\circ u\circ {\phi }^{-1}).$$

Theorem 101.

Let $M^n$ be a compact smooth manifold. Let $P:C^{\infty }(M,E)\to \Gamma (M,\tilde{E})$ be a local operator. Let $\Lambda ={\{(U_{\alpha },{\phi }_{\alpha },{\rho }_{\alpha },{\psi }_{\alpha })\}}_{1\le \alpha \le N}$ and $\tilde{\Lambda }={\{(U_{\alpha },{\phi }_{\alpha },{\tilde{\rho }}_{\alpha },{\psi }_{\alpha })\}}_{1\le \alpha \le N}$ be two augmented total trivialization atlases for E and $\tilde{E}$, respectively. Suppose the atlas ${\{(U_{\alpha },{\phi }_{\alpha })\}}_{1\le \alpha \le N}$ is GL compatible with itself. For each $1\le \alpha \le N$, let $Q^{\alpha }$ denote the local representation of P with respect to the total trivialization triples $(U_{\alpha },{\phi }_{\alpha },{\rho }_{\alpha })$ and $(U_{\alpha },{\phi }_{\alpha },{\tilde{\rho }}_{\alpha })$ of E and $\tilde{E}$, respectively. Suppose $e,\tilde{e}\in \mathbb{R}$, $1<q,\tilde{q}<\infty$, and for each $1\le \alpha \le N$, $1\le i\le \tilde{r}$, and $1\le j\le r$,

$$Q_{ij}^{\alpha }:(C_c^{\infty }({\phi }_{\alpha }(U_{\alpha })){,\parallel .\parallel }_{e,q})\to W_{loc}^{\tilde{e},\tilde{q}}({\phi }_{\alpha }(U_{\alpha }))$$

is well-defined and continuous and does not increase support. Then

•

$P(C^{\infty }(M,E))\subseteq W^{\tilde{e},\tilde{q}}(M,\tilde{E};\tilde{\Lambda })$,

•

$P:(C^{\infty }{(M,E),\parallel .\parallel }_{e,q})\to W^{\tilde{e},\tilde{q}}(M,\tilde{E};\tilde{\Lambda })$ is continuous and so it can be extended to a continuous linear map $P:W^{e,q}(M,E;\Lambda )\to W^{\tilde{e},\tilde{q}}(M,\tilde{E};\tilde{\Lambda })$.

Proof. 

First note that

$$\begin{array}{cc}\hfill & {\parallel Pu\parallel }_{W^{\tilde{e},\tilde{q}}(M,\tilde{E};\tilde{\Lambda })}=\sum _{\alpha =1}^N\sum _{i=1}^{\tilde{r}}{\parallel {\tilde{\rho }}_{\alpha }^i\circ ({\psi }_{\alpha }(Pu))\circ {\phi }_{\alpha }^{-1}\parallel }_{W^{\tilde{e},\tilde{q}}({\phi }_{\alpha }(U_{\alpha }))},\hfill \\ \hfill & {\parallel u\parallel }_{W^{e,q}(M,E;\Lambda )}=\sum _{\alpha =1}^N\sum _{j=1}^r{\parallel {\rho }_{\alpha }^j\circ ({\psi }_{\alpha }u)\circ {\phi }_{\alpha }^{-1}\parallel }_{W^{e,q}({\phi }_{\alpha }(U_{\alpha }))}.\hfill \end{array}$$

It is enough to show that for all $1\le \alpha \le N$, $1\le i\le \tilde{r}$

$$\parallel {\tilde{\rho }}_{\alpha }^i\circ ({\psi }_{\alpha }(Pu))\circ {\phi }_{\alpha }^{-1}{\parallel }_{W^{\tilde{e},\tilde{q}}({\phi }_{\alpha }(U_{\alpha }))}⪯\sum _{\beta =1}^N\sum _{j=1}^r{\parallel {\rho }_{\beta }^j\circ ({\psi }_{\beta }u)\circ {\phi }_{\beta }^{-1}\parallel }_{W^{e,q}({\phi }_{\beta }(U_{\beta }))}.$$

We have

$$\begin{array}{cc}\hfill \parallel {\tilde{\rho }}_{\alpha }^i& \circ ({\psi }_{\alpha }(Pu))\circ {\phi }_{\alpha }^{-1}{\parallel }_{W^{\tilde{e},\tilde{q}}({\phi }_{\alpha }(U_{\alpha }))}={\parallel ({\psi }_{\alpha }\circ {\phi }_{\alpha }^{-1})·({\tilde{\rho }}_{\alpha }^i\circ (Pu)\circ {\phi }_{\alpha }^{-1})\parallel }_{W^{\tilde{e},\tilde{q}}({\phi }_{\alpha }(U_{\alpha }))}\hfill \\ \hfill & \le \sum _{j=1}^r{\parallel ({\psi }_{\alpha }\circ {\phi }_{\alpha }^{-1})·Q_{ij}^{\alpha }({\rho }_{\alpha }^j\circ (\sum _{\beta =1}^N{\psi }_{\beta }u)\circ {\phi }_{\alpha }^{-1})\parallel }_{W^{\tilde{e},\tilde{q}}({\phi }_{\alpha }(U_{\alpha }))}\hfill \\ \hfill & (\mathrm{see}\mathrm{the}\mathrm{paragraph}\mathrm{above}\mathrm{Theorem}101)\hfill \\ \hfill & \le \sum _{\beta =1}^N\sum _{j=1}^r{\parallel ({\psi }_{\alpha }\circ {\phi }_{\alpha }^{-1})·Q_{ij}^{\alpha }({\rho }_{\alpha }^j\circ ({\psi }_{\beta }u)\circ {\phi }_{\alpha }^{-1})\parallel }_{W^{\tilde{e},\tilde{q}}({\phi }_{\alpha }(U_{\alpha }))}\hfill \\ \hfill & =\sum _{\beta =1}^N\sum _{j=1}^r{\parallel ({\psi }_{\alpha }\circ {\phi }_{\alpha }^{-1})·Q_{ij}^{\alpha }({\rho }_{\alpha }^j\circ (\xi {\psi }_{\beta }u)\circ {\phi }_{\alpha }^{-1})\parallel }_{W^{\tilde{e},\tilde{q}}({\phi }_{\alpha }(U_{\alpha }))},\hfill \end{array}$$

where $\xi \in C_c^{\infty }(U_{\alpha })$ is a fixed function such that $\xi =1$ on $\mathrm{supp}{\psi }_{\alpha }$. Using the assumption that $Q_{ij}^{\alpha }:(C_c^{\infty }({\phi }_{\alpha }(U_{\alpha })){,\parallel .\parallel }_{e,q})\to W_{loc}^{\tilde{e},\tilde{q}}({\phi }_{\alpha }(U_{\alpha }))$ is continuous we get

$$\begin{array}{cc}\hfill \parallel {\tilde{\rho }}_{\alpha }^i& \circ ({\psi }_{\alpha }(Pu))\circ {\phi }_{\alpha }^{-1}{\parallel }_{W^{\tilde{e},\tilde{q}}({\phi }_{\alpha }(U_{\alpha }))}⪯\sum _{\beta =1}^N\sum _{j=1}^r{\parallel {\rho }_{\alpha }^j\circ (\xi {\psi }_{\beta }u)\circ {\phi }_{\alpha }^{-1}\parallel }_{W^{e,q}({\phi }_{\alpha }(U_{\alpha }))}.\hfill \end{array}$$

Note that ${\rho }_{\alpha }^j\circ (\xi {\psi }_{\beta }u)\circ {\phi }_{\alpha }^{-1}=(\xi {\psi }_{\beta }\circ {\phi }_{\alpha }^{-1})({\rho }_{\alpha }^j\circ u\circ {\phi }_{\alpha }^{-1})$ has compact support in ${\phi }_{\alpha }(U_{\alpha }\cap U_{\beta })$. So, it follows from Corollary 6 that

$$\begin{array}{cc}\hfill & \parallel {\rho }_{\alpha }^j\circ (\xi {\psi }_{\beta }u)\circ {\phi }_{\alpha }^{-1}{\parallel }_{W^{e,q}({\phi }_{\alpha }(U_{\alpha }))}\simeq {\parallel {\rho }_{\alpha }^j\circ (\xi {\psi }_{\beta }u)\circ {\phi }_{\alpha }^{-1}\parallel }_{W^{e,q}({\phi }_{\alpha }(U_{\alpha }\cap U_{\beta }))}.\hfill \end{array}$$

Therefore,

$$\begin{array}{cc}\hfill \parallel {\tilde{\rho }}_{\alpha }^i& \circ ({\psi }_{\alpha }(Pu))\circ {\phi }_{\alpha }^{-1}{\parallel }_{W^{\tilde{e},\tilde{q}}({\phi }_{\alpha }(U_{\alpha }))}\hfill \\ \hfill & ⪯\sum _{\beta =1}^N\sum _{j=1}^r{\parallel {\rho }_{\alpha }^j\circ (\xi {\psi }_{\beta }u)\circ {\phi }_{\alpha }^{-1}\parallel }_{W^{e,q}({\phi }_{\alpha }(U_{\alpha }\cap U_{\beta }))}\hfill \\ \hfill & =\sum _{\beta =1}^N\sum _{j=1}^r{\parallel {\rho }_{\alpha }^j\circ (\xi {\psi }_{\beta }u)\circ {\phi }_{\beta }^{-1}\circ {\phi }_{\beta }\circ {\phi }_{\alpha }^{-1}\parallel }_{W^{e,q}({\phi }_{\alpha }(U_{\alpha }\cap U_{\beta }))}\hfill \\ \hfill & \stackrel{\mathrm{Theorem}80}{⪯}\sum _{\beta =1}^N\sum _{j=1}^r{\parallel {\rho }_{\alpha }^j\circ (\xi {\psi }_{\beta }u)\circ {\phi }_{\beta }^{-1}\parallel }_{W^{e,q}({\phi }_{\beta }(U_{\alpha }\cap U_{\beta }))}.\hfill \end{array}$$

So, it is enough to prove that $\parallel {\rho }_{\alpha }^j\circ (\xi {\psi }_{\beta }u)\circ {\phi }_{\beta }^{-1}{\parallel }_{W^{e,q}({\phi }_{\beta }(U_{\alpha }\cap U_{\beta }))}$ can be bounded by ${\sum }_{\beta =1}^N{\sum }_{j=1}^r{\parallel {\rho }_{\beta }^j\circ ({\psi }_{\beta }u)\circ {\phi }_{\beta }^{-1}\parallel }_{W^{e,q}({\phi }_{\beta }(U_{\beta }))}$. Since this can be done in the exact same way as the proof of Theorem 88, we do not repeat the argument here. □

Here we will discuss one simple application of the above theorem. Let $(M^n,g)$ be a compact Riemannian manifold with $g\in W^{s,p}(M,T^{2}M)$, $sp>n$, and $s\ge 1$. Consider $d:C^{\infty }(M)\to C^{\infty }(T^{*}M)$. The local representations are all assumed to be with respect to charts in a super nice total trivialization atlas that is GL compatible with itself. The local representation of d is $Q:C^{\infty }(\phi (U))\to C^{\infty }(\phi (U),{\mathbb{R}}^n)$ which is defined by

$$\begin{array}{cc}\hfill Q(f)(a)& =\tilde{\rho }\circ d({\rho }^{-1}\circ f\circ \phi )\circ {\phi }^{-1}(a)\hfill \\ \hfill & =\tilde{\rho }\circ (\frac{\partial f}{\partial x^i}{|}_{\phi ({\phi }^{-1}(a))}d{x}^i{|}_{{\phi }^{-1}(a)})\hfill \\ \hfill & =(\frac{\partial f}{\partial x^1}{|}_a,\dots ,\frac{\partial f}{\partial x^n}{|}_a).\hfill \end{array}$$

Here we used $\rho =Id$ and the fact that if $g:M\to \mathbb{R}$ is smooth, then

$$(dg)(p)=\frac{\partial (g\circ {\phi }^{-1})}{\partial x^i}{{|}_{\phi (p)}d{x}^i|}_p.$$

Clearly, each component of Q is a continuous operator from $(C_c^{\infty }(\phi (U)),\parallel .{\parallel }_{e,q})$ to $W^{e-1,q}(\phi (U))\hookrightarrow W_{loc}^{e-1,q}(\phi (U))$ (see Theorem 82; note that $\phi (U)={\mathbb{R}}^n$). Hence d can be viewed as a continuous operator from $W^{e,q}(M)$ to $W^{e-1,q}(T^{*}M)$.

Several other interesting applications of Theorem 101 can be found in [16].

11. Conclusions

Sobolev-Slobodeckij spaces play a key role in the study of elliptic differential operators in nonsmooth setting. In this manuscript, we focused on establishing certain fundamental properties of Sobolev-Slobodeckij spaces that are particularly useful in better understanding the behavior of elliptic differential operators on compact manifolds. In particular, we built a general framework for developing multiplication theorems, embedding results, etc. for Sobolev–Slobodeckij spaces on compact manifolds. We paid special attention to spaces with noninteger smoothness order and to general sections of vector bundles. We established in particular that, as long as $1<q<\infty$ and $e\ge 0$ or $e\in \mathbb{Z}$,

•

Various common standard characterizations of $W^{e,q}$ (as discussed in Section 9) are equivalent;

•

The local charts definition of $W^{e,q}$ is independent of the chosen atlas;

•

Nice properties of $W^{e,q}$ for smooth domains in ${\mathbb{R}}^n$ (such as embedding properties and multiplication properties) will carry over to $W^{e,q}$ of sections of vector bundles.

Furthermore, we noticed that the local representations of elements of $W^{e,q}$ (for functions on M or, more generally, sections of vector bundles) will not necessarily be in the corresponding Euclidean Sobolev-Slobodeckij space; they should be viewed as elements of locally Sobolev-Slobodeckij spaces on the Euclidean space (we have devoted a separate manuscript [17] to the study of the properties of locally Sobolev-Slobodeckij spaces on the Euclidean space). In the same spirit, in Section 10 we observed that locally Sobolev-Slobodeckij spaces can be considered as the appropriate target spaces in the study of the local representations of differential operators between Sobolev–Slobodeckij spaces of sections of vector bundles. For the case where $e<-1$ is noninteger, we were not able to prove the validity of these properties in a general setting; however, by introducing notions such as “geometrically Lipschitz atlases”, we found sufficient conditions that guarantee the validity of similar results as those we have for the case where $e\in \mathbb{Z}$.