Numerical Study of Natural Convection of Power Law Fluid in a Square Cavity Fitted with a Uniformly Heated T-Fin
Abstract
:1. Introduction
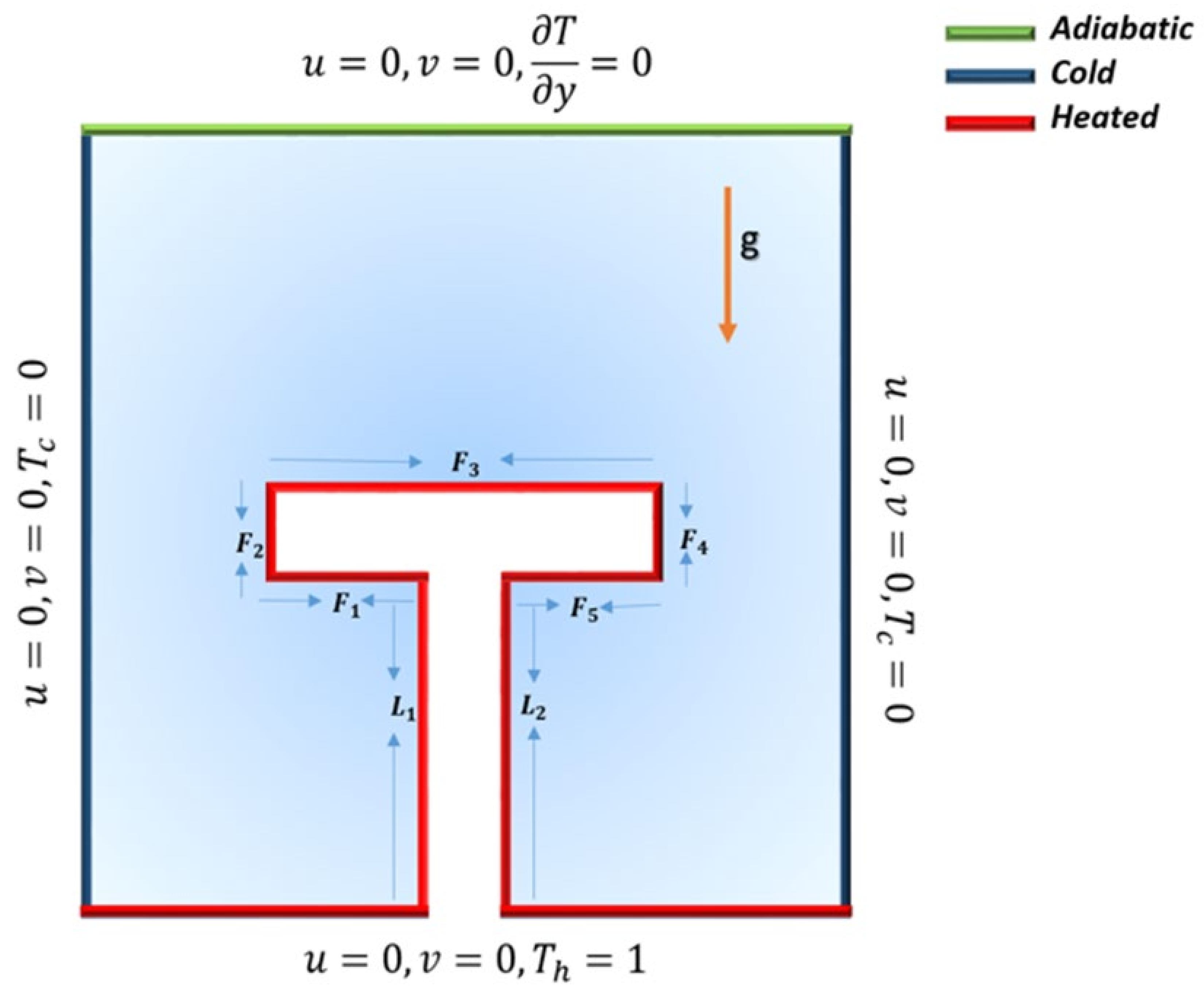
2. Problem Definition and Mathematical Formulation
3. Numerical Details
3.1. Discretization of Equations
3.2. Grid Independence Test
Quantities of Engineering Interest
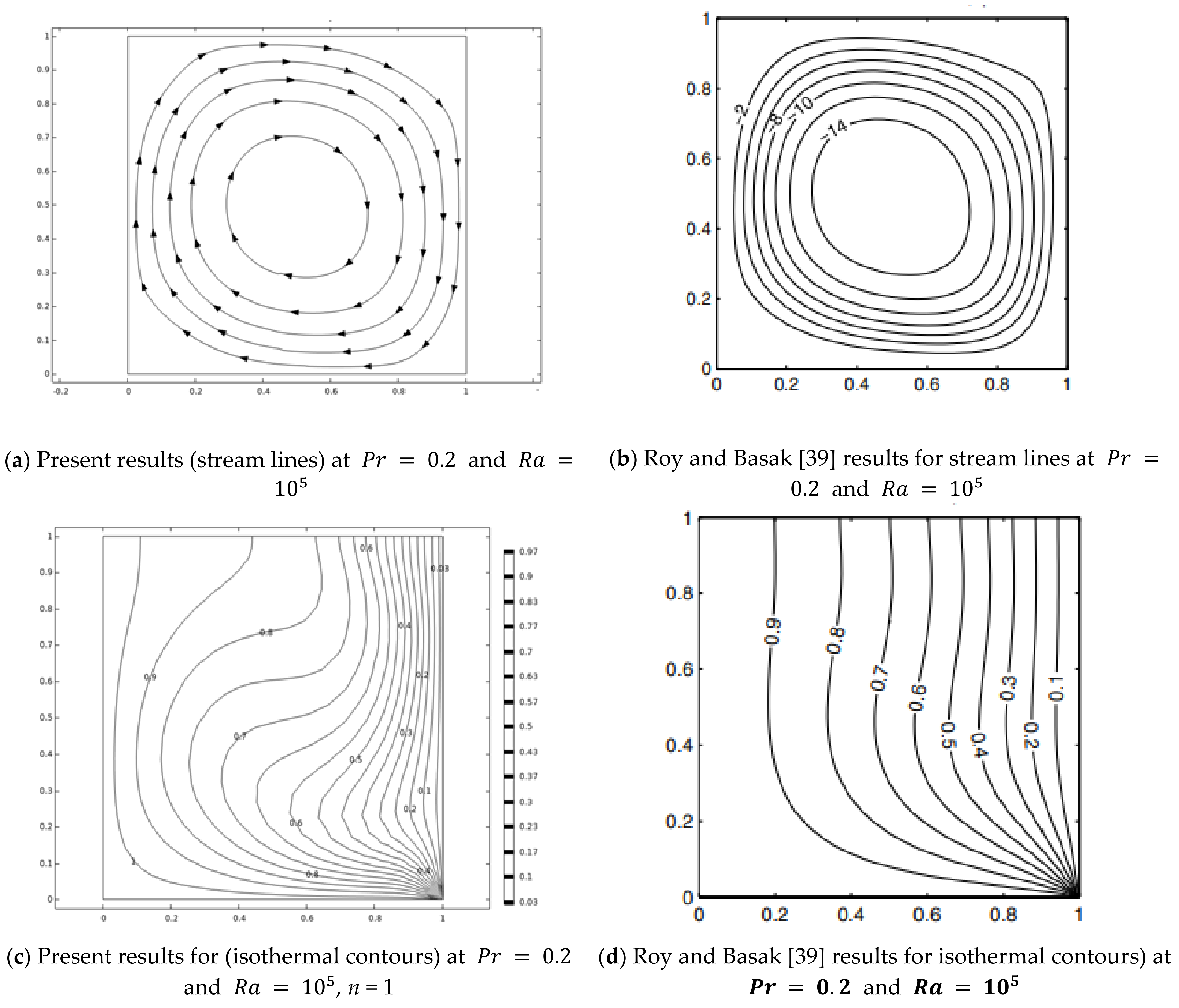
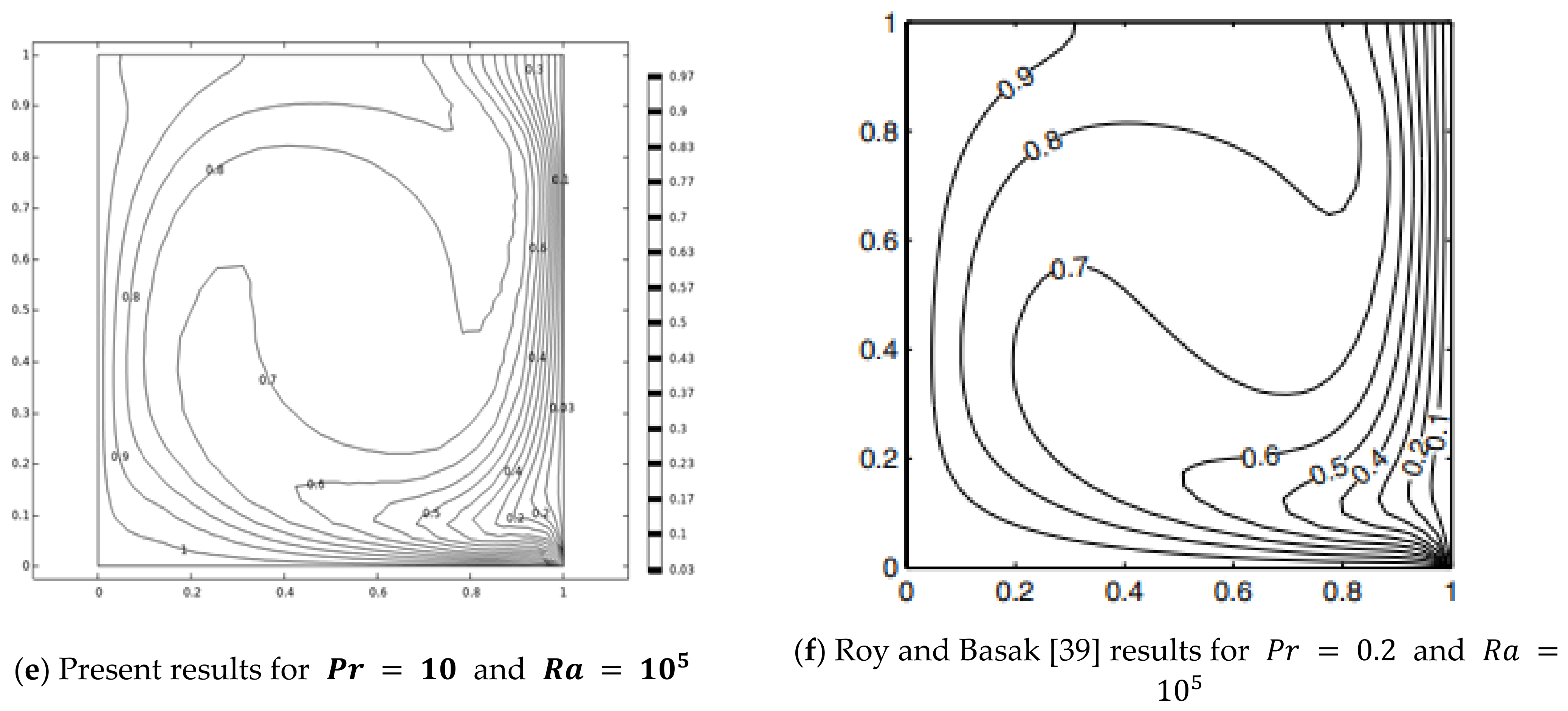
3.3. Result Validation
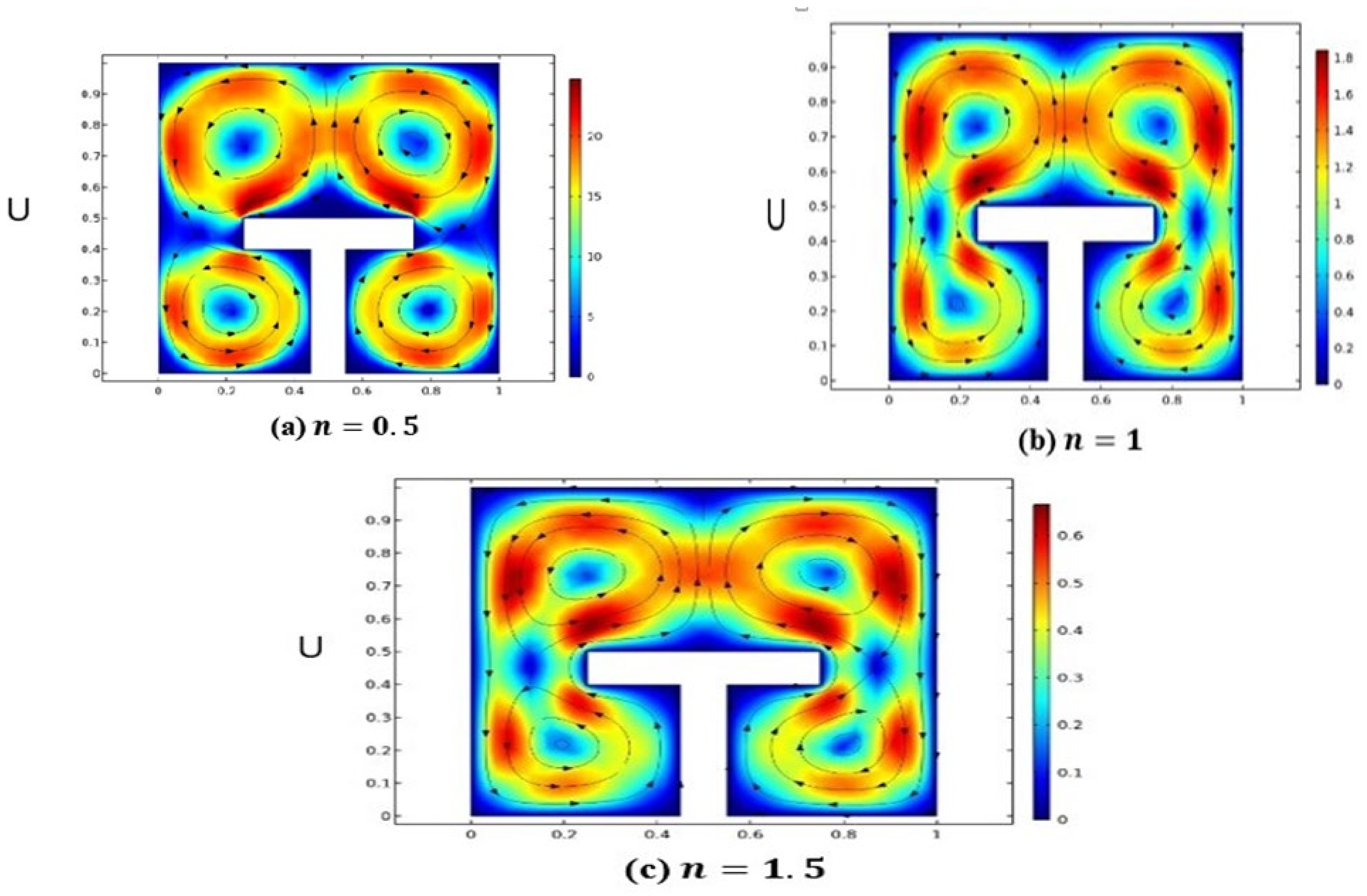
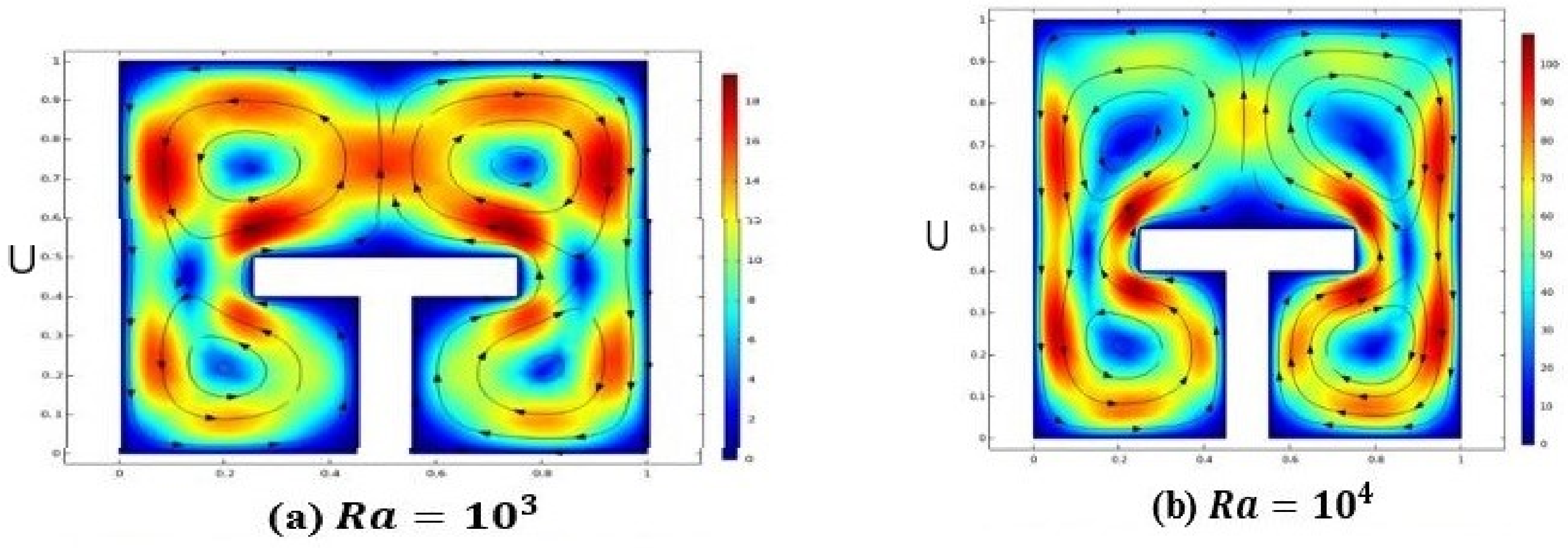
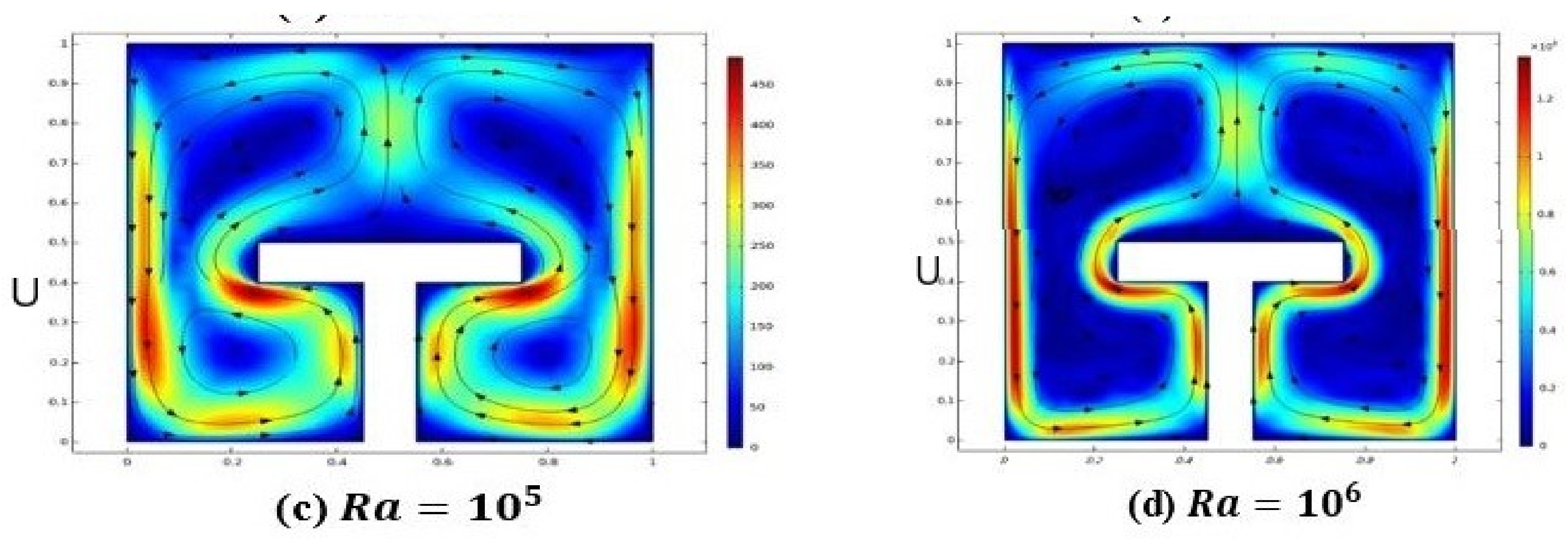
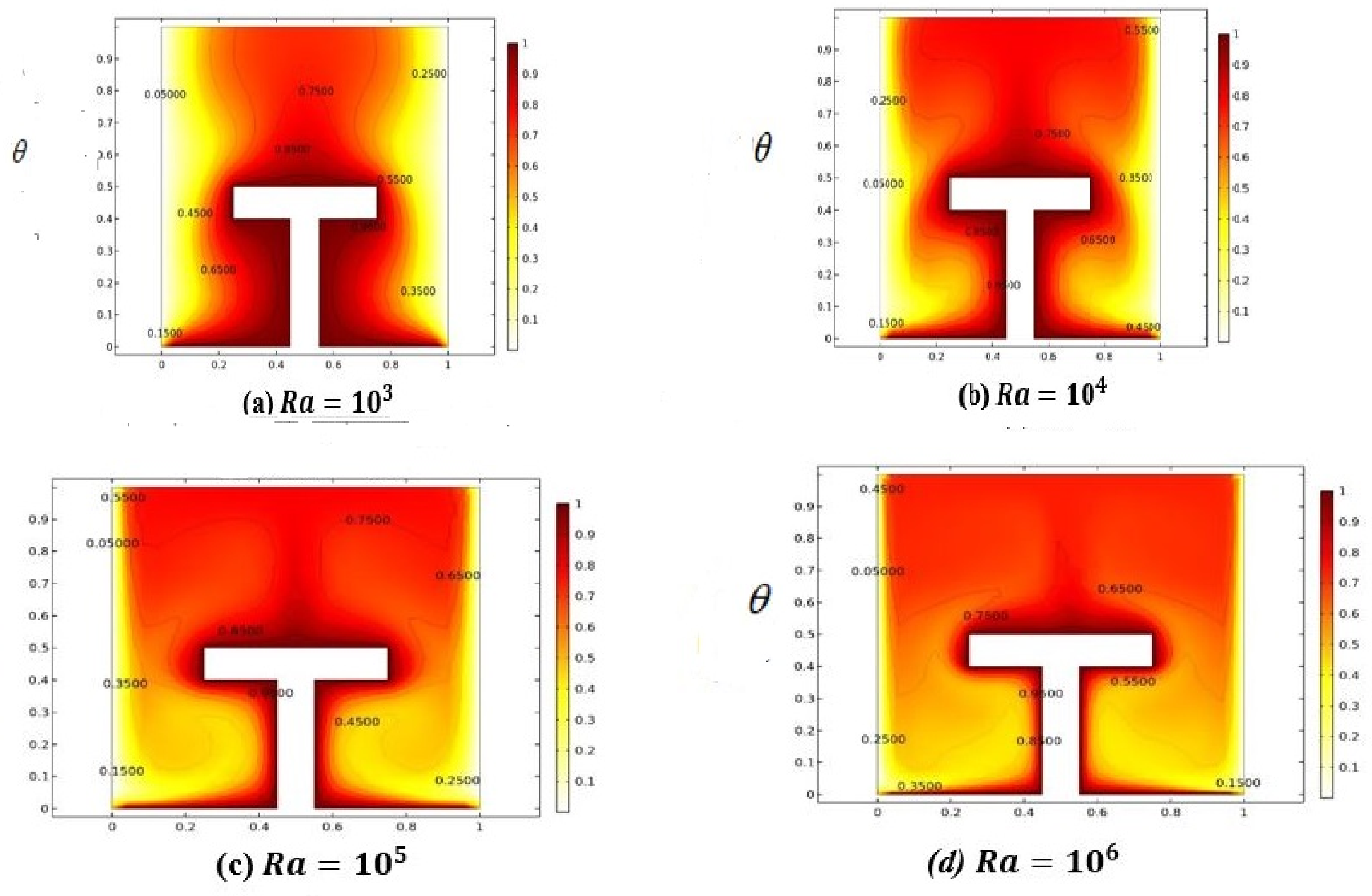
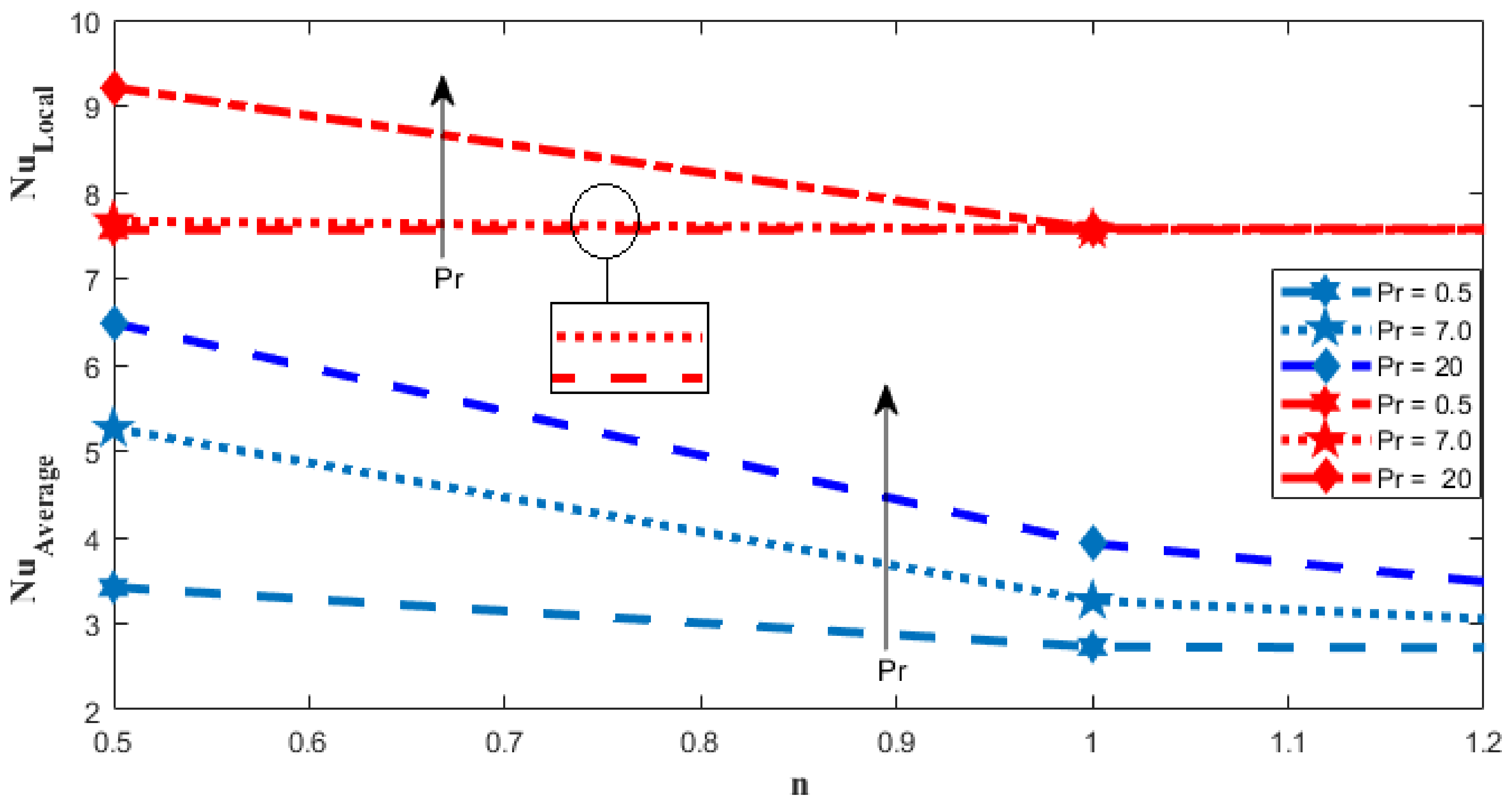
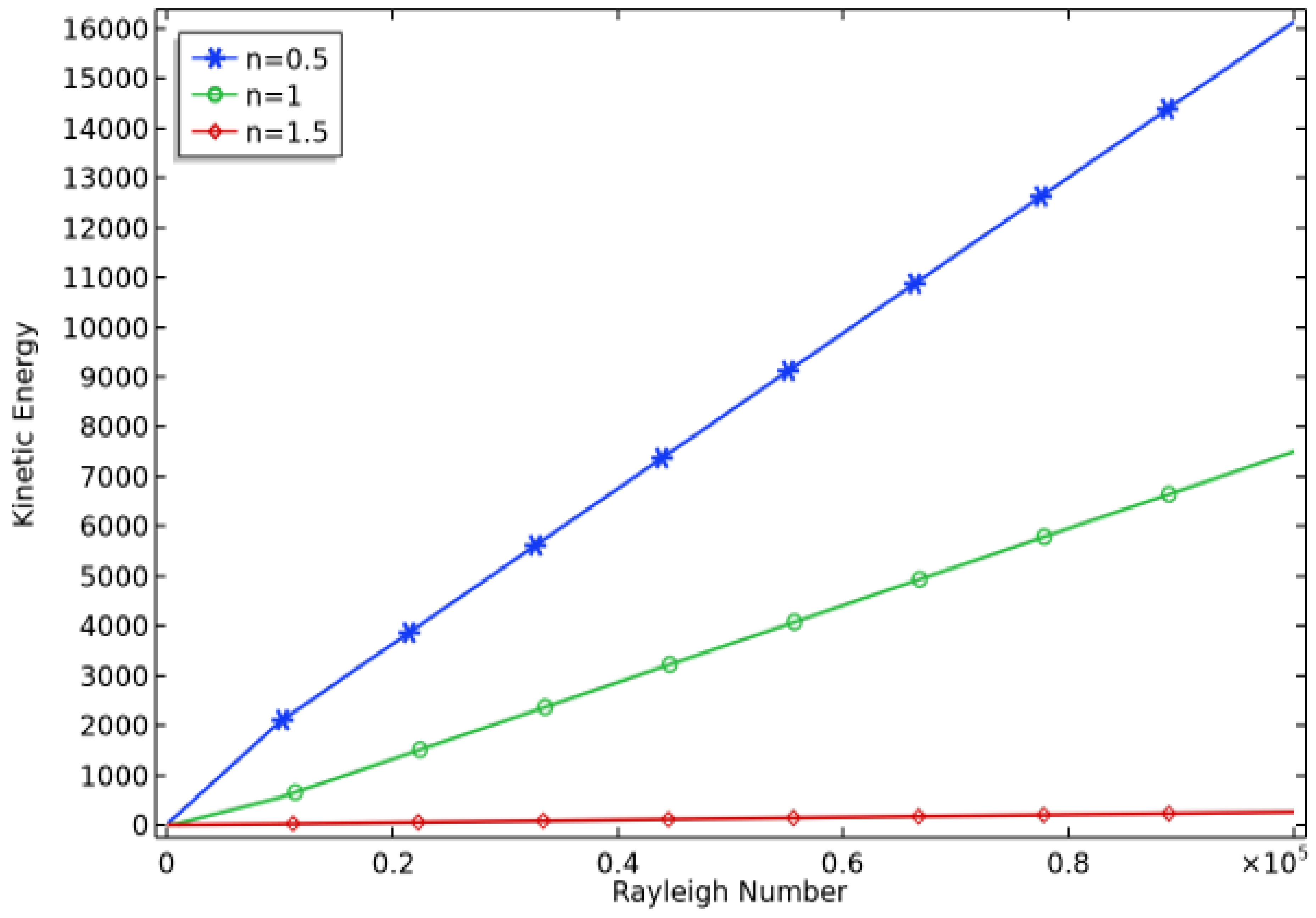
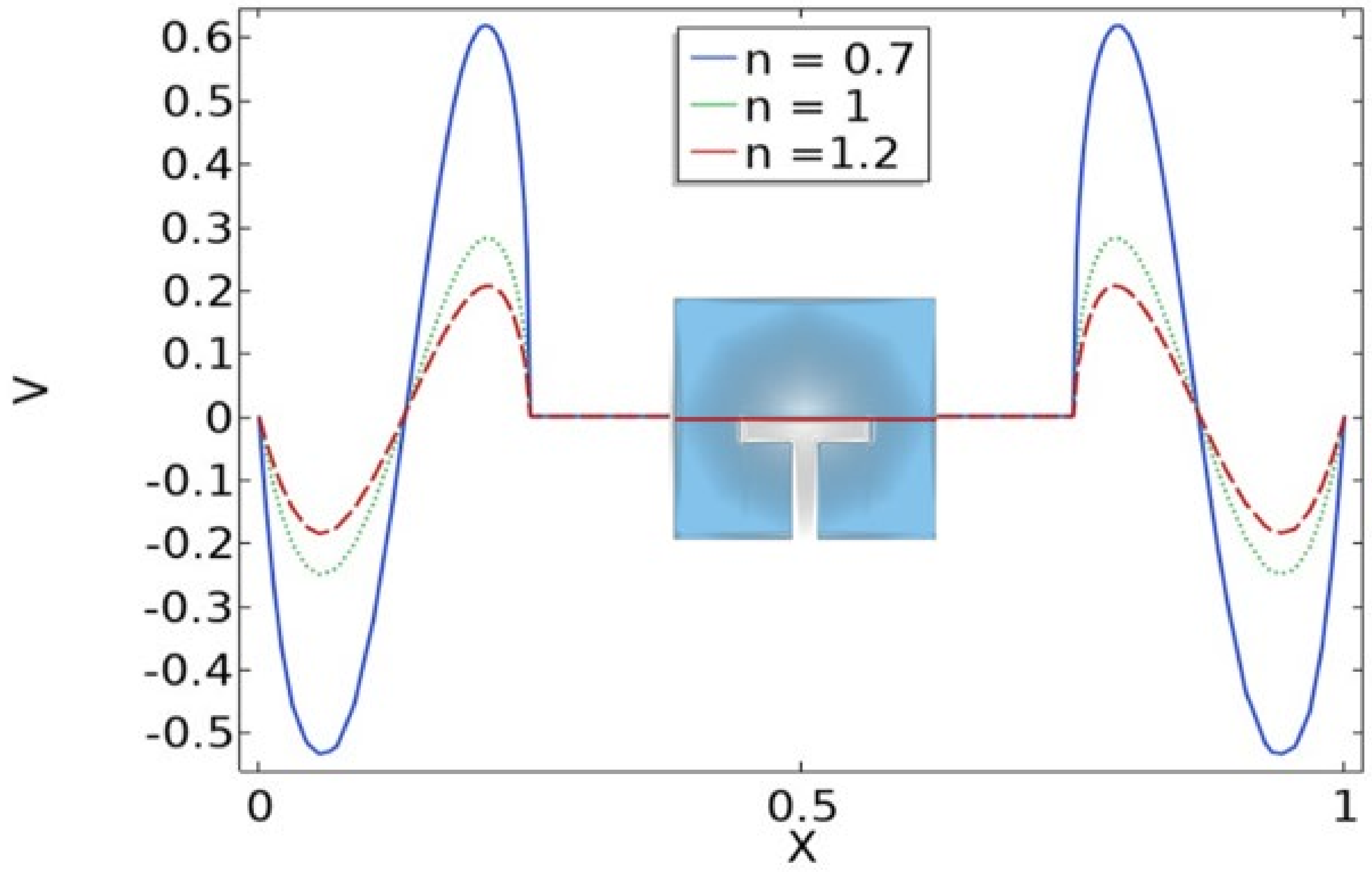
4. Discussion of Results
5. Conclusions
- •
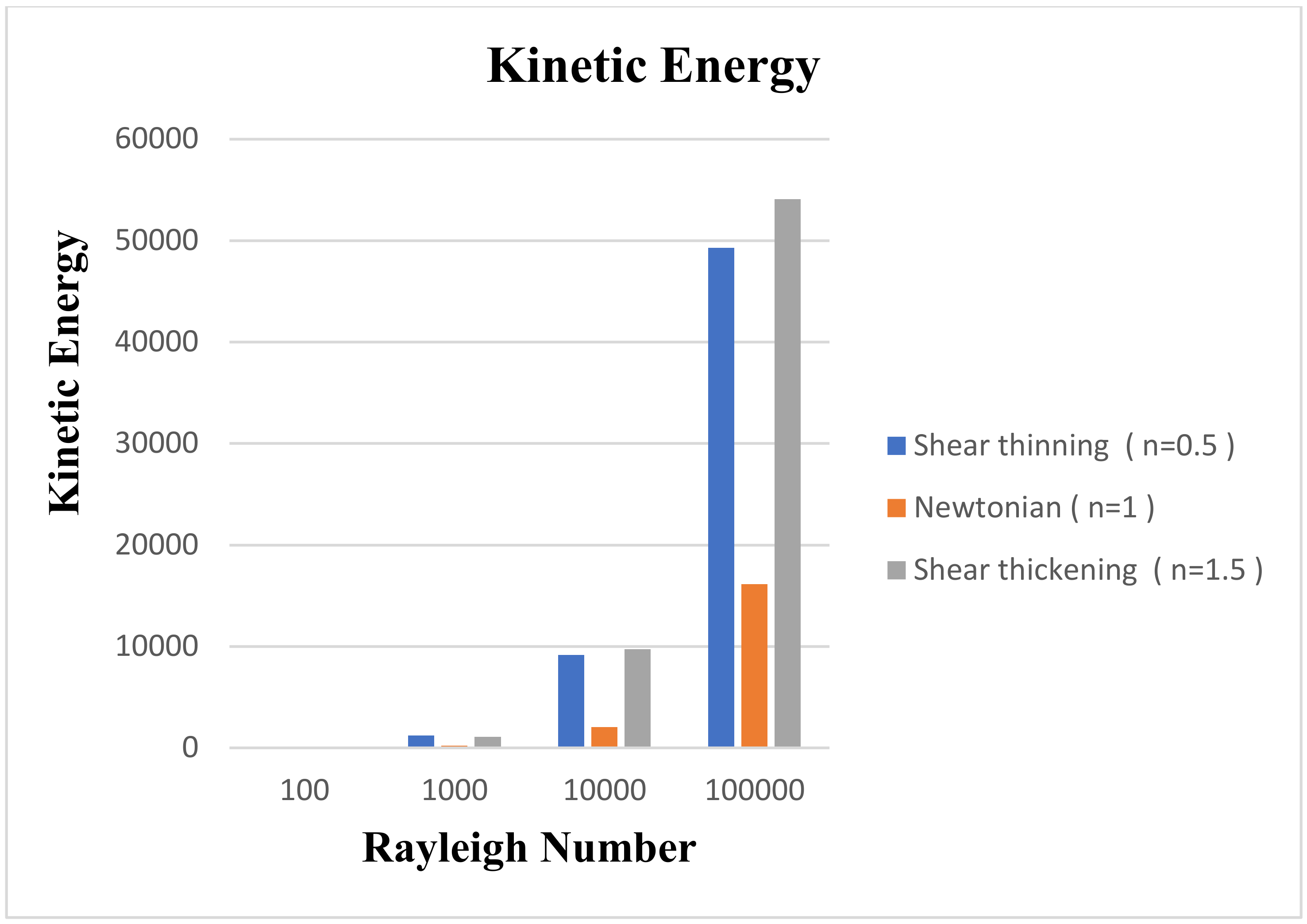
- It is inferred that kinetic energy and heat flux coefficient increase with an increase in the Rayleigh number.
- •
- It is deduced that the increment in the power-law index decreases the kinetic energy and local and average Nusselt numbers.
- •
- The magnitude of kinetic energy and Nusselt number for shear thinning fluid is comparatively higher than for shear thickening and Newtonian cases.
- •
- Increase in temperature distribution is observed against the Rayleigh number due to the generation of temperature differences.
- •
- Local and average heat transfer coefficients enhance with increases in the Prandtl number.
- •
- Magnitude of heat transmission enriches with an increase in the Rayleigh number.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Eckert, E.R.G.; Carlson, W.O. Natural Convection in an Air Layer Enclosed Between Two Vertical Plates with Different Temperatures. Int. J. Heat Mass Transf. 1961, 2, 106–120. [Google Scholar] [CrossRef]
- Newell, M.E.; Schmidt, F.W. Heat Transfer by Laminar Natural Convection within Rectangular Enclosures. ASME J. Heat Transf. 1970, 92, 159–168. [Google Scholar] [CrossRef]
- Bonnett, W.S.; McIntire, V.L. Dissipation effects in hydrodynamic stability of viscoelastic fluids. AIChE J. 1975, 21, 901–910. [Google Scholar] [CrossRef]
- Tamotsu, H.; Utaro, I.; Teiriki, T. Heat Transfer by Natural Convection in an Enclosed Cavity—A Part of Bottom is Heated. Kagaku Kogaku Ronbunshu 1975, 1, 450–453. [Google Scholar]
- Flack, R.D.; Konopnicki, T.; Rooke, J.H. The measurement of natural convective heat transfer in triangular enclosures. J. Heat Transf. 1979, 101, 770–782. [Google Scholar] [CrossRef]
- Davis, G.D.V. Natural convection of air in a square cavity: A bench mark numerical solution. Int. J. Num. Methods Fluids 1983, 3, 249–264. [Google Scholar] [CrossRef]
- Hasnaoui, M.; Bilgen, E.; Vasseur, P. Natural convection heat transfer in rectangular cavities heated from below. J. Thermophys. Heat Transf. 1992, 38, 255–264. [Google Scholar] [CrossRef]
- Aydin, O.; Yang, J. Natural convection in enclosures with localized heating from below and symmetrical cooling from sides. Int. J. Numer. Methods Heat Fluid Flow 2000, 10, 518–529. [Google Scholar] [CrossRef]
- Shojaeian, M.; Kosar, A. Convective heat transfer and entropy generation analysis on Newtonian and non-Newtonian fluid flows between parallel-plates under slip boundary conditions. Int. J. Heat Mass Transf. 2014, 70, 664–673. [Google Scholar] [CrossRef]
- Sharif, M.A.R.; Mohammad, T.R. Natural convection in cavities with constant flux heating at the bottom wall and isothermal cooling from the sidewalls. Int. J. Therm. Sci. 2005, 44, 865–878. [Google Scholar] [CrossRef]
- Alebrahim, A.; Bejan, A. Constructal trees of circular fins for conductive and convective heat transfer. Int. J. Heat Mass Transf. 1999, 42, 3585–3597. [Google Scholar] [CrossRef]
- Almogbel, M.; Bejan, A. Cylindrical trees of pin fins. Int. J. Heat Mass Transf. 2000, 43, 4285–4297. [Google Scholar] [CrossRef]
- Kraus, A.D.; Aziz, A.; Welty, J.R. Extended Surface Heat Transfer; John Wiley: New York, NY, USA, 2002. [Google Scholar]
- Lorenzini, G.; Biserni, C.; Isoldi, L.A.; Dos Santos, E.D.; Rocha, L.A.O. Constructal design applied to the geometric optimization of Y-shaped cavities embedded in a conducting medium. J. Electron. Packag. 2011, 133, 041008. [Google Scholar] [CrossRef]
- Abdi, A.; Martin, V.; Chiu, J.N. Numerical investigation of melting in a cavity with vertically oriented fins. Appl. Energy 2019, 235, 1027–1040. [Google Scholar] [CrossRef]
- Bendaraa, A.; Charafi, M.M.; Hasnaoui, A. Numerical study of natural convectionin a differentially heated square cavity filled with nanofluid in the presence of fins attached to walls in different locations. Phys. Fluids 2019, 31, 5355. [Google Scholar] [CrossRef]
- Shi, X.; Khodadadi, J.M. Laminar natural convection heat transfer in a differentially heated square cavity due to a thin fin on the hot wall. J. Heat Transf. 2003, 125, 624–634. [Google Scholar] [CrossRef]
- Horbach, C.D.S.; dos Santos, E.D.; Isoldi, L.A.; Rocha, L.A.O. Constructal design of Y-shaped conductive pathways for cooling a heat-generating body. Defect Diffus. Forum 2014, 348, 245–260. [Google Scholar] [CrossRef]
- Rehman, K.; Kouz, W.A.; Sherif, E.S.; AbdelMalek, Z. Hybrid meshed analysis on rhombus shaped solid material domain (RSSMD) equipped with non-Newtonian liquid stream. J. Sci. Adv. Mater. 2020, 5, 476–486. [Google Scholar] [CrossRef]
- Tavana, M.; Pourmehran, O.; Aghaei, A.; Sangara, J.A.; Gorji, B.M. Numerical Analysis of Fluid Flow and Heat Transfer in Microchannels with Various Internal Fins. Int. J. Artif. Intell. Mechatron. 2015, 3, 2320–2331. [Google Scholar]
- Scozia, R.; Frederick, R.L. Natural Convection in Slender Cavities with Multiple Fins Attached on an Active Wall. Numer. Heat Transf. 1991, 20, 127–158. [Google Scholar] [CrossRef]
- Facas, G.N. Natural Convection in a Cavity with Fins Attached to Both Vertical Walls. J. Thermophys. Heat Transf. 1993, 7, 555–560. [Google Scholar] [CrossRef]
- Bahiraei, M.; Heshmatian, S.; Goodarzi, M.; Moayedi, H. CFD analysis of employing a novel ecofriendly nanofluid in a miniature pin fin heat sink for cooling of electronic components: Effect of different configurations. Adv. Powder Technol. 2019, 30, 2503–2516. [Google Scholar] [CrossRef]
- Li, Z.; Sarfaraz, M.M.; Mazinani, A.; Hayat, T.; Alsulami, H. Pool boiling heat transfer to CuO-H2O nanofluid on finned surfaces. Int. J. Heat Mass Transf. 2020, 156, 119780. [Google Scholar] [CrossRef]
- Ozoe, H.; Churchill, S.W. Hydrodynamic stability and natural convection in Ostwald–de Waele and Ellis fluids: The development of a numerical solution. AIChE J. 1972, 18, 1196–1207. [Google Scholar] [CrossRef]
- Kaddiri, M.; Naïmi, M.; Raji, A.; Hasnaoui, M. Rayleigh Benard convection of non-Newtonian power-law fluids with temperature-dependent viscosity. ISRN Thermodyn. 2012, 2012, 10. [Google Scholar] [CrossRef] [Green Version]
- Kim, G.B.; Hyun, J.M.; Kwak, H.S. Transient buoyant convection of a power-law non-Newtonian fluid in an enclosure. Int. J. Heat Mass Transf. 2003, 46, 3605–3617. [Google Scholar]
- Makayssi, T.; Lamsaadi, M.; Naïmi, M.; Hasnaoui, M. Natural convection heat transfer in shallow horizontal rectangular enclosures uniformly heated from the side and filled with non-Newtonian power law fluids. Energy Convers. Manag. 2006, 47, 2535–2551. [Google Scholar]
- Abderrahmane, H.; Brahim, N.; Abdelfatah, B.; Nouereddine, A.M. Laminar natural convection of power-law fluid in a differentially heated inclined square cavity. Ann. Chim.-Sci. Mat. 2017, 41, 261–281. [Google Scholar] [CrossRef]
- Khezzar, L.; Siginer, D.; Vinogradov, I. Natural convection of power law fluids in inclined cavities. Therm. Sci. 2017, 53, 8–17. [Google Scholar] [CrossRef]
- Turan, O.; Sachdeva, A.; Chakraborty, N.; Poole, R.J. Laminar natural convection of power-law fluids in a square enclosure with differentially heated side walls subjected to constant temperatures. J. Non-Newton. Fluid Mech. 2011, 166, 1049–1063. [Google Scholar] [CrossRef]
- Ternik, P.; Rudolf, R. Laminar natural convection of non-Newtonian nanofluid in a square enclosure whit differentially heated side walls. Int. J. Simul. Modeling 2013, 12, 5–16. [Google Scholar] [CrossRef]
- Sojoudi, A.; Saha, S.C.; Gu, Y.; Hossain, M.A. Steady natural convection of non-Newtonian power-law fluid in a trapezoidal enclosure. Adv. Mech. Eng. 2013, 53, 653–668. [Google Scholar] [CrossRef] [Green Version]
- Turan, O.; Sachdeva, A.; Poole, R.J.; Chakraborty, N. Aspect ratio and boundary conditions effects on laminar natural convection of power-law fluids in a rectangular enclosure with differentially heated side walls. Int. J. Heat Mass Transf. 2013, 60, 722–738. [Google Scholar] [CrossRef]
- Ternik, P.; Buchmeister, J. Buoyacy-induced flow and heat transfer of power law fluids in a side heated square cavity. Int. J. Simul. Model. 2015, 14, 238–249. [Google Scholar] [CrossRef]
- Alloui, Z.; Vasseur, P. Natural convection of Carreau–Yasuda non-Newtonian fluids in a vertical cavity heated from the sides. Int. J. Heat Mass Transf. 2015, 84, 912–924. [Google Scholar] [CrossRef]
- Nirmalkar, N.; Chhabra, R.P.; Poole, R.J. Effect of shear-thinning behavior on heat transfer from a heated sphere in yield-stress fluids. Ind. Eng. Chem. Res. 2017, 53, 13490–13504. [Google Scholar] [CrossRef]
- Ouertatani, N.; Ben Cheikh, N.; Ben Beya, B.; Lili, T. Numerical simulation of two-dimensional Rayleigh–Bénard convection in an enclosure. Comptes Rendus Mécanique 2008, 336, 464–470. [Google Scholar] [CrossRef]
- Roy, S.; Basak, T. Finite element analysis of natural convection flows in a square cavity with non-uniformly heated wall(s). Int. J. Eng. Sci. 2005, 43, 668–680. [Google Scholar] [CrossRef]
- Nirmalkar, N.; Gupta, A.K.; Chhabra, R.P. Natural Convection from a Heated Sphere in Bingham Plastic Fluids. Ind. Eng. Chem. Res. 2014, 53, 17818–17832. [Google Scholar] [CrossRef]
- Gupta, S.; Patel, S.A.; Chhabra, R.P. Pulsatile flow of power-law fluids over a heated cylinder: Flow and heat transfer characteristics. Int. J. Therm. Sci. 2020, 152, 106330. [Google Scholar] [CrossRef]
- Mishra, L.; Chhabra, R.P. Combined effects of fluid yield stress and geometrical arrangement on natural convection in a square duct from two differentially heated horizontal cylinders. J. Therm. Sci. Eng. Appl. 2020, 011016. [Google Scholar] [CrossRef]
- Sasmal, C.; Gupta, A.K.; Chhabra, R.P. Natural convection heat transfer in a power-law fluid from a heated rotating cylinder in a square duct. Int. J. Heat Mass Transf. 2020, 1, 975–996. [Google Scholar] [CrossRef]
- Mishra, L.; Chhabra, R.R. Natural convection in power-law fluids in a square enclosure from two differentially heated horizontal cylinders. Heat Transf. Eng. 2018, 39, 819–842. [Google Scholar] [CrossRef]
- Raisi, A. Natural Convection of Non-Newtonian Fluids in a Square Cavity with a Localized Heat Source. Stroj. Vestnik/J. Mech. Eng. 2016, 62, 10–22. [Google Scholar] [CrossRef]


| Levels | Number of Elements | Degree of Greedom | Kinetic Energy | |
|---|---|---|---|---|
| Extremely Coarse | 454 | 1264 | 5.7142 | |
| Extra Coarse | 660 | 1808 | 6.2082 | |
| Coarser | 1008 | 2636 | 6.6154 | |
| Coarse | 1812 | 4556 | 7.2062 | |
| Normal | 2675 | 6528 | 8.5638 | |
| Fine | 4147 | 9772 | 8.8640 | |
| Finer | 10,680 | 24,368 | 8.8644 |
| n | [30] | [33] | |
|---|---|---|---|
| 0.6 | 6.9345 | 7.020 | 6.9872 |
| 0.8 | 5.5127 | − | 5.6200 |
| 1.0 | 4.6993 | 3.741 | 4.6990 |
| 1.2 | 3.1709 | − | 3.1705 |
| 1.4 | 3.7869 | 3.770 | 3.7870 |
| Power Law Index (n) | Local Nusselt Number | Kinetic Energy |
|---|---|---|
| 0.5 | 9.214687249 | 105.4262823501 |
| 1 | 7.579833344 | 34.408781197 |
| 1.5 | 7.566853799 | 95.137400379 |
| Ra | Shear Thinning n = 0.5 | Newtonian n = 1 | Shear Thickening n = 1.5 |
|---|---|---|---|
| 100 | 9.214 | 7.579 | 7.566 |
| 1000 | 14,364 | 8.528 | 7.607 |
| 10,000 | 23,208 | 14,055 | 8.253 |
| 100,000 | 36,322 | 25,311 | 11,063 |
| Rayleigh Number | Shear Thinning n = 0.5 | Newtonian n = 1 | Shear Thickening n = 1.5 |
|---|---|---|---|
| 100 | 105,426 | 34,408 | 95,137 |
| 1000 | 1,207,006 | 211,448 | 1,076,050 |
| 10,000 | 9,173,715 | 2,065,724 | 9,719,185 |
| 100,000 | 49,296,473 | 16,134,383 | 54,104,160 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bilal, S.; Khan, N.Z.; Shah, I.A.; Awrejcewicz, J.; Akgül, A.; Riaz, M.B. Numerical Study of Natural Convection of Power Law Fluid in a Square Cavity Fitted with a Uniformly Heated T-Fin. Mathematics 2022, 10, 342. https://doi.org/10.3390/math10030342
Bilal S, Khan NZ, Shah IA, Awrejcewicz J, Akgül A, Riaz MB. Numerical Study of Natural Convection of Power Law Fluid in a Square Cavity Fitted with a Uniformly Heated T-Fin. Mathematics. 2022; 10(3):342. https://doi.org/10.3390/math10030342
Chicago/Turabian StyleBilal, Sardar, Noor Zeb Khan, Imtiaz Ali Shah, Jan Awrejcewicz, Ali Akgül, and Muhammad Bilal Riaz. 2022. "Numerical Study of Natural Convection of Power Law Fluid in a Square Cavity Fitted with a Uniformly Heated T-Fin" Mathematics 10, no. 3: 342. https://doi.org/10.3390/math10030342
APA StyleBilal, S., Khan, N. Z., Shah, I. A., Awrejcewicz, J., Akgül, A., & Riaz, M. B. (2022). Numerical Study of Natural Convection of Power Law Fluid in a Square Cavity Fitted with a Uniformly Heated T-Fin. Mathematics, 10(3), 342. https://doi.org/10.3390/math10030342










