Abstract
The current research on iterative learning control focuses on the condition where the system relative degree is equal to 1, while the condition where the system relative degree is equal to 0 or greater than 1 is not considered. Therefore, this paper studies the monotonic convergence of the corresponding dynamic iterative learning controller systematically for discrete linear repetitive processes with different relative degrees. First, a 2D discrete Roesser model of the iterative learning control system is presented by means of 2D systems theory. Then, the monotonic convergence condition of the controlled system is analyzed according to the stability theory of linear repetitive process. Furthermore, the sufficient conditions of the controller existence are given in linear matrix inequality format under different relative degrees, which guarantees the system dynamic performance. Finally, through comparison with static controllers under different relative degrees, the simulation results show that the designed schemes are effective and feasible.
Keywords:
linear repetitive process; relative degrees; dynamic iterative learning control; monotonic convergence; linear matrix inequality MSC:
93C05
1. Introduction
Iterative learning control (hereafter abbreviated as ILC) is suitable for executing repetitive operation tasks in finite time. The strategy is to use the previous control experience and output error to repeatedly adjust the present system input, and then the system output is able to track the desired trajectory [1,2]. There are different application scenarios in the field of ILC. The research in [3,4] studied state-observer-based ILC algorithms and PD-type ILC algorithms, respectively, in systems with arbitrary relative degrees. The uncertain system survey in [5,6] is also an important domain for ILC application. Additionally, monotonic convergence and controller design have always been hot issues [7,8,9].
Linear repetitive processes under ILC are usually regarded as two-dimensional systems on the time and batch axes. Research on ILC system-design methods and convergence performance on the basis of 2D system theory has become an important direction for the development of ILC technology [10,11]. Based on the theory of 2D systems, the work in [12,13] discussed a comprehensive predictive ILC strategy to ensure the fast convergence performance of the learning process under model error and uncertain disturbance. In [14,15], a high-order ILC controller was proposed according to the stability theory of linear repetitive processes, which optimized the monotonic convergence and robust performance of the system.
Based on discrete linear repetitive processes of actuator failure, the authors of [16,17] proposed a comprehensive design method of an integrated iterative learning fault-tolerant controller with state feedback and gave sufficient conditions for a closed-loop system to remain stable in the case of failure using Lyapunov stability theory. In [18,19], a P-type ILC algorithm was proposed for high relative linear multivariable discrete systems with iterative initial error.
These existing design methods use static state feedback and feedforward information to improve the system performance. However, in some cases, the static iterative learning controller may be highly conservative, and it is difficult to meet certain performance requirements of the system. In this case, dynamic ILC control law is a better choice method. In terms of the error convergence between channels, relevant applications showed that the dynamic ILC outperforms the static controller. In [20,21], a dynamic ILC controller is proposed to make the system tracking error converge rapidly along the iterative direction.
The authors of [22,23] used 2D system theory to design the controller, but the stability analysis and applicable cases are not completely given. In [24,25], a dynamic filter is designed; however, it is difficult to control the system stability for uncertain systems. For the system with an uncertain ILC model, a dynamic filter was designed to make the system error converge in [26,27], while both of these papers did not consider the system fault.
The research in [28] introduced an ILC method on the basis of the iterative moving-average operator, which is applied in nonlinear dynamic systems with random variable test lengths. The work in [29,30] designed a dynamic ILC law based on the repetitive process setting method for three-dimensional cranes and space manipulator individually, while the research on ILC in systems with a relative degree greater than 1 is relatively rare, the above research only considers the ILC with a relative degree of 1 and does not consider the situation where the system relative degree is equal to 0 or greater than 1.
In view of this, this paper studies the system monotonic convergence under the dynamic ILC algorithm for discrete linear repetitive processes with different degrees of relativity. Combined with 2D system theory, a 2D discrete Roesser model of an ILC system is established. The stability theory of linear repetitive processes is used to analyze the system monotone convergence condition. The sufficient condition for the controller existence is given in linear matrix inequality (hereafter abbreviated as LMI) format, it guarantees the dynamic performance.
In this paper, for matrices X, and are the transpositions and orthogonal complements, respectively; and mean that X is positive definite and negative definite separately; I and 0 represent a unit and zero matrix, respectively; symbol “∀” represents the element transposition in a symmetrical position; represents the part of the matrix X; and represents a diagonal matrix.
2. Problem Description
We consider below the state space model with iteration as follows:
where the iteration period t satisfies ; system iteration times ; n, m, and l are the system state, input and output at time t and batch k; boundary condition represents the system initial status at batch k; and D are the corresponding system matrices of proper dimension.
Suppose that system (1) is stable and the relative degree , which has the following characteristics [31]:
- (1)
- if and the row is full of rank, then ;
- (2)
- if the system meets the following conditions:
- (a)
- for all , there are and ;
- (b)
- and the row is full of rank.
In ILC process of system (1), we make its desired trajectory and define the tracking error as follows:
For a given state space model (1), considering the different relative degrees of the system, this paper designs appropriate control inputs to make the tracking error monotonic convergent along the batch direction. At the same time, the system stability along the time axis is also guaranteed.
3. Iterative Learning Control for Linear Repetitive Processes
For batch , state space model [32] of discrete linear repetitive processes running on finite periods is as follows:
where n, m, l represent system state, input, output at time t and batch k, respectively. Set boundary conditions and as known vector functions, the stability condition of linear repetitive processes (3) satisfies the below lemmas.
Lemma 1
([32]). The linear repetitive process described in (3) is stable if and only if the following inequality is established:
(i) , its modulus is strictly less than 1 to ensure convergence along the batch.
(ii) , its modulus is strictly less than 1 to ensure convergence along time.
(iii) All the eigenvalues modulus of transfer function are strictly less than 1 on a unit circle of complex plane , thereby, ensuring convergence along time and the batch.
Lemma 2
([33]). Given a matrix with proper dimensions and M, there is for , and the below conditions are equivalent:
(1) There exists to hold the below inequality:
(2) There exists array to hold the below inequality:
To make system (3) convergent, we propose Theorem 1.
Theorem 1.
If matrices , exist, the following LMI is established:
Then, the linear repetitive process (3) is stable.
Proof of Theorem 1.
The is the frequency response matrix of transfer function matrix in Lemma 1, and then we can obtain
When , for , there is , which satisfies condition (iii) of Lemma 1. In addition, from (6), we find
As , the below inequalities hold, and then the following inequality is also true
where , condition (ii) and (i) of Lemma 1 are also satisfied, respectively. □
4. Design of a Dynamic Iterative Learning Control System
To obtain the form of (6) to ensure system (3) is stable, we propose Theorems 2 and 3 for dynamic ILC algorithms in systems with different relative degrees.
Lemma 3
(The Projection Theorem [34]). Let and Σ be real matrices of appropriate dimension where , and there is a matrix W that holds
if and only if the following inequalities hold:
Lemma 4
([35]). Suppose that W, L and V are given matrices of appropriate dimension. W and V are positive definite, and then is equivalent to
or
For system (1), the below ILC law is defined as:
where is the initial value of iterative control, and is the iteration learning update law, which is used to update the control system input signal. We simultaneously define
where represents the difference of along batch axis.
4.1. Zero Relativity ()
Considering the relativity of system (1), there is . The state equation of a dynamic iterative learning controller is as follows:
where is the dynamic ILC state vector. The below dynamic ILC update law is adopted as follows:
where the corresponding static ILC update law is In order to rewrite the dynamic ILC system into a discrete linear repetitive process, define
Then, a 2D dynamic model is obtained as follows:
where , , , .
Theorem 2.
Considering the 2D closed loop system (22) whose relativity , if positive definite symmetric matrix are existing, well-dimensioned matrices and and matrices and make the following linear matrix inequalities hold
Then, the 2D linear repetitive process (22) under dynamic ILC is stable along both the time and batch axes, the system tracking error has monotonic convergence, and the system controller matrices are
Proof of Theorem 2.
The inequality (23) can be rewritten to be
where , , , , , and take If inequality (25) is true, according to Lemma 3, the following linear matrix inequalities are also true
In Theorem 2, according to the matrix , we can conclude holds. Then, the inequality clearly holds.
According to inequality , we obtain
4.2. Higher Order Relativity ()
Considering that system (1) has high-order relativity , the system model satisfies . In order to compensate for higher order relativity, the state equation and dynamic iterative learning update law are designed as follows:
The static iterative learning update law for high relativity is , and thus we can find
and then
The corresponding 2D dynamic mode is
where , , , , .
Theorem 3.
Considering the 2D closed loop system (22) whose relativity , if positive definite symmetric matrices are existing, well-dimensioned matrices and and matrices and make the following linear matrix inequalities hold
Then, the 2D linear repetitive process (22) under dynamic ILC is stable along both the time and batch axes, the system tracking error has monotonic convergence, and the controller matrix of the system is
Proof of Theorem 3.
The proving process is same with Theorem 2 and, thus, is omitted here. □
There are two main steps to implement the dynamic ILC for linear repetitive process: step 1 is to use the LMI toolbox to obtain the dynamic ILC law factors , and shown in Algorithm 1, and step 2 is to iterate the input according to the dynamic learning control law along both the batch and time axes as demonstrated in Algorithm 2.
| Algorithm 1 Linear repetitive process dynamic ILC law calculation |
|
| Algorithm 2 Dynamic ILC for linear repetitive process algorithm |
|
5. Simulation Results
To verify the proposed dynamic ILC algorithm effectiveness, simulations were performed in MATLAB with the LMI toolbox for the systems with different relative degrees. For reasons of evaluating the system tracking error, the root mean square error is introduced as follows:
5.1. Condition 1: Relativity
Considering the system relativity , the coefficient of its state equation is , , , . Suppose that each iteration length of the system is , and the expected trajectory is as follows:
To further explore the advantages of dynamic ILC, we consider the corresponding static ILC under the same conditions, and the system law is
Using the same LMI solution, parameters of static ILC can be obtained as
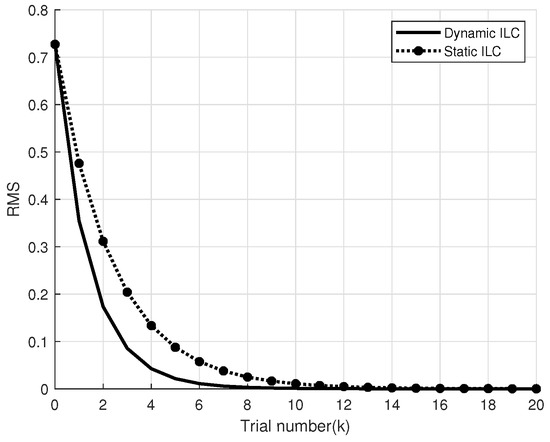
Figure 1.
The mean square error trajectory at relative degree .
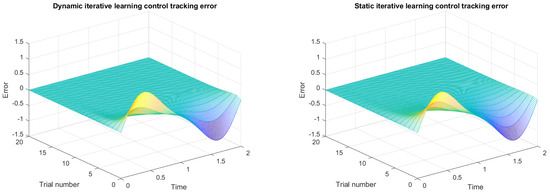
Figure 2.
The tracking error curve of ILC at relative degree .
5.2. Condition 2: Relativity
Considering the system relativity , taking the injection speed control of the injection molding process in [35] as the simulation objective, the constant matrix of its state equation is given as follows: , , . Define the expected trajectory as
The static ILC law under the same conditions is
The static ILC controller parameters are obtained using the same LMI solution method as follows:
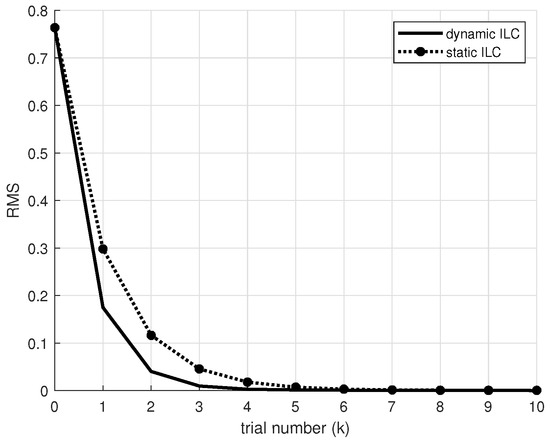
Figure 3.
The mean square error trajectory at relative degree .
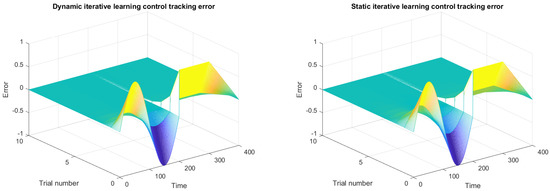
Figure 4.
The tracking error curve of ILC at relative degree .
5.3. Condition 3: Relativity
Considering the system relativity , the selected state space model parameters are as follows: , , . Suppose that each iteration length of the system is and the sampling time , then the expected trajectory is as follows:
The controller parameters can be obtained as
The static ILC law under the same conditions is
The parameters of the static ILC controller are obtained
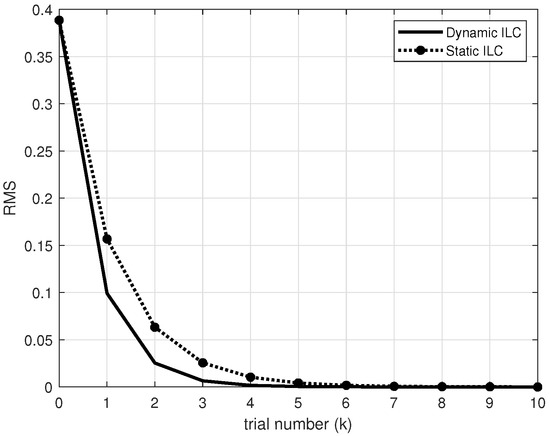
Figure 5.
The mean square error trajectory at relative degree .
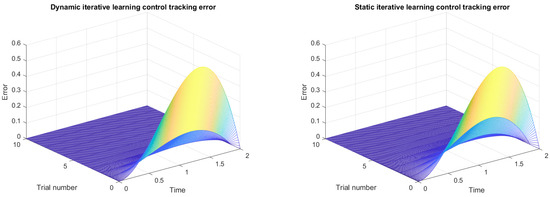
Figure 6.
The tracking error curve of ILC at relative degree .
The simulation results show that the actual system output gradually tracks the desired trajectory along an iterative axis, and the system remains stable under the dynamic ILC. Under the same conditions, compared with the static iterative learning controller, the control system using a dynamic iterative learning controller can achieve a better convergence effect.
6. Conclusions and Future Work
The monotonic convergence problem of dynamic ILC systems was studied in this paper in discrete linear repetitive processes with different relative degrees. First, the 2D discrete Roesser model of ILC system was established based on 2D system theory; secondly, the stability theory of linear repetitive processes was used to analyze the system monotone convergence, and sufficient conditions for the controller existence were given to simultaneously guarantee the dynamic performance; finally, the static controller and dynamic controller were simulated under different conditions, and the comparison showed the effectiveness of the dynamic ILC design schemes.
However, we know that the system matrix and D has difficulty maintaining accuracy for actual objects, and the system always has disturbances. For certain conditions, the dynamic iterative learning controller proposed in this paper is not suitable. Additionally, the ILC initial state issue studied in [36,37,38] is also critical for dynamic ILC algorithms, and thus how to eliminate the impacts of parameter uncertainty, disturbances and the initial state issue is one of our future jobs. Our subsequent research will also consider the actuator fault diagnosis and the reaction method, which is a category of fault-tolerant control.
Author Contributions
Investigation, R.Y. and L.W.; writing—original draft preparation, L.W.; writing—review and editing, L.D., R.Y. and Y.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Natural Science Foundation of the Higher Education Institutions of Jiangsu Province (No. 22KJB120009), the National Science Foundation of China (No. 62103293), the Natural Science Foundation of Jiangsu Province in China (No. BK20210709) and the Start-up Fund for Introducing Talent of Wuxi University (No. 2021r045).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All data generated or analyzed during this study are included in this article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chen, Y.; Chu, B.; Freeman, C.T. Iterative Learning Control for Robotic Path Following With Trial-Varying Motion Profiles. IEEE/ASME Trans. Mechatron. 2022, 27, 4697–4706. [Google Scholar] [CrossRef]
- Yan, Q.; Cai, J.; Ma, Y.; Yu, Y. Robust Learning Control for Robot Manipulators with Random Initial Errors and Iteration-Varying Reference Trajectories. IEEE Access 2019, 7, 32628–32643. [Google Scholar] [CrossRef]
- Bouakrif, F. Iterative learning control for MIMO nonlinear systems with arbitrary relative degree and no states measurement. Complexity 2013, 19, 37–45. [Google Scholar] [CrossRef]
- Fu, Q.; Du, L.; Xu, G.; Wu, J.; Yu, P. PD-type iterative learning control for linear continuous systems with arbitrary relative degree. Trans. Inst. Meas. Control 2018, 41, 2555–2562. [Google Scholar] [CrossRef]
- Cao, W.; Sun, M. Iterative learning based fault diagnosis for discrete linear uncertain systems. J. Syst. Eng. Electron. 2014, 25, 496–501. [Google Scholar] [CrossRef]
- Li, Z.; Hu, Y.; Li, D. Robust design of feedback feed-forward iterative learning control based on 2D system theory for linear uncertain systems. Int. J. Syst. Sci. 2015, 47, 2620–2631. [Google Scholar] [CrossRef]
- Wang, X.; Wang, J.; Shen, D.; Zhou, Y. Convergence analysis for iterative learning control of conformable fractional differential equations. Math. Methods Appl. Sci. 2018, 41, 8315–8328. [Google Scholar] [CrossRef]
- Tao, H.; Paszke, W.; Rogers, E.; Yang, H.; Gałkowski, K. Finite frequency range iterative learning fault-tolerant control for discrete time-delay uncertain systems with actuator faults. ISA Trans. 2019, 95, 152–163. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Chu, B.; Freeman, C.T.; Liu, Y. Generalized iterative learning control with mixed system constraints: A gantry robot based verification. Control Eng. Pract. 2020, 95, 104260. [Google Scholar] [CrossRef]
- Pakshin, P.V.; Emelianova, J.P.; Emelianov, M.A. Iterative Learning Control Design for Multiagent Systems Based on 2D Models. Autom. Remote Control 2018, 79, 1040–1056. [Google Scholar] [CrossRef]
- Wang, L.; Dong, W. Optimal Iterative Learning Fault-Tolerant Guaranteed Cost Control for Batch Processes in the 2D-FM Model. Abstr. Appl. D 2012, 2012, 748981. [Google Scholar] [CrossRef]
- Zhang, Q.; Yu, J.; Wang, L. 2D Terminal Constrained Model Predictive Iterative Learning Control of Batch Processes With Time Delay. IEEE Access 2019, 7, 126842–126856. [Google Scholar] [CrossRef]
- Wang, L.; Yu, J.; Li, P.; Li, H.; Zhang, R. A 2D-FM model-based robust iterative learning model predictive control for batch processes. ISA Trans. 2021, 110, 271–282. [Google Scholar] [CrossRef] [PubMed]
- Yu, M.; Chai, S. Adaptive iterative learning control for discrete-time nonlinear systems with multiple iteration-varying high-order internal models. Int. J. Robust Nonlinear Control 2021, 31, 7390–7408. [Google Scholar] [CrossRef]
- Yu, M.; Chai, S. A Survey on High-Order Internal Model Based Iterative Learning Control. IEEE Access 2019, 7, 127024–127031. [Google Scholar] [CrossRef]
- Zou, W.; Shen, Y.; Paszke, W.; Tao, H. Robust feedback feed-forward PD-type iterative learning control for uncertain discrete systems over finite frequency ranges. Trans. Inst. Meas. Control 2022, 44, 2850–2862. [Google Scholar] [CrossRef]
- Asl, R.M.; Madady, A. Stabilization of two-dimensional mixed continuous-discrete-time systems via dynamic output feedback with application to iterative learning control design. Trans. Inst. Meas. Control 2021, 44, 172–187. [Google Scholar] [CrossRef]
- Wei, Y.S.; Li, X.D. Iterative learning control for linear discrete-time systems with high relative degree under initial state vibration. IET Control Theory Ampmathsemicolon Appl. 2016, 10, 1115–1126. [Google Scholar] [CrossRef]
- Liu, Y.; Ruan, X.; Li, X. Optimized Iterative Learning Control for Linear Discrete-Time-Invariant Systems. IEEE Access 2019, 7, 75378–75388. [Google Scholar] [CrossRef]
- Hladowski, L.; Galkowski, K.; Rogers, E. Dynamic Output-Only Iterative Learning Control Design. IEEE Access 2021, 9, 147072–147081. [Google Scholar] [CrossRef]
- Li, X.; Xu, J.X.; Huang, D. Iterative learning control for nonlinear dynamic systems with randomly varying trial lengths. Int. J. Adapt. Control Signal Process. 2015, 29, 1341–1353. [Google Scholar] [CrossRef]
- Wu, S.; Zhang, R. A two-dimensional design of model predictive control for batch processes with two-dimensional (2D) dynamics using extended non-minimal state space structure. J. Process. Control 2019, 81, 172–189. [Google Scholar] [CrossRef]
- Wan, K.; Wei, Y.S. Adaptive ILC of Tracking Nonrepetitive Trajectory for Two-dimensional Nonlinear Discrete Time-varying Fornasini-Marchesini Systems with Iteration-varying Boundary States. Int. J. Control Autom. Syst. 2020, 19, 417–425. [Google Scholar] [CrossRef]
- Li, X. Robot target localization and interactive multi-mode motion trajectory tracking based on adaptive iterative learning. J. Ambient. Intell. Humaniz. Comput. 2020, 11, 6271–6282. [Google Scholar] [CrossRef]
- Zhao, X.; Geng, Y.; Yuan, C.; Wu, B. An Unscented Kalman Filter–based iterative learning controller for multibody rotating scan optical spacecraft. Trans. Inst. Meas. Control 2022, 44, 2418–2433. [Google Scholar] [CrossRef]
- Bifaretti, S.; Tomei, P.; Verrelli, C.M. A global robust iterative learning position control for current-fed permanent magnet step motors. Automatica 2011, 47, 227–234. [Google Scholar] [CrossRef]
- Hao, S.; Liu, T.; Paszke, W.; Galkowski, K. Robust iterative learning control for batch processes with input delay subject to time-varying uncertainties. IET Control Theory Ampmathsemicolon Appl. 2016, 10, 1904–1915. [Google Scholar] [CrossRef]
- Wang, L.; Shen, Y.; Yu, J.; Li, P.; Zhang, R.; Gao, F. Robust iterative learning control for multi-phase batch processes: An average dwell-time method with 2D convergence indexes. Int. J. Syst. Sci. 2017, 49, 324–343. [Google Scholar] [CrossRef]
- Hladowski, L.; Galkowski, K.; Rogers, E. Further results on dynamic iterative learning control law design using repetitive process stability theory. In Proceedings of the 2017 Tenth International Workshop on Multidimensional (nD) Systems (nDS), Zielona Góra, Poland, 13–15 September 2017. [Google Scholar] [CrossRef]
- Qiao, J.Z.; Wu, H.; Zhu, Y.; Xu, J.; Li, W. Anti-disturbance iterative learning tracking control for space manipulators with repetitive reference trajectory. Assem. Autom. 2019, 39, 401–409. [Google Scholar] [CrossRef]
- Meng, D.; Jia, Y.; Du, J.; Yu, F. Data-Driven Control for Relative Degree Systems via Iterative Learning. IEEE Trans. Neural Netw. 2011, 22, 2213–2225. [Google Scholar] [CrossRef]
- Rogers, E.; Galkowski, K.; Owens, D.H. Control Systems Theory and Applications for Linear Repetitive Processes; Springer: Berlin/Heidelberg, Germany, 2007; Volume 349, p. 32. [Google Scholar] [CrossRef]
- Rantzer, A. On the Kalman—Yakubovich—Popov lemma. Syst. Ampmathsemicolon Control Lett. 1996, 28, 7–10. [Google Scholar] [CrossRef]
- Gahinet, P.; Apkarian, P. A linear matrix inequality approach to H∞ control. Int. J. Robust Nonlinear Control 1994, 4, 421–448. [Google Scholar] [CrossRef]
- Shi, J.; Gao, F.; Wu, T.J. Robust design of integrated feedback and iterative learning control of a batch process based on a 2D Roesser system. J. Process. Control 2005, 15, 907–924. [Google Scholar] [CrossRef]
- Geng, Y.; Ruan, X.; Zhou, Q.; Yang, X. Robust adaptive iterative learning control for nonrepetitive systems with iteration-varying parameters and initial state. Int. J. Mach. Learn. Cybern. 2021, 12, 2327–2337. [Google Scholar] [CrossRef]
- Ayatinia, M.; Forouzanfar, M.; Ramezani, A. An LMI Approach to Robust Iterative Learning Control for Linear Discrete-time Systems. Int. J. Control Autom. Syst. 2022, 20, 2391–2401. [Google Scholar] [CrossRef]
- Tao, H.; Li, J.; Chen, Y.; Stojanovic, V.; Yang, H. Robust point-to-point iterative learning control with trial-varying initial conditions. IET Control Theory Appl. 2020, 14, 3344–3350. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).