A Memristor-Based Colpitts Oscillator Circuit
Abstract
:1. Introduction
2. Generalized Memristor Emulator
3. Memristive-Based Colpitts Circuit
4. Complex Dynamical Behaviors
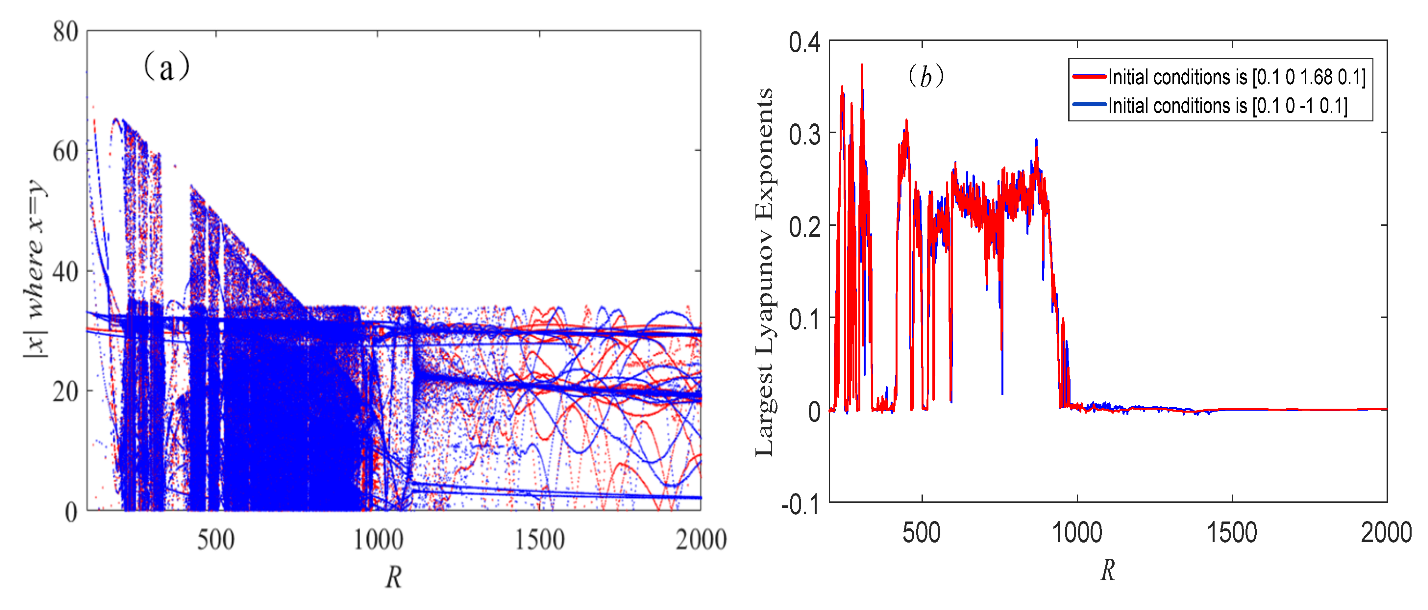
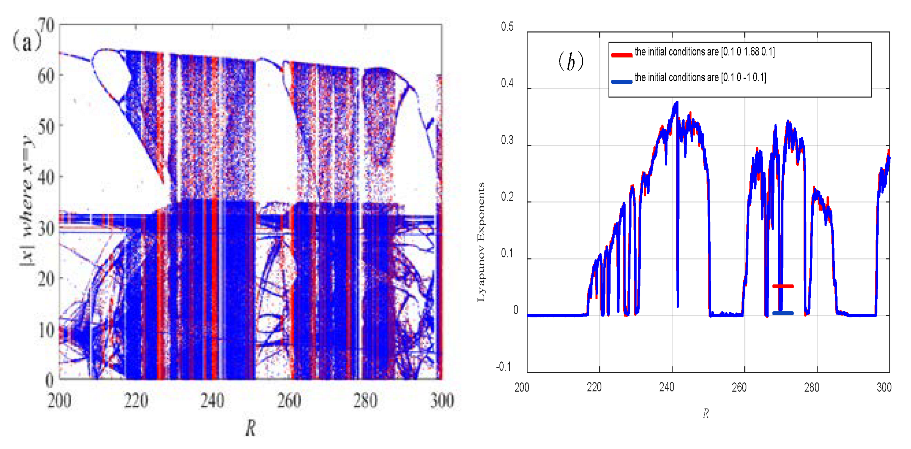
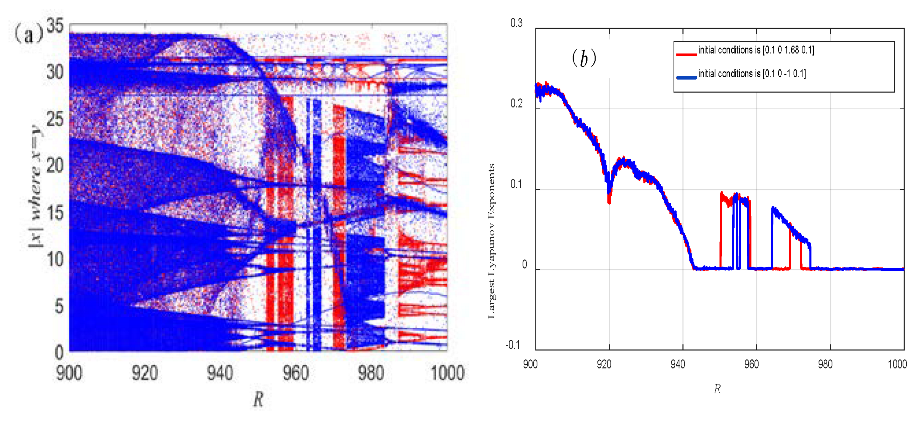
4.1. Phase Portraits with Respect to Variables R
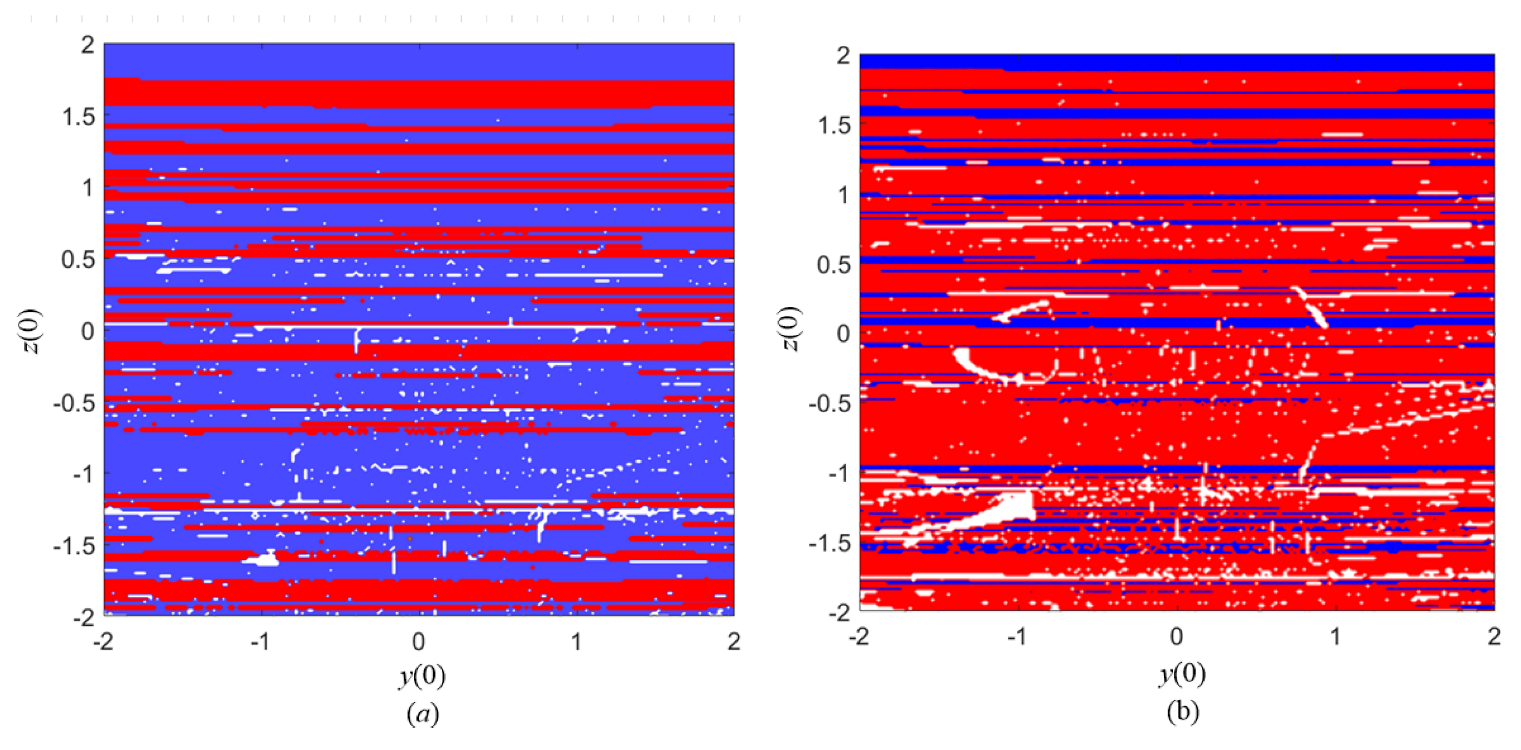
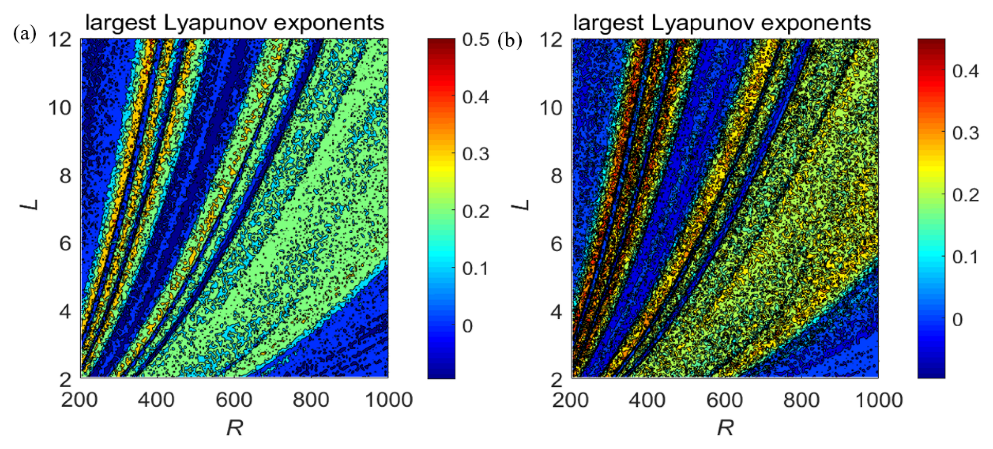
4.2. Basins of Attraction
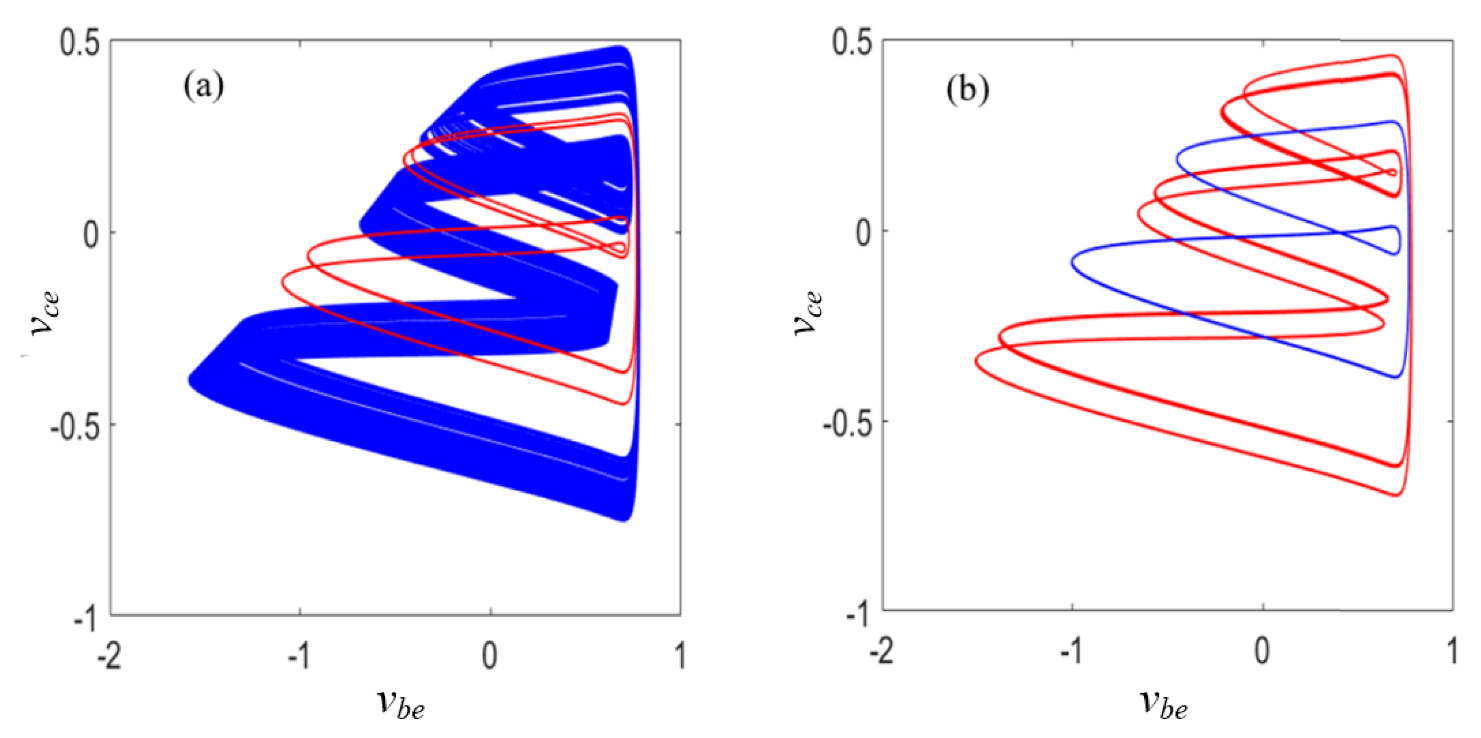
4.3. Coexisting Multiple Attractors
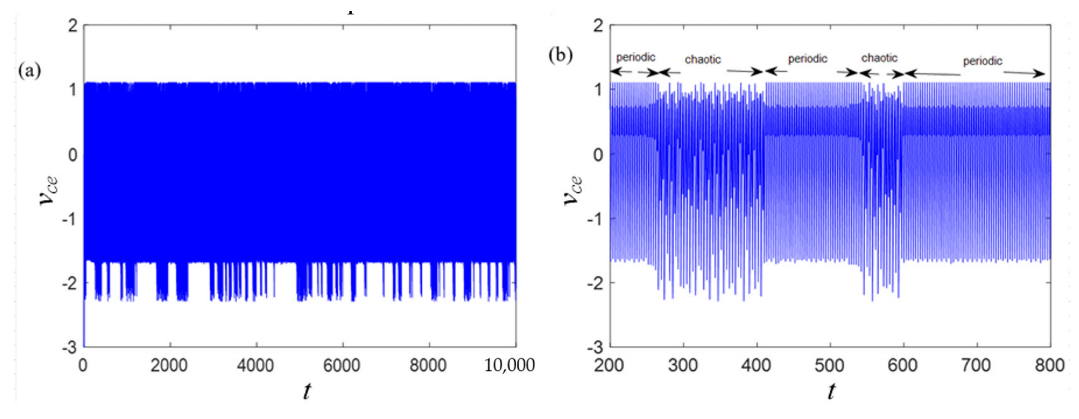
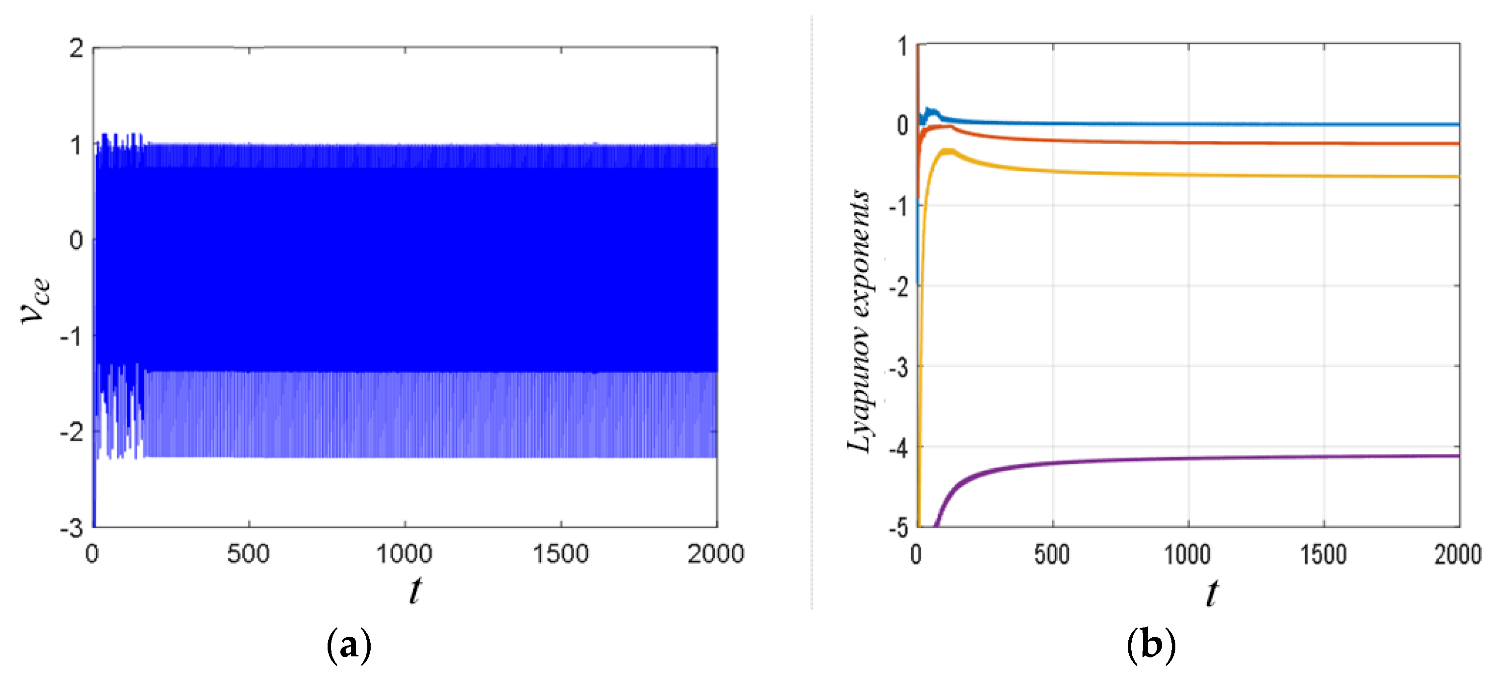
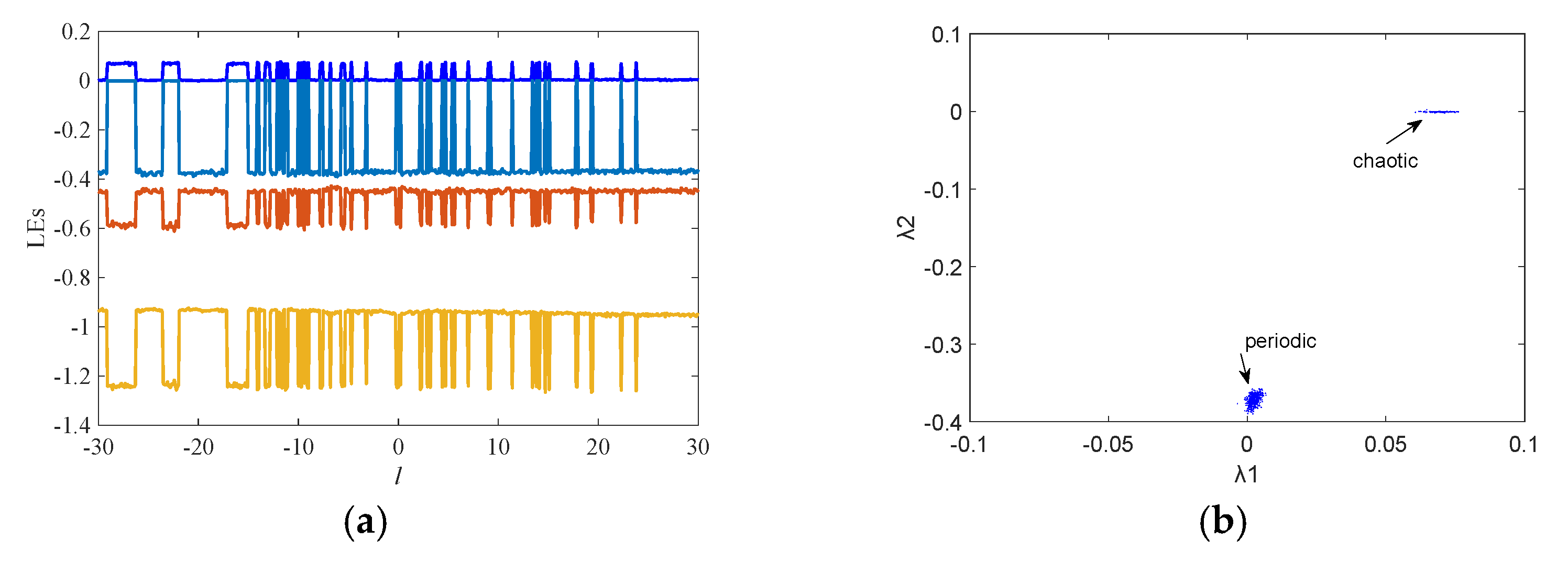
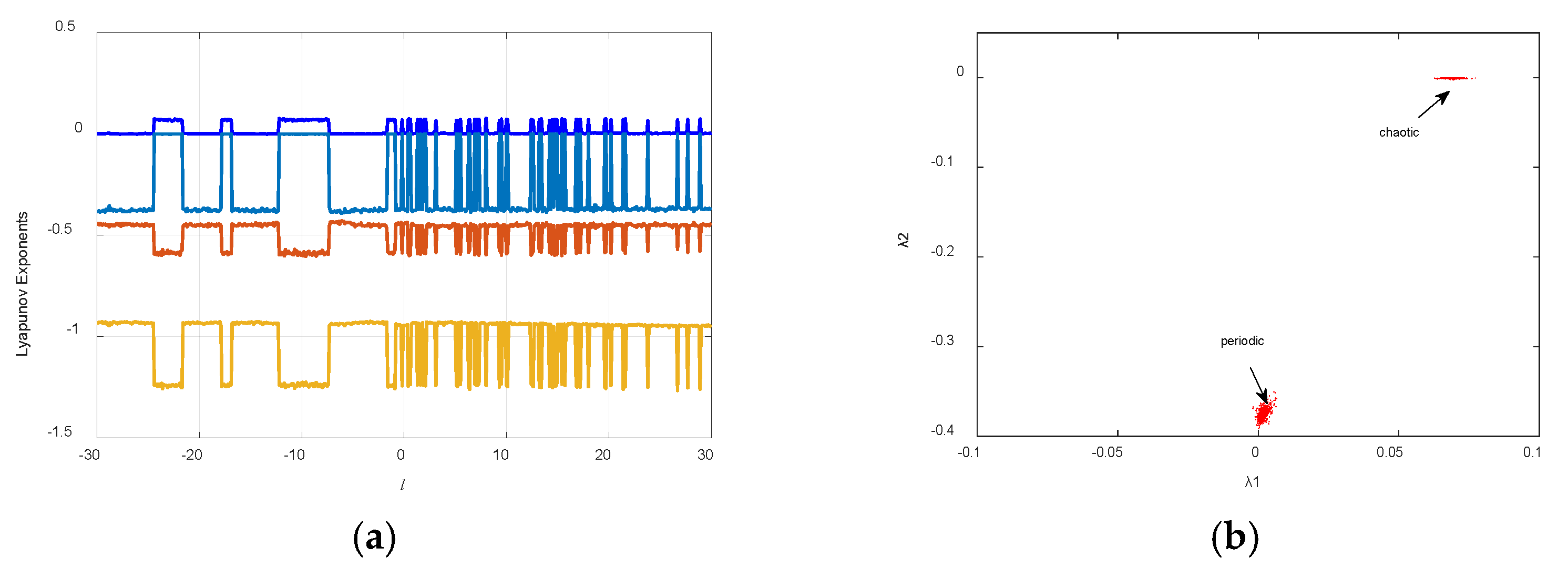
4.4. Intermittent Chaos and Transient Chaos
4.5. Offset Boosting
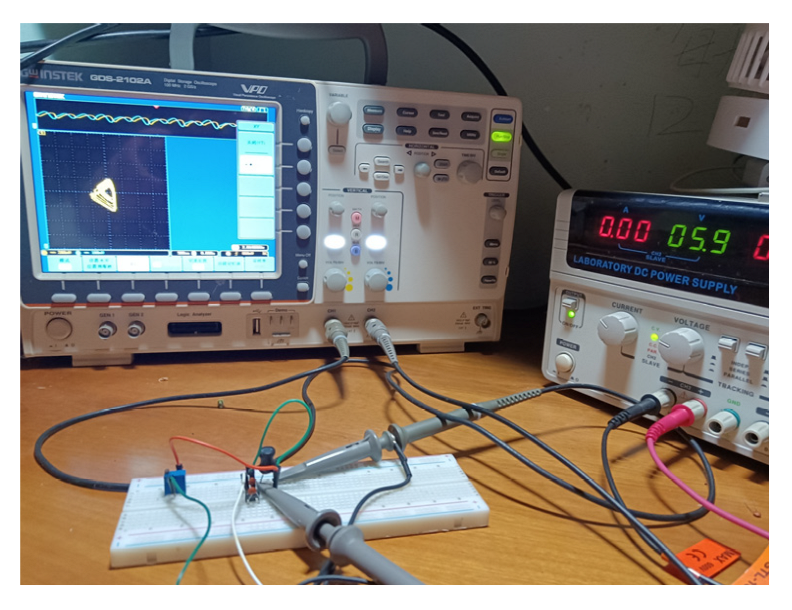
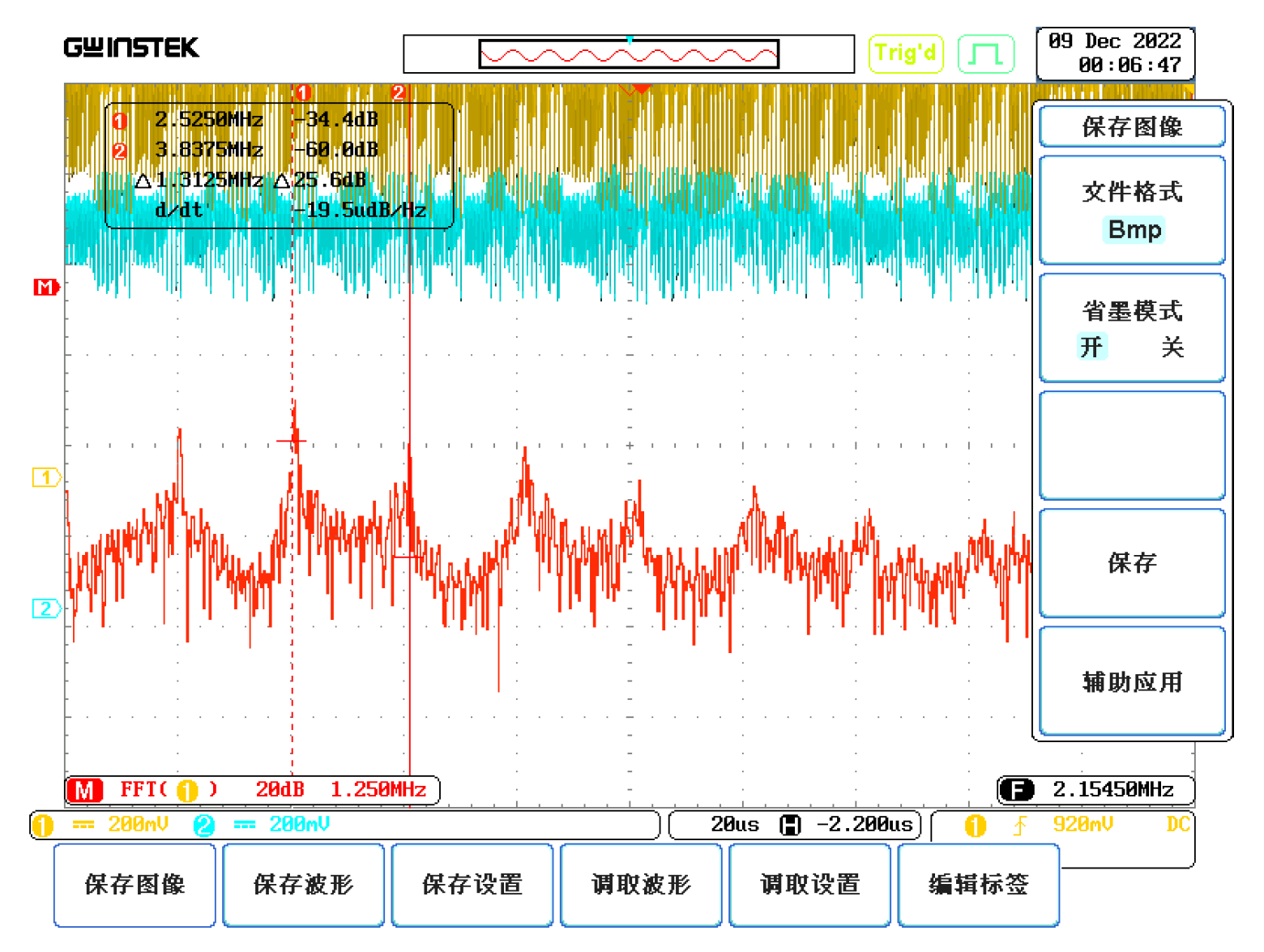
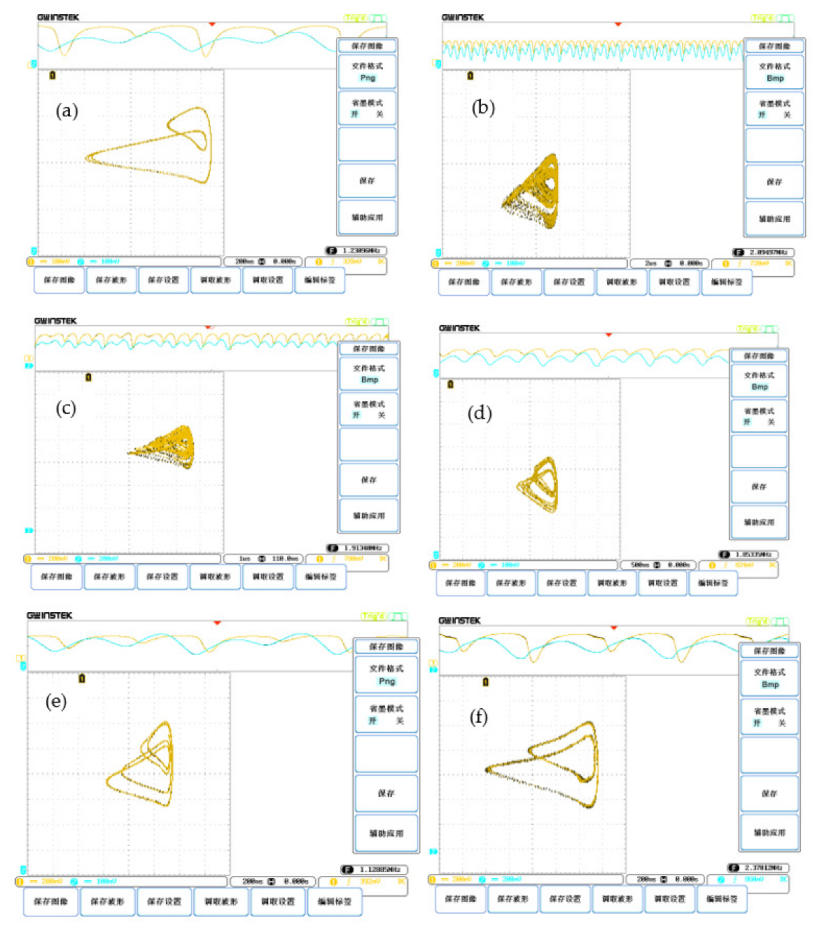
5. Hardware Experiments
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chua, L. Memristor-The missing circuit element. IEEE Trans. Circuit Theory 1971, 18, 507–519. [Google Scholar] [CrossRef]
- Strukov, D.B.; Snider, G.S.; Stewart, D.R.; Williams, R.S. The missing memristor found. Nature 2008, 453, 80–83. [Google Scholar] [CrossRef]
- Khalid, M.; Singh, J. Memristor based unbalanced ternary logic gates. Anal. Integr. Circuits Signal Process. 2016, 87, 399–406. [Google Scholar] [CrossRef]
- Wang, X.; Zhou, P.; Eshraghian, J.; Lin, C.; Iu, H.; Chang, T. High-Density Memristor-CMOS Ternary Logic Family. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 264–274. [Google Scholar] [CrossRef]
- Liu, P.; You, Z.; Wu Ji Liu, B.; Han, Y.; Chakrabarty, K. Fault Modeling and Efficient Testing of Memristor-Based Memory. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 11, 4444–4455. [Google Scholar] [CrossRef]
- Parshina, L.; Novodvorsky, O.; Khramova, O.; Gusev, D.; Polyakov, A.; Mikhalevsky, V.; Cherebilo, E. Laser synthesis of non-volatile memristor structures based on tantalum oxide thin films. Chaos Solitons Fractals 2021, 142, 110460. [Google Scholar] [CrossRef]
- Bharathi, M.; Wang, Z.; Guo, B.; Balraj, B.; Li, Q.; Shuai, J.; Guo, D. Memristors: Understanding, utilization and upgradation for neuromorphic computing. Nano 2020, 15, 15. [Google Scholar] [CrossRef]
- Li, Y.; Ang, K.W. Hardware Implementation of Neuromorphic Computing Using Large-Scale Memristor Crossbar Arrays. Adv. Intell. Syst. 2021, 3, 2000137. [Google Scholar] [CrossRef]
- Li, Z.; Zhou, H.; Wang, M.; Ma, M. Coexisting firing patterns and phase synchronization in locally active memristor coupled neurons with HR and FN models. Nonlinear Dyn. 2021, 104, 1455–1473. [Google Scholar] [CrossRef]
- Lin, H.; Wang, C.; Xu, C.; Zhang, X.; Iu, H.H.C. A Memristive Synapse Control Method to Generate diversified multistructure chaotic attractor. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2022, 1. [Google Scholar] [CrossRef]
- Wan, Q.; Yan, Z.; Li, F.; Chen, S.; Liu, J. Complex dynamics in a Hopfield neural network under electromagnetic induction and electromagnetic radiation. Chaos 2022, 32, 073107. [Google Scholar] [CrossRef]
- Lin, H.; Wang, C.; Cui, L.; Sun, Y.; Xu, C.; Yu, F. Brain-like initial-boosted hyperchaos and application in biomedical image encryption. IEEE Trans. Ind. Inform. 2022, 18, 8839–8850. [Google Scholar] [CrossRef]
- Ran, H.; Wen, S.; Li, Q.; Yang, Y.; Shi, K.; Feng, Y.; Zhou, P.; Huang, T. Memristor-Based Edge Computing of Blaze Block for Image Recognition. IEEE Trans. Neural Netw. Learn. Syst. 2020, 33, 2121–2131. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.; Liu, Z.; Tang, J.; Gao, B.; Zhang, Y.; Qian, H.; Wu, H. Memristor-Based Signal Processing for Edge Computing. Tsinghua Sci. Technol. 2022, 27, 455–471. [Google Scholar] [CrossRef]
- Li, C.; Li, H.; Xie, W.; Du, J. A S-type bistable locally active memristor model and its analog implementation in an oscillator circuit. Nonlinear Dyn. 2021, 1, 1041–1058. [Google Scholar] [CrossRef]
- Xie, W.; Wang, C.; Lin, H. A fractional-order multistable locally active memristor and its chaotic system with transient transition, state jump. Nonlinear Dyn. 2021, 104, 4523–4541. [Google Scholar] [CrossRef]
- Ma, M.; Yang, Y.; Qiu, Z.; Peng, Y.; Sun, Y.; Li, Z.; Wang, M. A locally active discrete memristor model and its application in a hyperchaotic map. Nonlinear Dyn. 2022, 107, 2935–2949. [Google Scholar] [CrossRef]
- Knowm Inc. Products. Available online: https://knowm.com/collections/all/ (accessed on 26 May 2020).
- Yesil, A. A New Grounded Memristor Emulator Based on MOSFET-C. AEU-Int. J. Electron. Commun. 2018, 91, 143–149. [Google Scholar] [CrossRef]
- Vista, J.; Ranjan, A. A Simple Floating MOS-Memristor for High-Frequency Applications. IEEE Trans. Very Large Scale Integr. Syst. 2019, 27, 1186–1195. [Google Scholar] [CrossRef]
- Ghosh, M.; Singh, A.; Borah, S.S.; Vista, J.; Ranjan, A.; Kumar, S. MOSFET-Based Memristor for High-Frequency Signal Processing. IEEE Trans. Electron. Devices 2022, 69, 2248–2255. [Google Scholar] [CrossRef]
- Corinto, F.; Ascoli, A. Memristive diode bridge with LCR filter. Electron. Lett. 2012, 48, 824–825. [Google Scholar] [CrossRef]
- Bao, B.C.; Yu, J.J.; Hu, F.W. Generalized memristor consisting of diode bridge with first order parallel RC filter. Int. J. Bifurc. Chaos 2014, 24, 1350143. [Google Scholar] [CrossRef]
- Wu, H.G.; Bao, B.C.; Liu, Z.; Xu, Q.; Jiang, P. Chaotic and periodic bursting phenomena in a memristive Wien-bridge oscillator. Nonlinear Dyn. 2015, 83, 893–903. [Google Scholar] [CrossRef]
- Bao, B.C.; Xu, L.; Wu, Z.M.; Chen, M.; Wu, H.G. Coexistence of multiple bifurcation modes in memristive diode-bridge based canonical Chua’s circuit. Int. J. Electron. 2018, 105, 1159–1169. [Google Scholar] [CrossRef]
- Kengne, J.; Leutcho, G.D.; Telem, A. Reversals of period doubling, coexisting multiple attractors, and offset boosting in a novel memristive diode bridge-based hyperjerk circuit. Analog. Integr. Circuits Signal Process. 2019, 101, 379–399. [Google Scholar] [CrossRef]
- Chithra, A.; Fozin, T.F.; Srinivasan, K.; Kengne, E.R.M.; Kouanou, A.T.; Mohamed, I.R. Complex Dynamics in a Memristive Diode Bridge-Based MLC Circuit: Coexisting Attractors and Double-Transient Chaos. Int. J. Bifurc. Chaos 2021, 31, 2150049. [Google Scholar] [CrossRef]
- Wang, N.; Zhang, G.; Bao, H. Bursting oscillations and coexisting attractors in a simple memristor-capacitor-based chaotic circuit. Nonlinear Dyn. 2019, 97, 1477–1494. [Google Scholar] [CrossRef]
- Li, F.; Tai, C.; Bao, H.; Luo, J.; Bao, B. Hyperchaos, quasi-period and coexisting behaviors in second-order-memristor-based jerk circuit. Eur. Phys. J. Spec. Top. 2020, 229, 1045–1058. [Google Scholar] [CrossRef]
- Kengne, L.K.; Pone, J.; Hilaire, F. On the dynamics of chaotic circuits based on memristive diode-bridge with variable symmetry: A case study. Chaos Solitons Fractals 2021, 145, 110795. [Google Scholar] [CrossRef]
- Wu, H.; Zhou, J.; Chen, M.; Xu, Q.; Bao, B. DC-offset induced asymmetry in memristive diode-bridge-based Shinriki oscillator. Chaos Solitons Fractals 2022, 154, 111624. [Google Scholar] [CrossRef]
- Ramadoss, J.; Kengne, J.; Telem AN, K.; Rajagopal, K. Broken symmetry and dynamics of a memristive diodes bridge-based Shinriki oscillator. Phys. A Stat. Mech. Its Appl. 2022, 588, 126562. [Google Scholar] [CrossRef]
- Sánchez-López, C. RuizBharathwaj Muthuswamy. Implementing Memristor Based Chaotic Circuits. Int. J. Bifurc. Chaos 2010, 20, 1002651. [Google Scholar]
- Kim, H.; Sah, M.P.; Yang, C.; Cho, S.; Chua, L.O. Memristor Emulator for Memristor Circuit Applications. IEEE Trans. Circuits Syst. I Regul. Pap. 2012, 59, 2422–2431. [Google Scholar]
- Yesil, A.; Babacan, Y.; Kacar, F. A new DDCC based memristor emulator circuit and its applications. Microelectron. J. 2014, 45, 282–287. [Google Scholar] [CrossRef]
- Sánchez-López, C.; Aguila-Cuapio, L.E. A 860 kHz grounded memristor emulator circuit. AEUE-Int. J. Electron. Commun. 2017, 73, 23–33. [Google Scholar] [CrossRef]
- Ranjan, R.K.; Rani, N.; Pal, R.; Paul, S.K.; Kanyal, G. Single CCTA based high frequency floating and grounded type of incremental/decremental memristor emulator and its application. Microelectron. J. 2017, 60, 119–128. [Google Scholar] [CrossRef]
- Vista, J.; Ranjan, A. Flux Controlled Floating Memristor Employing VDTA: Incremental or Decremental Operation. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2021, 40, 364–372. [Google Scholar] [CrossRef]
- Raj, A.; Singh, S.; Kumar, P. Dual mode, high frequency and power efficient grounded memristor based on OTA and DVCC. Analog. Integr. Circuits Signal Process. 2022, 110, 81–89. [Google Scholar] [CrossRef]
- Tekam, B.; Kengne, J.; Kenmoe, G.D. High frequency Colpitts’ oscillator: A simple configuration for chaos generation. Chaos Solitons Fractals 2019, 126, 351–360. [Google Scholar] [CrossRef]
- Sabarathinam, S.; Thamilmaran, K. Transient chaos in a globally coupled system of nearly conservative Hamiltonian Duffing oscillators. Chaos Solitons Fractals 2015, 73, 129–140. [Google Scholar] [CrossRef]
- Li, C.; Gu, Z.; Liu, Z.; Jafari, S.; Kapitaniak, T. Constructing chaotic repellors. Chaos Solitons Fractals 2021, 42, 110544. [Google Scholar] [CrossRef]
- Li, C.; Xiong, W.; Chen, G. Diagnosing multistability by offset boosting. Nonlinear Dyn. 2017, 90, 1335–1341. [Google Scholar] [CrossRef]
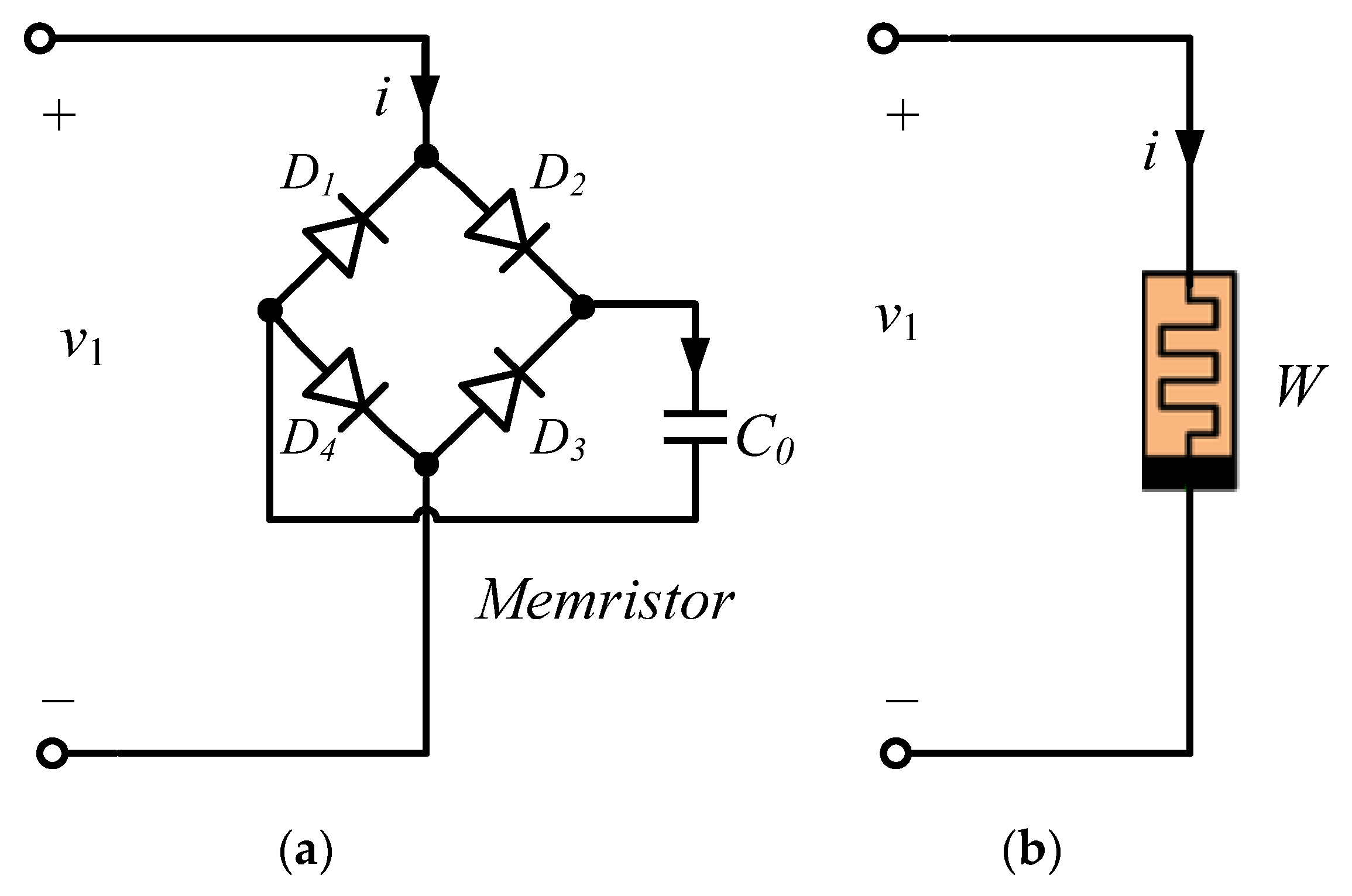
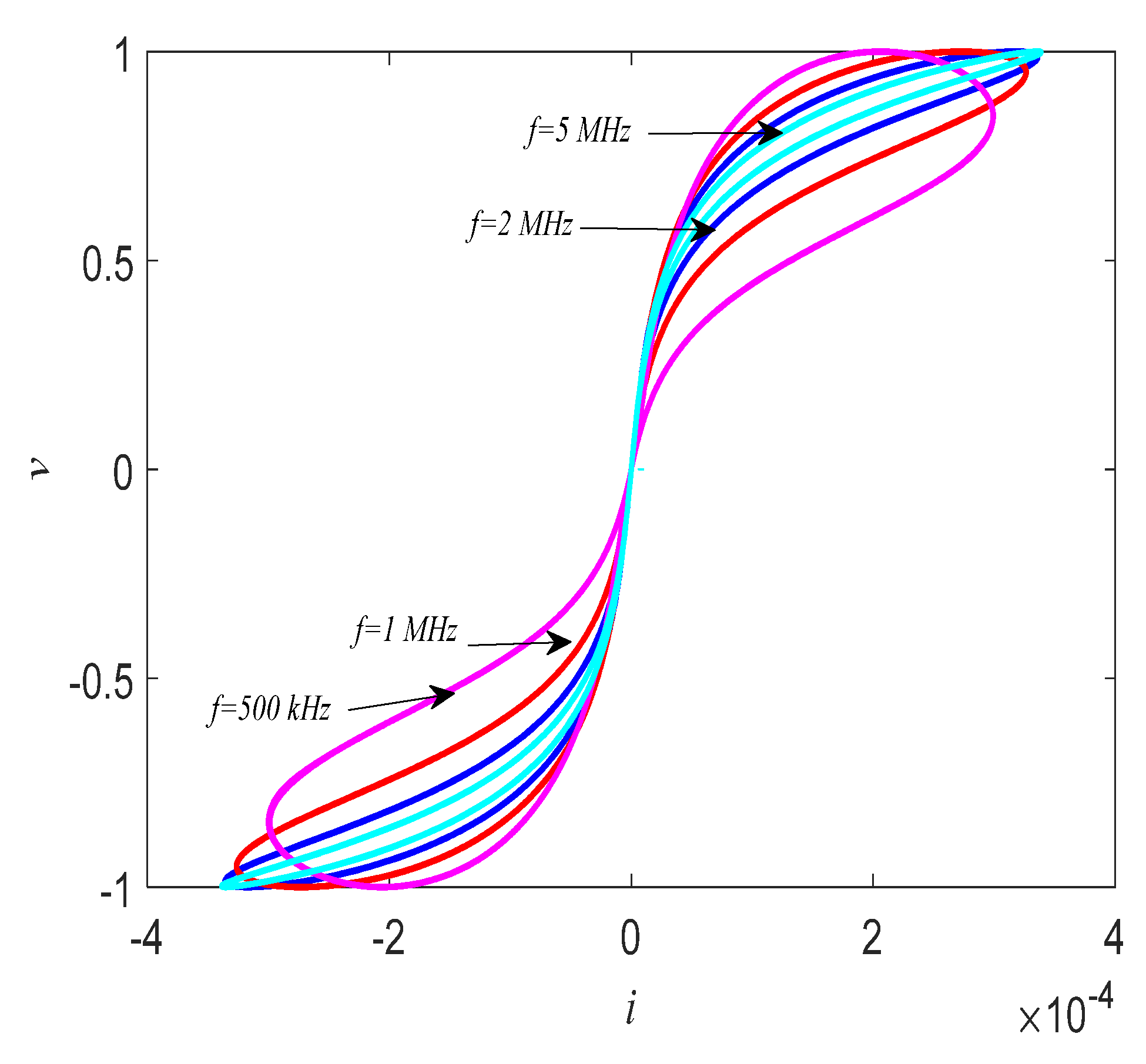
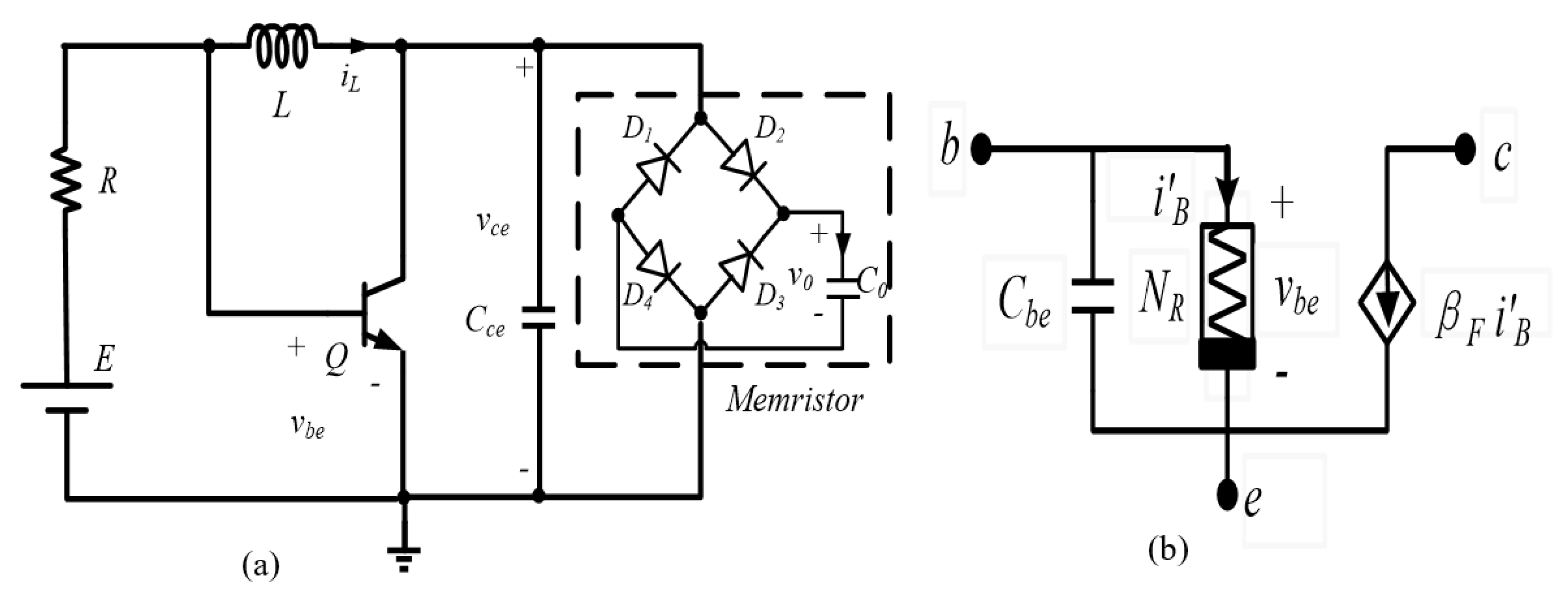
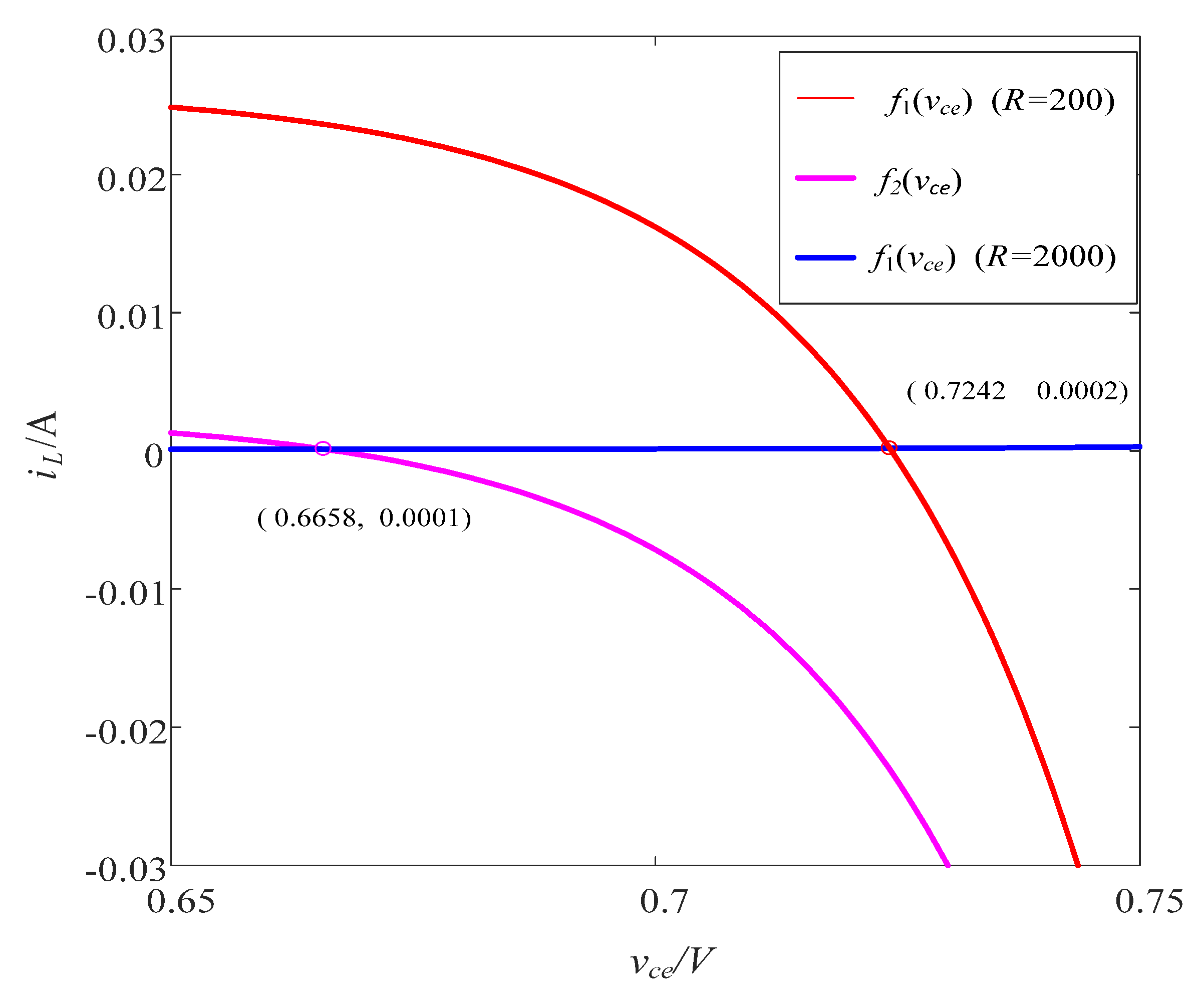


| Ref. | Essential Components | Power Supply | Floating/ Grounded | Operating Frequency |
|---|---|---|---|---|
| [19] | 7 MOSFETs | ±0.9 V DC voltages | Grounded | 50 MHz |
| [20] | 3 MOSFETs | 10 μA | Floating | 13 MHz |
| [21] | 4 MOSFETs | No | Floating | 50 MHz |
| [35] | DDCC | ±1.5 V DC | Grounded | 1 MHz |
| [36] | 1 CCII, 1 multiplier | ±10 V DC | Grounded | 860 kHz |
| [37] | CCTA | ±1.5 V DC | Floating/ grounded | hundreds of kHz |
| [38] | VDTA | ±0.9 V DC | Floating | 50 MHz |
| [39] | VDTA, OTA | ±0.9 V DC, ±1.2 V DC | Grounded | 1 MHz |
| Proposed work | Diode bridge | No | Floating | 5 MHz |
| Parameters | Significations | Values |
|---|---|---|
| Cce | Capacitance | 2.2 nF |
| L | Inductance | 4.7 μH |
| C0 | Capacitance | 100 pF |
| E | DC voltage source | 5.89 V |
| R/Ω | Equilibrium Point P | Eigenvalues |
|---|---|---|
| 200 | (0.7242, 0.7242, 0.0002, 0.5725) | |
| 500 | (0.7012, 0.7012, 0.0104, 0.5496) | |
| 800 | (0.6893, 0.6893, 0.0001, 0.5377) | |
| 1200 | (0.6790, 0.6790, 0.0001, 0.5274) | |
| 2000 | (0.6658, 0.6658, 0.0001, 0.5143) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, L.; You, Z.; Liang, X.; Li, X. A Memristor-Based Colpitts Oscillator Circuit. Mathematics 2022, 10, 4820. https://doi.org/10.3390/math10244820
Zhou L, You Z, Liang X, Li X. A Memristor-Based Colpitts Oscillator Circuit. Mathematics. 2022; 10(24):4820. https://doi.org/10.3390/math10244820
Chicago/Turabian StyleZhou, Ling, Zhenzhen You, Xiaolin Liang, and Xiaowu Li. 2022. "A Memristor-Based Colpitts Oscillator Circuit" Mathematics 10, no. 24: 4820. https://doi.org/10.3390/math10244820
APA StyleZhou, L., You, Z., Liang, X., & Li, X. (2022). A Memristor-Based Colpitts Oscillator Circuit. Mathematics, 10(24), 4820. https://doi.org/10.3390/math10244820






