Numerical Analysis of Fourier Finite Volume Element Method for Dirichlet Boundary Optimal Control Problems Governed by Elliptic PDEs on Complex Connected Domains
Abstract
1. Introduction
2. Optimality System
3. Fourier Finite Volume Element Method
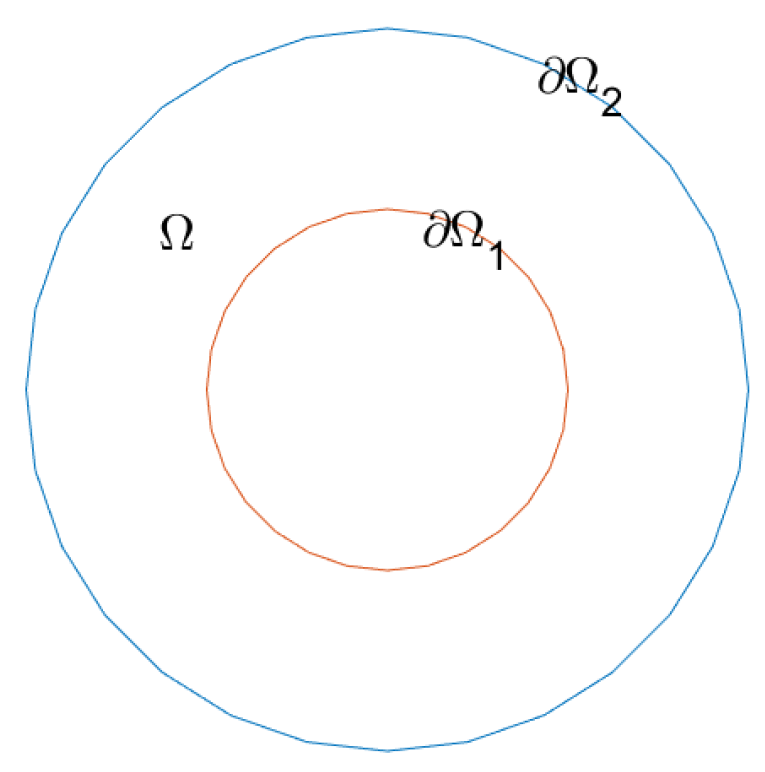
3.1. Polar Coordinates Transform
3.2. Fourier Expansion and Truncation
3.3. Finite Volume Element Method
4. A Priori Error Estimates
5. Numerical Experiments
| Algorithm 1: Algorithm for the solution of optimal control problem. |
|
5.1. Experiment 1
5.2. Experiment 2
6. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Han, Q.; Lin, F. Elliptic Partial Differential Equations; American Mathematical Soc.: Providence, RI, USA, 2011; Volume 1. [Google Scholar]
- Nirenberg, L. On elliptic partial differential equations. In Il Principio di Minimo e sue Applicazioni alle Equazioni Funzionali; Springer: Berlin/Heidelberg, Germany, 2011; pp. 1–48. [Google Scholar]
- Boureghda, A. Solution of an ice melting problem using a fixed domain method with a moving boundary. Bull. Math. Soc. Sci. Math. Roum. 2019, 62, 341–353. [Google Scholar]
- Gefen, A.; Weihs, D. Computer Methods in Biomechanics and Biomedical Engineering: Proceedings of the 14th International Symposium CMBBE, Tel Aviv, Israel, 2016; Springer: Cham, Switzerland, 2018. [Google Scholar] [CrossRef]
- Tröltzsch, F. Optimal Control of Partial Differential Equations: Theory, Methods, and Applications; American Mathematical Soc.: Providence, RI, USA, 2010; Volume 112. [Google Scholar]
- Lions, J.L. Optimal Control of Systems Governed by Partial Differential Equations; Springer: Berlin/Heidelberg, Germany, 1971. [Google Scholar]
- Hinze, M.; Pinnau, R.; Ulbrich, M.; Ulbrich, S. Optimization with PDE Constraints; Springer: Berlin/Heidelberg, Germany, 2008; Volume 23. [Google Scholar]
- Zamani, N.; Chuang, J. Optimal control of current in a cathodic protection system: A numerical investigation. Optim. Control Appl. Methods 1987, 8, 339–350. [Google Scholar] [CrossRef]
- Zhong, W.; Zhong, X. Elliptic partial differential equation and optimal control. Numer. Methods Partial Differ. Equ. 1992, 8, 149–169. [Google Scholar]
- Yousept, I. Optimal control of quasilinear H(curl)-elliptic partial differential equations in magnetostatic field problems. SIAM J. Control Optim. 2013, 51, 3624–3651. [Google Scholar] [CrossRef]
- Khursheed, A. The Finite Element Method in Charged Particle Optics; Springer: Boston, MA, USA, 1999. [Google Scholar]
- French, D.A.; Thomas King, J. Approximation of an elliptic control problem by the finite element method. Numer. Funct. Anal. Optim. 1991, 12, 299–314. [Google Scholar] [CrossRef]
- Yan, M.; Gong, W.; Yan, N. Finite element methods for elliptic optimal control problems with boundary observations. Appl. Numer. Math. 2015, 90, 190–207. [Google Scholar] [CrossRef]
- Christof, C.; Vexler, B. New regularity results and finite element error estimates for a class of parabolic optimal control problems with pointwise state constraints. ESAIM Control Optim. Calc. Var. 2021, 27, 4. [Google Scholar] [CrossRef]
- Liu, J.; Zhou, Z. Finite element approximation of time fractional optimal control problem with integral state constraint. AIMS Math. 2021, 6, 979–997. [Google Scholar] [CrossRef]
- Li, R.; Chen, Z.; Wu, W. Generalized Difference Methods for Differential Equations: Numerical Analysis of Finite Volume Methods; CRC Press: New York, NY, USA, 2000. [Google Scholar]
- Shen, J.; Tang, T.; Wang, L. Spectral Methods: Algorithms, Analysis and Applications; Springer: Berlin/Heidelberg, Germany, 2011; Volume 41. [Google Scholar]
- Pfeiffer, H.P.; Kidder, L.E.; Scheel, M.A.; Teukolsky, S.A. A multidomain spectral method for solving elliptic equations. Comput. Phys. Commun. 2003, 152, 253–273. [Google Scholar] [CrossRef]
- Tao, Z.Z.; Sun, B. Galerkin spectral method for elliptic optimal control problem with L2-norm control constraint. Discret. Contin. Dyn. Syst.-B 2022, 27, 4121. [Google Scholar] [CrossRef]
- Chen, R. On optimal boundary control of a class of system governed by parabolic partial differential equation. Sci. China Ser. A-Math. Phys. Astron. Technol. Sci. 1982, 25, 1205–1218. [Google Scholar]
- Casas, E.; Raymond, J.P. Error estimates for the numerical approximation of Dirichlet boundary control for semilinear elliptic equations. SIAM J. Control Optim. 2006, 45, 1586–1611. [Google Scholar] [CrossRef]
- Deckelnick, K.; Günther, A.; Hinze, M. Finite element approximation of Dirichlet boundary control for elliptic PDEs on two-and three-dimensional curved domains. SIAM J. Control Optim. 2009, 48, 2798–2819. [Google Scholar] [CrossRef]
- Gong, W.; Yan, N. Mixed finite element method for Dirichlet boundary control problem governed by elliptic PDEs. SIAM J. Control Optim. 2011, 49, 984–1014. [Google Scholar] [CrossRef]
- Pfefferer, J.; Winkler, M. Finite element error estimates for normal derivatives on boundary concentrated meshes. SIAM J. Control Optim. 2019, 57, 2043–2073. [Google Scholar] [CrossRef]
- Vexler, B. Finite element approximation of elliptic Dirichlet optimal control problems. Numer. Funct. Anal. Optim. 2007, 28, 957–973. [Google Scholar] [CrossRef]
- May, S.; Rannacher, R.; Vexler, B. Error analysis for a finite element approximation of elliptic Dirichlet boundary control problems. SIAM J. Control Optim. 2013, 51, 2585–2611. [Google Scholar] [CrossRef]
- Chang, L.; Gong, W.; Yan, N. Weak boundary penalization for Dirichlet boundary control problems governed by elliptic equations. J. Math. Anal. Appl. 2017, 453, 529–557. [Google Scholar] [CrossRef]
- Hu, W.; Shen, J.; Singler, J.R.; Zhang, Y.; Zheng, X. A superconvergent hybridizable discontinuous Galerkin method for Dirichlet boundary control of elliptic PDEs. Numer. Math. 2020, 144, 375–411. [Google Scholar] [CrossRef]
- Geveci, T. On the approximation of the solution of an optimal control problem governed by an elliptic equation. RAIRO. Anal. Numérique 1979, 13, 313–328. [Google Scholar] [CrossRef]
- Karkulik, M. A finite element method for elliptic Dirichlet boundary control problems. Comput. Methods Appl. Math. 2020, 20, 827–843. [Google Scholar] [CrossRef]
- Hinze, M.; Matthes, U. A note on variational discretization of elliptic Neumann boundary control. Control Cybern. 2009, 38, 577–591. [Google Scholar]
- Casas, E.; Dhamo, V. Error estimates for the numerical approximation of Neumann control problems governed by a class of quasilinear elliptic equations. Comput. Optim. Appl. 2012, 52, 719–756. [Google Scholar] [CrossRef]
- Gunzburger, M.D.; Lee, H.C.; Lee, J. Error estimates of stochastic optimal Neumann boundary control problems. SIAM J. Numer. Anal. 2011, 49, 1532–1552. [Google Scholar] [CrossRef]
- Krumbiegel, K.; Meyer, C.; Rösch, A. A priori error analysis for linear quadratic elliptic Neumann boundary control problems with control and state constraints. SIAM J. Control Optim. 2010, 48, 5108–5142. [Google Scholar] [CrossRef]
- Brenner, S.; Oh, M.; Sung, L.Y. P1 finite element methods for an elliptic state-constrained distributed optimal control problem with Neumann boundary conditions. Results Appl. Math. 2020, 8, 100090. [Google Scholar] [CrossRef]
- Akman, T.; Yücel, H.; Karasözen, B. A priori error analysis of the upwind symmetric interior penalty Galerkin (SIPG) method for the optimal control problems governed by unsteady convection diffusion equations. Comput. Optim. Appl. 2014, 57, 703–729. [Google Scholar] [CrossRef]
- Luo, X.; Chen, Y.; Huang, Y.; Hou, T. Some error estimates of finite volume element method for parabolic optimal control problems. Optim. Control Appl. Methods 2014, 35, 145–165. [Google Scholar] [CrossRef]
- Chen, Y.; Yi, N.; Liu, W. A Legendre–Galerkin spectral method for optimal control problems governed by elliptic equations. SIAM J. Numer. Anal. 2008, 46, 2254–2275. [Google Scholar] [CrossRef]
- Ravindran, S.S. Penalization of Dirichlet Boundary Control for Nonstationary Magneto-Hydrodynamics. SIAM J. Control Optim. 2020, 58, 2354–2382. [Google Scholar] [CrossRef]
- Chatzipantelidis, P.; Lazarov, R.; Thomée, V. Error estimates for a finite volume element method for parabolic equations in convex polygonal domains. Numer. Methods Partial. Differ. Equ. Int. J. 2004, 20, 650–674. [Google Scholar] [CrossRef]
- Bi, C.; Ginting, V. Two-grid finite volume element method for linear and nonlinear elliptic problems. Numer. Math. 2007, 108, 177–198. [Google Scholar] [CrossRef]
- Kumar, S.; Nataraj, N.; Pani, A.K. Finite volume element method for second order hyperbolic equations. Int. J. Numer. Anal. Model. 2008, 5, 132–151. [Google Scholar]
- Luo, X.; Chen, Y.; Huang, Y. Some Error Estimates of Finite Volume Element Approximation for Elliptic Optimal Control Problems. Int. J. Numer. Anal. Model. 2013, 10, 697–711. [Google Scholar]
- Cai, Z.; McCormick, S. On the accuracy of the finite volume element method for diffusion equations on composite grids. SIAM J. Numer. Anal. 1990, 27, 636–655. [Google Scholar] [CrossRef]
- Ewing, R.; Lazarov, R.; Lin, Y. Finite volume element approximations of nonlocal reactive flows in porous media. Numer. Methods Partial. Differ. Equ. Int. J. 2000, 16, 285–311. [Google Scholar] [CrossRef]
- Karaa, S.; Mustapha, K.; Pani, A.K. Finite volume element method for two-dimensional fractional subdiffusion problems. IMA J. Numer. Anal. 2017, 37, 945–964. [Google Scholar] [CrossRef]
- Li, R.; Gao, Y.; Chen, J.; Zhang, L.; He, X.; Chen, Z. Discontinuous finite volume element method for a coupled Navier-Stokes-Cahn-Hilliard phase field model. Adv. Comput. Math. 2020, 46, 1–35. [Google Scholar] [CrossRef]
- Lin, Y.; Liu, J.; Yang, M. Finite volume element methods: An overview on recent developments. Int. J. Numer. Anal. Model. Ser. B 2013, 4, 14–34. [Google Scholar]
- Gan, X.; Xu, D. An efficient symmetric finite volume element method for second-order variable coefficient parabolic integro-differential equations. Comput. Appl. Math. 2020, 39, 1–24. [Google Scholar] [CrossRef]
- Lou, Y.; Chen, C.; Xue, G. Two-grid finite volume element method combined with Crank-Nicolson scheme for semilinear parabolic equations. Adv. Appl. Math. Mech. 2021, 13, 892–913. [Google Scholar]
- Ewing, R.E.; Li, Z.; Lin, T.; Lin, Y. The immersed finite volume element methods for the elliptic interface problems. Math. Comput. Simul. 1999, 50, 63–76. [Google Scholar] [CrossRef]
- Kumar, S.; Nataraj, N.; Pani, A.K. Discontinuous Galerkin finite volume element methods for second-order linear elliptic problems. Numer. Methods Partial. Differ. Equ. Int. J. 2009, 25, 1402–1424. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, Z.; Li, Z. A Fourier finite volume element method for solving two-dimensional quasi-geostrophic equations on a sphere. Appl. Numer. Math. 2013, 71, 1–13. [Google Scholar]
- Lin, X.; Su, M.; Zhang, Z. Fourier Finite Volume Element Method for Two Classes of Optimal Control Problems Governed by Elliptic PDEs on Complex Connected Domain. Numer. Funct. Anal. Optim. 2020, 41, 379–412. [Google Scholar] [CrossRef]
- Hinze, M. A variational discretization concept in control constrained optimization: The linear-quadratic case. Comput. Optim. Appl. 2005, 30, 45–61. [Google Scholar] [CrossRef]
- Chen, R. Optimal boundary control of parabolic system on doubly connected region in new space. Sci. China (Sci. Sin.) Ser. A 1995, 8, 933–944. [Google Scholar]
- Djellab, N. Résolution Numérique de Problèmes D’équations aux Dérivées Partielles Issus de la Biologie et la Médecine. Ph.D. Thesis, Ferhat ABBAS University, Setif, Algeria, 2022. [Google Scholar]
- Ewing, R.E.; Lin, T.; Lin, Y. On the accuracy of the finite volume element method based on piecewise linear polynomials. SIAM J. Numer. Anal. 2002, 39, 1865–1888. [Google Scholar] [CrossRef]
- Qiu, Z.; Zeng, Z.; Mei, H.; Li, L.; Yao, L.; Zhang, L. A Fourier–Legendre spectral element method in polar coordinates. J. Comput. Phys. 2012, 231, 666–675. [Google Scholar] [CrossRef]
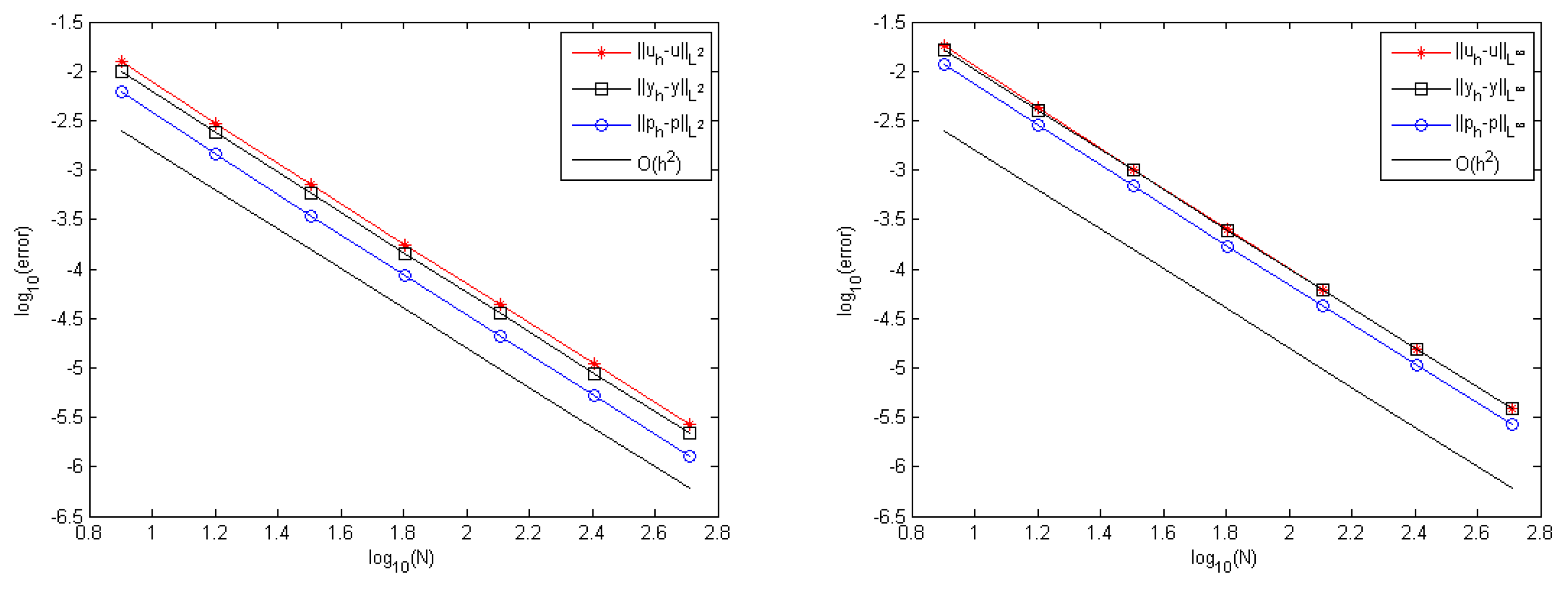
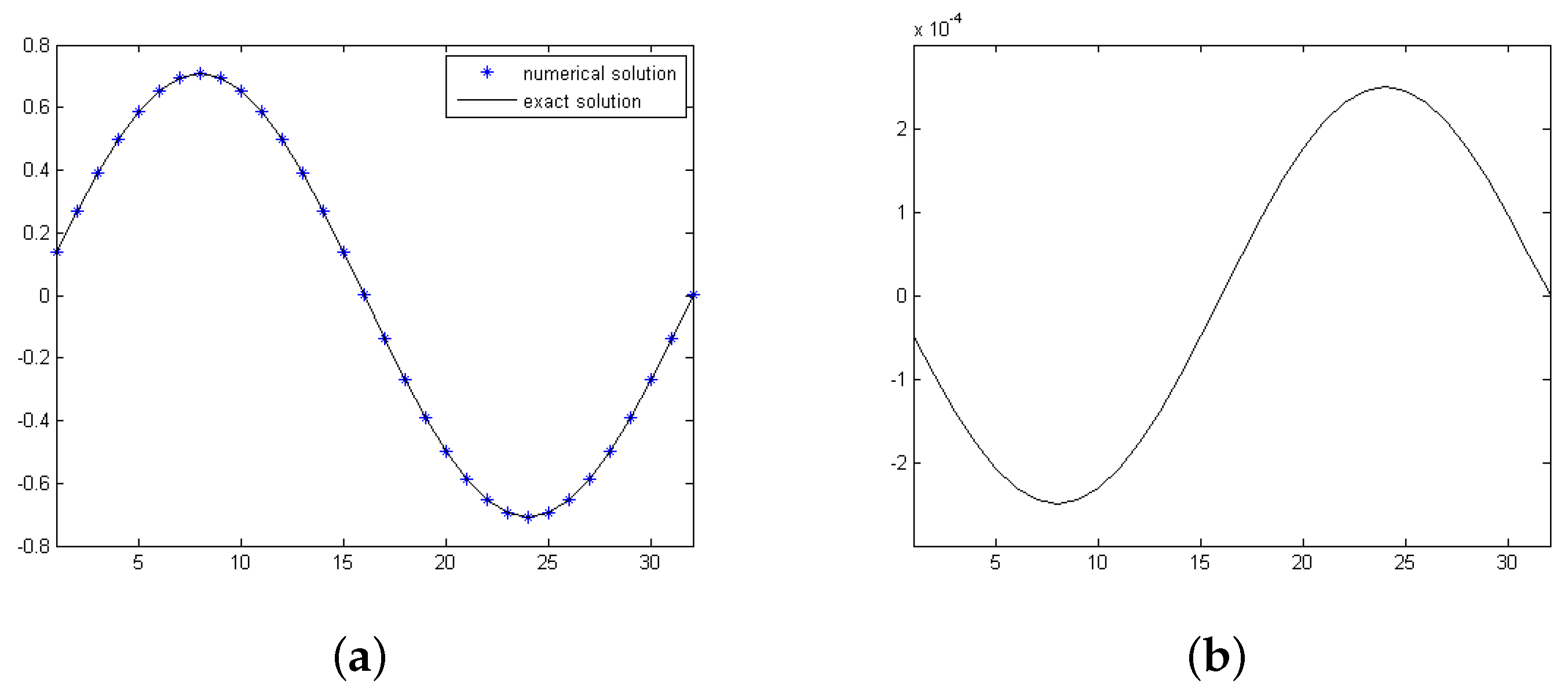
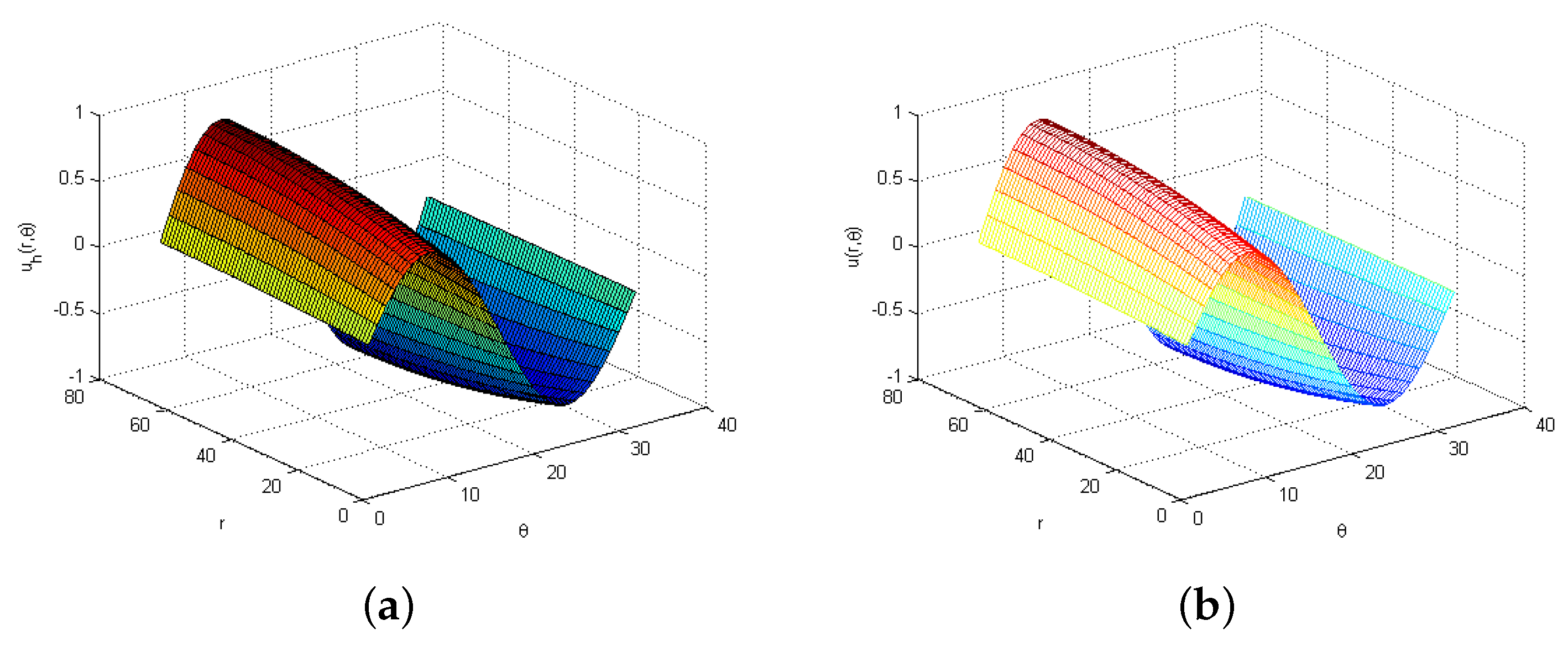
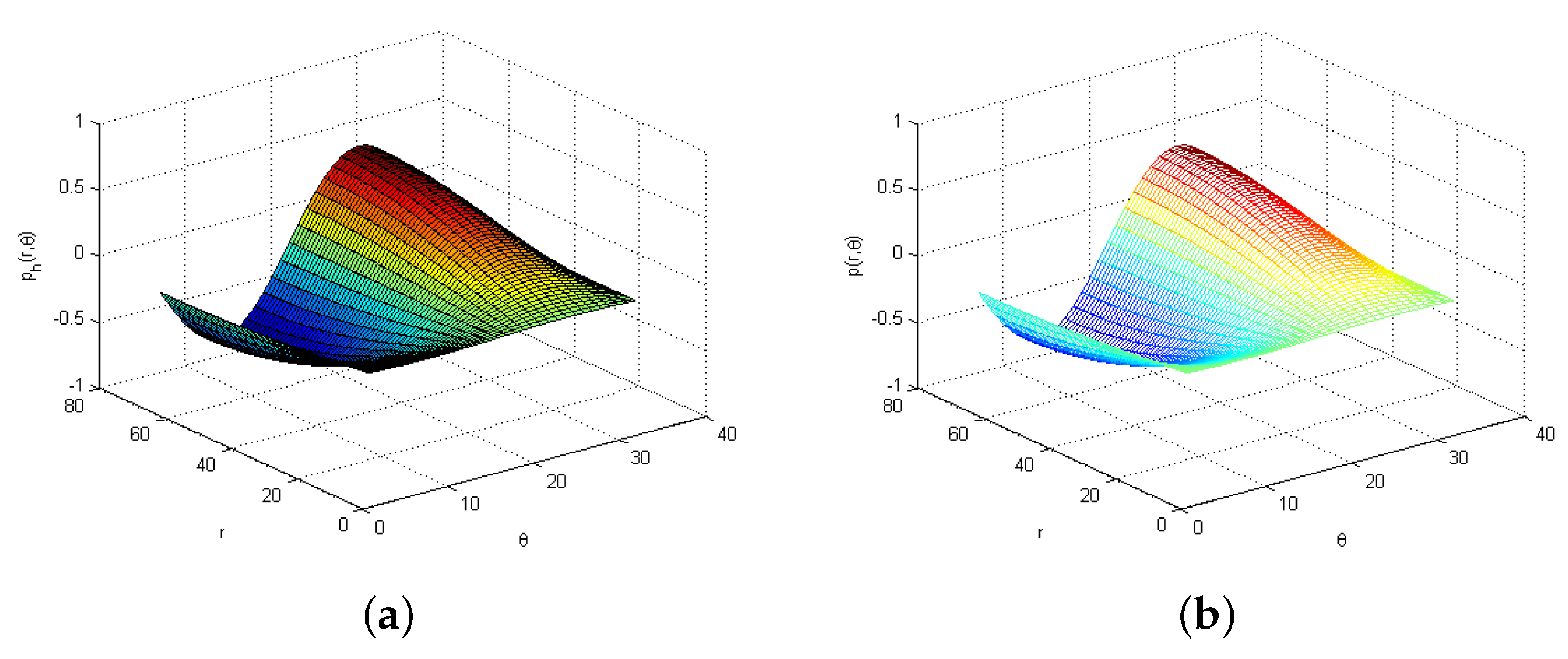
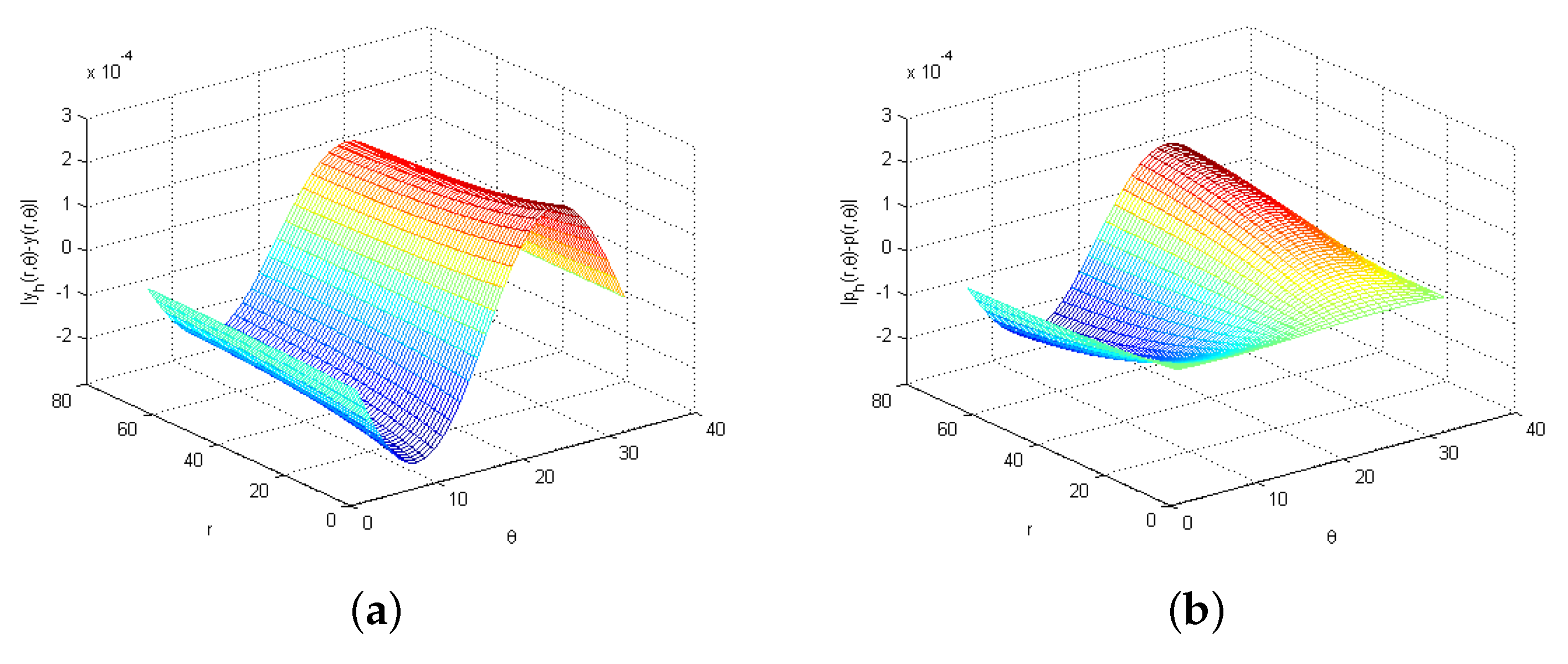
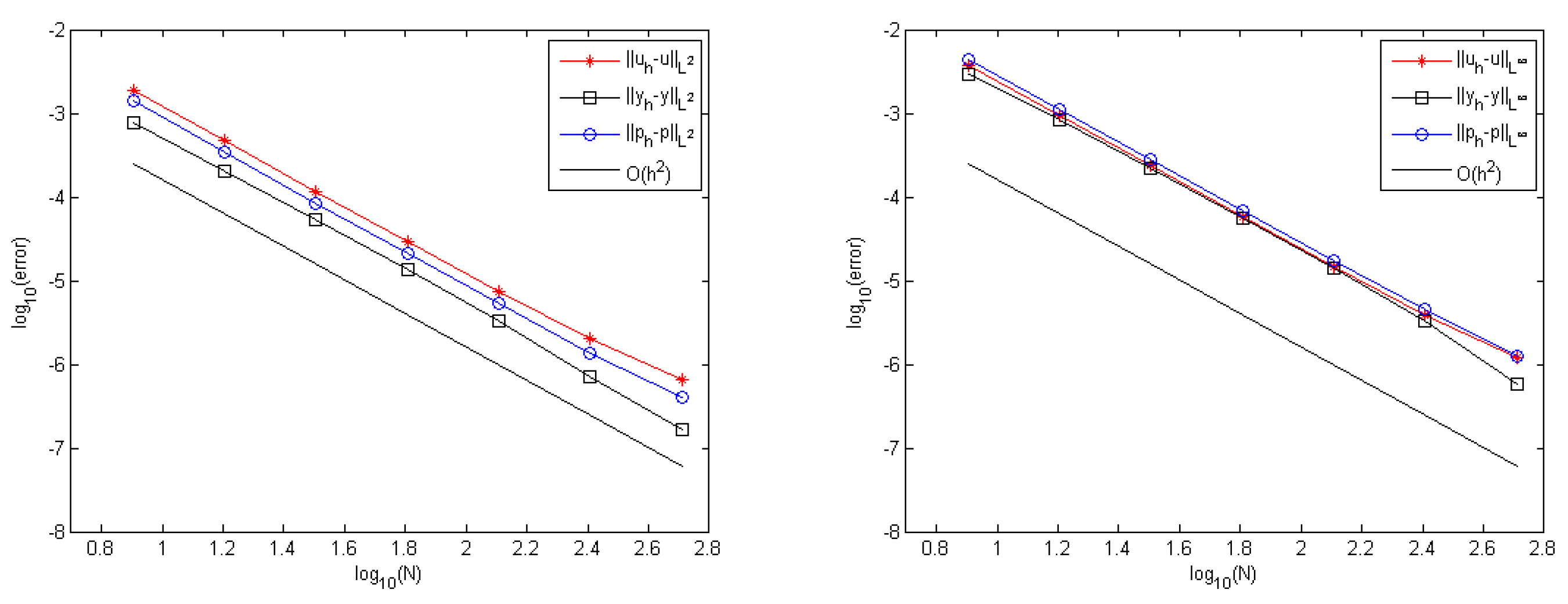
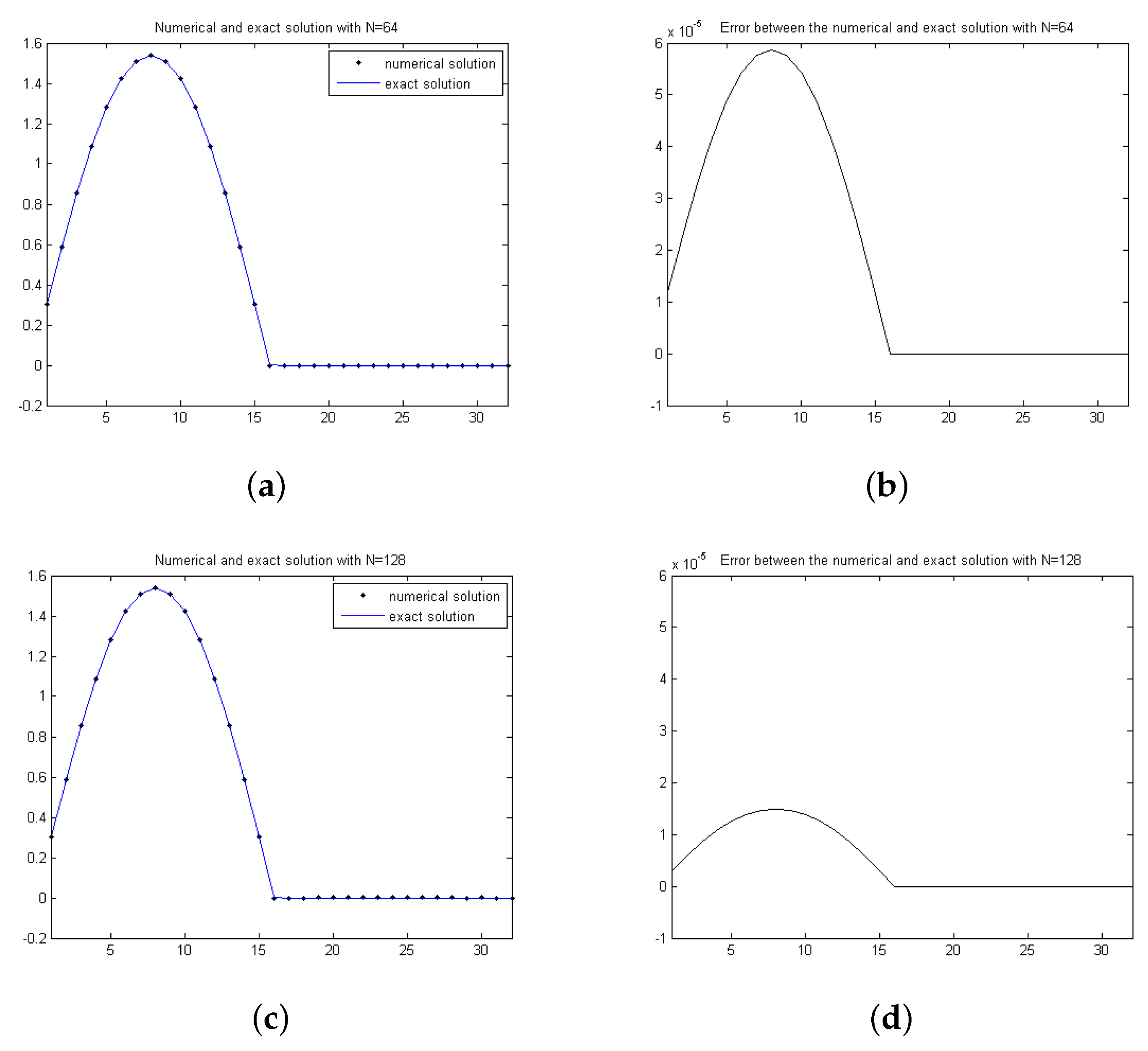
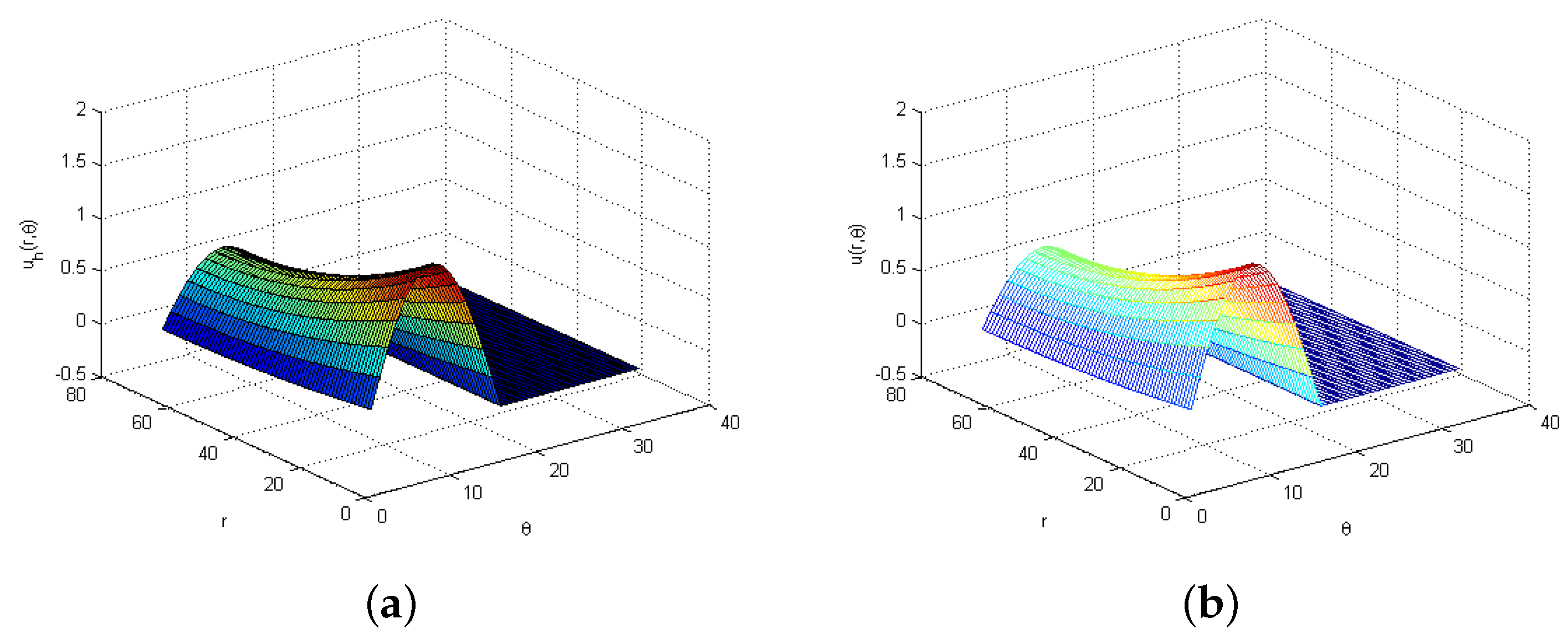
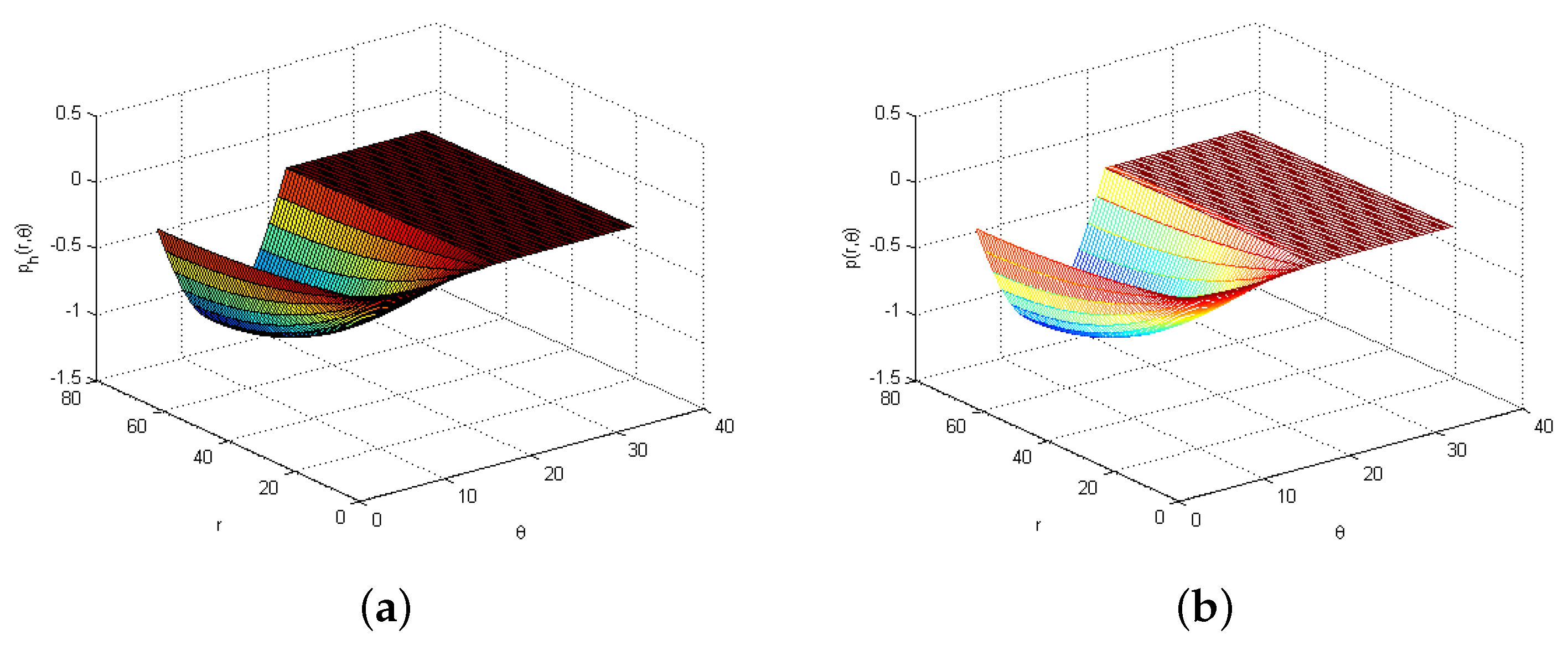
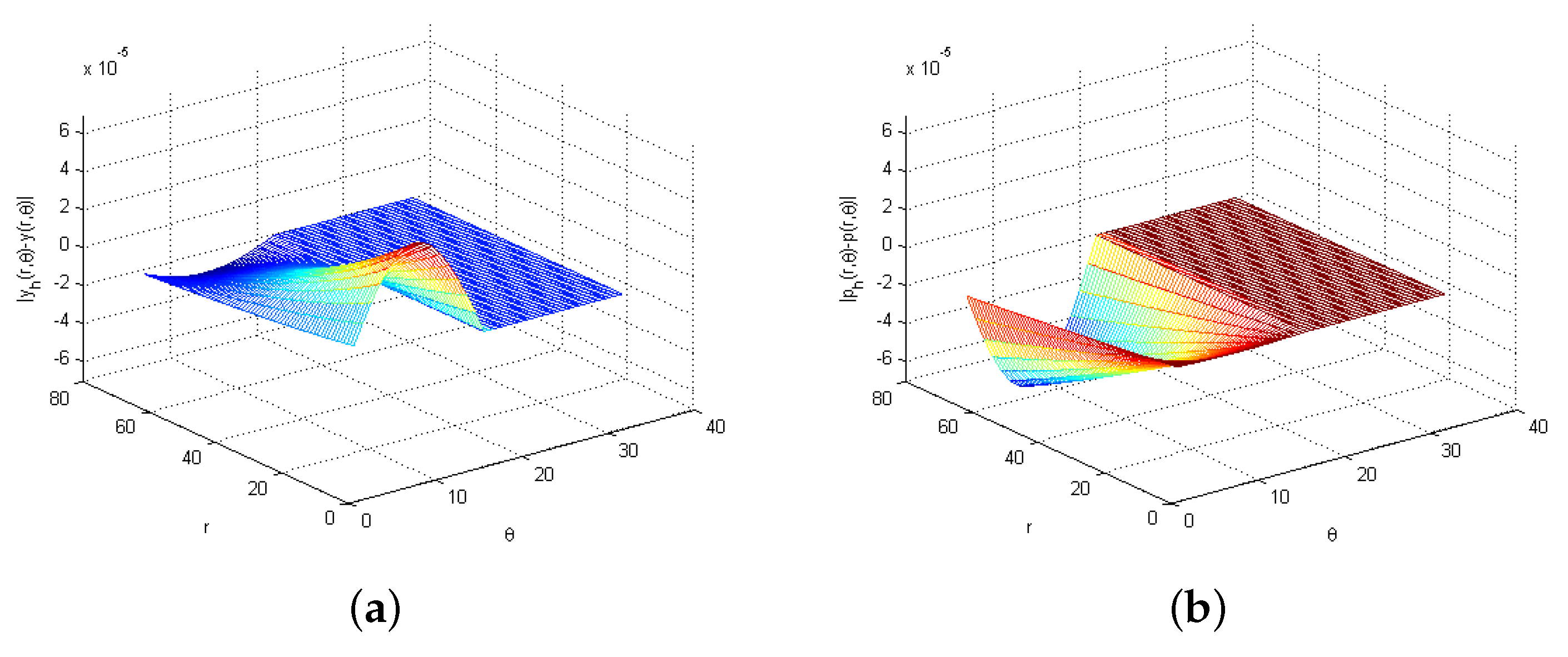
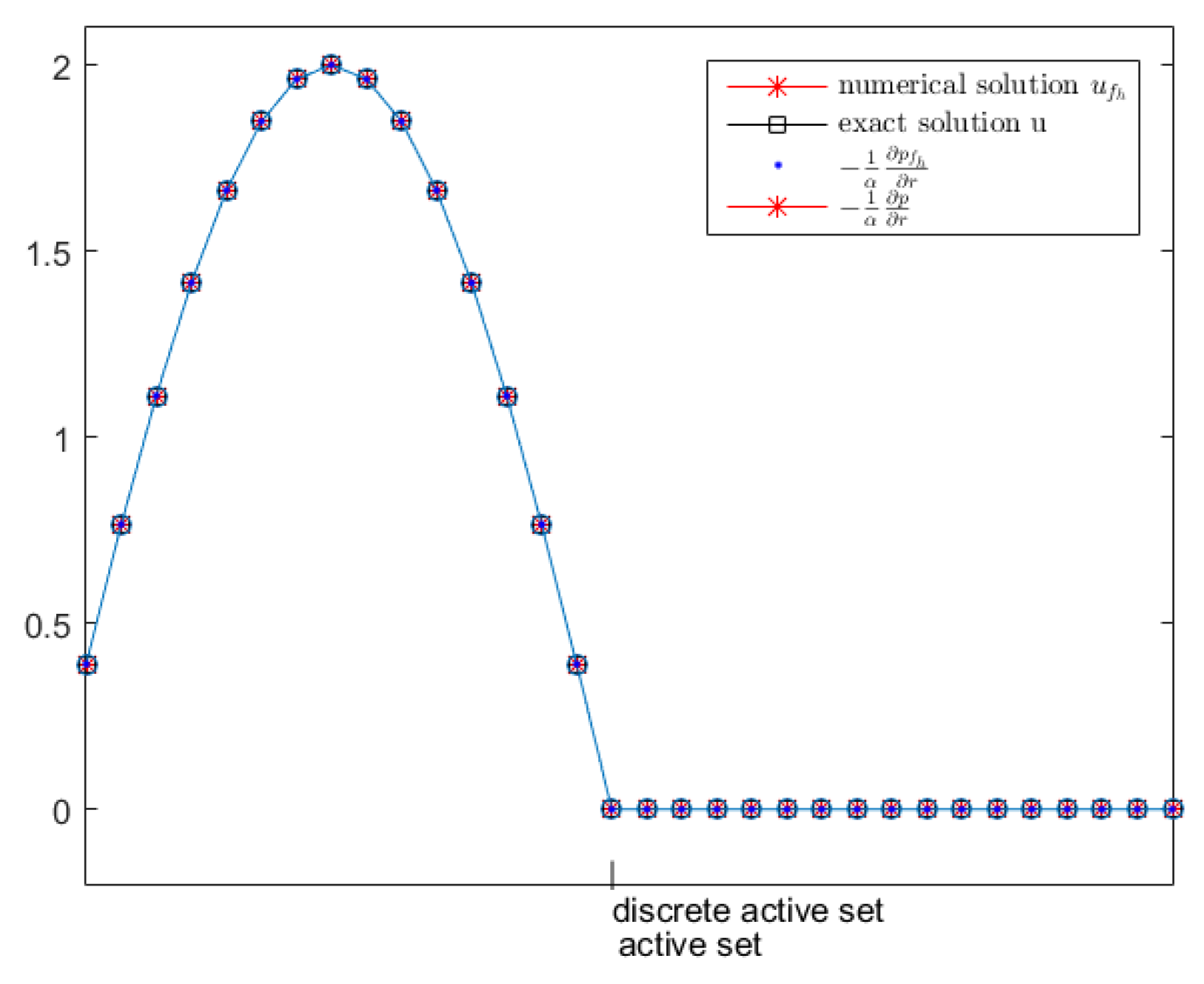
| (a) -norm | ||||||
| N | Order | Order | Order | |||
| 8 | ||||||
| 16 | 2.12 | 2.11 | 2.15 | |||
| 32 | 2.07 | 2.06 | 2.08 | |||
| 64 | 2.04 | 2.03 | 2.04 | |||
| 128 | 2.02 | 2.02 | 2.02 | |||
| 256 | 2.01 | 2.01 | 2.01 | |||
| 512 | 2.00 | 2.01 | 2.01 | |||
| (b) -norm | ||||||
| N | Order | Order | Order | |||
| 8 | ||||||
| 16 | 2.12 | 2.04 | 2.08 | |||
| 32 | 2.07 | 2.03 | 2.04 | |||
| 64 | 2.04 | 2.01 | 2.02 | |||
| 128 | 2.02 | 2.01 | 2.01 | |||
| 256 | 2.01 | 2.00 | 2.01 | |||
| 512 | 2.00 | 2.00 | 2.00 | |||
| (a) -norm | ||||||
| N | Order | Order | Order | |||
| 8 | ||||||
| 16 | 1.99 | 1.86 | 2.09 | |||
| 32 | 2.00 | 1.93 | 2.04 | |||
| 64 | 1.99 | 1.98 | 2.02 | |||
| 128 | 1.96 | 2.05 | 1.99 | |||
| 256 | 1.85 | 2.29 | 1.92 | |||
| (b) -norm | ||||||
| N | Order | Order | Order | |||
| 8 | ||||||
| 16 | 2.00 | 1.77 | 2.00 | |||
| 32 | 2.00 | 1.88 | 2.00 | |||
| 64 | 1.99 | 1.95 | 2.00 | |||
| 128 | 1.97 | 2.00 | 1.99 | |||
| 256 | 1.90 | 2.13 | 1.95 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, M.; Xie, L.; Zhang, Z. Numerical Analysis of Fourier Finite Volume Element Method for Dirichlet Boundary Optimal Control Problems Governed by Elliptic PDEs on Complex Connected Domains. Mathematics 2022, 10, 4779. https://doi.org/10.3390/math10244779
Su M, Xie L, Zhang Z. Numerical Analysis of Fourier Finite Volume Element Method for Dirichlet Boundary Optimal Control Problems Governed by Elliptic PDEs on Complex Connected Domains. Mathematics. 2022; 10(24):4779. https://doi.org/10.3390/math10244779
Chicago/Turabian StyleSu, Mengya, Liuqing Xie, and Zhiyue Zhang. 2022. "Numerical Analysis of Fourier Finite Volume Element Method for Dirichlet Boundary Optimal Control Problems Governed by Elliptic PDEs on Complex Connected Domains" Mathematics 10, no. 24: 4779. https://doi.org/10.3390/math10244779
APA StyleSu, M., Xie, L., & Zhang, Z. (2022). Numerical Analysis of Fourier Finite Volume Element Method for Dirichlet Boundary Optimal Control Problems Governed by Elliptic PDEs on Complex Connected Domains. Mathematics, 10(24), 4779. https://doi.org/10.3390/math10244779







