An Innovative Hunter-Prey-Based Optimization for Electrically Based Single-, Double-, and Triple-Diode Models of Solar Photovoltaic Systems

Abstract

The derivation of PV model parameters is crucial for the optimization, control, and simulation of PV systems. Although many parameter extraction algorithms have been developed to address this issue, they might have some limitations. This work presents an efficient hybrid optimization approach for reliably and effectively extracting PV parameters based on the hunter–prey optimizer (HPO) technique. The proposed HPO technique is a new population-based optimizer inspired by the behavior of prey and predator animals. In the proposed HPO mechanism, the predator attacks the prey that leaves the prey population. Accordingly, the position of a hunter is adjusted toward this distant prey, while the position of the prey is adjusted towards a secure place. The search agent’s position, which represents the best fitness function value, is considered a secure place. The proposed HPO technique worked as suggested when parameters are extracted from several PV models, including single-, double-, and triple-diode models. Moreover, a statistical error analysis was used to demonstrate the superiority of the proposed method. The proposed HPO technique outperformed other recently reported techniques in terms of convergence speed, dependability, and accuracy, according to simulation data.

1. Introduction

1.1. Motivation

Conventional energy has had substantial negative effects on the environment in the past decades. Therefore, the adoption of alternative renewable energy sources (RES) has drawn a lot of attention in recent years to increase environmental protection. Due to its widespread availability and cleanliness, solar photovoltaic energy is considered the most profitable RES. Hence, solar energy has been used for a variety of practical purposes, including the provision of hot water, agriculture, and the oil industry. Photovoltaic (PV) systems play a significant role in the development of RES all over the world in various applications because they can convert solar energy directly into electrical energy [1,2,3]. Therefore, accurate parameter extraction is pivotal for PV cell design improvements, the evaluation of PV cell performance, quality control, and the optimization of manufacturing processes. Hence, having practical parameter identification strategies is essential [4].

1.2. Literature Survey of Related Work

Through the mathematical modeling of the PV system, tremendous progress has been achieved over the past few decades in understanding how the properties of PV systems act. The most common models are those that fit measured current–voltage data from PV cells under all operating situations and emulate real PV cells’ behavior [5]. Usually, equivalent circuit models constructed of diodes are employed. Single- and double-diode models are the models that are employed most frequently in this regard. Additionally, the current–voltage (I–V) characteristic curve is described using the triple-diode model. These similar models require the estimation of five, seven, and nine parameters, respectively [6].

Due to its multi-modal, multi-variable, and non-linear characteristics, PV model parameter extraction is still a challenging issue. Using numerical optimization approaches, methods based on I–V characteristic curves are used to reduce the total error between the measured current and the emulated current. Although this kind of approach does not necessitate intricate analysis and derivation, it might use more computer resources. Deterministic and meta-heuristic approaches are two of the most often utilized numerical optimization techniques [7].

Deterministic and meta-heuristic approaches can locate the ideal solution quickly. However, their performance is highly dependent on the initial estimation. When using these techniques, there is a possibility that it could become trapped in a local optimum if the initial estimation provided is incorrect. Meta-heuristic approaches, which are based on natural occurrences, have drawn a lot of interest and are frequently used in engineering optimization, particularly in highly non-linear and complicated situations. Meta-heuristic approaches have the advantage of being straightforward, efficient, simple to use, and independent of the properties of the mathematical model of the system under study. Accordingly, a variety of meta-heuristic approaches have been employed in recent years to extract PV model parameters [8]. In this study, a thorough evaluation of meta-heuristic optimizers and associated variants that have been developed for PV model parameter extraction is conducted to demonstrate a comparison with these studies.

The extraction of unidentified parameters from a PV model is considered a complicated issue that has been studied by many researchers because of its non-linear, non-convex, and multiparametric properties. Myriad meta-heuristics have been established to extract the single-diode PV model’s parameters, such as the shuffled frog leaping algorithm [9], ant lion optimizer (ALO) [10], and an enhanced simplified swarm optimization [11]. Furthermore, a bacterial factorial optimization model has been illustrated, as depicted in [12], and has been validated through comparisons between experimental and simulation outcomes.

A plethora of optimizers have been demonstrated for single- and double-diode PV models such as a combined differential evolution/whale optimizer [4], self-adaptive ensemble with differential evolution [13], cat swarm optimization [14], opposition-based learning salp swarm optimizers [15], biography-based optimization [16], salp swarm algorithm [17], particle swarm optimizer (PSO) [18], and an improved shuffled complex evaluation model [19]. Moreover, an enhanced whale optimization algorithm has been characterized, as manifested in [20], to precisely extract the parameters of two actual PV stations and diverse PV modules. A combination of bee pollinator and flower pollination has been elaborated, as manifested in [21], to extract the single- and double-diode PV models’ parameters with diverse environmental circumstances. Moreover, a performance-guided JAYA optimizer has been highlighted, as manifested in [22], and applied for extracting the diverse PV module variables.

In [23,24], a supply–demand optimizer was demonstrated for the triple-diode model of a PV cell and practical PV power plant system. A genetic algorithm based on non-uniform mutation (GANUM) [25] has been illustrated to extract parameters from PV models in a reliable, accurate, and quick way. In that study, the GAMNU was employed on single- and double-diode PV models. However, it was not implemented on the triple-diode PV model. In [26], an artificial hummingbird optimizer was represented with a solar triple-diode PV model of the STM6-40/36 module, KC200GT module, and mSi cell.

The moth–flame optimization (MFO) [27], grey wolf optimization (GWO) [28,29], quantum chaos BOA (QCBOA) [30], particle swarm optimization (PSO) [31], Tunicate swarm algorithm (TSA) [32,33], heap-based algorithm [34], salp swarm algorithm (SSA) [17], and rat swarm optimization (RSO) [35] are examples of these optimizers. Nevertheless, most of the optimizers in the literature have some restrictions. For instance, in [36], when working with a PV cell double-diode model, the memetic adaptive differential evolution (MADE) algorithm performed poorly. In the same context, the exploitation of the artificial bee colony (ABC) was poor [37]. Although a quick convergence speed of the biogeography-based optimizer (BBO) was achieved, it was easily caught in local optimal values because of its elitist mechanism. Furthermore, the cuckoo search (CS) algorithm suffered from slow convergence [38].

1.3. Research Gap

A lot of merits are offered by meta-heuristic optimization procedures, which include protection against early assumptions, established conjunctions, and an absence of individuality scenario [39]. In the literature, many meta-heuristic optimization procedures have been employed to extract PV cell parameters. It was established by a variety of “no free lunch” (NFL) theories that every algorithms’ improved performance over one class of problems is counterbalanced by efficiency over another [40]. Naruei et al. recently introduced the innovative hunter–prey optimization (HPO) technique, a population-based effective method, in [41]. The HPO technique is influenced by the behavior of predatory animals, such as lions, leopards, and wolves, in addition to prey species, such as stags and gazelles. Animal hunting behavior can take on a variety of forms, and some of these forms have been optimized through combinatorial processes. In the HPO technique, a special model is used as opposed to the scenario used by the other approaches. In the suggested technique, which incorporates prey and predator populations, a predator attacks a victim who wanders far from their group. The animal places itself farther from danger as the hunter moves closer to this distant target. It was assumed that the search agent’s station, which had the greatest fitness value, was a secure area.

1.4. Paper Contribution

This research focuses on improving the electrical parameters of various equivalent circuit models of PV systems because of the specific features of the HPO technique. Based on the HPO technique, three models are created considering the composition of a single-, double-, and triple-diode. The proposed HPO technique is applied to several applications in the field of photovoltaic technologies, considering two industrial PV panels, while considering STM6-40/36 and RTC France modules, and it is compared to numerous current optimizers. The results generated by the HPO-based PV design are also assessed against several established techniques. The key contributions of this paper can be highlighted as follows:

• A promising algorithm is demonstrated in the field of photovoltaic technologies, modelling with real applications on a commercial STM6-40/36 module and RTC France cell;
• The simulated results demonstrate that the developed PV system equivalent model relying on the HPO technique is extremely efficient and produces superior outcomes when compared to other reported techniques;
• The convergence rate for the proposed HPO is great, with a high speed in focusing the search around the area of the global optimization of the minimum RMSE;
• The proposed HPO technique provides high accuracy in extracting the electrical PV parameters with significant coincidence between the simulated and experimental I–V and P–V characteristics.

1.5. Key Segments of the Paper

This paper is organized in five sections: Section 2 demonstrates the HPO steps, while Section 3 characterizes the mathematical representation of the three PV models. In addition to this, a detailed discussion of the obtained results using HPO and the reported optimizers is developed in Section 4. Moreover, concluding remarks for the paper are provided in Section 5.

2. Mathematical Model of the Hunter–Prey-Based Optimization

In the HPO technique, when a hunter travels in quest of prey, the prey often swarms; as a result, the hunter aims for prey that is distant from the swarm. The hunter pursues and strikes its prey after locating it. The prey looks for food while also running away from a predator’s danger and searches for a secure haven. Based on a fitness function, this protected region is considered to be the ideal place to find prey. In the proposed HPO technique, the initial population can be randomly set to $(\overrightarrow{x})=\left\{{\overrightarrow{x}}_1,{\overrightarrow{x}}_2,\dots ,{\overrightarrow{x}}_n\right\}$, and the objective function can be calculated as $(\overrightarrow{O})=\left\{O_1,O_2,\dots ,O_n\right\}$ for all population members. Several rules and tactics inspired by the proposed algorithm were used to regulate and direct the population in the search space. Every time an iteration occurred, the proposed algorithm’s rules were followed to update each population member’s position, which was then assessed using the objective function. Every time the procedure was repeated, the solutions improved. Equation (1) generates a random position for each person in the initial population within the search space. The lower and upper boundaries of the search space are represented in Equation (2).

Several rules and tactics inspired by the proposed optimizer were used to regulate and direct the population in the search space.

$$x_i=rand(1,d).*(ub-lb)+lb$$

(1)

$$lb=\left[l{b}_1,l{b}_2,\dots ,l{b}_d\right],ub=\left[u{b}_1,u{b}_2,\dots ,u{b}_d\right]$$

(2)

where X_i represents the prey or hunter position, lb illustrates the lower boundary for the issue variables, ub manifests the upper boundary for the issue variables, and d illustrates the variables number of the issue.

Using $O_i=f(\overrightarrow{x})$, each solution’s fitness was determined after determining each agent’s position and generating the initial population. Exploration and exploitation were the main pillars of the search mechanism. Exploration describes the algorithm’s propensity for highly chaotic behaviors that cause solutions to frequently change. Due to the large variations in the solutions, the search space was further explored to identify its most promising regions. Exploitation is the process of reducing random behaviors after promising areas have been identified, so that the algorithm can explore in and around the promising regions. The hunter position for the hunter search mechanism could be updated with Equation (3):

$$x_{i,j}(t+1)=x_{i,j}(t)+0.5\left[2CZ{P}_{pos(j)}-x_{i,j}(t)+(2(1-C)Z\mu (j)-x_{i,j}(t))\right]$$

(3)

where $x(t+1)$ and $x(t)$ represent the next hunter and current hunter positions, Z manifests an adaptive parameter, P_pos illustrates the prey position, and µ characterizes the mean of all positions, as depicted in Equation (4):

$$\begin{array}{l}P={\overrightarrow{R}}_1<C;\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}IDX=(P==0);\\ Z=R_2\otimes IDX+{\overrightarrow{R}}_3\otimes (\approx IDX)\end{array}$$

(4)

where P illustrates a random vector and its value is in the range [0, 1], which is equivalent to the issue variables’ number, R₁ and R₃ characterize random vectors and their value is in the range [0, 1], and R₂ is a random number and its value is in the range [0, 1]. Additionally, IDX represents the index numbers of the R₁ vector that achieve the constraint (P = 0).

C illustrates the balance parameter between exploitation and exploration, and its value reduces over the iterations from 1 to 0.02. This parameter, C, can be scientifically expressed as depicted in Equation (5):

$$C=1-it\left(\frac{0.98}{MaxIt}\right)$$

(5)

where (it) and MaxIt represent the current and the maximum iteration values, respectively.

To calculate the prey position (P_pos), firstly, the average of all positions (µ) was determined according to Equation (6):

$$\mu =\frac{1}{n}{\displaystyle \sum _{i=1}^n{\overrightarrow{x}}_i}$$

(6)

The distance was calculated according to the Euclidean distance, as illustrated in Equation (7):

$$D_{euc(i)}={\left({\displaystyle \sum _{j=1}^d{(x_{i,j}-{\mu }_j)}^2}\right)}^{1/2}$$

(7)

The maximum distance from the mean positions of the search agent was considered the prey position (Ppos), as illustrated in Equation (8):

$${\overrightarrow{P}}_{pos}={\overrightarrow{x}}_i{\left|i\hspace{0.17em}is\hspace{0.17em}index\hspace{0.17em}of\hspace{0.17em}Max\hspace{0.17em}(end)sort(D_{euc})\right.}_{ }$$

(8)

According to the hunting scenario, when the hunter takes the prey, the prey dies, and the hunter will search for a new prey. To overcome this issue, a decreasing mechanism was considered, as manifested in Equation (9):

$$kbest=round(C\times N)$$

(9)

where N represents the number of search agents.

Equation (8) can be modified and the prey position can be calculated according to Equation (10):

$${\overrightarrow{P}}_{pos}={\overrightarrow{x}}_i\left|i\hspace{0.17em}is\hspace{0.17em}sorted\hspace{0.17em}\hspace{0.17em}{D}_{euc}(kbest)\right.$$

(10)

When starting the algorithm, the Kbest value is equivalent to N. Hence, the last search agent, which is farthest from the search agents’ average position ($\mu$), is attacked by the hunter and selected as the prey. The hunter chooses the prey and attacks the last search agent that is furthest away from the average position of the search agents ($\mu$). The Kbest value steadily drops until it equals the search agent, which is located at the closest point to the average location of the search agents ($\mu$) at the end of the algorithm. It should be noted that the distance from the search agents’ average position determined how the search agents, in each iteration, were ranked ($\mu$). When being assaulted, the prey seeks to escape and get to a secure position.

It was supposed that the best secure position defined the optimal global position, since it allows the prey to have a chance of survival, while the hunter will select alternative prey. The prey position was updated as illustrated in Equation (6):

$$x_{i,j}(t+1)=T_{pos(j)}+CZ\cos (2\pi R_4)\times (T_{pos(j)}-x_{i,j}(t))$$

(11)

where R₄ characterizes a random number and its value is in the range [−1, 1], and T_pos represents the optimum global position. The COS function and its input parameter permit the next prey to be positioned at global optimum diverse angles and radials. Thus, the exploitation phase’s performance can be improved.

To select the prey and hunter in the HPO technique, Equations (3) and (11) were used:

$$x_{i,j}(t+1)=\left\{\begin{array}{}\hfill \mathrm{(12a)}& x_i(t)+0.5\left[(2CZ{P}_{pos}-x_i(t))+(2(1-c)Z\mu -x_i(t))\right]\hspace{0.17em}if\hspace{0.17em}\hspace{0.17em}{R}_5<\beta \hfill \hfill \mathrm{(12b)}& T_{pos}+CZ\cos (2\pi R_4)\times (T_{pos}-x_i(t))\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}else\hfill \end{array}\right.$$

where $\beta$ defines a regulatory parameter with a value of 0.1. The symbol (R₅) characterizes a random number and its value is in the range [0, 1]. The search agent would be a hunter if R₅ was less than $\beta$, and, consequently, the next position of the search agent, as manifested in Equation (12a), would be updated. However, the search agent will be prey in cases when R₅ is higher than $\beta$, and, consequently, the next position of the search agent, as manifested in Equation (12b), would be updated. The flowchart of the HPO technique is depicted in Figure 1.

3. Mathematical Model of the Electrical Representations of Solar PV Systems

To highlight the I–V properties of the PV modules, different equivalent circuits were designed. The single-, double-, and three-diode versions of PV-equivalent circuits are the most frequently utilized practically. The following is a description of these PV models [42]. In the last decades, the famous representation of PV cells is the Shockley diode-equivalent circuits.

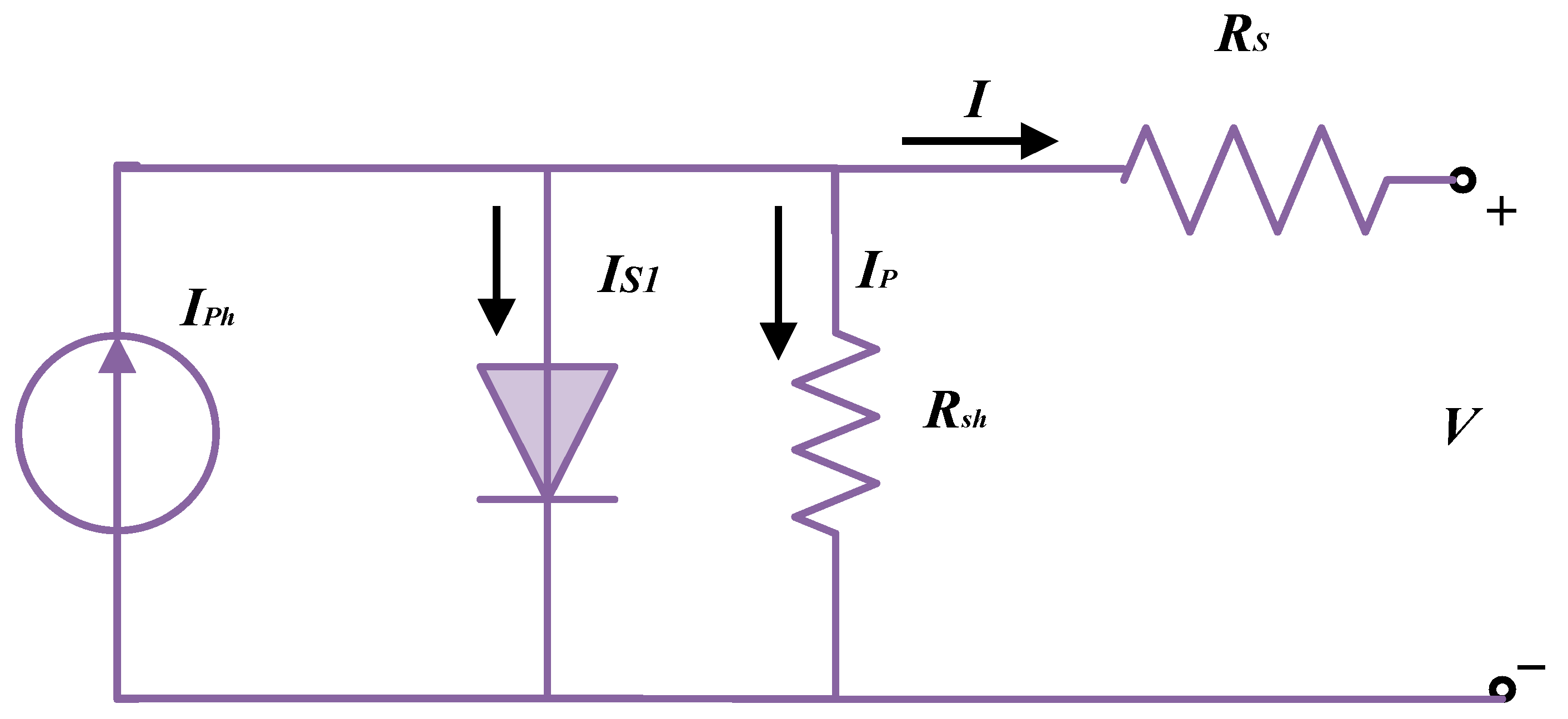
3.1. Single-Diode Model

To analyze the dynamic interactions between various components of a PV system, modeling has become an essential component. The SDM is widely utilized to represent solar cell characteristics. The equivalent circuit of SDM is manifested in Figure 2, where the PV cell is represented as a current source and placed in parallel with a single diode.

As illustrated in Figure 2, the key components of a single-diode model included in PV cells are a diode, two resistors, and a current source. In Equation (13), the load current equation applying Kirchoff’s Current Law of the single-diode model was mathematically formulated. The two lumped resistors manifested the losses, which were series resistance (R_S) and shunt resistance (R_Sh). The output current (I) was obtained using the Shockley diode equation, which is denoted in Equation (13) [4,39]:

$$I=I_{ph}-I_{S1}\left[\exp \left((V+I{R}_S)/{\eta }_1\hspace{0.17em}{V}_{th}\right)-1\right]-(V+I{R}_S)/R_{sh}$$

(13)

where I_S2 characterizes the reverse saturation current, whereas η₂ denotes the ideality factor of D2. In addition to this, the two symbols R_Sh and R_S show shunt and series resistances, respectively. Furthermore, I_Ph and I express the photocurrent of the cell and output current, respectively, while V shows the terminal voltage, and V_th can be mathematically characterized as in Equation (14), which depicts the thermal voltage of the PV cell:

$$V_{th}=K_{B}T/q_c$$

(14)

where the symbols (q_c) and (T) represent the electron’s charge and absolute temperature, respectively, while K_B elaborates Boltzmann’s constant.

Five unidentified parameters in this model were estimated from the I–V data of PV cells: I_S1, R_S, I_Ph, R_P, and η₁.

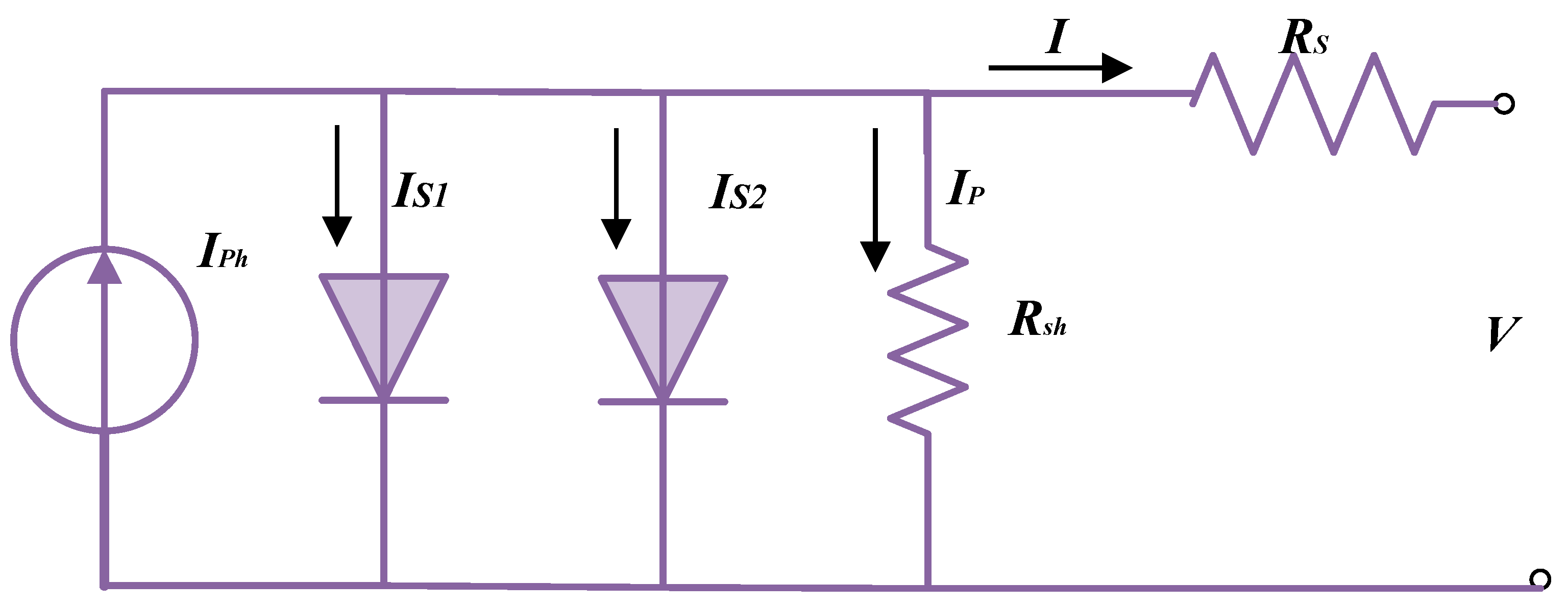
3.2. Double-Diode Model

This model was considered as a modified version of the single-diode model. In this version, an additional diode, which demonstrated a space charge recombination, was added in parallel in the basic single-diode model, as elaborated in Figure 3. In Equation (15), the load current equation of the double-diode model is mathematically formulated:

$$I=I_{Ph}-I_{S1}\left[\exp \left((V+I{R}_S)/{\eta }_1\hspace{0.17em}{V}_{th}\right)-1\right]-I_{S2}\left[\exp \left((V+I{R}_S)/{\eta }_2\hspace{0.17em}{V}_{th}\right)-1\right]-(V+I{R}_S)/R_{sh}$$

(15)

where I_S2 characterizes the reverse saturation current, while η₂ denotes the ideality factor of D2.

Seven unidentified parameters in this model were determined from the I–V data of PV cells: I_S1, I_S2, R_S, I_Ph, R_P, η₁, and η₂.

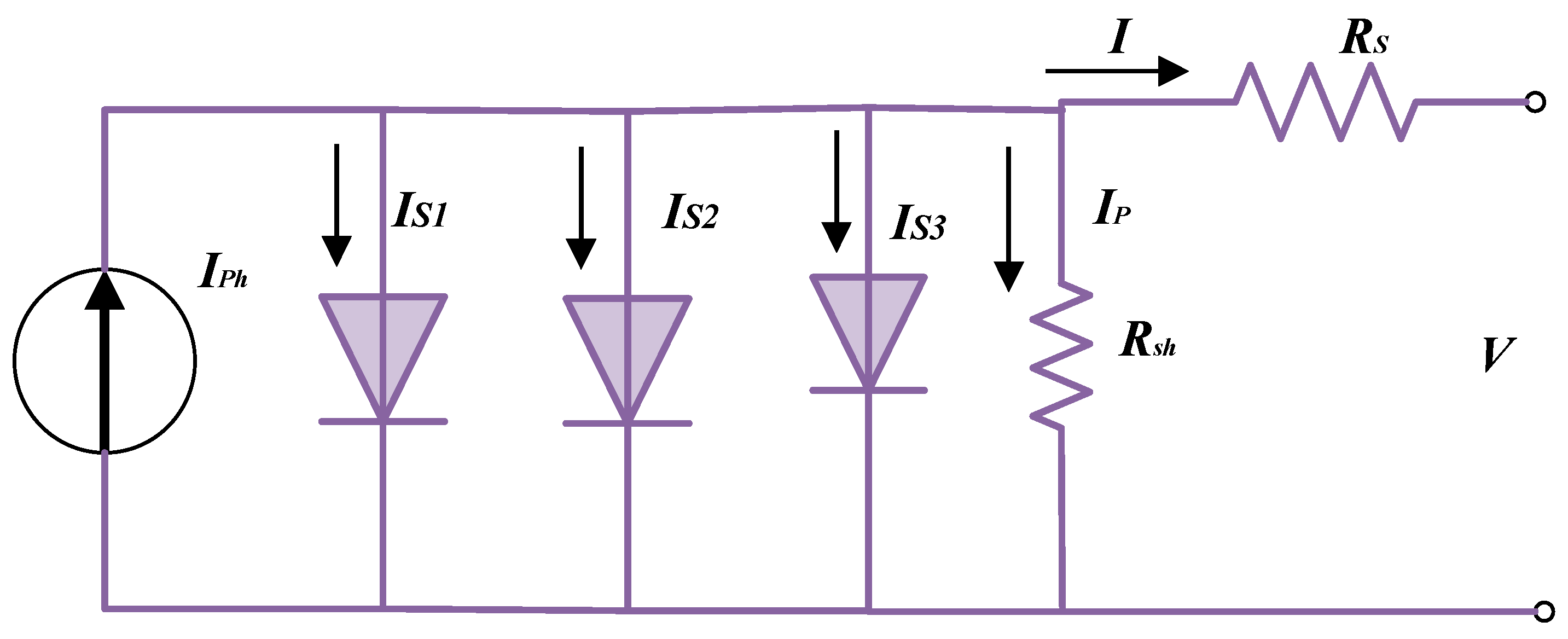
3.3. Photovoltaic Triple-Diode Model

This model was considered as a modified version of the double-diode model. In this version, an additional diode, which demonstrated a space charge recombination, was added in parallel in the basic double-diode model, as elaborated in Figure 4. The grain boundaries and leakage current effect (I_s3) were manifested in this model, where the leakage current flowed throughout the shunt resistance. Series resistance in the central part of the solar cell was represented by the resistance of semiconductors to the material. In Equation (16), the load current equation of the double-diode model is mathematically formulated [43]:

$$\begin{array}{ll}I=& I_{Ph}-I_{S1}\left[\exp \left((V+I{R}_S)/{\eta }_1\hspace{0.17em}{V}_{th}\right)-1\right]-I_{S2}\left[\exp \left((V+I{R}_S)/{\eta }_2\hspace{0.17em}{V}_{th}\right)-1\right]\\ & -I_{S3}\left[\exp \left((V+I{R}_S)/{\eta }_3\hspace{0.17em}{V}_{th}\right)-1\right]-(V+I{R}_S)/R_{sh}\end{array}$$

(16)

where I_S3 characterizes the reverse saturation current, while η₃ denotes the ideality factor of D3.

Nine unidentified parameters in this model were determined from the I–V data of PV cells: I_S1, I_S2, I_S3, R_S, I_Ph, R_P, η₁, η₃, and η₃ [44,45].

3.4. PV Modules Handling

The equations of the single-, double-, and triple-diode models were illustrated in terms of a PV module made up of N_p cells connected in parallel and N_s cells connected in series. Therefore, Equations (13), (15) and (16) were upgraded and modified to (17–19) for the single-, double-, and triple-diode models, respectively, as follows:

$$I=N_p\left(I_{ph}-I_{S1}\left[\exp \left((V+I{N}_s{R}_S/N_p)/({\eta }_1\hspace{0.17em}{N}_s{V}_{th})\right)-1\right]\right)-(V+I{N}_s{R}_S/N_p)/(N_s{N}_p{R}_{sh})$$

(17)

$$\begin{array}{ll}I=& N_p\left(I_{ph}-I_{S1}\left[\exp \left((V+I{N}_s{R}_S/N_p)/({\eta }_1\hspace{0.17em}{N}_s{V}_{th})\right)-1\right]\right)-I_{S2}\left[\exp \left((V+I{N}_s{R}_S/N_p)/({\eta }_2\hspace{0.17em}{N}_s{V}_{th})\right)-1\right]\\ & -(V+I{N}_s{R}_S/N_p)/(N_s{N}_p{R}_{sh})\end{array}$$

(18)

$$\begin{array}{ll}I=& N_p\left(I_{ph}-I_{S1}\left[\exp \left((V+I{N}_s{R}_S/N_p)/({\eta }_1\hspace{0.17em}{N}_s{V}_{th})\right)-1\right]\right)-I_{S2}\left[\exp \left((V+I{N}_s{R}_S/N_p)/({\eta }_2\hspace{0.17em}{N}_s{V}_{th})\right)-1\right]\\ & -I_{S3}\left[\exp \left((V+I{N}_s{R}_S/N_p)/({\eta }_3\hspace{0.17em}{N}_s{V}_{th})\right)-1\right]-(V+I{N}_s{R}_S/N_p)/(N_s{N}_p{R}_{sh})\end{array}$$

(19)

The PV cells/modules for single-, double- and triple-diode models had unaccounted for variables that could be computed numerically, analytically, or utilizing optimization methods.

3.5. Objective Function Formulation

The statistical analysis in this paper, which was based on the root-mean-square error ($\mathrm{RMSE}$) [46], was performed according to the following Equation:

$$\mathrm{RMSE}=\sqrt{\frac{1}{P}{{\displaystyle \sum }}_{J=1}^P{(I_{exp}^J-I_{cal}^J\left(V_{exp}^J,x\right))}^2}$$

(20)

where x defines the solution vector, P represents the number of iterations, and $I_{exp}^J$ and $V_{exp}^J$ characterize the measured current and voltage, respectively.

Equation (17) can be implemented for the single-, double-, and triple-diode solar PV model cell. In the single-, double-, and triple-diode models, the five, seven, and nine unknown parameters, respectively, were calculated.

4. Simulation Results

In this article, the STM6-40/36 and R.T.C France were studied under the proposed HPO. The mono-crystalline STM6-40/36 module comprises 36 cells connected in series with a cell size of 38 mm × 128 mm, a working temperature of 51 °C, and an irradiance of 1000 W/m² [47]. The commercial silicon solar R.T.C France works at a temperature of 33 °C and solar radiance of 1000 W/m². It has an open circuit voltage and a short-circuit current of 0.5727 V and 0.7605 A, respectively. In addition to that, the maximum point voltage and current of R.T.C France are 0.4590 V and 0.6755 A, respectively. The measured data contained 26 and 20 pairs of I and V values of the RTC France and STM6_40/36, respectively. The upper (ub) and lower limits (lb) for the extracted parameters of the STM6-40/36 and RTC France modules are characterized in

Table 1. Search range for the extracted parameters of PV modules under study.

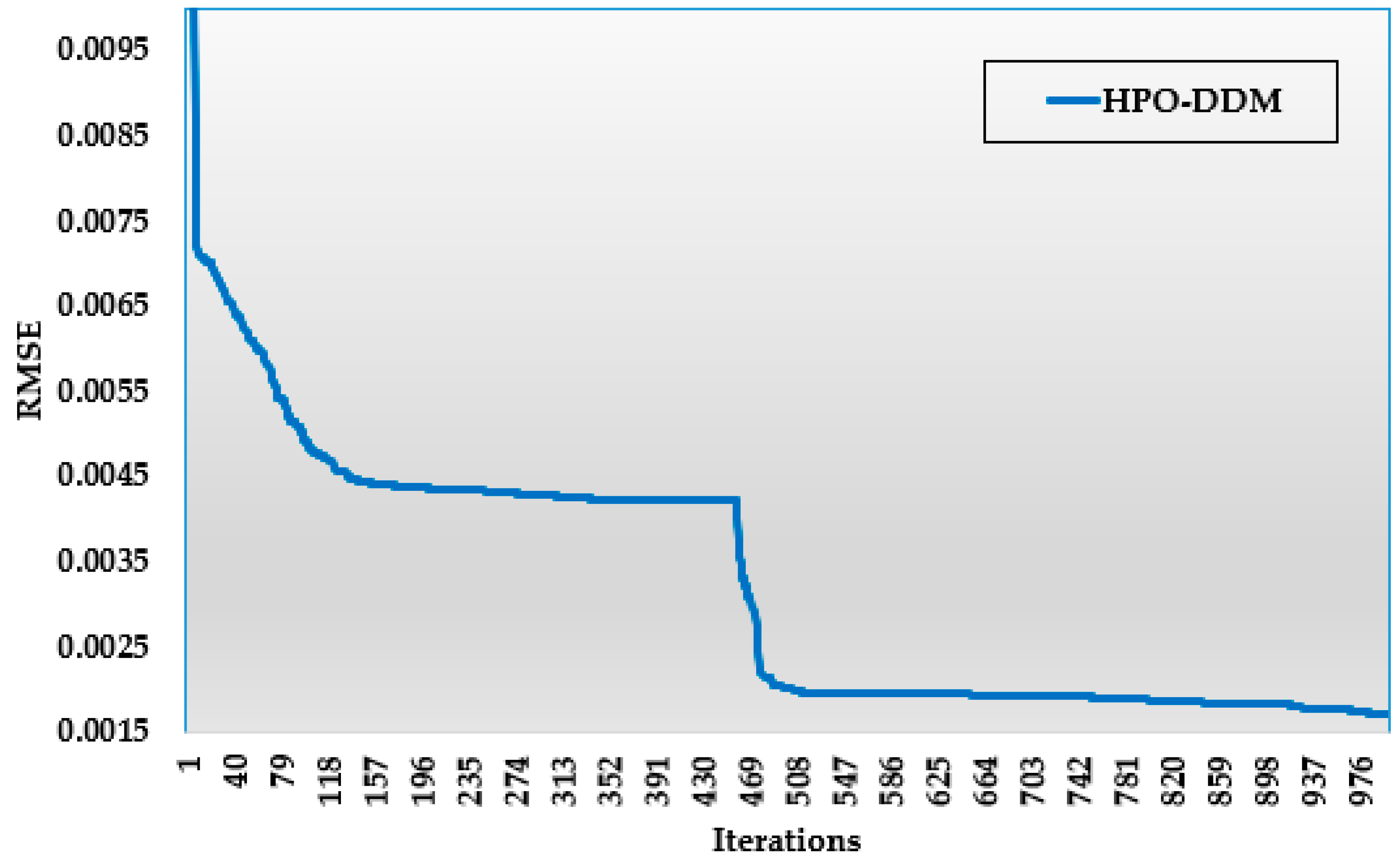
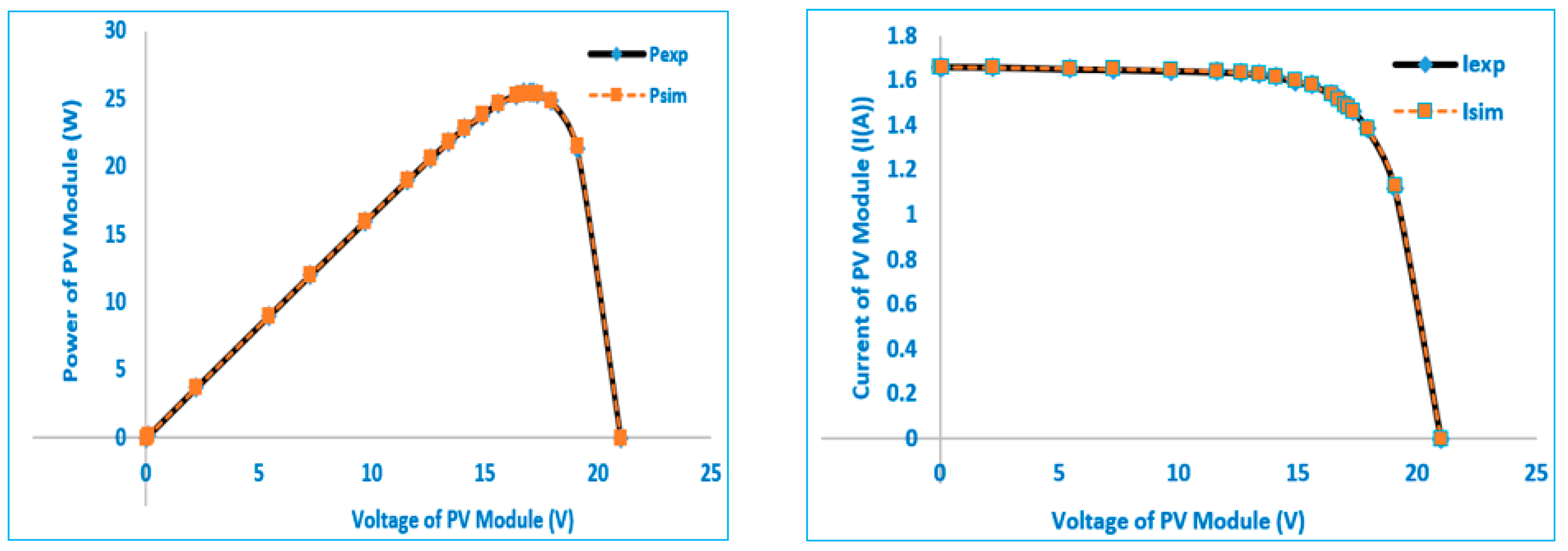
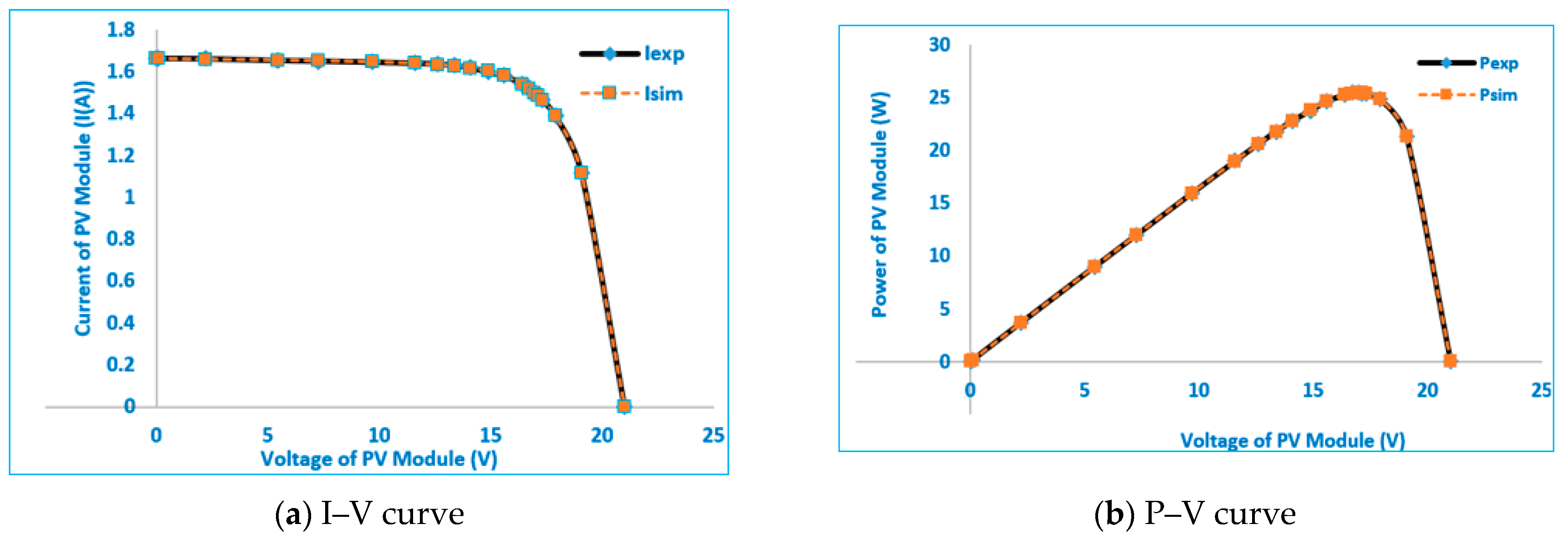
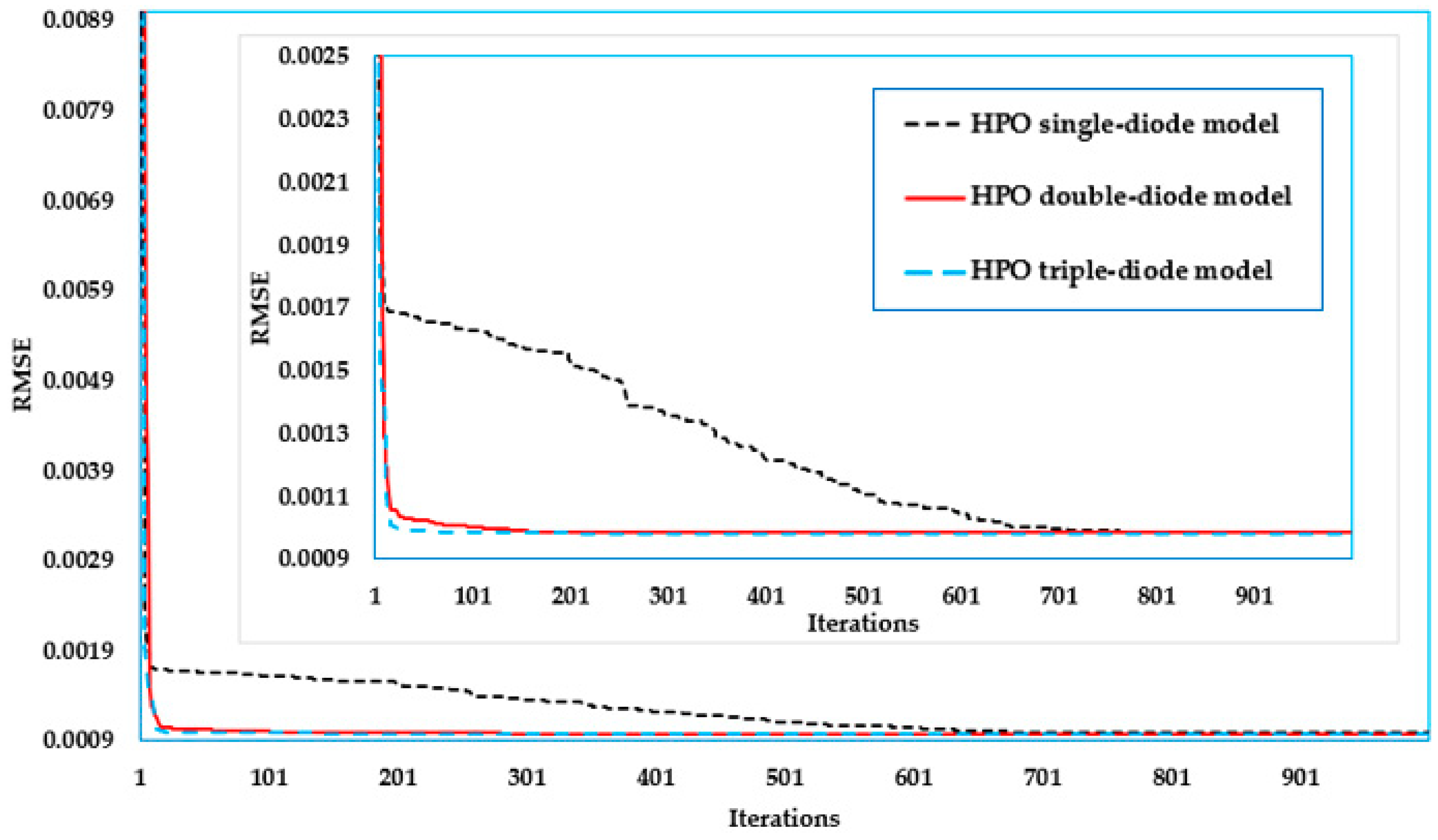
Parameter	STM6-40/36 PV Module		RTC France PV Cell
	lb	ub	lb	ub
IPh (A)	0	2	0	1
RS (Ω)	0	0.36	0	0.5
${\eta }_1, {\eta }_2$$, {\eta }_3$	1	2	1	2
Rsh (Ω)	0	100	0	100
$I_{S1}, I_{S2}, I_{S3}$ (μA)	0	50	0	1

.

4.1. Simulation Results for STM6_40/36 PV Module

4.1.1. Case 1: Single-Diode Model

Using this model, a comparison of the proposed HPO technique and other recent optimizers is depicted in

Table 2. Optimal results of the HPO and other reported techniques for the single-diode model of STM6_40/36.

Optimizer	IPh (A)	${\mathit{I}}_{\mathit{S}1} \left(\mathsf{\mu }\mathbf{A}\right)$	RS (Ω)	Rsh (Ω)	${\mathit{\eta }}_1$	RMSE	Improvement %
Proposed HPO	1.663905	1.74	0.004275	15.92749	1.520269	1.729814 × 10−3	-
EO [48]	1.663629	1.78	0.004205	16.24408	1.523146	1.733 × 10−3	0.1838
MPA [48]	1.65702	2.46	0.003831	31.50673	1.559041	3.496 × 10−3	50.5202
EMPA [48]	1.663418	2.03	0.003788	16.878	1.537713	1.769 × 10−3	2.2151
GTO [48]	1.663905	1.74	0.004274	15.92829	1.520303	1.73 × 10−3	0.0108
HBA [48]	1.661527	5.51	0.00001	23.6426	1.658694	3.33 × 10−3	48.0536
JFS [48]	1.662589	1.84	0.004105	16.96607	1.526795	1.807 × 10−3	4.2715
ImCSA [49]	1.663971	2	0.002914	15.84051	1.5335	1.794 × 10−3	3.5778
FBI [50]	1.66391	1.74	0.004281	15.91743	1.520073	1.73 × 10−3	0.0108
ISCE [19]	1.66390478	1.74	0.004274	15.9283	1.5203	1.73 × 10−3	0.0108
BHCS [38]	1.6639	1.74	0.00427	15.9283	1.5203	1.73 × 10−3	0.0108
TPBA [51]	1.6632	2.77	0.004186	16.7328	1.5656	1.774 × 10−3	2.4908
SA [52]	1.6609	5.90	0.0049499	26.7742	1.66602	3.399 × 10−3	49.1081

. For a comparative assessment, we included the following optimizers: equilibrium optimizer (EO) [48], marine predator algorithm (MPA) [48], enhanced MPA (EMPA) [48], gorilla troops optimization (GTO) [48], heap-based algorithm (HBA) [48], jellyfish search (JFS) [48], improved cuckoo search (ImCSA) algorithm [49], forensic-based investigation (FBI) [50], improved shuffled complex evolution (ISCE) [19], hybridizing cuckoo search/biogeography-based optimization (BHCS) [38], three-point-based approach (TPBA) [51], and simulated annealing (SA) [52]. This table illustrates the RMSE value and the estimations of five parameters calculated using other optimizers and the proposed HPO technique. For this model, the RMSE value obtained by the proposed HPO technique was the best (1.729814 × 10⁻³) among other optimizers in the literature. On the other hand, the EO, MPA, EMPA, GTO, HBA, JFS, ImCSA, FBI, ISCE, BHCS, TPBA, and SA optimizers obtained RMSE values of 1.733 × 10⁻³, 3.496 × 10⁻³, 1.769 × 10⁻³, 1.73 × 10⁻³, 3.33 × 10⁻³, 1.807 × 10⁻³, 1.794 × 10⁻³, 1.73 × 10⁻³, 1.73 × 10⁻³, 1.73 × 10⁻³, 1.774 × 10⁻³, and 3.399 × 10⁻³, respectively. Therefore, the improvement percentage due to the proposed HPO records was 0.1838, 50.5202, 2.2151, 0.0108, 48.0536, 4.2715, 3.5778, 0.0108, 0.0108, 0.0108, 2.4908, and 49.1081 % when compared with EO, MPA, EMPA, GTO, HBA, JFS, ImCSA, FBI, ISCE, BHCS, TPBA, and SA, respectively.

Additionally, the convergence rate for the proposed HPO technique is depicted in Figure 5. As shown, the performance of the applied HPO technique was great. As illustrated, it displays high speed in focusing the search around the area of the global optimization of the minimum RMSE.

Furthermore, Figure 6 and Figure 7 manifest the simulated and experimental I–V and P–V characteristics, respectively. It was demonstrated in both figures that the obtained curves using the proposed HPO technique were approximately aligned with the experimental data, which illustrates that the proposed HPO technique extracted the parameters accurately.

4.1.2. Case 2: Double-diode Model of STM6_40/36 PV Module

Using this model, a comparison of the proposed HPO technique and other optimizers is depicted in

Table 3. Optimal results of the HPO and other reported techniques for the double-diode model of STM6_40/36.

Optimizer	IPh (A)	${\mathit{I}}_{\mathit{S}1} \left(\mathsf{\mu }\mathbf{A}\right)$	${\mathit{I}}_{\mathit{S}2} \left(\mathsf{\mu }\mathbf{A}\right)$	RS (Ω)	Rsh (Ω)	${\mathit{\eta }}_1$	${\mathit{\eta }}_2$	RMSE	Improvement %
HPO	1.663702	4.06	5.57 × 10−4	0.008726	17.82614	1.688851	1	1.696271 × 10−3	-
EPSO [53]	1.6648	16.70	6.21 × 10−6	0.5000	16.858	1.16649	1.87067	1.8307 × 10−3	7.3430
LCROA [54]	1.6637	72.2	3.28 × 10−6	0.16717	16.7419	1.5739	2.000	1.712 × 10−3	0.9187
BA [55]	1.637941	1.59	3.94 × 10−5	0.003887	24.6958	1.504536	1.4783	2.194577 × 10−2	92.2706
DBA [55]	1.663860	1.80	3.66 × 10−6	0.004167	16.066503	1.524098	1.43939	1.731960 × 10−3	2.0606
NBA [55]	1.662865	6.60	1.61 × 10−6	0.004653	16.694049	1.678806	1.511867	1.82684 × 10−3	7.1473
FC-EPSO [56]	1.6634	1.85	9.72 × 10−5	0.01101	16.5914	1.5818	1.5445	1.772 × 10−3	4.2736

, which illustrates the RMSE value and the estimated values of seven parameters calculated using other optimizers and the proposed HPO technique. Additionally, the convergence rate for the proposed HPO technique is depicted in Figure 8. For this model, the RMSE value obtained using the proposed HPO technique (1.696271 × 10⁻³) was the best among all optimizers used from the literature, such as the ensemble particle swarm optimizer (EPSO) [53], improved Rao-based chaotic optimization (LCROA) [54], bat algorithm (BA) [55], the directional bat algorithm (DBA) [55], novel bat algorithm (NBA) [55], and fractional chaotic-ensemble particle-swarm optimizer (FC-EPSO) algorithm [56]. In this regard, EPSO, LCROA, BA, NBA, DBA, and FC-EPSO obtained RMSE values of 1.8307 × 10⁻³, 1.712 × 10⁻³, 2.194577 × 10⁻², 1.731960 × 10⁻³, 1.82684 × 10⁻³, and 1.772 × 10⁻³, respectively. Therefore, the improvement percentage using the proposed HPO was 7.343, 0.9187, 92.2706, 2.0606, 7.1473 and 4.2736 % compared to EPSO, LCROA, BA, NBA, DBA, and FC-EPSO, respectively.

The statistical analysis is demonstrated in

Table 4. Statistical analysis of HPO and other techniques for the double-diode model of STM6_40/36.

Optimizer	Min	Improvement %	Mean	Improvement %	Max	Improvement %	Std	Improvement %
HPO	0.001696271	-	0.003222066	-	0.003329899	-	0.000410222	-
BA [55]	2.1946 × 10−2	2.0250	0.092023	8.8801	0.01448059	1.1151	2.407 × 10−2	2.3660
DBA [55]	1.7319 × 10−3	0.0036	0.004934	0.1712	0.01372796	1.0398	2.893 × 10−3	0.2483
NBA [55]	1.8268 × 10−3	0.0131	0.0041404	0.0918	0.007598	0.4268	1.430 × 10−3	0.1020
LCROA [54]	1.712 × 10−3	0.0016	−	-	−	-	−	-
FC-EPSO [56]	1.772 × 10−3	0.0076	−	-	−	-	−	-
EPSO [53]	1.8307 × 10−3	0.0134	−	-	−	-	−	-

, which shows the quality of the HPO technique versus EPSO, LCROA, BA, NBA, DBA, and FC-EPSO. As shown, the competitive performance was notable for the proposed HPO technique in comparison with the other reported optimizers. The proposed HPO technique successfully achieved the lowest minimum, standard deviation (Std), maximum, and mean RMSE, with 0.001696271, 0.000410222, 0.003329899, and 0.003222066, respectively.

Furthermore, Figure 9 manifests the simulated and experimental I–V and P–V characteristics. It is demonstrated in this figure that the data calculated using the proposed HPO technique were approximately aligned with the experimental data, which illustrates that the proposed HPO technique extracted the parameters accurately. Moreover,

Table 5. Simulated and experimental current and power and the absolute errors established using the proposed HPO technique for DDM STM6-40/36 PV module.

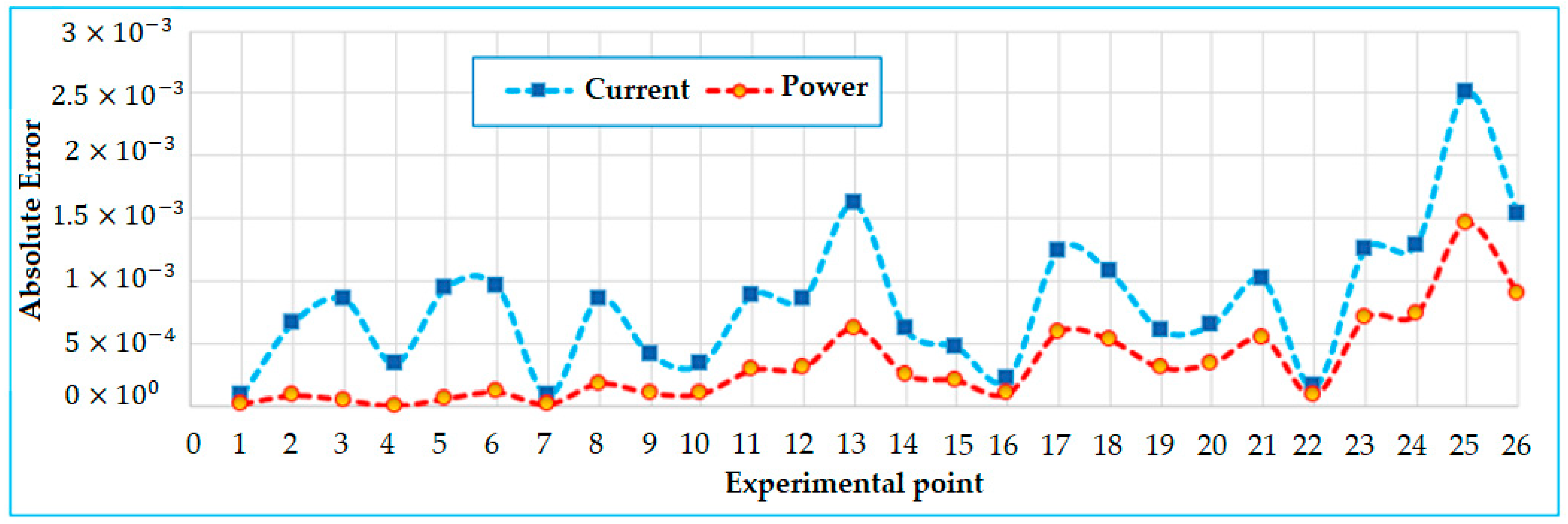
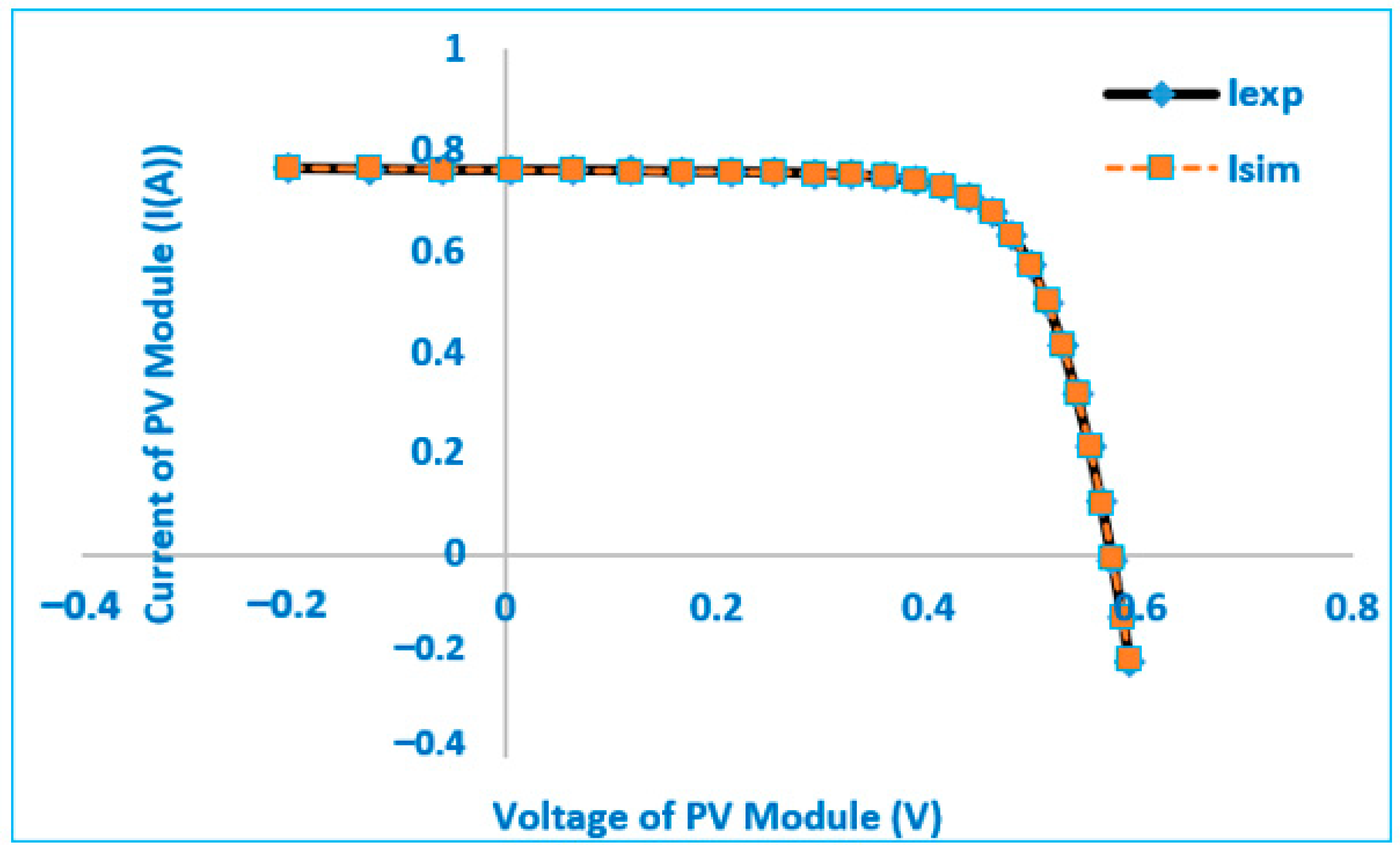
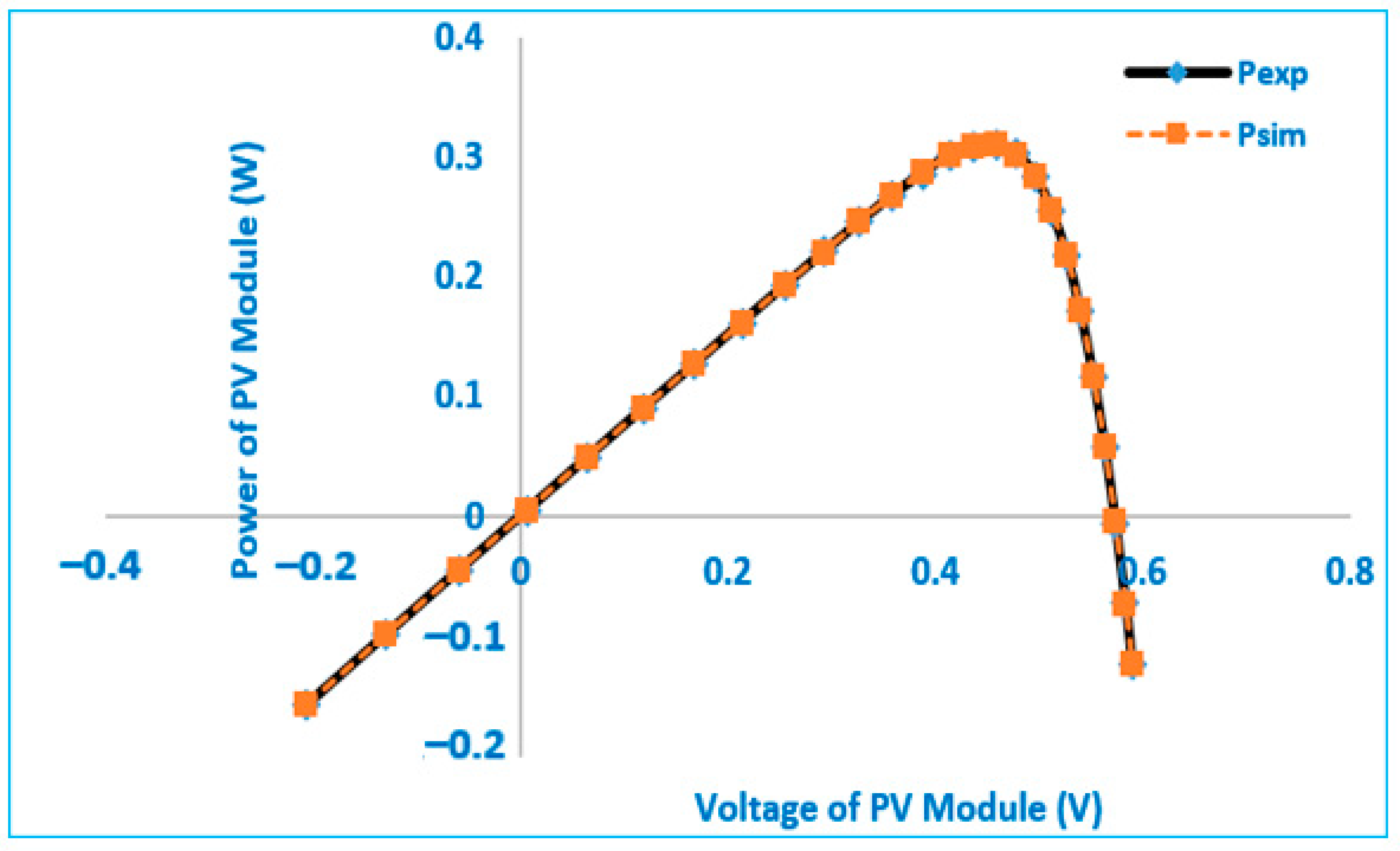
Point	Vexp	Iexp	Isim	Pexp	Psim	Absolut IAE	Absolut PAE
1	0	1.663	1.66155158	0	0	0.00144842	0
2	0.118	1.663	1.661412044	0.196234	0.196047	0.001587956	0.000187379
3	2.237	1.661	1.658898411	3.715657	3.710956	0.002101589	0.004701254
4	5.434	1.653	1.655006769	8.982402	8.993307	0.002006769	0.010904785
5	7.26	1.65	1.652569075	11.979	11.99765	0.002569075	0.018651483
6	9.68	1.645	1.648317804	15.9236	15.95572	0.003317804	0.032116347
7	11.59	1.64	1.642153043	19.0076	19.03255	0.002153043	0.024953773
8	12.6	1.636	1.63618594	20.6136	20.61594	0.00018594	0.002342849
9	13.37	1.629	1.629108637	21.77973	21.78118	0.000108637	0.00145248
10	14.09	1.619	1.619252298	22.81171	22.81526	0.000252298	0.003554873
11	14.88	1.597	1.602754697	23.76336	23.84899	0.005754697	0.085629887
12	15.59	1.581	1.580023152	24.64779	24.63256	0.000976848	0.015229061
13	16.4	1.542	1.539581627	25.2888	25.24914	0.002418373	0.039661322
14	16.71	1.524	1.518250212	25.46604	25.36996	0.005749788	0.096078953
15	16.98	1.5	1.49621083	25.47	25.40566	0.00378917	0.064340108
16	17.13	1.485	1.482357816	25.43805	25.39279	0.002642184	0.045260619
17	17.32	1.465	1.462947873	25.3738	25.33826	0.002052127	0.035542835
18	17.91	1.388	1.38662746	24.85908	24.8345	0.00137254	0.024582184
19	19.08	1.118	1.127166992	21.33144	21.50635	0.009166992	0.174906208
20	21.02	0	−0.001376261	0	−0.02893	0.001376261	0.028928997

illustrates the absolute error values of current and power for the measured and simulated data at the 20 experimental voltage points. It can be deduced that the difference in absolute error values between the measured and simulated data was relatively small.

4.1.3. Case 3: Triple-Diode Model of STM6_40/36 PV Module

The objective function in the triple-diode model was more complex because it had two additional parameters that increased the number of unknown variables to nine. The proposed HPO technique was applied to this model and the obtained parameters are tabulated in

Table 6. Optimal values of extracted parameters by HPO technique for the triple-diode model of STM6-120/36.

IPh	Rs	Rsh	IS1	η1	IS2	η2	IS3	η3	RMSE
1.663466	0.007732	19.21541	1.4 × 10−5	2	3.82 × 10−8	1.213937	0	2	1.7334461 × 10−3

. Based on this table, the proposed HPO technique obtained an RMSE value of 1.733446 × 10⁻³.

Table 7. Comparative assessment of the proposed HPO technique versus recently reported optimizers for the triple-diode model with STM6_40/36 PV module.

Optimizer	Min (RMSE)	Improvement %
Proposed HPO	1.733446 × 10−3	-
African Vultures Optimization (AVO)	3.5398 × 10−3	0.1806
HBO	3.331 × 10−3	0.1598
MPA	2.596 × 10−3	0.0863
JFS	2.113 × 10−3	0.0380
EMPA	1.850 × 10−3	0.0117
EO	1.738 × 10−3	0.0005
Social network search (SNS) [57]	2.30797 × 10−3	0.0575

shows a comparative assessment of the proposed HPO technique versus recently reported optimizers, and the great effectiveness of the proposed HPO technique can be derived as it had the minimum RMSE (1.733446 × 10⁻³) and the best outcome among all optimizers used.

Additionally, the convergence rate for the proposed HPO technique is depicted in Figure 10. As shown, the performance of the applied HPO technique was great. As illustrated, it exhibited a high speed in focusing the search around the area of the global optimization of the minimum RMSE.

Furthermore, Figure 11 manifests the simulated and experimental I–V and P–V characteristics. It is demonstrated in this figure that the data calculated using the proposed HPO technique were approximately aligned with the experimental data, which illustrates that the proposed HPO technique extracted the parameters accurately. Moreover,

Table 8. Simulated and experimental current and power and the absolute error established using the proposed HPO technique for TDM STM6-40/36 PV module.

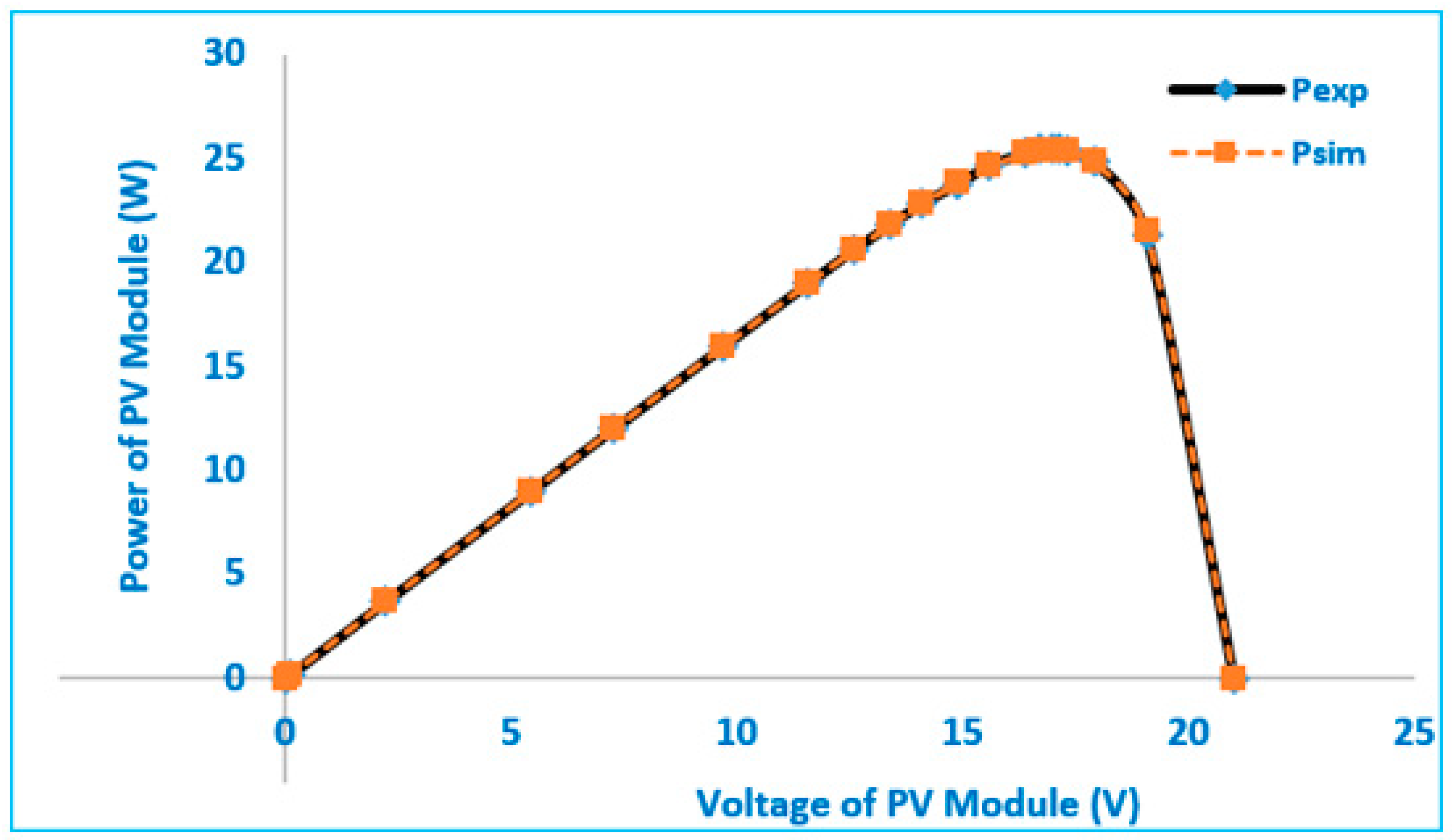
Point	Vexp	Iexp	Isim	Pexp	Psim	Absolut IAE	Absolut PAE
1	0	1.663	1.662793111	0	0	0.000206889	0
2	0.118	1.663	1.662621462	0.196234	0.196189	0.000378538	4.46675 × 10−5
3	2.237	1.661	1.659523942	3.715657	3.712355	0.001476058	0.003301942
4	5.434	1.653	1.654692858	8.982402	8.991601	0.001692858	0.009198993
5	7.26	1.65	1.651650964	11.979	11.99099	0.001650964	0.011985997
6	9.68	1.645	1.646510854	15.9236	15.93823	0.001510854	0.014625064
7	11.59	1.64	1.639749954	19.0076	19.0047	0.000250046	0.002898033
8	12.6	1.636	1.633709538	20.6136	20.58474	0.002290462	0.028859815
9	13.37	1.629	1.626837989	21.77973	21.75082	0.002162011	0.02890609
10	14.09	1.619	1.617488836	22.81171	22.79042	0.001511164	0.0212923
11	14.88	1.597	1.602039545	23.76336	23.83835	0.005039545	0.074988431
12	15.59	1.581	1.580589913	24.64779	24.6414	0.000410087	0.00639326
13	16.4	1.542	1.541877255	25.2888	25.28679	0.000122745	0.002013016
14	16.71	1.524	1.521049642	25.46604	25.41674	0.002950358	0.049300474
15	16.98	1.5	1.499402663	25.47	25.45986	0.000597337	0.010142784
16	17.13	1.485	1.485687804	25.43805	25.44983	0.000687804	0.011782077
17	17.32	1.465	1.466312804	25.3738	25.39654	0.001312804	0.022737767
18	17.91	1.388	1.388788295	24.85908	24.8732	0.000788295	0.014118357
19	19.08	1.118	1.11763777	21.33144	21.32453	0.00036223	0.006911339
20	21.02	0	1.56513 × 10−5	0	0.000329	1.56513 × 10−5	0.000328991

illustrates the absolute error values of current and power for the measured and simulated data at the 20 experimental voltage points. It can be deduced that the difference in absolute error values between the measured and simulated data was relatively small.

4.2. Simulation Results for RTC France Silicon Cell

For the RTC France silicon PV cell, the proposed HPO technique was applied to minimize the RMSE objective function considering the three diode models with five, seven, and nine unknown variables. The corresponding values are tabulated in

Table 9. Optimal values of extracted parameters using HPO technique for the three diode models with RTC France.

Model	Single Diode	Double Diode	Triple Diode
IPh (A)	0.760776	0.760779	0.76078
IS1 (μA)	0.323	0.252	0
IS2 (μA)	-	0.534	6.6 × 10−7
IS3 (μA)	-	-	2.36 × 10−7
η1	1.481183	1.460079	1
η2	-	2	2
η3	-	-	1.454796
RS (Ω)	0.036377	0.036629	0.036694
Rsh (Ω)	53.71846	54.94474	55.25778
RMSE (×10−4)	9.8602	9.83	9.825

, while Figure 12 displays the convergence trends of the proposed HPO technique for the three diode models. As shown, the proposed HPO technique successfully achieved RMSE values of 9.8602 × 10⁻⁴, 9.83 × 10⁻⁴, and 9.825 × 10⁻⁴ for the single-, double-, and triple-diode models, respectively. Furthermore, Figure 12 shows that the performance of the applied HPO technique was great, especially for the double- and triple-diode models. The proposed HPO technique displayed high speed in focusing the search around the area of the global optimization of the minimum RMSE.

Considering the single-diode model, a comparison of the proposed HPO technique and other optimizers is depicted in

Table 10. Comparative assessment of HPO for the single-diode model of RTC France versus reported optimizers.

Algorithms	RMSE (×10−4)
Proposed HPO	9.8602
GAMNU [25]	9.8618
BBO-M [58]	9.8634
TLBO [59]	9.8733
JAYA [62]	9.8946
IADE [59]	9.89
CSA [59]	9.91184
HS [61]	9.95146
CLPSO [63]	9.9633
ABC [60]	10
HHO [15]	12.6479
CPSO [59]	13.8607
GWO [29]	75.011

. It illustrates the RMSE values of the proposed HPO technique compared to other optimizers reported in the literature, such as the genetic algorithm based on non-uniform mutation (GAMNU) [25], biogeography-based optimizer with mutation strategies (BBO-M) [58], teaching–learning-based optimizer (TLBO), CPSO [59], HHO [15], ABC [60], HS [61], GWO [29], JAYA [62], and CLPSO [63]. As shown, the proposed HPO provided significant effectiveness in finding the minimum RMSE compared to its counterparts.

Considering the triple-diode model, Figure 13 displays the absolute error values of current and power for the measured and simulated data at the 26 experimental voltage points. It can be deduced that the difference in absolute error values between the measured and simulated data was relatively small.

Furthermore, Figure 14 and Figure 15 manifest the simulated and experimental I–V and P–V characteristics for the triple-diode model. It is demonstrated that the data calculated with the proposed HPO technique were approximately aligned with the experimental data, which illustrates that the proposed HPO technique extracted the parameters accurately.

5. Conclusions

In this article, a novel HPO technique has been developed for extracting the parameters of single-diode, double-diode, and triple-diode solar PV cell/panel models of R.T.C. France and STM-6/120. The proposed HPO was established to optimize the parameters to attain the best performance in terms of the RMSE value. According to the experimental results, the speed of convergence and accurate solution of PV cell/panel models manifested that the proposed HPO accomplished better solutions compared with optimizers recently reported in the literature. Moreover, the characteristic curves of P–V and I–V obtained with the HPO on the solar PV cell model illustrated solution stability effects. In addition to that, the statistical outcomes demonstrated that the proposed HPO had enhanced the solar PV model parameter extraction problem efficacy because the RMSE of the proposed HPO technique was lower than the recently reported optimizers. Furthermore, the convergence characteristics illustrated that the proposed HPO had a higher convergence trend than the optimizers recently reported in the literature. As future work, the developed HPO could be applied to several other power system optimizations such as combined heat and power dispatch, synchronous motor designs, optimal power flow, AC–DC power system operation [64], etc. Moreover, based on the successful application of the developed HPO in finding the optimal electrical parameters of PV, it could be extended for optimal allocations of PV sources in distribution and transmission networks.