Random Motions at Finite Velocity on Non-Euclidean Spaces

Abstract

In this paper, random motions at finite velocity on the Poincaré half-plane and on the unit-radius sphere are studied. The moving particle at each Poisson event chooses a uniformly distributed direction independent of the previous evolution. This implies that the current distance $d(P_0,P_t)$ from the starting point $P_0$ is obtained by applying the hyperbolic Carnot formula in the Poincaré half-plane and the spherical Carnot formula in the analysis of the motion on the sphere. We obtain explicit results of the conditional and unconditional mean distance in both cases. Some results for higher-order moments are also presented for a small number of changes of direction.

1. Introduction

Random processes on non-Euclidean spaces have been introduced and developed since 1959, when the paper by Gertsenshtein and Vasiliev [1] on hyperbolic Brownian motion appeared.

Starting from the 1990s, new and interesting applications of hyperbolic Brownian motion were considered, for example in [2,3]. Details on hyperbolic and fractional hyperbolic Brownian motion can be found in [4].

In this paper, as well as in Cammarota and Orsingher (2008), a finite-velocity random motion on the Poincaré half-plane is analyzed. The relevant difference from [5] is the assumption regarding the switching mechanism.

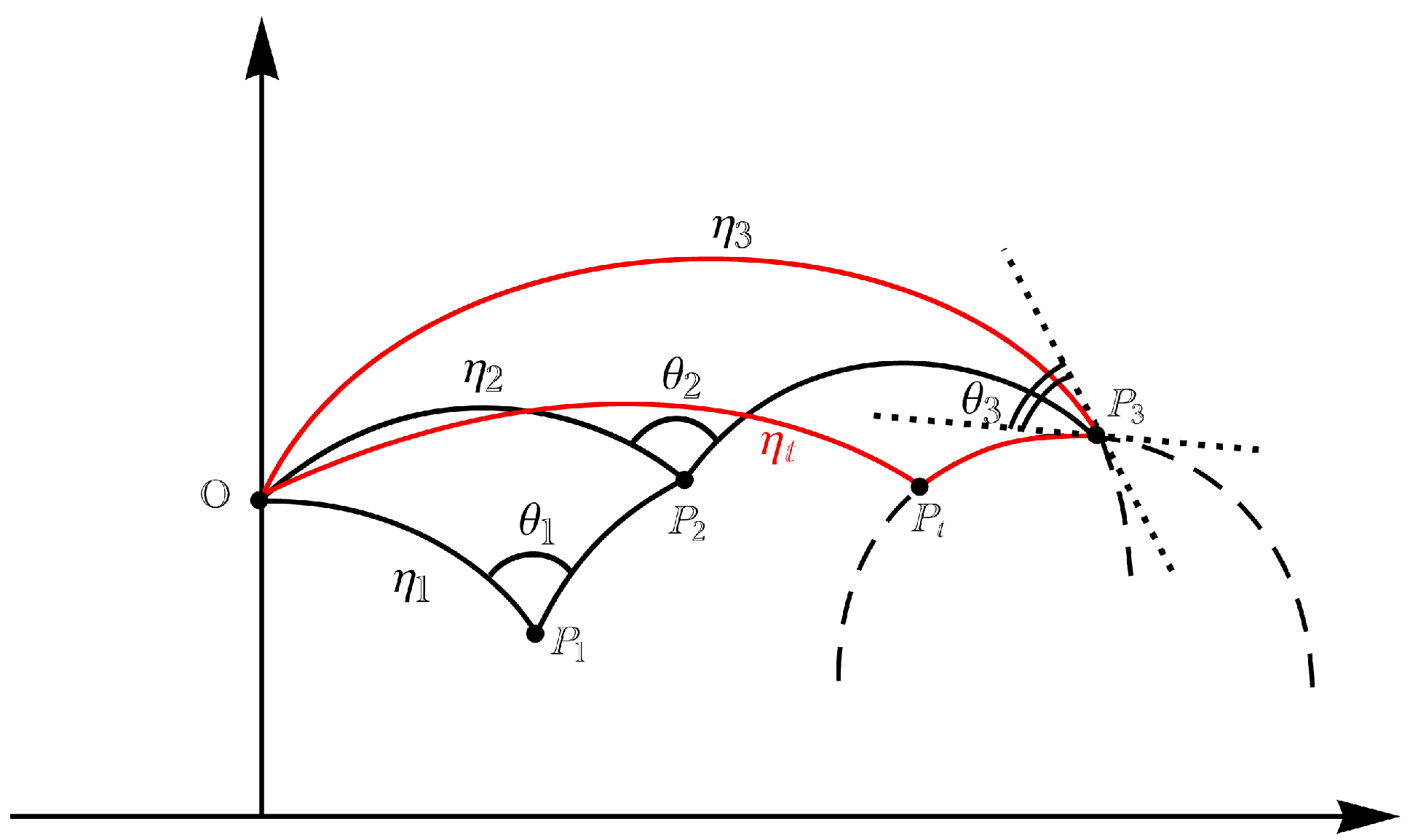
Our purpose is the study of the current distance from the starting point of a particle moving with constant hyperbolic velocity, which chooses a uniformly distributed orientation at Poisson-paced times. The main results concern the conditional and unconditional moments of the distance.

We start our analysis with some definitions. The Poincaré half-plane is defined as

$${\mathbb{H}}_2^{+}=\{(x,y):x\in \mathbb{R},y>0\}.$$

In ${\mathbb{H}}_2^{+}$, the distance measure is

$$d{s}^2=\frac{d{x}^2+d{y}^2}{y^2}$$

(1)

and the coordinates are either Cartesian $(x,y)$ or hyperbolic $(\eta ,\alpha )$, related to each other by the relationships

$$\left\{\begin{array}{c}x=\frac{\cos \alpha \sinh \eta }{\cosh \eta -\sinh \eta \sin \alpha }\hfill \\ y=\frac{1}{\cosh \eta -\sinh \eta \sin \alpha }\hfill \end{array}\right.$$

(2)

for $\eta >0$ and $0<\alpha <2\pi$ (see [6,7,8] for more details).

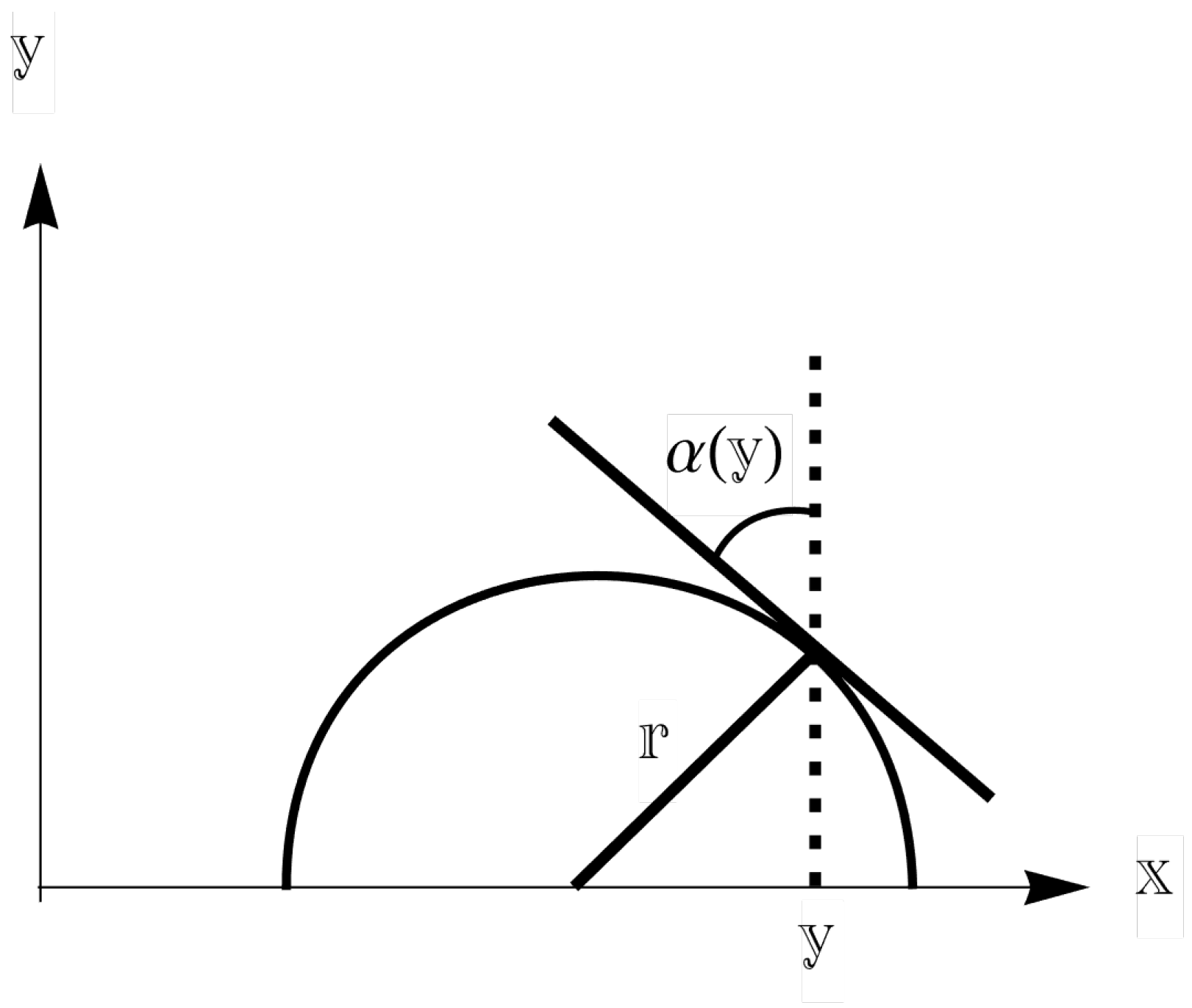
The geodesics on ${\mathbb{H}}_2^{+}$ are given by half-circles with the center on the $y=0$ line and upper straight-lines.

The structure of the Poincaré half-plane has a physical basis. The light passing through a non-homogeneous medium with a space-varying refraction coefficient obeying the relationship

$$\frac{\sin \alpha \left(y\right)}{y}=cost$$

(3)

describes half-circles with the origin on $y=0$. In (2), the angle is formed by the tangent to the point with ordinate y (see Figure 1).

The random motion analyzed here runs on the geodesics of ${\mathbb{H}}_2^{+}$ and moves with constant hyperbolic velocity

$$c=\frac{dy}{dx}=\frac{1}{y}\sqrt{d{x}^2+d{y}^2}$$

(4)

provided that $y>0$.

The direction of the motion changes at Poisson-paced times. The new directions are here assumed to be uniformly distributed on $[0,2\pi )$ and are independent from the previous line of motion. Given that $P_k=(X\left(T_k\right),Y\left(T_k\right))$ is the last position where a change of direction was recorded, in the paper [5], the new direction taken at each Poisson time is assumed to be orthogonal to the current geodesic joining $P_k$ and the origin $(0,1)$. This permits the authors to use the hyperbolic Pythagorean theorem to describe the geodesic distance as

$$\begin{array}{cc}\hfill \cosh \eta \left(t\right)& =\cosh d(P_0,P_t)=\cosh d(P_0,P_k)d(P_k,P_t)\hfill \\ \hfill & =\prod _{k=1}^{N\left(t\right)+1}\cosh d(P_{k-1},P_k)\hfill \\ \hfill & =\prod _{k=1}^{N\left(t\right)+1}\cosh c(t_k-t_{k-1})\hfill \end{array}$$

(5)

where $P_{N\left(t\right)+1}=P_t$ is the current position of the moving particle.

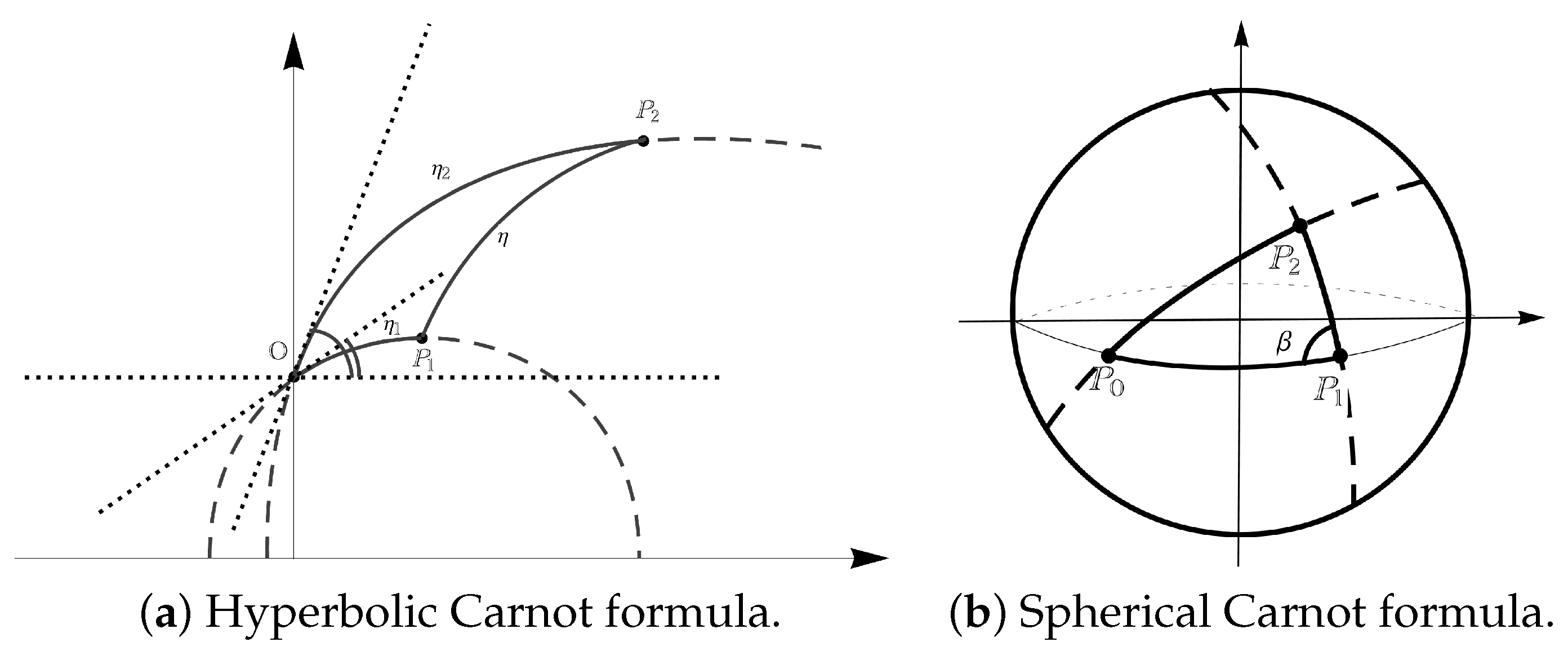
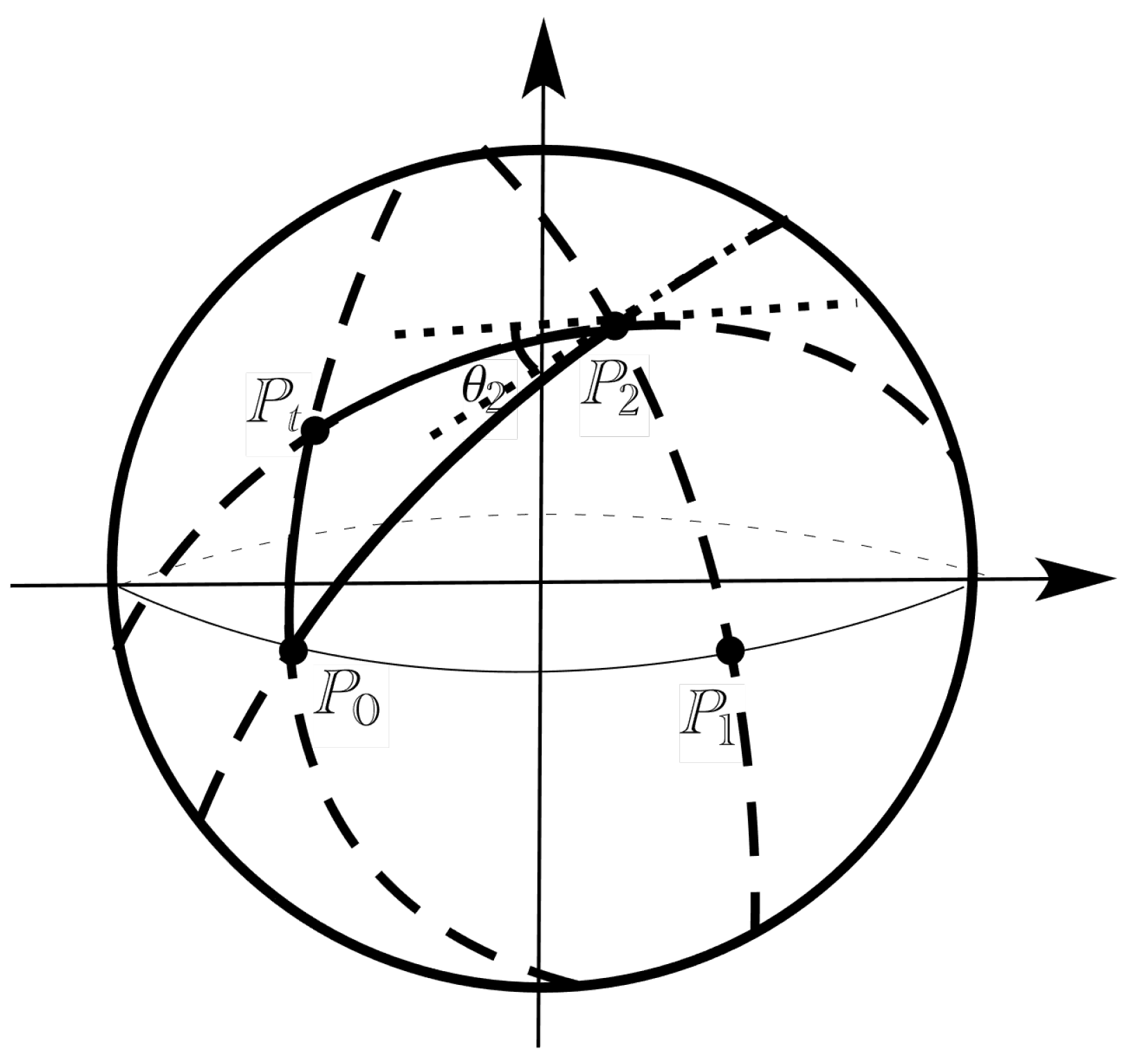
In the present paper, we must instead use the hyperbolic Carnot formula, which reads

$$\cosh \eta =\cosh {\eta }_1\cosh {\eta }_2-\sinh {\eta }_1\sinh {\eta }_2\cos \alpha$$

(6)

for the scalene hyperbolic triangle of Figure 2a below.

The application of the hyperbolic Carnot formula implies a considerable increase in the difficulties of the mathematical investigation, which is compensated for by the generalisation of the assumptions.

The task of our paper is thus the analysis of the process

$$\begin{array}{c}\cosh {\eta }_{\theta }\left(t\right)=\hfill \\ \hfill \prod _{k=1}^{N\left(t\right)+1}\cosh c(t_k-t_{k-1})-\sum _{k=1}^{N\left(t\right)}\cos {\theta }_k\sinh {\eta }_k\sinh c(t_{k+1}-t_k)\prod _{j=k+2}^{N\left(t\right)+1}\cosh c(t_j-t_{j-1}).\end{array}$$

(7)

In (7), we adopt the convention that for $j>N\left(t\right)+1$, the corresponding term is equal to one. Additionally, we set ${\eta }_k=\eta \left(t_k\right)$, for $k=1,\dots ,N\left(t\right)$.

First, we notice that for $\theta =\pm \frac{\pi }{2}$, the current distance (7) coincides with (5). Furthermore, for every $k=1,\dots ,n$, it is almost straightforward to see that

$$\mathbb{E}\left[\cosh {\eta }_{\theta }\left(t\right)\right|N\left(t\right)=n]=\mathbb{E}\left[\cosh \eta \left(t\right)\right|N\left(t\right)=n]$$

(8)

so that

$$\mathbb{E}\left[\cosh {\eta }_{\theta }\left(t\right)\right]={\mathrm{e}}^{-\frac{\lambda t}{2}}\left\{\cosh \frac{t\sqrt{{\lambda }^2+4c^2}}{2}+\frac{\lambda }{\sqrt{{\lambda }^2+4c^2}}\sinh \frac{t\sqrt{{\lambda }^2+4c^2}}{2}\right\}.$$

(9)

Additionally, because of the assumption of the uniform distribution of the random variables ${\theta }_k$ and the independence of ${\theta }_k$ from $\eta \left(t_k\right)$, we prove that the same relationship holds.

For conditional and unconditional moments, in general, we have that for $m>1$,

$$\mathbb{E}\left[{\cosh }^m{\eta }_{\theta }\left(t\right)\right|N\left(t\right)=n]\ne \mathbb{E}\left[{\cosh }^m\eta \left(t\right)\right|N\left(t\right)=n].$$

(10)

Therefore, in order to obtain meaningful results, we are forced to consider only the cases with small values of n and m.

We have also considered a finite velocity random motion on an elliptic space, represented by a unit-radius sphere. In this case, we must use the relationship of spherical trigonometry instead of those of hyperbolic trigonometry. Indeed, the spherical distance from the starting point is obtained by means of the spherical Carnot formula, which reads

$$\cos d(P_0,P_2)=\cos d(P_0,P_1)d(P_1,P_2)+\sin d(P_0,P_1)\sin d(P_1,P_2)\cos \beta$$

(11)

for the scalene spherical triangle of Figure 2b above.

Additionally, in this case, we generalize the results of Section 6 of [5] by allowing the particle to take uniformly distributed orientations at the Poisson events. In fact, the angles between the new geodesic step and the one joining $P_0$ and the current position are assumed to be independent and identically distributed, with a uniform distribution on $[0,2\pi )$.

Similarly to the motion analyzed on ${\mathbb{H}}_2^{+}$, we have proved that the conditional and unconditional expected value of the spherical distance from the starting point $d(P_0,P_t)$ coincides with that of the motion with orthogonal changes of direction. Therefore, we have that

$$\mathbb{E}\left[\cos d_{\theta }(P_0,P_t)\right|N\left(t\right)=n]=\mathbb{E}\left[\cos d_{\theta }(P_0,P_t)\right|N\left(t\right)=n]$$

(12)

and that

$$\begin{array}{c}\mathbb{E}\left[\cos d_{\theta }(P_0,P_t)\right]=\hfill \\ \hfill \frac{{\mathrm{e}}^{-\frac{\lambda t}{2}}}{2}\left[({\mathrm{e}}^{\frac{t}{2}\sqrt{{\lambda }^2-4c^2}}+{\mathrm{e}}^{-\frac{t}{2}\sqrt{{\lambda }^2-4c^2}})+\frac{\lambda }{\sqrt{{\lambda }^2-4c^2}}({\mathrm{e}}^{\frac{t}{2}\sqrt{{\lambda }^2-4c^2}}-{\mathrm{e}}^{-\frac{t}{2}\sqrt{{\lambda }^2-4c^2}})\right]\end{array}$$

(13)

where c is the constant spherical velocity. In this case, we need to consider the cases $\lambda <2c$, $\lambda =2c$ and $\lambda >2c$ separately, since a particle that moves along geodesic lines on the surface of a sphere can repeatedly cover a whole great circle. Thus, if t is sufficiently large and $\lambda <2c$, the support of the random distance $d_{\theta }(P_0,P_t)$ is the union of spheres with an additional spherical cap.

2. Description of the Model: Mean Values of the Hyperbolic Distance Travelled

The random motion considered here starts at the origin $O=(0,1)$ of the Poincaré half-plane and chooses its initial direction with uniform law in $[0,2\pi )$, moving with constant hyperbolic velocity $c=\frac{1}{y}\sqrt{d{x}^2+d{y}^2}$.

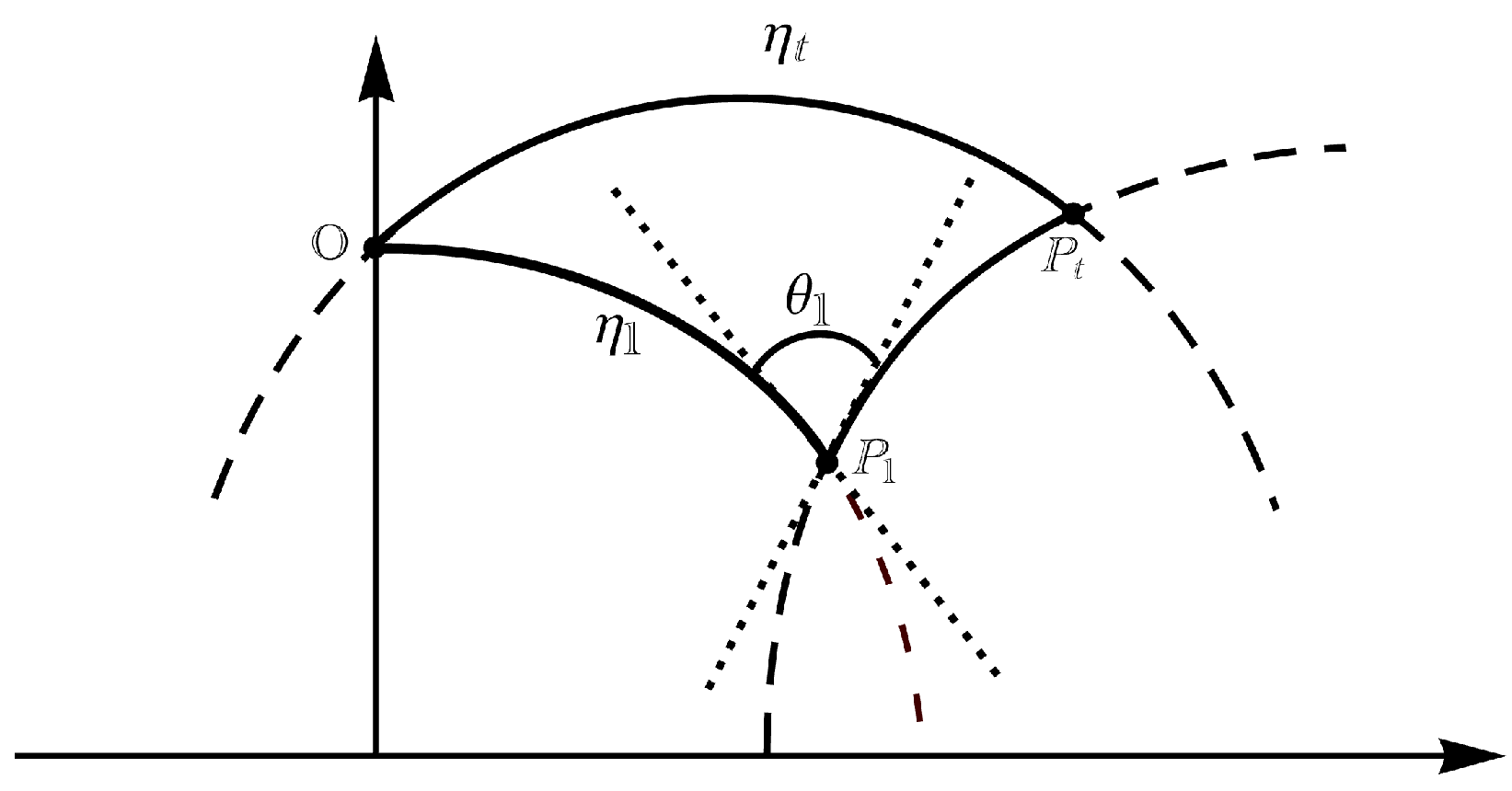
At Poisson times, the direction of the motion is changed and switches to a new orientation, independent of the current one. For example, if $N\left(t\right)=1$ and the random instant of change of direction is $t_1$, the particle at time t has a hyperbolic distance from the origin equal to

$$\cosh \eta \left(t\right)=\cosh c{t}_1\cosh c(t-t_1)-\sinh c{t}_1\sinh c(t-t_1)\cos {\theta }_1$$

(14)

where in (14), the hyperbolic Carnot formula has been applied (see Figure 3).

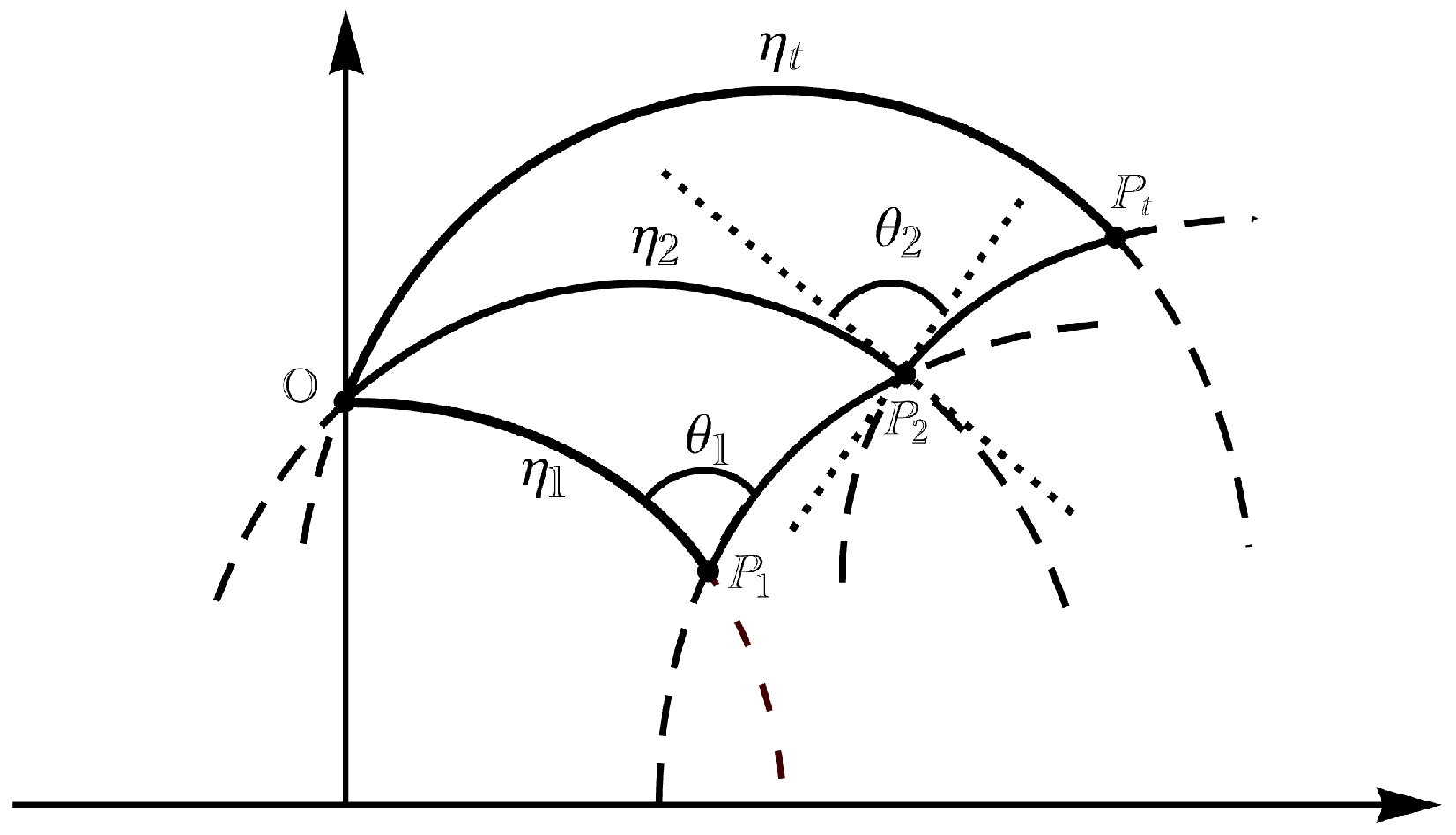
If $N\left(t\right)=2$, $t_1$ and $t_2$ are the instants of change of direction driven by the Poisson process. Therefore, the current hyperbolic distance from O (have a look at Figure 4) is given by

$$\begin{array}{cc}\hfill \cosh \eta \left(t\right)& =\cosh {\eta }_2\cosh c(t-t_2)-\sinh {\eta }_2\sinh c(t-t_2)\cos {\theta }_2\hfill \\ \hfill & =\left[\cosh c{t}_1\cosh c(t-t_1)-\sinh c{t}_1\sinh c(t-t_1)\cos {\theta }_1\right]\cosh c(t-t_2)\hfill \\ & -\sinh {\eta }_2\sinh c(t-t_2)\cos {\theta }_2\hfill \\ \hfill & =\cosh c{t}_1\cosh c(t_2-t_1)\cosh c(t-t_2)\hfill \\ \hfill & -\cos {\theta }_1\sinh {\eta }_1\sinh c(t_2-t_1)\cosh c(t-t_2)\hfill \\ \hfill & -\cos {\theta }_2\sinh {\eta }_2\sinh c(t-t_2).\hfill \end{array}$$

(15)

In order to give further insight, we consider the case of $N\left(t\right)=3$ (see Figure 5), where, after successively applying Formulas (14) and (15), we obtain that

$$\begin{array}{cc}\hfill \cosh \eta \left(t\right)& =\cosh {\eta }_3\cosh c(t-t_3)-\sinh {\eta }_3\sinh c(t-t_3)\cos {\theta }_3\hfill \end{array}$$

$$\begin{array}{cc}\hfill & =\cosh c{t}_1\cosh c(t_2-t_1)\cosh c(t_3-t_2)\cosh c(t-t_3)\hfill \\ \hfill & -\cos {\theta }_1\sinh {\eta }_1\sinh c(t_2-t_1)\cosh c(t_3-t_2)\cosh c(t-t_3)\hfill \\ & -\cos {\theta }_2\sinh {\eta }_2\sinh c(t_3-t_2)\cosh c(t-t_3)\hfill \\ & \cos {\theta }_3\sinh {\eta }_3\sinh c(t-t_3)\hfill \\ \hfill & =\prod _{k=1}^4\cosh c(t_k-t_{k-1})\hfill \\ & -\sum _{k=1}^3\cos {\theta }_k\sinh {\eta }_k\sinh c(t_{k+1}-t_k)\prod _{j=k+2}^4\cosh c(t_j-t_{j-1})\hfill \end{array}$$

(16)

with $t_4=t$ and $t_0=0$.

Inspired by (16), we can write the general expression of the hyperbolic distance when the number $N\left(t\right)$ of Poisson events is equal to n. We thus arrive at

$$\begin{array}{c}\cosh \eta \left(t\right)=\hfill \\ \hfill \prod _{k=1}^{n+1}\cosh c(t_k-t_{k-1})-\sum _{k=1}^n\cos {\theta }_k\sinh {\eta }_k\sinh c(t_{k+1}-t_k)\prod _{j=k+2}^{n+1}\cosh c(t_j-t_{j-1}).\end{array}$$

(17)

We note that for orthogonal deviations, that is for ${\theta }_k=\pm \frac{\pi }{2}$, $k=1,\dots ,n$, Formula (17) reduces to

$$\cosh \eta \left(t\right)=\prod _{k=1}^{n+1}\cosh c(t_k-t_{k-1})t_{n+1}=t.$$

Formula (17) can be proved by induction. First, it is straightforward to see that (17) holds for $n=1$. In fact, in this case, it reduces to Formula (14).

Then, we assume that it holds when $N\left(t\right)=n-1$; that is,

$$\begin{array}{c}\cosh \eta \left(t\right)=\hfill \\ \hfill \prod _{k=1}^n\cosh c(t_k-t_{k-1})-\sum _{k=1}^{n-1}\cos {\theta }_k\sinh {\eta }_k\sinh c(t_{k+1}-t_k)\prod _{j=k+2}^n\cosh c(t_j-t_{j-1}).\end{array}$$

(18)

Let $t_n$ be the n-th Poisson instant and let $t>t_n$ such that $N\left(t\right)=n$. Let ${\eta }_n$ be the hyperbolic distance of the particle from O at time $t_n$. Therefore, by applying once again the hyperbolic Carnot formula, we have that

$$\begin{array}{cc}\hfill \cosh & \eta \left(t\right)=\cosh {\eta }_n\cosh c(t-t_n)-\sinh {\eta }_n\sinh c(t-t_n)\cos {\theta }_n\hfill \\ \hfill & =\{\prod _{k=1}^n\cosh c(t_k-t_{k-1})\hfill \\ & -\sum _{k=1}^{n-1}\cos {\theta }_k\sinh {\eta }_k\sinh c(t_{k+1}-t_k)·\prod _{j=k+2}^n\cosh c(t_j-t_{j-1})\}\cosh c(t-t_n)\hfill \\ \hfill & -\sinh {\eta }_n\sinh c(t-t_n)\cos {\theta }_n\hfill \\ \hfill & =\prod _{k=1}^n\cosh c(t_k-t_{k-1})\cosh c(t-t_n)\hfill \\ & -\sum _{k=1}^{n-1}\cos {\theta }_k\sinh {\eta }_k·\sinh c(t_{k+1}-t_k)\prod _{j=k+2}^n\cosh c(t_j-t_{j-1})\cosh c(t-t_n)\hfill \\ \hfill & -\sinh {\eta }_n\sinh c(t-t_n)\cos {\theta }_n\hfill \\ & =\prod _{k=1}^{n+1}\cosh c(t_k-t_{k-1})\hfill \\ \hfill & -\sum _{k=1}^{n-1}\cos {\theta }_k\sinh {\eta }_k\sinh c(t_{k+1}-t_k){\displaystyle \prod _{j=k+2}^{n+1}}\cosh c(t_j-t_{j-1})\hfill \\ \hfill & -\sinh {\eta }_n\sinh c(t-t_n)\cos {\theta }_n\underset{=1}{\underbrace{\prod _{j=k+2}^{n+1}\cosh c(t_j-t_{j-1})}}\hfill \\ \hfill & =\prod _{k=1}^{n+1}\cosh c(t_k-t_{k-1})\hfill \\ \hfill & -\sum _{k=1}^n\cos {\theta }_k\sinh {\eta }_k\sinh c(t_{k+1}-t_k)\prod _{j=k+2}^{n+1}\cosh c(t_j-t_{j-1})\hfill \end{array}$$

where we have considered that for $k=n$, we obtain $j>n+1$, and therefore, the corresponding product is equal to one.

Remark 1.

By taking into account Formula (17), we have that the conditional mean distance is equal to

$$\begin{array}{cc}\hfill \mathbb{E}& \left[\cosh {\eta }_{\theta }\left(t\right)\right|N\left(t\right)=n]\hfill \\ \hfill & =\frac{1}{{\left(2\pi \right)}^n}\frac{n!}{t^n}{\int }_0^{t}d{t}_1{\int }_{t_1}^{t}d{t}_2\cdots {\int }_{t_{n-1}}^{t}d{t}_n{\int }_0^{2\pi }d{\theta }_1\cdots {\int }_0^{2\pi }d{\theta }_n\hfill \\ \hfill & \left(\prod _{k=1}^{n+1}\cosh c(t_k-t_{k-1})-\sum _{k=1}^n\cos {\theta }_k\sinh {\eta }_k\sinh c(t_{k+1}-t_k)·\prod _{j=k+2}^{n+1}\cosh c(t_j-t_{j-1})\right)\hfill \\ \hfill & =(\mathit{because}\mathit{of}\mathit{the}\mathit{independence}\mathit{of}{\eta }_k\mathit{from}{\theta }_k\mathit{and}\mathit{the}\mathit{independence}\hfill \\ \hfill & \mathit{of}{\theta }_k\mathit{among}\mathit{themselves})\hfill \\ \hfill & =\frac{n!}{t^n}{\int }_0^{t}d{t}_1{\int }_{t_1}^{t}d{t}_2\cdots {\int }_{t_{n-1}}^{t}d{t}_n\prod _{k=1}^{n+1}\cosh c(t_k-t_{k-1})\hfill \\ \hfill & =\frac{n!}{t^n}{I}_n\left(t\right).\hfill \end{array}$$

(19)

In the above step, the uniform distribution of the r.v.s. ${\theta }_k$ plays a crucial role.

The functions

$$I_n\left(t\right)={\int }_0^{t}d{t}_1{\int }_{t_1}^{t}d{t}_2\cdots {\int }_{t_{n-1}}^{t}d{t}_n\prod _{k=1}^{n+1}\cosh c(t_k-t_{k-1})$$

are solutions of the difference-differential equations

$$\frac{d^2}{d{t}^2}{I}_n=\frac{d}{dt}{I}_{n-1}+c^2{I}_n$$

(20)

The unconditional mean value $E\left(t\right)=\mathbb{E}\cosh \eta \left(t\right)=\mathbb{E}\left[\mathbb{E}\right(\cosh \eta \left(t\right)\left|N\right(t\left)\right)]$ satisfies the Cauchy problem

$$\left\{\begin{array}{c}\frac{d^2}{d{t}^2}E\left(t\right)+\lambda \frac{d}{dt}E\left(t\right)-c^{2}E\left(t\right)=0\hfill \\ E\left(0\right)=1\hfill \\ \frac{d}{dt}E\left(t\right){|}_{t=0}=0\hfill \end{array}\right.$$

(21)

(see [5] for details). The solution to (21) reads

$$\mathbb{E}\left[\cosh \eta \left(t\right)\right]={\mathrm{e}}^{-\frac{\lambda t}{2}}\left\{\cosh \frac{t\sqrt{{\lambda }^2+4c^2}}{2}+\frac{\lambda }{\sqrt{{\lambda }^2+4c^2}}\sinh \frac{t\sqrt{{\lambda }^2+4c^2}}{2}\right\}.$$

We note that the assumption of uniformly distributed deviations ${\theta }_k$ does not affect the mean value of the hyperbolic distance of the randomly moving particle.

For the higher-order conditional and unconditional moments $\mathbb{E}\left({\cosh }^m{\eta }_{\theta }\left(t\right)\right|N\left(t\right)=n)$ and $\mathbb{E}{\cosh }^m{\eta }_{\theta }\left(t\right)$, the results dramatically differ from those considered in the inspiring work [5].

3. Higher-Order Moments

The conditional m-th order moments of (17) have the form

$$\begin{array}{cc}\hfill \mathbb{E}({\cosh }^m& {\eta }_{\theta }\left(t\right)|N\left(t\right)=n)\hfill \\ \hfill & =\mathbb{E}\{\prod _{k=1}^{n+1}\cosh c(t_k-t_{k-1})-\sum _{k=1}^n\cos {\theta }_k\sinh {\eta }_k\sinh c(t_{k+1}-t_k)·\hfill \\ & ·\prod _{j=k+2}^{n+1}\cosh c(t_j-t_{j-1}){\}}^m\hfill \end{array}$$

(22)

which seems tractable only for small values of m and n.

The expression involves even-order powers of ${\cos }^m{\theta }_k$, which differ from zero, thus making the evaluation of (22) a hard task.

We restrict ourselves in the analysis of the higher moments of the hyperbolic distance to some special cases, which we present below.

$$\mathbb{E}\left({\cosh }^2{\eta }_{\theta }\left(t\right)\right|N\left(t\right)=1)=\frac{3}{8}{\cosh }^{2}ct+\frac{7}{16ct}\sinh ct\cosh ct+\frac{3}{16}$$

(23)

$$\begin{array}{c}\mathbb{E}\left({\cosh }^2{\eta }_{\theta }\left(t\right)\right|N\left(t\right)=2)\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=\frac{9}{64}{\cosh }^{2}ct+\frac{3}{32c^2{t}^2}{\sinh }^{2}ct+\frac{63}{128ct}\sinh ct\cosh ct+\frac{35}{128}\end{array}$$

(24)

$$\begin{array}{c}\mathbb{E}\left({\cosh }^3{\eta }_{\theta }\left(t\right)\right|N\left(t\right)=1)\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=\frac{5}{64}\cosh 3ct+\frac{37}{384ct}\sinh 3ct+\frac{21}{64}\cosh ct+\frac{39}{128ct}\sinh ct.\end{array}$$

(25)

Furthermore, we have that

$$\mathbb{E}\left({\cosh }^2{\eta }_{\theta }\left(t\right)\right|N\left(t\right)=3)>\mathbb{E}\left({\cosh }^2\eta \left(t\right)\right|N\left(t\right)=3).$$

(26)

This shows that the assumption of the uniform distribution of deviations ${\theta }_k$ implies a larger randomness of the sample paths.

For the sake of completeness, we give a hint for the derivation of (23).

$$\begin{array}{cc}\hfill \mathbb{E}& \left({\cosh }^2{\eta }_{\theta }\left(t\right)\right|N\left(t\right)=1)\hfill \\ \hfill & =\frac{1}{t}{\int }_0^t\left(\frac{1}{2\pi }{\int }_0^{2\pi }d{\theta }_1\right){\cosh }^{2}c{t}_1{\cosh }^{2}c(t-t_1)d{t}_1\hfill \\ \hfill & +\frac{1}{t}{\int }_0^t\left(\frac{1}{2\pi }{\int }_0^{2\pi }{\cos }^2{\theta }_{1}d{\theta }_1\right){\sinh }^{2}c{t}_1{\sinh }^{2}c(t-t_1)d{t}_1\hfill \\ \hfill & -\frac{2}{t}{\int }_0^t\left(\frac{1}{2\pi }{\int }_0^{2\pi }\cos {\theta }_{1}d{\theta }_1\right)\cosh c{t}_1\cosh c(t-t_1)\sinh c{t}_1\sinh c(t-t_1)d{t}_1.\hfill \end{array}$$

(27)

Fortunately, the third term in (27) is equal to zero, while the second one differs from zero because $\frac{1}{2\pi }{\int }_0^{2\pi }{\cos }^2{\theta }_{1}d{\theta }_1=\frac{1}{2}$. This entails that

$$\mathbb{E}\left({\cosh }^2{\eta }_{\theta }\left(t\right)\right|N\left(t\right)=1)>\mathbb{E}\left({\cosh }^2\eta \left(t\right)\right|N\left(t\right)=1).$$

(28)

More generally, we can compare the behaviour of the randomly moving particle in the case of uniformly distributed and orthogonal deviations by means of inequalities of the conditional moments of the hyperbolic distance.

The proof of (26) implies a more significant amount of calculation. Additionally,

$$\mathbb{E}[{\cosh }^2{\eta }_{\theta }\left(t\right)-{\cosh }^2\eta \left(t\right)|N\left(t\right)=1]=\frac{1}{2t}{\int }_0^t{\left[\sinh c{t}_1\sinh c(t-t_1)\right]}^{2}d{t}_1$$

(29)

shows that the difference between the terms of (28) is an increasing function of t.

For small values of t, we have the following asymptotic relationships:

$$\mathbb{E}\left[{\cosh }^2{\eta }_{\theta }\left(t\right)\right|N\left(t\right)=1]\sim 1+\frac{2}{3}{c}^2{t}^2$$

$$\mathbb{E}\left[{\cosh }^2{\eta }_{\theta }\left(t\right)\right|N\left(t\right)=2]\sim 1+\frac{1}{2}{c}^2{t}^2$$

$$\mathbb{E}\left[{\cosh }^3{\eta }_{\theta }\left(t\right)\right|N\left(t\right)=1]\sim 1+c^2{t}^2=\mathbb{E}\left[{\cosh }^2{\eta }_{\theta }\left(t\right)\right|N\left(t\right)=0].$$

4. Motion at Finite Velocity in the 3-Sphere

The starting point $P_0$ of the random motion on the surface $S_3$ is assumed to be on the equator. We suppose that the moving particle initially takes a uniformly distributed direction and runs with constant velocity c along arcs of great circumferences.

At the Poisson times $T_k$ and $k\ge 1$, the particle takes the new random orientation ${\theta }_k$ with uniform law in $[0,2\pi )$ independent of the previous directions. We are interested in the analysis of the current distance $d(P_0,P_t)$ of the point reached at time t from $P_0$.

In this framework, the sample paths described by the moving particle are represented by broken spherical arcs.

At time $T_2$, we have a spherical scalene triangle with vertices $P_0$, $P_1$ and $P_2$ (see Figure 2b).

At time $T_{k+1}\ge t>T_k$, we have a scalene triangle with sides $P_0{P}_t$, $P_k{P}_t$ and $P_0{P}_k$, so that the current distance $d(P_0,P_t)$ must be expressed by means of the spherical Carnot formula.

$$\cos d(P_0,P_t)=\cos d(P_0,P_k)\cos d(P_k,P_t)+\sin d(P_0,P_k)\sin d(P_k,P_t)\cos {\theta }_k$$

(30)

where ${\theta }_k$ is the angle between the spherical arcs $P_0{P}_k$ and $P_k{P}_t$ (see the Figure 6 below).

Differently from the paper by Cammarota and Orsingher (2008), where each step $P_k{P}_t$ is orthogonal to $P_0{P}_k$, here, we assume a more general choice of the orientations. This entails that we must use the Carnot spherical formula instead of the Pythagorean theorem, with a substantial increase in the necessary computation.

For $T_1<t\le T_2$, Formula (30) specializes as

$$\begin{array}{cc}\hfill \cos d(P_0,P_t)& =\cos d(P_0,P_1)\cos d(P_1,P_t)\hfill \\ & +\sin d(P_0,P_1)\sin d(P_1,P_t)\cos {\theta }_1\hfill \\ \hfill & =\cos c{t}_1\cos c(t-t_1)+\sin c{t}_1\sin c(t-t_1)\cos {\theta }_1.\hfill \end{array}$$

(31)

For $T_2<t\le T_3$, we have that

$$\begin{array}{cc}\hfill \cos & d(P_0,P_t)=\cos d(P_0,P_2)\cos d(P_2,P_t)\hfill \\ & +\sin d(P_0,P_2)\sin d(P_2,P_t)\cos {\theta }_2\hfill \\ \hfill & =\left[\cos d(P_0,P_1)\cos d(P_1,P_2)+\sin d(P_0,P_1)\sin d(P_1,P_2)\cos {\theta }_1\right]·\cos d(P_2,P_t)\hfill \\ & +\sin d(P_0,P_2)\sin d(P_2,P_t)\cos {\theta }_2\hfill \\ \hfill & =\cos d(P_0,P_1)\cos d(P_1,P_2)\cos d(P_2,P_t)\hfill \\ & +\cos d(P_2,P_t)\sin d(P_0,P_1)\sin d(P_1,P_2)\cos {\theta }_1\hfill \\ & +\sin d(P_0,P_2)\sin d(P_2,P_t)\cos {\theta }_2.\hfill \end{array}$$

(32)

Analogously for $T_3<t\le T_k$, we arrive at

$$\begin{array}{c}\cos d(P_0,P_t)=\hfill \\ \hfill \hspace{1em}\prod _{k=1}^4\cos d(P_{k-1},P_k)+\sum _{k=1}^3\cos {\theta }_k\sin d(P_0,P_k)\sin d(P_k,P_{k+1})\prod _{j=k+2}^4\cos d(P_{j-1},P_j).\end{array}$$

(33)

For the general case where $T_k<t\le T_{k+1}$, by generalizing (33), we obtain

$$\begin{array}{c}\cos d(P_0,P_t)=\hfill \\ \hfill \hspace{1em}\prod _{r=1}^{k+1}\cos d(P_{r-1},P_r)+\sum _{r=1}^k\cos {\theta }_r\sin d(P_0,P_r)\sin d(P_r,P_{r+1})\prod _{j=r+2}^{k+1}\cos d(P_{j-1},P_j).\end{array}$$

(34)

Formula (34) can be proved by induction as in the hyperbolic case. For the sake of brevity, we do not repeat such a proof.

By denoting the spherical velocity with c, that is,

$$c=\frac{ds}{dt}=\sqrt{{\sin }^{2}d\theta {\left(\frac{d\varphi }{dt}\right)}^2+{\left(\frac{d\theta }{dt}\right)}^2}$$

we can evaluate the conditional mean value of the distance $\cos d(P_0,P_t)$ in the following way:

$$\begin{array}{cc}\hfill \mathbb{E}& \left[\cosh d(P_0,P_t)\right|N\left(t\right)=n]\hfill \\ \hfill & =\frac{1}{{\left(2\pi \right)}^n}\frac{n!}{t^n}{\int }_0^{t}d{t}_1{\int }_{t_1}^{t}d{t}_2\cdots {\int }_{t_{n-1}}^{t}d{t}_n{\int }_0^{2\pi }d{\theta }_1\cdots {\int }_0^{2\pi }d{\theta }_n\hfill \\ \hfill & \left(\prod _{k=1}^{n+1}\cos c(t_k-t_{k-1})-\sum _{k=1}^n\cos {\theta }_k\sin d(P_0,P_k)\sin c(t_{k+1}-t_k)·\prod _{j=k+2}^{n+1}\cosh c(t_j-t_{j-1})\right)\hfill \\ \hfill & =\left(\mathrm{because}\mathrm{of}\mathrm{the}\mathrm{independence}\mathrm{of}{\eta }_k\mathrm{from}{\theta }_k\mathrm{and}\mathrm{that}\mathrm{of}{\theta }_k\mathrm{among}\mathrm{themselves}\right)\hfill \\ \hfill & =\frac{n!}{t^n}{\int }_0^{t}d{t}_1{\int }_{t_1}^{t}d{t}_2\cdots {\int }_{t_{n-1}}^{t}d{t}_n\prod _{k=1}^{n+1}\cos c(t_k-t_{k-1})\hfill \end{array}$$

(35)

because ${\int }_0^{2\pi }\cos {\theta }_{k}d{\theta }_k=0$ for all k, and $\sin d(P_0,P_k)$ does not depend on ${\theta }_k$.

This implies that the conditional mean value (35) coincides with that of the orthogonal spherical case studied in Cammarota and Orsingher (2008).

The relationship (35) permits us to argue that as in [5] and conclude that

$$\mathbb{E}\cos d(P_0,P_t)=E\left(t\right)$$

is a function satisfying the initial value problem

$$\left\{\begin{array}{c}\frac{d^2}{d{t}^2}E\left(t\right)=-\lambda \frac{d}{dt}E\left(t\right)-c^{2}E\left(t\right)\hfill \\ E\left(0\right)=1,\frac{d}{dt}E\left(t\right){|}_{t=0}=0\hfill \end{array}\right..$$

(36)

The solution to (36) reads

$$\begin{array}{c}\mathbb{E}\left[\cos d(P_0,P_t)\right]=\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\frac{{\mathrm{e}}^{-\frac{\lambda t}{2}}}{2}\left[({\mathrm{e}}^{\frac{t}{2}\sqrt{{\lambda }^2-4c^2}}+{\mathrm{e}}^{-\frac{t}{2}\sqrt{{\lambda }^2-4c^2}})+\frac{\lambda }{\sqrt{{\lambda }^2-4c^2}}({\mathrm{e}}^{\frac{t}{2}\sqrt{{\lambda }^2-4c^2}}-{\mathrm{e}}^{-\frac{t}{2}\sqrt{{\lambda }^2-4c^2}})\right].\end{array}$$

(37)

We have three relevant cases in the analysis of (37).

For $\lambda >2c$, that is, when the Poisson rate is sufficiently high, the particle barely leaves the neighborhood of the starting point and cannot run the whole great circumference. Loosely speaking, the support of $d(P_0,P_t)$ is a spherical cap centered at $P_0$, which never covers, on average, the whole unit-radius sphere. Thus, we have that

$$E\left(t\right)={\mathrm{e}}^{-\frac{\lambda t}{2}}\left(\cosh \frac{t}{2}\sqrt{{\lambda }^2-4c^2}+\frac{\lambda }{\sqrt{{\lambda }^2-4c^2}}\sinh \frac{t}{2}\sqrt{{\lambda }^2-4c^2}\right).$$

For $\lambda =2c$, Formula (37) yields

$$E\left(t\right)={\mathrm{e}}^{-\frac{\lambda t}{2}}\left(1+\frac{\lambda t}{2}\right).$$

In this case, the spherical cap in the mean coincides with the whole $S_3$, and the moving particle reaches one of the two poles.

For $\lambda <2c$, the particle performing the random motion repeatedly runs a distance, which, in the average, is bigger than the great circle and displays a periodical behaviour. Thus, we have that

$$E\left(t\right)={\mathrm{e}}^{-\frac{\lambda t}{2}}\left(\cos \frac{t}{2}\sqrt{4c^2-{\lambda }^2}+\frac{\lambda }{\sqrt{4c^2-{\lambda }^2}}\sin \frac{t}{2}\sqrt{4c^2-{\lambda }^2}\right).$$

We notice that the two formulas describing the mean distance of the moving particle from the starting point on the Poincaré half-plane and on the unit sphere strongly resemble each other. This is a consequence of the deep relationship between these spaces. In fact, ${\mathbb{H}}_2^{+}$ can be seen as a sphere with an imaginary radius given by the imaginary unit. Therefore, by considering an imaginary velocity for the moving particle, we may derive the results for the moments of the distance travelled on the sphere directly from those obtained on the half-plane.

In light of this, by substituting c with $ic$ in Formula (18), we obtain Formula (34). Additionally, from Formulas (23)–(26), we obtain that

$$\begin{array}{cc}\hfill \mathbb{E}\left[{\cos }^{2}d(P_0,P_t)\right|N\left(t\right)=1]& =\mathbb{E}\left[{\cosh }^{2}id(P_0,P_t)\right|N\left(t\right)=1]\hfill \\ \hfill & =\frac{3}{8}{\cosh }^2\left(ic\right)t+\frac{7}{16\left(ic\right)t}\sinh \left(ic\right)t\cosh \left(ic\right)t+\frac{3}{16}\hfill \\ \hfill & =\frac{3}{8}{\cos }^{2}ct+\frac{7}{16ct}\sin ct\cos ct+\frac{3}{16}\hfill \end{array}$$

(38)

and, similarly, also that

$$\mathbb{E}\left({\cos }^{2}d(P_0,P_t)\right|N\left(t\right)=2)=\frac{9}{64}{\cos }^{2}ct+\frac{3}{32c^2{t}^2}{\sin }^{2}ct+\frac{63}{128ct}\sin ct\cos ct+\frac{35}{128}$$

$$\mathbb{E}\left({\cos }^{3}d(P_0,P_t)\right|N\left(t\right)=1)=\frac{5}{64}\cos 3ct+\frac{37}{384ct}\sin 3ct+\frac{21}{64}\cos ct+\frac{39}{128ct}\sin ct.$$

Furthermore, we have that

$$\mathbb{E}\left({\cos }^2{d}_{\theta }(P_0,P_t)\right|N\left(t\right)=3)>\mathbb{E}\left({\cos }^{2}d(P_0,P_t)\right|N\left(t\right)=3)$$

where $d_{\theta }$ here denotes the spherical distance with uniform deviations, and d denotes the current spherical distance with orthogonal deviations (Cammarota and Orsingher 2008).

With the same approach, we may also derive the following asymptotic relationships:

$$\mathbb{E}\left[{\cos }^{2}d(P_0,P_t)\right|N\left(t\right)=1]\sim 1-\frac{2}{3}{c}^2{t}^2$$

$$\mathbb{E}\left[{\cos }^{2}d(P_0,P_t)\right|N\left(t\right)=2]\sim 1-\frac{1}{2}{c}^2{t}^2$$

$$\mathbb{E}\left[{\cos }^{3}d(P_0,P_t)\left(t\right)\right|N\left(t\right)=1]\sim 1-c^2{t}^2=\mathbb{E}\left[{\cosh }^{2}d(P_0,P_t)\right|N\left(t\right)=0].$$

The last results recall the analogous results for the motion on ${\mathbb{H}}_2^{+}$.

5. Conclusions

The crucial assumption that orthogonal deviations are replaced by uniformly distributed changes of direction make the random motion more general but at the same time involve a more complicated mathematical investigation.

The effect of this generalisation is perceived when higher moments are examined, whereas the conditional and unconditional mean distance from the starting point coincide with those obtained in [5].