Randomized Average Kaczmarz Algorithm for Tensor Linear Systems
Abstract
1. Introduction
2. Preliminaries
2.1. Notation
2.2. Tensor Basics
2.3. Randomized Average Block Kaczmarz Algorithm
| Algorithm 1 Randomized average block Kaczmarz (RABK) algorithm |
|
2.4. Randomized Regularized Kaczmarz Algorithm
| Algorithm 2 Randomized Regularized Kaczmarz Algorithm |
|
3. Tensor Randomized Average Kaczmarz Algorithm
| Algorithm 3 Tensor randomized average Kaczmarz (TRAK) algorithm |
|
| Algorithm 4 Matrix randomized average Kaczmarz (MRAK) algorithm |
|
4. Tensor Randomized Average Kaczmarz Algorithm with Random Sampling (TRAKS)
| Algorithm 5 Tensor randomized average Kaczmarz algorithm with random sampling (TRAKS) |
|
| Algorithm 6 Matrix randomized average Kaczmarz algorithm with random sampling (MRAKS) |
|
5. The Fourier Version of the Algorithms
| Algorithm 7 TRAK algorithm in the Fourier domain () |
|
| Algorithm 8 TRAKS algorithm in the Fourier domain () |
|
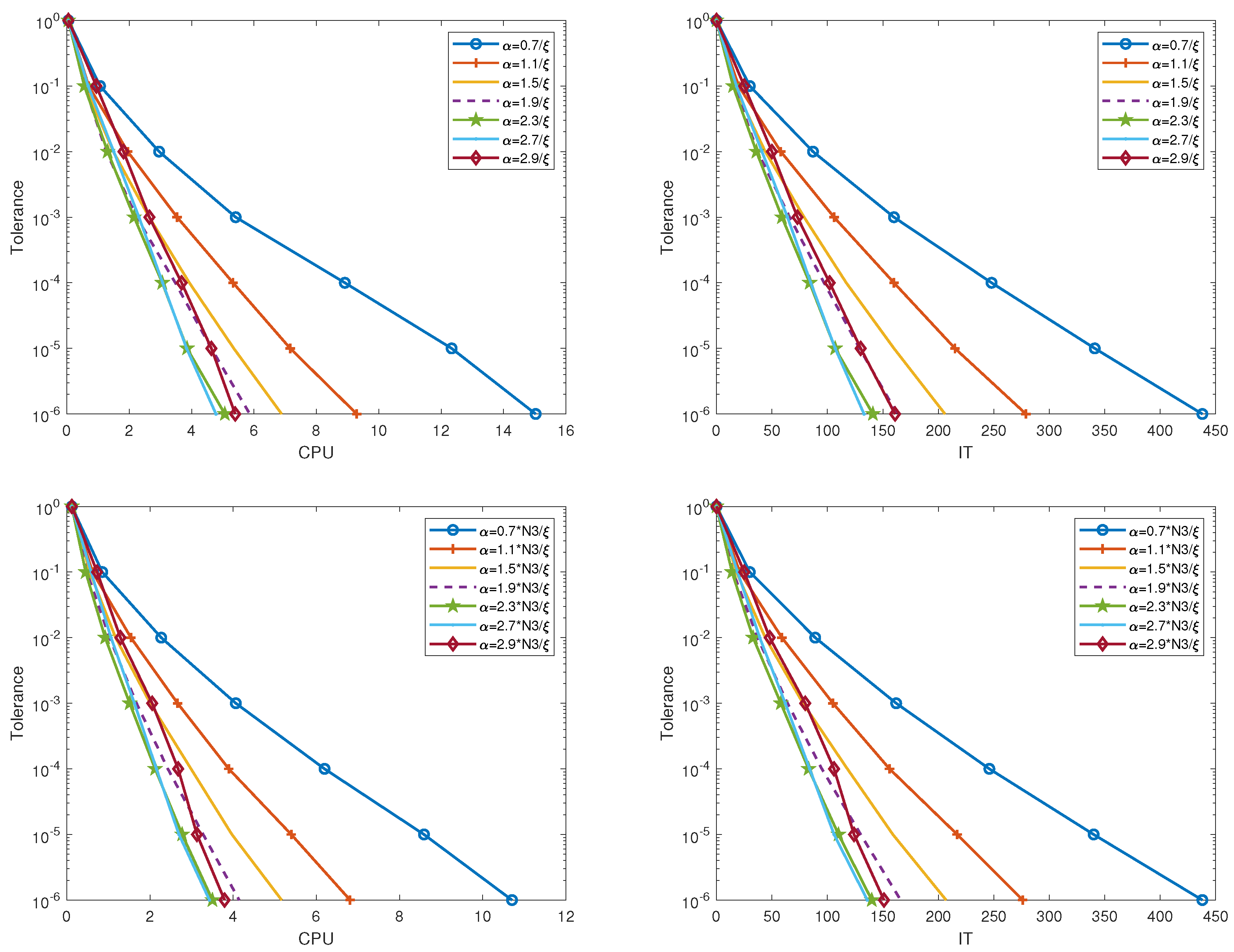
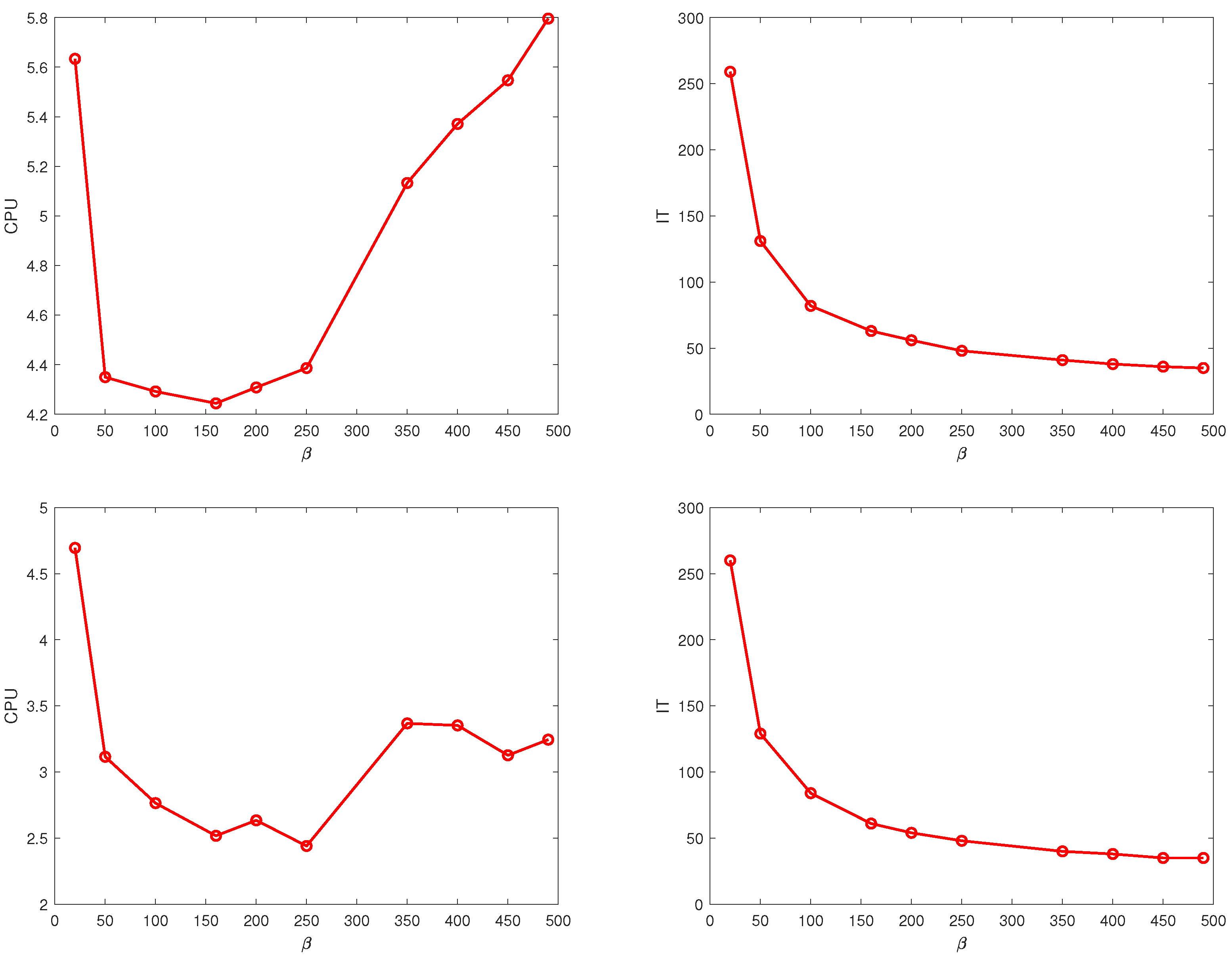
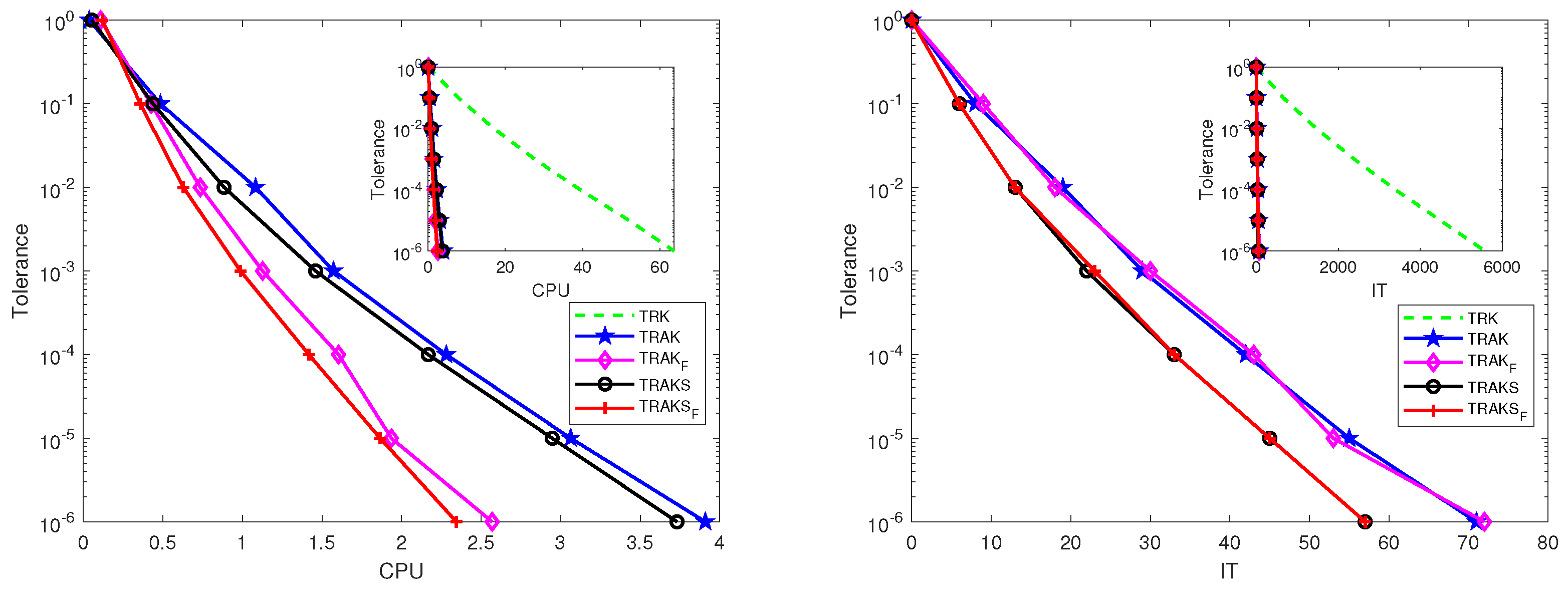
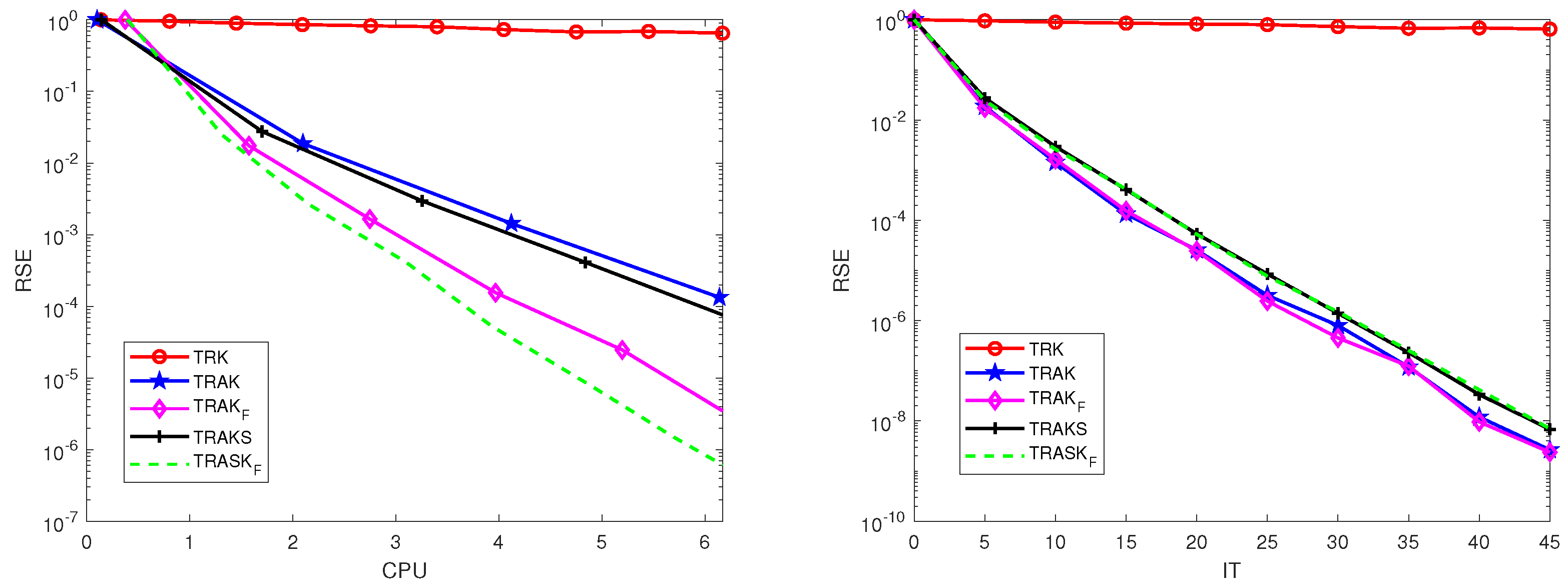
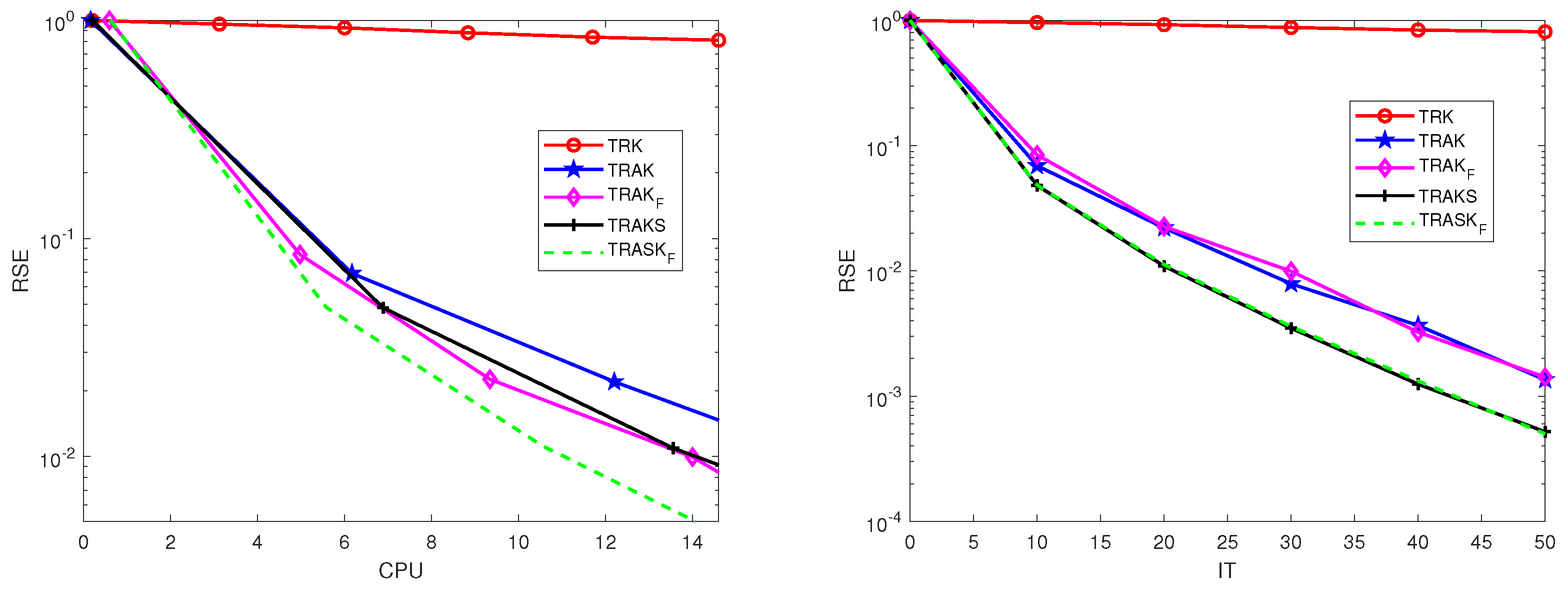
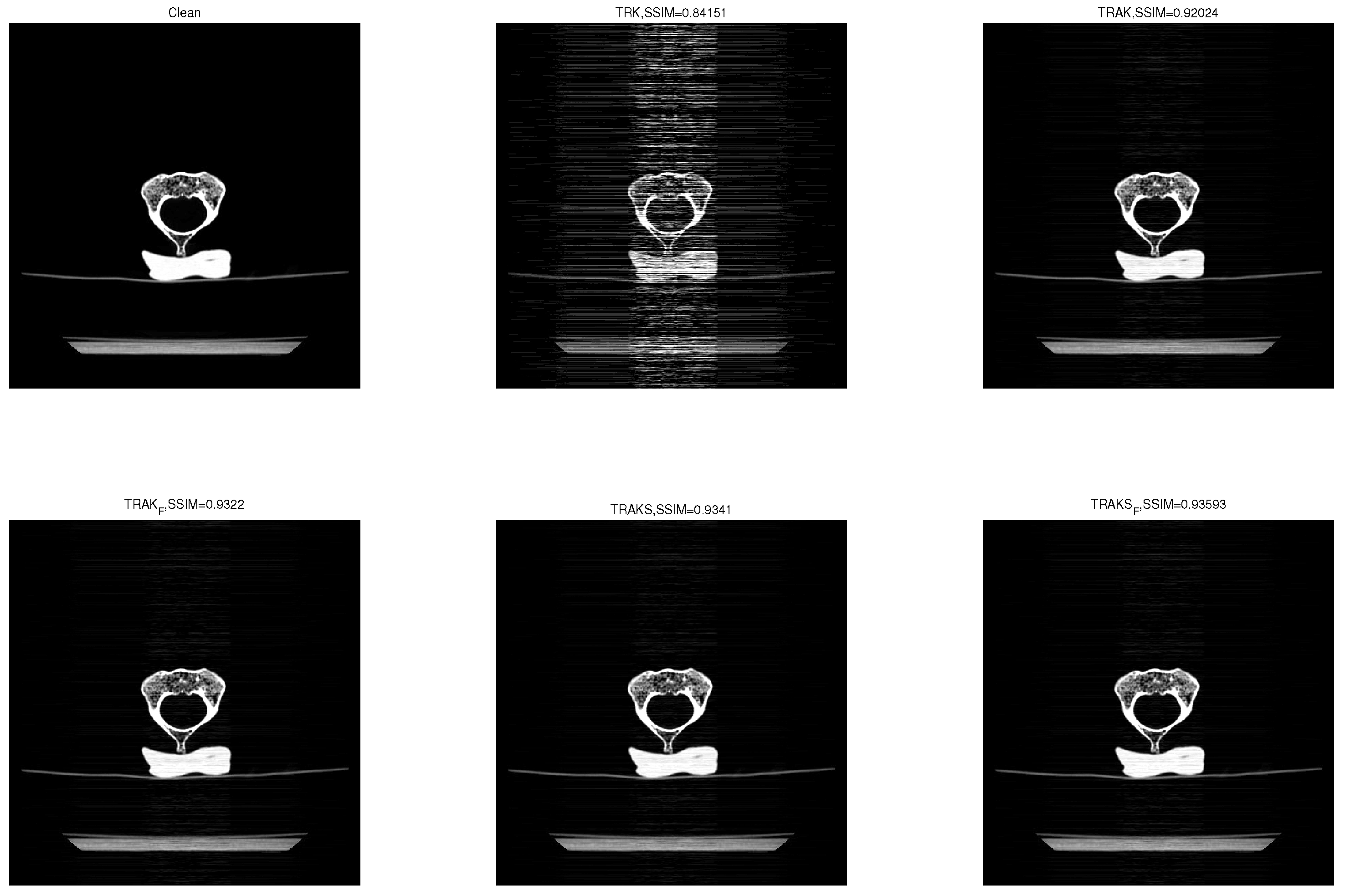
6. Numerical Experiments
6.1. Synthetic Data
6.2. 3D MRI Image Data
6.3. Video Data
6.4. CT Data
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kilmer, M.E.; Martin, C.D. Factorization strategies for third-order tensors. Linear Algebra Its Appl. 2011, 435, 641–658. [Google Scholar] [CrossRef]
- Newman, E.; Horesh, L.; Avron, H.; Kilmer, M. Stable tensor neural networks for rapid deep learning. arXiv 2018, arXiv:1811.06569. [Google Scholar]
- Soltani, S.; Kilmer, M.E.; Hansen, P.C. A tensor-based dictionary learning approach to tomographic image reconstruction. Bit Numer. Math. 2016, 56, 1425–1454. [Google Scholar] [CrossRef]
- Hua, Z.; Li, L.; Zhu, H. Tensor regression with applications in neuroimaging data analysis. J. Am. Stat. Assoc. 2013, 108, 540–552. [Google Scholar]
- Andersen, A.H.; Kak, A.C. Simultaneous algebraic reconstruction technique (SART): A superior implementation of the ART algorithm. Ultrason. Imaging 1984, 6, 81–94. [Google Scholar] [CrossRef] [PubMed]
- Peterson, J.E.; Paulsson, B.N.; McEvilly, T.V. Applications of algebraic reconstruction techniques to crosshole seismic data. Geophysics 1985, 50, 1566–1580. [Google Scholar] [CrossRef]
- Zouzias, A.; Freris, N.M. Randomized extended Kaczmarz for solving least squares. SIAM J. Matrix Anal. Appl. 2013, 34, 773–793. [Google Scholar] [CrossRef]
- Needell, D. Randomized Kaczmarz solver for noisy linear systems. BIT Numer. Math. 2010, 50, 395–403. [Google Scholar] [CrossRef]
- Moorman, J.D.; Tu, T.K.; Molitor, D.; Needell, D. Randomized Kaczmarz with averaging. Bit Numer. Math. 2021, 61, 337–359. [Google Scholar] [CrossRef]
- Necoara, I. Faster randomized block Kaczmarz algorithms. SIAM J. Matrix Anal. Appl. 2019, 40, 1425–1452. [Google Scholar] [CrossRef]
- Miao, C.Q.; Wu, W.T. On greedy randomized average block Kaczmarz method for solving large linear systems. J. Comput. Appl. Math. 2022, 413, 114372. [Google Scholar] [CrossRef]
- Elfving, T. Block-iterative methods for consistent and inconsistent linear equations. Numer. Math. 1980, 35, 1–12. [Google Scholar] [CrossRef]
- Eggermont, P.P.B.; Herman, G.T.; Lent, A. Iterative algorithms for large partitioned linear systems with applications to image reconstruction. Linear Algebra Its Appl. 1981, 40, 37–67. [Google Scholar] [CrossRef]
- Needell, D.; Tropp, J.A. Paved with good intentions: Analysis of a randomized block Kaczmarz method. Linear Algebra Its Appl. 2014, 441, 199–221. [Google Scholar] [CrossRef]
- Ma, A.; Molitor, D. Randomized Kaczmarz for tensor linear systems. BIT Numer. Math. 2022, 62, 171–194. [Google Scholar] [CrossRef]
- Tang, L.; Yu, Y.; Zhang, Y.; Li, H. Sketch-and-project methods for tensor linear systems. arXiv 2022, arXiv:2201.00667. [Google Scholar] [CrossRef]
- Chen, X.; Qin, J. Regularized Kaczmarz algorithms for tensor recovery. SIAM J. Imaging Sci. 2021, 14, 1439–1471. [Google Scholar] [CrossRef]
- Wang, X.; Che, M.; Mo, C.; Wei, Y. Solving the system of nonsingular tensor equations via randomized Kaczmarz-like method. J. Comput. Appl. Math. 2023, 421, 114856. [Google Scholar] [CrossRef]
- Kilmer, M.E.; Braman, K.; Hao, N.; Hoover, R.C. Third-order tensors as operators on matrices: A theoretical and computational framework with applications in imaging. SIAM J. Matrix Anal. Appl. 2013, 34, 148–172. [Google Scholar] [CrossRef]
- Jin, H.; Bai, M.; Benítez, J.; Liu, X. The generalized inverses of tensors and an application to linear models. Comput. Math. Appl. 2017, 74, 385–397. [Google Scholar] [CrossRef]
- Jiang, Y.; Wu, G.; Jiang, L. A Kaczmarz method with simple random sampling for solving large linear systems. arXiv 2020, arXiv:2011.14693. [Google Scholar]
- Carlton, M.A. Probability and Statistics for Computer Scientists. Am. Stat. 2008, 62, 271–272. [Google Scholar] [CrossRef]
- Wang, Q.; Li, W.; Bao, W.; Gao, X. Nonlinear Kaczmarz algorithms and their convergence. J. Comput. Appl. Math. 2022, 399, 113720. [Google Scholar] [CrossRef]
- Lu, C. Tensor-Tensor Product Toolbox. Carnegie Mellon University. 2018. Available online: https://github.com/canyilu/tproduct (accessed on 17 July 2022).
- Finding His Voice. Available online: https://archive.org/details/FindingH1929 (accessed on 15 August 2022).
- Bone and Joint ct-scan Data. Available online: https://isbweb.org/data/vsj/ (accessed on 25 August 2022).

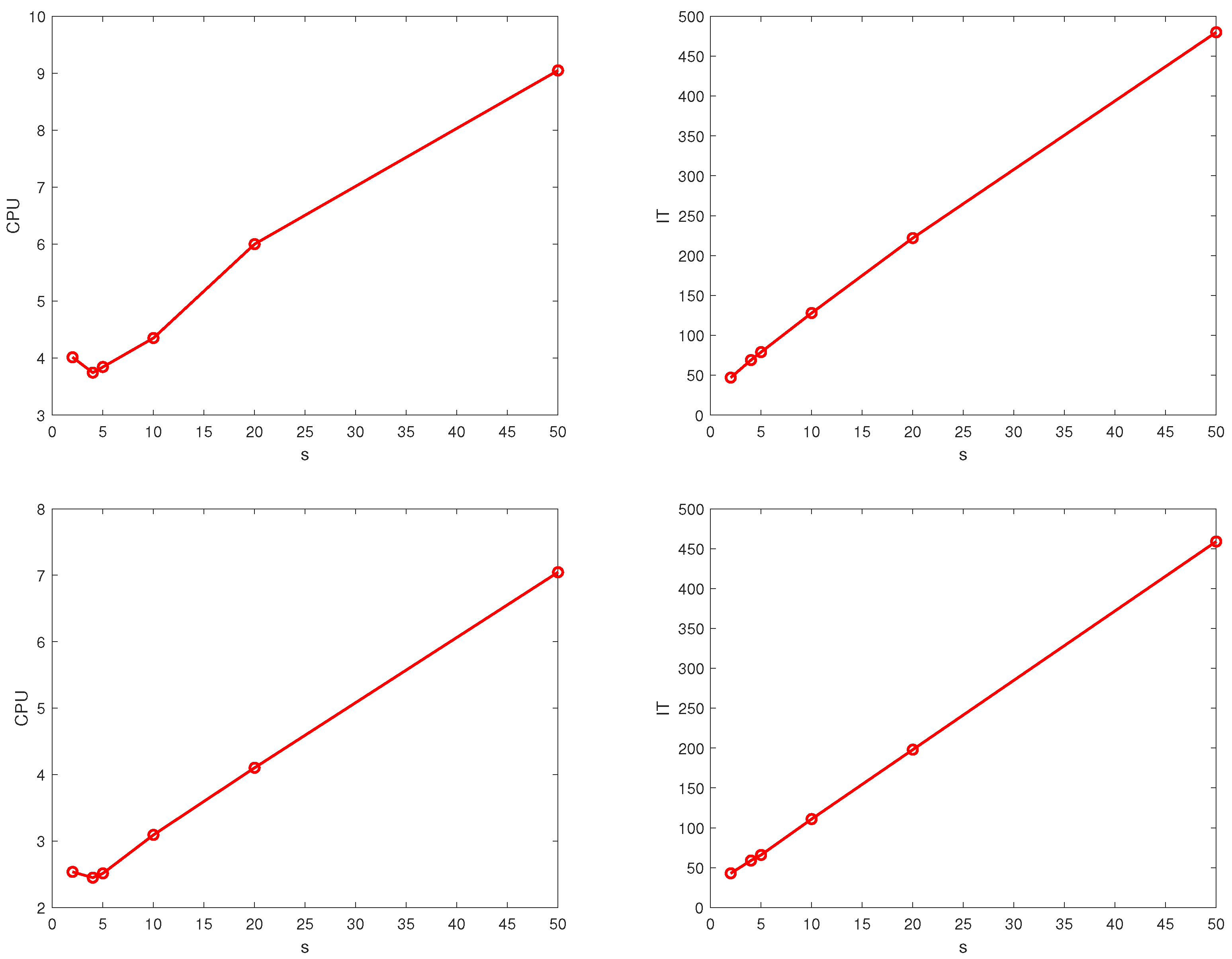


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bao, W.; Zhang, F.; Li, W.; Wang, Q.; Gao, Y. Randomized Average Kaczmarz Algorithm for Tensor Linear Systems. Mathematics 2022, 10, 4594. https://doi.org/10.3390/math10234594
Bao W, Zhang F, Li W, Wang Q, Gao Y. Randomized Average Kaczmarz Algorithm for Tensor Linear Systems. Mathematics. 2022; 10(23):4594. https://doi.org/10.3390/math10234594
Chicago/Turabian StyleBao, Wendi, Feiyu Zhang, Weiguo Li, Qin Wang, and Ying Gao. 2022. "Randomized Average Kaczmarz Algorithm for Tensor Linear Systems" Mathematics 10, no. 23: 4594. https://doi.org/10.3390/math10234594
APA StyleBao, W., Zhang, F., Li, W., Wang, Q., & Gao, Y. (2022). Randomized Average Kaczmarz Algorithm for Tensor Linear Systems. Mathematics, 10(23), 4594. https://doi.org/10.3390/math10234594





