Controllable Energy Consumption in a Sustainable Smart Manufacturing Model Considering Superior Service, Flexible Demand, and Partial Outsourcing

Abstract

The waste of energy in the present era is a dangerous signal for the future. All categories of consumers should come forward to moderate energy use and prevent wastage. This study focuses on a controllable energy consumption-based sustainable inventory model incorporating variable production rates, improved service, partial outsourcing planning, defective production, restoring reworkable items, disposing of non-reworkable items, and energy-saving steps. Reducing unusual energy consumption in production systems reduces carbon emissions and maximizes the system’s profit. An improved service level attracts customers, increases demand, and improves product reputation. Separate holding costs of reworked, defective, and perfect-quality items are considered for every lot delivered and reworked. The demand in the market is related to price and service. A traditional optimization technique examines the global optimization for the profit function and decision variables. Numerical illustrations as well as concave 3D graphs validate the analytical results and provide a sensitivity analysis for different parameters. The model is validated through special cases and comparison graphs.

1. Introduction

Industry managers aim to maximize profits by satisfying customer demands. Accordingly, the service level has recently emerged as one of the most significant parameters for measuring customer satisfaction. The introduction of a service level allows defective items to be rendered usable. Variable market demand can be controlled by variable production rates. Outsourcing supports the global reputation and boosts profit. The improvement of reworkable items increases the system’s profit, and the disposal of non-reworkable items reduces environmental pollution and carbon emissions. The unusual consumption of electrical energy through air handling and lighting costs is an environment-friendly concept with maximum profit and energy savings.

Energy saving can increase profits and be environmentally friendly (Kim [1]). Furthermore, partial outsourcing planning with defective production, reworking, and disposal represents a progressive mindset (Chiu et al. [2]). Demand can be increased by leveraging the concept of the service level. However, variable production rates, with variable demand and energy economic expansion (Hasan [3]), are challenging to implement in production systems. In light of the above, we propose an inventory model of partial outsourcing, imperfect production, reworking of items, disposal of scrap/nonreworkable items, energy-saving concepts, service facilities under variable production rates, and variable demand to optimize the total expected profit.

1.1. Research Question

• How does waste of energy impact the environment?
• How does the reworking of imperfect items affect the system profit?
• How do energy-saving steps affect a production inventory model?
• How does controllable energy consumption improve sustainability in the production-inventory model?

Motivated by the questions mentioned above, the proposed model has been derived.

1.2. Research Goal

The below-mentioned research gaps can be drawn based on the present literature.

• Many production models were discussed considering the manufacturing rate and partial outsourcing. However, most of the models included flexible production through the replenishment technique. However, the impacts of reworking the smart product with partial outsourcing under a flexible production system have not yet been studied.
• A mathematical model on variable demand and flexible production rates through smart production under sustainability exists. However, the idea of imperfect production and reworking them through different holding costs with price- and service-dependent demand has not been developed.
• Various studies discussed production models on various stages and manufacturing uptime-downtime. However, how a smart production model under sustainability can comprise the optimum profit through an imperfect production system under partial outsourcing and controlled energy consumption has rarely been investigated.

1.3. Contribution

(i)

Several production models considered variable demand and production systems. However, service-level and selling price-dependent demand with partial outsourcing, defective production, reworking of defective items, and disposal of non-reworkable scrap items present a significant gap in the literature.

(i)

Several models have considered an energy-saving investment plan. However, reducing unusual energy consumption through controllable air handling and lowering lighting costs to reduce carbon emissions and realize environmental benefits has scarcely been considered.

(iii)

Many production models assume a fixed setup cost. However, different holding costs for reworked and perfect and defective goods are considered here, which is practicable in a production system. Moreover, an inventory model with outsourcing and an in-house setup for the remaining products significantly contributes to the literature. This study introduces a sustainable smart production model with defective items, where demand is service-level and selling is price-dependent. The cost of production per unit depends on the production rate, as well as tool/die, labor, and development costs. Furthermore, defective items are reworked to increase the system’s profit, and the unusual energy consumption is reduced. Finally, the total expected profit (TEP) is optimized by optimizing the decision variables.

1.4. Structure of this Study

The remaining part of the paper is such that the literature review associated with this study is discussed in the next section. Table 1 provides the research gap among the previous authors. Section 3 shows the reason for the problem, mathematical notation, and assumptions. Mathematical modelling is derived in Section 4, and the methodology of the solution is discussed in Section 5. Numerical applications are established in Section 6 and Section 7 introduces a sensitivity analysis. Section 8 provides an overview of the conduct of this study, and the conclusions are drawn in Section 9.

Table 1. Author(s) contribution table.

Author(s)	Production Rate	Demand Type	Outsourcing	Reworking	Service Level	Energy Consumption	Model Type
Kim [1]	NA	NA	NA	NA	Yes	Yes	EA
Chiu et al. [2]	Constant	Constant	Yes	Yes	NA	NA	Inventory
Habib et al. [4]	Constant	Constant	NA	NA	NA	Yes	SCM
Glock [5]	Variable	Constant	NA	NA	NA	NA	Inventory
Singh & Sharma [6]	Variable	TD	NA	NA	NA	NA	Inventory
Gautam et al. [7]	Variable	Variable	NA	Yes	NA	NA	Production
Malik & Kim [8]	Variable	Fuzzy	NA	NA	NA	NA	SCM
Tang & Wang [9]	Constant	Stochastic	NA	Yes	NA	Yes	Inventory
Esmaeili et al. [10]	Constant	Constant	NA	Yes	Yes	NA	SCM
Sarkar et al. [11]	NA	Uncertain	NA	NA	NA	NA	Inventory
Xiang [12]	Variable	Stochastic	NA	Yes	NA	Yes	Supply chain
Jauhari et al. [13]	Constant	GTPQD	NA	Yes	NA	NA	SCM
Gahm et al. [14]	NA	NA	NA	NA	NA	Yes	EMQ
Xie et al. [15]	Constant	Constant	NA	NA	NA	Yes	Inventory
Bachar et al. [16]	Constant	Variable	Yes	Yes	NA	NA	Inventory
This Paper	Variable	SPSD	Yes	Yes	Yes	Yes	Inventory

NA, not applied; SPSD, selling price and service dependent; SCM, supply chain management EA, economic analysis, GTPQD, green technology, price- and quality-dependent, TD—time-dependent.

2. Related Literature Review

A controllable production rate is essential for controlling shortages. Moreover, this model’s important features are outsourcing, service facilities, rework, and energy consumption. The background of these concepts is discussed in this section.

2.1. Flexible Production Rate

Optimizing the volume of production is critical for any production manager. The production rate may be variable or constant depending on the market demand. Khouja and Mehrez [17] introduced an economic production quantity (EPQ) model in which they introduced the variable production rate under perfect and imperfect production. Eiamkanchanalai and Banerjee [18] extended the model mentioned above by incorporating idle capacity costs. An economic manufacturing quantity (EMQ) model in which flexible rate of manufacturing, corrective and preventive repair was proposed by Giri and Dohi [19]. Glock [5] focused on a production model which produced a single item in a single utilization and conveyed to the resulting phase in shipments under a variable production rate.

A smart production system with a flexible rate of production and flexible demand was derived by Singh and Sharma [6]. The impacts of inflation and the time worth of money were considered to upgrade the model to be more realistic. An incorporated production model for deteriorating products with variable production rates was discussed by Chan et al. [20]. Kim and Glock [21] developed a two-stage production system with a variable production rate with multiple equal machines. A variable imperfect production system was examined by Gautam et al. [7] under greening degree. Yadav et al. [22] proposed a flexible production model to control by-products. They considered rework to eliminate toxic waste from the production system.

Manna et al. [23] derived a production model with setup cost as interval-valued fuzzy number. The production system was emissions-controlled. Malik and Kim [8] considered a multi-constrained supply chain model with variable production rates under fuzzy demand. Xu et al. [24] discussed a influencing factor for renewable energy production in a large scale. Sarkar et al. [25] focussed on a model in which they incorporated flexible production, optimum energy utilization, and multi-type smart biofuel manufacturing with sustainability. Aouam et al. [26] proposed a supply chain management (SCM) with production capacity constraint for guarantee service. They solved the model by a mixed-integer programming. Ouaret [27] developed a production model where multiple products produced from a single machine. Thus, a random disturbances occurred in the system. They solved the problem using a dynamic programming.

Several researchers have developed different models that consider flexible production rates. However, an inventory model considering the flexible production rate, selling price, service-dependent demand, outsourcing, and exact total expected profit have not been considered.

2.2. Outsourcing

Outsourcing is an important global business strategy. Outsourcing has wide applications for assembling products. On the one hand, it is possible to produce a lot at a low cost. By contrast, in some cases, it can be purchased through outsourcing without production. Coman and Ronen [28] introduced a linear programming problem in which they considered outsourcing. An extended EPQ model with outsourcing with a secondary utilization, manufacturing planning, inventory control, and stochastic demand was considered by Lee and Lan [29]. Hahn et al. [30] developed a situation-based nonparametric positioning approach to identify valuable outsourcing choices at the essential level. An inventory model with reworking under a fixed and variable outsourcing strategy was introduced by Chiu et al. [31].

Chiu et al. [2] focused on their earlier model by associating a strategy for variable fabrication and disposal of scrap items. Chen et al. [32] studied outsourcing decisions under multidimensional uncertainties with two contingent outsourcing contracts. Niu and Mu [33] considered the supply chain parties’ choices over outsourcing original equipment from the manufacturers’ procurement. Tang and Wang [9] discussed a situation-based stochastic model by associating binomial distribution and transportation outsourcing. Recently, Bachar et al. [16] developed a model regarding the impact of partial outsourcing, green investment, and flexible demand. However, a production model considering variable production rates and flexible demand with outsourcing has not been considered. Therefore, the proposed study sought to fill this research gap.

2.3. Service Level

Companies focus on various strategies, for example, price discount approaches, cash-back arrangements, and promotions, to market the superiority of their goods. Accordingly, the facility level of any product is important to customers, who consider the service facilities available for products. Notably, after-sale service is considered to increase the demand and popularity of the items. Taleizadeh et al. [34] developed a multiproduct production system using a single machine with partial backorders and service-level constraints. Jodlbauer and Reitner [35] considered a stochastic multi-item cyclic production system through service level and safety stock. Different service contracts on three levels (among a customer, manufacturer, and an agent) to locate the best contract were discussed by Esmaeili et al. [10].

Bhat and Krishnamurthy [36] developed service-level limitations as per customer classes in each season and analyzed the influence of constraints of service level on the policy of optimization and cost under various occasional demand conditions. Level of service and environmental footprint were introduced as two objective functions in a multi-objective inventory problem by Rahimi et al. [37]. Gruson et al. [38] introduced different service levels for deterministic batch size problems. The effect of two popular levels of service estimates on the plan of a basic-level strategy was examined by Escalona et al. [39]. Sarkar et al. [40] developed a dual-channel SCM model under a flexible production system under a carbon tax policy.

Qin et al. [41] derived an analytical model from inspecting how the selling mode on an e-commerce platform influences logistic strategy. However, an inventory model with variable production rate, variable demand, outsourcing, and service facilities was not considered, but this is addressed in the current model.

2.4. Rework

Rework aims to reduce the cost of production, benefit the environment, and redefine defective products. It reduces raw material consumption, lowering the cost associated with defective products. Many researchers have shed light on this topic. An EPQ inventory model with reworking by synchronous and asynchronous process was introduced by Priyan et al. [42]. They used green investments to save the environment. Sarkar et al. [43] developed a smart production model with an online-to-offline (O2O) mechanism. They used an autonomation policy for detecting defective products for rework. Selling defective products at discounts and reworking in an EPQ model was formulated by Haider et al. [44]. A supply chain model considering stock- and price-dependent random demand with reworking and shortages was developed by Pal and Mahapatra [45].

Reworking was proposed for second-rate and nonconforming products to improve their quality conditions, as discussed by Gouiaa-Mtibaa et al. [46]. A closed-loop supply chain model was discussed by Jauhuri et al. [47] under green investment of energy use, whereas emissions of carbon, reworking, and waste disposal were presented by Jauhari et al. [13]. Xiang [12] presented a model for energy use with a social choice rule solved by using Nash learning. Sarkar et al. [48] focused on a model incorporating the rate of production, a multi-phase production system, selling price, optimum lot size, and defective production rate. The effect of reworking with service and outsourcing under a flexible production rate in an inventory model is an important gap in the literature. The proposed study allows the total expected profit to be determined, which benefits any inventory system.

2.5. Energy Saving

Energy management is critical to environmental protection. Excessive wastage harms the environment and increases expenses, which is undesirable in any manufacturing system. In addition, moderate energy use increases the service life of electric components. Tang et al. [49] introduced a nonlinear unit energy consumption cost function to express the associated production cost. Gahm et al. [14] introduced energy demand, energetic coverage, and energy supply in a review and research framework. An economic discussion of energy-saving techniques for complex production buildings was conducted by Kim [1]. An original strategy was given an identical circuit model for the estimation of filter residue load of diesel particulate, and the development of the correctness of the recovery timing was proposed by Du et al. [50].

Anyaoha and Zhang [51] discussed three types of palm oil processing industries and the importance of using renewable energy for emissions reduction. Meng et al. [52] identified national energy consumption during different production phases. Xie et al. [15] discussed the nonlinear connection between energy utilization change and green all-out factor efficiency. Peinado-Guerrero and Villalobos [53] focused on a study that discussed optimum energy storage for a bi-directional flow from modern grids. Moon et al. [54] presented a model that included controlled carbon emissions, effects of production costs, reliability, and variable setup costs. Kumar et al. [55] derived an SCM model on carbon emissions and advertisement-dependent demand. Sarkar et al. [56] derived a warehouse model based on radio-frequency identification (RFID) technology but without concerns about emissions from the system. Sarkar et al. [57] focused on a two-echelon supply chain model in which they considered reduction of setup costs, carbon emissions, and utilization of energy consumption. Sarkar and Seo derived [58] a supply chain model considering renewable energy with automation and flexibility in a production system.

Energy consumption critically affects air handling and lighting costs. This concept was incorporated into the present model. The impact of air handling and lighting costs on energy consumption was considered in an inventory model under a variable production rate, variable demand, partial outsourcing, and reworking to fill existing research gaps.

Different researchers have developed many research models with different strategies to optimize the total value of the system or system profit of the system. Most research studies were optimized according to the expected profit or cost. Several models were derived by considering the variable production rate, variable demand, outsourcing, and reworking in an inventory model. However, an inventory model was developed in this study considering selling price, service-dependent demand, variable production rate, varying lot size, and variable selling price under partial outsourcing and improved service facilities. None of these keywords were previously considered.

3. Problem Definition, Notation, and Assumptions

3.1. Problem Definition

The present model introduces a partial outsourcing plan and energy-saving concept. The variable-type production rate is considered here for the smart production system. Chiu et al. [2] considered a variable lot size with partial outsourcing only. However, the present study was based on a fixed production rate with a fixed demand without an energy-saving plan. Products of the production process may be perfect or defective. A portion of the perfect products produced is outsourced, and the remainder can fulfill the customers’ variable demands. The defective products are separated into reworkable and non-reworkable items. Reworkable items can be improved through rework investment planning. The scrapped, non-reworkable items are disposed of through a separate investment. This model aims to save energy. The manufacturing system can realize more profit through minimum air handling and lighting. However, service facilities win customer trust in the event of any needed repairs. Kim [1] considered air handling and lighting costs in their model. Furthermore, outsourcing planning, reworking, and disposal concepts considering environmental benefits and reduced carbon emission strategies have become popular in the competitive market. Accordingly, this study aims to optimize lot size, production rate, selling price, and service level by optimizing the total expected profit.

3.2. Notation

3.2.1. Decision Variables

P	Rate of production
Q	Lot size quantity
p	Selling price of the item
s	Service-related variable

3.2.2. Input Parameters

$T_{\sigma }$	Replenishment cycle time
$T_{1\sigma }$	Production uptime
$T_{2\sigma }$	Reworking time
$T_{3\sigma }$	Delivery time
$H_1$	Maximum level inventory of perfect quality when the in-house      fabrication time ends
$H_2$	Level of items of perfect quality, when the reworking process completes
H	Level of items of perfect quality, when outsourced items are received
K	In-house setup cost
h	Unit cost of holding
$R_c$	Unit cost of reworking
$h_1$	Holding cost per reworked item per year
$D_c$	Unit disposal cost
${\beta }_1$	The connecting variable between $O_{fc}$ and K, where $O_{fc}=(1+{\beta }_1)K$      and $-1<{\beta }_1<0$
${\beta }_2$	The connecting variable between $O_c$ and C, where $O_c=(1+{\beta }_2)C$ and ${\beta }_2>0$
$\varphi$	Overall scrap rate of imperfect items, where $\varphi =[\zeta +(1–\zeta ){\zeta }_1]$
$O_{fc}$	Fixed outsourcing setup (order) cost in a cycle
$O_c$	Unit outsourcing cost
$a_i$	Scaling parameters (i = 1,2,3,4)
$\delta$	Shape parameter related to service-related function
${\eta }_1$	Energy cost ($/unit energy consumption)
${\eta }_1^{{}^{\prime }}$	Cost of carbon emissions due to used energy ($/unit of energy utilization)
${\eta }_2$	Energy cost ($/unit energy utilization)
${\eta }_2^{{}^{\prime }}$	Cost of emissions of carbon due to the utilization of energy      ($/unit energy utilization)
$\sigma$	Fraction lot size (Q) that is outsourced $(0<\sigma <1)$
x	Randomly produced portion of defective items
$\psi$	Rate of imperfect items
${\psi }_1$	Rate of imperfect items after rework
D	Market demand
$P_1$	Reworking rate
$\zeta$	Amount of scrap items
${\zeta }_1$	Number of remanufactured items that fail during reworking and become scrap
$\phi$	Scaling parameter for the service investment function
${\sum }_{j=1}^{\Omega }{\xi }_j$	Total energy used by a fan (horsepower)
${\sum }_{j=1}^{\Omega }{\xi }_j^{{}^{\prime }}$	Energy used by a bulb
${\sum }_{j=1}^{\Omega }{\mu }_j$	Number of fixtures
${\sum }_{j=1}^{\Omega }{\zeta }_j$	Number of bulbs

3.3. Assumptions

The below-mentioned assumptions are considered to derive the proposed model.

• A deterministic manufacturing model with randomly produced defective items is used. Reworking is performed considering brand reputation, customer satisfaction, and market size. Because reworking is possible only with additional costs, only repairable defective items were reworked.
• Generally, the demand for any product can be used as a variable or constant. In this study, variable demand is considered, being dependent on service level and selling price, such that $D=(a_1-a_{2}p-a_3{p}^2)+a_4{s}^{\delta }$
• The variable production cost is considered. The cost of unit production (UPC) is a quadratic function of the variable manufacturing rate. The cost of raw material is fixed, the cost of development is inversely proportional to the variable production rate, and the die/tool cost is directly proportional to the variable production rate. Thus, $UPC=({\alpha }_{1}P+\frac{{\alpha }_2}{P}+{\alpha }_3)$.
• A fixed fraction, $\sigma$, of Q($0<\sigma <1$) is outsourced, considering partial outsourcing. The outsourcing end products are assumed to have the perfect quality, being deliverable after complete reworking. If $\sigma =0$, the system is upgraded to in-house manufacturing. If $\sigma =1$, the system is a purchase system.

4. Model Formulation

The current socio-economic situation renders outsourcing within the inventory system essential to satisfying customer prerequisites. Here, the production rate is considered flexible rather than constant, to cover the customer’s demand. The market’s demand is assumed to vary because of the selling price and the service level. Partial outsourcing is considered to be in balance with the workloads of the production equipment. A fraction $\sigma$ (where $0<\sigma <1$) of lot size Q is outsourced, which must be reworked to attain perfect quality. The planned time of receipt is at the end of the in-house rework process, as shown in Figure 1. In addition, the fixed setup cost, $O_{fc}$, and unit purchase cost, $O_c$, are associated with this outsourcing policy. The remaining portion, $(1-\sigma )Q$ (where $0<\sigma <1$), is fabricated using an in-house EMQ-based system at an annual rate of production of P.

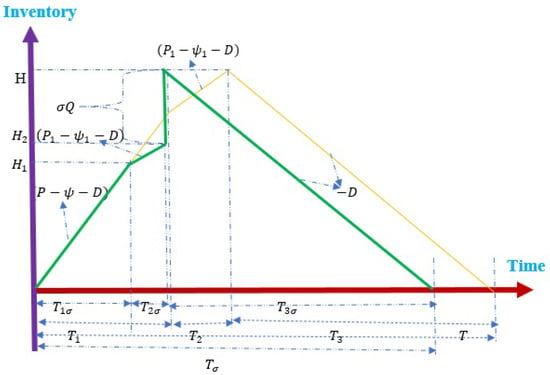
Figure 1. Comparison of status of items of perfect quality in the present system (in green) and in a system with no outsourcing option (in orange) [2] under energy-saving mode.

The manufacturing system produces some defective items x through the randomly generated defective rate $\psi$. Therefore, the total imperfect products are $(1-\sigma )Qx$. Defective products are further inspected and categorized as scrap ($\zeta$) and reworkable ($1-\zeta$) items. Reworking commences in each replenishment cycle when normal fabrication ends at a rate of $P_1$ units per year. A fraction of the remanufactured products ${\zeta }_1$ fails and becomes scrap. Because no shortages are allowed in the proposed model, $P-\psi -D$ must be greater than zero. Figure 2 indicates the progression of the defective products in the proposed model.

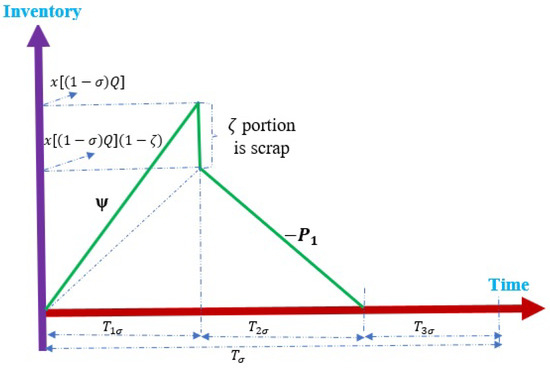
Figure 2. Status of defective products in the proposed model [2] under controllable energy consumption.

From the assumptions of the proposed system, as well as Figure 1 and Figure 2, the following expressions can be directly obtained.

$$\begin{array}{ccc}\hfill T_{1\sigma }& =& \frac{(1-\sigma )Q}{P}=\frac{H_1}{P-\psi -D}\hfill \end{array}$$

(1)

$$\begin{array}{ccc}\hfill T_{2\sigma }& =& \frac{x\left[\right(1-\sigma \left)Q\right](1-\zeta )}{P_1}\hfill \end{array}$$

(2)

$$\begin{array}{ccc}\hfill T_{3\sigma }& =& \frac{H}{D}=\frac{H_2+\sigma Q}{D}\hfill \end{array}$$

(3)

The total time of the replenishment period is the sum of $T_{1\sigma }$, $T_{2\sigma }$, and $T_{3\sigma }$. Therefore, the reduced expression for the total replenishment cycle is given by

$$\begin{array}{c}\hfill T_{\sigma }=T_{1\sigma }+T_{3\sigma }+T_{3\sigma }=\frac{Q(1-x\varphi (1-\sigma \left)\right)}{D}.\end{array}$$

(4)

However, the cycle time is generally determined by dividing the lot size quantity by the market’s demand.

The degree of the available stock of perfect quality at the end of in-house manufacturing is obtained by subtracting the imperfect quantity and demand of items from the rate of production:

$$\begin{array}{c}\hfill H_1=(P-\psi -D)T_{1\sigma }.\end{array}$$

(5)

The degree of the available stock of perfect quality at the end of the reworking process is obtained by the summation of the quantity of on-hand items of perfect quality and the remaining reworked products that cover the market demand.

$$\begin{array}{c}\hfill H_2=H_1+(P_1-{\psi }_1-D)T_{2\sigma }.\end{array}$$

(6)

The maximum degree of the available stock of perfect quality when outsourcing goods are received is obtained by the summation of the quantity of reworked perfect-quality items and outsourcing products.

$$\begin{array}{c}\hfill H=H_2+\sigma Q=D{T}_{3\sigma }\end{array}$$

(7)

The amount of imperfect products at the end of $T_{1\sigma }$ is given by:

$$\begin{array}{c}\hfill D{T}_{1\sigma }=xP{T}_{1\sigma }=x\left[(1-\sigma )Q\right].\end{array}$$

(8)

Furthermore, the total number of fragment products in each cycle is

$$\begin{array}{c}\hfill \zeta \left[xQ(1-\sigma )\right]+{\zeta }_1\left((1-\zeta )\left[xQ\right(1-\sigma \left)\right]\right)=\varphi x\left[(1-\sigma )Q\right],\end{array}$$

(9)

where $\varphi =[\zeta +{\zeta }_1(1-\zeta )]$.

4.1. Air Handling Costs (AC)

Energy wastage is a significant problem in all manufacturing systems. Each manufacturing system requires fans for holding items. The energy consumption of the fans should be reduced to reduce carbon emissions. Furthermore, the reduction of air handling costs reduces the total system cost. The cost of energy incurred from carbon emission and air handling is expressed as

$$\begin{array}{c}\hfill AC=\frac{{\Sigma }_{j=1}^{\Omega }{\xi }_j\times 746\times ({\eta }_1+{\eta }_1^{{}^{\prime }})\times 365}{1000\times \left[\frac{H_1}{2}\left(T_{1\sigma }\right)+\frac{H_1+H_2}{2}\left(T_{2\sigma }\right)+\frac{H}{2}\left(T_{3\sigma }\right)\right]}.\end{array}$$

(10)

4.2. Lighting Cost (LC)

Investment in lighting costs is the main expense for a stock system. Appropriate lighting is essential for stocking goods, reworking, and inspecting. However, the unusual energy consumption is detrimental to the manufacturing system and the environment. Optimizing the number of bulbs used in manufacturing systems is profitable and eco-friendly. The energy cost for lighting and related carbon emissions is given as follows:

$$\begin{array}{c}\hfill LC=\frac{{\Sigma }_{j=1}^{\Omega }{\xi }_j^{{}^{\prime }}\times {\Sigma }_{j=1}^{\Omega }{\mu }_j\times {\Sigma }_{j=1}^{\Omega }{\zeta }_j\times ({\eta }_2+{\eta }_2^{{}^{\prime }})\times 365}{1000\times \left[\frac{H_1}{2}\left(T_{1\sigma }\right)+\frac{H_1+H_2}{2}\left(T_{2\sigma }\right)+\frac{H}{2}\left(T_{3\sigma }\right)\right]}.\end{array}$$

(11)

4.3. Investment for Service (IS)

Increasing product popularity requires investing in services to fulfill the customers’ requirements. High quality of service improves the demand of the market. The proposed model has become highly dependable, with various service ventures for each customer. However, the demand for the items relies upon the availability of service facilities. The accessibility to service facilities improves trust between the customers and the manufacturer. The complete expense of the investment for service is as per the following.

$$\begin{array}{c}\hfill RIS=\phi \frac{s^2}{2}.\end{array}$$

(12)

4.4. Production Cost (PC)

Variable production may be the only direction for development under the current socioeconomic conditions. After outsourcing, the remaining items are fabricated at the annual production rate of P. The flexible production rate always balances the fluctuating demand of the market and meets the shortages. The stock availability of products attracts customers. Additionally, the availability of products improves the reputation. The unit cost of production is a function of the variable production rate, comprising the tool/die cost, development cost, and labor cost. The cost of production is expressed as follows:

$$\begin{array}{c}\hfill PC=({\alpha }_{1}P+\frac{{\alpha }_2}{P}+{\alpha }_3)(1-\sigma )Q.\end{array}$$

(13)

4.5. Outsourcing Cost (OC)

The outsourcing cost is related to the unit production cost through the connecting variable ${\beta }_2$ (${\beta }_2\ge 0$). Variable outsourcing of any production system improves the popularity of the products by compensating for shortages in the overall business process. Further, selling price-dependent demand and service facilities influences variable outsourcing. Therefore, the variable outsourcing cost is

$$\begin{array}{c}\hfill OC=O_c\sigma Q.\end{array}$$

(14)

4.6. Outsourcing Setup Cost (OSC)

Perfect quality is required in all the end products of outsourced items. Otherwise, management can suffer large economic losses and shuttered reputation. Therefore, an outsourcing setup is necessary to produce and hold high-quality items at any location safely. The outsourcing setup has significant effects on inventory management. The outsourcing setup cost is given by

$$\begin{array}{c}\hfill OSC=O_{fc}.\end{array}$$

(15)

4.7. In-House Setup Cost (SC)

By investing once in an in-house setup, the equipment can be prepared for producing different batches of goods over the entire and subsequent cycle time. Setup cost is an elementary cost for starting and maintaining business operations. Depending on the setup, the production process can quickly improve. In this case, an improved setup was required. The total in-house setup cost expression is

$$\begin{array}{c}\hfill SC=K.\end{array}$$

(16)

4.8. Reworking Cost (RC)

There are two solutions to defective production. The first involves incurring development costs to improve the manufacturing process. The second consists of introducing the reworking process. The method of reworking incurs a rework cost (RC), which is expressed as

$$\begin{array}{c}\hfill RC=R_c(1-\zeta )x\left[(1-\sigma )Q\right].\end{array}$$

(17)

4.9. Disposal Cost (DC)

All nonreworkable items are disposed of in an environmentally friendly way. However, this involves a disposal cost. If $D_c$ is the unit disposal cost, then the expression for the disposal cost is expressed as

$$\begin{array}{c}\hfill DC=D_c\varphi x\left[(1-\sigma )Q\right].\end{array}$$

(18)

4.10. Holding Cost for Rework Items (HCR)

Investment in holding cost generates a strong stock that holds all unsold items. This is an important component of the total production cost. In this study, holding costs are incurred for remanufactured, perfect-quality, and imperfect items. Because the remanufactured items are prepared to be sold in the market, it is necessary to invest in the holding cost for reworking. During the time interval $T_{2\sigma }$, only reworking is performed; thus, the holding cost of reworked goods is such that [2]:

$$\begin{array}{c}\hfill HCR=h_1\frac{P_1{T}_{2\sigma }}{2}\left(T_{2\sigma }\right).\end{array}$$

(19)

4.11. Holding Cost for Perfect Products and Defective Items (HCPD)

Perfect-quality items and imperfect products are held separately. The perfect-quality products must be stored in appropriate places, such as storerooms and warehouses, with appropriate environments. The total time interval is separated into three parts, $T_{1\sigma }$, $T_{2\sigma }$, and $T_{3\sigma }$, and the holding cost is calculated separately. In addition, the defective items to be outsourced for reworking should be held at this cost. The expression is given as follows: [2]

$$\begin{array}{c}\hfill HCPD=h\left[\frac{H_1+\psi T_{1\sigma }}{2}\left(T_{1\sigma }\right)+\frac{H_1+H_2}{2}\left(T_{2\sigma }\right)+\frac{H}{2}\left(T_{3\sigma }\right)\right].\end{array}$$

(20)

4.12. Total Cost (TC)

The total relevant per cycle cost, $TC(P,Q,p,s)$, for the proposed hybrid EMQ-based system includes the production cost, variable outsourcing and setup costs, available variable fabrication and setup costs, variable reworking cost, and removal cost for scraps, in addition to the holding costs of the inventory for reworked, perfect-quality, and defective items in the fabrication cycle. Thus, $TC(P,Q,p,s)$ is given as follows:

$$\begin{array}{ccc}\hfill TC& =& (PC+OC+OSC+SC+RC+DC+HCR+HCPD+IS+AC+LC)\hfill \\ & =& ({\alpha }_{1}P+\frac{{\alpha }_2}{P}+{\alpha }_3)(1-\sigma )Q+O_c\sigma Q+O_{fc}+K+R_c(1-\zeta )x\left[(1-\sigma )Q\right]\hfill \\ & +& D_c\varphi x\left[(1-\sigma )Q\right]+h_1\frac{P_1{T}_{2\sigma }}{2}\left(T_{2\sigma }\right)+h\left[\frac{H_1+\psi T_{1\sigma }}{2}\left(T_{1\sigma }\right)+\frac{H_1+H_2}{2}\left(T_{2\sigma }\right)+\frac{H}{2}\left(T_{3\sigma }\right)\right]+\phi \frac{s^2}{2}\hfill \\ & +& \frac{\left[{\Sigma }_{j=1}^{\Omega }{\xi }_j\times 746\times ({\eta }_1+{\eta }_1^{{}^{\prime }})\times 365\right]}{1000\times \left[\frac{H_1}{2}\left(T_{1\sigma }\right)+\frac{H_1+H_2}{2}\left(T_{2\sigma }\right)+\frac{H}{2}\left(T_{3\sigma }\right)\right]}+\frac{\left[{\Sigma }_{j=1}^{\Omega }{\xi }_j^{{}^{\prime }}\times {\Sigma }_{j=1}^{\Omega }{\mu }_j\times {\Sigma }_{j=1}^{\Omega }{\zeta }_j\times ({\eta }_2+{\eta }_2^{{}^{\prime }})\times 365\right]}{1000\times \left[\frac{H_1}{2}\left(T_{1\sigma }\right)+\frac{H_1+H_2}{2}\left(T_{2\sigma }\right)+\frac{H}{2}\left(T_{3\sigma }\right)\right]}.\hfill \end{array}$$

Substituting $O_{fc}$ in $\left[(1+{\beta }_1)K\right]$ and $O_c$ in $\left[(1+{\beta }_2)({\alpha }_{1}P+\frac{{\alpha }_2}{P}+{\alpha }_3)\right]$ in the above equation, we obtain the following:

$$\begin{array}{ccc}\hfill TC& =& ({\alpha }_{1}P+\frac{{\alpha }_2}{P}+{\alpha }_3)(1-\sigma )Q+\left[(1+{\beta }_2)({\alpha }_{1}P+\frac{{\alpha }_2}{P}+{\alpha }_3)\right]\sigma Q+\left[(1+{\beta }_1)K\right]\hfill \\ & +& K+R_c(1-\zeta )x\left[(1-\sigma )Q\right]+D_c\varphi x\left[(1-\sigma )Q\right]+h_1\frac{P_1{T}_{2\sigma }}{2}\left(T_{2\sigma }\right)\hfill \\ & +& h\left[\frac{H_1+\psi T_{1\sigma }}{2}\left(T_{1\sigma }\right)+\frac{H_1+H_2}{2}\left(T_{2\sigma }\right)+\frac{H}{2}\left(T_{3\sigma }\right)\right]+\phi \frac{s^2}{2}\hfill \\ & +& \frac{\left[{\Sigma }_{j=1}^{\Omega }{\xi }_j\times 746\times ({\eta }_1+{\eta }_1^{{}^{\prime }})\times 365\right]}{1000\times \left[\frac{H_1}{2}\left(T_{1\sigma }\right)+\frac{H_1+H_2}{2}\left(T_{2\sigma }\right)+\frac{H}{2}\left(T_{3\sigma }\right)\right]}+\frac{\left[{\Sigma }_{j=1}^{\Omega }{\xi }_j^{{}^{\prime }}\times {\Sigma }_{j=1}^{\Omega }{\mu }_j\times {\Sigma }_{j=1}^{\Omega }{\zeta }_j\times ({\eta }_2+{\eta }_2^{{}^{\prime }})\times 365\right]}{1000\times \left[\frac{H_1}{2}\left(T_{1\sigma }\right)+\frac{H_1+H_2}{2}\left(T_{2\sigma }\right)+\frac{H}{2}\left(T_{3\sigma }\right)\right]}.\hfill \end{array}$$

Using the anticipated values of x to adapt to the defective production rate in the manufacturing process, we replace all relevant variables from Equations (1)–(9) in Equation (20) to derive the expected cost of the system, E[TCU(P, Q, p, s)], as follows:

$$\begin{array}{ccc}\hfill E\left[TCU\right]& =& \frac{E\left[TC\right]}{E\left[T_{\sigma }\right]}=\frac{({\alpha }_{1}P+\frac{{\alpha }_2}{P}+{\alpha }_3)(1-\sigma )D}{(1-(1-\sigma \left)\varphi E\right[x\left]\right)}+\frac{D\left[K+(1+{\beta }_1)K\right]}{Q(1-(1-\sigma \left)\varphi E\right[x\left]\right)}\hfill \\ & +& \frac{D({\alpha }_{1}P+\frac{{\alpha }_2}{P}+{\alpha }_3)\left[\sigma (1+{\beta }_2)\right]}{(1-\varphi E[x\left]\right(1-\sigma \left)\right)}+\frac{D(1-\sigma )E\left[x\right][R_c(1-\zeta )+D_c\varphi ]}{(1-\varphi E[x\left]\right(1-\sigma \left)\right)}\hfill \\ & +& \frac{DQ[h_1(1-\zeta )-h]}{2(1-\varphi E[x\left]\right(1-\sigma \left)\right)}\left[\frac{E{\left[x\right]}^2{(1-\sigma )}^2(1-\zeta )}{P_1}\right]+\phi \frac{D{E}_0{s}^2}{2Q}\hfill \\ & +& \frac{hQ}{2(1-(1-\sigma \left)\varphi E\right[x\left]\right)}[{[1-\varphi E\left[x\right](1-\sigma )]}^2-\frac{(1-\sigma )D}{P}[(1+\sigma )\hfill \\ & -& 2\varphi E\left[x\right](1-\sigma )]+\frac{E\left[x\right](1-\sigma )(1-\zeta )D}{P_1}(\varphi (1-\sigma )E\left[x\right]-2\sigma )]\hfill \\ & +& \frac{\left[{\Sigma }_{j=1}^{\Omega }{\xi }_j\times 746\times ({\eta }_1+{\eta }_1^{{}^{\prime }})\times 365\right]}{1000\times T\times \left[\frac{H_1}{2}\left(T_{1\sigma }\right)+\frac{H_1+H_2}{2}\left(T_{2\sigma }\right)+\frac{H}{2}\left(T_{3\sigma }\right)\right]}+\frac{\left[{\Sigma }_{j=1}^{\Omega }{\xi }_j^{{}^{\prime }}\times {\Sigma }_{j=1}^{\Omega }{\mu }_j\times {\Sigma }_{j=1}^{\Omega }{\zeta }_j\times ({\eta }_2+{\eta }_2^{{}^{\prime }})\times 365\right]}{1000\times T\times \left[\frac{H_1}{2}\left(T_{1\sigma }\right)+\frac{H_1+H_2}{2}\left(T_{2\sigma }\right)+\frac{H}{2}\left(T_{3\sigma }\right)\right]}.\hfill \end{array}$$

Let

$$\begin{array}{c}\hfill E_0=\frac{1}{(1-(1-\sigma \left)\varphi E\right[x\left]\right)};E_1=\frac{E\left[x\right]}{(1-(1-\sigma \left)\varphi E\right[x\left]\right)}.\end{array}$$

Thus,

$$\begin{array}{ccc}\hfill E\left[TCU\right]& =& ({\alpha }_{1}P+\frac{{\alpha }_2}{P}+{\alpha }_3)(1-\sigma )D{E}_0+\frac{\left[D(1+{\beta }_1)K+K\right]E_0}{Q}\hfill \\ & +& D({\alpha }_{1}P+\frac{{\alpha }_2}{P}+{\alpha }_3)\left[\sigma (1+{\beta }_2)\right]E_0+D(1-\sigma )\left[R_c(1-\zeta )+D_c\varphi \right]E_1\hfill \\ & +& \frac{DQ[h_1(1-\zeta )-h]E_0}{2}\left[\frac{E{\left[x\right]}^2{(1-\sigma )}^2(1-\zeta )}{P_1}\right]+\phi \frac{D{E}_0{s}^2}{2Q}\hfill \\ & +& \frac{hQ{E}_0}{2}\left[E_0^{-2}-\frac{(1-\sigma )D}{P}[(1+\sigma )-2\varphi E\left[x\right](1-\sigma )]+\frac{E\left[x\right](1-\sigma )(1-\zeta )D}{P_1}\left(\varphi E\left[x\right](1-\sigma )-2\sigma \right)\right]\hfill \\ & +& \frac{\left[{\Sigma }_{j=1}^{\Omega }{\xi }_j\times 746\times ({\eta }_1+{\eta }_1^{{}^{\prime }})\times 365\right]}{1000\times T\times \left[\frac{H_1}{2}\left(T_{1\sigma }\right)+\frac{H_1+H_2}{2}\left(T_{2\sigma }\right)+\frac{H}{2}\left(T_{3\sigma }\right)\right]}+\frac{\left[{\Sigma }_{j=1}^{\Omega }{\xi }_j^{{}^{\prime }}\times {\Sigma }_{j=1}^{\Omega }{\mu }_j\times {\Sigma }_{j=1}^{\Omega }{\zeta }_j\times ({\eta }_2+{\eta }_2^{{}^{\prime }})\times 365\right]}{1000\times T\times \left[\frac{H_1}{2}\left(T_{1\sigma }\right)+\frac{H_1+H_2}{2}\left(T_{2\sigma }\right)+\frac{H}{2}\left(T_{3\sigma }\right)\right]}.\hfill \end{array}$$

4.13. Total Expected Profit (TEP)

The revenue is obtained in the following manner.

Revenue = $pD=p\left((a_1-a_{2}p-a_3{p}^2)+a_4{s}^{\delta }\right).$

Thus, the TEP is given as follows:

$$\begin{array}{ccc}\hfill TEP& =& TEP(P,Q,p,s)=((a_1-a_{2}p-a_3{p}^2)+a_4{s}^{\delta })p\hfill \\ & -& ((a_1-a_{2}p-a_3{p}^2)+a_4{s}^{\delta })[({\alpha }_{1}P+\frac{{\alpha }_2}{P}+{\alpha }_3)(1-\sigma )E_0\hfill \\ & +& ({\alpha }_{1}P+\frac{{\alpha }_2}{P}+{\alpha }_3)\left(\sigma (1+{\beta }_2)\right)E_0+(1-\sigma )\left(R_c(1-\zeta )+D_c\varphi \right)E_1\hfill \\ & +& \frac{Q[h_1(1-\zeta )-h]E_0}{2}\left(\frac{E{\left[x\right]}^2{(1-\sigma )}^2(1-\zeta )}{P_1}\right)+\frac{\left((1+{\beta }_1)K+K\right)E_0}{Q}\hfill \\ & +& \frac{hQ{E}_0}{2}\{\frac{E_0^{-2}}{D}-\frac{(1-\sigma )}{P}[(1+\sigma )-2\varphi E\left[x\right](1-\sigma )]+\phi \frac{E_0{s}^2}{2Q}\hfill \\ & +& \frac{E\left[x\right](1-\sigma )(1-\zeta )}{P_1}\left(\varphi E\left[x\right](1-\sigma )-2\sigma \right)\left\}\right]\hfill \\ & -& \frac{D{E}_0\left[\left\{{\Sigma }_{j=1}^{\Omega }{\xi }_j\times 746\times ({\eta }_1+{\eta }_1^{{}^{\prime }})\right\}+\left\{{\Sigma }_{j=1}^{\Omega }{\xi }_j^{{}^{\prime }}\times {\Sigma }_{j=1}^{\Omega }{\mu }_j\times {\Sigma }_{j=1}^{\Omega }{\zeta }_j\times ({\eta }_2+{\eta }_2^{{}^{\prime }})\right\}\right]\times 365}{1000\times Q\times \left[\frac{H_1}{2}\left(T_{1\sigma }\right)+\frac{H_1+H_2}{2}\left(T_{2\sigma }\right)+\frac{H}{2}\left(T_{3\sigma }\right)\right]}.\hfill \end{array}$$

5. Solution Methodology

The proposed study obtains the solution by utilizing the classical optimization method. The total profit is optimized with decision variables P, Q, p, and s. A Hessian matrix is used for the concavity of the objective function for the global optimum. Initially, the TEP is partially differentiated, and afterward, the value is likened to zero. In this way, the optimum values of the decision variables are expressed in the equation.

The maximum values of the decision variables are

$$\begin{array}{ccc}\hfill P^{*}& =& \sqrt{\frac{{\Theta }_2}{{\Theta }_1}\left[({\alpha }_1{P}^2-{\alpha }_2)\left\{(1-\sigma )E_0+\sigma (1+{\beta }_2)E_0\right\}+{\Theta }_1^{*}\right]},\hfill \end{array}$$

(21)

$$\begin{array}{ccc}\hfill Q^{*}& =& \sqrt{\frac{\left((1+{\beta }_1)K+K\right)E_0+{\Theta }_3}{{\Theta }_5+{\Theta }_4}},\hfill \end{array}$$

(22)

$$\begin{array}{ccc}\hfill p^{*}& =& \frac{3a_3{p}^2-a_4{s}^{\delta }-a_1-a_2{\Theta }_6}{2a_3{\Theta }_6-2a_2},\hfill \end{array}$$

(23)

$$\begin{array}{ccc}\hfill s^{*}& =& \sqrt{\frac{4a_4\delta (p-{\Theta }_7)}{\phi \times h{\left(E_0\right)}^2\{2s^{-\delta }(a_1-a_{2}p-a_3{p}^2)+a_4\left(\delta +2\right)\}}}.\hfill \end{array}$$

(24)

[See Appendix A for the calculation of first-order derivatives and the expression of ${\Theta }_1,{\Theta }_1^{*}$, ${\Theta }_2,{\Theta }_3,{\Theta }_4,{\Theta }_5,{\Theta }_6,{\Theta }_7.$ See Appendix B for the simplified expressions of different notations.]

Sufficient conditions and global optimality is fulfilled by utilizing the following expression:

Proposition 1.

TEP is convex at $P^{*}$, $Q^{*}$, $p^{*}$, and $s^{*}$, if

$X_1<0$;

$X_1{X}_2>X_5^2$;

$X_1(X_2{X}_3-X_8^2)+X_6(X_5{X}_8-X_6{X}_2)<X_5(X_5{X}_3-X_6{X}_8)$; ${\mathrm{Y}}_1>{\mathrm{Y}}_2$.

See Appendix B for proof.

6. Numerical Experiment

Three numerical examples are given to approve the proposed model. Parametric qualities are taken from [1,2]. Mathematica 11.3.0 is used to obtain the optimum output.

6.1. Example 1

The mathematical model is numerically examined. The following input parametric values are considered to validate the numerical example. $a_1$ = 2201; $a_2$ = 0.1; $a_3$ = 0.001; $a_4$ = 300; ${\alpha }_1$ = 20.11; ${\alpha }_2$ = 100.22; ${\alpha }_3$ = 0.001; $\delta$ = 5.85; $\lambda$ = 11; $\sigma$ = 0.4; $E\left[x\right]$ = 0.6; ${\zeta }_1$ = 0.059; ${\beta }_1$ = −0.4; ${\beta }_2$ = 0.2; $P_1$ = 350 (units/year); d = 40 (units/year); $d_1$ = 50 (units/year); $\zeta$ = 0.3; K = 400 ($/setup); h = 30 ($/unit/unit time); $h_1$ = 40 ($/unit/unit time); $R_c$ = 60 ($/unit); $D_c$ = 20 ($/unit); ${\sum }_{j=1}^{\Omega }{\xi }_j$ = 2.18 (horsepower—hp); ${\eta }_1$ = 0.75 ($/unit energy consumption); ${\eta }_1^{{}^{\prime }}$ = 0.05 ($/unit energy consumption); ${\sum }_{j=1}^{\Omega }{\xi }_j^{{}^{\prime }}$ = 20 (units); ${\eta }_2$ = 0.045 ($/unit energy consumption); ${\eta }_2^{{}^{\prime }}$ = 0.05 ($/unit energy consumption); ${\sum }_{j=1}^{\Omega }{\mu }_j$ = 150; and ${\sum }_{j=1}^{\Omega }{\zeta }_j$ = 150. Table 2 shows the optimum outputs, and Figure 3 and Figure 4 show graphical representations. These figures prove the concavity of the optimum output.

Table 2. Optimum results from Example 1.

Variables	P	Q	p	s	TEP
Optimum	2752.270	884.129	884.54	0.049	962,312.23
results	(units/year)	(units)	($/unit)	($/year)	($/year)

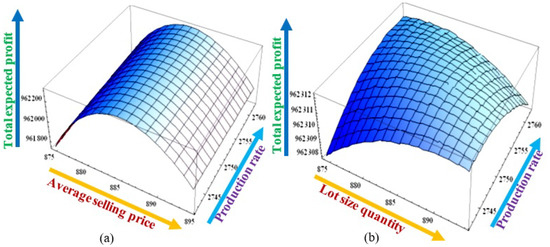
Figure 3. TEP as a function of (a) production rate and average selling price; (b) production rate and lot size quantity.

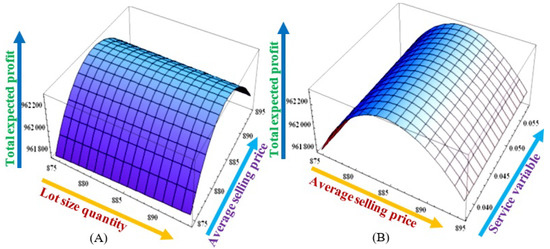
Figure 4. TEP as a function of (A) lot size quantity and average selling price and (B) average selling price and service-related variable.

6.2. Example 2

The below-mentioned values of the parameter were considered to validate the numerical example: $a_1$ = 1671; $a_2$ = 0.01; $a_3$ = 0.001; $a_4$ = 300; ${\alpha }_1$ = 20.11; ${\alpha }_2$ = 2.22; ${\alpha }_3$ = 0.001; $\delta$ = 5.85; $\lambda$ = 11; $\sigma$ = 0.4; $E\left[x\right]$ = 0.6; ${\zeta }_1$ = 0.059; ${\beta }_1$ = −0.4; ${\beta }_2$ = 0.2; $P_1$ = 350 (units/year); d = 40 (units/year); $d_1$ = 50 (units/year); $\zeta$ = 0.3; K = 400 ($/setup); h = 30 ($/unit/unit time); $h_1$ = 40 ($/unit/unit time); $R_c$ = 60 ($/unit); $D_c$ = 20 ($/unit); ${\sum }_{j=1}^{\Omega }{\xi }_j$ = 2.18 (horsepower); ${\eta }_1$ = 0.75 ($/unit energy consumption); ${\eta }_1^{{}^{\prime }}$ = 0.05 ($/unit energy consumption); ${\sum }_{j=1}^{\Omega }{\xi }_j^{{}^{\prime }}$ = 20 (units); ${\eta }_2$ = 0.045 ($/unit energy consumption); ${\eta }_2^{{}^{\prime }}$ = 0.05 ($/unit energy consumption); ${\sum }_{j=1}^{\Omega }{\mu }_j$ = 150; and ${\sum }_{j=1}^{\Omega }{\zeta }_j$ = 150. The optimum outputs are provided in Table 3.

Table 3. Optimum results from Example 2.

Variables	P	Q	p	s	TEP
Optimum	1659.20	810.57	755.29	0.049	791,253.31
results	(units/year)	(units)	($/unit)	($/year)	($/year)

6.3. Example 3

The below-mentioned input values of parameters are considered to validate the numerical example. The values of the input parameters are $a_1$ = 2201; $a_2$ = 1.3; $a_3$ = 0.002; $a_4$ = 300; ${\alpha }_1$ = 90.11; ${\alpha }_2$ = 80.22; ${\alpha }_3$ = 0.005; $\delta$ = 5.85; $\lambda$ = 11; $\sigma$ = 0.4; $E\left[x\right]$ = 0.6; ${\zeta }_1$ = 0.059; ${\beta }_1$ = −0.4; ${\beta }_2$ = 0.2; $P_1$ = 350 (units/year); d = 40 (units/year); $d_1$ = 50 (units/year); $\zeta$ = 0.3; K = 400 ($/setup); h = 30 ($/unit/unit time); $h_1$ = 40 ($/unit/unit time); $R_c$ = 60 ($/unit); $D_c$ = 20 ($/unit); ${\sum }_{j=1}^{\Omega }{\xi }_j$ = 2.18 (horsepower); ${\eta }_1$ = 0.75 ($/unit energy consumption); ${\eta }_1^{{}^{\prime }}$ = 0.05 ($/unit energy consumption); ${\sum }_{j=1}^{\Omega }{\xi }_j^{{}^{\prime }}$ = 20 (units); ${\eta }_2$ = 0.045 ($/unit energy consumption); ${\eta }_2^{{}^{\prime }}$ = 0.05 ($/unit energy consumption); ${\sum }_{j=1}^{\Omega }{\mu }_j$ = 150; and ${\sum }_{j=1}^{\Omega }{\zeta }_j$ = 150. The optimum outputs are provided in Table 4.

Table 4. Optimum results from Example 3.

Variables	P	Q	p	s	TEP
Optimum	1531.19	929.08	492.56	0.060	377,547.97
results	(units/year)	(units)	($/unit)	($/year)	($/year)

6.4. Special Cases

6.4.1. Constant Rate of Production

The proposed model determines a variable production rate and maximizes the TEP. The same parametric values used for Example 1 are considered, except for a fixed production rate of 2700 units per year. However, for the fixed rate of production, the numerically obtained total expected profit and the maximum values of other decision variables indicate that the TEP will decrease. The optimal outputs are shown in Table 5.

Table 5. Optimum outputs for the case of constant production rate.

Variables	Q	p	s	TEP
Optimum	909.38	885.77	0.049	962,297.65
results	(units)	($/unit)	($/year)	($/year)

6.4.2. Without Service Facilities

This example numerically obtains the total expected profit and maximum value of the remaining decision variables in the case of no investments for the service facilities. The results show a decrease in the TEP and an increase in the FPR. The same parametric values are described in the example with no investments toward the service facilities. The optimal outputs are summarized in Table 6.

Table 6. Optimum outputs for the case without service facilities.

Variables	P	Q	p	TEP
Optimum	2752.27	884.13	880.54	962,305.23
Results	(units/year)	(units)	($/unit)	($/year)

6.4.3. Without Outsourcing

The model considers the case of no outsourcing ($\sigma$ = 0) to calculate the nature of the total expected profit. The parametric values, as described in Example 1, are used without outsourcing. The optimal outputs are summarized in Table 7. The results of this numerical example show a decrease in the TEP and an increase in the FPR.

Table 7. Optimum results for the case without outsourcing.

Variables	P	Q	p	s	TEP
Optimum	1490.96	484.40	886.91	0.049	942,198.73
results	(units/year)	(units)	($/unit)	($/year)	($/year)

Figure 5 shows the TEP for different cases.

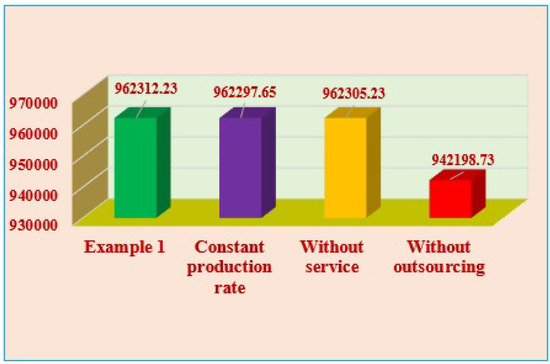
Figure 5. Comparison of the values of TEP obtained for Example 1 and its special cases.

6.5. Discussion

Numerical experiments and their comparison shows that TEP is optimized for the initially proposed model. All the profit is numerically validated utilizing Mathematica 11.3.0 software. Figure 5 indicates the correlation among the TEP of Example 1 of the present model and different special observations. In the special observation of a fixed production rate, the TEP is USD 962,297.65 per year. In the case without a service facility, the TEP is USD 962,305.23 per year. For the case without outsourcing, the TEP is USD 942,198.73 per year. Compared to such special observations, Example 1 gives the maximum TEP of USD 962,312.23 per year.

The present research provides the maximum profit compared to the earlier research concept based on the variable production rate with reworking, service, partial outsourcing, and an energy-saving mode under variable demands. However, partial outsourcing with the reworking of scrap items is introduced here, which are many supportive concepts for the manufacturing industry for examining their information investigation and optimum profit. Furthermore, FPR in smart production systems and controllable energy consumption attract customers. Otherwise, flexible demand helps to influence the vacillating market and is useful for effectively running a business process. Hence, the correlation among the different special cases help in the approval of the initial research concepts.

From the above numerical experiments and their comparison among the previous research articles, it can be concluded that the TEP is at its maximum for the originally proposed model. All cost amounts are numerically expressed using Mathematica 11.3.0 software. Figure 6 shows the comparison among the TEP of Example 1 of the proposed research, Sarkar et al. [57], Chiu et al. [2], and Mridha et al. [25]. In the research article by Sarkar et al. [57], only energy-saving policies are considered, while having a constant production rate and no outsourcing and service facility approaches. Their research concept gives a total profit of USD 895,017.85 per cycle. In addition to the previously stated research, the partial outsourcing concept of Chiu et al. [2] yields a total profit of USD 903,161.04 per cycle, and Mridha et al. [25] yield a total profit of USD 942,198.74 per cycle. Compared to this previous research, the proposed model in Example 1 gives a total profit of USD 962,312.23 per cycle.

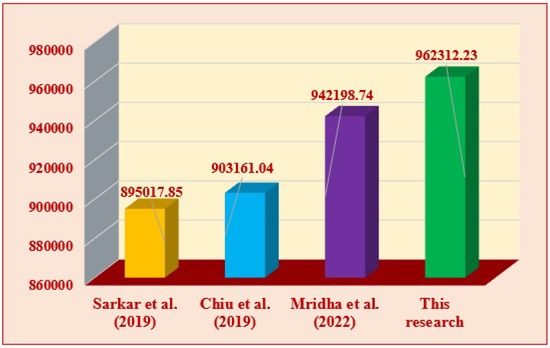
Figure 6. Comparison among the total expected profit of Example 1 and other studies in the literature review [2,25,57].

For the scientific community, the proposed research gives the highest total profit compared to the previous research due to the concept of a variable production rate with a variable demand, a partial outsourcing facility, an energy-saving approach, a service facility, and sustainability. However, partial outsourcing planning with the controllable energy consumption of the SSCM is considered here, which is very helpful for the production management for analyzing their data analysis and maximum profit. Hence, the comparison among the previous research helps in the validation of the original research idea.

7. Sensitivity Analysis

Significant observations regarding cost and scaling parameters are numerically calculated, and the changes in the effects of this parameter are described in Table 8 and Figure 7. Table 8 indicates how scaling parameters and cost influence TEP.

Table 8. Sensitivity analysis of key parameters of Example 1.

Parameters	Changes (%)	TEP (%)	Parameters	Changes (%)	TEP (%)
	−50	+0.06		−50	+0.003
	−25	+0.03		−25	+0.001
K	+25	−0.03	${\eta }_1$	+25	−0.001
	+50	−0.06		+50	−0.003
	−50	+0.06		−50	+0.0001
	−25	+0.03		−25	+0.00007
h	+25	−0.03	${\eta }_1^{{}^{\prime }}$	+25	−0.00007
	+50	−0.06		+50	−0.0001
	−50	+0.30		−50	+0.04
	−25	+0.13		−25	+0.02
$h_1$	+25	−0.13	${\eta }_2$	+25	−0.02
	+50	−0.30		+50	−0.04
	−50	+1.19		−50	+0.05
	−25	+0.60		−25	+0.02
$R_c$	+25	−0.60	${\eta }_2^{{}^{\prime }}$	+25	−0.02
	+50	−1.19		+50	−0.05
	−50	+0.20		−50	+3.34
	−25	+0.10		−25	+1.65
$D_c$	+25	−0.10	$a_2$	+25	−1.65
	+50	−0.20		+50	−3.34

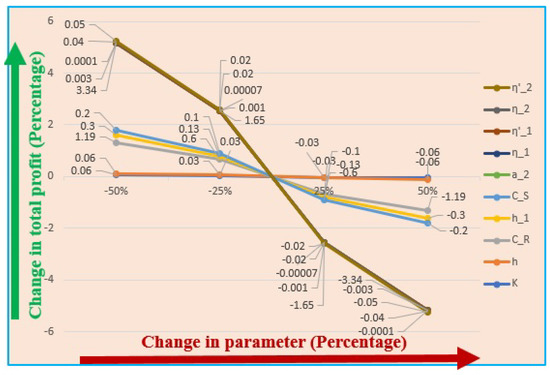
Figure 7. Changes in total profit versus parametric values.

• The most effective cost parameter is the reworking cost. This straightforwardly and undoubtedly influences the TEP. The increasing value of the reworking cost decreases the TEP, as indicated in the sensitivity table.
• The standard part of the demand function has the greatest impact on TEP, as indicated in Table 8. The value of the parameter decreases continuously with TEP. Typically, revenue, as well as TEP, increase as demand increases.
• The cost of carbon emissions has a small impact on the TEP. However, the TEP decreases as it increases.
• The holding cost of reworked items greatly impacts the TEP. Little changes in the cost parameters have huge effects on the TEP. The total expected profit decreases as it increases, and vice versa.
• Table 8 indicates the importance of the disposal cost. The TEP decreases as it increases and vice versa. Defective products should be properly disposed of to realize environmental benefits.
• The scaling parameters and remaining costs, such as setup cost, the in-house holding cost, cost of energy, and carbon emissions due to the use of energy, have a similar effect on TEP, as shown in Table 8.

8. Managerial Insights

The following are recommended to improve the industry.

• Variable production has a greater influence on market demand than constant demand, and variable production rates are very important for the production industry. However, the variable production rate can easily mitigate fluctuating market demand and increase competitiveness. The production manager should vary production for a smooth operation.
• The manager can invest in the in-house setup, by which they can produce more or outsource more products to control the demand of the market as well as consumer loyalty. The industry manager should ensure outsourced products have perfect quality; otherwise, they will face the prospect of losses and a bad reputation.
• All defective products should be separated carefully as reworkable and nonreworkable. Production managers should focus on reworking reworkable defective items to increase profits.
• Service facilities ensure customer trust in the longevity of their products. They also enjoy customer demand and popularity. Hence, the production manager incorporates service facilities into the business.
• Scrapped nonreworkable items are very harmful to the environment. The manager should dispose of the scrap nonreworkable items appropriately, thereby improving the environment by reducing carbon emissions and pollution.
• For any industry, unusual energy consumption increases the system’s total price and increases environmental pollution through carbon emissions. The manager should concentrate on reducing the unnecessary use of bulbs and fans used in production and holding. The model incorporates this concept to diminish the system’s total cost and maximize profit.

9. Conclusions

Currently, the demand of the market exhibits high vacillations. The proposed model showed that considering a variable production rate and service level increased the demand and TEP. The proposed model highlighted the effects of partial outsourcing and energy-saving steps. Furthermore, numerical examples showed that outsourcing and energy-saving efforts with reworking played a fundamental role in consumer loyalty in a sustainable inventory system. The study focused on the environmental benefits of reducing carbon emissions and energy saving. Service facilities, a significant contribution of this model, could increase market demand and improve product reputation. Mathematica 11.3.0 was used to prove global optimality and obtain numerical outputs. The TEP was maximized by optimizing the decision variables.

This study did not consider adjusting the discrete investment to reduce setup costs. This research can be extended by incorporating quality enhancement and setup cost reduction strategies (Woo et al. [59]). Stock-dependent holding costs, a nonlinear type of function under trade-credit, would broaden the applicability of the findings of our study (Cárdenas-Barrón et al. [60]). Future research should consider partial backordering and delay-in-payment. The present research model can be developed through the consideration of variance and variable lead times under a smart manufacturing system (Lyu et al. [61]), a sustainable approach along with a mark-up strategy with green investments (Bachar et al. [16]). Moreover, remanufacturing, warranty strategies, an autonomous inspection policy for detecting defective items, economic policies (Oryani et al. [62]) and O2O retailing strategies may be considered for further research.