Blockchain-Based Distributed Federated Learning in Smart Grid

Abstract

The participation of prosumers in demand-response programs is essential for the success of demand-side management in renewable-powered energy grids. Unfortunately, the engagement is still low due to concerns related to the privacy of their energy data used in the prediction processes. In this paper, we propose a blockchain-based distributed federated learning (FL) technique for energy-demand prediction that combines FL with blockchain to provide data privacy and trust features for energy prosumers. The privacy-sensitive energy data are stored locally at edge prosumer nodes without revealing it to third parties, with only the learned local model weights being shared using a blockchain network. The global federated model is not centralized but distributed and replicated over the blockchain overlay, ensuring the model immutability and provenance of parameter updates. We had proposed smart contracts to deal with the integration of local machine-learning prediction models with the blockchain, defining functions for the model parameters’ scaling and reduction of blockchain overhead. The centralized, local-edge, and blockchain-integrated models are comparatively evaluated for prediction of energy demand 24 h ahead using a multi-layer perceptron model and the monitored energy data of several prosumers. The results show only a slight decrease in prediction accuracy in the case of blockchain-based distributed FL with reliable data privacy support compared with the centralized learning solution.

1. Introduction

The increasing availability of energy storage technologies and the higher penetration of intermittent renewable energy sources at grid edge is pushing the energy grid towards decentralized management scenarios [1]. Among the different management options, demand-side management represents an effective method for unlocking a larger share of energy flexibility at the local level [2]. It leverages the control of electricity consumption of prosumers either by time-scheduling or power-modulating the loads. Examples include control of smart appliances, smart thermostats (for heating purposes), or the charging of electric vehicles (EVs). The success of demand-response (DR) programs depends on consumer engagement and accuracy of energy predictions a day in advance [3].

The load-flexibility schemes require the dispatch of the set-points to a greater number of assets during a broader timeframe, therefore energy prediction many steps in advance is required [4]. The stochastic nature of renewable energy production and the high variation of demand in the case of small prosumers induces a high level of uncertainty in the energy prediction [5]. Most of the state-of-the-art approaches deal with one-step-ahead energy prediction offering good accuracy, but on longer time frames as required in DR, the accuracy drops significantly [6]. With the advent of Internet of Things (IoT) smart-energy metering technology, a significant amount of energy data is becoming available. 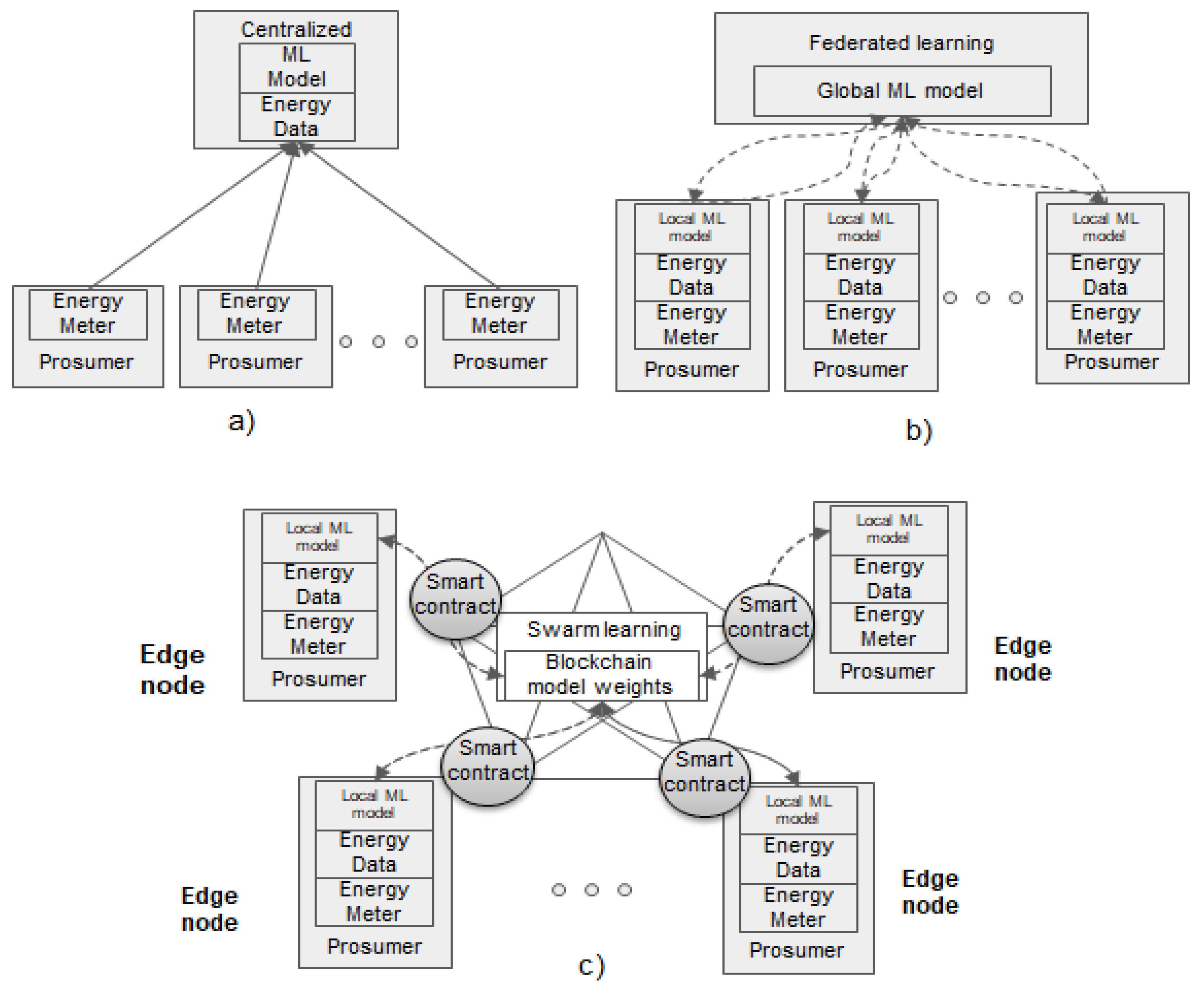Therefore energy utilities are storing energy data centralized in cloud-based systems and use big data and Machine Learning (ML) to predict energy production/consumption values [7]. Different time and energy scales (prosumers, communities, etc.) features are used to reduce the model uncertainty and improve prediction accuracy. In such approaches, ML models are trained with fine-grained data collected from prosumers to learn a prediction model. The models are then used to predict the energy demand and the signals for adjusting the energy demand during the implementation of the programs (see Figure 1a) [8,9,10].

To improve the accuracy of the predictions, energy features are used together with non-energy-related vectors and contextual features such as behavioral or social features [11]. Even though the accuracy in this centralized cloud-based case is better, it raises privacy concerns. Data privacy is one of the main obstacles to consumers’ engagement in DR programs [12]. In fact, due to privacy concerns, the adoption of smart meters in many European countries was delayed and the engagement of individual costumers and collectively operating households in DR programs is limited [13]. Even though a lot of work was put into privacy-preserving energy metering it is still an open research issue [14,15,16]. Efforts are made to provide trusted bidirectional connections among prosumers and utilities, but centralization is a key issue that makes data privacy sensitive [17]. In Europe, privacy-sensitive data need to be stored securely, following the current General Data Protection Regulation (GDPR) rules, thus privacy-based ML plays a major role in energy prediction [18]. The prediction process can be decentralized by employing privacy-preserving federated-learning (FL) infrastructures (see Figure 1b) [19]. The data are stored at the edge node in the prosumer premises reinforcing the privacy features and preventing potential data leakage. Thus, the local ML models are trained on prosumers’ sites and the global model is updated using the edge nodes information, but in this case, the model parameters are transferred and not the sensitive data [20,21]. The distribution of the model-learning process closer to the edge decreases latency and bandwidth costs as the energy data are stored locally and not transferred over the network, but the tradeoff is the decrease in prediction model accuracy [22].

In this context, distributed ledger technologies [23] can bring benefits in reinforcing the trust in DR program management due to the democratization and transparency features they provide [24]. For example, data provenance allows tracking the changes at any time by simply iterating through the blocks of the chain [25]. The immutability assures that any information stored in the chain remains unchanged and cannot be tampered with by a third party [26,27]. They are highly desirable features in the case of distributed ML. A public blockchain network can store the global model in FL cases promoting transparency and trust among prosumers [28]. As it is impossible to modify the data stored, it reduces the chances of fraud. The transactions on the blockchain are public and accessible, therefore, the transactions to update the global federated model are transparent and traceable [29].

A few approaches in the state of the art are joining FL models with blockchain technology [30,31,32,33,34] (see Figure 1c) to ensure data privacy and trust features and none to our knowledge on prosumers’ energy. In our case, the ML prediction models are trained at the prosumers’ using local energy-demand data, and the blockchain will store and update the global energy prediction model. We use a public blockchain as it does not limit the joining of new prosumers and define smart contracts to manage the federated model update, the model parameters’ replication, and dissemination. As result, the prosumers are more engaged because the concerns about energy data ownership, confidentiality, and privacy are decreased due to public blockchain integration and enabling model traceability for any state change.

In this paper we provide the following contributions:

• Blockchain-based distributed FL for the energy domain to support the privacy-preserving prediction of prosumers’ energy demand. The global model parameters are immutably stored and shared using blockchain network overlay.
• Smart contracts to update the global model parameters considering the challenges of integrating regression-based energy prediction, such as scaling the model parameters with prosumers’ size and blockchain transactional overhead.
• Comparative evaluation of prosumers’ energy-demand prediction using multi-layer perceptron (MLP) model distribution in three cases: centralized, local edge, and blockchain FL.

The rest of the paper is structured as follows. Section 2 presents the state-of-the-art approaches on distributed ML models for the energy domain. Section 3 presents the blockchain-based distributed FL model formalization for privacy-preserving energy-demand prediction and smart contracts for blockchain integration. Section 4 presents comparative energy-demand prediction results on three cases considering a MLP model and integration of prosumers’ energy data from meters. Section 5 presents a discussion of the approach, and Section 6 gives the conclusions and future work.

2. Related Work

Distributed ML techniques aim to add privacy-preserving features to the learning process [35,36]. FL solutions are only partially addressing the privacy and security issues. The centralization of the learned models makes them vulnerable to malicious attacks and may constitute a single point of failure [37]. FL aims to address the issues of security, trust, and privacy leakage, relevant in the smart energy grid scenarios, by combining blockchain technology [23] with FL and distributed optimization [33]. In the remainder of this section, we analyze the state-of-the-art FL solutions classified according to the distributed optimization algorithms used, and highlight the security issues that need to be addressed in smart energy grids. Then the few approaches on blockchain-based distributed FL concept are presented, showing their strengths concerning the FL models.

One of the first FL models was presented by Zinkevich et al., who propose a decentralized ML model, referred to as “one-shot parameter averaging”, based on parallel stochastic gradient descent (SGD) [38]. The proposed architecture trained local models using the SGD optimizer, and the central model was created using a single final communication round, which is suboptimal. Important aspects, such as the data distribution between nodes and applying one-shot parameter averaging on different ML architectures other than support vector machines (SVM), were not considered. Boyd et al. propose the alternating direction method of multipliers that is a form of distributed convex optimization tested on the lasso, sparse logistic regression, basis pursuit, covariance selection, and SVM [39]. The results showed that the convergence can be slow, due to the number of communication rounds. Shamir et al. [40] proposed the Distributed Approximate Newton (DANE) approach that considers the similarity among problems on different machines, converging in fewer communication rounds. Konečný et al. describe the concept of FL where a centralized model is trained, using multiple local datasets contained in local nodes, without exchanging data samples [41]. The solution was optimizing the communication rounds and the convergence time when considering the trade-off between accuracy and data privacy with good results. The primary methods to train FL models were analyzed by McMahan et al. [42]: Federated Stochastic Gradient Descent (FedSGD) that averages local nodes’ gradients at every step in the learning phase, and Federated Averaging (FedAvg), which averages the weights when all clients have finished computing their local models. Zhu et al. [43] showed that the accuracy can be heavily impacted if the training data are not independent and identically distributed (non-IID) among local nodes. Several solutions were proposed leveraging minimal data distribution between nodes, which can be a source of privacy leakage. In articles [44,45], a set of enhancements to the FedAvg and FedSGD algorithms are proposed. They tackle the problems of communication among devices, the correlation between data heterogeneity, and the convergence rate of the learning process. They show that even if it is more precise theoretically, the Federated Distributed Approximate NEwton (FedDANE) algorithm is outperformed in practice by FedProx. FedProx improves the convergence of the FedAvg algorithm by adding a proximal term for approximation as shown by Li et al. [46]. The impact of network communication and latency over a FL setup in a wireless environment is analyzed by Yang et al. in [47], the authors formulating an optimization problem for energy efficiency under latency constraints. Uddin et al. propose a novel FL approach that considers mutual information and proves the convergence of the solution on clinical datasets [48]. The authors refined their solution by introducing a Lagrangian-based loss function and applying the information bottleneck principle in [49].

FL has high applicability in smart energy grids’ management scenarios. The FL solutions can address issues related to data privacy and security [50]. Traditional architectures collect user data in centralized databases for further processing, but this imposes data privacy concerns and security issues. FL approaches are adapted to smart grid use cases such as energy forecasting and prosumer pattern classification by considering distributed deployment of smart meters at prosumer locations. A thorough review of applications for FL is done by Li et al. [44], identifying six directions of industry applications. Su et al. [51] investigate the applications of decentralized deep-learning technologies in smart grids and Husnoo et al. [52] discuss a FL framework for prosumers’ energy forecasting. It uses the Long Short-Term Memory (LSTM) neural network and the FedAvg algorithm [42]. Singh et al. [53] propose a serverless FL design for smart grids with good accuracy results on datasets. LSTM was used as the central model in an FL approach by Taïk et al. [54]. Without prosumer clustering, the accuracy was not good enough even after multiple communication rounds. FL was evaluated by Gholizadeh et al. [55], who propose a new clustering method to reduce the convergence time. Su et al. [56] propose a secure FL scheme enabling prosumers in a smart grid to share data considering non-IID effects. The method can train a two-layer deep reinforcement learning algorithm, showing promising results and communication efficiency. Wang et al. [57] propose using an FL approach to bridge data between smart meters and the social characteristics of prosumers. Saputra et al. [58] apply FL design for predicting the energy demand of EVs. The solution allows the charging station not to share data with the service provider, decreasing communication overhead, and improving prediction accuracy. In [59] Liu et al., an FL framework is proposed for energy grids to learn power consumption patterns and preserve power data security. The approach combines horizontal with vertical FL.

As the learning model and data distribution are also susceptible to attacks, a trade-off needs to be made between security and decentralization. Usynin et al. [60] tackle the model inversion attacks, where an attacker reverse-engineers the federated model and then discloses the training data. They propose techniques based on gradient methods to expose image data for attackers, showing how these attacks can be mitigated. Song et al. [61] describe an efficient privacy-preserving data aggregation model that joins the individual weights without revealing their models, thus decreasing the risk of data leaks. The algorithm is highly resilient in case of communication faults, being able to compute a reasonable model even in the case of when a high number of users disconnect. Ganjoo et al. [62] investigate the poisoning attacks on a FL design targeting to preserve data privacy, and Liu et al. [59] used encryption to preserve privacy in a FL system. Ma et al. [63] propose a solution to deal with Byzantine attacks in FL frameworks. They use a privacy-preserving gradient aggregation mechanism that is efficient, secured, and based on a two-party calculation protocol. Other techniques for privacy and security are based on multi-party computation and the additive homomorphic property of Paillier [64]. Key exchanges for authentication and data encryption are applied by Zhao et al. [65] in the context of the social Internet of vehicles. Finally, a thorough review of security and privacy problems in the context of FL is presented by Hou et al. [66], where the authors investigate model extraction and poisoning attacks as well as a solution for incentivizing the participants for commenting their resources and local results.

Table 1. FL relevance for smart grid.

Issues in Smart Grid Scenarios		FL Solutions
Data privacy preservation and security	Non-blockchain	Distributed perturbation [35], sequential learning [36], model inversion [60], data aggregation mechanism [61], poisoning attacks mitigation [37,62], Byzantine-robust FL [63], homomorphic encryption [64], collaborative authentication protocol [65]
	Blockchain enabled	Incentivization and avoidance of model poisoning [66], blockchain for data sharing and serverless computing [53], swarm learning [30]
Optimization of communication costs, devices, and data heterogeneity		DANE [40], FedDANE [45], Structured and sketched updates [41], FedAvg [42], iterative algorithms [47], FedProx [46]
Analytics and energy efficiency		AI of things [51], load forecasting [52,53,54], energy data sharing [53,56,58], prosumer profiling [57], learning consumption patterns [59]

summarizes the state of the art directions involving FL.

In this context, we aim to combine FL with blockchain to tackle issues such as model centralization, trust, and data privacy. Very few approaches were found in the literature. The concept was introduced by Warnat-Herresthal et al. [30], who propose a system design such as FL, which eliminates the need for the central coordinator. Instead, operations on the central model, such as averaging and distributing weights, are held directly on a decentralized smart contract. This approach increases security because each client can monitor the integrity and the changes made in the central model. Experimental results were conducted on IID clinical data used to classify diseases.

Analyzing the existing state of the art, few relevant literature approaches that tackle data privacy, learning-model centralization, and immutability in the context of ML-based prediction of energy demand and applications of FL in smart grid scenarios, are found. In this paper, we address the identified knowledge gap in the literature by proposing a distributed FL technique for energy-demand prediction that combines FL with blockchain to assure data privacy for individual energy prosumers. The privacy-sensitive energy data are stored locally at edge prosumer nodes without the need to reveal it to third parties, and only the learned local model weight is pushed to the blockchain. The global model is not centralized but distributed and replicated over the blockchain network thus being immutable and offering obfuscation and an anonymization method for the models, making it difficult for inversion attacks to reveal prosumer behavior.

3. Smart Contracts for Federated Learning

The proposed solution aims to avoid the privacy linkage in the case of energy data by keeping them on the prosumer nodes. The data of a prosumer are used to train a local ML model, and the global model is stored in a blockchain network and updated by the prosumers using smart contracts.

The prosumer ML model will learn a function ${\theta }_w:R^p\to R,$ that depends on a vector of weights $w\in R^p$. This model ${\theta }_w$ will be trained with $n$ datapoint pairs of the form $\left(x_i,y_i\right)$, where $x_i\in R^p$ are the timestamp-driven features and $y_i\in R$ are the energy values sampled by the meters. In the FL approach, $k$ nodes are used to train the global model function ${\theta }_w$, and keep the $n$ energy datapoints distributed in $k$ sets, each stored by an edge node and with a cardinality $n_i<n,i\in \left\{1..k\right\}$, such that ${\displaystyle \sum }_{i=1}^k{n}_i=n$ (see Figure 2).

The models are trained locally by each of the $k$ edge nodes associated with the energy prosumers, obtaining a set of parameter vectors $w_i$ for each learned function ${\theta }_{w_i}$ that minimizes a prediction error function:

$$f_w:R\to R, f_w\left(x_i,y_i\right)=Error\left(y_i,{\theta }_w\left(x_i\right)\right)$$

(1)

Each edge node $i$ solves an optimization problem that computes the best weight vector $w_i$ that minimizes the local prediction error on the local data sampled:

$$Edge node i:determine w_i to \underset{w_i}{min}\frac{1}{n_i}{\displaystyle \sum }_{j=1}^{n_i}{f}_{w_i}\left(x_i,y_i\right)$$

(2)

At central node level the goal is to determine a weight vector $w_F$ by defining a federated model function ${\theta }_{w_F}$ and considering the local model parameters:

$$determine w_F=\phi \left(w_1,w_2,\dots w_k\right) to \underset{w_F}{\mathit{min}}\frac{1}{n}{\displaystyle \sum }_{j=1}^n{f}_{w_F}\left(x_i,y_i\right)$$

(3)

The weight vector $w_F$ of the federated model is computed iteratively based on the edge models’ weights combined by a function $\phi$. There are two main solutions that can be used to update the federated weight vector. The first one is to use the SGD algorithm that updates the global model weights based on a weighted average of the edge nodes vectors of weights [38]. The second approach uses the DANE method that updates the federated weight based on the average gradient of the local weights [40,41]. It uses several stages in which the weight vector is updated with the gradient computed as the average of the gradients from the edge models.

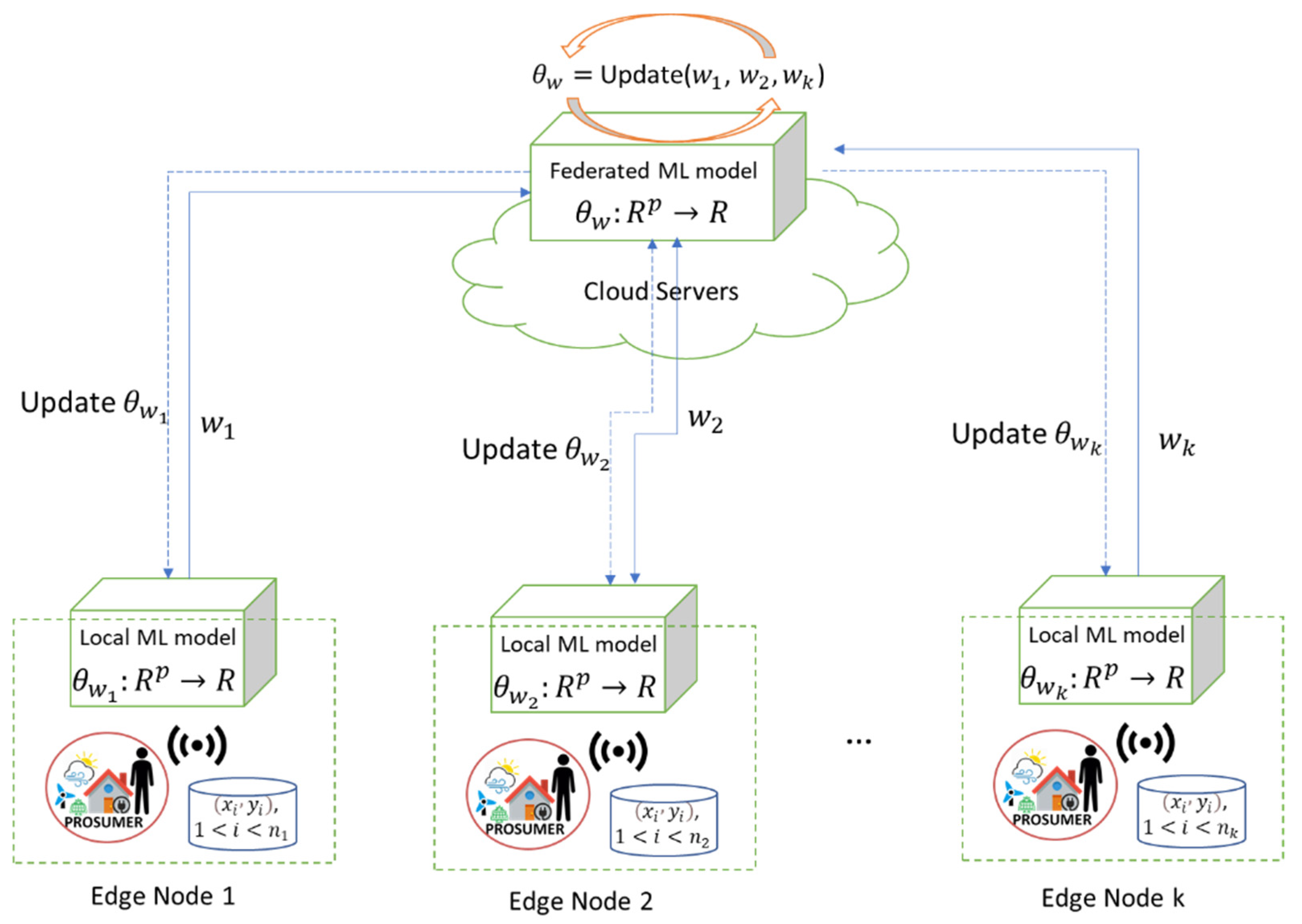
The federated ML optimization considers the acquisition of energy data by the $k$ edge nodes associated with prosumers (see Figure 3). An initial weight vector is computed to initialize the global model which is distributed to the edge prosumer nodes. Then, a loop of $s$ iterations gradually improve the federated weight vector $w_F$ (lines 4–9). Each iteration collects the local gradients, computes the global gradient, updates the federated weights, and distributes the weight vector $w_F^s$ to the edge nodes, to start a new local model training process. Finally, the algorithm returns the weight vector corresponding to the federated model learned after the iterations.

Our solution considers the federated approach for the energy prediction of prosumers and propose the adoption of blockchain and smart contracts to store and update the global ML model (see Figure 4). We define smart contracts to publish the local energy prediction models weight vectors on the blockchain network. Then we leverage on the blockchain to store the model in a tamper-proof manner and to replicate and disseminate the local models’ weight to all nodes participating to the network overlay.

Smart contracts are deployed on the blockchain network overlay to manage the weights vector of the global ML model that is shared and used for energy-demand prediction. The contracts contain methods to update the global model weights and their addresses are known by all nodes participating in the learning process. The main functions implemented in the smart contract are correlated to the FL steps (see

Table 2. FL concepts mapped to smart contract.

Decentralized Learning Steps	Smart Contract
Weight vector of global model	Int256 [] globalModelWeights
Initialize the global model	function setInitialWeights (int256[] memory weights)
Retrieve the initial weights of the global model	function getInitialWeights () public view returns (int256[] memory)
Push the edge nodes training results	function postLocalWeights(int256[] memory weights)
Update the global model weights using the local models	function updateGlobalModel () public view returns (int256[] memory)

for the mapping). The get functions are declared as a view because they do not alter the contract state, which means that participants will not pay gas when querying the central weights.

Figure 5 shows the smart contract function used to update the global mode weights. Due to the limitations of mapping, we used both accounts and accountPresent to keep track of edge prosumer participants and their addresses. The globalModelWeights is updated by averaging the values in localModelWeights, which is the mapping that stores weights from edge accounts. When updateGlobalModel is called, the globalModelWeights is reinitialized, then a loop goes through all the prosumer accounts, adds each local weight vector to the corresponding position in globalModelWeights, and finally, the global weights are divided by the total number of edge nodes participants, to determine the average.

The smart contract functions (defined in Table 2) are invoked by the edge nodes corresponding to the smart grid prosumers. The pseudocode of the edge prosumer nodes function for local ML model updating is shown in Figure 6. Because the algorithm runs in interaction rounds (i.e., either local or global model’s update) the edge nodes need to be synchronized to avoid inconsistent models’ update in which the local model weights are updated at around and are posted on blockchain for global model update only later at round. We use a timestamp-based synchronization between the edge nodes, defining a set of milestones to delimit training rounds. Each model training round will be delimited by time intervals to get the global model weights from the blockchain and to post the local model weights to the blockchain. Only local weights posted by edge nodes in these intervals are considered, otherwise are discarded.

The algorithm starts by Initializing Its local time with Universal Time Coordinated (UTC) and performing a milestone synchronization with the other edge prosumer nodes involved in training (lines 5–6). The node initializes the local model with the weights taken from the blockchain then it starts a loop of iterations to train the model with local data (lines 8–12). The local weights vector $w_L^s$ is sent to the blockchain using the smart contract methods when the local time reaches the milestone set for the post. When the local time reaches the get milestone, a new weight vector is taken from the blockchain using the Smart Contract to initialize the local model for the next iteration (lines 10–11).

4. Evaluation Results

To test the blockchain-based energy-demand prediction, the infrastructure presented by us in [67] was used to acquire the readings of prosumers’ energy consumption. In short each prosumer has installed power meters featuring the International Electrotechnical Commission (IEC) 62056 protocol and power quality analyzer that uses Hypertext Transfer Protocol (HTTP) to transfer energy data. The meters send data each five seconds using MQ Telemetry Transport (MQTT) messaging service and the data are stored in a local data model.

We have aggregated the energy measurements taken over five months at intervals of 15 min. The objective is to predict the next day’s demand for each prosumer using one value each hour, thus 24 energy values. As the prosumers can be of very different energy scales, a clustering algorithm is used to select those with a similar scale of energy consumption (i.e., concerning the maximum energy demand). The energy data are non-IID on the local edge nodes associated with the monitored prosumers. Also, they may have different consumption patterns. Thus, each local model was trained on local shuffled data samples received from energy meters for the first four months, with a validation split of 10%, and was tested on one month’s data.

The local prediction model on each prosumer edge node is a fully connected MLP, which uses a feedforward neural network. We trained and tested multiple MLP configurations to determine the meta-parameters (i.e., the vector of weights) to be used in the learning process. The number of epochs in each iteration was set to one because FedAvg is used to average the weights determined by local models after each epoch. The optimal number of averaging iterations was determined and fine-tuned during evaluation. Other tuned meta-parameters were the number of hidden layers, neurons, and the learning rate. In our feature selection process, we have found that the most relevant input features, besides energy consumption values, were linked to the date and time of the values.

The MLP model used for energy prediction features one hidden layer with 30 neurons, rectified linear unit (ReLu) activation function for the hidden layer, and linear activation for the output layer (see

Table 3. MLP configuration used for local energy prediction models.

MLP Configuration
Number of input neurons	26
Number of output neurons	24
Number of hidden layers	1
Number of neurons in hidden layer	30
Activation function at hidden layer	ReLu
Activation function at output layer	Linear
Optimizer	SGD
Loss function	MSE
Kernel initializer	He uniform
Batch size	32

). We have used the stochastic gradient descent with mean squared error (MSE) as loss function, a He uniform-variance scaling initializer, and a batch size of 32. As input for the model, the best results were obtained for 26 input features, out of which 24 were the hourly energy data of a day in the past, 1 is the day of the week, and 1 Boolean to indicate whether the forecasted day is on a weekend. Before each iteration, we applied a data normalization, using a min-max scaler to bring the data in the interval [−1, 1], before feeding them into the network. After each prediction, the inverse scaling function is used to de-normalize the results.

The smart contracts for blockchain integration and global ML model update were implemented using Solidity and deployed in a private Ethereum blockchain [68]. Ethereum was selected for the good support for implementing the smart contracts in a Turing complete language such as Solidity and for customizing chain specifications in terms of consensus algorithm, prefilled accounts, block genesis configuration, gas, etc.

The local models for the edge prosumer nodes were built using the Keras library [69]. The interaction between the edge prosumer nodes and the smart contract was enabled by a blockchain Application Programmable Interface (API), developed in NodeJS, using the web3 library [70]. The API creates for each edge prosumer node a secured blockchain account and enables function calls through HTTP GET and POST requests. In this way in each iteration, the edge prosumer nodes receive the central model weights from the blockchain, train the model and then post the newly trained local weights.

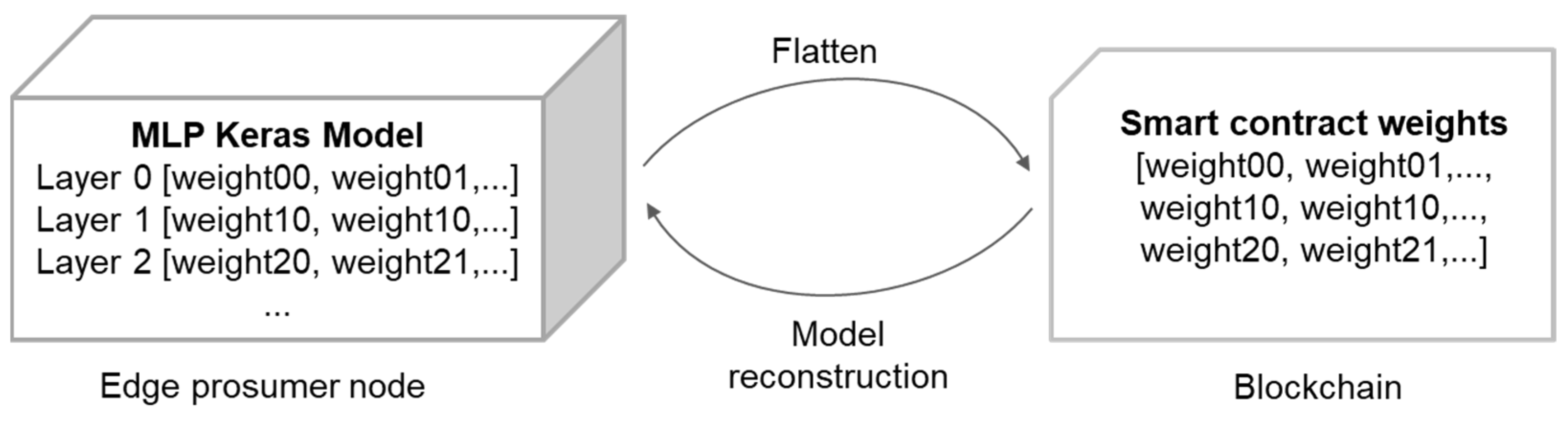
The smart contracts feature two state variables: an array representing the initial global model weights and a map to store the local weights for each edge prosumer node. To reduce the blockchain overhead, we used only one-dimensional arrays to store the weights of a local prediction model and gave the responsibility to update the array to the edge prosumer node. To store a weights’ array in the smart contract, the edge prosumer node must flatten the local model weights’ array before posting it. To reconstruct a model from a weights’ array received from the smart contract, the edge prosumer device must reshape the 1D array to the original Keras model (see Figure 7).

Three different prosumers’ energy-demand prediction test cases were set up using IID data and comparatively evaluated: centralized learning, edge learning, and distributed FL.

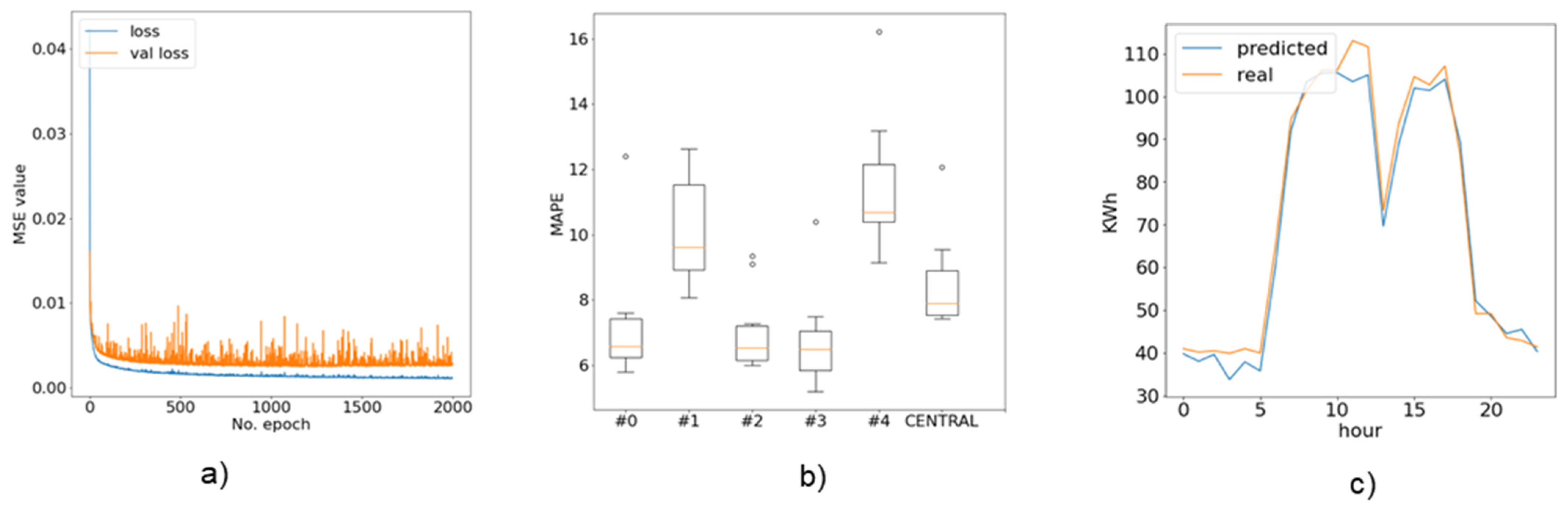
In centralized learning case, the edge prosumer nodes data were aggregated, and a single global model was trained using the entire dataset. After the tuning process, we found that a single hidden layer with 35 neurons, an SGD optimizer with a 0.9 learning rate, a batch size of 128 trained for 1100 epochs achieve the best results (see Figure 8). As expected, this learning approach obtains the highest accuracy (i.e., mean absolute percentage error—MAPE 9.51) but features-limited privacy-preserving support due to data movement and centralization features.

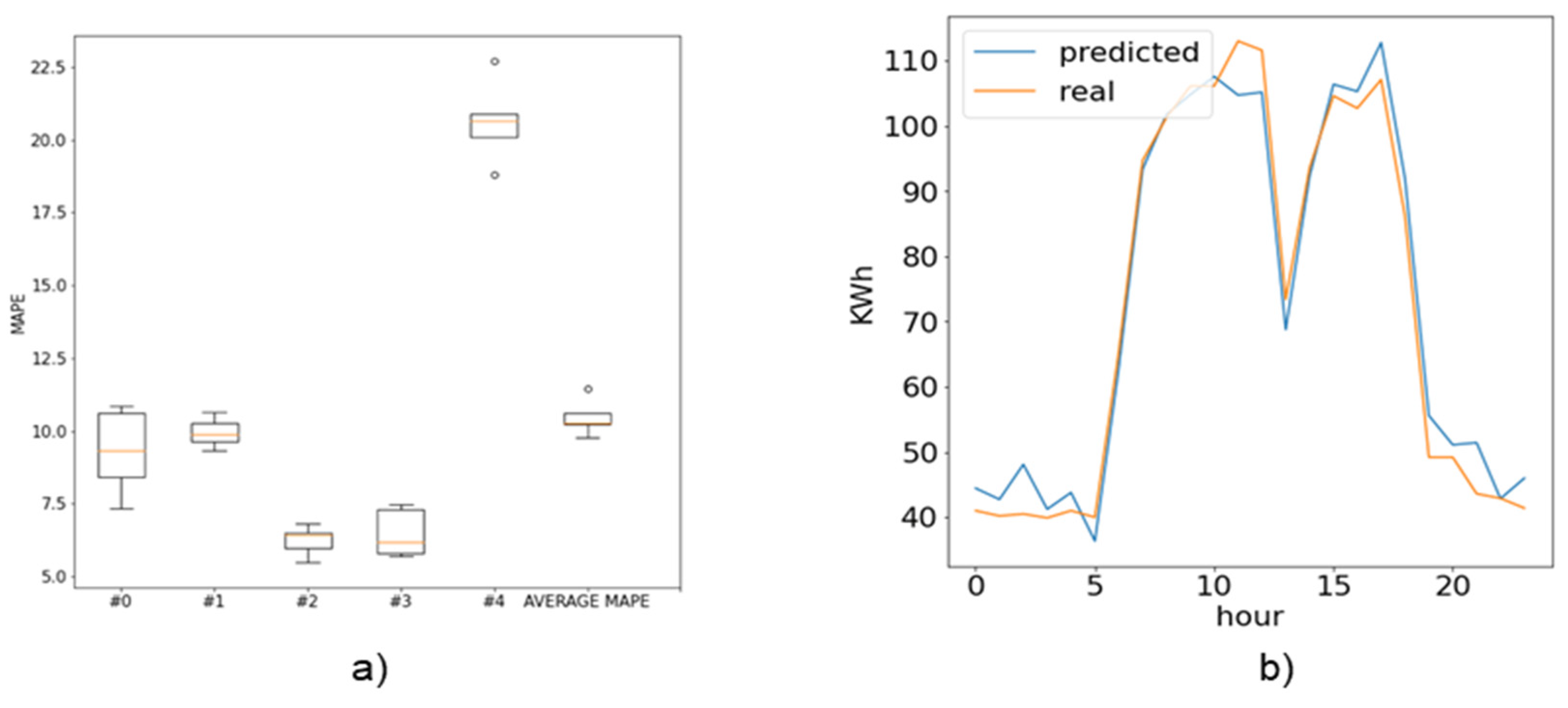
In the local edge approach, each edge prosumer node trains its model using only the local energy data. No exchange of model parameters or energy data is done with the other nodes. Each local node is responsible for storing its data and tuning the local model. Finally, we plotted accuracy for each prosumer node and determined the average MAPE to illustrate the aggregated accuracy results. In Figure 9 we can see that, even though the average MAPE is 10.82, some prosumers (e.g., prosumer #4) obtain high errors, due to low variance in local datasets.

In the blockchain-based distributed FL case, we tested two configurations: one with IID data, and one without IID data. For the IID configuration, the energy data were distributed randomly among edge prosumer nodes which facilitates the convergence of learning process (see Figure 10). To find the number of iterations for the learning model, the validation and train loss were compared during a long training session. In this case, the local energy data at the edge contained samples from every prosumer part of the test case. The accuracy of the prediction process is better but did not exceed the accuracy of the centralized approach. Nevertheless, such data distribution improves the convergence of the distributed FL prediction process.

In the distributed FL configuration with non-IID data, since only the data distribution is different from our model, we considered the setup and features as in the previous case.

The results show that the non-IID blockchain-based distributed FL model has slightly less accuracy (see Figure 11). But even so, the average MAPE is 14.35, which is good for the implementation of DR programs and meets the privacy-preserving need for prosumers’ energy data. Also, some prosumers can benefit from using such an approach as their MAPE value is better. For example, prosumer #4 had the worst MAPE value in the local edge test case but the accuracy was improved when using the proposed learning solution. This was caused by the limited variance in its local test case data, compared to a broader knowledge base received from the distributed learning blockchain model.

The performance of each evaluation case was determined using the mean absolute percentage error against the test energy data set (see

Table 4. Average MAPE results for prosumers’ test cases considered.

Prosumer	Centralized Learning	Local Learning	Blockchain-Based Distributed FL
			Non-IID	IID
0	7.58	7.96	10.80	8.83
1	12.03	9.95	16.22	11.74
2	7.15	7.63	13.97	7.66
3	7.43	6.70	11.08	8.27
4	13.37	21.85	19.69	17.02

). Even though individual tuning was done for each scenario, we can observe that our learning solution achieves comparable results with state-of-the-art centralized and local trained models, without violating the privacy laws.

As expected, the centralized model had the best performance, and locally trained models underperformed due to lack of data variability, the average minimum and maximum MAPE values being reported in

Table 5. Accuracy of the prediction process.

Test Case		MAPE
		Min	Average	Max
Blockchain-based federated learning	Non-IID	10.80	14.35	19.69
	IID	7.66	10.62	17.02
Centralized		7.15	9.51	13.37
Local		6.70	10.82	21.85

.

5. Discussion

Nowadays implementations of management solutions for local energy systems lack the human and social aspects such as the role of households, privacy, and local community sustainability goals. The emerging energy system paradigm shift towards more distributed generation is driven mainly by techno-economic progress and ambitious energy policy targets. They miss the engagement of prosumers and community members. With the proliferation of energy services and energy grid digitization, prosumers struggle to maintain the necessary level of control or awareness over the propagation of their sensitive data along different stakeholders involved in DR programs. Prosumers are losing control of energy data and they are not sure that the data are properly managed by utility companies. This constitutes a barrier to their involvement in energy programs. The blockchain-based distributed FL solution has the potential of mitigating their concerns as the energy data are kept on prosumer edge nodes, and only models’ parameters are being transferred. Blockchain offers a good and fully automated solution for implementing GDPR compliant data accountability and provenance tracking of local ML parameters complementing the FL architectures.

However, joining FL and blockchain brings some limitations and open challenges that need further investigation. One such limitation is the computational cost of blockchain integration that depends on the blockchain platform and type of setup used. The global model complexity is determined by factors such as the dimension of the weight vectors received from the edge prosumer nodes or the number of edge nodes. Thus, it is infeasible to use public blockchain deployments in conjunction with a complex ML model unless methods for the partial consideration of parameters in the global model or in a compressed manner are being integrated [33]. In this case, part of the model can remain personal for each prosumer and the parameters of the model in the blockchain can be eliminated [71].

The cost of gas for storing the global model and the computational cost for executing the smart contracts can be very high. Also, a significant element to be considered is the learning convergence time, which defines the number of communication rounds between edge prosumer devices and the smart contracts, and this could also significantly increase the blockchain cost on public deployments. Therefore, the blockchain-based distributed FL design is more suitable for private blockchain or networks with low computational costs such as platforms using Proof of Stake for validation.

Another limitation that may affect the accuracy of the blockchain-based distributed FL in the case of energy-demand prediction is the imbalances of the data used in training. Prosumers can have different energy scales and various energy patterns. When significantly different predictors share their model, there is a chance that some of them are trained and matched better, and others may be lacking behind. This case is usually present in non-IID FL models, and those participants should be identified and eliminated during the training. To deal with this issue, solutions such as FedProx can be integrated to address the statistical heterogeneity in FL [46]. It considers the heterogeneity of prosumers nodes in terms of computational resources and amount of data to allow for a different number of computations to be performed locally.

For our blockchain integration we recommend using a clustering algorithm on the initial portfolio of prosumers, and different FL models should be assigned to each cluster. Even if a clustering algorithm is used, the scaler should fit every participant without knowing the energy data samples. We used prosumers with similar energy amplitudes, so their values have been scaled between zero and the maximum demand. Normalized values will improve the convergence of the different models with different rates based on the prosumer scale. Finally, a zero-knowledge proof algorithm can be used to prove that a given participant belongs to a cluster without sharing its data.

In our study, we made sure that the local prediction models stored in the blockchain were associated only with residential household consumers. Also, the training had considered only verified data acquired by energy meters. However, there can be malicious participants that may interfere with the blockchain-based distributed FL process, by posting wrong weights that affect the accuracy of the global model. The issue should be addressed by conducting validations before accepting new edge prosumer nodes as participants. The validation could be made transparent, by defining new functionalities to the blockchain smart contract. Also, it may be done by a third-party stakeholder such as the Distribution System Operator, who has a high interest in the reliability and the security of the system. The blockchain offers good transaction traceability and can be used to identify the peers that mislead the learning model parameters [33]. The solution can be joined with the methods for incentivizing the prosumers’ participation in demand response. Therefore, the rewards can be connected to the quality of contribution to the learning and prediction on top of the rewards for flexibility committed.

The proposed distributed learning system should facilitate and encourage new participants to join and contribute to the energy-demand prediction. By joining the blockchain they will download and use the stored model. This could drastically reduce the time needed for a new participant to integrate local energy samples into the process without breaking data privacy. Also, it will improve the accuracy of the energy prediction in the case of a new participant that does not have any pre-trained ML model. The smart grid scenario could integrate a pre-validation of the new participant and prevent the access of malicious users.

Finally, our approach can be improved to consider the economics of privacy and the value of local ML models for energy-demand prediction. Model-sharing strategies could be implemented at the blockchain level to combine the benefits of both market-based and regulatory-oriented approaches. The prosumers may have financial benefits from sharing their ML models, and at the same time, the blockchain may allow the tracking of the parameters’ updating process and the penalization of illicit behavior. Thus, as future work, a market-based mechanism can be implemented at blockchain overlay in which edge prosumer nodes will gain financial revenue for training models and sharing them with others. A fee is paid to the edge prosumer nodes if their model updates improve the prediction accuracy. The edge nodes that only download the model and use it for local prediction without contributing to the training process will be charged. The trained models can be rated by edge nodes’ prosumers to eliminate potential malicious nodes.

6. Conclusions and Future Work

In this paper, we describe a blockchain-based distributed FL solution for predicting the energy demand of prosumers supporting their participation in grid management programs. We combine the FL model with blockchain to assure the privacy of energy-demand data used in the predictions. The ML models are trained at edge prosumer nodes using energy data that are locally stored and only the models’ parameters are shared using a blockchain. Therefore the global federated model parameters are stored in a tamper-proof manner as transactions in a blockchain are replicated among all nodes. Smart contracts are defined for managing the local ML models’ integration with blockchain-specifying functions to address the data imbalances, model parameters’ scaling, and reduction of blockchain overhead. The global prediction model is not centralized but distributed and replicated over the blockchain network, therefore becoming immutable, making it difficult for inversion attacks to reveal prosumer behavior.

We have provided a comparative evaluation of different ML model distributions such as centralized, local edge, and distributed FL. The results show that concerning the prediction of energy demand, our proposed solution’s impact on accuracy is limited compared to the centralized solution that, as expected, has the best prediction results, but is exposed to privacy leakage. This makes it a relevant technology for providing energy services because it addresses prosumers’ concerns related to the privacy of sensitive data and provides enough benefits in terms of prediction accuracy to reach the potential of DR.

As future work we plan to study the integration of complex deep-learning models such as convolutional neural networks (CNN) or LSTM to improve prosumers’ energy prediction accuracy. As the limitation of today’s blockchains in terms of block size, transactions’ dimensions, and gas consumption is well known, we plan to integrate advanced techniques for the partial integration of learned parameters or for models’ compression. Also, other types of blockchain platforms will be considered to address the overhead limitations and to incentivize prosumers’ contribution to the learning and prediction process going beyond today’s models in the energy domain which reward only the use of energy flexibility.