Convexity of the Capacity of One-Bit Quantized Additive White Gaussian Noise Channels

Abstract

In this study, the maximum error-free transmission rate of an additive white Gaussian noise channel with a symmetric analog-to-digital converter (ADC) was derived as a composite function of the binary entropy function, Gaussian Q-function, and the square root function, assuming that the composite function was convex on the set of all non-negative real numbers. However, because mathematically proving this convexity near zero is difficult, studies in this field have only presented numerical results for small values in the domain. Because the low-signal-to-noise (SNR) regime is considered to be a major application area for one-bit ADCs in wireless communication, deriving a concrete proof of the convexity of the composite function on small SNR values (non-negative values near zero) is important. Therefore, this study proposes a novel proof for convexity, which is satisfied for all non-negative values, based on the continuity of the involved functions.

1. Introduction

The capacity of a communication channel is defined as the maximum data rate that can be transmitted over the channel with an arbitrarily small error probability. In information theory, the channel capacity is given by the supremum of the mutual information between the input and output of the channel [1]. For example, consider the channel $Y=X+N$, where $X\in \mathbb{R}$ and $Y\in \mathbb{R}$ are input and output random variables, respectively; $N\in \mathbb{R}$ is an additive noise independent of X and follows a zero-mean Gaussian distribution; and $\mathbb{R}$ denotes the set of real numbers. This type of channel is referred to as an additive white Gaussian noise (AWGN) channel, and its capacity is given by $\frac{1}{2}{log}_2(1+\gamma )$, where $\gamma$ is the signal-to-noise ratio (SNR) defined as $\gamma \triangleq \frac{\mathbb{E}\left[\right|X{|}^2]}{\mathbb{E}\left[\right|N{|}^2]}$. In recent decades, extensive research on wireless communications has been conducted based on the aforementioned channel capacity and its convexity [2,3].

To satisfy the consistently increasing demand for data rates, recent standards for wireless communication have focused on a large amount of unused bandwidth in the millimeter-wave (mmWave) and terahertz frequency bands [4,5,6,7]. This is because using a significantly wider bandwidth available in a higher-frequency band, such as the mmWave band, is a good solution to satisfy the fast-growing demand for higher data rates. However, such an increase in the bandwidth can cause dissipation of an extensive amount of power when using conventional high-resolution analog-to-digital converters (ADCs) because the power consumption of ADCs linearly increases with increasing sampling rates [8]. This power consumption issue is critical for mobile devices because it is directly related to the battery lifetime as well as the available power resources for uplink communications.

Receiver structures based on low-resolution ADCs have attracted considerable attention as a useful solution for exploiting the abundant resources available in extremely high-frequency bands while achieving low power consumption [9]. In particular, an extreme case that uses one-bit ADCs at the receivers has been widely studied because it is the most power-efficient solution. Extensive studies have been devoted to the evaluation of the performance of communication channels with one-bit ADCs [9,10,11,12,13,14,15,16,17,18,19,20,21,22]. The capacity of a single-input and single-output (SISO) real-valued additive white Gaussian noise (AWGN) channel with one-bit ADCs was derived in [10]. In [10], a symmetric one-bit ADC was assumed, such that the channel output was given by $Y_Q=f_Q(X+N)$, where $f_Q(·)$ denotes the quantization function defined as

$$\begin{array}{cc}\hfill & f_Q\left(x\right)=\left\{\begin{array}{cc}1,\hfill & x\ge 0\hfill \\ -1,\hfill & x<0\hfill \end{array}\right..\hfill \end{array}$$

(1)

The channel capacity of this one-bit quantized AWGN channel was derived as $1-H_b\left(Q\left(\sqrt{\gamma }\right)\right)$ [10], where $H_b$ and Q denote the binary entropy and Gaussian Q-functions, respectively. Further extending this result, the capacity of complex fading channels with multiple transmit and receive antennas was considered in [11]. For example, assuming perfect channel state information at the transmitter, the capacity of a multiple-input and single-output (MISO) complex fading channel was derived for the given channel components. Moreover, certain upper and lower bounds were presented for multiple-input and multiple-output (MIMO) complex channels. Furthermore, numerous important studies have derived the capacities of various wireless channels with one-bit ADCs [12,13,14,15,16]. In [12], the tradeoffs between the achievable rates and energy rates were considered when one-bit ADC receivers were used. The authors of [13] used a one-bit ADC for an uplink massive MIMO system, and the corresponding throughput was analyzed. The performance of a one-bit quantized channel with limited channel state information at the transmitter was considered in [14]. In addition to using ADCs in receivers, the application of one-bit digital-to-analog converters to transmitters was considered in [15]. The secrecy capacity of a Gaussian wiretap channel with one-bit ADCs was analyzed in [16]. The detection performance of fading channels with one-bit ADCs was also studied [17,18,19,20,21,22].

Several studies so far have been based on the capacity $1-H_b\left(Q\left(\sqrt{\gamma }\right)\right)$ of the one-bit quantized SISO AWGN channel, which was first derived in [10]. However, when it was derived in [10], the authors assumed that the composite function $H_b\left(Q\left(\sqrt{x}\right)\right)$ was convex for $x\ge 0$, although the convexity was proved by restricting the domain to $x>c$ for a constant c. Thus, the authors did not provide a concrete mathematical proof when x was close to zero; only a numerical result was presented to support their claim of convexity when $0\le x\le c$ [10,23]. Because a low-SNR regime is an important application of a one-bit ADC [11], we need to prove the convexity on $0\le x\le c$ for the exact derivation of the capacity for all SNR regions. Systems with one-bit ADCs have been extensively studied for the further evolution of 5G and 6G communication. Thus, providing a concrete proof for the convexity of $H_b\left(Q\left(\sqrt{x}\right)\right)$, for all $x\ge 0$, will be an important supplement to the theoretical completeness of previous results derived assuming this convexity. Furthermore, the corresponding results can be used to derive unknown channel capacities with one-bit ADCs for various important communication applications, such as multiple-input and multiple-output channels. These results can also be used to solve various optimization problems associated with the design of appropriate resource allocation strategies as the convexity of the capacity function can guarantee the existence of a unique solution depending on the system parameters [24,25].

In this regard, this study proves that the composite function $H_b\left(Q\left(\sqrt{x}\right)\right)$ is convex for all possible values of the input SNR, i.e., for all $x\ge 0$.

2. Notations and Preliminaries

The function $logx$ denotes a logarithmic function with base e. In addition, we use the following notations throughout this paper for simplicity.

Notation 1. 

D is defined as the set of nonnegative real numbers: $D=\{x\in \mathbb{R}:x\ge 0\}$. The function $Q:D\to \mathbb{R}$ denotes the Gaussian Q-function defined as follows, and $Q_n\left(x\right)$ is defined as the n-th order derivative of $Q\left(x\right)$:

$$\begin{array}{cc}\hfill & Q\left(x\right)\triangleq {\int }_x^{\infty }\frac{1}{\sqrt{2\pi }}{e}^{-\frac{r^2}{2}}dr,\hfill \\ \hfill & Q_n\left(x\right)\triangleq \frac{d^n}{d{x}^n}Q\left(x\right).\hfill \end{array}$$

The function $H_b:[0,1]\to \mathbb{R}$ denotes the binary entropy function defined as

$$\begin{array}{cc}\hfill & H_b\left(x\right)=-x{log}_{2}x-(1-x){log}_2(1-x).\hfill \end{array}$$

Notation 2. 

The function $g:D\to \mathbb{R}$ is defined as follows, and $g_n\left(x\right)$ is defined as the n-th order derivative of $g\left(x\right)$ on D:

$$\begin{array}{cc}\hfill & g\left(x\right)\triangleq log\left(\frac{1-Q\left(x\right)}{Q\left(x\right)}\right),\hfill \\ \hfill & g_n\left(x\right)\triangleq \frac{d^n}{d{x}^n}log\left(\frac{1-Q\left(x\right)}{Q\left(x\right)}\right).\hfill \end{array}$$

Notation 3. 

The functions $t:D\to \mathbb{R}$ and $s:D\to \mathbb{R}$ are defined as follows, and $t_n\left(x\right)$ and $s_n\left(x\right)$ are defined as the n-th order derivatives of $t\left(x\right)$ and $s\left(x\right)$ on D, respectively:

$$\begin{array}{cc}\hfill & t\left(x\right)\triangleq \frac{Q_1\left(x\right)}{Q\left(x\right)},s\left(x\right)\triangleq \frac{Q_1\left(x\right)}{Q(-x)},\hfill \\ \hfill & t_n\left(x\right)\triangleq \frac{d^{n}t\left(x\right)}{d{x}^n},s_n\left(x\right)\triangleq \frac{d^{n}s\left(x\right)}{d{x}^n}.\hfill \end{array}$$

Based on direct differentiation using the chain rule, we can easily derive the followings (see Appendix A for the derivation):

$$\begin{array}{cc}\hfill & Q_1\left(x\right)=Q_1(-x)=-\frac{1}{\sqrt{2\pi }}{e}^{-\frac{x^2}{2}},Q_2\left(x\right)=-x{Q}_1\left(x\right),\hfill \end{array}$$

(2)

$$\begin{array}{ccc}\hfill & \frac{d}{dx}{H}_b\left(x\right)={log}_2(1-x)-{log}_{2}x,\hfill & \end{array}$$

(3)

$$\begin{array}{cc}\hfill & t_1\left(x\right)=-t\left(x\right)(x+t\left(x\right)),s_1\left(x\right)=-s\left(x\right)(x-s\left(x\right)),\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill & t_2\left(x\right)=-t_1\left(x\right)(x+t\left(x\right))-t\left(x\right)(1+t_1\left(x\right)),\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill & s_2\left(x\right)=-s_1\left(x\right)(x-s\left(x\right))-s\left(x\right)(1-s_1\left(x\right)),\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill & g_1\left(x\right)=-t\left(x\right)-s\left(x\right),g_2=(t\left(x\right)+s\left(x\right))(x+t\left(x\right)-s\left(x\right)).\hfill \end{array}$$

(7)

Moreover, the limiting value of $t_1\left(x\right)$ and $s_1\left(x\right)$ can be obtained as follows.

Lemma 1. 

The functions $t_1\left(x\right)$ and $s_1\left(x\right)$ have the following limits:

$$\begin{array}{cc}\hfill & \underset{x\to \infty }{lim}{t}_1\left(x\right)=-1,\underset{x\to 0}{lim}{s}_1\left(x\right)=\frac{4}{2\pi }.\hfill \end{array}$$

(8)

Moreover, for all $x\in D$, the following inequalities are satisfied:

$$\begin{array}{cc}\hfill & g\left(x\right)\ge 0,g_1\left(x\right)\ge 0,\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill & t\left(x\right)\le 0,s\left(x\right)\le 0,\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill & x+t\left(x\right)\le 0,\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill & t_1\left(x\right)\le 0,s_1\left(x\right)\ge 0.\hfill \end{array}$$

(12)

Proof. 

See Appendix A. □

Lemma 1 includes a summary of inequalities that are essential for deriving the main results presented in the following section. Each result in this lemma does not have a specific physical meaning. Nevertheless, the results play key roles in proving the convexity of $H_b(Q\left(\sqrt{x}\right)$ as described in the following section.

3. Proof of Convexity

Based on Lemma 1, we can derive the following results.

Lemma 2. 

For all $x\in D$, we have

$$\begin{array}{c}\hfill -1\le t_1\left(x\right)\le 0,0\le s_1\left(x\right)\le 1.\end{array}$$

(13)

Proof. 

By (8) and (12), it suffices to prove that $t_1\left(x\right)\ge -1$ and $s_1\left(x\right)\le 1$ for all $x>0$.

First, a proof by contradiction is used to prove that $t_1\left(x\right)\ge -1$ for all $x>0$. To this end, suppose that there exists a positive real value a that satisfies $t_1\left(a\right)<-1$, or equivalently, $t_1\left(a\right)=-1-{\delta }_0$ for some ${\delta }_0>0$. Because $t_1\left(x\right)$ is continuous for $x\ge 0$, there must be an open interval $(a,a+ϵ)$ inside domain D with some $ϵ>0$ on which $t_1\left(x\right)<-1$. Let ${ϵ}^{*}$ be the supremum of all possible values of $ϵ$. If ${ϵ}^{*}$ is finite, there exists a ${\delta }_1>0$ such that $t_1\left(x\right)<-1$ on $(a,a+{ϵ}^{*})$ and $t_1\left(x\right)\ge -1$ on $[a+{ϵ}^{*},a+{ϵ}^{*}+{\delta }_1)$, by the definition of ${ϵ}^{*}$. However, by (5), with the inequalities in Lemma 1, $t_1\left(x\right)<-1$ implies that $t_2\left(x\right)<0$ on $(a,a+{ϵ}^{*})$, which further implies that $t_1\left(x\right)$ is strictly decreasing on $(a,a+{ϵ}^{*})$. As $t_1\left(x\right)$ is strictly decreasing on $(a,a+{ϵ}^{*})$, we must have ${lim}_{x\to a+{ϵ}^{*}}{t}_1\left(x\right)\le t_1\left(a\right)=-1-{\delta }_0$. Because $t_1\left(x\right)$ is continuous, this contradicts the assumption that $t_1\left(x\right)\ge -1$ on $[a+{ϵ}^{*},a+{ϵ}^{*}+{\delta }_1)$, which was induced by assuming a finite value of ${ϵ}^{*}$. Similarly, if ${ϵ}^{*}$ diverges to infinity, then $t_1\left(x\right)$ must be strictly decreasing on $(a,\infty )$. As $t_1\left(a\right)=-1-{\delta }_0$, this implies that ${lim}_{x\to \infty }{t}_1\left(x\right)\le -1-{\delta }_0$, but this contradicts (8). Therefore, we conclude that $t_1\left(x\right)\ge -1$ for all $x>0$.

Similarly, a proof by contradiction is used to prove that $s_1\left(x\right)\le 1$ for all $x>0$. For the sake of contradiction, suppose that there exists a positive real value b that satisfies $s_1\left(b\right)>1$, or equivalently, $s_1\left(b\right)=1+{\rho }_0$, for some ${\rho }_0>0$. Because $s_1\left(x\right)$ is continuous for $x\ge 0$, there must be an open interval $(b-\tau ,b)$ inside domain D with some $\tau >0$ on which $s_1\left(b\right)>1$. Let ${\tau }^{*}$ be the supremum of all possible values of $\tau$. If ${\tau }^{*}<b$, there exists a ${\rho }_1>0$ such that $s_1\left(x\right)>1$ on $(b-{\tau }^{*},b)$ and $s_1\left(x\right)\le 1$ on $(b-{\tau }^{*}-{\rho }_1,b-{\tau }^{*}]$, by the definition of ${\tau }^{*}$. However, by (6), with the inequalities in Lemma 1, $s_1\left(x\right)>1$ implies that $s_2\left(x\right)<0$ on $(b-{\tau }^{*},b)$, which further implies that $s_1\left(x\right)$ is strictly decreasing on $(b-{\tau }^{*},b)$. As $s_1\left(x\right)$ is strictly decreasing on $(b-{\tau }^{*},b)$, we must have ${lim}_{x\to b-{\tau }^{*}}{s}_1\left(x\right)\ge s_1\left(b\right)=1+{\rho }_0$. Because $s_1\left(x\right)$ is continuous, this contradicts the assumption that $s_1\left(x\right)\le 1$ on $(b-{\tau }^{*}-{\rho }_1,b-{\tau }^{*}]$. Similarly, if ${\tau }^{*}=b$, $s_1\left(x\right)$ must be strictly decreasing on $[0,b)$. As $s_1\left(b\right)>1$, this implies that ${lim}_{x\to 0}{s}_1\left(x\right)>1$, but this contradicts (8). Therefore, we conclude that $s_1\left(x\right)\le 1$ for all $x>0$. □

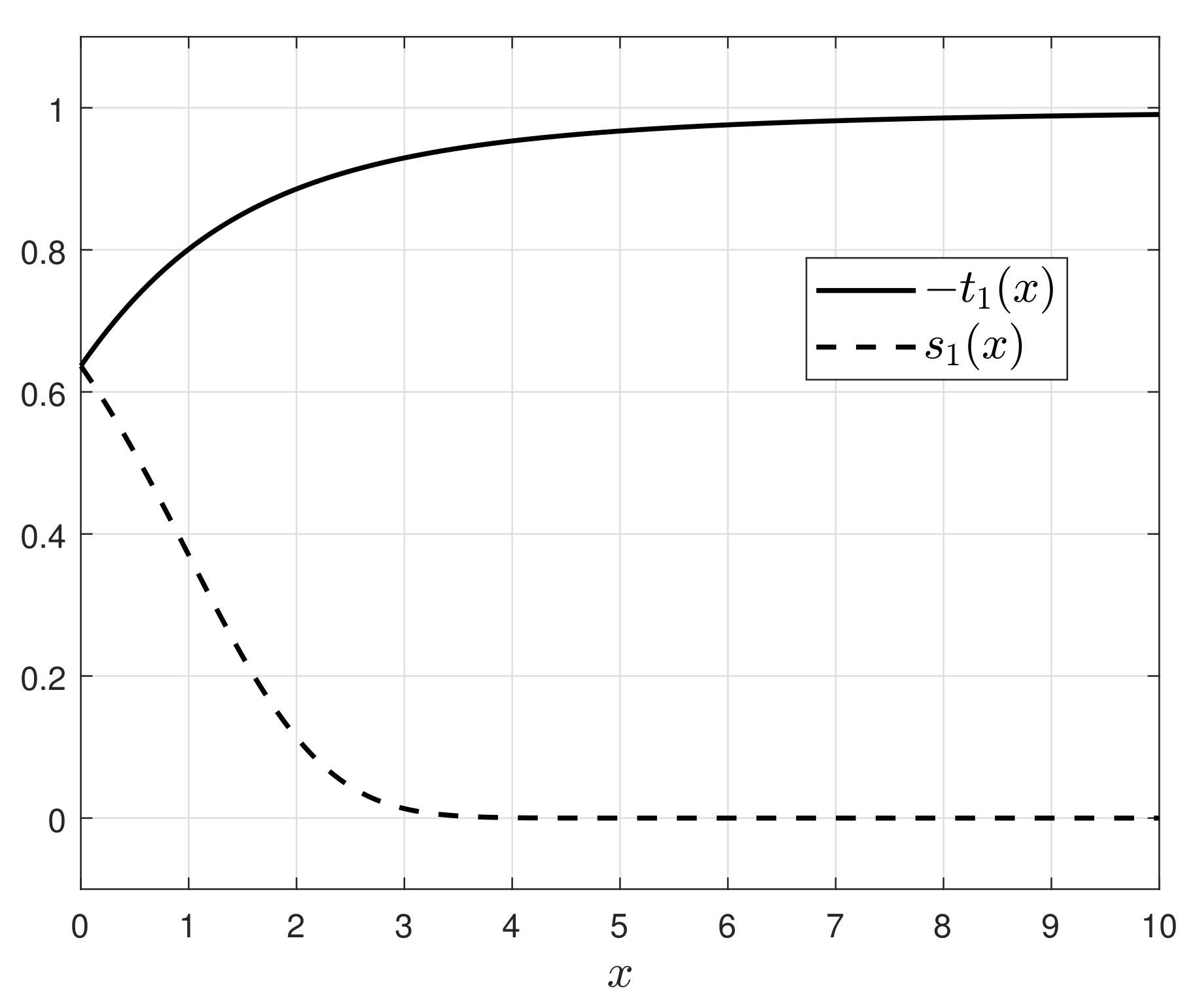
Figure 1 verifies Lemma 2, which can be used to derive the following result.

Lemma 3. 

For all $x\in D$, the following inequality is true.

$$\begin{array}{cc}\hfill & g\left(x\right)+x{g}_1\left(x\right)-g_2\left(x\right)\ge 0.\hfill \end{array}$$

(14)

Proof. 

From (7), we have $g\left(x\right)+x{g}_1\left(x\right)-g_2\left(x\right)=g\left(x\right)+(2x+t\left(x\right)-s\left(x\right))g_1\left(x\right)$. Because both $g\left(x\right)$ and $g_1\left(x\right)$ are nonnegative (9), it suffices to prove that $2x+t\left(x\right)-s\left(x\right)\ge 0$. By definition, ${lim}_{x\to 0}[t\left(x\right)-s\left(x\right)]=0$, such that ${lim}_{x\to 0}[2x+t\left(x\right)-s\left(x\right)]=0$. Thus, it suffices to prove that $\frac{d(2x+t(x)-s(x\left)\right)}{dx}=2+t_1\left(x\right)-s_1\left(x\right)\ge 0$, or equivalently, $s_1\left(x\right)-t_1\left(x\right)\le 2$. Because $s_1\left(x\right)\ge 0$ (by (12)) and $-t_1\left(x\right)\ge 0$ (by (10)), the triangle inequality implies that $s_1\left(x\right)-t_1\left(x\right)\le |t_1\left(x\right)|+|s_1\left(x\right)|$, and Lemma 2 further implies that $s_1\left(x\right)-t_1\left(x\right)\le |t_1\left(x\right)|+|s_1\left(x\right)|\le 2$. □

In Figure 2, function $g\left(x\right)+x{g}_1\left(x\right)-g_2\left(x\right)$ is depicted to demonstrate the result in Lemma 3.

Lemma 4. 

The composite function $H_b\left(Q\left(\sqrt{x}\right)\right)$ is convex on D if and only if

$$\begin{array}{c}\hfill \left(x+\frac{1}{x}\right)g\left(x\right)\ge g_1\left(x\right)\end{array}$$

(15)

on D.

Proof. 

A real-valued twice differentiable function of one variable is convex if and only if its derivative is nondecreasing (i.e., the second-order derivative is nonnegative). Thus, we investigate the derivative of $H_b\left(Q\left(\sqrt{x}\right)\right)$, which can be calculated using (2) and (3), as

$$\begin{array}{cc}\hfill \frac{d}{dx}{H}_b\left(Q\left(\sqrt{x}\right)\right)& ={log}_2\left(\frac{1-Q\left(\sqrt{x}\right)}{Q\left(\sqrt{x}\right)}\right)\left(-\frac{1}{\sqrt{2\pi }}{e}^{-\frac{x}{2}}\right)\left(\frac{1}{2\sqrt{x}}\right)\hfill \\ \hfill & =\frac{-e^{-\frac{x}{2}}}{2(log2)\sqrt{2\pi x}}log\left(\frac{1-Q\left(\sqrt{x}\right)}{Q\left(\sqrt{x}\right)}\right).\hfill \end{array}$$

Thus, $\frac{d}{dx}{H}_b\left(Q\left(\sqrt{x}\right)\right)$ is nondecreasing if and only if $\frac{d}{dx}v\left(x\right)\le 0$, where $v\left(x\right)=x^{-\frac{1}{2}}{e}^{-\frac{x}{2}}log\left(\frac{1-Q\left(\sqrt{x}\right)}{Q\left(\sqrt{x}\right)}\right)$. Then, $\frac{d}{dx}v\left(x\right)$ can be calculated as

$$\begin{array}{cc}\hfill & \frac{d}{dx}v\left(x\right)\hfill \\ \hfill & =-\frac{1}{2}{e}^{-\frac{x}{2}}{x}^{-\frac{3}{2}}\left[(x+1)log\left(\frac{1-Q\left(\sqrt{x}\right)}{Q\left(\sqrt{x}\right)}\right)-2x\frac{d}{dx}\left\{log\left(\frac{1-Q\left(\sqrt{x}\right)}{Q\left(\sqrt{x}\right)}\right)\right\}\right].\hfill \end{array}$$

Hence, $\frac{d}{dx}v\left(x\right)\le 0$ if and only if

$$\begin{array}{cc}\hfill \frac{1}{2}\left(1+\frac{1}{x}\right)log\left(\frac{1-Q\left(\sqrt{x}\right)}{Q\left(\sqrt{x}\right)}\right)& =\frac{1}{2}\left(1+\frac{1}{x}\right)g\left(\sqrt{x}\right)\hfill \\ \hfill & \ge \frac{d}{dx}\left\{log\left(\frac{1-Q\left(\sqrt{x}\right)}{Q\left(\sqrt{x}\right)}\right)\right\}=\frac{g_1\left(\sqrt{x}\right)}{2\sqrt{x}},\hfill \end{array}$$

or, by multiplying both sides by $2\sqrt{x}$, it follows that $\frac{d}{dx}v\left(x\right)\le 0$ if and only if

$$\begin{array}{c}\hfill \left(\sqrt{x}+\frac{1}{\sqrt{x}}\right)g\left(\sqrt{x}\right)\ge g_1\left(\sqrt{x}\right).\end{array}$$

Therefore, we conclude that $H_b\left(Q\left(\sqrt{x}\right)\right)$ is convex on D if and only if $(\sqrt{x}+\frac{1}{\sqrt{x}})g\left(\sqrt{x}\right)\ge g_1\left(\sqrt{x}\right)$ on D. Because the function $y=\sqrt{x}$ has a one-to-one correspondence from D to D, proving that $(y+\frac{1}{y})g\left(y\right)\ge g_1\left(y\right)$ for all $y\in D$ is equivalent to proving that $(\sqrt{x}+\frac{1}{\sqrt{x}})g\left(\sqrt{x}\right)\ge g_1\left(\sqrt{x}\right)$ for all $x\in D$; thus, the proof is complete. □

Lemma 5. 

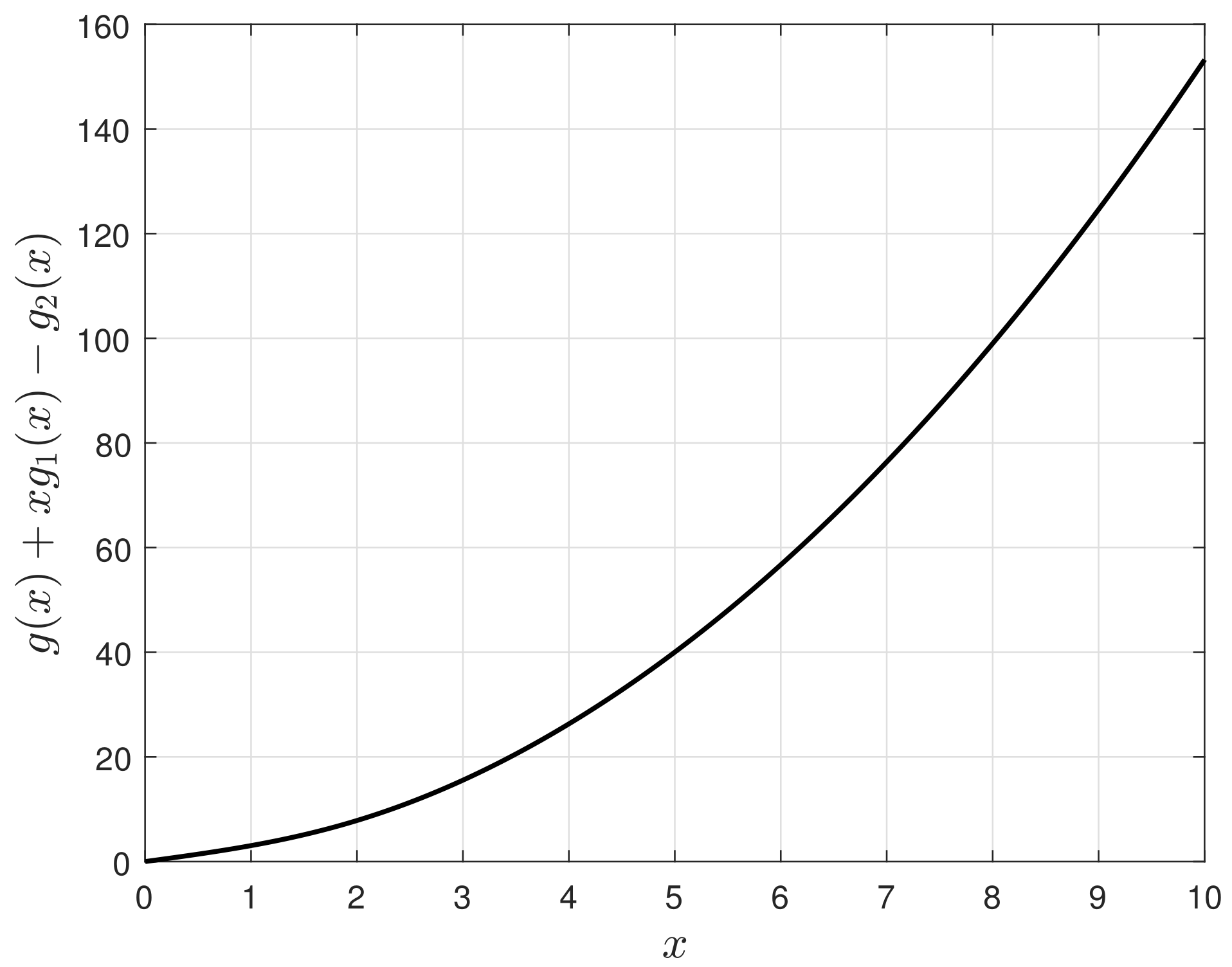
If $\frac{g\left(x\right)}{x}\le g_1\left(x\right)$ on a subset of D, then

$$\begin{array}{c}\hfill \frac{d}{dx}\left[\left(x+\frac{1}{x}\right)g\left(x\right)\right]-g_2\left(x\right)\ge 0\end{array}$$

(16)

on the subset.

Proof. 

The left-hand side of (16) can be calculated as

$$\begin{array}{cc}\hfill \frac{d}{dx}\left[\left(x+\frac{1}{x}\right)g\left(x\right)\right]-g_2\left(x\right)& =\left(1-\frac{1}{x^2}\right)g\left(x\right)+\left(x+\frac{1}{x}\right)g_1\left(x\right)-g_2\left(x\right)\hfill \\ \hfill & =\frac{1}{x}\left(g_1\left(x\right)-\frac{g\left(x\right)}{x}\right)+g\left(x\right)+x{g}_1\left(x\right)-g_2\left(x\right).\hfill \end{array}$$

As we know that $g\left(x\right)+x{g}_1\left(x\right)-g_2\left(x\right)\ge 0$ on D by Lemma 3, $g_1\left(x\right)-\frac{g\left(x\right)}{x}\ge 0$ implies that $\frac{d}{dx}\left[\left(x+\frac{1}{x}\right)g\left(x\right)\right]-g_2\left(x\right)\ge 0$. □

Theorem 1. 

The composite function $H_b\left(Q\left(\sqrt{x}\right)\right)$ is convex on D.

Proof. 

For simplicity, let $f\left(x\right)=\left(x+\frac{1}{x}\right)g\left(x\right)$. First, by applying L’Hôpital’s rule, we have

$$\underset{x\to 0}{lim}f\left(x\right)=\underset{x\to 0}{lim}\left[\frac{g\left(x\right)}{x}\right]=\underset{x\to 0}{lim}{g}_1\left(x\right).$$

Thus, by Lemma 4, the proof is complete if $f\left(x\right)\ge g_1\left(x\right)$ is true for all $x>0$.

For the sake of contradiction, suppose that there exists a real value $a>0$ on which $f\left(a\right)<g_1\left(a\right)$. Because both $f\left(x\right)$ and $g_1\left(x\right)$ are continuous, this implies that there exists an open interval $(a-ϵ,a)$ inside D on which $f\left(x\right)<g_1\left(x\right)$. Moreover, because ${lim}_{x\to 0}f\left(x\right)={lim}_{x\to 0}{g}_1\left(x\right)$, there must exist an ${ϵ}_0>0$ and a corresponding open interval $(a-{ϵ}_0,a)$ that satisfies

$$\begin{array}{c}\hfill f\left(x\right)<g_1\left(x\right)\mathrm{on}(a-{ϵ}_0,a)\end{array}$$

(17)

and

$$\begin{array}{c}\hfill \underset{x\to a-{ϵ}_0}{lim}f\left(x\right)=\underset{x\to a-{ϵ}_0}{lim}{g}_1\left(x\right).\end{array}$$

(18)

For example, ${ϵ}_0=a$ if $f\left(x\right)$ is strictly less than $g_1\left(x\right)$ for all x in $\in (0,a)$. Combining (17) and (18), we obtain $f\left(x\right)\le g_1\left(x\right)$ on $[a-{ϵ}_0,a)$. Because $f\left(x\right)=(x+\frac{1}{x})g\left(x\right)$ and $g\left(x\right)\ge 0$, this implies that $\frac{g\left(x\right)}{x}\le g_1\left(x\right)$ on $[a-{ϵ}_0,a)$. By Lemma 5, $\frac{g\left(x\right)}{x}\le g_1\left(x\right)$ further implies that

$$\begin{array}{c}\hfill \frac{d}{dx}\left[f\left(x\right)-g_1\left(x\right)\right]\ge 0\mathrm{on}[a-{ϵ}_0,a).\end{array}$$

(19)

Subsequently, (18) and (19) imply that $f\left(x\right)$ must be greater than or equal to $g_1\left(x\right)$ on $(a-{ϵ}_0,a)$. However, this contradicts (17) and thus, the proof is completed. □

4. Discussion and Conclusions

This letter provides a mathematical proof for the convexity of the capacity function of one-bit quantized AWGN channel. Specifically, the continuity of involved functions are used to provide a proof by contradiction. The corresponding result can be an important supplement for the theoretical completeness of previous studies as numerous important studies have derived the capacities of various wireless channels with one-bit ADCs assuming that the convexity is true without providing a mathematical proof when SNR is near zero.

For example, in the proof of Theorem 2 provided in [10], Jensen’s inequality was applied to the conditional entropy $H\left(Y_Q\right|X)$, which is derived as

$$\begin{array}{c}\hfill H\left(Y_Q\right|X)=\mathbb{E}\left[H_b\left(Q\left(\sqrt{\frac{{\left|X\right|}^2}{{\sigma }_N^2}}\right)\right)\right],\end{array}$$

if $Y_Q$ is the one-bit quantized output of an AWGN channel such that $Y_Q=f_Q(X+N)$, where X is the transmit signal, N is the zero-mean Gaussian noise with variance ${\sigma }_N^2$, and $f_Q$ is the quantization function defined in (1). The convexity of $H_b\left(Q\left(\sqrt{x}\right)\right)$ guarantees the following result based on Jensen’s inequality:

$$\begin{array}{c}\hfill H\left(Y_Q\right|X)\ge H_b\left(Q\left(\sqrt{\mathbb{E}\left[\frac{{\left|X\right|}^2}{{\sigma }_N^2}\right]}\right)\right).\end{array}$$

(20)

Because there exists a transmit signal distribution that satisfies the equality in (20) (e.g., binary phase shift keying (BPSK)), this result implies that the capacity of a one-bit quantized AWGN channel is given by $1-H_b\left(Q\left(\sqrt{\gamma }\right)\right)$, where $\gamma =\mathbb{E}[\frac{{\left|X\right|}^2}{{\sigma }_N^2}]$ is the SNR. Although this derivation of the capacity assumes the convexity of $H_b\left(Q\left(\sqrt{x}\right)\right)$, an analytical proof was presented assuming that $x\ge 2$, and only numerical results were provided for the case of $0\le x\le 2$. Thus, our complete proof of convexity can be a theoretical supplement to this result. 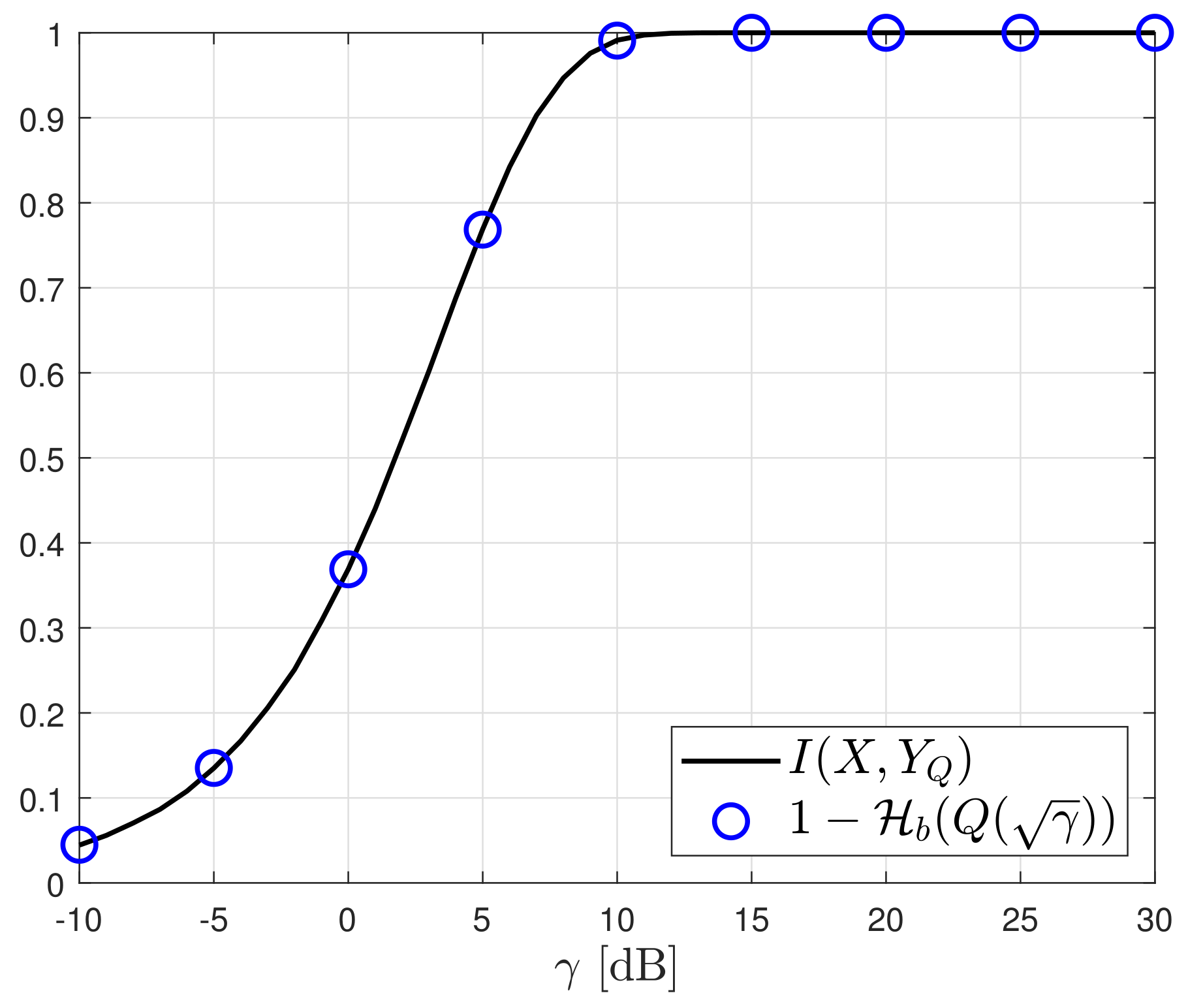In short, the proof guarantees that the capacity cannot be larger than $1-H_b\left(Q\left(\sqrt{\gamma }\right)\right)$ and that BPSK signaling achieves this upper bound. In Figure 3, the mutual information between X and $Y_Q$, denoted as $I(X,Y_Q)$, is compared with the capacity $1-H_b\left(Q\left(\sqrt{\gamma }\right)\right)$. BPSK signaling with equal probabilities is used as the probability distribution of X. The numerical results are consistent with the analysis results. In [11], authors extended this result to the multi-antenna complex fading channels. For MISO cases, the capacity was derived based on the convexity of $H_b\left(Q\left(\sqrt{x}\right)\right)$ on $x\ge 0$ by directly extending the capacity of the SISO channel with a one-bit ADC. Moreover, an upper bound for the capacity of the MIMO channels was derived, and this derivation was also based on the convexity of $H_b\left(Q\left(\sqrt{x}\right)\right)$. Thus, our results could supplement these results.

The convexity of the capacity function can also be used for optimization problems to provide appropriate resource allocation. In such cases, the convexity of the objective function can be used to clarify the existence of an optimal solution and identify it. For example, in [25], an optimal power allocation problem was formulated and solved based on the convexity of $H_b\left(Q\left(\sqrt{x}\right)\right)$; however, the convexity was assumed with only some numerical results.

With one-bit quantization, deriving the exact capacity is difficult because the quantization function is difficult to analyze. Thus, although analyzing the conventional capacity with infinite-resolution ADCs is feasible, obtaining the capacity for channels with one-bit ADCs may be extremely difficult. For example, the capacity of MIMO channels with one-bit ADCs is generally unknown, although the exact capacity of the MIMO channels with infinite-resolution ADCs is already known. Thus, our results can provide a valid mathematical basis for further derivations of unknown capacities and various optimization problems that use the capacity function of a one-bit quantized AWGN channel.