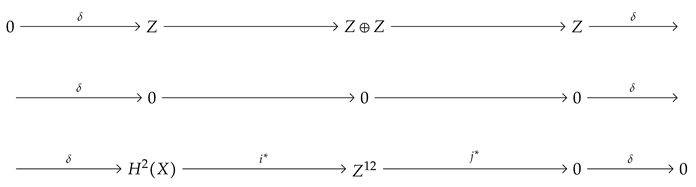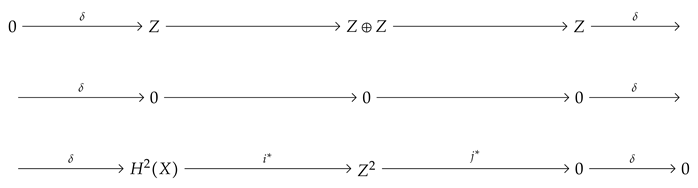1. Introduction
This paper aims to present the elements needed to endow a robot with an increased capacity for human life simulation. In this context, the terms fundamental interval of time, life frequency, life sequence, life programme, necessary energy, tensional coherence, tensional content and tensional information must be understood as specific terms of the life simulator and not necessarily of life. They could be treated as particular terms of life if they were highlighted and measured. However, such an approach would involve huge resources that would exceed the capabilities of current technologies.
A series of hypotheses necessary to describe the functionality of the life engine will be denoted by ().
The most important research topic for humans is undoubtedly life. To study life in its complexity we need an overall vision. Something such as Heisenberg’s uncertainty principle seems to manifest itself in the research approach to complex processes and phenomena. Thus, although humans have decoded DNA, they still cannot explain life in all its complexity. Moreover, they have no control over the critical events of life, and even more so, over genetics.
The triggering, maintaining and stopping of vital processes of life are determined by specific laws and mechanisms. Although some of these laws and mechanisms are not visible, the emergence, presence and disappearance of life amply and justify them. Two of these mechanisms are the topics of this paper: the energetic mechanism of life maintenance and the mechanism of the generation of tensional information.
The human species seems to have a limited capacity to understand the present. The present does not depend exclusively on the past. If so, then the status changes cannot be explained. No one can prove that the present belonged to the future. If we treat the present as a previous moment from the future, then the following issues can be explained: the superimposing of events over life moments, the beginning and the end of life and how life is maintained on a finite time horizon. In the following sections, we will consider this option, which is useful in the simulation approach to life. These aspects and the others that will be exposed in the paper suggest that a human being can be defined as a robot equipped with the consciousness of the moment that moves in a field of events. We define the consciouness of the moment as the living being’s ability to discern the details of the moment regarding both his/her own person and the environment of interaction. This robot, which we call a human effector, is the support on which life manifests itself.
Life manifests itself through biological constructs. The events that occur at the level of the human body are due to both the passage of time and the interaction environment. On the other hand, human beings interpret the events that take place in their interaction environments. Thus, the evolution of the biological construct together with our events and interpretations belong to life. The interactions between these components suggest that life is a mathematical category of categories.
Section 2 presents a convincing argument in order to support the idea that the life category is best represented by the following categories: biology, capacity of interpretation, life scenes and necessary energy.
Life as we perceive it manifests itself on a finite time horizon. There are at least two reasons to consider that the present, as a moment of life, is a running of the future. First of all, no one can influence the moments of his/her birth and death. Secondly, no one has full control over all events in his/her life.
However, how can we explain the course of life without knowing it? Suppose that the course of life is a sequence of events waiting to be passed through the filter of consciousness. The filter always works at the present moment. The flow of time brings these events into the sights of consciousness. All the events of the moment that take place at the level of the biological construct as well as at the level of the interaction environment generate a tension as an effect of the level of nervous excitement. The human effector must have the capacity to read these tensions.
The initial moment of life, the state of sleep, the state of wakefulness and the final moment of life cover completely our life, and therefore we will consider them as fundamental moments and states of life.
What does the human effector read at each and every moment? The presence of tensions means the presence of life and that is why we consider tensional information as vital.
Section 3 presents the construction and representation of the tensional information read by a reader in order to implement/simulate the fundamental moments and states of life. This construction is the exclusive creation of the authors.
The paper is organized as follows:
Section 1—Introduction;
Section 2—The issue of the present and the mechanism of human life;
Section 3—Topological modelling of the tensional information, where we present topological preliminaries, construction and representation of the tensional information, and representations of the fundamental moments and states of life;
Section 4—Conclusions.
2. The Issue of the Present and the Mechanism of Human Life—Hypotheses
The construction of a simulation mechanism for human life (HL) is an ambitious project. Human existence must be justified by deep reasons capable of explaining it. Their manifestation becomes possible in the presence of a generator of life.
Life [
1,
2] means more than its existence. It means biology, orientation by senses, interpretations, perceived frames of the life scenes and, so on. These aspects explain why human life is unique.
The meaning of life is unknown, as long as the human species is not capable of configuring the future in its smallest details. The human species indeed progresses, and its progress influences the future. What if this progress as well as all our actions belonged to our future? Let us consider the first moment of life. The whole life, except the first moment, is projected in the future. The passing of time will expand the past, contract the future up to the final moment of life and show us our future in every moment. So, the source of the present is always the future, whereas the source of the past is always the present (). Since is essential in the approach to life simulation we will treat the human effector in relation to this hypothesis.
Our inability to have memories from the future does not mean that the future does not exist. However, in every moment of life, we access a moment from the future. What reason can justify our inability to access the future? The stake of our life [
1,
2,
3] is hard to guess, as long as we are not the masters of our own lives. For example, we cannot control the initial moment of life or the transition to death. Moreover, no one can explain their own experience of these two important life events. A possible answer to the question above is given by the need to experience life in the most natural way possible. Why is that? If we have a future, then the future includes us, together with the life scenes, life events, and so on. A convincing answer in agreement to
would be that the whole life is a test that assesses how we interpret what happens to us.
A human being is a bio-psycho-social entity. So, the presence of life is a consequence of the synchronous functionality of these three attributes (). The biological attribute is represented by the biological programme, the psychological attribute is represented by the interpretations provided by the human entity at every moment of his/her life, whereas the social attribute is given by the programme of the life scenes that include social interactions. The biological, psychological and social programmes, function simultaneously, aligning a sequence of the biological programme with a sequence of the psychological programme and a sequence of the social one at every moment of life.
Human beings are simple effectors of their life programmes () as a consequence of . Their interpretations are generated by an internal source. These interpretations become possible in the presence of a capacity of interpretation. We advance the idea that this capacity depends on one’s own skills, on the ability to compare stimuli and to assign meaning to the comparisons that have been made, on relating one’s own initiatives to social norms and to one’s own beliefs.
How could we describe each moment of life? Two moments of life have the same chronology for all people: the initial and the final moment of life. On the other hand, there are two other states that complete our life: the state of wakefulness and the state of sleep. These states are important because most of our life is covered by them. Another important state is that of coma. However, life is continuous, and so are these moments and states. At the same time, the whole of life is a continuous state of tension (). So, all these four moments and states are tensions. To explain the continuity of human life, it is necessary to complete the list of the moments and states mentioned here with the transitions between them. Therefore, the human lifespan is a sum of the two moments mentioned above plus the periods recorded by the mentioned states plus the periods recorded by the transitions between these four moments and states of life.
Since life is a chronology of moments, states, events, interpretations, life scenes, and so on, we cannot disregard the notion of time. When does our life start? When does our life end? Do people’s lives have different units of time? How can we explain the continuity of life between two consecutive moments? How can we explain that people interpret the same life scene differently? In the following, we will present a possible mechanism that provides an answer to these questions, and is useful in the construction of a life simulator.
As we mentioned above, a human being is a bio-psycho-social entity. For every living entity, the specificity of life is represented by his/her interaction with the environment. At the level of cell division, we cannot talk about life because the only interactions are electrochemical in nature. On the other hand, after the moment of death for a short time, the electrochemical interactions continue to manifest inside the human body in the absence of life. So, there must be something, very special, which makes it possible to maintain the complex interactions between the inside and the outside of the human body (). We call this the necessary energy (NE). Therefore, the initial moment of life is given by the moment when the human body receives NE. At the same time, life ends when the human body no longer receives NE.
Human life depends on the presence of a source of energy that emits NE permanently to the human body (). The emission of NE is conducted with a certain frequency. What NE frequency does the human body receive? We could interpret a quantum of NE as a condition that has to maintain HL between two consecutive moments. At the same time, a human being becomes aware of the interaction environment only when he/she receives NE. To compute the NE frequency we need special watches. These watches should measure the fastest transformations that take place in the base anatomical units (BAU), as well as in the larger anatomical structures (LAS). In each and every BAU and LAS there are transitions between normal functionality, altered functionality and dis-functionality. So, for each BAU and LAS, we need a very accurate watch capable of measuring the intervals of time recorded for the transitions normal functionality to altered functionality, altered functionality to normal functionality and altered functionality to dis-functionality, and also the intervals of time recorded for each of these types of functionality. Another watch, which also acts at the biological level, measures the intervals of time necessary to cross the transitions “the initial moment of life to the state of sleep”, “the state of sleep to the state of wakefulness”, and vice versa, “the state of sleep to the final moment of life” and also the intervals of time recorded for each of these two states. All these intervals recorded over a lifetime allow us to compute the fundamental interval of time (FIT). This is given by the size of the interval of time that generates, by multiplication, the other recorded intervals of time. So, FIT works as a scaling factor for all intervals of time. At the same time, FIT has to be interpreted as a unit of time for life.
What is the connection between NE and FIT? First of all, NE assures the continuity of life. Secondly, the continuity of life presupposes a huge number of adaptive sequences, considered as frames of life, which are a consequence of the existence of FIT. To explain the continuity of life, FIT should coincide with the size of the interval of time in which the source of energy emits a NE quantum to the human body. We can interpret the measure as a veritable frequency of life that indicates the number of NE quatums received by the human body in a second. This should be a personalized constant for every human being. The number of life sequences throughout lifetime is given by the ratio . This number can be huge.
How can we explain the different interpretations given by human beings to the same life scene? FIT coincides with the interval between two frames of HL. Suppose that two human beings belong to the same life scene for 1.2 s, and have the following FITS: s, s. The first human being experiences four frames of life at 0 s, 0.4 s, 0.8 s, and 1.2 s, whereas the second one experiences seven frames of life at 0 s, 0.2 s, 0.4 s, 0.6 s, 0.8 s, 1 s, and 1.2 s. It is easy to observe that the second human being has three additional life frames at 0.2 s, 0.6 s and 1 s that can generate different interpretations.
Each and every human being has a unique life frequency. However, human beings belong to the human species. So, at the level of the human species there are a very large number of life frequencies. Moreover,, the human species is one of the species of the Universe. As a consequence, there are a huge number of life frequencies in the Universe. Sustaining life in the Universe can be explained by the presence of a unique source that emits NE using its proper frequency. To transmit NE to each human being, the proper frequency of the unique source is transformed by a block of multiplication into a personalized life frequency, as indicated in
Figure 1.
What can we say about the frequency of the NE source? From all FITS recorded in the Universe, we can compute a scaling factor. This scaling factor is the specific FIT of the NE source (FITNEs) and the value of the ratio 1/FITNEs is the emission frequency of the NE source. FITNEs is the time unit of life on the scale of the Universe.
2.1. Representation of the Category of Human Life
How can a human life be approached in its entirety? The specialized literature is rich in approaches to life from a physiological and interpretative perspective [
4,
5,
6,
7,
8]. Some longitudinal studies analyze the evolution of the human lifespan with the purpose of finding some of its particular aspects [
9]. Other studies highlight the role of technology in improving life quality and also in increasing lifespan [
10,
11,
12]. Using the hypothesis
and NE we can associate HL with a mathematical category [
13,
14] of categories (see
Figure 2). The objects of the mathematical category are: biology (B), capacity of interpretation (CI), life scenes (S) and NE. The arrows between these objects are denoted by (Fi) and represent functors.
The morphisms of the category Life are presented below:
To represent the fundamental moments and states of life, we define a subcategory at the level of category B, one whose objects are tensional coherences. The representations of the tensional coherences through topological spaces are the subject of
Section 3. These representations are important for our approach because they constitute the information read by the reader to implement the fundamental moments and states of life.
2.2. Logical Schemes of the Life Programme
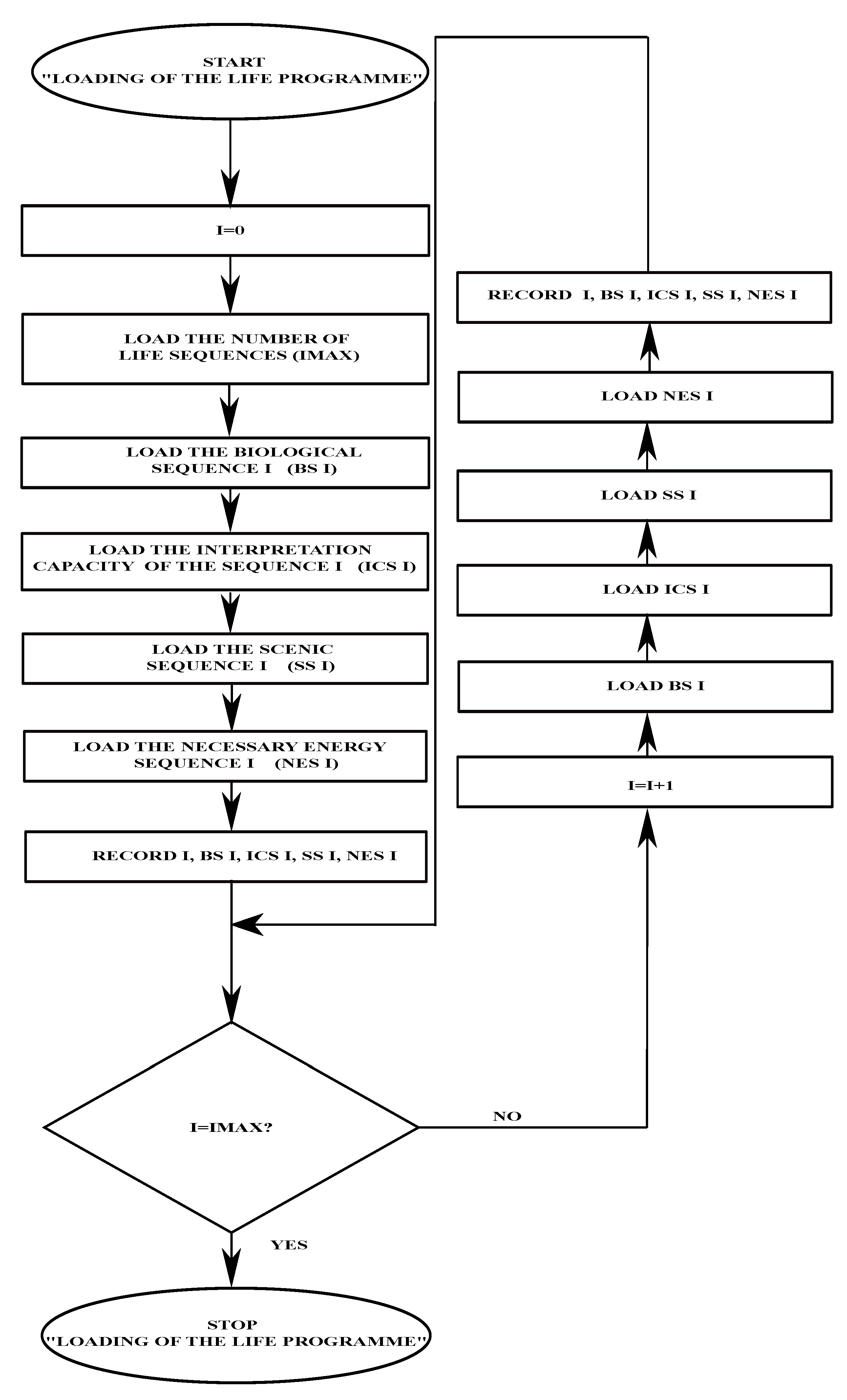
We consider that HL is the process of running life sequences through a complex software. Each life sequence includes the biological, psychological, and social events manifested in FIT and the quantum of NE received by the human body. All of these are the inputs of the life programme, whereas the output is represented by the interpretations recorded throughout life.
The present exists as a consequence of the existence of the future. So, the future must be configured before it is run. Alternatively, in order to run the present, we need a previous loading of the future. Running the life programme requires the loading of this programme (see
Figure 3 and
Figure 4).
3. Topological Modelling of Tensional Information
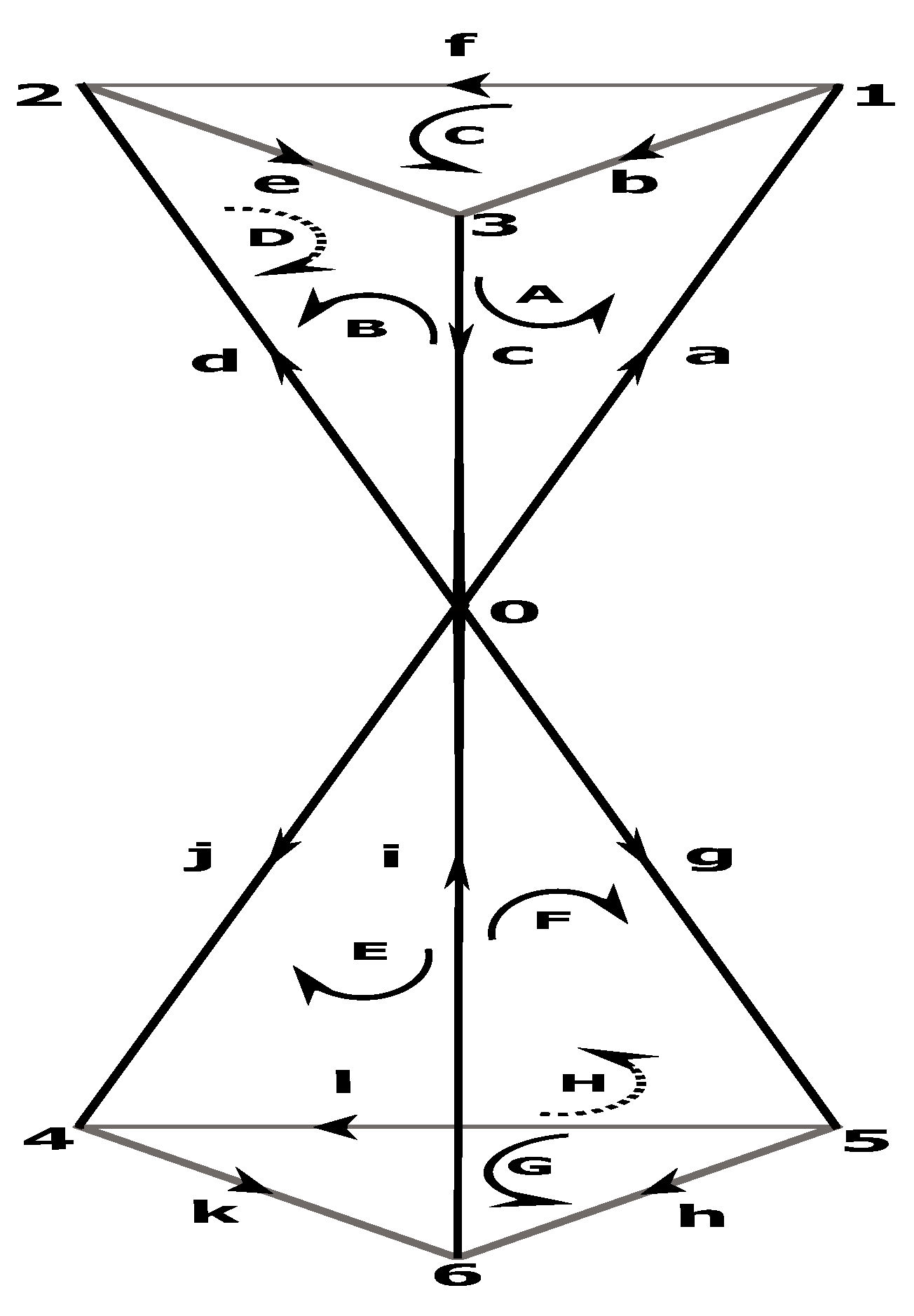
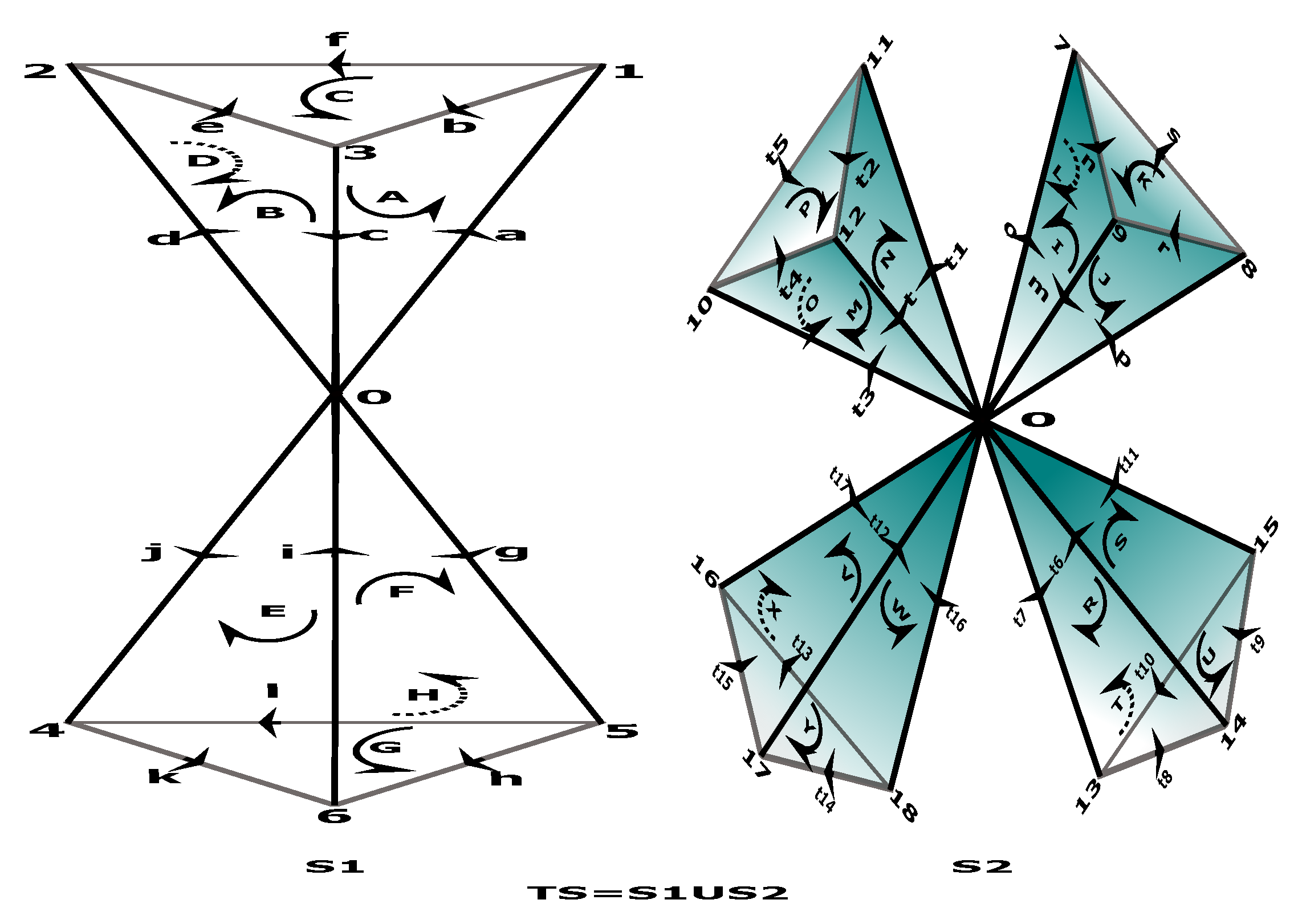
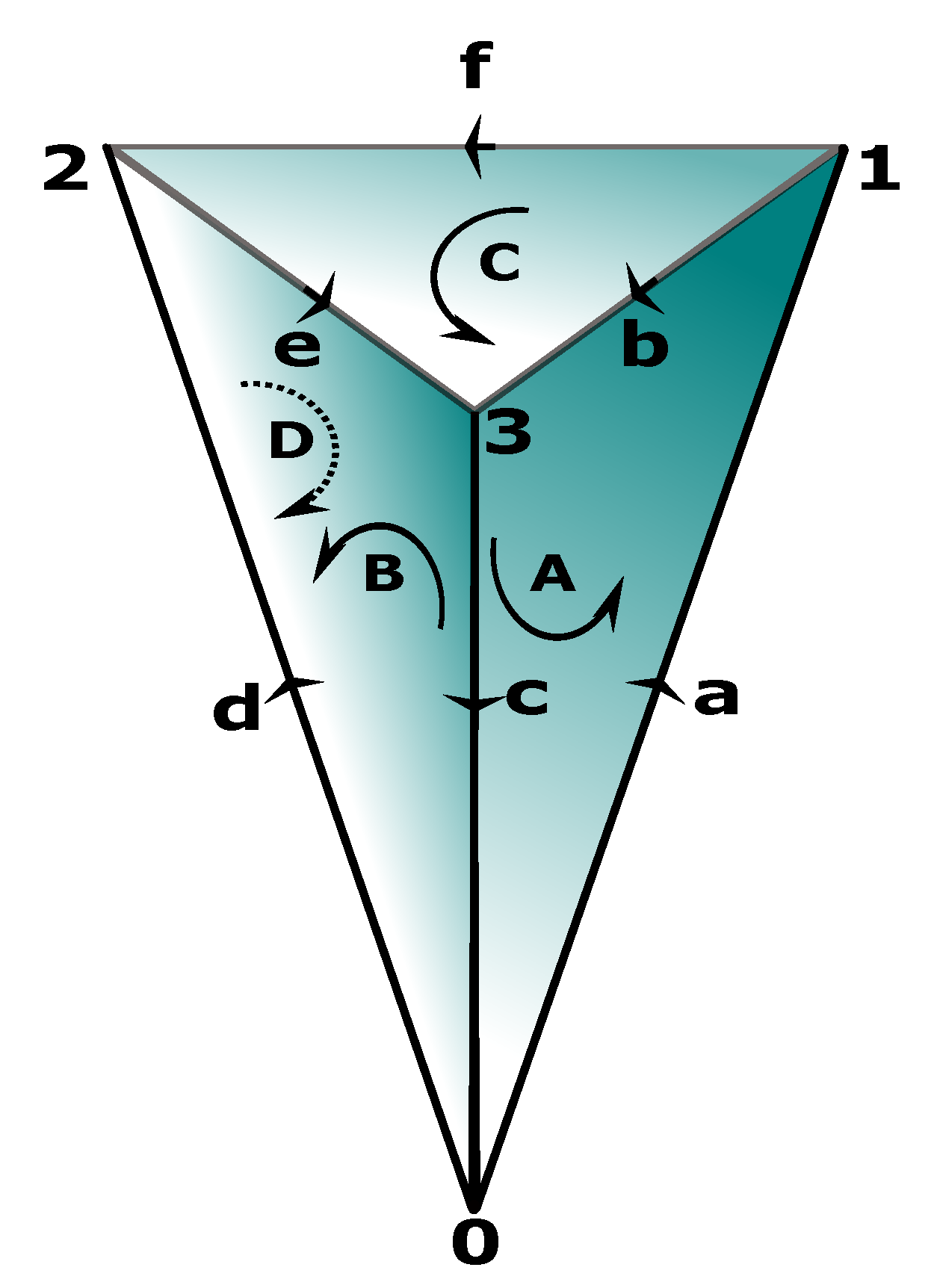
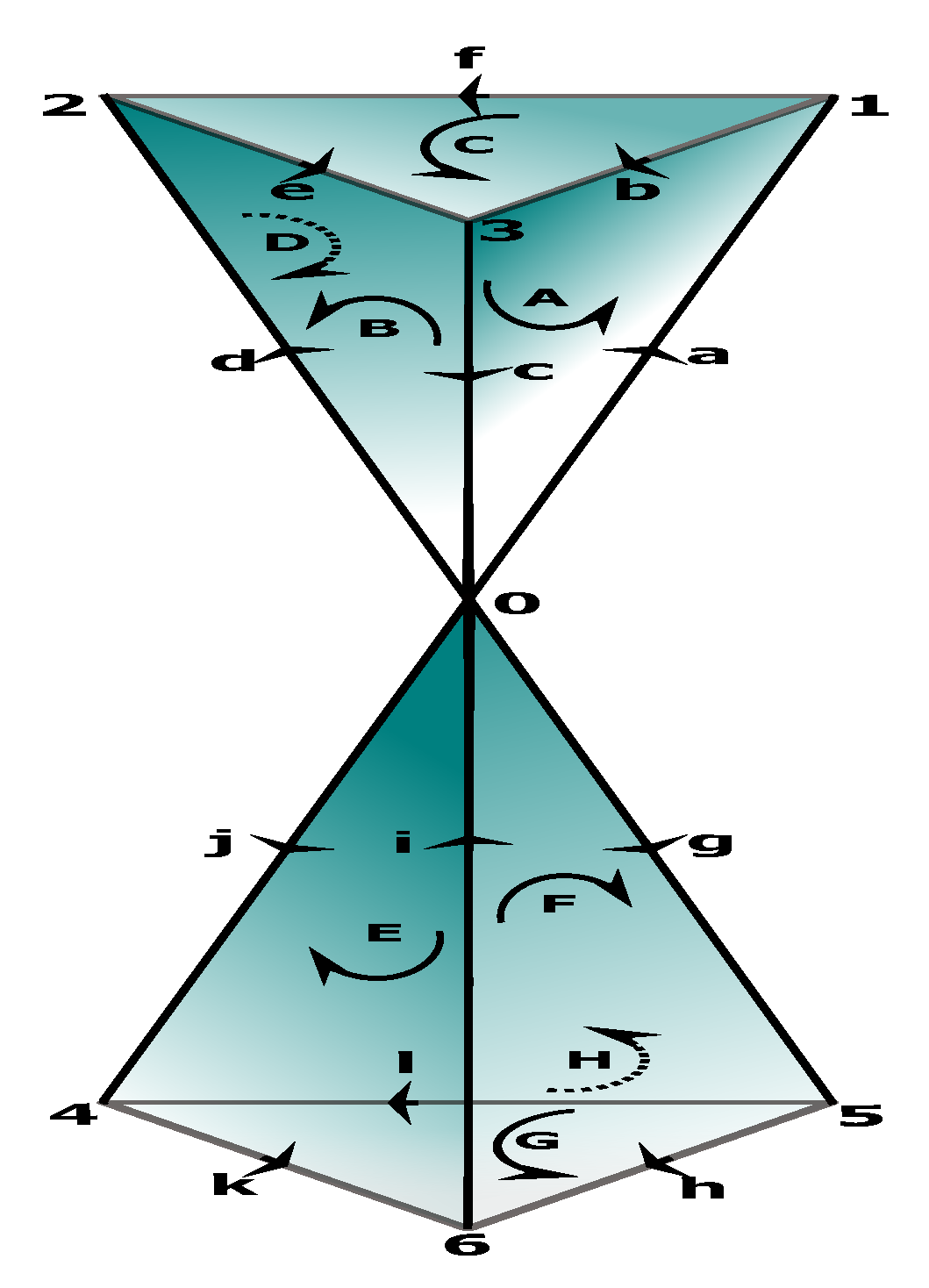
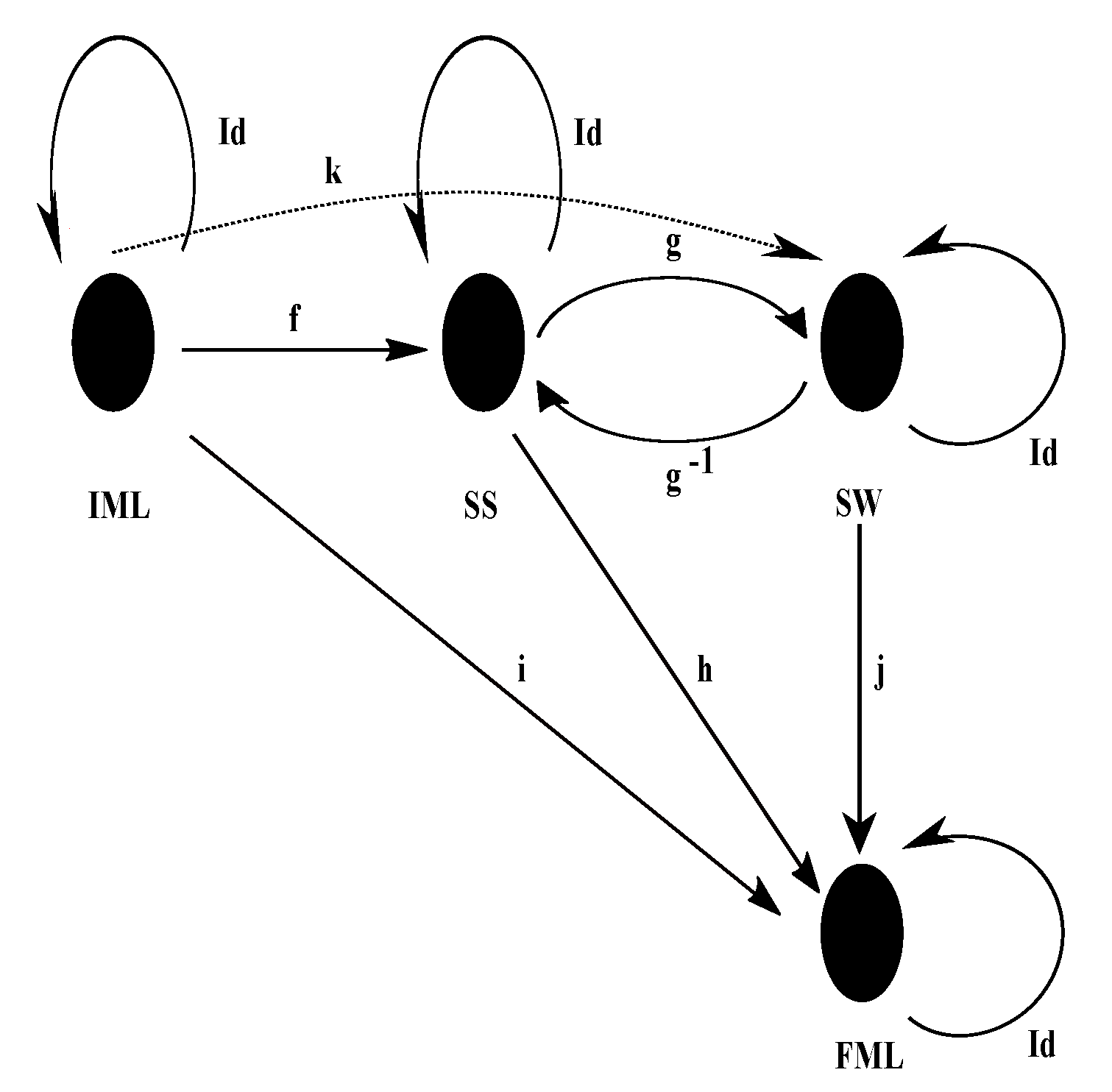
Our life is a continuous state of tension, and its fundamental moments and states are tensional coherences. The objects of the tensional coherence subcategory (see
Figure 5) are: the initial moment of life (IML), the state of sleep (SS), the state of wakefulness (SW), and the final moment of life (FML). The morphisms of the subcategory are:
,
f,
g,
,
h,
i,
j,
k.
In this section, we will present the tensional information read by the human effector to implement the fundamental moments and states of life, as well as the transitions between them.
3.1. Topological Preliminaries
Definition 1 ([
15]).
A topological space is an ordered pair , where X is a set and τ is a collection of subsets of X, satisfying the following axioms:- (1)
The empty set and X itself belong to τ.
- (2)
Any arbitrary (finite or infinite) union of members of τ still belongs to τ.
- (3)
The intersection of any finite number of members of τ still belongs to τ.
The elements of τ are called open sets and the collection of τ is called a topology on X.
Definition 2 ([
16]).
A topological space X is path-connected if for any there is a continuous map such that and . Definition 3 ([
16,
17]).
A topological space X is contractible if the identity map is homotopic to a constant map given by for some or IF. Theorem 1.
A contractible space is path-connected.
Proof of Theorem 1.
Let X be a contractible space and C the constant map given by for some . Since X is contractible there is a such that . Let be a continuous map. For each we define the map given by such that H ∘ r(0) = c and H ∘ r(1) = u. Thus, c and u are joined by the path H ∘r. □
Theorem 2.
A closed n-ball is contractible.
Proof of Theorem 2.
Obviously a closed n-ball is path connected. Let X be the space of a closed n-ball and , where . Then i: is the inclusion map and C is the constant map given by C for all . We define the homotopy H: by H for all and . Then, H = I = i ∘ C and H = C. Therefore, IC. □
Definition 4 ([
18]).
A set is convex if the line segment between any two points in C lies in C, i.e., if for any two points , and any with we have (see Figure 6 and Figure 7). Definition 5 ([
18]).
The convex hull of a set S is the smallest convex set containing S (see Figure 8). Definition 6 ([
19]).
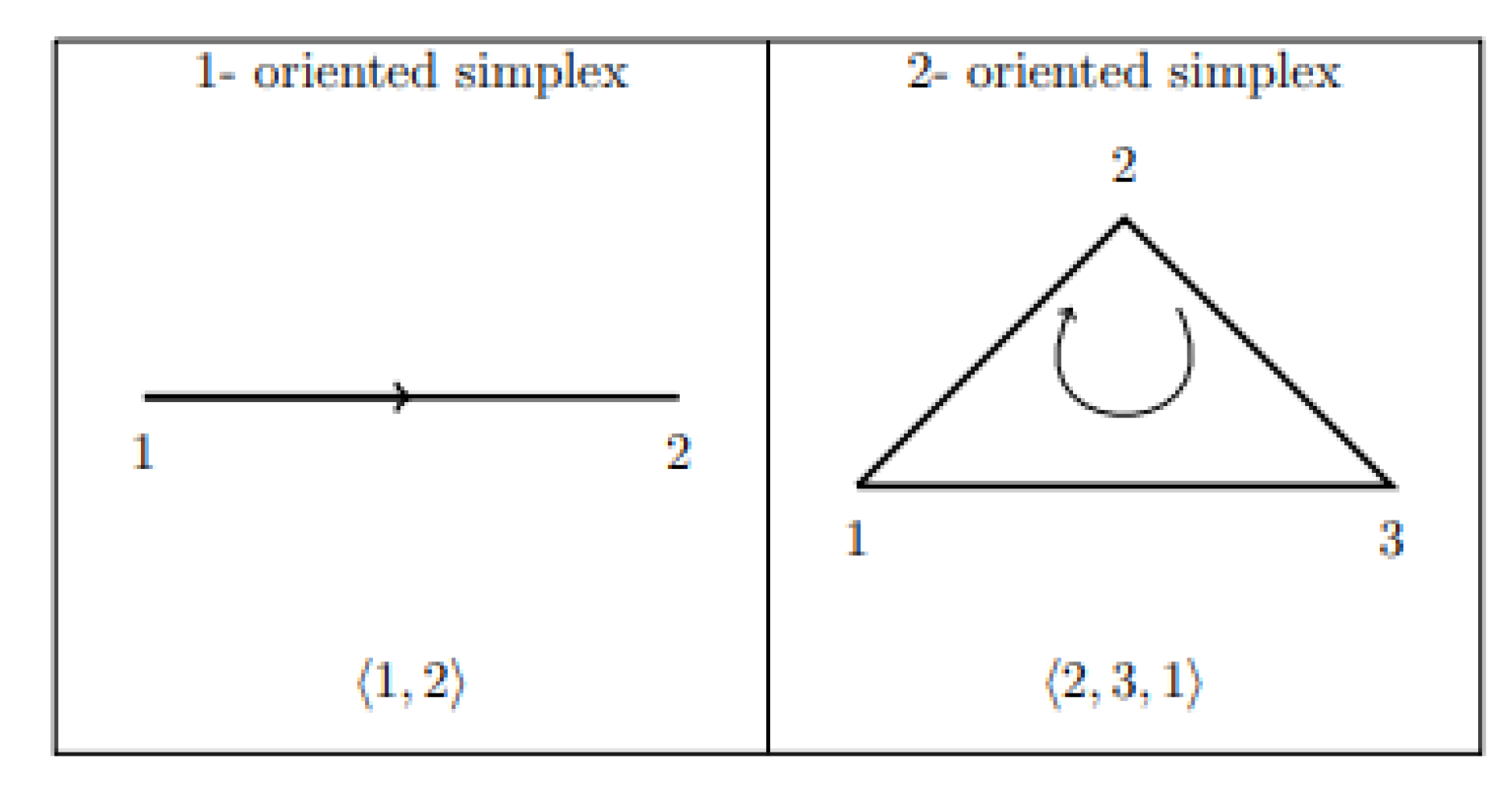
Let be a geometrically independent set in . We define the n-simplex σ spanned by to be the set of all points x of such that , where and for all i. The numbers are called the barycentric coordinates of the point x of σ with respect to . A 0-simplex is generated by one point, a 1-simplex is generated by two points, a 2-simplex is generated by three points, a 3-simplex is generated by four points, …, an n-simplex is generated by (n + 1) points (see
Figure 9).
Definition 7 ([
20]).
A simplex together with a specific choice of orientation is called an oriented simplex (see Figure 10). Definition 8 ([
21]).
A finite simplicial complex K is a finite collection of simplices in some euclidian space such that:- (1)
if , then every space of s also belongs to K.
- (2)
if then is either empty or a common face of s and of t.
Definition 9 ([
22]).
Let and be two groups. A group homomorphism from to is a function such that for all x, y we have . Theorem 3 ([
22,
23]).
(First Isomorphism Theorem) If is a group homomorphism, then Ker and G/Ker . Definition 10 ([
17]).
The sequence of the groups A, B and C ![Mathematics 10 04313 i001 Mathematics 10 04313 i001]() is a short exact sequence [24] if α is injective, β is surjective and Ker β = Im α.
is a short exact sequence [24] if α is injective, β is surjective and Ker β = Im α. Definition 11.
Any exact sequence that is not a short exact sequence is a long exact sequence.
Definition 12 ([
25]).
A cochain complex is a sequence of abelian groups (or modules over a ring) and their homomorphisms ![Mathematics 10 04313 i002 Mathematics 10 04313 i002]() such that
such that is called a coboundary operator.
The elements of Ker are called cocycles of dimension n and the elements of Im are called coboundaries of dimension n.
Example
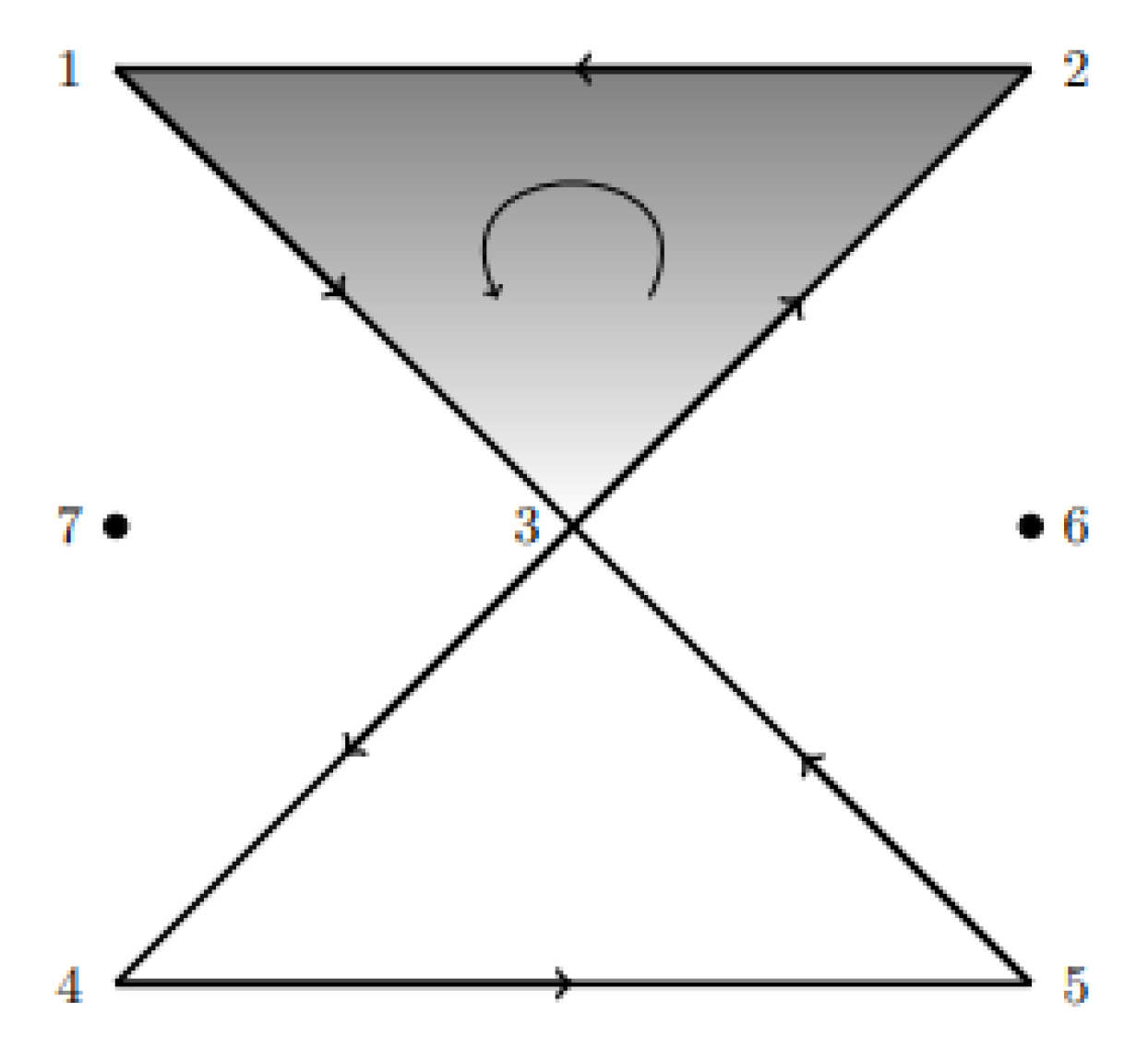
The simplicial complex K presented in
Figure 11 has seven 0-simplices, six 1-simplices and one 2-simplices. Thus
The cochain complex for this simplicial complex is
It is easy to verify the relation . For instance and .
Definition 13 ([
25]).
A chain complex is a sequence of abelian groups (or modules over a ring) and their homomorphisms indexed by integers ![Mathematics 10 04313 i004 Mathematics 10 04313 i004]() such that
such that Definition 14 ([
17]).
A boundary homomorphism is defined as follows: , , where σ is an oriented simplex and means that is omitted. The simplicial complex presented in
Figure 11 allows us to check the relation
. Considering the simplicial subcomplex
there is no problem to verify that
. Indeed,
.
Definition 15 ([
26]).
For the factor group is the n - dimensional cohomology group of G with coefficients in A. Moreover, the factor group can be computed using the formula Ker /Im , where is a coboundary operator.
Theorem 4.
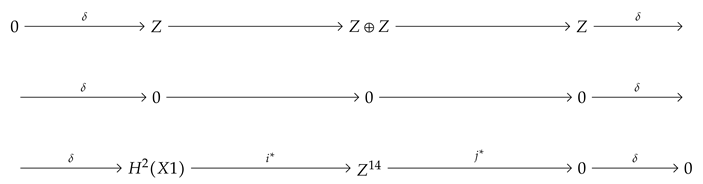
Let X be the space consisting of a single vertex . Then for n = 0, and for n ≠ 0.
Proof of Theorem 4.
As X has a single vertex, we obtain the sequence
![Mathematics 10 04313 i005 Mathematics 10 04313 i005]()
Im
. Since Im
we have ker
. Thus H
=
= Z. There are no n-simplices with
, and therefore
for
. □
Theorem 5.
The cohomology groups are: Z if n = and 0 if n∈N.
Proof of Theorem 5.
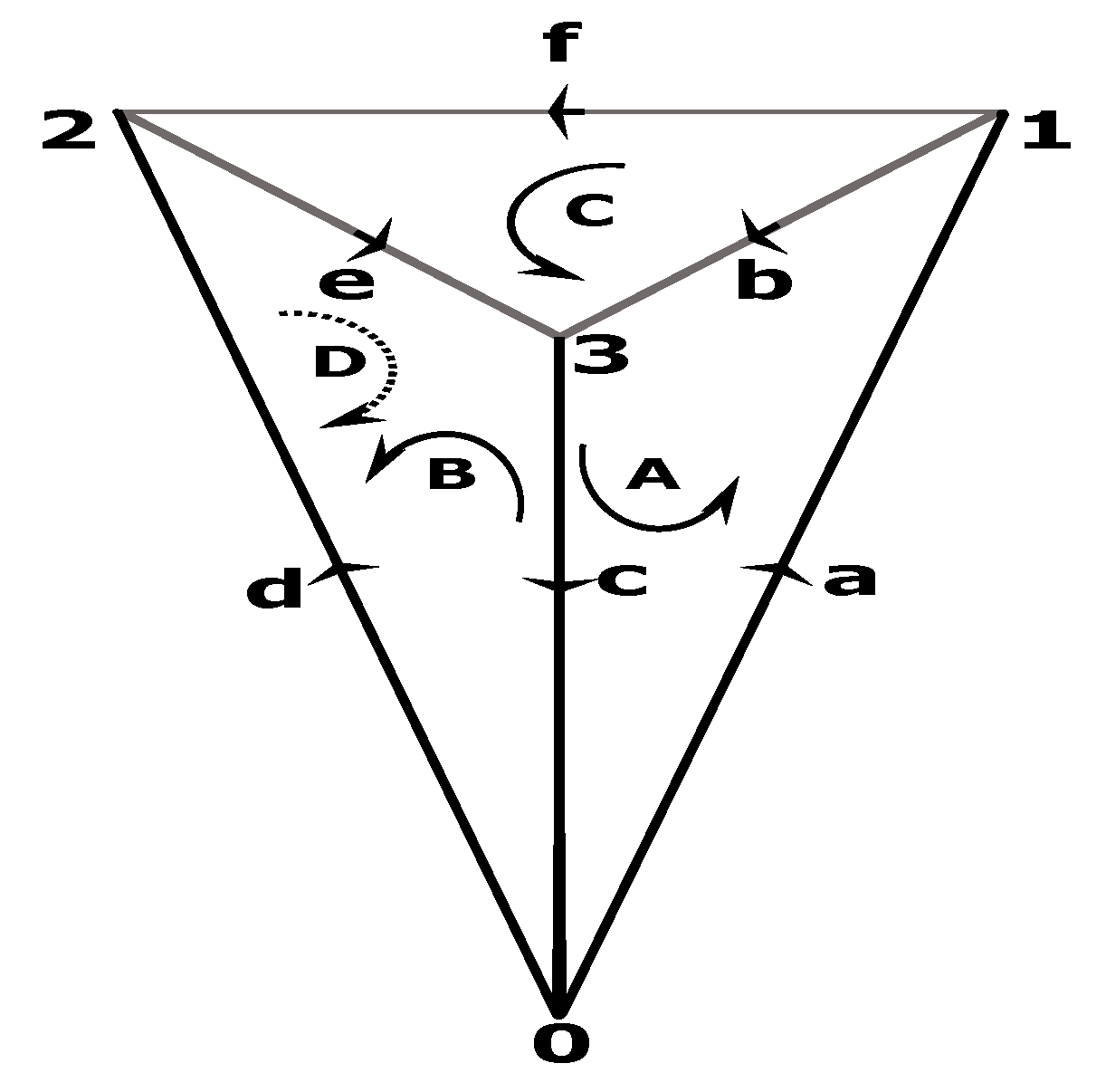
is homeomorphic to tetrahedron (see
Figure 12).
The simplices of tetrahedron are presented in
Table 1.
Now, let us compute
.
In order to compute 1-cochains, we need the following calculations:
Thus, we obtain 1-cochains,
To compute the cohomology groups of a 2-sphere we need to find ker , ker and ker .
ker
It is easy to see that ker .
ker
We get:
where
.
The solution of the equation
is
Hence
ker
Let us compute
, where
.
Solving the equation
we get the solution:
Hence, the group of one-dimensional cocycle is
Thus, we find 1-cocycles:
In the following, we will compute the coboundary groups , and .
It is clear that .
The rank of the matrix
is 3. The group of one dimensional coboundary is
Therefore, 1-coboundaries are:
The rank of 1-cochain matrix
is 3. The group of two dimensional coboundary is,
Since
we obtain
, so, 2-cocycles are
,
,
and
. Thus, the cohomology groups of a 2-sphere are:
□
Definition 16 ([
16]).
Let X be a space. Suppose G is an additive group of a commutative ring with identity. Let and . Suppose also is a simplex in X. and are a k and a l-simplex in X. The cup product is defined by the formula . Theorem 6 ([
17]).
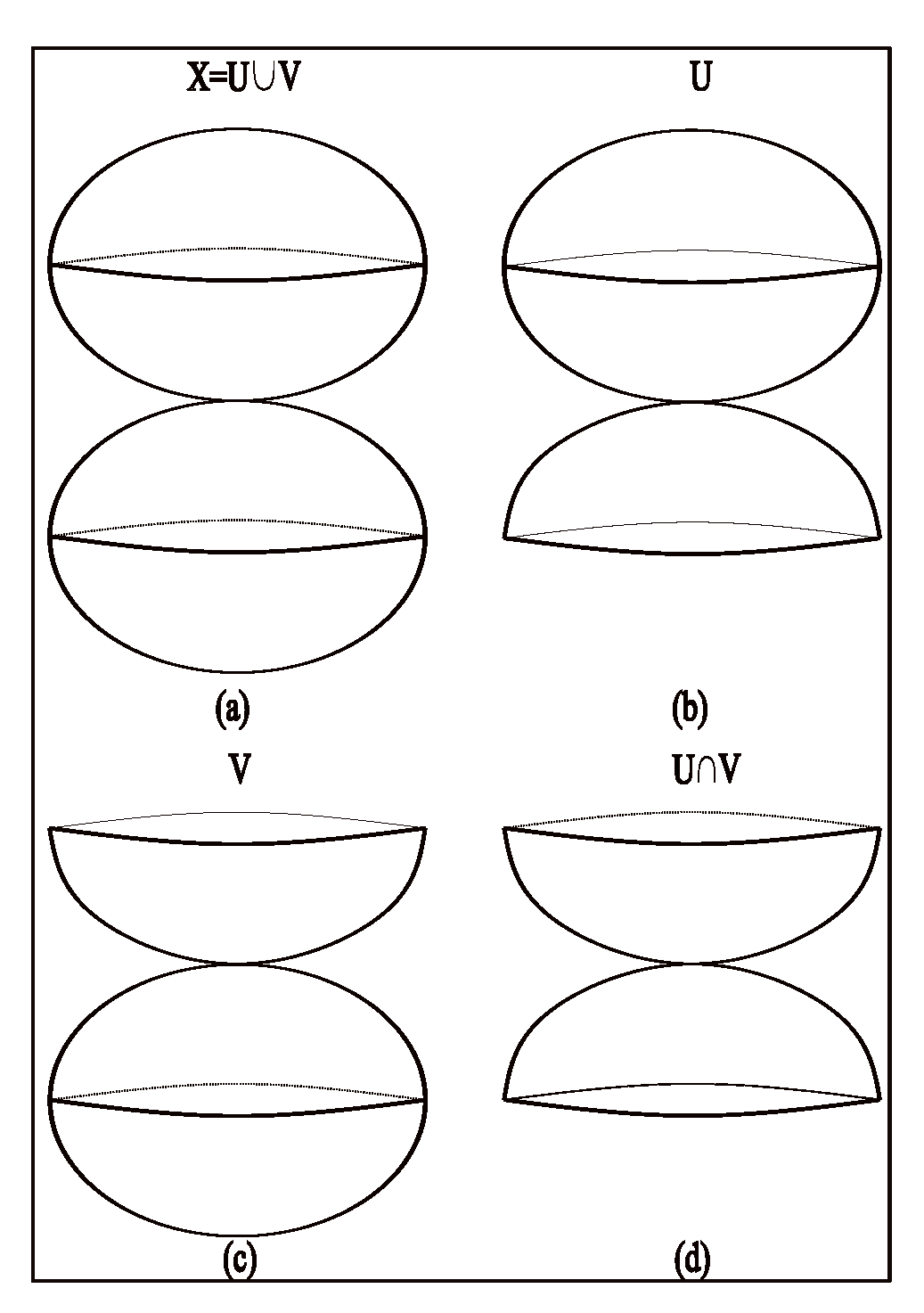
(Mayer-Vietoris sequence) Let X be a topological space, and let be subspaces such that X is the union of the interiors of A and B. Then, there exists a long exact sequence 3.2. Construction and Representation of Tensional Information
How can we explain the activation of the processes responsible for inducing the fundamental moments and states of life? These processes take place at the level of the nervous system. allows us to state that their activation can be explained as an effect of reading the representations of the fundamental moments and states by a device that operates at the level of the human effector.
3.2.1. The Hypothesis of the Division of Tensional Content
As we saw in the second section, a human effector constantly receives NE during his/her life. So, the received necessary energy (RNE) must be suddenly consumed in order to preserve it in time. How can we explain the mechanism of this consumption? To consume RNE, a device responsible for this mechanism should ensure the generation of needs, which manifest as tensions. Why is that? Because a good reason for the consumption of RNE is represented by the extinguishing of these tensions. The tensions must be cumulative in order to be treated globally as a tensional content (TC). To be perceived, the tensional content must have at least a minimal tensional coherence or a minimal tensional density. Therefore, from a statistical point of view, there is a perfect association between RNE and TC observed as a tensional quantity (fluid) necessary to consume RNE. As RNE is a constant, TC is obviously a constant over a lifetime. The maintenance of HL depends on the preservation of these constants.
However, human life cannot be reduced to its preservation. Otherwise, the whole existence of a human being would be exclusively monotonous.
What kind of mechanism is involved in the generation of tensional variation? This mechanism has to use TC to allow the simultaneous manifestation of both the tensional variation and life.
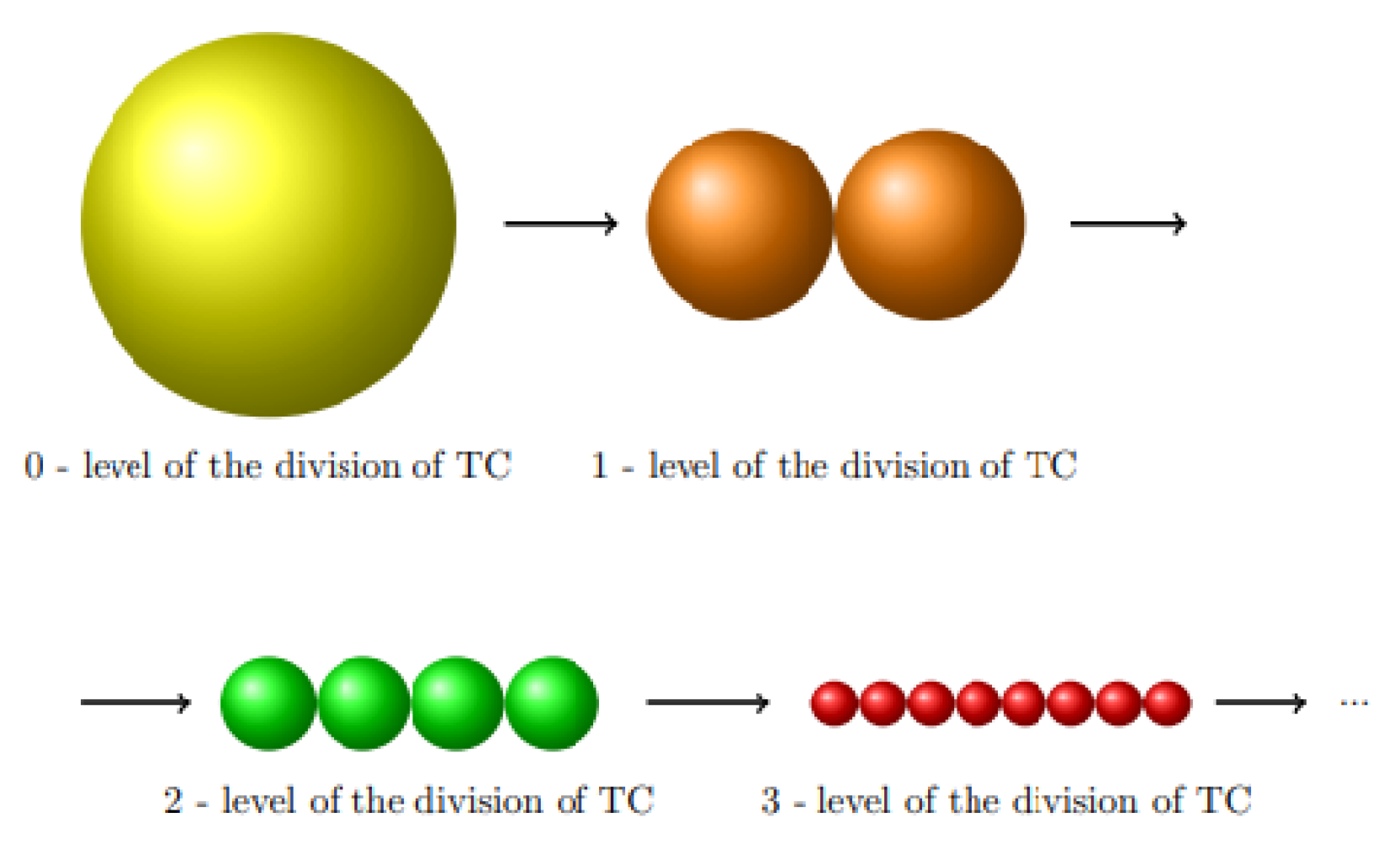
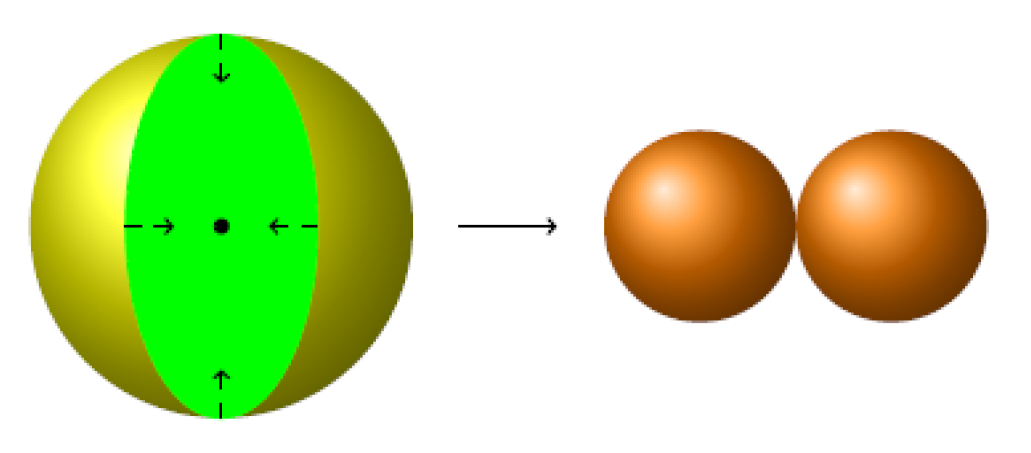
In the following, we will try to give a topological perspective to this mechanism. Let us represent tensional content by a ball of radius 1 mu, with the mass m. This representation allows us to compute tensional coherence using the well known formula,
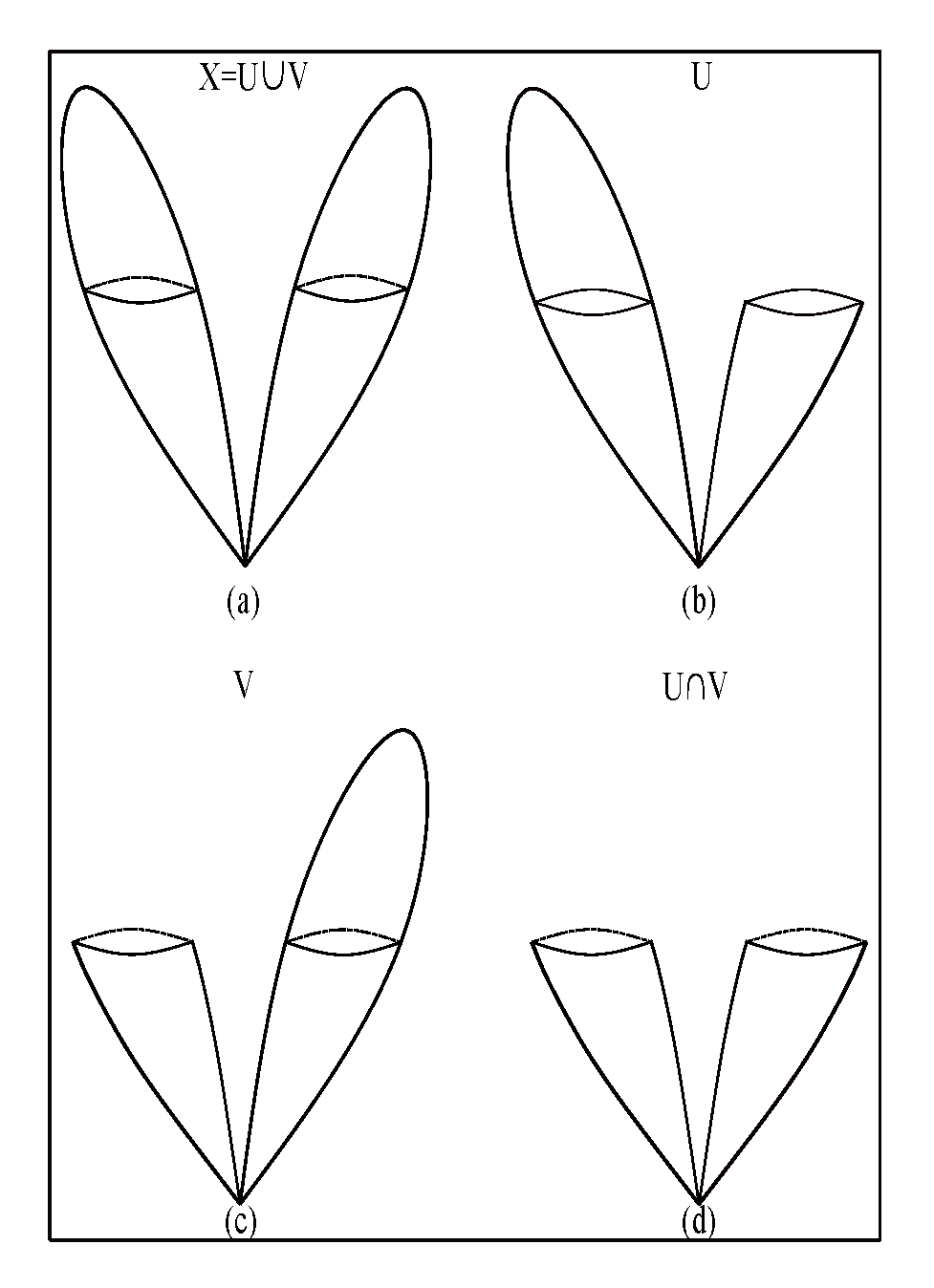
. Through a process of the type of cell division, two balls of radius 0.5 mu each result and this process may continue as in
Figure 13.
Thus, we obtain different levels of the division of TC with different tensional coherences (see
Table 2 ).
How can we explain the transition 0 - level of the division of TC to 1 - level of the division of TC (see
Figure 14)? A subspace of a ball is
, where
is a disk.
is contractible to a point (for instance to its center
). Indeed,
is path-connected. Let
, where
. Then i:
is the inclusion map and C
is the constant map given by C
for all
. We define the homotopy H
by H
for all
and
. Then H
= I
= i ∘ C and H
= C
. Thus I
C
.
Therefore, the first level of TC division is obtained by the contraction of the disk to its center. The following levels of TC division result in the same way.
Why does the TC division seem plausible? First of all, tensional content is a constant, as we have observed above. For a TC ball, with a radius r, a certain minimal tensional coherence for the preservation of life results. However, an increasing ball will determine the reduction of tensional coherence below the minimal level. Therefore, the repeated tensional division of TC leads to higher tensional coherences.
3.2.2. Diffuse Tension and Oriented Tension
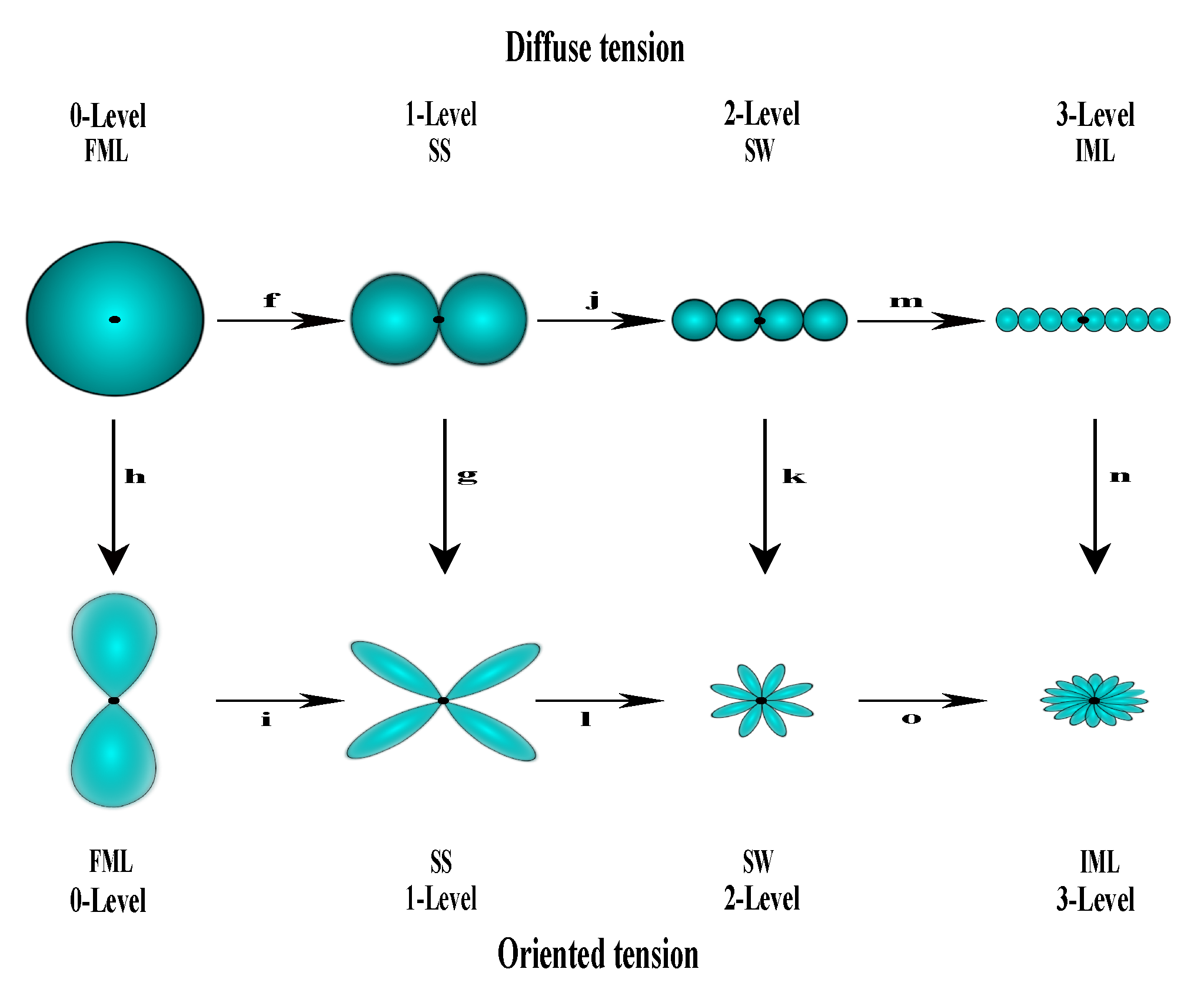
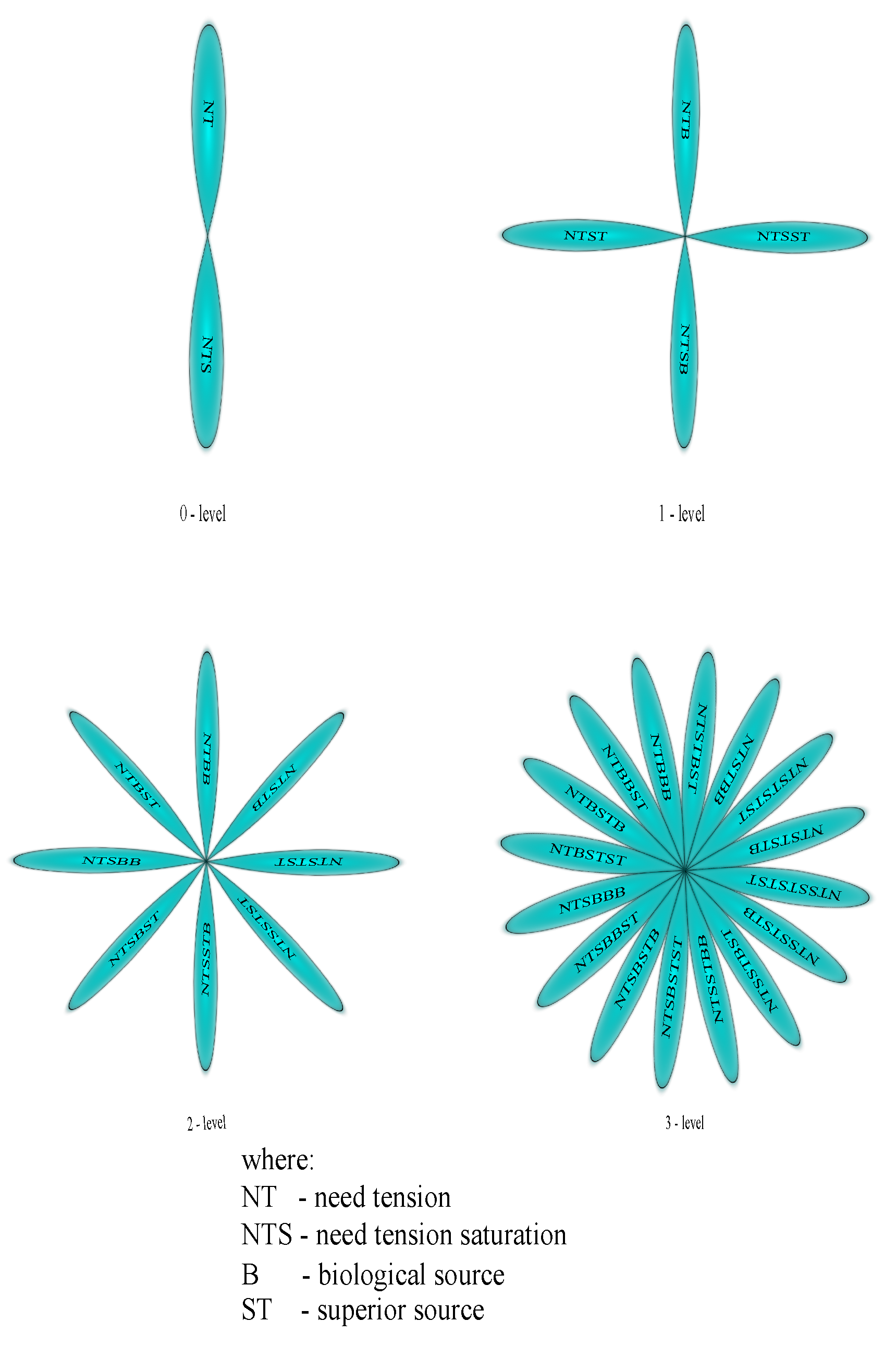
What is HL? In our opinion, HL is a continuous tension. Let us suppose that this tension is made up of two components: a diffuse tension (DT) and an oriented one (OT). The biological and psychological functionality (BPF) of any human being can be disrupted or not by tensions. However, BPF is conditioned and supported by the presence of tensions. We associate the BPF, which is not affected by tensions, with DT and the BPF, which is affected by tensions with OT. DT ensures the physical presence of the human being, whereas OT is the tensional component on which the consciousness of the moment manifests itself more or less intensely. Thus, it is clear that the coherence of DT is smaller than the coherence of OT. These two components are important because they ensure the preservation of life and the consumption of RNE.
How many levels of DT and OT division can be taken into account? Since there are four fundamental moments and states that can be described by their coherences, we will consider four levels of TC division.
The increase in the tensional coherence of each level of DT generates an increase in the tensional coherence of the correspondent level of OT, as indicated in
Figure 15.
Figure 15 should be understood only as a construction capable of explaining how the fundamental moments and states are generated from the tensional perspective.
The above diagram is commutative, where f, j, m, n, k, g, h, i, l, o are continuous maps. Moreover, this diagram suggests that IML and FML result from a multi-step process. Transformations of the cell division type of each level of DT (vertical maps) ensure the increase in tensional coherence, and also emphasize the sources of these tensions, as we will observe in the following.
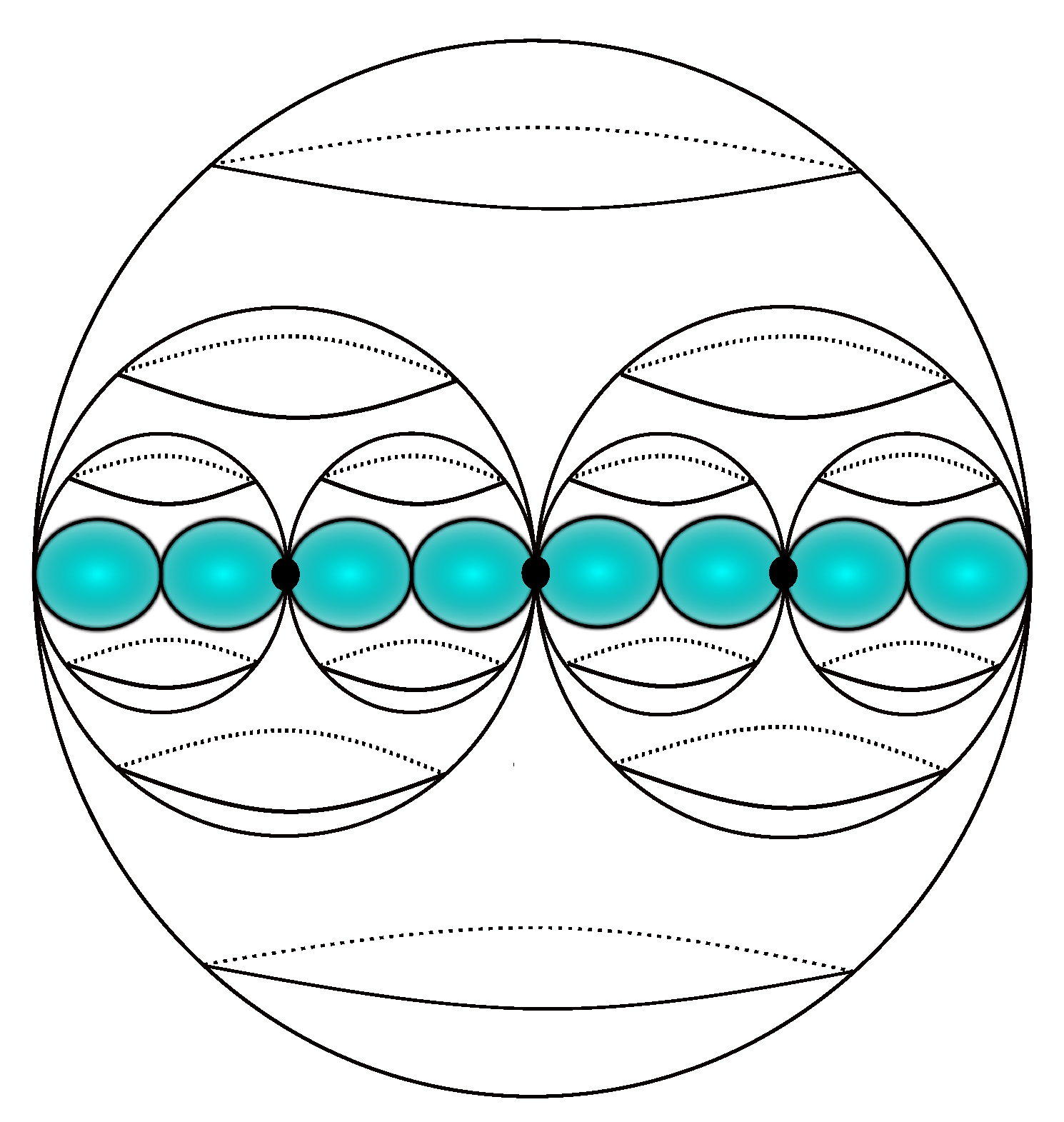
The successive transitions from the first to the last level of DT and OT presuppose the successive transfers of tensional content between these levels. Thus, the union of the levels of DT and OT are presented in
Figure 16 and
Figure 17. They are topological spaces that correspond to DT and OT at IML.
Let us define the sources of tension. Any tension perceived at the level of OT is generated by a need, and is limited by its saturation. Therefore, at the 0-level of OT, the tensional components are: the need tension (NT) and the need tension saturation (NTS). At the next level of OT, both NT and NTS have a biological source and a superior one. A superior source is a source that is not a biological one. Thus, at the first level, we have the following tensional components: the biological source of the need tension (NTB), the superior source of the need tension (NTST), the biological source of the need tension saturation (NTSB), and the superior source of the need tension saturation (NTSST). The following two levels (2-level and 3-level) can be described similarly (see
Figure 18).
3.3. Representations of the Fundamental Moments and States of Life
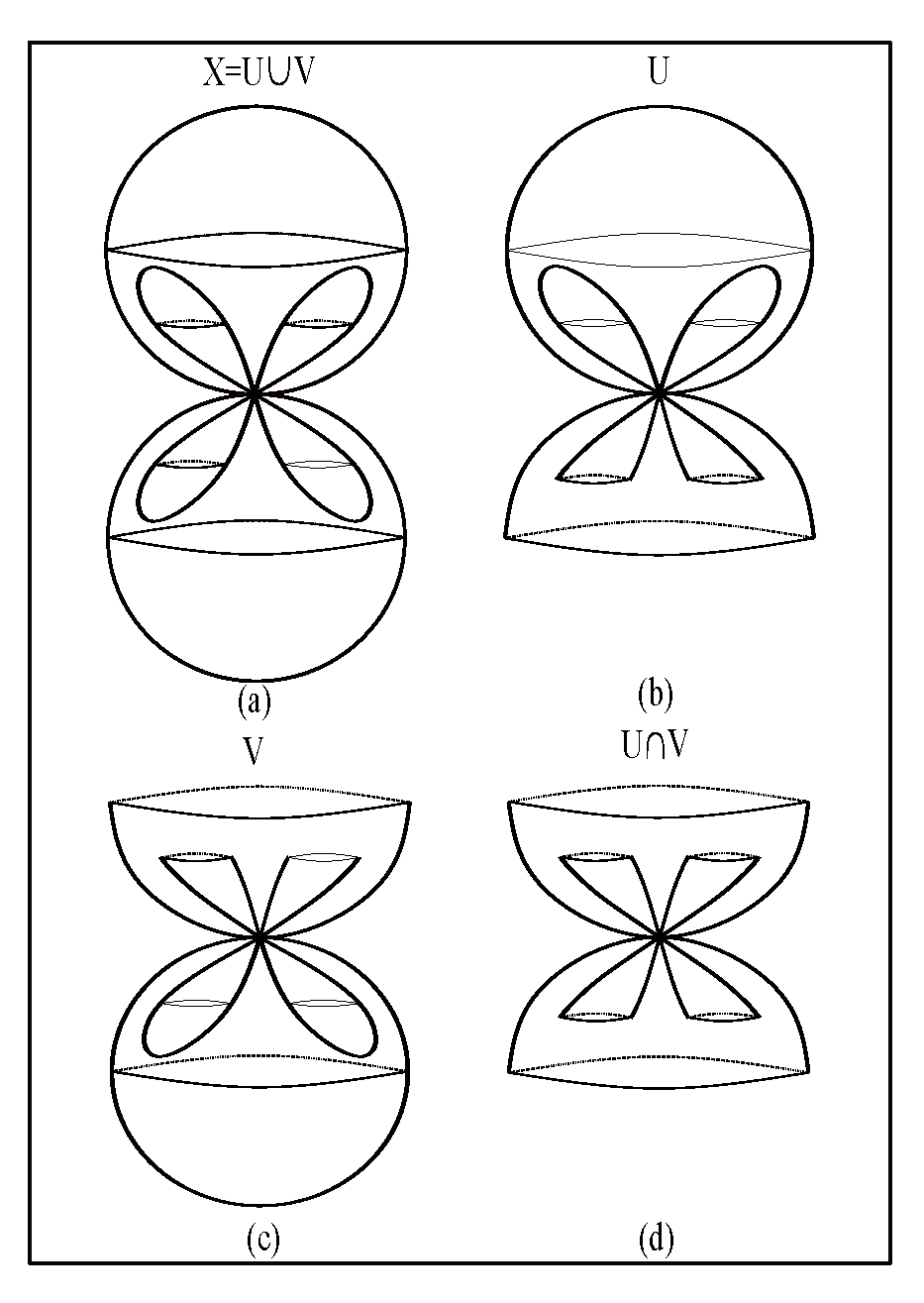
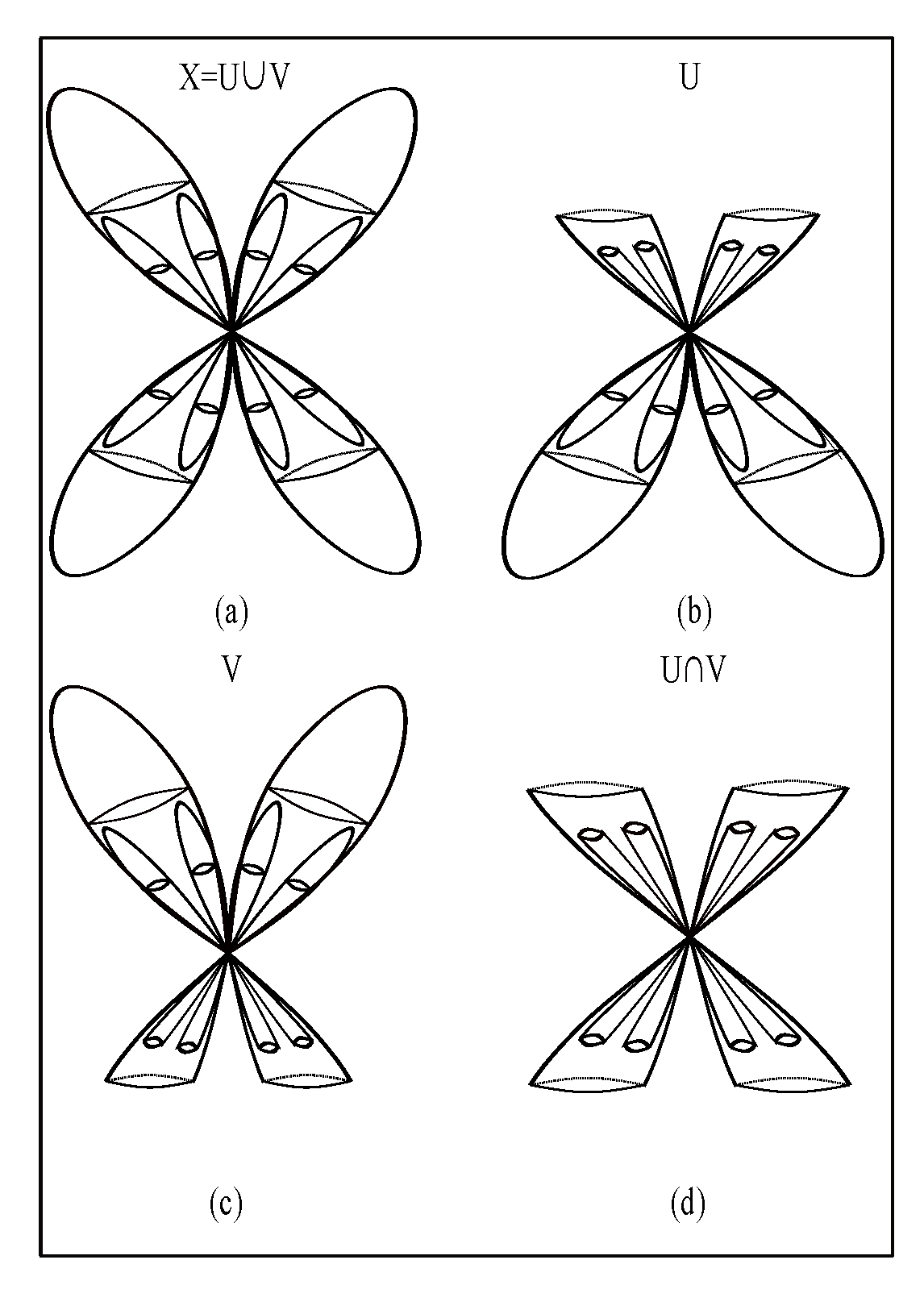
Why are the fundamental moments and states so important? In our opinion, two important aspects must be taken into account. First of all, each of them characterizes a particular tensional state determined by nervous stimulation. Secondly, the other tensional states appear against a background of fundamental moments and states. From the topological point of view, all the states that are not fundamental are representations equivalent to those that describe the fundamental states.
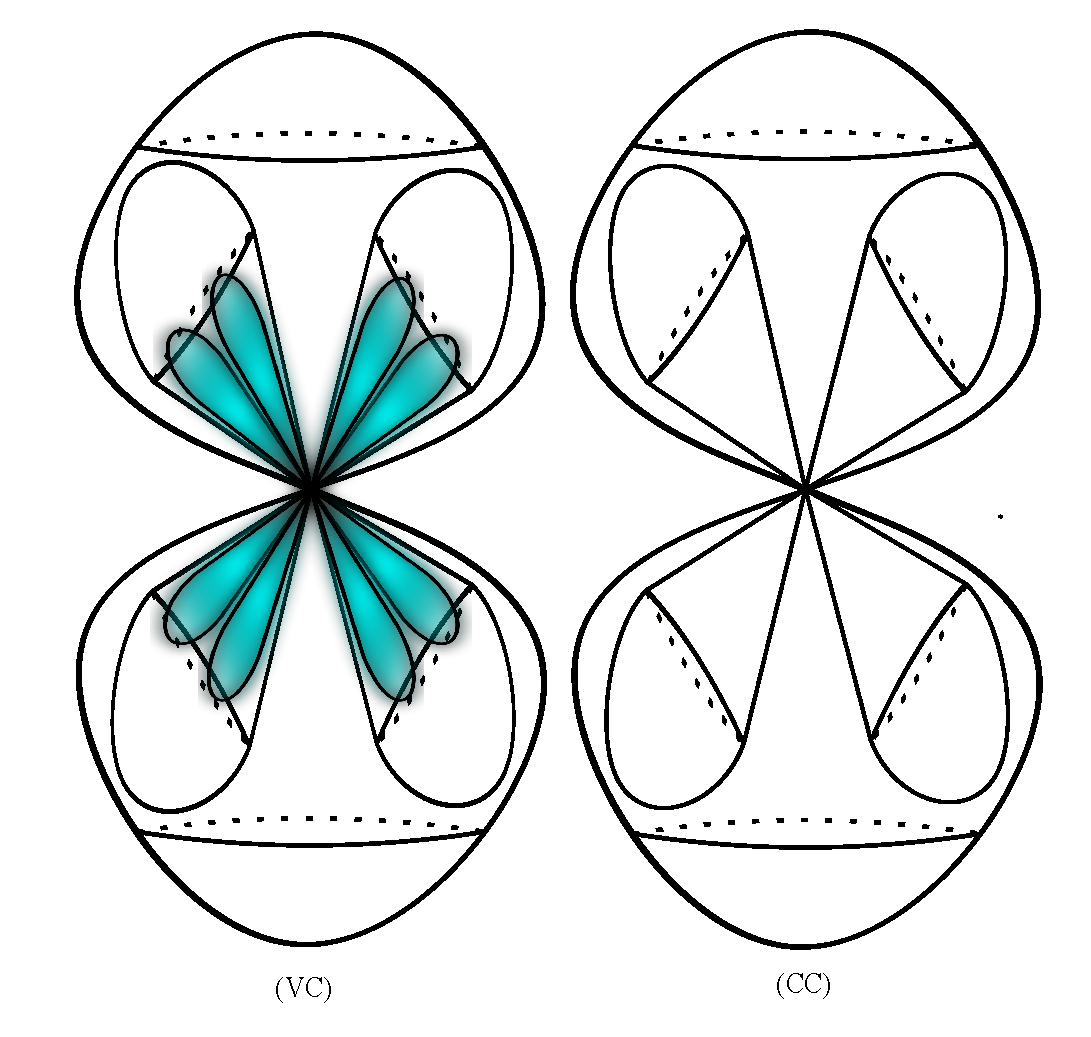
All moments of life must be read by a device that has to implement them as effective tensional states. That is why we will associate each of the fundamental and non-fundamental moments and states with a piece of tensional information (TI). The device contains two components: a component that treats TI as a necessity and a component that treats TI in terms of experiencing tension. Here, the term “necessity” must be understood as a mandatory moment of the predefined life. We call the first component the cold one (CC) and the second component the vulnerable one (VC).
How can we represent the fundamental moments and states of life? First of all, the levels of TC at DT division are essential because they explain, in terms of representations, the levels of TC at OT division. The exclusive specialization of our device in the reading of DT would ignore the sources of tensions that affect BPF and generate coherent behaviours focused on their extinction. Thus, the specialization of the device in the reading of both DT and OT, seems to be plausible.
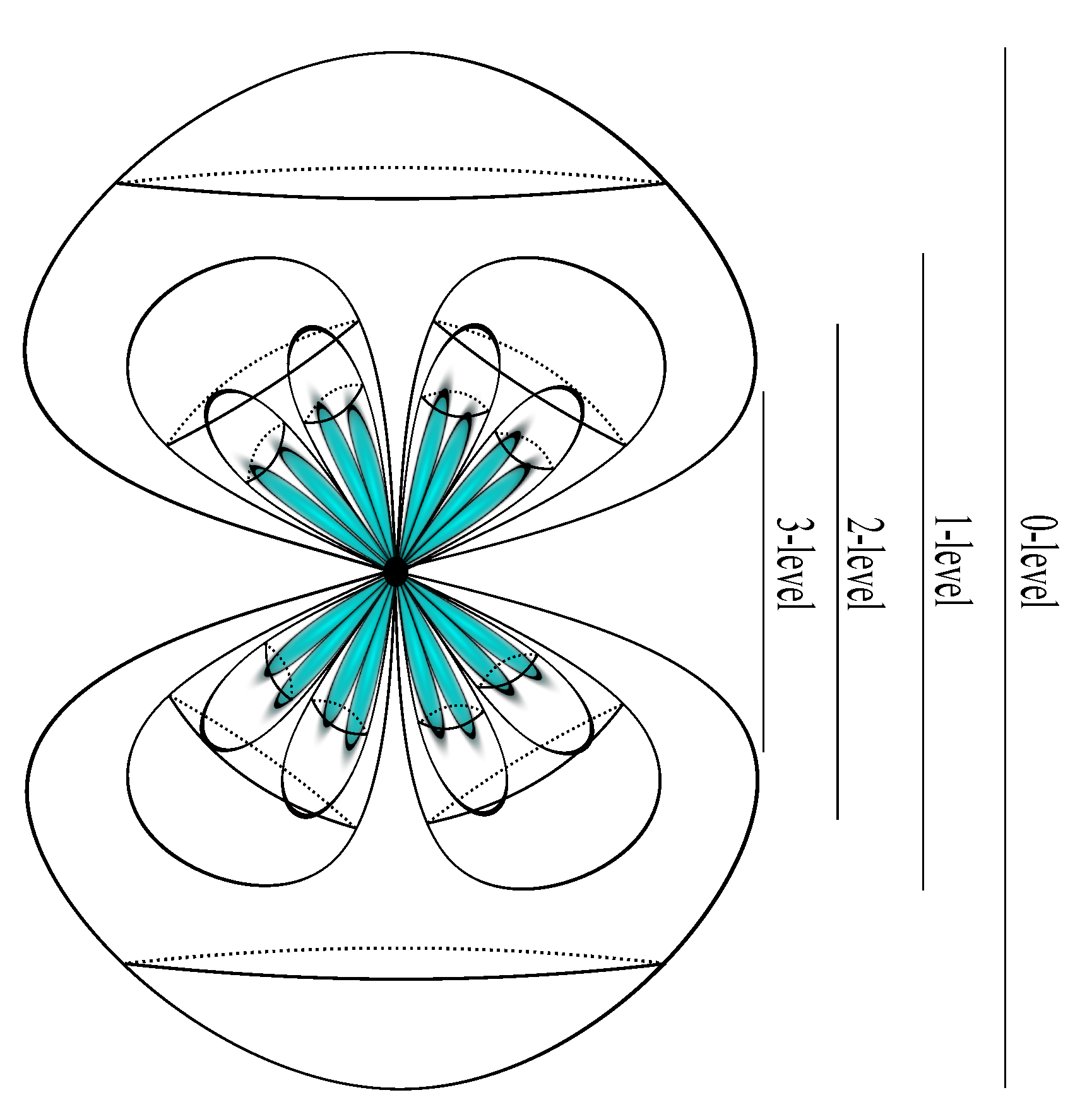
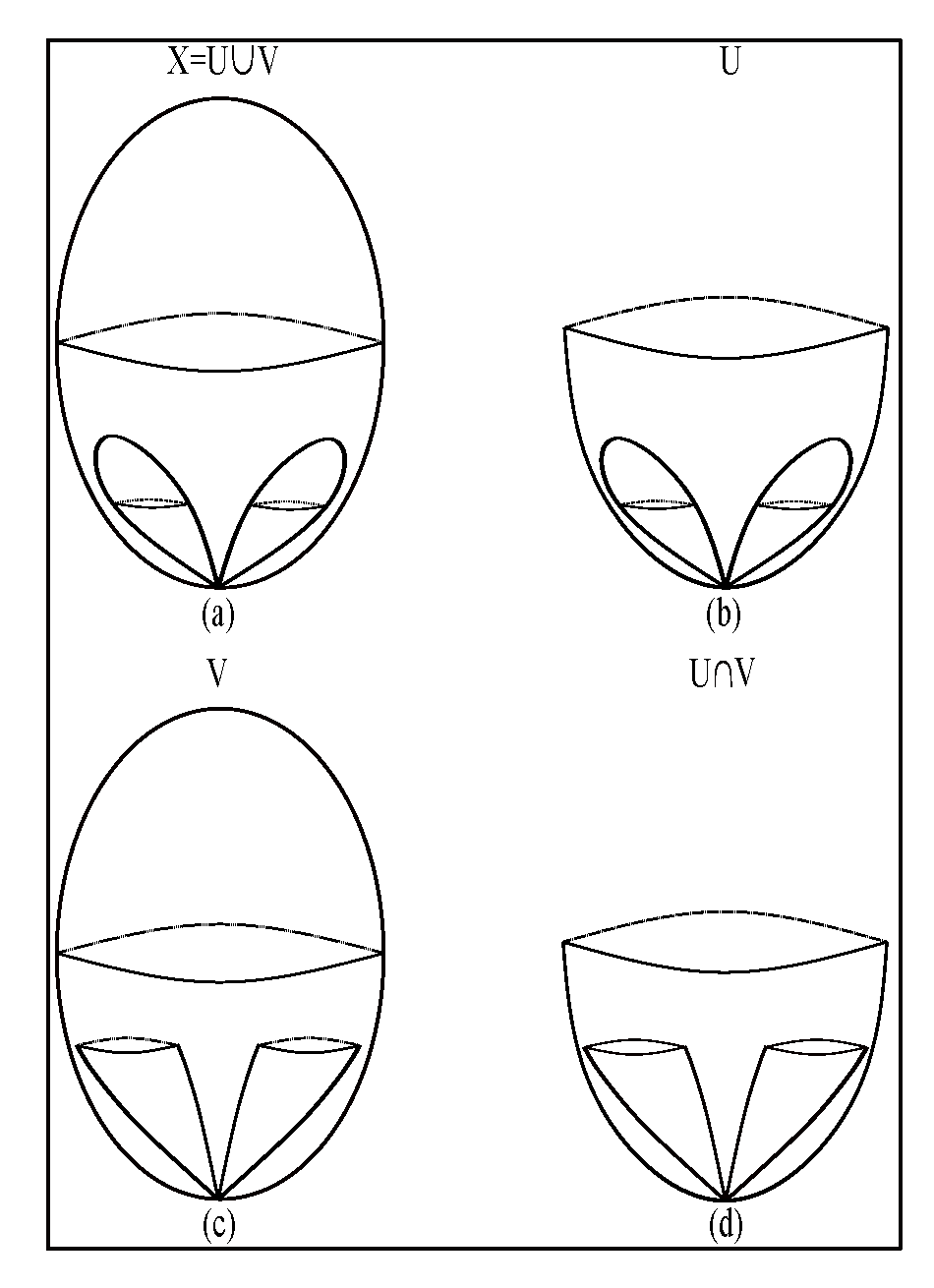
Taking into account that a higher level of TC at OT division is associated with a higher level of tensional coherence, the homeomorphic representation of the union of the levels of OT (see
Figure 17) indicates the TI read by the device through its component VC, at IML.
What is the TI read by CC at IML? CC reads a representation that defines a mandatory moment of life. From a certain point of view, this moment should not be affected by tensions, or its associated tensional state is the one that manifests at the potential level. So, for the same moment, we obtain two representations of TI: one that defines a potential tensional state and the other that defines the effective tensional one. The two must be equivalent. We will treat the equivalence issue in terms of homotopy equivalence. Thus, the topological spaces, which are presented in
Figure 17 and
Figure 19, are equivalent if the coloured areas, representing effective tensions, are contractible to their intersection point.
To prove that the two TIs of each pair presented above are different, their algebraic invariants are computed and presented in appendixes A-B and in
Table 3.
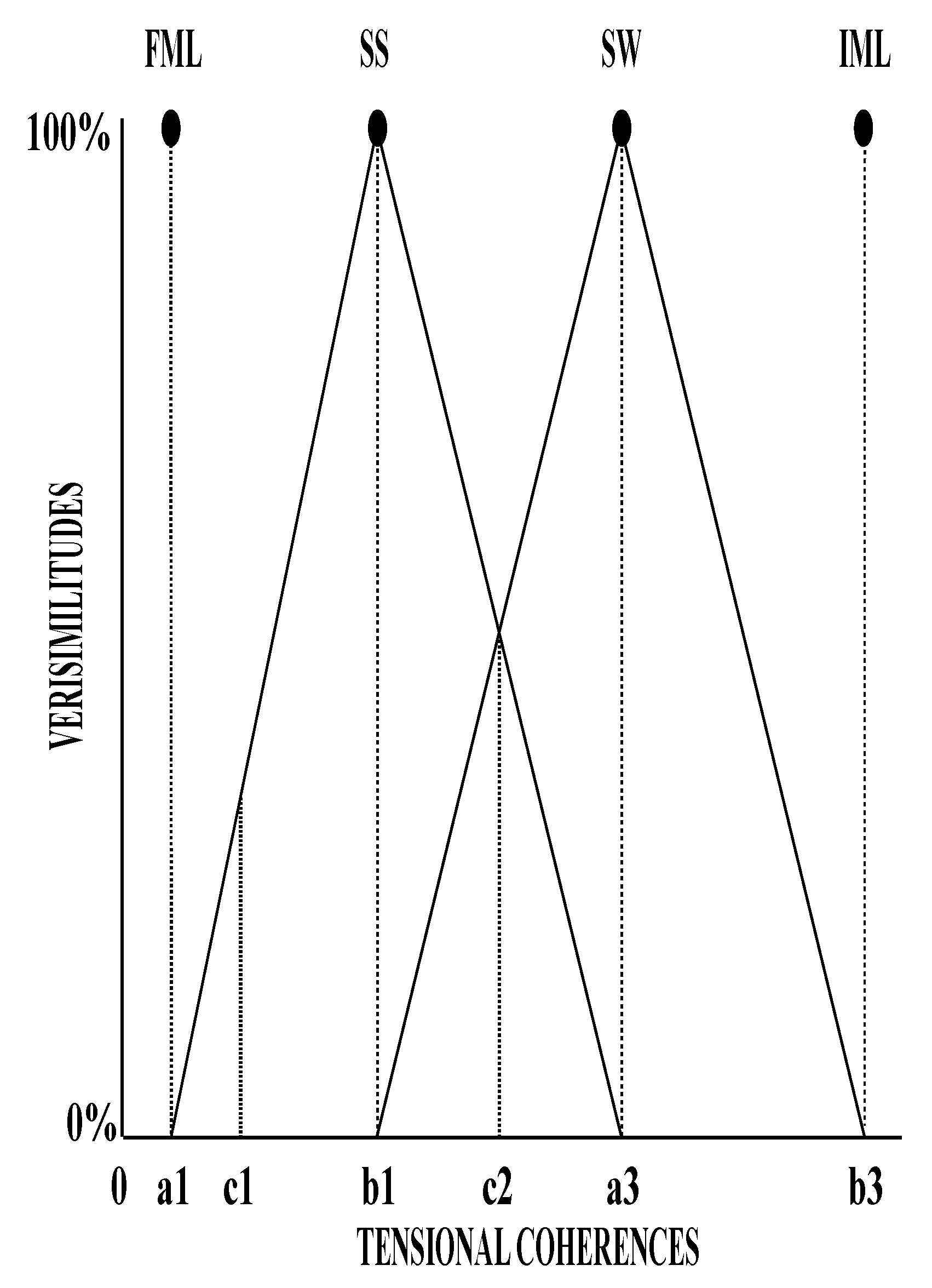
At the level of VC, the transitions between the four fundamental moments and states can be explained if SS and SW are treated as vague sets of tensional coherences (see
Figure 24).
The interval [b1,a3] crossed from right to the left and vice versa describes the transitions between SW and SS. SS is described by the tensional coherences that belong to the interval [c1,b1), and SW by the tensional coherences that belong to the interval (a3,b3]. So, at each and every moment of life, except the first moment, the reader reads a TI that is homeomorphic with the previous TI or a sequence of a homotopy. For the state of coma, the tensional coherences vary in the interval (a1,c1). The maximum verisimilitudes are reached by the coherences a1, b1, a3 and b3.
4. Conclusions
Human life is a running engine of the future. From this perspective, human life can be simulated by an artificial intelligence engine.
The running of life on the human effector presupposes the existence of vital information that must be read and implemented by a specialized device. Every moment of life is a more or less felt state of tension, and that is why tensional information is considered vital. The construction of this information is presented in
Section 3.2.
The paper treats the elements needed to simulate the presence of life from a tensional perspective. Our prospective concerns are aimed at identifying technical solutions for the simultaneous running of the biological, psychological and social programmes. Of course, the biological and psychological programmes can be adapted depending on the support on which the simulated life is run.
The tensional information describes the fundamental moments and states of life. Their representations through topological spaces are the subject of
Section 3. The algebraic invariants of these representations are presented in
Table 3. At every moment of life, except the first moment, a specialized device reads a TI that is homeomorphic with the previous TI or a sequence of a homotopy.
Human life seems to function as a mathematical category of categories (see
Section 2). This category without the NE object can represent an authentic life engine that consumes energy and generates interpretations.
What maintains vital processes? The paper presents the hypothesis of the existence of a source that transmits energy to the human body with a certain frequency. The frequency depends on FIT used to highlight all the events that take place at the level of all biological structures. The number of life sequences is calculated as the ratio between lifetime expressed in seconds and FIT. An energy quantum received by the human body must maintain life processes between two consecutive moments of life, and activate the consciousness of the moment.
One of the prospective problems of the human species is the survival on distant planets in the Universe, where human presence is reduced. A major danger with potential life-threatening effects is represented by the increased possibility of depression manifesting in such hostile environments. The construction of robots endowed with a vast knowledge base and also with the capacity to simulate human presence over long time horizons would considerably reduce this danger. We expect that our work will be useful in this endeavor.
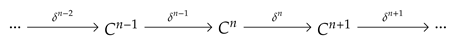 such that
such that 
 such that
such that  Im . Since Im we have ker . Thus H = = Z. There are no n-simplices with , and therefore for . □
Im . Since Im we have ker . Thus H = = Z. There are no n-simplices with , and therefore for . □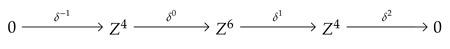
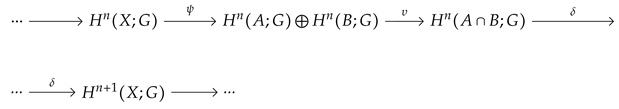


 Since, Ker then / Ker = Im , or / Ker . So, .
Since, Ker then / Ker = Im , or / Ker . So, .