Abstract
In this paper, bifurcations in the solution of the Navier–Stokes equations are studied and multiple solutions of the driven semi-elliptical cavity flow are presented. The two-dimensional steady incompressible driven viscous flow in a semi-elliptical cavity is solved numerically. To this end, the problem is formulated using an elliptic coordinate system that transforms the geometry conformally and provides a body fitted coordinate system. The presented results show that above a bifurcation Reynolds number the solution of the governing flow equations bifurcates and there exist multiple solutions for a particular Reynolds number when the aspect ratio of the semi-elliptical cavity geometry is 0.26 ⩽D⩽ 0.8. The bifurcation Reynolds numbers for different aspect ratios and also multiple solutions at different Reynolds numbers are presented in detail.
Keywords:
Navier–Stokes equations; semi-elliptical cavity flow; bifurcation Reynolds number; multiplicity of solutions MSC:
76D05; 35Q30
1. Introduction
The governing Navier–Stokes equations in fluid mechanics are the nonlinear systems of equations and they can possess more than one solution by nature [1,2]. The non-uniqueness of solutions of the Navier–Stokes Equations is primarily due to the nonlinearity of the differential equations, or variation of geometric or fluid mechanical parameters [1]. Finding and dealing with flow problems that have multiple solutions is a challenging and arduous task. These flow problems with multiple solutions exhibit interesting flow features; therefore, they are interesting and intriguing for applied mathematicians and fluid dynamics researchers.
In the literature, there are some studies that present particular fluid flow problems that have multiple solutions at a given Reynolds number. As an example of such flow problems that have multiple solutions, Lemée et al. [3] and Prasad et al. [4] presented multiple solutions to square cavity flow driven by two opposite-facing walls. Similarly, Wahba [5] and Perumal et al. [6] presented multiple solutions of square cavity flow driven by two non-facing walls. Moreover, Zhuo et al. [7], Wahba [5] and Perumal et al. [6] presented multiple solutions of square cavity flow driven by four side walls. These studies are examples for flow problems with square cavity geometry that has multiple solutions.
As an example of different geometry flow problems, Albensoeder et al. [8] studied the rectangular cavity flow driven by two facing side walls using the finite volume method. Their [8] results showed that the solution of two-dimensional steady incompressible flow in a rectangular cavity has several bifurcations and they [8] have presented different non-unique solutions of rectangular cavity flow for different aspect ratios. Chen et al. [9] also studied the two-sided driven rectangular cavity flow and presented multiple solutions.
We note that these flow problems, i.e., the square cavity flow driven by two opposite-facing walls [3,4] or driven by two non-facing walls [5,6] or driven by four side walls [7], have mirror symmetry in geometry and also in boundary conditions. The same is true for the rectangular geometry flow problem which is driven by two facing side walls also. In these flow problems, it is possible to draw a mirror symmetry line such that across this line the geometry and also boundary conditions have mirror symmetry. Although these flow problems have mirror symmetry by definition, the multiple solutions can exhibit mirror symmetric and non-symmetric behavior [8].
Unlike the mirror-symmetric flow problems mentioned above, Erturk [10] has presented multiple solutions for arc-shaped cavity flow. The arc-shaped cavity flow problem, by definition, does not have a mirror-symmetry line. Erturk [10] showed that above a bifurcation Reynolds number, the driven flow in an arc-shaped cavity with an arc length ratio less than 1/2, has two different multiplicity solutions at a given particular Reynolds number. Erturk [10] presented bifurcation Reynolds numbers for arc-shaped cavity geometry with different arc length ratios and also presented multiple solutions of arc-shaped cavity flow at various Reynolds numbers.
The driven semi-elliptical cavity flow problem looks very similar to the driven arc-shaped cavity flow problem considered by Erturk [10] in terms of the geometry with a straight moving lid at the top together with a non-moving stationary curved bottom wall at the bottom.
In the literature, to the best of our knowledge, there are only two studies that consider the flow in a semi-elliptical cavity with an aspect ratio less than unity (). Idris et al. [11] studied the lid-driven cavity flow inside a semi-ellipse shallow cavity using a non-uniform mesh. They [11] considered three different aspect ratios (1:4, 1:3 and 3:8) for the semi-ellipse geometry and presented solutions for a range of Reynolds numbers between and . Ren and Guo [12] studied the steady flow in a two-dimensional lid-driven semi-elliptical cavity using the lattice Boltzmann simulation method. They [12] considered a wide range of aspect ratios for the elliptic cavity with values less and also greater than unity (). They presented detailed solutions of steady flow in a semi-elliptical cavity up to . Aside from these two studies [11,12], the flow in a semi-elliptical cavity is not completely understood, especially in terms of bifurcation of the solution at high Reynolds numbers and this constitutes the main motivation of the present study.
At high Reynolds numbers (high inertial forces, i.e., high velocity, with respect to small viscous forces, i.e., very small viscosity) stationary flow loses stability and undergoes transition to turbulence eventually [13]. By nature, turbulence is three-dimensional and unsteady. Along with transient solutions, stationary steady solutions of Navier–Stokes equations still exists at high Reynolds number regimes. For the theory of the Navier–Stokes model, it is important to study the stationary solution at high Reynolds numbers even when the flow loses stability [14,15,16].
The aim of this study is then to solve the semi-elliptical cavity flow numerically, especially at high Reynolds numbers and present bifurcation Reynolds number and also present multiple solutions of the Navier–Stokes equations as the Reynolds number increases for different aspect ratios of the elliptic cavity geometry. In Section 2, the numerical simulation details are given. Comparison of the numerical solutions with the available solutions found in the literature, discussions of the bifurcation and detailed multiple solutions of the semi-elliptical cavity flow are presented in Section 3. Finally, in Section 4, the conclusions are presented.
2. Numerical Method
The schematic and the geometry of the driven semi-elliptical cavity flow problem is given in Figure 1a. The top wall of the semi-elliptical cavity is moving while the curved bottom wall is stationary. The incompressible two-dimensional viscous flow inside the driven semi-elliptical cavity is governed by the Navier–Stokes equation and we consider the streamfunction and vorticity formulation of the Navier–Stokes equation as the following
where is the Reynolds number based on the top wall velocity (U) and the width of the top wall (L) which are both equal to unity.
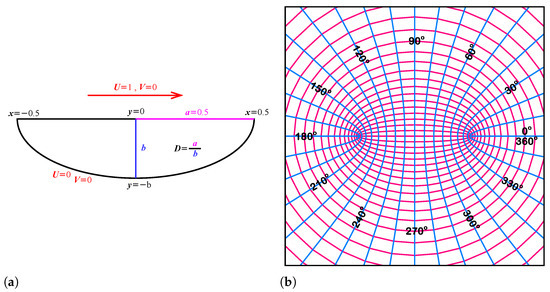
Figure 1.
The schematic of driven semi-elliptical cavity flow, the geometry and the elliptic coordinate system. (a) Schematic of semi-elliptical cavity flow. (b) Elliptic coordinate system.
By nature, the geometry of the semi-elliptical cavity flow problem suggests that the problem is best solved by using an elliptic coordinate system since the elliptic coordinate system transforms the geometry conformally and automatically generate a body fitted coordinate system. The elliptic coordinate system consists of confocal ellipses and hyperbolae, as shown in Figure 1b. The transformation from elliptic coordinates () to the Cartesian () coordinates is given by
where i is the imaginary number, the elliptic coordinates and and also c is the elliptical eccentricity such that
and a and b denote the semi-major and semi-minor axes of the ellipse as shown in Figure 1a. In our case, the length of the top wall of the ellipse is equal to unity such that . Different ellipses are defined by the vertical-to-horizontal semi-axis ratio, i.e., the aspect ratio (D), defined as the following
The Cartesian coordinates can be defined in terms of elliptic coordinates as the following
Using the elliptic coordinate transformation (3), the streamfunction and vorticity equations in elliptic coordinates are given by
where J denotes the Jacobian of the transformation and it is defined as the following
We note that the governing equations of the driven semi-elliptical cavity flow are nonlinear ((8) and (9)); therefore, they are solved in an iterative manner. For this, we assign pseudo time derivatives to the governing equations as the following
and then solve these equations through the pseudo time until steady state solution (i.e., ) is obtained. We use the ADI (Alternating Implicit Direction) method in order to advance the above equations in the pseudo time. The ADI method involves a two step iteration process. In the first step, using the following implicit system, the solution is advanced to intermediate half time level by using a tri-diagonal solver.
Here, the superscript denotes the pseudo time level. After obtaining the solution at the intermediate half time level (i.e., and ), in the second step, using the following implicit system, the solution is advanced to a new time level (i.e., and ) again using a tri-diagonal solver.
We note that in order to start the iteration process we assign initially guessed values to the variables (i.e., , ) and then using the ADI method as described above advance the solution in the pseudo time.
Using the chain rule, in elliptic coordinate system the U and V velocities in x- and y-directions are defined as the following
The no-slip no-penetration boundary conditions state that on the top moving wall the fluid velocities are U = 1 and V = 0 and on the curved bottom wall they are U = 0 and V = 0, as shown in Figure 1a. These boundary conditions state that on the wall the value of the streamfunction is zero (i.e., = 0). Using the streamfunction Equation (8) and also Equation (17), the value of the vorticity on the wall is calculated as the following
where subscript 0 refers to wall grid points, 1 refers to adjacent grid points next to the wall, refers to grid spacing and U refers to wall velocity such that it is equal to 1 on the top moving wall and 0 on the stationary curved bottom wall.
During the numerical iterations, the following residuals are monitored at each pseudo time step
where subscripts show the grid index and max denote the maximum absolute value in the whole computational domain. By definition, these residuals show the change in the streamfunction and vorticity variables between two consecutive pseudo time steps normalized by the streamfunction and vorticity value at the previous pseudo time step. In the present study we continue the iterations until both and are less than , which means that at the convergence the streamfunction and vorticity values change only 0.00000001% between two iteration steps at a grid point as the maximum and even less in the other grid points in the computational domain. This convergence criterion is used for every multiple solution presented in the current study.
The numerical algorithm followed in the present study is given schematically in Figure 2.
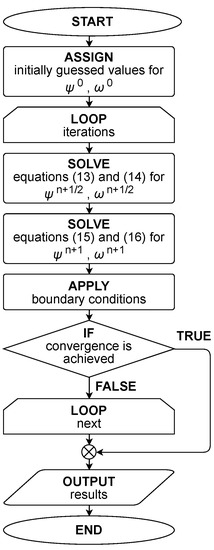
Figure 2.
The numerical algorithm.
3. Results and Discussions
Figure 3 shows semi-elliptical cavity geometries that are considered in the present study. In the present study, numerical solutions of driven semi-elliptical cavity flow with aspect ratios (D) of 0.26, 0.5 and 0.8 will be presented in detail even though many more aspect ratios are considered. In all of the considered aspect ratio ellipses, first grid refined studies are carried out such that all of the solutions presented here are grid independent solutions.
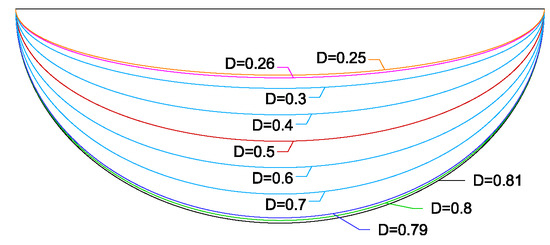
Figure 3.
Semi-elliptical cavity geometries with different aspect ratios.
First, we compare our numerical solutions with those of Idris et al. [11] and Ren and Guo [12] and consider the same semi-ellipse cases and Reynolds numbers. Idris et al. [11] considered aspect ratios of 1:4, 1:3 and 3:8 in their study. Their definition of aspect ratio corresponds to , 0.6667 (2/3) and 0.75, respectively, with the definition used in the present study. For these aspect ratios, Idris et al. [11] present numerical data for minimum and also maximum streamfunction values at the primary and secondary vortex centers and the (x,y) location of the these centers for , 500, 1000, 1500 and 2000. Table 1 tabulates present results at the same Reynolds numbers along with those from Idris et al. [11].

Table 1.
Comparison of flow properties for , 0.6667 and 0.75 aspect ratio semi-ellipses.
In their study, Ren and Guo [12] also considered aspect ratios of and 0.5 for Reynolds number of 500, 1000, 3000 and 5000. Table 2 tabulates present data for the same cases in comparison with those of Ren and Guo [12].

Table 2.
Comparison of flow properties for and 0.5 aspect ratio semi-ellipses.
Both Table 1 and Table 2 show that our numerical results are in very good agreement with those of Idris et al. [11] and Ren and Guo [12], although we believe that our results are more accurate due to the body fitted fine mesh used in the numerical simulation together with the very low residuals considered for the convergence.
In a study, Erturk [10] considered the flow inside a driven arc-shaped cavity and reported that when the arc length ratio is less than 1/2, above a bifurcation Reynolds number the arc-shaped cavity flow has multiple solutions for a given particular Reynolds number. Erturk [10] finds that below a bifurcation Reynolds number, a single solution exists for the governing Navier–Stokes equations for the arc-shaped cavity flow; however, above the bifurcation Reynolds number, two different solutions exist for a given particular Reynolds number. Erturk [10] also finds that this bifurcation Reynolds number varies as the arc length ratio changes. For arc-shaped cavity geometries with various arc length ratios, Erturk [10] presented the bifurcation Reynolds number at which multiple solutions start to exist and also presented the two different solutions of the Navier–Stokes equations at various Reynolds numbers above the bifurcation Reynolds number. Erturk [10] called the only solution that exists below the bifurcation Reynolds number the “1st solution” and also the new solution that starts to exist above the bifurcation Reynolds number the “2nd solution”. In order to obtain the “1st solution” and also the “2nd solution”, Erturk [10] made the following statements:
- Below the bifurcation Reynolds number, if the homogeneous solution is used as an initial guess for the iterations, the obtained solution is the 1st solution.
- Above the bifurcation Reynolds number, if the homogeneous solution is used as an initial guess for the iterations, the solution always converges to the 2nd solution.
- Below the bifurcation Reynolds number, the 2nd solution does not exist. The 2nd solution exists only above the bifurcation Reynolds number.
- If the 1st solution with previous smaller Reynolds number is used as an initial guess for the iterations, it is possible to obtain the 1st solution even above the bifurcation Reynolds number. The 1st solution exists above the bifurcation Reynolds number.
In the present study, we use the same classification used in Erturk [10] and name the only solution “1st solution” when the Reynolds number is below the bifurcation Reynolds number and also name the new solution that starts to appear above the bifurcation Reynolds number “2nd solution”. In order to obtain the bifurcation Reynolds number and also the multiple solutions of the flow problem we follow the procedure given by Erturk [10].
First, we start with a semi-ellipse with aspect ratio. In order to obtain the bifurcation Reynolds number whereby the governing flow equations start to have multiple solutions, we solve the flow problem at incrementally increasing Reynolds numbers using the homogeneous initial guess for the numerical iterations. Figure 4 shows the streamfunction contours of the solutions obtained at and also at when homogeneous initial guess is used for the considered aspect ratio ellipse (). One can see that when the Reynolds number is incremented only by “1”, the vortex structure of the flow and the solution of the governing equations change dramatically. For aspect ratio semi-ellipse, the bifurcation Reynolds number is and starting from this Reynolds number and above a second solution starts to exist at any considered Reynolds number. We note that we considered only integer values.

Figure 4.
Bifurcation of the solution in driven semi-elliptical cavity flow with aspect ratio. (a) (1st solution). (b) (2nd solution).
Below the bifurcation Reynolds number, only one solution exists for the governing flow equations, i.e., the 1st solution, even if different initial guesses are used for the iterations. Figure 5 shows the evolution of the 1st solution at various Reynolds numbers below the bifurcation Reynolds number of .
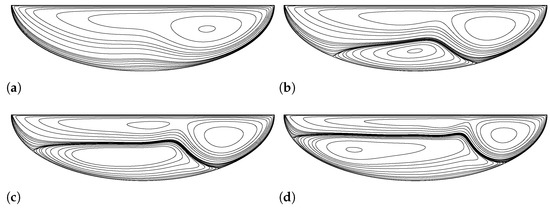
Figure 5.
The evolution of the 1st solution of driven semi-elliptical cavity flow until for aspect ratio. (a) (1st solution). (b) (1st solution). (c) (1st solution). (d) (1st solution).
In order to obtain the 1st solution above the bifurcation Reynolds number, for example, at , we use the 1st solution at as initial guess for the iterations. The obtained 1st solution at is given in Figure 6a. In order to obtain the 2nd solution above the bifurcation Reynolds number, for example, at , we use the 2nd solution at as initial guess for the iterations. The obtained 2nd solution at is given in Figure 6b. Then, using the corresponding 1st or 2nd solutions at previous smaller Reynolds numbers, we solve for the 1st or 2nd solutions at higher Reynolds numbers. We note that we advance the Reynolds number by incrementing 1000. Using the previous 1st solution at smaller Reynolds number as initial guess for the next higher Reynolds number, we were able to obtain the 1st solution until 14,000 at maximum. Moreover, using the previous 2nd solution at smaller Reynolds number as initial guess for the next higher Reynolds number, we were able to obtain the 2nd solution until 30,000 at maximum. Figure 6 shows the streamfunction contours of both the 1st and 2nd solutions at various same Reynolds numbers until 14,000, i.e., until the maximum Reynolds number for the 1st solution. Above 14,000, only the 2nd solution exists and Figure 7 shows the streamfunction contours of the 2nd solution at various Reynolds numbers until 30,000.

Figure 6.
The 1st and 2nd solutions of driven semi-elliptical cavity flow with aspect ratio at various same Reynolds numbers. (a) (1st solution). (b) (2nd solution). (c) 10,000 (1st solution). (d) 10,000 (2nd solution). (e) 14,000 (1st solution). (f) 14,000 (2nd solution).

Figure 7.
The evolution of the 2nd solution of driven semi-elliptical cavity flow above 14,000 for aspect ratio. (a) 15,000 (2nd solution). (b) 20,000 (2nd solution). (c) 25,000 (2nd solution). (d) 30,000 (2nd solution).
For future references, for the 1st and 2nd solutions given in Figure 4, Figure 5, Figure 6 and Figure 7 we tabulate the streamfunction () and vorticity () values at the center of the strongest clockwise rotating vortex (i.e., at the location of ) and also at the center of the strongest counterclockwise rotating vortex (i.e., at the location of ) together with the x-y locations of these centers for the 1st solution in Table 3 and the same for the 2nd solution in Table 4.

Table 3.
Minimum and maximum streamfunction values in the 1st solution, corresponding vorticity values and (x,y) locations for aspect ratio.

Table 4.
Minimum and maximum streamfunction values in the 2nd solution, corresponding vorticity values and (x,y) locations for aspect ratio.
After obtaining the 1st and 2nd solutions of the flow in a driven semi-elliptical cavity with aspect ratio, we then extend the analysis for smaller aspect ratios. We first solve the semi-elliptical cavity flow with aspect ratio and then solve it for aspect ratio by repeating the same procedure we follow for the aspect ratio semi-ellipse as described above. For and aspect ratio semi-elliptical cavity flows, the bifurcation Reynolds numbers are 5546 and 6673, respectively. The and aspect ratio semi-ellipse cavity geometries are shown in blue color in Figure 3 for comparison with other semi-ellipse geometries. Following this, we then repeat the same analysis for aspect ratio semi-elliptical cavity flow. However, for this aspect ratio, we did not observe any bifurcation in the solution as the Reynolds number increases such that there was only one solution for any considered Reynolds number. Multiplicity in the solution does not arise for the aspect ratio semi-elliptical cavity flow case. This fact shows that there is a minimum aspect ratio for semi-elliptical cavity flow to have multiplicity in the solution. In order to find this minimum aspect ratio for the semi-elliptical cavity flow to have multiple solutions, we start to solve for different aspect ratio cases incrementing the aspect ratio by 0.01. For any aspect ratio semi-ellipse with and above, we find bifurcation in the solution at a certain Reynolds number such that there exists multiplicity in the solution. However, for any aspect ratio semi-ellipse with and below, there is no bifurcation in the solution such that only one solution exists for every Reynolds number. Thus, the minimum aspect ratio for the semi-elliptical cavity flow such that multiplicity in the solution exists is .
For this obtained minimum aspect ratio semi-elliptical cavity flow, Figure 8 shows the solution for and also for when homogeneous initial guess is used for the iterations. As seen in Figure 8a at in the 1st solution, there is one counter-rotating vortex just above the curved bottom wall. However, at in Figure 8b which is the bifurcation Reynolds number, different than the 1st solution, there are two separate counter-rotating vortices just above the curved bottom wall in the 2nd solution.

Figure 8.
Bifurcation of the solution in driven semi-elliptical cavity flow with aspect ratio. (a) (1st solution). (b) (2nd solution).
Figure 9 shows the evolution of the 1st solution of the driven semi-elliptical cavity flow with at various Reynolds numbers below the bifurcation Reynolds number.
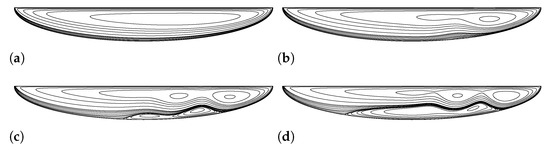
Figure 9.
The evolution of the 1st solution of driven semi-elliptical cavity flow until for aspect ratio. (a) (1st solution). (b) (1st solution). (c) (1st solution). (d) (1st solution).
For aspect ratio semi-ellipse, we were able to advance the 1st solution until a Reynolds number of 16,000. Figure 10 shows both the 1st and 2nd solutions at various same Reynolds numbers until 16,000.
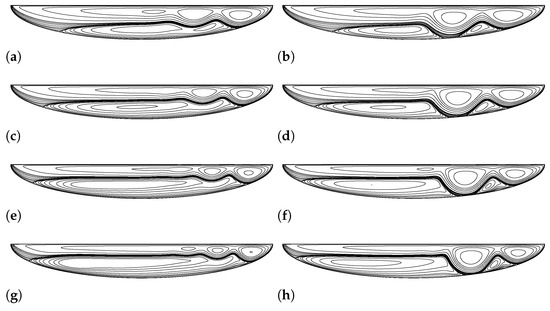
Figure 10.
The 1st and 2nd solutions of driven semi-elliptical cavity flow with aspect ratio at various same Reynolds numbers. (a) (1st solution). (b) (2nd solution). (c) (1st solution). (d) 10,000 (2nd solution). (e) 13,000 (1st solution). (f) 13,000 (2nd solution). (g) 16,000 (1st solution). (h) 16,000 (2nd solution).
Above 16,000, only the 2nd solution exists for the driven semi-elliptical cavity flow with aspect ratio. For this case, we were able to advance the 2nd solution until a Reynolds number of 23,000. Figure 11 shows the 2nd solution at various Reynolds numbers until 23,000 for aspect ratio semi-elliptical cavity flow.
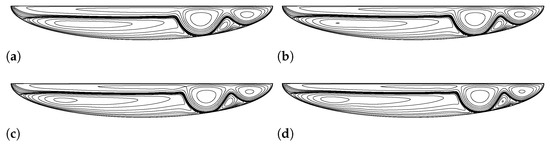
Figure 11.
The evolution of the 2nd solution of driven semi-elliptical cavity flow above 16,000 for aspect ratio. (a) 17,000 (2nd solution). (b) 19,000 (2nd solution). (c) 21,000 (2nd solution). (d) 23,000 (2nd solution).
Similarly, for future references, for the driven semi-elliptical cavity flow with aspect ratio , we tabulate the streamfunction () and vorticity () values at the center of the strongest clockwise rotating vortex (i.e., at the location of ) and also at the center of the strongest counterclockwise rotating vortex (i.e., at the location of ) together with the x–y locations of these centers for the 1st solution in Table 5 and the same for the 2nd solution in Table 6.

Table 5.
Minimum and maximum streamfunction values in the 1st solution, corresponding vorticity values and (x,y) locations for aspect ratio.

Table 6.
Minimum and maximum streamfunction values in the 2nd solution, corresponding vorticity values and (x,y) locations for aspect ratio.
Then, we start examining solutions of the semi-elliptical cavity flow with aspect ratios above . We first solve for , and aspect ratio semi-elliptical cavity flows and we obtain the bifurcation Reynolds number for these flows as 5084, 5968 and 7182, respectively. However, for aspect ratio, we did not observe any bifurcation in the solution such that there was no multiplicity in the solution as the Reynolds number increases. For this aspect ratio semi-ellipse, we obtain only one solution for any considered Reynolds number. This fact shows that there is a maximum aspect ratio for semi-elliptical cavity flow to have multiplicity in the solution as well. In order to find this maximum aspect ratio such that the flow in a semi-elliptical cavity exhibits multiple solutions, we use the following procedure. First, we choose a high Reynolds number which is above an expected bifurcation Reynolds number, for example, 12,000. We note that for semi-elliptical cavity flow with aspect ratio, the bifurcation Reynolds number is 7182; therefore, 12,000 should be well beyond a possible bifurcation. At this high Reynolds number (above bifurcation Reynolds number), i.e., 12,000, when the homogeneous initial guess is used for the iterations, the solution obtained is the 2nd solution as stated by Erturk [10]. We also note that this is true if there is bifurcation in the solution such that the flow has multiple solutions. Using this chosen Reynolds number, we then solve the flow in a semi-elliptical cavity by changing the aspect ratio with 0.01 increments in order to see at which aspect ratio the flow starts to change behavior. Figure 12 shows the solutions we obtain when homogeneous initial guess is used for 12,000 and for , 0.8, 0.81 and 0.82 aspect ratio semi-elliptical cavity flows. As seen in Figure 12, above when the aspect ratio is incremented by only 0.01, i.e., at , the solution changes dramatically. We note that beyond this aspect ratio () the solution resembles the 1st solution. After several numerical experimentations, we did not find any multiplicity in the solution for aspect ratio ellipse and above. Thus we find the maximum aspect ratio that the semi-elliptical cavity flow exhibits multiplicity in the solutions as .
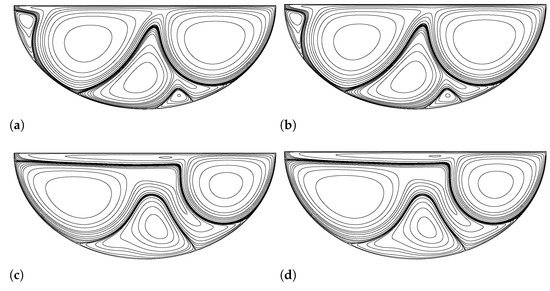
Figure 12.
The solution of semi-elliptical cavity flow at 12,000 with various aspect ratios. (a) . (b) . (c) . (d) .
For this obtained maximum aspect ratio semi-elliptical cavity flow, Figure 13 shows the solution for and also for when the homogeneous initial guess is used for the iterations. As seen in Figure 13, for aspect ratio semi-ellipse when the Reynolds number is incremented just by 1 from to 7182, the flow topology changes dramatically. Thus, for aspect ratio semi-ellipse, the bifurcation Reynolds number is .

Figure 13.
Bifurcation of the solution in driven semi-elliptical cavity flow with aspect ratio. (a) (1st solution). (b) (2nd solution).
Figure 14 shows the evolution of the 1st solution at various Reynolds numbers which are below the bifurcation Reynolds number () for aspect ratio.

Figure 14.
The evolution of the 1st solution of driven semi-elliptical cavity flow until for aspect ratio. (a) (1st solution). (b) (1st solution). (c) (1st solution). (d) (1st solution).
For aspect ratio semi-ellipse, we were able to obtain the 2nd solution until 19,000 at maximum, while on the other hand we obtained the 1st solution until 25,000 at maximum. In Figure 15, we give both the 1st and 2nd solutions at various same Reynolds numbers until 19,000. Moreover, Figure 16 shows the evolution of the 1st solution above 19,000 until 25,000.

Figure 15.
The 1st and 2nd solutions of driven semi-elliptical cavity flow with aspect ratio at various same Reynolds numbers. (a) (1st solution). (b) (2nd solution). (c) = 10,000 (1st solution). (d) 10,000 (2nd solution). (e) 15,000 (1st solution). (f) 15,000 (2nd solution). (g) 19,000 (1st solution). (h) 19,000 (2nd solution).
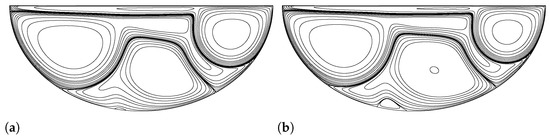
Figure 16.
The evolution of the 1st solution of driven semi-elliptical cavity flow above 19,000 for aspect ratio. (a) 20,000 (1st solution). (b) 25,000 (1st solution).
Similarly, for future references, for the driven semi-elliptical cavity flow with aspect ratio, we tabulate the streamfunction () and vorticity () values at the center of the strongest clockwise rotating vortex (i.e., at the location of ) and also at the center of the strongest counterclockwise rotating vortex (i.e., at the location of ) together with the x–y locations of these centers for the 1st solution in Table 7 and the same for the 2nd solution in Table 8.

Table 7.
Minimum and maximum streamfunction values in the 1st solution, corresponding vorticity values and (x,y) locations for .

Table 8.
Minimum and maximum streamfunction values in the 2nd solution, corresponding vorticity values and (x,y) locations for .
If we look at the solutions given above in Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15 and Figure 16, we can notice that the 1st and 2nd solutions of the driven semi-elliptical cavity flow have different characteristics and behavior with respect to the Reynolds number. One of the main differences between the 1st and 2nd solutions is that in the 2nd solution there are two strong local vortex centers in the main clockwise vortex near the top lid; however, there is one in the 1st solution. The schematic views of the vortices in the 1st and 2nd solutions are given in Figure 17. In Figure 17, the center of the vortex close to the top moving lid is colored with blue for the 1st solution and the two local centers for the 2nd solution are colored with red and green. In Figure 18, we plot the streamfunction values at the center of these vortex centers (blue, red and green) and also the vorticity values at the same centers in Figure 19 with respect to the Reynolds number.
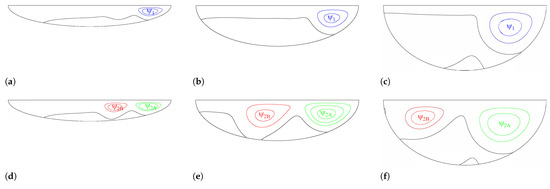
Figure 17.
The schematic view of the vortices and local vortex centers with blue, red and green color codes in the 1st and 2nd solutions for the considered aspect ratio semi-ellipses. (a) 1st solution, . (b) 1st solution, . (c) 1st solution, . (d) 2nd solution, . (e) 2nd solution, . (f) 2nd solution, .

Figure 18.
Variation of streamfunction values at the center of the local vortex centers in 1st and 2nd solutions with respect to the Reynolds number with color codes blue, red and green. (a) Streamfunction () values, . (b) Streamfunction () values, . (c) Streamfunction () values, .

Figure 19.
Variation of vorticity values at the center of the local vortex centers in 1st and 2nd solutions with respect to the Reynolds number with color codes blue, red and green. (a) Vorticity () values, . (b) Vorticity () values, . (c) Vorticity () values, .
In Figure 18, in the 1st solution (blue color) in aspect ratio, the streamfunction value increases (in absolute value sense) as the Reynolds number increases at small Reynolds numbers and then starts to decrease (in absolute value sense) afterwards. However in and aspect ratios, the streamfunction value decreases continuously (in absolute value sense) as the Reynolds number increases in the 1st solution (blue color).
On the other hand, in Figure 18, in the 2nd solution (red and green colors), at small Reynolds numbers the streamfunction value at the local center close to the top right corner of the semi-elliptical cavity (green color) is greater than (in absolute value sense) that at the local center close to the center top of the semi-elliptical cavity (red color) for aspect ratio. However, as the Reynolds number increases while the streamfunction at the green center decreases (in absolute value sense) that at the red center increases such that red value becomes greater than the green value (in absolute value sense). The same is also true for aspect ratio. For aspect ratio, even though the trend is the same, the streamfunction at the green center stays greater than (in absolute value sense) that at the red center at all Reynolds numbers.
In Figure 19, in the 1st solution (blue color) the vorticity value at the vortex center increases (in absolute value sense) as the Reynolds number increases for all the aspect ratios considered. The same is also true for the 2nd solution at the green center. In the 2nd solution the vorticity value at the red center first decreases slightly (in absolute value sense) then starts to increase as the Reynolds number increases for aspect ratio. In aspect ratio, the vorticity value at the red center almost stays constant with respect to the Reynolds number. However, in aspect ratio, the vorticity value at the red center continuously decreases (in absolute value sense) as the Reynolds number increases.
As mentioned above, the bifurcation Reynolds number of the driven semi-elliptical cavity flow at which the governing equations start to exhibit multiplicity of solutions changes as the aspect ratio of the semi-ellipse changes. In Figure 20, we plot the variation of the bifurcation Reynolds number for different aspect ratios. Figure 20 shows that starting from the minimum aspect ratio (), as the aspect ratio increases the bifurcation Reynolds number at first decreases and then starts to increase afterwards while having the minimum bifurcation Reynolds number at .
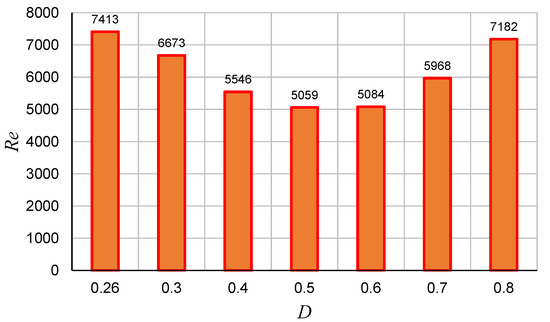
Figure 20.
Bifurcation Reynolds numbers for different aspect ratio (D) semi-ellipses.
4. Conclusions
The semi-elliptical cavity flow is solved numerically for various Reynolds numbers and also for various aspect ratios. The elliptic coordinate system which transforms the geometry conformally and also provides a body fitted coordinate system is used in the formulation. The steady governing flow equations are solved until very low residual levels for numerical accuracy. For the considered driven semi-elliptical cavity flow, the following is concluded:
- The solution of Navier–Stokes equations for incompressible 2D steady flow in a driven semi-elliptical cavity bifurcates at a bifurcation Reynolds number and beyond this bifurcation Reynolds number at least two different solutions exist for the governing equations.
- The solution of Navier–Stokes equations for incompressible 2D steady flow in a driven semi-elliptical cavity bifurcates only for semi ellipses with a vertical-to-horizontal semi-axis ratio (aspect ratio) .
- We did not observe bifurcation for semi-ellipses with and aspect ratios. For these aspect ratio (vertical-to-horizontal semi-axis ratio) semi-ellipses, we find only a single solution for each Reynolds number.
- For semi-ellipses with aspect ratios , the bifurcation Reynolds number at which the Navier–Stokes equations start to have multiple solutions at first starts to decrease as D increases; then, after having a minimum around , the bifurcation Reynolds number starts to increase as D increases further.
Although with the present study at least two different multiplicity solutions of the driven semi-elliptical cavity flow are presented, whether or not the driven semi-elliptical cavity flow has any more multiplicity solutions is an open question for further investigations. Finally detailed streamfunction and vorticity data from the driven semi-elliptical cavity flow are tabulated for future reference.
Author Contributions
Methodology, E.E.; analysis, E.E.; writing, review and editing, E.E. and T.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Schlichting, H.; Gersten, K. Boundary-Layer Theory; Springer: Berlin, Germany, 2017. [Google Scholar] [CrossRef]
- Shankar, P.; Deshpande, M. Fluid Mechanics in the Driven Cavity. Annu. Rev. Fluid Mech. 2000, 32, 93–136. [Google Scholar] [CrossRef]
- Lemée, T.; Kasperski, G.; Labrosse, G.; Narayanan, R. Multiple Stable Solutions in the 2D Symmetrical Two-Sided Square Lid-Driven Cavity. Comput. Fluids 2015, 119, 204–212. [Google Scholar] [CrossRef]
- Prasad, C.; Dass, A. Use of an HOC Scheme to Determine the Existence of Multiple Steady States in the Antiparallel Lid-Driven Flow in a Two-Sided Square Cavity. Comput. Fluids 2016, 140, 297–307. [Google Scholar] [CrossRef]
- Wahba, E. Multiplicity of States for Two-Sided and Four-Sided Lid Driven Cavity Flows. Comput. Fluids 2009, 38, 247–253. [Google Scholar] [CrossRef]
- Perumal, D.; Dass, A. Multiplicity of Steady Solutions in Two-Dimensional Lid-Driven Cavity Flows by Lattice Boltzmann Method. Comput. Math. Appl. 2011, 61, 3711–3721. [Google Scholar] [CrossRef]
- Zhuo, C.; Zhong, C.; Guo, X.; Cao, J. Numerical Investigation of Four-Lid-Driven Cavity Flow Bifurcation Using the Multiple-Relaxation-Time Lattice Boltzmann Method. Comput. Fluids 2015, 110, 136–151. [Google Scholar] [CrossRef]
- Albensoeder, S.; Kuhlmann, H.; Rath, H. Multiplicity of Steady Two-Dimensional Flows in Two-Sided Lid-Driven Cavities. Theor. Comput. Fluid Dyn. 2001, 14, 223–241. [Google Scholar] [CrossRef]
- Chen, K.T.; Tsai, C.C.; Luo, W.J.; Chen, C.N. Multiplicity of Steady Solutions in A Two-Sided Lid-Driven Cavity with Different Aspect Ratios. Theor. Comput. Fluid Dyn. 2013, 27, 767–776. [Google Scholar] [CrossRef]
- Erturk, E. Multiplicity of Steady State Solutions in 2-D Incompressible Viscous Wall Driven Arc-Shaped Cavity Flow. J. Appl. Fluid Mech. 2021, 14, 1147–1163. [Google Scholar] [CrossRef]
- Idris, M.; Irwan, M.; Ammar, N. Steady State Vortex Structure of Lid Driven Flow Inside Shallow Semi-Ellipse Cavity. J. Mech. Eng. Sci. 2012, 2, 206–216. [Google Scholar] [CrossRef]
- Ren, J.; Guo, P. Lattice Boltzmann Simulation of Steady Flow in a Semi-Elliptical Cavity. Commun. Comput. Phys. 2017, 21, 692–717. [Google Scholar] [CrossRef]
- Erturk, E. Discussions on Driven Cavity Flow. Int. J. Numer. Methods Fluids 2009, 60, 275–294. [Google Scholar] [CrossRef]
- Erturk, E. Stationary Solutions of Incompressible Viscous Flow in a Wall-Driven Semi-Circular Cavity. Acta Polytech. 2021, 61, 516–525. [Google Scholar] [CrossRef]
- Christov, C.; Marinova, R.; Marinov, T. Identifying the Stationary Viscous Flows Around a Circular Cylinder at High Reynolds Numbers. Lect. Notes Comput. Sci. 2008, 4818, 175–183. [Google Scholar] [CrossRef]
- Erturk, E.; Gokcol, O. Numerical Solutions of Steady Incompressible Flow Around a Circular Cylinder up to Reynolds Number 500. Int. J. Mech. Eng. Technol. 2018, 9, 1368–1378. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).