High-Dimensional Precision Matrix Estimation through GSOS with Application in the Foreign Exchange Market
Abstract
1. Introduction
Estimation, Literature Review
2. The Proposed Method
| Algorithm 1 GSOS based on dpglasso approach |
|
Glasso Scenario
| Algorithm 2 GSOS based on glasso approach |
|
3. Simulation
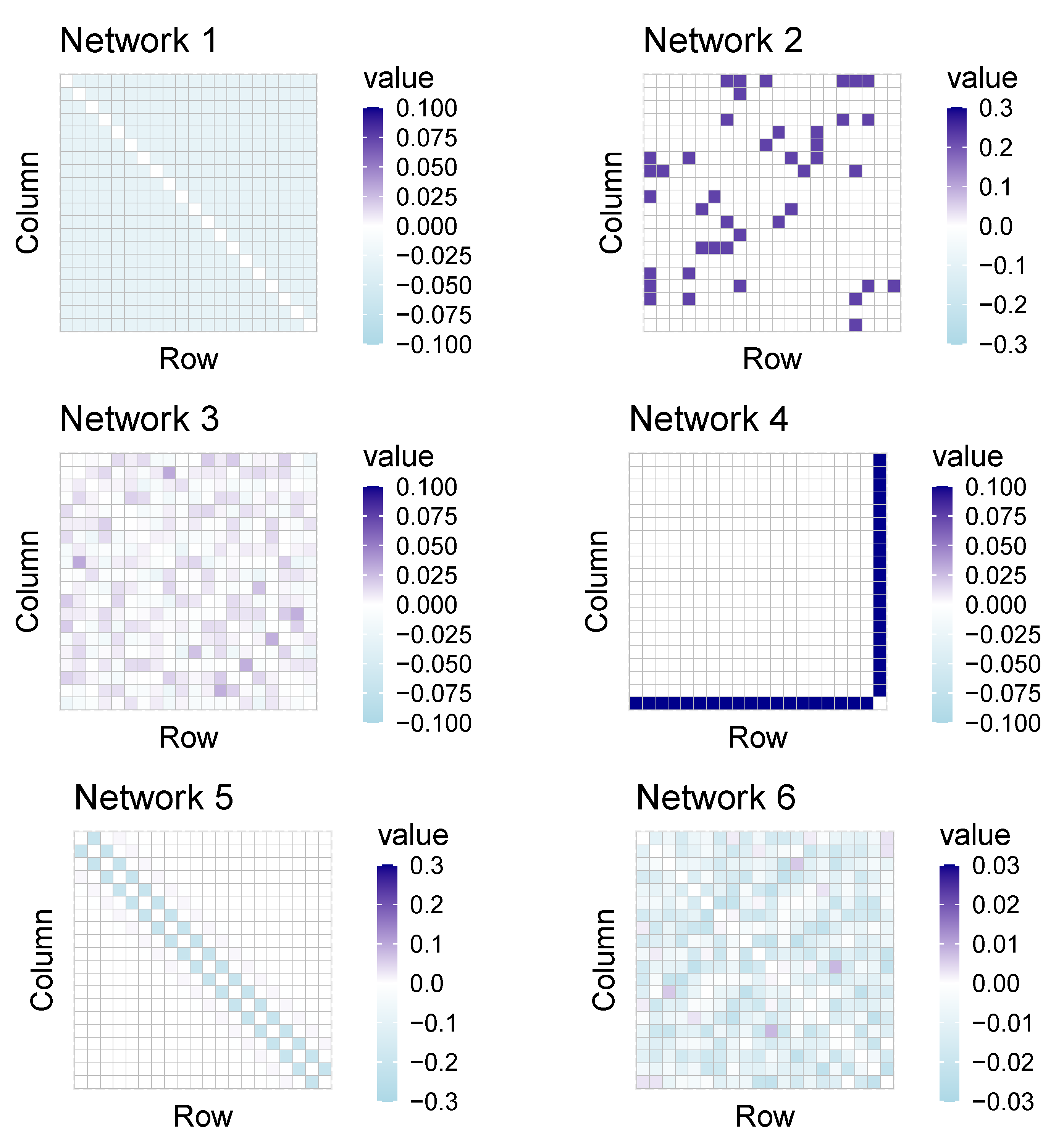
- Network 1: A model with compound symmetry structure where and for . In this model, the covariance matrix is structured and non-sparse;
- Network 2. The prototype matrix is used to standardize the precision matrix to possess a unit diagonal. Let , where each off-diagonal entry in is generated independently and equals with probability , or 0 with probability . a is chosen such that the condition number of the matrix is equal to p. Here we have an unstructured and sparse precision matrix;
- Network 3. The precision matrix is defined , where is an matrix with and comes from . The precision matrix of this model is unstructured and non-sparse;
- Network 4. A star model with , and otherwise. This local area network has a structured and sparse precision matrix;
- Network 5. A moving average (MA) model with , and . This covariance matrix is structured and sparse;
- Network 6. A diagonally dominant model. Consider , where is a matrix with zero diagonal elements. Each off-diagonal element of is drawn from a standard uniform distribution. Compute a matrix , where and is the largest row sum of the absolute values of the elements of the matrix . Finally, each off-diagonal element of is chosen as and , where is drawn from uniform distribution with minimum 0 and maximum . This covariance matrix is unstructured and non-sparse.
3.1. Performance Measures
Loss Functions
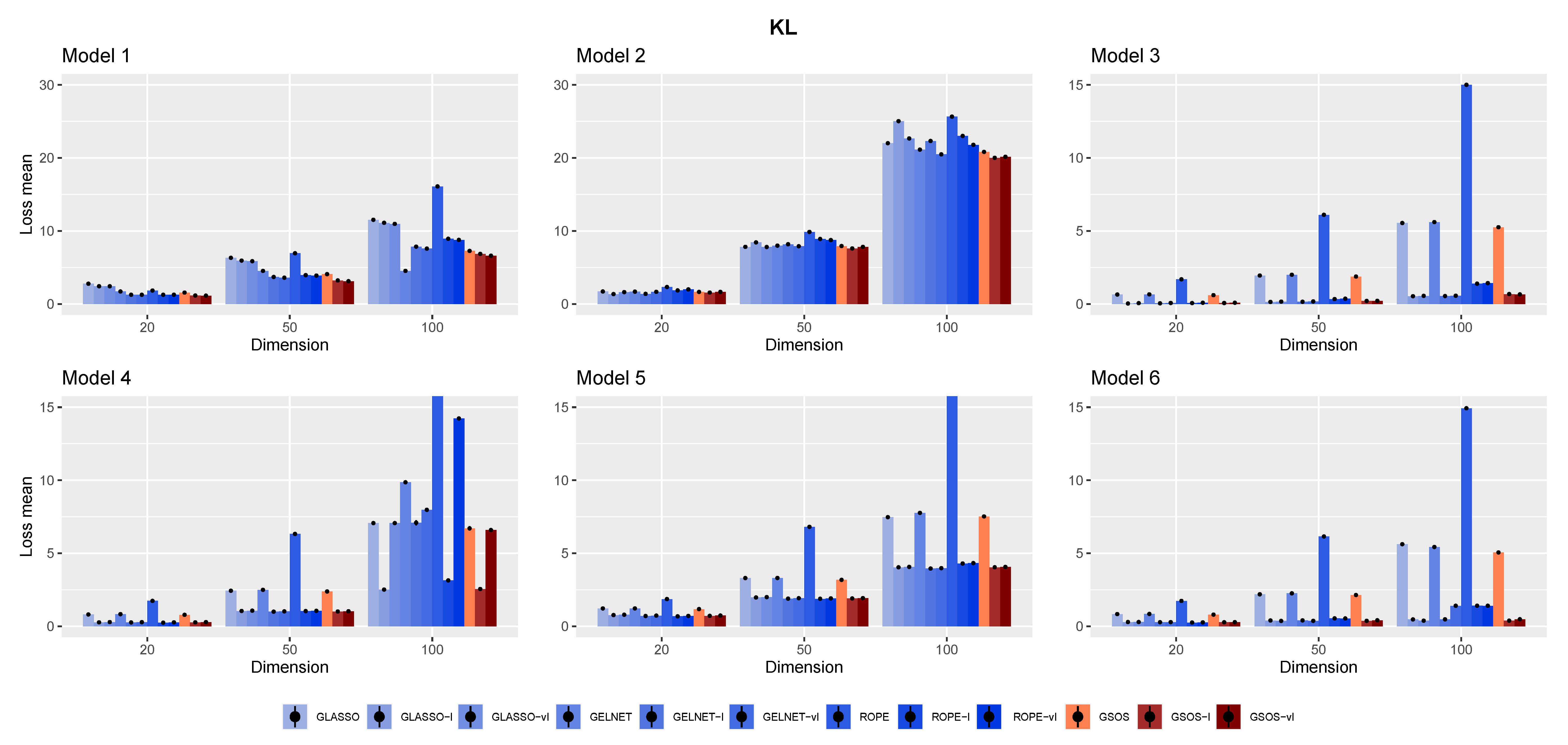
- The Kullback–Leibler loss: ;
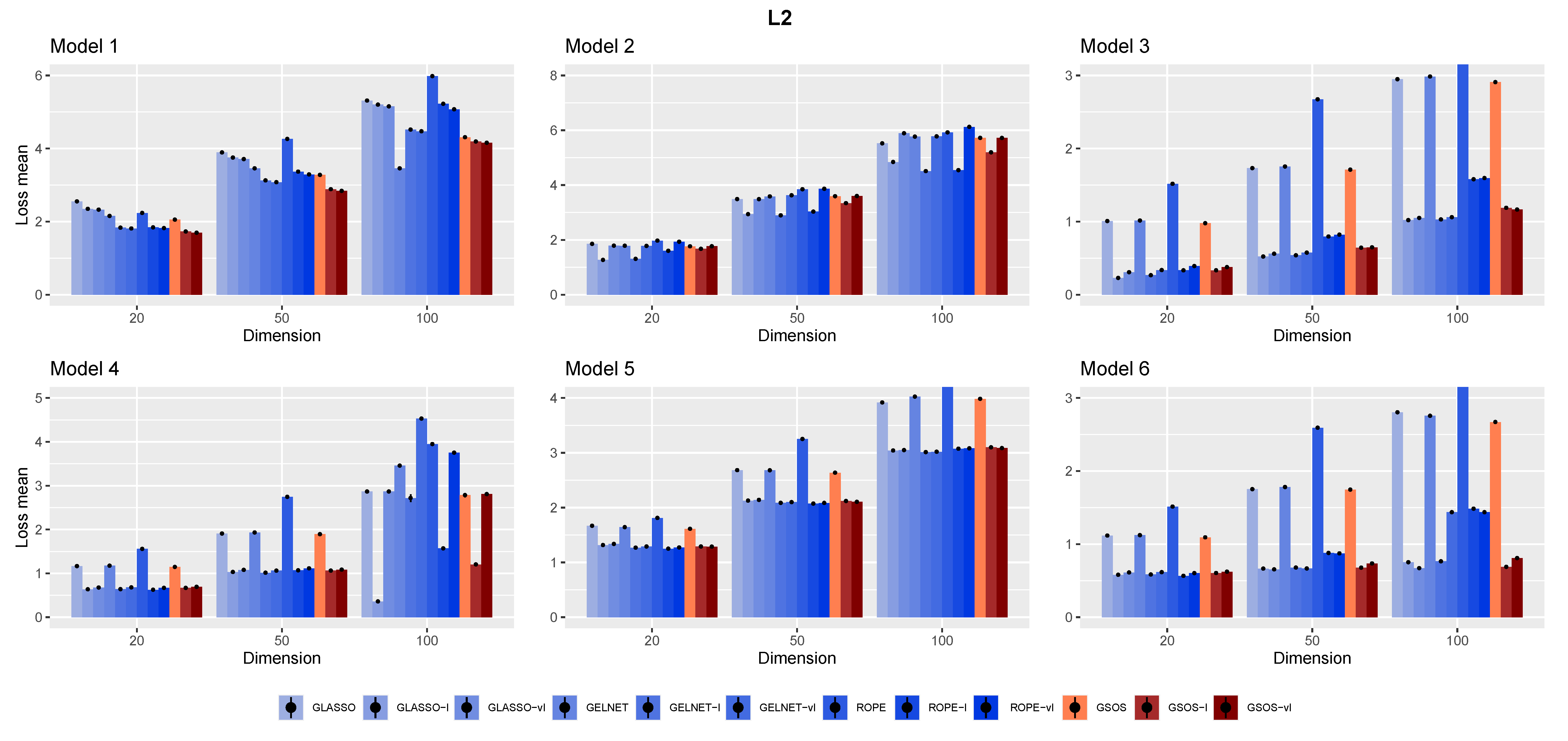
- The loss: ;
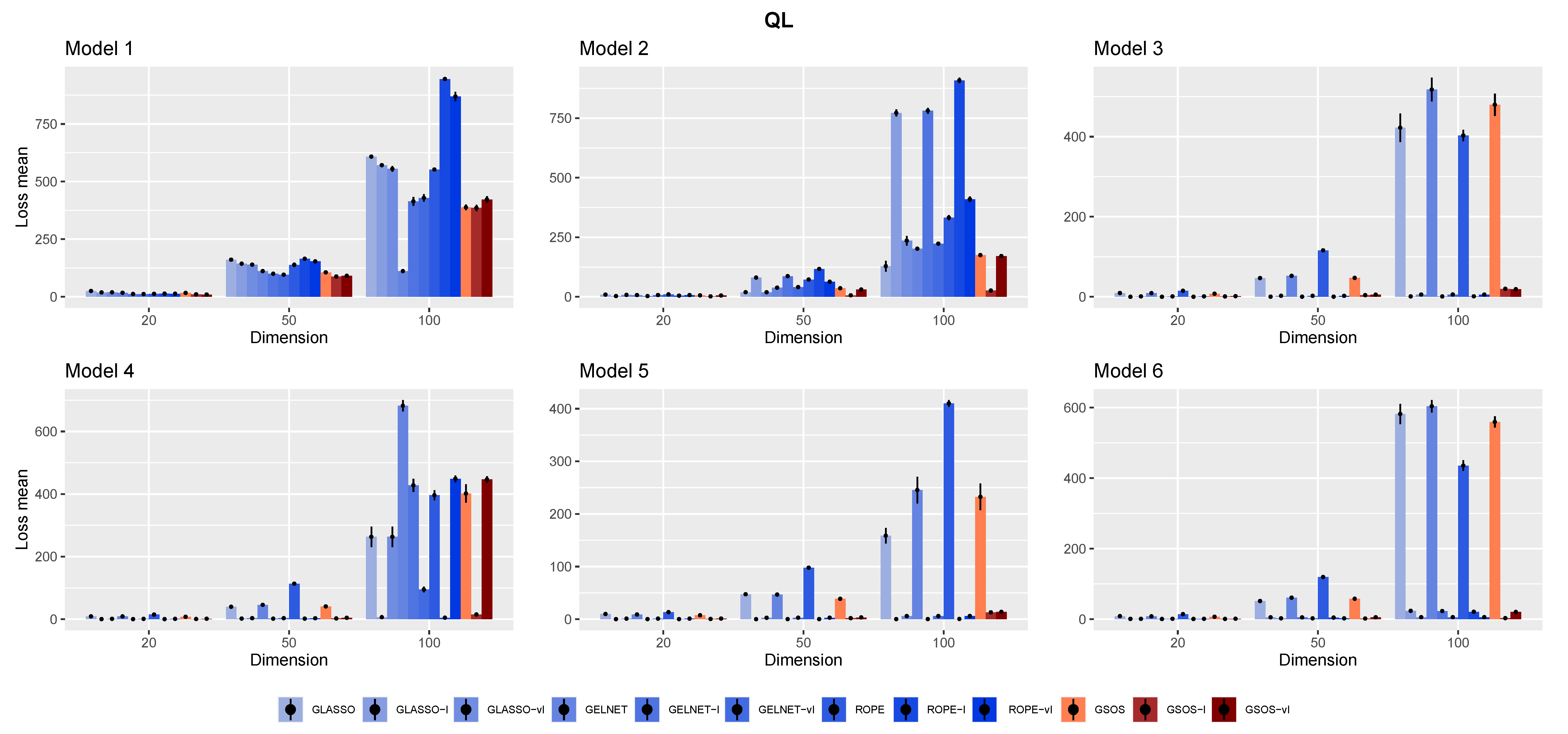
- The quadratic loss: ;
- The spectral norm loss: , where is the largest eigenvalue of the matrix .
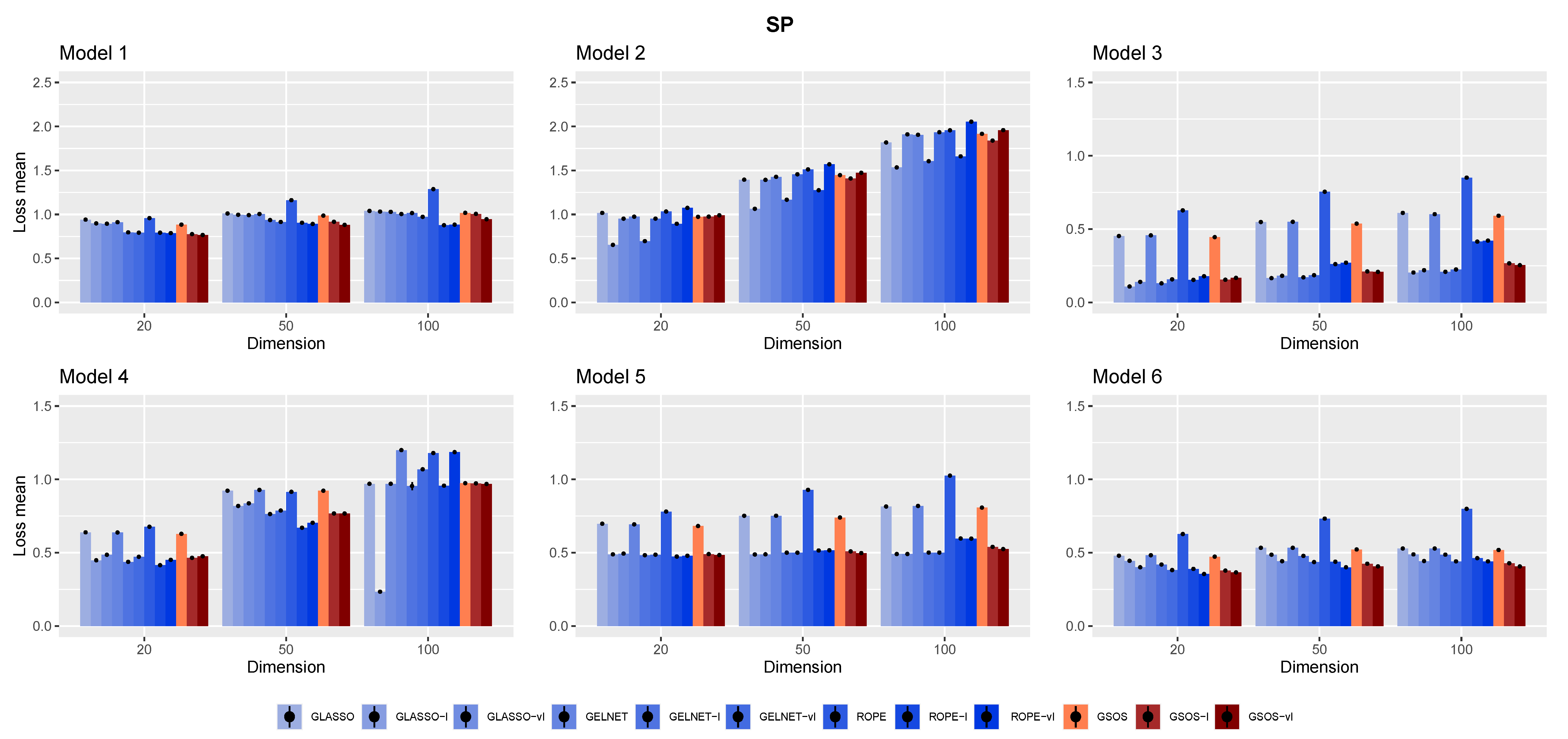
3.2. Simulation Results
- In general, as mentioned in [15], it is advantageous to include a target in the methods, since each approach works better with the appropriate target;
- Compared to other alternatives, GSOS is often a considerable contender for high-dimensional precision matrix estimation;
- The question of which target is more effective remains. However, in most cases, our simulations suggest that the identity target matrix works better.
4. Real Data
Real Data Results
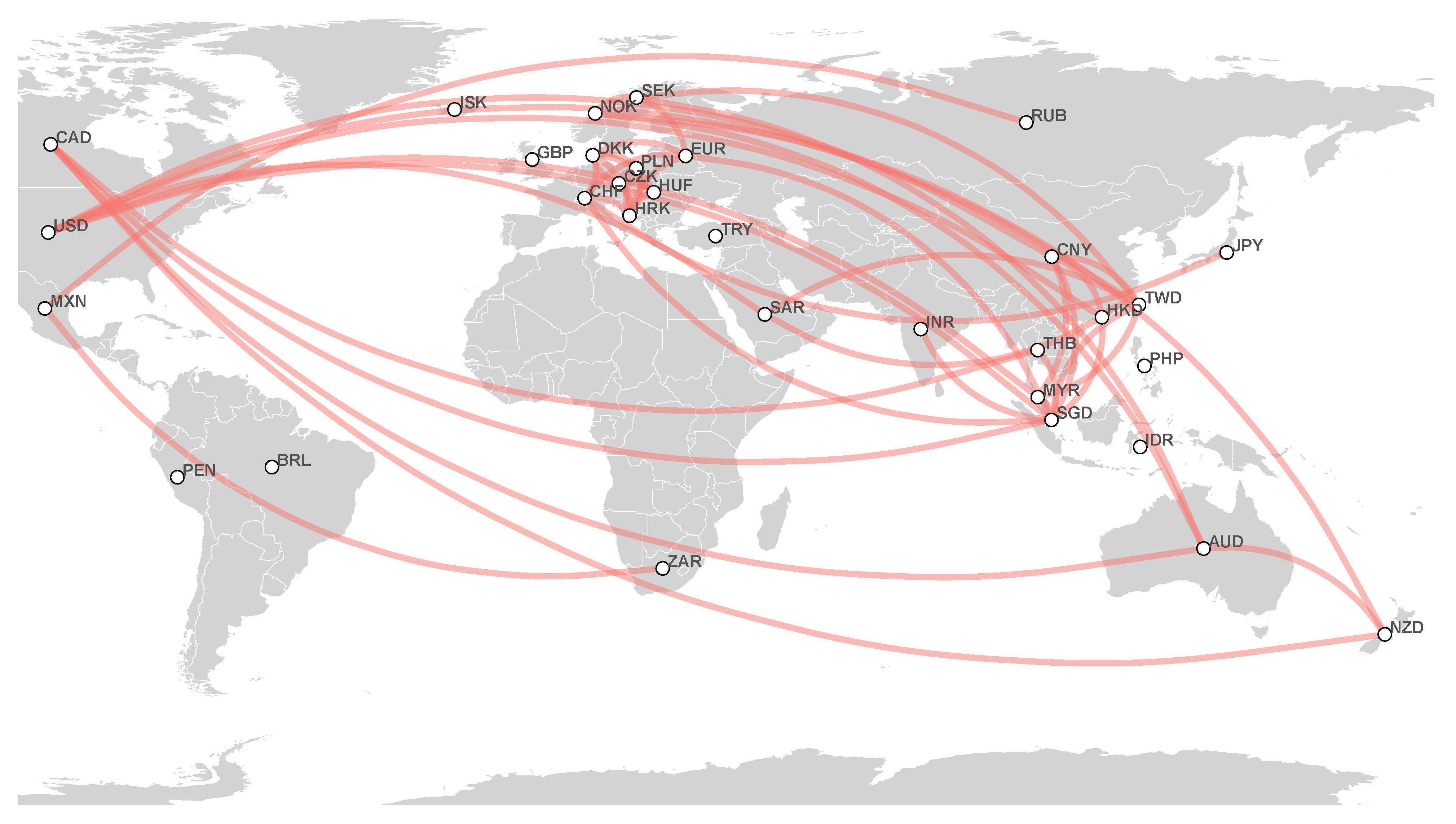
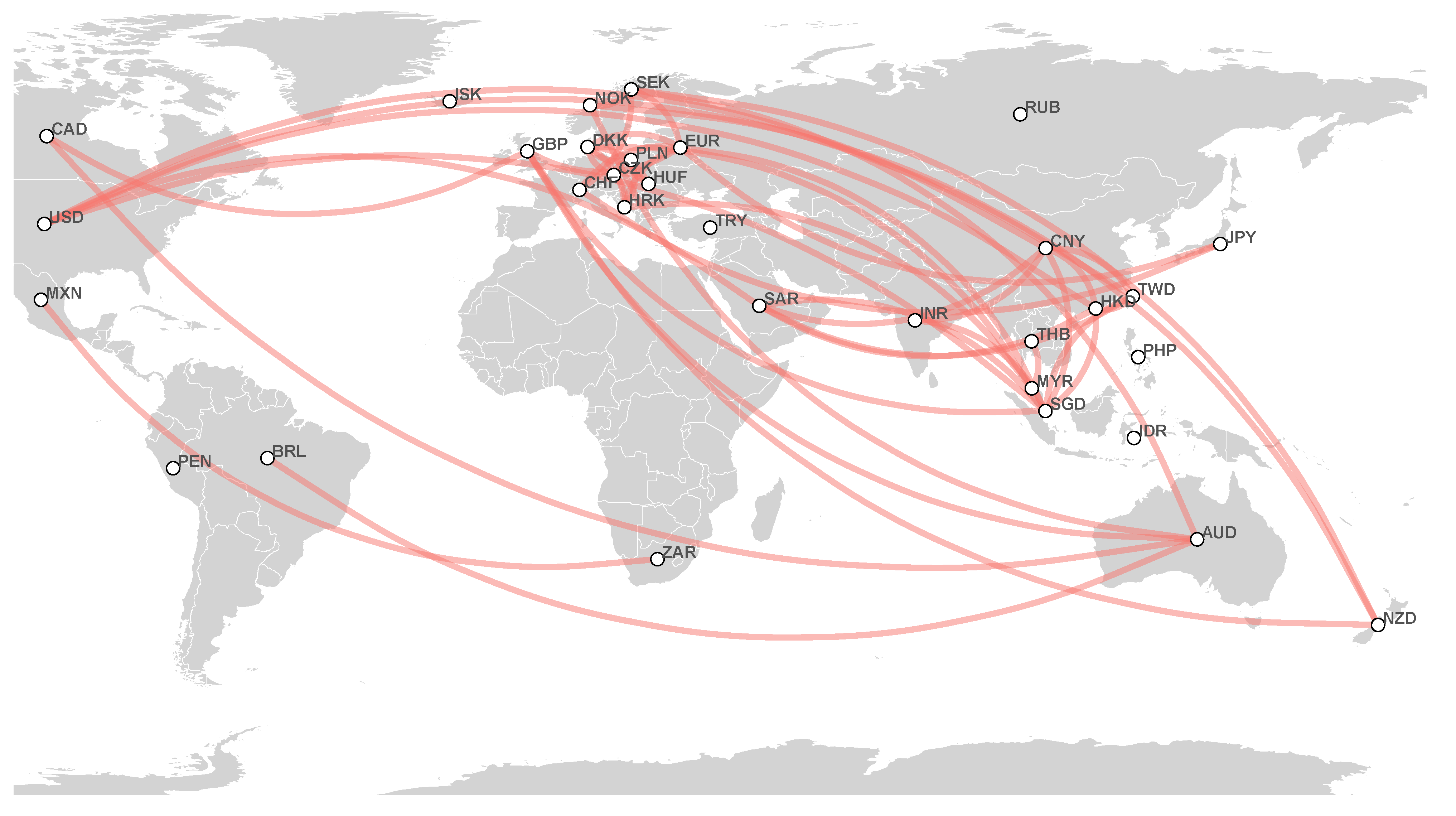
- 2018–2021 network: First, strong partial correlations appear between European currencies: DKK, HRK, CZK, PLN, HUF, CHF, and EUR. Additionally, we find a cluster that consists of HKD, SAR, CNY, TWD, SGD, and USD. Considering a smaller threshold, one notices the partial correlation between the Oceania couple of AUD and NZD and CAD, and the joining of EUR to the USD-based cluster, which connects European currencies to this cluster. Finally, a rather interesting cluster centered around a Latin American currency, MXN, appears, which consists of BRL, ZAR, and RUB;
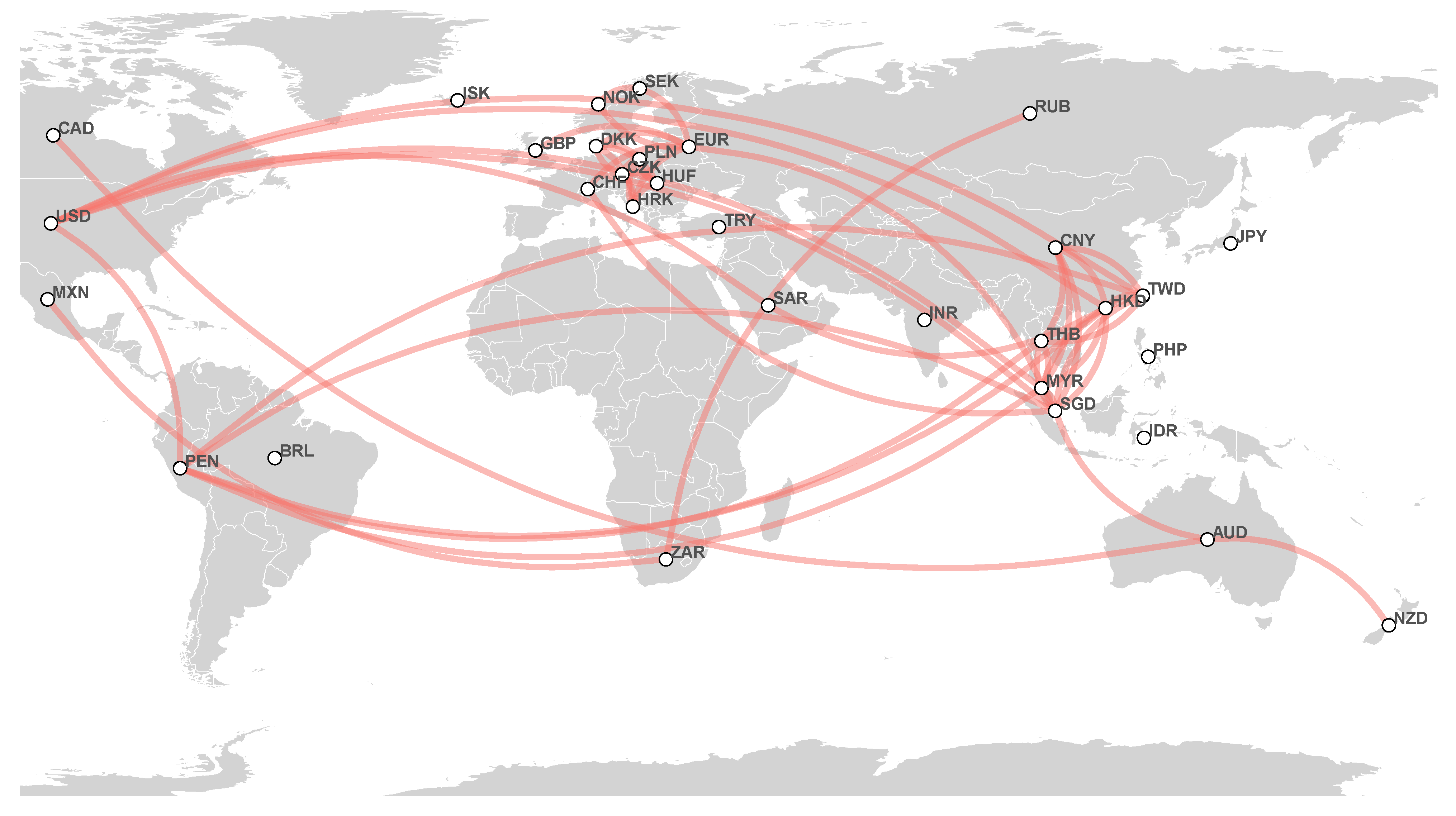
- 2018 network: We observe strong correlations between European currencies: DKK, HRK, CZK, PLN, HUF, and EUR. The USD-based cluster here consists of HKD, PEN, TWD, SGD, CNY, THB, and MYR. The EUR currency connects these two major clusters. We find the relation between the Oceania couple AUD and NZD and CAD for a smaller threshold. In addition, a cluster between the Latin American, African, and Asian currencies MXN, ZAR, and RUB is noteworthy;
- 2019 network: Similar to the 2018 network, we have strong and connected European currencies: DKK, HRK, CZK, PLN, and HUF. The USD-based cluster is formed by HKD, SAR, TWD, SGD, CNY, and MYR at first; by considering a smaller threshold, we find other currencies such as PEN and THB. We observe that EUR connects these two clusters, and another cluster consists of AUD, NZD, NOK, and SEK;
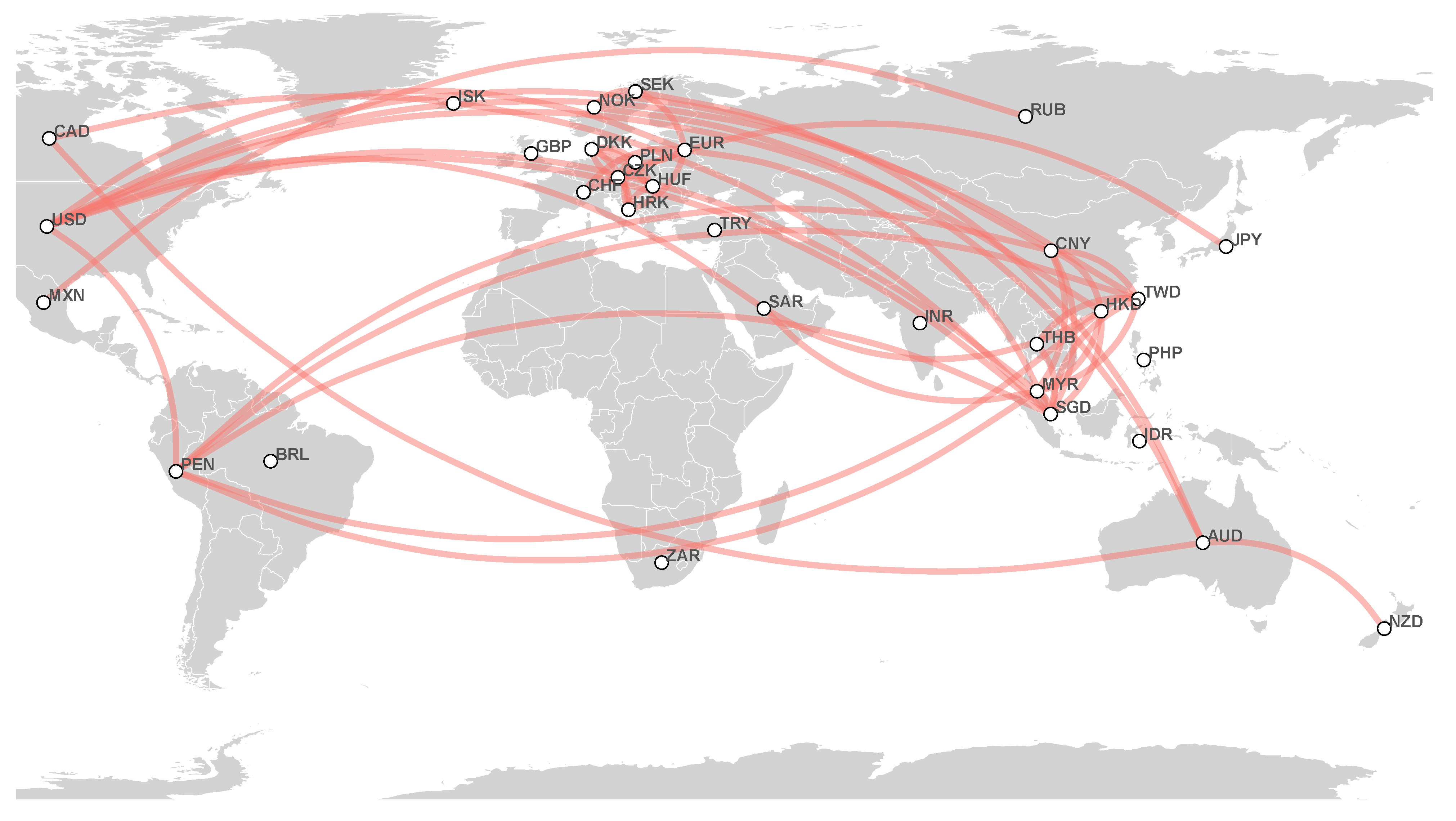
- 2020 network: This year, we observe the USD cluster as follows: HKD, SAR, TWD, SGD, and CNY. We can see MYR, PHP, and THB as a disjointed clique (every two distinct vertices are adjacent). Regarding European currencies, EUR and CHF have a connecting role between this cluster and the USD-based cluster. The European currency cluster consists of DKK, HRK, CZK, PLN, and HUF. In addition, we observe two other clusters: the Oceania couple AUD and NZD with CAD and GBP, and MXN, BRL, ZAR, and RUB. These two clusters have a connection to European currencies by SEK;
- 2021 network: As previously, we observe that the USD-based cluster consists of HKD, SAR, TWD, CNY, and SGD. DKK, HRK, CZK, HUF, PLN, CHF, SEK, and EUR form a European currency cluster, which is connected to the USD cluster by EUR. In addition, we discover an interesting cluster centered around AUD consisting of NZD, CAD, NOK, and GBP. Considering a smaller threshold, we find more relations in the last cluster and considerable partial correlations between AUD, NZD, NOK, and SEK. This year, we see a strong partial correlation between GBP and SGD, which has never been observed before. Finally, we have a small cluster consisting of three Latin American, Asian, and African currencies: MXN, RUB, and ZAR.
5. Discussion
5.1. Summary
5.2. Contributions
5.3. Strengths and Limitations
5.4. Future Work
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| GLASSO | Graphical lasso with zero target matrix |
| GLASSO-I | Graphical lasso with identity target matrix |
| GLASSO-vI | Graphical lasso with scalar target matrix |
| GELNET | Graphical elastic net with zero target matrix |
| GELNET-I | Graphical elastic net with identity target matrix |
| GELNET-vI | Graphical elastic net with scalar target matrix |
| ROPE | ROPE with zero target matrix |
| ROPE-I | ROPE with identity target matrix |
| ROPE-vI | ROPE with scalar target matrix |
| GSOS | GSOS with zero target matrix |
| GSOS-I | GSOS with identity target matrix |
| GSOS-vI | GSOS with scalar target matrix |
Appendix A
References
- Friedman, J.; Hastie, T.; Tibshirani, R. Sparse inverse covariance estimation with the graphical lasso. Biostatistics 2008, 9, 432–441. [Google Scholar] [CrossRef] [PubMed]
- Fan, J.; Feng, Y.; Wu, Y. Network exploration via the adaptive LASSO and SCAD penalties. Ann. Appl. Stat. 2009, 3, 521. [Google Scholar] [CrossRef] [PubMed]
- Bien, J.; Tibshirani, R.J. Sparse estimation of a covariance matrix. Biometrika 2011, 98, 807–820. [Google Scholar] [CrossRef] [PubMed]
- Witten, D.M.; Friedman, J.H.; Simon, N. New insights and faster computations for the graphical lasso. J. Comput. Gr. Stat. 2011, 20, 892–900. [Google Scholar] [CrossRef]
- Mazumder, R.; Hastie, T. The graphical lasso: New insights and alternatives. Electron. J. Stat. 2012, 6, 2125. [Google Scholar] [CrossRef]
- Danaher, P.; Wang, P.; Witten, D.M. The joint graphical lasso for inverse covariance estimation across multiple classes. J. R. Stat. Soc. Ser. B (Statist. Methodol.) 2014, 76, 373–397. [Google Scholar] [CrossRef]
- Avagyan, V.; Alonso, A.M.; Nogales, F.J. Improving the graphical lasso estimation for the precision matrix through roots of the sample covariance matrix. J. Comput. Graph. Stat. 2017, 26, 865–872. [Google Scholar] [CrossRef]
- Warton, D.I. Penalized normal likelihood and ridge regularization of correlation and covariance matrices. J. Am. Stat. Assoc. 2008, 103, 340–349. [Google Scholar] [CrossRef]
- Van Wieringen, W.N.; Peeters, C.F. Ridge estimation of inverse covariance matrices from high-dimensional data. Comput. Stat. Data Anal. 2016, 103, 284–303. [Google Scholar] [CrossRef]
- van Wieringen, W.N. The generalized ridge estimator of the inverse covariance matrix. J. Comput. Graph. Stat. 2019, 28, 932–942. [Google Scholar] [CrossRef]
- Kuismin, M.; Kemppainen, J.; Sillanpää, M. Precision matrix estimation with ROPE. J. Comput. Graph. Stat. 2017, 26, 682–694. [Google Scholar] [CrossRef][Green Version]
- Rothman, A.J. Positive definite estimators of large covariance matrices. Biometrika 2012, 99, 733–740. [Google Scholar] [CrossRef]
- Atchadé, Y.F.; Mazumder, R.; Chen, J. Scalable computation of regularized precision matrices via stochastic optimization. arXiv 2015, arXiv:1509.00426. [Google Scholar]
- Bernardini, D.; Paterlini, S.; Taufer, E. New estimation approaches for graphical models with elastic net penalty. arXiv 2021, arXiv:2102.01053. [Google Scholar] [CrossRef]
- Kovács, S.; Ruckstuhl, T.; Obrist, H.; Bühlmann, P. Graphical Elastic Net and Target Matrices: Fast Algorithms and Software for Sparse Precision Matrix Estimation. arXiv 2021, arXiv:2101.02148. [Google Scholar]
- Yuan, M.; Lin, Y. Model selection and estimation in the Gaussian graphical model. Biometrika 2007, 94, 19–35. [Google Scholar] [CrossRef]
- Banerjee, O.; El Ghaoui, L.; d’Aspremont, A. Model selection through sparse maximum likelihood estimation for multivariate Gaussian or binary data. J. Mach. Learn. Res. 2008, 9, 485–516. [Google Scholar]
- Yuan, M. Efficient computation of ℓ1 regularized estimates in Gaussian graphical models. J. Comput. Graph. Stat. 2008, 17, 809–826. [Google Scholar] [CrossRef]
- Guo, J.; Levina, E.; Michailidis, G.; Zhu, J. Joint estimation of multiple graphical models. Biometrika 2011, 98, 1–15. [Google Scholar] [CrossRef]
- Shan, L.; Kim, I. Joint estimation of multiple Gaussian graphical models across unbalanced classes. Comput. Stat. Data Anal. 2018, 121, 89–103. [Google Scholar] [CrossRef]
- Londschien, M.; Kovács, S.; Bühlmann, P. Change-point detection for graphical models in the presence of missing values. J. Comput. Graph. Stat. 2021, 30, 768–779. [Google Scholar] [CrossRef]
- Boyd, S.; Boyd, S.P.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Basnarkov, L.; Stojkoski, V.; Utkovski, Z.; Kocarev, L. Correlation patterns in foreign exchange markets. Phys. A Stat. Mech. Its Appl. 2019, 525, 1026–1037. [Google Scholar] [CrossRef]
- Fenn, D.J.; Porter, M.A.; Mucha, P.J.; McDonald, M.; Williams, S.; Johnson, N.F.; Jones, N.S. Dynamical clustering of exchange rates. Quant. Financ. 2012, 12, 1493–1520. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2022. [Google Scholar]

| Currencies | |||
|---|---|---|---|
| AUD | Australian dollar | MXN | Mexican peso |
| BRL | Brazilian real | MYR | Malaysian ringgit |
| CAD | Canadian dollar | NOK | Norwegian krone |
| CHF | Swiss franc | NZD | New Zealand dollar |
| CNY | Chinese renminbi | PEN | Peruvian nuevo sol |
| CZK | Czech koruna | PHP | Philippines peso |
| DKK | Danish krone | PLN | Polish zloty |
| EUR | Euro | RUB | Russian ruble |
| GBP | British pound | SAR | Saudi Arabian riyal |
| HKD | Hong Kong dollar | SEK | Swedish krona |
| HRK | Croatian kuna | SGD | Singapore dollar |
| HUF | Hungarian forint | THB | Thailand baht |
| IDR | Indonesian rupiah | TRY | Turkish lira |
| ISK | Icelandic krona | TWD | Taiwanese dollar |
| INR | Indian rupee | USD | US dollar |
| JPY | Japanese yen | ZAR | South African rand |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kheyri, A.; Bekker, A.; Arashi, M. High-Dimensional Precision Matrix Estimation through GSOS with Application in the Foreign Exchange Market. Mathematics 2022, 10, 4232. https://doi.org/10.3390/math10224232
Kheyri A, Bekker A, Arashi M. High-Dimensional Precision Matrix Estimation through GSOS with Application in the Foreign Exchange Market. Mathematics. 2022; 10(22):4232. https://doi.org/10.3390/math10224232
Chicago/Turabian StyleKheyri, Azam, Andriette Bekker, and Mohammad Arashi. 2022. "High-Dimensional Precision Matrix Estimation through GSOS with Application in the Foreign Exchange Market" Mathematics 10, no. 22: 4232. https://doi.org/10.3390/math10224232
APA StyleKheyri, A., Bekker, A., & Arashi, M. (2022). High-Dimensional Precision Matrix Estimation through GSOS with Application in the Foreign Exchange Market. Mathematics, 10(22), 4232. https://doi.org/10.3390/math10224232







