A Finite Volume Method to Solve the Ill-Posed Elliptic Problems

Abstract

In this paper, we propose a finite volume element method of primal-dual type to solve the ill-posed elliptic problem, that is, the elliptic problem with lacking or overlapping boundary value condition. We first establish the primal-dual finite volume element scheme by introducing the Lagrange multiplier $\lambda$ and prove the well-posedness of the discrete scheme. Then, the error estimations of the finite volume solution are derived under some proper norms including the $H^1$-norm. Numerical experiments are provided to verify the effectiveness of the proposed finite volume element method at last.

1. Introduction

In this present paper, we consider the finite volume element method for solving the following second-order ill-posed elliptic problem

$$\left\{\begin{array}{c}-div(a\nabla u)=f,x\in \mathsf{\Omega },\hfill \\ {u|}_{{\mathsf{\Gamma }}_d}=g_1,\frac{\partial u}{\partial n}{|}_{{\mathsf{\Gamma }}_n}=g_2,\hfill \end{array}\right.$$

(1)

where $\mathsf{\Omega }$ is a bounded polygonal domain in $R^2$ with boundary $\partial \mathsf{\Omega }$, ${\mathsf{\Gamma }}_d$ and ${\mathsf{\Gamma }}_n$ are two parts of the boundary $\partial \mathsf{\Omega }$ and $meas({\mathsf{\Gamma }}_d)\ne 0$, n is the unit external normal vector on $\partial \mathsf{\Omega }$, $f\in L^2(\mathsf{\Omega })$, $g_1\in H^1({\mathsf{\Gamma }}_d)$ and $g_2\in L_2({\mathsf{\Gamma }}_n)$ are known real-valued functions, $a(x)\in W^{1,\infty }(\mathsf{\Omega })$ is assumed to be such that $0<a_0\le a(x)\le a_1$. When ${\mathsf{\Gamma }}_d\cup {\mathsf{\Gamma }}_n\ne \partial \mathsf{\Omega }$ or ${\mathsf{\Gamma }}_d\cap {\mathsf{\Gamma }}_n\ne \varnothing$, elliptic problem (1) is called ill-posed, caused by the ill-posed boundary conditions. For example, in some engineering projects such as the dam with underground boundary, the ultra-high temperature surface of the spaceships, in these cases, part boundary conditions cannot be measured. This kind of ill-posed elliptic problem is to resolve a problem with lacking boundary conditions on part of the domain boundary [1].

Ill-posed elliptic problems have attracted many researchers since the 1960s due to their wide applications such as geophysics, steady-state inverse heat conduction, wave propagation, cardiology, electromagnetic scattering enzymatic reactions, bifurcation phenomena, phenomena in chemistry and plasma physics, and so on [2,3,4]. In 1902, Hadamard [5] first introduced the concept of the well-posed Cauchy problem, and later in 1923, he published the well-known example in [6] at Yale University. He illustrated the ill-posedness of the Cauchy problem for the Laplace equation (${\mathsf{\Gamma }}_d={\mathsf{\Gamma }}_n\subset \partial \mathsf{\Omega }$ and $a(x)=1$ in problem (1)). The work of Hadamard laid the foundation of the theory for the ill-posed Cauchy problems of elliptic equations. From then on, the theory has been further developed.

For severely ill-posed problems, the common numerical methods may not achieve optimal error estimates without some proper strategies. In [7], a stabilized finite element method was proposed in which a primal and an adjoint problem were solved simultaneously. Yagola et al. [8] discussed regularizing algorithms using a priori information. Klibanov [9] discussed a universal method of the regularization for ill-posed Cauchy problems by constructing Tikhonov functionals. Chung et al. [10] proposed a least squares formulation for the ill-posed problems and Qian [11] proposed a wavelet dual least squares method for the ill-posed elliptic problems. Cheng et al. [12] developed a numerical method for the ill-posed Cauchy problem of the Laplace equation where the essence of the method is to transform the Cauchy problem into a moment problem whose numerical method has been studied extensively. We refer the readers to [13,14,15,16] for more details on how to handle the severely ill-posed problems numerically.

Burman has conducted a series of research about ill-posed elliptic problems. In 2013, he proposed a stabilized finite element method to solve nonsymmetric indefinite problems [7] where the main idea is to solve a primal and an adjoint problem simultaneously. In 2014 [17], he further developed the analysis for the stabilized finite element method proposed in [7] where the weak continuous dependence was assumed so that the error estimate can be derived. In 2018, Burman et al. [18] showed that the stabilization methods for solving the ill-posed convection-dominated convection-diffusion problems are better than that of the Tikhonov regularization method. Wang et al. [2,19] devised a well-posed numerical scheme for a type of ill-posed elliptic problem by using a new primal-dual weak Galerkin finite element method where weak gradients were used in [19] while weak Laplacian was used in [2]. However, in their methods, the well-posedness of the discrete scheme was based on the uniqueness of the exact solution of the ill-posed problem and the error estimates were given only in some semi-norms. To the authors’ best knowledge, there is no research on the finite volume element method (FVE) for solving the ill-posed elliptic problem. The advantage of the FVE method [20,21,22,23,24,25] over some other numerical methods is that it can preserve some conservation properties of the original problem locally which are essential in some practical applications. Motivated by the work of Burman [7,17,18] and Wang [2,19], this paper aims to propose a finite volume element method for solving the ill-posed elliptic problem (1). The main difficulty of this problem is that the bilinear form of the variational equation derived from the ill-posed elliptic problem contains an individual boundary integral term because of lacking or overlap boundary conditions, so it is not positive definite on the solution space. Therefore, based on this bilinear form, the well-posedness of the discrete solution cannot be assured and it is very difficult to derive the error estimates in the $H^1$ and $L^2$ norms. To overcome this difficulty, the key technique in our paper is to introduce the primal-dual finite volume scheme and add proper stability terms on ${\mathsf{\Gamma }}_d$ and ${\mathsf{\Gamma }}_n$. Compared with the research works of Burman [7,17,18] and Wang [2,19], the advantage of our method is that our stability analysis and error estimates do not depend on some additional assumptions on the ill-posed problem. Our discrete scheme admits a unique solution and can achieve the optimal convergence order in some proper norms, including the $H^1$-norm.

According to the research in [1,26] we know that the ill-posed elliptic problem (1) has a solution $u\in H^1(\mathsf{\Omega })$ when boundary data $g_1\times g_2$ belong to a dense subset of $H^{\frac{1}{2}}({\mathsf{\Gamma }}_d)\times H^{\frac{1}{2}}({\mathsf{\Gamma }}_n)$. If the solution exists, it must be unique when ${\mathsf{\Gamma }}_d\cap {\mathsf{\Gamma }}_n$ is a nontrivial portion of the domain boundary. In this paper, we assume that the solution of the ill-posed elliptic problem (1) exists and possesses a certain smoothness needed for our analysis.

Throughout this paper, we use the notations $W^{m,p}(D)$ to indicate the standard Sobolev spaces on domain $D\subseteq \mathsf{\Omega }$ equipped with the norm ${\parallel ·\parallel }_{m,p,D}$ and seminorm ${|·|}_{m,p,D}$. When $p=2$, we denote $H^m(D)=W^{m,2}{(D),\parallel ·\parallel }_{m,D}={\parallel ·\parallel }_{m,2,D}$ and ${|·|}_{m,D}={|·|}_{m,2,D}$, and we omit subscript D if $D=\mathsf{\Omega }$. We also denote the letter C as a positive constant independent of the mesh size h.

This paper is organized as follows. We first establish a primal-dual finite volume scheme and prove the well-posedness of the discrete scheme in Section 2. In Section 3, we do the error analysis of the primal-dual finite volume scheme. Section 4 is devoted to the numerical experiments to illustrate the theoretical analysis.

2. Finite Volume Element Formulation

Let ${\mathcal{T}}_h$ be a quasi-regular triangulation of $\mathsf{\Omega }$ where $h=\underset{K\in {\mathcal{T}}_h}{max}\left\{h_K\right\}$, $h_K$ is the diameter of element K. We assume that the triangulation is such that the endpoints of ${\mathsf{\Gamma }}_d$ and ${\mathsf{\Gamma }}_n$ are the nodal points of ${\mathcal{T}}_h$. Denote $N_h$ the set of all nodal points of ${\mathcal{T}}_h$, ${\mathcal{E}}_h$ the set of all edges of ${\mathcal{T}}_h$ and ${\mathcal{E}}_h^0={\mathcal{E}}_h\backslash \partial \mathsf{\Omega }$. 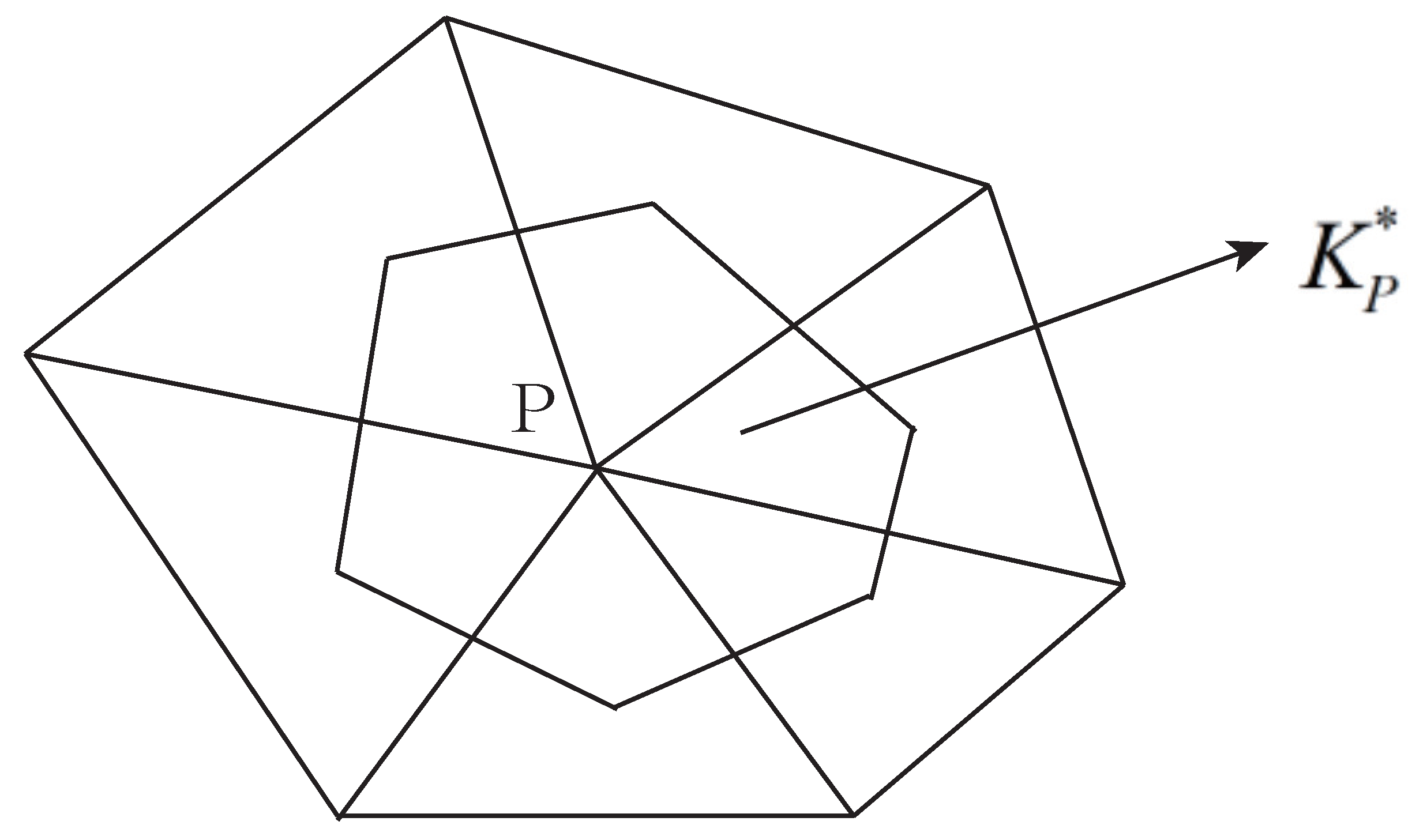With the triangulation ${\mathcal{T}}_h$, we construct a barycenter dual partition ${\mathcal{T}}_h^{*}$ by connecting the midpoints of the three edges to the barycenter of each element $K\in {\mathcal{T}}_h$ by straight lines. So, for each point $P\in N_h$, there is a polygonal element $K_P^{*}\in {\mathcal{T}}_h^{*}=\bigcup \left\{K_P^{*}\right\}$ which is the dual element or the control volume of point P, see Figure 1. Let ${\mathcal{S}}_h$ and ${\mathcal{S}}_h^{*}$ be the trail function space and the test function space, respectively,

$${\mathcal{S}}_h=\{u_h\in C(\overline{\mathsf{\Omega }})\cap H^1(\mathsf{\Omega }):u_h{\mid }_K\in P_1(K),\forall K\in {\mathcal{T}}_h\},$$

(2)

$${\mathcal{S}}_h^{*}=\{v_h\in L^2(\mathsf{\Omega }):v_h{\mid }_{K_P^{*}}=constant,\forall K_P^{*}\in {\mathcal{T}}_h^{*}\},$$

(3)

where $P_k(K)$ is the set of all k-th order polynomials on K.

For function $u\in C(\overline{\mathsf{\Omega }})$, define the interpolation operator ${\gamma }_h^{*}:C(\overline{\mathsf{\Omega }})\to {\mathcal{S}}_h^{*}$ by

$${\gamma }_h^{*}u{\mid }_{K_P^{*}}=u(P){\chi }_{{}_P}(x),K_P^{*}\in {\mathcal{T}}_h^{*},$$

(4)

where ${\chi }_{{}_P}(x)$ is the characteristic function of the dual element $K_P^{*}$. Thus,

$${\gamma }_h^{*}u(x)=\sum _{P\in N_h}u(P){\chi }_{{}_P}(x),x\in \mathsf{\Omega }.$$

(5)

It can be proved that ${\gamma }_h^{*}$ is a one to one mapping from ${\mathcal{S}}_h$ to ${\mathcal{S}}_h^{*}$, that is, ${\gamma }_h^{*}{\mathcal{S}}_h={\mathcal{S}}_h^{*}$.

For smooth function $u(x)$, we can obtain from the Green formula that

$$-{\int }_{K_P^{*}}div(a\nabla u)vd{K}_P^{*}=-{\int }_{\partial K_P^{*}}a\frac{\partial u}{\partial n}vds,\forall v\in {\mathcal{S}}_h^{*}.$$

(6)

Consequently, when $u\in H^{1+s}(\mathsf{\Omega })(s\ge \frac{1}{2})$ is the solution of problem (1), u satisfies the variational equation

$$a_h(u,{\gamma }_h^{*}{v}_h)=(f,{\gamma }_h^{*}{v}_h)+{\int }_{{\mathsf{\Gamma }}_n}a(x)g_2(x){\gamma }_h^{*}{v}_{h}ds,\forall v_h\in {\mathcal{S}}_h,$$

(7)

where

$$a_h(u,{\gamma }_h^{*}{v}_h)=-\sum _{K_P^{*}\in {\mathcal{T}}_h^{*}}{\int }_{\partial K_P^{*}\backslash {\mathsf{\Gamma }}_n}a(x)\frac{\partial u}{\partial n}{\gamma }_h^{*}{v}_{h}ds,\forall v_h\in {\mathcal{S}}_h.$$

(8)

and

$${\int }_{{\mathsf{\Gamma }}_n}a(x)g_2(x){\gamma }_h^{*}{v}_{h}ds=\sum _{K_P^{*}\in {\mathcal{T}}_h^{*}}{\int }_{\partial K_P^{*}\cap {\mathsf{\Gamma }}_n}a(x)g_2(x){\gamma }_h^{*}{v}_{h}ds=\sum _{K\in {\mathcal{T}}_h}{\int }_{\partial K\cap {\mathsf{\Gamma }}_n}a(x)g_2(x){\gamma }_h^{*}{v}_{h}ds.$$

(9)

In view of the ill boundary condition in general, the variational form (7) is not well-posed. In order to define a well-posed discrete scheme, we first introduce the jump $\left[u\right]$ of function u across element edge e by

$$\begin{array}{c}\hfill {\left[u\right]|}_e=u{\mid }_{K_1}{\mathbf{n}}_1+u{\mid }_{K_2}{\mathbf{n}}_2,e\in {\mathcal{E}}_h^0{,\left[u\right]|}_e=u\mathbf{n},e\in \partial \mathsf{\Omega },\end{array}$$

(10)

where e is the common edge of elements $K_1$ and $K_2$, ${\mathbf{n}}_1,{\mathbf{n}}_2$ are the unit external normal vectors to $K_1$ and $K_2$, respectively. Furthermore, for vector function w,

$${\left[\mathbf{w}\right]|}_e{=\mathbf{w}|}_{K_1}·{\mathbf{n}}_1+\mathbf{w}{{|}_{K_2}·{\mathbf{n}}_2,e\in {\mathcal{E}}_h^0,\left[\mathbf{w}\right]|}_e=\mathbf{w}·\mathbf{n},e\in \partial \mathsf{\Omega }.$$

(11)

For any $u,v\in {\mathcal{S}}_h+H^{1+s}(\mathsf{\Omega }),s\ge \frac{1}{2}$, denote

$$S_d(u,v)={\int }_{{\mathsf{\Gamma }}_d}{h}_{\mu }^{-1}uvds=\sum _{e\subset {\mathsf{\Gamma }}_d}{\int }_e{h}_{\mu }^{-1}uvds,$$

(12)

$$S_{n,d}(u,v)={\int }_{{\mathsf{\Gamma }}_d\cup {\mathsf{\Gamma }}_n}{h}_{\mu }^{-1}uvds=\sum _{e\subset {\mathsf{\Gamma }}_d\cup {\mathsf{\Gamma }}_n}{\int }_e{h}_{\mu }^{-1}uvds,$$

(13)

$$S(u,v)={\int }_{{\mathcal{E}}_h^0\cup {\mathsf{\Gamma }}_n}{h}_{\mu }[\nabla u][\nabla v]ds=\sum _{e\in {\mathcal{E}}_h^0\cup {\mathsf{\Gamma }}_n}{\int }_e{h}_{\mu }[\nabla u][\nabla v]ds,$$

(14)

where $h_{\mu }{\mid }_e=h_e=meas(e)$.

From Equation (7), we see that when the solution of problem (1) $u\in H^{1+s}(\mathsf{\Omega })(s\ge \frac{1}{2})$, u and the Lagrange multiplier $\lambda =0$ satisfies the following primal-dual variation equations with stabilizers

$$\left\{\begin{array}{c}{S}_d(u,v_h)+S(u,v_h)-a_h(v_h,{\gamma }_h^{*}\lambda )={\int }_{{\mathsf{\Gamma }}_d}{h}_{\mu }^{-1}{g}_1{v}_{h}ds+{\int }_{{\mathsf{\Gamma }}_n}{h}_{\mu }{g}_2\frac{\partial v_h}{\partial n}ds,\forall v_h\in {\mathcal{S}}_h,\hfill \\ S_{n,d}(\lambda ,w_h)+a_h(u,{\gamma }_h^{*}{w}_h)=(f,{\gamma }_h^{*}{w}_h)+{\int }_{{\mathsf{\Gamma }}_n}a{g}_2{\gamma }_h^{*}{w}_{h}ds,\forall w_h\in {\mathcal{S}}_h.\hfill \end{array}\right.$$

(15)

Based on the weak form (15), we define the primal-dual finite volume element approximation of problem (1): find $(u_h,{\lambda }_h)\in {\mathcal{S}}_h\times {\mathcal{S}}_h$ such that

$$\left\{\begin{array}{c}{S}_d(u_h,v_h)+S(u_h,v_h)-a_h(v_h,{\gamma }_h^{*}{\lambda }_h)={\int }_{{\mathsf{\Gamma }}_d}{h}_{\mu }^{-1}{g}_1{v}_{h}ds+{\int }_{{\mathsf{\Gamma }}_n}{h}_{\mu }{g}_2\frac{\partial v_h}{\partial n}ds,\forall v_h\in {\mathcal{S}}_h,\hfill \\ S_{n,d}({\lambda }_h,w_h)+a_h(u_h,{\gamma }_h^{*}{w}_h)=(f,{\gamma }_h^{*}{w}_h)+{\int }_{{\mathsf{\Gamma }}_n}a{g}_2{\gamma }_h^{*}{w}_{h}ds,\forall w_h\in {\mathcal{S}}_h.\hfill \end{array}\right.$$

(16)

Obviously, the discrete scheme (16) is consistent.

Next, we recall some known results which will play an important role in our analysis. Let $I_h:C(\overline{\mathsf{\Omega }})\to S_h$ be the standard linear interpolation operator. The approximation property of $I_h$, trace inequality and finite element inverse inequality are as follows

$$\parallel v-I_h{v\parallel }_{m,p,K}\le C{h}_K^{2-m}{\parallel v\parallel }_{2,p,K},0\le m\le 2,1<p\le \infty ,$$

(17)

$${\parallel v\parallel }_{0,p,\partial K}\le C{h}_K^{-\frac{1}{p}}{(\parallel v\parallel }_{0,p,K}+h_K{\parallel \nabla v\parallel }_{0,p,K}),v\in W^{1,p}(K),1\le p\le \infty ,$$

(18)

$$\parallel v_h{\parallel }_{m,p,\partial K}\le C{h}_K^{-\frac{1}{p}}{\parallel v_h\parallel }_{m,p,K},v_h\in P_k(K),m=0,1,1\le p\le \infty .$$

(19)

$$\parallel v_h{\parallel }_{m,p,K}\le C{h}_K^{\frac{2}{p}-\frac{2}{q}}{\parallel v_h\parallel }_{m,q,K},v_h\in P_k(K),m=0,1,1\le q\le p\le \infty .$$

(20)

Lemma 1 

([27]). Let $K\in {\mathcal{T}}_h$ and $e\subset \partial K$ be an edge of K. Then, for $v_h\in {\mathcal{S}}_h$, the following results hold

$${\int }_K(v_h-{\gamma }_h^{*}{v}_h)=0,{\int }_e(v_h-{\gamma }_h^{*}{v}_h)ds=0.$$

(21)

Lemma 2. 

Let $K\in {\mathcal{T}}_h$. Then, for $w_h\in {\mathcal{S}}_h,1\le q\le \infty$, the interpolation operator ${\gamma }_h^{*}$ has the following approximation properties

$$\parallel w_h-{\gamma }_h^{*}{w}_h{\parallel }_{0,q,K}\le C{h}_K{\parallel \nabla w_h\parallel }_{0,q,K},$$

(22)

$$\parallel w_h-{\gamma }_h^{*}{w}_h{\parallel }_{0,q,\partial K}\le C{h}_K^{1-\frac{1}{q}}{\parallel \nabla w_h\parallel }_{0,q,K}.$$

(23)

Proof. 

Let P be a vertex of element K. Denote $\widehat{K}=K_P^{*}\bigcap K$ the one third part of element K, then ${\gamma }_h^{*}{w}_h=w_h(P)$ on $\widehat{K}$. Following the inverse inequality, we can obtain

$$\begin{array}{cc}\hfill & \parallel w_h-{\gamma }_h^{*}{w}_h{\parallel }_{0,q,\widehat{K}}={\parallel w_h-w_h(P)\parallel }_{0,q,\widehat{K}}\hfill \\ \hfill & \le h_{\widehat{K}}|\widehat{K}{|}^{\frac{1}{q}}|\nabla w_h{|}_{0,\infty ,\widehat{K}}\le C{h}_{\widehat{K}}\parallel \nabla w_h{\parallel }_{0,q,\widehat{K}}\le C{h}_K{\parallel \nabla w_h\parallel }_{0,q,K},\hfill \end{array}$$

(24)

which gives estimation (22). In order to prove (23), we let $\widehat{\tau }=\partial K\bigcap \partial \widehat{K}$, by using trace inequality (18) and (22) we have

$$\begin{array}{cc}\hfill \parallel w_h-{\gamma }_h^{*}{w}_h{\parallel }_{0,q,\widehat{\tau }}& \le C{h}_{\widehat{K}}^{-\frac{1}{q}}(\parallel w_h-{\gamma }_h^{*}{w}_h{\parallel }_{0,q,\widehat{K}}+h_{\widehat{K}}\parallel \nabla w_h{\parallel }_{0,q,\widehat{K}})\hfill \\ \hfill & \le C{h}_{\widehat{K}}^{1-\frac{1}{q}}\parallel \nabla w_h{\parallel }_{0,q,\widehat{K}}\le C{h}_K^{1-\frac{1}{q}}{\parallel \nabla w_h\parallel }_{0,q,K},\hfill \end{array}$$

(25)

which completes the proof. □

The basic idea of our forthcoming analysis is to regard the FVE method as a disturbance of the FEM [24,27,28], so we need to give the relationship between the bilinear form of FVE and that of FEM.

Define the bilinear form of FVE and FEM, respectively,

$$\begin{array}{cc}\hfill & a_V(w_h,{\gamma }_h^{*}{v}_h)=-\sum _{K_P^{*}\in {\mathcal{T}}_h^{*}}{\int }_{\partial K_P^{*}}a\frac{\partial w_h}{\partial n}{\gamma }_h^{*}{v}_{h}ds,\forall w_h,v_h\in {\mathcal{S}}_h,\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill & a(w_h,v_h)={\int }_{\mathsf{\Omega }}a\nabla w_h\nabla v_h,\forall w_h,v_h\in {\mathcal{S}}_h.\hfill \end{array}$$

(27)

Lemma 3 

([27]). Let the algebraic sum space $V(h)=H^{\frac{3}{2}}(\mathsf{\Omega })+{\mathcal{S}}_h$. For all $w\in V(h),v_h\in {\mathcal{S}}_h$, we have

$$a_V(w,{\gamma }_h^{*}{v}_h)-a(w,v_h)=\sum _{K\in {\mathcal{T}}_h}{\int }_{\partial K}\mathbf{n}·(a▽w)({\gamma }_h^{*}{v}_h-v_h)ds+\sum _{K\in {\mathcal{T}}_h}{(-div(a\nabla w),{\gamma }_h^{*}{v}_h-v_h)}_K.$$

(28)

From Lemma 3, we can obtain the following estimate between the bilinear form of FVE and that of FEM.

Lemma 4. 

For all $w_h,v_h\in {\mathcal{S}}_h$, we have

$$|a(w_h,v_h)-a_V(w_h,{\gamma }_h^{*}{v}_h)|\le Ch\parallel \nabla w_h\parallel \parallel \nabla v_h\parallel .$$

(29)

Proof. 

From Lemma 3, Lemma 1, Lemma 2 and noting that $w_h$ is a piecewise linear function on ${\mathcal{T}}_h$, we can derive

$$\begin{array}{cc}\hfill & |a(w_h,v_h)-a_V(w_h,{\gamma }_h^{*}{v}_h)|\le |\sum _{K\in {\mathcal{T}}_h}{\int }_{\partial K}a\frac{\partial w_h}{\partial n}({\gamma }_h^{*}{v}_h-v_h)ds|+|\sum _{K\in {\mathcal{T}}_h}{\int }_{K}div(a\nabla w_h)({\gamma }_h^{*}{v}_h-v_h)|\hfill \\ \hfill & =|\sum _{K\in {\mathcal{T}}_h}{\int }_{\partial K}(a-a^c)\frac{\partial w_h}{\partial n}({\gamma }_h^{*}{v}_h-v_h)ds|+|\sum _{K\in {\mathcal{T}}_h}{\int }_K\nabla a·\nabla w_h({\gamma }_h^{*}{v}_h-v_h)|\hfill \\ \hfill & \le |a-a^c{|}_{\infty }\sum _{K\in {\mathcal{T}}_h}({\int }_{\partial K}|\frac{\partial w_h}{\partial n}{|}^2{)}^{\frac{1}{2}}({\int }_{\partial K}|{\gamma }_h^{*}{v}_h-v_h{|}^2{)}^{\frac{1}{2}}+Ch\parallel \nabla w_h\parallel \parallel \nabla v_h\parallel \hfill \\ \hfill & \le {Ch|a|}_{1,\infty }\sum _{K\in {\mathcal{T}}_h}\parallel \nabla w_h{\parallel }_{\partial K}{h}_K^{\frac{1}{2}}\parallel \nabla v_h{\parallel }_K+Ch\parallel \nabla w_h\parallel \parallel \nabla v_h{\displaystyle \parallel }\hfill \\ \hfill & \le {Ch|a|}_{1,\infty }\sum _{K\in {\mathcal{T}}_h}{h}_K^{-\frac{1}{2}}\parallel \nabla w_h{\parallel }_K{h}_K^{\frac{1}{2}}\parallel \nabla v_h{\parallel }_K+Ch\parallel \nabla w_h\parallel \parallel \nabla v_h\parallel \hfill \\ \hfill & \le Ch\parallel \nabla w_h\parallel \parallel \nabla v_h\parallel .\hfill \end{array}$$

(30)

where $a^c{|}_{{}_K}=\frac{1}{|K|}{\int }_{{}_K}adx$ is the mean of $a(x)$ on element K. The proof is completed. □

From Lemma 4 and $a(u,v)=(a\nabla u,\nabla v)$, we see that when h is sufficiently small, the following inequality holds

$$a_V(u_h,{\gamma }_h^{*}{u}_h)\ge C_0{\parallel \nabla u_h\parallel }^2,\forall u_h\in {\mathcal{S}}_h.$$

(31)

By the definitions of $a_h(·,·)$ and $a_V(·,·)$, we have

$$a_h(u,{\gamma }_h^{*}v)=a_V(u,{\gamma }_h^{*}v)+{\int }_{{\mathsf{\Gamma }}_n}a\frac{\partial u}{\partial n}{\gamma }_h^{*}vds,\forall u\in V(h),v\in {\mathcal{S}}_h.$$

(32)

Lemma 5. 

For sufficiently small h, we have

$$a_h(w_h,{\gamma }_h^{*}{w}_h)\ge {\gamma }_0\parallel \nabla w_h{\parallel }^2-C_1{\int }_{{\mathsf{\Gamma }}_n}{h}_{\mu }^{-1}{|w_h|}^{2}ds,\forall w_h\in {\mathcal{S}}_h,$$

(33)

where ${\gamma }_0$ is a constant.

Proof. 

By using Lemma 1, Lemma 2 and the inverse inequality, we obtain

$$\begin{array}{cc}\hfill & {\int }_{{\mathsf{\Gamma }}_n}a\frac{\partial w_h}{\partial n}{\gamma }_h^{*}{v}_{h}ds={\int }_{{\mathsf{\Gamma }}_n}a\frac{\partial w_h}{\partial n}({\gamma }_h^{*}{v}_h-v_h)ds+{\int }_{{\mathsf{\Gamma }}_n}a\frac{\partial w_h}{\partial n}{v}_{h}ds\hfill \\ \hfill & =\sum _{K\in {\mathcal{T}}_h}{\int }_{{\mathsf{\Gamma }}_n\cap \partial K}(a-a^c)\frac{\partial w_h}{\partial n}({\gamma }_h^{*}{v}_h-v_h)ds+\sum _{K\in {\mathcal{T}}_h}{\int }_{{\mathsf{\Gamma }}_n\cap \partial K}a\frac{\partial w_h}{\partial n}{v}_{h}ds\hfill \\ \hfill & \le Ch\sum _{K\in {\mathcal{T}}_h}\parallel \nabla w_h{\parallel }_{\partial K}\parallel {\gamma }_h^{*}{v}_h-v_h{\parallel }_{\partial K}+C\sum _{K\in {\mathcal{T}}_h}{\parallel h_{\mu }^{\frac{1}{2}}\nabla w_h\parallel }_{\partial K\cap {\mathsf{\Gamma }}_n}{({\int }_{{\mathsf{\Gamma }}_n\cap \partial K}{h}_{\mu }^{-1}{v}_h^{2}ds)}^{\frac{1}{2}}\hfill \\ \hfill & \le Ch\parallel \nabla w_h\parallel \parallel \nabla v_h\parallel +C\parallel \nabla w_h\parallel {({\int }_{{\mathsf{\Gamma }}_n}{h}_{\mu }^{-1}{v}_h^{2}ds)}^{\frac{1}{2}},\hfill \end{array}$$

(34)

We complete the proof by combining (31) and (32). □

Theorem 1. 

Assume that either ${\mathsf{\Gamma }}_n\ne \varnothing$ or ${\mathsf{\Gamma }}_d$ is not a straight line, then the solution $(u_h,{\lambda }_h)\in {\mathcal{S}}_h\times {\mathcal{S}}_h$ of finite volume element scheme (16) exists uniquely.

Proof. 

We just need to prove that the discrete linear homogeneous equations (16) only have the trivial solutions. Let $f(x)=g_1(x)=g_2(x)=0$ in (16) and take $v_h=u_h,w_h={\lambda }_h$, we can derive by adding the two equations

$$S_d(u_h,u_h)+S(u_h,u_h)+S_{n,d}({\lambda }_h,{\lambda }_h)=0.$$

(35)

With the definitions of $S_d(u,v),S_{n,d}(u,v)$ and $S(u,v)$, we obtain

$$u_h{|}_{{\mathsf{\Gamma }}_d}=0,\frac{\partial u_h}{\partial n}{|}_{{\mathsf{\Gamma }}_n}=0,[\nabla u_h]{|}_e=0,e\in {\mathcal{E}}_h^0,{\lambda }_h{{|}_{{\mathsf{\Gamma }}_d}={\lambda }_h|}_{{\mathsf{\Gamma }}_n}=0.$$

(36)

Notice that $\nabla u_h$ is piecewise constant on ${\mathcal{T}}_h$, then by $[\nabla u_h]{|}_e=0$ we know that $\nabla u_h$ is a constant on the whole domain $\mathsf{\Omega }$ and $u_h$ is a single linear polynomial on $\mathsf{\Omega }$. Thus, by $\frac{\partial u_h}{\partial n}{|}_{{\mathsf{\Gamma }}_n}=0$, $u_h{|}_{{\mathsf{\Gamma }}_d}=0$ and the condition of Theorem 1, we can assert that $u_h=0$ on $\mathsf{\Omega }$. Furthermore, from the first homogeneous Equation in (16) we can obtain

$$a_h(v_h,{\gamma }_h^{*}{\lambda }_h)=0,\forall v_h\in {\mathcal{S}}_h.$$

(37)

Taking $v_h={\lambda }_h$ in (37), using Lemma 5 and ${\lambda }_h{|}_{{\mathsf{\Gamma }}_n}=0$ we can deduce $\parallel \nabla {\lambda }_h\parallel =0$, that is, ${\lambda }_h$ is a constant. Furthermore, ${\lambda }_h{|}_{{\mathsf{\Gamma }}_d}=0$ implies that ${\lambda }_h\equiv 0$ on $\mathsf{\Omega }$. □

Theorem 1 gives the well-posedness of the primal-dual finite volume element scheme (16).

3. Error Estimation

In this section, we do the error analysis of the primal-dual finite volume element method (16).

Introduce the semi-norm notations

$${|u|}_{{\mathsf{\Gamma }}_d}=S_d^{\frac{1}{2}}{(u,u),|u|}_{{\mathsf{\Gamma }}_{n,d}}=S_{n,d}^{\frac{1}{2}}(u,u),{|u|}_S=S^{\frac{1}{2}}(u,u).$$

(38)

Lemma 6. 

Let $e_u=u_h-I_{h}u\in {\mathcal{S}}_h$, then the following estimate holds

$$|a_h(u-I_{h}u,{\gamma }_h^{*}{v}_h){|\le Ch\parallel u\parallel }_2(\parallel \nabla v_h\parallel +|v_h{|}_{{\mathsf{\Gamma }}_{n,d}}),\forall v_h\in {\mathcal{S}}_h.$$

(39)

Proof. 

From (32), we first have

$$a_h(u-I_{h}u,{\gamma }_h^{*}{v}_h)=a_V(u-I_{h}u,{\gamma }_h^{*}{v}_h)+{\int }_{{\mathsf{\Gamma }}_n}a\frac{\partial (u-I_{h}u)}{\partial n}{\gamma }_h^{*}{v}_{h}ds.$$

(40)

Using Lemma 3, Lemma 2, trace inequality (18) and the approximation property of $I_{h}u$, we obtain

$$\begin{array}{cc}\hfill & |a_V(u-I_{h}u,{\gamma }_h^{*}{v}_h)|\le |a(u-I_{h}u,v_h)|+\sum _{K\in {\mathcal{T}}_h}{|a|}_{\infty }\parallel \nabla (u-I_{h}u){\parallel }_{0,\partial K}{\parallel {\gamma }_h^{*}{v}_h-v_h\parallel }_{0,\partial K}\hfill \\ \hfill & +\sum _{K\in {\mathcal{T}}_h}{[|\nabla a|}_{\infty }\parallel \nabla (u-I_{h}u){\parallel }_{0,K}+{|a|}_{\infty }{\parallel \Delta u\parallel }_{0,K}]{\parallel {\gamma }_h^{*}{v}_h-v_h\parallel }_{0,K}\hfill \\ \hfill & \le {Ch\parallel u\parallel }_2\parallel \nabla v_h\parallel .\hfill \end{array}$$

(41)

It follows from Lemma 2 and trace inequality (18) that

$$\begin{array}{cc}\hfill |{\int }_{{\mathsf{\Gamma }}_n}a\frac{\partial (u-I_{h}u)}{\partial n}{\gamma }_h^{*}{v}_{h}ds|& \le \sum _{e\in {\mathsf{\Gamma }}_n}|{\int }_{e}a\frac{\partial (u-I_{h}u)}{\partial n}({\gamma }_h^{*}{v}_h-v_h)ds|+\sum _{e\in {\mathsf{\Gamma }}_n}|{\int }_{e}a\frac{\partial (u-I_{h}u)}{\partial n}{v}_{h}ds|\hfill \\ \hfill & \le {Ch\parallel u\parallel }_2\parallel \nabla v_h\parallel +\sum _{e\in {\mathsf{\Gamma }}_n}|{\int }_{e}a{h}_{\mu }^{\frac{1}{2}}\frac{\partial (u-I_{h}u)}{\partial n}{h}_{\mu }^{-\frac{1}{2}}{v}_{h}ds|\hfill \\ \hfill & \le {Ch\parallel u\parallel }_2\parallel \nabla v_h{\parallel +Ch\parallel u\parallel }_2{|v_h|}_{{\mathsf{\Gamma }}_{n,d}}.\hfill \end{array}$$

(42)

Combining (40), (41) and (42), we complete the proof. □

Lemma 7. 

Let $(u,\lambda =0)$ be the solution of problem (15) and $(u_h,{\lambda }_h)\in {\mathcal{S}}_h\times {\mathcal{S}}_h$ be the solution of problem (16). Denote error functions $e_u=u_h-I_{h}u,e_{\lambda }={\lambda }_h-\lambda ={\lambda }_h$. Then, the following error estimate holds

$$\parallel \nabla e_{\lambda }\parallel \le C(|e_u{|}_{{\mathsf{\Gamma }}_d}+|e_u{|}_S+|e_{\lambda }{|}_{{\mathsf{\Gamma }}_{n,d}}{)+Ch\parallel u\parallel }_2.$$

(43)

Proof. 

Subtracting (15) from (16), it leads to

$$S_d(e_u,v_h)+S(e_u,v_h)-a_h(v_h,{\gamma }_h^{*}{e}_{\lambda })=S_d(u-I_{h}u,v_h)+S(u-I_{h}u,v_h),\forall v_h\in {\mathcal{S}}_h,$$

(44)

$$S_{n,d}(e_{\lambda },w_h)+a_h(e_u,{\gamma }_h^{*}{w}_h)=a_h(u-I_{h}u,{\gamma }_h^{*}{w}_h),\forall w_h\in {\mathcal{S}}_h.$$

(45)

Taking $v_h=e_{\lambda }$ in (44), we obtain from (17)–(19) that

$$\begin{array}{cc}\hfill |a_h(e_{\lambda },{\gamma }_h^{*}{e}_{\lambda })|& =|S_d(e_u,e_{\lambda })+S(e_u,e_{\lambda })-S_d(u-I_{h}u,e_{\lambda })-S(u-I_{h}u,e_{\lambda })|\hfill \\ \hfill & \le |e_u{|}_{{\mathsf{\Gamma }}_d}|e_{\lambda }{|}_{{\mathsf{\Gamma }}_d}+|e_u{|}_S|e_{\lambda }{|}_S+{Ch\parallel u\parallel }_2|e_{\lambda }{|}_{{\mathsf{\Gamma }}_d}+{Ch\parallel u\parallel }_2\parallel \nabla e_{\lambda }\parallel \hfill \\ \hfill & \le |e_u{|}_{{\mathsf{\Gamma }}_d}|e_{\lambda }{|}_{{\mathsf{\Gamma }}_d}+C|e_u{|}_S\parallel \nabla e_{\lambda }{\parallel +Ch\parallel u\parallel }_2(|e_{\lambda }{|}_{{\mathsf{\Gamma }}_d}+\parallel \nabla e_{\lambda }\parallel ).\hfill \end{array}$$

(46)

Hence, by using Lemma 5 we have

$$\begin{array}{cc}\hfill {\gamma }_0{\parallel \nabla e_{\lambda }\parallel }^2& \le |e_u{|}_{{\mathsf{\Gamma }}_d}|e_{\lambda }{|}_{{\mathsf{\Gamma }}_d}+C|e_u{|}_S\parallel \nabla e_{\lambda }{\parallel +Ch\parallel u\parallel }_2(|e_{\lambda }{|}_{{\mathsf{\Gamma }}_d}+\parallel \nabla e_{\lambda }\parallel )\hfill \\ \hfill & +C_1{\int }_{{\mathsf{\Gamma }}_n}{h}_{\mu }^{-1}{|e_{\lambda }|}^{2}ds.\hfill \end{array}$$

(47)

By using the Cauchy inequality it yields that

$$\parallel \nabla e_{\lambda }{\parallel }^2\le C(|e_u{|}_{{\mathsf{\Gamma }}_d}^2+|e_u{|}_S^2+|e_{\lambda }{|}_{{\mathsf{\Gamma }}_{n,d}}^2)+C{h}^2{\parallel u\parallel }_2^2,$$

(48)

which completes the proof. □

Theorem 2. 

Under the assumptions of Lemma 7, the following error estimates hold

$$|e_u{|}_{{\mathsf{\Gamma }}_d}+|e_u{|}_S\le Ch{\parallel u\parallel }_2,$$

(49)

$$\parallel \nabla e_{\lambda }\parallel +|e_{\lambda }{|}_{{\mathsf{\Gamma }}_{n,d}}\le Ch{\parallel u\parallel }_2.$$

(50)

Proof. 

Setting $v_h=e_u,w_h=e_{\lambda }$ in error Equations (44) and (45), respectively, and adding these two equations, we obtain

$$S_d(e_u,e_u)+S(e_u,e_u)+S_{n,d}(e_{\lambda },e_{\lambda })=S_d(u-I_{h}u,e_u)+S(u-I_{h}u,e_u)+a_h(u-I_{h}u,{\gamma }_h^{*}{e}_{\lambda }).$$

(51)

By the definitions of $S_d(u,v)$ and $S(u,v)$, estimates (17) and (18), we have

$$\begin{array}{c}\hfill |S_d(u-I_{h}u,e_u)|\le |u-I_h{u|}_{{\mathsf{\Gamma }}_d}|e_u{|}_{{\mathsf{\Gamma }}_d}\le {Ch\parallel u\parallel }_2{|e_u|}_{{\mathsf{\Gamma }}_d},\end{array}$$

(52)

$$\begin{array}{c}\hfill |S(u-I_{h}u,e_u)|\le |u-I_h{u|}_S|e_u{|}_S\le {Ch\parallel u\parallel }_2{|e_u|}_S.\end{array}$$

(53)

From Lemma 6 and Lemma 7, it yields that

$$\begin{array}{cc}\hfill |a_h(u-I_{h}u,{\gamma }_h^{*}{e}_{\lambda })|& \le {Ch\parallel u\parallel }_2(|e_{\lambda }{|}_{{\mathsf{\Gamma }}_{n,d}}+\parallel \nabla e_{\lambda }\parallel )\hfill \\ \hfill & \le {Ch\parallel u\parallel }_2{(h\parallel u\parallel }_2+|e_u{|}_{{\mathsf{\Gamma }}_d}+|e_u{|}_S+|e_{\lambda }{|}_{{\mathsf{\Gamma }}_{n,d}}).\hfill \end{array}$$

(54)

Taking these estimates into (51) together with the Cauchy inequality we obtain

$$|e_u{|}_{{\mathsf{\Gamma }}_d}^2+|e_u{|}_S^2+|e_{\lambda }{|}_{{\mathsf{\Gamma }}_{n,d}}^2\le C{h}^2{\parallel u\parallel }_2^2.$$

(55)

Then, the conclusions of Theorem 2 follow from (55) and Lemma 7. □

Introduce the notations

$$|||u_h{|||}_{\mathsf{\Gamma }}^2=||\nabla u_h{||}^2+|u_h{|}_{{\mathsf{\Gamma }}_d}^2,|||u_h{|||}_S^2=|u_h{|}_{{\mathsf{\Gamma }}_d}^2+{|u_h|}_S^2.$$

(56)

Obviously, $|||u_h{|||}_{\mathsf{\Gamma }}$ defines a norm on $H^1(\mathsf{\Omega })$ and $|||u_h{|||}_S$ is also a norm on $S_h$ under the condition of Theorem 1. Then, Theorem 2 implies the following error estimates

$$|||u_h-I_h{u|||}_S+|||\lambda -{\lambda }_h{|||}_{\mathsf{\Gamma }}\le Ch{\parallel u\parallel }_2.$$

(57)

Theorem 3. 

Suppose the boundary condition satisfies ${\mathsf{\Gamma }}_n\subset {\mathsf{\Gamma }}_d$. Let u and $u_h$ be the solutions of problem (1) and (16), respectively, then the following gradient error estimate holds

$$\parallel \nabla (u_h-I_{h}u){\parallel \le Ch\parallel u\parallel }_2.$$

(58)

Proof. 

When ${\mathsf{\Gamma }}_n\subset {\mathsf{\Gamma }}_d$, $S_{n,d}(u,v)=S_d(u,v)$ and ${|u|}_{{\mathsf{\Gamma }}_d}={|u|}_{{\mathsf{\Gamma }}_{n,d}}$. Take $w_h=e_u$ in (45) we have from Lemma 6

$$\begin{array}{cc}\hfill |a_h(e_u,{\gamma }_h^{*}{e}_u)|& \le |S_d(e_{\lambda },e_u)|+|a_h(u-I_{h}u,{\gamma }_h^{*}{e}_u)|\hfill \\ \hfill & \le |e_{\lambda }{|}_{{\mathsf{\Gamma }}_d}|e_u{|}_{{\mathsf{\Gamma }}_d}+{Ch\parallel u\parallel }_2(\parallel \nabla e_u\parallel +|e_u{|}_{{\mathsf{\Gamma }}_d}).\hfill \end{array}$$

(59)

It follows from Lemma 5 that

$${\gamma }_0\parallel \nabla e_u{\parallel }^2\le |e_{\lambda }{|}_{{\mathsf{\Gamma }}_d}^2+|e_u{|}_{{\mathsf{\Gamma }}_d}^2+C|e_u{|}_{{\mathsf{\Gamma }}_d}^2+C{h}^2{\parallel u\parallel }_2^2+\frac{{\gamma }_0}{2}\parallel \nabla e_u{\parallel }^2+C{|e_u|}_{{\mathsf{\Gamma }}_d}^2,$$

(60)

Combining with Theorem 2, it yields the desired result.

Lemma 8. 

On space $H^1(\mathsf{\Omega })$, the norm ${|||w|||}_{\mathsf{\Gamma }}={(|w|}_{{\mathsf{\Gamma }}_d}^2+{\parallel \nabla w\parallel }^2{)}^{\frac{1}{2}}$ is equivalent to the $H^1$-norm ${\parallel w\parallel }_1$.

Proof. 

Let $w\in H^1(\mathsf{\Omega })$. We only need to prove $\parallel w\parallel \le C(|w{|}_{{\mathsf{\Gamma }}_d}+\parallel \nabla w\parallel )$. Introduce the following auxiliary problem

$$\left\{\begin{array}{c}-▵\psi =w,\psi \in H^2(\mathsf{\Omega }),\hfill \\ {\psi |}_{{\mathsf{\Gamma }}_d}=0,\frac{\partial \psi }{\partial n}{|}_{{({\mathsf{\Gamma }}_d)}^c}=0,\hfill \\ {\parallel \psi \parallel }_2\le C\parallel w\parallel ,\hfill \end{array}\right.$$

(61)

where ${({\mathsf{\Gamma }}_d)}^c$ is the supplementary set of ${\mathsf{\Gamma }}_d$. By Green formula, we arrive at

$$\begin{array}{cc}\hfill {\parallel w\parallel }^2& =(\nabla w,\nabla \psi )-{\int }_{{\mathsf{\Gamma }}_d}\frac{\partial \psi }{\partial n}wds\hfill \\ \hfill & \le \parallel \nabla w\parallel \parallel \nabla \psi \parallel +|{\int }_{{\mathsf{\Gamma }}_d}{h}_{\mu }^{\frac{1}{2}}\frac{\partial \psi }{\partial n}{h}_{\mu }^{-\frac{1}{2}}wds|\hfill \\ \hfill & \le \parallel \nabla w\parallel \parallel \nabla \psi \parallel +C_{tra}{\parallel \psi \parallel }_2{|w|}_{{\mathsf{\Gamma }}_d}\hfill \\ \hfill & \le C(|w{|}_{{\mathsf{\Gamma }}_d}+\parallel \nabla w\parallel )\parallel w\parallel ,\hfill \end{array}$$

(62)

where $C_{tra}$ is a constant related to the trace inequality. This implies that $\parallel w\parallel \le C(|w{|}_{{\mathsf{\Gamma }}_d}+\parallel \nabla w\parallel )$. □

Theorem 4. 

Under the assumption of Theorem 3, the following error estimate holds

$$\parallel u-u_h{\parallel }_1\le Ch{\parallel u\parallel }_2.$$

(63)

Proof. 

With Lemma 8, Theorem 2, Theorem 3 and the triangle inequality, we obtain the desired result. □

4. Numerical Experiment

In this section, we provide two numerical examples to illustrate the effectiveness of the proposed primal-dual finite volume element method (16). In the numerical experiment, all computations are carried out by using Matlab R2019a.

We consider problem (1) on the domain ${[0,1]}^2$ with $a(x)=1$. The source term $f=f(x,y)$ is determined by the exact solution $u(x,y)$ with the formula $f=-div(a\nabla u)$. The boundary data $g_1=u(x,y)$ on ${\mathsf{\Gamma }}_d$ and $g_2=\frac{\partial u}{\partial n}$ on ${\mathsf{\Gamma }}_n$ depends on the given exact solution $u(x,y)$.

In the numerical examples, we first partition the domain $\mathsf{\Omega }$ into the squares with mesh size $1/N$. Then, each square is divided into two triangles by the diagonal line connection which results in a uniform triangulation ${\mathcal{T}}_h$ whose mesh size is $h=\sqrt{2}/N$. Based on the uniform triangulation, we construct the barycenter dual partition ${\mathcal{T}}_h^{*}$ by connecting the midpoints of the three edges to the barycenter of each element in ${\mathcal{T}}_h$ with straight lines.

The error estimation of the primal-dual finite volume element solution is computed in the following three norms

$$\begin{array}{cc}\hfill \parallel \nabla (u-u_h)\parallel & ={(\sum _{K\in {\mathcal{T}}_h}(\nabla (u-u_h),\nabla (u-u_h)))}^{\frac{1}{2}},\hfill \end{array}$$

(64)

$$\begin{array}{cc}\hfill |||u-u_h{|||}_S& =(|u-u_h{|}_{{\mathsf{\Gamma }}_d}^2+|u-u_h{{|}_S^2)}^{\frac{1}{2}}\hfill \\ & ={(S_d(u-u_h,u-u_h)+S(u-u_h,u-u_h))}^{\frac{1}{2}},\hfill \end{array}$$

(65)

$$\begin{array}{cc}\hfill \parallel u-u_h\parallel & ={(\sum _{K\in {\mathcal{T}}_h}{(u-u_h,u-u_h)}_{{}_K})}^{\frac{1}{2}}.\hfill \end{array}$$

(66)

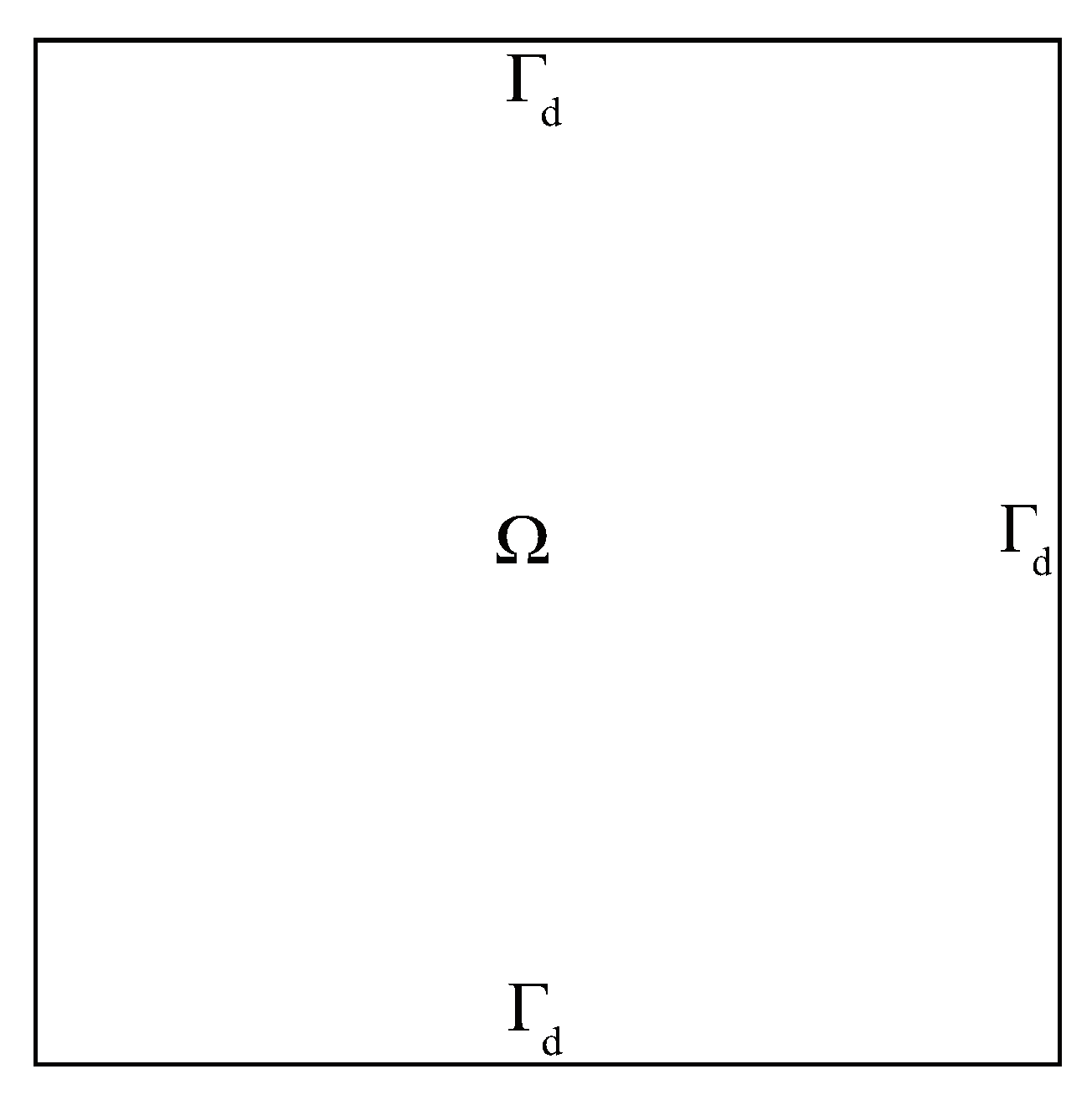
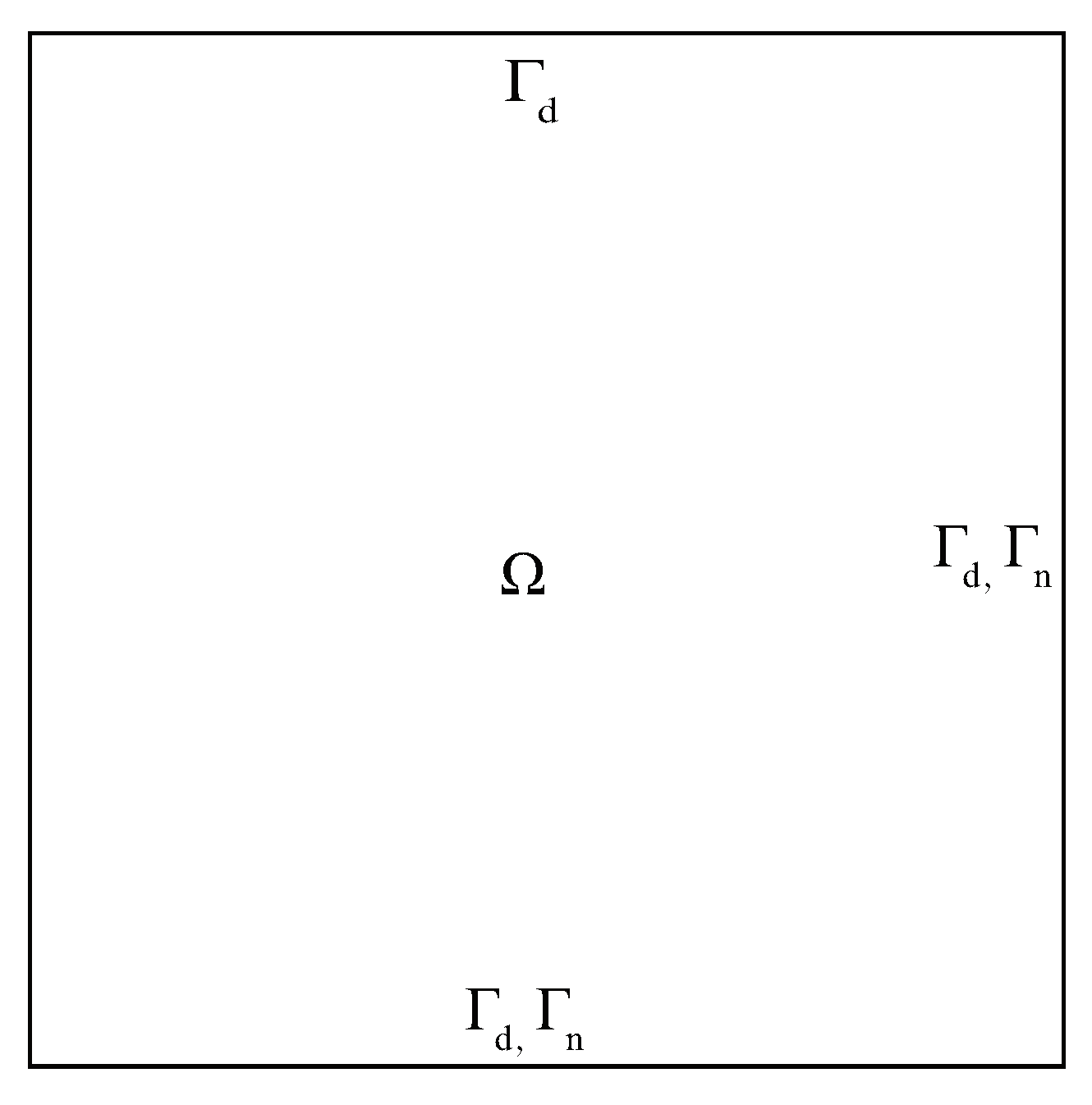
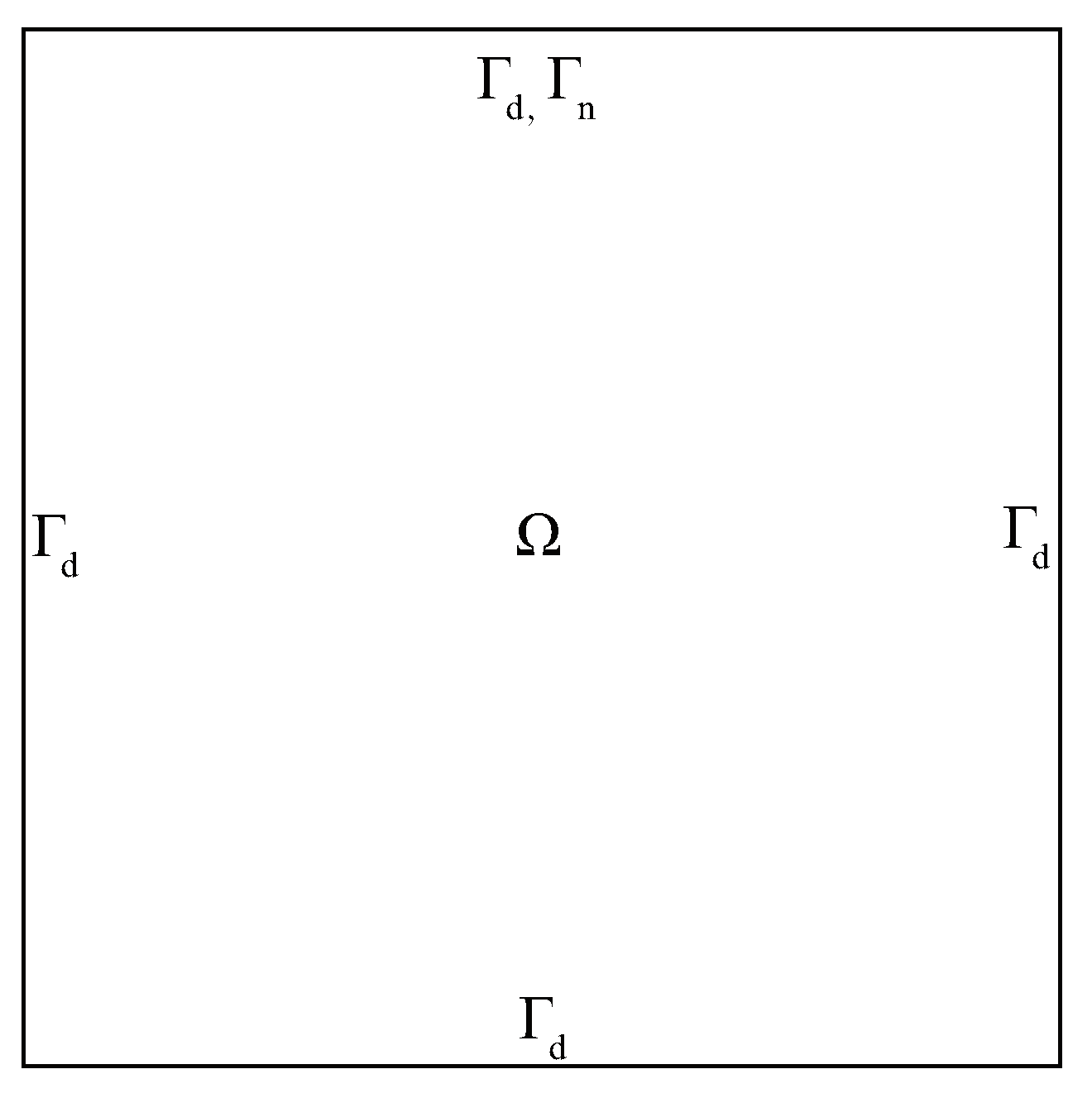
Example 1.

In this experiment, the exact solution is $u(x)=x^2+y^2$. We consider three boundary conditions as follows

B.C. I: Lacking boundary condition (See Figure 2.)

$${\mathsf{\Gamma }}_d:=\{y=0;x\in (0,1)\}\cup \{x=1;y\in (0,1)\}\cup \{y=1;x\in (0,1)\}.$$

B.C. II: Lacking and overlap boundary condition (See Figure 3.)

$$\begin{array}{cc}\hfill & {\mathsf{\Gamma }}_d:=\{y=0;x\in (0,1)\}\cup \{x=1;y\in (0,1)\}\cup \{y=1;x\in (0,1)\},\hfill \\ \hfill & {\mathsf{\Gamma }}_n:=\{y=0;x\in (0,1)\}.\hfill \end{array}$$

B.C. III: Overlap boundary condition (See Figure 4.)

$$\begin{array}{cc}\hfill & {\mathsf{\Gamma }}_d:=\{y=0;x\in (0,1)\}\cup \{x=1;y\in (0,1)\}\cup \{y=1;x\in (0,1)\cup \{x=0;y\in (0,1)\},\hfill \\ \hfill & {\mathsf{\Gamma }}_n:=\{x=0;y\in (0,1)\}\cup \{y=0;x\in (0,1)\}.\hfill \end{array}$$

The errors and convergence rates of the numerical solution for the above three kinds of boundary conditions are shown in

Table 1. Experiment results for the exact solution $u=x^2+y^2$ with B.C. I.

N	$\parallel \mathit{\nabla }(\mathit{u}-{\mathit{u}}_{\mathit{h}})\parallel$		$|||\mathit{u}-{\mathit{u}}_{\mathit{h}}{|||}_{\mathit{S}}$		$\parallel \mathit{u}-{\mathit{u}}_{\mathit{h}}\parallel$
	Error	Order	Error	Order	Error	Order
4	0.2757	N/A	0.4144	N/A	6.6300 × 10${}^{-2}$	N/A
8	0.1301	1.0835	0.2032	1.0281	2.2700 × 10${}^{-2}$	1.5463
16	0.0597	1.1238	0.0967	1.0713	6.4000 × 10${}^{-3}$	1.8265
32	0.0291	1.0367	0.0475	1.0256	1.8000 × 10${}^{-3}$	1.8301
64	0.0144	1.0150	0.0236	1.0091	4.7860 × 10${}^{-4}$	1.9111
128	0.0072	1.0000	0.0118	1.0000	1.2875 × 10${}^{-4}$	1.8942

,

Table 2. Experiment results for the exact solution $u=x^2+y^2$ with B.C. II.

N	$\parallel \mathit{\nabla }(\mathit{u}-{\mathit{u}}_{\mathit{h}})\parallel$		$|||\mathit{u}-{\mathit{u}}_{\mathit{h}}{|||}_{\mathit{S}}$		$\parallel \mathit{u}-{\mathit{u}}_{\mathit{h}}\parallel$
	Error	Order	Error	Order	Error	Order
4	0.2392	N/A	0.3898	N/A	5.5900 × 10${}^{-2}$	N/A
8	0.1155	1.0503	0.1921	1.0209	2.1300 × 10${}^{-2}$	1.3920
16	0.0486	1.2489	0.0873	1.1378	6.2000 × 10${}^{-3}$	1.7805
32	0.0223	1.1239	0.0410	1.0904	1.7000 × 10${}^{-3}$	1.8667
64	0.0108	1.0460	0.0200	1.0356	4.5130 × 10${}^{-4}$	1.9134
128	0.0053	1.0270	0.0099	1.0145	1.2153 × 10${}^{-4}$	1.8928

and

Table 3. Experiment results for the exact solution $u=x^2+y^2$ with B.C III.

N	$\parallel \mathit{\nabla }(\mathit{u}-{\mathit{u}}_{\mathit{h}})\parallel$		$|||\mathit{u}-{\mathit{u}}_{\mathit{h}}{|||}_{\mathit{S}}$		$\parallel \mathit{u}-{\mathit{u}}_{\mathit{h}}\parallel$
	Error	Order	Error	Order	Error	Order
4	0.2482	N/A	0.4199	N/A	5.8400 × 10${}^{-2}$	N/A
8	0.1276	0.9599	0.2070	1.0204	2.0000 × 10${}^{-2}$	1.5460
16	0.0628	1.0228	0.1048	0.9820	6.5000 × 10${}^{-3}$	1.6215
32	0.0305	1.0420	0.0532	0.9781	1.9000 × 10${}^{-3}$	1.7744
64	0.0149	1.0335	0.0268	0.9892	5.5340 × 10${}^{-4}$	1.7796
128	0.0074	1.0097	0.0135	0.9893	1.5403 × 10${}^{-4}$	1.8451

, respectively.

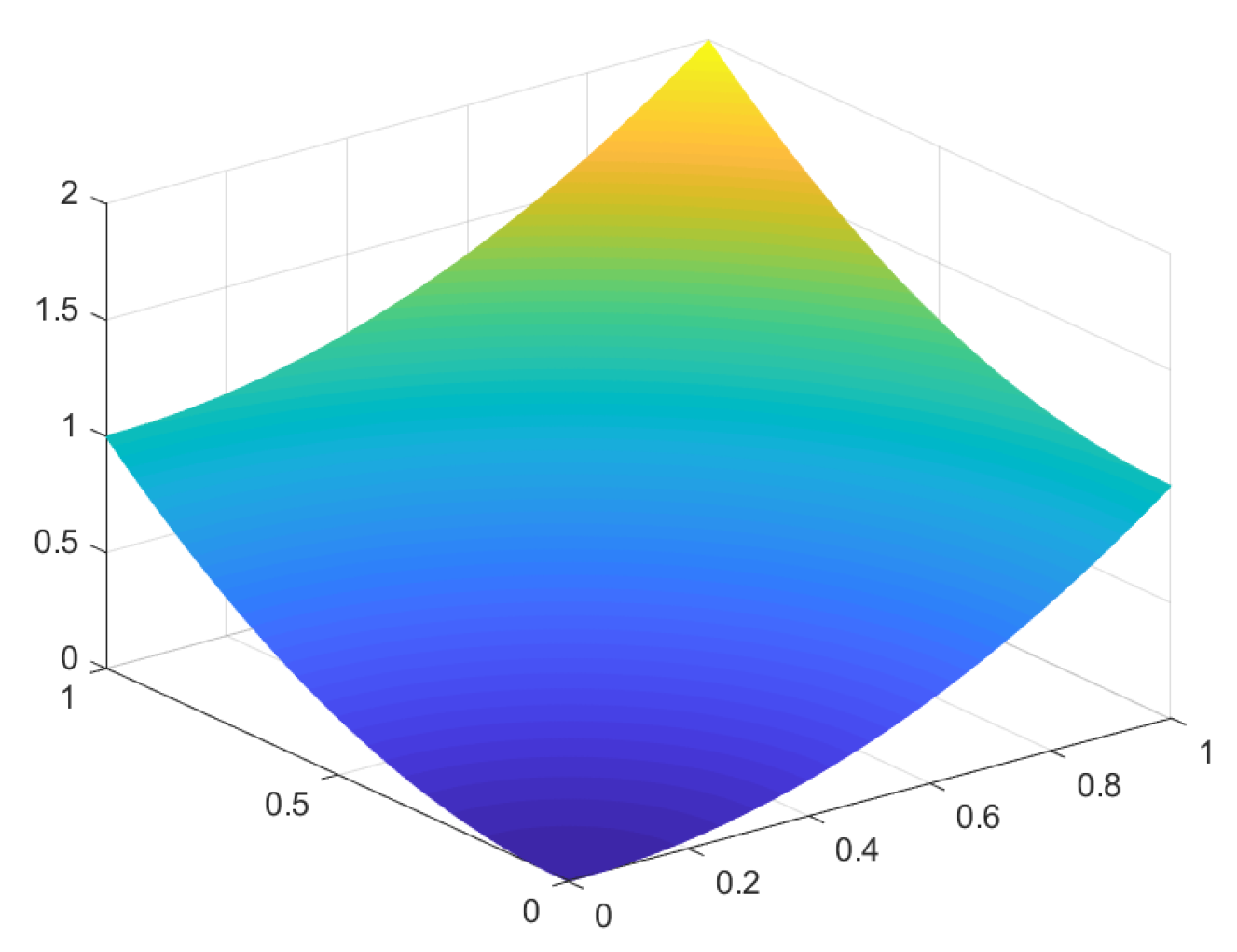
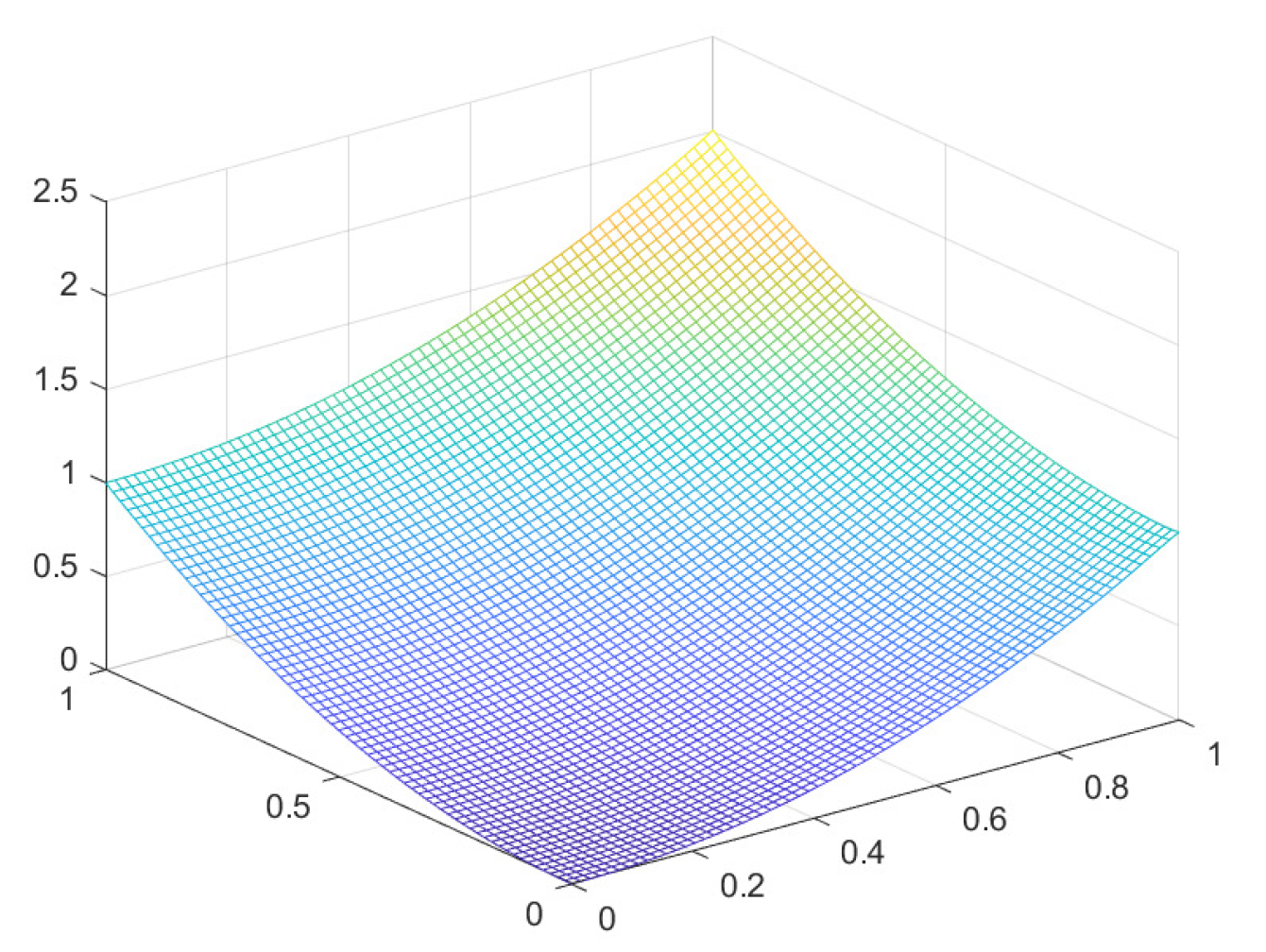
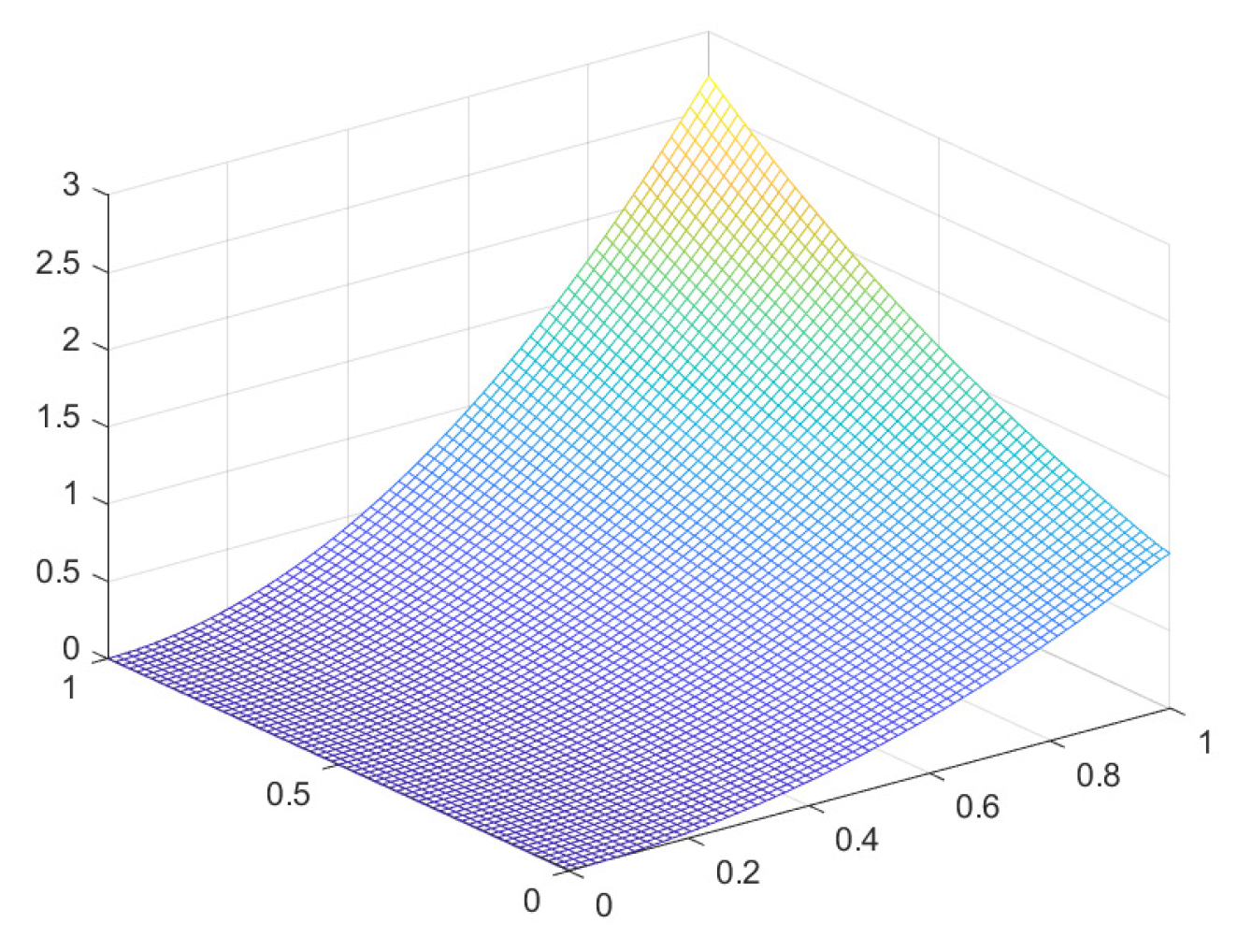
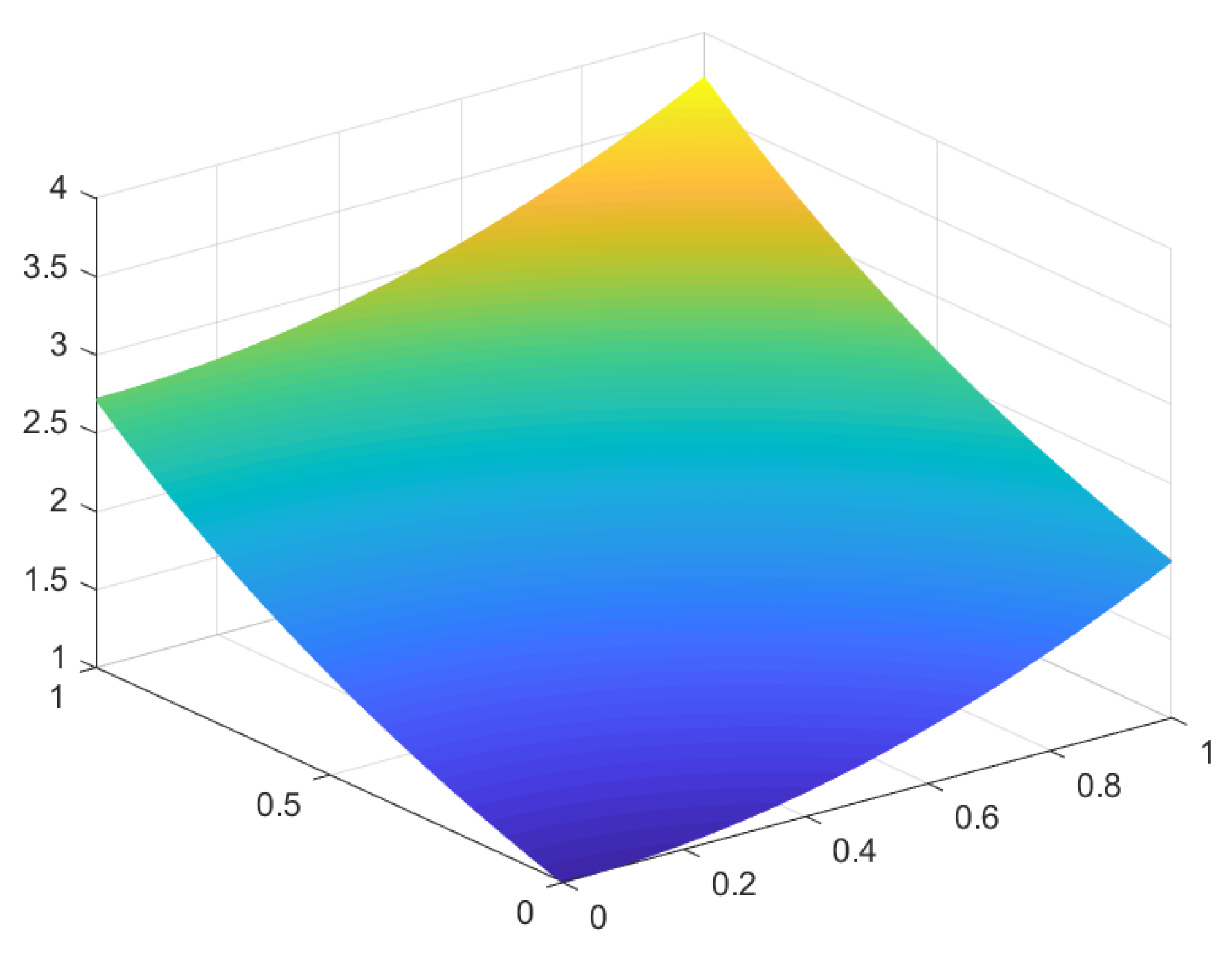
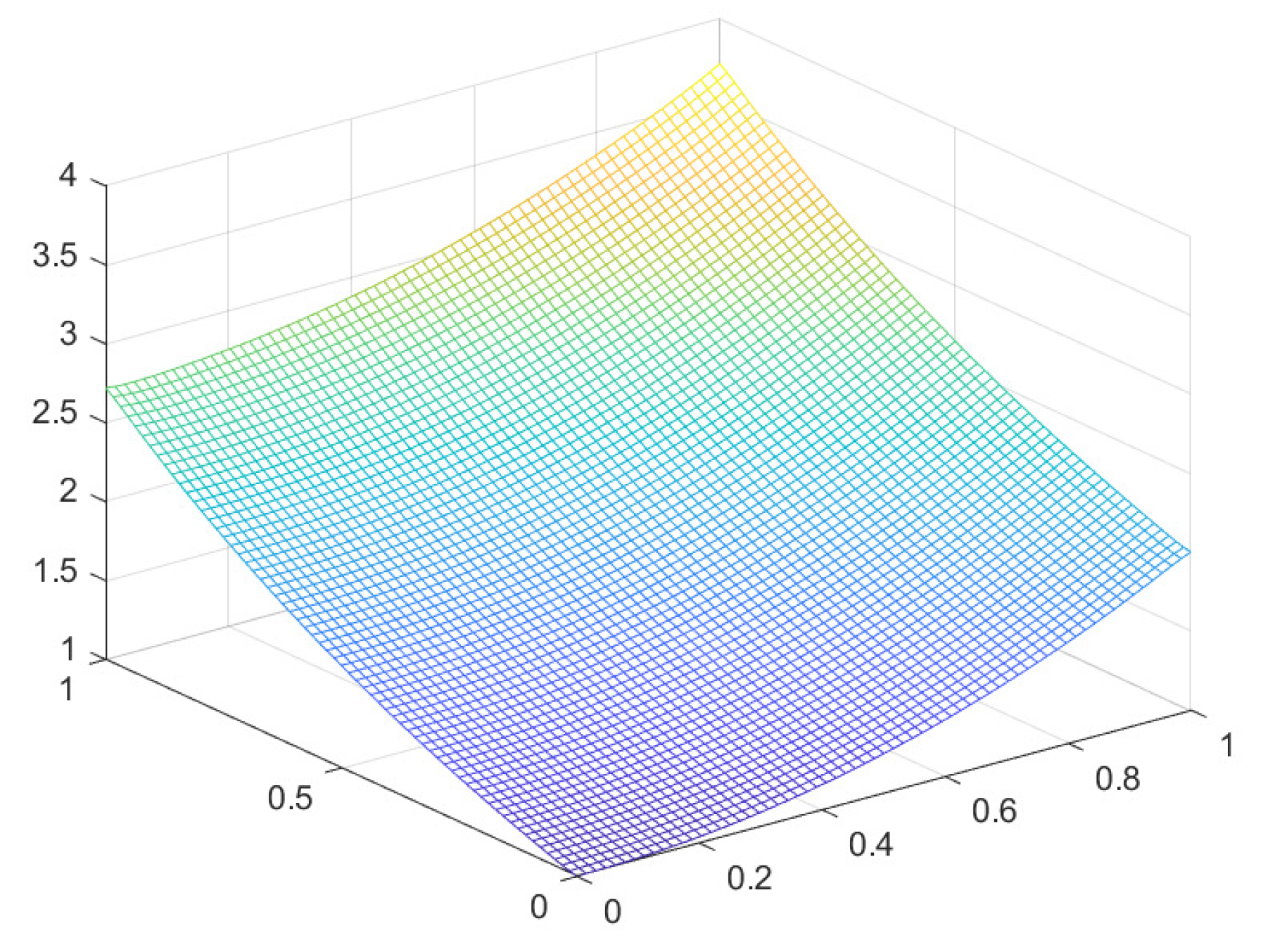
The exact solution u and the numerical solution $u_h$ of B.C. I are shown in Figure 5 and Figure 6, respectively.

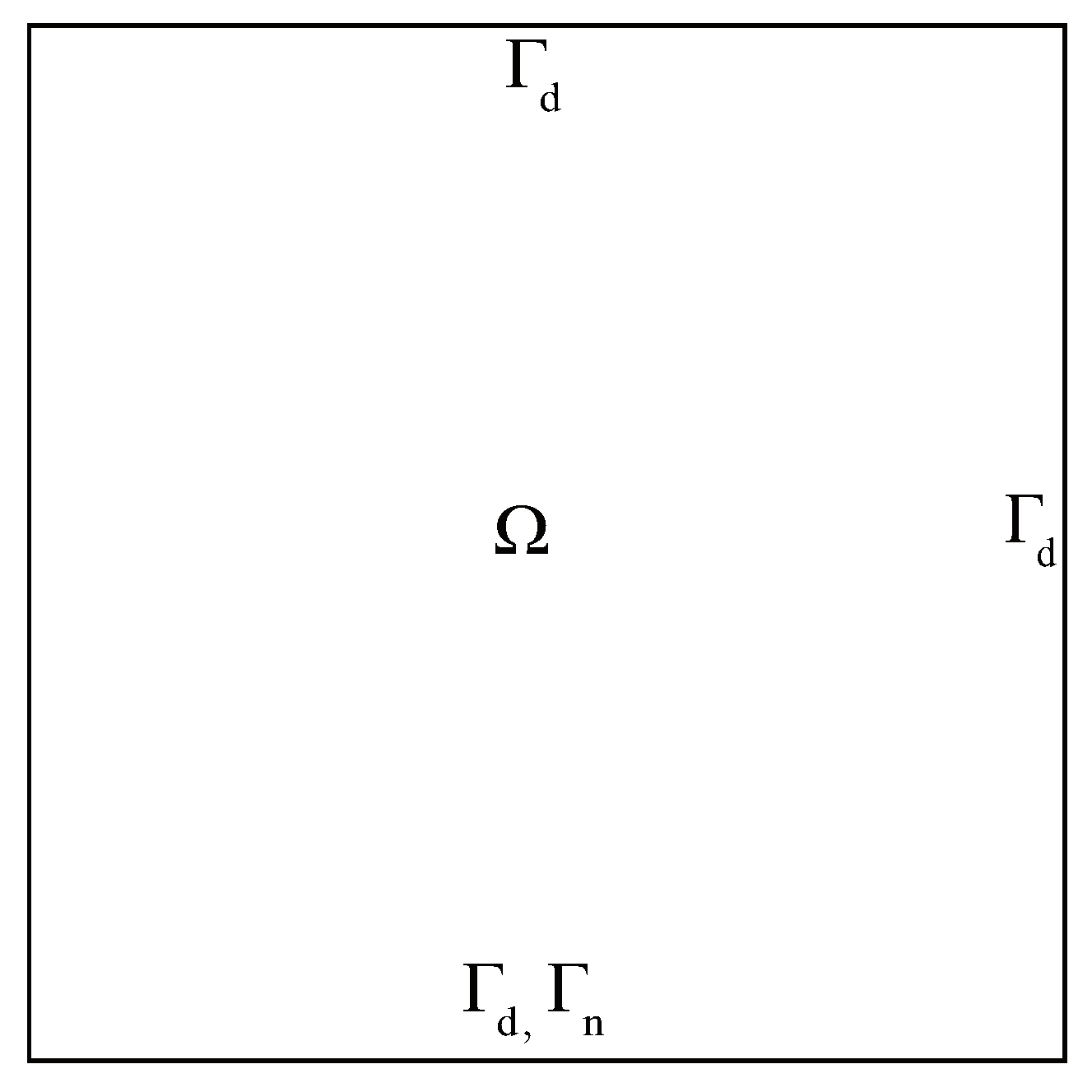
Example 2.

In this experiment, the exact solution is $u(x)=x^2{e}^y$. We consider three boundary conditions as follows

B.C. I: Lacking boundary condition (See Figure 2).

$${\mathsf{\Gamma }}_d:=\{y=0;x\in (0,1)\}\cup \{x=1;y\in (0,1)\}\cup \{y=1;x\in (0,1)\}.$$

B.C. IV: Lacking and overlap boundary condition (See Figure 7).

$$\begin{array}{cc}\hfill & {\mathsf{\Gamma }}_d:=\{y=0;x\in (0,1)\}\cup \{x=1;y\in (0,1)\}\cup \{y=1;x\in (0,1)\},\hfill \\ \hfill & {\mathsf{\Gamma }}_n:=\{y=0;x\in (0,1)\}\cup \{x=1;y\in (0,1)\}.\hfill \end{array}$$

B.C. V: Overlap boundary condition (See Figure 8).

$$\begin{array}{cc}\hfill & {\mathsf{\Gamma }}_d:=\{y=0;x\in (0,1)\}\cup \{x=1;y\in (0,1)\}\cup \{y=1;x\in (0,1)\cup \{x=0;y\in (0,1)\},\hfill \\ \hfill & {\mathsf{\Gamma }}_n:=\{y=1;x\in (0,1)\}.\hfill \end{array}$$

The errors and convergence rates of the numerical solution for the above three kinds of boundary conditions are shown in

Table 4. Experiment results for the exact solution $u=x^2{e}^y$ with B.C. I.

N	$\parallel \mathit{\nabla }(\mathit{u}-{\mathit{u}}_{\mathit{h}})\parallel$		$|||\mathit{u}-{\mathit{u}}_{\mathit{h}}{|||}_{\mathit{S}}$		$\parallel \mathit{u}-{\mathit{u}}_{\mathit{h}}\parallel$
	Error	Order	Error	Order	Error	Order
4	0.5723	N/A	0.8975	N/A	1.2870 × 10${}^{-1}$	N/A
8	0.2541	1.1714	0.3911	1.1984	3.9100 × 10${}^{-2}$	1.7188
16	0.1159	1.1325	0.1817	1.1060	1.1000 × 10${}^{-2}$	1.8297
32	0.0573	1.0163	0.0908	1.0008	3.1000 × 10${}^{-3}$	1.8272
64	0.0287	0.9975	0.0462	0.9748	8.7486 × 10${}^{-4}$	1.8251
128	0.0144	0.9950	0.0234	0.9814	2.4102 × 10${}^{-4}$	1.8599

,

Table 5. Experiment results for the exact solution $u=x^2{e}^y$ with B.C. IV.

N	$\parallel \mathit{\nabla }(\mathit{u}-{\mathit{u}}_{\mathit{h}})\parallel$		$|||\mathit{u}-{\mathit{u}}_{\mathit{h}}{|||}_{\mathit{S}}$		$\parallel \mathit{u}-{\mathit{u}}_{\mathit{h}}\parallel$
	Error	Order	Error	Order	Error	Order
4	0.5365	N/A	0.9491	N/A	1.2670 × 10${}^{-1}$	N/A
8	0.3092	0.7950	0.5265	0.8501	5.0000 × 10${}^{-2}$	1.3414
16	0.1702	0.8613	0.2978	0.8221	1.8000 × 10${}^{-2}$	1.4739
32	0.0891	0.9337	0.1617	0.8810	5.9000 × 10${}^{-3}$	1.6092
64	0.0458	0.9601	0.0851	0.9261	1.8000 × 10${}^{-3}$	1.7127
128	0.0233	0.9750	0.0438	0.9582	5.0591 × 10${}^{-4}$	1.8310

and

Table 6. Experiment results for the exact solution $u=x^2{e}^y$ with B.C. V.

N	$\parallel \mathit{\nabla }(\mathit{u}-{\mathit{u}}_{\mathit{h}})\parallel$		$|||\mathit{u}-{\mathit{u}}_{\mathit{h}}{|||}_{\mathit{S}}$		$\parallel \mathit{u}-{\mathit{u}}_{\mathit{h}}\parallel$
	Error	Order	Error	Order	Error	Order
4	0.5050	N/A	0.8853	N/A	1.1150 × 10${}^{-1}$	N/A
8	0.2001	1.3356	0.3580	1.3062	3.2100 × 10${}^{-2}$	1.7964
16	0.0901	1.1511	0.1537	1.2198	8.9000 × 10${}^{-3}$	1.8507
32	0.0435	1.0505	0.0722	1.0900	2.5000 × 10${}^{-3}$	1.8319
64	0.0216	1.0100	0.0355	1.0242	7.0990 × 10${}^{-4}$	1.8162
128	0.0108	1.0000	0.0177	1.0041	1.9578 × 10${}^{-4}$	1.8584

, respectively.

The exact solution u and the numerical solution $u_h$ of B.C. V. are shown in Figure 9 and Figure 10, respectively.

Example 3.

In this experiment, the exact solution is $u(x)=x^2+e^y$. We consider three boundary conditions as follows:

B.C. I: Lacking boundary condition (See Figure 2).

$${\mathsf{\Gamma }}_d:=\{y=0;x\in (0,1)\}\cup \{x=1;y\in (0,1)\}\cup \{y=1;x\in (0,1)\}.$$

B.C. II: Lacking and overlap boundary condition (See Figure 3).

$$\begin{array}{cc}\hfill & {\mathsf{\Gamma }}_d:=\{y=0;x\in (0,1)\}\cup \{x=1;y\in (0,1)\}\cup \{y=1;x\in (0,1)\},\hfill \\ \hfill & {\mathsf{\Gamma }}_n:=\{y=0;x\in (0,1)\}.\hfill \end{array}$$

B.C. V: Overlap boundary condition (See Figure 8).

$$\begin{array}{cc}\hfill & {\mathsf{\Gamma }}_d:=\{y=0;x\in (0,1)\}\cup \{x=1;y\in (0,1)\}\cup \{y=1;x\in (0,1)\cup \{x=0;y\in (0,1)\},\hfill \\ \hfill & {\mathsf{\Gamma }}_n:=\{y=1;x\in (0,1)\}.\hfill \end{array}$$

The errors and convergence rates of the numerical solution for the above three kinds of boundary conditions are shown in

Table 7. Experiment results for the exact solution $u=x^2{e}^y$ with B.C. I.

N	$\parallel \mathit{\nabla }(\mathit{u}-{\mathit{u}}_{\mathit{h}})\parallel$		$|||\mathit{u}-{\mathit{u}}_{\mathit{h}}{|||}_{\mathit{S}}$		$\parallel \mathit{u}-{\mathit{u}}_{\mathit{h}}\parallel$
	Error	Order	Error	Order	Error	Order
4	0.4205	N/A	0.6184	N/A	1.0720 × 10${}^{-1}$	N/A
8	0.1972	1.0924	0.3112	0.9907	3.5800 × 10${}^{-2}$	1.5823
16	0.0920	1.1000	0.1495	1.0577	1.0300 × 10${}^{-2}$	1.7973
32	0.0446	1.0446	0.0729	1.0362	2.8000 × 10${}^{-3}$	1.8791
64	0.0221	1.0130	0.0360	1.0179	7.5851 × 10${}^{-4}$	1.8842
128	0.0110	1.0065	0.0179	1.0080	2.0323 × 10${}^{-4}$	1.9001

,

Table 8. Experiment results for the exact solution $u=x^2{e}^y$ with B.C. II.

N	$\parallel \mathit{\nabla }(\mathit{u}-{\mathit{u}}_{\mathit{h}})\parallel$		$|||\mathit{u}-{\mathit{u}}_{\mathit{h}}{|||}_{\mathit{S}}$		$\parallel \mathit{u}-{\mathit{u}}_{\mathit{h}}\parallel$
	Error	Order	Error	Order	Error	Order
4	0.3758	N/A	0.5988	N/A	9.5300 × 10${}^{-2}$	N/A
8	0.1962	0.9376	0.3303	0.8583	3.8300 × 10${}^{-2}$	1.3151
16	0.0898	1.1275	0.1617	1.0318	1.1900 × 10${}^{-2}$	1.6864
32	0.0426	1.0759	0.0783	1.0462	3.4000 × 10${}^{-3}$	1.8074
64	0.0209	1.0274	0.0385	1.0242	9.2049 × 10${}^{-4}$	1.8851
128	0.0104	1.0069	0.0191	1.0113	2.4911 × 10${}^{-4}$	1.8856

and

Table 9. Experiment results for the exact solution $u=x^2{e}^y$ with B.C. V.

N	$\parallel \mathit{\nabla }(\mathit{u}-{\mathit{u}}_{\mathit{h}})\parallel$		$|||\mathit{u}-{\mathit{u}}_{\mathit{h}}{|||}_{\mathit{S}}$		$\parallel \mathit{u}-{\mathit{u}}_{\mathit{h}}\parallel$
	Error	Order	Error	Order	Error	Order
4	0.3638	N/A	0.5879	N/A	8.8300 × 10${}^{-2}$	N/A
8	0.2526	0.5263	0.3864	0.6055	3.6600 × 10${}^{-2}$	1.2706
16	0.1489	0.7625	0.2381	0.6985	1.4600 × 10${}^{-2}$	1.3259
32	0.0762	0.9665	0.1292	0.8820	4.7000 × 10${}^{-3}$	1.6352
64	0.0384	0.9887	0.0669	0.9495	1.4000 × 10${}^{-3}$	1.7472
128	0.0192	1.0000	0.0340	0.9765	3.8797 × 10${}^{-4}$	1.8514

, respectively.

The exact solution u and the numerical solution $u_h$ of B.C. V are shown in Figure 11 and Figure 12, respectively.

5. Conclusions

We consider how to solve numerically an ill-posed elliptic problem with missing or overlap boundary conditions. A primal-dual finite volume scheme with proper stabilized terms is proposed and analyzed. We first prove the well-posedness of the discrete scheme. Then, we derive the gradient error estimate of $O(h)$-order and some other error estimates under proper norms. Numerical experiments verify the effectiveness of the proposed primal-dual finite volume element method.