Mathematical Correlation Study of Nanofluid Flow Merging Points in Entrance Regions
Abstract
1. Introduction
2. Geometry Description and Computational Method
Geometry Details
3. Mathematical Formulation and Nanofluid Properties
4. Numerical Scheme and Boundary Condition
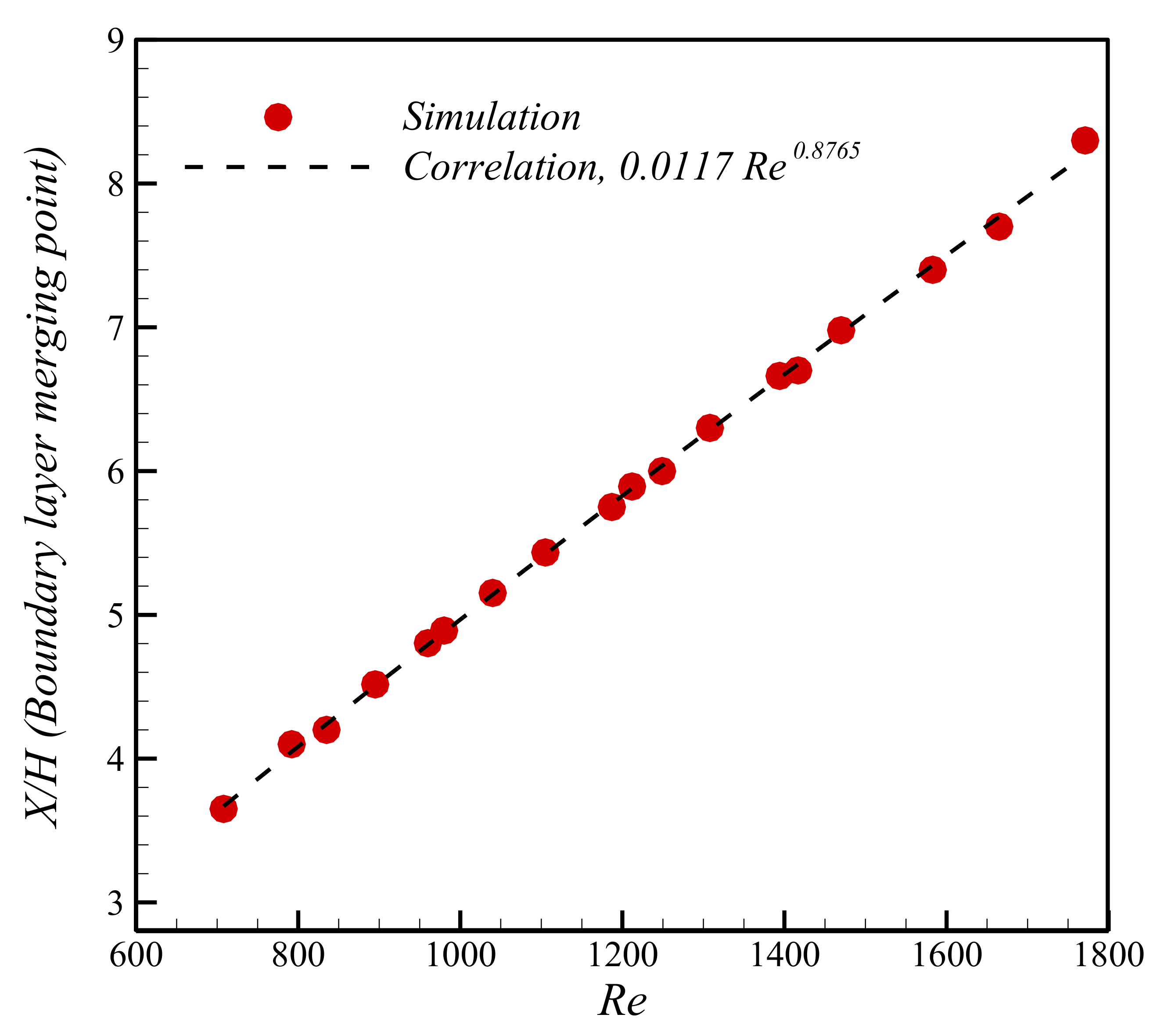
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Channel cross section (m2) | |
| Hydraulic diameter (m) | |
| Nanoparticle diameter (nm) | |
| Parallel plates distance (m) | |
| P | Pressure (Pa) |
| Reynolds number (-) | |
| Nanolayer thickness (nm) | |
| Fluid velocity in x and y direction (m/s) | |
| Channel width (m) | |
| Greek letter | |
| Nanofluid volume fraction (-) | |
| Viscosity (Pa.s) | |
| Density (kg/m3) | |
| Subscript | |
| l | fluid |
References
- Baghban, A.; Sasanipour, J.; Pourfayaz, F.; Ahmadi, M.H.; Kasaeian, A.; Chamkha, A.J.; Oztop, H.F.; Chau, K. Towards experimental and modeling study of heat transfer performance of water-SiO2 nanofluid in quadrangular cross-section channels. Eng. Appl. Comput. Fluid Mech. 2019, 13, 453–469. [Google Scholar] [CrossRef]
- Ramezanizadeh, M.; Alhuyi Nazari, M.; Ahmadi, M.H.; Chau, K. Experimental and numerical analysis of a nanofluidic thermosyphon heat exchanger. Eng. Appl. Comput. Fluid Mech. 2019, 13, 40–47. [Google Scholar] [CrossRef]
- Ahmadi, M.H.; Mohseni-Gharyehsafa, B.; Farzaneh-Gord, M.; Jilte, R.D.; Kumar, R.; Chau, K. Applicability of connectionist methods to predict dynamic viscosity of silver/water nanofluid by using ANN-MLP, MARS and MPR algorithms. Eng. Appl. Comput. Fluid Mech. 2019, 13, 220–228. [Google Scholar] [CrossRef]
- Ahmadi, M.H.; Ghahremannezhad, A.; Chau, K.-W.; Seifaddini, P.; Ramezannezhad, M.; Ghasempour, R. Development of simple-to-use predictive models to determine thermal properties of Fe2O3/water-ethylene glycol nanofluid. Computation 2019, 7, 18. [Google Scholar] [CrossRef]
- Bhushan, S.; Walters, D.K. Development of Parallel Pseudo-Spectral Solver Using Influence Matrix Method and Application to Boundary Layer Transition. Eng. Appl. Comput. Fluid Mech. 2014, 8, 158–177. [Google Scholar] [CrossRef]
- Pettersson, K.; Rizzi, A. Comparing different CFD methods accuracy in computing local boundary layer properties. Eng. Appl. Comput. Fluid Mech. 2009, 3, 98–108. [Google Scholar] [CrossRef][Green Version]
- Savkiv, V.; Mykhailyshyn, R.; Fendo, O.; Mykhailyshyn, M. Orientation Modeling of Bernoulli Gripper Device with Off-Centered Masses of the Manipulating Object. Procedia Eng. 2017, 187, 264–271. [Google Scholar] [CrossRef]
- Bejan, A. Convection Heat Transfer; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Cengel, Y. Heat and Mass Transfer: Fundamentals and Applications; McGraw-Hill Higher Education: New York, NY, USA, 2014. [Google Scholar]
- Fox, R.W.; McDonald, A.T.; Pritchard, P.J. Introduction to Fluid Mechanics; John Wiley and Sons: Chichester, UK, 1998. [Google Scholar]
- Incropera, F.P.; Lavine, A.S.; Bergman, T.L.; DeWitt, D.P. Fundamentals of Heat and Mass Transfer; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Nakayama, Y. Introduction to Fluid Mechanics; Butterworth-Heinemann: Oxford, UK, 2018. [Google Scholar]
- White, F.M. Fluid Mechanics; McGraw-Hill: New York, NY, USA, 1999. [Google Scholar]
- Yunus, A.C. Fluid Mechanics: Fundamentals and Applications (Si Units); Tata McGraw Hill Education Private Limited: New York, NY, USA, 2010. [Google Scholar]
- Krishna, M.V.; Chamkha, A.J. Hall and ion slip effects on MHD rotating boundary layer flow of nanofluid past an infinite vertical plate embedded in a porous medium. Results Phys. 2019, 15, 102652. [Google Scholar] [CrossRef]
- Madhu, M.; Kishan, N.; Chamkha, A. Boundary layer flow and heat transfer of a non-Newtonian nanofluid over a non-linearly stretching sheet. Int. J. Numer. Methods Heat Fluid Flow 2016, 26, 2198–2217. [Google Scholar] [CrossRef]
- Mahdavi, M.; Sharifpur, M.; Meyer, J.P. Simulation study of convective and hydrodynamic turbulent nanofluids by turbulence models. Int. J. Therm. Sci. 2016, 110, 36–51. [Google Scholar] [CrossRef]
- Mahdavi, M.; Sharifpur, M.; Ghodsinezhad, H.; Meyer, J.P. A new combination of nanoparticles mass diffusion flux and slip mechanism approaches with electrostatic forces in a natural convective cavity flow. Int. J. Heat Mass Transf. 2017, 106, 980–998. [Google Scholar] [CrossRef][Green Version]
- Sharifpur, M.; Tshimanga, N.; Meyer, J.P.; Manca, O. Experimental investigation and model development for thermal conductivity of α-Al2O3-glycerol nanofluids. Int. Commun. Heat Mass Transf. 2017, 85, 12–22. [Google Scholar] [CrossRef]
- Suzzi, N.; Lorenzini, M. Viscous heating of a laminar flow in the thermal entrance region of a rectangular channel with rounded corners and uniform wall temperature. Int. J. Therm. Sci. 2019, 145, 106032. [Google Scholar] [CrossRef]
- Yutaka, A.; Hiroshi, N.; Faghri, M. Developing laminar flow and heat transfer in the entrance region of regular polygonal ducts. Int. J. Heat Mass Transf. 1988, 31, 2590–2593. [Google Scholar] [CrossRef]
- Chebbi, R. Laminar flow of power-law fluids in the entrance region of a pipe. Chem. Eng. Sci. 2002, 57, 4435–4443. [Google Scholar] [CrossRef]
- Ma, J.-F.; Shen, X.-R.; Zhang, M.-K.; Zhang, B.-Z. Laminar Developing Flow in the Entrance Region of Rotating Curved Pipes. J. Hydrodyn. 2006, 18, 418–423. [Google Scholar] [CrossRef]
- Lin, C.; Zhang, P.; Ebadian, M.A. Laminar forced convection in the entrance region of helical pipes. Int. J. Heat Mass Transf. 1997, 40, 3293–3304. [Google Scholar] [CrossRef]
- Al-Nassri, S.A.; Unny, T. Developing laminar flow in the inlet length of a smooth pipe. Appl. Sci. Res. 1981, 36, 313–332. [Google Scholar] [CrossRef]
- Fargie, D.; Martin, W. Developing laminar flow in a pipe of circular cross-section. Proc. R. Soc. Lond. A Math. Phys. Sci. 1971, 321, 461–476. [Google Scholar]
- Mohanty, A.K.; Asthana, S.B.L. Laminar flow in the entrance region of a smooth pipe. J. Fluid Mech. 1979, 90, 433–447. [Google Scholar] [CrossRef]
- Mohanty, A.K.; Das, R. Laminar flow in the entrance region of a parallel plate channel. AIChE J. 1982, 28, 830–833. [Google Scholar] [CrossRef]
- Su, L.; Duan, Z.; He, B.; Ma, H.; Ding, G. Laminar flow and heat transfer in the entrance region of elliptical minichannels. Int. J. Heat Mass Transf. 2019, 145, 118717. [Google Scholar] [CrossRef]
- Durst, F.; Ray, S.; Ünsal, B.; Bayoumi, O.A. The Development Lengths of Laminar Pipe and Channel Flows. J. Fluids Eng. Trans. ASME 2005, 127, 1154–1160. [Google Scholar] [CrossRef]
- Ahmadi, M.H.; Sadeghzadeh, M.; Maddah, H.; Solouk, A.; Kumar, R.; Chau, K.-W. Precise smart model for estimating dynamic viscosity of SiO2/ethylene glycol–water nanofluid. Eng. Appl. Comput. Fluid Mech. 2019, 13, 1095–1105. [Google Scholar] [CrossRef]
- Bhushan, S.; Muthu, S. Parallel performance assessment of a pseudo-spectral solver for transition and turbulent boundary layer flows. Eng. Appl. Comput. Fluid Mech. 2019, 13, 763–781. [Google Scholar] [CrossRef]
- Ghalandari, M.; Koohshahi, E.M.; Mohamadian, F.; Shamshirband, S.; Chau, K.W. Numerical simulation of nanofluid flow inside a root canal. Eng. Appl. Comput. Fluid Mech. 2019, 13, 254–264. [Google Scholar] [CrossRef]
- Baghban, A.; Jalali, A.; Shafiee, M.; Ahmadi, M.H.; Chau, K.-W. Developing an ANFIS-based swarm concept model for estimating the relative viscosity of nanofluids. Eng. Appl. Comput. Fluid Mech. 2019, 13, 26–39. [Google Scholar] [CrossRef]
- Mahdavi, M.; Sharifpur, M.; Ahmadi, M.H.; Meyer, J.P. Nanofluid flow and shear layers between two parallel plates: A simulation approach. Eng. Appl. Comput. Fluid Mech. 2020, 14, 1536–1545. [Google Scholar] [CrossRef]
- Granados-Ortiz, F.-J.; Leon-Prieto, L.; Ortega-Casanova, J. Computational study of the application of Al2O3 nanoparticles to forced convection of high-Reynolds swirling jets for engineering cooling processes. Eng. Appl. Comput. Fluid Mech. 2021, 15, 1–22. [Google Scholar] [CrossRef]
- Fereidoon, A.; Saedodin, S.; Hemmat Esfe, M.; Noroozi, M.J. Evaluation of mixed convection in inclined square lid-driven cavity filled with Al2O3/water nano-fluid. Eng. Appl. Comput. Fluid Mech. 2013, 7, 55–65. [Google Scholar] [CrossRef]
- Mahdavi, M.; Sharifpur, M.; Ghodsinezhad, H.; Meyer, J.P. Experimental and Numerical Investigation on a Water-Filled Cavity Natural Convection to Find the Proper Thermal Boundary Conditions for Simulations. Heat Transf. Eng. 2018, 39, 359–373. [Google Scholar] [CrossRef]
- Mahdavi, M.; Sharifpur, M.; Meyer, J.P. A novel combined model of discrete and mixture phases for nanoparticles in convective turbulent flow. Phys. Fluids 2017, 29, 082005. [Google Scholar] [CrossRef]
- Mahdavi, M.; Sharifpur, M.; Meyer, J.P. Natural convection study of Brownian nano-size particles inside a water-filled cavity by Lagrangian-Eulerian tracking approach. In Heat Transfer. International Conference on Heat Transfer, Fluid Mechanics and Thermodynamics (HEFAT2016), Costa del Sol, Malaga, Spain 11–13 July 2016; University of Pretoria: Pretoria, South Africa, 2016; p. 17. [Google Scholar]
- Mahdavi, M.; Sharifpur, M.; Meyer, J.P. Implementation of diffusion and electrostatic forces to produce a new slip velocity in the multiphase approach to nano fluids. Powder Technol. 2017, 307, 153–162. [Google Scholar] [CrossRef]
- Teng, T.-P.; Hung, Y.-H.; Jwo, C.-S.; Chen, C.-C.; Jeng, L.-Y. Pressure drop of TiO2 nanofluid in circular pipes. Particuology 2011, 9, 486–491. [Google Scholar] [CrossRef]
- Bahremand, H.; Abbassi, A.; Saffar-Avval, M. Experimental and numerical investigation of turbulent nanofluid flow in helically coiled tubes under constant wall heat flux using Eulerian–Lagrangian approach. Powder Technol. 2014, 269, 93–100. [Google Scholar] [CrossRef]
- Ansys-Fluent 19.3 Theory Guide; ANSYS Inc.: Canonsburg, PA, USA, 2019.
- Sharifpur, M.; Yousefi, S.; Meyer, J.P. A new model for density of nanofluids including nanolayer. Int. Commun. Heat Mass Transf. 2016, 78, 168–174. [Google Scholar] [CrossRef]
- Corcione, M. Empirical correlating equations for predicting the effective thermal conductivity and dynamic viscosity of nanofluids. Energy Convers. Manag. 2011, 52, 789–793. [Google Scholar] [CrossRef]


| Component | Density (kg/m3) | Thermal Conductivity (W/m.K) | Specific Heat (J/kg.K) | Particle Diameter (nm) |
|---|---|---|---|---|
| Water | 998.2 | 0.6 | 4181 | - |
| 3880 | 36 | 773 | 150 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mahdavi, M.; Sharifpur, M.; Abd El-Rahman, M.; Meyer, J.P. Mathematical Correlation Study of Nanofluid Flow Merging Points in Entrance Regions. Mathematics 2022, 10, 4148. https://doi.org/10.3390/math10214148
Mahdavi M, Sharifpur M, Abd El-Rahman M, Meyer JP. Mathematical Correlation Study of Nanofluid Flow Merging Points in Entrance Regions. Mathematics. 2022; 10(21):4148. https://doi.org/10.3390/math10214148
Chicago/Turabian StyleMahdavi, Mostafa, Mohsen Sharifpur, Magda Abd El-Rahman, and Josua P. Meyer. 2022. "Mathematical Correlation Study of Nanofluid Flow Merging Points in Entrance Regions" Mathematics 10, no. 21: 4148. https://doi.org/10.3390/math10214148
APA StyleMahdavi, M., Sharifpur, M., Abd El-Rahman, M., & Meyer, J. P. (2022). Mathematical Correlation Study of Nanofluid Flow Merging Points in Entrance Regions. Mathematics, 10(21), 4148. https://doi.org/10.3390/math10214148









