Bimodal-Distributed Binarized Neural Networks

Abstract

Binary neural networks (BNNs) are an extremely promising method for reducing deep neural networks’ complexity and power consumption significantly. Binarization techniques, however, suffer from ineligible performance degradation compared to their full-precision counterparts. Prior work mainly focused on strategies for sign function approximation during the forward and backward phases to reduce the quantization error during the binarization process. In this work, we propose a bimodal-distributed binarization method (BD-BNN). The newly proposed technique aims to impose a bimodal distribution of the network weights by kurtosis regularization. The proposed method consists of a teacher–trainer training scheme termed weight distribution mimicking (WDM), which efficiently imitates the full-precision network weight distribution to their binary counterpart. Preserving this distribution during binarization-aware training creates robust and informative binary feature maps and thus it can significantly reduce the generalization error of the BNN. Extensive evaluations on CIFAR-10 and ImageNet demonstrate that our newly proposed BD-BNN outperforms current state-of-the-art schemes.

1. Introduction

Deep neural networks (DNNs) are currently widely used for a variety of tasks, including computer vision [1,2,3], natural language processing [4], control of autonomous vehicles [5], and even disease diagnosis in the medical domain [6,7]. The large size of most of such models, however, makes them expensive (in terms of hardware power consumption and inference time) to deploy on devices with constrained resources, such as devices with limited bandwidth to memory or edge devices which are limited by computational and memory resources. To cope with the huge demand of resources made by DNNs, academic and industrial researchers have attempted to compress these models and relax the inference cost. The leading compression methods include pruning [8,9], low-rank decomposition [10,11], quantization [12,13] and knowledge distillation [14].

Quantization techniques aim to reduce the number of bits being used to represent a value in the model, both in weights and activations. We can trade the numerical precision of the DNN’s parameters and activations with the overall accuracy of the results; i.e., we can reduce the communication and computational cost of the system, from 32 bits long (standard representation of numbers when a full precision is used) to a few bits long. Binarization can be considered to be an extreme case of quantization where the values of the weights and activations are represented by only a single bit, which means getting a 32× memory footprint reduction and a higher computational reduction by transforming the expensive matrix computation into cheaper XNOR and popcount operations [15].

Notwithstanding the immense interest in BNNs, the challenge remains to close the accuracy gap between the full-precision (FP) and binarized versions. The importance of maintaining the appropriate data distribution is a key issue in many works, specifically in DNN compression studies; while [12] uses a normally distributed prior for the weights and activations, ref. [13] uses a log-normal distribution prior for the neural gradients. In both cases, they show that the choice of distribution approximation has a significant impact on the final model’s accuracy. KURE [16] represents a step forward, by offering matching between the data distribution and the task. The authors show that uniform distribution is more robust under quantization noise and suggest a technique that allows for the uniformization the distribution of the weights.

In this paper, we suggest a method to manipulate the weight distribution so that it is better suited for being transferred to adopt a bimodal distribution. The manipulation is done with a unique combination of a bimodal regularization term and a novel training regime of weight regularization mimicking alongside knowledge distillation (KD). This distribution is capable of reducing the quantization error under model binarization. Our experiments show state-of-the-art results in a variety of BNNs, without increasing the number of parameters. For example, we achieved a 60.6% accuracy in the standard binarized ResNet-18 on the ImageNet dataset, on which the previous state-of-the-art result was 60.2%.

This paper makes the following contributions:

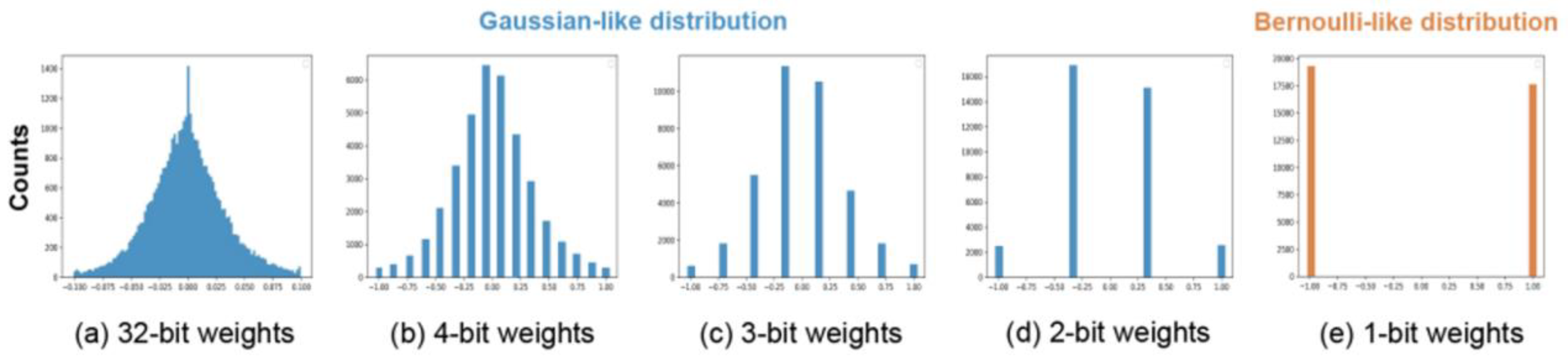
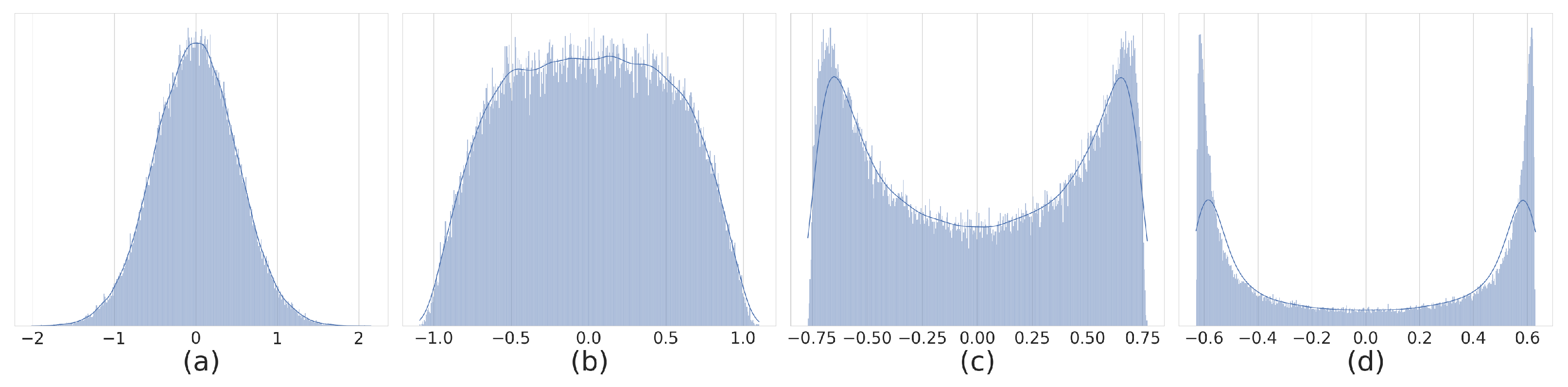
• We introduce a regularization term to manipulate the weight distribution such that it becomes a bimodal distribution that, in turn, reduces the quantization error.
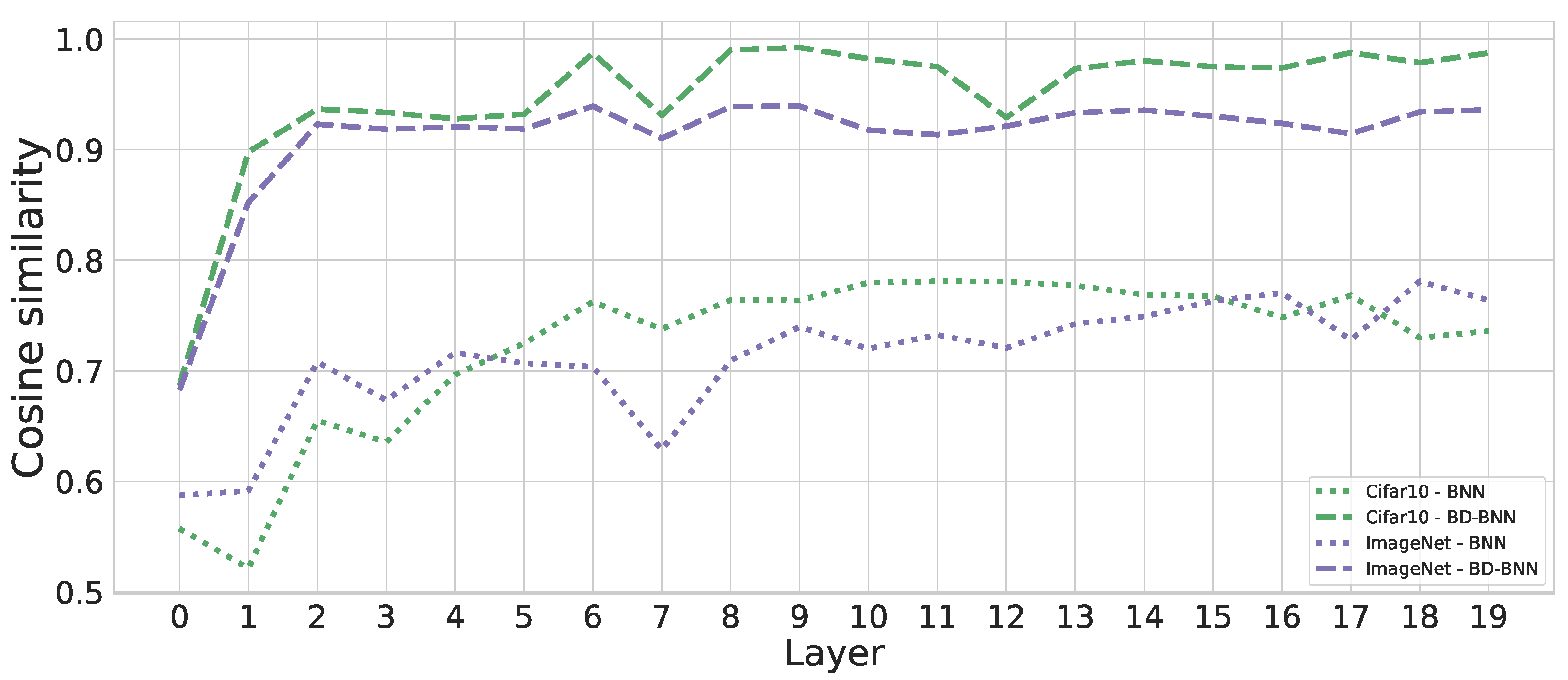
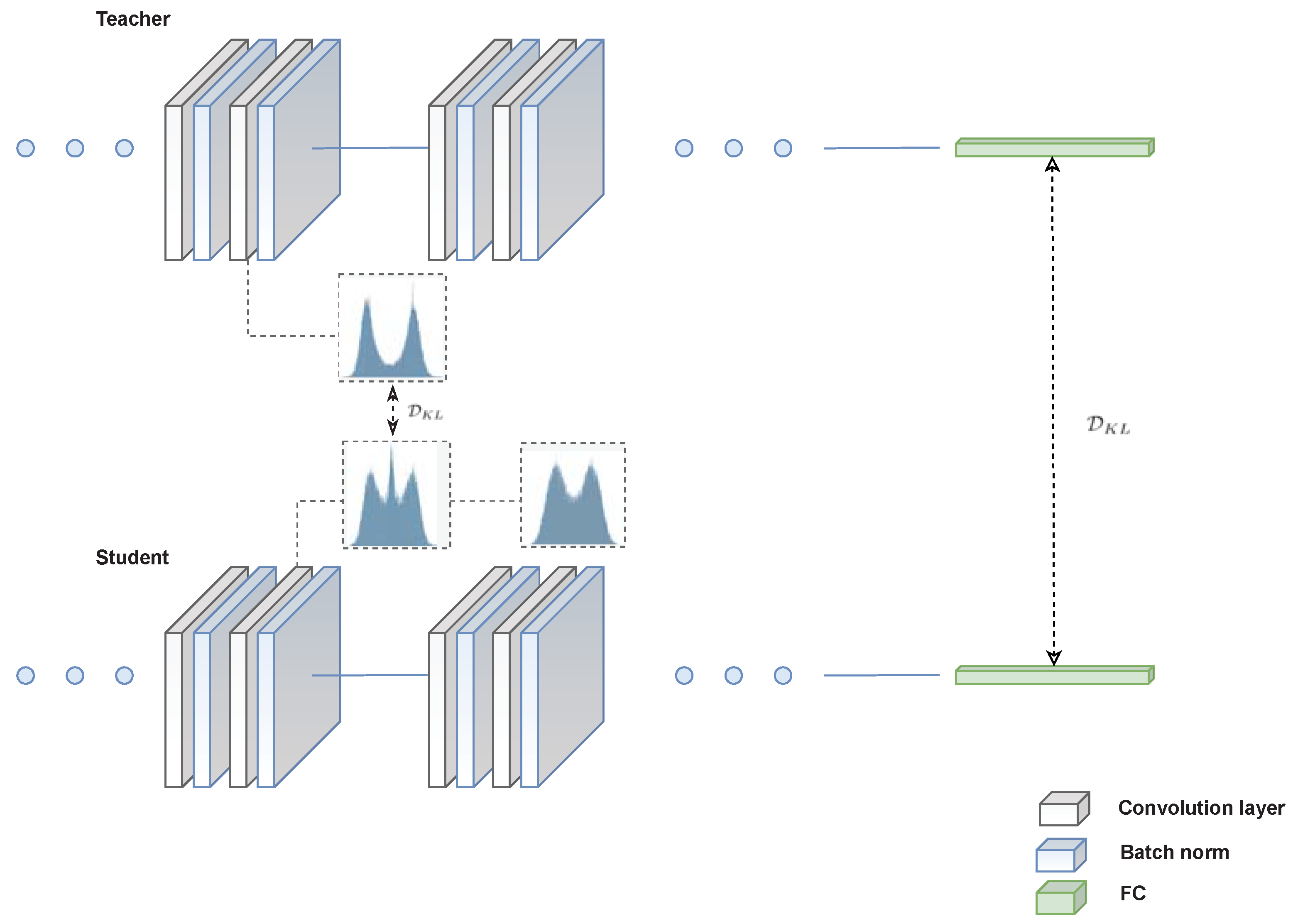
• We propose weight distribution mimicking (WDM) as a training scheme that establishes a better match between the teacher and student distribution for an FP 32 teacher and binary student.
• We are the first to analyze the distribution of the gradients of the loss term with regularization for BNNs.
• We analyze the proposed method in a variety of BNNs and achieve state-of-the-art results without increasing the number of parameters.

2. Background

BNN is a form of extreme quantization that has been broadly studied in the past few years, beginning with the pioneering binarization work of [17], which showed decent performance in the one-bit quantization of the forward pass, adopting the straight-through-estimator (STE) [18] to approximate the binarized gradients. The advantages of such extremely compressed networks is fairly obvious. Due to their very-low bit representation, BNNs can be implemented and embedded on tiny restricted devices and save a significant amount of storage, computation cost, and energy consumption. This makes BNNs appealing for implementation on low memory devices or when the computation is bounded. In addition, BNNs are usually implemented by using the XNOR function as a substance for the convolution operation. This simple logic gate is much faster than computing the standard matrix multiplication needed in CNN and is much cheaper to produce. Figure 1 shows the memory consumption and speed improvement of a BNN in comparison to a regular 32-bit floating-point architecture. As we can see in the figure, the memory size decreases significantly when using binary precision. Furthermore, the figure shows that the when the network is larger and has more parameters (channel size and filter size), the benefits of the binary precision are more prominent. This is because the more memory and computation time that the original 32-bit networks requires, the more efficient its binary counterpart is in comparison.

Despite the superiority of BNNs in memory saving and computation reduction, they suffer a drastic drop in accuracy compared to their real-valued counterparts. There are two main reasons for the performance degradation: large quantization error in the forward propagation and gradient mismatch during backpropagation. Specifically, quantization error refers to the residual between the full-precision weights or activations vector and its quantized version and can be measured by:

$$\begin{array}{c}\hfill MSE\left(X_q\right)=\frac{1}{n}\sum _{i=1}^n{(X-X_q)}^2\end{array}$$

(1)

The representational ability of BNNs is limited, especially in contrast to the full-precision vectors that hold an almost unlimited representation space. Such a representation gap easily results in a large accumulated error when mapping the real-valued weights into the binary space. This is a significantly larger information gap than the one caused by regular quantization.

A good visualization of this effect is shown in Figure 2. Because $X_q$ is of a Bernoulli-like distribution (in case of binarization) it is possible to assume that a bimodal distribution will minimize the quantization error. In comparison to the normal distribution, these vectors usually hold; this is the premise of this work. For this reason, known quantization techniques do not usually work when the quantization goes as far as 1 bit. Moreover, unlike quantization, training a BNN usually begins from scratch and not with pre-trained weights. We believe that the reason for this is that the optimization process needs to reach a different optimal point for the model. The minima reached with higher precision weights and activations does not suit the one for 1-bit precision, and the model needs to converge to a different point.

The backpropagation process in BNNs has to be different from a normal DNN training scheme because the derivative of the sign function is zero almost everywhere. Updating the weights during the training process has to be performed differently. Usually, this is performed by saving the real valued weights and using a straight-through estimator (STE) as the derivative. The simple STE was first presented in [18].

This identity and clip function takes the clipping attribute of binarization into account to reduce the gradient error. However, it can only pass the gradient information inside the clipping interval. Outside [−1, +1], the gradient is clamped to 0. This means that once the value jumps outside the clamping interval, it can no longer be updated. This characteristic greatly harms the updating ability of backward propagation, increases the difficulty of optimization, and decreases the accuracy in practice. The following works have chosen different functions for the backpropagation process and demonstrated their superiority over the standard STE. Some of these works are mentioned later on.

3. Related Work

A lot of research has been conducted to reduce the gap between binarized DNNs and their FP counterparts. This effort usually includes optimization and improvement of the naive binarization process which is often based on loss function improvement, gradient approximation, quantization error minimization, and various changes to the model structure and architectures.

To reduce the quantization error, XNOR-Net [15] uses two different channel-wise scaling factors for the weights and activations. Bi-Real-Net [19] combines additional shortcuts and a replacement of the sign function with a polynomial function for the activations to reduce the information loss caused by the binarization. IR-Net [20] combines a technique to reduce the information entropy loss in the forward pass with an error decay estimator (EDE) that replaces the STE in the backward pass.

Real-to-Bin [21] suggests changing the order of the ResNet block using a two-stage optimization strategy and introduces a progressive teacher–student technique. SD-BNN [22] proposes removing the commonly used scaling factor for weights and activations and replaces them with a self-distribution factor that is learnable and applied before the binarization. RBNN [23] explores the effect of the angular bias on the quantization error and suggests a method that reduces the angle between the FP weights and their binarized version. The authors of this work also suggested a new backpropagation method that meets their needs more efficiently. The authors of [24] combined a reverse-order initialization with smooth progressive quantization and binarized KD. They used the output heatmaps of the teacher network as soft labels for the binary cross entropy loss. FDA [25] suggested estimating the gradient of the sign function in the Fourier frequency domain.

A different approach that has been taken by other related works is to consider the DNN’s distribution to improve performance. KURE [16] applies a regularization to the weights to make them uniformly distributed, which improves the network robustness. In both [12,13], a prior distribution is used to reduce the quantization error. While the former work uses a normal distribution prior for the weights and activations, the latter uses a log-normal distribution prior for the neural gradients.

In this work, we focus on DNN binarization that does not change the number of parameters of the original network, in contrast to recent known methods, such as ReActNet [26] that show impressive binarization results at the cost of increasing the number of parameters.

4. Preliminaries

In this section, we review and provide the notation for BNN, kurtosis and KD.

4.1. BNNs

DNNs usually comprise two integral parts. One is the feature extractor, and the other is a regressor or classifier. The feature extractor commonly uses a basic block based on some multiplication of weights and activations, such as a convolution layer, because the convolution operation is shift invariant and the structure of the network creates informative features for the learning task. The convolution operation is defined as

$$Z_i=A_i\times W_i$$

where $A_i\in {\mathbb{R}}^{K_i,L_i}$ is a two-dimensional input signal (also called activation) to the convolution and $W_i={W_{i,j}...}_{c_i}$ is a set of c two-dimensional weights $W_{i,j}\in {\mathbb{R}}^{M_i,N_i}$, both represented in floating point values over 32 bits. They also both use floating-point multiply–accumulate (MAC) operations. A layer uses $c\times (K_i-M_i)\times L_i-N_i$ times $M_i\times N_i$ MAC operations. One can see that CNNs have a very low speed and a high memory consumption due to the hardware’s computational and communication limitations. BNNs, on the other hand, quantize the weights and activations to 1-bit representations and use 1-bit operations by simply defining the binary projections using the sign function.

$$B_x=sign\left(x\right)=\left\{\begin{array}{cc}+1,\hfill & x\ge 0\hfill \\ -1,\hfill & else\hfill \end{array}\right.$$

where x is the floating-point parameter and B is its binary equivalent. $B_w$ and $B_a$ denote the binary weight and activations, respectively. Accordingly, for BNNs, the convolution operation can be expressed as:

$$Z=I\times W\approx B_w\times B_a=(B_w\otimes B_a)·\alpha$$

where ⊗ is the bitwise XNOR operation and $\alpha$ is a 32-bit scaling factor that is added to minimize the quantization error. BNNs enable the user to reduce the latency and increase the throughput, as they now have a 32 times lower memory footprint and thus have a reduced access to memory needed. This is in addition to operations that are 58 times faster as compared with 32-bit MAC operations [15].

4.2. Knowledge Distillation

KD is a technique for transferring knowledge from one model, referred to as a teacher, to another, referred to as a student [14]. Generally, a large DNN serves as a teacher and a more compact model serves as a student.

Knowledge transferring is done by adding a distillation loss to the student target:

$${\mathcal{L}}_{KD}=D_{KL}(z_T\left|\right|z_S)$$

(2)

where $D_{KL}$ refers to Kullback–Leibler divergence, and $z_T$ and $z_S$ are the output of the last fully connected layer in the teacher and student network, respectively.

KD is a very common technique for improving the generalization of the student [27]. Some studies have shown improvements even when using the exact same model for the teacher and the student [27,28,29]. This regime is typically called self-distillation. KD also leads to a tremendous improvement in model compression [14,29,30], when the common setup for quantization is to use the FP model as teacher and the quantized model as a student [31,32].

4.3. Kurtosis

Let X be a random variable such that $X\in {\mathcal{R}}^d$ from a known probability distribution function (PDF). A common statistical analysis of a variable distribution is to look at the moments of the variable and the most common moments are the first and second moments $\mu \left[X\right]=\mathbb{E}\left(x\right)$) and ${\sigma }^2\left[X\right]=\mathbb{E}\left[{(X-\mathbb{E}\left(x\right))}^2\right]$. A deeper analysis of the distribution can be done using the third and fourth moments – skewness and kurtosis.

The kurtosis of a random variable is defined as follows:

$$Kurtosis\left[X\right]=\left[\mathbb{E}{\left(\frac{X-\mu }{\sigma }\right)}^4\right]$$

(3)

where $\mu$ and $\sigma$ are the first and second moments of X.

The kurtosis, also called ’tailedness’, is a scale and shift-invariant measurement that helps explain how much of the PDF is dense around the mean. For example, for a uniform distribution, kurtosis = 1.8 and for a distribution with that kurtosis, there is an equal possibility of being far and close to the mean. In this paper, we use the kurtosis as a proxy of the weight distribution and define a kurtosis loss term that, by minimizing it, helps us mimic a desired distribution. We show that subtracting the cumulative distribution function (CDF) of this distribution from the CDF of the network weights (i.e., distribution shifting) leads to a distribution with a bimodal notion that is optimal for binarization.

5. Method

In this section, we first explore the effects of the fourth moment on the weight distribution. We demonstrate in Figure 3 how the changes in distribution affect the network’s feature maps. Then, we discuss the KD technique, which supports our goal of achieving bimodal distributions that are more “binary friendly”. Lastly, we present our bimodal distribution-aware training method.

5.1. Weight Distribution Regularization

DNNs’ weights and activations usually follow a Gaussian or Laplace distribution [12]. For BNNs, this distribution may not be optimal. We would like to manipulate the distribution without harming the performance, so that we can actually reduce the quantization error and thus increase the performance. In this work, we follow the work done by [16] and use the kurtosis as a proxy for the probability distribution. Kurtosis regularization is applied to the model loss function, $\mathcal{L}$, as follows:

$$\mathcal{L}={\mathcal{L}}_p+\lambda {\mathcal{L}}_K$$

(4)

where ${\mathcal{L}}_p$ is the target loss function. In common classification and regression tasks, ${\mathcal{L}}_p$ represents the cross entropy (CE) and mean squared error (MSE) loss. ${\mathcal{L}}_K$ is the kurtosis term and $\lambda$ is the coefficient. ${\mathcal{L}}_K$ is defined as

$${\mathcal{L}}_K=\frac{1}{L}\sum _{i=1}^L{\left|Kurtosis\left[W_i\right]-K_T\right|}^2$$

(5)

where L is the number of layers and $K_T$ is the target of the kurtosis regularization.

In this work, we explore the effect of the gradients of ${\mathcal{L}}_K$ in general, and the value of $K_T$ on the model weight distributions. Recall that DNN parameters are commonly optimized by the steepest descent optimization algorithm. To perform the optimization process, we use the Jacobian of the loss function, as in Equation (4).

We assume that $W\sim \mathcal{N}({\mu }_W,{\sigma }_W)$, as assumed in [12]. To ease the notation, we drop the distribution parameters from now on.

The Jacobian of ${\mathcal{L}}_p$ does not affect the weight distribution, as it is linear with W [33]

$$\nabla {\mathcal{L}}_p\propto W\Rightarrow W-\nabla {\mathcal{L}}_p\sim \mathcal{N}.$$

Because we want to explain how the Jacobian affects the distribution shift of the weights, we will focus on analyzing the gradients of Equation (5) with respect to W.

$$\frac{\partial {\mathcal{L}}_K}{\partial W_i}=\frac{8}{\sigma }·\underset{{\tilde{\mu }}_3}{\underbrace{\frac{{(W_i-\mu )}^3}{{\sigma }^3}}}·\underset{\kappa }{\underbrace{\left|\frac{{(W_i-\mu )}^4}{{\sigma }^4}-K_T\right|}}$$

(6)

Here, we derive the partial derivative of the kurtosis loss with respect to one layer of the weights $W_i$. This gradient term consists of a constant coefficient which does not affect the distribution and two additional parts: the third moment, denoted by ${\tilde{\mu }}_3$, and the distance of the kurtosis from $K_T$, which is denoted by $\kappa$. ${\tilde{\mu }}_3$, essentially an odd power of the data, symmetrically shifts weights away from the center of the distribution function. Means, weights with small magnitude, will have gradients with an even smaller magnitude of the skewness component.

$$|W_i|\le |W_j|\Rightarrow {\tilde{\mu }}_3\left(W_i\right)\le \left(\right|W_j|-|W_i\left|\right){\tilde{\mu }}_3\left(W_j\right)$$

$\kappa$ holds the desired tail shape of the shifted distribution.

When $K_T=3$, we maintain a normal distribution of the gradient, and the weight distribution remains normal, as we know for a sum of two random variables with the same $\mu$. While [16] holds for quantization, a uniform distribution is optimal and is achieved by $K_T=1.8$. We hold that BNNs are more efficient when the weight distribution is bimodal and symmetrically shifted away from the mean. The gradient of ${\mathcal{L}}_K$ is uniform, and when $K_T=-1.2$, the weights are shifted uniformly away from the mean. In practice, this creates a bimodal distribution after a few epochs, but the generalization error increases and harms the FP32 model. An intermediate value, such as $K_T=1$, might not be a kurtosis value of a well-defined distribution, but can slowly move towards the desired distribution of W. In Figure 4, we show empirically that we end up with a bimodal distribution, and we do not see any noticeable harm to the model generalization.

In support of this claim, we show in Figure 5 that for $K_T=1$, the cosine similarity between the FP weights and the binary weights is considerably lower.

As seen in Figure 6, by setting different values of $K_T$ for each layer, we can control the weight distribution of the DNN. We can achieve the desired bimodal distribution by setting different $K_T$ values for different layers as long as we ensure that the mean of all $K_T$ values is equal to the value of the desired one. We carefully chose them as a set of hyperparameters, so the desired distribution exists in all layers without extending the training process. We used this in order to train a teacher network that will be more suitable for KD with our BNN student. For simplicity, the BNN uses a fixed value $K_T$.

5.2. Weight Distribution Mimicking

The reason that BNNs have difficulties obtaining a high performance mainly lies in the information loss resulting from the very low precision of weights and activations. While the quantization loss is tremendous when using ultra-low representation, shifting a FP network and using it as a guide can help minimize this loss. To bridge this information gap, we propose a teacher–student weight distribution mimicking (WDM) training scheme, as presented in Figure 7. WDM uses the information from the FP network teacher to obtain a lower loss on the BNN student by minimizing the distance between the distributions. This method is agnostic to KD and can work in parallel. For that reason, we also add KD and achieve better results.

$${\mathcal{L}}_{WDM}=\sum _{i=1}^L{D}_{KL}(\mathcal{D}\left(W_{i,T}\right)\left|\right|\mathcal{D}\left(W_{i,S}\right))+\beta {\mathcal{L}}_{KD}(y_T,y_S)$$

(7)

where we denote the i-th layer of weights in the teacher network as $W_{i,T}$ and the i-th layer of the student BNN as $W_{i,S}$. L is the number of convolution layers, $\mathcal{D}$ is the distribution of the weights, $y_T$ and $y_S$ are the predictions of the teacher and student, respectively, and $D_{KL}$ refers to the Kullback–Leibler divergence. The proposed method uses a fixed teacher, meaning we only optimize the student network and use the teacher as a model towards our desired behavior. Unlike KD, the goal of WDM is to help guide the BNN to realize how the final distribution of the weights should be at each layer, regardless of the features and predictions. Moreover, low-bit representation networks have difficulties following the distribution guidance from the kurtosis regularization and require longer training to do so. Using the WDM scheme helps reduce the time it takes to shift the BNN weight distribution.

5.3. BD-BNN

Our bimodal distribution-aware BNN (BD-BNN) is trained in a teacher–student fashion through two main steps:

(1) We train an FP-32 network and a BNN with the same architecture but with 1-bit representation with weight distribution regularization, where the FP-32 network has different $K_T$ values for each layer, as described in Section 5.1. The objective function is Equation (4) for both networks.

(2) We fix the FP-32 network as a teacher and the BNN as the student in our WDM training scheme, as described in Section 5.2, and use simple KD [14] on top, as shown in Figure 7. We call the student BNN BD-BNN. The objective of the BD-BNN in this stage is to aggregate the loss from Equation (4) with the one from Equation (7) as follows:

$$\mathcal{L}={\mathcal{L}}_{CE}+\lambda {\mathcal{L}}_K+\alpha {\mathcal{L}}_{WDM}$$

(8)

In the BD-BNN optimization process, we use known gradient approximation [19,23]. The weight distribution of BD-BNN shifts at each stage of the training, so the final weight distribution is optimal for the binarization process, as seen in Figure 8. We found that, on average, around 50% of the weights changed their sign in BD-BNN as compared to binarization of a pre-trained network.

6. Results

In this section, we evaluate our BD-BNN method on two common image classification datasets, CIFAR-10 [34] with ResNet-18/20 [1] and VGG-small [35], and ImageNet [36] with ResNet-18 [1]. The first convolution layer and the last fully connected layer are not binarized. We follow the training strategy explained in Section 5.3 and compare our BD-BNN with state-of-the-art existing methods. Our source code, experimental settings, training logs, and binary models are available at. https://github.com/BlueAnon/BD-BNN. Accessed data for the experiments for CIFAR-10 and ImageNet can be found at https://www.cs.toronto.edu/~kriz/cifar.html and https://www.image-net.org/ (accessed on 28 October 2022) respectively.

6.1. CIFAR-10

For the CIFAR-10 dataset, we trained all networks on the training set and the results reported are on the test set. We used an SGD optimizer with a weight decay of 0.001 for better L2 regularization. The learning rate was set to 0.1 and gradually decayed to 0. All convolution layers were binarized, including 1 × 1 conv. For gradient approximation, we used the method described in [23]. We compare our method with several other state-of-the-art binary methods including IR-Net [20] and RBNN [23] for the ResNet-18 structure, IR-Net [20], RBNN [23], FDA-Net [25], XNOR-Net [15] and DSQ [37] for the ResNet-20 structure, and VGG-small. In

Table 1. Performance comparison with state-of-the-art methods on CIFAR-10. W/A denotes the bit length of weights and activations.

Network	Method	Bit-Width (W/A)	Acc (%)
ResNet-18	FP32	32/32	93.00
	IR-Net [20]	1/1	91.50
	RBNN [23]	1/1	92.20
	BD-BNN (Ours)	1/1	92.46
ResNet-20	FP32	32/32	91.70
	DoReFa-Net [38]	1/1	79.30
	XNOR-Net [15]	1/1	85.23
	DSQ [37]	1/1	84.11
	IR-Net [20]	1/1	85.40
	FDA-BNN [25]	1/1	86.20
	RBNN [23]	1/1	86.50
	BD-BNN (Ours)	1/1	86.50
VGG-small	FP32	32/32	93.80
	BNN [17]	1/1	89.90
	XNOR-Net [15]	1/1	89.80
	DSQ [37]	1/1	91.72
	IR-Net [20]	1/1	90.40
	RBNN [23]	1/1	91.30
	FDA-BNN [25]	1/1	92.54
	BD-BNN (Ours)	1/1	92.7

, we compare our BD-BNN, method with several existing binarization methods, achieving around a 0.2% accuracy improvement in all the listed architectures. ResNet-20 used the Bi-Real structure, which includes a second skip connection in the ResNet block.

6.2. ImageNet

ImageNet is a much more challenging dataset due to its large scale and great diversity. It contains over 1.2 million training images from 1000 different categories. For ImageNet, we used the training set to train all networks and the results reported are on the test set, as was performed previously. We used an ADAM optimizer with a momentum of 0.9 and a learning rate set to 1 × 10${}^{-3}$. All methods listed in

Table 2. Performance comparison with state-of-the-art methods on ImageNet. W/A denotes the bit length of weights and activations. We report the top-1 and top-5 performances in terms of accuracy. ’*’ indicates that ReAct-Net partial structure was used.

Network	Method	Bit-Width (W/A)	Top-1 (%)	Top-5 (%)
ResNet-18	FP	32/32	69.6	89.2
	IR-Net [20]	1/1	58.1	80.0
	RBNN [23]	1/1	59.9	81.9
	Bi-Real-Net [19]	1/1	56.4	79.5
	XNOR-Net [15]	1/1	51.2	73.2
	BNN [17]	1/1	42.2	67.1
	DeReFa-Net [38]	1/1	53.4	67.7
	FDA-BNN [25]	1/1	60.2	82.3
	BD-BNN (Ours)	1/1	60.6	82.49
	ReActNet * [26]	1/1	62.1	83.53
	BD-BNN * (Ours)	1/1	63.27	84.42

, except [17], do not binarize the down-sampling layer in the shortcut branch of the ResNet block. Similar to [24], we also trained the network in two stages. First, we trained with binary activations and FP weights, and then we trained the full binary network. Furthermore, we used the architecture suggested in [19] that adds a skip connection to each ResNet block. We used STE gradient approximation as in [19,26]. We compared BD-BNN with IR-Net [20], RBNN [23], FDA-Net [25], XNOR-Net [15], Bi-real Net [19], BNN [17] and DoReFa [38]. For the ResNet-18 architecture, we demonstrate two different settings. The first one is the one described above, and for the second, we used PRelu as the non-linearity function and added a bias to the activations. This setting was used in ReAct-Net [26]. In contrast to ReAct-Net [26], however, we kept the ResNet structure as is. We trained ReAct-Net with our settings and compared our method to it. All experiments are listed in Table 2. As seen from the table, our BD-BNN achieves a 0.5–1.2% accuracy improvement over ResNet-18.

6.3. Ablation Study

In this section, we specify the contribution of each component of the method described in this paper. We test BD-BNN on CIFAR10 with ResNet-20 architecture. As shown in

Table 3. Ablation Study—Exploration of BD-BNN. WDR and WDM stand for weight distribution regularization and weight distribution mimicking, respectively.

Method	W/A	Acc
FP	32/32	91.7%
BNN	1/1	83.9%
BNN + WDR	1/1	85.25%
BNN + WDR + KD	1/1	85.69%
BNN + WDR + WDM	1/1	86.50%

, each addition contributes to the BNN performance. We conclude from the study that our WDM outperforms the commonly used KD training scheme. When put together, our method surpasses other state-of-the-art binary methods and achieves highly accurate BNNs.

In addition, we tested the effect of the WDM described in Section 5.2. We tried different teacher–student settings on ResNet-18 with the ImageNet dataset. The goal of this ablation is to determine which setting is best for binary networks. We used teachers that were trained with and without weight distribution regularization using the fourth momentum and trained a BNN student with a similar structure using the loss specified in Section 5.2.

Table 4. Ablation Study—WDM scheme analysis with different training of teacher–student.

Teacher	Student	Acc
FP	BNN	58.45%
FP + WDR	BNN	56.32%
FP	BNN + WDR	55.25%
FP + WDR	BNN + WDR	60.5%

shows that the best setting is to train a teacher with kurtosis and let the student try and mimic the teacher’s behavior, also using kurtosis. It also shows, as expected, that a teacher and a student that train with different methods show poor results when compared to ones that use the same method.

7. Discussion

Binarization is one of the dominant methods for reducing the inference complexity of DNNs, with the ability to reduce the memory footprint by 32× and to accelerate the deployment by 58× [15]. Despite this promising compression ability, there is still a gap between the accuracy of the binarized network and its full-precision counterpart.

In this work, we took one step further in reducing this gap and presented a novel method for binarization-aware training. Our approach is based on manipulating the weight distribution of the binary neural network for better performance. We show that a bimodal distribution achieves better results and higher cosine similarity than common binarization methods. We incorporate the fourth-moment weight regularization to the loss function. As a result, the weight distribution shifts and is more suitable for binary models. In addition, we presented a new teacher–student weight mimicking method that helps minimize the binarization error. Those two components form our presented method, BD-BNN, which outperforms state-of-the-art BNNs by up to 1.2% top-1 accuracy on ImageNet.

In light of our research, we propose several directions for further work, such as integrating $K_T$ as part of the learning process. Because different layers in the network have slightly different distributions, we believe that setting a different $K_T$ for each layer can improve performance. However, in this work we have conducted a rough parameter search in order to determine each layer’s suitable value. We suggest integrating this to the learning process and learning the correct values of $K_T$ for each layer of the BNN to optimize the results. Another aspect that has yet to be explored is transitioning from a quantized network to a binarized method using BD-BNN. Usually in BNN training we begin from nothing and do not initialize the weights with pre-trained ones. However, initializing the weights could mean a shorter training process and an easy transition from a quantized net to a binary one. We believe that using our method we can manipulate a quantized network distribution to be bimodal and doing so allows a better transition for binarization.