Robust Output Tracking of Boolean Control Networks over Finite Time
Abstract
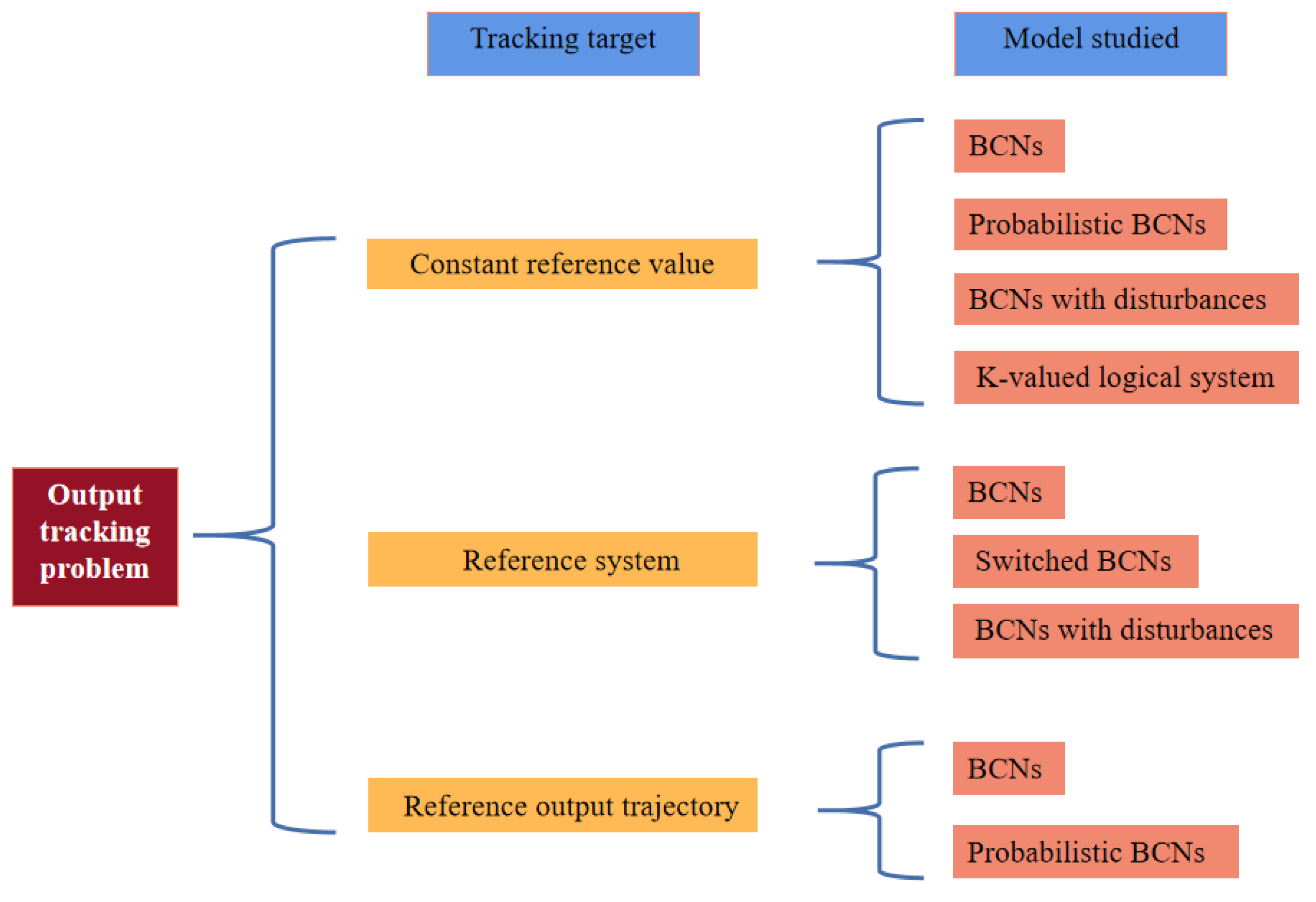
1. Introduction
2. Preliminaries
3. Main Results
3.1. Trackability of a Reference Output Trajectory
| Algorithm 1 Design of controller for tracking a reference output trajectory |
Input: and Output:G
|
3.2. Trackability of the Outputs of a Reference System
| Algorithm 2 Design of controller for tracking the outputs of a reference system over finite time |
Input: Output:R
|
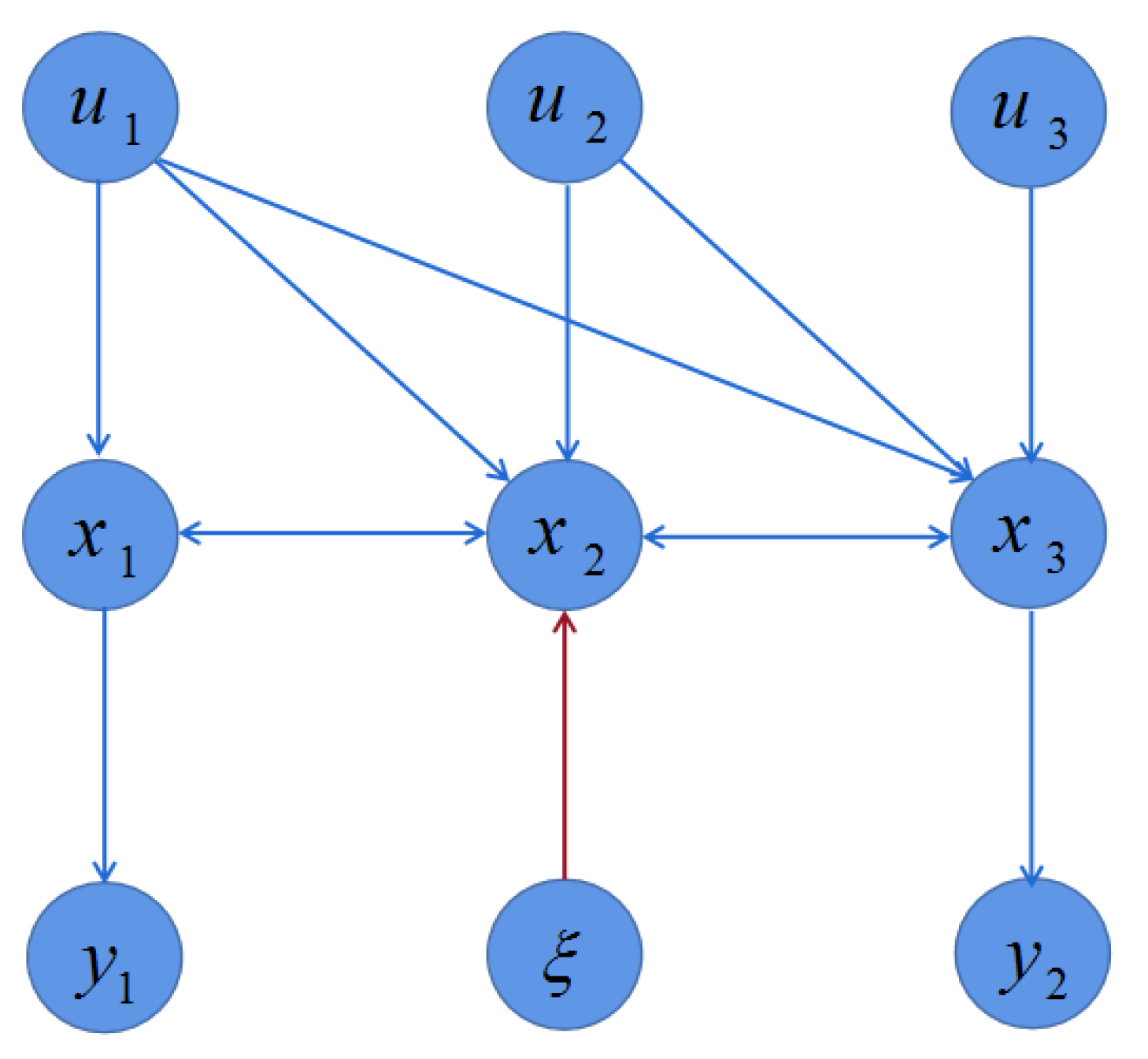
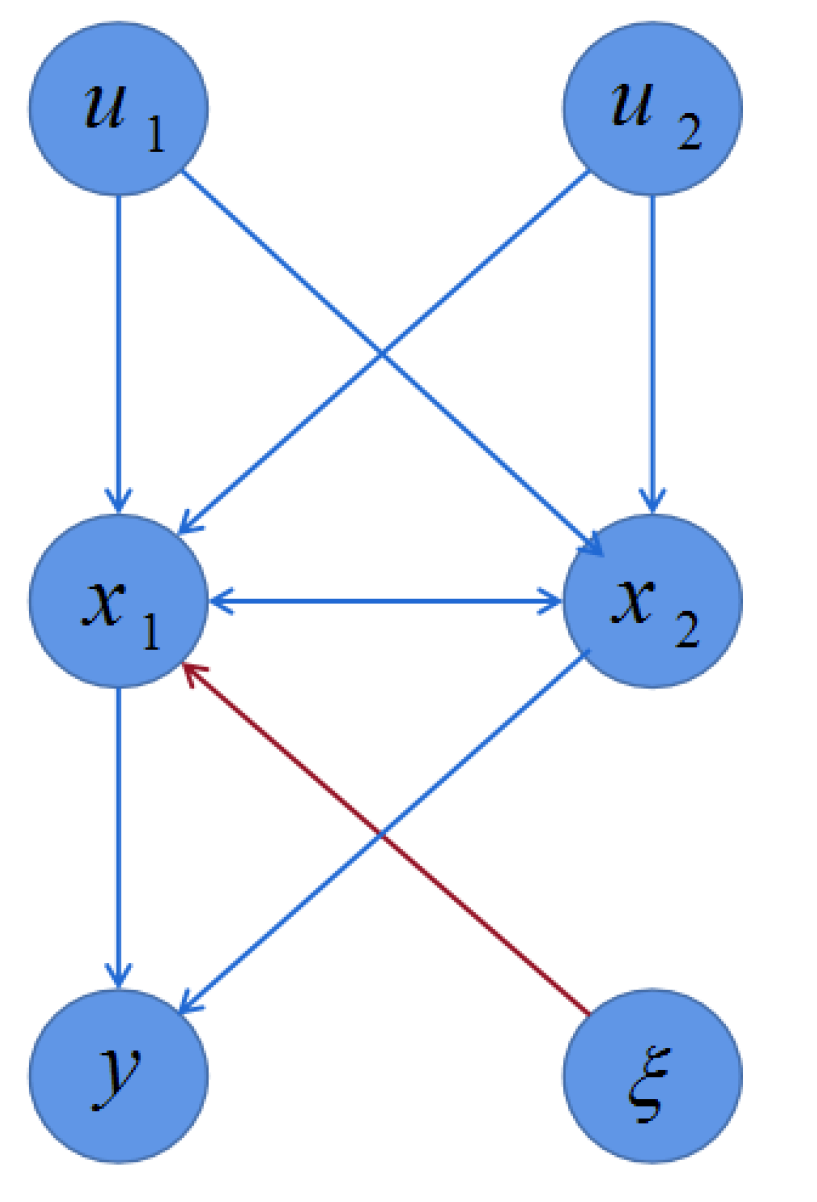
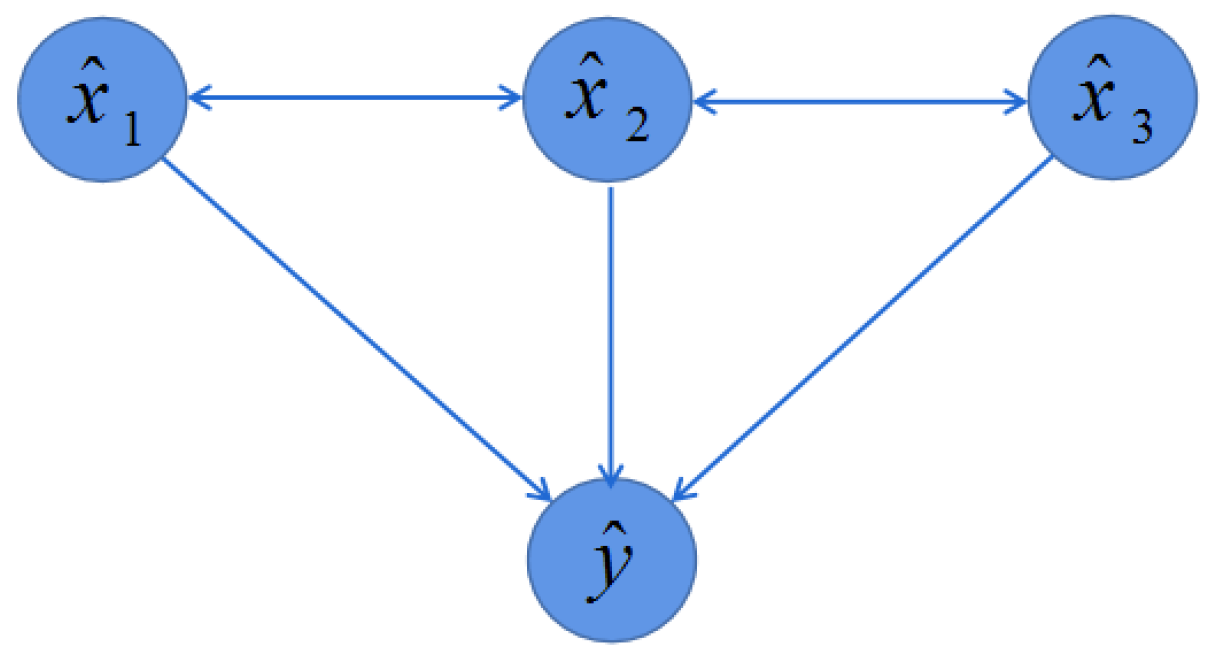
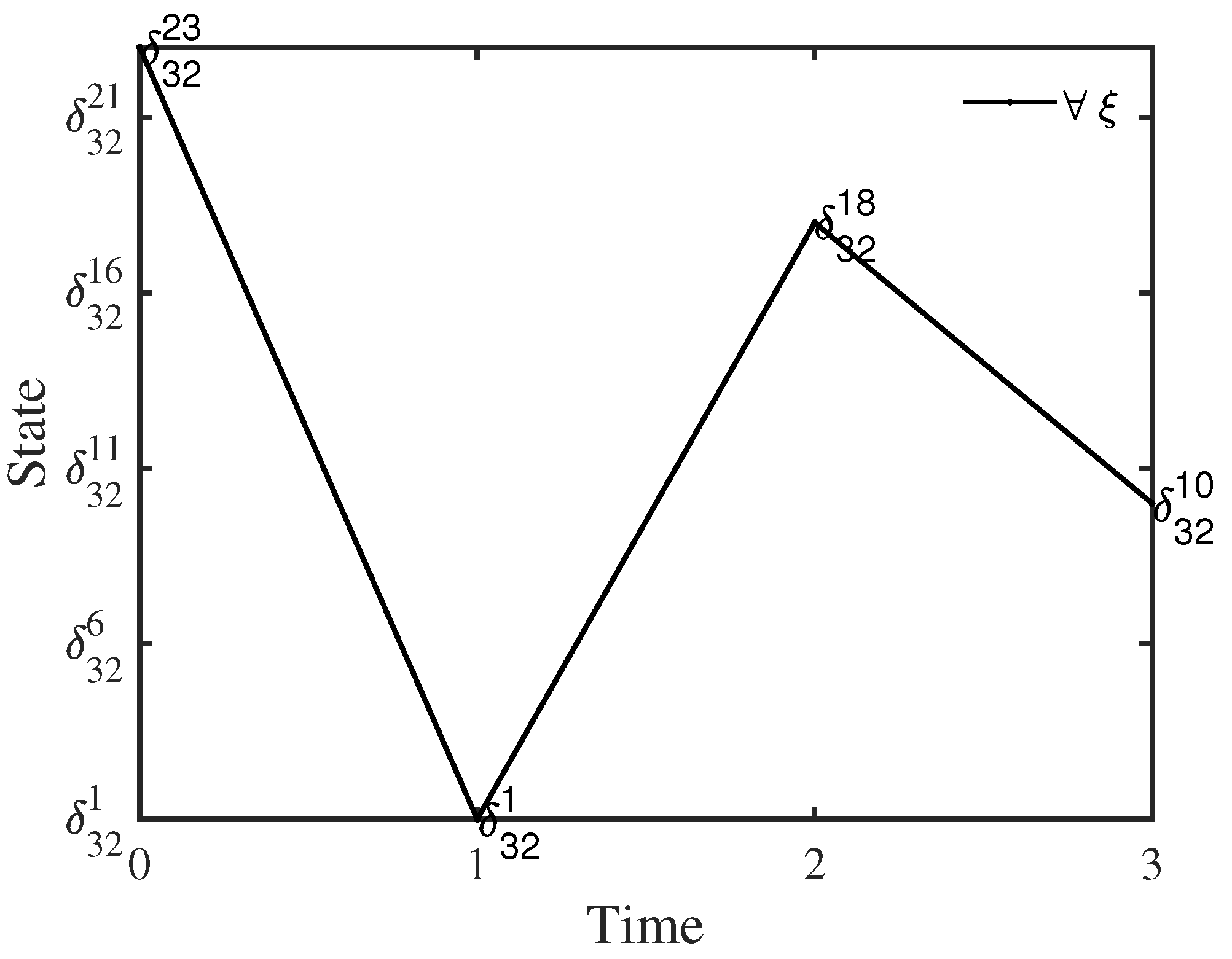
4. Illustrative Examples
| t | 1 | 2 | 3 | 4 |
| Y |
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kauffman, S.A. Metabolic stability and epigenesis in randomly constructed genetic nets. J. Theor. Bio. 1969, 22, 437–467. [Google Scholar] [CrossRef]
- Hassoun, M.H. Fundamentals of Artificial Neural Networks; MIT Press: Cambridge, MA, USA, 1995. [Google Scholar]
- Bloomingdale, P.; Nguyen, V.A.; Niu, J.; Mager, D.E. Boolean network modeling in systems pharmacology. J. Pharmacokinet. Phar. 2018, 45, 159–180. [Google Scholar] [CrossRef]
- Shen, X.; Wu, Y.; Shen, T. Logical control scheme with real-time statistical learning for residual gas fraction in IC engines. Sci. China Inf. Sci. 2018, 61, 010203. [Google Scholar] [CrossRef]
- Vadivel, R.; Hammachukiattikul, P.; Gunasekaran, N.; Saravanakumar, R.; Dutta, H. Strict dissipativity synchronization for delayed static neural networks: An event-triggered scheme. Chaos Soliton Fract. 2021, 150, 111212. [Google Scholar] [CrossRef]
- Vadivel, R.; Suresh, R.; Hammachukiattikul, P.; Unyong, B.; Gunasekaran, N. Event-triggered L-2-L-infinity filtering for network-based neutral systems with time-varying delays via T-S fuzzy approach. IEEE Access 2021, 9, 145133–145147. [Google Scholar] [CrossRef]
- Cheng, D.; Qi, H.; Li, Z. Analysis and Control of Boolean Networks: A Semi-Tensor Product Approach; Springer: London, UK, 2011. [Google Scholar]
- Guo, Y.; Zhou, R.; Wu, Y.; Gui, W.; Yang, C. Stability and set stability in distribution of probabilistic Boolean networks. IEEE Trans. Automat. Contr. 2018, 64, 736–742. [Google Scholar] [CrossRef]
- Li, H.; Wang, S.; Li, X.; Zhao, G. Perturbation analysis for controllability of logical control networks. SIAM J. Control Optim. 2020, 58, 3632–3657. [Google Scholar] [CrossRef]
- Feng, J.; Li, Y.; Fu, S.; Lyu, H. New method for disturbance decoupling of Boolean networks. IEEE Trans. Automat. Contr. 2022, 67, 4794–4800. [Google Scholar] [CrossRef]
- Li, R.; Yang, M.; Chu, T. State feedback stabilization for disturbance decoupling of Boolean control networks. IEEE Trans. Aut. Contr. 2013, 58, 1853–1857. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, Z.; Han, X.; Liu, Z. Stabilization of probabilistic finite automata based on semi-tensor product of matrices. J. Franklin Inst. 2020, 357, 5173–5186. [Google Scholar] [CrossRef]
- Zhao, G.; Li, H.; Duan, P.; Alsaadi, F. Survey on applications of semi-tensor product method in networked evolutionary games. J. Appl. Anal. Comput. 2019, 10, 32–54. [Google Scholar] [CrossRef]
- Zhong, J.; Lin, D. Driven stability of nonlinear feedback shift registers with inputs. IEEE Trans. Commun. 2016, 64, 2274–2284. [Google Scholar] [CrossRef]
- Lu, J.; Li, M.; Liu, Y.; Ho, D.; Kurths, J. Nonsingularity of Grain-like cascade FSRs via semi-tensor product. Sci. China Inf. Sci. 2018, 61, 010204. [Google Scholar] [CrossRef]
- Wu, Y.; Le, S.; Zhang, K.; Sun, X. Ex-ante agent transformation of Bayesian games. IEEE Trans. Automat. Contr. 2021, 67, 5793–5808. [Google Scholar] [CrossRef]
- Le, S.; Wu, Y.; Toyoda, M. A congestion game framework for service chain composition in NFV with function benefit. Inf. Sci. 2020, 514, 512–522. [Google Scholar] [CrossRef]
- Li, B.; Lu, J. Boolean-network-based approach for construction of filter generators. Sci. China Inf. Sci. 2020, 63, 212206. [Google Scholar] [CrossRef]
- Julius, A.; Halasz, A.; Sakar, M.; Rubin, H.; Kumar, V.; Pappas, G. Stochastic modeling and control of biological systems: The lactose regulation system of Escherichia coli. IEEE Trans. Automat. Contr. 2018, 53, 51–65. [Google Scholar] [CrossRef]
- Yerudkar, A.; Del Vecchio, C.; Glielmo, L. Output tracking control design of switched Boolean control networks. IEEE Control Syst. Lett. 2020, 4, 355–360. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Y.; Cheng, D. Output tracking of Boolean control networks. IEEE Trans. Automat. Contr. 2019, 65, 2730–2735. [Google Scholar] [CrossRef]
- Zhang, Z.; Leifeld, T.; Zhang, P. Finite horizon tracking control of Boolean control networks. IEEE Trans. Automat. Contr. 2017, 63, 1798–1805. [Google Scholar] [CrossRef]
- Zhang, Q.; Feng, J.; Jiao, T. Finite horizon tracking control of probabilistic Boolean control networks. J. Franklin Inst. 2021, 358, 9909–9928. [Google Scholar] [CrossRef]
- Li, H.; Song, P.; Yang, Q. Pinning control design for robust output tracking of k-valued logical networks. J. Franklin Inst. 2017, 354, 3039–3053. [Google Scholar] [CrossRef]


| Notations | Definitions |
|---|---|
| set of real numbers | |
| set of real matrices | |
| the r-th column of matrix C | |
| n-order identity matrix | |
| () | |
| set of logical matrices | |
| the cardinality of a set | |
| ⊗ | the Kronecker product |
| * | the Khatri–Rao product |
| () | the column vector of length r with all entries equal to 0 (1) |
| set of integer numbers x satisfying | |
| transposition of matrix A | |
| the -element of matrix A |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Zhao, X.; Fu, S.; Xia, J. Robust Output Tracking of Boolean Control Networks over Finite Time. Mathematics 2022, 10, 4078. https://doi.org/10.3390/math10214078
Zhao Y, Zhao X, Fu S, Xia J. Robust Output Tracking of Boolean Control Networks over Finite Time. Mathematics. 2022; 10(21):4078. https://doi.org/10.3390/math10214078
Chicago/Turabian StyleZhao, Yuan, Xiaoyu Zhao, Shihua Fu, and Jianwei Xia. 2022. "Robust Output Tracking of Boolean Control Networks over Finite Time" Mathematics 10, no. 21: 4078. https://doi.org/10.3390/math10214078
APA StyleZhao, Y., Zhao, X., Fu, S., & Xia, J. (2022). Robust Output Tracking of Boolean Control Networks over Finite Time. Mathematics, 10(21), 4078. https://doi.org/10.3390/math10214078






