A Comprehensive Analysis of Chinese, Japanese, Korean, US-PIMA Indian, and Trinidadian Screening Scores for Diabetes Risk Assessment and Prediction
Abstract
1. Introduction
2. Literature Review
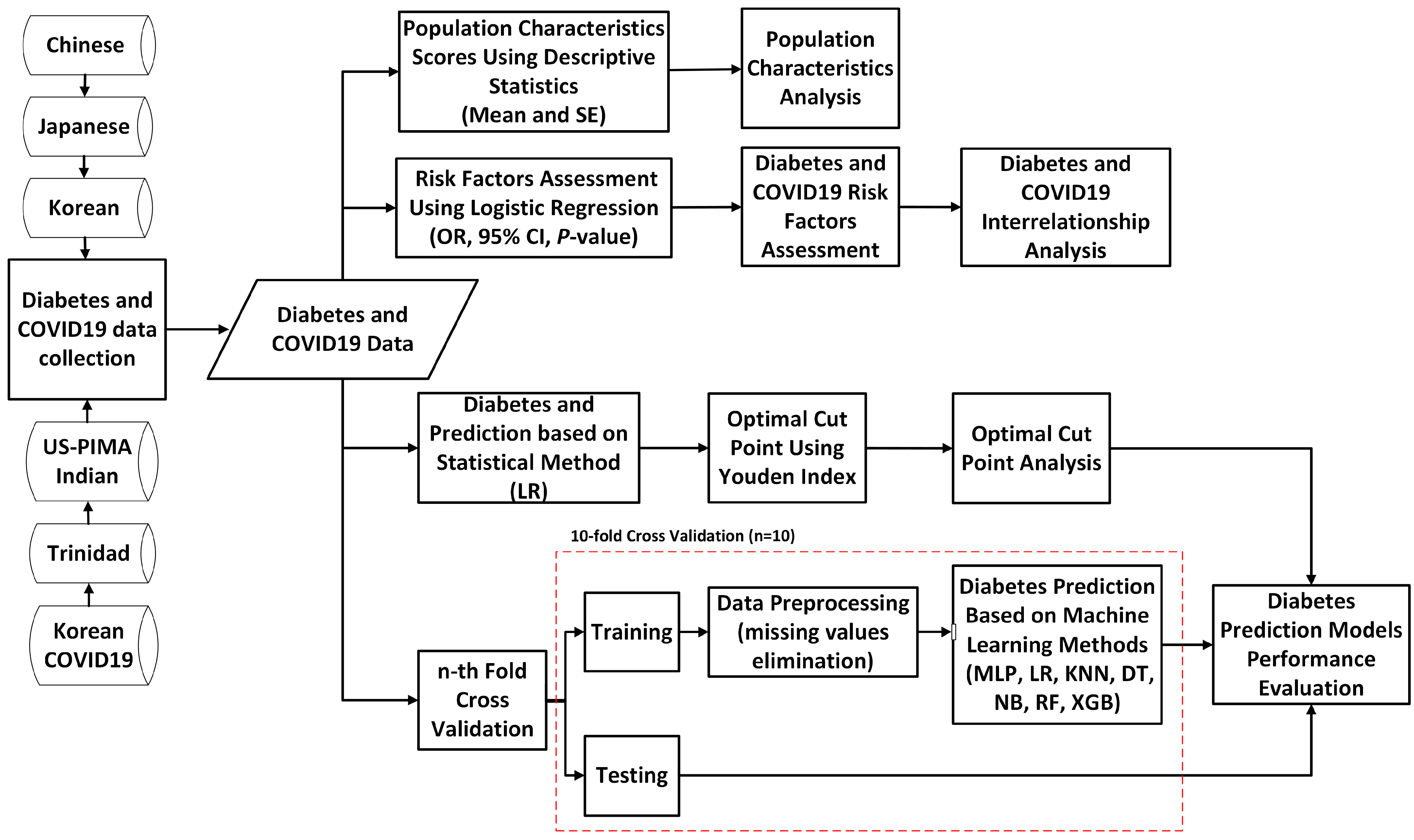
3. Materials and Methods
3.1. Study Populations and Data Sources
3.2. Proposed Study Design
3.3. Chi-Squared Test of Association
3.4. Model Evaluation
4. Results and Discussions
4.1. Descriptive Statistics Analysis
4.2. Diabetes Risk Factors and Significant Analysis
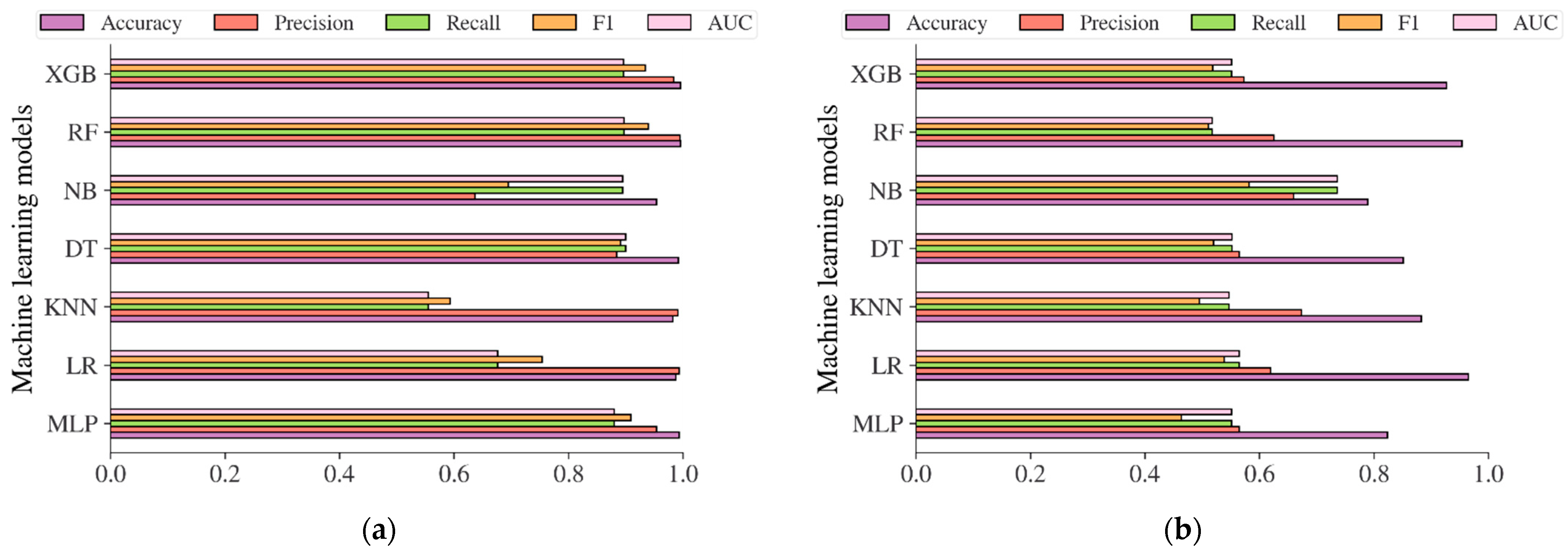
4.3. Diabetes Prediction Based on Machine Learning Methods
4.4. Comparison with Earlier Works
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pate, A.; Emsley, R.; Ashcroft, D.M.; Brown, B.; van Staa, T. The Uncertainty with Using Risk Prediction Models for Individual Decision Making: An Exemplar Cohort Study Examining the Prediction of Cardiovascular Disease in English Primary Care. BMC Med. 2019, 17, 134. [Google Scholar] [CrossRef]
- Chen, L. Overview of Clinical Prediction Models. Ann. Transl. Med. 2020, 8, 71. [Google Scholar] [CrossRef] [PubMed]
- Murphy, J.M. Performance of Screening and Diagnostic Tests: Application of Receiver Operating Characteristic Analysis. Arch. Gen. Psychiatry 1987, 44, 550. [Google Scholar] [CrossRef] [PubMed]
- Rossello, X.; Dorresteijn, J.A.; Janssen, A.; Lambrinou, E.; Scherrenberg, M.; Bonnefoy-Cudraz, E.; Cobain, M.; Piepoli, M.F.; Visseren, F.L.; Dendale, P. Risk Prediction Tools in Cardiovascular Disease Prevention: A Report from the ESC Prevention of CVD Programme Led by the European Association of Preventive Cardiology (EAPC) in Collaboration with the Acute Cardiovascular Care Association (ACCA) and the Association of Cardiovascular Nursing and Allied Professions (ACNAP). Eur. J. Psychiatry Nurs. 2019, 18, 534–544. [Google Scholar] [CrossRef]
- Fitriyani, N.L.; Syafrudin, M.; Alfian, G.; Rhee, J. HDPM: An Effective Heart Disease Prediction Model for a Clinical Decision Support System. IEEE Access 2020, 8, 133034–133050. [Google Scholar] [CrossRef]
- Alfian, G.; Syafrudin, M.; Fitriyani, N.L.; Anshari, M.; Stasa, P.; Svub, J.; Rhee, J. Deep Neural Network for Predicting Diabetic Retinopathy from Risk Factors. Mathematics 2020, 8, 1620. [Google Scholar] [CrossRef]
- Fitriyani, N.L.; Syafrudin, M.; Alfian, G.; Rhee, J. Development of Disease Prediction Model Based on Ensemble Learning Approach for Diabetes and Hypertension. IEEE Access 2019, 7, 144777–144789. [Google Scholar] [CrossRef]
- Alfian, G.; Syafrudin, M.; Ijaz, M.; Syaekhoni, M.; Fitriyani, N.; Rhee, J. A Personalized Healthcare Monitoring System for Diabetic Patients by Utilizing BLE-Based Sensors and Real-Time Data Processing. Sensors 2018, 18, 2183. [Google Scholar] [CrossRef]
- American Diabetes Association. Standards of Medical Care in Diabetes–2006. Diabetes Care 2006, 29, s4–s42. [Google Scholar] [CrossRef]
- World Health Organization. Global Status Report on Non-communicable Diseases 2014. Available online: https://www.who.int/nmh/publications/ncd-status-report-2014/en (accessed on 9 August 2022).
- Complication of Diabetes. Available online: https://www.diabetes.org.uk/guide-to-diabetes/complications (accessed on 9 August 2022).
- Global Report of Diabetes. Available online: https://apps.who.int/iris/bitstream/handle/10665/204871/9789241565257_eng.pdf?sequence=1 (accessed on 9 August 2022).
- Diabetes. Available online: https://www.who.int/health-topics/diabetes (accessed on 9 August 2022).
- Kianpour, F.; Fararouei, M.; Hassanzadeh, J.; Mohammadi, M.; Dianatinasab, M. Performance of Diabetes Screening Tests: An Evaluation Study of Iranian Diabetes Screening Program. Diabetol. Metab. Syndr. 2021, 13, 13. [Google Scholar] [CrossRef]
- Buijsse, B.; Simmons, R.K.; Griffin, S.J.; Schulze, M.B. Risk Assessment Tools for Identifying Individuals at Risk of Developing Type 2 Diabetes. Epidemiol. Rev. 2011, 33, 46–62. [Google Scholar] [CrossRef] [PubMed]
- Meng, L.; Kwon, K.-S.; Kim, D.J.; Lee, Y.; Kim, J.; Kshirsagar, A.V.; Bang, H. Performance of Diabetes and Kidney Disease Screening Scores in Contemporary United States and Korean Populations. Diabetes Metab. J. 2022, 46, 273–285. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.; Yang, S.; Huang, Z.; He, J.; Wang, X. Type 2 Diabetes Mellitus Prediction Model Based on Data Mining. Inform. Med. Unlocked 2018, 10, 100–107. [Google Scholar] [CrossRef]
- Meng, X.-H.; Huang, Y.-X.; Rao, D.-P.; Zhang, Q.; Liu, Q. Comparison of Three Data Mining Models for Predicting Diabetes or Prediabetes by Risk Factors. Kaohsiung J. Med. Sci. 2013, 29, 93–99. [Google Scholar] [CrossRef] [PubMed]
- Muktabhant, B.; Sanchaisuriya, P.; Sarakarn, P.; Tawityanon, W.; Trakulwong, M.; Worawat, S.; Schelp, F.P. Use of Glucometer and Fasting Blood Glucose as Screening Tools for Diabetes Mellitus Type 2 and Glycated Haemoglobin as Clinical Reference in Rural Community Primary Care Settings of a Middle Income Country. BMC Public Health 2012, 12, 349. [Google Scholar] [CrossRef] [PubMed]
- Agarwal, M.M. Gestational Diabetes Mellitus: Screening with Fasting Plasma Glucose. WJD 2016, 7, 279. [Google Scholar] [CrossRef]
- Mannucci, E.; Ognibene, A.; Sposato, I.; Brogi, M.; Gallori, G.; Bardini, G.; Cremasco, F.; Messeri, G.; Rotella, C.M. Fasting Plasma Glucose and Glycated Haemoglobin in the Screening of Diabetes and Impaired Glucose Tolerance. Acta Diabetol. 2003, 40, 181–186. [Google Scholar] [CrossRef]
- Katulanda, G.W.; Katulanda, P.; Dematapitiya, C.; Dissanayake, H.A.; Wijeratne, S.; Sheriff, M.H.R.; Matthews, D.R. Plasma Glucose in Screening for Diabetes and Pre-Diabetes: How Much Is Too Much? Analysis of Fasting Plasma Glucose and Oral Glucose Tolerance Test in Sri Lankans. BMC Endocr. Disord. 2019, 19, 11. [Google Scholar] [CrossRef]
- Rosén, A.; Otten, J.; Stomby, A.; Vallin, S.; Wennberg, P.; Brunström, M. Oral Glucose Tolerance Testing as a Complement to Fasting Plasma Glucose in Screening for Type 2 Diabetes: Population-Based Cross-Sectional Analyses of 146 000 Health Examinations in Västerbotten, Sweden. BMJ Open 2022, 12, e062172. [Google Scholar] [CrossRef]
- Goyal, A.; Gupta, Y.; Kubihal, S.; Kalaivani, M.; Bhatla, N.; Tandon, N. Utility of Screening Fasting Plasma Glucose and Glycated Hemoglobin to Circumvent the Need for Oral Glucose Tolerance Test in Women with Prior Gestational Diabetes. Adv. Ther. 2021, 38, 1342–1351. [Google Scholar] [CrossRef]
- Nomura, K.; Inoue, K.; Akimoto, K. A Two-Step Screening, Measurement of HbA1c in Association with FPG, May Be Useful in Predicting Diabetes. PLoS ONE 2012, 7, e36309. [Google Scholar] [CrossRef] [PubMed]
- Lim, W.-Y.; Ma, S.; Heng, D.; Tai, E.S.; Khoo, C.M.; Loh, T.P. Screening for Diabetes with HbA1c: Test Performance of HbA1c Compared to Fasting Plasma Glucose among Chinese, Malay and Indian Community Residents in Singapore. Sci. Rep. 2018, 8, 12419. [Google Scholar] [CrossRef] [PubMed]
- Nomura, S.; Sakamoto, H.; Rauniyar, S.K.; Shimada, K.; Yamamoto, H.; Kohsaka, S.; Ichihara, N.; Kumamaru, H.; Miyata, H. Analysis of the Relationship between the HbA1c Screening Results and the Development and Worsening of Diabetes among Adults Aged over 40 Years: A 4-Year Follow-up Study of 140,000 People in Japan—The Shizuoka Study. BMC Public Health 2021, 21, 1880. [Google Scholar] [CrossRef] [PubMed]
- Bender, W.; McCarthy, C.; Elovitz, M.; Parry, S.; Durnwald, C. Universal HbA1c Screening and Gestational Diabetes: A Comparison with Clinical Risk Factors. J. Mater.-Fetal Neonatal Med. 2021, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Zhou, X.; Pang, Z.; Gao, W.; Wang, S.; Zhang, L.; Ning, F.; Qiao, Q. Performance of an A1C and Fasting Capillary Blood Glucose Test for Screening Newly Diagnosed Diabetes and Pre-Diabetes Defined by an Oral Glucose Tolerance Test in Qingdao, China. Diabetes Care 2010, 33, 545–550. [Google Scholar] [CrossRef] [PubMed]
- Fadl, H.; Östlund, I.; Nilsson, K.; Hanson, U. Fasting Capillary Glucose as a Screening Test for Gestational Diabetes Mellitus. BJOG: Int. J. Obstet. Gynaecol. 2006, 113, 1067–1071. [Google Scholar] [CrossRef]
- Anderson, V.; Ye, C.; Sermer, M.; Connelly, P.W.; Hanley, A.J.G.; Zinman, B.; Retnakaran, R. Fasting Capillary Glucose as a Screening Test for Ruling Out Gestational Diabetes Mellitus. J. Obstet. Gynaecol. Can. 2013, 35, 515–522. [Google Scholar] [CrossRef]
- Priya, M.; Mohan Anjana, R.; Pradeepa, R.; Jayashri, R.; Deepa, M.; Bhansali, A.; Mohan, V. Comparison of Capillary Whole Blood Versus Venous Plasma Glucose Estimations in Screening for Diabetes Mellitus in Epidemiological Studies in Developing Countries. Diabetes Technol. Ther. 2011, 13, 586–591. [Google Scholar] [CrossRef]
- Landberg, E.; Nevander, S.; Hadi, M.; Blomberg, M.; Norling, A.; Ekman, B.; Lilliecreutz, C. Evaluation of Venous Plasma Glucose Measured by Point-of-Care Testing (Accu-Chek Inform II) and a Hospital Laboratory Hexokinase Method (Cobas C701) in Oral Glucose Tolerance Testing during Pregnancy—A Challenge in Diagnostic Accuracy. Scand. J. Clin. Lab. Investig. 2021, 81, 607–614. [Google Scholar] [CrossRef]
- Foss-Freitas, M.C.; de Andrade, R.C.; Figueiredo, R.C.; Pace, A.E.; Martinez, E.Z.; Dal Fabro, A.L.; Franco, L.J.; Foss, M.C. Comparison of Venous Plasma Glycemia and Capillary Glycemia for the Screening of Type 2 Diabetes Mellitus in the Japanese-Brazilian Community of Mombuca (Guatapará-SP). Diabetol. Metab. Syndr. 2010, 2, 6. [Google Scholar] [CrossRef]
- American Diabetes Association. Using Capillary Blood Glucose for Eligibility Screening in Community-Based Diabetes Prevention Study. Available online: https://professional.diabetes.org/abstract/using-capillary-blood-glucose-eligibility-screening-community-based-diabetes-prevention (accessed on 25 August 2022).
- American Diabetes Association. Understanding A1C Diagnosis. Available online: https://diabetes.org/diabetes/a1c/diagnosis (accessed on 25 August 2022).
- The Global Health Observatory. Available online: https://www.who.int/data/gho/indicator-metadata-registry/imr-details/2380 (accessed on 25 August 2022).
- Fluss, R.; Faraggi, D.; Reiser, B. Estimation of the Youden Index and Its Associated Cutoff Point. Biom. J. 2005, 47, 458–472. [Google Scholar] [CrossRef] [PubMed]
- Perkins, N.J.; Schisterman, E.F. The Youden Index and the Optimal Cut-Point Corrected for Measurement Error. Biom. J. 2005, 47, 428–441. [Google Scholar] [CrossRef] [PubMed]
- Zafari, N.; Lotfaliany, M.; Mansournia, M.A.; Khalili, D.; Azizi, F.; Hadaegh, F. Optimal Cut-Points of Different Anthropometric Indices and Their Joint Effect in Prediction of Type 2 Diabetes: Results of a Cohort Study. BMC Public Health 2018, 18, 691. [Google Scholar] [CrossRef] [PubMed]
- Baek, J.H.; Kim, H.; Kim, K.Y.; Jung, J. Insulin Resistance and the Risk of Diabetes and Dysglycemia in Korean General Adult Population. Diabetes Metab. J. 2018, 42, 296. [Google Scholar] [CrossRef]
- Xu, T.; Wang, J.; Fang, Y. A Model-Free Estimation for the Covariate-Adjusted Youden Index and Its Associated Cut-Point: A Model-Free Estimation for the Covariate-Adjusted Youden Index and Its Associated Cut-Point. Statist. Med. 2014, 33, 4963–4974. [Google Scholar] [CrossRef] [PubMed]
- Schisterman, E.F.; Perkins, N.J.; Liu, A.; Bondell, H. Optimal Cut-Point and Its Corresponding Youden Index to Discriminate Individuals Using Pooled Blood Samples. Epidemiology 2005, 16, 73–81. [Google Scholar] [CrossRef]
- Wu, Y.; Hu, H.; Cai, J.; Chen, R.; Zuo, X.; Cheng, H.; Yan, D. Machine Learning for Predicting the 3-Year Risk of Incident Diabetes in Chinese Adults. Front. Public Health 2021, 9, 626331. [Google Scholar] [CrossRef]
- Cai, X.; Zhu, Y.; Liu, S.; Wu, T.; Hong, J.; Ahmat, A.; Aierken, X.; Li, N. A Prediction Model Based on Noninvasive Indicators to Predict the 8-Year Incidence of Type 2 Diabetes in Patients with Nonalcoholic Fatty Liver Disease: A Population-Based Retrospective Cohort Study. BioMed Res. Int. 2021, 2021, 5527460. [Google Scholar] [CrossRef]
- Liu, Y.; Xiao, X.; Sun, C.; Tian, S.; Sun, Z.; Gao, Y.; Li, Y.; Cheng, J.; Lv, Y.; Li, M.; et al. Ideal Glycated Hemoglobin Cut-off Points for Screening Diabetes and Prediabetes in a Chinese Population. J. Diabetes Investig. 2016, 7, 695–702. [Google Scholar] [CrossRef]
- Mohapatra, S.K.; Swain, J.K.; Mohanty, M.N. Detection of Diabetes Using Multilayer Perceptron. In International Conference on Intelligent Computing and Applications; Bhaskar, M.A., Dash, S.S., Das, S., Panigrahi, B.K., Eds.; Advances in Intelligent Systems and Computing; Springer: Singapore, 2019; Volume 846, pp. 109–116. ISBN 9789811321818. [Google Scholar]
- Butt, U.M.; Letchmunan, S.; Ali, M.; Hassan, F.H.; Baqir, A.; Sherazi, H.H.R. Machine Learning Based Diabetes Classification and Prediction for Healthcare Applications. J. Healthc. Eng. 2021, 2021, 9930985. [Google Scholar] [CrossRef]
- Aishwarya, J.; Vakula, R.J. Performance Evaluation of Machine Learning Models for Diabetes Prediction. Int. J. Innov. Technol. Explor. Eng. (IJITEE) 2019, 8, 11. [Google Scholar] [CrossRef]
- Rajendra, P.; Latifi, S. Prediction of Diabetes Using Logistic Regression and Ensemble Techniques. Comput. Methods Programs Biomed. Update 2021, 1, 100032. [Google Scholar] [CrossRef]
- Joshi, R.D.; Dhakal, C.K. Predicting Type 2 Diabetes Using Logistic Regression and Machine Learning Approaches. Int. J. Environ. Res. Public Health 2021, 18, 7346. [Google Scholar] [CrossRef] [PubMed]
- Bani-Salameh, H.; Alkhatib, S.M.; Abdalla, M.; Al-Hami, M.; Banat, R.; Zyod, H.; Alkhatib, A.J. Prediction of Diabetes and Hypertension Using Multi-Layer Perceptron Neural Networks. Int. J. Model. Simul. Sci. Comput. 2021, 12, 2150012. [Google Scholar] [CrossRef]
- Oza, A.; Bokhare, A. Diabetes Prediction Using Logistic Regression and K-Nearest Neighbor. In Congress on Intelligent Systems; Springer: Singapore, 2022; pp. 407–418. [Google Scholar] [CrossRef]
- Diabetes Prediction Using Machine Learning KNN-Algorithm Technique. Available online: https://ijisrt.com/assets/upload/files/IJISRT22MAY682.pdf (accessed on 29 August 2022).
- Sarker, I.; Faruque, M.D.; Alqahtani, H.; Kalim, A. K-Nearest Neighbor Learning Based Diabetes Mellitus Prediction and Analysis for EHealth Services. ICST Trans. Scalable Inf. Sys. 2020, 7, 162737. [Google Scholar] [CrossRef]
- Posonia, A.M.; Vigneshwari, S.; Rani, D.J. Machine Learning Based Diabetes Prediction Using Decision Tree J48. In Proceedings of the 2020 3rd International Conference on Intelligent Sustainable Systems (ICISS), Thoothukudi, India, 3–5 December 2020; pp. 498–502. [Google Scholar]
- Ramezankhani, A.; Hadavandi, E.; Pournik, O.; Shahrabi, J.; Azizi, F.; Hadaegh, F. Decision Tree-Based Modelling for Identification of Potential Interactions between Type 2 Diabetes Risk Factors: A Decade Follow-up in a Middle East Prospective Cohort Study. BMJ Open 2016, 6, e013336. [Google Scholar] [CrossRef]
- Dwivedi, K.; Sharan, H.O.; Vishwakarma, V. Analysis of Decision Tree for Diabetes Prediction. Int. J. Eng. Tech. Res. (IJETR) 2019, 9, 3–6. [Google Scholar] [CrossRef]
- Permana, B.A.C.; Ahmad, R.; Bahtiar, H.; Sudianto, A.; Gunawan, I. Classification of Diabetes Disease Using Decision Tree Algorithm (C4.5). J. Phys. Conf. Ser. 2021, 1869, 012082. [Google Scholar] [CrossRef]
- Priya, K.L.; Charan Reddy Kypa, M.S.; Sudhan Reddy, M.M.; Mohan Reddy, G.R. A Novel Approach to Predict Diabetes by Using Naive Bayes Classifier. In Proceedings of the 2020 4th International Conference on Trends in Electronics and Informatics (ICOEI)(48184), Tirunelveli, India, 15–17 June 2020; pp. 603–607. [Google Scholar]
- Marathe, N.; Gawade, S.; Kanekar, A. Prediction of Heart Disease and Diabetes Using Naive Bayes Algorithm. Int. J. Sci. Res. Comput. Sci. Eng. Inf. Technol. 2021, 7, 447–453. [Google Scholar] [CrossRef]
- Prakash, A.; Anand, R.; Abinayaa, S.S.; Kalyan Chakravarthy, N.S. Normalized Naïve Bayes Model to Predict Type–2 Diabetes Mellitus. In Proceedings of the 2021 Emerging Trends in Industry 4.0 (ETI 4.0), Raigarh, India, 19–21 May 2021; pp. 1–5. [Google Scholar]
- Sharmila Agnal, E.S.A. Analyzing Diabetic Data Using Naive-Bayes Classifier. Eur. J. Mol. Amp Clin. Med. 2020, 7, 2687–2699. Available online: https://ejmcm.com/article_2022.html (accessed on 10 September 2022).
- Real Time Diabetes Prediction Using Naïve Bayes Classifier on Big Data of Healthcare. Available online: https://www.irjet.net/archives/V7/i5/IRJET-V7I521.pdf (accessed on 10 September 2022).
- VijiyaKumar, K.; Lavanya, B.; Nirmala, I.; Caroline, S.S. Random Forest Algorithm for the Prediction of Diabetes. In Proceedings of the 2019 IEEE International Conference on System, Computation, Automation and Networking (ICSCAN), Pondicherry, India, 29–30 March 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Ooka, T.; Johno, H.; Nakamoto, K.; Yoda, Y.; Yokomichi, H.; Yamagata, Z. Random Forest Approach for Determining Risk Prediction and Predictive Factors of Type 2 Diabetes: Large-Scale Health Check-up Data in Japan. BMJNPH 2021, 4, 140–148. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Zhai, M.; Ren, Z.; Ren, H.; Li, M.; Quan, D.; Chen, L.; Qiu, L. Exploratory Study on Classification of Diabetes Mellitus through a Combined Random Forest Classifier. BMC Med. Inform. Decis. Mak. 2021, 21, 105. [Google Scholar] [CrossRef] [PubMed]
- Diabetes Analysis and Prediction Using Random Forest, KNN, Naïve Bayes, and J48: An Ensemble Approach. Available online: http://www.ijstr.org/final-print/sep2019/Diabetes-Analysis-And-Prediction-Using-Random-Forest-Knn-Nave-Bayes-And-J48-An-Ensemble-Approach.pdf (accessed on 12 September 2022).
- Liu, Q.; Zhang, M.; He, Y.; Zhang, L.; Zou, J.; Yan, Y.; Guo, Y. Predicting the Risk of Incident Type 2 Diabetes Mellitus in Chinese Elderly Using Machine Learning Techniques. J. Pers. Med. 2022, 12, 905. [Google Scholar] [CrossRef] [PubMed]
- Xu, Z.; Wang, Z. A Risk Prediction Model for Type 2 Diabetes Based on Weighted Feature Selection of Random Forest and XGBoost Ensemble Classifier. In Proceedings of the 2019 Eleventh International Conference on Advanced Computational Intelligence (ICACI), Guilin, China, 7–9 June 2019; pp. 278–283. [Google Scholar] [CrossRef]
- Li, M.; Fu, X.; Li, D. Diabetes Prediction Based on XGBoost Algorithm. IOP Conf. Ser. Mater. Sci. Eng. 2020, 768, 072093. [Google Scholar] [CrossRef]
- Behera, D.K.; Dash, S.; Behera, A.K.; Dash, C.H.S.K. Extreme Gradient Boosting and Soft Voting Ensemble Classifier for Diabetes Prediction. In Proceedings of the 2021 19th OITS International Conference on Information Technology (OCIT), Bhubaneswar, India, 16–18 December 2021; pp. 191–195. [Google Scholar] [CrossRef]
- Wang, L.; Wang, X.; Chen, A.; Jin, X.; Che, H. Prediction of Type 2 Diabetes Risk and Its Effect Evaluation Based on the XGBoost Model. Healthcare 2020, 8, 247. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, X.-P.; Yuan, J.; Cai, B.; Wang, X.-L.; Wu, X.-L.; Zhang, Y.-H.; Zhang, X.-Y.; Yin, T.; Zhu, X.-H.; et al. Association of Body Mass Index and Age with Incident Diabetes in Chinese Adults: A Population-Based Cohort Study. BMJ Open 2018, 8, e021768. [Google Scholar] [CrossRef]
- Okamura, T.; Hashimoto, Y.; Hamaguchi, M.; Obora, A.; Kojima, T.; Fukui, M. Low Urine PH Is a Risk for Non-Alcoholic Fatty Liver Disease: A Population-Based Longitudinal Study. Clin. Res. Hepatol. Gastroenterol. 2018, 42, 570–576. [Google Scholar] [CrossRef]
- National Health Insurance Sharing Service (NHISS) Korea. Available online: https://nhiss.nhis.or.kr/bd/ab/bdabf003cv.do (accessed on 30 June 2022).
- PIMA Indian Diabetes Dataset. Available online: https://www.kaggle.com/datasets/uciml/pima-indians-diabetes-database (accessed on 30 June 2022).
- The Sex Independent Angle of Type 2 Diabetes. Available online: https://data.mendeley.com/datasets/dtxy4j6pcn/1 (accessed on 30 June 2022).
- [NeurIPS 2020] Data Science for COVID19 (DS4C). Available online: https://www.kaggle.com/datasets/kimjihoo/coronavirusdataset (accessed on 17 October 2022).
- Chun, S.-Y.; Kim, D.W.; Lee, S.A.; Lee, S.J.; Chang, J.H.; Choi, Y.J.; Kim, S.W.; Song, S.O. Does Diabetes Increase the Risk of Contracting COVID-19? A Population-Based Study in Korea. Diabetes Metab. J. 2020, 44, 897–907. [Google Scholar] [CrossRef]
- You, J.H.; Lee, S.A.; Chun, S.-Y.; Song, S.O.; Lee, B.-W.; Kim, D.J.; Boyko, E.J. Clinical Outcomes of COVID-19 Patients with Type 2 Diabetes: A Population-Based Study in Korea. Endocrinol. Metab. 2020, 35, 901–908. [Google Scholar] [CrossRef]
- Guidelines for the Prevention, Management, and Care of Diabetes Mellitus. Available online: https://applications.emro.who.int/dsaf/dsa664.pdf (accessed on 26 August 2022).
- Diagnosis and Management of Type 2 Diabetes. Available online: https://apps.who.int/iris/rest/bitstreams/1274478/retrieve (accessed on 26 August 2022).
- Diabetes Risk Factors. Available online: https://www.cdc.gov/diabetes/basics/risk-factors.html (accessed on 26 August 2022).
- Ramnanansingh, T.G.; Nayak, S.B. Application of a Novel Sex Independent Anthropometric Index, Termed Angle Index, in Relation to Type 2 Diabetes: A Trinidadian Case–Control Study. BMJ Open 2019, 9, e024029. [Google Scholar] [CrossRef]
- Singhal, R.; Rana, R. Chi-Square Test and Its Application in Hypothesis Testing. J. Pract. Cardiovasc. Sci. 2015, 1, 69. [Google Scholar] [CrossRef]
- Franke, T.M.; Ho, T.; Christie, C.A. The Chi-Square Test: Often Used and More Often Misinterpreted. Am. J. Eval. 2012, 33, 448–458. [Google Scholar] [CrossRef]
- Trevethan, R. Sensitivity, Specificity, and Predictive Values: Foundations, Pliabilities, and Pitfalls in Research and Practice. Front. Public Health 2017, 5, 307. [Google Scholar] [CrossRef]
- Lee, Y.; Bang, H.; Kim, H.C.; Kim, H.M.; Park, S.W.; Kim, D.J. A Simple Screening Score for Diabetes for the Korean Population. Diabetes Care 2012, 35, 1723–1730. [Google Scholar] [CrossRef] [PubMed]
- Bang, H. Development and Validation of a Patient Self-Assessment Score for Diabetes Risk. Ann. Intern. Med. 2009, 151, 775. [Google Scholar] [CrossRef]
- Kwon, K.-S.; Bang, H.; Bomback, A.S.; Koh, D.-H.; Yum, J.-H.; Lee, J.-H.; Lee, S.; Park, S.K.; Yoo, K.-Y.; Park, S.K.; et al. A Simple Prediction Score for Kidney Disease in the Korean Population: Prediction of Kidney Disease. Nephrology 2012, 17, 278–284. [Google Scholar] [CrossRef]
- Hypertension Control. Available online: http://apps.who.int/iris/bitstream/handle/10665/38276/WHO_TRS_862.pdf?sequence=1 (accessed on 24 August 2022).
- Li, S.; Guo, S.; He, F.; Zhang, M.; He, J.; Yan, Y.; Ding, Y.; Zhang, J.; Liu, J.; Guo, H.; et al. Prevalence of Diabetes Mellitus and Impaired Fasting Glucose, Associated with Risk Factors in Rural Kazakh Adults in Xinjiang, China. Int. J. Environ. Res. Public Health 2015, 12, 554–565. [Google Scholar] [CrossRef]
- Wu, M.; Wen, J.; Qin, Y.; Zhao, H.; Pan, X.; Su, J.; Du, W.; Pan, E.; Zhang, Q.; Zhang, N.; et al. Familial History of Diabetes Is Associated with Poor Glycaemic Control in Type 2 Diabetics: A Cross-Sectional Study. Sci. Rep. 2017, 7, 1432. [Google Scholar] [CrossRef]
- Unal, I. Defining an Optimal Cut-Point Value in ROC Analysis: An Alternative Approach. Comput. Math. Methods Med. 2017, 2017, 3762651. [Google Scholar] [CrossRef]
- Parikh, R.; Mathai, A.; Parikh, S.; Chandra Sekhar, G.; Thomas, R. Understanding and Using Sensitivity, Specificity and Predictive Values. Indian J. Ophthalmol. 2008, 56, 45. [Google Scholar] [CrossRef]





| Characteristic | China Population (n = 211,833) | Japan Population (n = 15,464) | Korea Population (n = 837,174) | US-PIMA Indian Population (n = 768) | Trinidad Population (n = 121) |
|---|---|---|---|---|---|
| Age, year | 42.1 ± 0.027 | 43.71 ± 0.072 | 43.19 ± 0.018 | 33.25 ± 0.424 | - |
| Male/Female, % | 54.82/45.18 | 45.49/54.51 | 57.40/42.60 | - | - |
| BMI, kg/m2 | 23.24 ± 0.007 | 22.12 ± 0.025 | 23.59 ± 0.0036 | 31.99 ± 0.284 | 29.18 ± 0.70 |
Obesity Status, % (WHO/Asia Criteria)
| 71.28/49.60 25.47/39.64 3.23/10.52 0.02/0.24 | 83.68/65.08 14.60/29.46 1.71/5.30 0.01/0.16 | 68.91/44.91 27.33/43.56 3.75/11.18 0.01/0.35 | 15.23/7.94 23.31/17.97 48.70/41.80 12.76/32.29 | 25.62/11.57 38.02/33.88 30.58/43.80 5.79/10.74 |
| SBP/ DBP, mmHg | 119.06 ± 0.04/ 74.18 ± 0.02 | 114.50 ± 0.12/ 71.58 ± 0.08 | 120.18 ± 0.02/ 74.96 ± 0.01 | -/ 79.11 ± 0.70 | 145.12 ± 1.94/ 87.24 ± 0.98 |
| Family history of diabetes, % | 2.05 | - | - | - | - |
| Exercise, % | - | 17.52 | - | - | - |
| Current smoker, % | 28.43 | 41.60 | - | - | - |
| Alcohol intake, % | 28.43 | 23.66 | - | - | - |
Outcomes-related
| 88.47 ± 0.02 - - 82.78 ± 0.04 23.55 ± 0.04 24.70 ± 0.02 49.83 ± 0.04 23.95 ± 0.05 24.08 ± 0.04 1.97 | - 5.17 ± 0.003 92.97 ± 0.06 198.20 ± 0.27 80.79 ± 0.47 56.54 ± 0.13 - 19.99 ± 012 18.40 ± 0.07 2.41 | 98.71 ± 0.03 - - - - - - - - 11.53 | - - 120.89 ± 1.15 - - - - - - 34.90 | 126.24 ± 5.19 - - 191.09 ± 4.38 157.46 ± 9.30 47.08 ± 1.19 111.73 ± 4.00 - - 58.68 |
| Diabetes Risk Factors | OR (95% CI) | p-Value |
|---|---|---|
| Age, year | ||
| 35–44 | 2.91 (2.54–3.34) | <0.001 |
| ≥45 | 11.18 (9.92–12.59) | <0.001 |
| Male, % | 2.14 (2.00–2.29) | <0.001 |
| BMI, kg/m2 (Asia criteria) | ||
| 23–27.4 | 3.83 (3.51–4.17) | <0.001 |
| ≥27.5 | 9.56 (8.72–10.49) | <0.001 |
| Hypertension (based on SBP/DBP) | 3.16 (2.96–3.37) | <0.001 |
| Cholesterol, mg/dL | 1.99 (1.87–2.12) | <0.001 |
| Triglyceride, mg/dL | 0.99 (0.24–4.02) | <0.001 |
| Smoking | 0.98 (0.92–1.05) | <0.001 |
| Alcohol | 0.98 (0.92–1.05) | <0.001 |
| Family history of diabetes | 2.08 (1.78–2.43) | <0.001 |
| Diabetes Risk Factors | OR (95% CI) | p-Value |
|---|---|---|
| Age, year | ||
| 35–44 | 2.65 (1.50–2.58) | 0.230 |
| ≥45 | 4.53 (2.58–7.95) | <0.001 |
| Male, % | 2.80 (2.20–3.57) | <0.001 |
| BMI, kg/m2 (Asia criteria) | ||
| 23–27.4 | 2.97 (2.35–3.76) | <0.001 |
| ≥27.5 | 8.78 (6.59–11.68) | <0.001 |
| Hypertension (based on SBP/DBP) | 2.81 (2.23–3.53) | <0.001 |
| Cholesterol, mg/dL | 1.94 (1.57–2.40) | <0.001 |
| Triglyceride, mg/dL | 5.10 (2.07–3.16) | <0.001 |
| Smoking | 2.25 (1.82–2.78) | <0.001 |
| Alcohol | 1.31 (1.04–1.64) | 0.534 |
| Exercise | 0.74 (0.55–1.00) | <0.001 |
| Diabetes Risk Factors | OR (95% CI) | p-Value |
|---|---|---|
| Male, % | 1.11 (1.10–1.13) | <0.001 |
| Age, year | ||
| 35–44 | 4.33 (4.16–4.51) | <0.001 |
| ≥45 | 24.11 (23.28–24.96) | <0.001 |
| BMI, kg/m2 (Asia criteria) | ||
| 23–27.4 | 2.01 (1.98–2.04) | <0.001 |
| ≥27.5 | 3.04 (2.98–3.10) | <0.001 |
| Hypertension (based on SBP/DBP) | 1.98 (1.95–2.01) | <0.001 |
| Diabetes Risk Factors | OR (95% CI) | p-Value |
|---|---|---|
| Age, year | ||
| 35–44 | 3.08 (2.10–4.51) | <0.001 |
| ≥45 | 2.83 (1.91–4.20) | <0.001 |
| BMI, kg/m2 (WHO criteria) | ||
| 25–30 | 3.45 (1.61–7.43) | 0.350 |
| ≥30 | 10.32 (5.10–20.87) | <0.001 |
| Hypertension (based on DBP) | 1.69 (1.22–2.35) | 0.678 |
| Diabetes Risk Factors | OR (95% CI) | p-Value |
|---|---|---|
| BMI, kg/m2 (WHO criteria) | ||
| 25–30 | 1.80 (0.72–4.52) | 0.410 |
| ≥30 | 3.69 (1.39–9.78) | 0.432 |
| Hypertension (based on SBP/DBP) | 1.99 (0.95–4.16) | 0.485 |
| Cholesterol, mg/dL | 1.04 (0.50–2.17) | 0.691 |
| Triglycerides, mg/dL | 1.78 (0.84–3.77) | 0.601 |
| Risk Factors | OR (95% CI) | p-Value |
|---|---|---|
| Age, year | ||
| <20 | 8.69 (2.53–29.91) | <0.001 |
| 20–29 | 2.76 (1.26–6.03) | <0.001 |
| 30–39 | 2.43 (1.57–3.75) | <0.001 |
| 40–49 | 1.27 (0.93–1.74) | <0.001 |
| 50–59 | 1.33 (1.08–1.66) | <0.001 |
| 60–69 | 5.18 (4.10–6.55) | <0.001 |
| ≥70 | 3.62 (2.71–4.83) | <0.001 |
| Gender | ||
| Male | 1.16 (1.20–1.33) | <0.001 |
| Female | 1.28 (1.12–1.47) | <0.001 |
| Diabetes | 1.21 (1.10–1.34) | <0.001 |
| Model Population | Chinese | Japanese | Korean | US-PIMA Indian | Trinidadian | |
|---|---|---|---|---|---|---|
| Diagnostic Test | FPG | FPG | HbA1C | FBS | 2hPG | FBG |
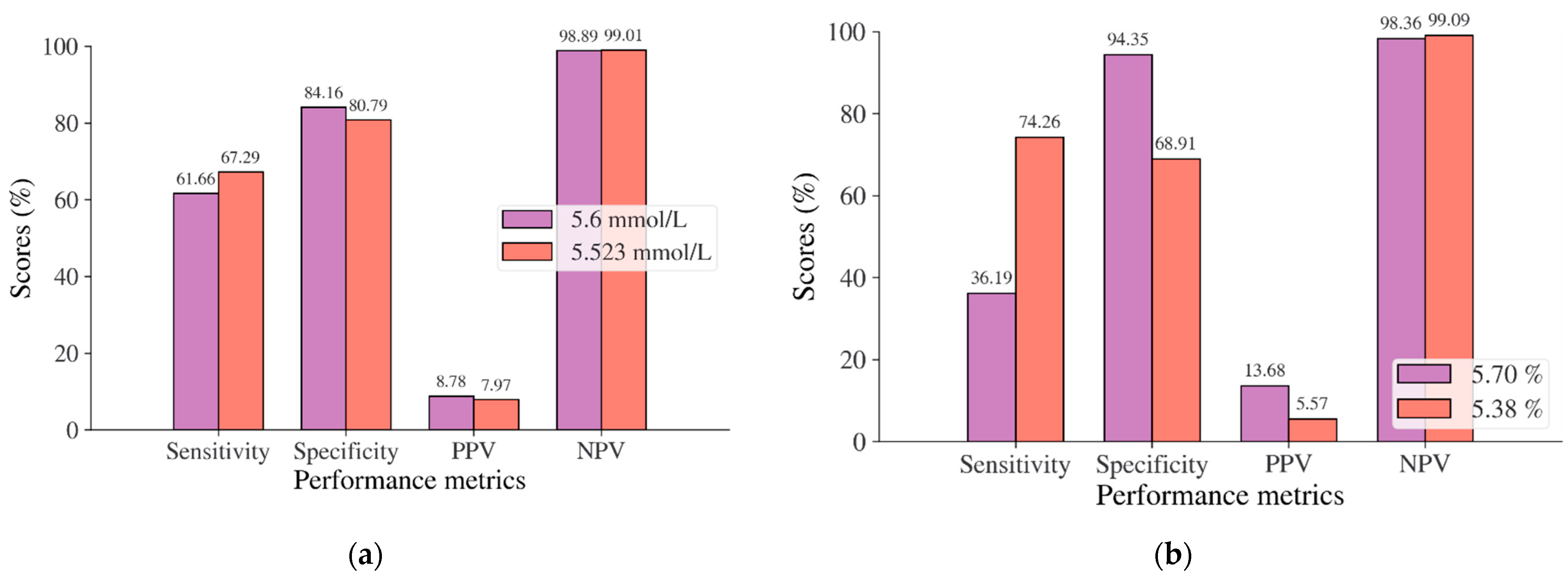
| Cut point as recommended by ADA and WHO | ≥7 mmol/L | ≥5.6 mmol/L | ≥5.7% | ≥126 mg/dL | ≥140 mg/dL | ≥126 mg/dL |
| Optimal cut point | 6.205 | 5.523 | 5.375 | 105.50–106.50 | 123.50 | 107.50 |
| Percentage of high risk, ADA and WHO/optimal cut points (%) | 1.96/4.09 | 16.94/20.37 | 6.38/32.13 | 7.47/20.70 | 25.65/41.93 | 35.59/50.85 |
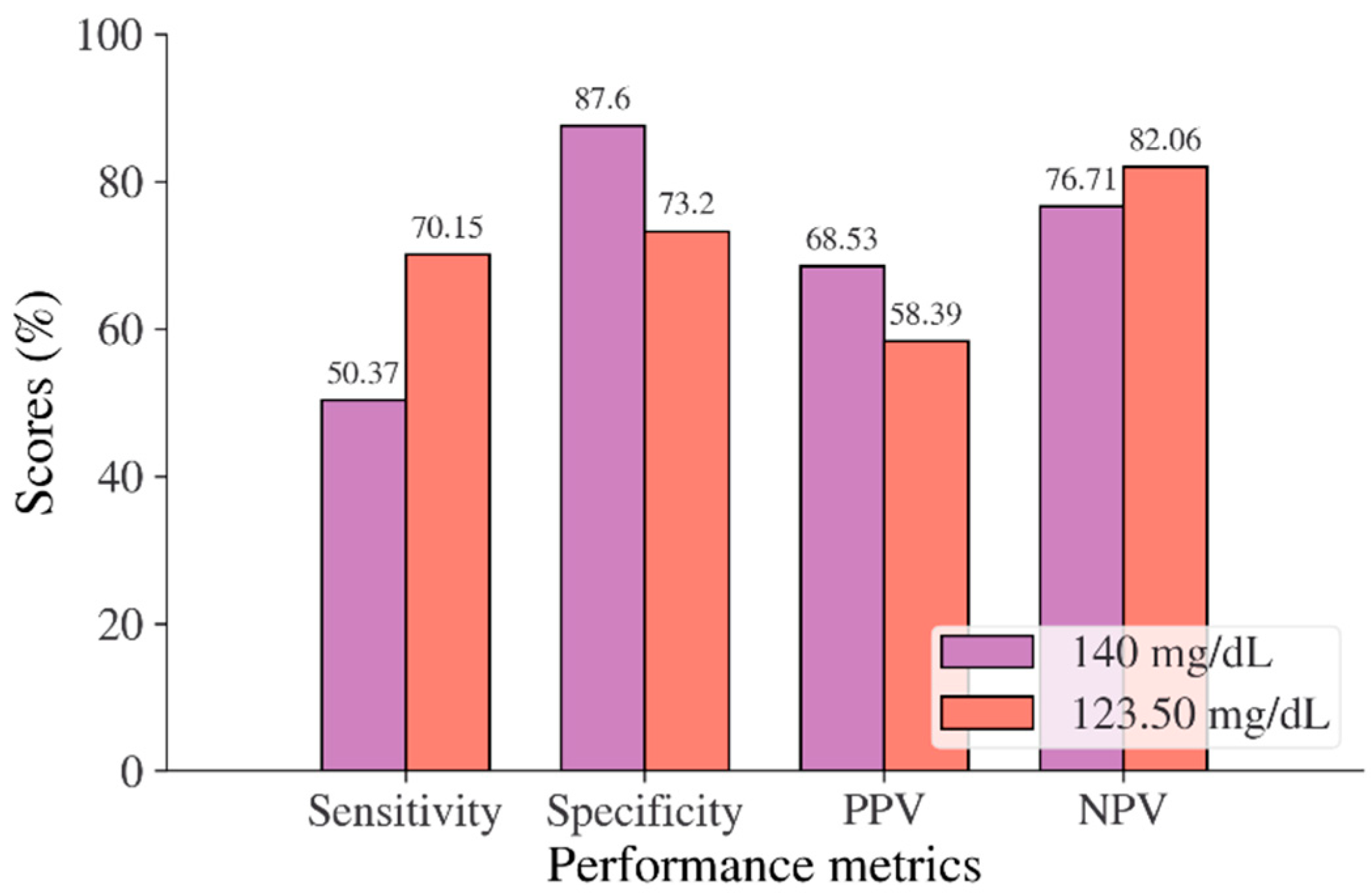
| Sensitivity, ADA, and WHO/optimal cut points (%) | 81.93/88.95 | 61.66/67.29 | 36.19/76.26 | 46.26/72.69 | 50.37/70.15 | 65.22/81.16 |
| Specificity, ADA, and WHO/optimal cut points (%) | 100/97.44 | 84.16/80.79 | 94.35/68.91 | 97.59/86.07 | 87.60/73.20 | 100/91.84 |
| PPV, ADA, and WHO/optimal cut points (%) | 100/41.07 | 8.78/7.97 | 13.68/5.57 | 71.41/40.48 | 68.53/58.39 | 100/93.33 |
| NPV, ADA, and WHO/optimal cut points (%) | 99.64/99.77 | 98.89/99.01 | 98.36/99.09 | 93.31/96.03 | 76.71/82.06 | 67.12/77.59 |
| LR+, ADA, and WHO/optimal cut points | ~/34.75 | 3.89/3.50 | 6.41/2.39 | 19.17/5.22 | 4.06/2.62 | ~/9.942 |
| LR−, ADA, and WHO/optimal cut points | 0.18/0.11 | 0.46/0.40 | 0.68/0.37 | 0.55/0.32 | 0.57/0.41 | 0.35/0.205 |
| Youden index, ADA, and WHO/optimal cut points (%) | 81.92/86.39 | 45.82/48.08 | 30.55/43.17 | 43.85/58.76 | 37.97/43.35 | 65.22/73.00 |
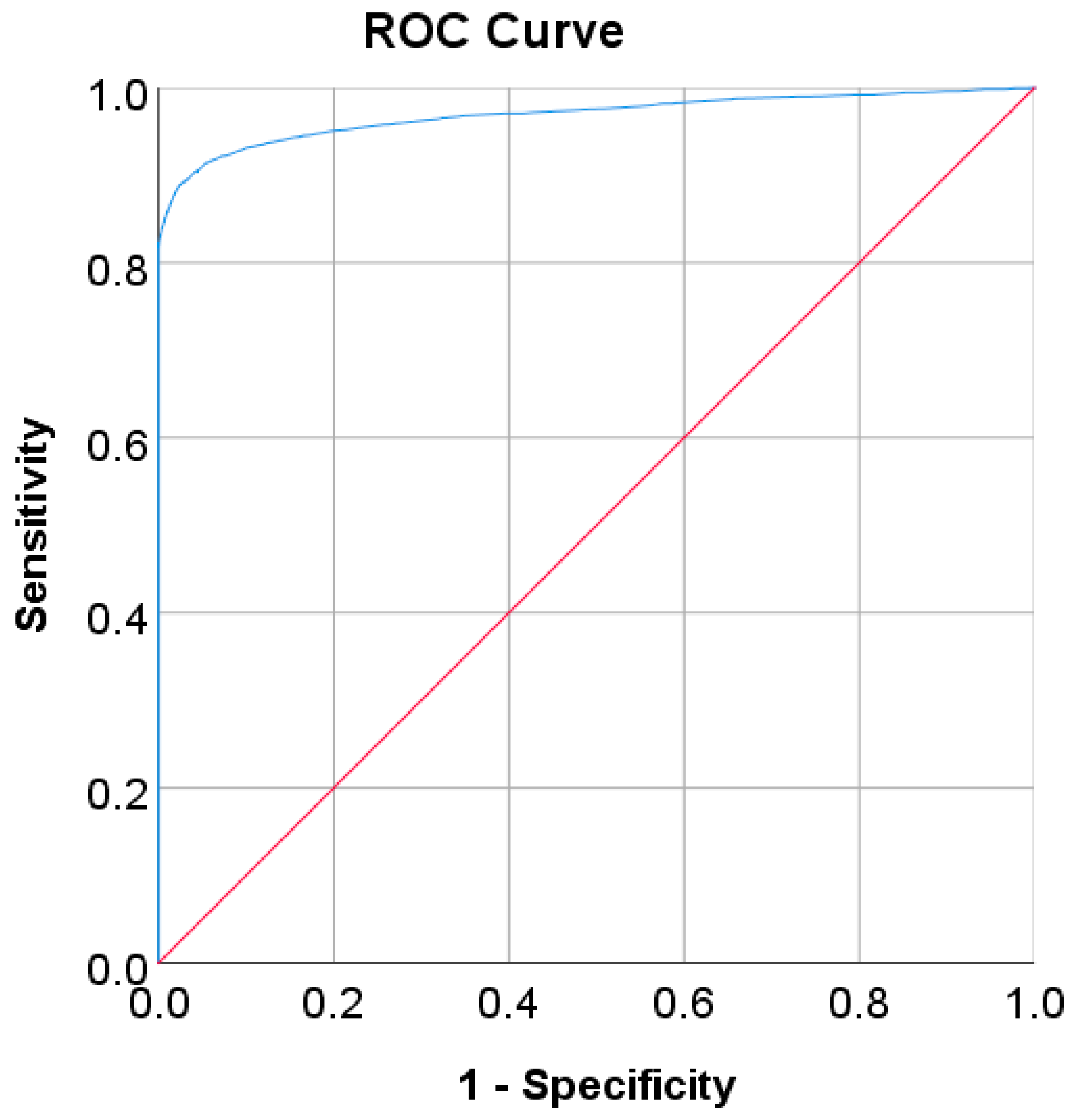
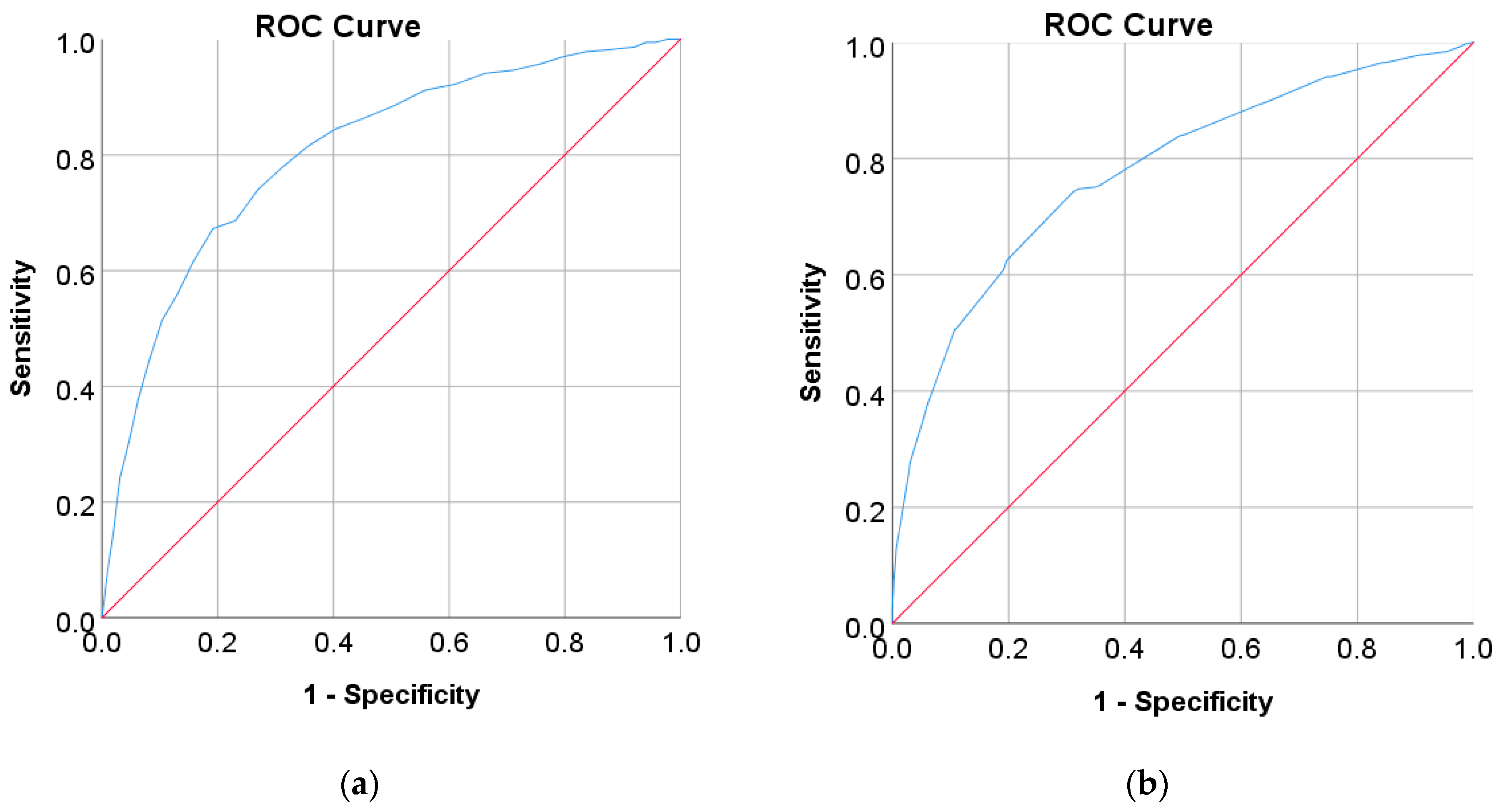
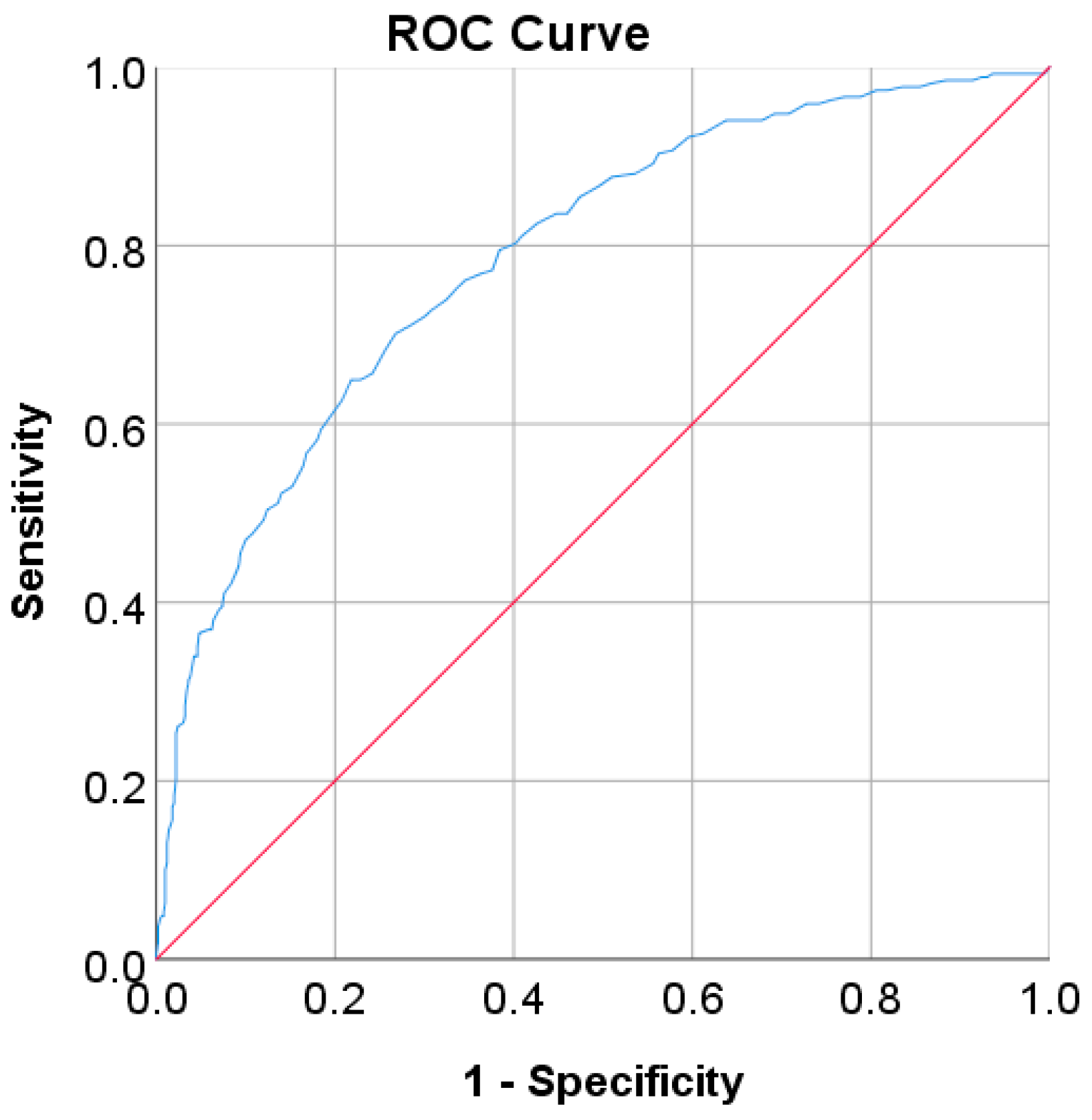
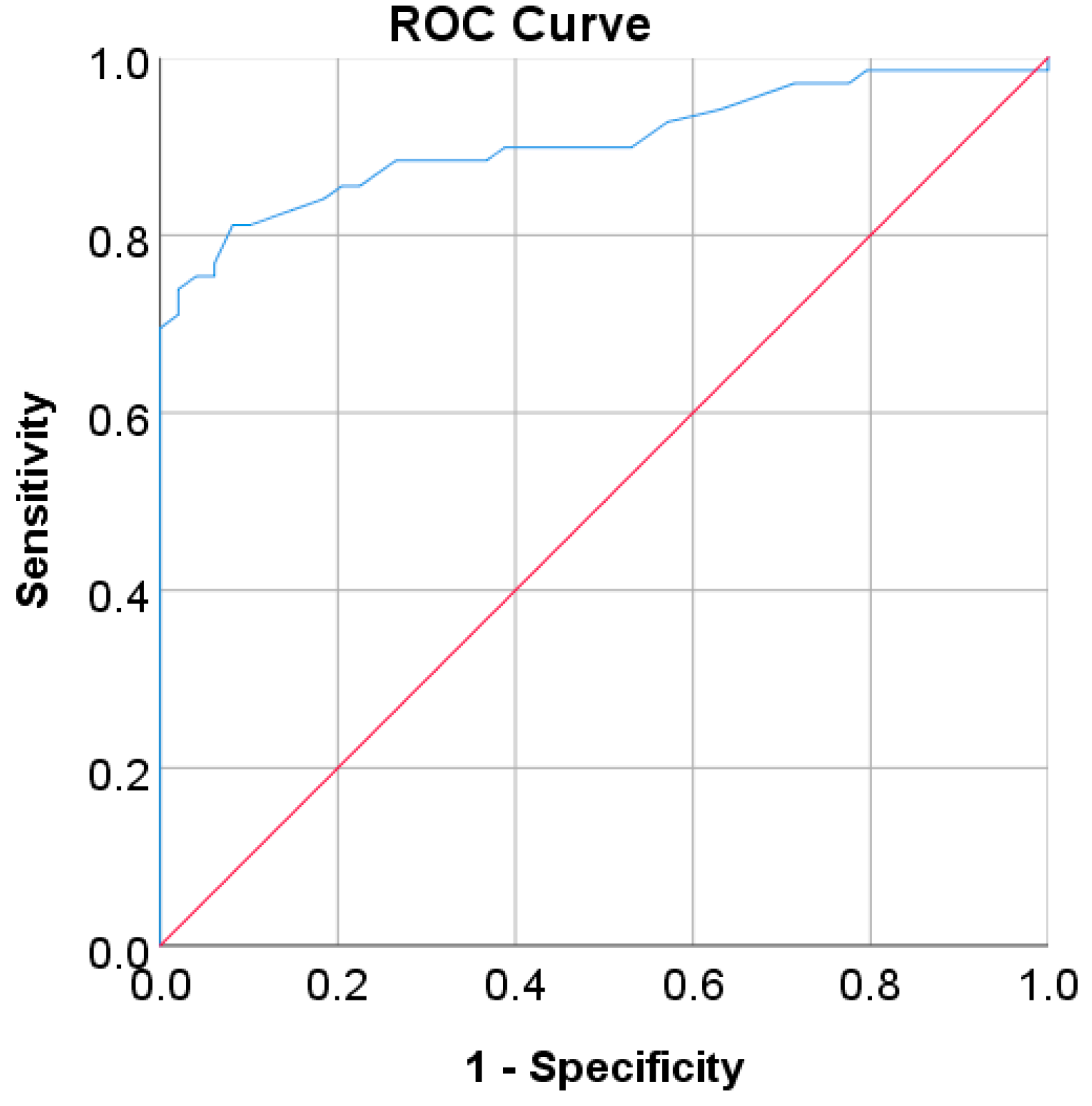
| AUC | 0.97 | 0.80 | 0.78 | 0.85 | 0.79 | 0.905 |
| SE | 0.002 | 0.012 | 0.013 | 0.001 | 0.017 | 0.028 |
| 95% CI | 0.965–0.972 | 0.782–0.828 | 0.752–0.804 | 0.847–0.850 | 0.755–0.822 | 0.850–0.960 |
| p-value | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 |
| Dataset | Author | Year | Method | AUC |
|---|---|---|---|---|
| Chinese | Wu et al. [44] | 2021 | XGBoost | 0.93 |
| Proposed study | 2022 | LR | 0.97 | |
| Japanese (NAFLD) | Cai et al. [45] | 2021 | Cox regression | 0.80 |
| Proposed study | 2022 | LR | 0.80 | |
| Korean (NHISS) | Alfian et al. [6] | 2020 | DNN + RFE | 0.80 |
| Proposed study | 2022 | LR | 0.85 | |
| US-PIMA Indian | Sarker et al. [55] | 2018 | Optimal KNN | 0.73 |
| Aiswarya and Vakula [49] | 2019 | LR | 0.736 | |
| Bani-Salameh et al. [52] | 2021 | MLP | 0.77 | |
| Proposed study | 2022 | LR | 0.79 | |
| Trinidadian | Ramnansingh and Nayak [85] | 2019 | Binomial LR | 0.72 |
| Proposed study | 2022 | LR | 0.905 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fitriyani, N.L.; Syafrudin, M.; Ulyah, S.M.; Alfian, G.; Qolbiyani, S.L.; Anshari, M. A Comprehensive Analysis of Chinese, Japanese, Korean, US-PIMA Indian, and Trinidadian Screening Scores for Diabetes Risk Assessment and Prediction. Mathematics 2022, 10, 4027. https://doi.org/10.3390/math10214027
Fitriyani NL, Syafrudin M, Ulyah SM, Alfian G, Qolbiyani SL, Anshari M. A Comprehensive Analysis of Chinese, Japanese, Korean, US-PIMA Indian, and Trinidadian Screening Scores for Diabetes Risk Assessment and Prediction. Mathematics. 2022; 10(21):4027. https://doi.org/10.3390/math10214027
Chicago/Turabian StyleFitriyani, Norma Latif, Muhammad Syafrudin, Siti Maghfirotul Ulyah, Ganjar Alfian, Syifa Latif Qolbiyani, and Muhammad Anshari. 2022. "A Comprehensive Analysis of Chinese, Japanese, Korean, US-PIMA Indian, and Trinidadian Screening Scores for Diabetes Risk Assessment and Prediction" Mathematics 10, no. 21: 4027. https://doi.org/10.3390/math10214027
APA StyleFitriyani, N. L., Syafrudin, M., Ulyah, S. M., Alfian, G., Qolbiyani, S. L., & Anshari, M. (2022). A Comprehensive Analysis of Chinese, Japanese, Korean, US-PIMA Indian, and Trinidadian Screening Scores for Diabetes Risk Assessment and Prediction. Mathematics, 10(21), 4027. https://doi.org/10.3390/math10214027









